RANS-Based Aerothermal Database of LS89 Transonic Turbine Cascade Under Adiabatic and Cooled Wall Conditions
Abstract
1. Introduction
2. Experimental Reference
3. Numerical Setup
3.1. Governing Equations
3.2. Computational Setup
3.2.1. Boundary Conditions
3.2.2. Solver Setting
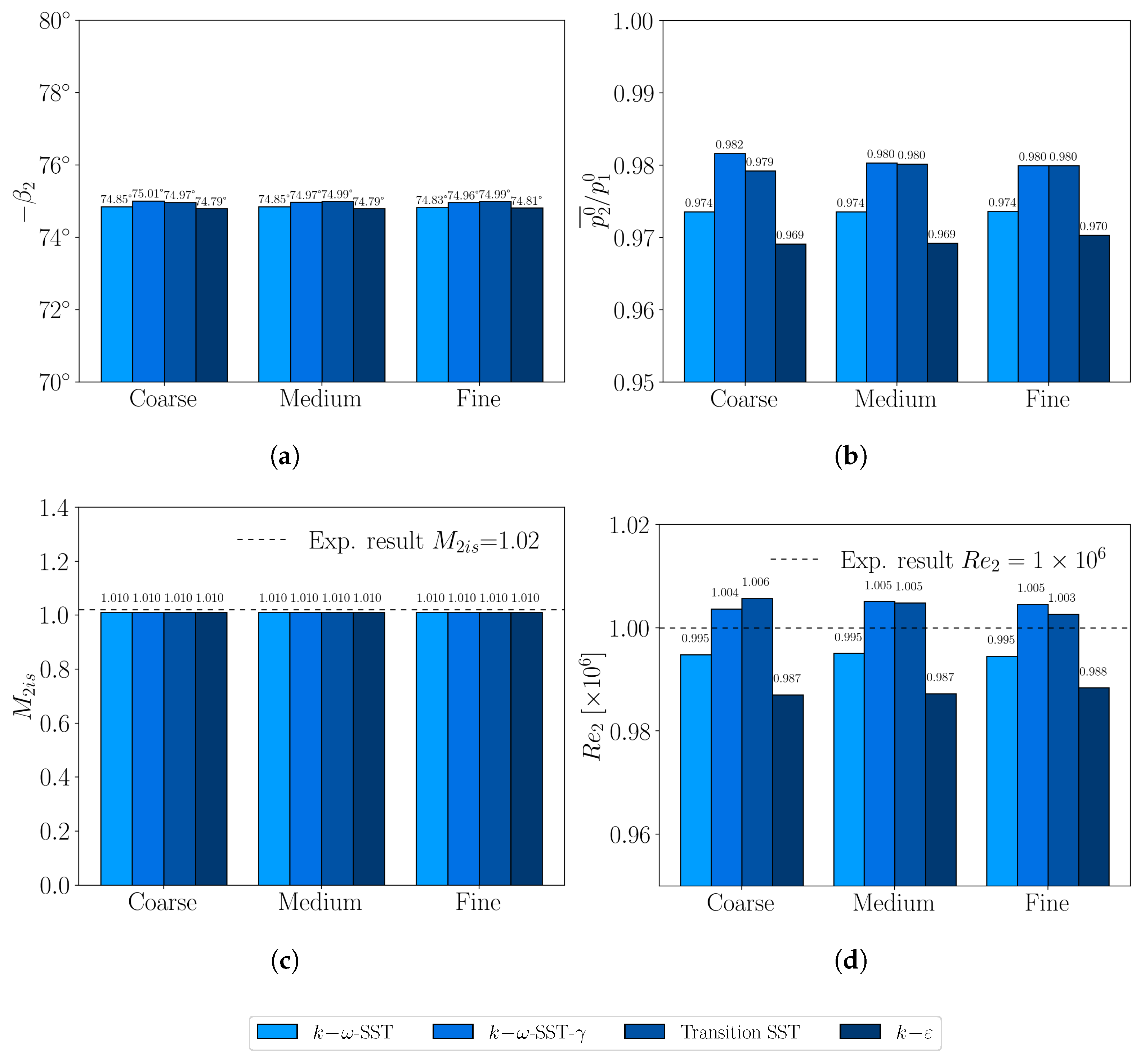
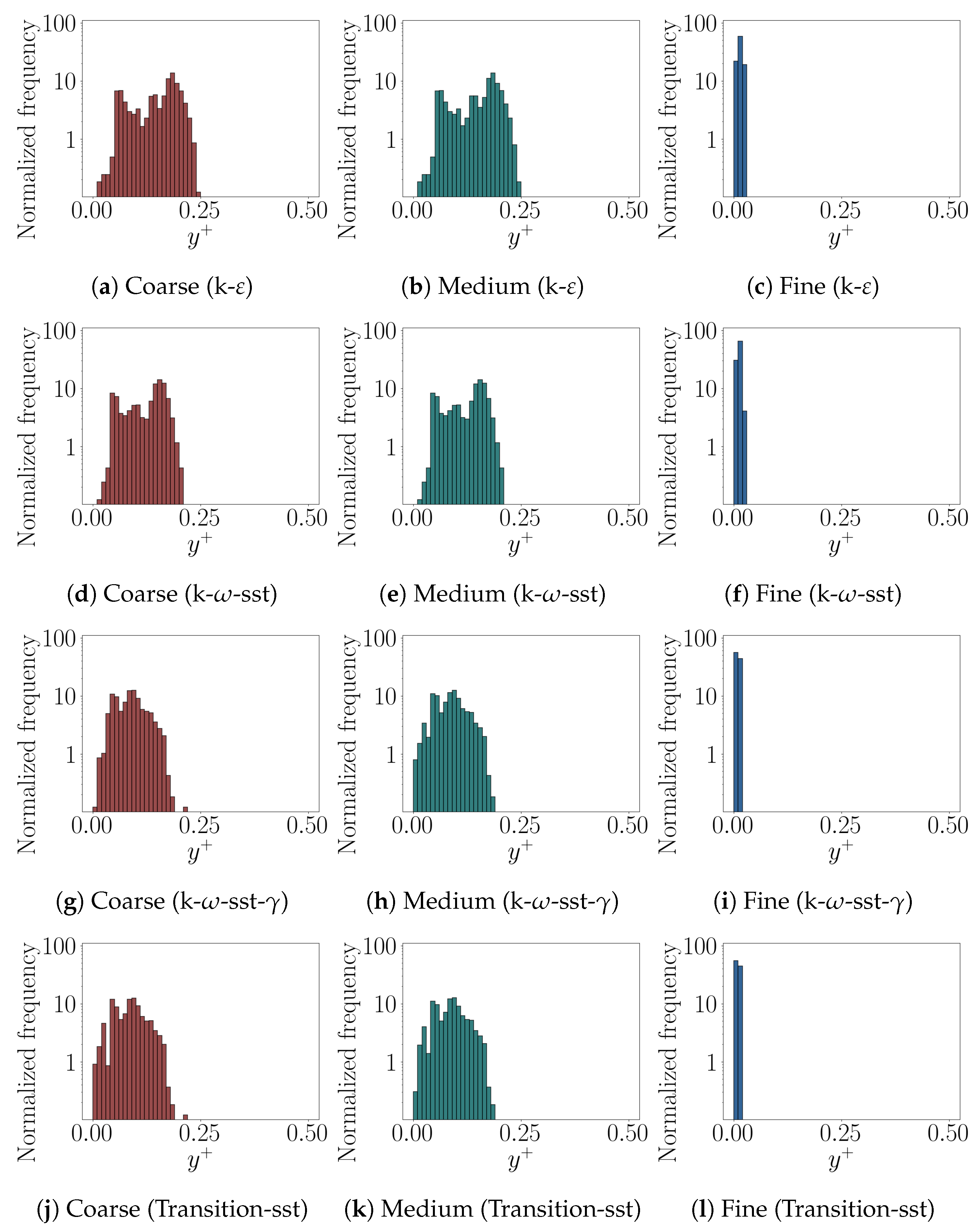
3.3. Validation and Mesh Convergence Analysis
3.3.1. Global Quantities
3.3.2. Near-Wall Quantities
4. Results and Discussion
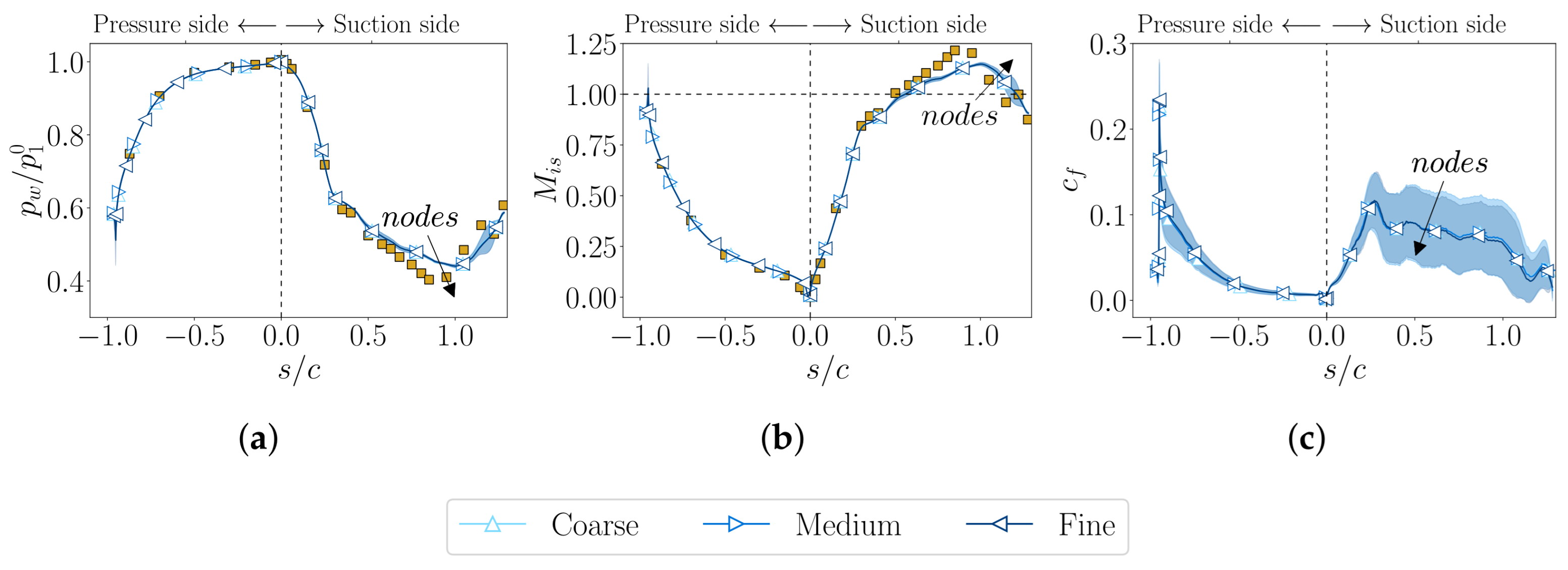
4.1. Adiabatic Wall Arrangement
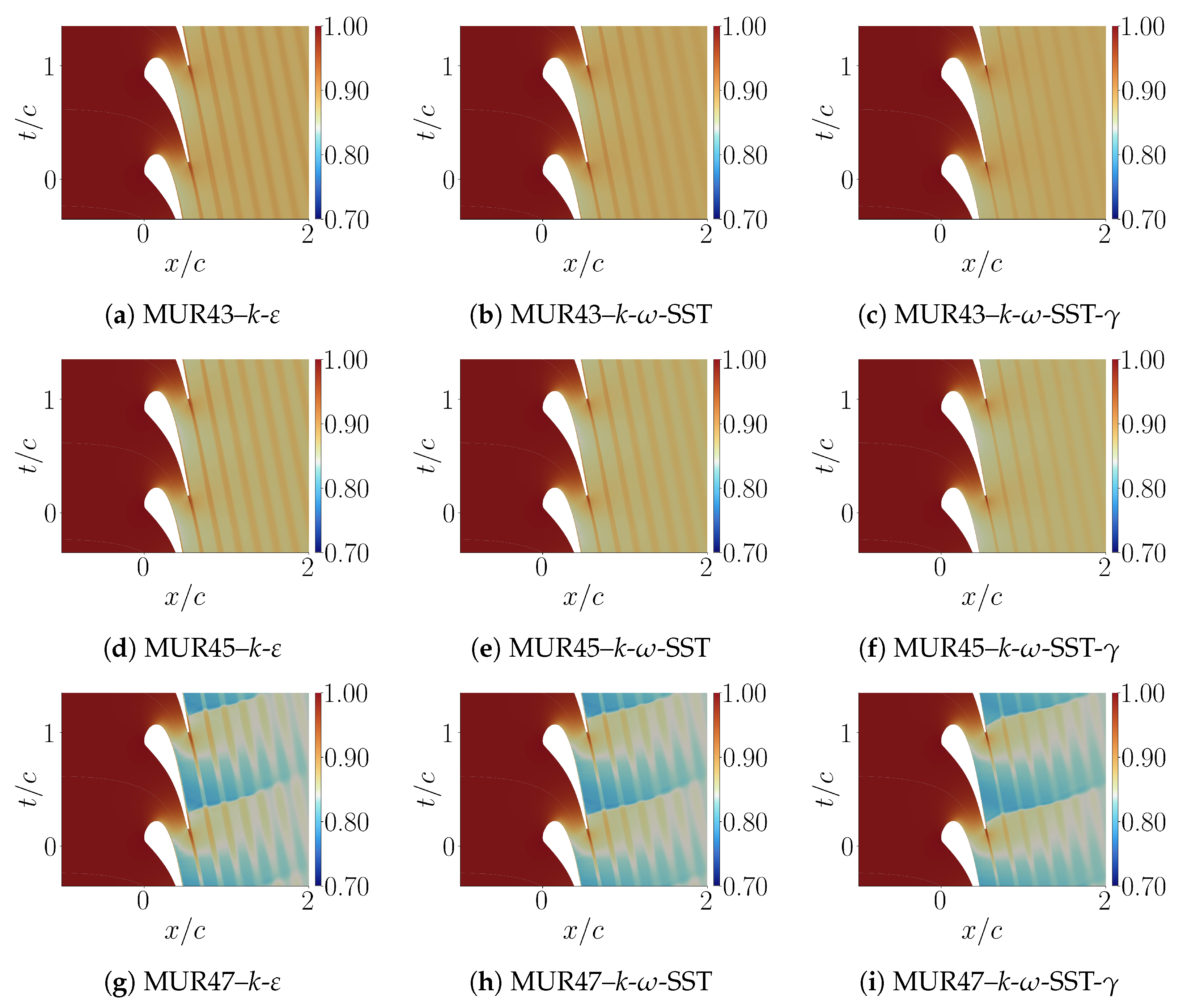
4.1.1. Flow Qualitative Description
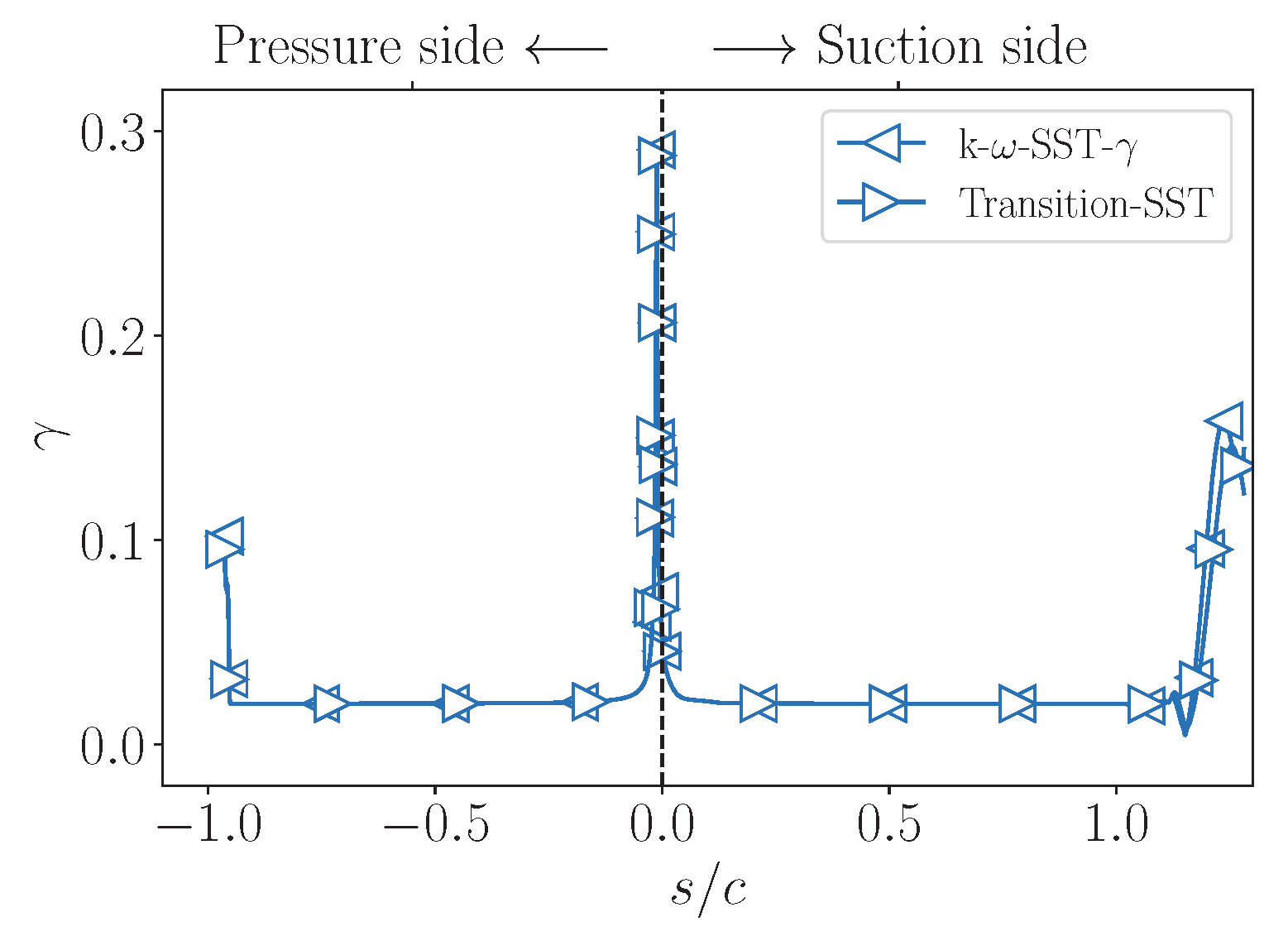
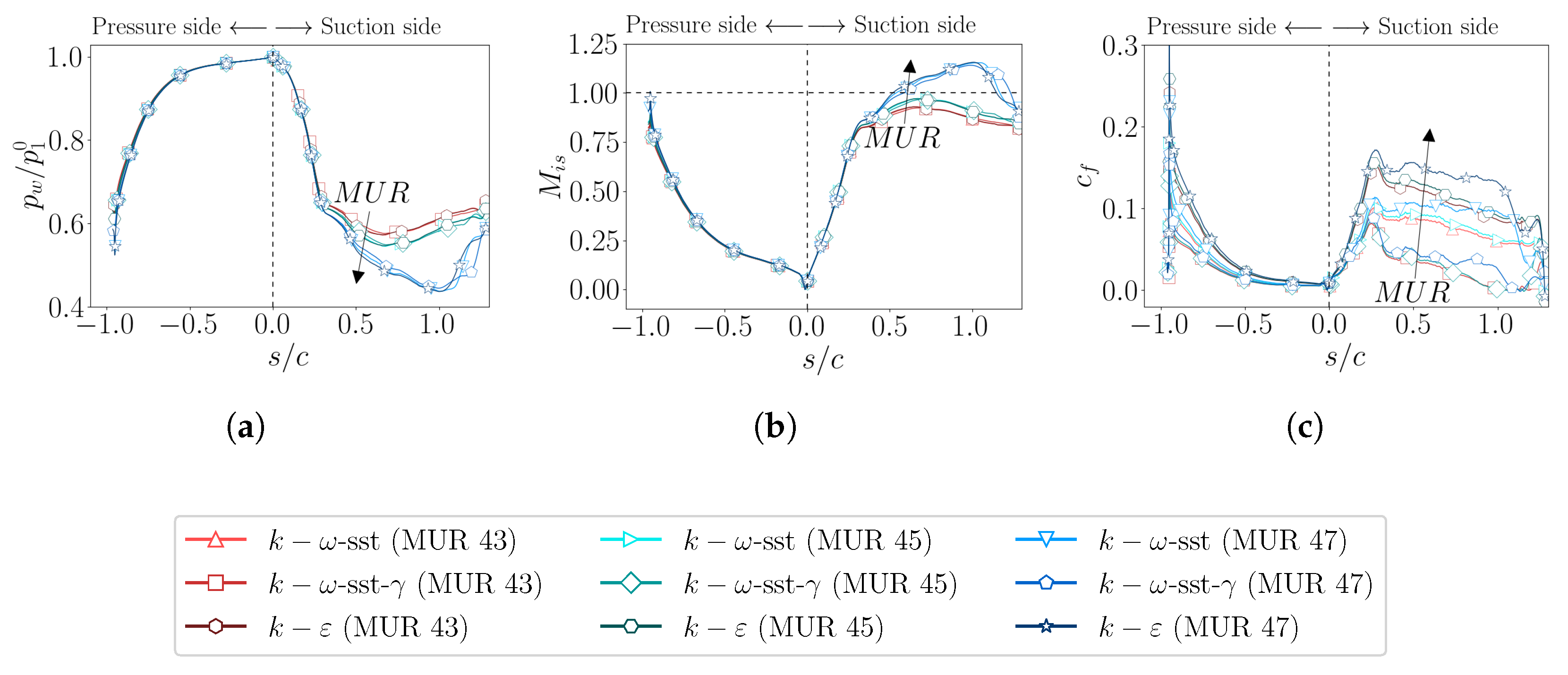
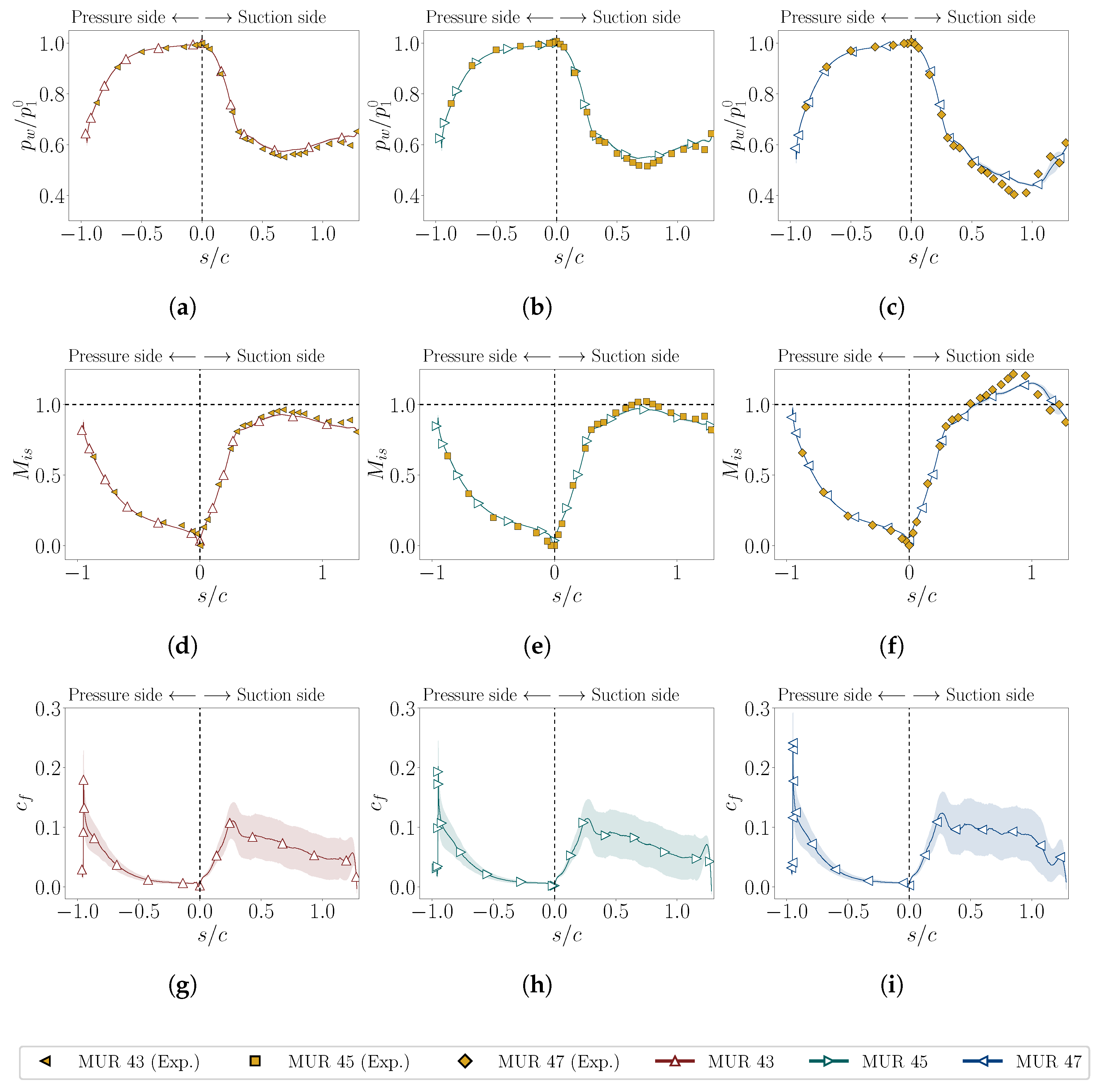
4.1.2. Near Wall Quantities
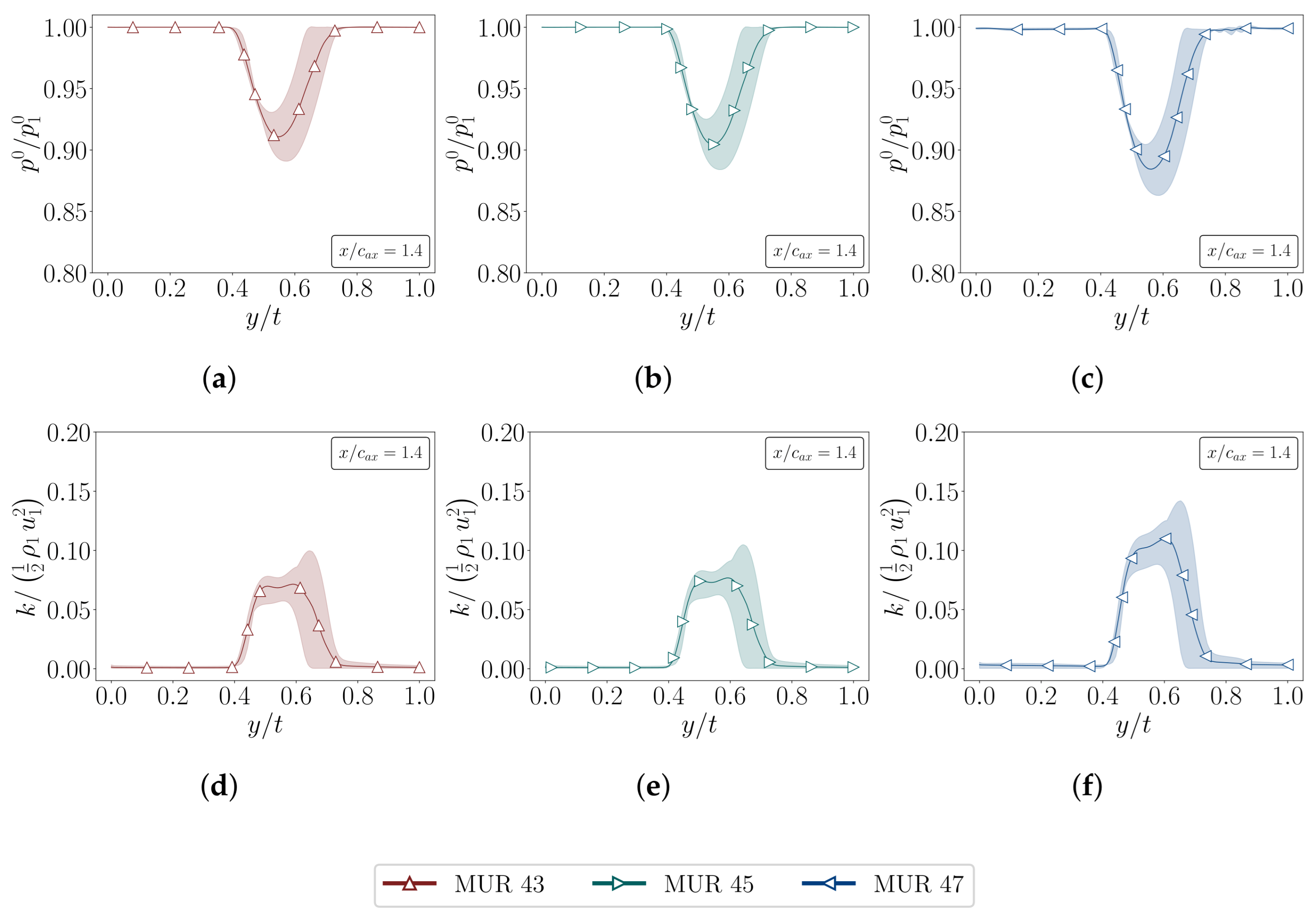
4.1.3. Wake Characterization
4.2. Diabatic Wall Arrangements
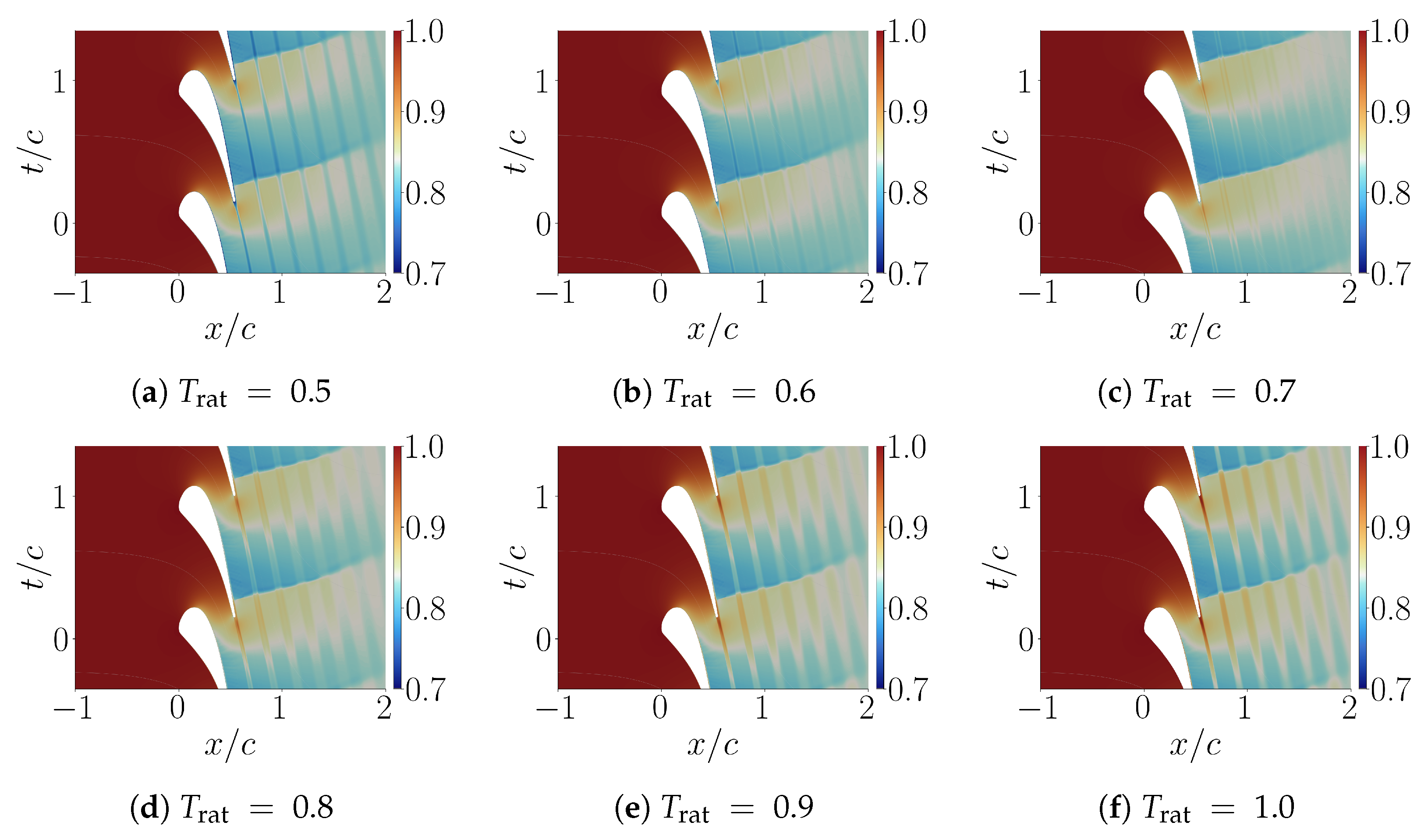
4.2.1. Flow Qualitative Description
4.2.2. Near-Wall Quantities
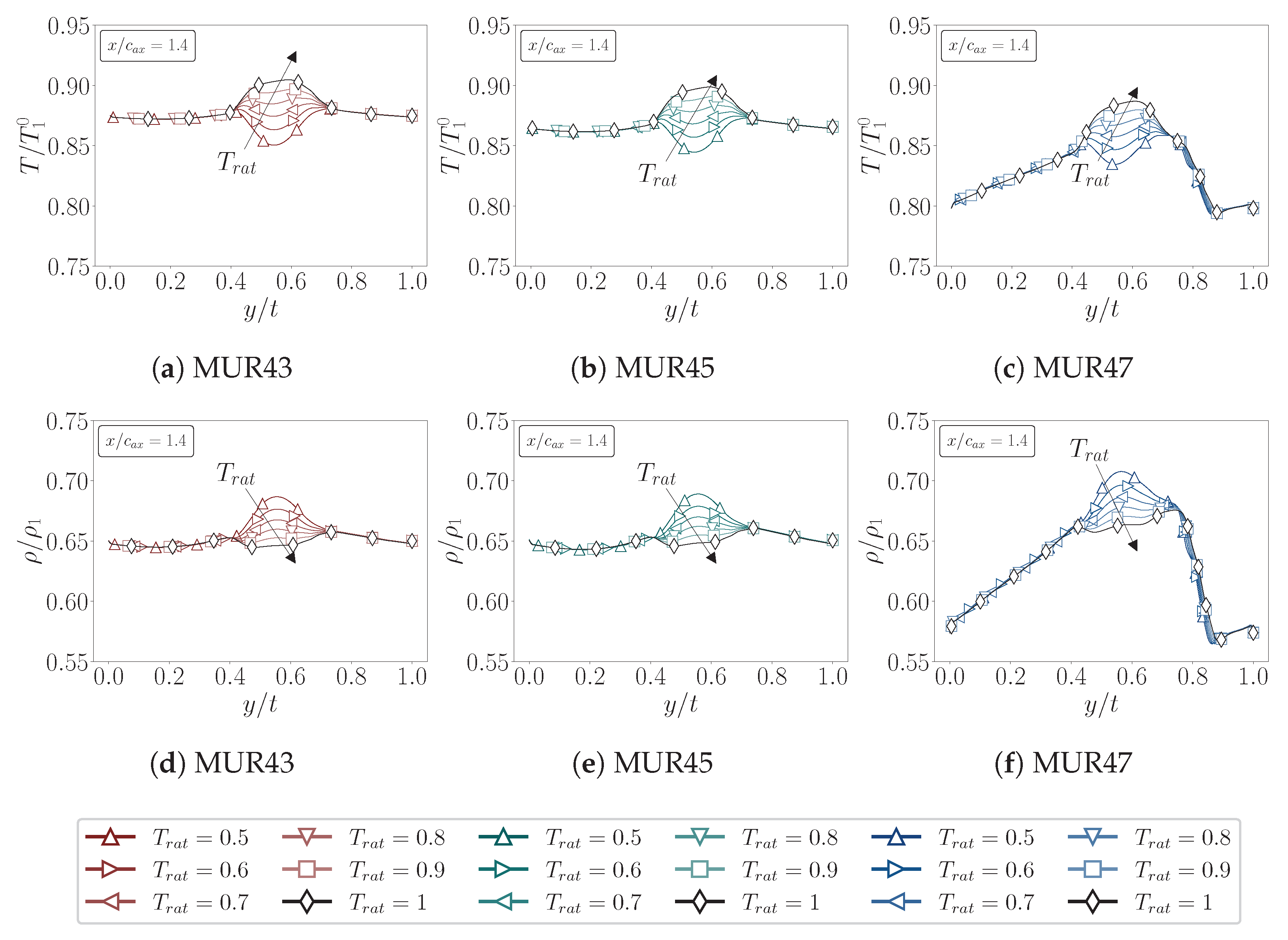
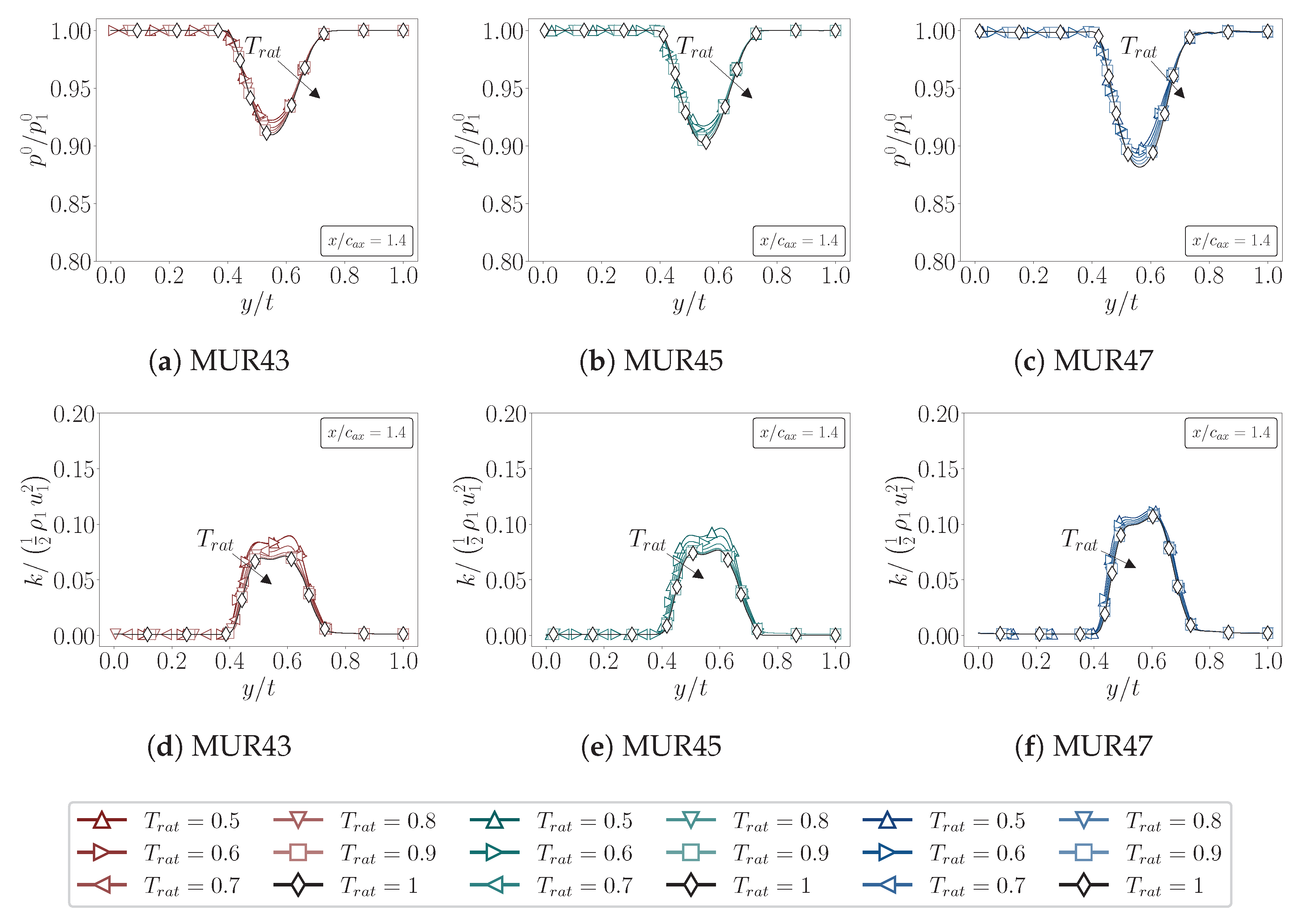
4.2.3. Wake Characterization
5. Conclusions
- A systematic mesh convergence analysis confirmed grid-independent solutions for global quantities, with near-exact agreement against experimental data for exit angle, outlet Mach number, and Reynolds number. Remaining discrepancies were primarily attributed to turbulence model dependence rather than discretization.
- None of the considered RANS turbulence models consistently outperformed the others. To mitigate closure-induced variability, a model-averaging strategy was adopted, reducing uncertainty and providing more robust predictions, particularly for near-wall shear and wake quantities.
- Wall pressure and isentropic Mach number distributions were shown to be largely insensitive to wall cooling, whereas viscous and thermal quantities (skin friction and heat transfer coefficients) displayed a strong nonlinear dependence on wall-to-recovery temperature ratio.
- Wake characteristics, including total pressure deficit and turbulent kinetic energy, are strongly influenced by wall cooling at low Mach numbers, with colder walls deepening the pressure deficit and increasing turbulence intensity. Notably, the RANS solutions show an opposite trend to DNS/LES, predicting higher turbulence levels with stronger cooling, a discrepancy that reflects the limitations of closures calibrated primarily for adiabatic walls.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- De Vanna, F.; Benini, E. Impact of wall cooling on transonic gas turbine stators aerothermodynamics: Insights from Wall-Modeled LES. Appl. Therm. Eng. 2025, 272, 126396. [Google Scholar] [CrossRef]
- Bogard, D.G.; Thole, K.A. Gas Turbine Film Cooling. J. Propuls. Power 2012, 22, 249–270. [Google Scholar] [CrossRef]
- Bolaina, C.; Teloxa, J.; Varela, C.; Sierra, F.Z. Thermomechanical stress distributions in a gas turbine blade under the effect of cooling flow variations. J. Turbomach. 2013, 135, 064501. [Google Scholar] [CrossRef]
- Mukherjee, D. Stresses in Turbine Blades Due to Temperature and Load Variation. In Proceedings of the ASME 1978 International Gas Turbine Conference and Products Show, London, UK, 9–13 April 1978; American Society of Mechanical Engineers: New York, NY, USA, 1978; Volume 79726, p. V01BT02A057. [Google Scholar] [CrossRef]
- Sierra, F.Z.; Narzary, D.; Bolaina, C.; Han, J.C.; Kubiak, J.; Nebradt, J. Heat Transfer and Thermal Mechanical Stress Distributions in Gas Turbine Blades. In Proceedings of the ASME Turbo Expo 2009: Power for Land, Sea, and Air, Orlando, FL, USA, 8–12 June 2009; Volume 48845, pp. 115–126. [Google Scholar] [CrossRef]
- Colban, W.; Gratton, A.; Thole, K.A.; Haendler, M. Heat Transfer and Film-Cooling Measurements on a Stator Vane with Fan-Shaped Cooling Holes. J. Turbomach. 2005, 128, 53–61. [Google Scholar] [CrossRef]
- Andreini, A.; Caciolli, G.; Da Soghe, R.; Facchini, B.; Mazzei, L. Numerical Investigation on the Heat Transfer Enhancement due to Coolant Extraction on the Cold Side of Film Cooling Holes. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Volume 5B: Heat Transfer, Düsseldorf, Germany, 16–20 June 2014; p. V05BT14A004. [Google Scholar] [CrossRef]
- Chi, Z.; Wang, L. Scale cooling–A novel fractal cooling structure for turbine vanes. J. Turbomach. 2025, 147, 061012. [Google Scholar] [CrossRef]
- Zhang, F.; Liu, C.; Wang, W.; Ye, L.; Li, B.; Liu, F. Film superposition prediction method for film cooling layouts with same opening ratio on the turbine blade. Appl. Therm. Eng. 2023, 233, 121105. [Google Scholar] [CrossRef]
- Bernardini, M.; Asproulias, I.; Larsson, J.; Pirozzoli, S.; Grasso, F. Heat transfer and wall temperature effects in shock wave turbulent boundary layer interactions. Phys. Rev. Fluids 2016, 1, 084403. [Google Scholar] [CrossRef]
- Kahveci, H.S.; Haldeman, C.W.; Mathison, R.M.; Dunn, M.G. Heat Transfer for the Film-Cooled Vane of a 1-1/2 Stage High-Pressure Transonic Turbine—Part I: Experimental Configuration and Data Review With Inlet Temperature Profile Effects. J. Turbomach. 2012, 135, 021027. [Google Scholar] [CrossRef]
- Kahveci, H.S.; Haldeman, C.W.; Mathison, R.M.; Dunn, M.G. Heat Transfer for the Film-Cooled Vane of a 1-1/2 Stage High-Pressure Transonic Turbine—Part II: Effect of Cooling Variation on the Vane Airfoil and Inner End Wall. J. Turbomach. 2012, 135, 021028. [Google Scholar] [CrossRef]
- Zhang, Q.; O’Dowd, D.O.; He, L.; Wheeler, A.P.S.; Ligrani, P.M.; Cheong, B.C.Y. Overtip Shock Wave Structure and Its Impact on Turbine Blade Tip Heat Transfer. J. Turbomach. 2011, 133, 041001. [Google Scholar] [CrossRef]
- Azad, G.S.; Han, J.C.; Teng, S.; Boyle, R.J. Heat Transfer and Pressure Distributions on a Gas Turbine Blade Tip. J. Turbomach. 2000, 122, 717–724. [Google Scholar] [CrossRef]
- Azad, G.S.; Han, J.C.; Boyle, R.J. Heat Transfer and Flow on the Squealer Tip of a Gas Turbine Blade. J. Turbomach. 2000, 122, 725–732. [Google Scholar] [CrossRef]
- Sampson, M.; Fairbanks, A.; Moseley, J.; Ligrani, P.M.; Xu, H.; Fox, M. Linear Cascade and Wind Tunnel Development for Turbine Blade Tip Heat Transfer Investigations With and Without Film Cooling. In Proceedings of the ASME Turbo Expo 2019: Turbomachinery Technical Conference and Exposition, Volume 5A: Heat Transfer, Phoenix, AZ, USA, 17–21 June 2019; p. V05AT13A007. [Google Scholar] [CrossRef]
- Giel, P.W.; Van Fossen, G.J.; Boyle, R.J.; Thurman, D.R.; Civinskas, K.C. Blade Heat Transfer Measurements and Predictions in a Transonic Turbine Cascade. In Proceedings of the ASME 1999 International Gas Turbine and Aeroengine Congress and Exhibition, Volume 3: Heat Transfer; Electric Power; Industrial and Cogeneration, Indianapolis, IN, USA, 7–10 June 1999; p. V003T01A029. [Google Scholar] [CrossRef]
- Chen, D.; Du, Q.; Xu, Q.; Xu, G.; Liu, H.; Li, H. Film cooling and aerodynamic loss performance of turbine vanes with fan-shaped and wave-trenched holes. Appl. Therm. Eng. 2023, 230, 120643. [Google Scholar] [CrossRef]
- Abuaf, N.; Bunker, R.; Lee, C.P. Heat Transfer and Film Cooling Effectiveness in a Linear Airfoil Cascade. J. Turbomach. 1997, 119, 302–309. [Google Scholar] [CrossRef]
- Tallman, J.A.; Haldeman, C.W.; Dunn, M.G.; Tolpadi, A.K.; Bergholz, R.F. Heat Transfer Measurements and Predictions for a Modern, High-Pressure, Transonic Turbine, Including Endwalls. J. Turbomach. 2009, 131, 021001. [Google Scholar] [CrossRef]
- Bianchini, C.; Andrei, L.; Andreini, A.; Facchini, B. Numerical Benchmark of Nonconventional RANS Turbulence Models for Film and Effusion Cooling. J. Turbomach. 2013, 135, 041026. [Google Scholar] [CrossRef]
- Ravelli, S.; Barigozzi, G. Comparison of RANS and Detached Eddy Simulation Modeling Against Measurements of Leading Edge Film Cooling on a First-Stage Vane. J. Turbomach. 2017, 139, 051005. [Google Scholar] [CrossRef]
- Jones, F.B.; Fox, D.W.; Bogard, D.G. Evaluating the Usefulness of RANS in Film Cooling. In Proceedings of the ASME Turbo Expo 2019: Turbomachinery Technical Conference and Exposition, Volume 5A: Heat Transfer, Phoenix, AZ, USA, 17–21 June 2019; p. V05AT12A019. [Google Scholar] [CrossRef]
- Rosafio, N.; Lopes, G.; Salvadori, S.; Lavagnoli, S.; Misul, D.A. RANS Prediction of Losses and Transition Onset in a High-Speed Low-Pressure Turbine Cascade. Energies 2023, 16, 7348. [Google Scholar] [CrossRef]
- Müller-Schindewolffs, C.; Baier, R.D.; Seume, J.R.; Herbst, F. Direct numerical simulation based analysis of RANS predictions of a low-pressure turbine cascade. J. Turbomach. 2017, 139, 081006. [Google Scholar] [CrossRef]
- Gourdain, N.; Gicquel, L.Y.; Collado, E. Comparison of RANS and LES for prediction of wall heat transfer in a highly loaded turbine guide vane. J. Propuls. Power 2012, 28, 423–433. [Google Scholar] [CrossRef]
- Marconcini, M.; Pacciani, R.; Arnone, A.; Michelassi, V.; Pichler, R.; Zhao, Y.; Sandberg, R. Large eddy simulation and RANS analysis of the end-wall flow in a linear low-pressure-turbine cascade–Part II: Loss generation. J. Turbomach. 2019, 141, 051004. [Google Scholar] [CrossRef]
- Denton, J.D. Some Limitations of Turbomachinery CFD. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea, and Air, Volume 7: Turbomachinery, Parts A, B, and C, Glasgow, UK, 14–18 June 2010; pp. 735–745. [Google Scholar] [CrossRef]
- Huang, J.; Nicholson, G.L.; Duan, L.; Choudhari, M.M.; Bowersox, R.D.W. Simulation and modeling of cold-wall hypersonic turbulent boundary layers on flat plate. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar] [CrossRef]
- Borghi, M.R.; Spiegel, S.C.; Yoder, D.A.; Georgiadis, N.J.; Wernet, M.P. Turbulent simulations of cooling jets in crossflow. In Proceedings of the AIAA Scitech 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar] [CrossRef]
- Pichler, R.; Zhao, Y.; Sandberg, R.; Michelassi, V.; Pacciani, R.; Marconcini, M.; Arnone, A. Large-Eddy Simulation and RANS Analysis of the End-Wall Flow in a Linear Low-Pressure Turbine Cascade, Part I: Flow and Secondary Vorticity Fields Under Varying Inlet Condition. J. Turbomach. 2019, 141, 121005. [Google Scholar] [CrossRef]
- Sandrin, S.; Mazzei, L.; Da Soghe, R.; Fontaneto, F. Computational Fluid Dynamics Prediction of External Thermal Loads on Film-Cooled Gas Turbine Vanes: A Validation of Reynolds-Averaged Navier–Stokes Transition Models and Scale-Resolving Simulations for the VKI LS-94 Test Case. Fluids 2024, 9, 91. [Google Scholar] [CrossRef]
- Hassan, J.S.; Yavuzkurt, S. Comparison of four different two-equation models of turbulence in predicting film cooling performance. In Proceedings of the ASME Turbo Expo 2006: Power for Land, Sea, and Air, Barcelona, Spain, 8–11 May 2006; Volume 4238, pp. 701–710. [Google Scholar] [CrossRef]
- BiAn, X.; Wang, Q.; Su, X.; Yuan, X. Interaction mechanisms of shock waves with the boundary layer and wakes in a highly-loaded NGV using hybrid RANS/LES. Chin. J. Aeronaut. 2020, 33, 149–160. [Google Scholar] [CrossRef]
- Heyse, J.F.; Mishra, A.A.; Iaccarino, G. Estimating RANS model uncertainty using machine learning. J. Glob. Power Propuls. Soc. 2021, 2021, 1–14. [Google Scholar] [CrossRef]
- Schobeiri, M.T.; Nikparto, A. A Comparative Numerical Study of Aerodynamics and Heat Transfer on Transitional Flow Around a Highly Loaded Turbine Blade With Flow Separation Using RANS, URANS and LES. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Volume 5C: Heat Transfer, Düsseldorf, Germany, 16–20 June 2014; p. V05CT17A001. [Google Scholar] [CrossRef]
- Duraisamy, K.; Iaccarino, G.; Xiao, H. Turbulence Modeling in the Age of Data. Annu. Rev. Fluid Mech. 2019, 51, 357–377. [Google Scholar] [CrossRef]
- He, W.; Deng, Q.; Zhou, W.; Gao, T.; Feng, Z. Film cooling and aerodynamic performances of a turbine nozzle guide vane with trenched cooling holes. Appl. Therm. Eng. 2019, 150, 150–163. [Google Scholar] [CrossRef]
- Xiao, H.; Cinnella, P. Quantification of model uncertainty in RANS simulations: A review. Prog. Aerosp. Sci. 2019, 108, 1–31. [Google Scholar] [CrossRef]
- Edeling, W.; Cinnella, P.; Dwight, R.P. Predictive RANS simulations via Bayesian Model-Scenario Averaging. J. Comput. Phys. 2014, 275, 65–91. [Google Scholar] [CrossRef]
- Wang, J.X.; Sun, R.; Xiao, H. Quantification of uncertainties in turbulence modeling: A comparison of physics-based and random matrix theoretic approaches. Int. J. Heat Fluid Flow 2016, 62, 577–592. [Google Scholar] [CrossRef]
- Arts, T.; Lambert de Rouvroit, M.; Rutherford, A. Aerothermal Investigation of a Highly Loaded Transonic Linear Turbine Guide Vane Cascade. A Test Case for Inviscid and Viscous Flow Computations; VKI LS 1990-06; Von Karman Institute for Fluid Dynamics: Sint-Genesius-Rode, Belgium, 1990. [Google Scholar]
- De Vanna, F.; Benini, E. Wall-Modeled LES of a Transonic Gas Turbine Vane—Part I: Model Setup and Assessment of Turbulent Length Scales. J. Turbomach. 2025, 147, 111015. [Google Scholar] [CrossRef]
- De Vanna, F.; Benini, E. Wall-Modeled LES of a Transonic Gas Turbine Vane—Part II: Mach Number Effect and Losses Prediction. J. Turbomach. 2025, 147, 111016. [Google Scholar] [CrossRef]
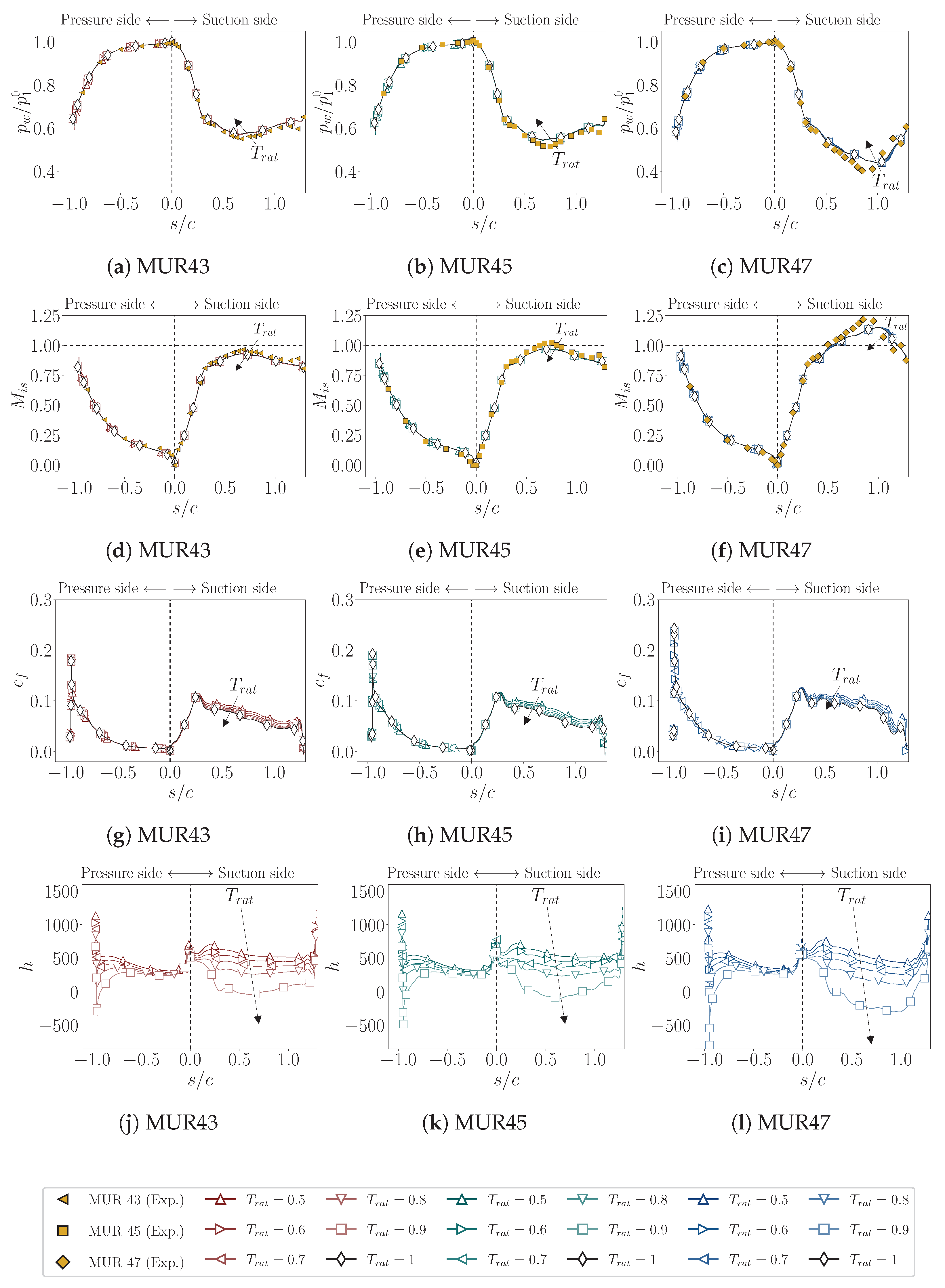
| Parameters | Variable | Value | Unit |
|---|---|---|---|
| Chord | c | 67.647 | [mm] |
| Axial chord | 38.8 | [mm] | |
| Stagger angle | 55 | [°] | |
| Pitch | t | 57.5 | [mm] |
| Case | [Pa] | [Pa] | [K] | [−] | [%] | [−] |
|---|---|---|---|---|---|---|
| MUR43 | 143,500 | 90,405 | 420 | 0.840 | 5 | 10 |
| MUR45 | 147,500 | 89,583 | 420 | 0.875 | 5 | 10 |
| MUR47 | 159,600 | 83,661 | 420 | 1.020 | 5 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fornasari, D.; Regazzo, S.; Benini, E.; De Vanna, F. RANS-Based Aerothermal Database of LS89 Transonic Turbine Cascade Under Adiabatic and Cooled Wall Conditions. Energies 2025, 18, 5321. https://doi.org/10.3390/en18195321
Fornasari D, Regazzo S, Benini E, De Vanna F. RANS-Based Aerothermal Database of LS89 Transonic Turbine Cascade Under Adiabatic and Cooled Wall Conditions. Energies. 2025; 18(19):5321. https://doi.org/10.3390/en18195321
Chicago/Turabian StyleFornasari, Davide, Stefano Regazzo, Ernesto Benini, and Francesco De Vanna. 2025. "RANS-Based Aerothermal Database of LS89 Transonic Turbine Cascade Under Adiabatic and Cooled Wall Conditions" Energies 18, no. 19: 5321. https://doi.org/10.3390/en18195321
APA StyleFornasari, D., Regazzo, S., Benini, E., & De Vanna, F. (2025). RANS-Based Aerothermal Database of LS89 Transonic Turbine Cascade Under Adiabatic and Cooled Wall Conditions. Energies, 18(19), 5321. https://doi.org/10.3390/en18195321









