Heat Pump Optimization—Comparative Study of Different Optimization Algorithms and Heat Exchanger Area Approximations
Abstract
1. Introduction
2. Materials and Method
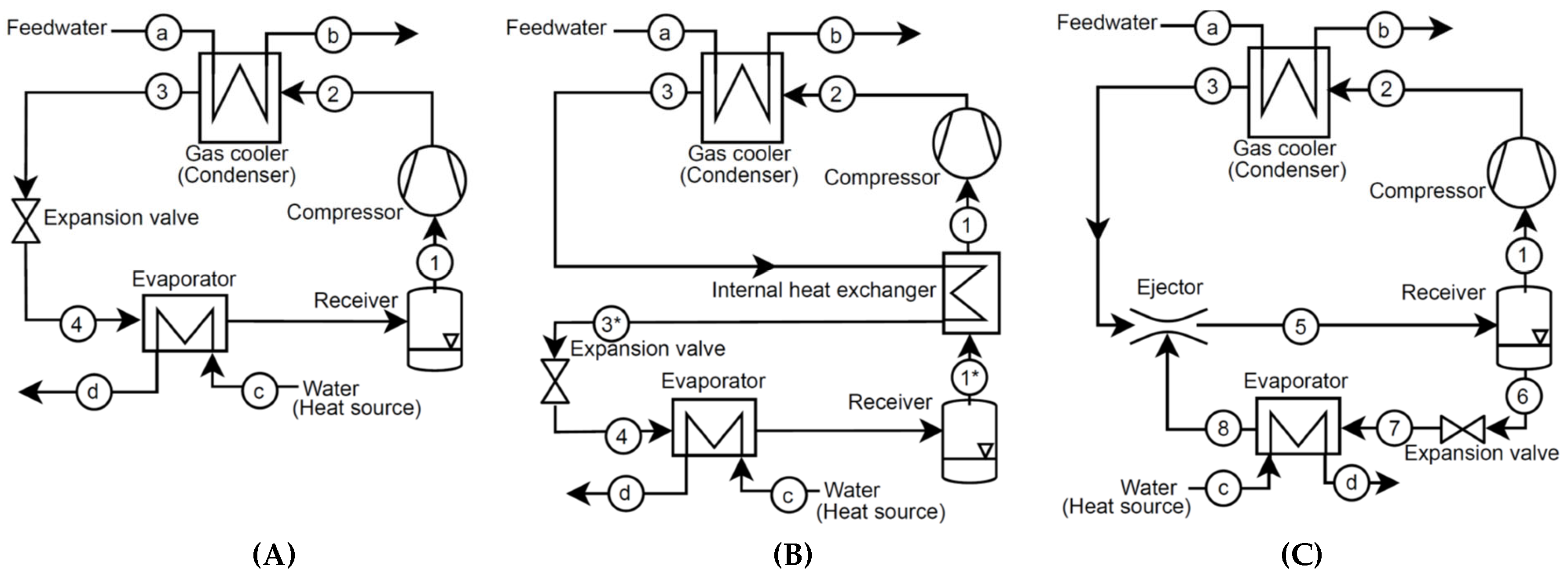
2.1. Heat Pump Processes
2.2. Process Modelling
2.2.1. Compressor and Ejector Performance
2.2.2. Modeling of HEs
2.2.3. HE Area Integral Approximations
2.3. Optimization
Optimization Scheme
2.4. Error Estimates, Run Time, and Definition of Failed Cases
2.5. Case Studies
3. Results and Discussion
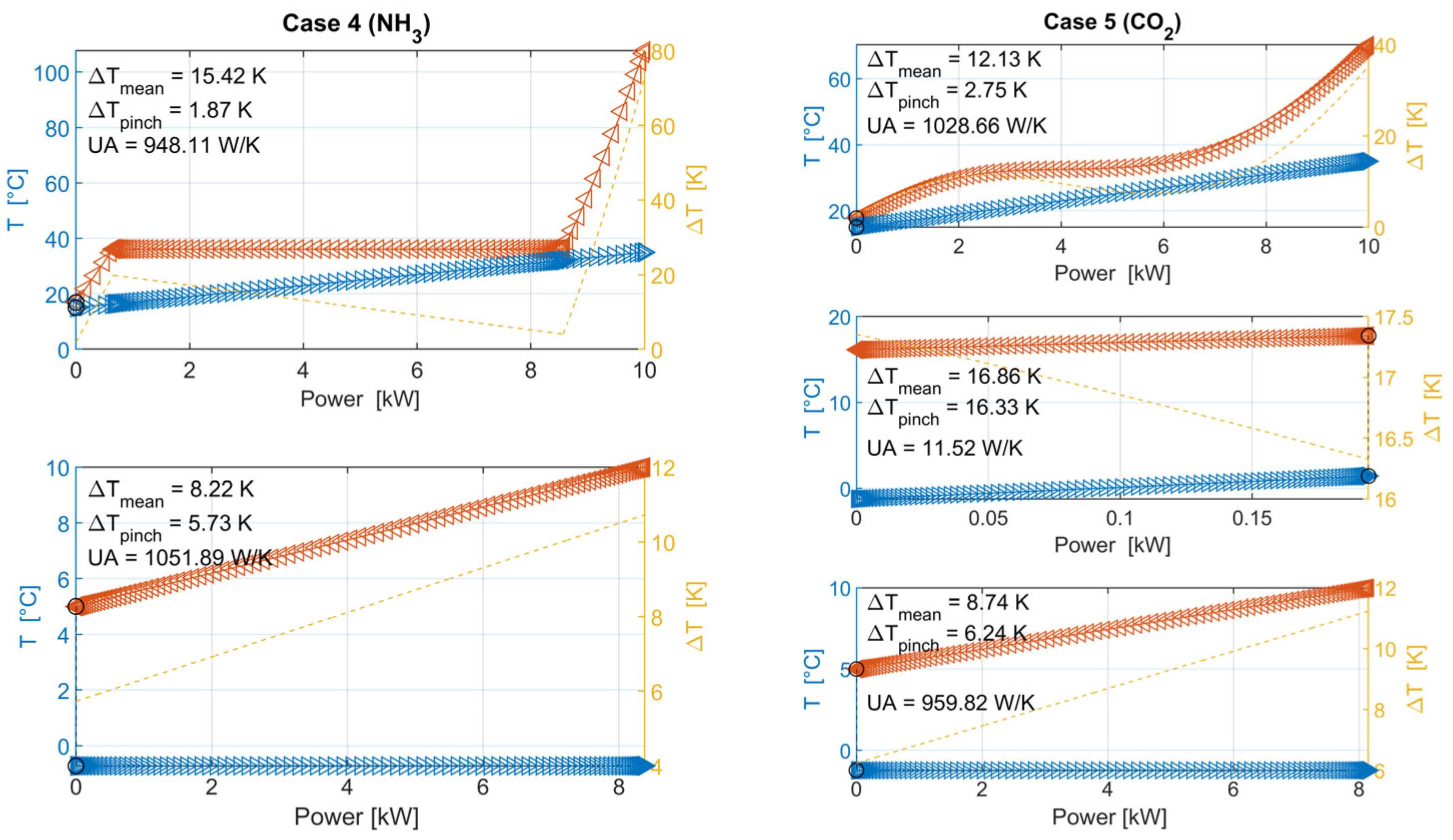
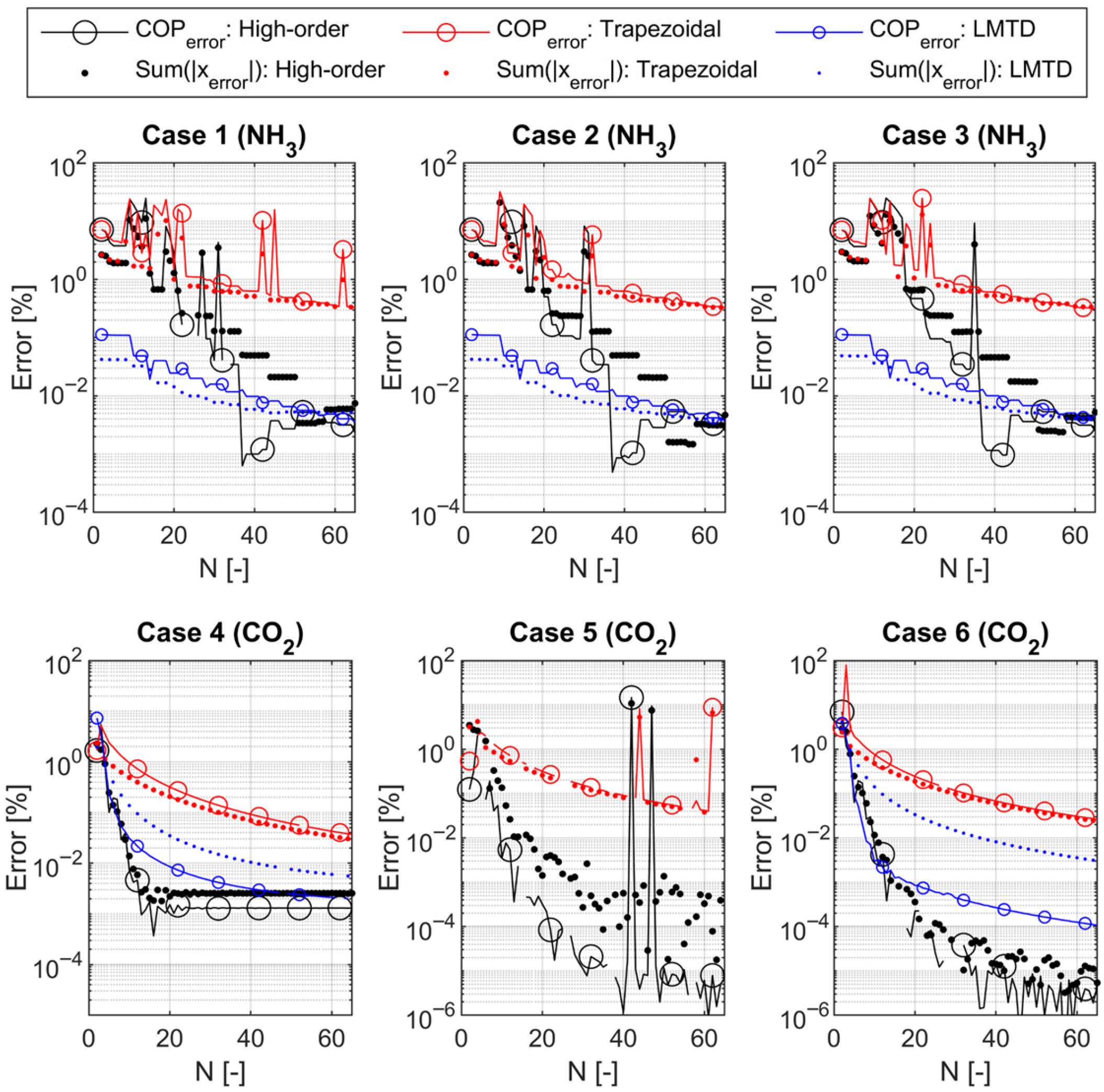
3.1. Model Verification
3.2. Required Modeling Precision
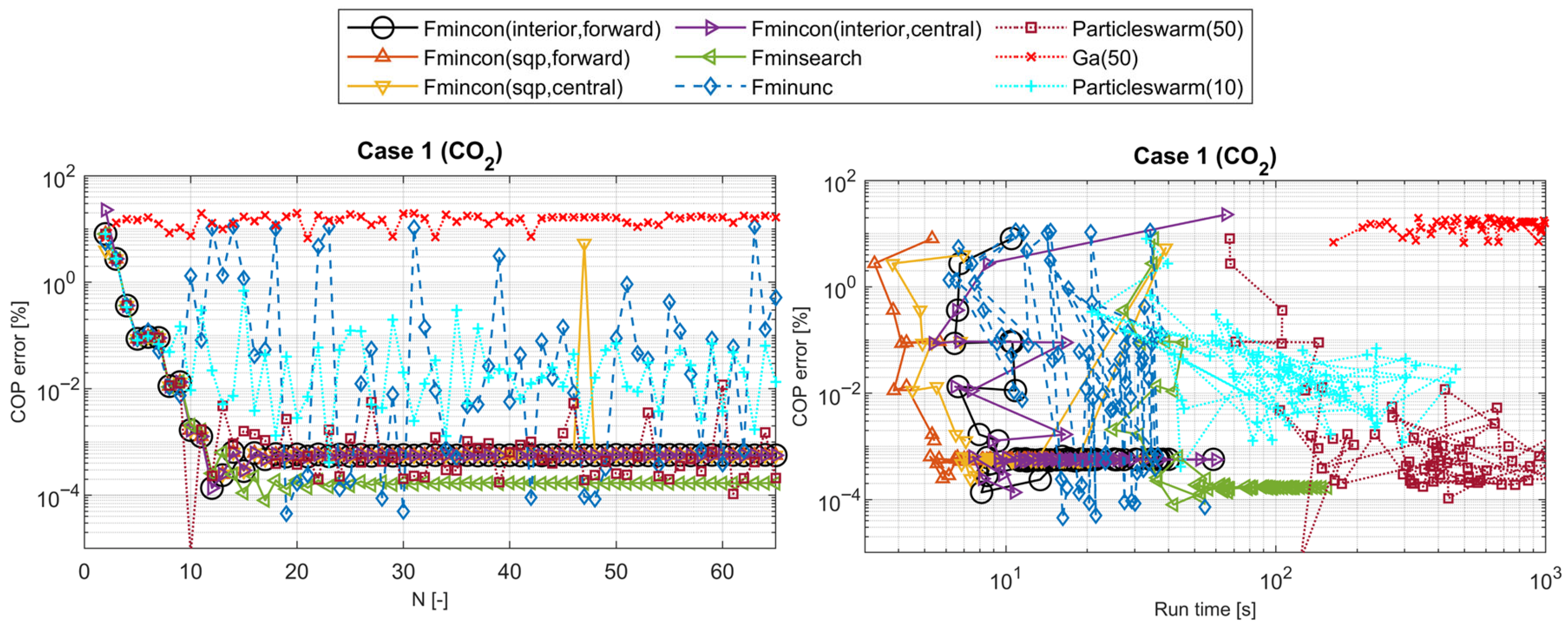
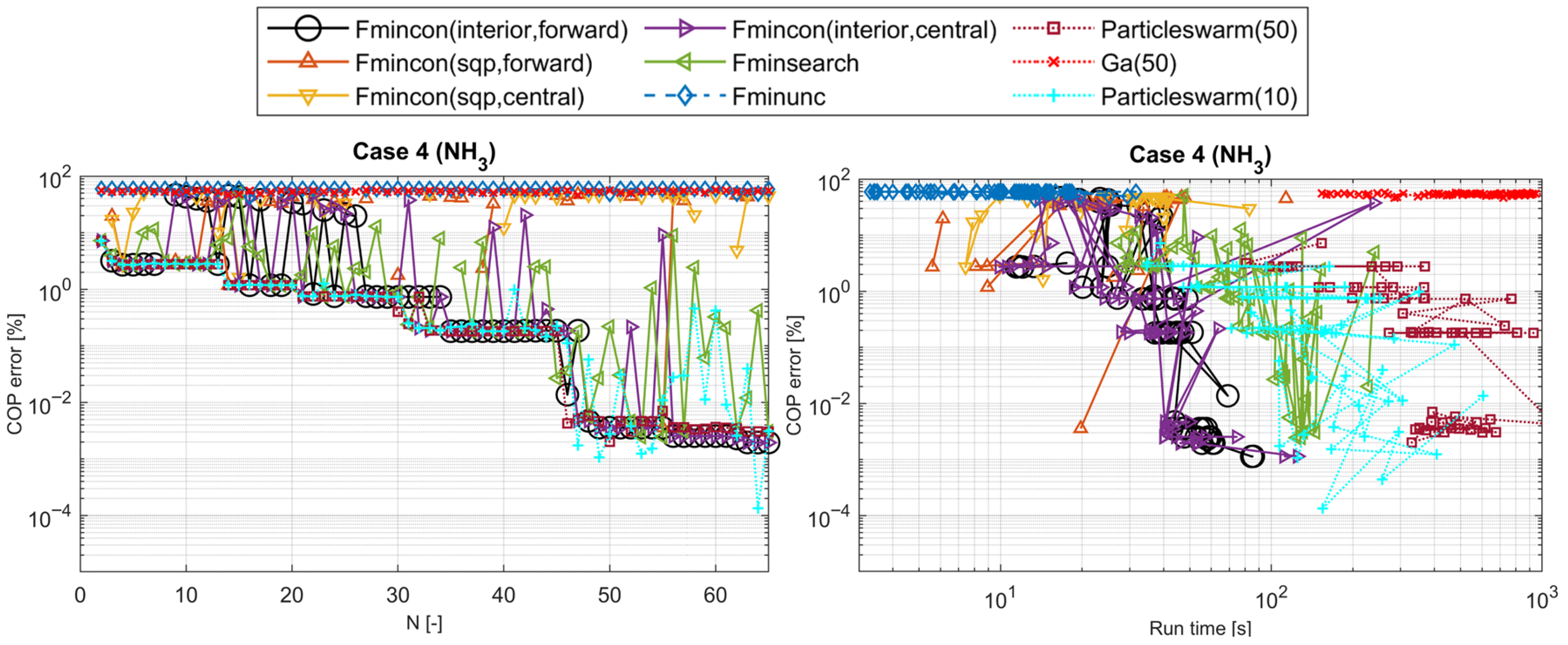
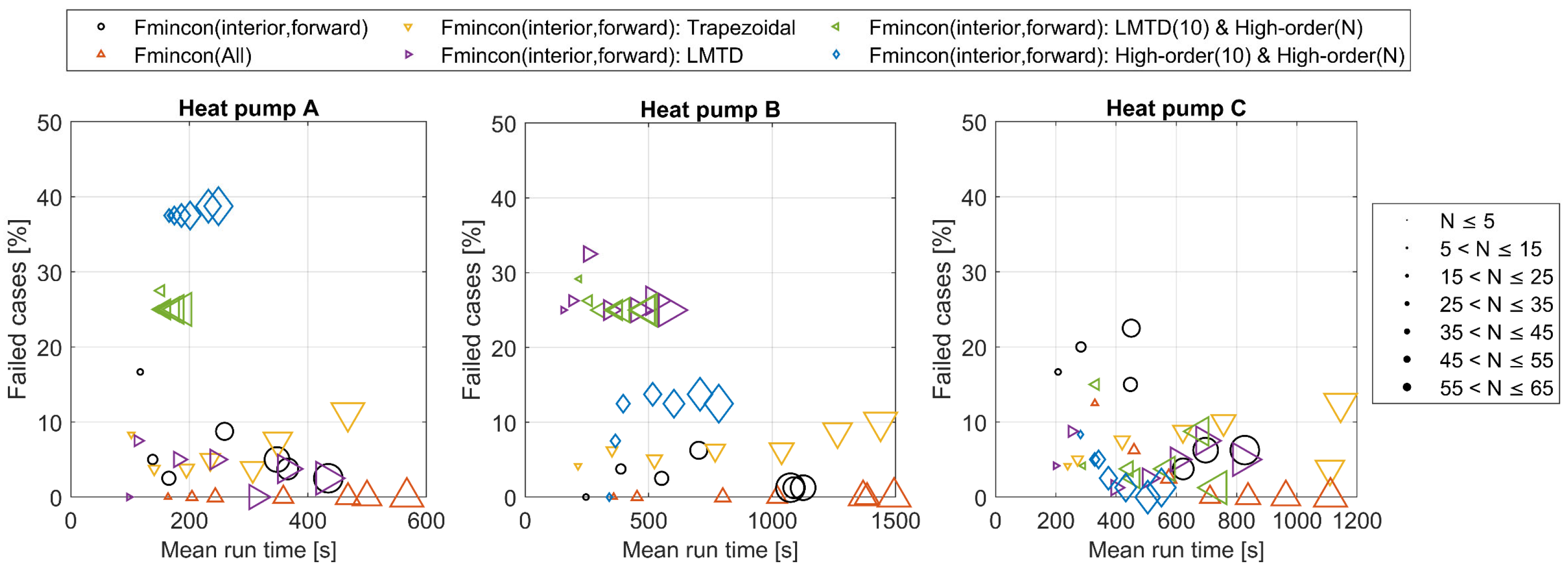
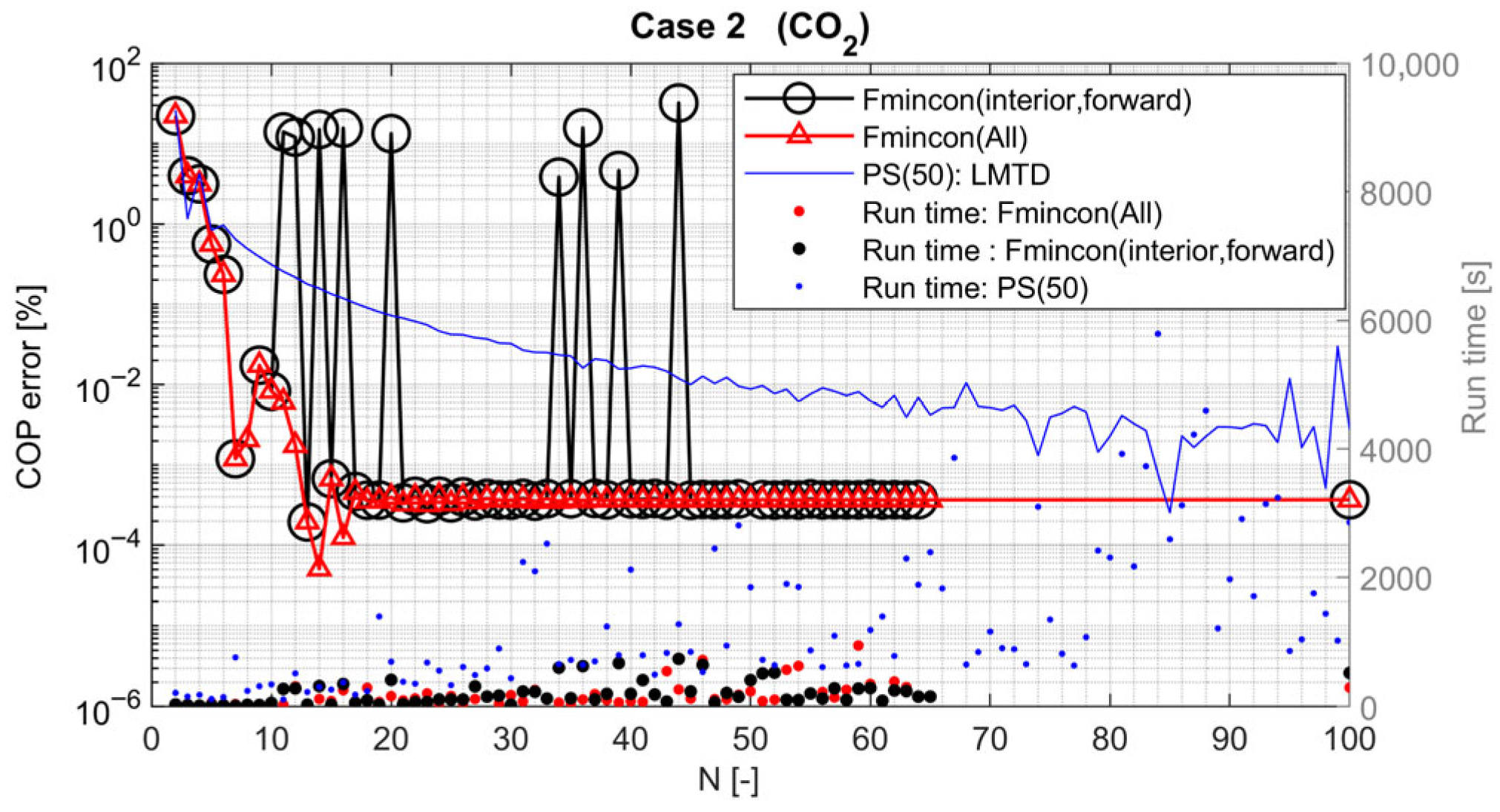
3.3. Optimization Algorithms
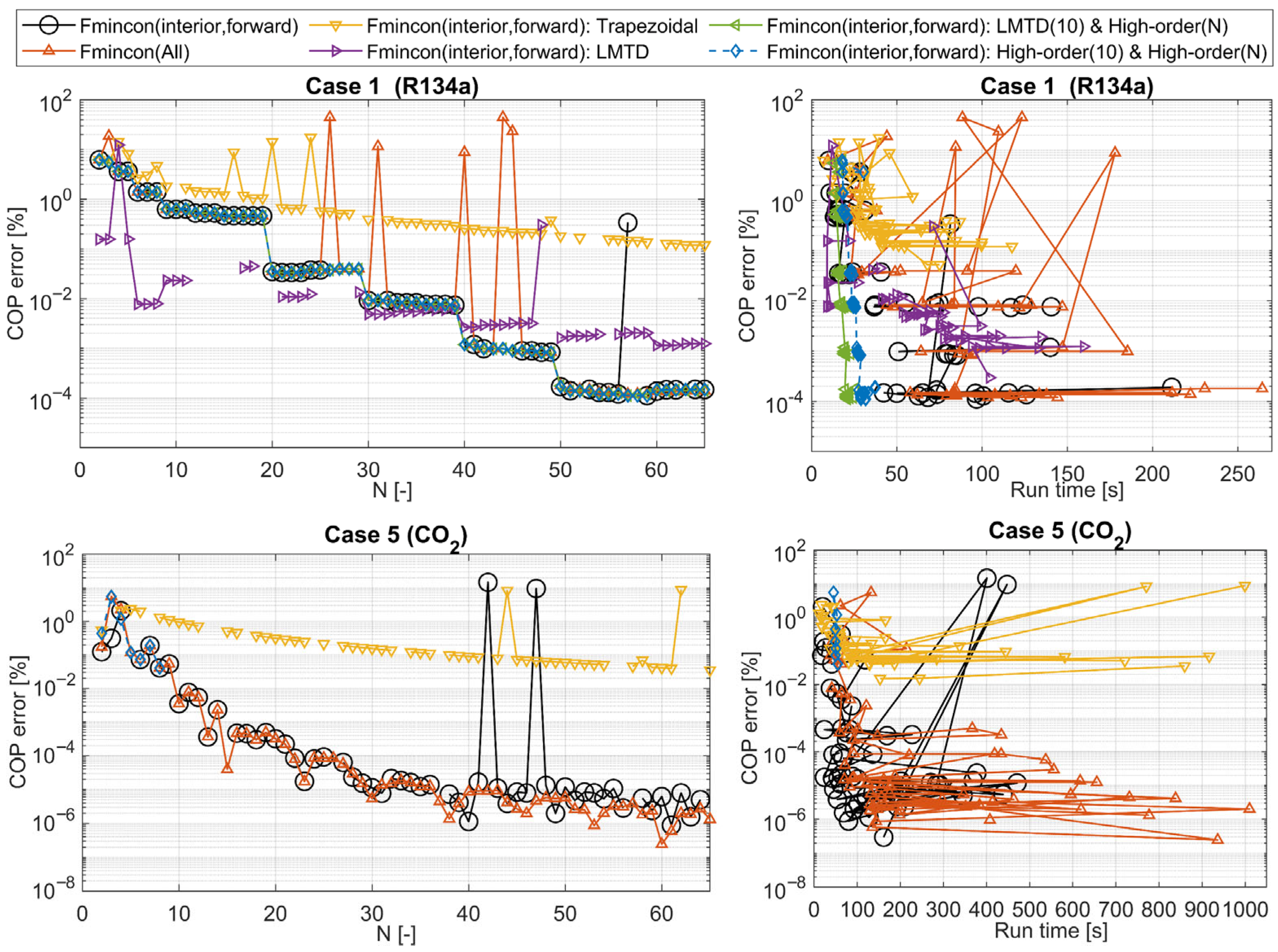
3.4. Sequential Optimization Methods
3.4.1. Fmincon(All)
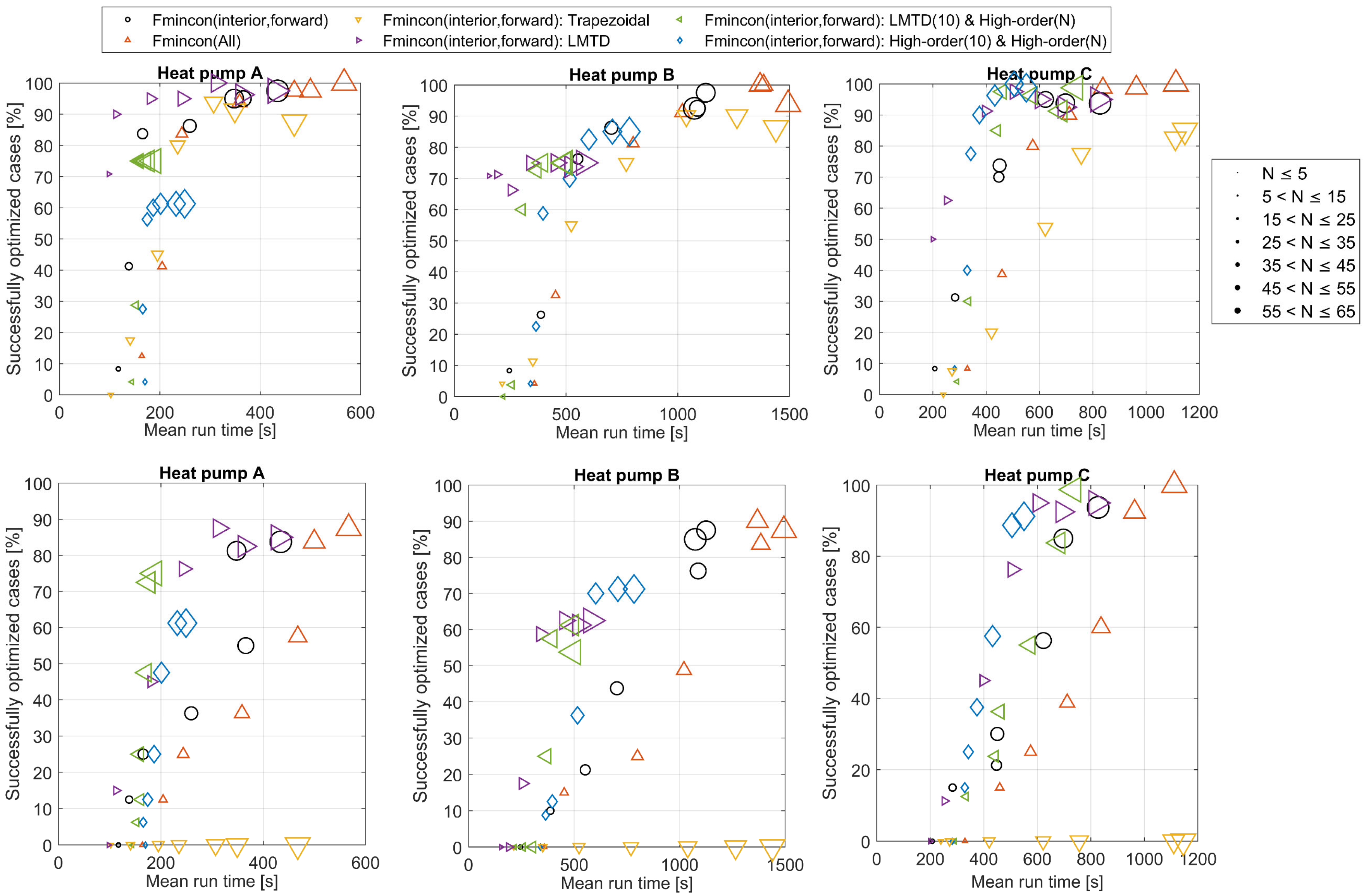
3.4.2. Improving the Initial Guess
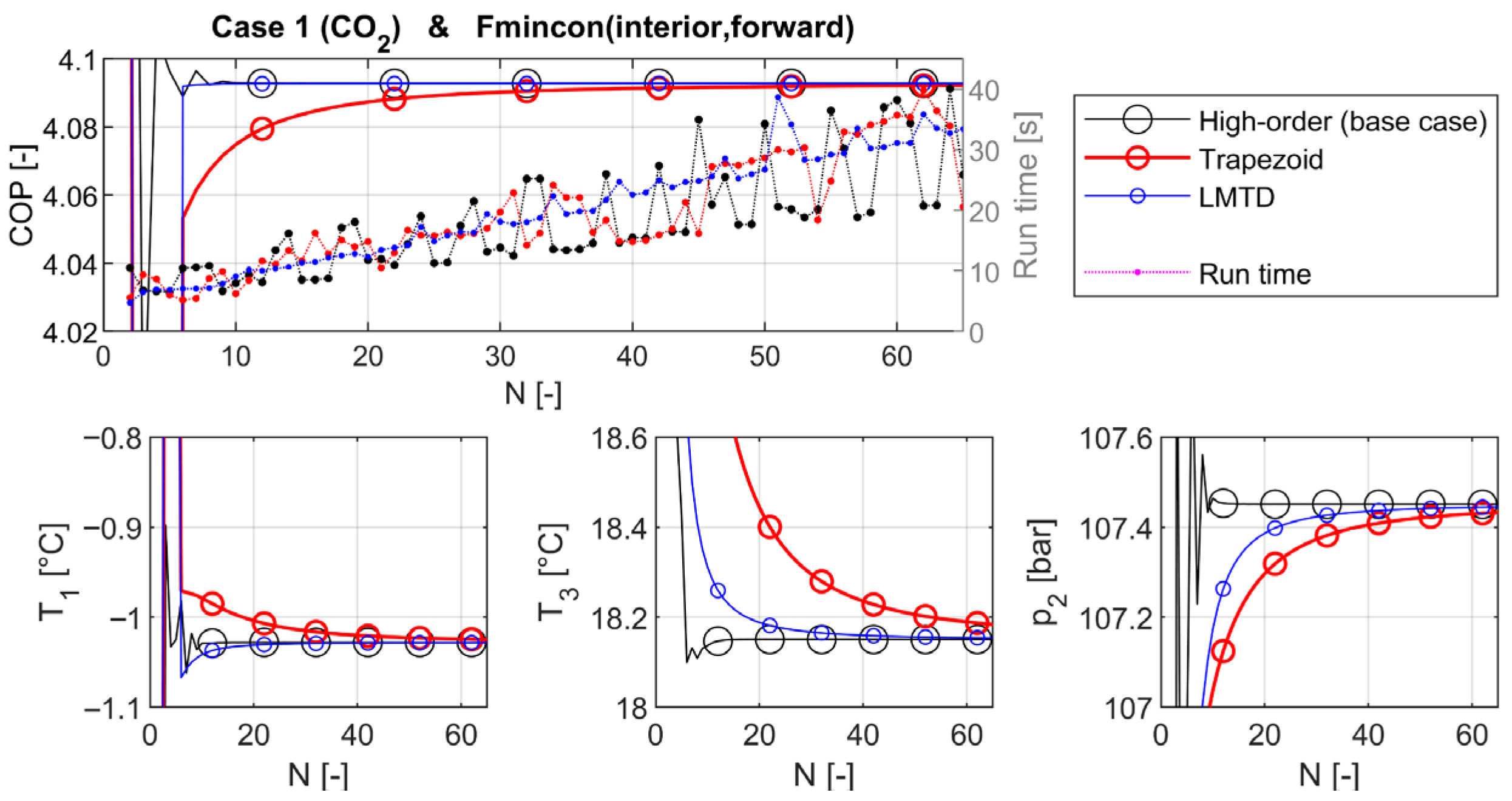
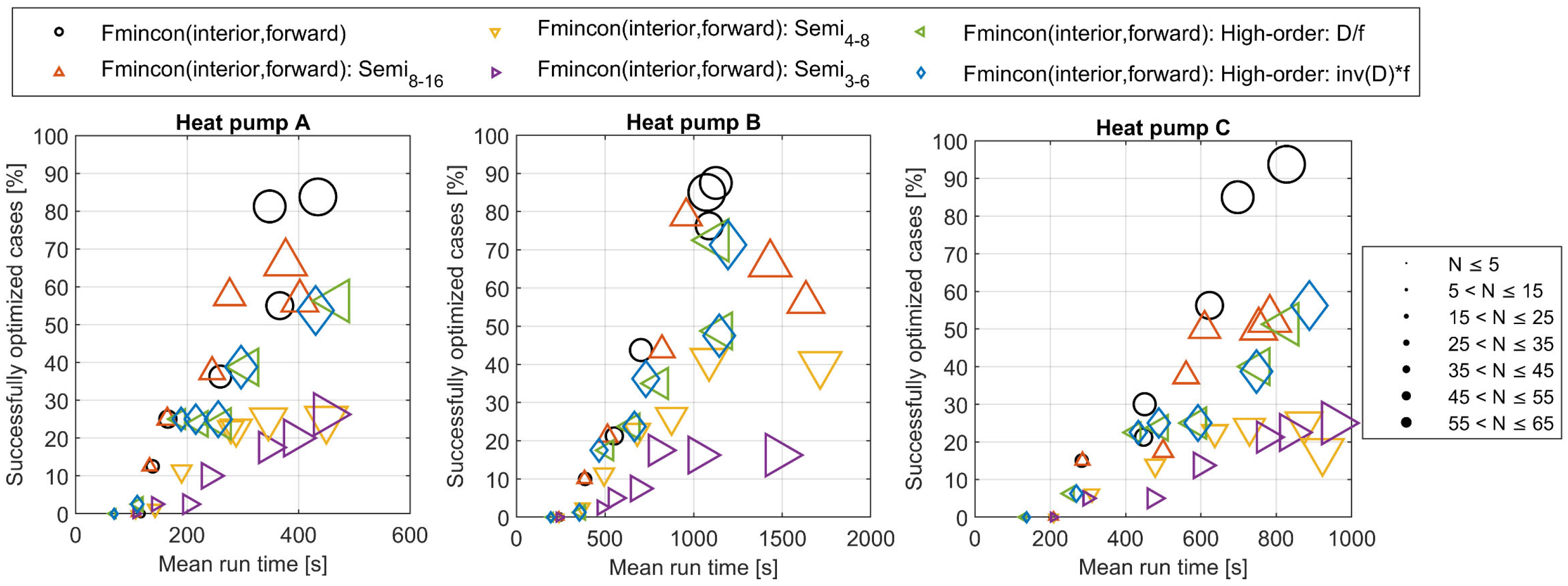
3.5. Performance of the HE Area Approximations
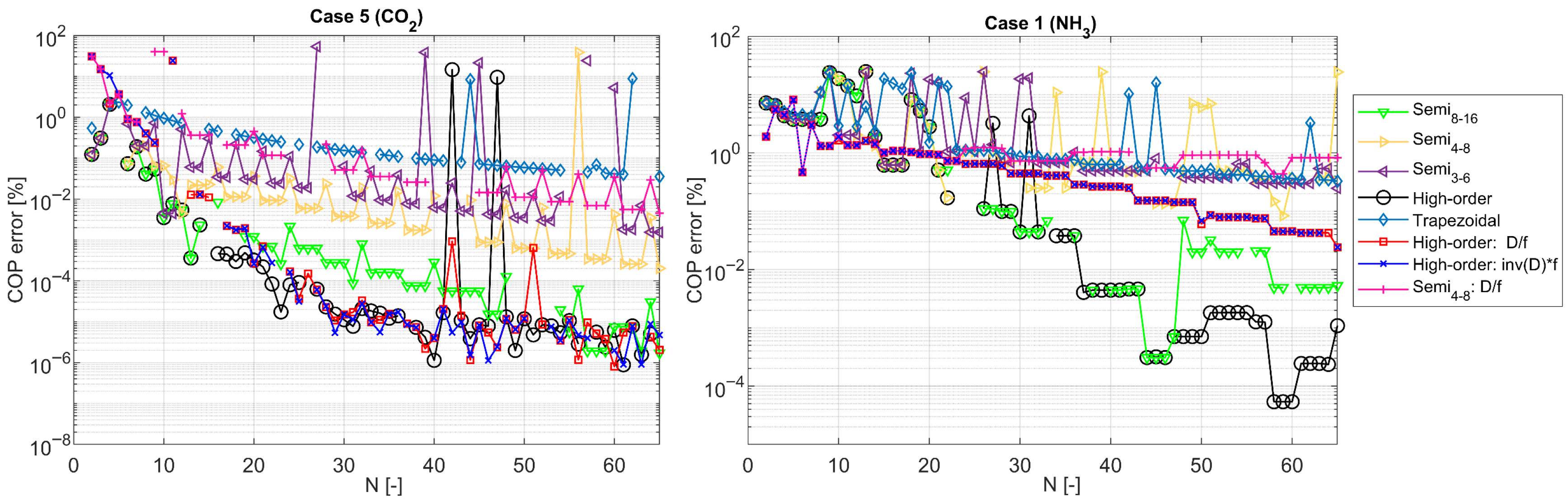
3.5.1. High-Order
3.5.2. Trapezoidal
3.5.3. High-Order Alternatives
3.5.4. Semi High-Order
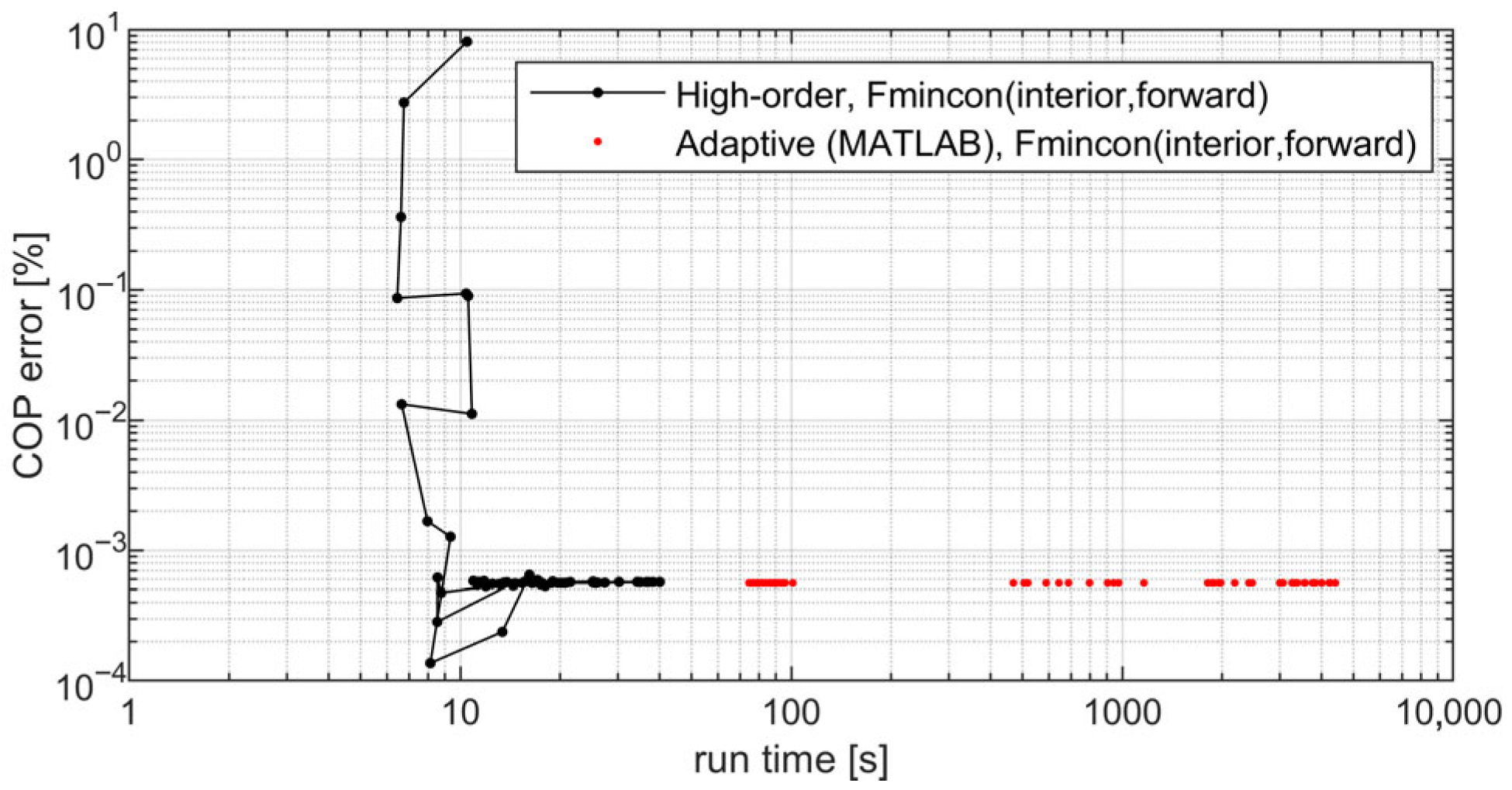
3.5.5. Adaptive Methods
3.5.6. LMTD
3.5.7. Possible Applications and Real Heat Transfer Models
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Allen, B.; Savard-Goguen, M.; Gosselin, L. Optimizing heat exchanger networks with genetic algorithms for designing each heat exchanger including condensers. Appl. Therm. Eng. 2009, 29, 3437–3444. [Google Scholar] [CrossRef]
- Amalfi, R.L.; Vakili-Farahani, F.; Thome, J.R. Flow boiling and frictional pressure gradients in plate heat exchangers. Part 2: Comparison of literature methods to database and new prediction methods. Int. J. Refrig. 2016, 61, 185–203. [Google Scholar] [CrossRef]
- Austbø, B.; Løvseth, S.W.; Gundersen, T. Annotated bibliography—Use of optimization in LNG process design and operation. Comput. Chem. Eng. 2014, 71, 391–414. [Google Scholar] [CrossRef]
- Ayub, Z.H. Plate Heat Exchanger Literature Survey and New Heat Transfer and Pressure Drop Correlations for Refrigerant Evaporators. Heat Transf. Eng. 2003, 24, 3–16. [Google Scholar] [CrossRef]
- Ayub, Z.H.; Khan, T.S.; Salam, S.; Nawazc, K.; Ayub, A.H.; Khan, M.S. Literature survey and a universal evaporation correlation for plate type heat exchangers. Int. J. Refrig. 2019, 99, 408–418. [Google Scholar] [CrossRef]
- Bell, I.H.; Wronski, J.; Quoilin, S.; Lemort, V. Pure and Pseudo-pure Fluid Thermophysical Property Evaluation and the Open-Source Thermophysical Property Library CoolProp. Ind. Eng. Chem. Res. 2014, 53, 2498–2508. [Google Scholar] [CrossRef]
- Brodal, E.; Eiksund, O. Optimization study of heat pumps using refrigerant blends—Ejector versus expansion valve systems. Int. J. Refrig. 2020, 111, 136–146. [Google Scholar] [CrossRef]
- Brodal, E.; Jackson, S.; Eiksund, O. Performance and design study of optimized LNG Mixed Fluid Cascade processes. Energy 2019, 189, 116207. [Google Scholar] [CrossRef]
- Brodal, E.; Jackson, S.; Eiksund, O. Comparing optimization schemes for solving case studies with multiple heat exchangers using high-order pinch point temperature difference methods. Comput. Chem. Eng. 2023, 180, 108474. [Google Scholar] [CrossRef]
- Brodal, E.; Jackson, S.; Hailu, G. UA and pinch point temperature difference modeling—Finding the best heat exchanger schemes. Comput. Chem. Eng. 2022, 169, 108085. [Google Scholar] [CrossRef]
- Byrd, R.H.; Hribar, M.E.; Nocedal, J. An interior point algorithm for large-scale nonlinear programming. SIAM J. Optim. 1999, 9, 877–900. [Google Scholar] [CrossRef]
- Chen, Y.-G. Pinch point analysis and design considerations of CO2 gas cooler for heat pump water heaters. Int. J. Refrig. 2016, 69, 136–146. [Google Scholar] [CrossRef]
- Dai, B.; Dang, C.; Li, M.; Tian, H.; Ma, Y. Thermodynamic performance assessment of carbon dioxide blends with low-global warming potential (GWP) working fluids for a heat pump water heater. Int. J. Refrig. 2015, 56, 1–14. [Google Scholar] [CrossRef]
- Dimian, A.C.; Bildea, C.S.; Kiss, A.A. Chapter 13—Pinch Point Analysis. Comput. Aided Chem. Eng. 2014, 35, 525–564. [Google Scholar]
- Duran, M.A.; Grossmann, I.E. Simultaneous optimization and heat integration of chemical processes. AIChE J. 1986, 32, 123–138. [Google Scholar] [CrossRef]
- Elbel, S.; Hrnjak, P. Experimental validation of a prototype ejector designed to reduce throttling losses encountered in transcritical R744 system operation. Int. J. Refrig. 2008, 31, 411–422. [Google Scholar] [CrossRef]
- Eldeeb, R.; Aute, V.; Radermacher, R. A survey of correlations for heat transfer and pressure drop for evaporation and condensation in plate heat exchangers. Int. J. Refrig. 2016, 65, 12–26. [Google Scholar] [CrossRef]
- Elias, A.M.; Giordano, R.d.C.; Secchi, A.R.; Furlan, F.F. Integrating pinch analysis and process simulation within equa-tion-oriented simulators. Comput. Chem. Eng. 2019, 130, 106555. [Google Scholar] [CrossRef]
- Fu, C.; Gundersen, T. Heat and work integration: Fundamental insights and applications to carbon dioxide capture processes. Energy Convers. Manag. 2016, 121, 36–48. [Google Scholar] [CrossRef]
- Gao, K.; Wu, J.; Bell, I.; Lemmon, E. Thermodynamic properties of ammonia for temperatures from the melting line to 725 K and pressures to 1000 MPa. J. Phys. Chem. Ref. Data 2020. [Google Scholar]
- Hansen, P.C. Discrete Inverse Problems: Insight and Algorithms; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2010. [Google Scholar]
- Hesthaven, J.S.; Gottlieb, S.; Gottlieb, D. Spectral Methods for Time-Dependent Problems; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Kemp, I.C. Preface. In Pinch Analysis and Process Integration, 2nd ed.; Butter-worth-Heinemann: Oxford, UK, 2007; pp. xiv–xv. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995. [Google Scholar]
- Kim, S.Y.; Bagajewicz, M. Global optimization of heat exchanger networks using a new generalized superstruc-ture. Chem. Eng. Sci. 2016, 147, 30–46. [Google Scholar] [CrossRef]
- Kim, Y.; Lim, J.; Shim, J.Y.; Hong, S.; Lee, H.; Cho, H. Optimization of Heat Exchanger Network via Pinch Analysis in Heat Pump-Assisted Textile Industry Wastewater Heat Recovery System. Energies 2022, 15, 3090. [Google Scholar] [CrossRef]
- Kruzel, M.; Bohdal, T.; Dutkowski, K.; Wołosz, K.J.; Robakowski, G. The Heat Transfer Coefficient During Pool Boiling of Refrigerants in a Compact Heat Exchanger. Energies 2025, 18, 4030. [Google Scholar] [CrossRef]
- Lemmon, E.W.; McLinden, M.O.; Wagner, W. Thermodynamic Properties of Propane. III. A Reference Equation of State for Temperatures from the Melting Line to 650 K and Pressures up to 1000 MPa. J. Chem. Eng. Data 2009, 54, 3141–3180. [Google Scholar] [CrossRef]
- Levy, S. Genetic Algorithms in Search Optimization and Machine Learning; New Whole Earth LLC: Chicago, IL, USA, 1991; 126p. [Google Scholar]
- Longo, G.A.; Righetti, G.; Zilio, C. A new computational procedure for refrigerant condensation inside herringbone-type Brazed Plate Heat Exchangers. Int. J. Heat Mass Transf. 2015, 82, 530–536. [Google Scholar] [CrossRef]
- Matlab. 9.8.0.1323502 (R2020a), The MathWorks Inc.: Natick, MS, USA, 2020.
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Powell, M.J.D. A Fast Algorithm for Nonlinearly Constrained Optimization Calculations; Springer: Berlin/Heidelberg, Germany, 2006; pp. 144–157. [Google Scholar]
- Rao, R.V.; Saroj, A.; Ocloń, P.; Taler, J. Design Optimization of Heat Exchangers with Advanced Optimization Techniques: A Review. Arch. Comput. Methods Eng. 2019, 27, 517–548. [Google Scholar] [CrossRef]
- Ren, C.; Song, Q.; Sun, S.; Zhang, C.; Wang, D. Experimental Study on Flow Boiling Heat Transfer of Zeotropic Mixture R290/R601a in a Mini-Channel. Energies 2025, 18, 2074. [Google Scholar] [CrossRef]
- Shampine, L. Vectorized adaptive quadrature in MATLAB. J. Comput. Appl. Math. 2008, 211, 131–140. [Google Scholar] [CrossRef]
- Shanno, D.F. Conditioning of Quasi-Newton Methods for Function Minimization. Math. Comput. 1970, 24, 647–656. [Google Scholar] [CrossRef]
- Span, R.; Wagner, W. A New Equation of State for Carbon Dioxide Covering the Fluid Region from the Triple-Point Temperature to 1100 K at Pressures up to 800 MPa. J. Phys. Chem. Ref. Data 1996, 25, 1509–1596. [Google Scholar] [CrossRef]
- Spellucci, P. A new technique for inconsistent QP problems in the SQP method. Math. Methods Oper. Res. 1998, 47, 355–400. [Google Scholar] [CrossRef]
- Szymczak, P.; Jasiński, P.B.; Łęcki, M. Numerical Study of the Condenser of a Small CO2 Refrigeration Unit Operating Under Supercritical Conditions. Energies 2025, 18, 2992. [Google Scholar] [CrossRef]
- Tillner-Roth, R.; Baehr, H.D. An International Standard Formulation for the Thermodynamic Properties of 1,1,1,2-Tetrafluoroethane (HFC-134a) for Temperatures from 170 K to 455 K and Pressures up to 70 MPa. J. Phys. Chem. Ref. Data 1994, 23, 657–729. [Google Scholar] [CrossRef]
- Trefethen, L.N. Spectral Methods in Matlab; SIAM: Philadelphia, PA, USA, 2000. [Google Scholar]
- Vikse, M.; Watson, H.A.; Kim, D.; Barton, P.I.; Gundersen, T. Optimization of a dual mixed refrigerant process using a nonsmooth approach. Energy 2020, 196, 116999. [Google Scholar] [CrossRef]
- Kumar, D.V.; Vijayaraghavan, S.; Thakur, P. Analytical and experimental investigation on heat transfer and flow parameters of Multichannel louvered fin cross flow heat exchanger using iterative LMTD and ∊-NTU method. Mater. Today Proc. 2022, 52, 1240–1248. [Google Scholar] [CrossRef]
- Watson, H.A.J.; Khan, K.A.; Barton, P.I. Multistream heat exchanger modeling and design. AIChE J. 2015, 61, 3390–3403. [Google Scholar] [CrossRef]

| Initial Guess
| LB | UB | |||
|---|---|---|---|---|---|
| T1 | T1 | T8 | 273.15 K (1 − 0.01 (0.5 − rand)) | 0 K | 500 K |
| T3 | T3 | T3 | 223.15 K (1 − 0.01 (0.5 − rand)) | 0 K | 500 K |
| p2 | p2 | p2 | 95 bar (1 − 0.01 (0.5 − rand)) | 1 bar | 1000 bar |
| - | T1* | - | 15 °C (1 − 0.01 (0.5 − rand)) | 1 × 10−6 °C | 100 °C |
| - | - | pr | 4 (1 − 0.01 (0.5 − rand)) | 1 | 45 |
| Case 1 (R) | Case 2 (R) | Case 3 (R) | Case 4 (R) | Case 5 (R) | Case 6 (R) | |
|---|---|---|---|---|---|---|
| Heat pump | A | B | C | A | B | C |
| 70 °C | 70 °C | 70 °C | 35 °C | 35 °C | 35 °C |
| Heat Pump | Inputs Process Scheme | Inputs Optimization Scheme |
|---|---|---|
| A | , , , , , , , , and | and |
| B | , , , , , , , , , and | and |
| C | , , , , , , , ,, | , and |
| Heat Pump | Outputs Process Scheme | Outputs Optimization Scheme |
|---|---|---|
| A | , , and COP | and |
| B | , ,, and COP | and |
| C | , , , and COP | and |
| Heat Pump | COP Error Less Than | Best Optimization Scheme | |
|---|---|---|---|
| Optimization Algorithm | Grid Size | ||
| A | 1.00% | Fmincon(interior) | |
| B | 1.00% | Fmincon(interior,forward) | |
| C | 1.00% | Fmincon(interior,forward) | |
| A | 0.01% | Fmincon(interior) | |
| B | 0.01% | Fmincon(interior,forward) | |
| C | 0.01% | Fmincon(interior) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brodal, E. Heat Pump Optimization—Comparative Study of Different Optimization Algorithms and Heat Exchanger Area Approximations. Energies 2025, 18, 5270. https://doi.org/10.3390/en18195270
Brodal E. Heat Pump Optimization—Comparative Study of Different Optimization Algorithms and Heat Exchanger Area Approximations. Energies. 2025; 18(19):5270. https://doi.org/10.3390/en18195270
Chicago/Turabian StyleBrodal, Eivind. 2025. "Heat Pump Optimization—Comparative Study of Different Optimization Algorithms and Heat Exchanger Area Approximations" Energies 18, no. 19: 5270. https://doi.org/10.3390/en18195270
APA StyleBrodal, E. (2025). Heat Pump Optimization—Comparative Study of Different Optimization Algorithms and Heat Exchanger Area Approximations. Energies, 18(19), 5270. https://doi.org/10.3390/en18195270






