Multi-Parameter Optimization Design of the Impeller for a Hydrogen Liquefaction Turbine Expander
Abstract
1. Introduction
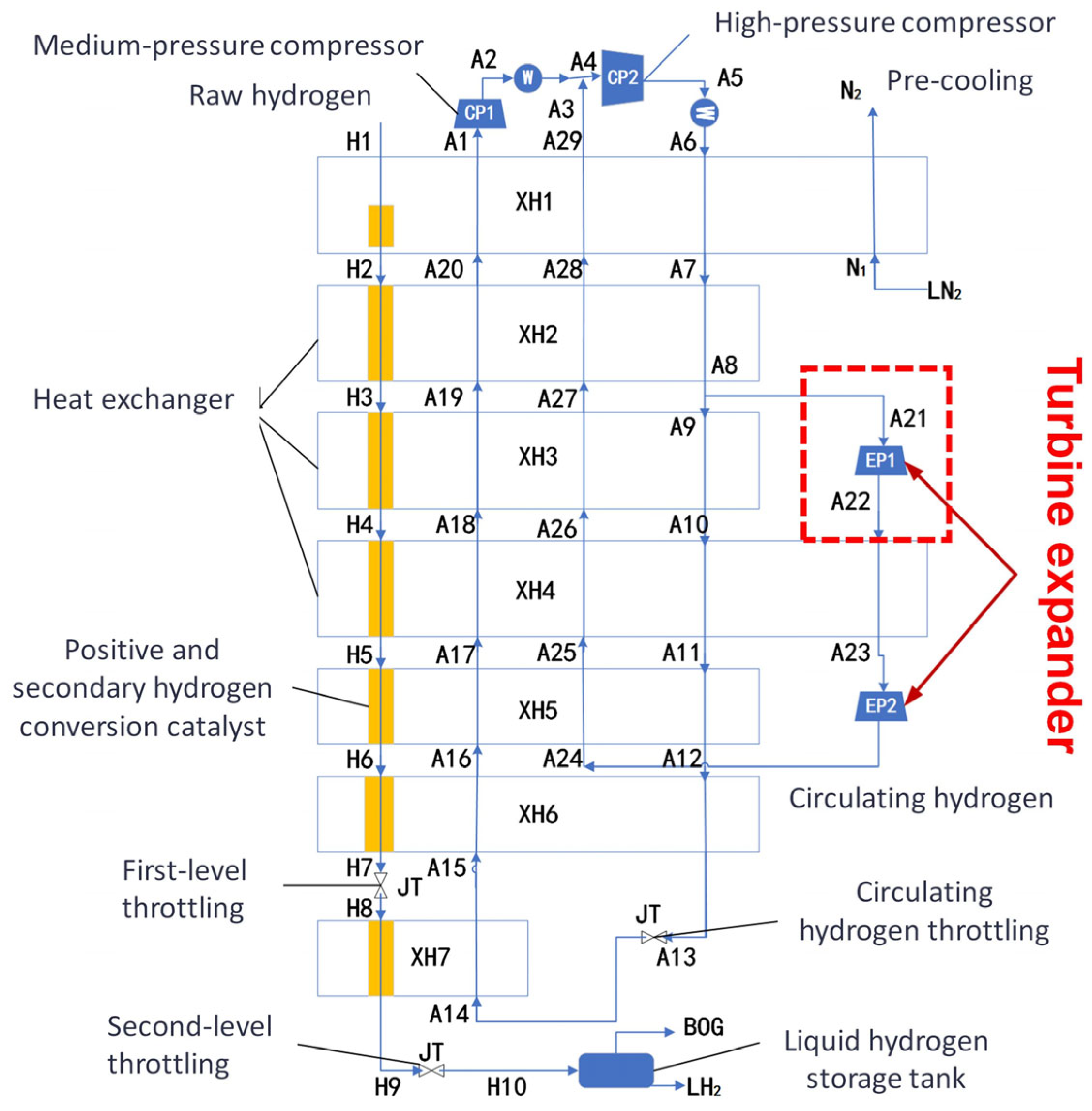
2. The Design of the Turbine Expander Impeller
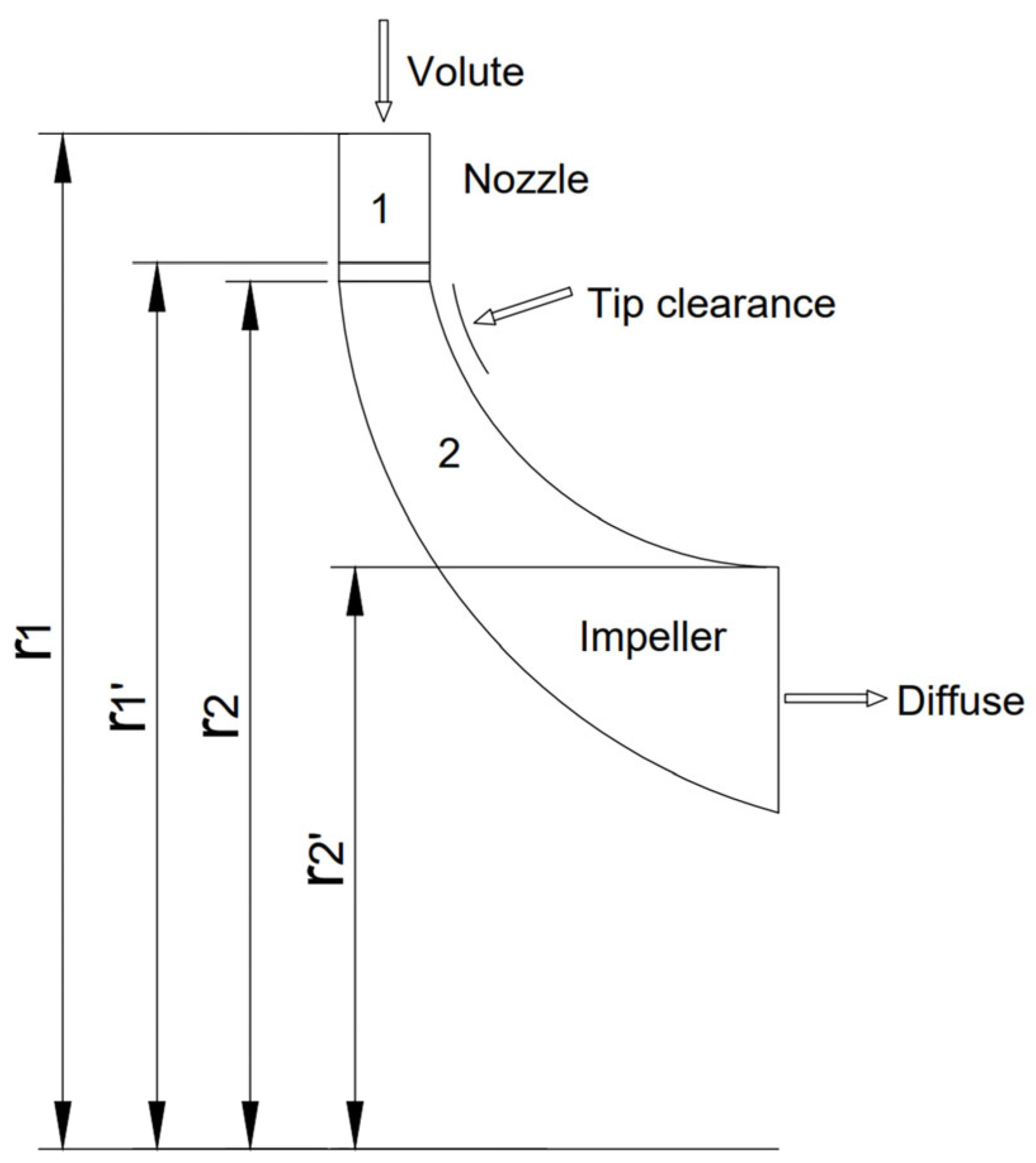
2.1. Calculation of Dimensional Parameters for Turbine Expander Impeller
2.2. Modeling and Simulation
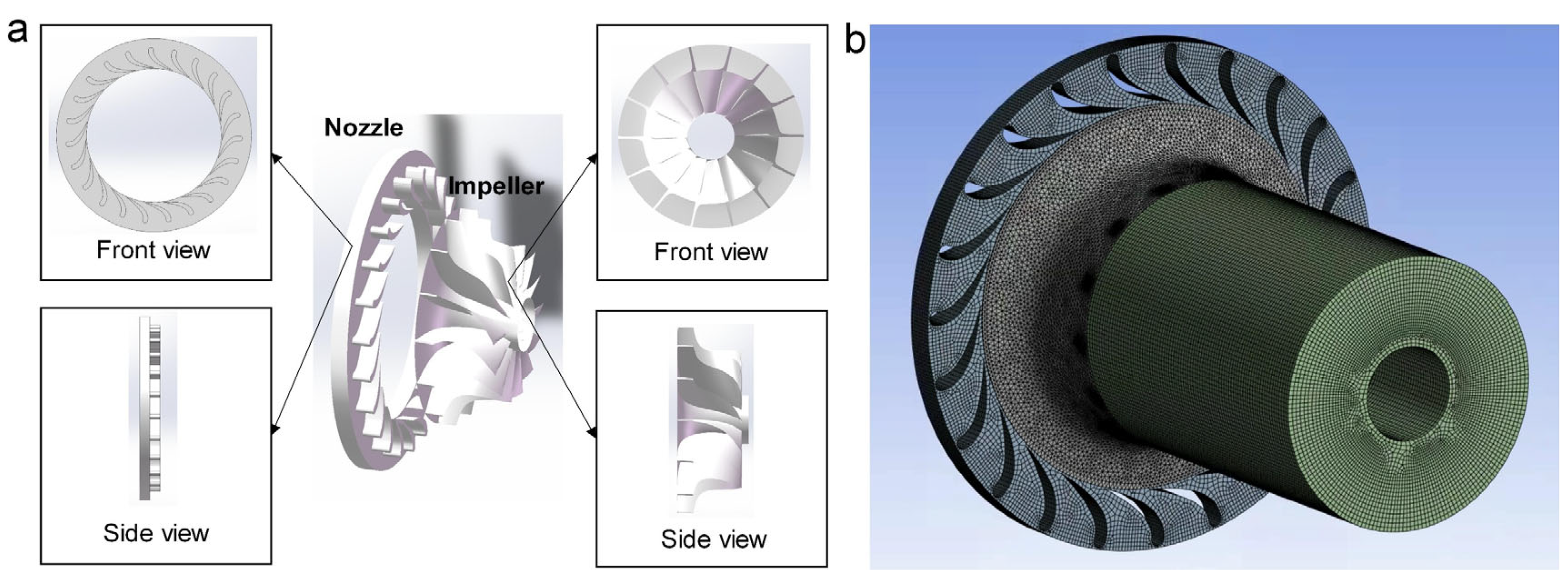
2.2.1. Modeling of the Nozzle and Impeller
2.2.2. Control Equations and Turbulence Models
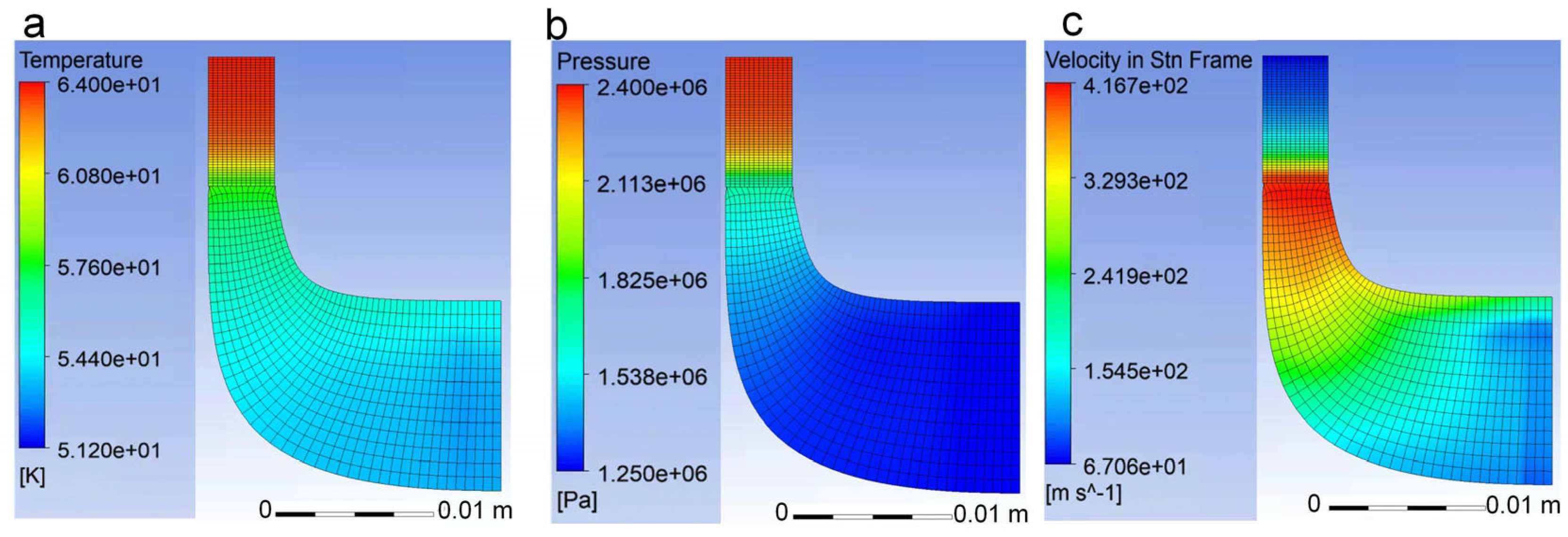
2.2.3. Model Validation
3. Result and Discussion
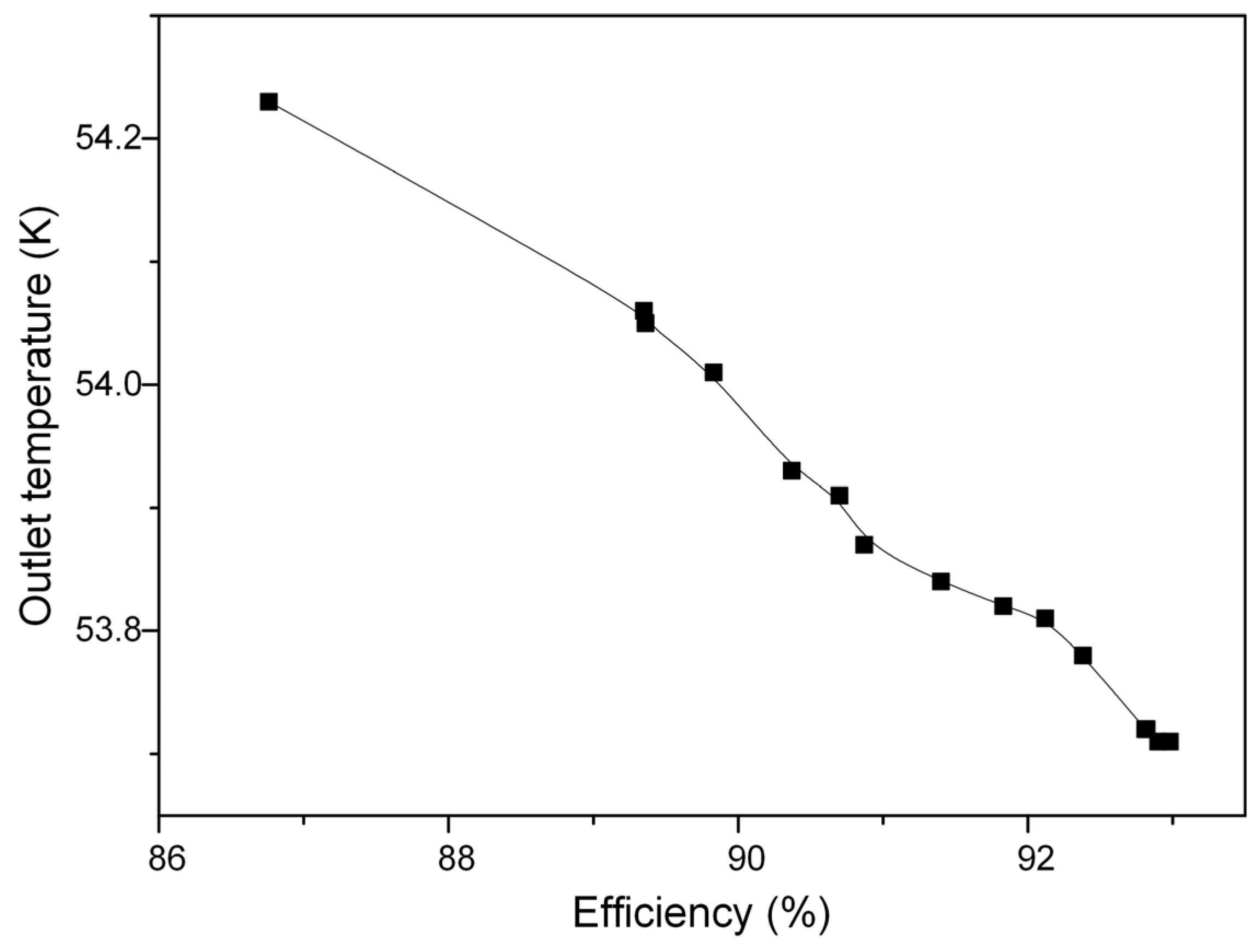
3.1. Simulation Results of Turbine Expanders Under Different One-Dimensional Design Parameter
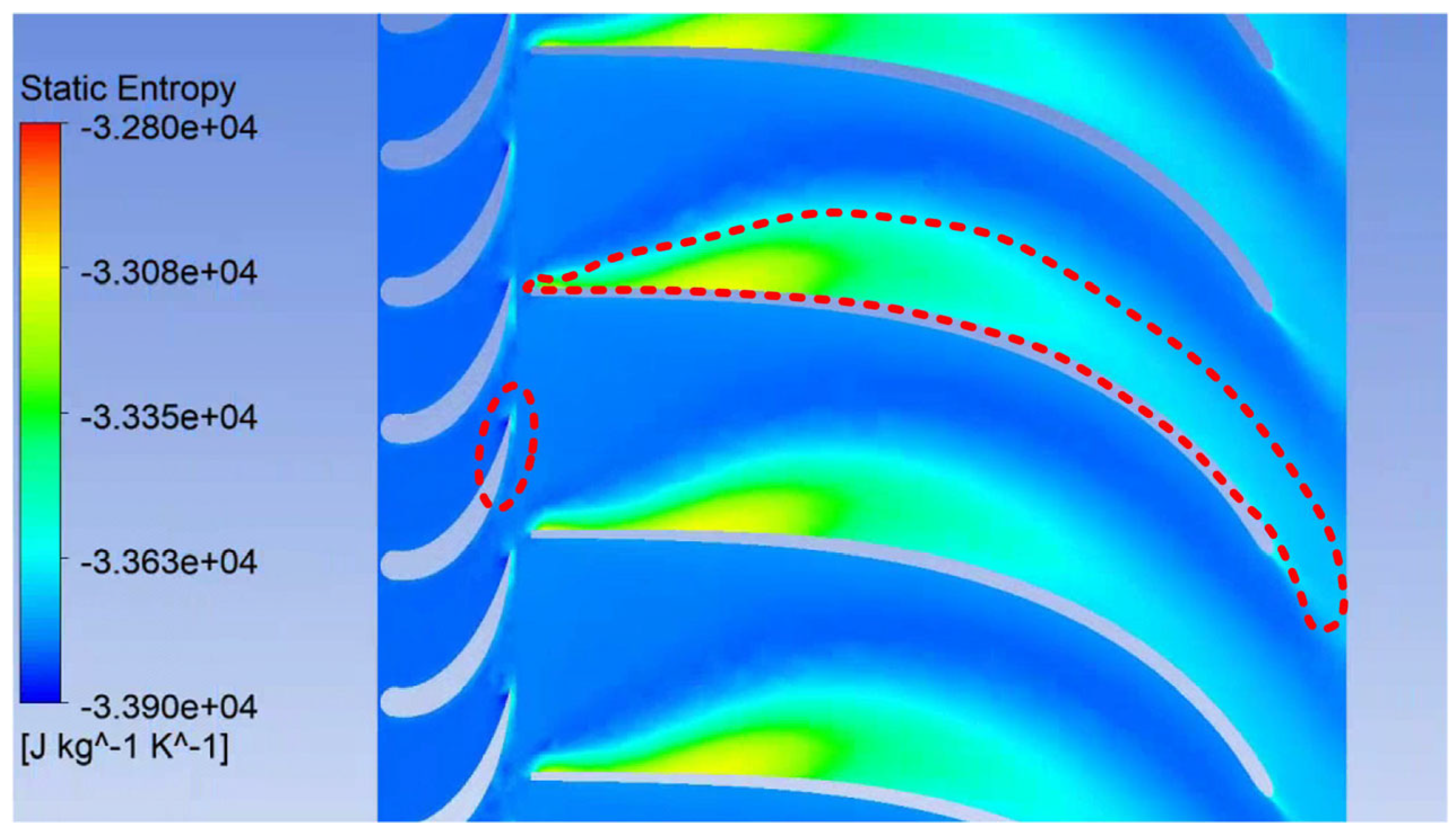
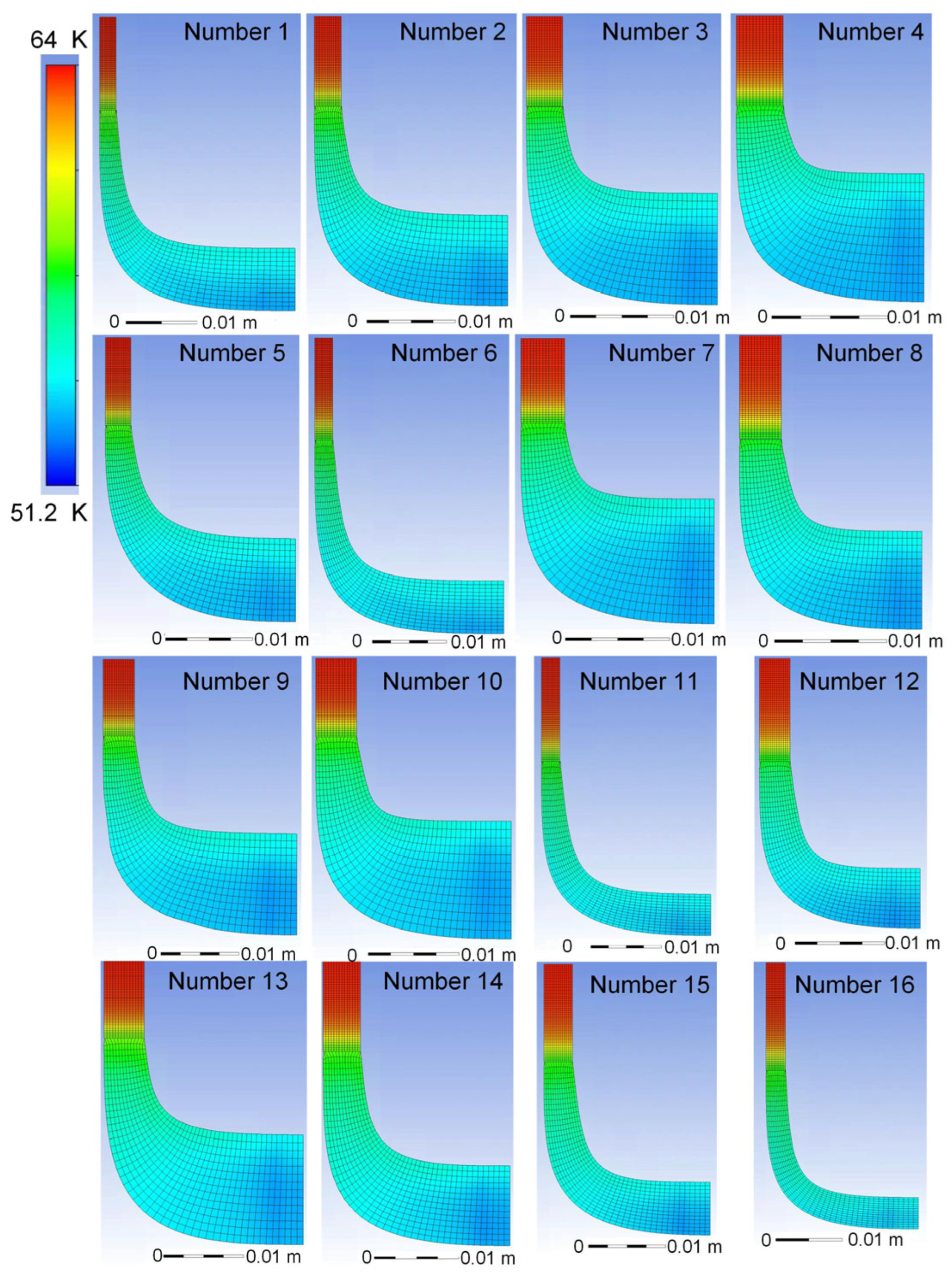
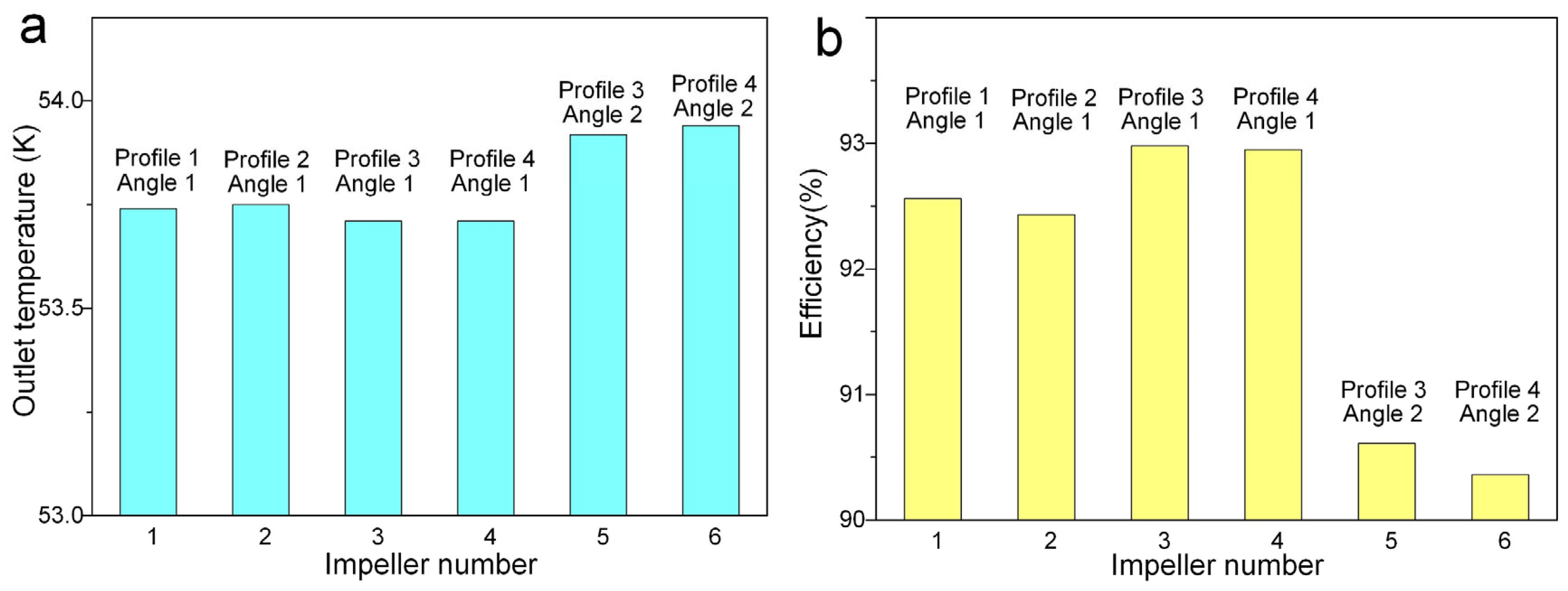
3.2. Analysis of the Influence of Meridional Profile on the Performance of Expander Impellers
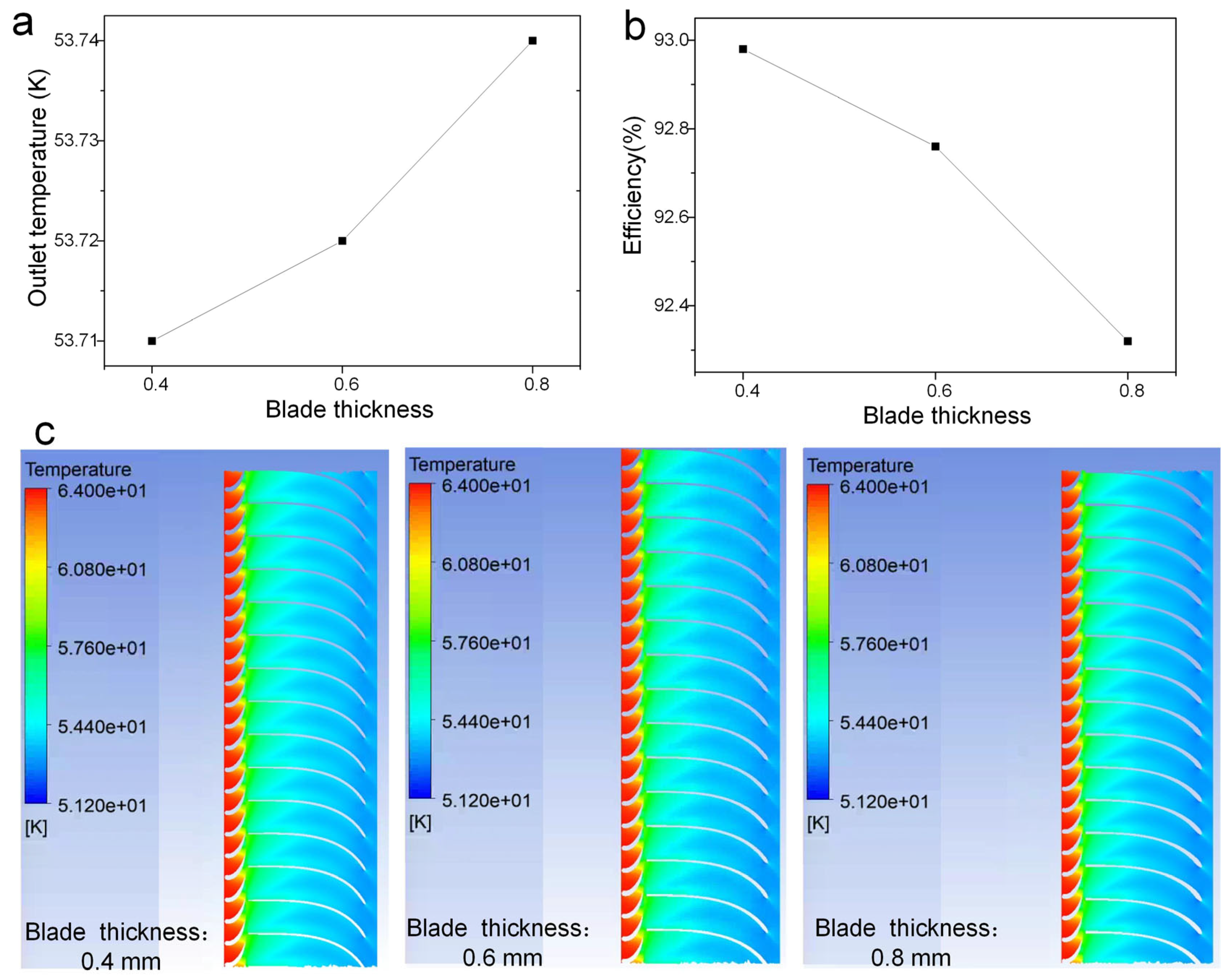
3.3. Analysis of the Influence of Blade Parameters on the Performance of Expander Impellers
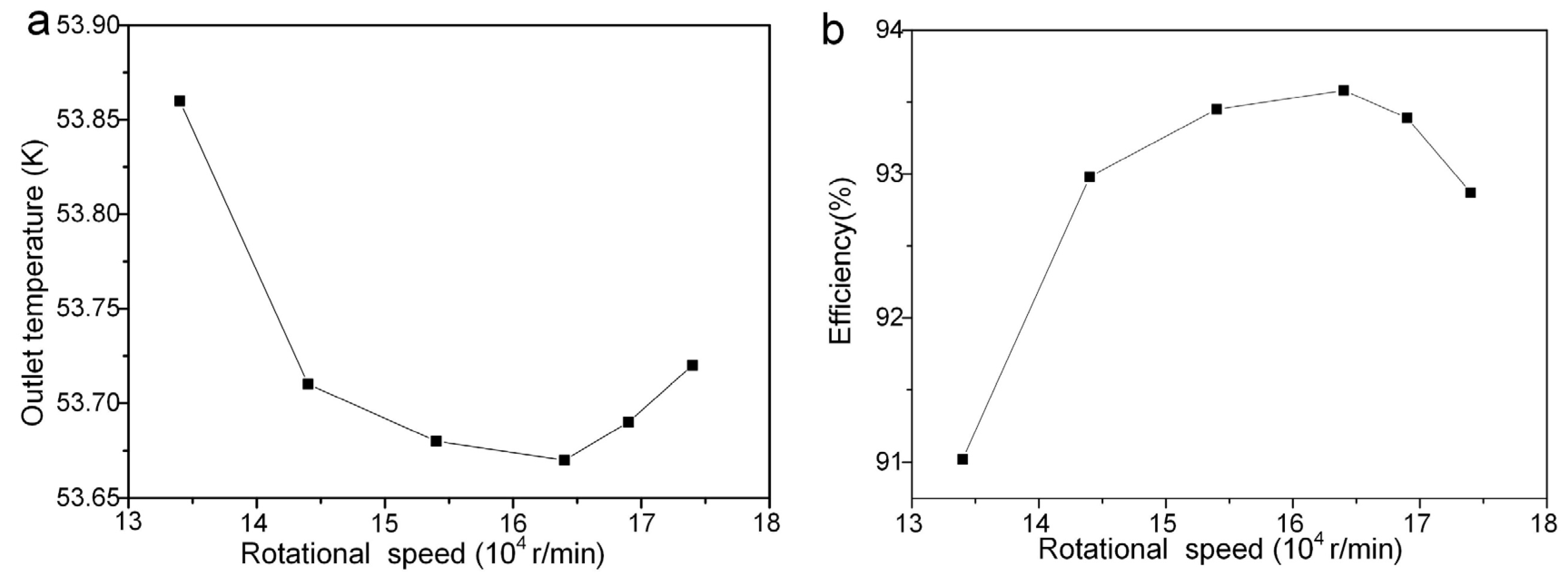
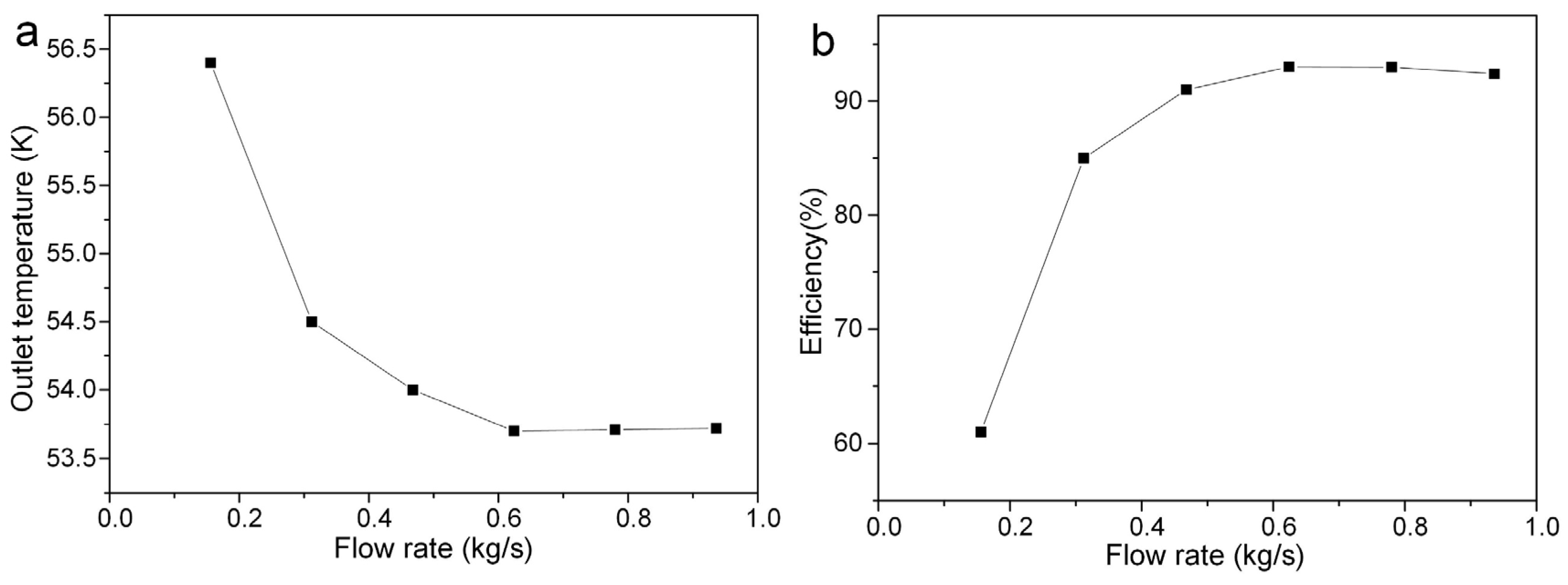
3.4. Analysis of the Influence of Operating Parameters Such as Rotational Speed and Flow Rate on the Performance of Expander Impellers
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, S.H.; Qiu, C.X.; Shen, Y.W.; Tao, X.; Gan, Z.H. Thermodynamic and economic analysis of new coupling processes with large-scale hydrogen liquefaction process and liquid air energy storage. Energy 2024, 286, 129563. [Google Scholar] [CrossRef]
- Faye, O.; Szpunar, J.A. An Efficient Way To Suppress the Competition between Adsorption of H2 and Desorption of nH2–Nb Complex from Graphene Sheet: A Promising Approach to H2 Storage. J. Phys. Chem. C 2018, 122, 28506–28517. [Google Scholar] [CrossRef]
- Zheng, J.P.; Chen, L.B.; Wang, J.; Xi, X.T.; Zhu, H.L.; Zhou, Y.; Wang, J.J. Thermodynamic analysis and comparison of four insulation schemes for liquid hydrogen storage tank. Energy Convers. Manag. 2019, 186, 526–534. [Google Scholar] [CrossRef]
- Teng, J.J.; Wang, K.; Zhu, S.L.; Bao, S.R.; Zhi, X.Q.; Zhang, X.B.; Qiu, L.M. Comparative study on thermodynamic performance of hydrogen liquefaction processes with various ortho-para hydrogen conversion methods. Energy 2023, 271, 127016. [Google Scholar] [CrossRef]
- Chang, H.M.; Ryu, K.N.; Baik, J.H. Thermodynamic design of hydrogen liquefaction systems with helium or neon Brayton refrigerator. Cryogenics 2018, 91, 68–76. [Google Scholar] [CrossRef]
- Asadnia, M.; Mehrpooya, M. A novel hydrogen liquefaction process configuration with combined mixed refrigerant systems. Int. J. Hydrogen Energy 2017, 42, 15564–15585. [Google Scholar] [CrossRef]
- Zhou, K.M.; Chen, L.; Li, S.F.; Zhao, K.; Zhang, Z.; Chen, S.T.; Hou, Y. Comparative analysis of energy losses in hydrogen and helium turbo-expanders for hydrogen liquefiers. Appl. Therm. Eng. 2023, 227, 120322. [Google Scholar] [CrossRef]
- Zhu, Z.C.; Lou, S.M.; Zhang, Y.M.; An, L.L.; Liu, Y.; Li, X.J. The design and research of two-stage series-connected helium turbine expanders for hydrogen liquefaction system. Appl. Therm. Eng. 2024, 249, 123396. [Google Scholar] [CrossRef]
- Yang, J.; Li, Y.Z.; Tan, H.B. Study on Performance Comparison of Two Hydrogen Liquefaction Processes Based on the Claude Cycle and the Brayton Refrigeration Cycle. Processes 2023, 11, 932. [Google Scholar] [CrossRef]
- Zhou, K.M.; Zhao, K.; Chen, L.; Zhang, Z.; Deng, K.Y.; Chen, S.T.; Hou, Y. High-efficiency control strategies of a hydrogen turbo-expander for a 5 t/d hydrogen liquefier. Energy 2024, 297, 131326. [Google Scholar] [CrossRef]
- Aasadnia, M.; Mehrpooya, M. Large-scale liquid hydrogen production methods and approaches: A review. Appl. Energy 2018, 212, 57–83. [Google Scholar] [CrossRef]
- Krasae-in, S.; Stang, J.H.; Neksa, P. Development of large-scale hydrogen liquefaction processes from 1898 to 2009. Int. J. Hydrogen Energy 2010, 35, 4524–4533. [Google Scholar] [CrossRef]
- Yuksel, Y.E.; Ozturk, M.; Dincer, I. Analysis and assessment of a novel hydrogen liquefaction process. Int. J. Hydrogen Energy 2017, 42, 11429–11438. [Google Scholar] [CrossRef]
- Baker, C.R.; Shaner, R.L. A study of the efficiency of hydrogen liquefaction. Int. J. Hydrogen Energy 1978, 3, 321–334. [Google Scholar] [CrossRef]
- Bracha, M.; Lorenz, G.; Patzelt, A.; Wanner, M. Large-scale hydrogen liquefaction in Germany. Linde-Rep. Sci. Technol. 1994, 19, 53–59. [Google Scholar] [CrossRef]
- Krasae-In, S.; Stang, J.H.; Neksa, P. Simulation on a proposed large-scale liquid hydrogen plant using a multi-component refrigerant refrigeration system. Int. J. Hydrogen Energy 2010, 35, 12531–12544. [Google Scholar] [CrossRef]
- Ansarinasab, H.; Mehrpooya, M.; Mohammadi, A. Advanced exergy and exergoeconomic analyses of a hydrogen liquefaction plant equipped with mixed refrigerant system. J. Clean. Prod. 2017, 144, 248–259. [Google Scholar] [CrossRef]
- Valenti, G.; Macchi, E. Proposal of an innovative, high-efficiency, large-scale hydrogen liquefier. Int. J. Hydrogen Energy 2008, 33, 3116–3121. [Google Scholar] [CrossRef]
- Song, P.; Sun, J.J.; Wang, K. Swirling and cavitating flow suppression in a cryogenic liquid turbine expander through geometric optimization. Proc. Inst. Mech. Eng. Part A-J. Power Energy 2015, 229, 628–646. [Google Scholar] [CrossRef]
- Huang, N.; Li, Z.L.; Zhu, B.S. Cavitating Flow Suppression in the Draft Tube of a Cryogenic Turbine Expander through Runner Optimization. Processes 2020, 8, 270. [Google Scholar] [CrossRef]
- Fiaschi, D.; Manfrida, G.; Maraschiello, F. Thermo-fluid dynamics preliminary design of turbo-expanders for ORC cycles. Appl. Energy 2012, 97, 601–608. [Google Scholar] [CrossRef]
- Jumonville, J. Tutorial on Cryogenic Turboexpanders; Texas A&M University, Turbomachinery Laboratory: College Station, TX, USA, 2010; Available online: https://hdl.handle.net/1969.1/163027 (accessed on 12 September 2025).
- Persky, R.; Sauret, E. Loss models for on and off-design performance of radial inflow turbomachinery. Appl. Therm. Eng. 2019, 150, 1066–1077. [Google Scholar] [CrossRef]
- Sun, Z.; Yao, Q.; Jin, H.; Xu, Y.; Hang, W.; Chen, H.; Li, K.; Shi, L.; Gu, J.; Zhang, Q.; et al. A novel in-situ sensor calibration method for building thermal systems based on virtual samples and autoencoder. Energy 2024, 297, 131314. [Google Scholar] [CrossRef]
- Li, L.; Xu, P.; Li, Q.H.; Yin, Z.C.; Zheng, R.Y.; Wu, J.F.; Bao, J.J.; Bai, W.Y.; Qi, H.; Tan, D.P. Multi-field coupling particle flow dynamic behaviors of the microreactor and ultrasonic control method. Powder Technol. 2025, 454, 120731. [Google Scholar] [CrossRef]
- Wang, H.; Yang, J.; Dong, X.; Guo, H.; Zhao, Y. Thermodynamic analysis and optimization of 10 t/d hydrogen liquefaction process. CIESC J. 2022, 73, 12. [Google Scholar] [CrossRef]
- Ferrario, F.; Busini, V. Statistical analysis of modelling approaches for CFD simulations of high-pressure natural gas releases. Results Eng. 2024, 21, 101770. [Google Scholar] [CrossRef]
- Menter, F.R. Review of the shear-stress transport turbulence model experience from an industrial perspective. Int. J. Comput. Fluid Dyn. 2009, 23, 305–316. [Google Scholar] [CrossRef]
- Li, X.M.; Li, J.; Pan, W.; Zou, Y.C.; Li, Q. Investigation on tip leakage flow characteristics of radial inflow micro turbine used in helium liquefying system. Int. J. Refrig. 2019, 98, 51–60. [Google Scholar] [CrossRef]
- Che, X.J.; Li, H.K.; Zhang, Z.N.; Chen, Y.B.; Cai, B.A.; Liu, K.X.; Cai, W.H. A novel optimum design method and performance analysis of cryogenic hydrogen turbo-expander for hydrogen liquefaction. Cryogenics 2025, 145, 103996. [Google Scholar] [CrossRef]
- Niu, B.; Chen, L.; Deng, K.; Wang, H.; Qu, J.; Li, S.; Zhang, Z.; Chen, S.; Hou, Y. Genetic algorithm based optimization design and coupling performance analysis of multi-stage series hydrogen turbo-expanders. Energy 2025, 335, 138128. [Google Scholar] [CrossRef]
- Zhou, K.M.; Chen, L.; Wang, H.D.; Deng, K.Y.; Zhang, Z.; Chen, S.T.; Hou, Y. Comparison of mean-line methods for hydrogen turbo-expanders in hydrogen liquefiers. Case Stud. Therm. Eng. 2024, 60, 104632. [Google Scholar] [CrossRef]
- Lim, H.; Seo, J.; Park, M.; Choi, B.; Park, J.; Bang, J.; Lee, D.; Kim, B.; Kim, S.; Lim, Y.; et al. A Numerical Study on Blade Design and Optimization of a Helium Expander for a Hydrogen Liquefaction Plant. Appl. Sci. 2022, 12, 1411. [Google Scholar] [CrossRef]
- Liu, H.M.; Zuo, J.S.; Qiu, S.; Liang, Y.W.; Ke, C.L.; Liu, L.Q.; Peng, N.; Xiong, L.Y.; Li, K.R.; Zhang, X.H. Simulative and experimental analysis of high-speed helium turbo-expanders in a 5t/day hydrogen liquefier. Int. J. Hydrogen Energy 2025, 133, 152–164. [Google Scholar] [CrossRef]






| Design Parameters | Value | Design Parameters | Value |
|---|---|---|---|
| Impeller inlet diameter D1 (mm) | 49.6 | Nozzle outlet diameter Dn (mm) | 51.7 |
| Impeller outlet outer diameter D2′ (mm) | 36.6 | Nozzle blade outer diameter D0 (mm) | 67.5 |
| Impeller outlet inter diameter D2″ (mm) | 12.6 | Nozzle height lN (mm) | 4.2 |
| Blade inlet height l1 (mm) | 4.3 | Nozzle blade outlet span tN (mm) | 7.1 |
| Blade outlet height l2 (mm) | 12 | Nozzle blade chord length b (mm) | 11.8 |
| Rotational speed (r/min) | 144,000 | Number of nozzles | 23 |
| Number of blades | 14 |
| Number | Outlet Temperature (K) | Efficiency (%) | Number | Outlet Temperature (K) | Efficiency (%) |
|---|---|---|---|---|---|
| 1 | 54.05 | 89.36 | 9 | 53.81 | 92.12 |
| 2 | 53.93 | 90.37 | 10 | 53.72 | 92.81 |
| 3 | 53.84 | 91.40 | 11 | 54.01 | 89.83 |
| 4 | 53.78 | 92.38 | 12 | 53.87 | 90.87 |
| 5 | 53.91 | 90.70 | 13 | 53.72 | 92.81 |
| 6 | 54.06 | 89.35 | 14 | 53.71 | 92.90 |
| 7 | 53.71 | 92.98 | 15 | 53.82 | 91.83 |
| 8 | 53.72 | 92.82 | 16 | 54.23 | 86.76 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Liu, P.; Cheng, H.; Zhao, Z.; Li, F.; Yang, J.; Wang, K. Multi-Parameter Optimization Design of the Impeller for a Hydrogen Liquefaction Turbine Expander. Energies 2025, 18, 5142. https://doi.org/10.3390/en18195142
Zhang X, Liu P, Cheng H, Zhao Z, Li F, Yang J, Wang K. Multi-Parameter Optimization Design of the Impeller for a Hydrogen Liquefaction Turbine Expander. Energies. 2025; 18(19):5142. https://doi.org/10.3390/en18195142
Chicago/Turabian StyleZhang, Xiaohui, Pei Liu, Hao Cheng, Zehui Zhao, Fangqiu Li, Jiayi Yang, and Ke Wang. 2025. "Multi-Parameter Optimization Design of the Impeller for a Hydrogen Liquefaction Turbine Expander" Energies 18, no. 19: 5142. https://doi.org/10.3390/en18195142
APA StyleZhang, X., Liu, P., Cheng, H., Zhao, Z., Li, F., Yang, J., & Wang, K. (2025). Multi-Parameter Optimization Design of the Impeller for a Hydrogen Liquefaction Turbine Expander. Energies, 18(19), 5142. https://doi.org/10.3390/en18195142







