McCARD/MASTER Hanbit Unit 3 Multi-Cycle Analyses with Monte Carlo-Based Reflector Cross-Section Generation
Abstract
1. Introduction
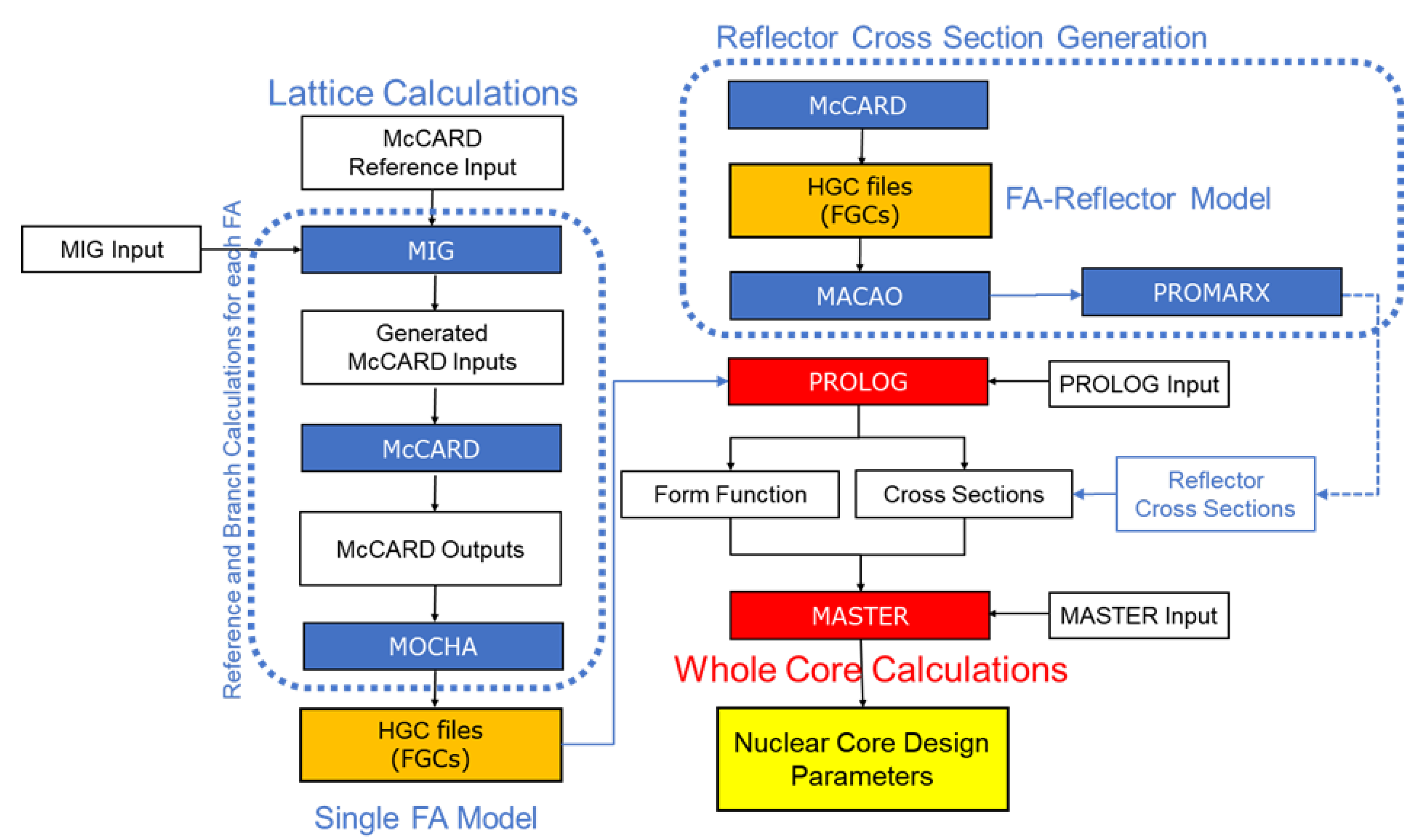
2. Monte Carlo-Based Two-Step Code System for a PWR Core Design
2.1. McCARD/MASTER Two-Step Code System
2.2. Monte Carlo Reflector Cross-Section Generation
3. McCARD/MASTER Multi-Cycle Core Analyses for Hanbit Unit 3
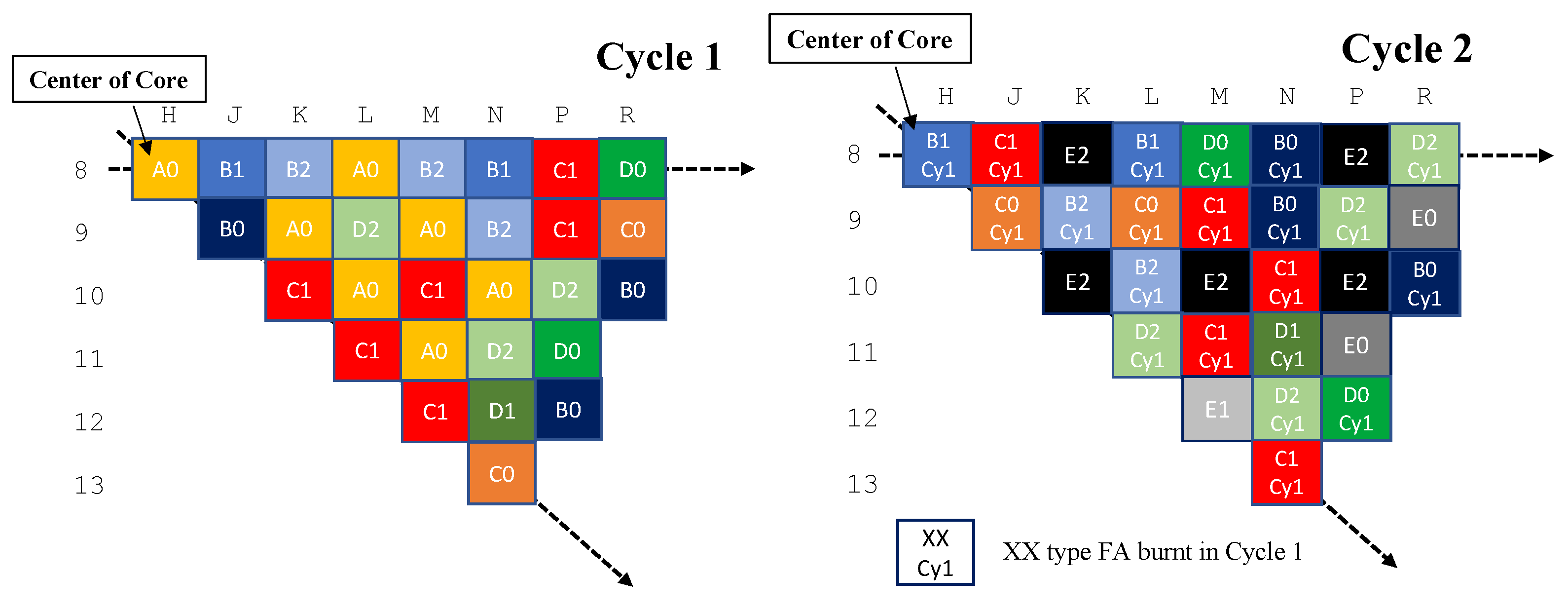
3.1. Commercial PWR Hanbit Unit 3
3.2. Few-Group Constant and Reflector Cross-Section Generation for Hanbit Unit 3
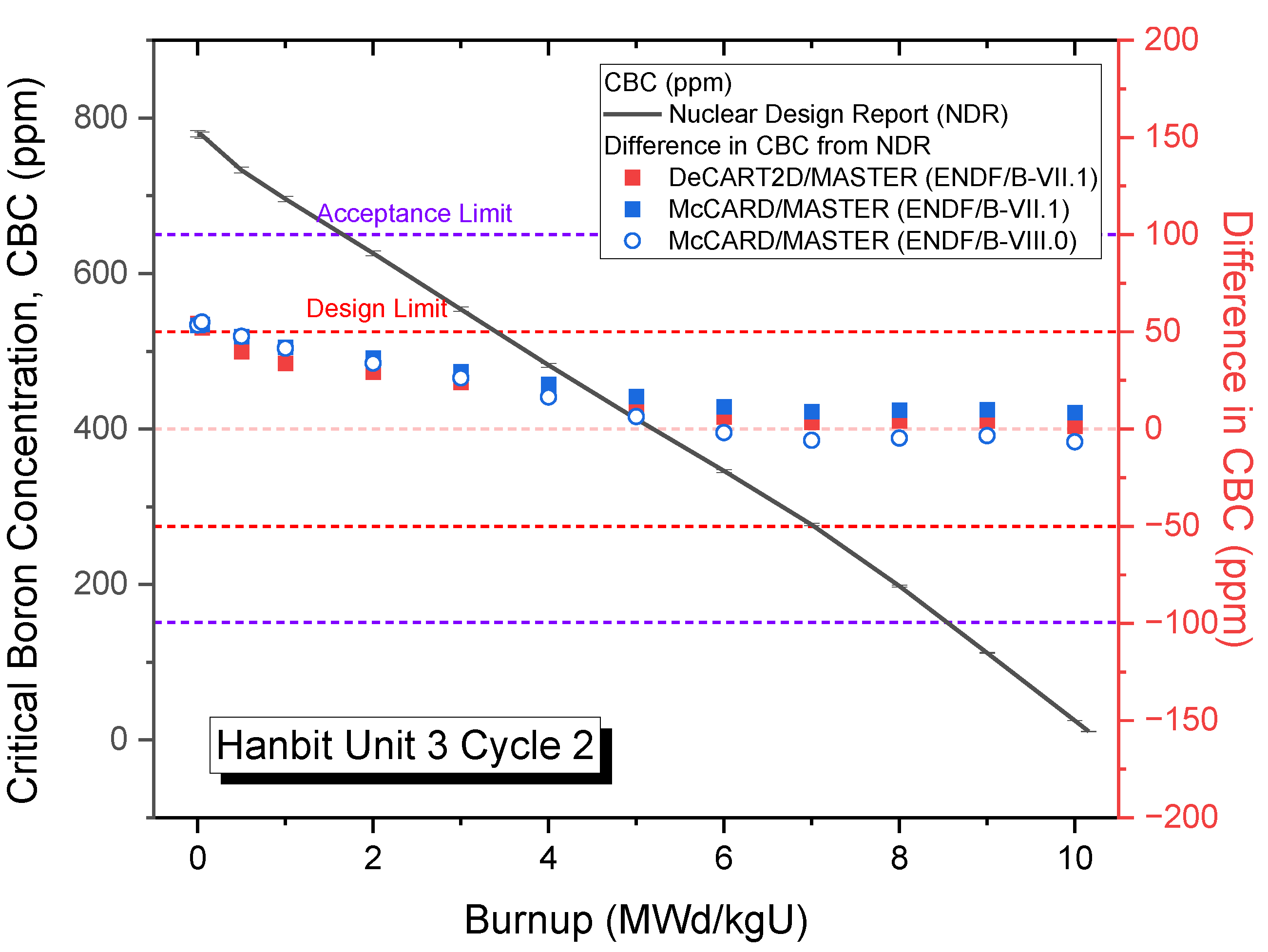
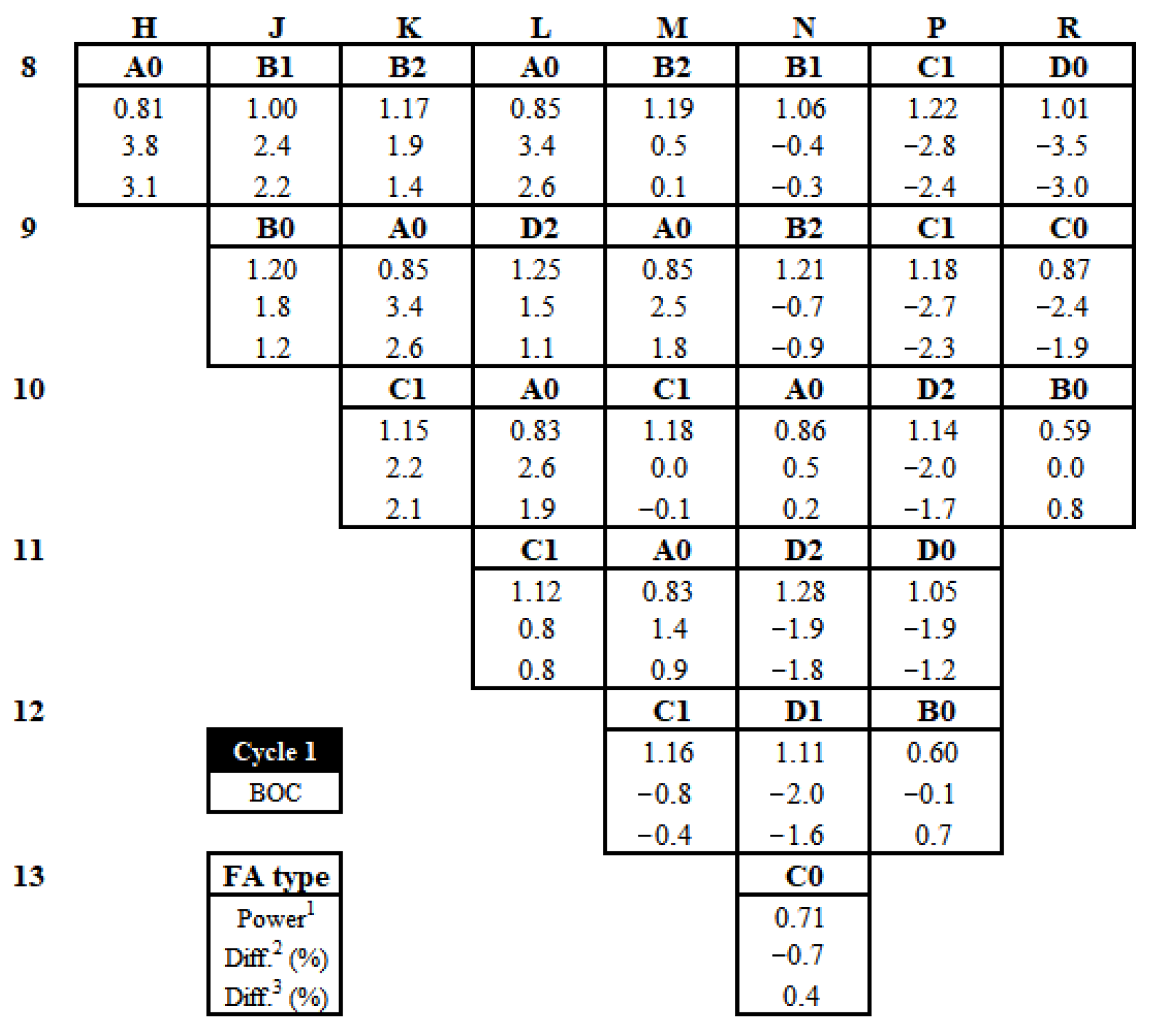
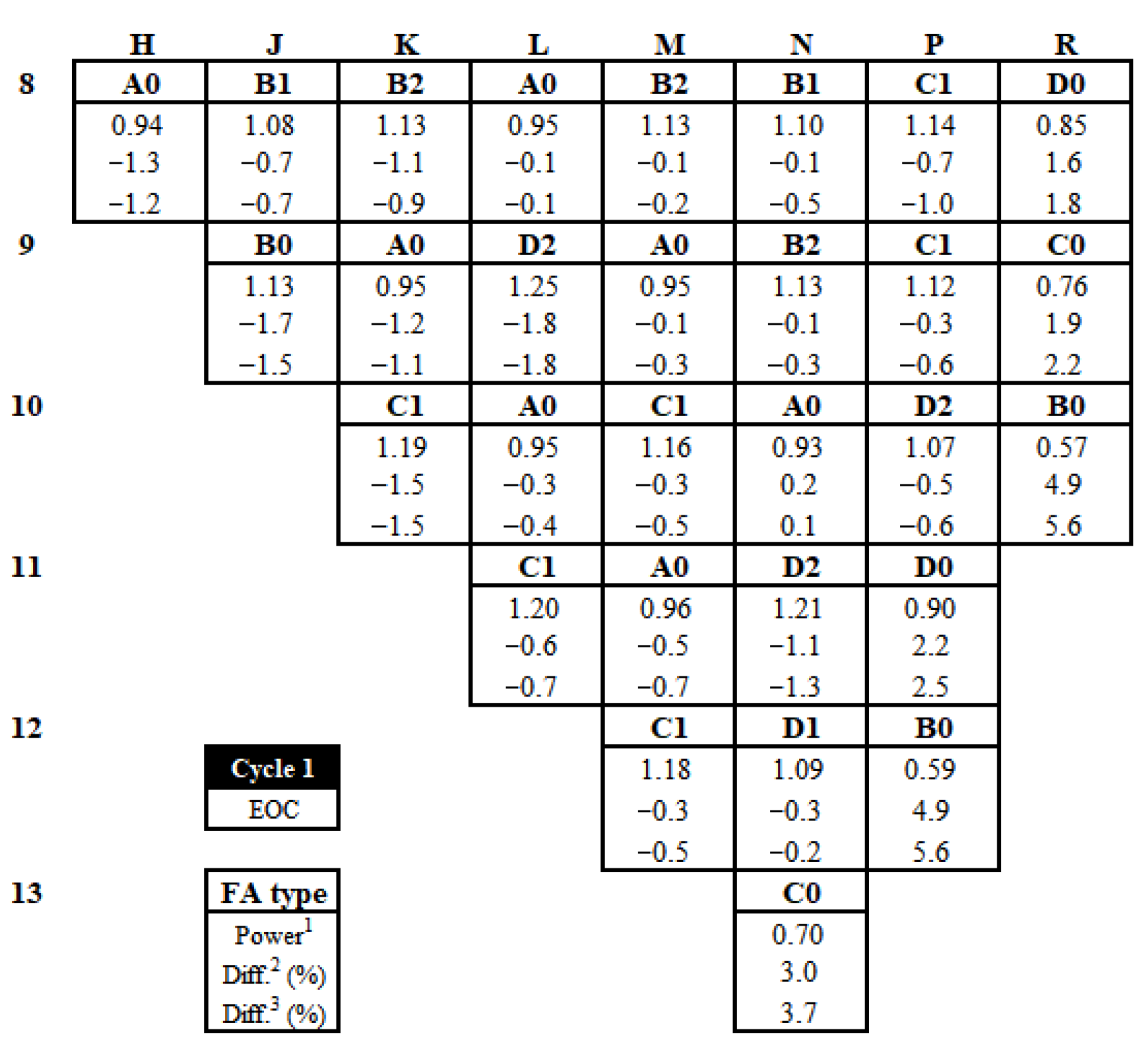
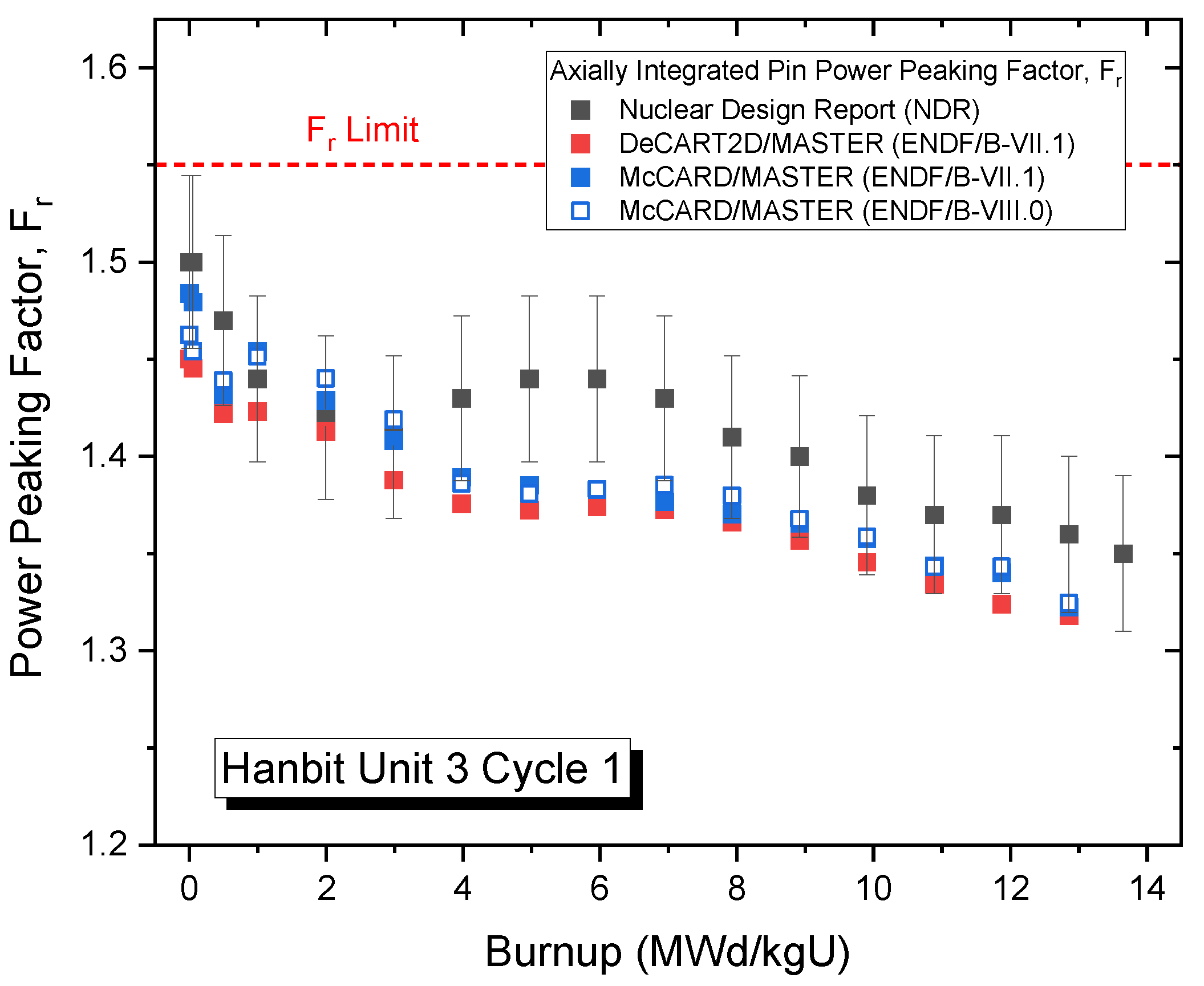
3.3. Whole-Core Analyses for Hanbit Unit 3 Cycles 1 and 2
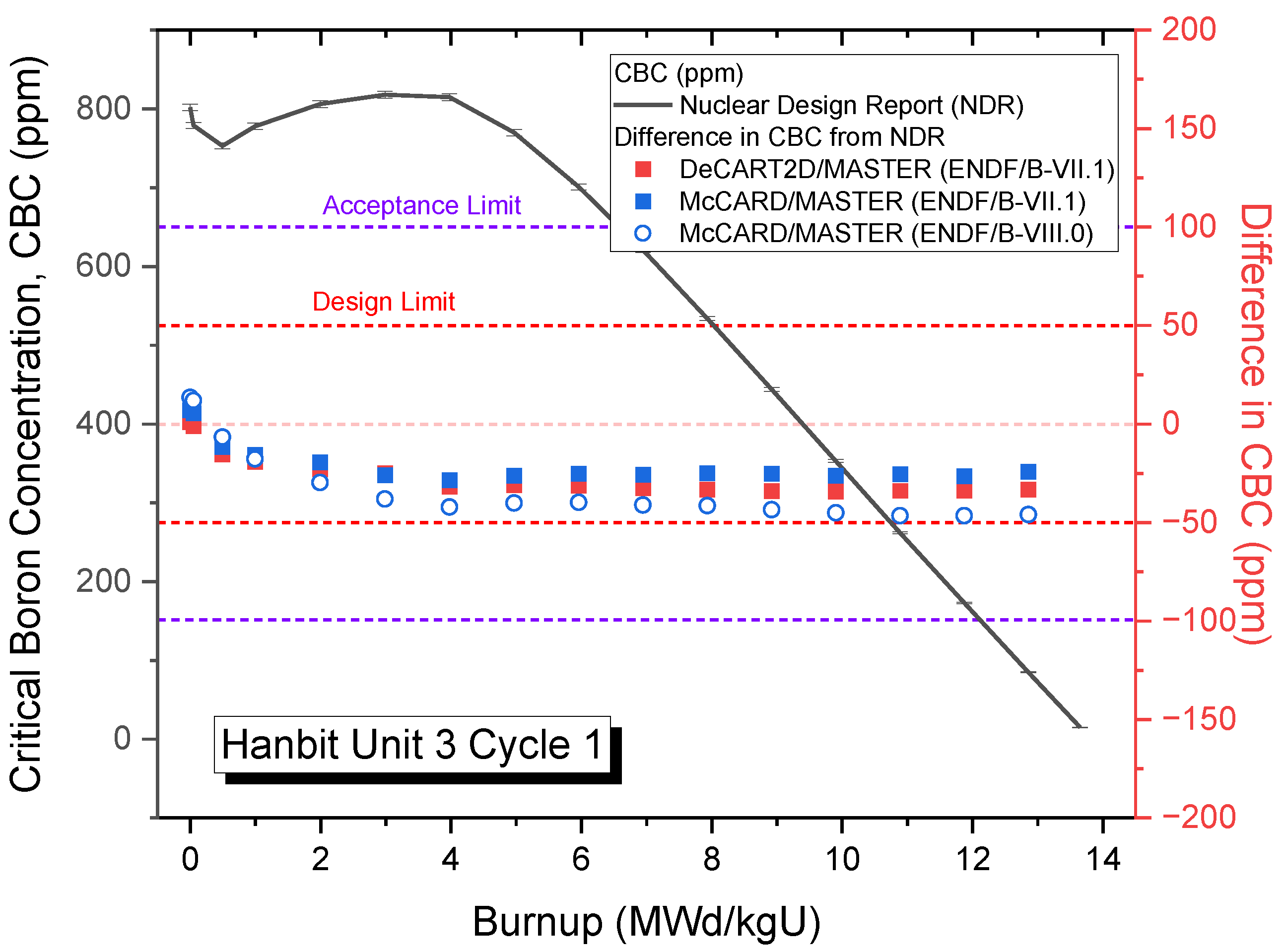
3.3.1. Critical Boron Concentrations for Hanbit Unit 3 Cycles 1 and 2
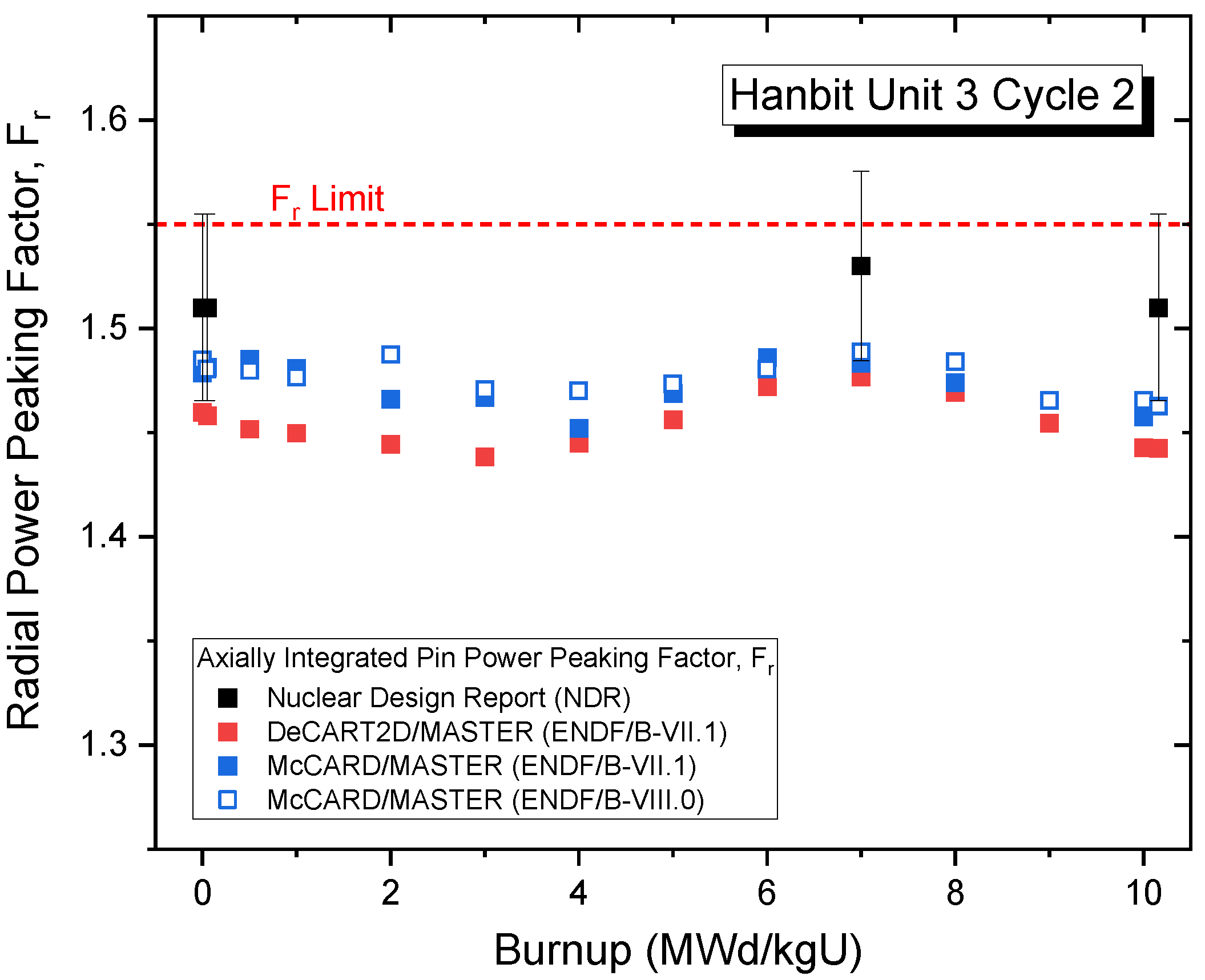
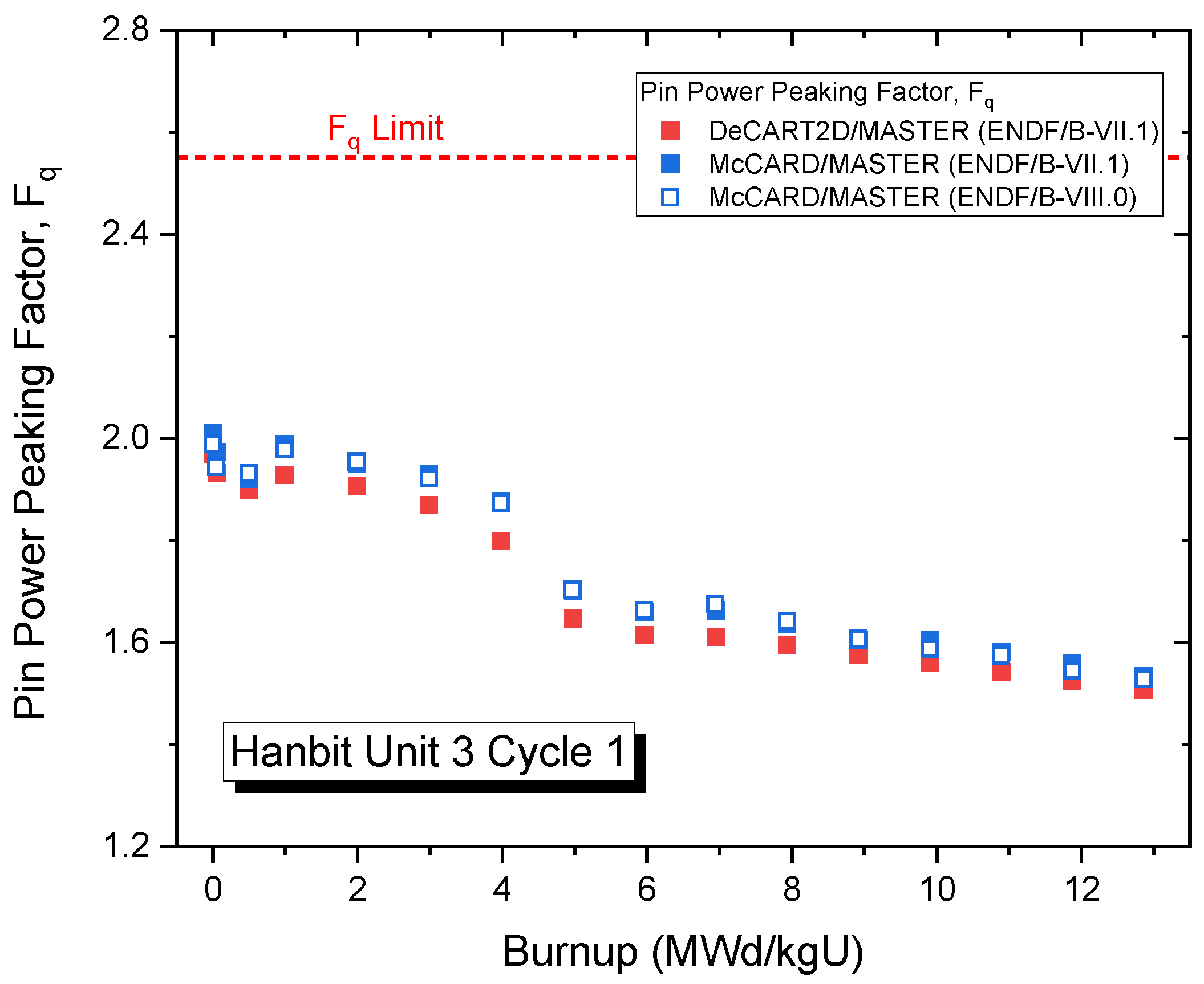
3.3.2. Power Distributions and Power-Peaking Factors for Hanbit Unit 3 Cycles 1 and 2
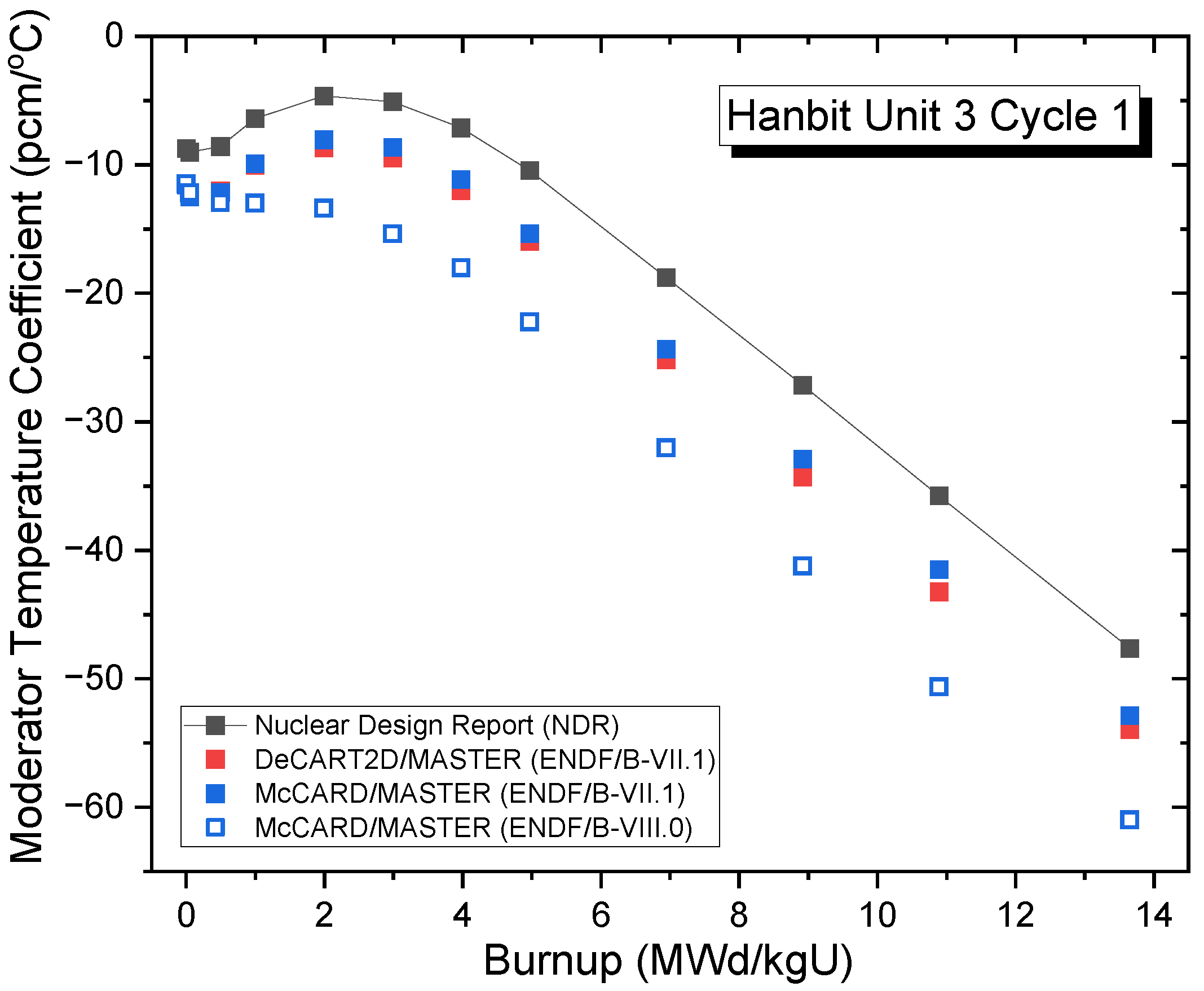
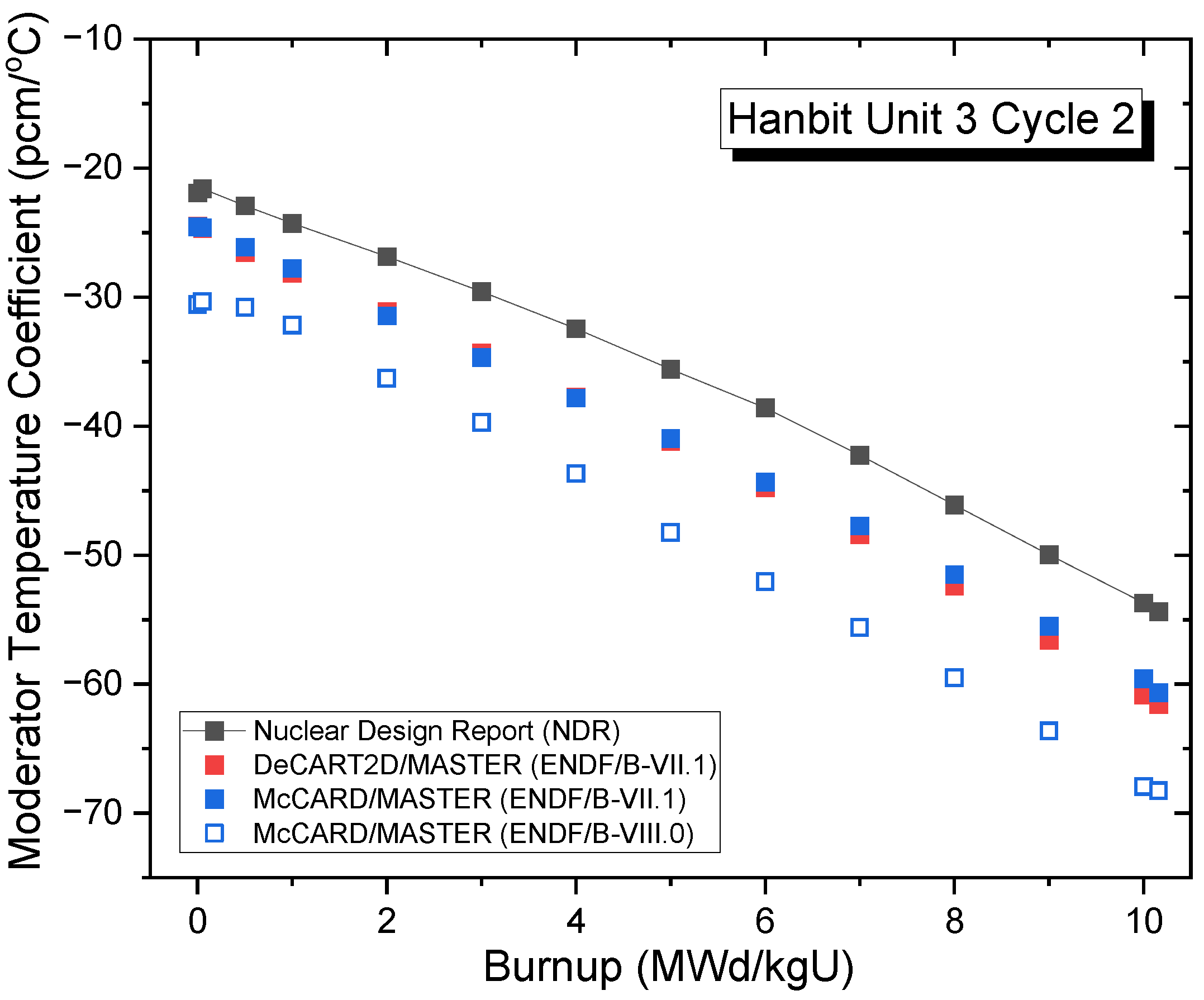
3.3.3. Temperature Coefficients for Hanbit Unit 3 Cycles 1 and 2
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ADF | Assembly discontinuity factor |
| BOC | Beginning of the cycle |
| BP | Burnable poison |
| CBC | Critical boron concentration |
| CE | Combustion engineering |
| CZP | Cold zero power |
| DF | Discontinuity factor |
| EOC | End of cycle |
| FA | Fuel assembly |
| FGC | Few-group constant |
| FTC | Fuel temperature coefficient |
| HFP | Hot full power |
| MACAO | Multi-assembly cross-section and ADF organizer |
| MC | Monte Carlo |
| MTC | Moderator temperature coefficient |
| NDR | Nuclear design report |
| PWR | Pressurized water reactor |
| RMS | Root mean square |
| SENM | Source expansion nodal method |
References
- Smith, K.S. Assembly Homogenization Techniques for Light Water Reactor Analysis. Prog. Nucl. Energy 1986, 17, 303–335. [Google Scholar] [CrossRef]
- Redmond, E.L., II. Multi-Group Cross Section Generation via Monte Carlo Method. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1997. [Google Scholar]
- Shim, H.J.; Cho, J.Y.; Song, J.S.; Kim, C.H. Generation of Few Group Diffusion Theory Constants by Monte Carlo Code. Trans. Am. Nucl. Soc. 2008, 99, 343. [Google Scholar]
- Park, H.J.; Shim, H.J.; Joo, H.G.; Kim, C.H. Generation of Few-Group Diffusion Theory Constants by Monte Carlo Code McCARD. Nucl. Sci. Eng. 2012, 172, 66–77. [Google Scholar] [CrossRef]
- Fridman, E.; Leppanen, J. On the Use of the Serpent Monte Carlo Code for Few-Group Cross Section Generation. Ann. Nucl. Energy 2010, 38, 1399–1405. [Google Scholar] [CrossRef]
- Yoo, S.Y.; Shim, H.J.; Kim, C.H. Monte Carlo Few-Group Constant Generation for CANDU 6 Core Analysis. Sci. Technol. Nucl. Install. 2015, 2015, 284642. [Google Scholar] [CrossRef]
- Nguyen, T.D.C.; Lee, H.; Lee, D. Use of Monte Carlo code MCS for multigroup cross section generation for fast reactor analysis. Nucl. Eng. Technol. 2021, 53, 2788–2802. [Google Scholar] [CrossRef]
- Shim, H.J.; Han, B.S.; Jung, J.S.; Park, H.J.; Kim, C.H. McCARD: Monte Carlo Code for Advanced Reactor Design and Analysis. Nucl. Eng. Technol. 2012, 44, 161–176. [Google Scholar] [CrossRef]
- Park, H.J.; Shim, H.J.; Joo, H.G.; Kim, C.H. Uncertainty quantification of few-group Diffusion Theory Constants Generated by the B1 Theory-Augmented Monte Carlo Method. Nucl. Sci. Eng. 2013, 175, 28–43. [Google Scholar] [CrossRef]
- Wu, Y.; Song, Q.; Feng, K.; Vidal, J.F.; Gu, H.; Guo, H. Multigroup cross-sections generated using Monte-Carlo method with flux-moment homogenization technique for fast reactor analysis. Nucl. Eng. Technol. 2023, 55, 2474–2482. [Google Scholar] [CrossRef]
- Li, J.; Seker, V.; Ward, A.; Downar, T. Uncertainty Propagation of Monte Carlo Cross-Section Generation for Graphite-Moderated Pebble Bed Reactors. Nucl. Sci. Eng. 2025, 199, 772–792. [Google Scholar] [CrossRef]
- Yoon, J.I.; Joo, H.G. Two-Level Coarse Mesh Finite Difference Formulation with Multigroup Source Expansion Nodal Kernels. J. Nucl. Sci. Technol. 2008, 45, 668–682. [Google Scholar] [PubMed]
- Cho, J.Y.; Shim, C.; Han, T.Y.; Lee, K.; Lee, C.; Song, J.S.; Park, S.Y.; Park, H.J.; Jeong, H.J.; Jo, C.K.; et al. DeCART2D v1.1 User’s Manual; KAERI/UM-40/2016; Korea Atomic Energy Research Institute: Daejeon, Republic of Korea, 2016. [Google Scholar]
- Zee, S.Q.; Lee, C.G.; Lee, C.C.; Song, J.S.; Kim, S.J.; Kim, H.Y.; Lim, C.J.; Yoo, C.S.; Baek, B.C.; Yoo, H.S.; et al. Nuclear Design Report for Yonggwang Unit 3 Cycle 1; KAERI/TR-542/95; Korea Atomic Energy Research Institute: Daejeon, Republic of Korea, 1995. [Google Scholar]
- Yoo, C.S.; Ryu, H.S.; Baek, B.C.; Park, J.H.; Cho, Y.C.; Park, S.Y.; Song, J.S. Nuclear Design Report for Yonggwang Unit 3 Cycle 2; KAERI/TR-605/96; Korea Atomic Energy Research Institute: Daejeon, Republic of Korea, 1996. [Google Scholar]
- Cho, J.Y.; Jeong, H.J.; Song, J.S.; Park, S.Y.; Lee, K.; Lee, C.; Shim, C.; Park, H.J.; Choi, Y.; Koo, B.S. MASTER v4.0 User’s Manual; KAERI/UM-41/2016; Korea Atomic Energy Research Institute: Daejeon, Republic of Korea, 2016. [Google Scholar]
- Shim, C.B.; Lee, K.H.; Cho, J.Y. Improvement of Axial Reflector Cross Section Generation Model for PWR Core Analysis. In Proceedings of the Transactions of the Korean Nuclear Society Autumn Meeting, Gyeongju, Republic of Korea, 27–28 October 2016. [Google Scholar]
- APR-1400 Design Control Document Tier 2; APR1400-K-X-FS-14002-NP. Korea Electric Power Corporation: Naju-si, Republic of Korea; Korea Hydro & Nuclear Power Co., Ltd.: Gyeongju-si, Republic of Korea, 2018.
- Park, H.J.; Kang, H.; Lee, H.C.; Cho, J.Y. Comparison of ENDF/B-VIII.0 and ENDF/B-VII.1 in Criticality, Depletion Benchmark, and Uncertainty Analyses by McCARD. Ann. Nucl. Energy 2019, 131, 443–459. [Google Scholar]
- Cabellos, O.; Castro, E.; Ahnert, C.; Holgado, C. Propagation of Nuclear Data Uncertainties for PWR Core Analysis. Nucl. Eng. Technol. 2014, 46, 299–312. [Google Scholar] [CrossRef]


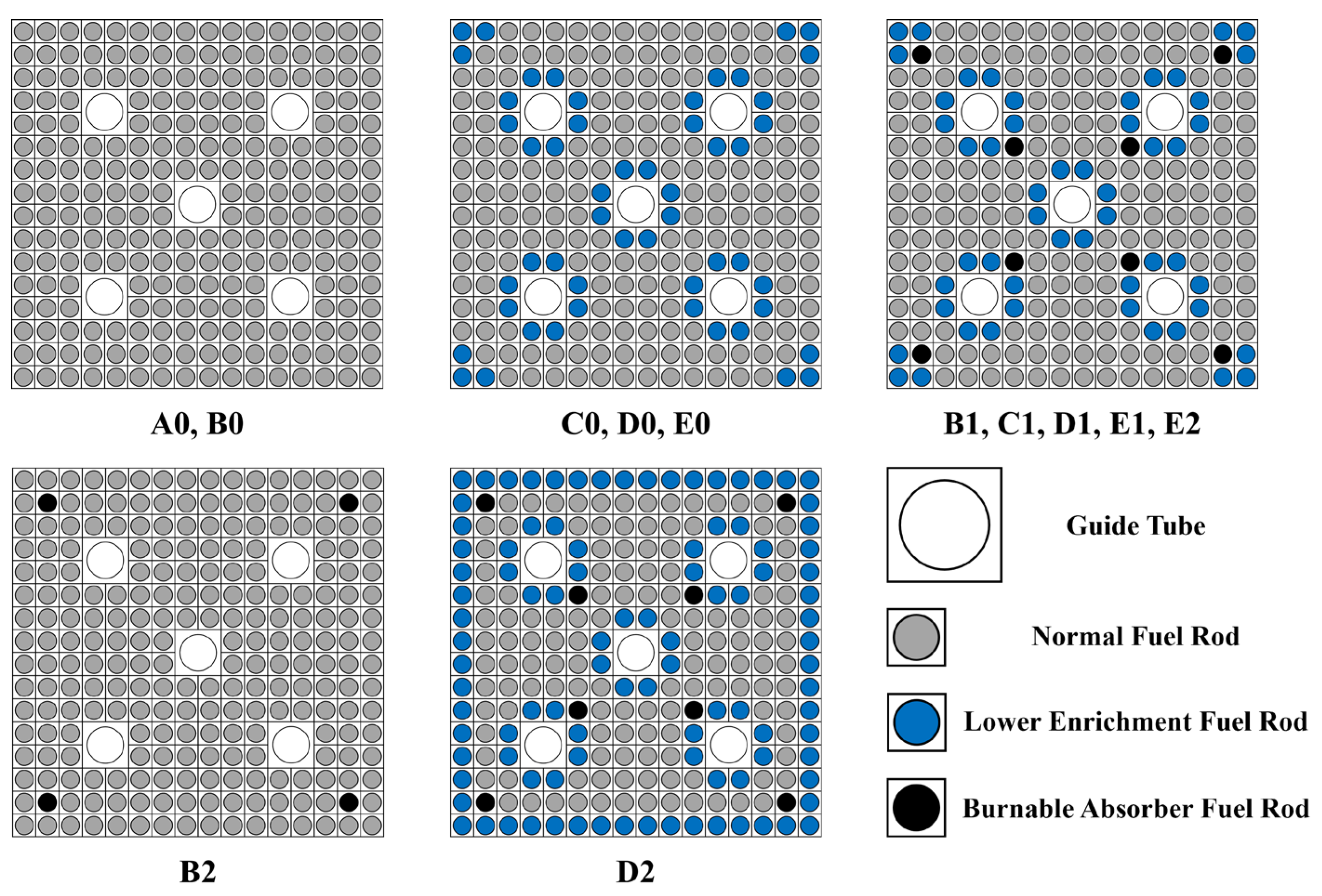







| FA Type | U-235 Enrichment (w/o) | Number of Fuel Rods | Number of BA 1 Rods | BA Content (w/o) | ||
|---|---|---|---|---|---|---|
| Normal Fuel Rod | Lower-Enrichment Fuel Rod | Normal Fuel Rod | Lower-Enrichment Fuel Rod | |||
| A0 | 1.3 | — | 236 | 0 | 0 | — |
| B0 | 2.3 | — | 236 | 0 | 0 | — |
| B1 | 2.3 | 1.3 | 176 | 52 | 8 | 4.0 |
| B2 | 2.3 | — | 232 | 0 | 4 | 4.0 |
| C0 | 2.8 | 2.3 | 184 | 52 | 0 | — |
| C1 | 2.8 | 2.3 | 176 | 52 | 8 | 4.0 |
| D0 | 3.3 | 2.8 | 184 | 52 | 0 | — |
| D1 | 3.3 | 2.8 | 176 | 52 | 8 | 4.0 |
| D2 | 3.3 | 2.8 | 128 | 100 | 8 | 4.0 |
| E0 | 4.0 | 3.6 | 184 | 52 | 0 | — |
| E1 | 4.0 | 3.6 | 176 | 52 | 8 | 6.0 |
| E2 | 3.6 | 3.1 | 176 | 52 | 8 | 6.0 |
| Parameter | Unit | Variation Conditions | |
|---|---|---|---|
| Reference Calculation | Branch Calculation | ||
| Boron Concentration (CSB) | ppm | 500 | 1000 |
| Fuel Temperature (Tf) | K | 900 | 700 |
| Moderator Temperature (Tm) | K | 585 | 605, 565, 535, 485, 405, 295 |
| Parameter | Cross-Section | Difference Rate (%) | |||
|---|---|---|---|---|---|
| McCARD (Barn) | Rel. SD 1 (%) | DeCART2D (Barn) | |||
| Buckling | 4.419 × 10−3 | 0.138 | 4.433 × 10−3 | −0.329 | |
| Group 1 (Fast) | 1.430 × 100 | 0.021 | 1.429 × 100 | 0.409 | |
| 8.529 × 10−3 | 0.084 | 8.558 × 10−3 | −0.336 | ||
| 5.859 × 10−3 | 0.067 | 5.857 × 10−3 | 0.062 | ||
| Group 2 (Thermal) | 4.797 × 10−1 | 0.023 | 4.830 × 10−1 | −0.682 | |
| 7.117 × 10−2 | 0.033 | 7.185 × 10−2 | −0.942 | ||
| 1.128 × 10−1 | 0.042 | 1.137 × 10−1 | −0.832 | ||
| Scattering Matrix | 4.827 × 10−1 | 0.013 | 4.844 × 10−1 | −0.339 | |
| 1.674 × 10−2 | 0.039 | 1.682 × 10−2 | −0.512 | ||
| 2.144 × 10−4 | 0.986 | 2.124 × 10−4 | 0.956 | ||
| 1.135 × 100 | 0.021 | 1.129 × 100 | 0.458 | ||
| Data | ENDF/B-VII.1 | ENDF/B-VIII.0 | Difference (%) | |||
|---|---|---|---|---|---|---|
| Cross-Section (Barn) | Rel. SD 1 (%) | Cross-Section (Barn) | Rel. SD 1 (%) | |||
| Buckling | 4.419 × 10−3 | 0.138 | 4.416 × 10−3 | 0.158 | −0.067 | |
| Group 1 (Fast) | 1.430 × 100 | 0.021 | 1.429 × 100 | 0.020 | −0.065 | |
| 8.529 × 10−3 | 0.084 | 8.578 × 10−3 | 0.096 | 0.564 | ||
| 5.859 × 10−3 | 0.067 | 5.867 × 10−3 | 0.060 | 0.106 | ||
| Group 2 (Thermal) | 4.797 × 10−1 | 0.023 | 4.885 × 10−1 | 0.022 | 1.824 | |
| 7.117 × 10−2 | 0.033 | 7.243 × 10−2 | 0.034 | 1.773 | ||
| 1.128 × 10−1 | 0.042 | 1.146 × 10−1 | 0.043 | 1.616 | ||
| Scattering Matrix | 4.827 × 10−1 | 0.013 | 4.837 × 10−1 | 0.011 | 0.194 | |
| 1.674 × 10−2 | 0.039 | 1.685 × 10−2 | 0.044 | 0.677 | ||
| 2.144 × 10−4 | 0.986 | 2.200 × 10−4 | 1.160 | 2.614 | ||
| 1.135× 100 | 0.021 | 1.118× 100 | 0.019 | −1.158 | ||
| Case | Fuel Temperature Coefficient (pcm/°C) | ||||
|---|---|---|---|---|---|
| NDR | DeCART2D/MASTER | McCARD/MASTER | |||
| ENDF/B-VII.1 | ENDF/B-VII.1 | ENDF/B-VIII.0 | |||
| Cycle 1 | BOC | −2.82 | −2.54 | −2.42 | −2.40 |
| EOC | −2.90 | −2.47 | −2.64 | −2.67 | |
| Cycle 2 | BOC | −2.75 | −2.43 | −2.40 | −2.67 |
| EOC | −2.90 | −2.61 | −2.79 | −2.88 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.W.; Park, H.J. McCARD/MASTER Hanbit Unit 3 Multi-Cycle Analyses with Monte Carlo-Based Reflector Cross-Section Generation. Energies 2025, 18, 5065. https://doi.org/10.3390/en18195065
Park JW, Park HJ. McCARD/MASTER Hanbit Unit 3 Multi-Cycle Analyses with Monte Carlo-Based Reflector Cross-Section Generation. Energies. 2025; 18(19):5065. https://doi.org/10.3390/en18195065
Chicago/Turabian StylePark, Jeong Woo, and Ho Jin Park. 2025. "McCARD/MASTER Hanbit Unit 3 Multi-Cycle Analyses with Monte Carlo-Based Reflector Cross-Section Generation" Energies 18, no. 19: 5065. https://doi.org/10.3390/en18195065
APA StylePark, J. W., & Park, H. J. (2025). McCARD/MASTER Hanbit Unit 3 Multi-Cycle Analyses with Monte Carlo-Based Reflector Cross-Section Generation. Energies, 18(19), 5065. https://doi.org/10.3390/en18195065






