Research on Adaptive Control Optimization of Battery Energy Storage System Under High Wind Energy Penetration
Abstract
1. Introduction
2. Introduction to Research System, Grouping and Inventory Model
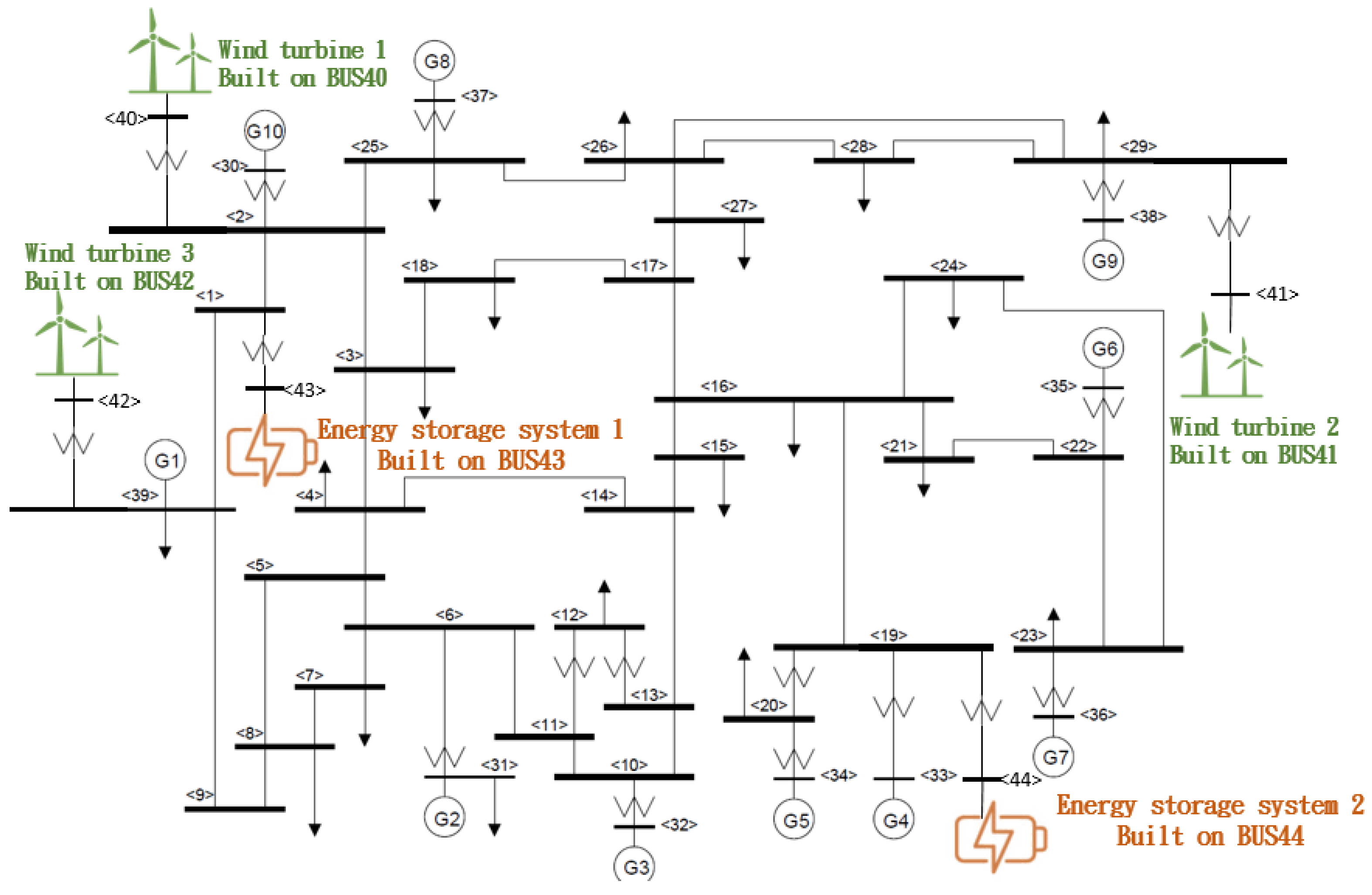
2.1. IEEE 39-Bus New England Power System
2.2. General Model of WECC Wind Turbine
2.3. WECC Energy Storage General Model
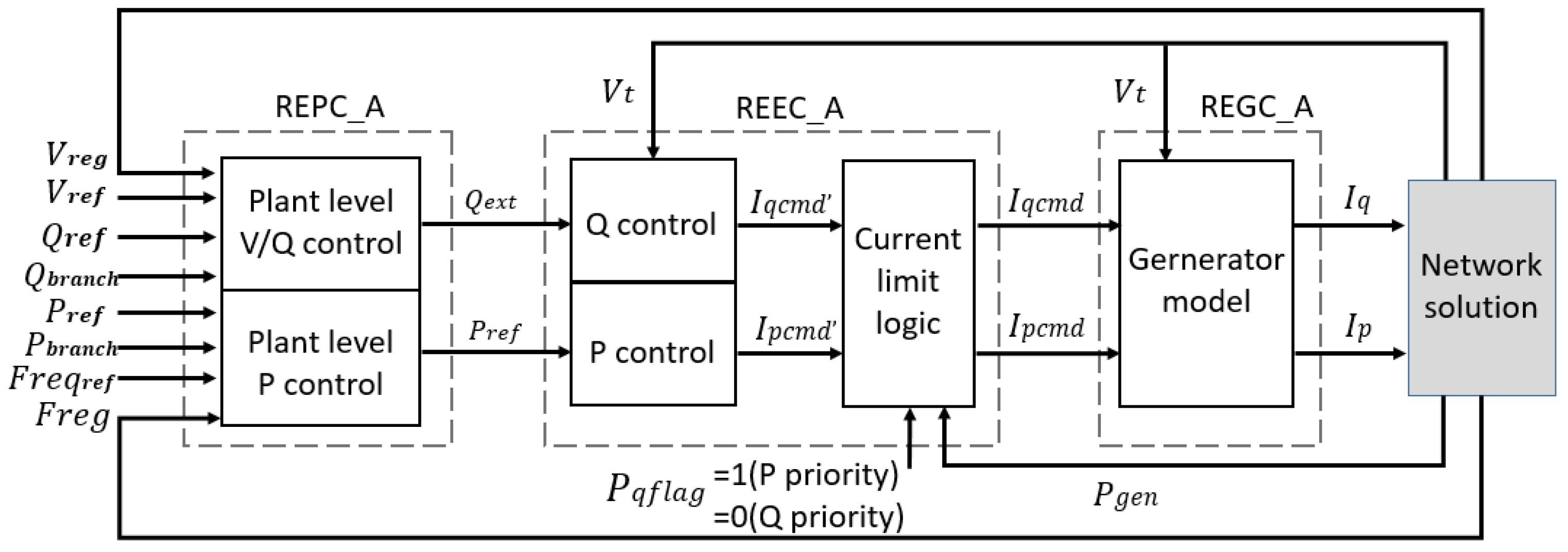
2.3.1. REPC_A Model
2.3.2. REEC_C Model
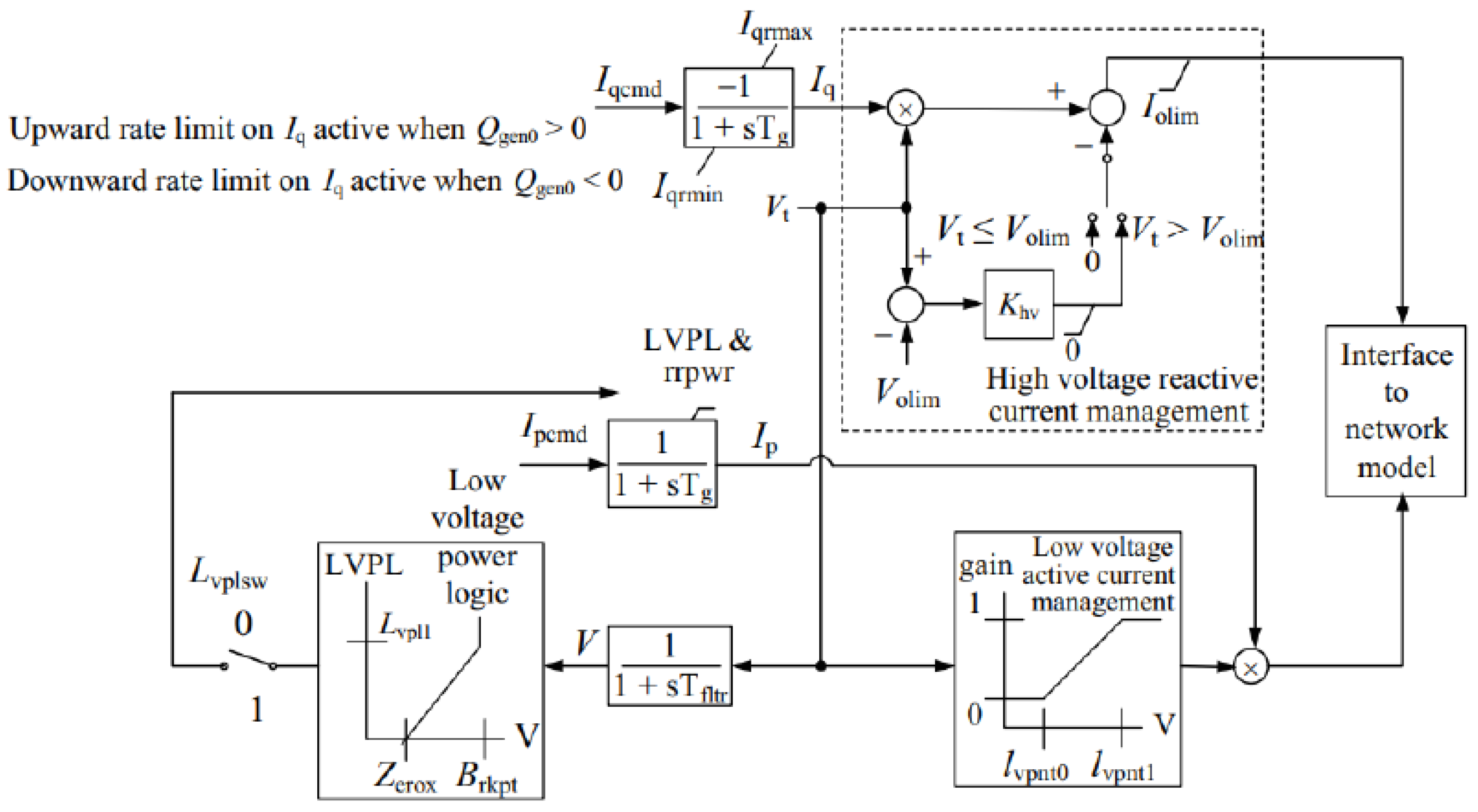
2.3.3. REGC_A Model
2.4. Summarize
3. Energy Storage Control Strategy Optimization Combining OAT and IPSO
3.1. Key Parameter Identification Method
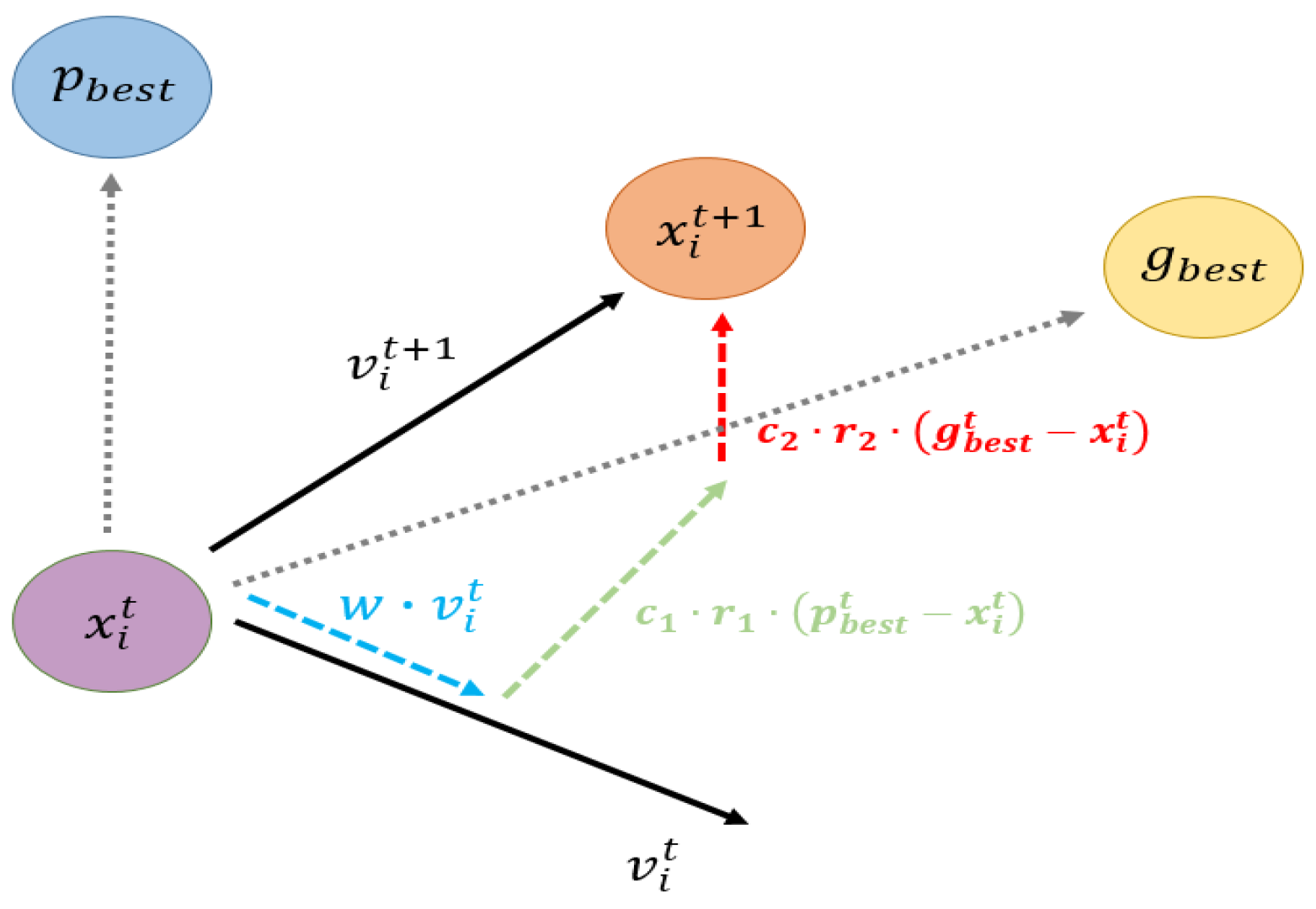
3.2. Improved Particle Swarm Optimization Method
3.3. Objective Function
4. Research Results
4.1. Overall Research Process
4.2. OAT Parameter Sensitivity Analysis Results
4.3. IPSO Results
4.3.1. Algorithm Comparison
4.3.2. Simulation Scenario Settings
4.3.3. Case 1: One Switch Is Disconnected
4.3.4. The Second Case: Two Wind Turbines Are Reduced to Half Load
4.3.5. Case 3: Three Wind Turbines Reduced to Half Load
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gayathri, K.; Jena, M.K.; Moharana, A.K. Impact of Different Penetration Level of Type-IV Renewable Energy Resources on Power System Dynamics. In Proceedings of the 2021 9th IEEE International Conference on Power Systems (ICPS), Kharagpur, India, 16–18 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Olivares, D.E.; Mehrizi-Sani, A.; Etemadi, A.H.; Cañizares, C.A.; Iravani, R.; Kazerani, M.; Hajimiragha, A.H.; Gomis-Bellmunt, O.; Saeedifard, M.; Palma-Behnke, R.; et al. Trends in Microgrid Control. IEEE Trans. Smart Grid 2014, 5, 1905–1919. [Google Scholar] [CrossRef]
- Alqahtani, S.; Shaher, A.; Garada, A.; Cipcigan, L. Frequency Stability in Renewable-Rich Modern Power Systems, Saudi Grid Case Study. In Proceedings of the 2022 57th International Universities Power Engineering Conference (UPEC), Istanbul, Turkey, 30 August 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, W.; Yang, L.; Qi, Y.; Zhao, J.; Zhang, M.; Shi, T. Parameter optimization method of energy storage controller based on power system transient stability. In Proceedings of the 2024 3rd International Conference on Smart Grids and Energy Systems (SGES), Zhengzhou, China, 25–27 October 2024; pp. 204–210. [Google Scholar] [CrossRef]
- Wang, R. Parameter Identification of Photovoltaic Cell Model Based on Enhanced Particle Swarm Optimization. Sustainability 2021, 13, 840. [Google Scholar] [CrossRef]
- Balamurali, A.; Mollaeian, A.; Sangdehi, S.M.; Kar, N.C. Parameter identification of permanent magnet synchronous machine based on metaheuristic optimization. In Proceedings of the 2015 IEEE International Electric Machines & Drives Conference (IEMDC), Coeur d’Alene, ID, USA, 10–13 May 2015; pp. 1729–1734. [Google Scholar] [CrossRef]
- Wan, Y.; Xing, M.; Wang, H. Parameter Identification of PSS/E Wind Turbine Generator Model Using Improved Particles Swarm Optimization Algorithm. In Proceedings of the 2023 6th International Conference on Energy, Electrical and Power Engineering (CEEPE), Guangzhou, China, 12–14 May 2023; pp. 350–355. [Google Scholar] [CrossRef]
- Singh, S.V.; Revathi, V.; Babu, B.S.; Bhavana, M.; Singh, N.; Nagamani, G. Enhancing Microgrid Stability: Optimal BESS Sizing via Modified PSO for Frequency Control and Cost Efficiency. In Proceedings of the 2024 7th International Conference on Contemporary Computing and Informatics (IC3I), Greater Noida, India, 18–20 September 2024; pp. 627–632. [Google Scholar] [CrossRef]
- Ayaz, M.; Dur-e-Zehra; Rizv, S.M.H.; Akbar, M. Optimal Load Frequency Control Using Particle Swarm Optimization for Power System Stability. In Proceedings of the 2024 International Conference on Engineering & Computing Technologies (ICECT), Islamabad, Pakistan, 23 May 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Huang, H.-C. Intelligent motion controller design for four-wheeled omnidirectional mobile robots using hybrid GA-PSO algorithm. In Proceedings of the 2011 IEEE International Conference on Systems, Man, and Cybernetics, Anchorage, AK, USA, 9–12 October 2011; pp. 2267–2272. [Google Scholar] [CrossRef]
- Ahmad, S.R.C.; Sendrasaran, K.; Naidu, K.; Awalin, L.J. Hybrid PSO-FA Optimization for Photovoltaic and Biomass Systems with Battery Energy Storage System (BESS) in Water Treatment Plant. In Proceedings of the 2022 IEEE International Conference on Power and Energy (PECon), Langkawi, Kedah, Malaysia, 5–6 December 2022; pp. 431–436. [Google Scholar] [CrossRef]
- Tjandra, R.; Wen, S.; Zhou, D.; Tang, Y. Optimal Sizing of BESS for Hybrid Electric Ship Using Multi-Objective Particle Swarm Optimization. In Proceedings of the 2019 10th International Conference on Power Electronics and ECCE Asia (ICPE 2019—ECCE Asia), Busan, Republic of Korea, 27–30 May 2019; pp. 1460–1466. [Google Scholar] [CrossRef]
- Irshad, K.; Khan, A.I.; Zayed, M.E.; Algarni, S.; Alqahtani, T. Performance analysis of air conditioning system integrated with thermal energy storage using enhanced machine learning modelling coupled with fire hawk optimizer. J. Build. Eng. 2024, 98, 111308. [Google Scholar] [CrossRef]
- Guddanti, B.; Roychowdhury, R.; Illindala, M.S. Evaluation of Modified Global Sensitivity Analysis Techniques for Power System Dynamic Studies. In Proceedings of the 2022 IEEE Industry Applications Society Annual Meeting (IAS), Detroit, MI, USA, 9–14 October 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, P.; Zhao, F.; Guo, Y.; Zhao, H.; Zhao, Y.; Dong, L. Sensitivity analysis of the row model’s input parameters. In Proceedings of the 2014 The Third International Conference on Agro-Geoinformatics, Beijing, China, 11–14 August 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P. How to avoid a perfunctory sensitivity analysis. Environ. Model. Softw. 2010, 25, 1508–1517. [Google Scholar] [CrossRef]
- Abera, B.; Wik, T.; Bekele, G.; Mamo, M. Parametric Sensitivity Analysis of the Modified AMOCO Model for an Anaerobic Digester. In Proceedings of the 2024 IEEE PES/IAS PowerAfrica, Johannesburg, South Africa, 7–11 October 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, W.; Wang, W.; Pan, Z. Grid Forming Control with Inertial and Virtual Admittance Characteristics for Grid-tied Converters. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; pp. 6164–6189. [Google Scholar] [CrossRef]
- Li, X.; Li, D.; Liu, Y.; Li, H. Study on Power Low Frequency Oscillation Caused by Primary Frequency Modulation. In Proceedings of the 2020 IEEE 9th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 11–13 December 2020; pp. 2271–2276. [Google Scholar] [CrossRef]
- Tian, Y.; Chen, Y.; Wei, W.; Xia, Y. A Review on Control Strategies of Grid-connected Energy Storage Systems for Frequency Regulation. In Proceedings of the 2023 5th International Academic Exchange Conference on Science and Technology Innovation (IAECST), Guangzhou, China, 8–10 December 2023; pp. 1319–1325. [Google Scholar] [CrossRef]
- Ren, Y.; Meng, Q.; Xu, C. Research on Frequency Modulation Control Strategy of Power System Based on Optimized Design of Energy Storage SOC. In Proceedings of the 2024 IEEE 7th International Conference on Information Systems and Computer Aided Education (ICISCAE), Dalian, China, 27–29 September 2024; pp. 682–686. [Google Scholar] [CrossRef]
- New England IEEE 39-Bus System. Available online: https://icseg.iti.illinois.edu/ieee-39-bus-system-2/ (accessed on 19 August 2025).
- WT3-Gerneric-Wind-Model. Available online: https://www.esig.energy/wiki-main-page/wt3-generic-wind-model/#Generator.2FConverter_Model_.28WT3G.29 (accessed on 16 August 2025).
- Lee, C.-C.; Hsin, Y.-M.; Dai, S.-C.; Kuo, C.-C. Optimal Modeling for Dynamic Response of Energy Storage Systems. Appl. Sci. 2023, 13, 4943. [Google Scholar] [CrossRef]
- WECC REMWG. Modeling Renewable Energy/Battery Energy Storage System Hybrid Power Plants; Western Electricity Coordinating Council: Salt Lake City, UT, USA, 2020. [Google Scholar]
- Zhu, X.; Liu, R.; Wang, S. Implementation of Parameter Estimation in Mechanistic Models by Dynamic Optimization. In Proceedings of the 2006 6th World Congress on Intelligent Control and Automation, Dalian, China, 21–23 June 2006; pp. 7683–7687. [Google Scholar] [CrossRef]
- Li, X. Application of Particle Swarm Optimization Algorithm in Computer Neural Network. In Proceedings of the 2017 International Conference on Computer Systems, Electronics and Control (ICCSEC), Dalian, China, 25–27 December 2017; pp. 446–449. [Google Scholar] [CrossRef]
- Robinson, J.; Sinton, S.; Rahmat-Samii, Y. Particle swarm, genetic algorithm, and their hybrids: Optimization of a profiled corrugated horn antenna. In Proceedings of the IEEE Antennas and Propagation Society International Symposium (IEEE Cat. No.02CH37313), San Antonio, TX, USA, 16–21 June 2002; Volume 1, pp. 314–317. [Google Scholar] [CrossRef]
- Zhang, X.; Zou, D.; Shen, X. A Novel Simple Particle Swarm Optimization Algorithm for Global Optimization. Mathematics 2018, 6, 287. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings. IEEE World Congress on Computational Intelligence (Cat. No.98TH8360), Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar] [CrossRef]
- Khaleghi, S.; Moghaddam, R.K.; Mousavi, A.E.; Ghahremani, E. Solution to economic dispatch problem with valve-point loading effect using IPSO algorithm. In Proceedings of the 2014 International Congress on Technology, Communication and Knowledge (ICTCK), Mashhad, Iran, 26–27 November 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Uriarte, A.; Melin, P.; Valdez, F. An improved Particle Swarm Optimization algorithm applied to Benchmark Functions. In Proceedings of the 2016 IEEE 8th International Conference on Intelligent Systems (IS), Sofia, Bulgaria, 4–6 September 2016; pp. 128–132. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhao, L.; Lee, W.-J. Robustness Analysis of Dynamic Equivalent Model of DFIG Wind Farm for Stability Study. IEEE Trans. Ind. Appl. 2018, 54, 5682–5690. [Google Scholar] [CrossRef]
- Li, W.T.; Shi, X.W.; Hei, Y.Q.; Liu, S.F.; Zhu, J. A Hybrid Optimization Algorithm and Its Application for Conformal Array Pattern Synthesis. IEEE Trans. Antennas Propag. 2010, 58, 3401–3406. [Google Scholar] [CrossRef]
- Siemens Industry, Inc.; Siemens Power Technologies International. PSS®E 33.4 Model Library/Program Operation Manual; Siemens Industry, Inc.: Schenectady, NY, USA, 2013. [Google Scholar]















| Model | Parameter Source |
|---|---|
| 39Bus-System | IEEE 39-Bus System Information |
| WT3 | ESIG default |
| REPC_A | WECC default |
| REEC_C | WECC default |
| REGC_A | WECC default |
| Parameter | Denotation | Significance |
|---|---|---|
| The lowest frequency point obtained during the simulation | Determine the lowest point of frequency drop | |
| Simulate the final frequency value | Determine the frequency point of the last rebound | |
| Frequency standard deviation after steady state | Reflects the oscillation degree and stability of the system in the steady state stage | |
| Amplitude of frequency fluctuation after steady state | Measure the steady-state oscillation amplitude of the system | |
| Oscillations | Frequency oscillation times after steady state | Reflects the system damping effect and stability |
| Model | Parameter | Denotation |
|---|---|---|
| REPC_A | Tfltr | Voltage or reactive power measurement filter time constant (s) |
| Kp | Reactive power PI control proportional gain (pu) | |
| Ki | Reactive power PI control integral gain (pu) | |
| Tft | Lead time constant (s) | |
| Tfv | Lag time constant (s) | |
| Kpg | Proportional gain for power control (pu) | |
| Kig | Proportional gain for power control (pu) | |
| Tp | Real power measurement filter time constant (s) | |
| Tg | Power Controller lag time constant (s) | |
| REEC_C | Trv | Voltage filter time constant |
| Kqv | gain during over and undervoltage conditions | |
| Tp | Filter time constant for electrical power | |
| Tiq | Time constant on delay s4 | |
| Tpord | Power filter time constant | |
| REGC_A | Tg | Converter time constant (s) |
| Khv | Overvoltage compensation gain used in the high voltage reactive current management |
| Ranking | Parameter | Score |
|---|---|---|
| 1 | Kpg (REPC) | 10 |
| 2 | Kig (REPC) | 7.77 |
| 3 | Tp (REPC) | 6.86 |
| 4 | Tg (REPC) | 6.85 |
| 5 | Tpord (REEC) | 6.2 |
| 6 | Tg (REGC) | 5.71 |
| 7 | Tp (REEC) | 4.51 |
| 8 | Tiq (REEC) | 4.09 |
| 9 | Trv (REEC) | 4.01 |
| 10 | Khv (REGC) | 0 |
| 11 | Tfv (REPC) | 0 |
| 12 | Ki (REPC) | 0 |
| 13 | Tfltr (REGC) | 0 |
| 14 | Tfltr (REPC) | 0 |
| 15 | Kqv (REEC) | 0 |
| 16 | Kp (REPC) | 0 |
| 17 | Tft (REPC) | 0 |
| Model | Parameter |
|---|---|
| REPC_A | Kpg |
| Kig | |
| Tp | |
| Tg | |
| REEC_C | Tp |
| Trv | |
| Tiq | |
| Tpord | |
| REGC_A | Tg |
| Parameter | Denotation | Value |
|---|---|---|
| SWARMSIZE | The number of particles per generation | 10 |
| MAXITER | Maximum iteration number | 20 |
| INERTIA_W_MAX | Initial inertia weight | 0.9 |
| INERTIA_W_MIN | final inertia weight | 0.4 |
| C_MAX | Learning factor upper limit | 2.5 |
| C_MIN | Learning factor lower limit | 0.5 |
| Model | Parameter | Value |
|---|---|---|
| REPC_A | Kpg | 0.0001–50 |
| Kig | 0.0001–50 | |
| Tp | 0.02–0.5 | |
| Tg | 0.05–0.5 | |
| REEC_A | Tp | 0.0001–0.1 |
| Trv | 0.0001–0.1 | |
| Tiq | 0.0001–0.1 | |
| Tpord | 0.01–0.1 | |
| REGC_A | Tg | 0.01–0.05 |
| Model | Parameter | Value |
|---|---|---|
| REPC_A | Kpg | 5.78525 |
| Kig | 33.20066 | |
| Tp | 0.43394 | |
| Tg | 0.24379 | |
| REEC_A | Tp | 0.03235 |
| Trv | 0.01906 | |
| Tiq | 0.00819 | |
| Tpord | 0.04740 | |
| REGC_A | Tg | 0.04032 |
| Model | Parameter | Value |
|---|---|---|
| REPC_A | Kpg | 2.59187 |
| Kig | 17.53082 | |
| Tp | 0.497 | |
| Tg | 0.08561 | |
| REEC_C | Tp | 0.07276 |
| Trv | 0.07684 | |
| Tiq | 0.05206 | |
| Tpord | 0.01401 | |
| REGC_A | Tg | 0.03006 |
| Model | Parameter | Value |
|---|---|---|
| REPC_A | Kpg | 2.59187 |
| Kig | 17.53082 | |
| Tp | 0.497 | |
| Tg | 0.08561 | |
| REEC_A | Tp | 0.07276 |
| Trv | 0.07684 | |
| Tiq | 0.05206 | |
| Tpord | 0.01401 | |
| REGC_A | Tg | 0.03006 |
| Simulated Situation | Fan 1 Output Power | Fan 2 Output Power | Fan 3 Output Power | Total Fan Output Power | Instantaneous Total Power Loss of Fan | BESS1 Instantaneous Maximum Output Power | BESS 2 Instantaneous Maximum Output Power | BESS Instantaneous Maximum Total Output Power | BESS 1 Lowest Frequency | BESS 2 Lowest Frequency |
|---|---|---|---|---|---|---|---|---|---|---|
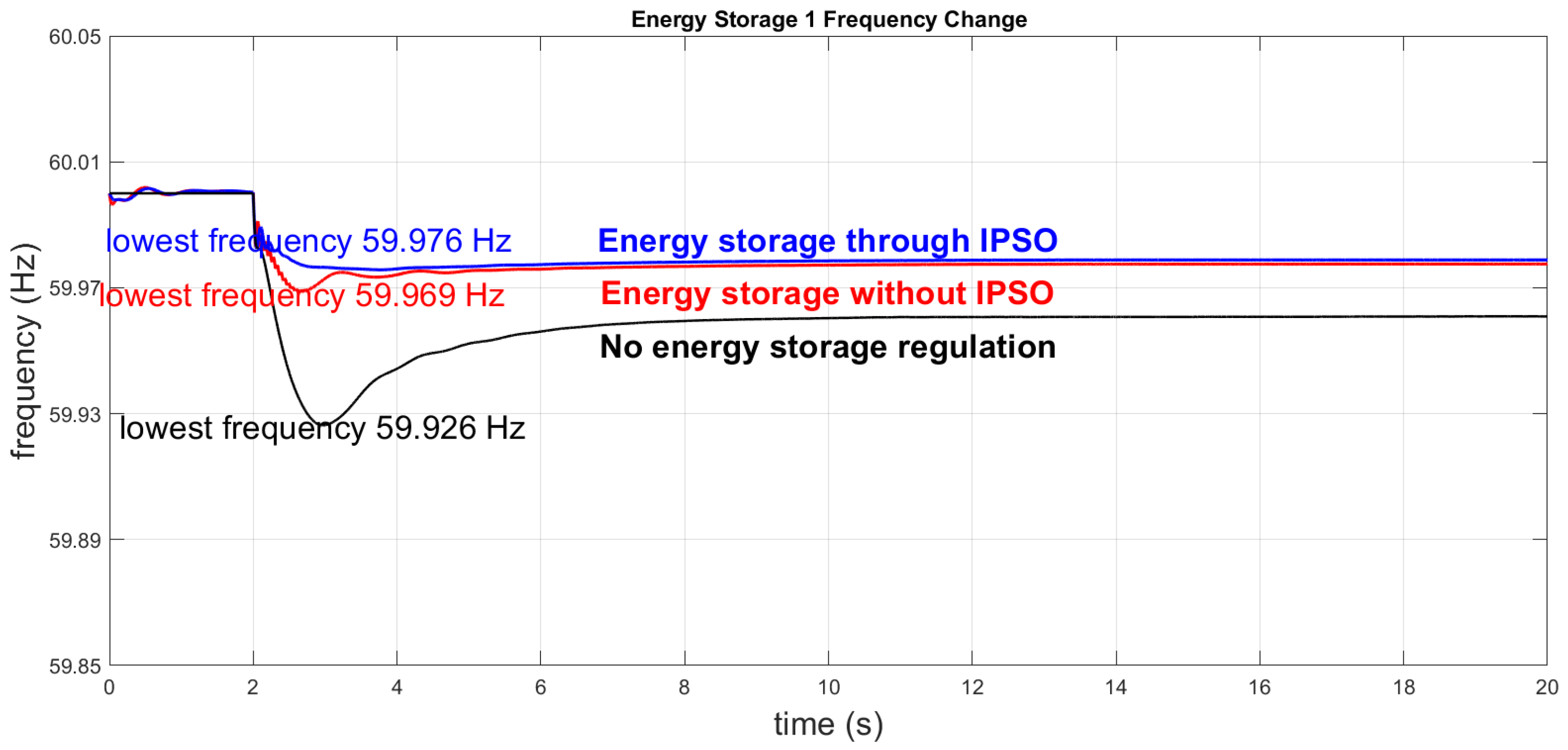
| Case 1 | 0 pu | 2 pu | 2 pu | 4 pu | 2 pu | 0.983 pu | 1.213 pu | 2.166 pu | 59.976 Hz | 59.976 Hz |
| Case 2 | 1 pu | 1 pu | 2 pu | 4 pu | 2 pu | 1.067 pu | 1.244 pu | 2.312 pu | 59.976 Hz | 59.976 Hz |
| Case 3 | 1 pu | 1 pu | 1 pu | 3 pu | 3 pu | 1.498 pu | 1.445 pu | 2.918 pu | 59.976 Hz | 59.976 Hz |
| Simulated Situation | Frequency Index | NO BESS | BESS Without IPSO | BESS with IPSO | Improvement (%) |
|---|---|---|---|---|---|
| Case 1 | 59.928 Hz | 59.971 Hz | 59.976 Hz | 0.00833% | |
| 59.958 Hz | 59.975 Hz | 59.978 Hz | 0.005% | ||
| 0.002456 Hz | 0.002135 Hz | 0.000067 Hz | 96.8% | ||
| 0.007141 Hz | 0.006541 Hz | 0.000289 Hz | 95.58% | ||
| Oscillations | 0 | 0 | 0 | ||
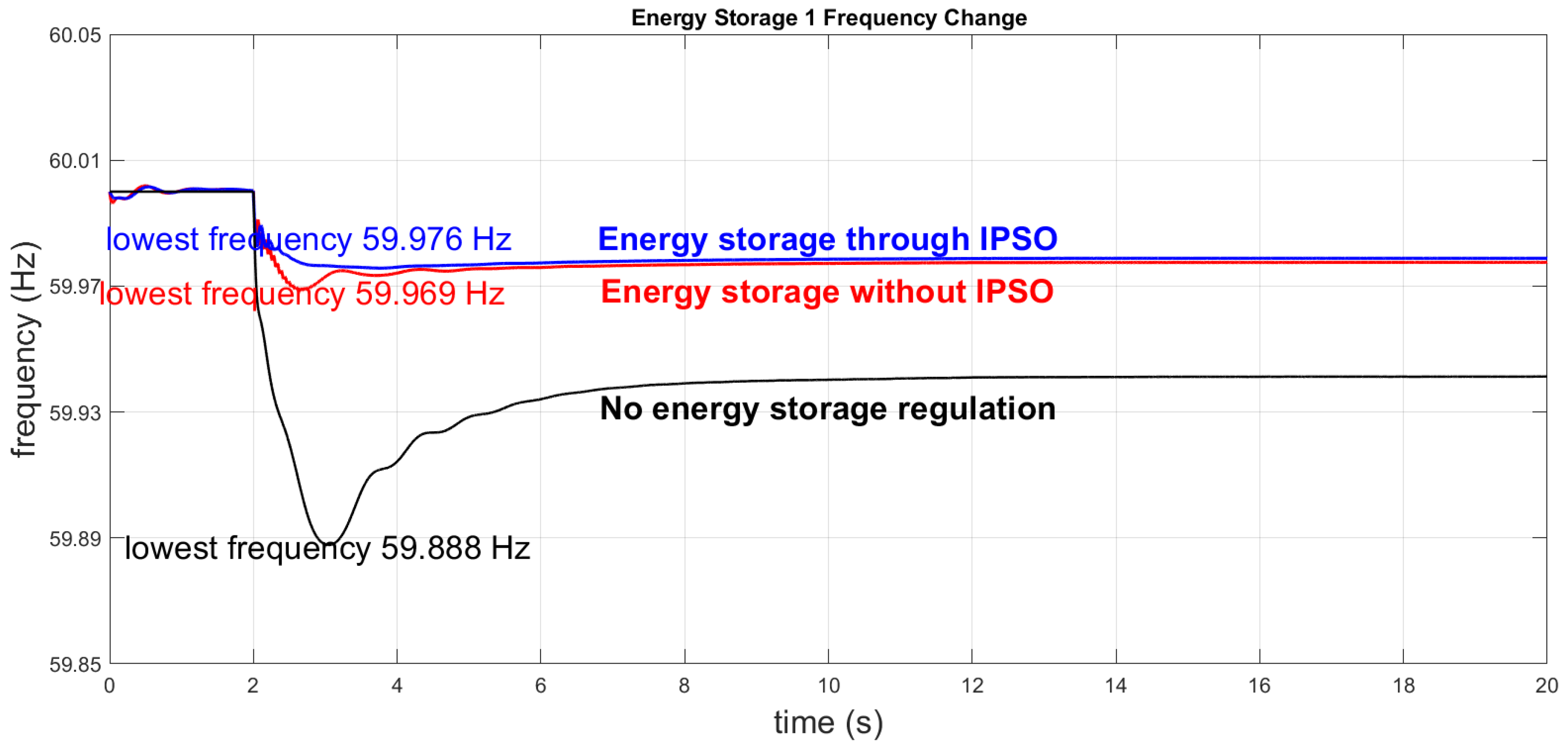
| Case 2 | 59.926 Hz | 59.969 Hz | 59.976 Hz | 0.011% | |
| 59.958 Hz | 59.976 Hz | 59.9788 Hz | 0.011% | ||
| 0.002146 Hz | 0.00211 Hz | 0.0000755 Hz | 96.42% | ||
| 0.001068 Hz | 0.000904 Hz | 0.000311 Hz | 65.59% | ||
| Oscillations | 0 | 0 | 0 | ||
| Case 3 | 59.884 Hz | 59.967 Hz | 59.976 Hz | 0.15% | |
| 59.943 Hz | 59.974 Hz | 59.975 Hz | 0.0016% | ||
| 0.001911 Hz | 0.001987 Hz | 0.000131 Hz | 93.4% | ||
| 0.007652 Hz | 0.007694 Hz | 0.000641 Hz | 91.6% | ||
| Oscillations | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.-H.; Chen, Y.-C.; Hung, C.-C. Research on Adaptive Control Optimization of Battery Energy Storage System Under High Wind Energy Penetration. Energies 2025, 18, 5057. https://doi.org/10.3390/en18195057
Wang M-H, Chen Y-C, Hung C-C. Research on Adaptive Control Optimization of Battery Energy Storage System Under High Wind Energy Penetration. Energies. 2025; 18(19):5057. https://doi.org/10.3390/en18195057
Chicago/Turabian StyleWang, Meng-Hui, Yi-Cheng Chen, and Chun-Chun Hung. 2025. "Research on Adaptive Control Optimization of Battery Energy Storage System Under High Wind Energy Penetration" Energies 18, no. 19: 5057. https://doi.org/10.3390/en18195057
APA StyleWang, M.-H., Chen, Y.-C., & Hung, C.-C. (2025). Research on Adaptive Control Optimization of Battery Energy Storage System Under High Wind Energy Penetration. Energies, 18(19), 5057. https://doi.org/10.3390/en18195057






