Numerical Simulation and Theoretical Analysis of Wave Loads on Truss Legs for Offshore Energy Platforms
Abstract
1. Introduction
2. Research Method
2.1. Theoretical Method
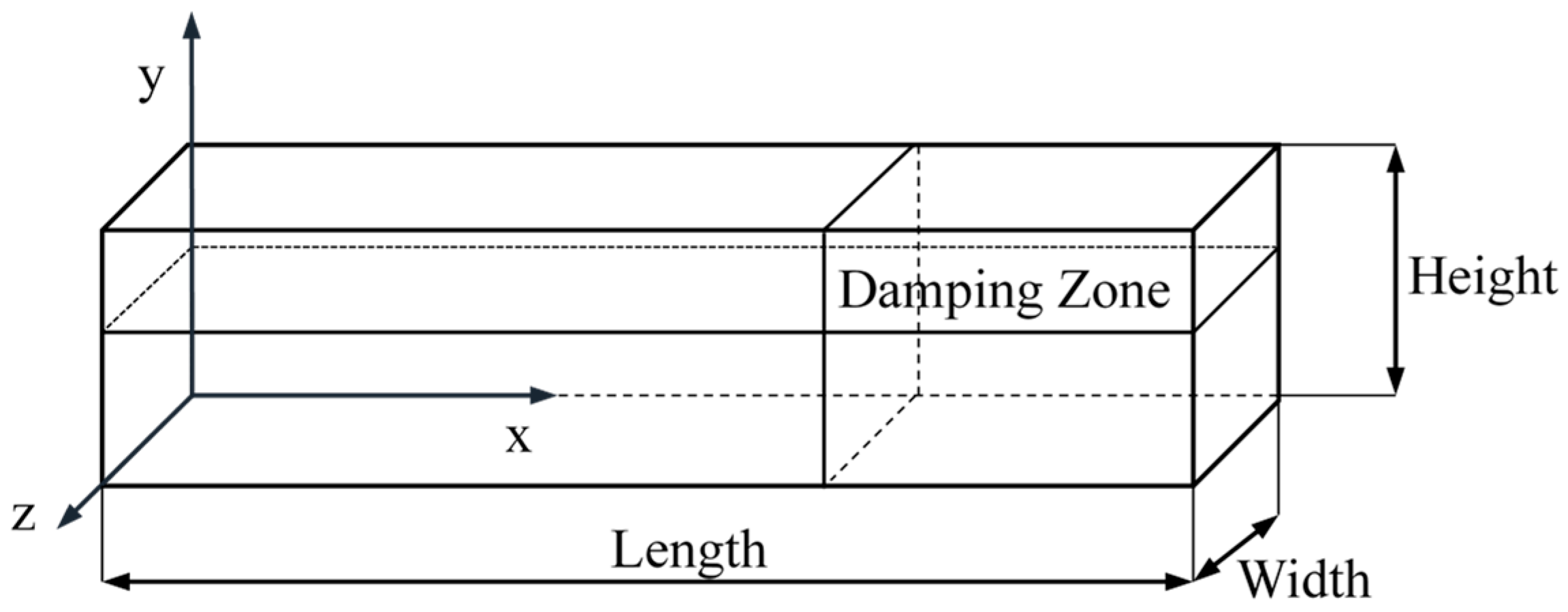
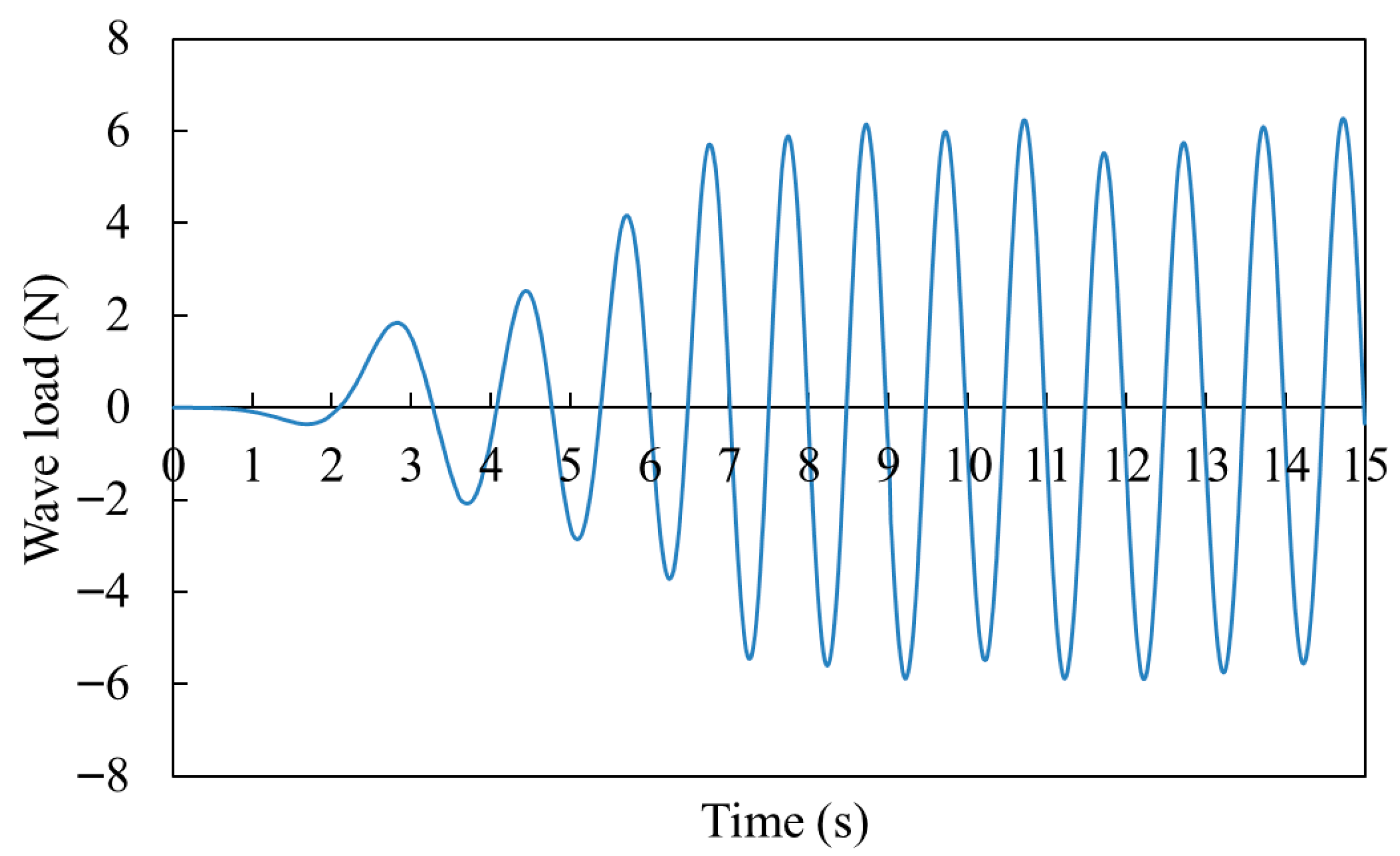
2.2. Numerical Method
3. Results and Discussion
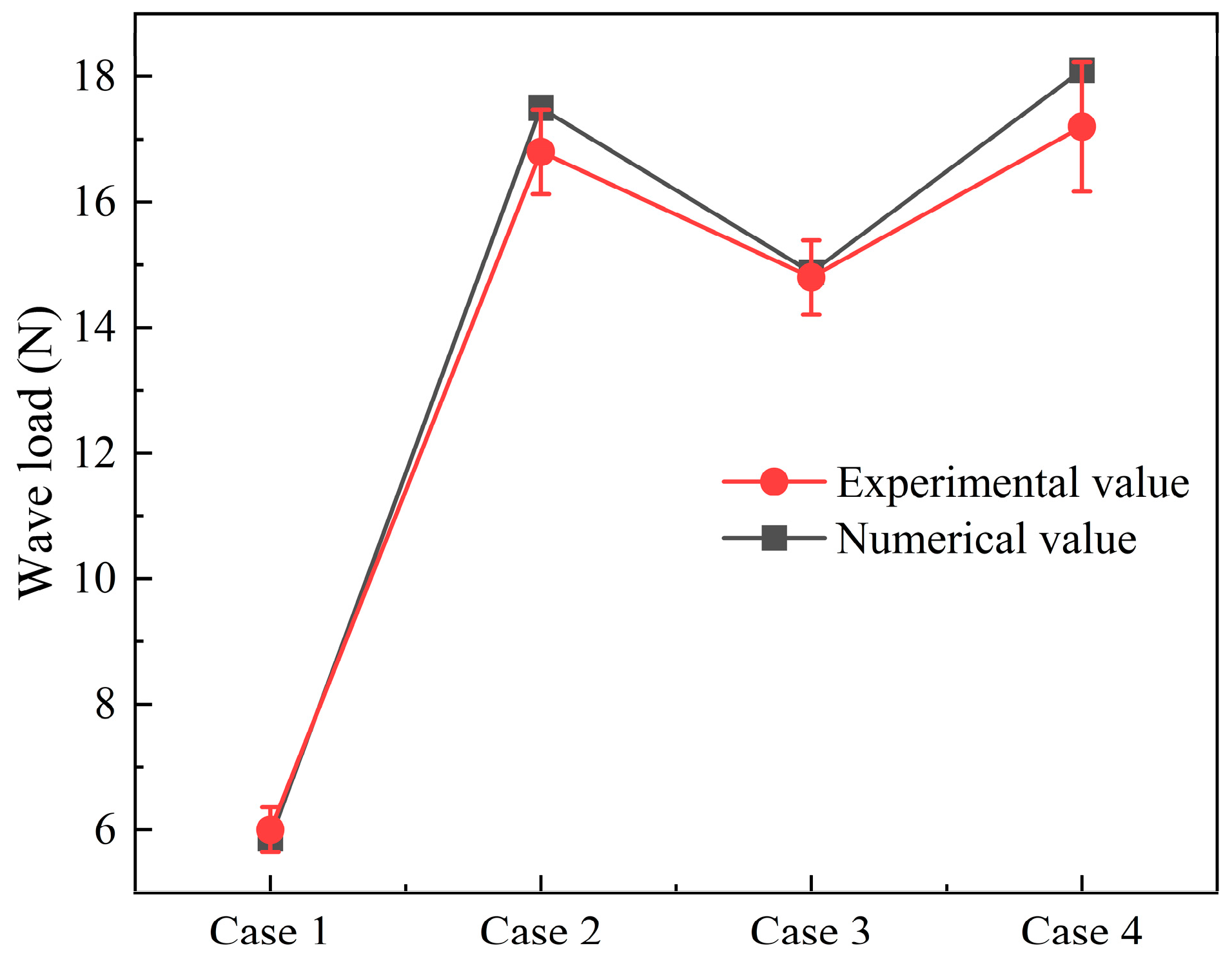
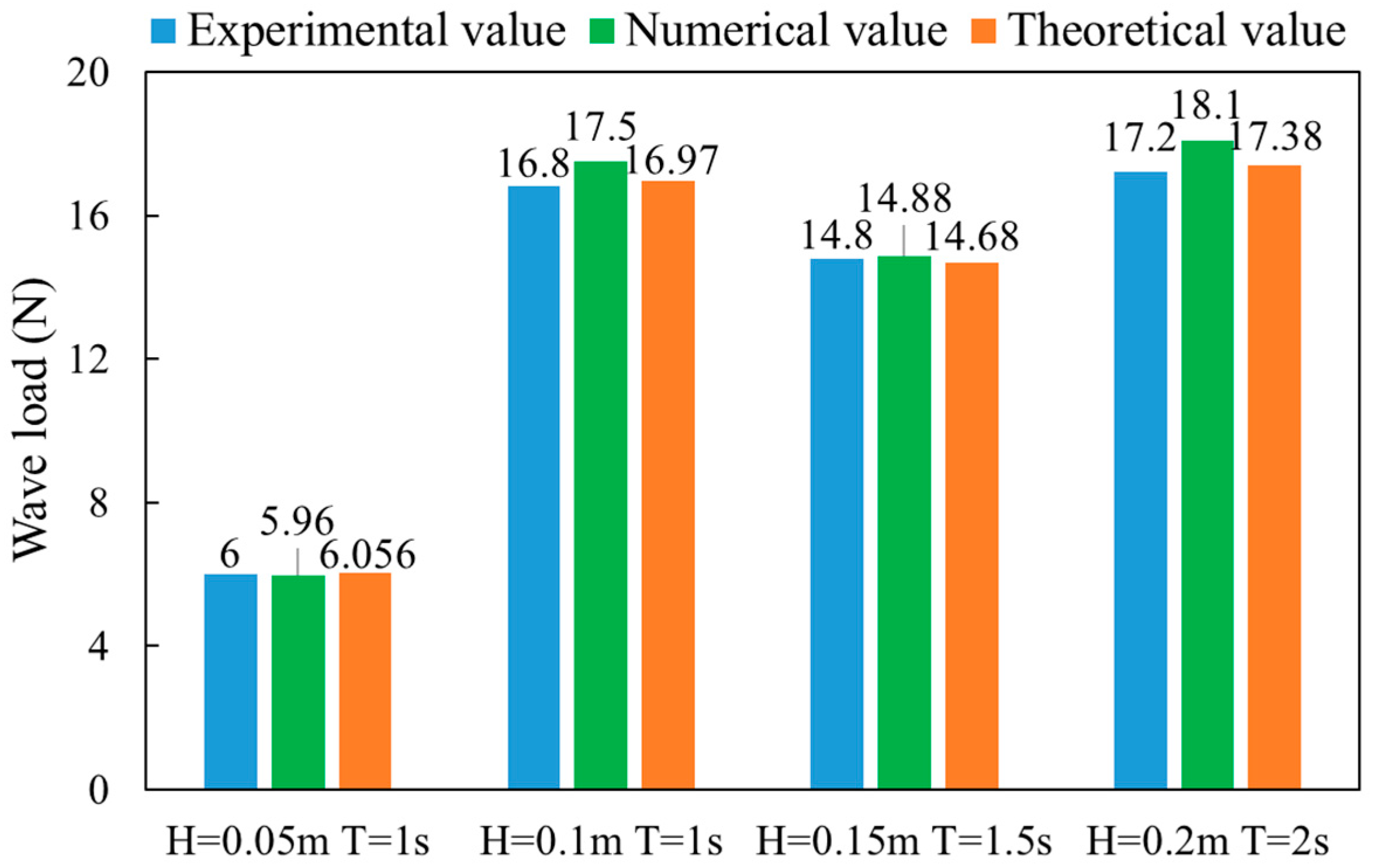
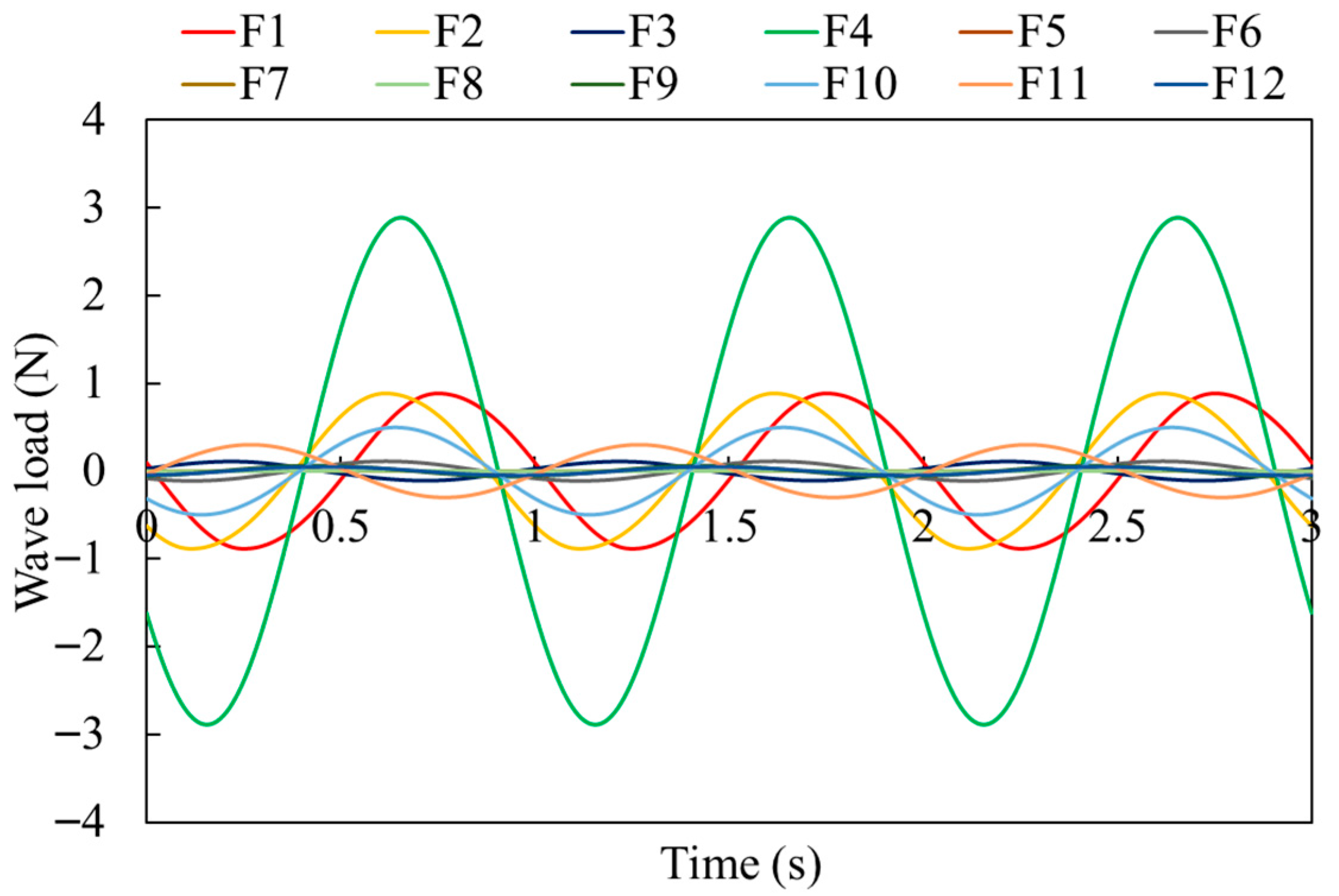
3.1. Wave Loads of the Truss Leg Under Different Wave Conditions
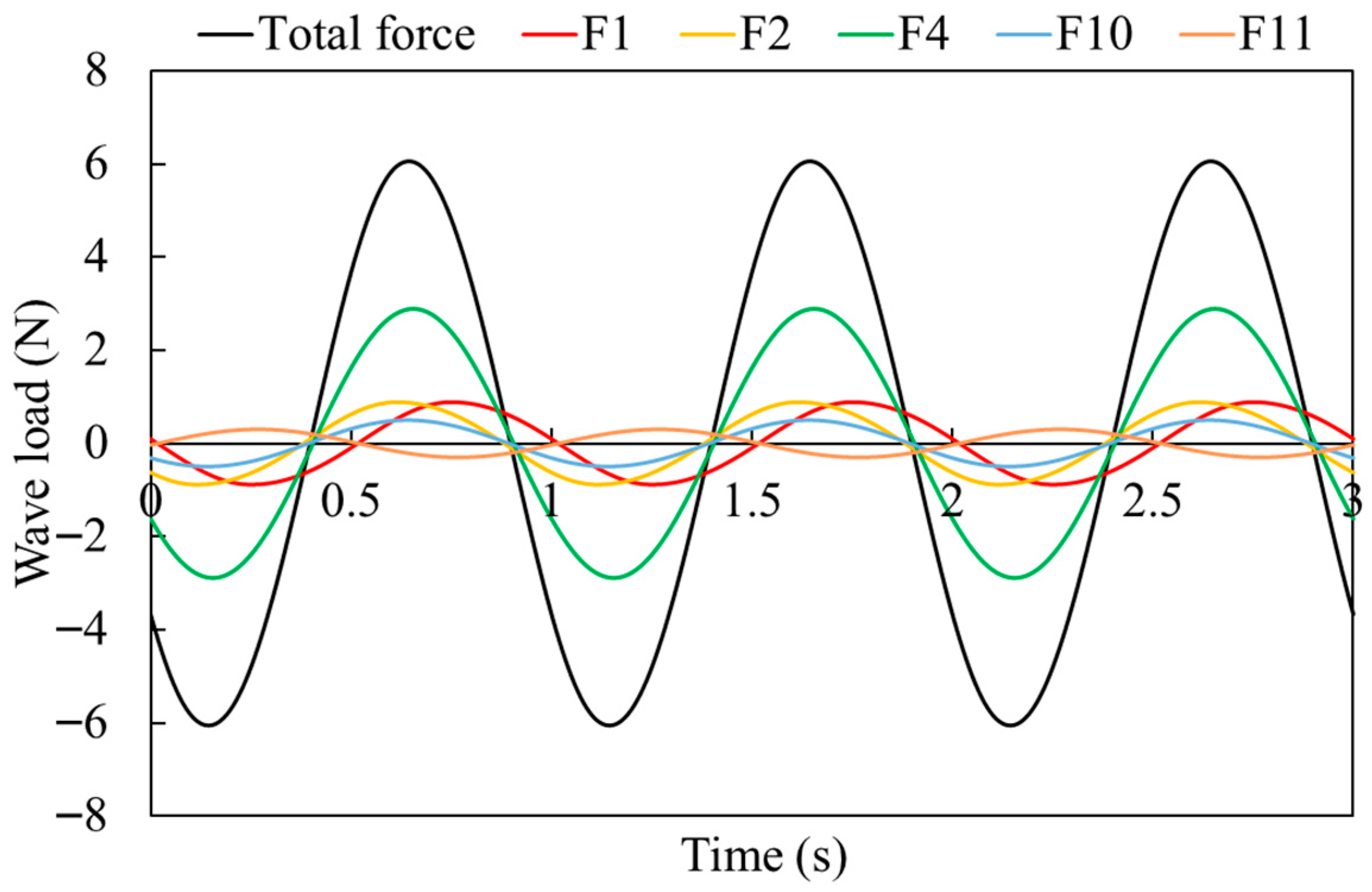
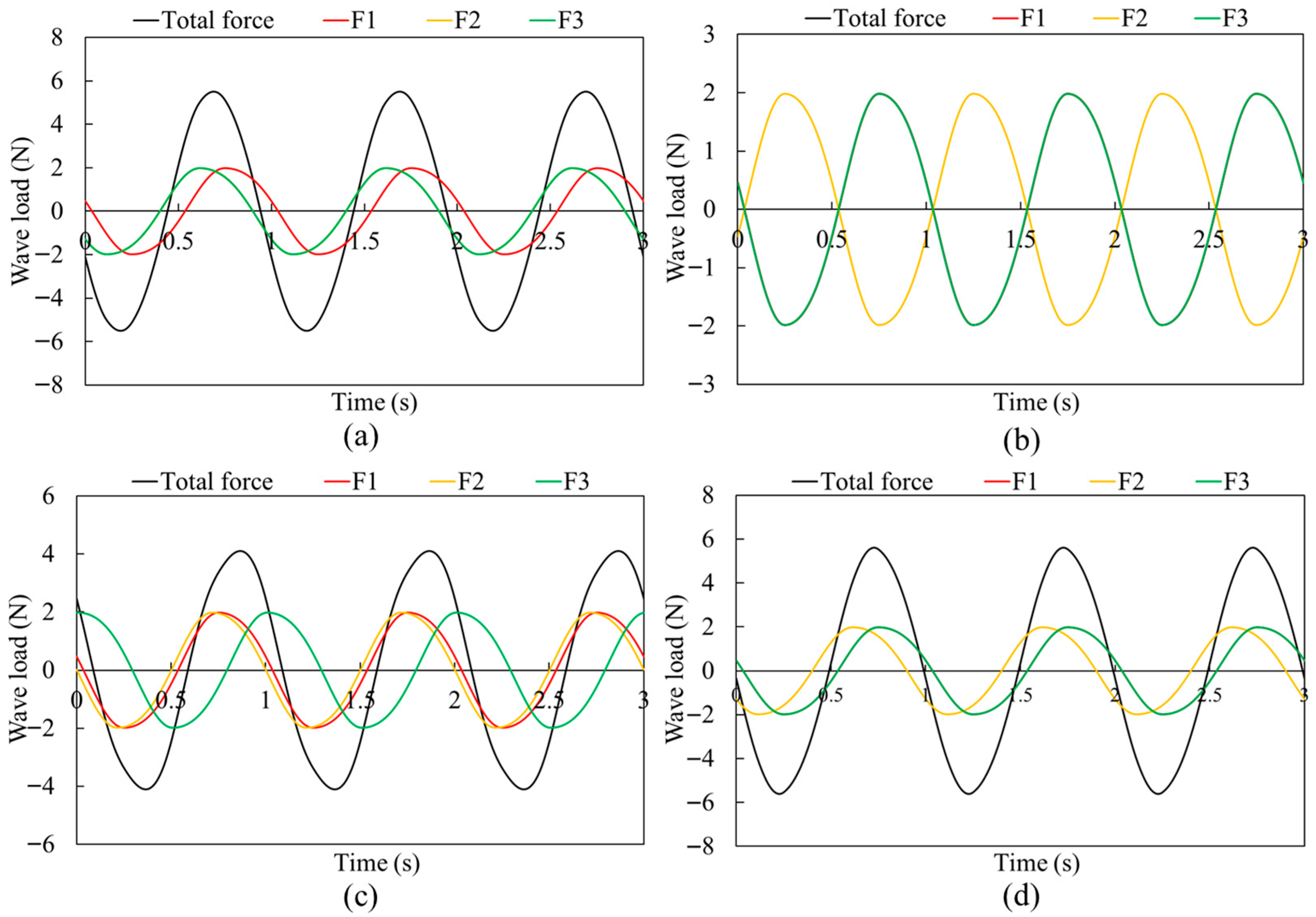
3.2. Effect of the Components on the Total Force
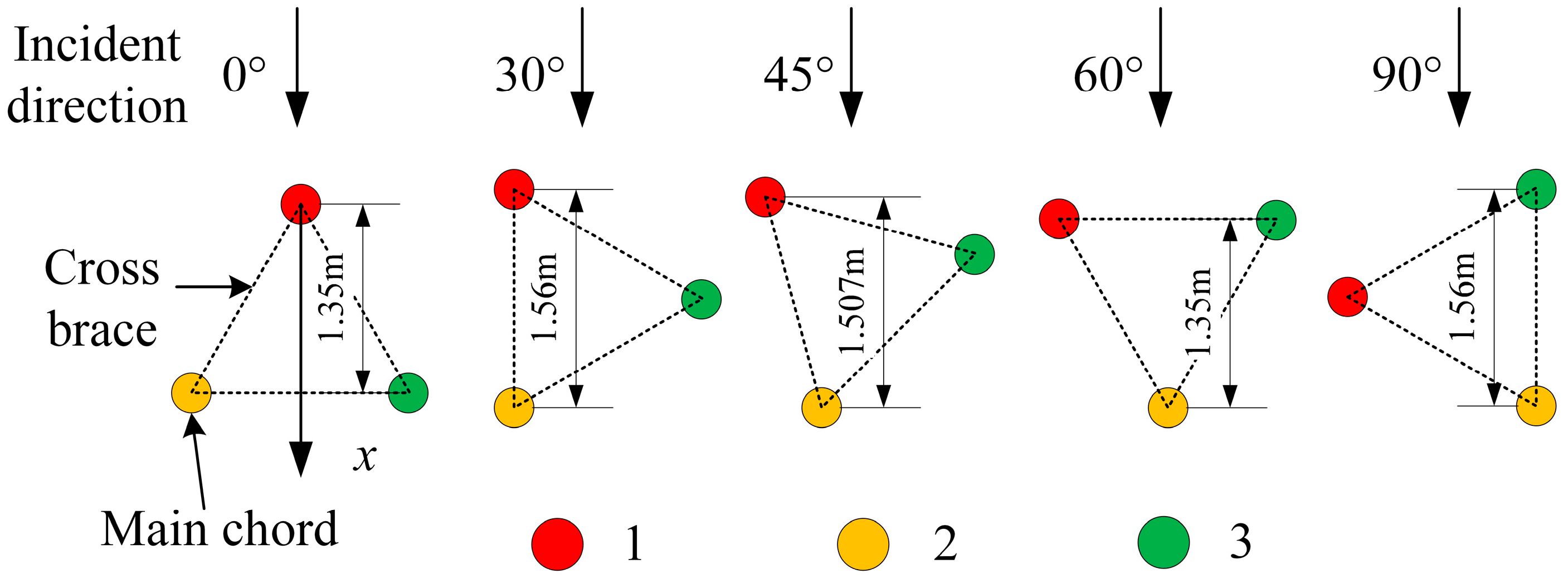
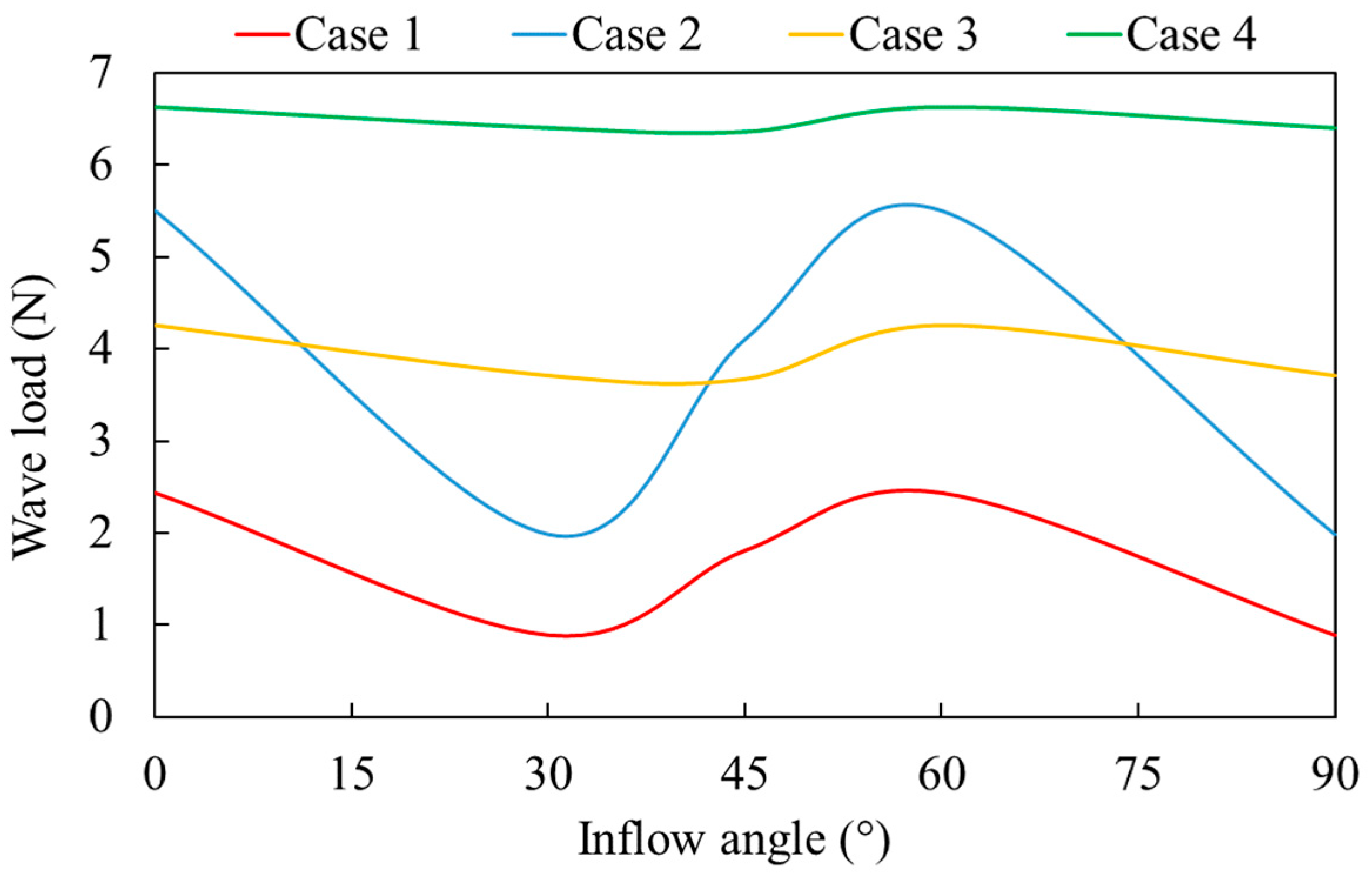
3.3. Effect of the Inflow Angle on the Total Force
4. Conclusions
- (1)
- Significant differences exist among the component forces. Two key factors affect these forces: locations and phase differences. Components near the free surface experience significantly larger forces. Additionally, phase differences between component units lead to variations in force magnitude, with in-phase components exhibiting higher forces. The phase relationship between the peak forces of components also considerably influences the total force. The maximum total force is negatively correlated with the phase difference between the peaks of the major component forces.
- (2)
- The influence of inflow angle on total force is periodic with a 60° cycle. The effect is most pronounced when the wavelength is comparable to the pile spacing. For much longer wavelengths, the inflow angle has a negligible impact.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Morison, J.R.; Johnson, J.W.; Schaaf, S.A. The force exerted by surface waves on piles. J. Pet. Technol. 1950, 2, 149–154. [Google Scholar] [CrossRef]
- Keulegan, G.H.; Carpenter, L.H. Forces on cylinders and plates in an oscillating fluid. JRNBS 1958, 60, 423–440. [Google Scholar] [CrossRef]
- Chakrabarti, S.K.; Wolbert, A.L.; Tam, W.A. Wave forces on vertical circular cylinder. J. Waterw. Harb. Coast. Eng. Div. 1976, 102, 203–221. [Google Scholar] [CrossRef]
- Sarpkaya, T. Force on a circular cylinder in viscous oscillatory flow at low keulegan—Carpenter numbers. J. Fluid Mech. 1986, 165, 61–71. [Google Scholar] [CrossRef]
- Raed, K.; Soares, C. Variability effect of the drag and inertia coefficients on the morison wave force acting on a fixed vertical cylinder in irregular waves. Ocean Eng. 2018, 159, 66–75. [Google Scholar] [CrossRef]
- Liu, G.; Li, H.; Qiu, Z.; Leng, D.; Li, Z.; Li, Z.; Li, W. A mini review of recent progress on vortex-induced vibrations of marine risers. Ocean Eng. 2020, 195, 106704. [Google Scholar] [CrossRef]
- Sundar, V.; Vengatesan, V.; Anandkumar, G.; Schlenkhoff, A. Hydrodynamic coefficients for inclined cylinders. Ocean Eng. 1998, 25, 277–294. [Google Scholar] [CrossRef]
- Chakrabarti, S.K. Wave forces on vertical array of tubes. Proc. Civ. Eng. Ocean 1979, 1, 241–259. [Google Scholar]
- Bonakdar, L.; Oumeraci, H. Pile group effect on the wave loading of a slender pile: A small-scale model study. Ocean Eng. 2015, 108, 449–461. [Google Scholar] [CrossRef]
- Bonakdar, L.; Oumeraci, H.; Etemad-Shahidi, A. Wave load formulae for prediction of wave-induced forces on a slender pile within pile groups. Coast. Eng. 2015, 102, 49–68. [Google Scholar] [CrossRef]
- Liu, S.; Ong, M.C.; Obhrai, C.; Seng, S. Computational fluid dynamics simulations of regular and irregular waves past a horizontal semi-submerged cylinder. J. Offshore Mech. Arct. Eng. 2018, 140, 031801. [Google Scholar] [CrossRef]
- Deng, X.; Liu, S.; Ong, M.C.; Ji, C. Numerical simulations of free-surface waves past two vertically aligned horizontal circular cylinders. Ocean Eng. 2019, 172, 550–561. [Google Scholar] [CrossRef]
- Koterayama, W.; Matsumoto, N. Experimental study of hydrodynamic forces and wave forces exerted on a truss structure. Ocean Eng. 1982, 9, 221–234. [Google Scholar] [CrossRef]
- Tian, X.; Liu, Y.; Liu, G.; Xie, Y.; Wang, S. Experimental study on influencing factors of hydrodynamic coefficient for jack-up platform. Ocean Eng. 2019, 193, 106588. [Google Scholar] [CrossRef]
- Xie, Y.; Huang, J.; Li, X.; Tian, X.; Liu, G.; Leng, D. Experimental study on hydrodynamic characteristics of three truss-type legs of jack-up offshore platform. Ocean Eng. 2021, 234, 109305. [Google Scholar] [CrossRef]
- Ye, H.; Yu, D.; Ye, J.; Yang, Z. Numerical analysis of dynamics of jack-up offshore platform and its seabed foundation under ocean wave. Appl. Sci. 2022, 12, 3299. [Google Scholar] [CrossRef]
- Gao, J.; Shang, Y.; Ding, L.; Feng, X. Simulation of overall performance of jack up platforms under multiple working conditions. In Methods and Applications for Modeling and Simulation of Complex Systems; Springer: Singapore, 2024; Volume 2170, pp. 3–13. [Google Scholar]
- Finnegan, W.; Goggins, J. Numerical simulation of linear water waves and wave–structure interaction. Ocean Eng. 2012, 43, 23–31. [Google Scholar] [CrossRef]
- Prasad, D.D.; Ahmed, M.R.; Lee, Y.H.; Sharma, R.N. Validation of a piston type wave-maker using numerical wave tank. Ocean Eng. 2017, 131, 57–67. [Google Scholar] [CrossRef]
- Tian, X.; Wang, Q.; Liu, G.; Deng, W.; Gao, Z. Numerical and experimental studies on a three-dimensional numerical wave tank. IEEE Access 2018, 6, 6585–6593. [Google Scholar] [CrossRef]
- Qiao, D.; Feng, C.; Yan, J.; Liang, H.; Ning, D.; Li, B. Numerical simulation and experimental analysis of wave interaction with a porous plate. Ocean Eng. 2020, 218, 108106. [Google Scholar] [CrossRef]
- Oliveira, D.; Lopes de Almeida, J.P.P.G.; Santiago, A.; Rigueiro, C. Development of a cfd-based numerical wave tank of a novel multipurpose wave energy converter. Renew. Energy 2022, 199, 226–245. [Google Scholar] [CrossRef]
- De Vita, F.; Di Mascio, A.; Onorato, M. A navier–stokes numerical wave tank with a pressure-based relaxation zone method. Ocean Eng. 2022, 266, 113207. [Google Scholar] [CrossRef]
- Yu, X.; Shao, Y.; Fuhrman, D.R.; Zhang, Y. A viscous numerical wave tank based on immersed-boundary generalized harmonic polynomial cell (ib-ghpc) method: Accuracy, validation and application. Coast. Eng. 2023, 180, 104273. [Google Scholar] [CrossRef]



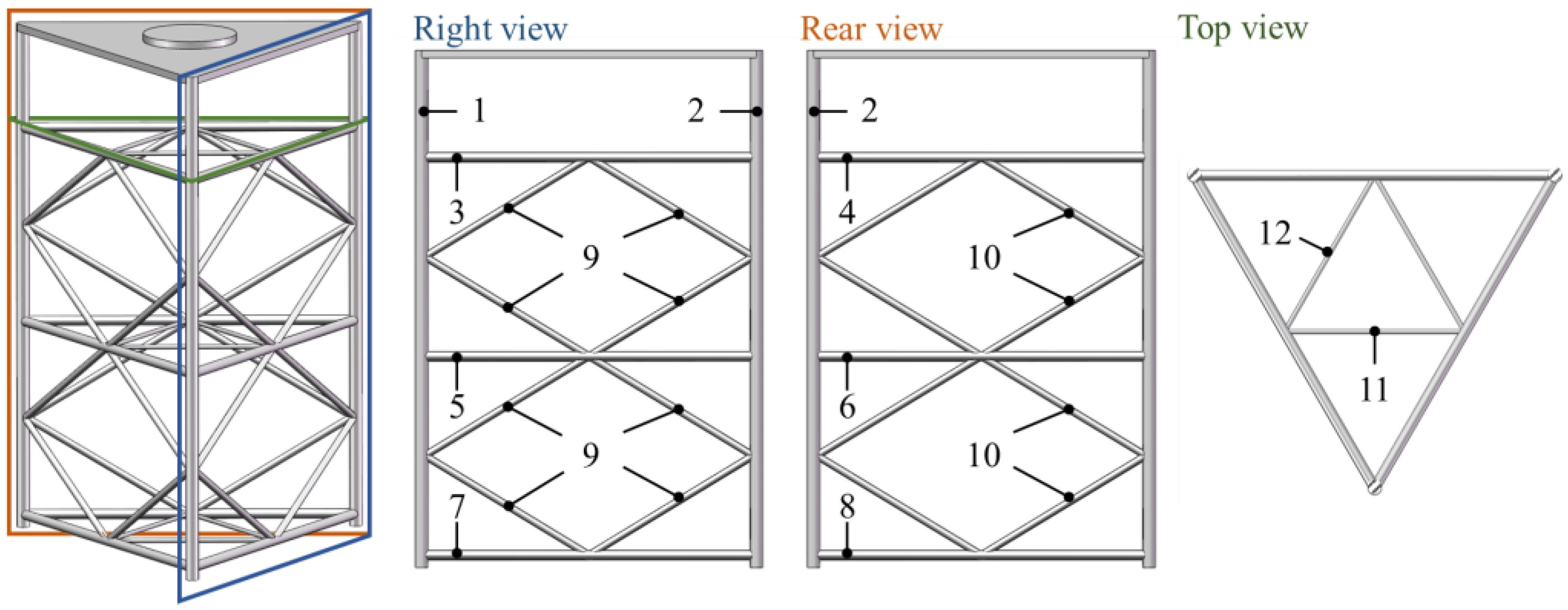


| Mesh Type | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| L/Δx | 20 | 40 | 60 | 80 |
| H/Δy | 5 | 10 | 15 | 20 |
| Δx (m) | 0.08 | 0.04 | 0.027 | 0.02 |
| Δy (m) | 0.02 | 0.01 | 0.0067 | 0.005 |
| Δx/Δy | 4 | 4 | 4 | 4 |
| Mesh Type | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Wave height (m) | 0.09532 | 0.09786 | 0.09863 | 0.09889 |
| Relative tolerance | 4.68% | 2.14% | 1.37% | 1.11% |
| Dimension | Main Chord | Cross Brace | Inclined Brace | Inner Cross Brace |
|---|---|---|---|---|
| Diameter (m) | 0.051 | 0.038 | 0.027 | 0.016 |
| Length (m) | 2.1 | 1.56 | 0.88 | 0.78 |
| Parameters | Values | |||
|---|---|---|---|---|
| Symbol | Case 1 | Case 2 | Case 3 | Case 4 |
| Wave height (m) | 0.05 | 0.1 | 0.15 | 0.2 |
| Wave period (s) | 1 | 1 | 1.5 | 2 |
| Inflow angle (°) | 0, 30, 45, 60, and 90 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, H.; Xie, Y.; Chen, D.-L.; Huang, J.; Zhou, C.-L.; Li, X.; Liu, G.; Zhu, J. Numerical Simulation and Theoretical Analysis of Wave Loads on Truss Legs for Offshore Energy Platforms. Energies 2025, 18, 5032. https://doi.org/10.3390/en18185032
Yuan H, Xie Y, Chen D-L, Huang J, Zhou C-L, Li X, Liu G, Zhu J. Numerical Simulation and Theoretical Analysis of Wave Loads on Truss Legs for Offshore Energy Platforms. Energies. 2025; 18(18):5032. https://doi.org/10.3390/en18185032
Chicago/Turabian StyleYuan, Haoxun, Yingchun Xie, Di-Lin Chen, Jintong Huang, Cheng-Long Zhou, Xiangkun Li, Guijie Liu, and Jinchi Zhu. 2025. "Numerical Simulation and Theoretical Analysis of Wave Loads on Truss Legs for Offshore Energy Platforms" Energies 18, no. 18: 5032. https://doi.org/10.3390/en18185032
APA StyleYuan, H., Xie, Y., Chen, D.-L., Huang, J., Zhou, C.-L., Li, X., Liu, G., & Zhu, J. (2025). Numerical Simulation and Theoretical Analysis of Wave Loads on Truss Legs for Offshore Energy Platforms. Energies, 18(18), 5032. https://doi.org/10.3390/en18185032






