Optimizing the Thermodynamic Performance of the Fuel/Lubricating Oil Heat Exchanger for an Aeroengine
Abstract
1. Introduction
2. Correlation Formulas
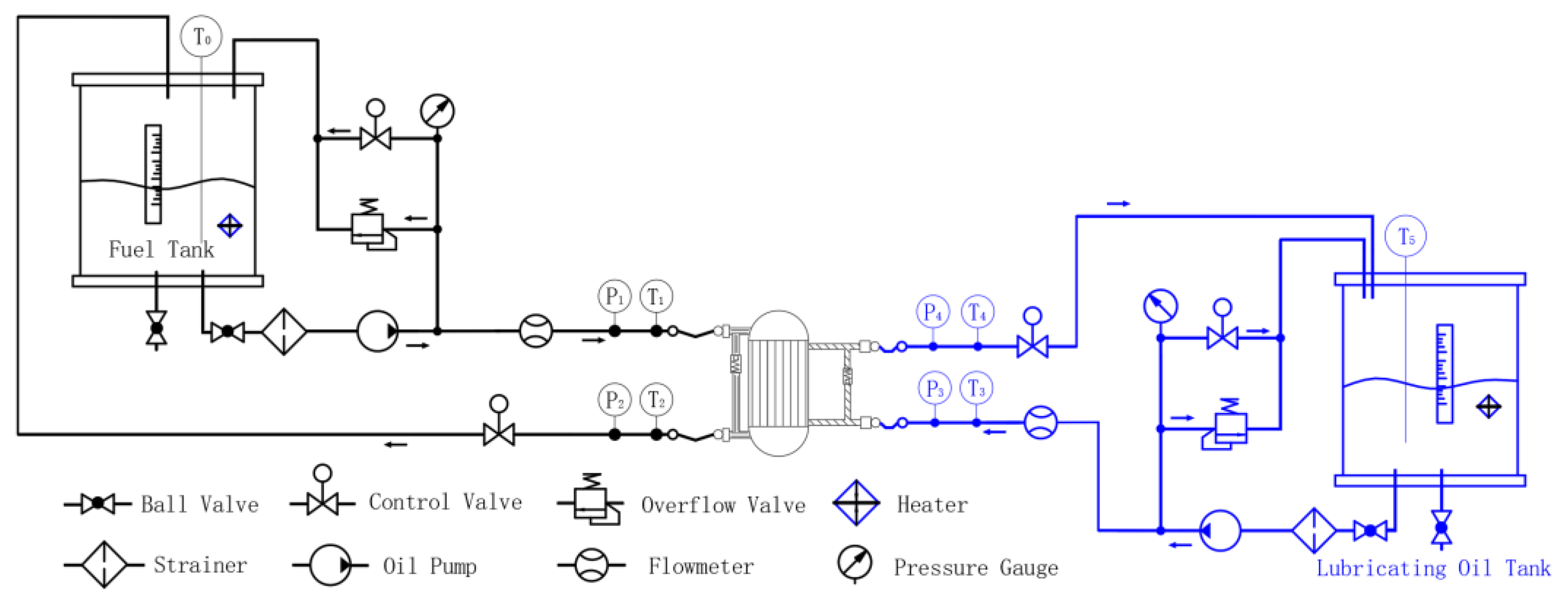
3. Experimental Sections
4. Results and Discussion
4.1. Calculation and Analysis for Original Structure
4.1.1. Model Building
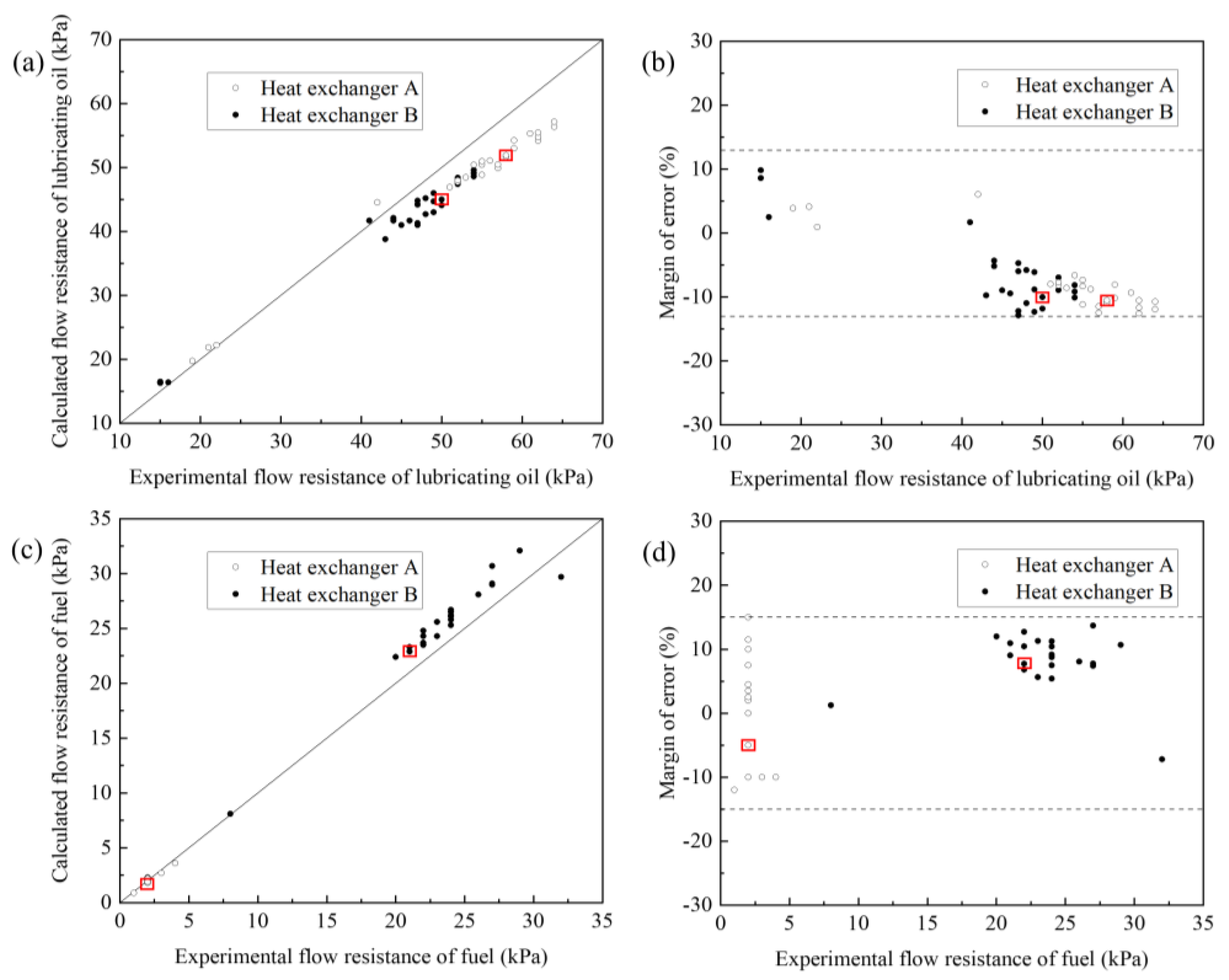
4.1.2. Comparison Between Experimental and Calculated Results
4.1.3. Thermal Resistance and Velocity Analysis
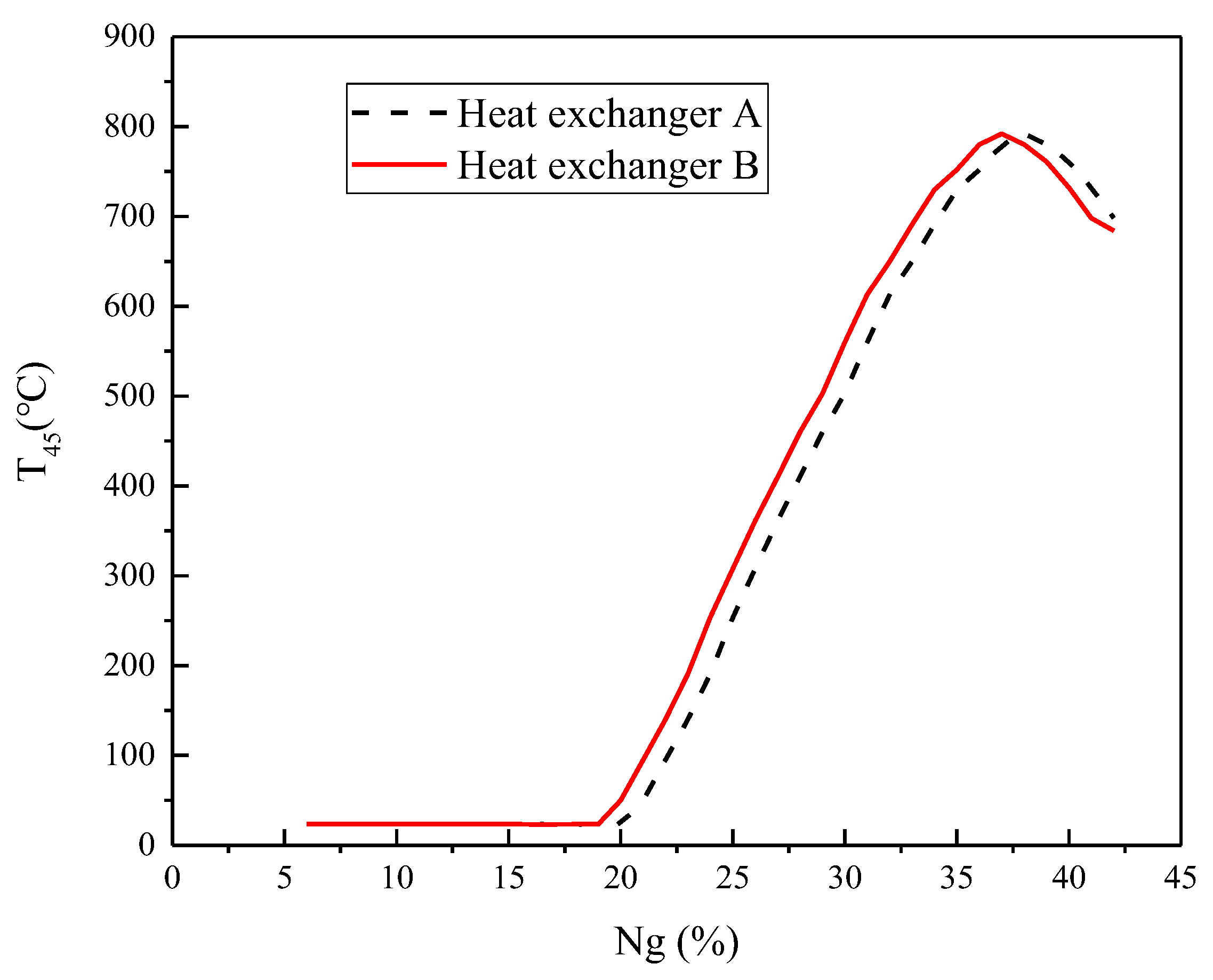
4.1.4. Whole Aeroengine Test
4.2. Structural Analysis and Improvement
4.2.1. Model Building
4.2.2. Geometric Parameters of Twisted Tape Inserts
- 1.
- Influence of the Twist Ratio and Thickness on the Tube-Side Heat Transfer Coefficient
- 2.
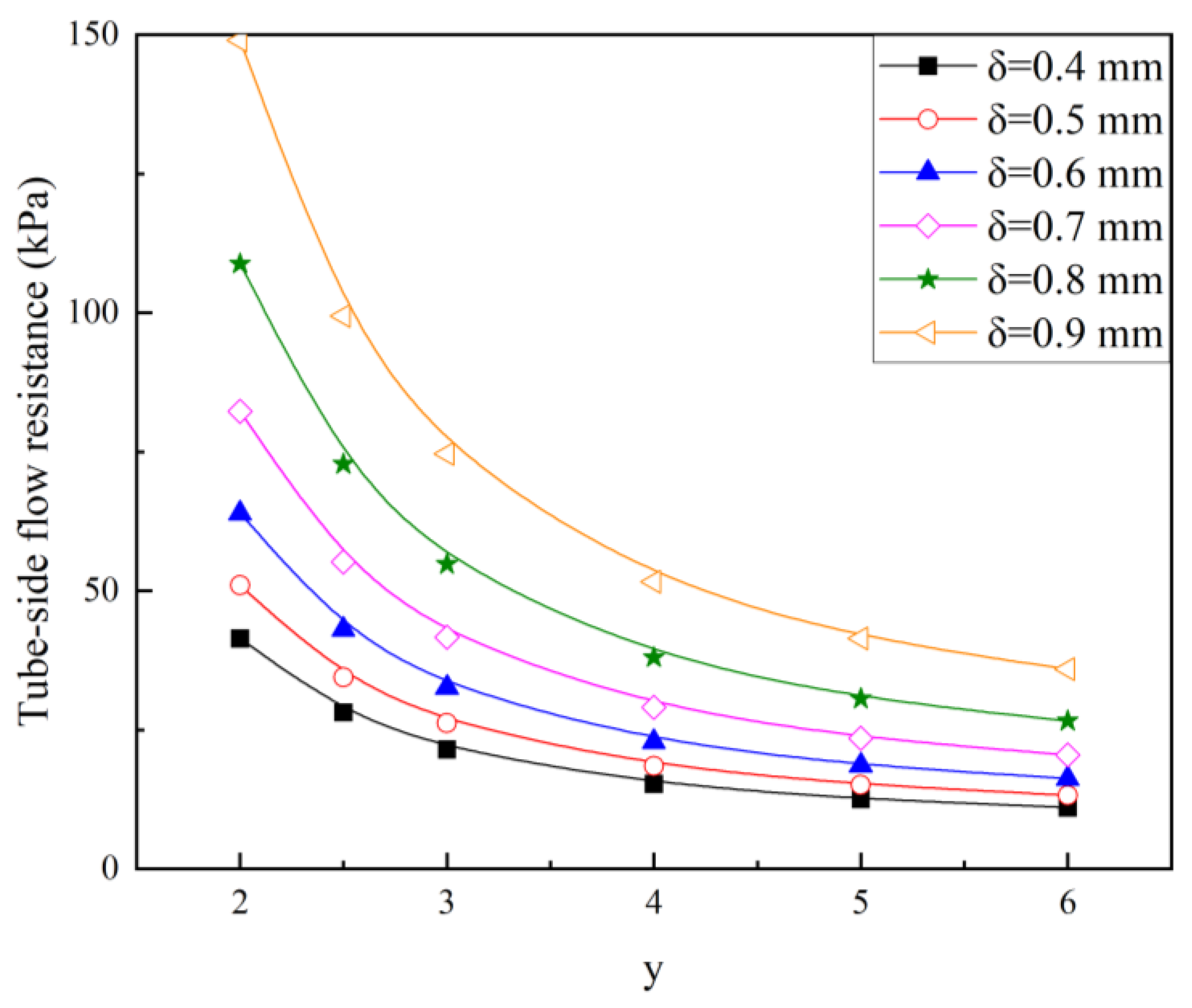
- Influence of the Twist Ratio and Thickness on the Tube-Side Flow Resistance
- 3.
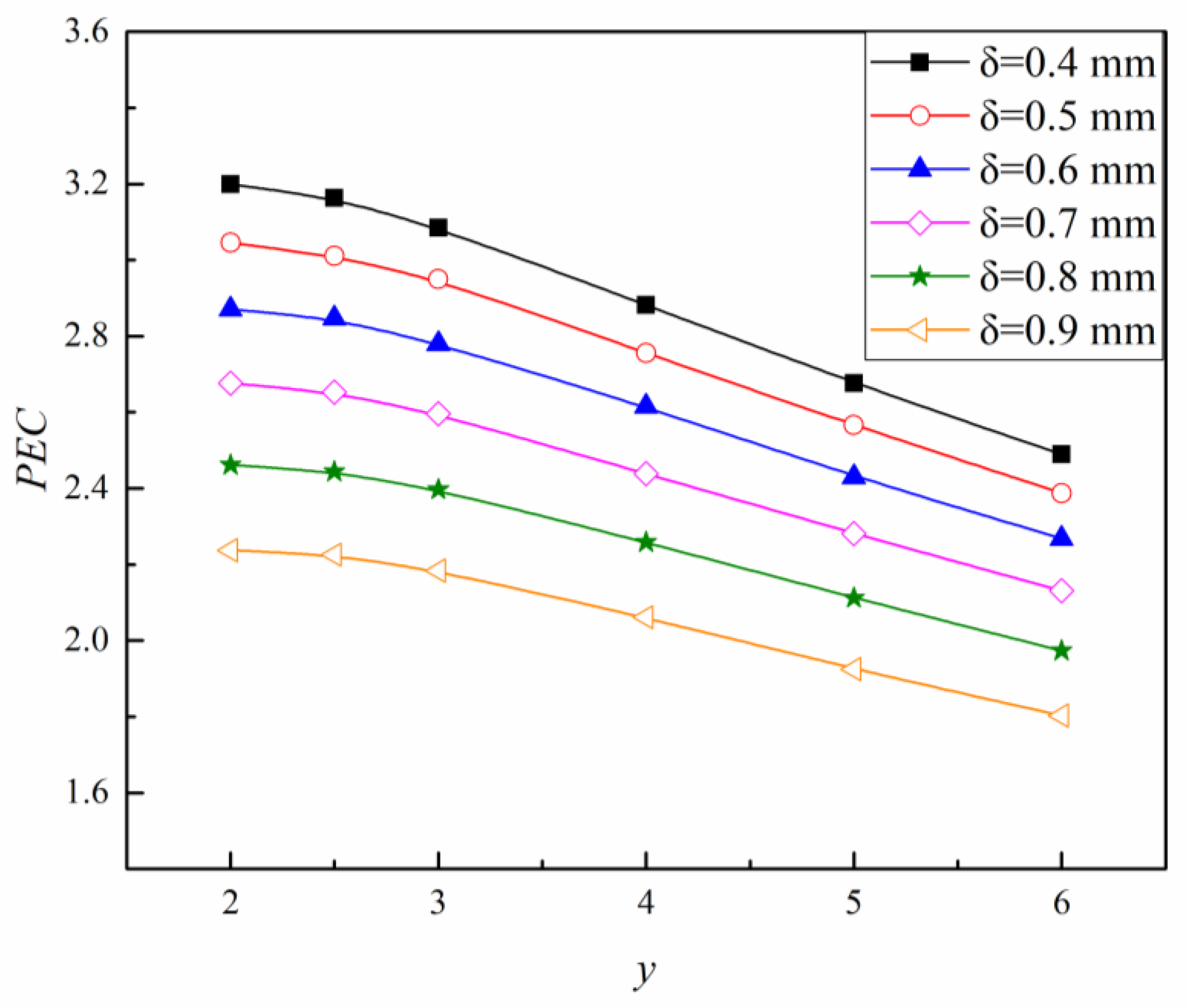
- Influence of the Twist Ratio and Thickness on the PEC
- 4.
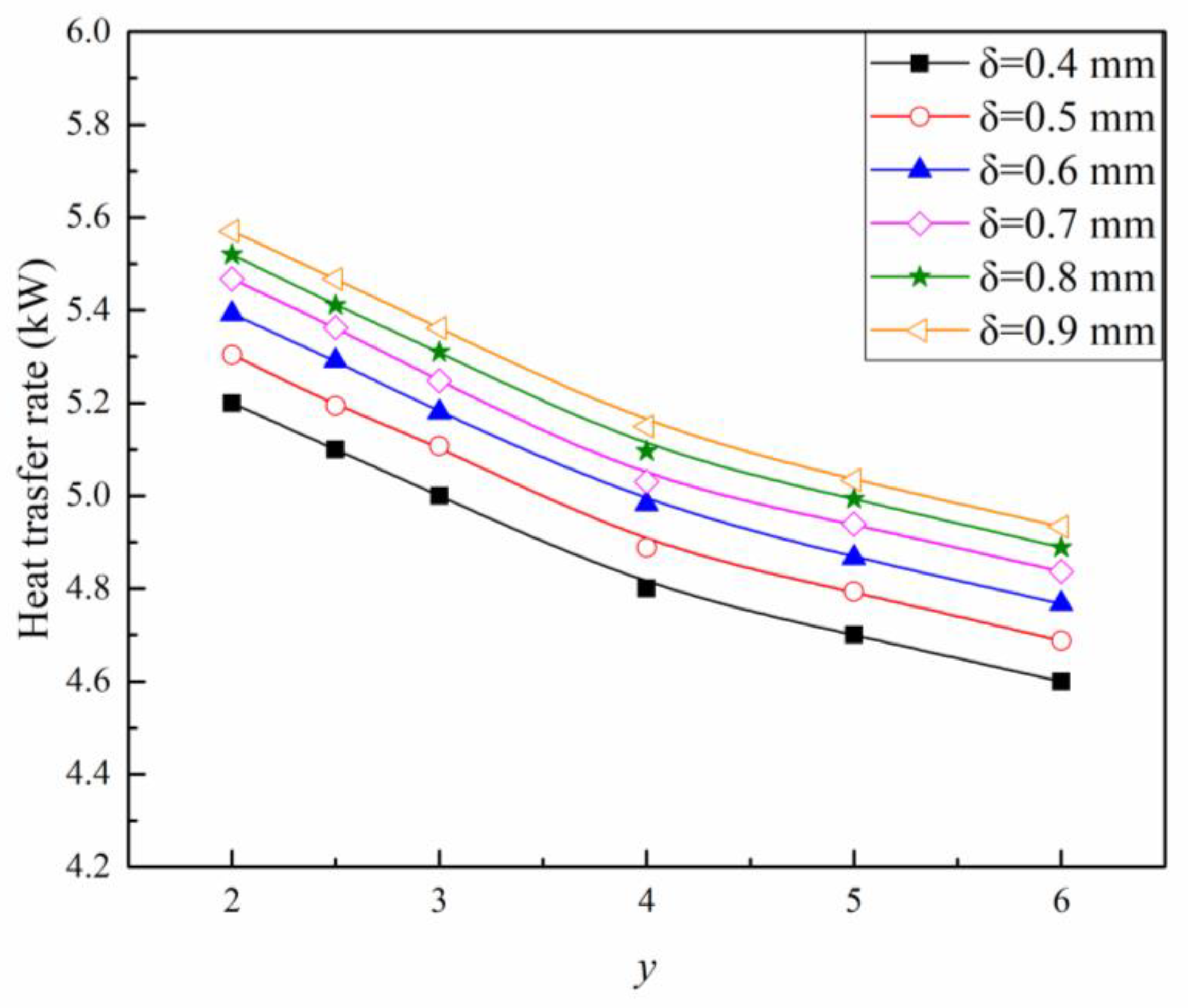
- Influence of the Twist Ratio and Thickness on the Heat Transfer Rate
4.2.3. Comparison Between Experimental and Calculated Results
4.2.4. Thermal Resistance and Velocity Analysis
4.2.5. Performance Evaluation and Whole Aeroengine Test
5. Conclusions
- (1)
- The HTRI-calculated results for heat exchanger A demonstrated excellent agreement with experimental data, showing maximum deviations of ±2% for outlet temperatures and ±15% for flow resistances. The model quantitatively identified that 84.6% of total thermal resistance resided on the tube side (fuel flow), providing critical guidance for optimization. The whole aeroengine test indicated that slow tube-side fuel velocity (0.25 m/s) prolonged fuel filling time, adversely affecting fuel ignition and aeroengine starting.
- (2)
- Based on HTRI-calculated results, whole aeroengine test data, and the technical requirements, the fuel/lubricating oil heat exchanger B incorporating twisted tape inserts was proposed. The thickness and the twist ratio of twisted tapes were finally determined to be 0.5 mm and 4, respectively.
- (3)
- Experimental verification of heat exchanger B confirmed the calculation model’s accuracy, maintaining prediction errors within ±2% for temperatures and ±15% for flow resistances, well within acceptable engineering tolerances. The optimized design achieved remarkable performance improvements with 82.6% reduction in tube-side thermal resistance, 213% increase in overall heat transfer coefficient, and 18.0% reduction in total heat exchanger mass.
- (4)
- Finally, the integrated experimental-computational workflow confirmed that the improved fuel/lubricating oil heat exchanger B simultaneously addressed conflicting requirements of mass reduction, flow resistance control, and heat transfer rate enhancement at the same time. Moreover, the system-level test (whole aeroengine test) indicated that the structural optimization directly improved ignition reliability, confirming excellent aeroengine starting compatibility.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Glossary
| Nomenclature | |
| A | heat transfer area, namely, outer wall area (m2) |
| Ai | inner wall area (m2) |
| Am | log mean heat transfer area of inner wall and outer wall (m2) |
| Ao | outer wall area (m2) |
| b | tube wall thickness (m) |
| cp | heat capacity (J/(kg·K)) |
| di | tube inner diameter (m) |
| do | tube outer diameter (m) |
| D | hydrodynamic diameter of the tube (m) |
| H | pitch of twisted tape inserts (mm) |
| l | tube length (m) |
| K | overall heat transfer coefficient (W/(m2·K)) |
| Q | heat transfer rate (W) |
| Rsi | tube-side fouling resistance (m2·K/W) |
| Rso | shell-side fouling resistance (m2·K/W) |
| y | twist ratio |
| Greek symbols | |
| α | tube-side heat transfer coefficient (J/(m2·K)) |
| αi | tube-side heat transfer coefficient (J/(m2·K)) |
| αs | shell-side heat transfer coefficient (J/(m2·K)) |
| δ | thickness of twisted tape inserts (mm) |
| flow resistance (kPa) | |
| Δtm | logarithmic mean temperature difference (K) |
| maximum end temperature difference (K) | |
| minimum end temperature difference (K) | |
| λ | coefficient of thermal conductivity (W/(m·K)) |
| viscosity (mPa·s) | |
| density (kg/m3) | |
References
- Che, M.; Elbel, S. Experimental study of local air-side heat transfer coefficient on real-scale heat exchanger fins by employing an absorption-based mass transfer method. Appl. Therm. Eng. 2021, 189, 116718. [Google Scholar] [CrossRef]
- Wang, S.; Wen, J.; Li, Y. An experimental investigation of heat transfer enhancement for a shell-and-tube heat exchanger. Appl. Therm. Eng. 2009, 29, 2433–2438. [Google Scholar] [CrossRef]
- Raei, B.; Shahraki, F.; Jamialahmadi, M.; Peyghambarzadeh, S. Different methods to calculate heat transfer coefficient in a double-tube heat exchanger: A comparative study. Exp. Heat Transf. 2018, 31, 32–46. [Google Scholar] [CrossRef]
- Samadifar, M.; Toghraie, D. Numerical simulation of heat transfer enhancement in a plate-fin heat exchanger using a new type of vortex generators. Appl. Therm. Eng. 2018, 133, 671–681. [Google Scholar] [CrossRef]
- Li, L.; Du, X.; Yang, L.; Xu, Y.; Yang, Y. Numerical simulation on flow and heat transfer of fin structure in air-cooled heat exchanger. Appl. Therm. Eng. 2013, 59, 77–86. [Google Scholar] [CrossRef]
- Gu, J. Calculating method and experimental verification of heat transfer characteristics for tube and shell type fuel and oil heat exchanger. Aeroengine 2013, 39, 65–69. [Google Scholar]
- Cai, H.; Weng, Z.; Liao, Y.; Gu, K.; Wang, J. Research on an arc air-lubricating oil radiator equipped in internal surface of air intake for the aero engine. J. Therm. Sci. 2020, 29, 687–696. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Y.; Pang, L.; Xu, Z. Research on the fin performance of air-oil heat exchanger for aircraft engine. In Proceedings of the International Conference on Man-Machine-Environment System Engineering, Singapore, 23–25 October 2021; Springer: Berlin/Heidelberg, Germany, 2022; pp. 419–426. [Google Scholar]
- Donohue, D.A. Heat transfer and pressure drop in heat exchangers. Ind. Eng. Chem. 1949, 41, 2499–2511. [Google Scholar] [CrossRef]
- Kern, D.Q. Process Heat Transfer; Tata McGraw-Hill Education: New York, NY, USA, 1997. [Google Scholar]
- Bell, K.J. Final Report of the Cooperative Research Program on Shell and Tube Heat Exchangers; University of Delaware, Engineering Experimental Station: Newark, DE, USA, 1963. [Google Scholar]
- Palen, J.; Taborek, J. Solution of shell side flow pressure drop and heat transfer by stream analysis method. Chem. Eng. Prog. Symp. Ser. 1969, 65, 53–63. [Google Scholar]
- Tinker, T. Shell side characteristics of shell and tube heat exchangers. Gen. Discuss. Heat Transf. 1951, 80, 89–116. [Google Scholar]
- Hu, Q.; Qu, X.; Peng, W.; Wang, J. Experimental and numerical investigation of turbulent heat transfer enhancement of an intermediate heat exchanger using corrugated tubes. J. Heat Mass Transf. 2022, 185, 122385. [Google Scholar] [CrossRef]
- Kirkar, S.M.; Gönül, A.; Celen, A.; Dalkilic, A.S. Multi-objective optimization of single-phase flow heat transfer characteristics in corrugated tubes. Int. J. Therm. Sci. 2023, 186, 108119. [Google Scholar] [CrossRef]
- Wu, J.; Lu, S.; Wang, C.; Li, J. Numerical study on heat transfer characteristics of helically coiled grooved elliptical tube heat exchanger. Int. J. Heat Fluid Flow 2024, 110, 109622. [Google Scholar] [CrossRef]
- Al-Obaidi, A.R. The influence of different twisted tape inserts configurations on thermo-hydraulic performance and enhancement of heat transfer in the 3D circular tube. Korean J. Chem. Eng. 2023, 40, 770–790. [Google Scholar] [CrossRef]
- Liaw, K.L.; Kurnia, J.C.; Sasmito, A.P. Enhancing supercritical carbon dioxide heat transfer in helical tube heat exchangers with twisted tape inserts: A computational investigation. Int. J. Heat Mass Transf. 2024, 227, 125598. [Google Scholar] [CrossRef]
- Chompookham, T.; Chingtuaythong, W.; Chokphoemphun, S. Influence of a novel serrated wire coil insert on thermal characteristics and air flow behavior in a tubular heat exchanger. Int. J. Therm. Sci. 2022, 171, 107184. [Google Scholar] [CrossRef]
- García, A.; Herrero-Martin, R.; Pérez-García, J.; Solano, J. Validation of a new methodological approach for the selection of wire-coil inserts in thermal equipment. Appl. Therm. Eng. 2023, 218, 119273. [Google Scholar] [CrossRef]
- Rashid, F.L.; Dhaidan, N.S.; Mahdi, A.J.; Azziz, H.N.; Parveen, R.; Togun, H.; Homod, R.Z. Heat transfer enhancement of phase change materials using letters-shaped fins: A review. Int. Commun. Heat Mass Transf. 2024, 159, 108096. [Google Scholar] [CrossRef]
- Khudhur, D.S.; Al-Zuhairy, R.C.; Kassim, M.S. Thermal analysis of heat transfer with different fin geometry through straight plate-fin heat sinks. Int. J. Therm. Sci. 2022, 174, 107443. [Google Scholar] [CrossRef]
- Boujelbene, M.; Mohammed, H.I.; Sultan, H.S.; Eisapour, M.; Chen, Z.; Mahdi, J.M.; Cairns, A.; Talebizadehsardari, P. A comparative study of twisted and straight fins in enhancing the melting and solidifying rates of PCM in horizontal double-tube heat exchangers. Int. Commun. Heat Mass Transf. 2024, 151, 107224. [Google Scholar] [CrossRef]
- Xu, P.; Wen, J.; Wang, S.; Chen, Q.; Li, Y. Numerical simulation on flow and heat transfer performances of serrated and wavy fins in plate-fin heat exchanger for hydrogen liquefaction. Int. J. Hydrogen Energy 2023, 48, 20680–20693. [Google Scholar] [CrossRef]
- Cheng, Z.; Xu, R.; Jiang, P. Morphology, flow and heat transfer in triply periodic minimal surface based porous structures. Int. J. Heat Mass Transf. 2021, 170, 120902. [Google Scholar] [CrossRef]
- Du, L.; Hu, W. An overview of heat transfer enhancement methods in microchannel heat sinks. Chem. Eng. Sci. 2023, 280, 119081. [Google Scholar] [CrossRef]
- Dagdevir, T.; Ozceyhan, V. An experimental study on heat transfer enhancement and flow characteristics of a tube with plain, perforated and dimpled twisted tape inserts. Int. J. Therm. Sci. 2021, 159, 106564. [Google Scholar] [CrossRef]
- Soltani, M.M.; Gorji-Bandpy, M.; Vaisi, A.; Moosavi, R. Heat transfer augmentation in a double-pipe heat exchanger with dimpled twisted tape inserts: An experimental study. Heat Mass Transf. 2022, 58, 1591–1606. [Google Scholar] [CrossRef]
- Hamza, N.F.A.; Aljabair, S. Evaluation of thermal performance factor by hybrid nanofluid and twisted tape inserts in heat exchanger. Heliyon 2022, 8, e11950. [Google Scholar] [CrossRef] [PubMed]
- Man, C.; Lv, X.; Hu, J.; Sun, P.; Tang, Y. Experimental study on effect of heat transfer enhancement for single-phase forced convective flow with twisted tape inserts. Int. J. Heat Mass Transf. 2017, 106, 877–883. [Google Scholar] [CrossRef]
- Mashayekhi, R.; Arasteh, H.; Talebizadehsardari, P.; Kumar, A.; Hangi, M.; Rahbari, A. Heat Transfer Enhancement of nanofluid flow in a tube equipped with rotating twisted tape inserts: A two-phase approach. Heat Transf. Eng. 2022, 43, 608–622. [Google Scholar] [CrossRef]
- Esmaeilzadeh, E.; Almohammadi, H.; Nokhosteen, A.; Motezaker, A.; Omrani, A. Study on heat transfer and friction factor characteristics of γ-Al2O3/water through circular tube with twisted tape inserts with different thicknesses. Int. J. Therm. Sci. 2014, 82, 72–83. [Google Scholar] [CrossRef]
- Zeng, M.; Tang, L.; Lin, M.; Wang, Q. Optimization of heat exchangers with vortex-generator fin by Taguchi method. Appl. Therm. Eng. 2010, 30, 1775–1783. [Google Scholar] [CrossRef]
- Siavashi, M.; Bahrami, H.R.T.; Aminian, E. Optimization of heat transfer enhancement and pumping power of a heat exchanger tube using nanofluid with gradient and multi-layered porous foams. Appl. Therm. Eng. 2018, 138, 465–474. [Google Scholar] [CrossRef]
- Setareh, M.; Saffar, M.; Abdullah, A. Experimental and numerical study on heat transfer enhancement using ultrasonic vibration in a double-pipe heat exchanger. Appl. Therm. Eng. 2019, 159, 113867. [Google Scholar] [CrossRef]
- Ghalambaz, M.; Arasteh, H.; Mashayekhi, R.; Keshmiri, A.; Talebizadehsardari, P.; Yaïci, W. Investigation of overlapped twisted tapes inserted in a double-pipe heat exchanger using two-phase nanofluid. Nanomaterials 2020, 10, 1656. [Google Scholar] [CrossRef] [PubMed]
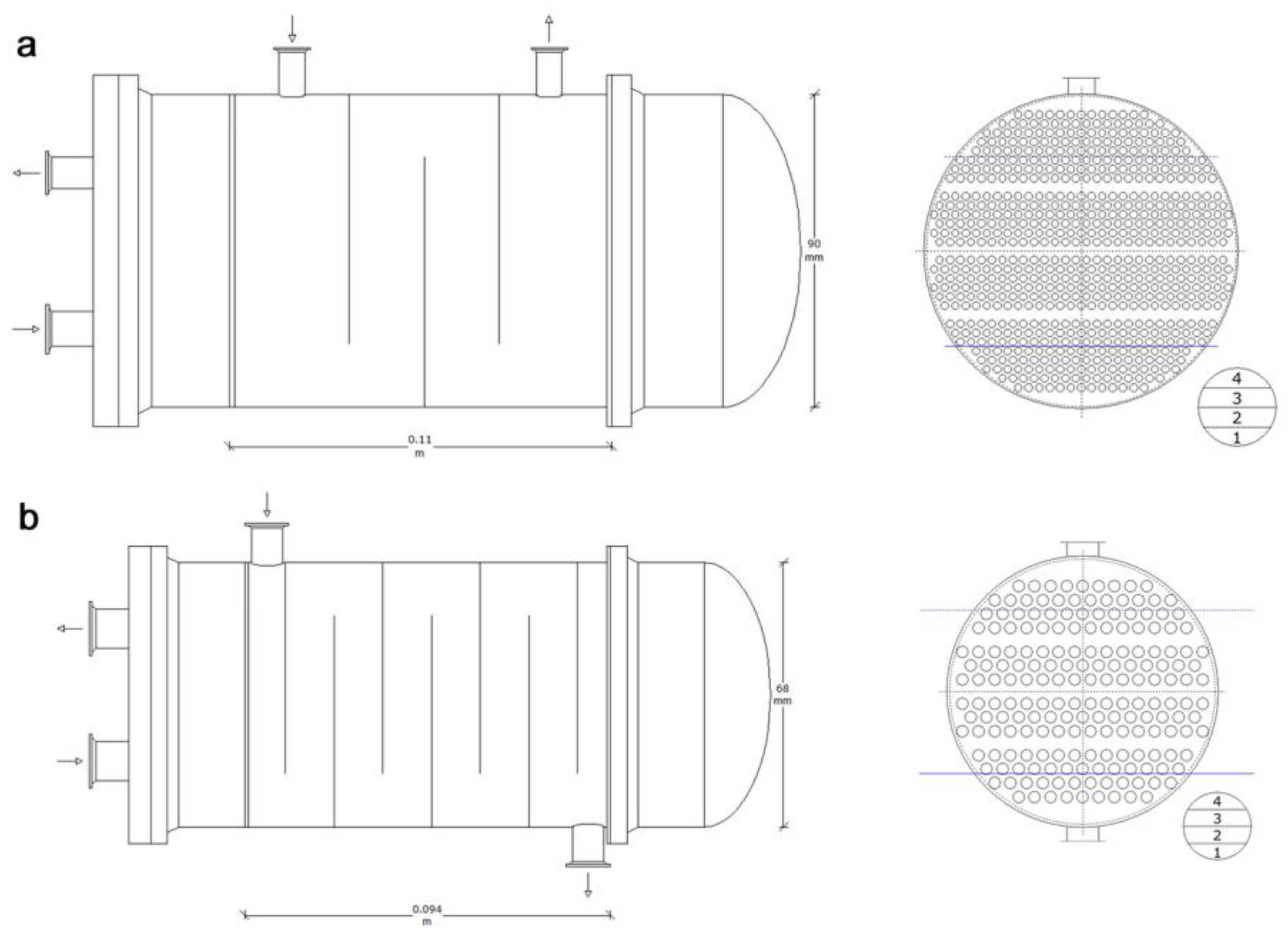



| Parameters (Unit) | Heat Exchanger A | Heat Exchanger B |
|---|---|---|
| Tube numbers | 662 | 186 |
| Tube size (mm) | 2.36 × 0.3 | 3 × 0.35 |
| Tube length (mm) | 110 | 110 |
| Tube type and material | plain tubes, aluminum alloy 3A21 | plain tubes with twisted tape inserts, aluminum alloy 3A21 |
| Tube pitch (mm) | 3 | 4 |
| Tube layout angle (°) | 30 | 30 |
| Tube passes | 4 | 4 |
| Shell passes | 1 | 1 |
| Shell inner diameter (mm) | 90 | 68 |
| Baffle spacing (mm) | 21.5 | 21.5 |
| Baffle cut (%) | 20 | 20 |
| Baffle numbers | 3 | 7 |
| Weight (kg) | 1.78 | 1.46 |
| Performance Parameters | Heat Exchanger A | Heat Exchanger B | ||||
|---|---|---|---|---|---|---|
| Experimental Results | Calculated Results | Error | Experimental Results | Calculated Results | Error | |
| Outlet temperature of lubricating oil | 96.5 °C | 97.7 °C | 1.2% | 97.2 °C | 96.7 °C | −0.5% |
| Outlet temperature of fuel | 86.8 °C | 87.4 °C | 0.7% | 89.2 °C | 90.0 °C | 0.9% |
| Flow resistance of lubricating oil | 58 kPa | 52.3 kPa | −10% | 49 kPa | 46.0 kPa | −6.1% |
| Flow resistance of fuel | 2 kPa | 1.9 kPa | −5% | 17 kPa | 18.5 kPa | 8.8% |
| Reynolds number of lubricating oil | 511 | 588 | 15.1% | 1428 | 1637 | 14.6% |
| Reynolds number of fuel | 95 | 91 | −4.3% | 462 | 495 | 7.1% |
| Parameters (Unit) | Heat Exchanger A | Heat Exchanger B |
|---|---|---|
| Heat transfer rate (kW) | 4.40 | 4.89 |
| Heat transfer area (m2) | 0.527 | 0.188 |
| Shell-side heat transfer coefficient (W/(m2·K)) | 2070.4 | 2186.2 |
| Tube-side heat transfer coefficient (W/(m2·K)) | 501.4 | 2995.4 |
| Overall heat transfer coefficient (W/(m2·K)) | 316.5 | 990.9 |
| Shell-side thermal resistance (m2·K/W) | 0.000483 | 0.000457 |
| Tube-side thermal resistance (m2·K/W) | 0.002674 | 0.000464 |
| Tube wall thermal resistance (m2·K/W) | 0.000002 | 0.000002 |
| Shell-side velocity (m/s) | 0.71 | 0.85 |
| Tube-side velocity (m/s) | 0.25 | 0.53 |
| Crossflow velocity (m/s) | 0.75 | 0.84 |
| Window velocity (m/s) | 0.44 | 0.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Shen, H.; Zeng, G.; Jiang, H.; Li, W.; An, S. Optimizing the Thermodynamic Performance of the Fuel/Lubricating Oil Heat Exchanger for an Aeroengine. Energies 2025, 18, 4955. https://doi.org/10.3390/en18184955
Li G, Shen H, Zeng G, Jiang H, Li W, An S. Optimizing the Thermodynamic Performance of the Fuel/Lubricating Oil Heat Exchanger for an Aeroengine. Energies. 2025; 18(18):4955. https://doi.org/10.3390/en18184955
Chicago/Turabian StyleLi, Guangle, Haijun Shen, Guangle Zeng, Huiqing Jiang, Wang Li, and Shuai An. 2025. "Optimizing the Thermodynamic Performance of the Fuel/Lubricating Oil Heat Exchanger for an Aeroengine" Energies 18, no. 18: 4955. https://doi.org/10.3390/en18184955
APA StyleLi, G., Shen, H., Zeng, G., Jiang, H., Li, W., & An, S. (2025). Optimizing the Thermodynamic Performance of the Fuel/Lubricating Oil Heat Exchanger for an Aeroengine. Energies, 18(18), 4955. https://doi.org/10.3390/en18184955






