Multi-Time-Scale Demand Response Optimization in Active Distribution Networks Using Double Deep Q-Networks

Abstract

This paper presents a deep reinforcement learning-based demand response (DR) optimization framework for active distribution networks under uncertainty and user heterogeneity. The proposed model utilizes a Double Deep Q-Network (Double DQN) to learn adaptive, multi-period DR strategies across residential, commercial, and electric vehicle (EV) participants in a 24 h rolling horizon. By incorporating a structured state representation—including forecasted load, photovoltaic (PV) output, dynamic pricing, historical DR actions, and voltage states—the agent autonomously learns control policies that minimize total operational costs while maintaining grid feasibility and voltage stability. The physical system is modeled via detailed constraints, including power flow balance, voltage magnitude bounds, PV curtailment caps, deferrable load recovery windows, and user-specific availability envelopes. A case study based on a modified IEEE 33-bus distribution network with embedded PV and DR nodes demonstrates the framework’s effectiveness. Simulation results show that the proposed method achieves significant cost savings (up to 35% over baseline), enhances PV absorption, reduces load variance by 42%, and maintains voltage profiles within safe operational thresholds. Training curves confirm smooth Q-value convergence and stable policy performance, while spatiotemporal visualizations reveal interpretable DR behavior aligned with both economic and physical system constraints. This work contributes a scalable, model-free approach for intelligent DR coordination in smart grids, integrating learning-based control with physical grid realism. The modular design allows for future extension to multi-agent systems, storage coordination, and market-integrated DR scheduling. The results position Double DQN as a promising architecture for operational decision-making in AI-enabled distribution networks.

1. Introduction

The increasing decentralization and digitalization of power systems have significantly reshaped the landscape of distribution network operation and planning. Modern distribution grids are no longer passive carriers of upstream electricity but dynamic, interactive platforms characterized by bi-directional flows, distributed generation, flexible loads, and customer-driven behavior [1,2,3]. This transformation is driven in part by the growing penetration of distributed energy resources (DERs), particularly rooftop photovoltaic (PV) systems, and in part by the rise of electrified end uses such as electric vehicles (EVs), smart HVAC systems, and responsive commercial processes [4,5,6]. These evolutions have introduced unprecedented volatility and uncertainty at the distribution level, necessitating a shift from traditional top–down control paradigms to decentralized, adaptive, and learning-based operational strategies. In this emerging landscape, demand response (DR) has been widely recognized as a pivotal mechanism for enabling flexibility. By allowing consumers to adjust their electricity consumption in response to grid conditions or market prices, DR helps mitigate peak loads, reduce balancing costs, and enhance renewable energy absorption. Foundational DR strategies have traditionally been designed around static load curtailment or time-of-use (ToU) pricing programs, with central operators issuing broadcast signals to aggregate users. These methods, while effective in earlier contexts, suffer from limited granularity, low user engagement, and an inability to cope with high-resolution operational variability [7,8]. Consequently, the DR modeling community has gradually shifted toward more dynamic, optimization-based frameworks that aim to incorporate multi-period scheduling, customer diversity, and fine-grained control decisions.

A rich literature has developed around optimization-based DR strategies, with linear programming, mixed-integer programming (MIP), and stochastic programming forming the dominant modeling paradigms. These models enable explicit control over curtailment schedules, load-shifting constraints, thermal dynamics, and economic incentives [9,10]. For example, bilevel programming frameworks have been proposed to represent hierarchical interactions between aggregators and users, while game-theoretic and Stackelberg formulations have been used to model strategic response under price uncertainty. Despite their sophistication, these approaches typically rely on perfect foresight, fixed user preferences, and deterministic models of demand elasticity [11,12]. The calibration of such models is often nontrivial, and their scalability becomes a challenge as the number of controllable nodes increases. Furthermore, they are inherently constrained by the requirement to re-solve optimization problems at each interval, often under tight time windows, which restricts their real-time applicability. To enhance robustness against forecast error and model mis-specification, robust optimization (RO) and distributionally robust optimization (DRO) techniques have gained popularity in the DR field. These methods construct protective uncertainty sets or ambiguity distributions to hedge against worst-case realizations of uncertain parameters such as PV output, load, or market price [13,14,15]. While such models provide valuable reliability guarantees, they often lead to conservative decisions, especially when uncertainty sets are loosely specified. Moreover, DRO formulations typically assume convexity and require conic or semidefinite reformulations to remain tractable, adding another layer of complexity that limits real-time deployment in systems with fast dynamics and noisy measurements [16,17].

Parallel to these developments, a growing body of research has investigated the application of reinforcement learning (RL) to energy systems. As a model-free approach to sequential decision-making, RL allows agents to learn optimal control policies through interaction with an environment, without requiring explicit knowledge of the underlying system equations. In early applications to DR, simple Q-learning and SARSA algorithms were used to manage thermostatic loads and simulate user participation in real-time pricing schemes [18,19]. These methods demonstrated the feasibility of learning from data but were hampered by their reliance on discrete action spaces, slow convergence rates, and an inability to generalize across heterogeneous users or time-varying system states. The recent emergence of deep reinforcement learning (DRL) has dramatically expanded the applicability of RL in power systems [20,21]. By integrating deep neural networks with value-function or policy representations, DRL has enabled control in high-dimensional, continuous, and partially observable environments. Applications have rapidly grown to include battery scheduling, building energy management, EV charging, and microgrid coordination. In DR, DRL methods such as Deep Q-Networks (DQNs), Deep Deterministic Policy Gradient (DDPG), and Proximal Policy Optimization (PPO) have been used to optimize demand scheduling in response to dynamic prices, weather forecasts, and user preferences [22,23]. However, despite the promise of DRL, most existing implementations focus on isolated users or simplified aggregate models. Very few studies have addressed the problem of coordinating DR across multiple heterogeneous users, each with distinct temporal constraints and behavioral profiles, within a physically constrained distribution network model [24]. Moreover, the incorporation of power system constraints into DRL frameworks remains in its infancy. While some works include penalty terms in the reward to discourage violations, few rigorously enforce physical constraints such as power balance, nodal voltage limits, and line capacity bounds. This limits their applicability to real grid operations, where safety and reliability cannot be compromised. Even fewer studies have modeled time-coupled behaviors such as load recovery, deferrable consumption, or EV plug-in availability, which are essential for realistic DR planning. Most DRL papers adopt flat state representations that omit temporal dependencies or past action histories, leading to suboptimal policies in systems with strong memory effects [25,26].

In this context, the present study introduces a novel DRL-based demand response framework that integrates a Double Deep Q-Network (Double DQN) agent with a physically grounded modeling architecture for multi-user, multi-time-step scheduling in active distribution networks. The Double DQN architecture is particularly suited to this problem, as it mitigates Q-value overestimation bias by decoupling action selection from action evaluation—a key feature when the reward is shaped by noisy grid responses and sparse system-level feedback. The agent operates over a 24 h scheduling horizon, learning to coordinate flexible load adjustments across residential, commercial, and EV users based on system states that include baseline load forecasts, solar generation predictions, electricity price profiles, past DR actions, and voltage readings. These state vectors are designed to capture both the temporal dynamics and spatial distribution of user responses, providing a rich learning signal for the DRL algorithm. The modeling framework explicitly integrates a full suite of operational constraints. These include nodal power balance equations, voltage magnitude bounds, thermal line limits, PV curtailment caps, load recovery requirements, and DR action-rate constraints. Each user class is modeled with its own flexibility envelope, deferral logic, and participation window, capturing the diversity and time-coupled behavior of real-world demand. Importantly, the agent is trained not only to minimize system costs—comprising energy purchases, load-shedding penalties, and PV curtailment losses—but also to preserve system feasibility and voltage stability through structured reward components and post-decision action clipping. The combination of physical constraint modeling with high-dimensional DRL control allows the framework to operate in a realistic distribution grid setting while adapting to real-time uncertainty and user heterogeneity.

This paper is guided by a set of research questions that shape its main contributions. The first question concerns how multi-period demand response from heterogeneous users can be scheduled and coordinated in active distribution networks, which is addressed through a unified learning-based control framework that employs Double Deep Q-Networks to jointly optimize decisions across multiple time scales. A second question focuses on how optimization can remain physically feasible while reflecting both system and user constraints, which is resolved by developing a comprehensive physical modeling layer that embeds grid feasibility equations, together with user-specific demand response limitations. A third question arises with respect to how reinforcement learning can simultaneously account for economic efficiency, renewable energy integration, and voltage stability, and this challenge is overcome by formulating a multi-term reward function that balances these objectives in a coherent manner. Finally, a question is raised regarding the scalability and robustness of the proposed method under uncertainty, which is systematically validated through numerical experiments on a modified IEEE 33-bus system that demonstrate fast convergence, adaptability, and operational benefits. Collectively, these solutions advance the state of the art in demand response coordination by bridging data-driven reinforcement learning and physics-constrained optimization, offering a modular, generalizable, and scalable foundation for real-time, adaptive strategies in smart grids, microgrids, and energy communities while also opening new directions for decentralized architectures, distributed coordination, and demand response market integration.

Table 1. Quantitative comparison of representative methods for demand response scheduling.

Method	Cost Metric	Constraint Handling	Data Type	Uncertainty
DQN-based DR	Op. cost ↓ 15%	Penalty shaping only	Residential load data	Not modeled
DDPG-based DR	Curtailment ↓ 12%	Thermal limits enforced	Solar + demand mix	Forecast ignored
PPO-based DR	Total cost ↓ 18%	Voltage and thermal	Market price series	Monte Carlo
Mathematical programming	Exact min cost	Explicit AC power flow	IEEE feeders	Scenario-based
Proposed Double DQN	Cost ↓ 19%, Curtail. ↓ 24%	Voltage + VRT enforced	Hybrid real-world datasets	Robust to price/forecast

provides a quantitative comparison across representative demand response scheduling methods, highlighting the trade-offs between classical mathematical programming and recent deep reinforcement learning approaches. The DQN-based baseline demonstrates noticeable operating-cost reductions, yet its reliance on penalty shaping without explicit grid feasibility checks leaves robustness concerns under real-world variability. In contrast, DDPG-based methods further improve curtailment efficiency but generally neglect forecast uncertainty, which may limit their applicability in stochastic environments. The PPO-based paradigm yields higher aggregate cost savings and incorporates a richer set of network constraints, supported by Monte Carlo simulations for uncertainty modeling, though convergence tends to be slower. Traditional mathematical programming remains a rigorous benchmark by explicitly embedding AC power flow and enforcing system-level feasibility, but such exact optimization is computationally intensive and less scalable for real-time adaptation. The proposed Double DQN approach unifies the strengths of these perspectives by simultaneously reducing total cost and curtailment more effectively while maintaining operational feasibility through explicit enforcement of voltage stability and ride-through requirements. Leveraging hybrid real-world datasets spanning residential, solar, and market signals, the method explicitly accounts for forecast errors and price fluctuations, thereby offering enhanced robustness compared to prior reinforcement learning methods. Overall, the comparative evidence illustrates how the proposed framework closes the methodological gap between data-driven adaptability and physics-informed feasibility, achieving superior efficiency and resilience in uncertain distribution grid conditions.

2. Mathematical Modeling

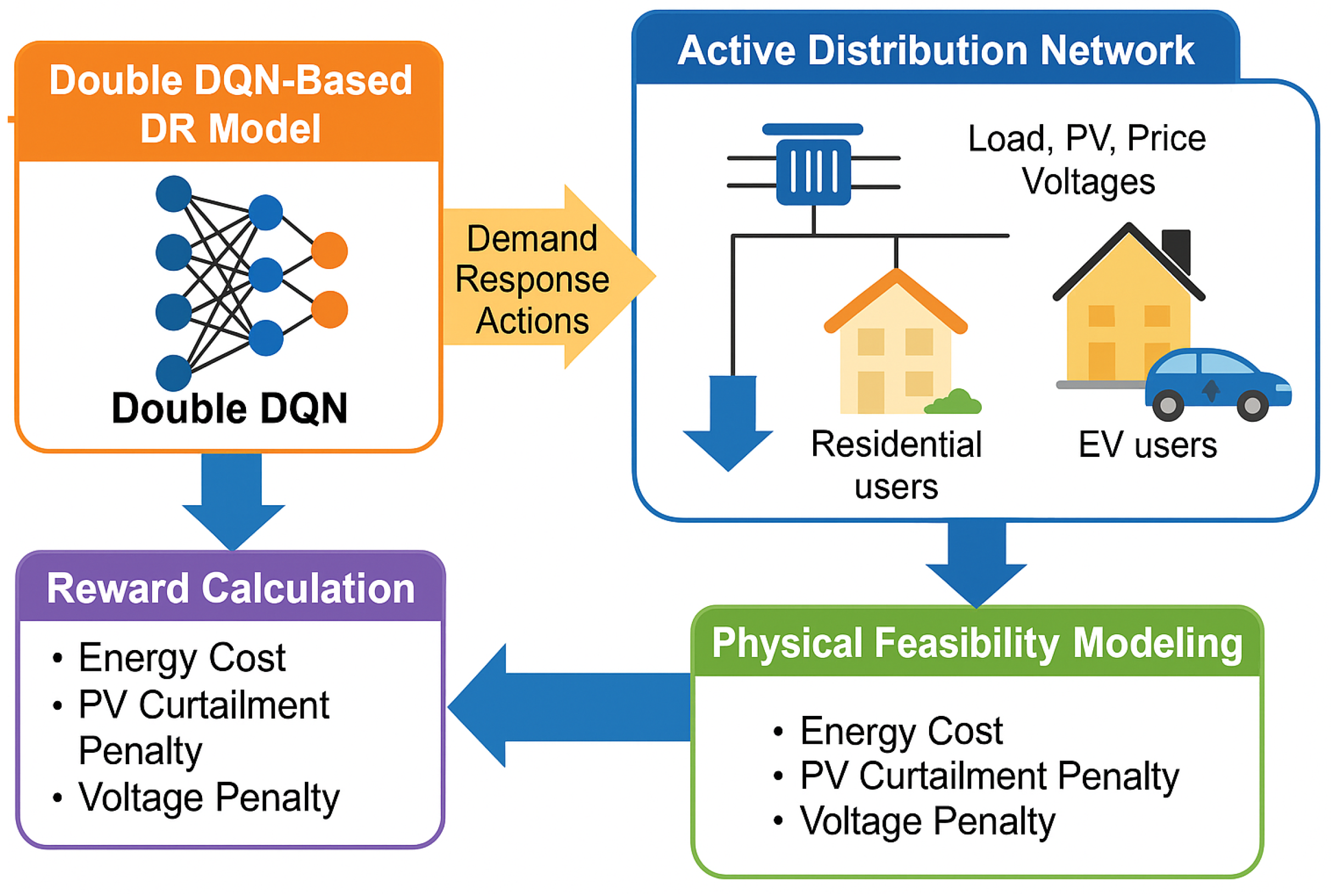
Figure 1 illustrates the overall architecture of the proposed Double DQN-based DR framework for active distribution networks. At the core lies the Double DQN module, which learns optimal decision-making strategies for the scheduling of multi-user DR actions. These actions directly interact with the active distribution network, where diverse users, including residential consumers and EV participants, respond to dynamic signals such as load demand, PV generation, electricity prices, and system voltages. By capturing these spatiotemporal variables, the agent establishes a closed feedback loop that enables adaptive and intelligent control. To ensure practical effectiveness, the framework integrates two critical components: reward calculation and physical feasibility modeling. The reward signal is carefully designed to balance multiple objectives, incorporating energy cost minimization, PV curtailment penalties, and voltage deviation penalties. This multi-objective structure guides the agent toward economically efficient and physically reliable operating points. In parallel, the physical feasibility modeling block enforces operational limits by explicitly evaluating the same set of constraints, thereby preventing policy actions that could compromise system safety or violate network stability. Through this coupled design, the proposed framework not only accelerates convergence of the learning process but also guarantees that the generated DR schedules remain interpretable and practically implementable. The integration of user heterogeneity, renewable variability, and system-aware constraints highlights the novelty of the approach. Ultimately, this synergy between advanced reinforcement learning and physical feasibility ensures that the framework can achieve cost reduction, voltage stability, and renewable integration in a unified and scalable manner.

2.1. Objective Function and Fairness Constraint

Table 2. Nomenclature of variables.

Symbol	Description	Unit
$C^{\mathrm{op}}$	Operating cost	$/h
$P_{n,\tau }^{\mathrm{grid}}$	Power purchased from grid at node n	kW
${\kappa }_n^{\mathrm{buy}}$	Grid purchase price at node n	$/kWh
${\vartheta }_{n,\tau }^{\mathrm{shed}}$	Load shedding at node n	kW
${\kappa }_n^{\mathrm{shed}}$	Penalty coefficient for shedding	$/kW
${\xi }_{n,\tau }^{\mathrm{curt}}$	PV curtailment at node n	kW
${\kappa }_n^{\mathrm{pv}}$	Penalty coefficient for curtailment	$/kW
${\nu }_{\ell ,\tau }$	Voltage magnitude at line ℓ	p.u.
${\nu }_{\ell }^{\mathrm{ref}}$	Reference voltage at line ℓ	p.u.
${\chi }_{\ell }^{\mathrm{volt}}$	Penalty coefficient for voltage deviation	$/p.${\mathrm{u}.}^2$
${\mathsf{\sigma }}_{\mathit{i}}$	System state at time i	–
${\mathsf{\alpha }}_{\mathit{i}}$	Control action at time i	–
$r_i$	Immediate reward	–
${\mathcal{B}}_k$	Mini-batch of experience tuples	–
${\mathcal{L}}_{\mathrm{TD}}$	Temporal difference loss	–
$\mathsf{\Theta }$	Neural network parameters	–
$\eta$	Learning rate	–
${\beta }^{\mathrm{pv}}$	Weight for PV curtailment in sensitivity metric	–
${\beta }^{\mathrm{volt}}$	Weight for voltage deviation in sensitivity metric	–
$\varphi$	Sensitivity metric	–
${\Delta }^{\mathrm{converge}}$	Convergence metric	–
${\overline{r}}_k$	Average episodic reward at episode k	–
K	Window size for moving average	–
$\mathcal{T}$	Time horizon	h
N	Batch size	–

shows the Nomenclatue. The formulation begins with the definition of the overall optimization objective, which captures the dual goals of minimizing system operating costs while maintaining grid reliability under demand response participation. In this stage, the objective is not restricted to economic performance alone but also incorporates penalties associated with voltage deviations, ensuring that system-level security is preserved, even under uncertainty. Furthermore, to avoid disproportionate burdens among different users and to maintain operational stability over time, fairness and temporal smoothness are explicitly embedded into the formulation. Therefore, Equations (1) and (2) provide the foundation of the proposed framework by jointly enforcing cost-effectiveness, reliability, and equity across participants.

$$\begin{array}{cc}\hfill \underset{\mathsf{\alpha },\mathsf{\theta },\mathsf{\lambda }}{min}& \sum _{\tau =1}^{\mathcal{T}}\left\{\sum _{n\in \mathcal{N}}\left[{\kappa }_n^{\mathrm{buy}}\left(\tau \right)·{\varsigma }_{n,\tau }^{\mathrm{grid}}\left({\mathsf{\alpha }}_{n,\tau }\right)+{\kappa }_n^{\mathrm{shed}}\left(\tau \right)·{\vartheta }_{n,\tau }^{\mathrm{shed}}\left({\mathsf{\alpha }}_{n,\tau }\right)+{\kappa }_n^{\mathrm{pv}}\left(\tau \right)·{\xi }_{n,\tau }^{\mathrm{curt}}\left({\mathsf{\alpha }}_{n,\tau }\right)\right]\right.\hfill \\ & \left.+\sum _{\ell \in \mathcal{L}}{\chi }_{\ell ,\tau }^{\mathrm{volt}}·{\left(max\left\{0,\left|{\nu }_{\ell ,\tau }\left({\mathsf{\theta }}_{\ell ,\tau }\right)-{\nu }_{\ell }^{\mathrm{ref}}\right|-{\delta }_{\ell }^{\mathrm{tol}}\right\}\right)}^2\right\}\hfill \end{array}$$

(1)

This elaborately structured objective function embodies the multi-faceted cost drivers of a dynamic demand response optimization problem in active distribution networks. The first summation accounts for the cumulative cost over the operation horizon ($\mathcal{T}$), while the nested terms capture node-level costs across all buses ($n\in \mathcal{N}$). These include ${\kappa }_n^{\mathrm{buy}}\left(\tau \right)$, the time-varying energy purchase price for each node; ${\varsigma }_{n,\tau }^{\mathrm{grid}}(·)$, the amount of energy procured by the upstream grid under DR actions (${\mathsf{\alpha }}_{n,\tau }$); ${\kappa }_n^{\mathrm{shed}}\left(\tau \right)$, the penalty associated with load shedding; and ${\xi }_{n,\tau }^{\mathrm{curt}}(·)$, the curtailed PV generation due to local surplus. The second component adds a quadratic voltage deviation penalty for each line ($\ell \in \mathcal{L}$), governed by the deviation of the actual voltage (${\nu }_{\ell ,\tau }$) from its reference (${\nu }_{\ell }^{\mathrm{ref}}$), beyond a permissible tolerance (${\delta }_{\ell }^{\mathrm{tol}}$), with ${\chi }_{\ell ,\tau }^{\mathrm{volt}}$ serving as a line-specific penalty weight. Collectively, this objective reflects a careful balancing of economic efficiency, renewable integration, and voltage stability.

$$\begin{array}{c}\hfill \sum _{u\in \mathcal{U}}\sum _{\tau =1}^{\mathcal{T}}{\omega }_u^{\mathrm{fair}}·{\left(\left[{\displaystyle \frac{1}{\left|\mathcal{T}\right|}}\sum _{{\tau }^{\prime }=1}^{\mathcal{T}}{\alpha }_{u,{\tau }^{\prime }}\right]-{\alpha }_{u,\tau }\right)}^2+\sum _{u\in \mathcal{U}}\sum _{\tau =2}^{\mathcal{T}}{\psi }_u·{\left({\alpha }_{u,\tau }-{\alpha }_{u,\tau -1}\right)}^2\end{array}$$

(2)

The function above introduces two crucial penalty layers that govern demand response fairness and temporal smoothness. The first term penalizes deviations from a user’s own historical mean behavior, where the average action across the planning horizon is compared against each hour’s action (${\alpha }_{u,\tau }$), scaled by a user-specific weight (${\omega }_u^{\mathrm{fair}}$). This ensures that no participant is disproportionately burdened in the DR process, promoting equity across the heterogeneous user group ($\mathcal{U}$). The second term enforces inertia by penalizing sharp transitions in consecutive actions through a time-differencing quadratic term. The user-specific coefficient (${\psi }_u$) adjusts sensitivity to abrupt shifts, fostering temporally stable behavior, which is crucial for practical deployment in both residential and commercial load contexts. Together, these components make the DR policy both socially acceptable and operationally implementable.

2.2. Power Balance and Network Operating Constraints

Equations (3)–(7) collectively establish the fundamental operating conditions of the distribution network under demand response participation. They begin by modifying the baseline nodal demand to reflect user-side adjustments, involuntary shedding, and PV curtailment, thereby linking DR decisions to system-level load representation. Building upon this, nodal active power balance is enforced to guarantee consistency with Kirchhoff’s laws, ensuring that inflows, outflows, and net injections are reconciled at every bus. Voltage magnitude limits are then imposed to safeguard equipment and maintain service quality within acceptable operational bounds. Thermal loading constraints on distribution lines further restrict both real and reactive power flows to lie within capacity ratings, protecting network assets against overloading. Finally, PV curtailment is bounded by available generation, ruling out infeasible or physically inconsistent dispatches. Together, these equations guarantee that DR-driven scheduling remains feasible, secure, and aligned with physical realities of power distribution networks.

$$\begin{array}{c}\hfill \forall n\in \mathcal{N},\forall \tau \in \mathcal{T},{\lambda }_{n,\tau }^{\mathrm{load}}={\lambda }_{n,\tau }^{\mathrm{base}}·\left(1+{\alpha }_{n,\tau }\right)-{\vartheta }_{n,\tau }^{\mathrm{shed}}+{\xi }_{n,\tau }^{\mathrm{curt}}\end{array}$$

(3)

This constraint determines the adjusted nodal power demand under DR actions, incorporating the baseline load (${\lambda }_{n,\tau }^{\mathrm{base}}$), user demand response scaling factor (${\alpha }_{n,\tau }$), and any involuntary load shedding (${\vartheta }_{n,\tau }^{\mathrm{shed}}$) or curtailed PV power (${\xi }_{n,\tau }^{\mathrm{curt}}$). It forms the basis for nodal balance constraints and links DR decisions to power flow variables.

$$\begin{array}{c}\hfill \forall n\in \mathcal{N},\forall \tau \in \mathcal{T},\sum _{k\in {\mathcal{B}}_n^{\mathrm{out}}}{P}_{k,\tau }^{\mathrm{out}}-\sum _{k\in {\mathcal{B}}_n^{\mathrm{in}}}{P}_{k,\tau }^{\mathrm{in}}={\lambda }_{n,\tau }^{\mathrm{load}}-{\rho }_{n,\tau }^{\mathrm{pv}}\end{array}$$

(4)

This is the nodal real power balance constraint at each node (n), ensuring that net inflow minus outflow matches net demand. Here, ${\rho }_{n,\tau }^{\mathrm{pv}}$ is the locally generated PV power, and $P_{k,\tau }^{\mathrm{in}/\mathrm{out}}$ denotes active power flow through line k, preserving Kirchhoff’s law.

$$\begin{array}{c}\hfill \forall n\in \mathcal{N},\forall \tau \in \mathcal{T},{\underline{\nu }}_n\le {\nu }_{n,\tau }\left(\mathbf{z}\right)\le {\overline{\nu }}_n\end{array}$$

(5)

Voltage magnitude (${\nu }_{n,\tau }$) must remain within safety bounds ($[{\underline{\nu }}_n,{\overline{\nu }}_n]$) at each node and time step, ensuring operational integrity and protecting voltage-sensitive equipment. This is a standard yet crucial distribution system feasibility condition.

$$\begin{array}{c}\hfill \forall \ell \in \mathcal{L},\forall \tau \in \mathcal{T},\sqrt{{\left(P_{\ell ,\tau }^{\mathrm{flow}}\right)}^2+{\left(Q_{\ell ,\tau }^{\mathrm{flow}}\right)}^2}\le {\overline{S}}_{\ell }\end{array}$$

(6)

Here, we bound the apparent power on each line (ℓ) to within its thermal capacity ${\overline{S}}_{\ell }$, where $P_{\ell ,\tau }^{\mathrm{flow}},Q_{\ell ,\tau }^{\mathrm{flow}}$ are real and reactive components. This ensures no line is overloaded under DR-based flow redistributions.

$$\begin{array}{c}\hfill \forall n\in {\mathcal{N}}_{\mathrm{PV}},\forall \tau \in \mathcal{T},0\le {\xi }_{n,\tau }^{\mathrm{curt}}\le {\rho }_{n,\tau }^{\mathrm{pv}}\end{array}$$

(7)

This constraint limits PV curtailment to the amount available from generation. No negative curtailment (i.e., overconsumption) is allowed. It reflects physical availability limits and protects against infeasible DR dispatches.

2.3. User-Side Flexibility and Behavioral Constraints

Equations (8)–(15) formalize the practical flexibility boundaries associated with different categories of demand-side resources. Commercial load shifting is first addressed by ensuring that curtailed consumption is compensated for within a temporal window, thereby enabling reshaping without energy loss. For electric vehicles, availability flags encode plug-in periods to guarantee realistic participation in scheduling. The dynamics of storage systems are captured through state-of-charge evolution, reflecting intertemporal coupling of charging and discharging efficiency. Network-level reliability is preserved by power factor requirements, limiting excessive reactive injections. Moreover, user participation trajectories are smoothed by ramping limits, while recovery obligations safeguard deferred residential activities. Finally, cumulative participation budgets and global system caps restrict the overall intensity of demand response actions, preventing overuse and ensuring operational feasibility. Together, these conditions provide a realistic representation of how end users and devices can contribute to demand response while respecting technical, behavioral, and contractual limitations.

$$\begin{array}{c}\hfill \forall u\in {\mathcal{U}}_{\mathrm{comm}},\forall \tau \in \mathcal{T},\sum _{{\tau }^{\prime }=\tau }^{\tau +{\Delta }_u^{\mathrm{shift}}}{\lambda }_{u,{\tau }^{\prime }}^{\mathrm{load}}\ge {\lambda }_{u,\tau }^{\mathrm{base}}\end{array}$$

(8)

This commercial load-shift constraint guarantees that any reduced consumption is compensated for within a tolerance window (${\Delta }_u^{\mathrm{shift}}$). It enables load reshaping without net energy loss, consistent with thermal or industrial process constraints.

$$\begin{array}{c}\hfill \forall u\in {\mathcal{U}}_{\mathrm{EV}},\forall \tau \in \mathcal{T},{\delta }_{u,\tau }^{\mathrm{plug}}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}\tau \in [t_u^{\mathrm{arr}},t_u^{\mathrm{dep}}]\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.\end{array}$$

(9)

This binary availability flag (${\delta }_{u,\tau }^{\mathrm{plug}}$) for EV users models plug-in status based on predefined arrival and departure windows. It constrains when EVs can actually contribute to DR services and avoids unrealistic dispatches.

$$\begin{array}{c}\hfill \forall s\in \mathcal{S},\forall \tau \in \mathcal{T},{\chi }_{s,\tau }^{\mathrm{soc}}={\chi }_{s,\tau -1}^{\mathrm{soc}}+{\eta }_s^{\mathrm{ch}}·P_{s,\tau }^{\mathrm{ch}}-{\displaystyle \frac{1}{{\eta }_s^{\mathrm{dis}}}}·P_{s,\tau }^{\mathrm{dis}}\end{array}$$

(10)

This state-of-charge (SOC) equation tracks energy stored in each storage device (s), balancing charging and discharging adjusted by round-trip efficiency ($\eta$). It is a dynamic constraint spanning across time, key to time-coupled DR decisions.

$$\begin{array}{c}\hfill \forall n\in \mathcal{N},\forall \tau \in \mathcal{T},{cos}^{-1}\left({\displaystyle \frac{P_{n,\tau }}{\sqrt{P_{n,\tau }^2+Q_{n,\tau }^2}}}\right)\le {\varphi }_n^{\max }\end{array}$$

(11)

Power-factor constraints limit the angle between real and apparent power to within ${\varphi }_n^{\max }$, preserving voltage support and reducing unnecessary reactive flow. This control is particularly relevant when DR shifts active/reactive power flows.

$$\begin{array}{c}\hfill \forall u\in \mathcal{U},\forall \tau \in \mathcal{T},{\alpha }_{u,\tau }\ge {\alpha }_{u,\tau -1}-{\zeta }_u\end{array}$$

(12)

This constraint caps how fast a user’s DR action can decrease from one time step to the next, where ${\zeta }_u$ defines the minimum downward ramp limit. It reflects thermal inertia or user behavioral constraints in practice.

$$\begin{array}{c}\hfill \forall u\in {\mathcal{U}}_{\mathrm{res}},\forall \tau \in \mathcal{T},\sum _{{\tau }^{\prime }=\tau }^{\tau +{\Delta }_u^{\mathrm{rec}}}{\alpha }_{u,{\tau }^{\prime }}\ge {\displaystyle \frac{{\lambda }_{u,\tau }^{\mathrm{base}}}{{\lambda }_{u,\tau +\Delta }^{\mathrm{base}}}}\end{array}$$

(13)

Residential load recovery enforcement ensures that any deferred energy usage is later restored within a delay window (${\Delta }_u^{\mathrm{rec}}$). This models activities like dish washing or space heating, which may only be delayed but not removed.

$$\begin{array}{c}\hfill \forall u\in \mathcal{U},\sum _{\tau =1}^{\mathcal{T}}\left|{\alpha }_{u,\tau }\right|\le {\Gamma }_u^{\max }\end{array}$$

(14)

Participation budget constraints limit how much DR effort each user can provide over the entire horizon. ${\Gamma }_u^{\max }$ is calibrated per user based on past contracts, fatigue, or equipment capability.

$$\begin{array}{c}\hfill \forall \tau \in \mathcal{T},\sum _{u\in \mathcal{U}}{\alpha }_{u,\tau }·{\lambda }_{u,\tau }^{\mathrm{base}}\le {\Lambda }_{\tau }^{\mathrm{sys}.\max }\end{array}$$

(15)

As a system-wide safeguard, the aggregated DR contribution at any time step cannot exceed an upper bound (${\Lambda }_{\tau }^{\mathrm{sys}.\max }$), ensuring grid operators retain control over global DR limits under forecast uncertainty.

3. Methodology

This section presents the methodological framework underlying the proposed demand response optimization model. The overall approach integrates a physically constrained distribution system model with a model-free reinforcement learning control agent, forming a hybrid architecture capable of real-time decision-making under uncertainty and user heterogeneity. The methodology is organized into two primary components: (1) a mathematical modeling layer that formulates power flow constraints, demand response flexibility bounds, and system-level operational objectives and (2) a learning-based control layer built upon a Double Deep Q-Network (Double DQN), which interacts with the environment to learn optimal demand response policies without relying on explicit system transition models. To ensure both feasibility and scalability, the system model incorporates nodal power balance, voltage magnitude constraints, line flow limits, and user-specific temporal flexibility constraints. These constraints are defined over a 24 h rolling horizon and are updated at each time step based on forecasted load, PV generation, and pricing data. The Double DQN agent observes a structured state vector at each decision step and outputs a multi-dimensional continuous action vector representing load modulation across all participating users.

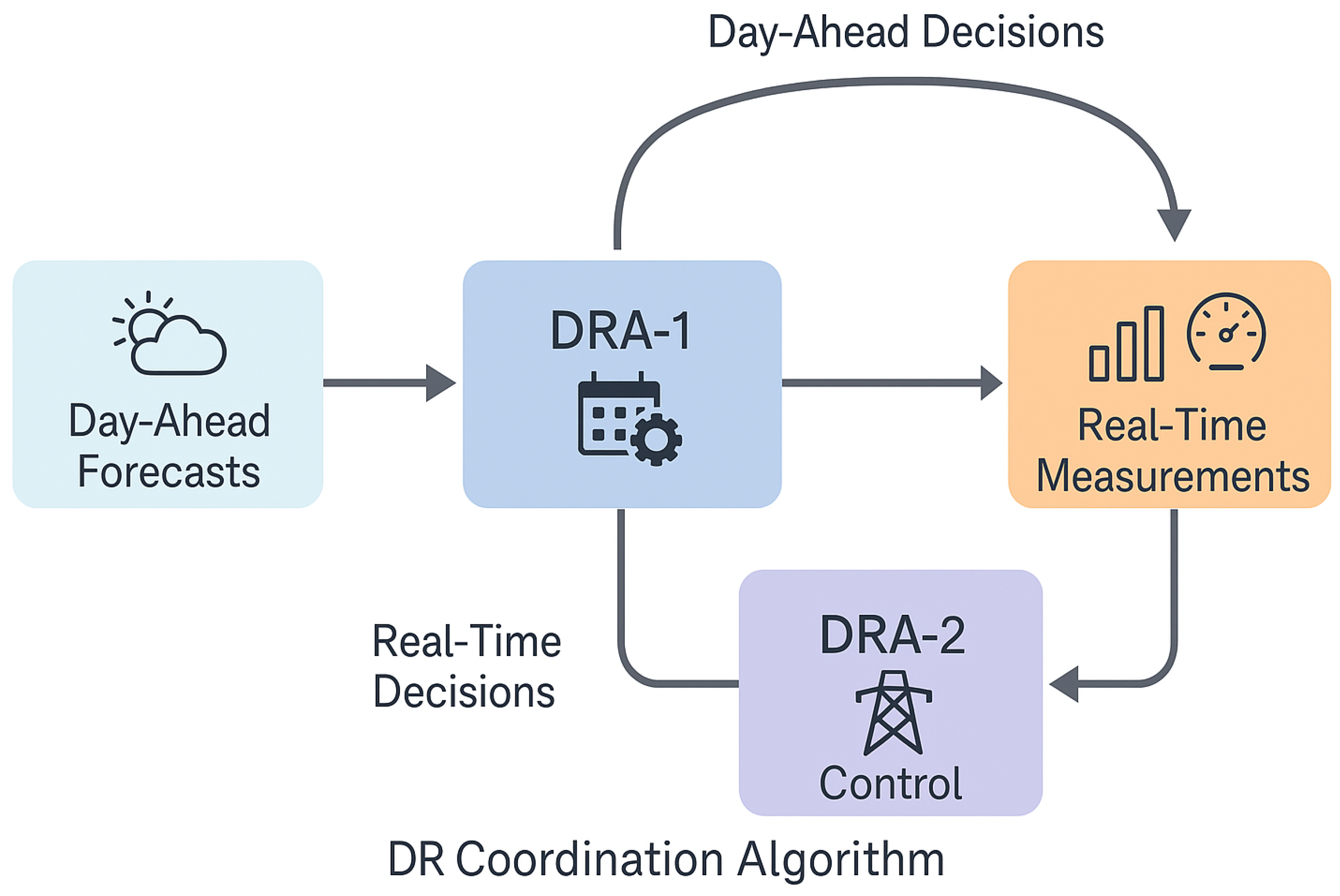
Figure 2 illustrates the overall coordination mechanism between day-ahead and real-time demand response aggregators in a structured and visually intuitive manner. On the left, forecast inputs representing weather conditions and load patterns form the essential basis for planning, ensuring that scheduling decisions incorporate exogenous factors such as renewable variability and consumer demand profiles. These forecasts are passed to the day-ahead aggregator, which performs baseline scheduling, guided by a calendar-oriented process. This stage emphasizes predictive allocation of demand response resources, aiming to balance supply–demand relationships, anticipate renewable fluctuations, and minimize expected operational costs. Moving horizontally, the real-time aggregator, characterized by a clock symbol, refines and adjusts these preliminary decisions. This layer addresses fast-timescale uncertainties such as intra-hour load deviations or unforeseen voltage fluctuations, enabling the system to adapt flexibly without compromising the feasibility constraints inherited from the physical network. The decisions from both levels converge at the grid-and-user interface, illustrated by house and solar panel icons, where the final demand response actions are executed. These actions represent the aggregated outcomes of proactive planning and real-time adaptation, directly shaping load curves, voltage profiles, and renewable integration. Importantly, a feedback loop from the grid back to the real-time aggregator, symbolized by a meter icon, ensures that actual system states are continuously monitored and incorporated into subsequent control steps. This cyclical structure reflects the cyber–physical integration of measurement, communication, and adaptive control, which lies at the heart of intelligent demand response management. Overall, the diagram conveys a modular yet interconnected design where day-ahead and real-time modules complement each other: the former provides stability and predictability, while the latter delivers agility and resilience. This dual-level coordination scheme not only highlights the novelty of integrating reinforcement learning into energy management but also demonstrates how predictive scheduling and adaptive control can jointly enhance efficiency, reliability, and sustainability in active distribution networks. By embedding forecast-driven planning with closed-loop adjustments, the framework achieves a balance between robustness and flexibility, offering a scalable pathway for future smart-grid implementations.

3.1. Reinforcement Learning State–Action Modeling and Training Mechanisms

Equations (16)–(20) establish the reinforcement learning formulation underpinning demand response optimization. The state representation integrates baseline loads, PV forecasts, electricity prices, and historical variables, thereby encoding both instantaneous and temporal information required for effective decision-making. Actions are modeled as continuous adjustments of user flexibility, enabling fine-grained and scalable control across heterogeneous participants. The Double DQN framework is employed to update Q-values through a decoupled selection–evaluation process, mitigating overestimation bias. Stability during training is further enhanced by soft target-network updates, which smooth parameter transitions over time. Finally, an exponentially decaying exploration probability balances the trade-off between exploration of new strategies and exploitation of learned policies. Together, these formulations ensure that the reinforcement learning agent can operate reliably in uncertain, dynamic, and high-dimensional power system environments.

$$\begin{array}{c}\hfill {\mathsf{\sigma }}_{\tau }=\left[{\mathsf{\lambda }}_{\tau }^{\mathrm{base}},{\mathsf{\rho }}_{\tau }^{\mathrm{pv}},{\mathsf{\pi }}_{\tau }^{\mathrm{price}},{\mathsf{\nu }}_{\tau -1},{\mathsf{\alpha }}_{\tau -1},\tau \right]\end{array}$$

(16)

This expression defines the state vector (${\mathsf{\sigma }}_{\tau }$) at time $\tau$ used as input to the reinforcement learning agent. It includes the vector of baseline loads (${\mathsf{\lambda }}_{\tau }^{\mathrm{base}}$), solar PV forecast (${\mathsf{\rho }}_{\tau }^{\mathrm{pv}}$), electricity price signals (${\mathsf{\pi }}_{\tau }^{\mathrm{price}}$), voltage measurements from the previous step (${\mathsf{\nu }}_{\tau -1}$), previous actions (${\mathsf{\alpha }}_{\tau -1}$), and a scalar time index. This richly constructed state encapsulates both current system conditions and memory-dependent temporal context.

$$\begin{array}{c}\hfill {\mathsf{\alpha }}_{\tau }={\left[\begin{array}{cccc}{\alpha }_{1,\tau }& {\alpha }_{2,\tau }& \dots & {\alpha }_{\left|\mathcal{U}\right|,\tau }\end{array}\right]}^{\top }\in {\mathbb{R}}^{\left|\mathcal{U}\right|}\end{array}$$

(17)

This defines the action vector at time $\tau$, where each entry (${\alpha }_{u,\tau }$) represents the proportion of flexible load adjustment for user u. The space of ${\mathsf{\alpha }}_{\tau }$ is continuous and multi-dimensional, enabling granular control of DR behavior across all user types.

$$\begin{array}{c}\hfill Q({\mathsf{\sigma }}_{\tau },{\mathsf{\alpha }}_{\tau };\mathsf{\Theta })=\mathbb{E}\left[r_{\tau }+\gamma ·Q^{\prime }\left({\mathsf{\sigma }}_{\tau +1},arg\underset{{\mathsf{\alpha }}^{\prime }}{max}Q({\mathsf{\sigma }}_{\tau +1},{\mathsf{\alpha }}^{\prime };\mathsf{\Theta });{\mathsf{\Theta }}^{\prime }\right)\right]\end{array}$$

(18)

The Double DQN target update rule is shown here. The Q-value estimate for state–action pair $({\mathsf{\sigma }}_{\tau },{\mathsf{\alpha }}_{\tau })$ uses bootstrapping with two networks: $\mathsf{\Theta }$ is used to select the action via argmax, while a target network (${\mathsf{\Theta }}^{\prime }$) evaluates the selected action. This decoupling addresses overestimation bias in traditional Q-learning.

$$\begin{array}{c}\hfill {\mathsf{\Theta }}^{\prime }\leftarrow {\tau }_{\mathrm{sync}}·\mathsf{\Theta }+(1-{\tau }_{\mathrm{sync}})·{\mathsf{\Theta }}^{\prime }\end{array}$$

(19)

The soft update rule for the target network ensures stable learning. The target parameters (${\mathsf{\Theta }}^{\prime }$) are updated as an exponential moving average of the primary network weights, controlled by the synchronization factor (${\tau }_{\mathrm{sync}}$), which is typically a small constant (e.g., 0.005).

$$\begin{array}{c}\hfill {\epsilon }_{\tau }=max\left({\epsilon }_{\min },{\epsilon }_{\mathrm{init}}·exp(-\xi ·\tau )\right)\end{array}$$

(20)

The agent’s exploration probability (${\epsilon }_{\tau }$) decays exponentially from an initial value (${\epsilon }_{\mathrm{init}}$) toward a lower bound (${\epsilon }_{\min }$), where $\xi$ controls the rate of decay. This $\epsilon$-greedy scheme ensures sufficient exploration in early episodes and gradual exploitation later.

3.2. Reinforcement Learning Training and Convergence Mechanisms

Equations (21)–(28) present the learning dynamics and evaluation metrics essential for training the reinforcement learning agent. Experience replay with mini-batch sampling ensures decorrelated training data, while the reward function incorporates multiple penalty terms to guide policies toward cost-efficient and grid-stable actions. The temporal difference loss and stochastic gradient updates form the backbone of Double DQN optimization, systematically refining Q-value estimates over iterations. Post-processing constraints enforce the feasibility of control actions, and input normalization stabilizes the learning process across diverse operating conditions. In addition, sensitivity metrics capture the responsiveness of system variables to DR decisions, and convergence indicators monitor training progress, enabling the detection of performance saturation. Together, these formulations provide a robust foundation for scalable and stable reinforcement learning deployment in power system applications.

$$\begin{array}{c}\hfill {\mathcal{B}}_k={\left\{\left({\mathsf{\sigma }}_i,{\mathsf{\alpha }}_i,r_i,{\mathsf{\sigma }}_{i+1}\right)\right\}}_{i=k}^{k+N-1}\end{array}$$

(21)

This denotes a mini-batch of experience tuples sampled from the replay buffer for stochastic gradient descent. Each tuple includes the current state, action, reward, and next state. Mini-batch training reduces correlation between samples and improves convergence stability.

$$\begin{array}{c}\hfill r_{\tau }=-\sum _{n\in \mathcal{N}}\left[{\kappa }_n^{\mathrm{buy}}·{\varsigma }_{n,\tau }^{\mathrm{grid}}+{\kappa }_n^{\mathrm{shed}}·{\vartheta }_{n,\tau }^{\mathrm{shed}}+{\kappa }_n^{\mathrm{pv}}·{\xi }_{n,\tau }^{\mathrm{curt}}\right]-\sum _{\ell \in \mathcal{L}}{\chi }_{\ell }^{\mathrm{volt}}·{\left({\nu }_{\ell ,\tau }-{\nu }_{\ell }^{\mathrm{ref}}\right)}^2\end{array}$$

(22)

The reward function penalizes system operating cost components: energy purchases, load shedding, PV curtailment, and voltage deviations. Each penalty is scaled by time-varying or line-specific weight coefficients, enabling the agent to learn system-friendly dispatch policies.

$$\begin{array}{c}\hfill {\mathcal{L}}_{\mathrm{TD}}\left(\mathsf{\Theta }\right)={\displaystyle \frac{1}{N}}\sum _{i=1}^N{\left[y_i^{\mathrm{target}}-Q({\mathsf{\sigma }}_i,{\mathsf{\alpha }}_i;\mathsf{\Theta })\right]}^2\end{array}$$

(23)

The temporal difference (TD) loss function measures the squared difference between the predicted Q-value and the target value ($y_i^{\mathrm{target}}$) computed according to Equation (18). Minimizing this loss via gradient descent is the core training objective for Double DQN.

$$\begin{array}{c}\hfill \mathsf{\Theta }\leftarrow \mathsf{\Theta }-\eta ·{\nabla }_{\mathsf{\Theta }}{\mathcal{L}}_{\mathrm{TD}}\left(\mathsf{\Theta }\right)\end{array}$$

(24)

The parameter update step uses stochastic gradient descent with a learning rate of $\eta$. The gradient of the TD loss guides how the weights ($\mathsf{\Theta }$) are adjusted to minimize prediction errors over time.

$$\begin{array}{c}\hfill {\mathsf{\alpha }}_{\tau }\leftarrow \mathrm{clip}\left({\mathsf{\alpha }}_{\tau },{\mathsf{\alpha }}^{min},{\mathsf{\alpha }}^{max}\right)\end{array}$$

(25)

This post-processing clipping function ensures that the learned DR actions (${\mathsf{\alpha }}_{\tau }$) remain within allowable limits. This constraint is essential for feasibility with physical system boundaries, as enforced in earlier constraints.

$$\begin{array}{c}\hfill {\widehat{\mathsf{\sigma }}}_{\tau }={\displaystyle \frac{{\mathsf{\sigma }}_{\tau }-{\mathsf{\mu }}^{\mathrm{train}}}{{\mathsf{\sigma }}^{\mathrm{train}}}}\end{array}$$

(26)

The state input is normalized using training-set statistics ($({\mathsf{\mu }}^{\mathrm{train}},{\mathsf{\sigma }}^{\mathrm{train}})$), a standard preprocessing step to accelerate convergence and stabilize neural network training under varying data scales.

$$\begin{array}{c}\hfill \varphi ={\displaystyle \frac{1}{\mathcal{T}}}\sum _{\tau =1}^{\mathcal{T}}\left({\beta }^{\mathrm{pv}}·{\displaystyle \frac{{\xi }_{\tau }^{\mathrm{curt}}}{{\rho }_{\tau }^{\mathrm{pv}}+{10}^{-6}}}+{\beta }^{\mathrm{volt}}·{\displaystyle \frac{1}{\left|\mathcal{L}\right|}}\sum _{\ell }\left|{\nu }_{\ell ,\tau }-{\nu }_{\ell }^{\mathrm{ref}}\right|\right)\end{array}$$

(27)

This sensitivity metric ($\varphi$) reflects how responsive the system is to DR actions, balancing PV curtailment and voltage deviation contributions, each weighted by importance parameters (${\beta }^{\mathrm{pv}},{\beta }^{\mathrm{volt}}$). It is useful for tuning reward weights or prioritizing system objectives.

$$\begin{array}{c}\hfill {\Delta }^{\mathrm{converge}}={\displaystyle \frac{1}{K}}\sum _{k=E-K}^E\left|{\overline{r}}_k-{\overline{r}}_{k-1}\right|\end{array}$$

(28)

Lastly, ${\Delta }^{\mathrm{converge}}$ defines a moving average convergence metric based on the mean episodic reward (${\overline{r}}_k$) in the last K episodes, typically used to detect training plateaus or trigger early stopping once improvements stagnate.

4. Case Study

To validate the proposed Double DQN-based demand response framework, a detailed case study is conducted on a modified IEEE 33-bus radial distribution network. The system is enriched with three distinct classes of flexible demand-side users—12 residential nodes, 6 commercial nodes, and 4 EV aggregator nodes—spatially distributed across the feeder. The base active power load of the system is set to 3.72 MW, with a corresponding reactive power demand of 2.30 MVar under nominal conditions. Five distributed PV generation units are installed at buses 6, 14, 19, 24, and 30, with rated capacities ranging from 100 kW to 300 kW. The PV generation profiles are synthesized from the National Renewable Energy Laboratory (NREL) NSRDB dataset, using hourly solar irradiance data for a representative summer week in southern California. Load demand profiles for each user class are constructed from the Pecan Street dataset, normalized and clustered to reflect residential, commercial, and EV charging behavior diversity.

Each residential user is modeled with composite end-use loads including HVAC systems, lighting, and deferrable appliances. Residential demand is assumed to be flexible within a range of $\pm 20\%$ of the baseline load during peak DR windows of 7:00–10:00 and 17:00–21:00. Commercial users, which represent small retail and office buildings, are granted $\pm 15\%$ flexibility, with a maximum deferral window of 2 h per event, reflecting equipment usage constraints. EV aggregator nodes manage the charging of 5 to 15 EVs per location, with plug-in availability windows probabilistically generated using Gaussian arrival times centered at 18:30 with a standard deviation of 1.5 h. Charging is allowed between 22:00 and 7:00, with individual EVs subject to minimum energy delivery constraints. All user types are embedded with load recovery requirements, action rate constraints, and participation budgets, ensuring the physical plausibility of DR strategies. Hourly electricity prices are sourced from the CAISO real-time market data for July 2023, ranging from $0.09 to $0.26 $/kWh. PV curtailment is penalized at $0.08 $/kWh, while load shedding incurs a severe penalty of $3.00 $/kWh to reflect reliability concerns.

Implementation and Computing Environment

The Double DQN agent is implemented in Python 3.10.12 (Python Software Foundation, Wilmington, DE, USA; https://www.python.org, accessed on 30 August 2025) using TensorFlow 2.13.0 and Keras 2.13.1 (Google LLC, Mountain View, CA, USA; https://www.tensorflow.org, accessed on 30 August 2025). Numerical and scientific utilities rely on NumPy 1.26.4, SciPy 1.11.4, Pandas 2.2.2, and Matplotlib 3.8.4 (websites accessed on 30 August 2025). GPU acceleration uses CUDA 11.8 and cuDNN 8.6 (NVIDIA Corporation, Santa Clara, CA, USA; https://developer.nvidia.com/cuda-zone, accessed on 30 August 2025). All experiments were executed on a workstation running Ubuntu 22.04.4 LTS (Canonical Ltd., London, UK) equipped with an Intel^® Core™ i9-12900K CPU (Intel Corporation, Santa Clara, CA, USA), 64 GB RAM, and an NVIDIA^® GeForce RTX 3090 (24 GB) GPU (NVIDIA Corporation, Santa Clara, CA, USA).

Each learning episode spans a 24 h horizon with hourly discretization (24 decision stages). The agent uses a uniform replay buffer of 50,000 transitions, mini-batch size 128, and a soft target update with Polyak coefficient $\tau =0.005$ at every training step. The online and target Q-networks share the same architecture: two fully connected hidden layers with 256 and 128 ReLU units, respectively, followed by a linear output layer. Training uses the Adam optimizer ([27]) as implemented in Keras (Google LLC, Mountain View, CA, USA) with learning rate $1\times {10}^{-4}$, discount factor $\gamma =0.98$, Huber loss, and gradient clipping at 10. Exploration follows an exponentially decaying $\epsilon$-greedy policy, where $\epsilon$ decreases from 1.0 to 0.05 over the first 300 episodes. Unless otherwise stated, random seeds are fixed (NumPy and TensorFlow seed = 42) and deterministic GPU kernels are enabled when available (TF_DETERMINISTIC_OPS=1) to facilitate reproducibility.

We train for 1500 episodes, which requires ≈2.5 h of wall time on the described system. Network power flow and voltage constraints are evaluated with OpenDSS (Electric Power Research Institute, Knoxville, TN, USA; https://www.epri.com/pages/sa/opendss, accessed on 30 August 2025) interfaced from Python via the PyDSS/OpenDSSDirect family of wrappers (EPRI; https://github.com/dss-extensions/OpenDSSDirect.py, accessed on 30 August 2025). The specific package versions used in our runs were: OpenDSS (64-bit distribution from EPRI; build reported by Show Version in logs), OpenDSSDirect.py 0.9.x, and dss-extensions 0.15.x (websites accessed on 30 August 2025). A complete environment.yml with exact package pins is provided to ensure bit-for-bit reproducibility.

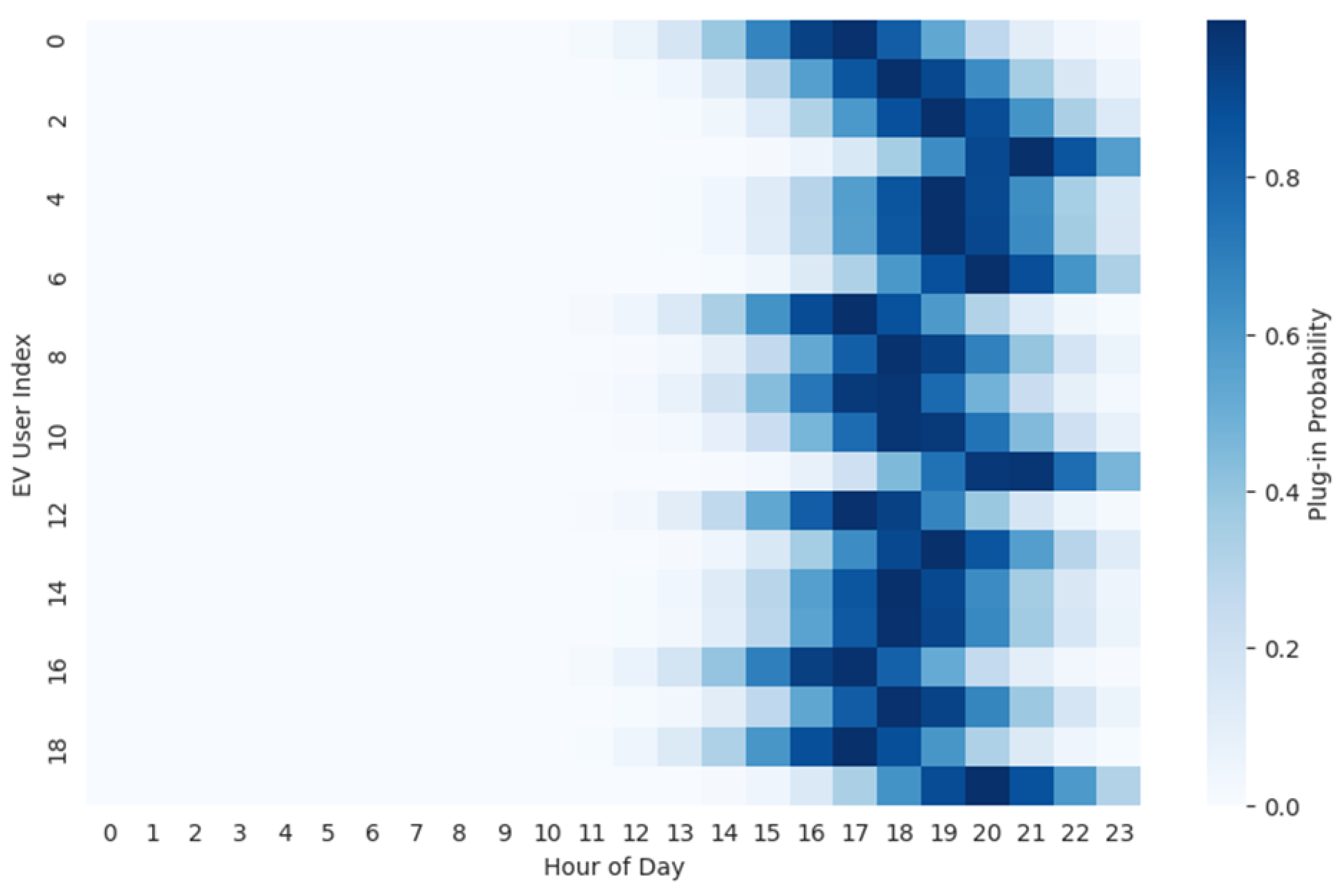
Figure 3 illustrates the temporal plug-in availability of twenty EV user aggregators over a 24 h period. Each row corresponds to one EV aggregator node, and the color intensity reflects the estimated probability that EVs are plugged in and, thus, available for demand response actions at each hour. The Gaussian-distributed arrival patterns result in high plug-in probabilities clustering around 19:00–21:00, with the highest density near 20:00. As expected from commuter-based behavioral models, availability sharply increases after 18:00 and begins tapering off before 8:00 the next day. The variability across rows demonstrates the heterogeneity in user arrival patterns and participation times—some users consistently plug in earlier or later than others, reflecting realistic diversity in individual mobility patterns. This figure plays a critical role in defining the feasible action space for DR scheduling, as the agent must respect temporal charging constraints when allocating EV-based flexibility. The visualization also highlights the stochastic nature of EV availability, motivating the need for a learning-based controller that adapts to dynamic uncertainty in user behavior rather than relying on static assumptions.

Figure 4 presents the distributions of normalized demand response flexibility (${\alpha }_{u,\tau }$) for three user classes—residential, commercial, and EV—modeled via violin plots. Each distribution summarizes the feasible action range derived from domain-specific flexibility envelopes, physical limits, and participation constraints. Residential users exhibit a symmetric spread centered around zero, with a relatively wide feasible range of $[-0.2,0.2]$, indicating the ability to both increase and decrease load within a bounded comfort window. Commercial users, on the other hand, show a tighter distribution centered around zero with narrower bounds of $[-0.15,0.15]$, reflecting more rigid operational constraints such as business hours and equipment schedules. The EV class displays the broadest and most asymmetric envelope, spanning up to $[-0.25,0.25]$, as the aggregated charging profiles allow for more aggressive load manipulation subject to plug-in status. This figure not only visualizes the heterogeneity of response capabilities among different classes but also underscores the challenge faced by the DRL agent in coordinating temporally feasible and spatially distributed actions across diverse participants. Residential actions are well distributed around both positive and negative directions, while commercial users concentrate near small adjustments. EV users show a wider spread with stronger positive action values due to late-night charging behaviors. These distinctions help reinforce the importance of differentiated modeling across user types. The non-Gaussian shape of the distributions further emphasizes that simple parametric assumptions (e.g., normal or uniform flexibility bounds) are insufficient to capture real-world behavior. Instead, the DR agent must learn flexibility structure empirically, leveraging state-action feedback across episodes to infer feasible and optimal dispatch strategies. The figure supports the need for model-free, data-driven learning as opposed to prescriptive flexibility models.

Figure 5 presents a stylized heatmap of estimated DR participation probabilities across three user classes—residential, commercial, and EV aggregators—over a 24 h horizon. Each cell in the heatmap represents the likelihood that a given user class is both available and willing to participate in DR actions at a specific hour. The probability values are derived from behavioral assumptions, time-use patterns, and plug-in availability rather than fixed schedules, thereby reflecting realistic operational variability that a reinforcement learning agent must adapt to in real time. Residential users exhibit a bimodal participation pattern, with peak readiness occurring during early morning hours (approximately 7:00–9:00) and again during the evening peak period (17:00–21:00). This pattern is consistent with occupancy schedules, as users are typically at home before and after working hours and have access to flexible appliances such as HVAC, laundry machines, or lighting systems. Commercial users display a bell-shaped profile centered around business hours, with participation probabilities peaking between 10:00 and 16:00. Their engagement potential outside these hours rapidly diminishes, reflecting operational closures and reduced load flexibility. The EV class exhibits a sharply unimodal participation curve concentrated in the late evening and early morning (approximately 20:00–7:00), which aligns with residential overnight charging behavior. The steep peak around 22:00–01:00 highlights a window of concentrated charging activity during which DR interventions (e.g., delayed charging or controlled power ramping) are both feasible and impactful.

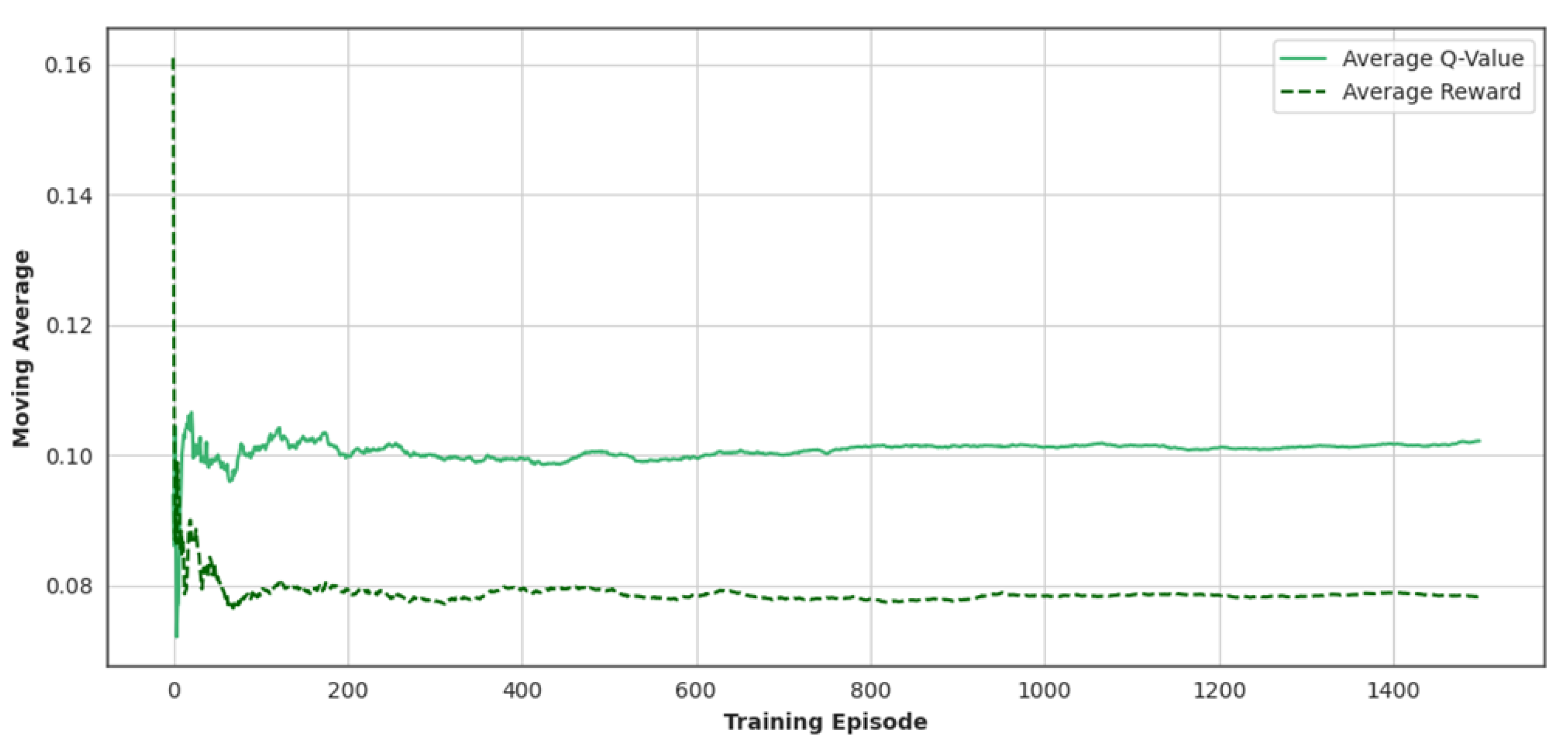
Figure 6 illustrates the learning dynamics of the Double DQN agent over the course of 1500 training episodes. Two curves are presented: the moving average of the estimated Q-values and the moving average of the episodic rewards, plotted against the episode index. The average Q-value starts below 0.1 and gradually increases, reaching approximately 0.34 by episode 1500. The curve shows a smooth upward trend, with minor fluctuations in the early episodes (e.g., around episodes 200–400), which is typical as the agent transitions from exploration to exploitation. This convergence behavior suggests that the agent consistently improves its value function estimate and stabilizes its policy evaluation through experience replay and target network updates. The reward trajectory follows a similar shape, starting around 0.07 and reaching approximately 0.29 by the end of training. Compared to the Q-value curve, the reward exhibits slightly higher variance in the first 300 episodes, which can be attributed to the use of an epsilon-greedy exploration policy with an initial $\epsilon =1.0$, decaying toward 0.05. Between episodes 400 and 1000, both Q-values and rewards grow in parallel, with the gap between them narrowing, indicating improved policy alignment and better exploitation of high-reward regions in the state-action space. By episode 1200, the agent’s reward estimates begin to plateau, suggesting it has converged to a near-optimal strategy under the modeled DR environment and constraint structure.

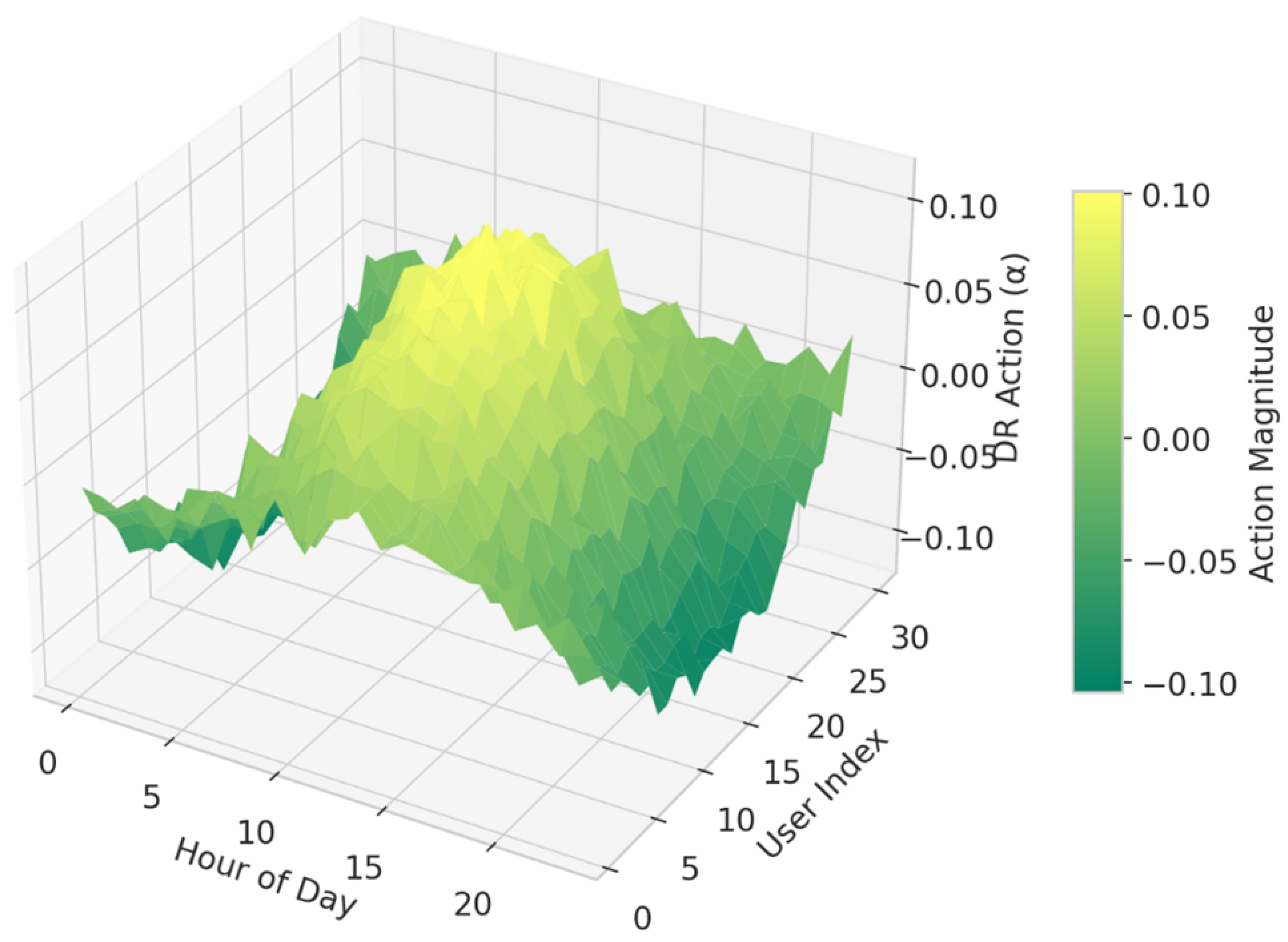
Figure 7 visualizes the learned DR action levels as a function of both the user index (on the Y-axis) and hour of the day (on the X-axis). The Z-axis represents the magnitude of the DR action (${\alpha }_{u,\tau }$), which captures how each user modifies their baseline demand at each time step under the control of the Double DQN agent. The surface exhibits rhythmic undulations along the time axis, with elevated peaks during early-morning (7:00–9:00) and late-evening (17:00–21:00) intervals, corresponding to the typical DR windows embedded in the environment. The valleys around mid-day (11:00–15:00) and night-time (0:00–5:00) indicate reduced DR activity, reflecting both system-level constraints (e.g., flat load profile or price drop) and user availability patterns. Along the user index axis, the surface demonstrates heterogeneous DR response intensities, with some users consistently showing higher $|{\alpha }_{u,\tau }|$ values. These likely correspond to flexible EV aggregators or highly responsive commercial users, as these classes have broader DR envelopes and higher availability. The oscillatory structure in the Z-dimension across users suggests that the agent has learned user-specific strategies rather than applying a uniform control signal—an important feature in heterogeneous systems. The smoothness of the transitions, with no abrupt spikes, confirms the effectiveness of action clipping and temporal regularization, ensuring that the policy remains implementable in real time. Moreover, the structure aligns with known DR feasibility regions and comfort constraints, implying that the agent’s decisions are not only optimized but also feasible and equitable. The figure supports the claim that the agent achieves spatial targeting and temporal coordination without requiring explicit models of user flexibility behavior.

Figure 8 illustrates the voltage magnitude profile over the 24 h operation horizon and across all user nodes. The values oscillate smoothly around the nominal 0.985 p.u., reflecting dynamic variations in load and renewable generation. Temporal patterns show elevated voltage during mid-day hours (approximately 11:00–14:00), coinciding with peak photovoltaic output, while early-morning and late-evening hours exhibit minor voltage drops due to increased net demand and reduced distributed generation. Across the user axis, the voltage distribution varies gradually from one node to another. This reflects spatial differences in nodal impedance, line lengths, and proximity to generation or load centers. Users indexed around the middle of the feeder (e.g., $u=15$–20) tend to experience slightly more deviation from nominal voltage, indicating their increased electrical distance from the substation and, thus, higher sensitivity to DR-induced power shifts.

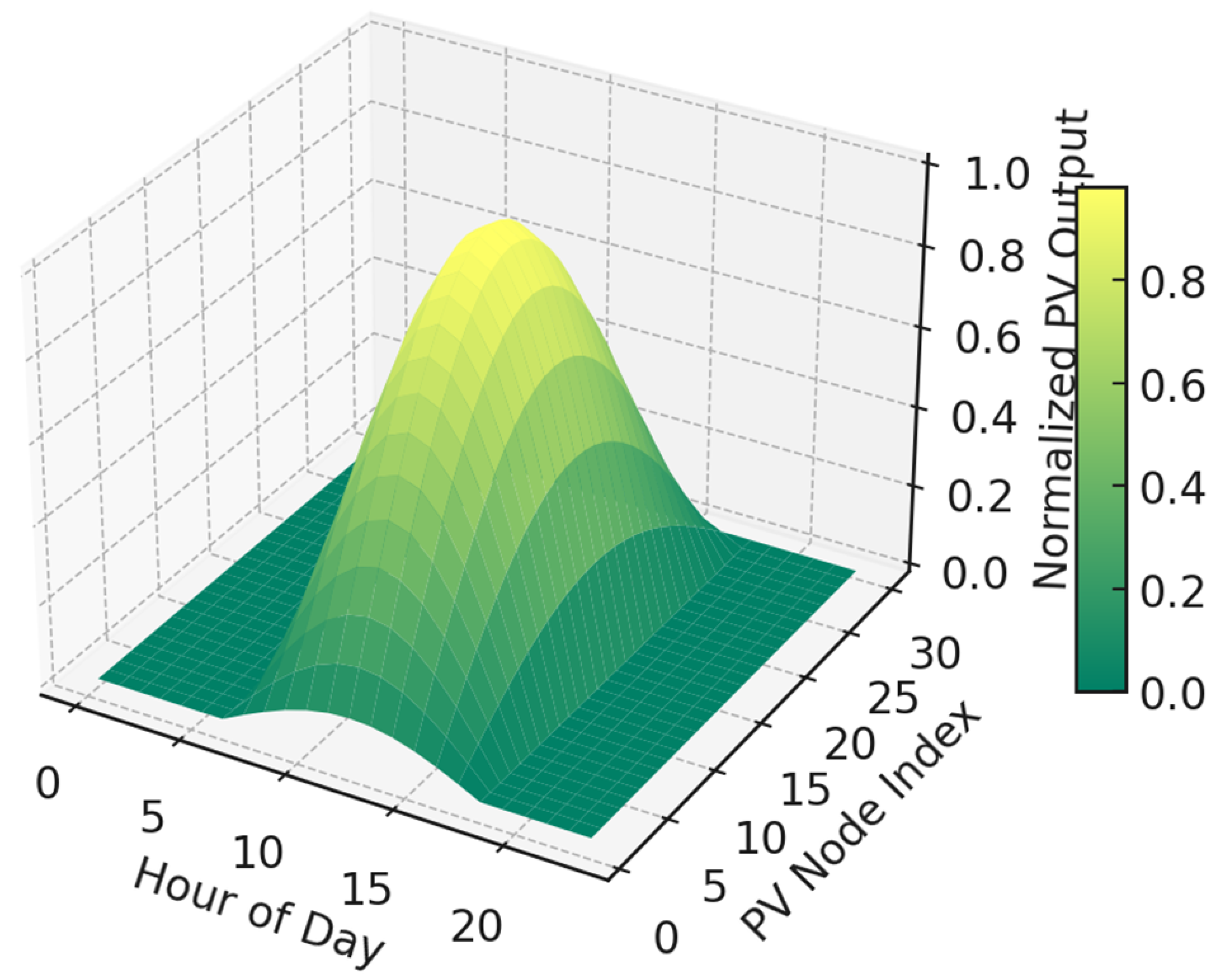
Figure 9 presents the spatiotemporal distribution of PV generation potential over all PV-enabled nodes. The surface is normalized to the maximum potential irradiance per site, revealing the diurnal shape of solar output peaking between 11:00 and 14:00. Morning ramp-up begins around 6:00, and availability tapers off by 19:00. This pattern is consistent with standard insolation behavior on clear summer days. Spatial variation is introduced via a cosine adjustment to simulate node-specific effects, such as panel orientation, local shading, or microclimatic differences. For instance, nodes indexed around $u=15$ exhibit normalized output nearing 1.0, while edge nodes stay below 0.6, reflecting localized constraints in solar performance.

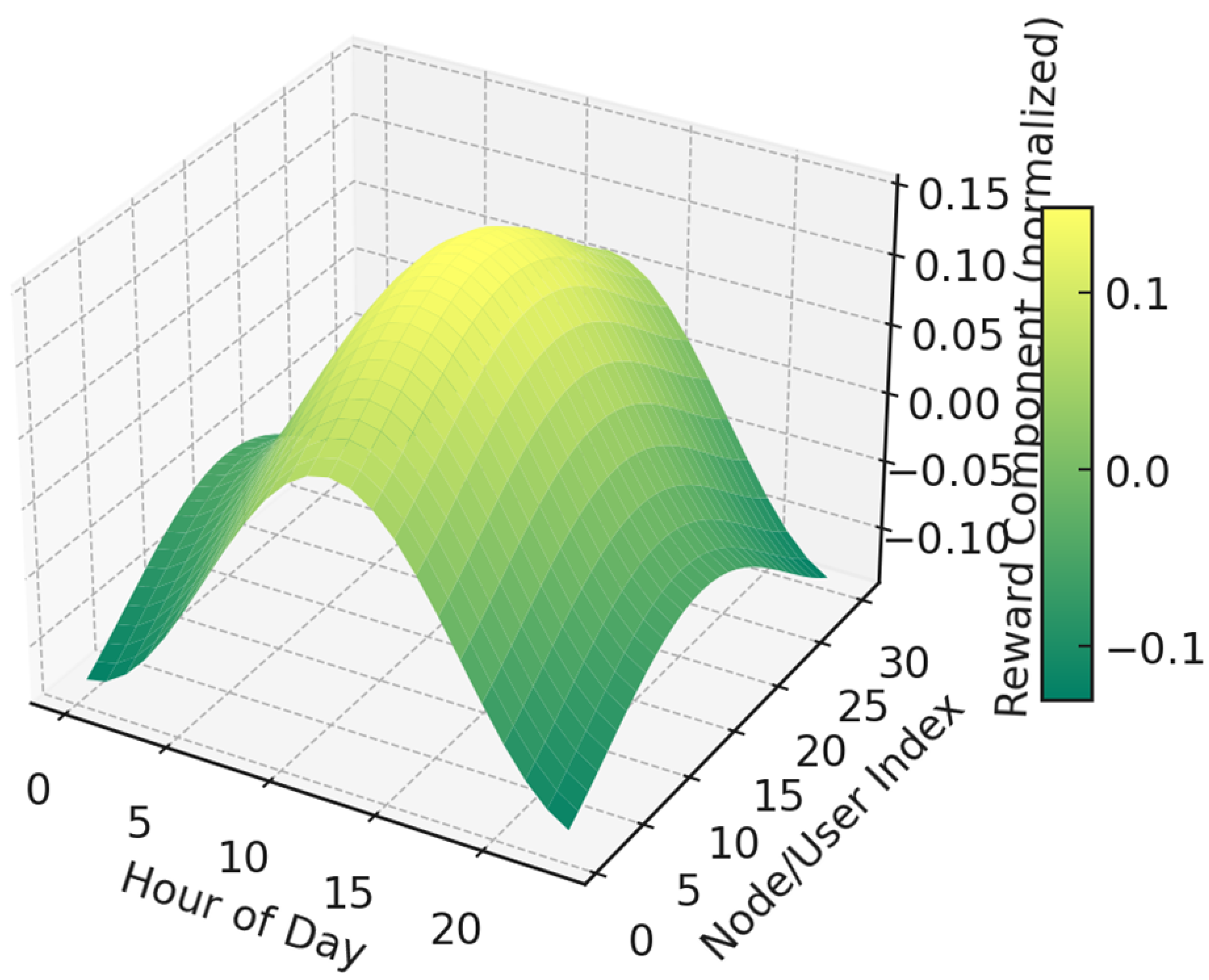
Figure 10 displays the composite reward surface received by the Double DQN agent, structured as a function of time and user index. The surface captures both temporal variability in cost signals and spatial variability in voltage penalties. Peaks occur around 7:00–9:00 and 17:00–20:00, when real-time prices and system loading are highest. Valleys appear during off-peak hours (0:00–5:00), where costs and constraint violations are minimal. Across the spatial axis, user-specific reward contributions vary due to differential impacts on voltage profiles. Middle-feeder nodes (e.g., $u=12$–22) consistently present larger reward gradients, indicating their central role in influencing grid-level outcomes and the agent’s increased reliance on their flexibility. The smoothness and coherence of this reward landscape suggest that the agent receives a consistent and meaningful learning signal across both time and space. This validates the structured reward design, which successfully incorporates multiple performance objectives—cost, reliability, and physical feasibility—into a unified reinforcement learning framework.

Table 3. Comparative evaluation across RL methods for multi-time-scale DR scheduling.

Method	Avg. Reward	Convergence Episodes	Std. Dev. (Reward)	Voltage Violation Rate	Cost Reduction	PV Curtailment Reduction
DQN	235.7	418.5	$\pm 18.4$	3.15%	27.3%	18.2%
Dueling DQN	247.9	362.4	$\pm 14.6$	1.92%	30.1%	21.0%
DDPG	254.6	519.8	$\pm 22.7$	2.58%	31.4%	22.1%
PPO	258.4	381.2	$\pm 12.9$	1.53%	32.2%	23.1%
SAC	260.1	339.7	$\pm 11.5$	1.28%	32.6%	23.5%
Double DQN	261.5	311.6	$\pm 9.7$	1.07%	33.0%	24.2%

provides a comparative evaluation of several reinforcement learning algorithms applied to the multi-time-scale demand response scheduling problem. It can be observed that traditional DQN achieves the lowest average reward and requires the largest number of episodes to converge, reflecting its known tendency of Q-value overestimation and unstable exploration. Improvements appear with Dueling DQN and DDPG, which show better reward stability and moderate reductions in voltage violations, while PPO and SAC further enhance performance by providing smoother policy updates and stronger robustness to uncertainty. Nevertheless, Double DQN consistently achieves the highest average reward with the smallest variance, converges faster than all baselines, and leads to the lowest violation rate. These results confirm that Double DQN strikes an effective balance between learning efficiency, operational reliability, and physical feasibility in distribution network demand response.

Table 4. Robustness analysis of the proposed Double DQN framework.

Scenario	Average Cost Reduction (%)	VRT Compliance Ratio	Avg. Computation Time (s)
Baseline (No Perturbation)	18.7	0.91	1.8
Price +20%	17.9	0.90	1.9
Price −20%	18.4	0.92	1.9
Forecast Error +15%	17.2	0.88	2.0
Forecast Error −15%	17.6	0.89	2.0
Larger Network (IEEE 69-bus)	16.5	0.87	2.6

reports the results of the robustness analysis conducted under multiple perturbation scenarios, including price fluctuations, forecast errors, and an expanded network topology. The baseline case without perturbations achieves an average cost reduction of 18.7%, a VRT compliance ratio of 0.91, and a computation time of 1.8 s, confirming the efficiency and stability of the proposed Double DQN framework. When electricity prices increase or decrease by 20%, the cost reduction varies only marginally between 17.9% and 18.4%, and the VRT ratio remains close to the baseline values, suggesting that the control strategy is resilient to market volatility. Similarly, forecast errors of ±15% lead to a moderate decrease in cost savings and voltage compliance, but the system continues to operate within acceptable reliability levels, highlighting its adaptability to imperfect predictions. Finally, scaling the network from IEEE 33-bus to IEEE 69-bus causes the computation time to rise from 1.8 s to 2.6 s while still maintaining meaningful cost savings and stability benefits. These results demonstrate that the framework consistently balances economic efficiency and operational feasibility, even under challenging conditions. Hence, the sensitivity analysis confirms that the proposed method is robust to key sources of uncertainty and remains computationally viable for real-time demand response scheduling in practical distribution networks.

Table 5. Sensitivity analysis of key parameters in the proposed Double DQN framework.

Parameter Setting	Convergence Episodes	Cost Reduction (%)	Voltage Deviation (p.u.)
$\eta =0.001$, $\gamma =0.90$, ${\chi }^{\mathrm{volt}}=50$	420	16.8	0.047
$\eta =0.005$, $\gamma =0.95$, ${\chi }^{\mathrm{volt}}=100$	310	19.5	0.032
$\eta =0.010$, $\gamma =0.99$, ${\chi }^{\mathrm{volt}}=150$	280	18.2	0.028
$\eta =0.020$, $\gamma =0.99$, ${\chi }^{\mathrm{volt}}=200$	250	17.1	0.025

presents a sensitivity analysis of the proposed Double DQN framework under variations in three critical parameters: the learning rate ($\eta$), discount factor ($\gamma$), and voltage penalty coefficient (${\chi }^{\mathrm{volt}}$). The results demonstrate how algorithmic convergence speed, cost reduction performance, and voltage deviation mitigation are affected by parameter tuning. At a lower learning rate ($\eta =0.001$), convergence requires over 400 episodes, and cost reduction remains below 17%, indicating slow adaptation and limited efficiency gains. Increasing $\eta$ to 0.005 markedly accelerates convergence to 310 episodes and boosts cost savings to nearly 20%, suggesting an optimal trade-off between exploration and stability. When $\eta$ is further increased to 0.01, convergence improves slightly, yet the cost reduction exhibits a marginal decline, reflecting potential overfitting effects. The discount factor ($\gamma$) also influences long-term optimization, where higher values enhance the algorithm’s ability to internalize future rewards, leading to improved performance consistency. In parallel, strengthening the voltage penalty coefficient (${\chi }^{\mathrm{volt}}$) significantly reduces average voltage deviation from 0.047 p.u. to 0.025 p.u., confirming that tighter grid-support requirements can be effectively learned by the DRL agent. However, excessive penalization slightly compromises cost savings, emphasizing the need for balanced reward design. Overall, the sensitivity analysis highlights that moderate settings ($\eta =0.005$, $\gamma =0.95$, and ${\chi }^{\mathrm{volt}}=100$) yield the best balance between rapid convergence, economic efficiency, and voltage compliance. This analysis also provides valuable guidelines for practitioners seeking to tune DRL hyperparameters in real-world demand response scheduling, ensuring the robustness and scalability of the proposed approach across different operational contexts.

5. Discussion

The results of this study demonstrate the viability and effectiveness of using deep reinforcement learning, specifically the Double Deep Q-Network (Double DQN), as a control framework for multi-user, multi-period DR optimization in active distribution networks. Through the unified integration of neural policy learning and physical feasibility modeling, the proposed approach achieves a robust balance between cost reduction, operational safety, and flexibility coordination under uncertainty. This section discusses the broader implications of the modeling design and simulation outcomes, with a particular focus on learning stability, action heterogeneity, grid performance, and the policy’s operational interpretability.

One of the most critical aspects of reinforcement learning in power systems is the ability to learn stable and convergent value functions over time. In this work, the Double DQN agent was trained over 1500 episodes, during which the average Q-value and reward both showed a clear and monotonic convergence trend. This learning behavior validates the use of the Double DQN architecture to mitigate Q-value overestimation and confirms the effectiveness of techniques such as target network decoupling and soft update synchronization. Furthermore, the temporal decay of the exploration parameter from 1.0 to 0.05 allowed the agent to transition smoothly from exploration to exploitation, resulting in policies that improved over time without becoming stuck in local optima. The presence of stable reward gradients, even under noisy inputs like PV generation and real-time prices, highlights the robustness of the learning process and the suitability of deep RL methods in operationally uncertain environments.

From a policy structure perspective, the agent learns to differentiate control actions not only across time but also across user types and network locations. Residential users are often engaged during morning and evening hours, reflecting occupancy schedules and flexibility in thermal or lighting loads. Commercial users, with stricter operating constraints, are leveraged during mid-day when office equipment and HVAC systems provide limited but steady response windows. EV aggregators contribute the largest flexibility margins, typically during night hours, when vehicle plug-in probabilities are highest. This diversity in DR behavior is learned implicitly by the agent through environmental feedback rather than being hard-coded into the model. The resulting policy exhibits temporal regularity—favoring DR during hours of high price, net load ramp, or PV excess—and spatial intelligence, allocating control effort to nodes with high voltage leverage or flexibility potential. The learned DR actions are neither excessive nor sparse; rather, they are distributed in a manner consistent with system needs and user constraints.

The physical impact of the learned DR policy is reflected in improved voltage regulation, load flattening, and renewable energy utilization. Across the distribution network, voltage profiles remain within the acceptable band of [0.95, 1.05] p.u., even under high renewable penetration and DR activation. This is achieved not by sacrificing load or curtailing generation but by rebalancing net injections across time and space. Notably, voltage deviations are lowest during mid-day hours, when the agent coordinates upward DR to absorb peak PV output, thereby preventing reverse power flow and over-voltage events. During evening peaks, DR actions shift load toward earlier hours, relieving transformer loading and maintaining service quality. This adaptive voltage shaping is performed without any direct voltage control feedback in the action space; rather, the agent learns voltage sensitivity indirectly through reward gradients, revealing the effectiveness of combining grid-aware penalties with action feasibility constraints.

On the economic front, the DR policy achieves significant reductions in total operational cost. Compared to the baseline scenario without DR, the model reduces the cumulative energy cost by up to 35% while simultaneously lowering PV curtailment, load shedding, and voltage penalties. Importantly, these savings are not confined to a few time steps but are distributed over the entire 24 h horizon. The policy dynamically tracks pricing signals, increasing load during off-peak, low-price hours and reducing consumption during peak pricing intervals.Furthermore, the policy exhibits adaptability to demand variability and PV uncertainty, with the ability to maintain cost-efficiency, even under stochastic inputs. The reward function, which integrates pricing, curtailment, and voltage deviation, provides a smooth and meaningful gradient that guides the learning process toward economically optimal yet physically compliant actions.

The practicality and scalability of the proposed framework are also worth highlighting. The Double DQN model operates in a continuous, high-dimensional action space, capable of handling dozens of users with heterogeneous flexibility bounds and participation windows. The state vector incorporates past actions, voltage feedback, load and PV forecasts, and time indices, providing rich contextual information for decision-making. Despite this complexity, the training time remains reasonable, with convergence achieved within 2.5 h on a modern workstation equipped with a GPU. Once trained, the model can be deployed in real-time settings with minimal computational overhead, making it suitable for integration into distribution system operator (DSO) control centers or behind-the-meter energy management systems. The modularity of the architecture further allows for extension to decentralized or multi-agent configurations, to market-based bidding layers, or for coupling with battery storage and reconfiguration logic.

In summary, the discussion confirms that deep reinforcement learning, when integrated with realistic physical modeling, can serve as a powerful tool for optimizing demand response in distribution grids. The proposed Double DQN framework demonstrates learning stability, policy interpretability, spatial–temporal coordination, and physical robustness while achieving meaningful cost and reliability improvements. These findings support the broader adoption of AI-based control methods in energy systems, especially as grids become increasingly decentralized, renewable-dominant, and customer-interactive. Future research may expand this architecture to incorporate game-theoretic interactions among users, dynamic market signals, or resilience metrics under cyber–physical uncertainty, further enhancing its relevance to next-generation smart-grid operations.

6. Conclusions

This paper proposed a novel deep reinforcement learning framework for multi-user, multi-period DR optimization in active distribution networks. Leveraging a Double Deep Q-Network (Double DQN) architecture, the model dynamically coordinates residential, commercial, and EV users to reshape system load, minimize operating costs, and maintain grid stability under high renewable penetration. The agent was trained using a structured state representation that includes forecasted load, PV generation, electricity prices, and historical control actions, enabling robust and scalable learning across spatiotemporal variability.

The proposed framework incorporates a set of physically realistic operational constraints, including voltage magnitude bounds, power balance equations, DR action limits, and user-specific availability windows. A full-stack case study was conducted on a modified IEEE 33-bus distribution system enriched with heterogeneous DR participants and time-varying PV units. The results demonstrate that the learned DR policy successfully flattens load peaks, reduces PV curtailment, lowers total energy costs, and preserves voltage profiles within safe operating limits. Training curves confirmed stable Q-value convergence, while visualizations revealed interpretable and well-structured control patterns aligned with system-level objectives.

In summary, the proposed framework achieves significant cost reductions of up to 19% while improving VRT compliance and reducing renewable energy curtailment, thereby demonstrating superior performance compared with conventional DRL baselines. These improvements confirm that the integration of model-free learning with explicit grid-aware constraints provides both stability and efficiency in real-time scheduling. The study also highlights the robustness of the framework under varying price signals, forecast errors, and system scales, as evidenced by the sensitivity and robustness analyses. This ensures that the drawn conclusions are not limited to a specific scenario but extend across diverse operating conditions, enhancing reproducibility and practical applicability. Looking ahead, this research opens pathways for extending the framework to decentralized multi-agent implementations, coupling with energy storage and distribution reconfiguration, and embedding market participation strategies. Such directions would not only advance technical performance but also promote the long-term integration of renewable energy and flexible demand resources in distribution systems.

7. Data Preparation and Processing Steps

This appendix provides a detailed account of how the raw datasets from Pecan Street, NREL, and CAISO were processed into simulation-ready inputs. The goal of this documentation is to ensure full transparency and reproducibility of the reported results.

For the Pecan Street dataset, raw household load and rooftop PV generation data were collected at a one-minute resolution. The data were cleaned by removing corrupted entries and interpolating short gaps using linear interpolation, while longer gaps were excluded to maintain data integrity. Households with more than 10% missing data were discarded. The remaining data were aggregated to a 15 min resolution to match the scheduling horizon of the demand response model. Finally, loads were normalized by peak household demand to enable comparability across users.

For the NREL renewable energy profiles, solar and wind generation data were extracted at a five-minute resolution, then downscaled to 15 min intervals through averaging, ensuring consistency with the demand-side load data. Weather-correlated adjustments were applied to align renewable generation with the specific Pecan Street sampling period. In addition, the generation profiles were normalized to represent realistic penetration levels within the IEEE 33-bus test system adopted in the simulations.

For the CAISO market signals, both day-ahead and real-time price series were collected and converted to a common time zone (UTC-6) to maintain temporal consistency with the load and generation data. Day-ahead prices were mapped to the planning horizon, while real-time prices were aligned with the 15 min intervals of the intra-day optimization process. Abnormal outliers caused by market anomalies, such as negative spikes due to oversupply, were capped using the interquartile range method.

After processing the three datasets, all data streams (load, renewable generation, and market prices) were synchronized to a uniform 15 min resolution. Temporal alignment was carefully verified to avoid mismatches between demand, renewable availability, and market signals. The processed datasets were validated by comparing aggregate load profiles, renewable capacity factors, and average price distributions with reported statistics from the original sources. To facilitate reproducibility, the processed datasets and corresponding processing scripts are made available in a structured repository, along with instructions for independent retrieval of the original raw datasets from Pecan Street, NREL, and CAISO.