Power System Modeling and Simulation for Distributed Generation Integration: Honduras Power System as a Case Study
Abstract
1. Introduction
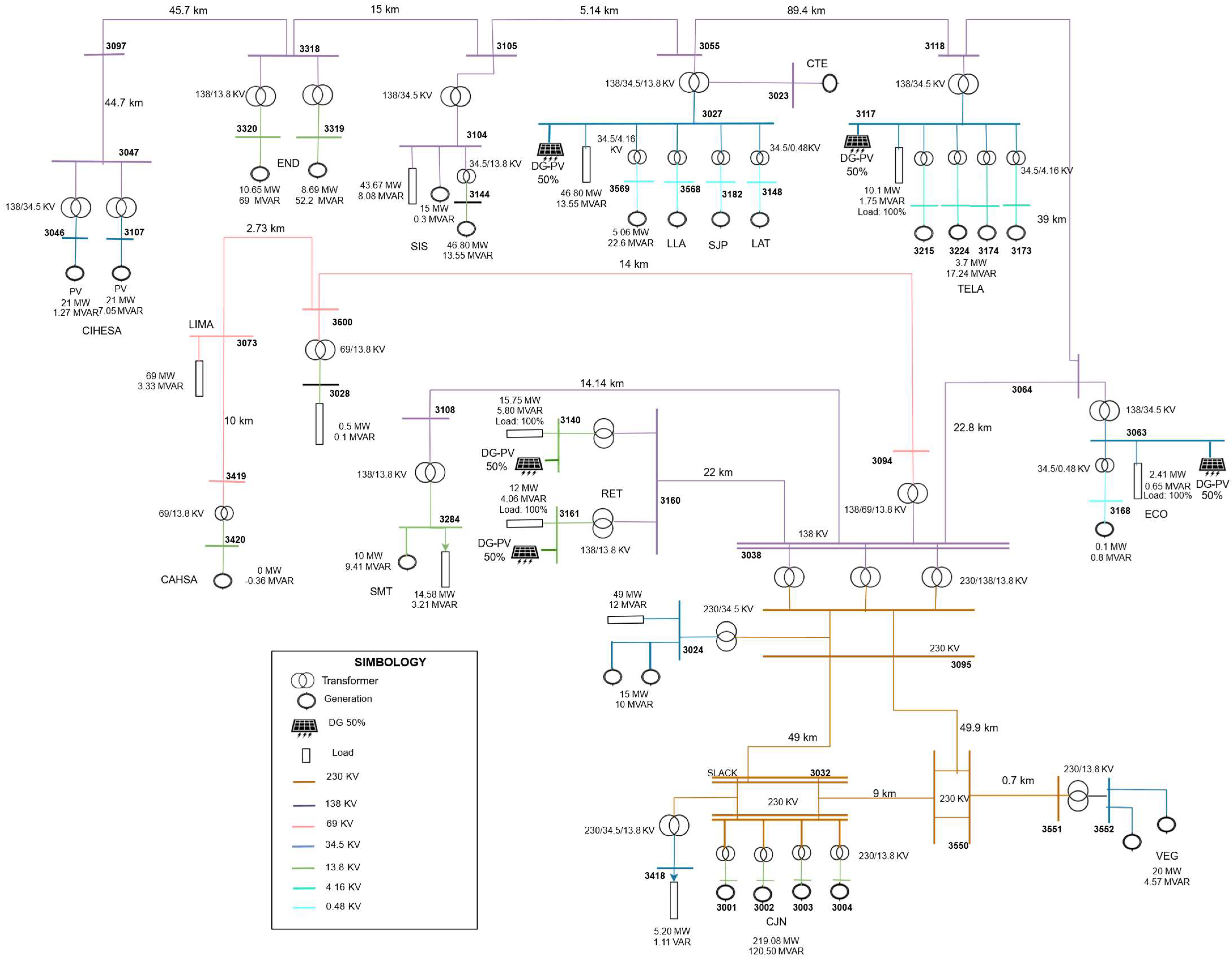
2. Problem Formulation and Description
- Generation: One hundred and fourteen buses in service with 2033.79 MW and forty-two buses out of service with 8.00 MW, for a total of one hundred and fifty-six buses.
- Lines: One hundred and thirty-eight lines in service and three out of service.
- Two-winding transformers: One hundred and eighty-four units in service and ten units out of service.
- Three-winding transformers: Forty-nine units in service; zero units out of service.
- Load: Eighty-seven buses in service with 2005 MW, and fifteen out of service with 161 MW.
- Generation: Nineteen buses with 425 MW of active power and 182.69 MVAR of reactive power.
- Lines: Sixteen active lines.
- Two-winding transformers: Twenty-eight units in service.
- Three-winding transformers: Seven units in service.
- Load: Eleven buses with 204.94 MW of active power and 50.39 MVAR of reactive power demand.
3. Methodology
3.1. Simulation Tools
- Pandas: Used for manipulating and analyzing tabular data, especially for loading, filtering, and transforming information from Excel spreadsheets. Its DataFrame structure facilitates the efficient handling of large volumes of electrical data [45].
- Os: Verifies the existence of the input Excel file and performs basic checks of the working environment [46].
- Pandapower: The main library for modeling, simulating, and analyzing electrical networks. It enables the creation of network elements (buses, lines, transformers, loads, and generators), the execution of load flows, the analysis of voltage and loss profiles, and the evaluation of distributed generation injection scenarios [44,47].
- Matplotlib.pyplot (v3.5.3): Used for displaying results. It is mainly used to generate bar and line graphs representing voltage profiles and line loads, among others [48].
- NumPy: Provides low-level mathematical tools and vectorized operations that optimize the calculations required for comparative analyses [49].
- Pandapower. topology: Provides useful functions for the network topological analysis, such as island detection, connected components, and routes among buses [41].
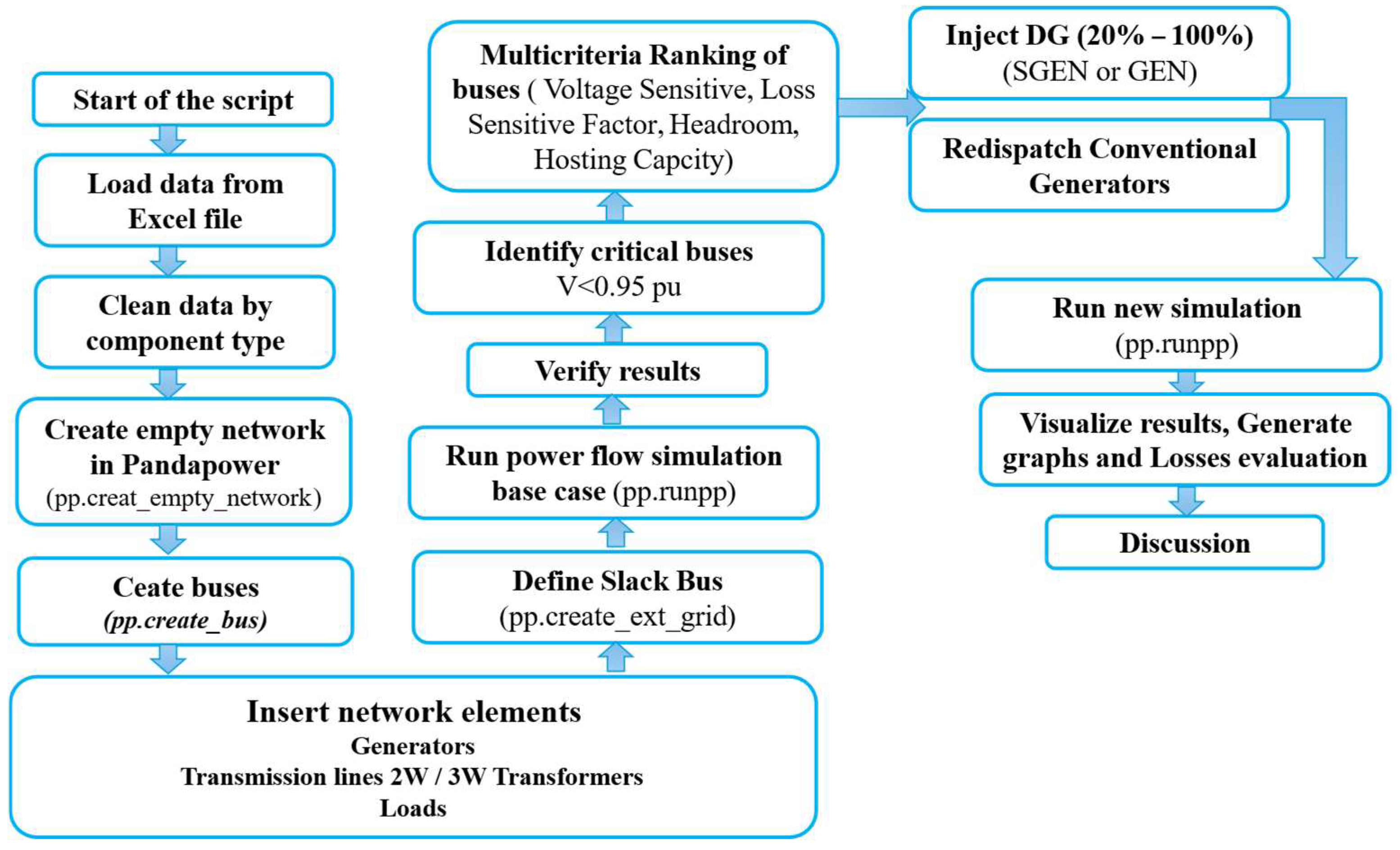
3.2. Proposed Methodology
3.2.1. Data Collection and Cleaning
3.2.2. Network Modeling in Pandapower
3.2.3. Simulation of Base Case
3.2.4. Bus Selection Using Multi-Criteria Analysis
3.2.5. DG Injection Scenarios
3.2.6. Application of Redispatch
3.2.7. Evaluation of Results
3.2.8. Validation and Discussion
4. Simulation Results and Discussion
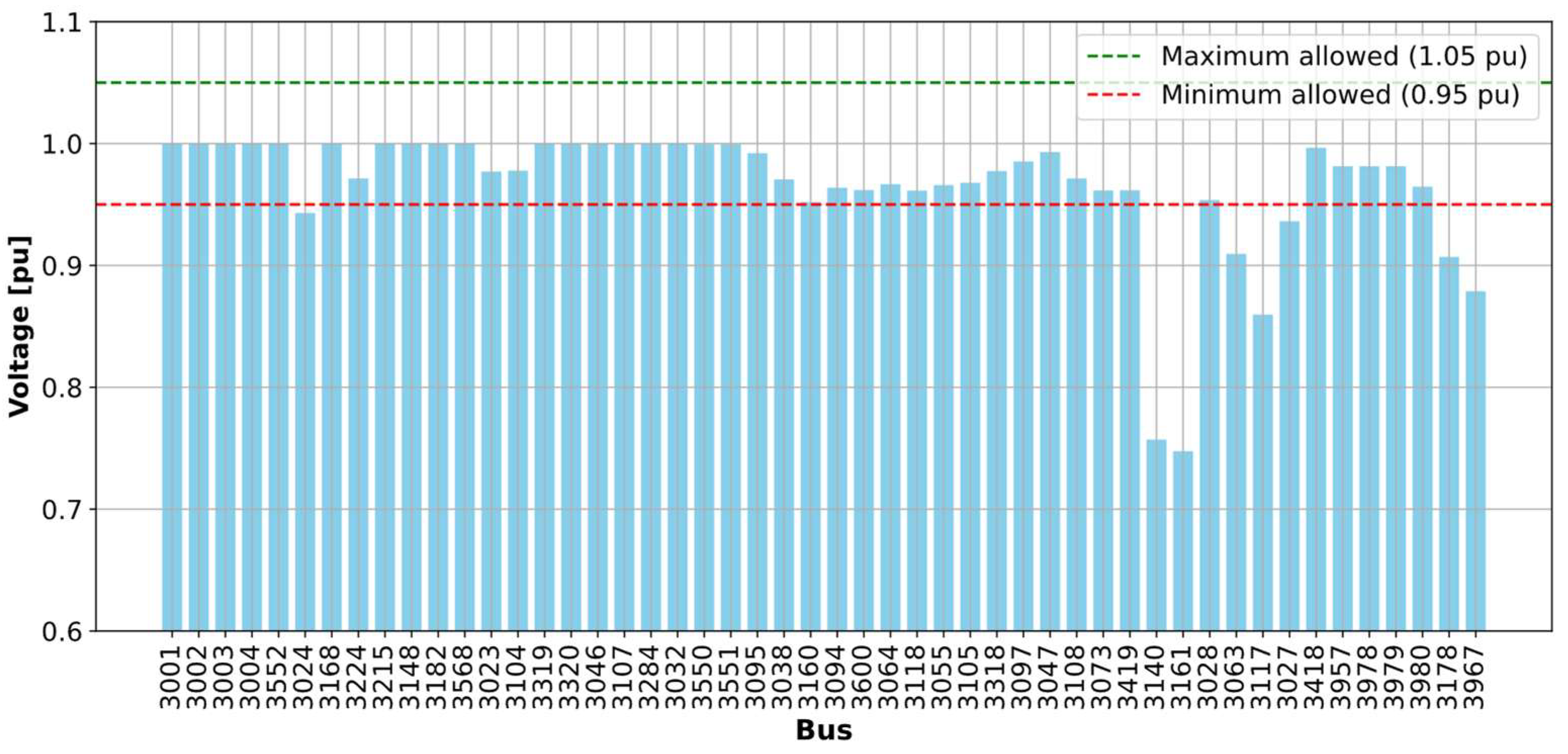
4.1. Base Scenario: No Distributed Generation
4.2. Base Scenario: With Distributed Generation
4.2.1. GEM: Voltage-Regulating Generator
- A voltage-regulating generator can regulate the voltage at the buses to which it is connected.
- It controls its reactive power injection (Q) to maintain a target voltage value (p.u.).
- It is used in load flow analysis as a controlled source of active and reactive power.
- In real applications, this behavior corresponds to that of synchronous generators, such as those used in large-scale hydroelectric, thermal, or wind power plants, as well as advanced reactive compensation devices, such as STATCOMs (static synchronous compensators) and photovoltaic inverters with advanced voltage control functions.
4.2.2. SGEM: Static Generator
- Proportional to base dispatch (the main criterion): Those who generate more cut back more. This is the typical AGC distribution, modeled according to the following.Let .
- Fallback proportional to maximum capacity: When distribution proportional to base dispatch is not applicable, a neutral criterion is adopted that uses the generators’ nominal capacity as a weighting factor. In these cases, the algorithm uses an alternative allocation scheme proportional to the maximum available power.Let .
- Equal shares: This is used to distribute the total adjustment equally among all eligible generators, regardless of their operating point or size. To do this, is used.
- Space to reduce (downward redispatch): The “enforce_limits_and_redistribute” routine imposes limits and corrects any imbalance in the total by redistributing iteratively. If there is still “surplus” power, meaning more reduction is needed, it is distributed only among units with a reduction margin, using weights as shown,Let .
- Upward headroom (upward redispatch): If there is a power shortage, it is necessary to increase generation. The following expression is then used when it is necessary to increase generation, and it is desired that those with more actual margin toward maximum power participate more.Let .
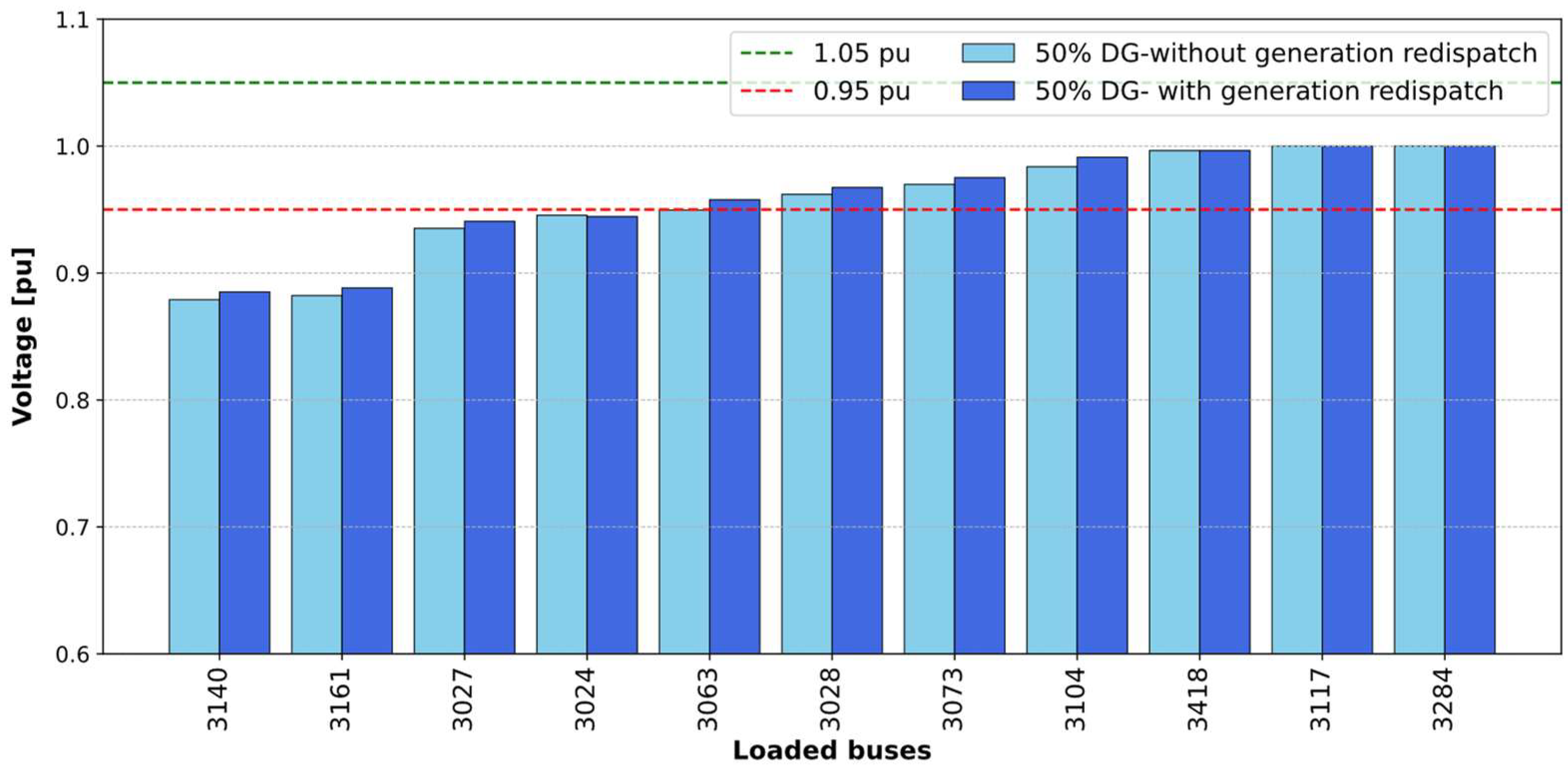
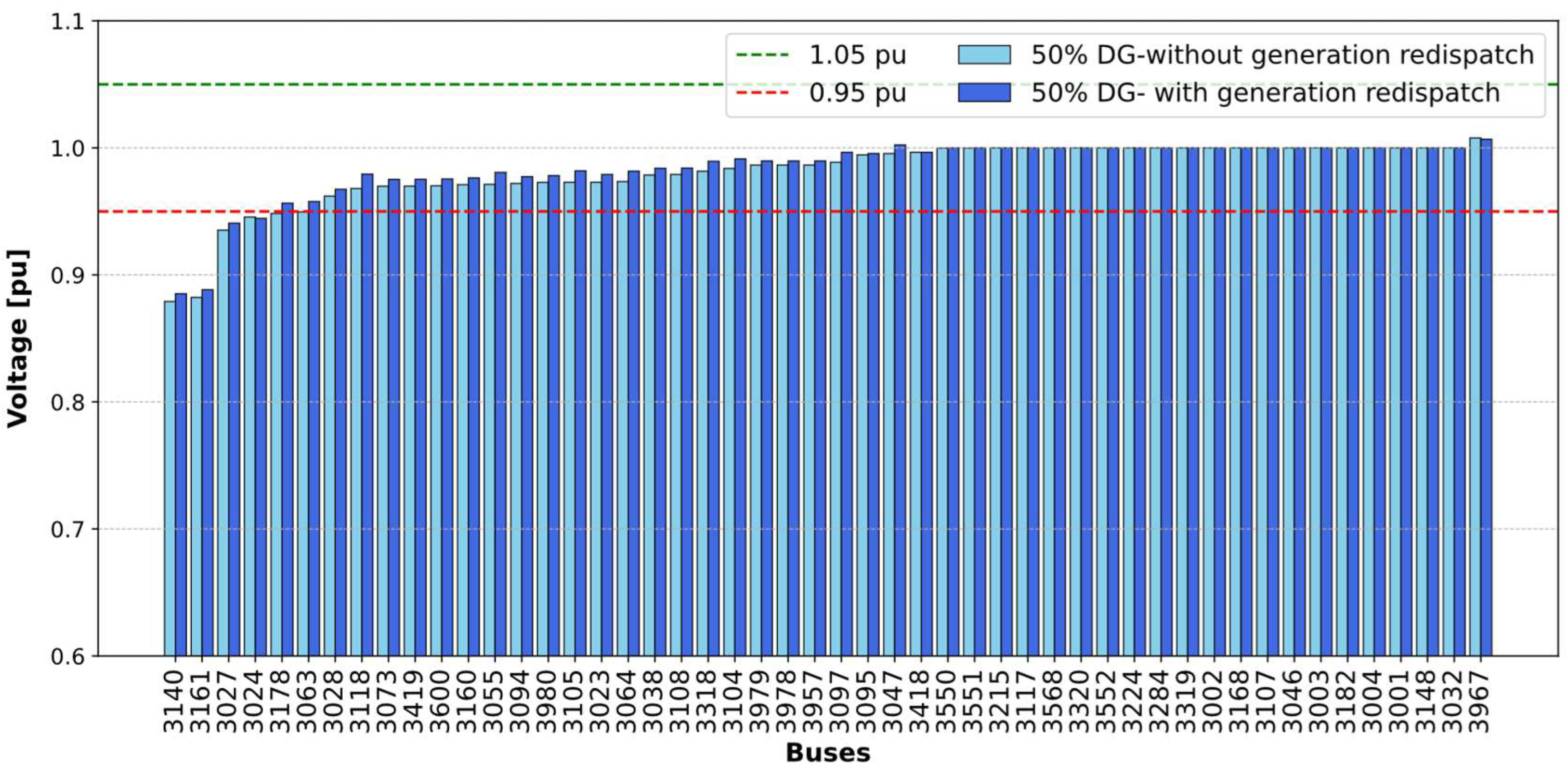
4.3. Comparison of Scenarios
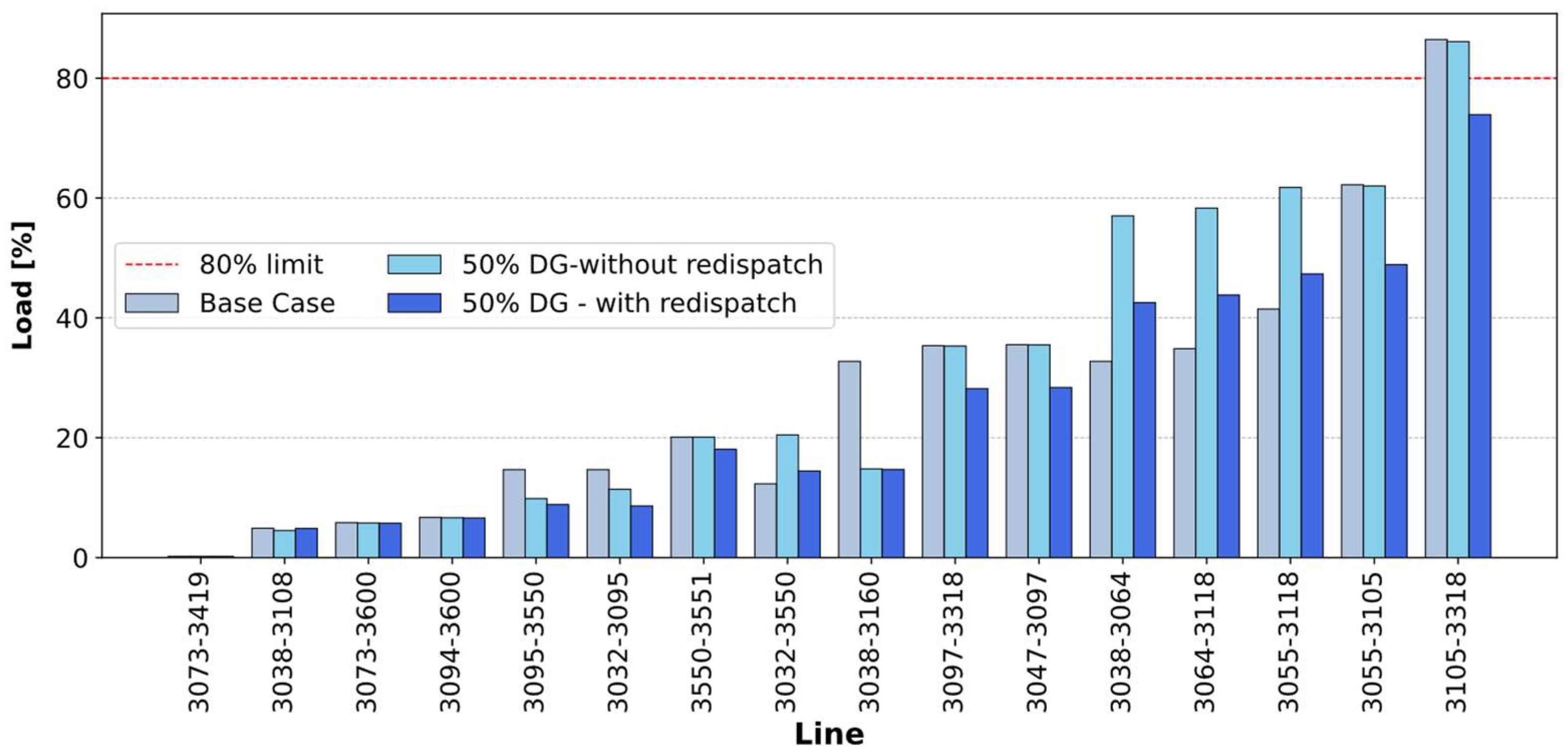
4.4. Result and Analysis
4.5. Limitation of Model for Future Studies
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
References
- RENRenewables Global Status Report. Available online: https://www.ren21.net/reports/global-status-report/ (accessed on 27 June 2025).
- Viaintermedia.com. IRENA Reports Record-Breaking Annual Growth in Renewable Power Capacity, Renewable Energy Magazine, at the Heart of Clean Energy Journalism. Available online: https://www.renewableenergymagazine.com/panorama/irena-reports-recordbreaking-annual-growth-in-renewable-20250328 (accessed on 27 June 2025).
- Hassan, Q.; Algburi, S.; Sameen, A.Z.; Al-Musawi, T.J.; Al-Jiboory, A.K.; Salman, H.M.; Ali, B.M.; Jaszczur, M. A comprehensive review of international renewable energy growth. Energy Built Environ. 2024. [Google Scholar] [CrossRef]
- Global overview—Renewables 2024—Analysis, IEA. Available online: https://www.iea.org/reports/renewables-2024/global-overview (accessed on 27 June 2025).
- Tabora, J.M.; Júnior, U.C.P.; Rodrigues, C.E.M.; Bezerra, U.H.; Tostes, M.E.d.L.; de Albuquerque, B.S.; de Matos, E.O.; Nascimento, A.A.D. Hybrid System Assessment in On-Grid and Off-Grid Conditions: A Technical and Economical Approach. Energies 2021, 14, 5284. [Google Scholar] [CrossRef]
- Renewables—Energy System, IEA. Available online: https://www.iea.org/energy-system/renewables (accessed on 27 June 2025).
- Renewables Readiness Assessment: Honduras. Available online: https://sen.hn/wp-content/uploads/2024/09/IRENA_RRA_Honduras_2023_ES.pdf (accessed on 27 June 2025).
- Honduras Presentation—Accelerating Renewables in the Regional Market—23 May. IRENA. Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Presentations/Regional-focus/2018/May/CD-MER-presentation---Accelerating-renewables-in-the-regional-market---23-May.pdf (accessed on 27 June 2025).
- Honduras Wind Electricity Capacity—Data, Chart. TheGlobalEconomy.com. Available online: https://www.theglobaleconomy.com/Honduras/wind_electricity_capacity/ (accessed on 27 June 2025).
- «SIE». Available online: https://siehonduras.olade.org/default.aspx (accessed on 4 September 2025).
- Reza, M.; Slootweg, J.; Schavernaker, P.; van der Sluis, L. Investigating impacts of distributed generation on transmission system stability. In Proceedings of the 2003 IEEE Bologna Power Tech. Conference Proceedings, Bologna, Italy, 23–26 June 2003; pp. 389–395. [Google Scholar] [CrossRef]
- Ahmadi, B.; Ceylan, O.; Ozdemir, A. Optimal allocation of multi-type distributed generators for minimization of power losses in distribution systems. In Proceedings of the 2019 20th International Conference on Intelligent System Application to Power Systems (ISAP), New Delhi, India, 10–14 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Iweh, C.D.; Gyamfi, S.; Tanyi, E.; Effah-Donyina, E. Distributed Generation and Renewable Energy Integration into the Grid: Prerequisites, Push Factors, Practical Options, Issues and Merits. Energies 2021, 14, 5375. [Google Scholar] [CrossRef]
- Ahmed, K.; Hussain, I.; Seyedmahmoudian, M.; Stojcevski, A.; Mekhilef, S. Voltage Stability and Power Sharing Control of Distributed Generation Units in DC Microgrids. Energies 2023, 16, 7038. [Google Scholar] [CrossRef]
- Madjovski, D.; Dumancic, I.; Tranchita, C. Dynamic Modeling of Distribution Power Systems with Renewable Generation for Stability Analysis. Energies 2024, 17, 5178. [Google Scholar] [CrossRef]
- Kabir, S.; Krause, O.; Bansal, R.; Ravishanker, J. Dynamic voltage stability analysis of sub-transmission networks with large-scale photovoltaic systems. In Proceedings of the 2014 IEEE PES General Meeting | Conference & Exposition, National Harbor, MD, USA, 27–31 July 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Furukakoi, M.; Senjyu, T.; Funabashi, T. Voltage stability improvement of power system using a shunt capacitor. Renew. Energy Power Qual. J. 2016, 339–344. [Google Scholar] [CrossRef]
- Lammert, G.; Premm, D.; Ospina, L.D.P.; Boemer, J.C.; Braun, M.; van Cutsem, T. Control of Photovoltaic Systems for En-hanced Short-Term Voltage Stability and Recovery. IEEE Trans. Energy Convers. 2019, 34, 243–254. [Google Scholar] [CrossRef]
- Fang, J.; Li, X.; Li, H.; Tang, Y. Stability Improvement for Three-Phase Grid-Connected Converters Through Impedance Reshaping in Quadrature-Axis. IEEE Trans. Power Electron. 2017, 33, 8365–8375. [Google Scholar] [CrossRef]
- Nazifa, S.; Islam, R.; Kabir, A.; Hasan, M. Analysis of the Impact of PV Penetration in Distribution Network: A Case Study in IEEE 14 Bus System. In Proceedings of the 2021 International Conference on Automation, Control and Mechatronics for Industry 4.0 (ACMI), Rajshahi, Bangladesh, 8–9 July 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Kwasinski, A.; Onwuchekwa, C.N. Dynamic Behavior and Stabilization of DC Microgrids with Instantaneous Constant-Power Loads. IEEE Trans. Power Electron. 2010, 26, 822–834. [Google Scholar] [CrossRef]
- Olamaei, J.; Niknam, T.; Gharehpetian, G. Application of particle swarm optimization for distribution feeder reconfiguration considering distributed generators. Appl. Math. Comput. 2008, 201, 575–586. [Google Scholar] [CrossRef]
- AlRashidi, M.; AlHajri, M. Optimal planning of multiple distributed generation sources in distribution networks: A new approach. Energy Convers. Manag. 2011, 52, 3301–3308. [Google Scholar] [CrossRef]
- Hizarci, H.; Demirel, O.; Turkay, B.E. Distribution network reconfiguration using time-varying acceleration coefficient assisted binary particle swarm optimization. Eng. Sci. Technol. Int. J. 2022, 35, 101230. [Google Scholar] [CrossRef]
- Tabora, J.M.; Velasquez, Y.G.; Rivera, D.A.; Quijano, D.A.; Melgar-Dominguez, O.D. A Multiobjective Strategy for Generation Expansion Planning to Enable Increased Penetration of Variable Renewable Energy Sources. IEEE Access 2024, 12, 187665–187675. [Google Scholar] [CrossRef]
- Tiwari, D.; Zideh, M.J.; Talreja, V.; Verma, V.; Solanki, S.K.; Solanki, J. Power Flow Analysis Using Deep Neural Networks in Three-Phase Unbalanced Smart Distribution Grids. IEEE Access 2024, 12, 29959–29970. [Google Scholar] [CrossRef]
- Palaniyappan, B.; T, V.; Chandrasekaran, G. Solving electric power distribution uncertainty using deep learning and incentive-based demand response. Util. Policy 2023, 82, 101579. [Google Scholar] [CrossRef]
- Lopes, J.C.; Sousa, T.; Benedito, R.d.S.; Trigoso, F.B.M.; Medina, D.O.G. Application of Battery Energy Storage System in Photovoltaic Power Plants Connected to the Distribution Grid. In Proceedings of the 2019 IEEE PES Innovative Smart Grid Technologies Conference-Latin America (ISGT Latin America), Gramado, Brazil, 15–18 September 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, Z.; Li, X.; Li, G.; Zhou, M.; Lo, K.L. Energy storage control for the Photovoltaic generation system in a micro-grid. In Proceedings of the 2010 5th International Conference on Critical Infrastructure (CRIS), Beijing, China, 20–22 September 2010; pp. 1–5. [Google Scholar] [CrossRef]
- Sarasua, J.I.; Martínez-Lucas, G.; García-Pereira, H.; Navarro-Soriano, G.; Molina-García, Á.; Fernández-Guillamón, A. Hybrid frequency control strategies based on hydro-power, wind, and energy storage systems: Application to 100% renewable scenarios. IET Renew. Power Gener. 2022, 16, 1107–1120. [Google Scholar] [CrossRef]
- Charlangsut, N.; Rugthaicharoencheep, N. Enhancing Voltage and Power Stability in Distribution System with Photovoltaic from the Benefits of Battery Energy Storage. Energies 2025, 18, 577. [Google Scholar] [CrossRef]
- Gómez-Ramírez, G.A.; Meza, C.; Mora-Jiménez, G.; Morales, J.R.R.; García-Santander, L. The Central American Power System: Achievements, Challenges, and Opportunities for a Green Transition. Energies 2023, 16, 4328. [Google Scholar] [CrossRef]
- Khalid, M. Smart grids and renewable energy systems: Perspectives and grid integration challenges. Energy Strat. Rev. 2024, 51, 101299. [Google Scholar] [CrossRef]
- Marinescu, B.; Gomis-Bellmunt, O.; Dorfler, F.; Schulte, H.; Sigrist, L. Dynamic Virtual Power Plant: A New Concept for Grid Integration of Renewable Energy Sources. IEEE Access 2022, 10, 104980–104995. [Google Scholar] [CrossRef]
- Pirooz, A.A.S.; Sanjari, M.J.; Kim, Y.-J.; Moore, S.; Turner, R.; Weaver, W.W.; Srinivasan, D.; Guerrero, J.M.; Shahidehpour, M. Adaptation of High Spatio-Temporal Resolution Weather/Load Forecast in Real-World Distributed Energy-System Operation. Energies 2023, 16, 3477. [Google Scholar] [CrossRef]
- Khalil, M.; Sheikh, S.A. Advancing Green Energy Integration in Power Systems for Enhanced Sustainability: A Review. IEEE Access 2024, 12, 151669–151692. [Google Scholar] [CrossRef]
- Centro Nacional de Despacho—Un Objetivo, una Pasión Servirte con Energía. Available online: https://cnd.enee.hn/ (accessed on 27 June 2025).
- Paye, J.C.H.; Vieira, J.P.A.; Tabora, J.M.; Leão, A.P.; Cordeiro, M.A.M.; Junior, G.C.; de Morais, A.P.; Farias, P.E. High Impedance Fault Models for Overhead Distribution Networks: A Review and Comparison with MV Lab Experiments. Energies 2024, 17, 1125. [Google Scholar] [CrossRef]
- Bolgaryn, R.; Banerjee, G.; Meinecke, S.; Maschke, H.; Marten, F.; Richter, M.; Liu, Z.; Lytaev, P.; Alfakhouri, B.; Kisse, J.; et al. Open Source Simulation Software pandapower and pandapipes: Recent Developments. In Proceedings of the 2023 Open Source Modelling and Simulation of Energy Systems (OSMSES), Aachen, Germany, 27–29 March 2023; pp. 1–8. [Google Scholar] [CrossRef]
- Bolgaryn, R.; Prade, E.; Banerjee, G.; Drauz-Mauel, S.; Lohmeier, D.; Lytaev, P.; Marten, F.; Meinecke, S.; Vogt, M.; Xiang, Y.; et al. Further developments in pandapower and pandapipes. In Proceedings of the 2024 Open Source Modelling and Simulation of Energy Systems (OSMSES), Vienna, Austria, 3–4 September 2024; pp. 1–8. [Google Scholar] [CrossRef]
- Bolgaryn, R.; Banerjee, G.; Cronbach, D.; Drauz, S.; Liu, Z.; Majidi, M.; Maschke, H.; Wang, Z.; Thurner, L. Recent Developments in Open Source Simulation Software pandapower and pandapipes. In Proceedings of the 2022 Open Source Modelling and Simulation of Energy Systems (OSMSES), Aachen, Germany, 4–5 April 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Junior, L.C.d.S.; Tabora, J.M.; Reis, J.; Andrade, V.; Carvalho, C.; Manito, A.; Tostes, M.; Matos, E.; Bezerra, U. Demand-Side Management Optimization Using Genetic Algorithms: A Case Study. Energies 2024, 17, 1463. [Google Scholar] [CrossRef]
- Huang, M.; Chen, R.; Zhong, H. Research on an Automatic Conversion Method of Power Flow Input Data from PSD-BPA to Pandapower. In Proceedings of the 2020 IEEE 4th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chongqing, China, 12–14 June 2020; pp. 494–498. [Google Scholar] [CrossRef]
- Thurner, L.; Scheidler, A.; Schafer, F.; Menke, J.-H.; Dollichon, J.; Meier, F.; Meinecke, S.; Braun, M. Pandapower—An Open-Source Python Tool for Convenient Modeling, Analysis, and Optimization of Electric Power Systems. IEEE Trans. Power Syst. 2018, 33, 6510–6521. [Google Scholar] [CrossRef]
- McKinney, W. Data structures for statistical computing in python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; Volume 445, pp. 51–56. [Google Scholar]
- Miscellaneous Operating System Interfaces, Python Documentation. Available online: https://docs.python.org/3/library/os.html (accessed on 27 June 2025).
- Dugan, R.C.; McDermott, T.E. An open source platform for collaborating on smart grid research. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–29 July 2011; IEEE: New York, NJ, USA; pp. 1–7. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Andrade, V.B.; Paixão, U.C., Jr.; Moreira, C.E.; Soares, T.M.; Tabora, J.M.; Tostes, M.E.d.L.; Bezerra, U.H.; Albuquerque, B.S.; Gouveia, L.D.S. Modelagem de um sistema de distribuição real desbalanceado e análise do impacto da geração distribuída utilizando o software OpenDSS. Simpósio Bras. Sist. Elétricos 2020, 1. [Google Scholar] [CrossRef]
- Gupta, M.; Abhyankar, A.R. Examining Impact of Distribution System Characteristics on Transmission Security Assessment of Future Power Systems. IEEE Access 2022, 10, 16388–16399. [Google Scholar] [CrossRef]
- Khani, D.; Yazdankhah, A.S.; Kojabadi, H.M. Impacts of distributed generations on power system transient and voltage stability. Int. J. Electr. Power Energy Syst. 2012, 43, 488–500. [Google Scholar] [CrossRef]
- Narang, D.; Mahmud, R.; Ingram, M.; Hoke, A. An Overview of Issues Related to IEEE Std 1547-2018 Requirements Regarding Voltage and Reactive Power Control; NREL/TP-5D00-77156; National Renewable Energy Laboratory: Golden, CO, USA, 2021. [Google Scholar]
- ExpControl, OpenDSS Documentation. Available online: https://opendss.epri.com/ExpControl.html (accessed on 27 June 2025).
- Mahbub, M. Power System Analysis by John Grainger. Available online: https://www.academia.edu/41974390/Power_System_Analysis_by_John_Grainger (accessed on 30 June 2025).
- Nagrath, I.J.; Kothari, D.P.; Desai, R.C. Modern Power System Analysis. IEEE Trans. Syst. Man. Cybern. 1982, 12, 96. [Google Scholar] [CrossRef]
- Kayal, P.; Chanda, S.; Chanda, C.K. An analytical approach for allocation and sizing of distributed generations in radial distribution network. Int. Trans. Electr. Energy Syst. 2017, 27, e2322. [Google Scholar] [CrossRef]
- Elkholy, A. Optimal Planning of Multiple PV-DG in Radial Distribution Systems Using Loss Sensitivity Analysis and Genetic Algorithm. J. Power Energy Eng. 2025, 13, 1–22. [Google Scholar] [CrossRef]
- Umoh, V.; Davidson, I.; Adebiyi, A.; Ekpe, U. Methods and Tools for PV and EV Hosting Capacity Determination in Low Voltage Distribution Networks—A Review. Energies 2023, 16, 3609. [Google Scholar] [CrossRef]
- Ela, E.; Milligan, M.; Bloom, A.; Botterud, A.; Townsend, A.; Levin, T. Evolution of Wholesale Electricity Market Design with Increasing Levels of Renewable Generation; NREL/TP-5D00-61765; National Renewable Energy Laboratory: Golden, CO, USA, 2014. [Google Scholar] [CrossRef]
- Pisciella, P.; Vespucci, M.T.; Viganò, G.; Rossi, M.; Moneta, D. Optimal Power Flow Analysis in Power Dispatch for Distribution Networks. In NAO 2017. Springer Proceedings in Mathematics & Statistics; Numerical Analysis and Optimization; Al-Baali, M., Grandinetti, L., Purnama, A., Eds.; Springer: Cham, Switzerland, 2018; Volume 235. [Google Scholar] [CrossRef]
- AC Power Flow. Available online: https://matpower.app/manual/matpower/ACPowerFlow.html (accessed on 27 June 2025).
- Red Externa—Documentación de Pandapower 3.1.3. Available online: https://pandapower.readthedocs.io/en/latest/elements/ext_grid.html (accessed on 27 June 2025).
- Control de Área. Available online: https://www.powerworld.com/WebHelp/Content/MainDocumentation_HTML/Area_Control.htm (accessed on 27 June 2025).
- Salimon, S.A.; Adepoju, G.A.; Adebayo, I.G.; Howlader, H.O.R.; Ayanlade, S.O.; Adewuyi, O.B. Impact of Distributed Generators Penetration Level on the Power Loss and Voltage Profile of Radial Distribution Networks. Energies 2023, 16, 1943. [Google Scholar] [CrossRef]



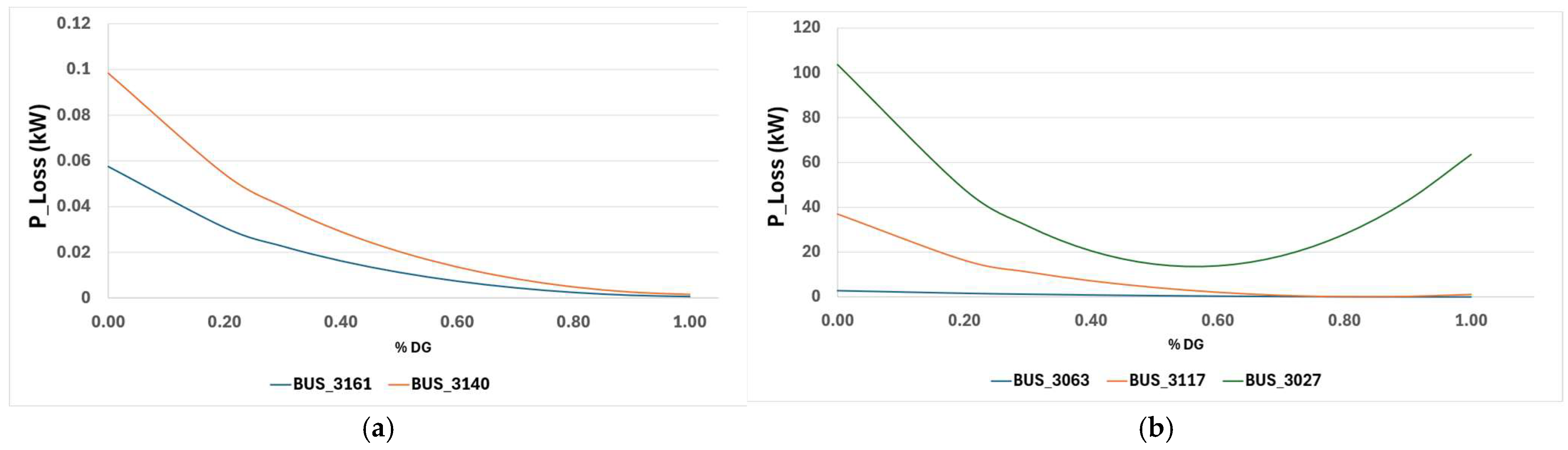
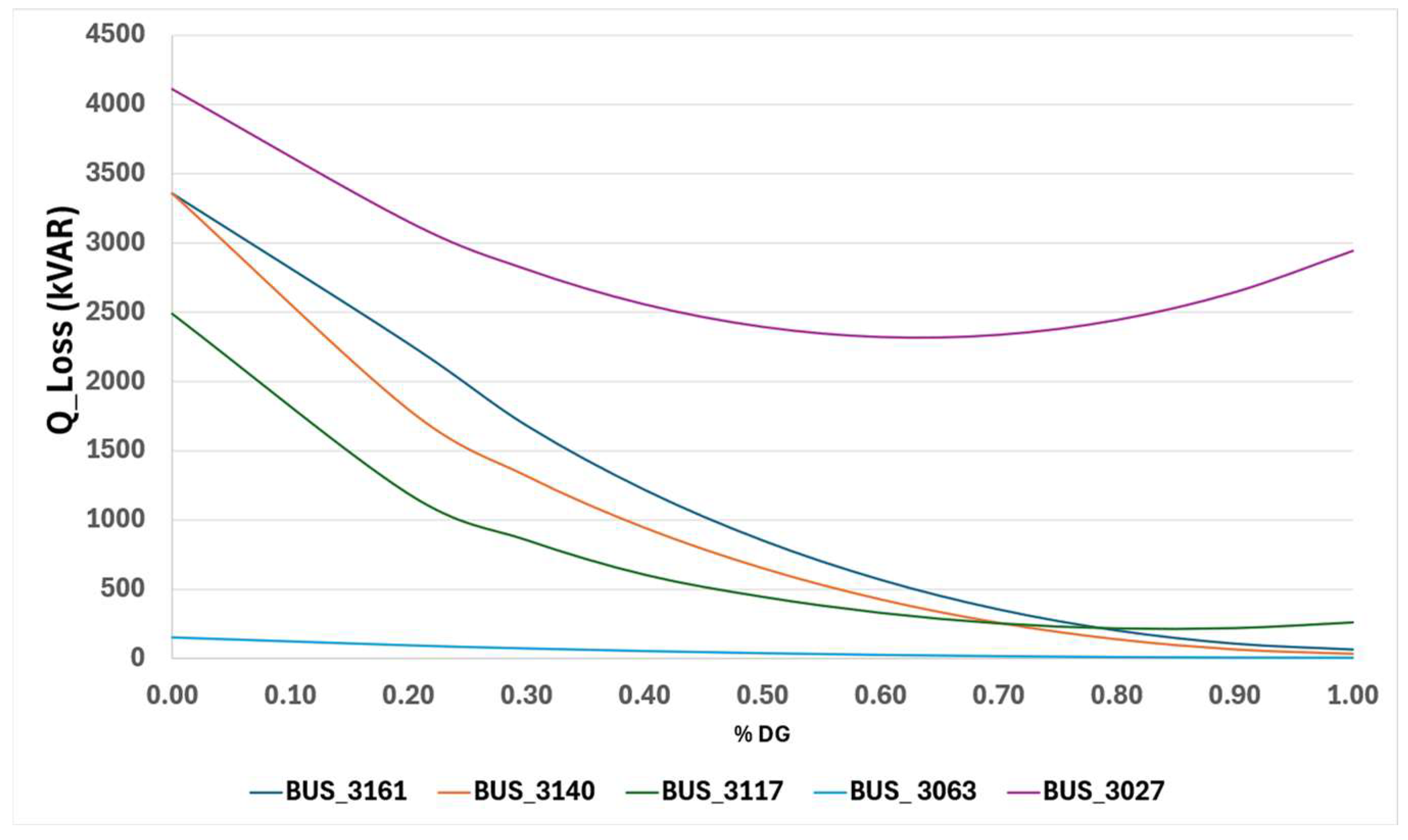
| Component | Active Power (MW) | Reactive Power (MVAR) |
|---|---|---|
| Total generation | 425.65 | 182.69 |
| Line losses | 4.44 | −17.21 |
| 2-winding transformer losses | 0.00 | 81.30 |
| 3-winding transformer losses | 0.53 | 11.44 |
| Total losses | 4.98 | 75.52 |
| Net delivered power | 420.67 | 107.17 |
| Demand | 202.92 | 50.39 |
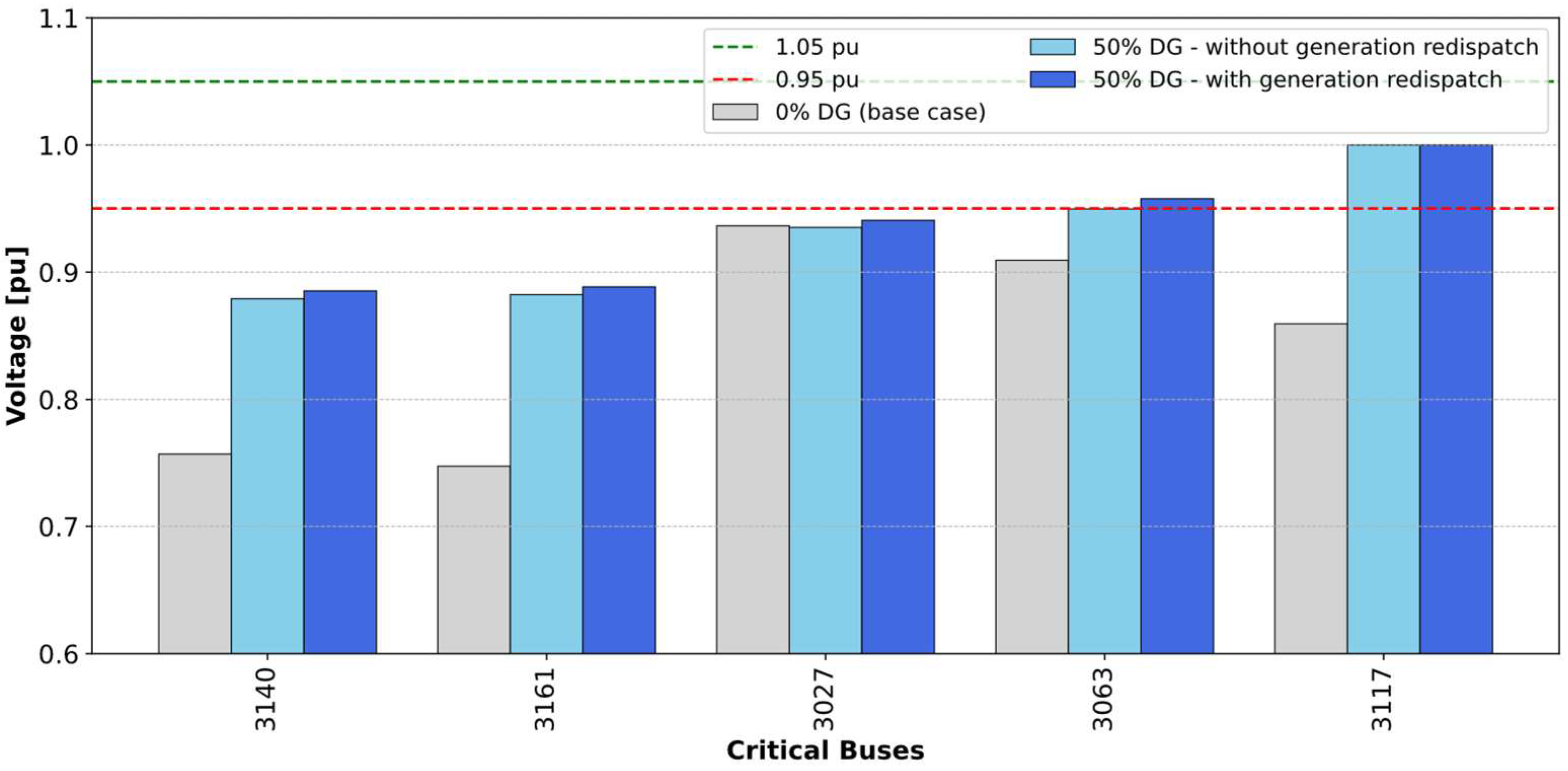
| Bus | Vbase_p.u. | dV_per_MW | LSF | Headroom_% | Hosting_cap_MW | Score |
|---|---|---|---|---|---|---|
| 3117 | 0.859547439 | 0.053911943 | −0.030377789 | 66.64711225 | 6.76 | 0.778314451 |
| 3161 | 0.747437422 | 0.02254533 | −0.031551214 | 32.17465971 | 3.86 | 0.49270371 |
| 3063 | 0.909439021 | 0.010660418 | 0.000330068 | 95.21906934 | 2.85 | 0.466494992 |
| 3140 | 0.756863237 | 0.01538126 | −0.02972196 | 11.28243275 | 3.52 | 0.390005769 |
| 3027 | 0.936448298 | 0.00089639 | 0.066078892 | 32.2324752 | 15.08 | 0.1518708 |
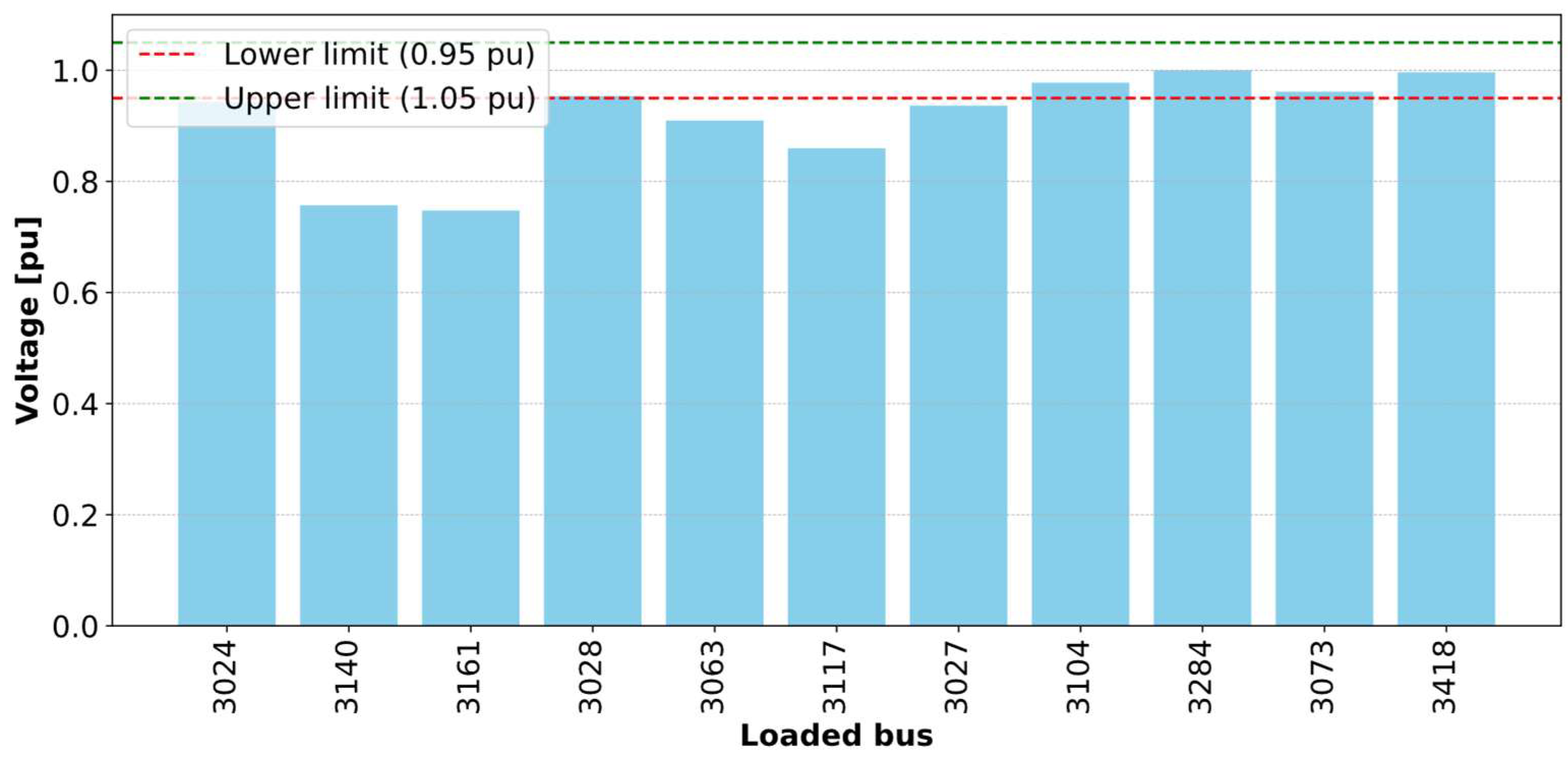
| Buses | Voltage (kV) | Voltage (p.u.) | Active Load (MW) | Reactive Load (MVAR) |
|---|---|---|---|---|
| 3161 | 13.8 | 0.747557 | 12 | 4.0774 |
| 3140 | 13.8 | 0.756975 | 15.75 | 5.8072 |
| 3117 | 34.5 | 0.859609 | 10.57 | 1.7537 |
| 3063 | 34.5 | 0.909510 | 2.41 | 0.6536 |
| 3027 | 34.5 | 0.936297 | 46.80 | 13.5518 |
| Bus | 0% | 20% | 30% | 40% | 50% | 60% | 70% | 80% | 90% | 100% |
|---|---|---|---|---|---|---|---|---|---|---|
| 3161 | 0.7474 | 0.8285 | 0.8506 | 0.8712 | 0.8883 | 0.9028 | 0.9152 | 0.9257 | 0.9345 | 0.9419 |
| 3140 | 0.75768 | 0.827 | 0.85 | 0.8691 | 0.8851 | 0.8987 | 0.9104 | 0.9204 | 0.9288 | 0.9358 |
| 3117 | 0.8594 | 0.9583 | 0.9807 | 0.9989 | 1 | 1 | 1 | 1 | 1 | 1 |
| 3063 | 0.9094 | 0.9345 | 0.9433 | 0.951 | 0.9577 | 0.9637 | 0.969 | 0.9737 | 0.9778 | 0.9813 |
| 3027 | 0.9364 | 0.942 | 0.9422 | 0.9418 | 0.9407 | 0.939 | 0.9366 | 0.9337 | 0.9301 | 0.9259 |
| Bus | Voltage (kV) | Voltage (p.u.) Before | Active Power (MW) | Reactive Power (MVAR) | Voltage (p.u.) After |
|---|---|---|---|---|---|
| 3161-GEN | 13.8 | 0.747557 | 3.86 | 1.21 | 0.8883 |
| 3140-GEN | 13.8 | 0.756975 | 3.52 | 1.59 | 0.8851 |
| 3117-GEN | 34.5 | 0.859609 | 6.73 | 0.58 | 1.00 |
| 3063-GEN | 34.5 | 0.909510 | 2.85 | 0.32 | 0.9577 |
| 3027-SGEN | 34.5 | 0.936297 | 15.07 | −4.75 | 0.9407 |
| Bus | V (kV) | V (p.u.) Before | V (p.u.) After | Improvement | Bus | V (kV) | V (p.u.) Before | V (p.u.) After | Improvement |
|---|---|---|---|---|---|---|---|---|---|
| 3140 | 13.8 | 0.757 | 0.885 | 0.128 | 3064 | 138 | 0.967 | 0.982 | 0.015 |
| 3161 | 13.8 | 0.747 | 0.888 | 0.141 | 3038 | 138 | 0.971 | 0.984 | 0.013 |
| 3027 | 34.5 | 0.936 | 0.941 | 0.004 | 3108 | 138 | 0.971 | 0.984 | 0.013 |
| 3024 | 35.19 | 0.943 | 0.945 | 0.002 | 3318 | 138 | 0.978 | 0.989 | 0.012 |
| 3178 | 13.8 | 0.907 | 0.956 | 0.050 | 3104 | 34.5 | 0.979 | 0.991 | 0.012 |
| 3063 | 34.5 | 0.909 | 0.958 | 0.048 | 3979 | 13.8 | 0.981 | 0.990 | 0.008 |
| 3028 | 13.8 | 0.954 | 0.967 | 0.014 | 3978 | 13.8 | 0.981 | 0.990 | 0.008 |
| 3118 | 138 | 0.961 | 0.979 | 0.018 | 3957 | 13.8 | 0.981 | 0.990 | 0.008 |
| 3073 | 69 | 0.962 | 0.975 | 0.014 | 3097 | 138 | 0.986 | 0.996 | 0.011 |
| 3419 | 69 | 0.962 | 0.975 | 0.014 | 3095 | 230 | 0.992 | 0.996 | 0.003 |
| 3600 | 69 | 0.962 | 0.976 | 0.014 | 3047 | 138 | 0.993 | 1.002 | 0.009 |
| 3160 | 138 | 0.952 | 0.976 | 0.024 | 3418 | 34.5 | 0.997 | 0.997 | 0.000 |
| 3055 | 138 | 0.966 | 0.981 | 0.014 | 3550 | 230 | 0.999 | 1.000 | 0.001 |
| 3094 | 69 | 0.964 | 0.977 | 0.014 | 3551 | 230 | 0.999 | 1.000 | 0.001 |
| 3980 | 13.8 | 0.965 | 0.978 | 0.014 | 3117 | 34.5 | 0.860 | 1.000 | 0.140 |
| 3105 | 138 | 0.968 | 0.982 | 0.014 | 3224 | 4.725 | 0.971 | 1.000 | 0.029 |
| 3023 | 13.8 | 0.977 | 0.979 | 0.002 | 3967 | 13.8 | 0.879 | 1.007 | 0.128 |
| Component | Active Power (MW) Before | Reactive Power (MVAR) Before | Active Power (MW) After | Reactive Power (MVAR) After |
|---|---|---|---|---|
| Total generation | 425.65 | 182.69 | 425.65 | 163.86 |
| Line losses | 4.44 | −17.21 | 4.37 | −18.10 |
| 2-winding transformer losses | 0.00 | 81.30 | 0.00 | 57.18 |
| 3-winding transformer losses | 0.53 | 11.44 | 0.14 | 2.09 |
| Total losses | 4.98 | 75.52 | 4.52 | 41.77 |
| Net delivered power | 420.67 | 107.17 | 421.14 | 122.69 |
| Demand | 202.92 | 50.39 | 202.92 | 50.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramos-Gómez, J.I.; Molina-García, A.; Muñoz-Tabora, J. Power System Modeling and Simulation for Distributed Generation Integration: Honduras Power System as a Case Study. Energies 2025, 18, 4777. https://doi.org/10.3390/en18174777
Ramos-Gómez JI, Molina-García A, Muñoz-Tabora J. Power System Modeling and Simulation for Distributed Generation Integration: Honduras Power System as a Case Study. Energies. 2025; 18(17):4777. https://doi.org/10.3390/en18174777
Chicago/Turabian StyleRamos-Gómez, Jhonny Ismael, Angel Molina-García, and Jonathan Muñoz-Tabora. 2025. "Power System Modeling and Simulation for Distributed Generation Integration: Honduras Power System as a Case Study" Energies 18, no. 17: 4777. https://doi.org/10.3390/en18174777
APA StyleRamos-Gómez, J. I., Molina-García, A., & Muñoz-Tabora, J. (2025). Power System Modeling and Simulation for Distributed Generation Integration: Honduras Power System as a Case Study. Energies, 18(17), 4777. https://doi.org/10.3390/en18174777








