Optimisation of a Kind of Vertical Axis Darrieus Turbine—Davidson Hill Venturi Cross-Flow Turbines
Abstract
1. Introduction
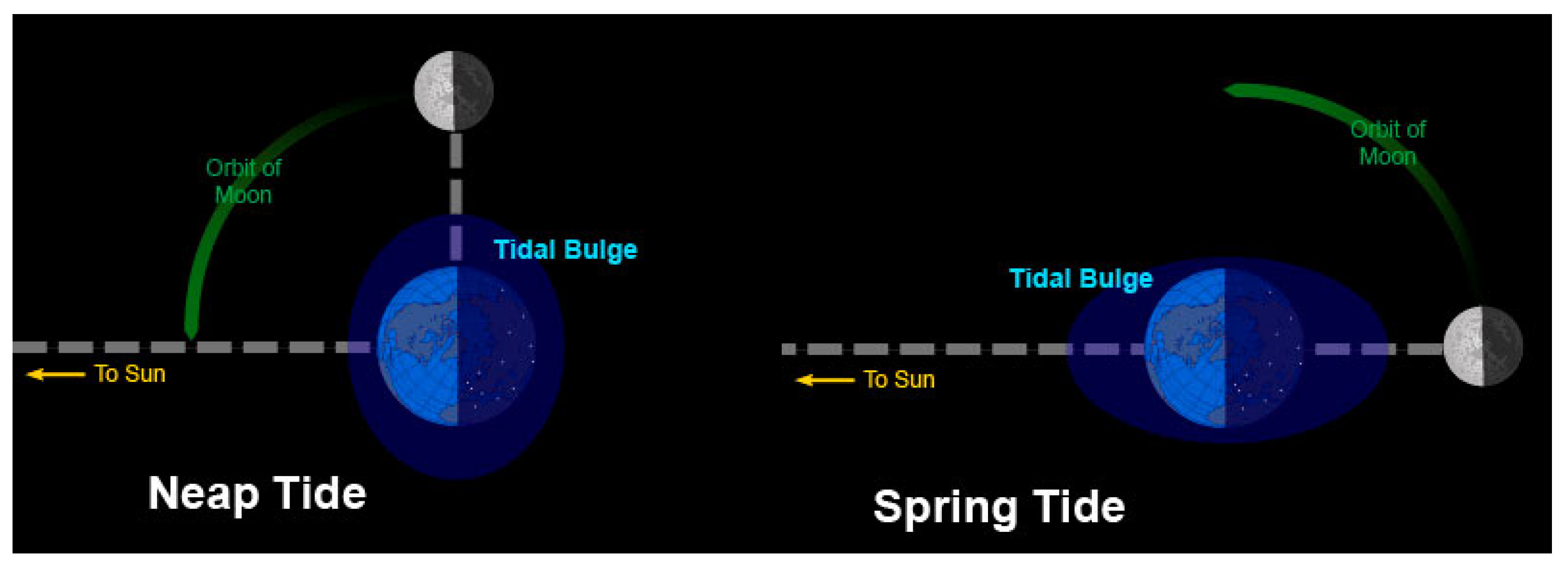
1.1. Tidal Energy
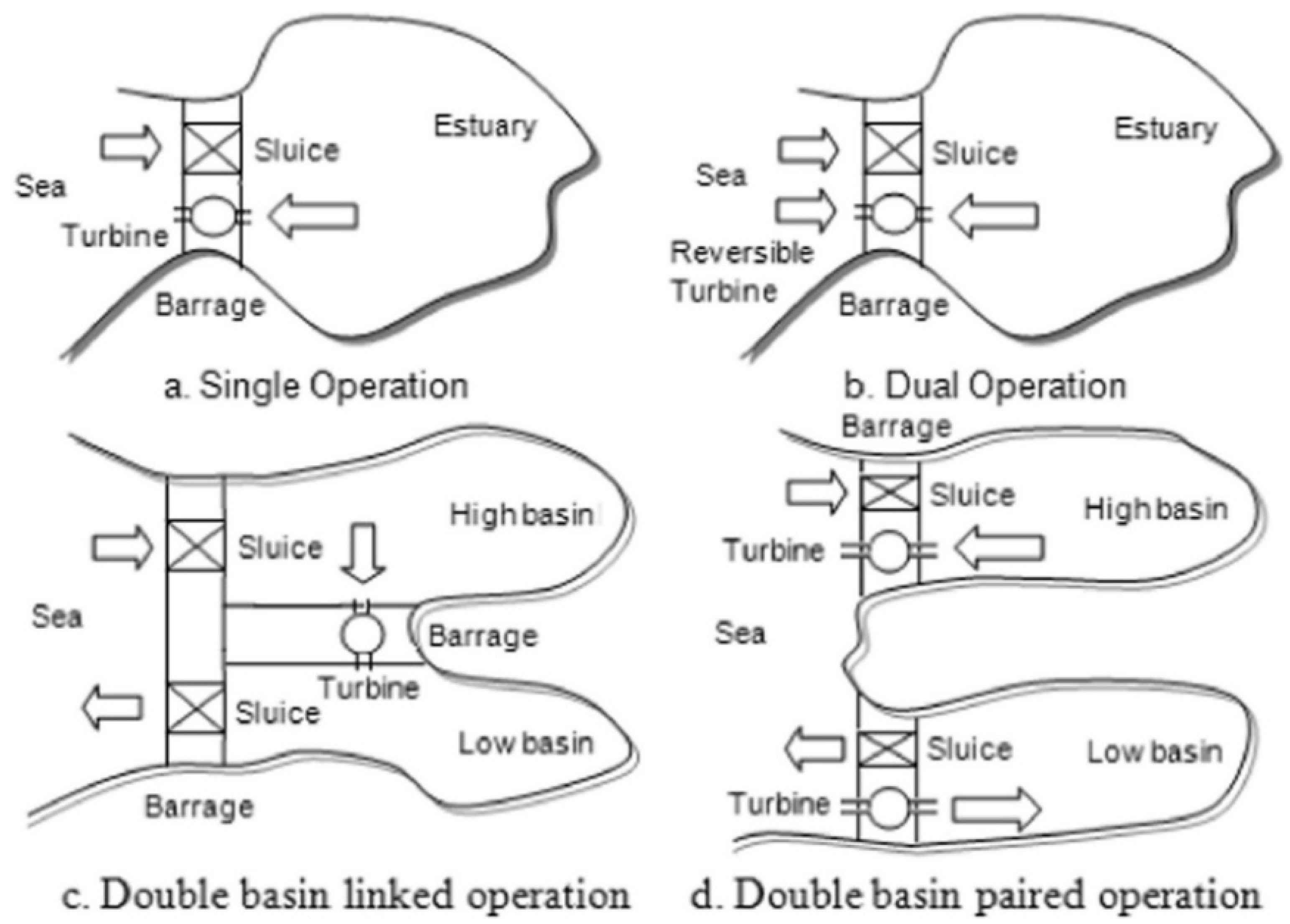
1.2. Tidal Power
- is sea water density ();
- is gravitational constant (9.81 ).
1.3. Location
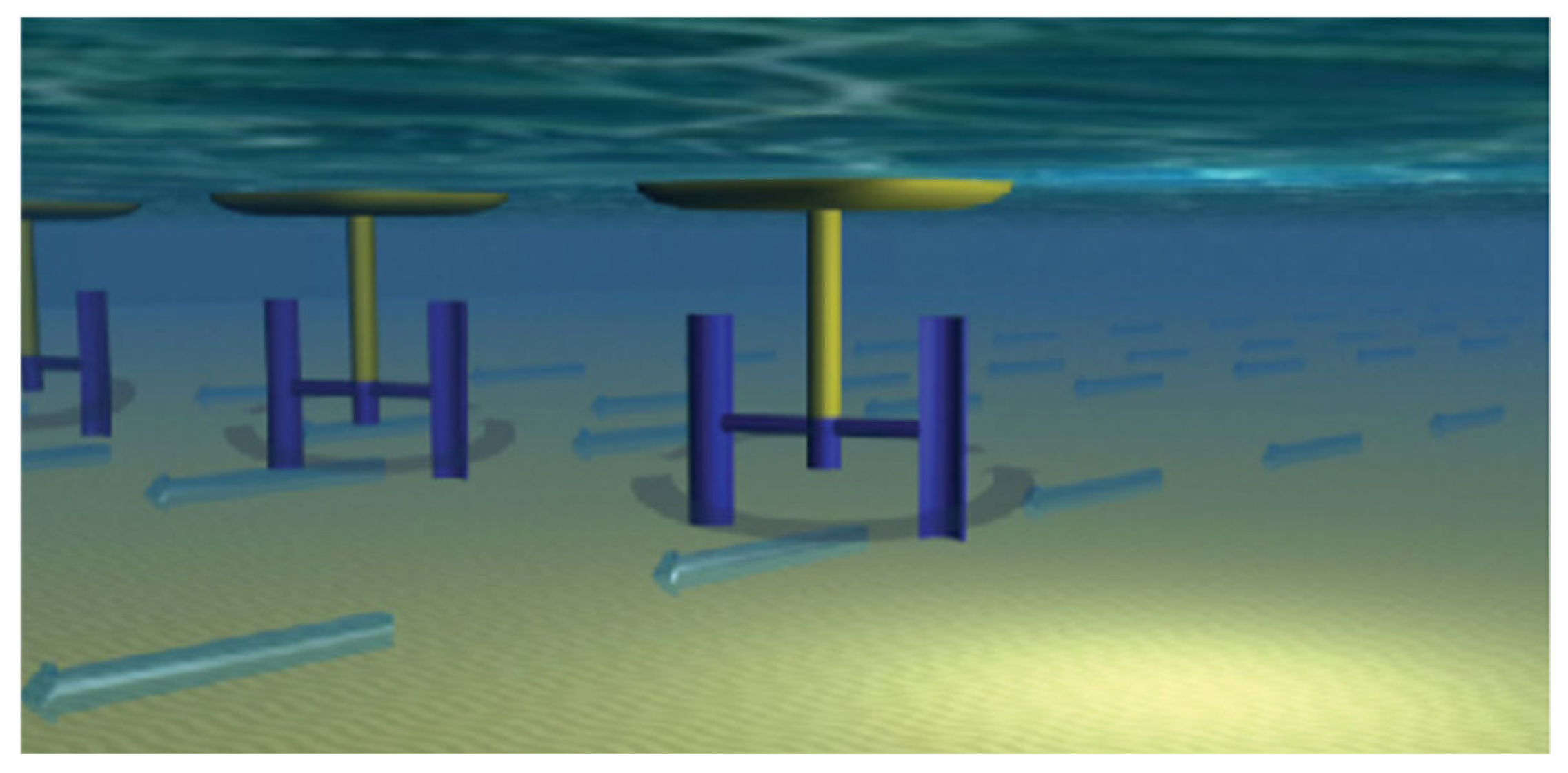
1.4. Tidal Turbines
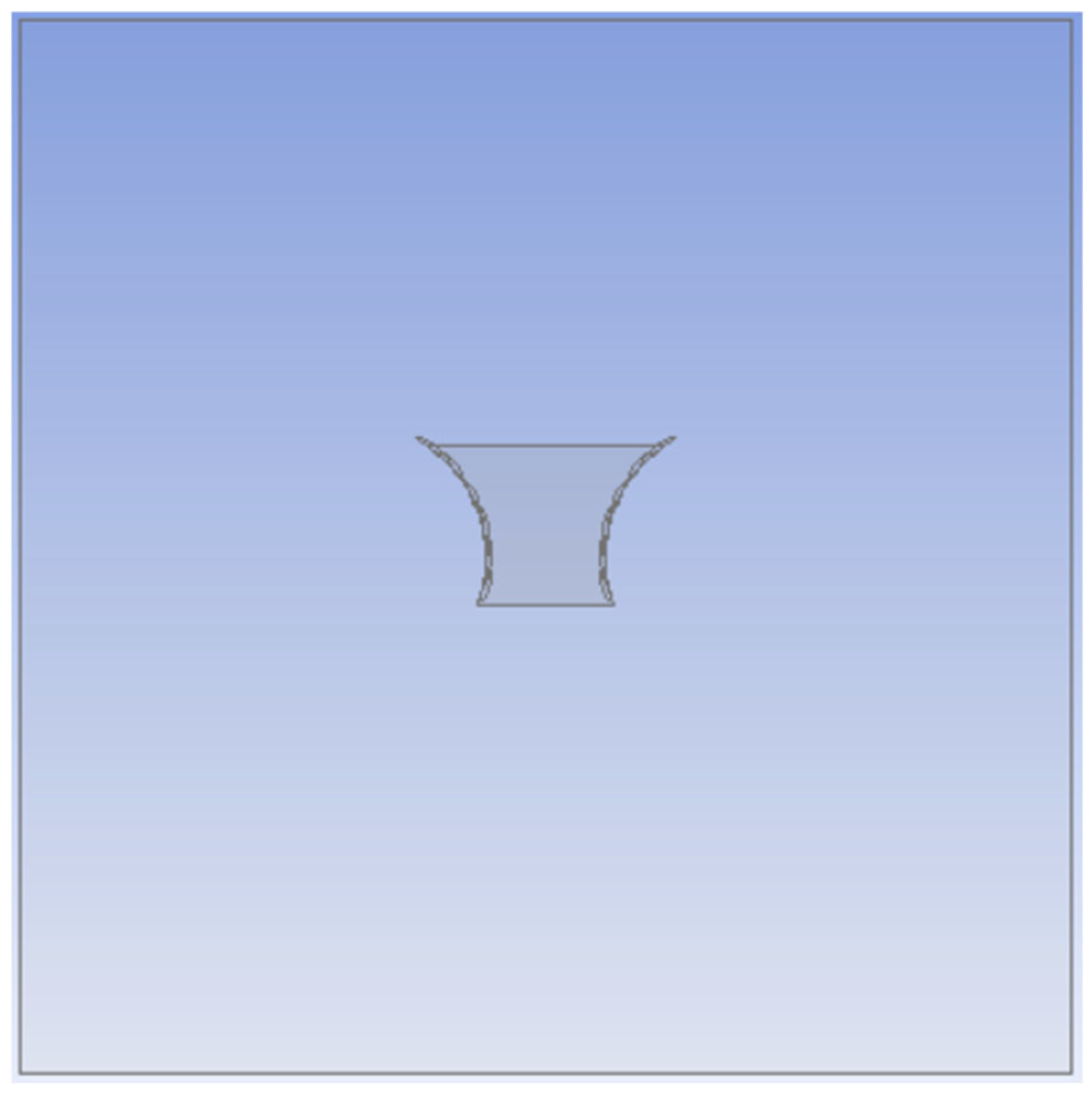
1.5. Davidson Hill Venturi System
1.6. Aim and Objective
- Establish the tidal turbine model;
- Adjust the parameters of hydrofoil and rotor blades;
- Simulate the model by Computational Fluid Dynamics software;
- Compare the simulation results and complete the analysis and discussion;
- Conclude the optimal parameter to increase the performance of the DHV tidal turbine.
2. Literature Review
2.1. Effect to Tidal Energy
2.2. Turbine Structure
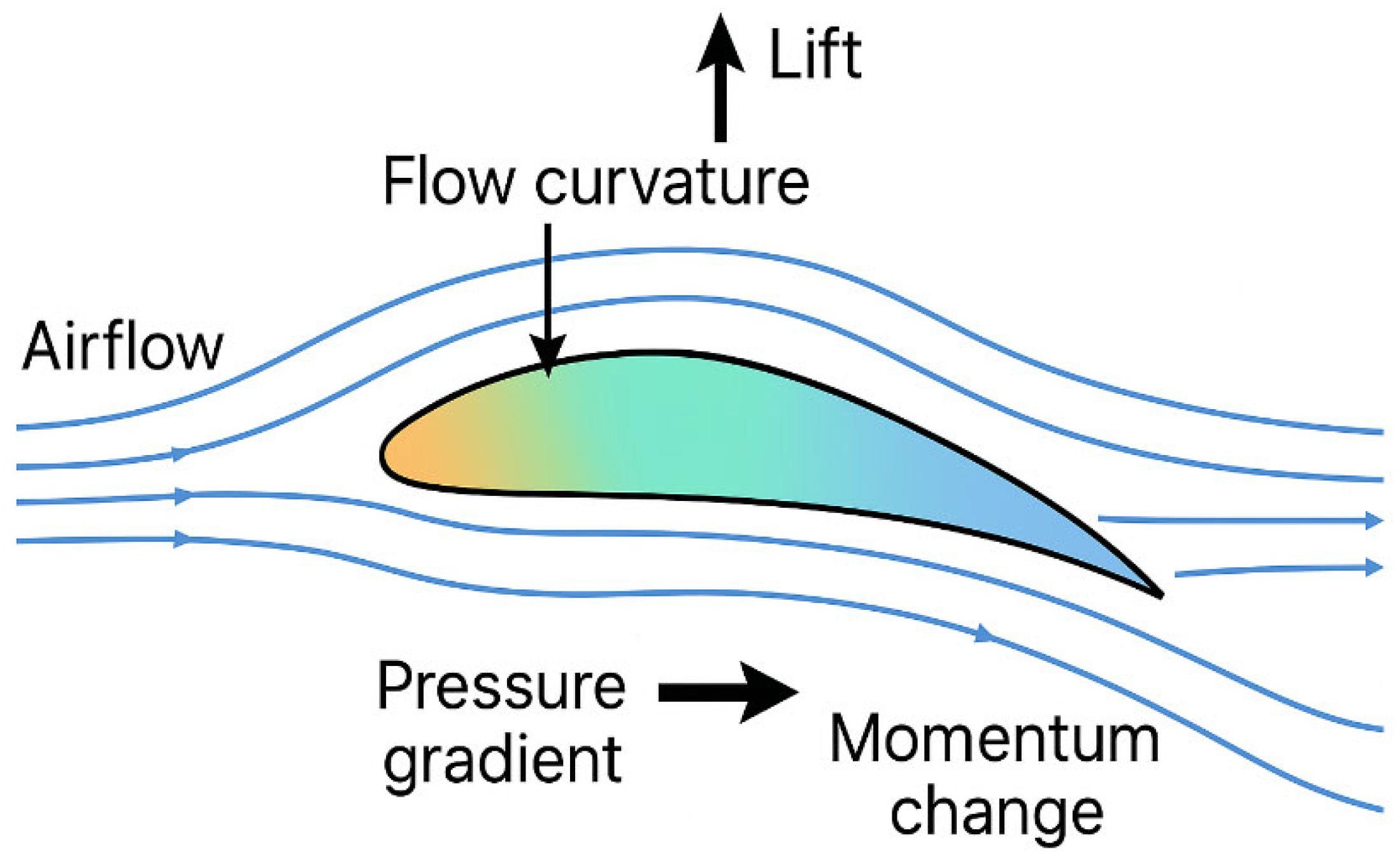
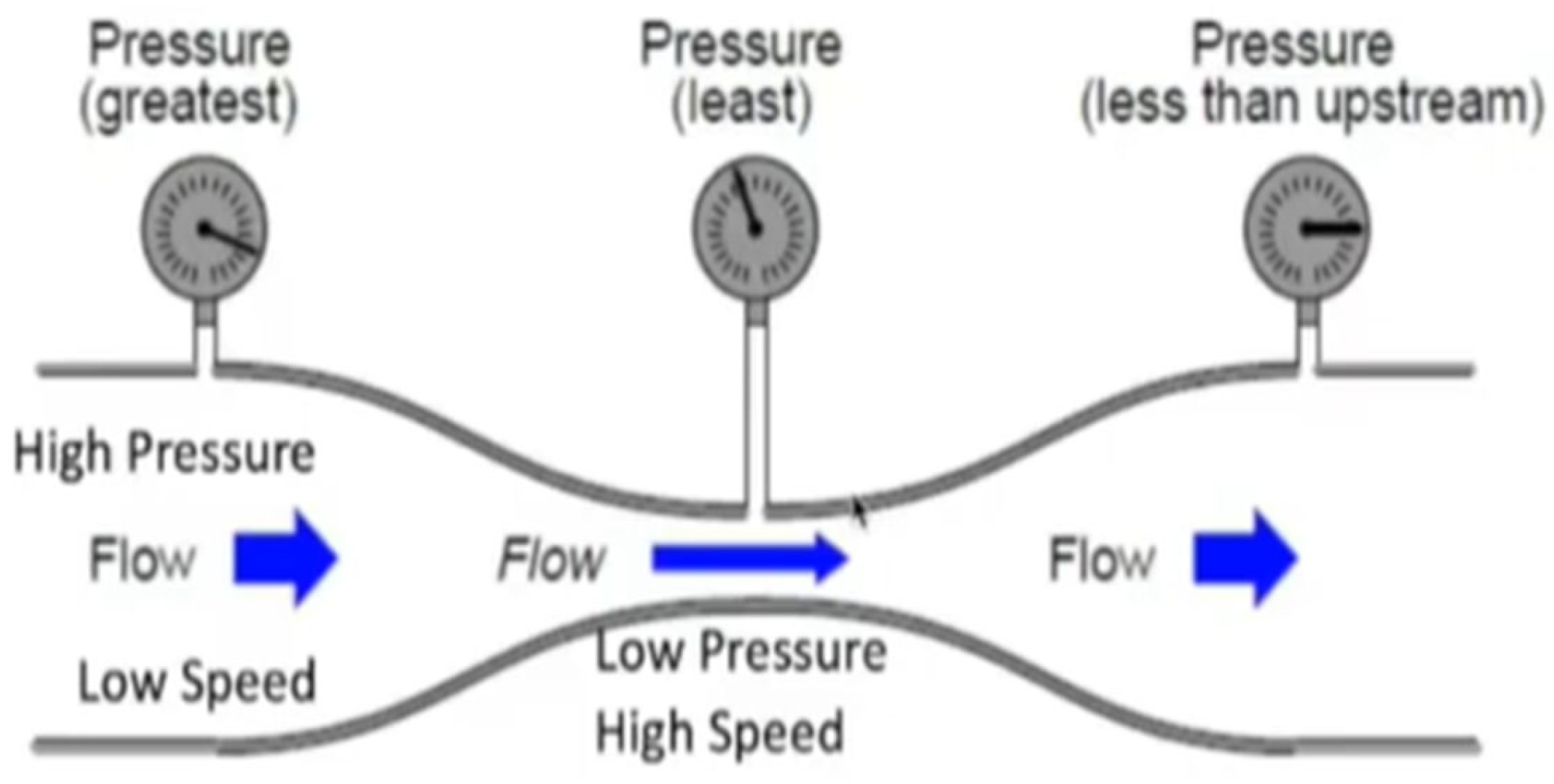
2.3. Darrieus Turbines
2.4. CFD Simulation
3. Methodology
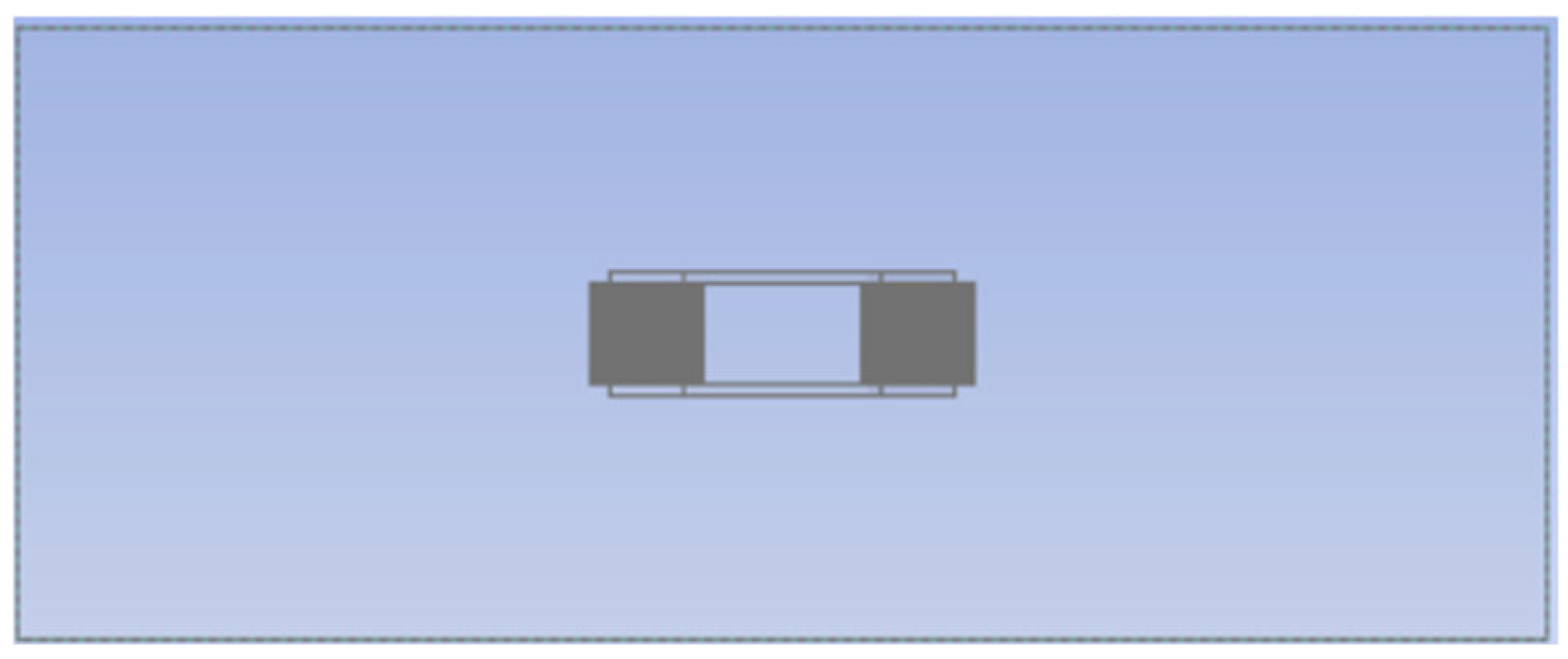
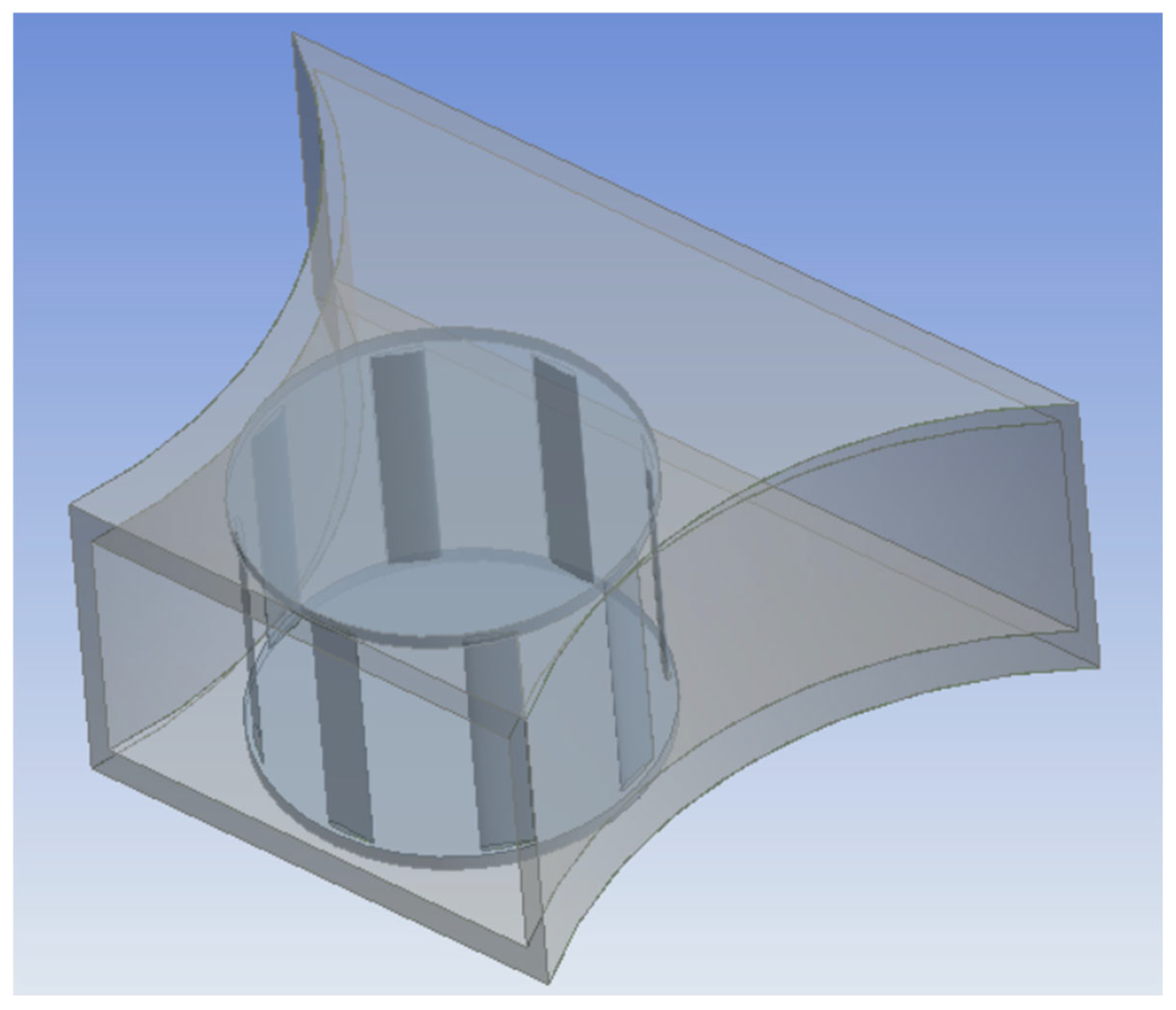
3.1. Model Geometry
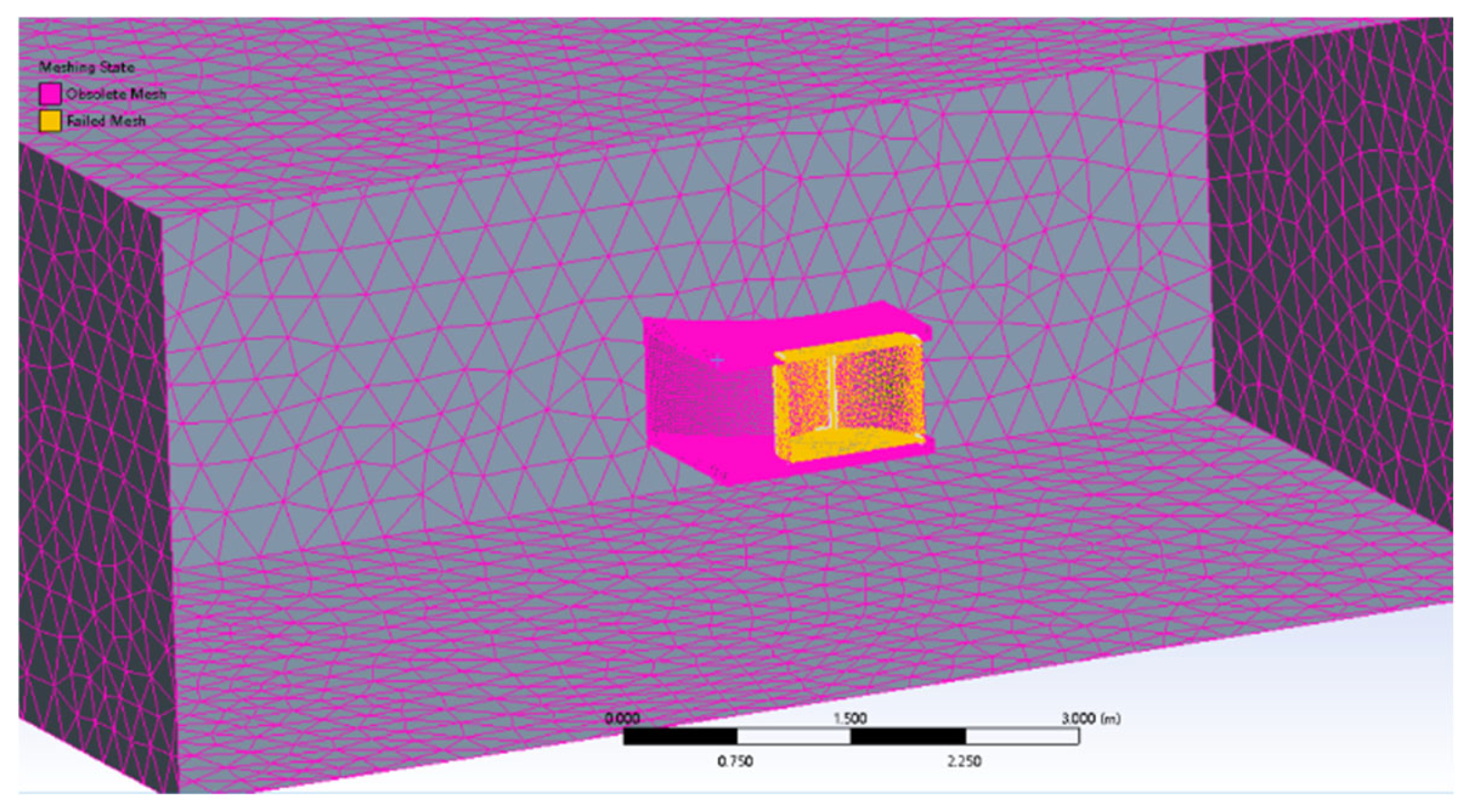
3.2. Meshing Design
3.3. Boundary Condition
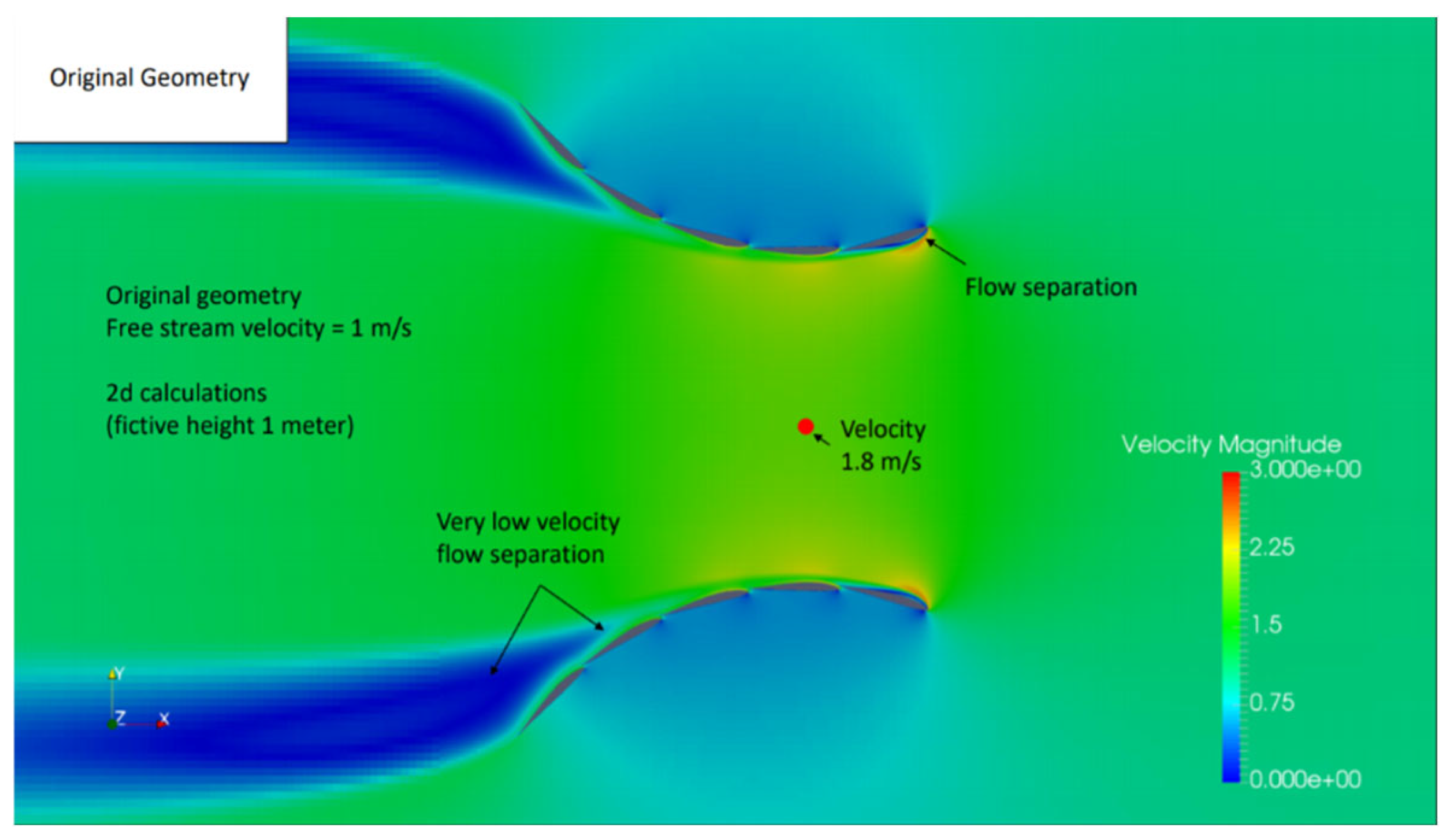
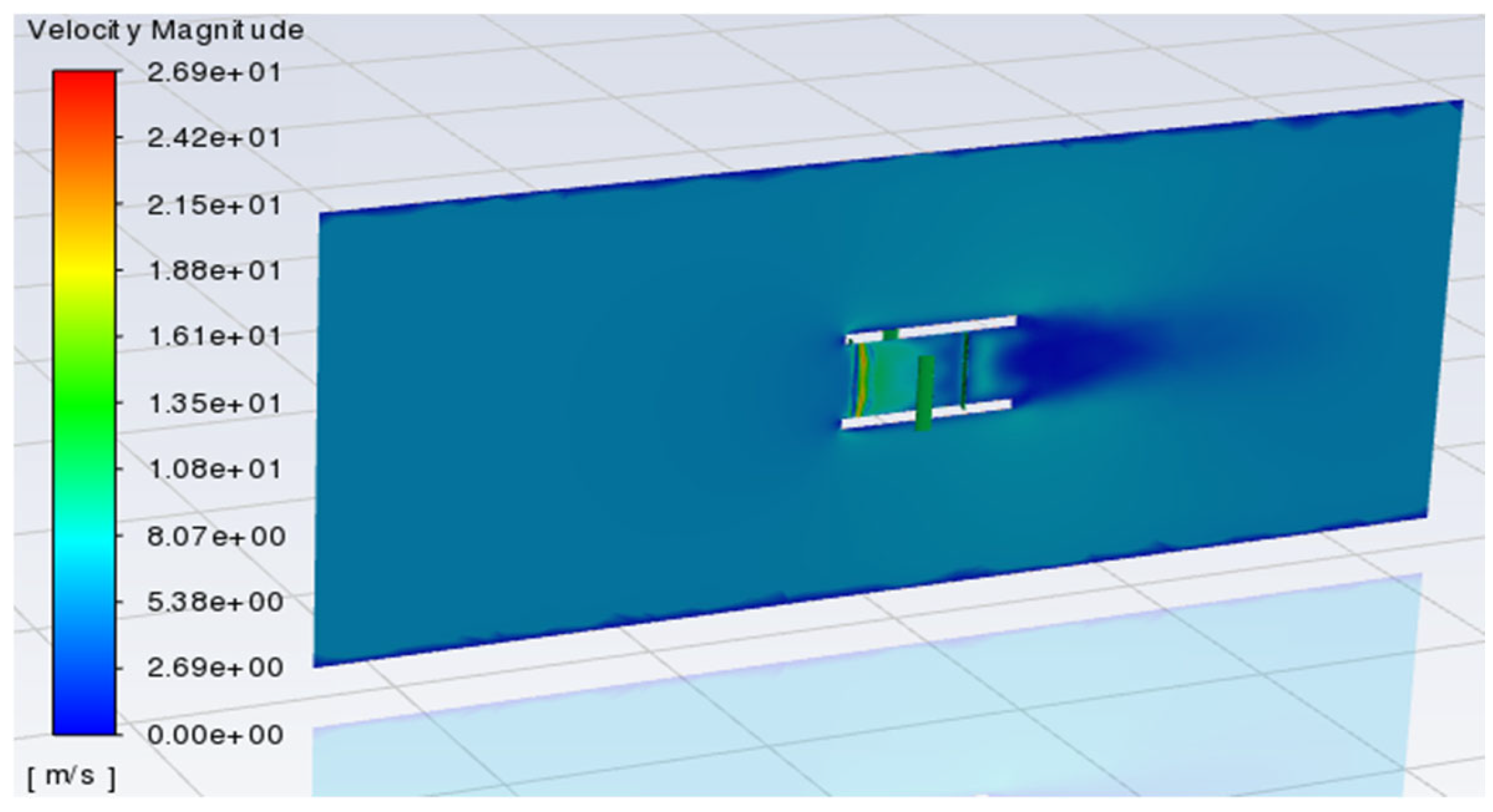
4. Results
- is the kinetic energy at the central point of the input surface of the turbine;
- is the kinetic energy at the central point of the outflow surface of the turbine;
- is the unit mass flow rate at the central point of the input surface of the turbine;
- is the unit mass flow rate at the central point of the outflow surface of the turbine.
- is the mass flow through the turbine in unit time.
5. Discussion
- There was a large difference in meshing size between the element around the turbine and the surrounding element, which caused the connection problem between two sizes of element. In group A, the meshing size in the surrounding computational domain is 0.03 m to save computational capacity, while the meshing size attached to the hydrofoil is only 0.01 m because of the tiny dimension of the hydrofoil geometry, which is established based on the data profile with the unit below 0.01 m.
- The result from this research is obtained from the 3D model, which is a more complex model than the previous study. Thus, the meshing problem can be amplified by the effect from the steam flow on different heights.
- The boundary layer is not considered in detail in group A because of the limitation of the element size. The element number in the above meshing document is already approaching 512,000, while the number is higher in the condition with inflation attached with the hydrofoil on the side panel of the turbine.
- One of the observation methods used in group B involved selecting nine points, and a local velocity was found, which can cause inaccurate data and low risk resistance from the accident condition.
- Because of the limitation of the project period, the comparison cases used in group B only include two models. Based on the results obtained from the two models, it is not easy to conclude the tendency directly and there is a high possibility of being impacted by the error data.
- It is important to increase the number of measuring points at the opening to improve the accuracy and representativeness of the velocity.
- For the performance of the venturi structure in tidal turbine, the mass change during the turbine operation should be considered. As the DHV used the hydrofoil structure on the side panel which allow the fluid flows in through the interval of the hydrofoil, the energy capture should also calculate the energy reduction that occurs in the increasing mass.
- Multiple models during the simulation process should be established to increase fault tolerance, so that the capacity of resisting disturbance and accuracy of the data can be highly ensured.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khan, N.; Abas, N. Powering the people beyond 2050. Sci. Echnol. Dev. 2012, 31, 131–151. [Google Scholar]
- Abas, N.; Kalair, A.; Khan, N. Review of fossil fuels and future energy technologies. Futures 2015, 69, 31–49. [Google Scholar] [CrossRef]
- Turcotte, D.L.; Schubert, G. Geodynamics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Williams, G.E. Geological constraints on the Precambrian history of Earth’s rotation and the Moon’s orbit. Rev. Geophys. 2000, 38, 37–59. [Google Scholar] [CrossRef]
- Khan, N.; Kalair, A.; Abas, N.; Haider, A. Ocean tidal, wave and thermal energy technologies. Renew. Sustain. Energy Rev. 2017, 72, 590–604. [Google Scholar] [CrossRef]
- Khanjanpour, M.H.; Javadi, A.A. Optimization of a Horizontal Axis Tidal (HAT) turbine for powering a Reverse Osmosis (RO) desalination system using Computational Fluid Dynamics (CFD) and Taguchi method. Energy Convers. Manag. 2021, 231, 113833. [Google Scholar] [CrossRef]
- Ibrahim, W.I.; Mohamed, M.R.; Ismail, R.M.T.R.; Leung, P.K.; Xing, W.W.; Shah, A.A. Hydrokinetic energy harnessing technologies: A review. Energy Rep. 2021, 7, 2021–2042. [Google Scholar] [CrossRef]
- Khan, M.J.; Bhuyan, G.; Iqbal, M.T.; Quaicoe, J.E. Hydrokinetic energy conversion systems and assessment of horizontal and vertical axis turbines for river and tidal applications: A technology status review. Appl. Energy 2009, 86, 1823–1835. [Google Scholar] [CrossRef]
- Gabl, R.; Burchell, J.; Hill, M.; Ingram, D.M. Sensitivity analysis of a Venturi shaped structure for cross-flow turbines. Eng. Appl. Comput. Fluid Mech. 2022, 16, 2243–2269. [Google Scholar] [CrossRef]
- DHV Turbines Ltd. 2021. Available online: http://www.dhvturbines.com/?cv=1 (accessed on 23 August 2021).
- EU-OEA. European Ocean Energy Association. Available online: https://www.oceanenergy-europe.eu/ocean-energy/ (accessed on 23 August 2021).
- López, I.; Andreu, J.; Ceballos, S.; de Alegría, I.M.; Kortabarria, I. Review of wave energy technologies and the necessary power-equipment. Renew Sustain. Energy Rev. 2013, 27, 413–434. [Google Scholar] [CrossRef]
- Met Office. Climate Zones. 2018. Available online: https://weather.metoffice.gov.uk/climate/climate-explained/climate-zones (accessed on 17 August 2021).
- Priegue, L.; Stoesser, T. The influence of blade roughness on the performance of a vertical axis tidal turbine. Int. J. Mar. Energy 2017, 17, 136–146. [Google Scholar] [CrossRef]
- Islam, M.; Ting, D.S.K.; Fartaj, A. Aerodynamic models for darrieus-type straight-bladed vertical axis wind turbines. Renew. Sustain. Energy Rev. 2008, 12, 1087–1109. [Google Scholar] [CrossRef]
- Brahimi, M.T.; Allet, A.; Paraschivoiu, I. Aerodynamic analysis models for vertical-axis wind turbines. Int. J. Rotating Mach. 1995, 2, 15–21. [Google Scholar] [CrossRef]
- Dai, Y.M.; Gardiner, N.; Sutton, R.; Dyson, P.K. Hydrodynamic analysis models for the design of Darrieus-type vertical-axis marine current turbines. J. Eng. Marit. Environ. 2011, 225, 295–307. [Google Scholar] [CrossRef]
- Patel, V.; Eldho, T.I.; Prabhu, S.V. Experimental investigations on Darrieus straight blade turbine for tidal current application and parametric optimization for hydro farm arrangement. Int. J. Mar. Energy 2017, 17, 110–135. [Google Scholar] [CrossRef]
- Hirsch, H.; Mandal, A.C. A cascade theory for the aerodynamic performance of darrieus wind turbines. Wind. Eng. 1987, 11, 164–175. [Google Scholar]
- Chen, J.; Yang, H.; Yang, M.; Xu, H.; Hu, Z. A comprehensive review of the theoretical approaches for the airfoil design of lift-type vertical axis wind turbine. Renew. Sustain. Energy Rev. 2015, 51, 1709–1720. [Google Scholar] [CrossRef]
- Chen, J.; Chen, L.; Xu, H.; Yang, H.; Ye, C.; Liu, D. Performance improvement of a vertical axis wind turbine by comprehensive assessment of an airfoil family. Energy 2016, 114, 318–331. [Google Scholar] [CrossRef]
- Patel, V.; Bhat, G.; Eltho, T.I.; Prabhu, S.V. Influence of overlap ratio and apsect ratio on the performance of Savonius hydrokinetic turbine. Int. J. Energy Res. 2016, 41, 829–844. [Google Scholar] [CrossRef]
- Joo, S.; Choi, H.; Lee, J. Aerodynamic characteristics of two-bladed H-Darrieus at various solidities and rotating speeds. Energy 2015, 90, 439–451. [Google Scholar] [CrossRef]
- Tummala, A.; Velamati, R.K.; Sinha, D.K.; Indraja, V.; Krishna, V.H. A review on small scale wind turbines. Renew. Sustain. Energy Rev. 2016, 56, 1351–1371. [Google Scholar] [CrossRef]
- Singh, M.A.; Biswas, A.; Misra, R.D. Investigation of self-starting and high rotor solidity on the performance of a three S1210 blade H-type Darrieus rotor. Renew. Energy 2015, 76, 381–387. [Google Scholar] [CrossRef]
- Hwang, I.S.; Lee, Y.H.; Kim, S.J. Optimization of cycloidal water turbine and the performance improvement by individual blade control. Appl. Energy 2009, 86, 1532–1540. [Google Scholar] [CrossRef]
- Mohamed, M.H.; Ali, A.M.; Hafiz, A.A. CFD analysis for H-rotor Darrieus turbine as a low speed wind energy converter. Eng. Sci. Technol. Int. J. 2015, 18, 1–13. [Google Scholar] [CrossRef]
- Ferrer, E.; Willden, R.H.J. Blade–wake interactions in cross-flow turbines. Int. J. Mar. Energy 2015, 11, 71–83. [Google Scholar] [CrossRef]
- Shiono, M.; Suzuki, K.; Kiho, S. An experimental study of the characteristics of a darrieus turbine for tidal power generation. Electr. Eng. Jpn. 2000, 132, 38–47. [Google Scholar] [CrossRef]
- Chen, W.-H.; Lam, T.T.; Chang, M.-H.; Jin, L.; Chueh, C.-C.; Augusto, G.L. Optimizing H-Darrieus Wind Turbine Performance with Double-Deflector Design. Energies 2024, 17, 503. [Google Scholar] [CrossRef]
- Mohamed, M.H. Performance investigation of H-rotor Darrieus turbine with new airfoil shapes. Energy 2012, 47, 522–530. [Google Scholar] [CrossRef]
- Tjiu, W.; Marnoto, T.; Mat, S.; Ruslan, M.H. Darrieus vertical axis wind turbine for power generation I: Assessment of Darrieus VAWT configurations. Renew. Energy 2015, 75, 50–67. [Google Scholar] [CrossRef]
- Antheaume, S.; Maître, T.; Achard, J.L. Hydraulic Darrieus turbines efficiency for free fluid flow conditions versus power farms conditions. Renew. Energy 2008, 33, 2186–2198. [Google Scholar] [CrossRef]
- Giorgetti, S.; Pellegrini, G.; Zanforlin, S. CFD investigation on the aerodynamic interferences between medium-solidity Darrieus Vertical Axis Wind Turbines. Energy Procedia 2015, 81, 227–239. [Google Scholar] [CrossRef]
- Shaheen, M.; Abdallah, S. Development of efficient vertical axis wind turbine clustered farms. Renew. Sustain. Energy Rev. 2016, 63, 237–244. [Google Scholar] [CrossRef]
- Maslov, N.; Charpentier, J.F.; Claramunt, C. A modelling approach for a cost-based evaluation of the energy produced by a marine energy farm. Int. J. Mar. Energy 2015, 9, 1–19. [Google Scholar] [CrossRef]
- Ross, I.; Altman, A. Wind tunnel blockage corrections: Review and application to Savonius vertical-axis wind turbines. J. Wind. Eng. Ind. Aerodyn. 2011, 99, 523–538. [Google Scholar] [CrossRef]
- Fiedler, A.J.; Tullis, S. Blade offset and pitch effects on a high solidity vertical axis wind turbine. Wind. Eng. 2009, 33, 237–246. [Google Scholar] [CrossRef]
- Priegue, L.; Stoesser, T.; Runge, S. Effect of blade parameters on the performance of a cross-flow turbine. In Proceedings of the E-Proceedings of the 36th IAHR World Congress, The Hague, The Netherlands, 28 June–3 July 2015. [Google Scholar]
- Miller, M.A.; Duvvuri, S.; Hultmark, M. Solidity effects on the performance of vertical-axis wind turbines. Flow 2021, 1, E9. [Google Scholar] [CrossRef]
- Gorlov, A. Unidirectional Helical Reaction Turbine. U.S. Patent No 5,451,137, 19 September 1995. [Google Scholar]
- Islam, M.; Ting, D.; Fartaj, A. Desirable airfoil features for smaller-capacity straight-bladed VAWT. Wind. Eng. 2007, 31, 165–196. [Google Scholar] [CrossRef]
- Soraghan, C. Influence of lift to drag ratio on optimal aerodynamic performance of straight blade vertical axis wind turbines. In Proceedings of the Europe’s Premier Wind Energy Event, Vienna, Austria, 4–7 February 2013. [Google Scholar]
- Castiglione, T.; Barbarelli, S.; Zupone, G.L.; Bova, S. Flow-field and wake analysis of novel double-rotor open-center tidal current turbine by CFD simulations. Ocean Eng. 2021, 222, 108597. [Google Scholar] [CrossRef]
- Mason-Jones, A.; O′Doherty, T.; O′Doherty, D.M.; Evans, P.S.; Wooldridge, C.F. Characterisation of a HATT using CFD and ADCP site data. In Proceedings of the 10th World Renewable Energy Congress, Grasgow, UK, 19–25 July 2008. [Google Scholar]
- Harrison, M.E.; Batten, W.M.J.; Myers, L.E.; Bahaj, A.S. A comparison between CFD simulations and experiments for predicting the far wake of horizontal axis tidal turbines. In Proceedings of the 8th European Wave and Tidal Ensergy Conference, Uppsala, Sweden, 7–10 September 2009. [Google Scholar]
- Li, Y.; Çalişal, S.M. A discrete vortex method for simulating a stand-alone tidal-current turbine: Modeling and validation. J. Offshore Mech. Arct. Eng. 2010, 132, 031102. [Google Scholar] [CrossRef]
- Harrison, M.E.; Batten, W.M.J.; Bahaj, A.S. A Blade Element Actuator Disc Approach Applied to Tidal Stream Turbines. In Proceedings of the OCEANS 2010 MTS/IEEE SEATTLE, Seattle, WA, USA, 20–23 September 2010; pp. 1–8. [Google Scholar]
- Belloni, C.S.K.; Willden, R.H.J.; Houlsby, G.T. An investigation of ducted and open-centre tidal turbines employing CFD-embedded BEM. Renew. Energy 2017, 108, 622–634. [Google Scholar] [CrossRef]
- Myers, L.E.; Bahaj, A.S. Experimental analysis of the flow field around horizontal axis tidal turbines by use of scale mesh disk rotor simulators. Ocean Eng. 2009, 37, 218–227. [Google Scholar] [CrossRef]
- Allsop, S.; Peyrard, C.; Thies, P.R.; Boulougouris, E.; Harrison, G.P. Hydrodynamic analysis of a ducted, open centre tidal stream turbine using blade element momentum theory. Ocean Eng. 2017, 141, 531–542. [Google Scholar] [CrossRef]
- Maître, T.; Amet, E.; Pellone, C. Modeling of the flow in a darrieus water turbine: Wall grid refinement analysis and comparison with experiments. Renew. Energy 2013, 51, 497–512. [Google Scholar] [CrossRef]
- Roa, A.M.; Aumelas, V.; Maître, T.; Pellone, C. Numerical and experimental analysis of a Darrieus-type cross flow water turbine in bare and shrouded configurations. IOP Conf. Ser. Earth Environ. Sci. 2010, 12, 012113. [Google Scholar] [CrossRef]
- McNaughton, J.; Billard, F.; Revell, A. Turbulence modelling of low reynolds number flow effects around a vertical axis turbine at a range of tip-speed ratios. J. Fluids Struct. 2014, 47, 124–138. [Google Scholar] [CrossRef]
- Howell, R.; Qin, N.; Edwards, J.; Durrani, N. Wind tunnel and numerical study of a small vertical axis wind turbine. Renew. Energy 2010, 35, 412–422. [Google Scholar] [CrossRef]
- Marsh, P.; Ranmuthugala, D.; Penesis, I.; Thomas, G. Numerical investigation of the influence of blade helicity on the performance characteristics of vertical axis tidal turbines. Renew. Energy 2015, 81, 926–935. [Google Scholar] [CrossRef]
- Rodi, W.; Constantinescu, G.; Stoesser, T. Large-eddy simulation in hydraulics. In IAHR Monographs; CRC Press: Leiden, The Netherlands, 2013; ISBN 9781138000247. [Google Scholar]
- Stoesser, T. Large-eddy simulation in hydraulics: Quo vadis? J. Hydraul. Res. 2014, 52, 441–452. [Google Scholar] [CrossRef]
- Kear, M.; Evans, B.; Ellis, R.; Rolland, S. Computational aerodynamic optimisation of vertical axis wind turbine blades. Appl. Math. Model. 2015, 40, 1038–1051. [Google Scholar] [CrossRef]



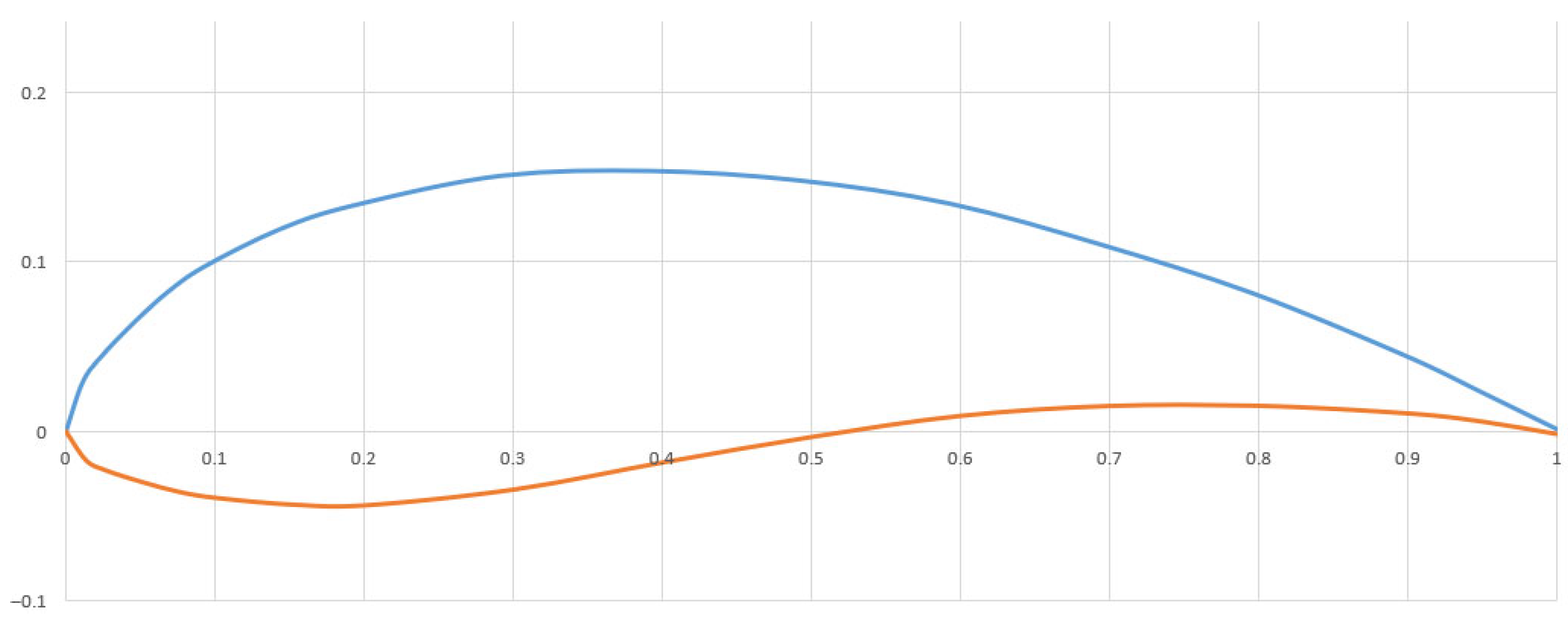








| Upper Line (Blue) | Lower Line (Red) | ||
|---|---|---|---|
| Coordinate (X) mm | Coordinate (Y) mm | Coordinate (X) mm | Coordinate (Y) mm |
| 0 | 0 | 0 | 0 |
| 3.46652 | 9.03444 | 4.2344 | −5.30248 |
| 7.17004 | 13.65436 | 8.28236 | −7.1416 |
| 14.70348 | 20.53684 | 16.30244 | −9.39784 |
| 22.28432 | 26.47132 | 24.30356 | −11.2464 |
| 29.94416 | 30.99012 | 32.26044 | −12.3366 |
| 45.38708 | 37.66088 | 48.12364 | −13.5406 |
| 60.95008 | 42.06592 | 63.92996 | −13.6449 |
| 92.25304 | 47.59592 | 95.37196 | −10.6966 |
| 123.8056 | 48.49336 | 126.7065 | −5.7038 |
| 155.5004 | 46.71428 | 158.0537 | −1.02384 |
| 187.3311 | 42.41352 | 189.4483 | 2.86612 |
| 219.3388 | 34.80108 | 220.9472 | 4.71156 |
| 251.4223 | 25.77612 | 252.544 | 4.75896 |
| 283.6384 | 14.22632 | 284.2199 | 3.35592 |
| 299.8018 | 7.44496 | 300.102 | 1.83596 |
| 316 | 0.474 | 316 | −0.474 |
| Model with Four Blades | Model with Eight Blades | |
|---|---|---|
| Velocity 1 () | 5.660685 | 4.435567 |
| Velocity 2 () | 2.616285 | 2.081603 |
| Energy reduction () | 142.677 A | 52.095 A |
| Efficiency | 78% | 59% |
| Four-Blade Turbine | Eight-Blade Turbine | |
|---|---|---|
| Area (net angular impulse ) | 290 | 273 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Hill, M.; Burchell, J. Optimisation of a Kind of Vertical Axis Darrieus Turbine—Davidson Hill Venturi Cross-Flow Turbines. Energies 2025, 18, 4763. https://doi.org/10.3390/en18174763
Wang H, Hill M, Burchell J. Optimisation of a Kind of Vertical Axis Darrieus Turbine—Davidson Hill Venturi Cross-Flow Turbines. Energies. 2025; 18(17):4763. https://doi.org/10.3390/en18174763
Chicago/Turabian StyleWang, Han, Mark Hill, and Joseph Burchell. 2025. "Optimisation of a Kind of Vertical Axis Darrieus Turbine—Davidson Hill Venturi Cross-Flow Turbines" Energies 18, no. 17: 4763. https://doi.org/10.3390/en18174763
APA StyleWang, H., Hill, M., & Burchell, J. (2025). Optimisation of a Kind of Vertical Axis Darrieus Turbine—Davidson Hill Venturi Cross-Flow Turbines. Energies, 18(17), 4763. https://doi.org/10.3390/en18174763






