A Physics-Informed Variational Autoencoder for Modeling Power Plant Thermal Systems
Abstract
1. Introduction
2. Materials and Methods
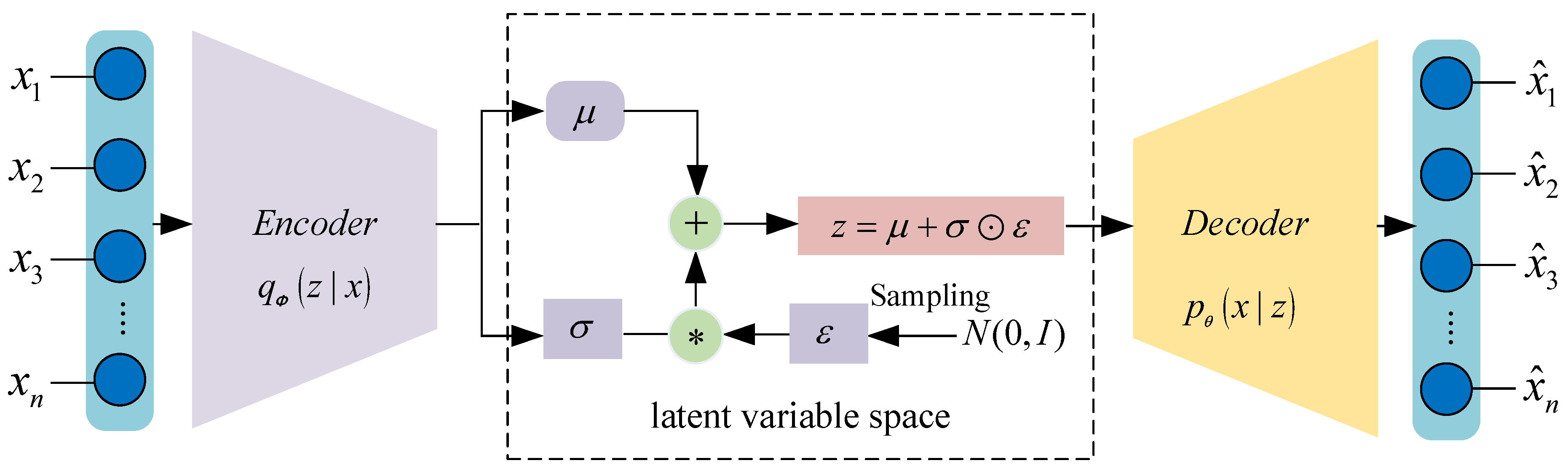
2.1. Variational Autoencoder, VAE
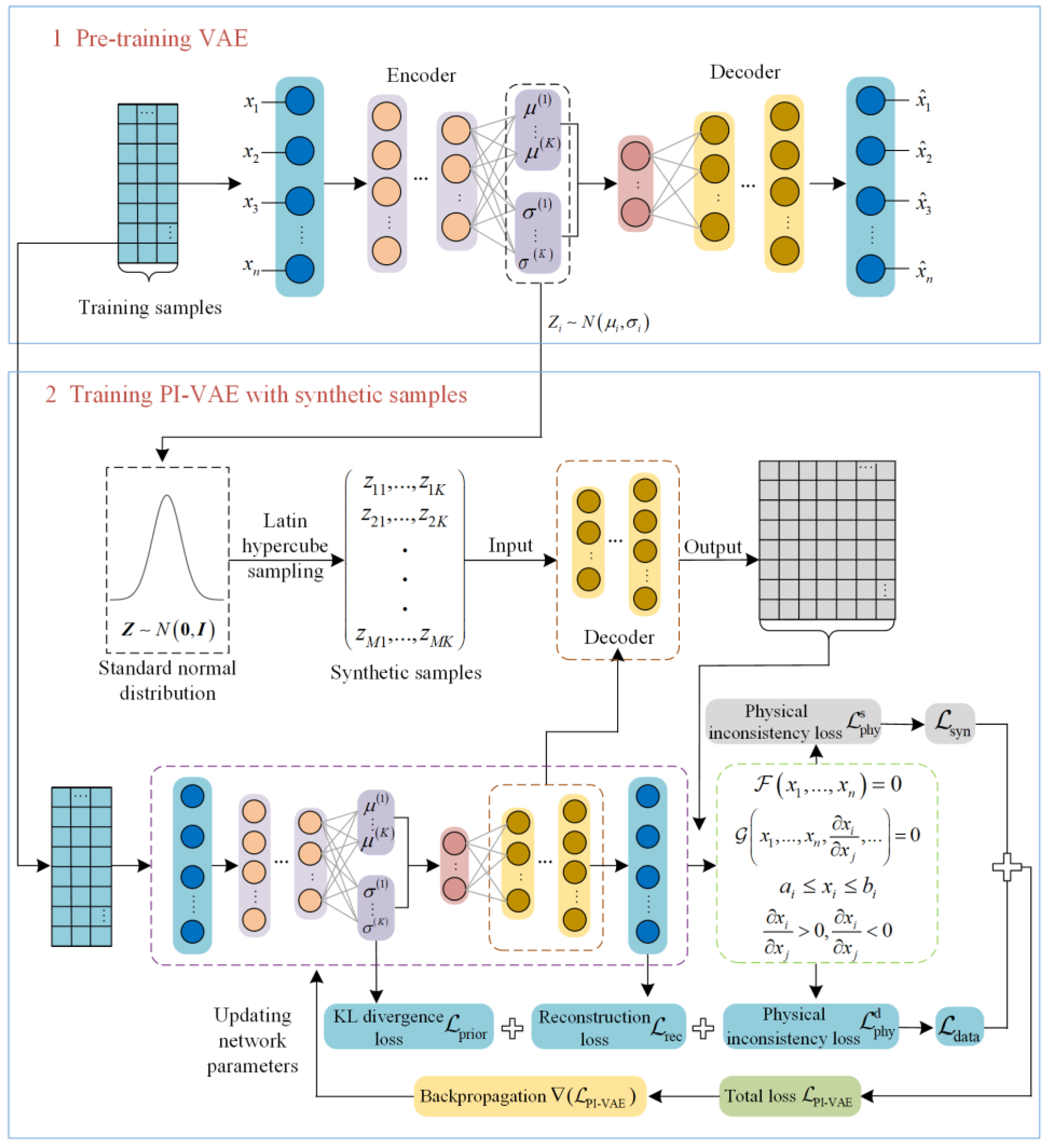
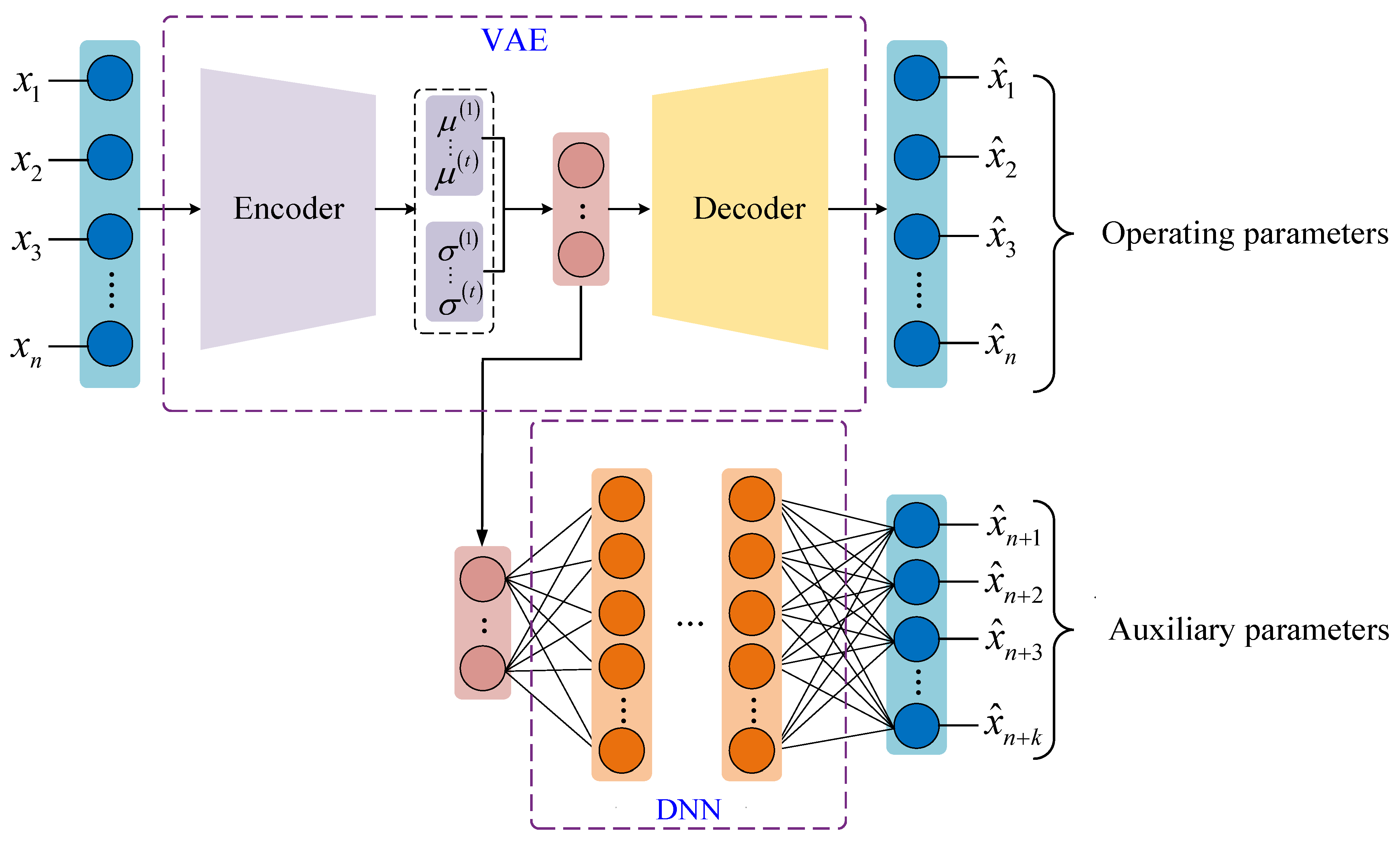
2.2. Physics-Informed Variational Autoencoder, PI-VAE
2.2.1. Physical Constraint
- (1)
- Equality constraint
- (2)
- Inequality constraint
2.2.2. Physical Inconsistency Loss Function
- (1)
- The loss function of the algebraic equations and transcendental equations can be uniformly expressed as:
- (2)
- The loss function of the partial differential equations can be expressed as:
- (3)
- The loss function of the boundary conditions can be expressed as:
- (4)
- The loss function of the monotonicity constraints can be expressed as:
2.2.3. Synthetic Sample Generation
| Algorithm 1. LHS-based sampling method for latent variables |
| Input: latent variable dimension , number of samples . Initialization: sample set . Iteration For do Randomize to generate sequence Iteration For do Generate a uniform random number Compute Obtain by inverse function mapping Add to the -th dimension sampling sequence End the iteration. End the iteration. Combine the sampling points from each dimension to form the final sample set . |
2.2.4. Training the PI-VAE Model
| Algorithm 2. Training algorithm for the PI-VAE model |
| Input: normalized training dataset . Initialization: Randomly initialize network parameters and Given synthetic sample size , batch size , learning rate , maximum number of iterations and , weighting coefficients , and . VAE pre-training stage: Iteration For do Select a mini-batch from Compute mean and variance via the encoder: Generate latent variable using the reparameterization trick: , where Reconstruct via the decoder: Compute the VAE loss for using Equation (5) Compute the gradient and update by descending the gradient Until converges, end the iteration. PI-VAE training stage: Generate synthetic dataset using the sampling method from Algorithm 1. Iteration For do Select a mini-batch from Reconstruct the training data batch to get Compute the VAE loss for using Equation (5) Compute the physical inconsistency loss on using Equation (27) Select a mini-batch from Obtain via the decoder: Compute the physical inconsistency loss on using Equation (29) Compute the total PI-VAE loss: Compute the gradient and update by descending the gradient Until converges, end the iteration. |
3. Results and Discussion
3.1. Numerical Case
3.1.1. Model Structure and Parameter Setting
3.1.2. Construction and Combination of Physical Constraints
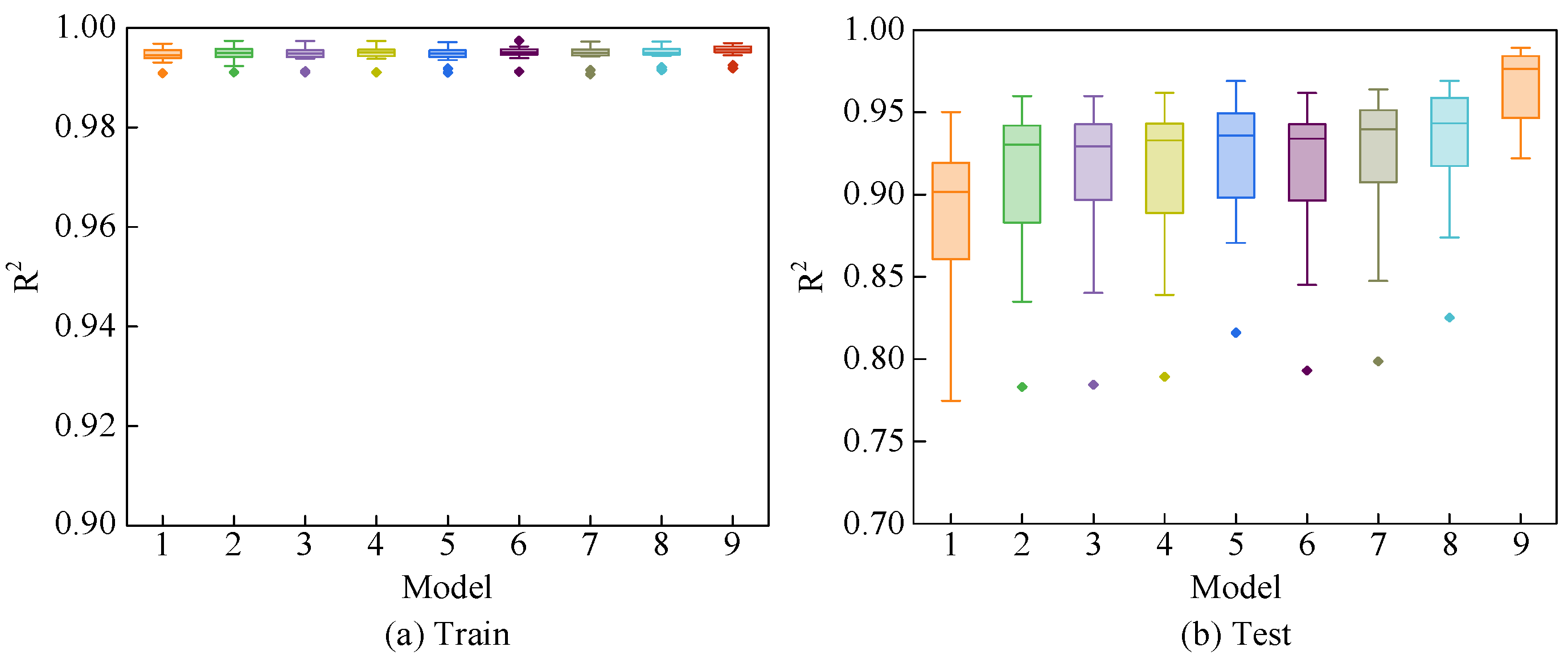
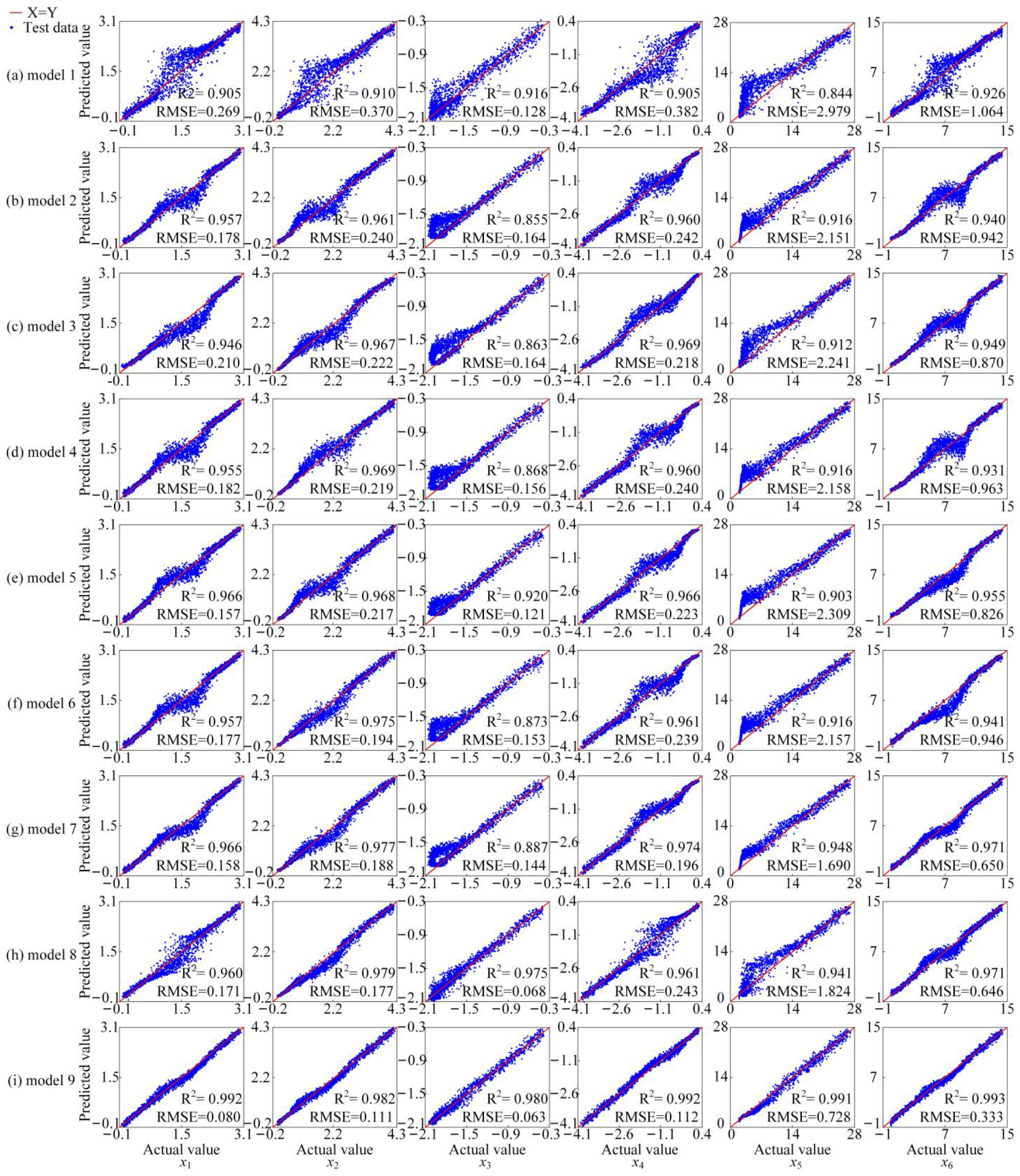
3.1.3. Performance Analysis with Different Combinations of Physical Constraints
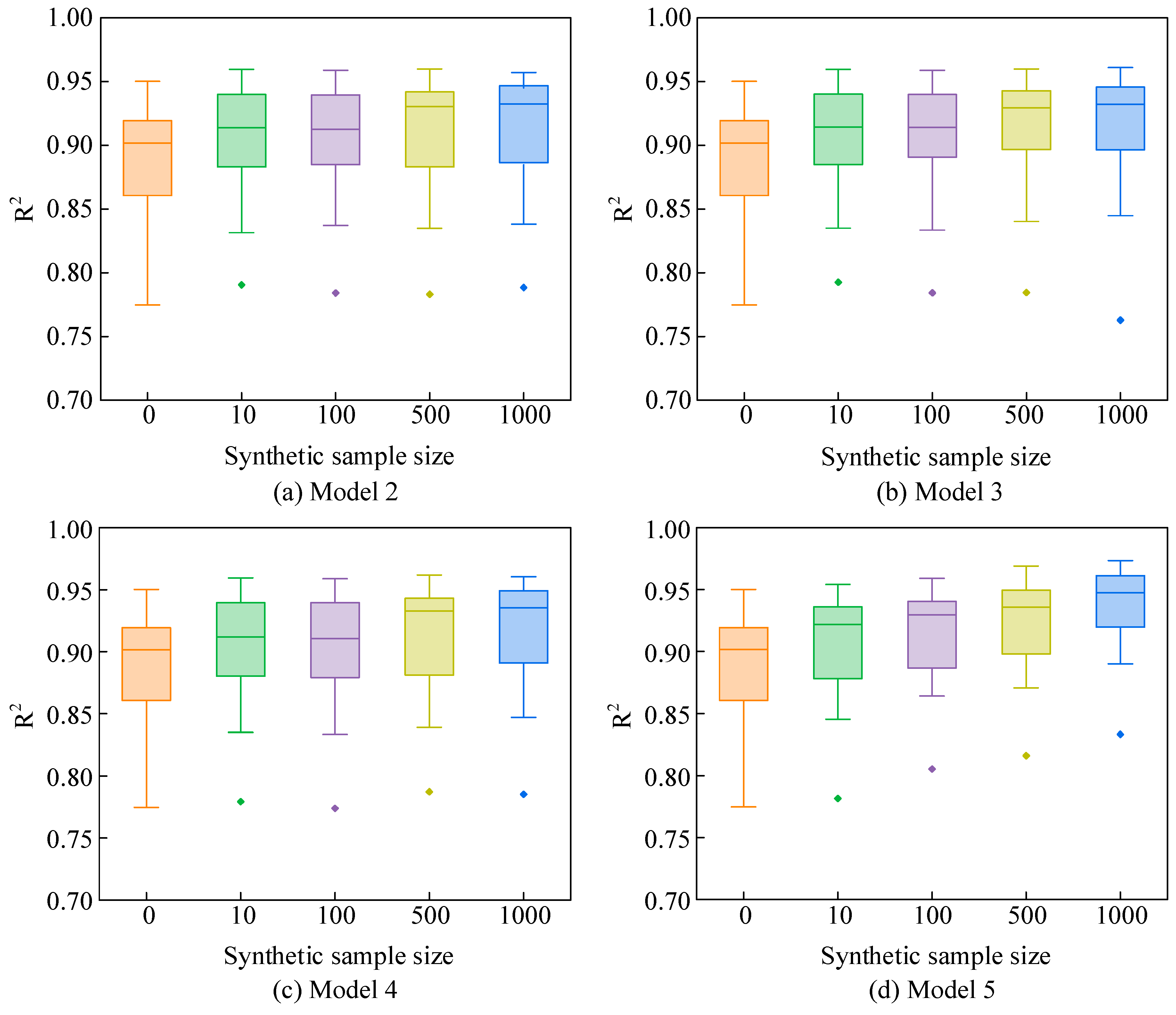
3.1.4. Performance Analysis with Different Synthetic Sample Sizes
3.2. HPFW System Case
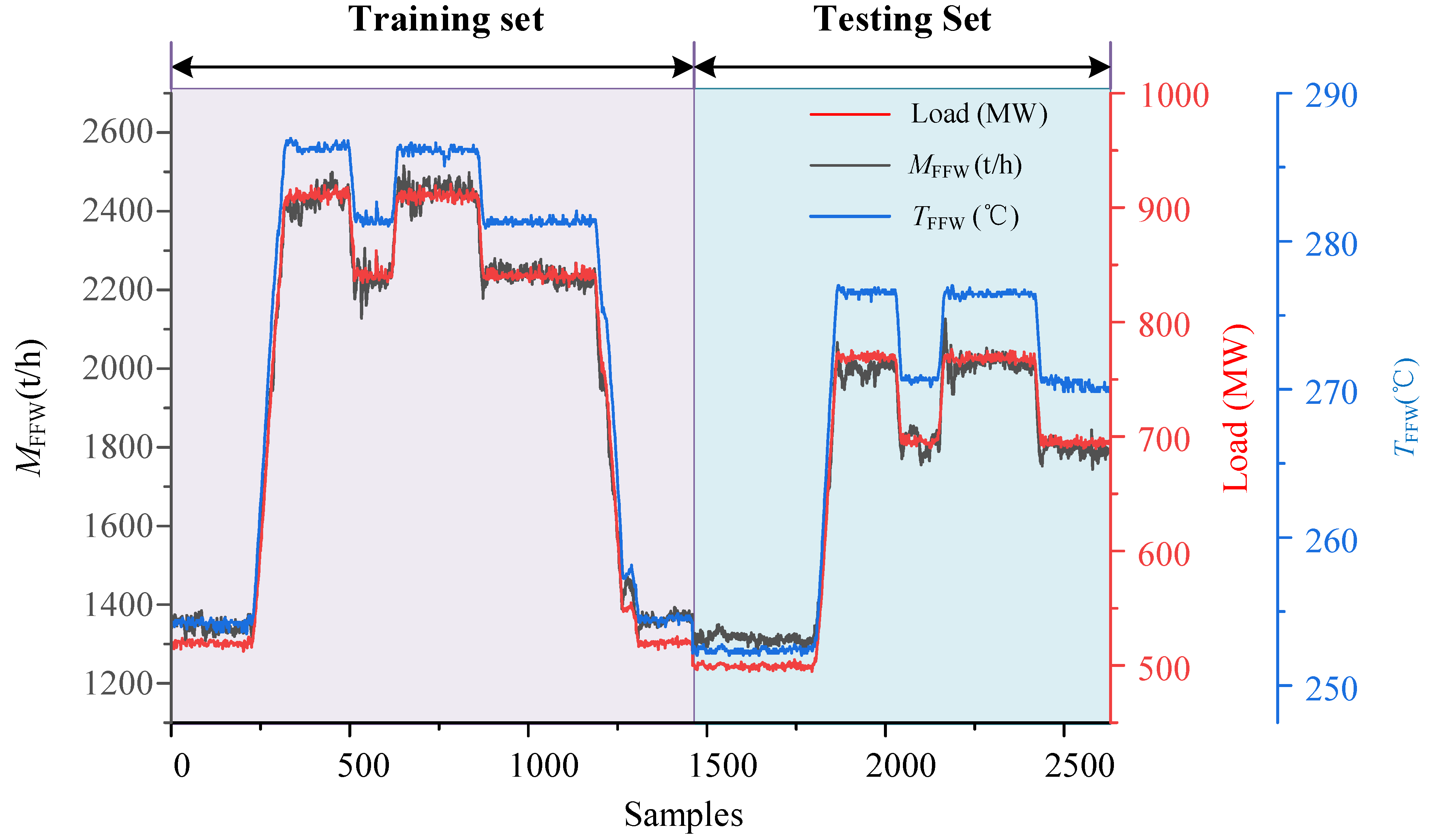
3.2.1. Research Object and Model Training
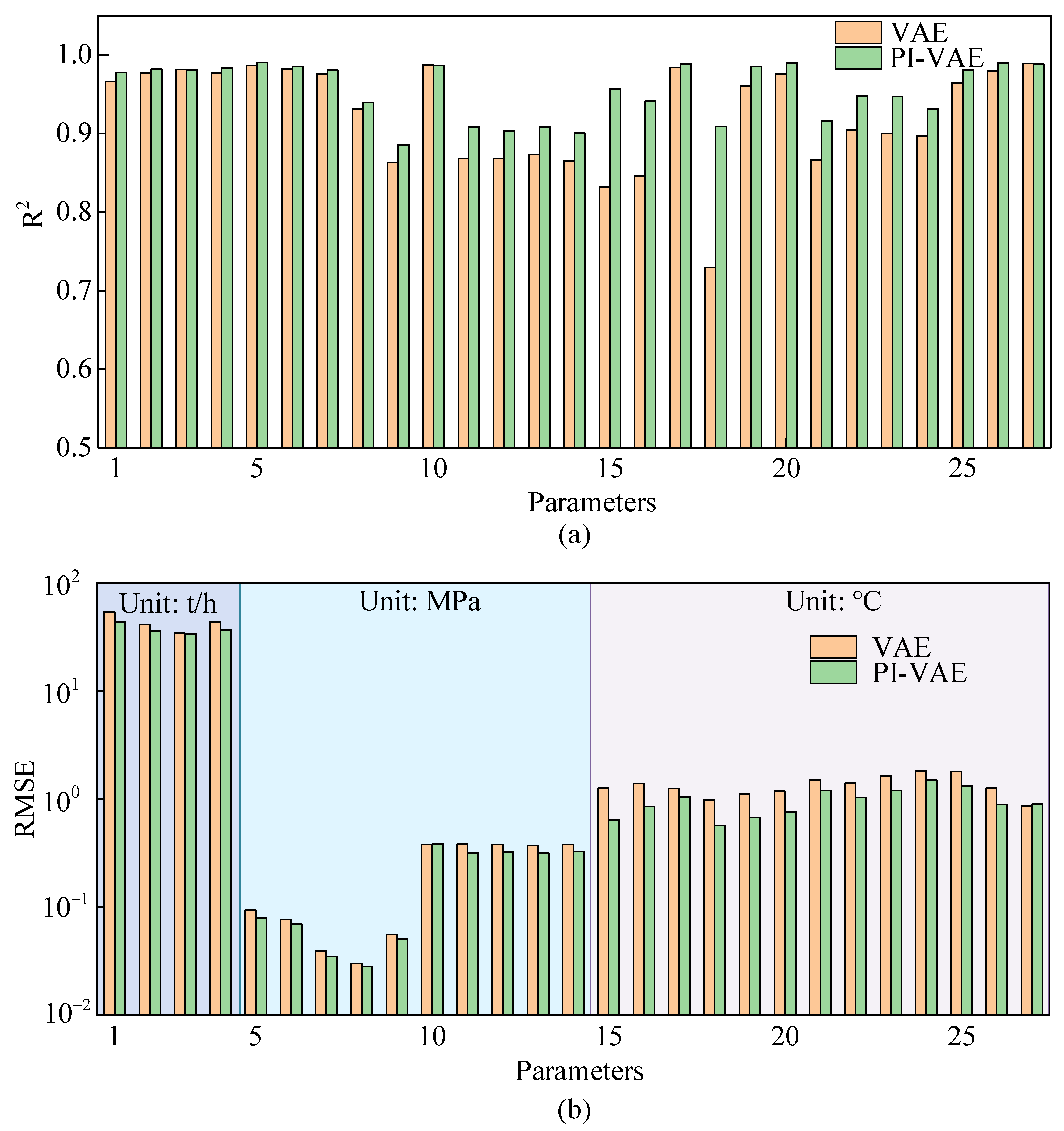
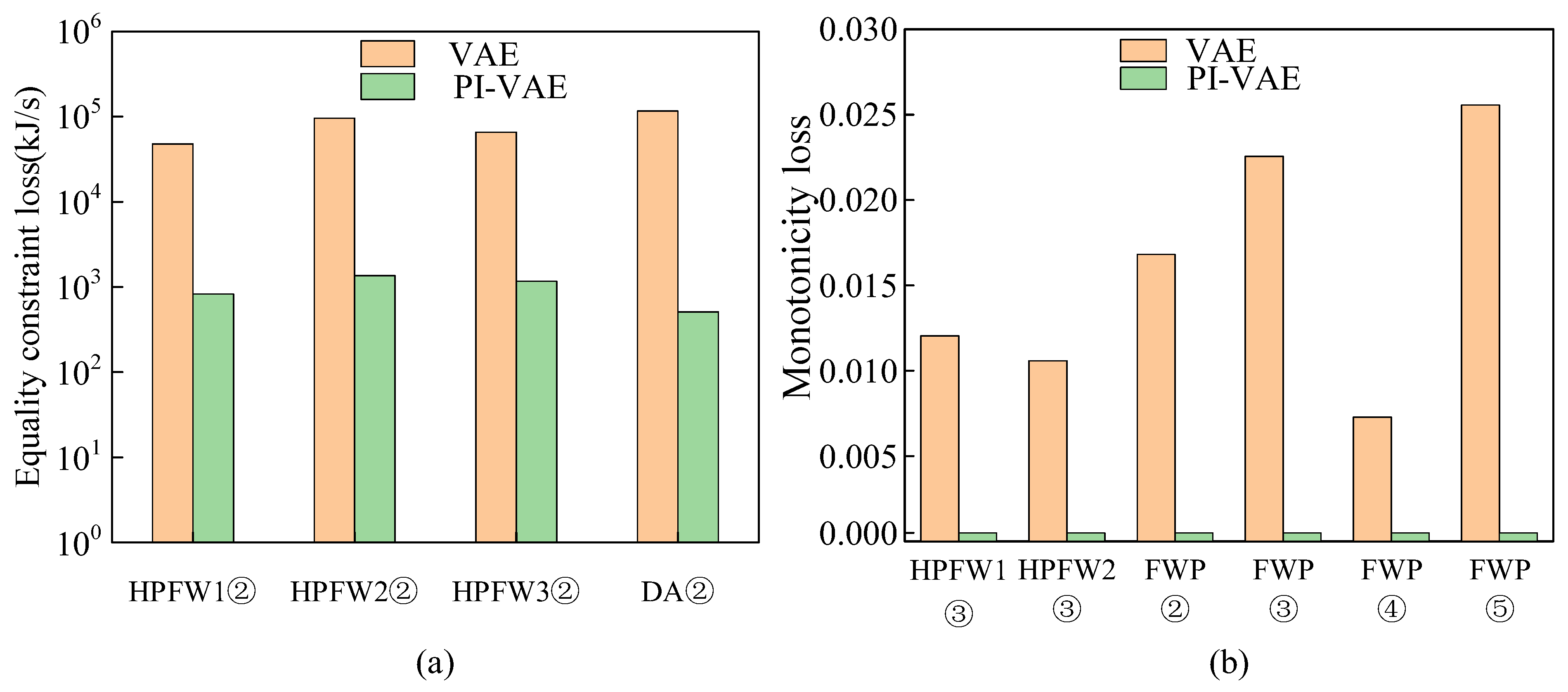
3.2.2. Model Performance Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ge, Z. Review on data-driven modeling and monitoring for plant-wide industrial processes. Chemom. Intell. Lab. Syst. 2017, 171, 16–25. [Google Scholar] [CrossRef]
- Ren, S.; Jin, Y.; Zhao, J.; Cao, Y.; Si, F. Nonlinear process monitoring based on generic reconstruction-based auto-associative neural network. J. Frankl. Inst. 2023, 360, 5149–5170. [Google Scholar] [CrossRef]
- Zhu, Y.; Yu, C.; Jin, W.; Shi, L.; Chen, B.; Xu, P. Mechanism-enhanced data-driven method for the joint optimization of boiler combustion and selective catalytic reduction systems considering gas temperature deviations. Energy 2024, 291, 130432. [Google Scholar] [CrossRef]
- Zhou, D.; Huang, D. A review on the progress, challenges and prospects in the modeling, simulation, control and diagnosis of thermodynamic systems. Adv. Eng. Inform. 2024, 60, 102435. [Google Scholar] [CrossRef]
- Chen, C.; Liu, M.; Li, M.; Wang, Y.; Wang, C.; Yan, J. Digital twin modeling and operation optimization of the steam turbine system of thermal power plants. Energy 2024, 290, 129969. [Google Scholar] [CrossRef]
- Zhang, S.; Zhao, C. Concurrent analysis of variable correlation and data distribution for monitoring large-scale processes under varying operation conditions. Neurocomputing 2019, 349, 225–238. [Google Scholar] [CrossRef]
- Chang, J.; Wang, X.; Zhou, Z.; Chen, H.; Niu, Y. CFD modeling of hydrodynamics, combustion and NOx emission in a tangentially fired pulverized-coal boiler at low load operating conditions. Adv. Powder Technol. 2021, 32, 290–303. [Google Scholar] [CrossRef]
- Yang, Y.; Nikolaidis, T.; Jafari, S.; Pilidis, P. Gas turbine engine transient performance and heat transfer effect modelling: A comprehensive review, research challenges, and exploring the future. Appl. Therm. Eng. 2024, 236, 121523. [Google Scholar] [CrossRef]
- Wang, J.; Feng, Y.; Ye, S.; Zhang, Y.; Ma, Z.; Dong, F. NOx emission prediction of coal-fired power units under uncertain classification of operating conditions. Fuel 2023, 343, 127840. [Google Scholar] [CrossRef]
- Song, H.; Liu, X.; Song, M. Comparative study of data-driven and model-driven approaches in prediction of nuclear power plants operating parameters. Appl. Energy 2023, 341, 121077. [Google Scholar] [CrossRef]
- Fenza, G.; Gallo, M.; Loia, V.; Orciuoli, F.; Herrera-Viedma, E. Data set quality in Machine Learning: Consistency measure based on Group Decision Making. Appl. Soft Comput. 2021, 106, 107366. [Google Scholar] [CrossRef]
- Lv, Y.; Romero, C.E.; Yang, T.; Fang, F.; Liu, J. Typical condition library construction for the development of data-driven models in power plants. Appl. Therm. Eng. 2018, 143, 160–171. [Google Scholar] [CrossRef]
- Vabalas, A.; Gowen, E.; Poliakoff, E.; Casson, A.J. Machine learning algorithm validation with a limited sample size. PLoS ONE 2019, 14, e0224365. [Google Scholar] [CrossRef]
- Azodi, C.B.; Tang, J.; Shiu, S.-H. Opening the Black Box: Interpretable Machine Learning for Geneticists. Trends Genet. 2020, 36, 442–455. [Google Scholar] [CrossRef]
- Bradley, W.; Kim, J.; Kilwein, Z.; Blakely, L.; Eydenberg, M.; Jalvin, J.; Laird, C.; Boukouvala, F. Perspectives on the integration between first-principles and data-driven modeling. Comput. Chem. Eng. 2022, 166, 107898. [Google Scholar] [CrossRef]
- Soofi, Y.J.; Gu, Y.; Liu, J. An adaptive Physics-based feature engineering approach for Machine Learning-assisted alloy discovery. Comput. Mater. Sci. 2023, 226, 112248. [Google Scholar] [CrossRef]
- Zhu, H.; Tsang, E.C.C.; Wang, X.-Z.; Aamir Raza Ashfaq, R. Monotonic classification extreme learning machine. Neurocomputing 2017, 225, 205–213. [Google Scholar] [CrossRef]
- Pan, C.; Dong, Y.; Yan, X.; Zhao, W. Hybrid model for main and side reactions of p-xylene oxidation with factor influence based monotone additive SVR. Chemom. Intell. Lab. Syst. 2014, 136, 36–46. [Google Scholar] [CrossRef]
- Ji, W.; Deng, S. Autonomous Discovery of Unknown Reaction Pathways from Data by Chemical Reaction Neural Network. J. Phys. Chem. A 2021, 125, 1082–1092. [Google Scholar] [CrossRef] [PubMed]
- Ji, W.; Richter, F.; Gollner, M.J.; Deng, S. Autonomous kinetic modeling of biomass pyrolysis using chemical reaction neural networks. Combust. Flame 2022, 240, 111992. [Google Scholar] [CrossRef]
- Raissi, M.; Yazdani, A.; Karniadakis, G.E. Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations. Science 2020, 367, 1026–1030. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Wu, Y.; Sicard, B.; Gadsden, S.A. Physics-informed machine learning: A comprehensive review on applications in anomaly detection and condition monitoring. Expert Syst. Appl. 2024, 255, 124678. [Google Scholar] [CrossRef]
- Cuomo, S.; Di Cola, V.S.; Giampaolo, F.; Rozza, G.; Raissi, M.; Piccialli, F. Scientific Machine Learning Through Physics–Informed Neural Networks: Where we are and What’s Next. J. Sci. Comput. 2022, 92, 88. [Google Scholar] [CrossRef]
- Cai, S.Z.; Mao, Z.P.; Wang, Z.C.; Yin, M.L.; Karniadakis, G.E. Physics-informed neural networks (PINNs) for fluid mechanics: A review. Acta Mech. Sin. 2021, 37, 1727–1738. [Google Scholar] [CrossRef]
- Jalili, D.; Jang, S.; Jadidi, M.; Giustini, G.; Keshmiri, A.; Mahmoudi, Y. Physics-informed neural networks for heat transfer prediction in two-phase flows. Int. J. Heat Mass Transf. 2024, 221, 125089. [Google Scholar] [CrossRef]
- Alber, M.; Buganza Tepole, A.; Cannon, W.R.; De, S.; Dura-Bernal, S.; Garikipati, K.; Karniadakis, G.; Lytton, W.W.; Perdikaris, P.; Petzold, L.; et al. Integrating machine learning and multiscale modeling—Perspectives, challenges, and opportunities in the biological, biomedical, and behavioral sciences. npj Digit. Med. 2019, 2, 115. [Google Scholar] [CrossRef]
- Zideh, M.J.; Chatterjee, P.; Srivastava, A.K. Physics-Informed Machine Learning for Data Anomaly Detection, Classification, Localization, and Mitigation: A Review, Challenges, and Path Forward. IEEE Access 2024, 12, 4597–4617. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Haghighat, E.; Raissi, M.; Moure, A.; Gomez, H.; Juanes, R. A physics-informed deep learning framework for inversion and surrogate modeling in solid mechanics. Comput. Methods Appl. Mech. Eng. 2021, 379, 113741. [Google Scholar] [CrossRef]
- Li, P.; Pei, Y.; Li, J. A comprehensive survey on design and application of autoencoder in deep learning. Appl. Soft Comput. 2023, 138, 110176. [Google Scholar] [CrossRef]
- Chen, X.; Zhao, C. Conditional discriminative autoencoder and condition-driven immediate representation of soft transition for monitoring complex nonstationary processes. Control Eng. Pract. 2022, 122, 105090. [Google Scholar] [CrossRef]
- Kim, H.; Ko, J.U.; Na, K.; Lee, H.; Kim, H.-S.; Son, J.-D.; Yoon, H.; Youn, B.D. Opt-TCAE: Optimal temporal convolutional auto-encoder for boiler tube leakage detection in a thermal power plant using multi-sensor data. Expert Syst. Appl. 2023, 215, 119377. [Google Scholar] [CrossRef]
- Khalid Fahmi, A.-T.W.; Reza Kashyzadeh, K.; Ghorbani, S. Fault detection in the gas turbine of the Kirkuk power plant: An anomaly detection approach using DLSTM-Autoencoder. Eng. Fail. Anal. 2024, 160, 108213. [Google Scholar] [CrossRef]
- Alemi, A.; Poole, B.; Fischer, I.; Dillon, J.; Saurous, R.A.; Murphy, K. Fixing a Broken ELBO. In Proceedings of the 35th International Conference on Machine Learning; Proceedings of Machine Learning Research; Stockholmsmässan, Stockholm Sweden; 10–15 July 2018; Jennifer, D., Andreas, K., Eds.; PMLR: Cambridge, MA, USA, 2018; Volume 80, pp. 159–168. [Google Scholar]
- Kingma, D.P.; Welling, M. An introduction to variational autoencoders. Found. Trends® Mach. Learn. 2019, 12, 307–392. [Google Scholar] [CrossRef]
- Styan, G.P.H. Hadamard products and multivariate statistical analysis. Linear Algebra Its Appl. 1973, 6, 217–240. [Google Scholar] [CrossRef]
- Margossian, C.C. A review of automatic differentiation and its efficient implementation. WIREs Data Min. Knowl. Discov. 2019, 9, e1305. [Google Scholar] [CrossRef]
- Wu, C.; Zhu, M.; Tan, Q.; Kartha, Y.; Lu, L. A comprehensive study of non-adaptive and residual-based adaptive sampling for physics-informed neural networks. Comput. Methods Appl. Mech. Eng. 2023, 403, 115671. [Google Scholar] [CrossRef]
- Sholokhov, A.; Liu, Y.; Mansour, H.; Nabi, S. Physics-informed neural ODE (PINODE): Embedding physics into models using collocation points. Sci. Rep. 2023, 13, 10166. [Google Scholar] [CrossRef]
- Shields, M.D.; Zhang, J. The generalization of Latin hypercube sampling. Reliab. Eng. Syst. Saf. 2016, 148, 96–108. [Google Scholar] [CrossRef]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-generation Hyperparameter Optimization Framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2623–2631. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, C.; Liu, M.; Chong, D.; Yan, J. Improving operational flexibility by regulating extraction steam of high-pressure heaters on a 660 MW supercritical coal-fired power plant: A dynamic simulation. Appl. Energy 2018, 212, 1295–1309. [Google Scholar] [CrossRef]
- Guo, S.; Liu, P.; Li, Z. Enhancement of performance monitoring of a coal-fired power plant via dynamic data reconciliation. Energy 2018, 151, 203–210. [Google Scholar] [CrossRef]



| Model | Description | Value |
|---|---|---|
| PI-VAE | Network structure | 6-16-8-2-8-16-6 |
| Activation function | “Relu” | |
| KL divergence loss weight | 0.1 | |
| Physical inconsistency loss weight | 0.1 | |
| Physical inconsistency loss weight | 0.2 | |
| Optimizer | “Adam” | |
| Learning rate | 0.001 | |
| Batch size of training samples | 100 | |
| Maximum number of training iterations | 5000 | |
| Number of synthetic samples | 500 | |
| VAE | Network structure | 6-16-8-2-8-16-6 |
| Activation function | “Relu” | |
| KL divergence loss weight | 0.1 | |
| Optimizer | “Adam” | |
| Learning rate | 0.001 | |
| Batch size of training samples | 50 | |
| Maximum number of training iterations | 3000 |
| No. | Mathematical Expression | Description |
|---|---|---|
| ① | Monotonicity | |
| ② | Monotonicity | |
| ③ | Incomplete partial differential equation | |
| ④ | Incomplete partial differential equation | |
| ⑤ | Partial differential equation | |
| ⑥ | Partial differential equation | |
| ⑦ | Partial differential equation | |
| ⑧ | Partial differential equation | |
| ⑨ | Partial differential equation |
| Model | Combination | Description |
| 1 | - | - |
| 2 | ① | |
| 3 | ①, ② | |
| 4 | ③ | |
| 5 | ③, ④ | |
| 6 | ⑤ | |
| 7 | ⑤, ⑨ | |
| 8 | ⑤, ⑥, ⑨ | |
| 9 | ⑤, ⑥, ⑦, ⑧, ⑨ |
| No. | Variable | Description | Unit |
|---|---|---|---|
| 1 | Outlet feed water mass flow rate of the HPFW1 | t/h | |
| 2 | Outlet mass flow rate of the FWP | t/h | |
| 3 | Inlet condensate mass flow rate of the DA | t/h | |
| 4 | Outlet feed water mass flow rate of the DA | t/h | |
| 5 | Extraction steam pressure to the HPFW1 | MPa | |
| 6 | Extraction steam pressure to the HPFW2 | MPa | |
| 7 | Extraction steam pressure to the HPFW3 | MPa | |
| 8 | Extraction steam pressure to the DA | MPa | |
| 9 | Inlet condensate pressure of the DA | MPa | |
| 10 | Outlet pressure of the FWP | MPa | |
| 11 | Inlet pressure of the HPFW1 | MPa | |
| 12 | Inlet pressure of the HPFW2 | MPa | |
| 13 | Inlet pressure of the HPFW1 | MPa | |
| 14 | Outlet pressure of the HPFW1 | MPa | |
| 15 | Extraction steam temperature of the HPFW1 | °C | |
| 16 | Extraction steam temperature of the HPFW2 | °C | |
| 17 | Extraction steam temperature of the HPFW3 | °C | |
| 18 | Extraction steam temperature of the DA | °C | |
| 19 | Inlet condensate temperature of the DA | °C | |
| 20 | Outlet temperature of the FWP | °C | |
| 21 | Inlet feed water temperature of the HPFW3 | °C | |
| 22 | Inlet feed water temperature of the HPFW2 | °C | |
| 23 | Inlet feed water temperature of the HPFW1 | °C | |
| 24 | Outlet temperature of the HPFW1 | °C | |
| 25 | Drain temperature of the HPFW1 | °C | |
| 26 | Drain temperature of the HPFW2 | °C | |
| 27 | Drain temperature of the HPFW3 | °C |
| Device | No. | Physical Constraint Expression | Description |
|---|---|---|---|
| HPFW1 | ① | Mass balance | |
| ② | Energy balance | ||
| ③ | Monotonicity | ||
| HPFW2 | ① | Mass balance | |
| ② | Energy balance | ||
| ③ | Monotonicity | ||
| HPFW3 | ① | Mass balance | |
| ② | Energy balance | ||
| FWP | ① | Mass balance | |
| ② | Monotonicity | ||
| ③ | Monotonicity | ||
| ④ | Monotonicity | ||
| ⑤ | Monotonicity | ||
| DA | ① | Mass balance | |
| ② | Energy balance |
| Variable | Description | Unit |
|---|---|---|
| Extraction steam mass flow rate to the HPFW1 | t/h | |
| Extraction steam mass flow rate to the HPFW2 | t/h | |
| Extraction steam mass flow rate to the HPFW3 | t/h | |
| Extraction steam mass flow rate to the deaerator | t/h | |
| Drain mass flow rate of the HPFW1 | t/h | |
| Drain mass flow rate of the HPFW2 | t/h | |
| Drain mass flow rate of the HPFW3 | t/h |
| Model | Descriptions | Value |
|---|---|---|
| PI-VAE | VAE network structure | 27-40-15-5-15-40-27 |
| DNN structure | 5-10-20-7 | |
| Activation function | “Relu” | |
| KL divergence loss weight | 0.1 | |
| Physical inconsistency loss weight | 0.002 | |
| Physical inconsistency loss weight | 0.003 | |
| Optimizer | “Adam” | |
| Learning rate | 0.001 | |
| Batch size of training samples | 500 | |
| Maximum number of training iterations | 5000 | |
| Number of synthetic samples | 2000 | |
| VAE | Network structure | 27-40-15-5-15-40-27 |
| Activation function | “Relu” | |
| KL divergence loss weight | 0.1 | |
| Optimizer | “Adam” | |
| Learning rate | 0.001 | |
| Batch size of training samples | 500 | |
| Maximum number of training iterations | 3000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, B.; Ren, S.; Weng, Q.; Si, F. A Physics-Informed Variational Autoencoder for Modeling Power Plant Thermal Systems. Energies 2025, 18, 4742. https://doi.org/10.3390/en18174742
Zhu B, Ren S, Weng Q, Si F. A Physics-Informed Variational Autoencoder for Modeling Power Plant Thermal Systems. Energies. 2025; 18(17):4742. https://doi.org/10.3390/en18174742
Chicago/Turabian StyleZhu, Baoyu, Shaojun Ren, Qihang Weng, and Fengqi Si. 2025. "A Physics-Informed Variational Autoencoder for Modeling Power Plant Thermal Systems" Energies 18, no. 17: 4742. https://doi.org/10.3390/en18174742
APA StyleZhu, B., Ren, S., Weng, Q., & Si, F. (2025). A Physics-Informed Variational Autoencoder for Modeling Power Plant Thermal Systems. Energies, 18(17), 4742. https://doi.org/10.3390/en18174742






