Experimental Investigation of the Capture Performance Model for a Novel Omnidirectional Wave Energy Converter
Abstract
1. Introduction
2. Method
2.1. System Description
2.2. Experimental Setup
3. Data Processing
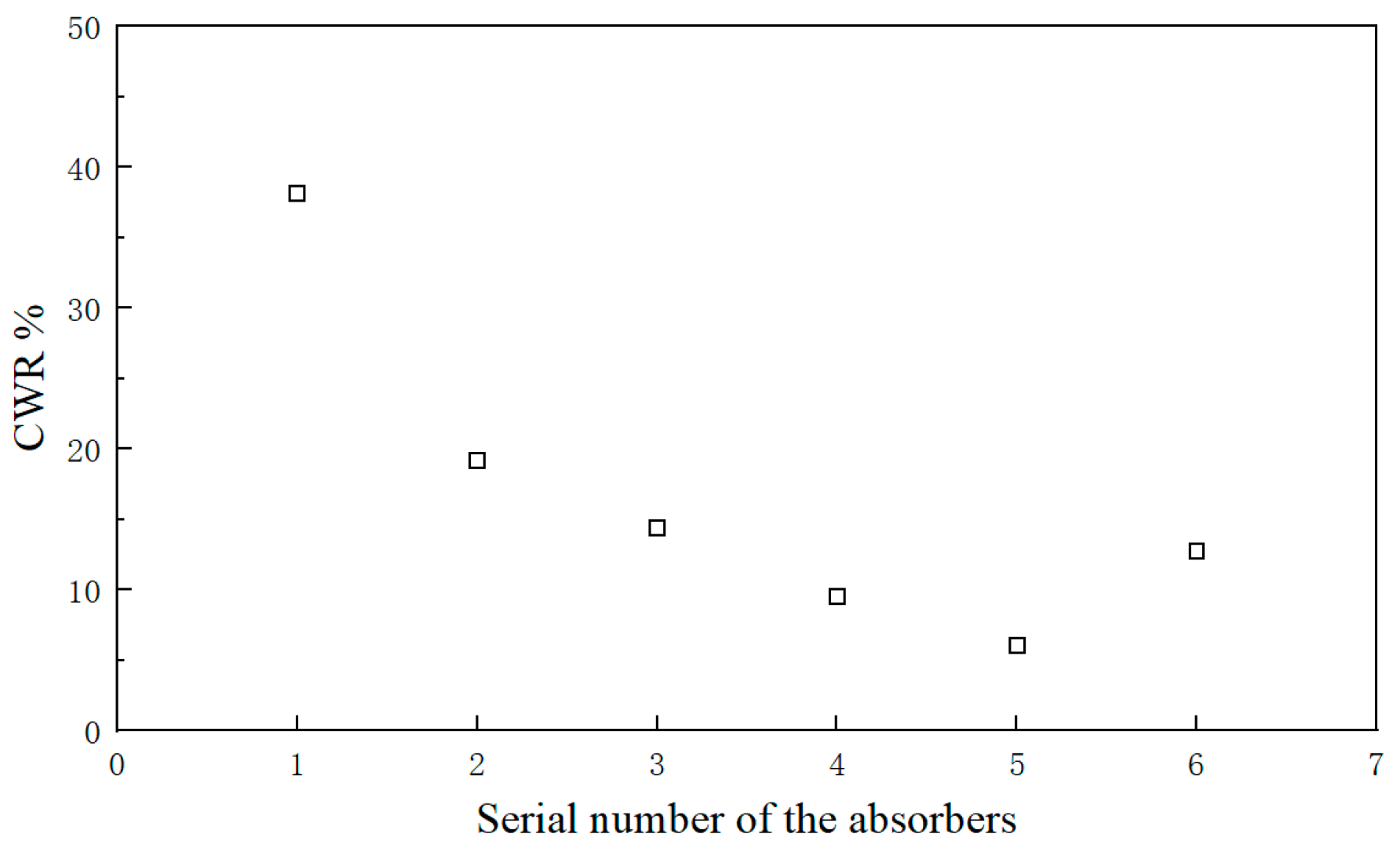
4. Result and Discussion
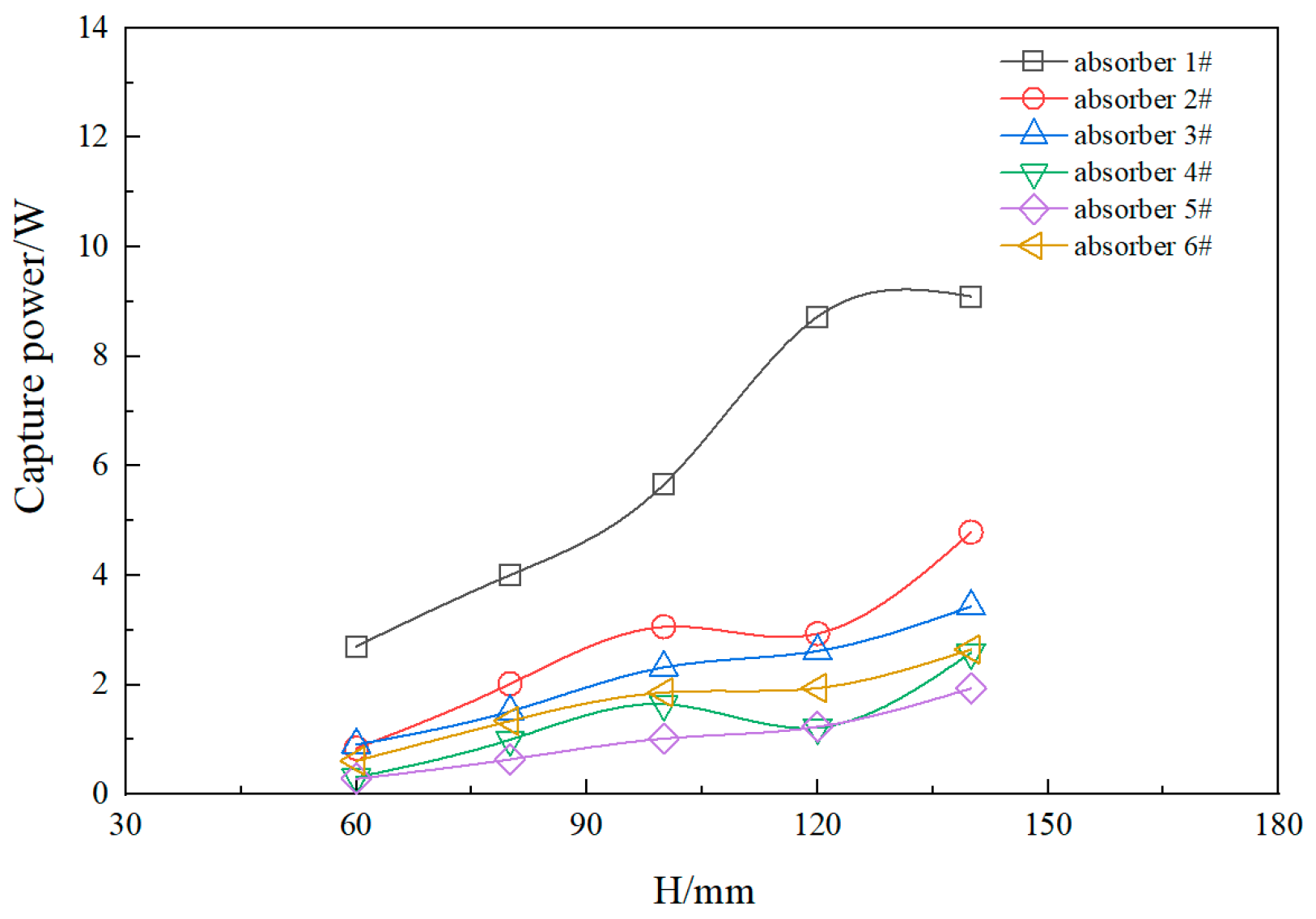
4.1. Effect of Wave Height
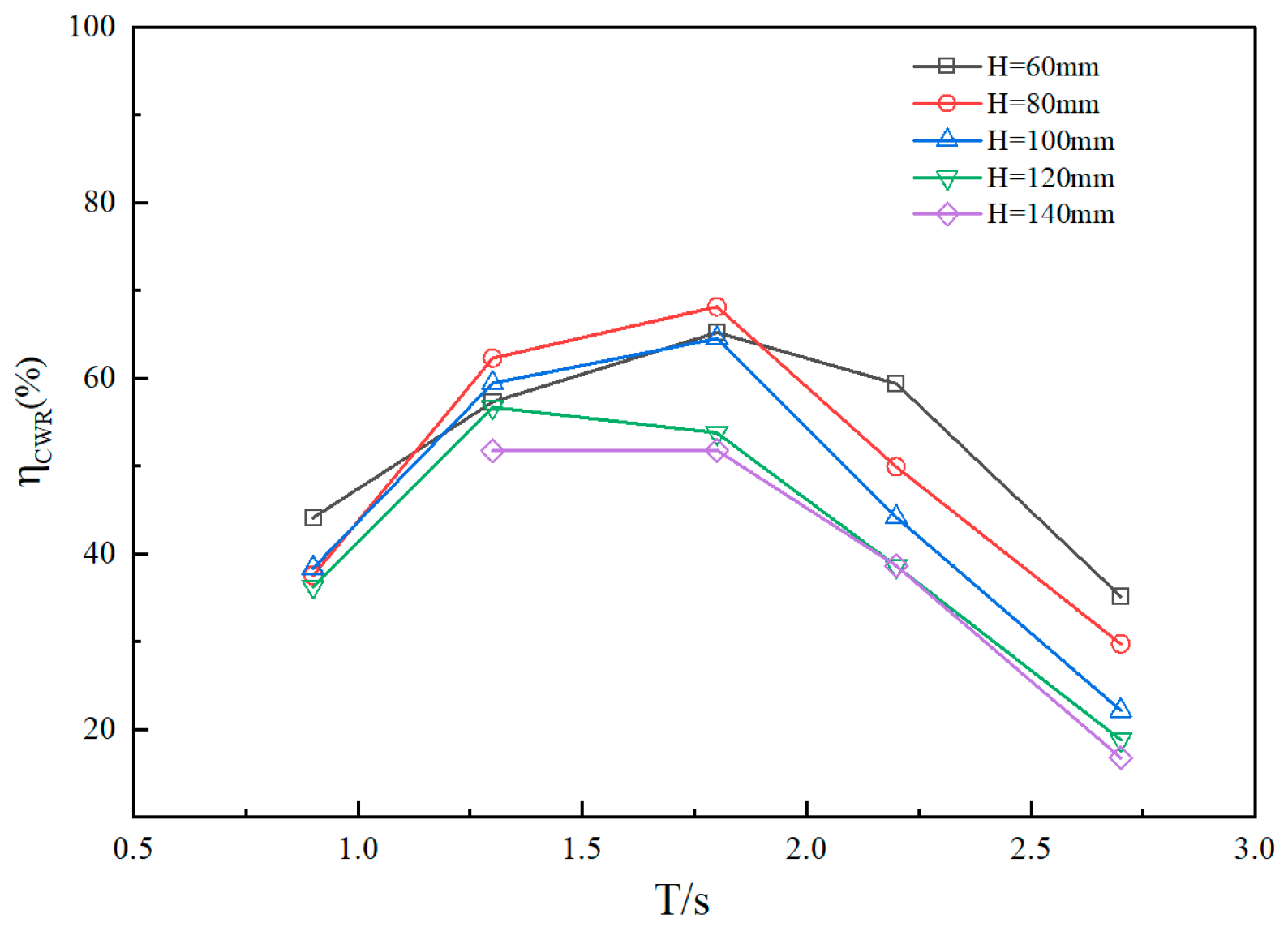
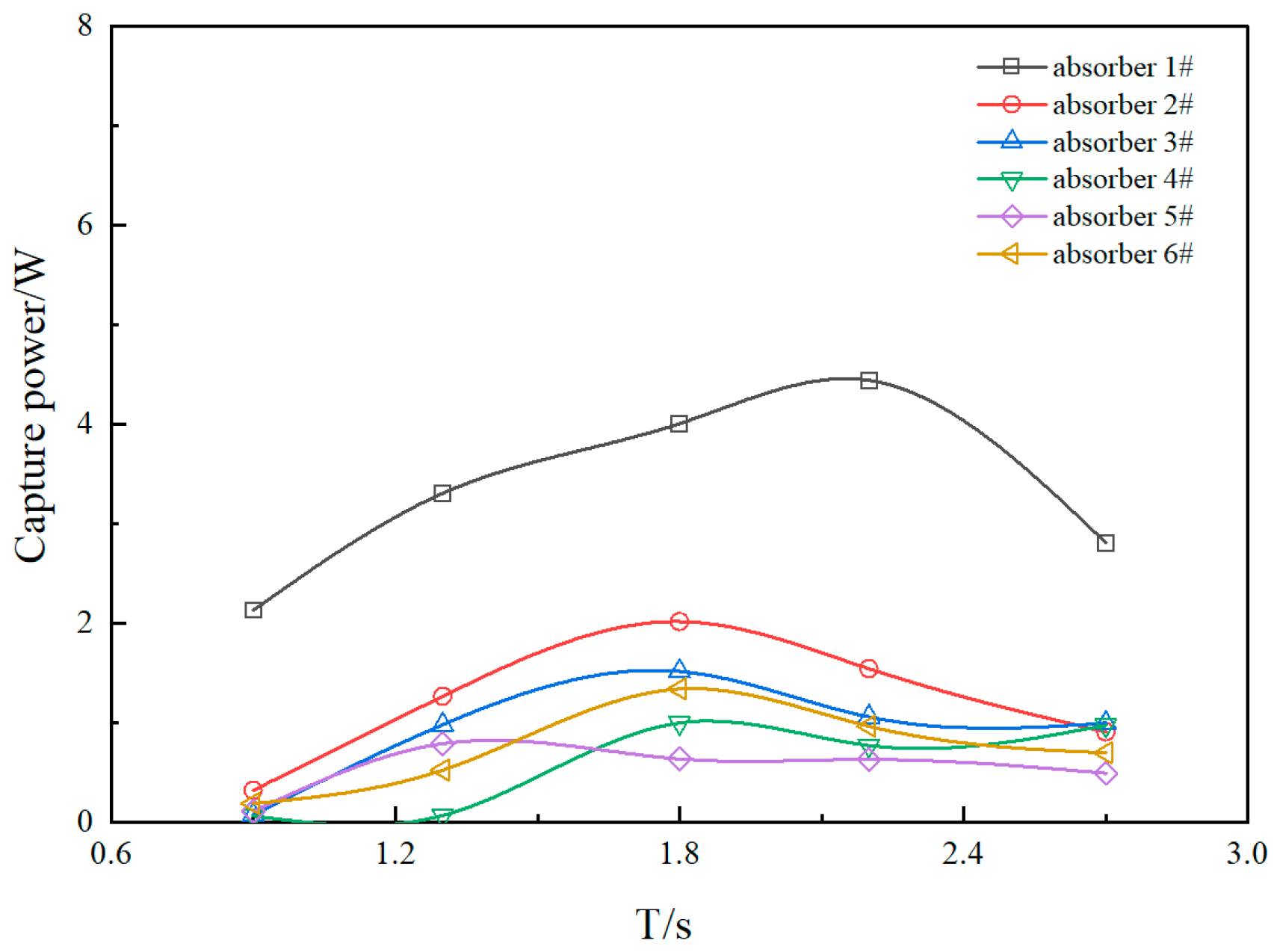
4.2. Effect of Wave Period
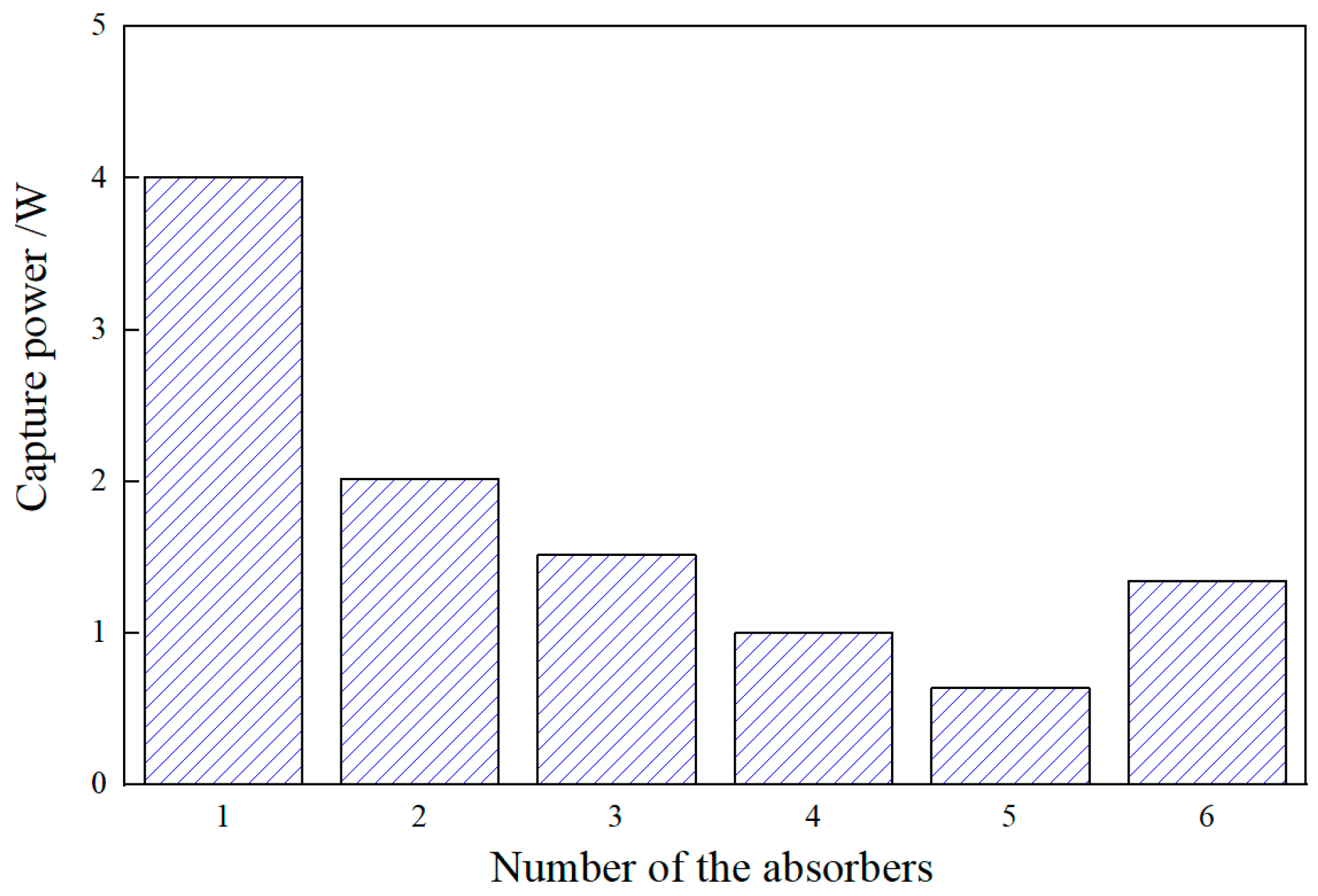
4.3. Effect of Freedom
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| CFD | computational fluid dynamics |
| CWR | capture width ratio |
| DOF | degrees of freedom |
| MB-MDOF | multi-body multi-degree-of-freedom |
| OB | oscillating buoy |
| OBWECs | oscillating buoy wave energy converters |
| OOBWEC | omnidirectional oscillating buoy WEC |
| OP | overtopping devices |
| OWC | oscillating water columns |
| PTO | power Take-Off |
| SDOF | single degree-of-freedom |
| SB-MDOF | systematically divided into two distinct classes: single-body multi-degree-of-freedom |
| WEC | wave energy converter |
References
- Leonard, M.D.; Michaelides, E.E.; Michaelides, D.N. Energy storage needs for the substitution of fossil fuel power plants with renewables. Renew. Energy 2020, 145, 951–962. [Google Scholar] [CrossRef]
- Guo, C.; Sheng, W.; De Silva, D.G.; Aggidis, G. A review of the levelized cost of wave energy based on a techno-economic model. Energies 2023, 16, 2144. [Google Scholar] [CrossRef]
- He, F.; Liu, Y.; Pan, J.; Ye, X.; Jiao, P. Advanced ocean wave energy harvesting: Current progress and future trends. J. Zhejiang Univ. Sci. 2023, 24, 91–108. [Google Scholar] [CrossRef]
- Seongho, A.; Vincent, S.N. Investigation of Mixed Long-Term Nonstationary Trends in Global Wave Energy Systems. J. Clean. Prod. 2024, 476, 143758. [Google Scholar] [CrossRef]
- Falcao, A.F.O. Wave energy utilization: A review of the technologies. Renew. Sustain. Energy 2010, 14, 899–918. [Google Scholar] [CrossRef]
- Shi, H.; Liu, Z. Research progress and development trend of ocean wave energy. Ocean. Sci. Technol. Feral. 2021, 39, 22–28. [Google Scholar]
- Farrok, O.; Farah, M.M.; Islam, M.R. Introduction to the Principles of Wave Energy Conversion. In Oceanic Wave Energy Conversion; Springer: Singapore, 2024; pp. 1–15. [Google Scholar]
- López, I.; Andreu, J.; Ceballos, S.; de Alegría, I.M.; Kortabarria, I. Review of wave energytechnologies and the necessary power-equipment. Renew. Sustain. Energy Rev. 2013, 27, 413–434. [Google Scholar] [CrossRef]
- Ma, Y.; Tan, Q.; Niu, B.; Hu, C.; Men, X. Research progress of floating multi-energy combined power generation device. Chin. J. Ship Res. 2024, 19, 3–20. (In Chinese) [Google Scholar]
- Parsa, K.; Mekhiche, M.; Sarokhan, J.; Stewart, D. Performance of OPT’s Commercial PB3 Power Buoy During 2016 Ocean Deployment and Comparison to Projected Model Results. In Proceedings of the ASME 2017 36th International Conference on Ocean, Offshore and Arctic Engineering, Trondheim, Norway, 25–30 June 2017. [Google Scholar]
- Waters, R.; Stålberg, M.; Danielsson, O.; Svensson, O.; Gustafsson, S.; Strömstedt, E.; Eriksson, M.; Sundberg, J.; Leijon, M. Experimental results from sea trials of an offshore wave energy system. Appl. Phys. Lett. 2007, 90, 034105. [Google Scholar] [CrossRef]
- Weber, J.; Mouwen, F.; Parish, A.; Robertson, D. Wavebob-research & development network and tools in context of systems engineerings. In Proceedings of the 8th EuroPean Wave Tidal Energy Conference, Uppsala, Sweden, 7 September 2009; pp. 416–420. [Google Scholar]
- Dalton, G.J.; Alcorn, R.; Lewis, T. Case study feasibility analysis of the pelamis wave energyconvertor in lreland, portugal and north america. Renew. Energy 2010, 35, 443–455. [Google Scholar] [CrossRef]
- Palha, A.; Mendes, L.; Fortes, C.J.; Brito-Melo, A.; Sarmento, A. The impact of wave energy farms in the shorelinewave climate: Portuguese pilot zone case study using pelamis energy wave devices. Renew. Energy 2010, 35, 62–77. [Google Scholar] [CrossRef]
- Zhang, C.; Huang, S.; You, Y.G.; Sheng, S.W. Numerical research and open sea tests of a 100 kW modified Edinburgh Duck wave energy convertor. Front. Energy Res. 2019, 7, 9. [Google Scholar] [CrossRef]
- OPT. Ocean Power Technologies Announces Results for the Fiscal Fourth Quarter and Full Year Ended 30 April 2014; OPT: Richmond, CA, USA, 2014. [Google Scholar]
- Murray, R.; Rastegar, J.; Ahmadian, M.; Ghasemi-Nejhad, M.N. Novel Two-Stage Piezoelectric-Based Ocean Wave Energy Harvesters for Moored or Unmoored Buoys. In Proceedings of the Active and Passive Smart Structures and Integrated System 2009, San Diego, CA, USA, 8–12 March 2009. [Google Scholar]
- Zhang, Y.Q.; You, Y.G.; Shneng, S.W.; Wang, W.S. Analysis and optimization of hydrodynamic performance of eagle wave energy generator. Ship Mech. 2017, 21, 533–540. [Google Scholar]
- Sheng, S.W.; Zhang, Y.Q.; Wang, K.L.; Ye, Y.; You, Y.G. Research on power generation system of eagle wave power plant. Renew. Energy 2015, 33, 1422–1426. [Google Scholar]
- Shi, H.; Huang, S.; Cao, F. Hydrodynamic performance and power absorption of a multi-freedom buoy wave energy device. Ocean. Eng. 2019, 172, 541–549. [Google Scholar] [CrossRef]
- Azam, A.; Ahmed, A.; Li, H.; Tairab, A.M.; Jia, C.; Li, N.; Zhang, Z. Design and analysis of the optimal spinning top-shaped buoy for wave energy harvesting in low energy density seas for sustainable marine aquaculture. Ocean. Eng. 2022, 255, 111434. [Google Scholar] [CrossRef]
- Xi, L.T.; Li, X.F.; Song, L.J.; Yang, S.B.; Huang, Z.Z. Simulation and Evaluation of Wave Energy Resources in the South China Sea. Renew. Energy 2021, 39, 561–568. [Google Scholar]
- Zhang, Y.; You, Y.; Hu, J.; Wu, B. Investigation of wave energy resource evaluation for A finite water depth at random wave sea states. Acta Energiae Solaris Sin. 2012, 33, 1060–1066. [Google Scholar]
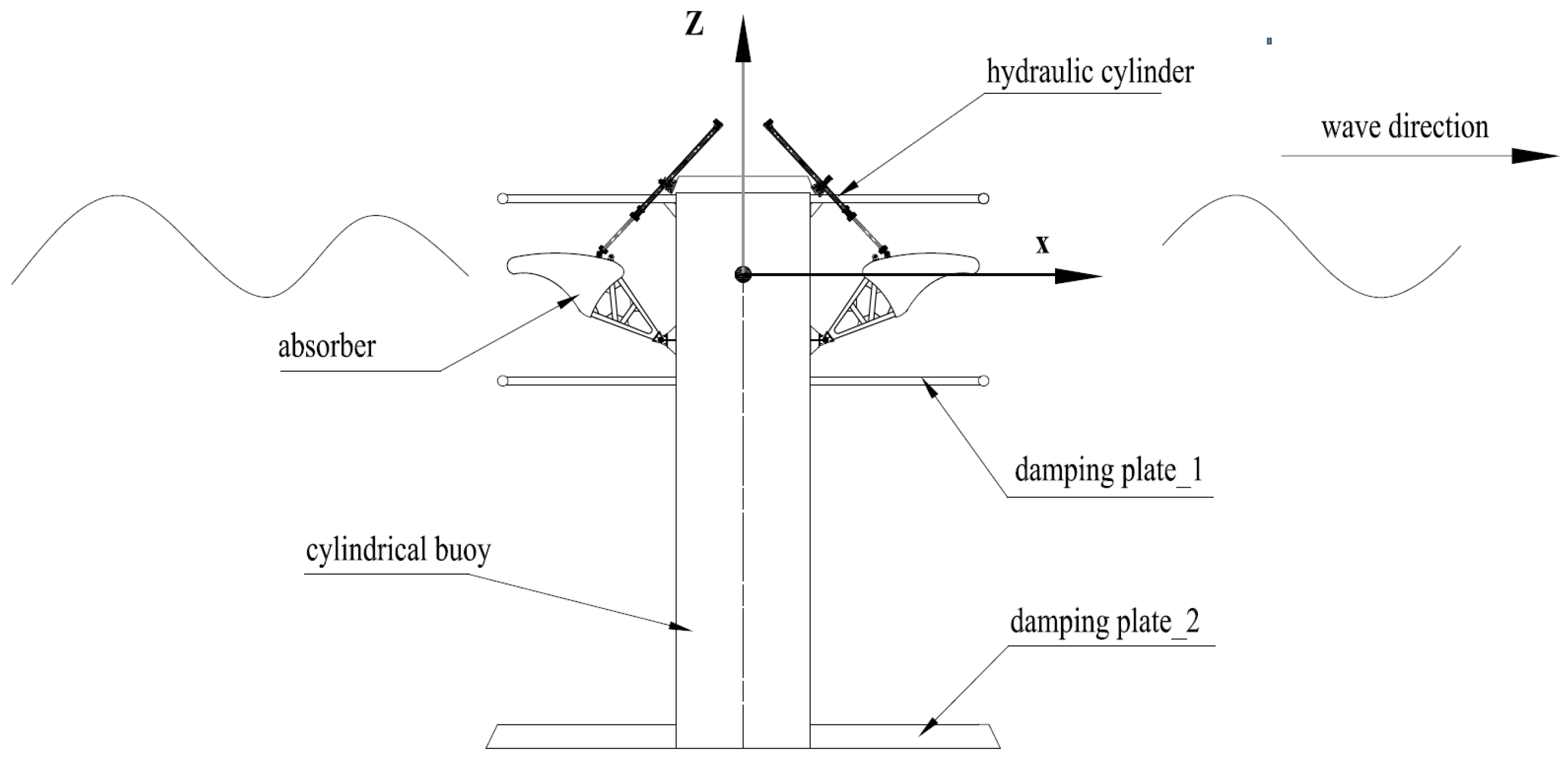


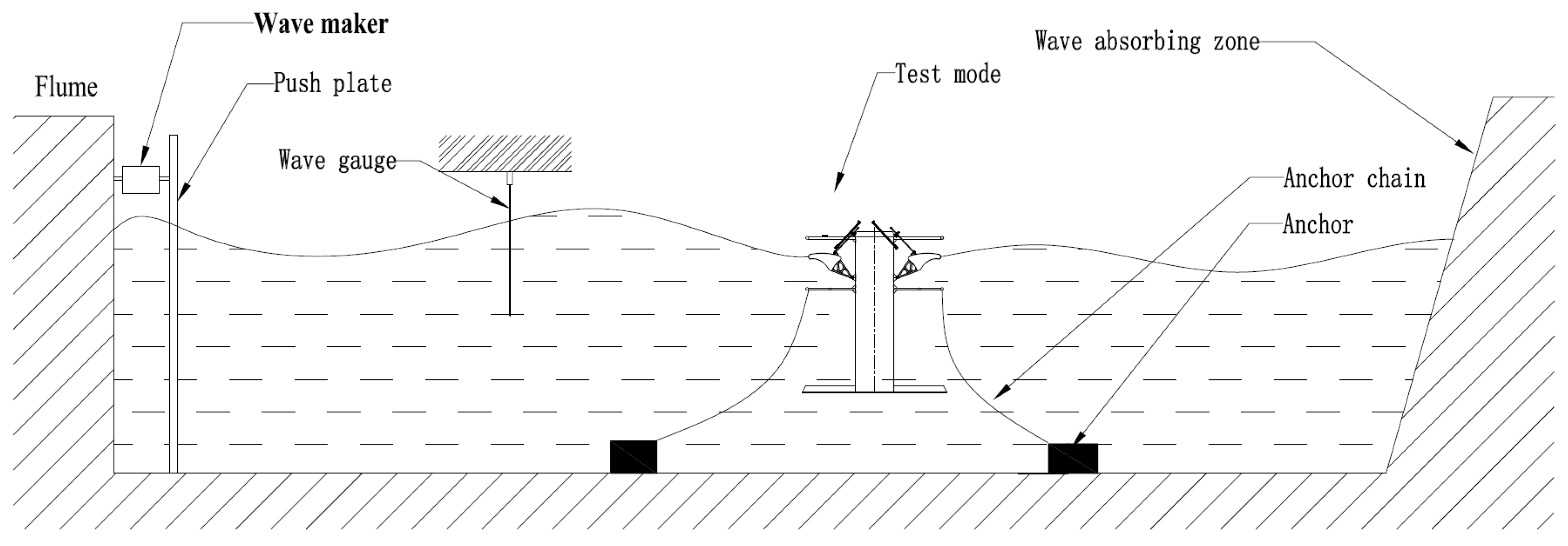
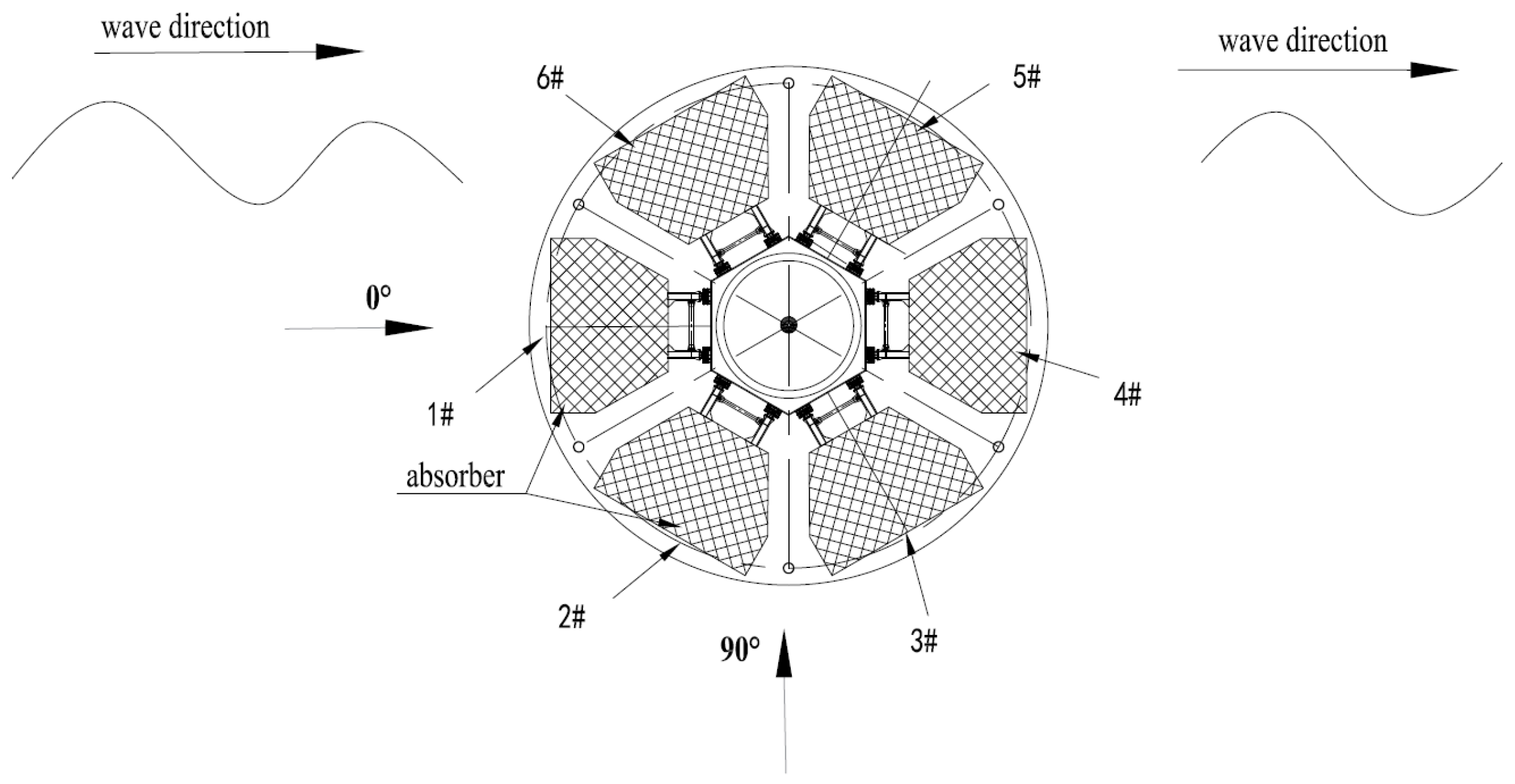

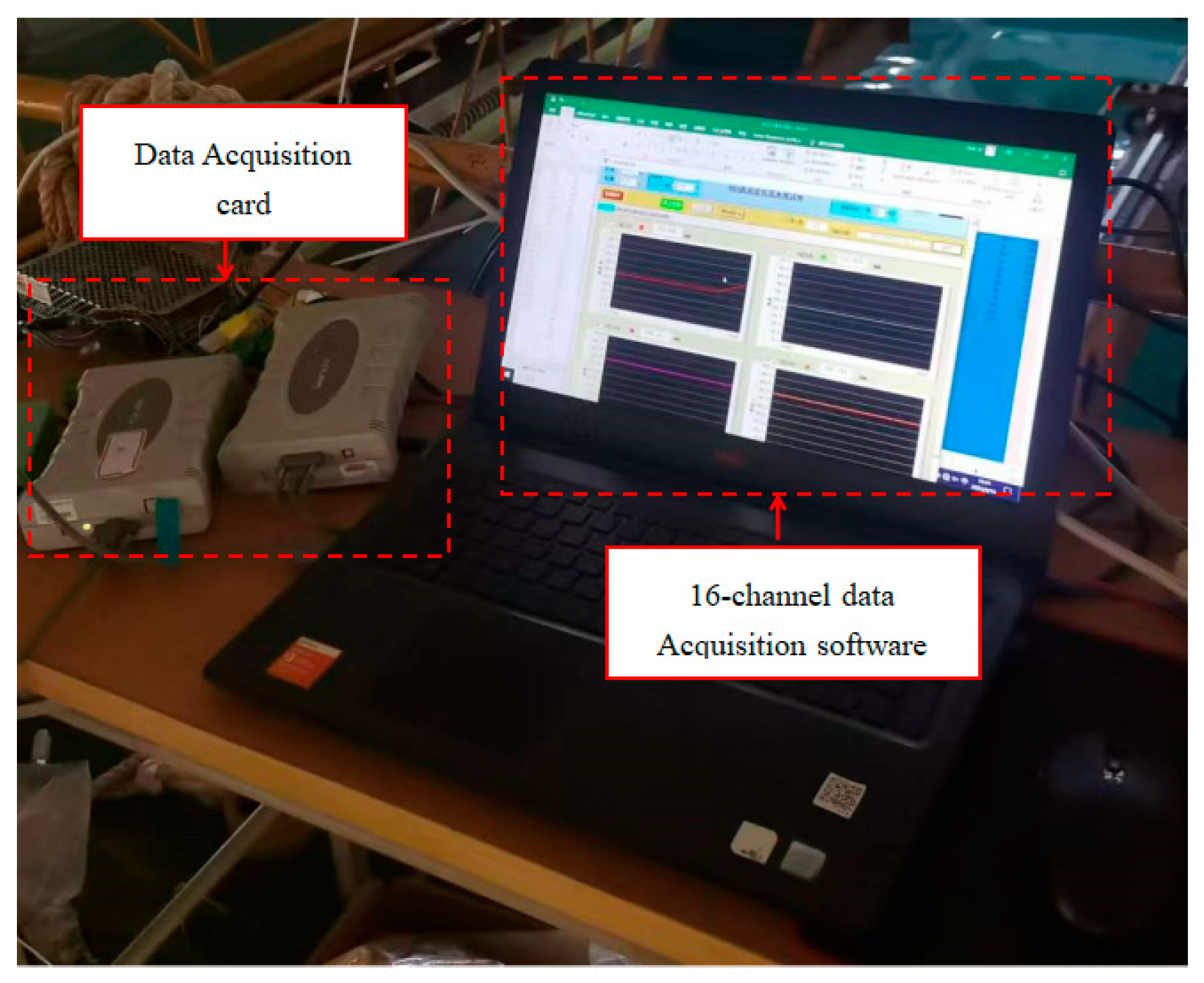

| NO. | Parameters | Data |
|---|---|---|
| 1 | Total length (m) | 2.14 |
| 2 | Total width (m) | 2.14 |
| 3 | Total height (m) | 2.38 |
| 4 | Operating draft (m) | 1.97 |
| 5 | Number of absorbers | 6 |
| 6 | Width of absorbers (m) | 0.8 |
| 7 | Weight (kg) | 360 |
| Physical Quantities | Symbolic | Ratio |
|---|---|---|
| linear scale | Ls/Lm | |
| period | Ts/Tm | |
| area | As/Am | |
| volumes | ||
| force | Fs/Fm | |
| power | Ps/Pm |
| Case | Real Sea | Wave Flume | ||
|---|---|---|---|---|
| Mean Height (m) | Mean Period (s) | Mean Height (m) | Mean Period (s) | |
| 1–4 | 0.3~0.6 | 2 | 0.06~0.12 | 0.9 |
| 5–9 | 0.3~0.7 | 3 | 0.06~0.14 | 1.3 |
| 10–14 | 0.3~0.7 | 4 | 0.06~0.14 | 1.8 |
| 15–19 | 0.3~0.7 | 5 | 0.06~0.14 | 2.2 |
| 20–24 | 0.3~0.7 | 6 | 0.06~0.14 | 2.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Liu, J.; Wang, Z.; Lin, Z.; Zhang, G.; Zhang, Y. Experimental Investigation of the Capture Performance Model for a Novel Omnidirectional Wave Energy Converter. Energies 2025, 18, 4729. https://doi.org/10.3390/en18174729
Wang W, Liu J, Wang Z, Lin Z, Zhang G, Zhang Y. Experimental Investigation of the Capture Performance Model for a Novel Omnidirectional Wave Energy Converter. Energies. 2025; 18(17):4729. https://doi.org/10.3390/en18174729
Chicago/Turabian StyleWang, Wensheng, Jingfeng Liu, Zhenpeng Wang, Zhaoji Lin, Guoyu Zhang, and Yaqun Zhang. 2025. "Experimental Investigation of the Capture Performance Model for a Novel Omnidirectional Wave Energy Converter" Energies 18, no. 17: 4729. https://doi.org/10.3390/en18174729
APA StyleWang, W., Liu, J., Wang, Z., Lin, Z., Zhang, G., & Zhang, Y. (2025). Experimental Investigation of the Capture Performance Model for a Novel Omnidirectional Wave Energy Converter. Energies, 18(17), 4729. https://doi.org/10.3390/en18174729





