Combined Effect of ABL Profile and Rotation in Wind Turbine Wakes: New Three-Dimensional Wake Model
Abstract
1. Introduction
2. Reference Analytical Wake Models
2.1. Turbulence Optimized Park Model
2.2. Bastankhah Wake Model
2.3. Zong Wake Model
3. Analysis of Far Wakes Under ABL Inflow and Rotation
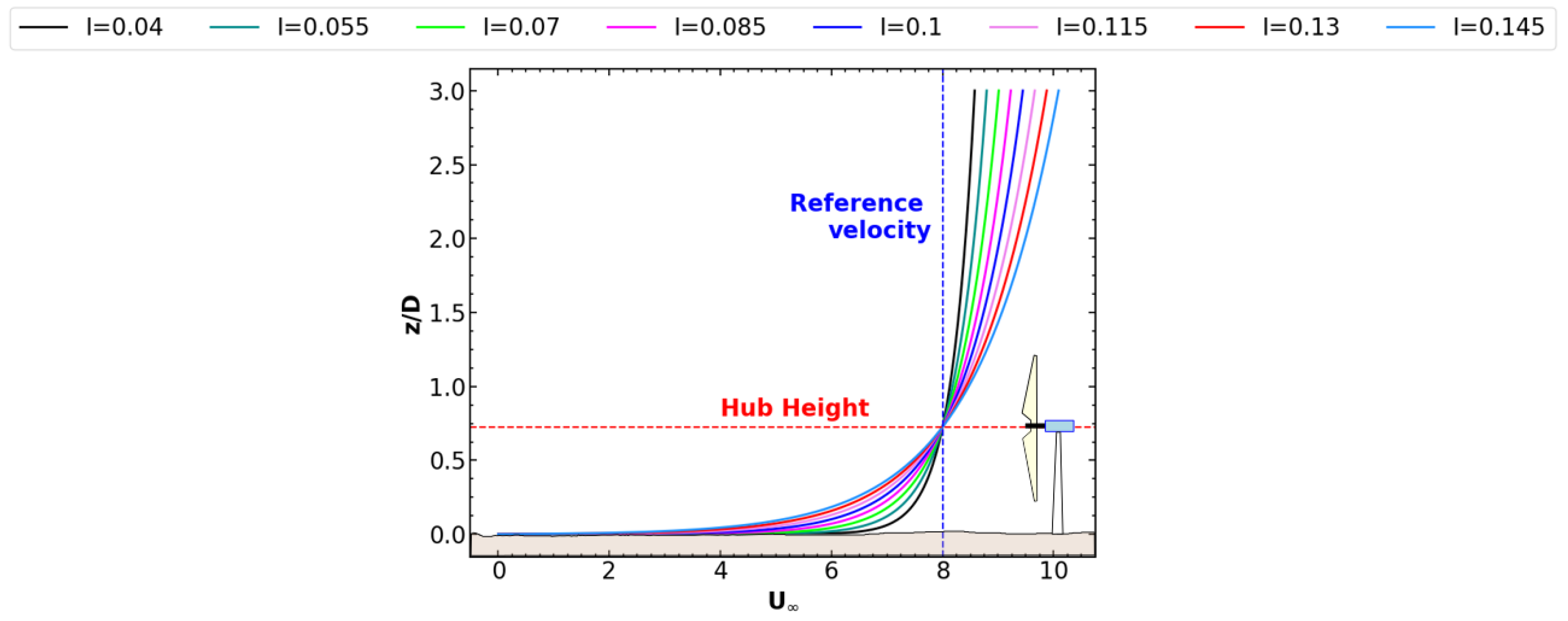
3.1. Numerical Setup
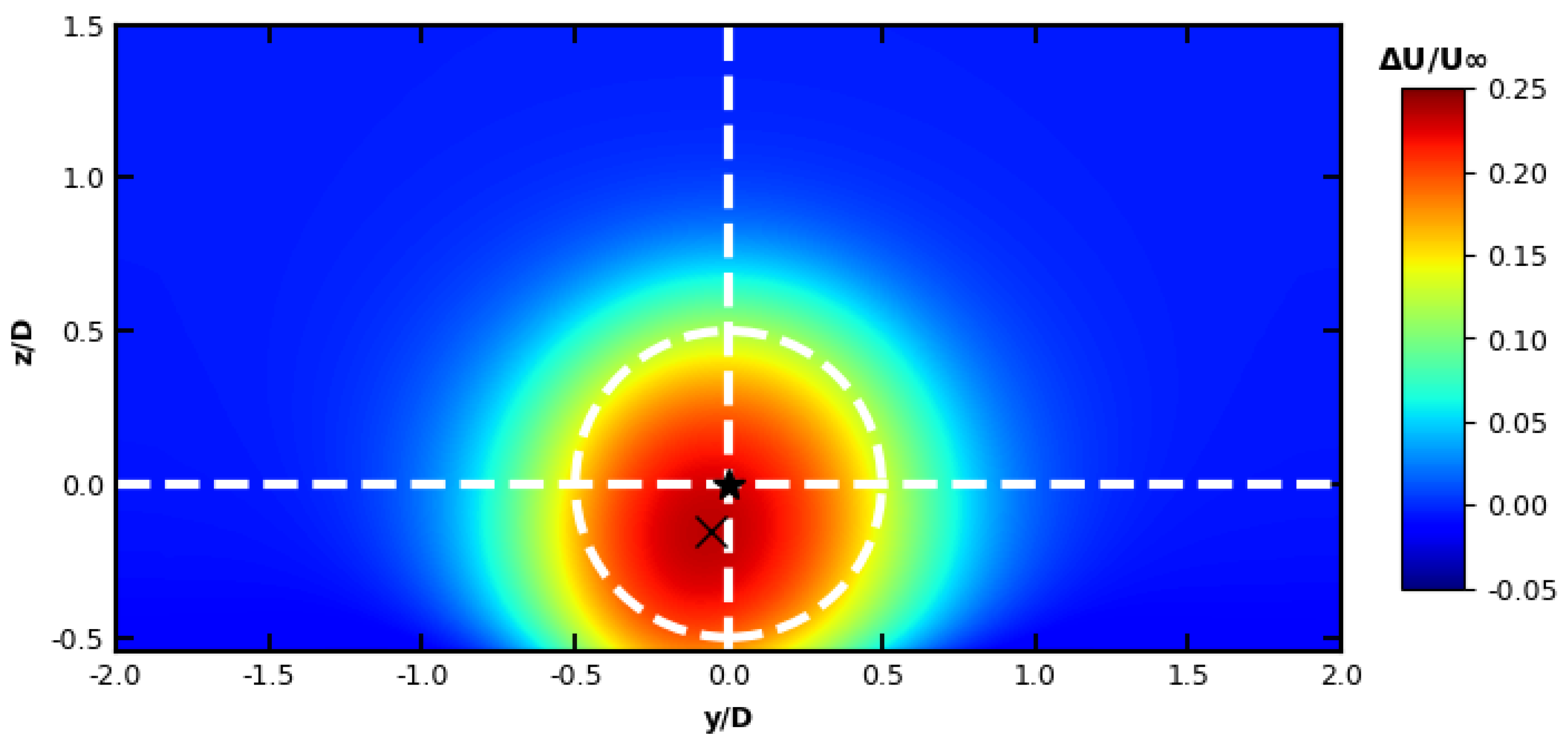
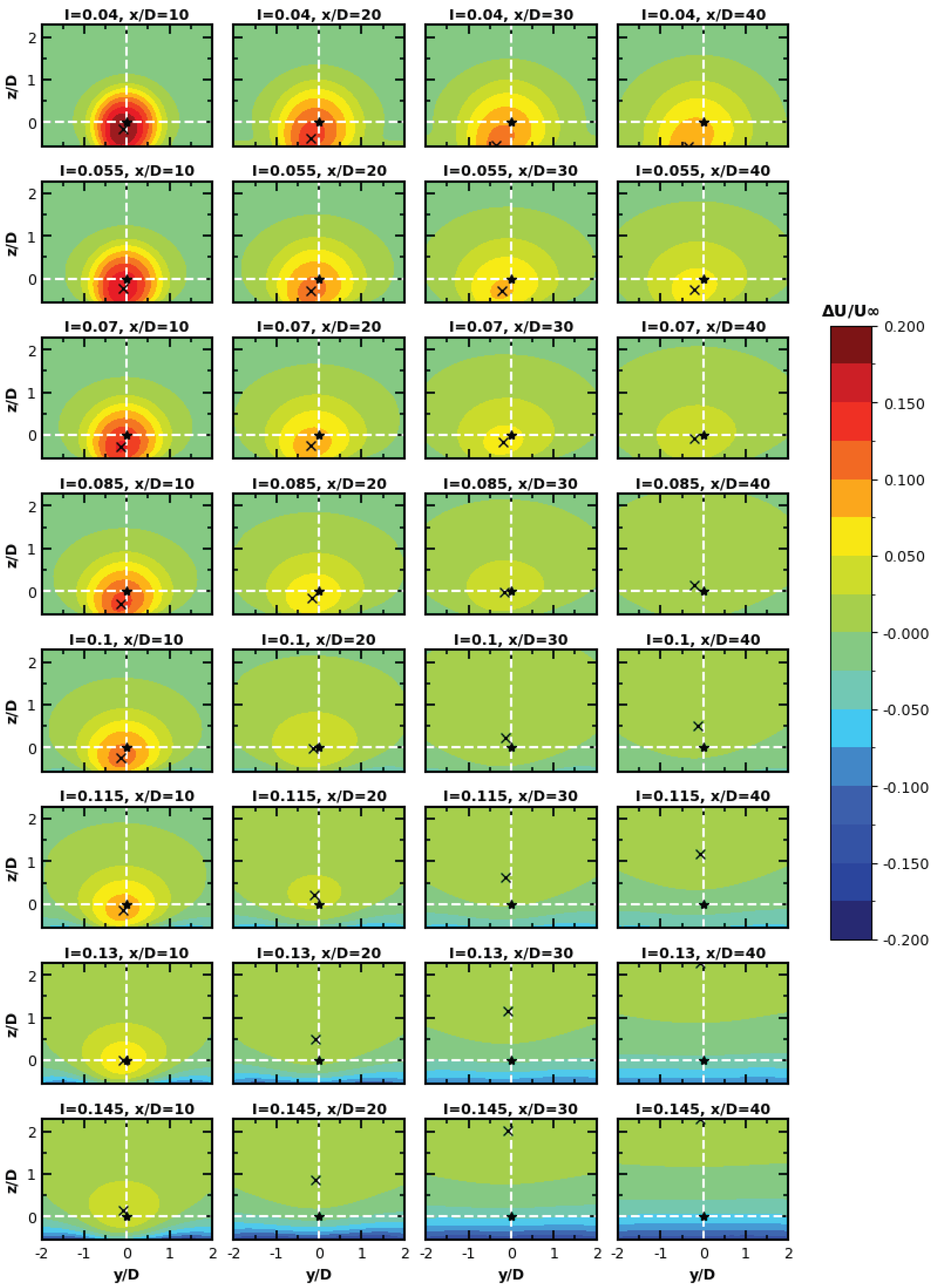
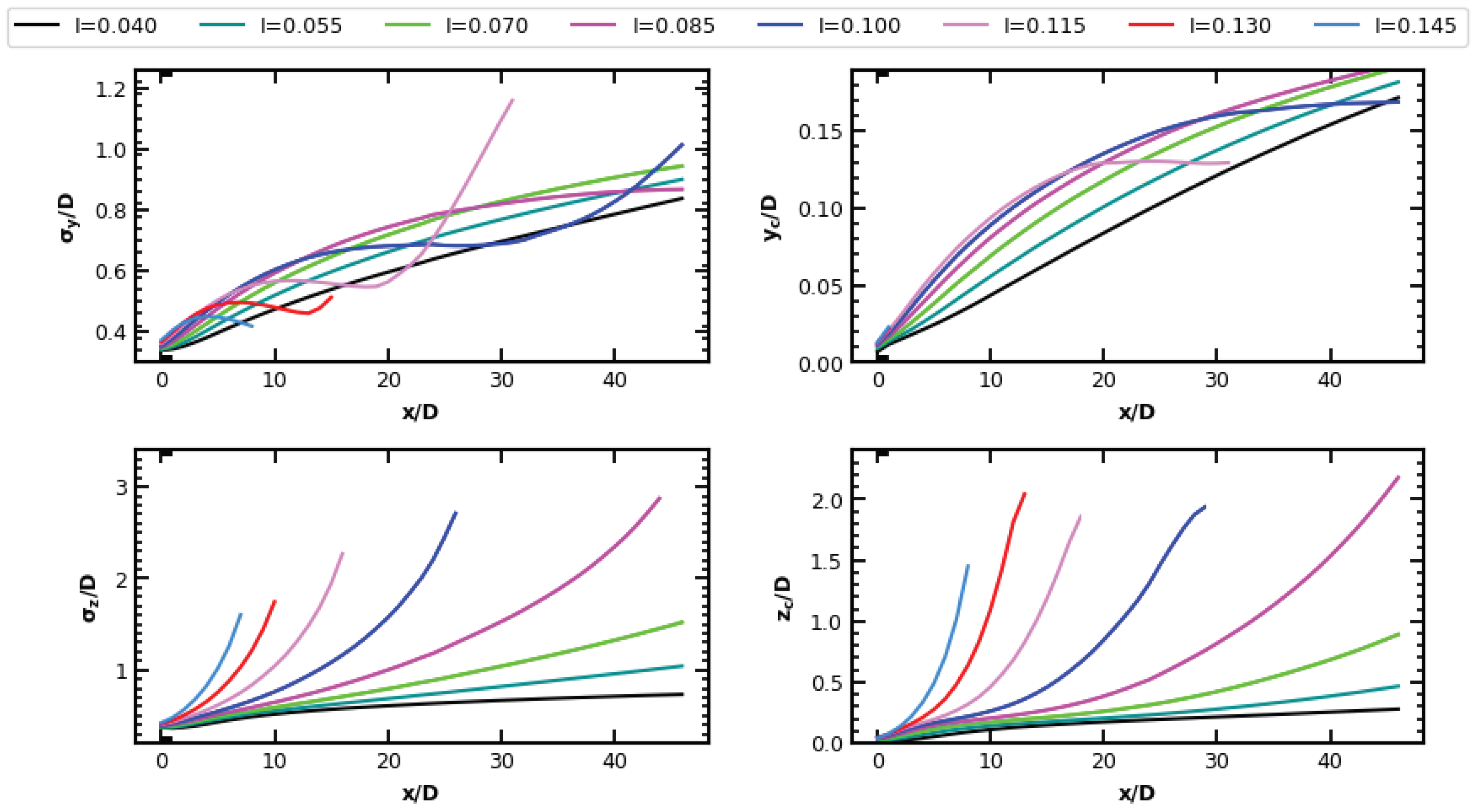
3.2. Wake Center Shift
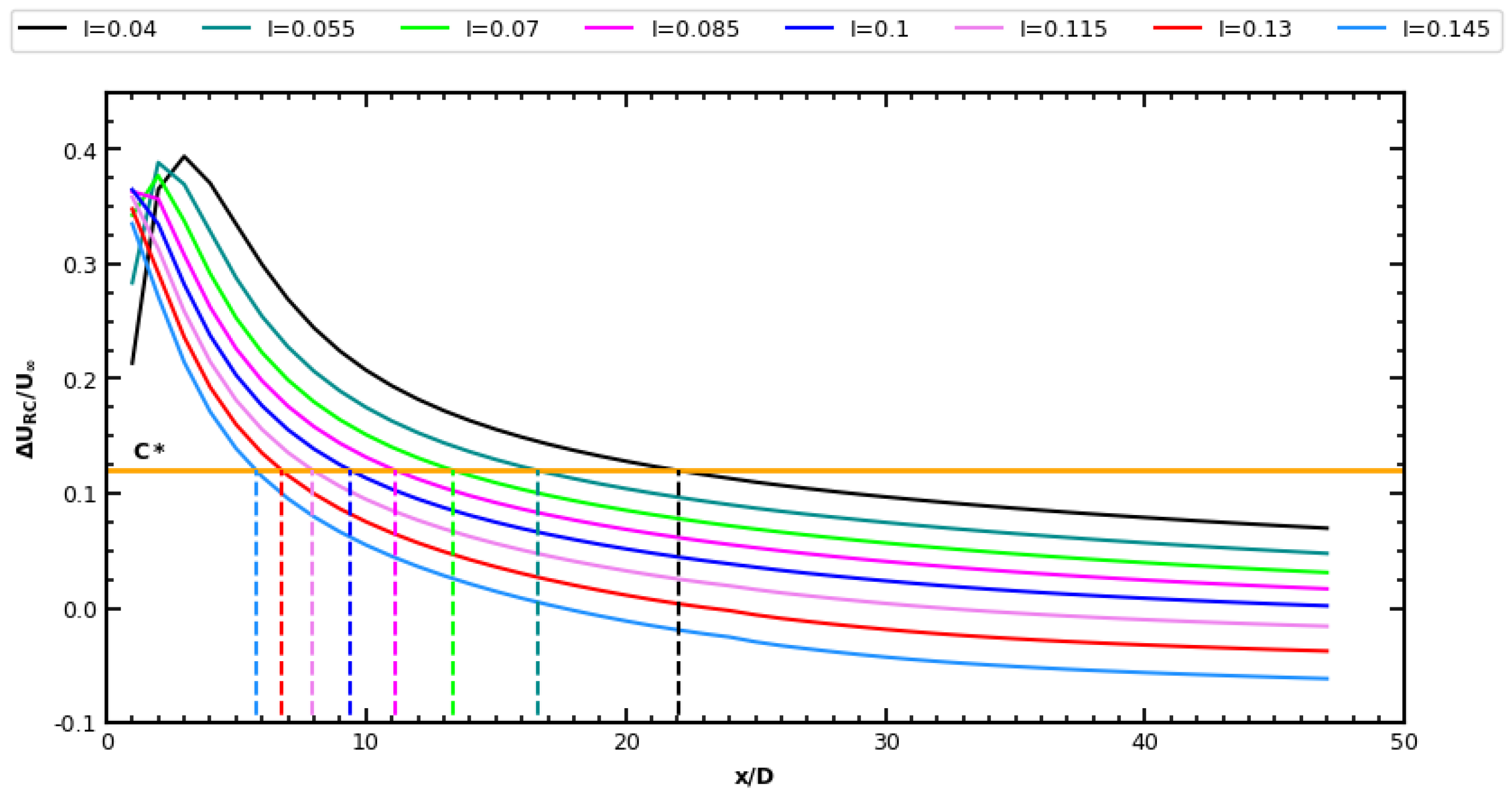
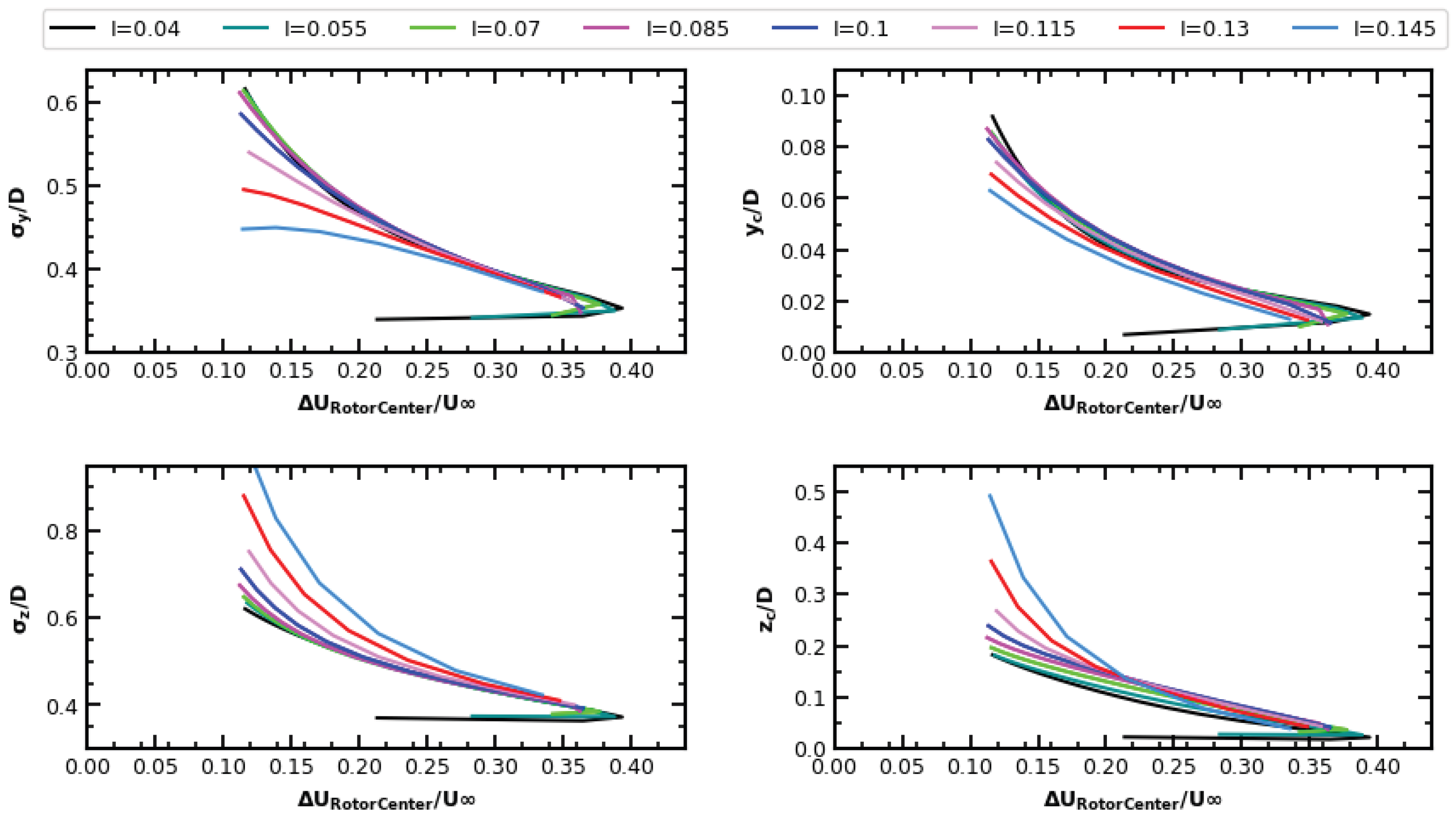
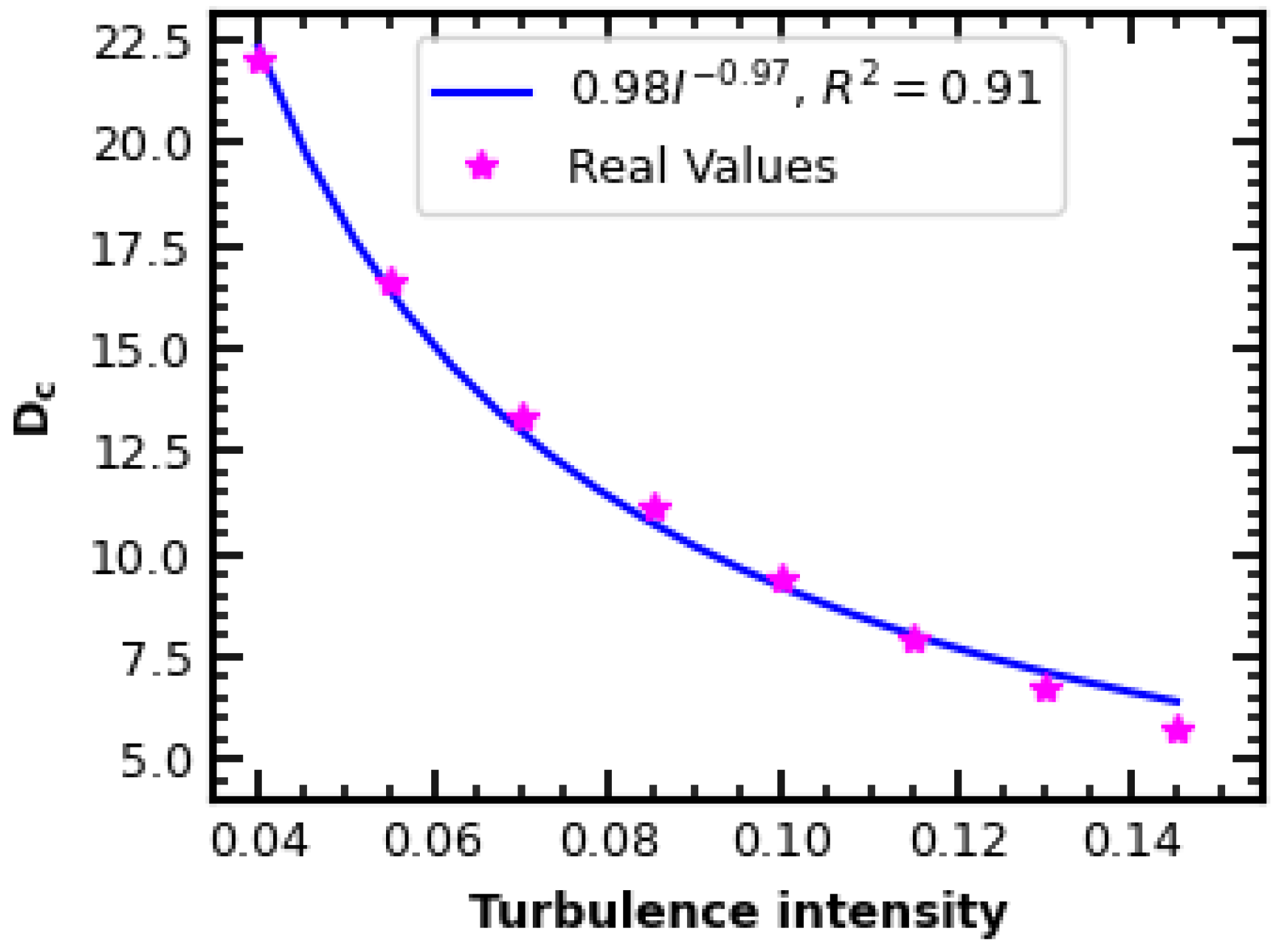
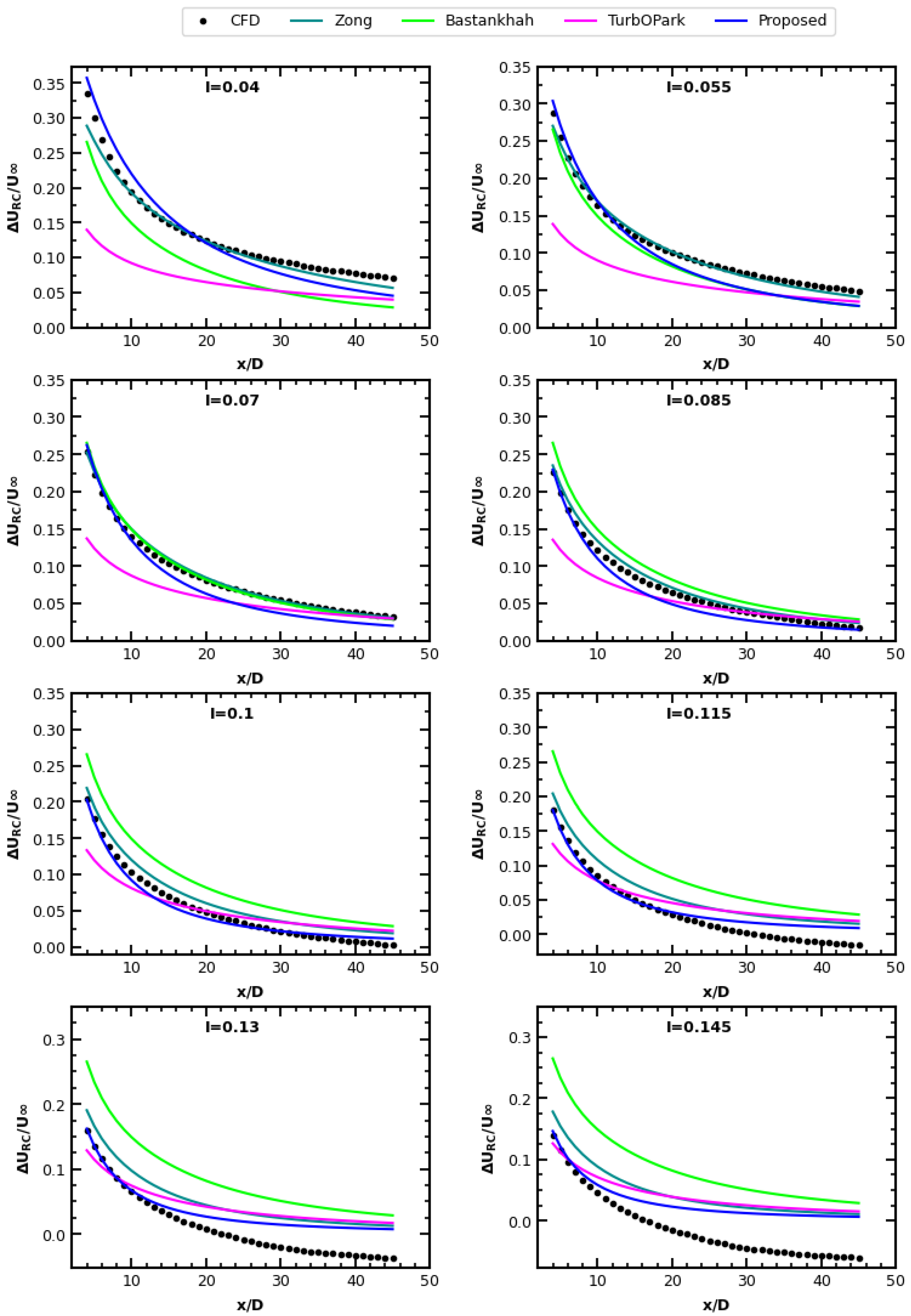
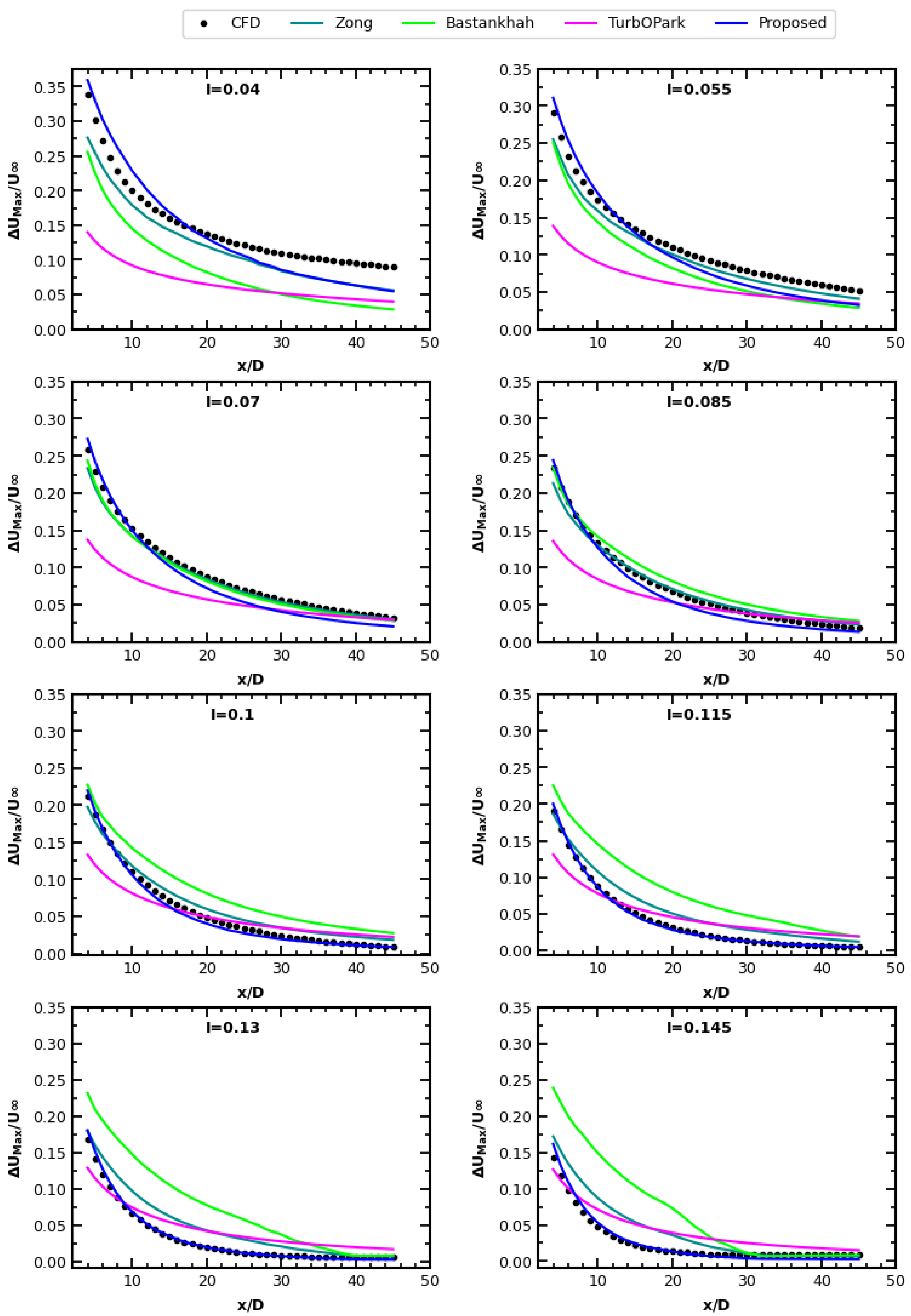
3.3. Wake Scaling in Terms of Turbulence
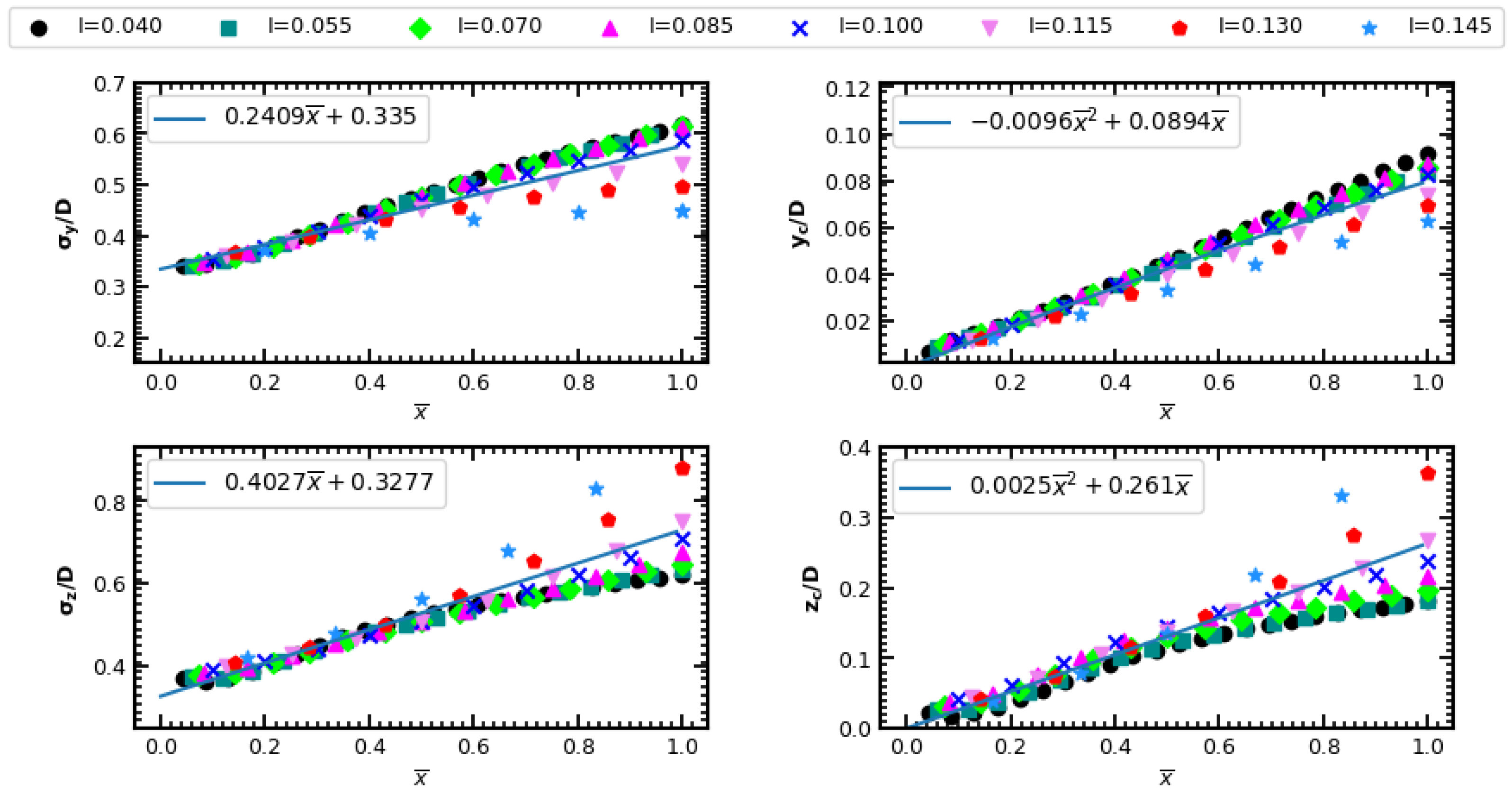
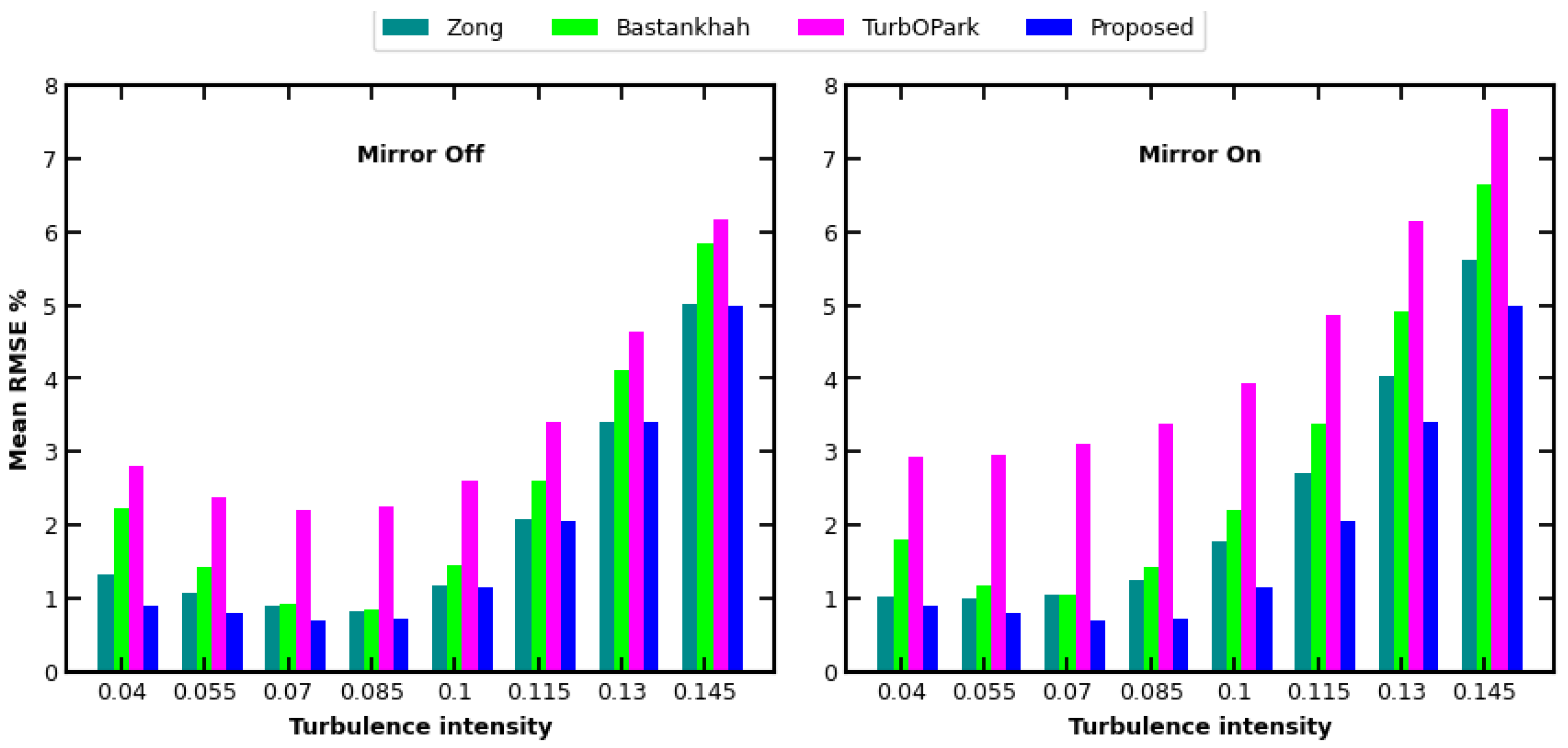
4. New 3D Gaussian Wake Model
5. Conclusions and Perspectives
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
References
- Brindley, G.; Willems, G.; Ramirez, L.; Cole, P.; Klonari, V.; Bickley, J. Wind Energy in Europe 2023 Statistics and the Outlook for 2024–2030; Technical Report; Wind Europe: Brussels, Belgium, 2023. [Google Scholar]
- Joyce Lee, F.Z. Global Wind Report 2022; Technical Report; Global Wind Energy Council (GWEC): Brussels, Belgium, 2022. [Google Scholar]
- Platis, A.; Siedersleben, S.K.; Bange, J.; Lampert, A.; Bärfuss, K.; Hankers, R.; Cañadillas, B.; Foreman, R.; Schulz-Stellenfleth, J.; Djath, B.; et al. First in situ evidence of wakes in the far field behind offshore wind farms. Sci. Rep. 2018, 8, 2163. [Google Scholar] [CrossRef]
- Moriarty, P.; Hamilton, N.; Debnath, M.; Herges, T.; Isom, B.; Lundquist, J.K.; Maniaci, D.; Naughton, B.; Pauly, R.; Roadman, J.; et al. American WAKE Experiment (AWAKEN); NREL: Golden, CO, USA, 2020. [Google Scholar]
- 4C Offshore. 4C Offshore—Offshore Wind Farm Map. 2023. Available online: https://map.4coffshore.com/offshorewind (accessed on 8 December 2023).
- Letsch, B.; Barriatto, L. Long Distance Offshore Wakes. Brazil Windpower. 2023. Available online: https://abeeolica.org.br/wp-content/uploads/2023/11/4.2AP-1690897876-Long-offshore-wakes_BWP2023_Reformatado.pdf (accessed on 21 May 2025).
- Schneemann, J.; Rott, A.; Dörenkämper, M.; Steinfeld, G.; Kühn, M. Cluster wakes impact on a far-distant offshore wind farm’s power. Wind. Energy Sci. 2020, 5, 29–49. [Google Scholar] [CrossRef]
- Technology, P. Formosa 1 Offshore Wind Farm. 2019. Available online: https://www.power-technology.com/projects/formosa-1-offshore-wind-farm/ (accessed on 8 December 2023).
- Cañadillas, B.; Foreman, R.; Barth, V.; Siedersleben, S.; Lampert, A.; Platis, A.; Djath, B.; Schulz-Stellenfleth, J.; Bange, J.; Emeis, S.; et al. Offshore wind farm wake recovery: Airborne measurements and its representation in engineering models. Wind Energy 2020, 23, 1249–1265. [Google Scholar] [CrossRef]
- da Silva, A.I.R.D.; Leite, G.d.N.P.; Araújo, A.M.; Villa, A.A.O.; da Costa, A.C.A.; Moreno, C.A.S.; Weschenfelder, F.; Droguett, E.L. Aerodynamic interference caused by wake effects of repowered wind farms on the annual energy production in neighboring wind farms. Sustain. Energy Technol. Assess. 2024, 64, 103704. [Google Scholar]
- Feroz, R.M.A.; Javed, A.; Syed, A.H.; Kazmi, S.A.A.; Uddin, E. Wind speed and power forecasting of a utility-scale wind farm with inter-farm wake interference and seasonal variation. Sustain. Energy Technol. Assess. 2020, 42, 100882. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, X. Upward Shift of Wind Turbine Wakes in Large Wind Farms. Energies 2023, 16, 8051. [Google Scholar] [CrossRef]
- Zhang, F.; Yang, X.; He, G. Multiscale analysis of a very long wind turbine wake in an atmospheric boundary layer. Phys. Rev. Fluids 2023, 8, 104605. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Chaouat, B. The state of the art of hybrid RANS/LES modeling for the simulation of turbulent flows. Flow Turbul. Combust. 2017, 99, 279–327. [Google Scholar] [CrossRef]
- Porté-Agel, F.; Bastankhah, M.; Shamsoddin, S. Wind-Turbine and Wind-Farm Flows: A Review. Bound.-Layer Meteorol. 2020, 174, 1–59. [Google Scholar] [CrossRef]
- Tian, L.; Song, Y.; Zhao, N.; Shen, W.; Zhu, C.; Wang, T. Effects of turbulence modelling in AD/RANS simulations of single wind & tidal turbine wakes and double wake interactions. Energy 2020, 208, 118440. [Google Scholar]
- Vanderwende, B.J.; Kosović, B.; Lundquist, J.K.; Mirocha, J.D. Simulating effects of a wind-turbine array using LES and RANS. J. Adv. Model. Earth Syst. 2016, 8, 1376–1390. [Google Scholar] [CrossRef]
- Katic, I.; Højstrup, J.; Jensen, N. A Simple Model for Cluster Efficiency. Eur. Wind. Energy Assoc. Conf. Exhib. 1987, 1, 407–410. [Google Scholar]
- Frandsen, S.; Barthelmie, R.; Pryor, S.; Rathmann, O.; Larsen, S.; Højstrup, J.; Thøgersen, M. Analytical modelling of wind speed deficit in large offshore wind farms. Wind Energy 2006, 9, 39–53. [Google Scholar] [CrossRef]
- Larsen, G. A Simple Stationary Semi-Analytical Wake Model; Number 1713(EN) in Denmark. Forskningscenter Risoe; Risoe-R, Risø National Laboratory for Sustainable Energy, Technical University of Denmark: Lyngby, Denmark, 2009. [Google Scholar]
- Bastankhah, M.; Porté-Agel, F. A new analytical model for wind-turbine wakes. Renew. Energy 2014, 70, 116–123. [Google Scholar] [CrossRef]
- Niayifar, A.; Porté-Agel, F. Analytical modeling of wind farms: A new approach for power prediction. Energies 2016, 9, 741. [Google Scholar] [CrossRef]
- Pedersen, J.G.; Svensson, E.; Poulsen, L.; Nygaard, N.G. Turbulence Optimized Park model with Gaussian wake profile. J. Phys. Conf. Ser. 2022, 2265, 022063. [Google Scholar] [CrossRef]
- Zong, H.; Porté-Agel, F. A momentum-conserving wake superposition method for wind farm power prediction. J. Fluid Mech. 2020, 889, A8. [Google Scholar] [CrossRef]
- Vahidi, D.; Porté-Agel, F. A new streamwise scaling for wind turbine wake modeling in the atmospheric boundary layer. Energies 2022, 15, 9477. [Google Scholar] [CrossRef]
- Souaiby, M.; Porté-Agel, F. An improved analytical framework for flow prediction inside and downstream of wind farms. Renew. Energy 2024, 225, 120251. [Google Scholar] [CrossRef]
- Carbajo Fuertes, F.; Markfort, C.D.; Porté-Agel, F. Wind turbine wake characterization with nacelle-mounted wind lidars for analytical wake model validation. Remote Sens. 2018, 10, 668. [Google Scholar] [CrossRef]
- Barasa, M.; Xuemin, L.; Zhang, Y.; Weiming, X. The impact of the atmospheric boundary layer on the asymmetric wake profile: A bivariate analysis. Sustain. Energy Technol. Assess. 2022, 53, 102563. [Google Scholar] [CrossRef]
- Lopes, A.M.; Vicente, A.H.; Sánchez, O.H.; Daus, R.; Koch, H. Operation assessment of analytical wind turbine wake models. J. Wind. Eng. Ind. Aerodyn. 2022, 220, 104840. [Google Scholar] [CrossRef]
- Snaiki, R.; Makki, S. A new analytical wind turbine wake model considering the effects of coriolis force and yawed conditions. J. Wind. Eng. Ind. Aerodyn. 2024, 250, 105767. [Google Scholar] [CrossRef]
- Larsen, G.C.; Madsen, H.A.; Thomsen, K.; Larsen, T.J. Wake meandering: A pragmatic approach. Wind. Energy Int. J. Prog. Appl. Wind. Power Convers. Technol. 2008, 11, 377–395. [Google Scholar] [CrossRef]
- Li, Z.; Yang, X. Resolvent-based motion-to-wake modelling of wind turbine wakes under dynamic rotor motion. J. Fluid Mech. 2024, 980, A48. [Google Scholar] [CrossRef]
- Brugger, P.; Markfort, C.D.; Porté-Agel, F. Improvements to the dynamic wake meandering model by incorporating the turbulent Schmidt number. Wind. Energy Sci. 2024, 9, 1363–1379. [Google Scholar] [CrossRef]
- Nygaard, N.G.; Steen, S.T.; Poulsen, L.; Pedersen, J.G. Modelling cluster wakes and wind farm blockage. J. Phys. Conf. Ser. 2020, 1618, 062072. [Google Scholar] [CrossRef]
- Bastankhah, M.; Porté-Agel, F. Experimental and theoretical study of wind turbine wakes in yawed conditions. J. Fluid Mech. 2016, 806, 506–541. [Google Scholar] [CrossRef]
- Greenshields, C. OpenFOAM v11 User Guide; The OpenFOAM Foundation: London, UK, 2023. [Google Scholar]
- Shih, T.H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-ε eddy viscosity model for high reynolds number turbulent flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Yang, Y.; Gu, M.; Chen, S.; Jin, X. New inflow boundary conditions for modelling the neutral equilibrium atmospheric boundary layer in computational wind engineering. J. Wind. Eng. Ind. Aerodyn. 2009, 97, 88–95. [Google Scholar] [CrossRef]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; National Renewable Energy Lab.(NREL): Golden, CO, USA, 2009. [Google Scholar] [CrossRef]
- Mikkelsen, R.F. Actuator Disc Methods Applied to Wind Turbines. Ph.D. Thesis, Technical University of Denmark, Kongens Lyngby, Denmark, 2004. [Google Scholar]
- Jimenez, A.; Crespo, A.; Migoya, E.; García, J. Advances in large-eddy simulation of a wind turbine wake. J. Phys. Conf. Ser. 2007, 75, 012041. [Google Scholar] [CrossRef]
- Navarro Diaz, G.P.; Otero, A.D.; Asmuth, H.; Sørensen, J.N.; Ivanell, S. Actuator line model using simplified force calculation methods. Wind. Energy Sci. 2023, 8, 363–382. [Google Scholar] [CrossRef]
- Porté-Agel, F.; Wu, Y.T.; Lu, H.; Conzemius, R.J. Large-eddy simulation of atmospheric boundary layer flow through wind turbines and wind farms. J. Wind. Eng. Ind. Aerodyn. 2011, 99, 154–168. [Google Scholar] [CrossRef]
- Diaz, G.P.N.; Saulo, A.C.; Otero, A.D. Wind farm interference and terrain interaction simulation by means of an adaptive actuator disc. J. Wind. Eng. Ind. Aerodyn. 2019, 186, 58–67. [Google Scholar] [CrossRef]
- Diaz, G.P.N.; Saulo, A.C.; Otero, A.D. Full wind rose wind farm simulation including wake and terrain effects for energy yield assessment. Energy 2021, 237, 121642. [Google Scholar] [CrossRef]
- Diaz, G.P.N.; Saulo, A.C.; Otero, A.D. Comparative study on the wake description using actuator disc model with increasing level of complexity. J. Phys. Conf. Ser. 2019, 1256, 012017. [Google Scholar] [CrossRef]
- Asmuth, H.; Diaz, G.P.N.; Madsen, H.A.; Branlard, E.; Forsting, A.R.M.; Nilsson, K.; Jonkman, J.; Ivanell, S. Wind turbine response in waked inflow: A modelling benchmark against full-scale measurements. Renew. Energy 2022, 191, 868–887. [Google Scholar] [CrossRef]
- Bastankhah, M.; Mohammadi, M.M.; Lees, C.; Diaz, G.P.N.; Buxton, O.R.; Ivanell, S. A fast-running physics-based wake model for a semi-infinite wind farm. J. Fluid Mech. 2024, 985, A43. [Google Scholar] [CrossRef]
- Bodini, N.; Lundquist, J.K.; Moriarty, P. Wind plants can impact long-term local atmospheric conditions. Sci. Rep. 2021, 11, 22939. [Google Scholar] [CrossRef]
- Ishihara, T.; Qian, G.W. A new Gaussian-based analytical wake model for wind turbines considering ambient turbulence intensities and thrust coefficient effects. J. Wind. Eng. Ind. Aerodyn. 2018, 177, 275–292. [Google Scholar] [CrossRef]
- Sørensen, J.N.; Mikkelsen, R.F.; Henningson, D.S.; Ivanell, S.; Sarmast, S.; Andersen, S.J. Simulation of wind turbine wakes using the actuator line technique. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373, 20140071. [Google Scholar] [CrossRef] [PubMed]
- Pedersen, M.M.; Forsting, A.M.; van der Laan, P.; Riva, R.; Romàn, L.A.A.; Risco, J.C.; Friis-Møller, M.; Quick, J.; Christiansen, J.P.S.; Rodrigues, R.V.; et al. PyWake 2.5.0: An Open-Source Wind Farm Simulation Tool; Technical University of Denmark: Kongens Lyngby, Denmark, 2023. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martinez-Trespalacios, J.A.; Barile, D.A.; Millan-Gandara, J.L.; Useche, J.; Otero, A.D. Combined Effect of ABL Profile and Rotation in Wind Turbine Wakes: New Three-Dimensional Wake Model. Energies 2025, 18, 4726. https://doi.org/10.3390/en18174726
Martinez-Trespalacios JA, Barile DA, Millan-Gandara JL, Useche J, Otero AD. Combined Effect of ABL Profile and Rotation in Wind Turbine Wakes: New Three-Dimensional Wake Model. Energies. 2025; 18(17):4726. https://doi.org/10.3390/en18174726
Chicago/Turabian StyleMartinez-Trespalacios, José A., Dimas A. Barile, John L. Millan-Gandara, Jairo Useche, and Alejandro D. Otero. 2025. "Combined Effect of ABL Profile and Rotation in Wind Turbine Wakes: New Three-Dimensional Wake Model" Energies 18, no. 17: 4726. https://doi.org/10.3390/en18174726
APA StyleMartinez-Trespalacios, J. A., Barile, D. A., Millan-Gandara, J. L., Useche, J., & Otero, A. D. (2025). Combined Effect of ABL Profile and Rotation in Wind Turbine Wakes: New Three-Dimensional Wake Model. Energies, 18(17), 4726. https://doi.org/10.3390/en18174726





