Deep Neural Network-Based Optimal Power Flow for Active Distribution Systems with High Photovoltaic Penetration

Abstract

The integration of photovoltaic (PV) generation into distribution systems supports decarbonization and cost reduction but introduces challenges for secure and efficient operation due to voltage fluctuations and power flow variability. Traditional centralized optimal power flow (OPF) methods require full system observability and significant computational resources, limiting their real-time applicability in active distribution systems. This paper proposes a deep neural network (DNN)-based OPF control framework designed for active distribution systems with high PV penetration under limited measurement availability. The proposed method leverages offline convex chance-constrained OPF (convex-CCOPF) solutions, generated through iterative simulations across a wide range of PV and load conditions, to train the DNN to approximate optimal control actions, including on-load tap changer (OLTC) positions and inverter reactive power dispatch. To address observability constraints, the DNN is trained using a reduced set of strategically selected measurement points, making it suitable for real-world deployment in distribution systems with sparse sensing infrastructure. The effectiveness of the proposed framework is validated on the IEEE 33-bus test system under varying operating conditions. The simulation results demonstrate that the DNN achieves near-optimal performance with a significantly reduced computation time compared to conventional OPF solvers while maintaining voltage profiles within permissible limits and minimizing power losses.

1. Introduction

The large-scale deployment of distributed energy resources (DERs) has significantly transformed the structure and operation of modern distribution systems. Among these resources, photovoltaic (PV) generation has experienced the most rapid growth due to the declining cost of solar technology, supportive government policies, and global decarbonization initiatives [1,2,3]. This expansion enables cost-effective and sustainable electricity supply but also introduces new operational complexities. PV generation is inherently intermittent and non-dispatchable, depending heavily on solar irradiance and weather conditions [4,5]. These characteristics lead to rapid and unpredictable power fluctuations, resulting in voltage deviations, reverse power flows, and bidirectional energy transfers in distribution feeders [6,7,8]. Furthermore, the increasing adoption of electric vehicles and other DERs compounds these challenges, making voltage regulation a critical requirement for maintaining secure and efficient distribution system operation [9,10].

Traditional voltage regulation devices, such as on-load tap changers (OLTCs), line voltage regulators, and capacitor banks, were primarily designed for radial distribution systems with unidirectional power flows and slowly varying loads [11,12]. In active distribution systems with high PV penetration, these devices are subject to excessive switching operations and increased degradation, which shorten their operational lifetime [13,14]. Moreover, their slow response limits their effectiveness in mitigating rapid voltage variations caused by fluctuating PV generation [15]. To address these challenges, numerous studies have proposed centralized optimal power flow (OPF)-based coordination strategies to jointly manage OLTCs, capacitor banks, and inverter-based resources [16,17,18]. Such approaches can achieve near-optimal voltage profiles by solving nonlinear optimization problems that capture system constraints and DER operating limits. Recent advances, including dynamic OPF models based on linear second-order cone relaxation [19] and recursive conic approximation methods for bipolar DC grids [20], have further improved computational efficiency compared to conventional OPF formulations. Nevertheless, despite their reduced computational burden, these methods still require a large number of real-time measurements and extensive communication infrastructure, which pose significant barriers to practical deployment in large-scale distribution systems.

In response to these challenges, numerous studies have investigated distributed voltage control strategies. A distributed optimization framework using the alternating direction method of multipliers (ADMM) was presented in [17], effectively improving voltage regulation while reducing dependence on detailed global system information. A distributed hierarchical control method was proposed in [21] to coordinate PV inverters and OLTCs, significantly reducing voltage deviations while limiting tap operations. In [22], a multi-agent consensus-based algorithm for Volt-VAR control (VVC) was developed, enabling local controllers to collaboratively maintain voltage profiles with minimal communication.

To enhance dynamic performance and integrate multiple device types, hybrid hierarchical frameworks have also been introduced. In [23], a bi-level distributed control scheme was developed, where an upper-level consensus algorithm determines reactive power setpoints for inverter clusters and a lower-level ADMM-based controller adjusts individual inverter outputs, enabling coordinated VVC without centralized computation. In [24], a hierarchical multi-stage framework was proposed that leverages high-resolution phasor measurements from µPMUs and a central phasor data concentrator (PDC) to coordinate inverter responses across multiple stages, improving voltage regulation performance under dynamic PV variations. Adaptive hierarchical designs were explored in [25], employing distributed model predictive control with ADMM-based coordination to dynamically adjust control actions for varying operating conditions. Although these distributed and hybrid approaches improve responsiveness and reduce reliance on centralized computation, they still rely on iterative optimization processes to reach convergence, which hinders their ability to deliver real-time control and may degrade performance under rapid PV fluctuations or highly uncertain operating conditions.

Recent studies have demonstrated the potential of deep neural networks (DNNs) to approximate OPF solutions and provide fast, high-quality control actions for active distribution systems. In [26], a data-driven coordinated voltage control strategy was proposed for active distribution systems. This approach learns the relationship between PV inverter outputs and system voltages directly from data, which are then used in a coordinated framework to determine reactive power setpoints for inverters, improving voltage regulation without relying on explicit system models or computationally intensive OPF solvers. Building on this concept, the authors of [27] presented DeepOPF, a neural-network-based surrogate for DC-OPF that replaces iterative solvers with a direct mapping model. While this approach achieved solution quality comparable to classical OPF with much faster computation, it requires voltage and power measurements from all system nodes, which may limit its practical deployment in real-world distribution systems. In [28], a DNN-based autonomous control framework was developed for predicting OLTC tap positions in feeders with high penetrations of DERs and electric vehicles. Although it demonstrated effective control of OLTC tap operations, it did not include reactive power control, limiting its ability to fully coordinate inverter-based resources. In contrast, [29] proposed a proxy-based model trained on chance-constrained OPF solutions to determine reactive power setpoints for smart inverters. While this enabled efficient VVC, it only managed the reactive power of smart inverters and did not incorporate OLTC or other device controls, thereby limiting its impact on broader system voltage coordination. In [30], a robust local coordination framework was introduced where a DNN emulated the outputs of a linearized CCOPF to coordinate inverters, OLTC, and static voltage controllers using only local information. This decentralized approach reduces communication requirements and computational burden. However, its reliance on local information may compromise global optimization, and the use of a linearized OPF to generate training data can limit its accuracy in highly nonlinear operating regions.

To overcome these gaps, we propose a deep learning-based framework for coordinated voltage regulation in distribution systems with high PV penetration. Two task-specific DNN models are developed: a regression model to predict continuous reactive power setpoints for PV inverters and a classification model to determine discrete OLTC tap positions. These models are trained on a comprehensive synthetic dataset of load and solar irradiance scenarios, ensuring robust performance across diverse operating conditions. The key contributions of this work are as follows:

• Leveraging a scenario-based convex-CCOPF formulation to generate high-quality training data that account for errors introduced by measurement noise and communication delays;
• Reducing measurement and communication requirements by relying only on data exchange between the substation and PV buses;
• Enabling fast, OPF-quality decision-making for the reactive power of multiple inverters and OLTC tap positions through a data-driven approach.

In contrast to prior DNN-based OPF approaches that approximate the entire optimization problem with a single model and rely on full-system observability, our framework introduces a dual-DNN architecture tailored to heterogeneous control devices—discrete OLTCs and continuous PV inverters—while requiring only limited, practically measurable inputs. Combined with scenario-based training under uncertainty, this design achieves near-optimal voltage regulation with significantly reduced computation and communication requirements, thereby enhancing both robustness and real-world applicability. The rest of this paper is organized as follows: Section 2 introduces the convex-CCOPF formulation used to generate training data. Section 3 describes the proposed DNN-based framework for coordinated voltage regulation. Section 4 presents the testing process and simulation results, evaluating the performance of the proposed method against benchmark approaches. Finally, Section 5 concludes the paper and outlines directions for future work.

2. Convex-CCOPF Formulation

Traditional OPF formulations are inherently non-convex due to the nonlinearities in power flow equations, making them computationally demanding and prone to convergence to local minima. These drawbacks limit their applicability for real-time operation and large-scale scenario generation. To overcome these challenges, we adopt a convex relaxation of the OPF problem, ensuring global optimality and computational efficiency. Such convex formulations have been widely recognized for providing tractable and reliable solutions in distribution-level optimization problems.

2.1. Distribution System Model

Consider G(N, E) as a graph representing a radial distribution system, where N denotes the set of buses and E represents the distribution lines connecting them. The buses are indexed as $i=1, 2, \dots , \left|N\right|$. The complex voltage at bus i is denoted by $V_i$, while $I_{\mathit{ij}}$, $P_{\mathit{ij}}$, and $Q_{\mathit{ij}}$ represent the complex current, active power, and reactive power flows, respectively, from bus i to bus j. At each bus i, $p_i^c$ and $q_i^c$ are the active and reactive power demands, respectively, while $p_i^g$ and $q_i^g$ are the active and reactive power generated by the connected PV. If no load is connected to bus i, $p_i^c$ and $q_i^c$ are set to zero. Similarly, $p_i^g$ and $q_i^g$ are set to zero for buses without PV connections. The resistance and reactance of the line connecting bus i and bus j are represented by $r_{\mathit{ij}}$ and $x_{\mathit{ij}}$, respectively.

2.2. Distribution Power Flow (DistFlow)

As described in [31], the power flow equations representing the distribution system can be written as follows:

$$P_{\mathit{ij}}-\sum _{k:(j,k)\in E}{P}_{\mathit{jk}}=r_{\mathit{ij}}{\left|I_{\mathit{ij}}\right|}^2+p_j^c-p_j^g$$

(1)

$$Q_{\mathit{ij}}-\sum _{k:(j,k)\in E}{Q}_{\mathit{jk}}=x_{\mathit{ij}}{\left|I_{\mathit{ij}}\right|}^2+q_j^c-q_j^g$$

(2)

$${\left|V_j\right|}^2={\left|V_i\right|}^2-2\left(r_{\mathit{ij}}{P}_{\mathit{ij}}+x_{\mathit{ij}}{Q}_{\mathit{ij}}\right)+\left({r_{\mathit{ij}}}^2+{x_{\mathit{ij}}}^2\right){\left|I_{\mathit{ij}}\right|}^2$$

(3)

$${\left|I_{\mathit{ij}}\right|}^2={\displaystyle \frac{{P_{\mathit{ij}}}^2+{Q_{\mathit{ij}}}^2}{{\left|V_i\right|}^2}}$$

(4)

2.3. Online Load Tap Changer (OLTC)

The OLTC is widely used in distribution systems to regulate bus voltage by adjusting the transformer turn ratio. By changing its tap position, the OLTC modifies the effective voltage at the distribution bus relative to the substation voltage.

Let $T_p$ denote the tap position (in per-unit steps) and a represent the step size of the OLTC. The relationship between the distribution bus voltage $V_1$ and the substation voltage $V_{\mathit{sub}}$ can be expressed as follows:

$${\left|V_1\right|}^2={\left(1-{aT}_p\right)}^2{V_{\mathit{sub}}}^2$$

(5)

2.4. Operational Constrains

To ensure reliable system operation, the following physical and operational constraints are imposed in the OPF formulation.

2.4.1. Voltage Magnitude Limits

The voltage magnitude at each bus is constrained to remain within the allowable range, expressed as

$${V_{\mathit{min}}}^2{\le \left|V_i\right|}^2\le {V_{\mathit{max}}}^2$$

(6)

where $V_{\mathit{min}}$ and $V_{\mathit{max}}$ denote the minimum and maximum voltage limits, respectively. Maintaining voltage within this range is critical for protecting customer equipment and ensuring compliance with distribution system operational standards under variable PV output.

2.4.2. PV Generation and Inverter Capability

The instantaneous active power capability of each PV depends on its peak capacity $p_{\mathit{pv},i}^{\mathit{peak}}$ and the solar irradiance $G_i$ at its location. This relationship determines the available PV power at bus i. In addition, the inverter output is constrained such that the combined active and reactive power does not exceed its rated apparent power $s_{\mathit{inv},i}^{\mathit{rate}}$. These constraints ensure that each PV operates within safe limits while adapting to varying solar conditions. The following equations are imposed to constrain the PV generation and inverter capabilities:

$$p_i^g=p_{\mathit{pv},i}^{\mathit{peak}}\times G_i$$

(7)

$${\left(p_i^g\right)}^2+{\left(q_i^g\right)}^2\le {\left(s_{\mathit{inv},i}^{\mathit{rate}}\right)}^2$$

(8)

2.4.3. Power Flow and Thermal Limits

The power flow in each distribution line must not exceed its thermal limit:

$${P_{\mathit{ij}}}^2+{Q_{\mathit{ij}}}^2\le {\left(S_{\mathit{ij}}^{\max }\right)}^2$$

(9)

where $S_{ij}^{\max }$ denotes the maximum apparent power capacity of the distribution line between bus i and j. This constraint prevents overheating and ensures that conductors operate within their safe thermal limits.

2.5. Objective Function

The objective of the optimization is to ensure secure and efficient operation of the active distribution system by co-optimizing inverter reactive power dispatch and the OLTC position. It integrates multiple performance goals into a single cost function that minimizes renewable energy curtailment, system losses, and voltage deviations, while also limiting excessive OLTC tap changes to prevent mechanical degradation. The overall objective can be expressed as

$$\underset{X}{\min }\left({\omega }_1\sum _{\left(i,j\right)\in E}{r}_{\mathit{ij}}{\left|I_{\mathit{ij}}\right|}^2+{\omega }_2\sum _{i\in N}\left|{\left|V_i\right|}^2-{V_N}^2\right|+{\omega }_3\left|T_p-T_{\mathit{prev}}\right|\right)$$

(10)

where ${\omega }_1$, ${\omega }_2$, and ${\omega }_3$ are weighting coefficients that balance system efficiency, voltage profile quality, and OLTC mechanical degradation, respectively. $V_N$ and $T_{\mathit{prev}}$ denote the nominal voltage and the OLTC position in the previous state, respectively. Optimization is performed over the decision variable set $X=\left(P, Q, {\left|I\right|}^2, p^g, p^c, q^g, q^c, {\left|V\right|}^2, T_p\right)$.

2.6. Model Convexification

While the DistFlow formulation provides a tractable representation of power flows in radial distribution systems, several constraints involve nonlinear relationships among branch currents, power flows, and bus voltages, rendering the model non-convex. To address this, a convex relaxation is applied to ensure global optimality and improve computational efficiency.

To address the non-convexity arising from the nonlinear constraints in (4), the relaxation approach proposed in [4] is applied. The equality constraints are relaxed into second-order cone inequalities as follows:

$${\left|I_{\mathit{ij}}\right|}^2\ge {\displaystyle \frac{{P_{\mathit{ij}}}^2+{Q_{\mathit{ij}}}^2}{{\left|V_i\right|}^2}}$$

(11)

The nonlinear nature of constraints (1)–(3) arises from their dependence on the current–flow equality in (4), which couples power flows with bus voltages in a non-convex form. By relaxing (4) into its second-order cone form, as expressed in (11), this coupling becomes convex. Consequently, replacing (4) with its convexified form renders the power balance and voltage drop constraints in (1)–(3) convex with respect to the decision variables.

The nonlinear constraint in (5) can be convexified by neglecting the quadratic term ${\left({aT}_p\right)}^2$, which is negligible compared to the linear components and has little impact on the optimized solution. After this simplification, constraint (5) can be rewritten in a convex form as follows:

$${\left|V_1\right|}^2=\left(1-{2aT}_p\right){V_{\mathit{sub}}}^2$$

(12)

2.7. Scenario-Based Convex-CCOPF

In practical distribution systems, the input data for OPF, such as load demands and PV outputs, are often affected by measurement and communication errors. To account for these uncertainties, the convex-OPF is extended into a scenario-based chance-constrained formulation. This method balances robustness and computational tractability by ensuring that network constraints are satisfied with high probability rather than under every possible realization of uncertainty.

Let uncertain load and PV generations be represented as random vectors:

$$\xi =\left\{p^c,{ q}^c,{ p}^g,{ q}^g \right\}$$

(13)

a set of $N_s$ scenarios $\left\{{\xi }^{\left(1\right)},{\xi }^{\left(2\right)}, \dots {,\xi }^{\left(N_s\right)}\right\}$ is generated by perturbing the nominal profiles with zero-mean Gaussian noise:

$${\xi }^{\left(k\right)}=\stackrel{-}{\xi }\times (1+{\delta }^{\left(k\right)}),{\delta }^{\left(k\right)}~N(0,{\sigma }^2)$$

(14)

in this study, the standard deviation σ was set to 0.1, with 400 scenarios generated and subsequently reduced to 20 representative cases using a clustering algorithm.

The scenario-based CCOPF minimizes the expected operating cost by extending the deterministic objective across all scenarios:

$$\underset{X}{\min }\left({\omega }_1\sum _{k=1}^{N_s}\sum _{(i,j)\in E}{r}_{\mathit{ij}}{\left|{I_{\mathit{ij}}}^{\left(k\right)}\right|}^2+{\omega }_2\sum _{k=1}^{N_s}\sum _{i\in N}\left|{\left|{V_i}^{\left(k\right)}\right|}^2-{V_N}^2\right|+{\omega }_3\left|T_p-T_{\mathit{prev}}\right|\right)$$

(15)

where $\left|{{\mathrm{I}}_{\mathrm{ij}}}^{\left(k\right)}\right|$ and $\left|{{\mathrm{V}}_{\mathrm{i}}}^{\left(k\right)}\right|$ are the branch currents and bus voltages under scenario k, respectively. The coefficients ${\omega }_1$, ${\omega }_2$, and ${\omega }_3$ are constrained to be non-negative and normalized to sum to one, and their final values were determined through iterative simulations as 0.485, 0.485, and 0.030.

The deterministic power flow equations, device operating limits, overload conditions, and voltage magnitude constraints are reformulated for each scenario k, yielding an additional dimension of variables and constraints. To avoid over-conservatism, bus voltage magnitude and thermal operation limit are enforced in a probabilistic form, expressed as chance constraints:

$$\mathrm{P}\left\{{V_{min}}^2{\le \left|{V_i}^{\left(k\right)}\right|}^2\le {V_{max}}^2,\forall k\right\}\ge 1-{\mathsf{\epsilon }}_v$$

(16)

$$\mathrm{P}\left\{{\left({P_{ij}}^{\left(k\right)}\right)}^2+{\left({Q_{ij}}^{\left(k\right)}\right)}^2\le {\left(S_{ij}^{max}\right)}^2,\forall k\right\}\ge 1-{\mathsf{\epsilon }}_{th}$$

(17)

where ${\mathsf{\epsilon }}_v$ and ${\mathsf{\epsilon }}_{th}$ denote the allowable probabilities of voltage and thermal violations, respectively. In this study, ${\mathsf{\epsilon }}_v$ is set to 5%, while ${\mathsf{\epsilon }}_{th}$ is set to 15%, with the apparent power capacity of each distribution line limited to 6.6 MVA. The higher threshold for thermal violations reflects the relatively large PV capacities connected to the system, which can cause substantial line loading under high irradiance conditions.

3. Proposed DNN-Based OPF

Although the scenario-based convex-CCOPF formulation provides global optimal solutions, solving it online for every operating timestep is computationally intensive, particularly in distribution systems with high PV penetration and frequent variations in load and generation. Moreover, the scenario-based convex-CCOPF requires full system state measurements, which are often impractical in real-world distribution systems. To overcome these challenges, we propose a DNN-based approach that approximates the scenario-based convex-CCOPF solution in real time. The DNN is trained to map a limited set of real-time measurements, reflecting the partial observability of practical systems, to near-optimal control actions. Once trained, it enables fast and efficient decision-making.

3.1. Structure of the Proposed Method

In this study, two separate DNNs are designed to estimate the optimal setpoints for PV inverters and the OLTC, respectively. The first DNN is formulated as a regression model to predict continuous setpoints for reactive power injections of the PV inverters. The second DNN is formulated as a classification model to determine the discrete tap position of the OLTC, which is inherently a categorical decision variable. This separation allows each DNN to specialize in its respective control task, thereby improving accuracy and computational efficiency: the regression DNN focuses on continuous inverter control, while the classification DNN handles discrete tap adjustments for system-wide voltage regulation. Although their outputs differ, both DNNs share the same input feature set, carefully selected to capture key operating conditions of the distribution system while remaining practical for real-world implementation.

The input features used for the proposed DNN models are illustrated in Figure 1, which shows their relation to the distribution system in a simplified form. These include: (1) the previous OLTC tap position, which provides information about the transformer’s configuration and serves as a baseline for predicting the next tap adjustment; (2) the feeder active and reactive power at the substation, representing the overall loading condition and the power exchange with the upstream grid; (3) the magnitude of branch currents flowing into PV buses, which reflects local power flow patterns and loading conditions; (4) the active and reactive power outputs of PV inverters, indicating their real-time contribution to the grid and remaining reactive capability; and (5) the voltage magnitudes at PV buses, serving as direct indicators of the local voltage profile and highlighting buses that may require corrective action. The figure illustrates a single PV connection for clarity; however, if additional PV units are connected to the network, the corresponding features (3)–(5) for those PV buses are also included in the DNN input set.

This set of features has been chosen for two main reasons. First, it provides a comprehensive view of the distribution system’s operating state by incorporating substation-level, feeder-level, and PV-bus-level measurements that are strongly correlated with voltage behavior. Second, although the proposed framework is tested on a conceptual system without a specific measurement setup, the feature selection is based on the reasonable assumption that measurements at PV buses are available. Focusing on PV buses is practical, as they are critical points for observing voltage variations and power flow changes in distribution systems with high PV penetration. This assumption aligns with typical data collection practices in real-world distribution systems, making the approach conceptually feasible for practical applications. By using this reduced yet strategically chosen feature set, the DNNs can effectively approximate the optimal OPF solutions while keeping the input dimensionality low. Consequently, training stability is improved, and fast, real-time inference is achieved.

3.2. Training Dataset Generation

The workflow for generating the training dataset used in this study is illustrated in Figure 2. The process begins by loading the distribution system model, including line and bus parameters, as well as PV and OLTC configurations. Next, load profiles and solar irradiance data are imported to establish the baseline operating conditions. A power flow analysis is then conducted to obtain the pre-optimized state of the distribution system, and selected results from this step are recorded as input features for training.

To account for measurement and communication errors, the baseline load profile and solar irradiance values are not used directly. Instead, zero-mean Gaussian random noise is added to these deterministic values, creating multiple perturbed realizations that represent possible true system conditions. These realizations are then used to form a scenario-based convex-CCOPF problem, which ensures that operational constraints such as voltage and flow limits are satisfied with a specified probability. In this formulation, the scenario-based convex-CCOPF is solved to obtain an optimal solution that satisfies the operational constraints across all generated scenarios within the predefined violation probability. The resulting PV inverter setpoints and OLTC tap positions are stored as labels for the training dataset.

This process is repeated until the target dataset size is achieved. The collected data are then preprocessed, including normalization and feature scaling, and subsequently used to train two DNNs: a regression model for PV inverter setpoints and a classification model for OLTC tap positions.

3.3. DNN Models and Training Process

Each DNN is implemented as a fully connected feed-forward network with one to five hidden layers. The hidden layers use either ReLU or tanh activation functions, while the output layers are task-specific: linear activation for the regression model and softmax activation for the classification model. To enhance generalization and mitigate overfitting, dropout regularization and batch normalization are applied. Hyperparameter tuning is performed using Bayesian optimization, exploring a search space that includes the number of hidden layers, neurons per layer, activation functions, dropout rates, and learning rates.

Before training, all input features and regression outputs are normalized to zero-mean and unit variance to improve numerical stability, while the classification labels (OLTC tap positions) are shifted to a non-negative range and one-hot encoded for categorical prediction. The models are trained using the Adam optimizer, with mean absolute error (MAE) loss for the regression network and categorical cross-entropy loss for the classification network. Early stopping, adaptive learning rate reduction, and model checkpointing are employed to ensure convergence and prevent overfitting. The dataset generated from the scenario-based convex-CCOPF process is split into training, validation, and test sets, with an 80–20 split used for training and validation.

4. Numerical Simulation Results

4.1. Simulation Setup

This section presents the evaluation of the proposed DNN-based OPF method’s performance. Its effectiveness is assessed by comparing it with two benchmark approaches: deterministic convex-OPF and scenario-based chance-constrained OPF. All tasks were implemented in Python 3.13.7. The power flow calculations were performed using Pandapower [32], while the optimization problems were formulated in CVXPY [33,34] and solved using Gurobi [35]. The machine learning models were implemented and trained in TensorFlow, with Keras Tuner employed for hyperparameter optimization [36,37]. All simulations and training were conducted on a Windows 11 workstation equipped with an Intel(R) Core(TM) i7–9700 CPU (3.00 GHz) and 16 GB of RAM.

Figure 3 illustrates the workflow used to test and compare the performance of the proposed DNN-based OPF method. After loading the distribution system model and importing the load and solar irradiance profiles, noise is added to account for real-world measurement errors and communication uncertainties. The processed inputs are then evaluated using three different methods: (1) the proposed DNN-based approach, which generates inverter setpoints and OLTC positions directly from the trained neural networks; (2) deterministic convex-CCOPF, which solves the standard OPF problem without considering uncertainty; and (3) scenario-based convex-CCOPF, which provides a robust optimization benchmark under noisy conditions.

The control actions of each method are applied to the distribution system through a power flow simulation to verify their feasibility and evaluate optimization performance. The resulting system states are recorded for comparison. This process is repeated iteratively for all test cases until the predefined number of scenarios is completed, ensuring a comprehensive evaluation of the proposed method against both deterministic and scenario-based convex-CCOPF approaches.

4.2. Testing System and Dataset

To evaluate the proposed approach, simulations are conducted on a modified IEEE 33-bus radial distribution system as shown in Figure 4. The system operates at a nominal voltage of 12.66 kV with a total apparent power base of 10 MVA. The line and bus parameters are adopted from [38]. Three PV plants are integrated at buses 3, 12, and 30, respectively, each with a peak capacity of 3 MW. To enhance operational flexibility, the associated inverters are sized with a 20% capacity margin, resulting in an inverter rating of 3.6 MVA for each plant. A power transformer equipped with an OLTC is installed at the substation (bus 1). The OLTC has 33 discrete tap positions (±16 around the nominal position), with a step size of 0.00625 per unit (p.u.), and permits up to three tap changes per control interval.

To generate the training dataset, 3000 synthetic load scenarios were created to represent a wide range of operating conditions. For each scenario, the total apparent system load was uniformly sampled within the range of 0.2 to 0.6 p.u., while the system power factor was drawn from 0.9 to 1.0 p.u. The corresponding total active and reactive powers were then computed from these values. At the bus level, the apparent load share of each bus was independently sampled from a uniform distribution between 0 and 1, and the bus-specific power factors were likewise generated within 0.9–1.0. The resulting active and reactive bus loads were subsequently scaled to ensure that the sum of all bus-level loads matched the pre-determined total system load for each scenario. In addition, solar irradiance data from a selected geographical location were incorporated to reflect realistic PV generation conditions in the training dataset.

Overall, this process yielded 3000 datasets that effectively captured a broad spectrum of operating conditions, thereby minimizing the risk of overfitting. To further ensure generalization, the dataset was randomly shuffled and divided into training (80%) and validation (20%) subsets for DNN development, while a separate set of unseen operating conditions was reserved exclusively for testing the final model performance. This data handling strategy, combined with the inherent variability introduced during scenario generation, ensured that the proposed DNN models maintained robustness and predictive accuracy when applied to unseen cases. Using this synthetic dataset, the hyperparameters of the DNN models were systematically fine-tuned through Bayesian optimization with Keras Tuner, and the optimized parameters are summarized in

Table 1. Optimized hyperparameters of the DNN-based OPF.

DNN Models	Layers	Number of Node	Activation Function	Dropout (%)	Learning Rate
Regression DNN	Dense 1	16	ReLU	0	0.0001–0.1
	Dense 2	128	ReLU	10
	Output	3	linear	0
Classification DNN	Dense 1	112	tanh	5
	Dense 2	72	tanh	25
	Dense 3	96	tanh	40
	Dense 4	32	tanh	0
	Output	33	softmax	0

.

4.3. Testing Results

To evaluate the performance of the proposed method, historical daily bus-level load data were used. Figure 5 illustrates the total active and reactive power of all buses over time, along with the corresponding solar irradiance profiles. The dataset represents a full day of operation with a 15–minute time resolution, capturing typical variations in both load demand and solar generation. The active and reactive loads exhibit morning and evening peaks, while the solar irradiance profile follows a bell-shaped curve during daylight hours, providing diverse operating conditions for testing the proposed framework.

Figure 6 illustrates the voltage profiles across the IEEE 33-bus system using four strategies: no OPF, deterministic convex-CCOPF, scenario-based convex-CCOPF, and the proposed DNN-based OPF. Without optimization (no OPF), the system exhibits significant voltage deviations, particularly at downstream buses (18–31), where voltages rise above 1.08 p.u. due to uncontrolled PV outputs and load variations. On the other hand, the deterministic convex-CCOPF method improves voltage regulation through a structured optimization approach but remains sensitive to PV output fluctuations and load variations, resulting in occasional voltage spikes or drops. The scenario-based convex-CCOPF further enhances performance by accounting for multiple uncertainty scenarios, including unpredictable load variations, PV output fluctuations, measurement errors, and communication errors. This comprehensive consideration results in a more uniform and stable voltage profile across all buses, maintaining voltages near the ideal range. Similarly, the DNN-based OPF achieves results comparable to the scenario-based convex-CCOPF under limited measurement availability. It maintains voltages within acceptable limits (≈0.95–1.05 p.u.). This comparison demonstrates that the DNN-based approach can effectively learn and replicate optimal control behaviors even under complex conditions and can therefore be regarded as a robust and practical solution for voltage regulation in modern distribution systems with high PV penetration.

Figure 7 presents the OLTC tap position profiles under the three optimization methods. Over the course of the simulated day, the deterministic convex-CCOPF results in 4 tap operations, while the scenario-based convex-CCOPF increases this to 6 operations due to its scenario-driven adjustments. In comparison, the proposed DNN-based OPF performs 10 tap changes, reflecting its greater responsiveness to system condition variations. Although the DNN-based method exhibits more frequent switching than the benchmark approaches, the increase remains moderate and does not impose excessive operational stress on the OLTC. This behavior highlights the method’s ability to leverage real-time inference for more proactive voltage regulation, while still maintaining practicality given the reduced measurement requirements. Overall, the results indicate that the proposed approach achieves improved adaptability with only a slight increase in tap operation frequency.

Figure 8 illustrates the loss profiles and objective function values for the four OPF methods, while

Table 2. Total energy losses of different OPF methods.

Method	Total Energy Loss (MWh)
No OPF	3.559177
convex-CCOPF	6.431050
Scenario-based convex-CCOPF	5.835950
DNN-based OPF	5.625800

summarizes their total daily energy losses. The no-OPF case records the lowest total energy loss of 3.56 MWh, since no control actions are imposed on the system. However, as shown in Figure 8b, this case results in the highest objective function value due to severe voltage fluctuations and repeated violations of operational constraints. By contrast, the convex-CCOPF, scenario-based convex-CCOPF, and DNN-based OPF methods achieve improved voltage regulation and secure operation, reflected in much lower objective function values. Their corresponding total energy losses are 6.43 MWh, 5.84 MWh, and 5.63 MWh, respectively. Although these values are higher than the no-OPF case, they represent a necessary trade-off between minimizing losses and ensuring feasibility under voltage and thermal constraints. Among them, the proposed DNN-based OPF achieves the lowest energy loss while maintaining real-time applicability, demonstrating its potential as a practical solution for large-scale deployment.

The computation times of the three OPF methods are summarized in

Table 3. Comparison of Computation Times for OPF Methods.

Method	Computation Time (s)	Relative Reduction Compared to Scenario-Based Convex-CCOPF (%)	Relative Reduction Compared to Convex-CCOPF (%)
Scenario-Based Convex-CCOPF	557.33	-	-
Convex-CCOPF	48.35	91.33	-
Proposed DNN-Based OPF	11.98	97.85	75.21

. Among the tested approaches, the scenario-based convex-CCOPF exhibited the highest computational burden, requiring 557.33 s due to the need to solve multiple scenarios simultaneously. The deterministic convex-CCOPF was significantly faster, with a computation time of 48.35 s. In contrast, the proposed DNN-based OPF achieved the shortest time at only 11.98 s, even when including data preprocessing. This corresponds to a reduction of nearly 98% compared to the scenario-based convex-CCOPF and approximately 75% compared to the deterministic convex-CCOPF. These results clearly highlight the efficiency of the proposed method, demonstrating its strong potential for real-time and large-scale distribution system applications.

5. Conclusions

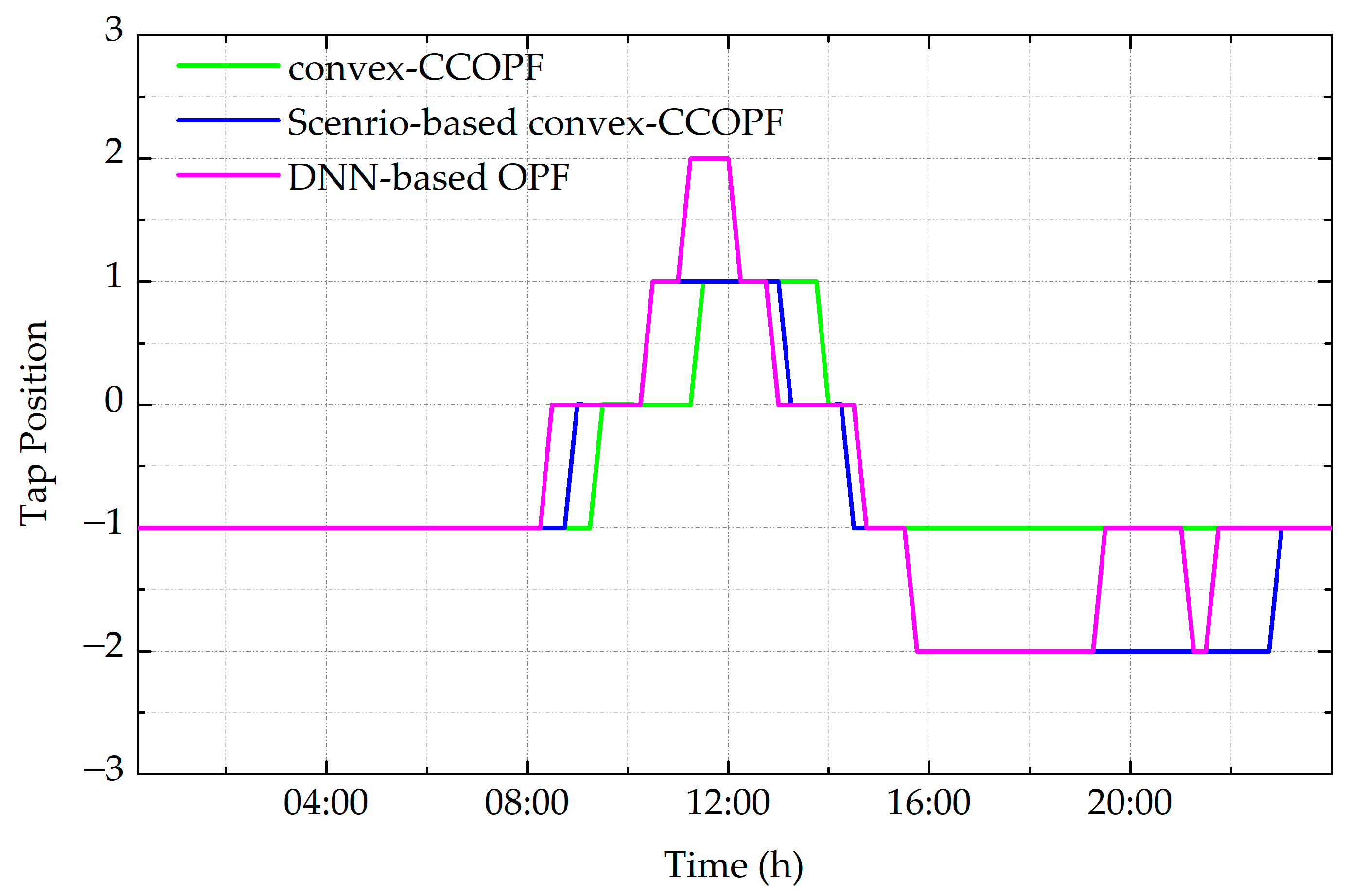
This study presents a novel deep learning-based framework for coordinated voltage regulation in active distribution systems with high PV penetration. By combining two specialized deep neural networks—a regression model for continuous reactive power control of PV inverters and a classification model for discrete OLTC tap selection—the framework successfully achieves near-optimal voltage profiles while reducing energy losses. Simulation results on the IEEE 33-bus test system demonstrated that the proposed approach reduced total energy losses to 5.63 MWh, compared with 6.43 MWh under convex-CCOPF, while also offering significant computational advantages. The DNN-based OPF required only 11.98 s to compute, nearly 98% faster than scenario-based convex-CCOPF (557.33 s) and 75% faster than deterministic convex-CCOPF (48.35 s), confirming its suitability for real-time applications. In terms of OLTC operation, the proposed method performed slightly more tap changes (10 per day) than the benchmark methods (4–6 per day), but this increase is offset by the reduced measurement requirements and improved overall loss performance. Importantly, the framework relies only on substation-to-PV-bus measurements rather than full-system observability, making it more practical for real-world deployment where measurement infrastructure is limited.

The key findings can be summarized as follows: (1) the effectiveness of the proposed two-stage DNN-based OPF in coordinating PV inverters and OLTC for voltage regulation; (2) the reduction in energy losses compared with deterministic and scenario-based convex-CCOPF methods; and (3) the substantially lower computational time achieved by the DNN-based OPF, demonstrating its suitability for real-time applications.

Beyond the specific test case, the proposed method demonstrates scalability and generalization potential. While validated on the IEEE 33-bus system, its reliance on PV-bus features and OLTC states makes it inherently adaptable to larger radial networks. For meshed distribution systems, extensions such as feature expansion to account for loop flows and enriched scenario-based training would be required, but the underlying framework remains applicable. Taken together, these results highlight that the proposed DNN-based OPF provides an efficient, scalable, and practically feasible solution for modern distribution systems with high levels of PV penetration. Future research will focus on extending the proposed framework to incorporate additional control devices, such as capacitor banks, step voltage regulators, and distributed energy storage systems, in order to enhance flexibility and reliability of active distribution networks. Particular attention will be paid to addressing the technical challenges that arise in such multi-device environments, including potential communication failures and the need to ensure stable operation under rapidly changing conditions. In addition, future work will involve validating the proposed framework in real-time environments, where issues such as measurement noise, communication delays, and data uncertainty must be carefully managed.