Influence of Asymmetric Three-Phase Cable Cross-Sections on Conducted Emission Measurements
Abstract
1. Introduction
2. Circuit Model of CE Setup
2.1. EMI Source and Power Supply Filter
2.2. LISN and AC Net
2.3. Power Supply Cable and Matrix Transfer Fuction
2.3.1. Lossless Homogeneous Medium: Quadrilateral Structure
2.3.2. Lossless Inhomogeneous Medium: Quadrilateral Structure
3. Definition of Modal Quantities
3.1. Lossless Homogeneous Medium: Transfer Function Matrix
3.2. Lossless Inhomogeneous Medium: Transfer Function Matrix
4. Cable Insertion Ratio
4.1. Cable Insertion Ratio, IRMTL: Quadrilateral Structure
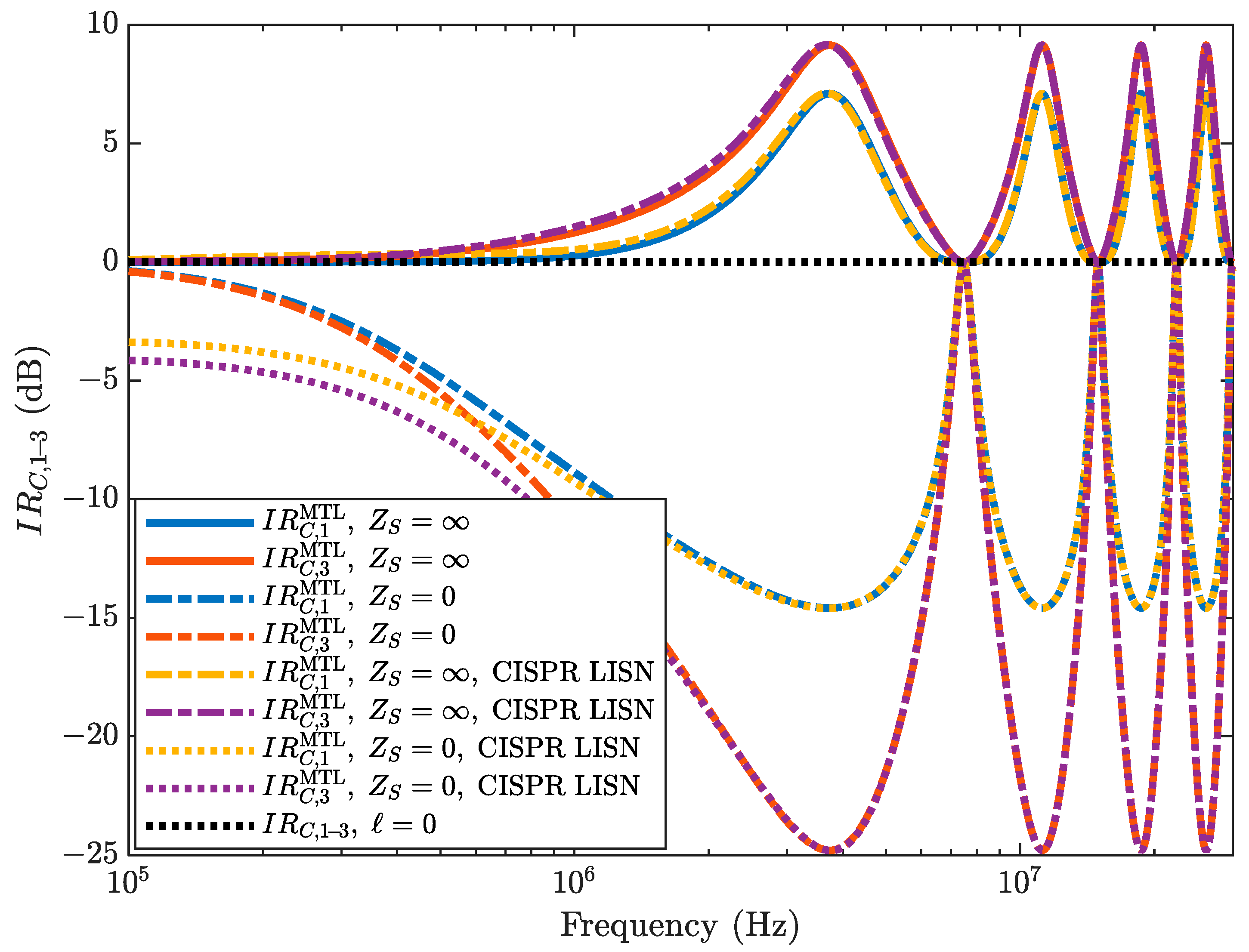
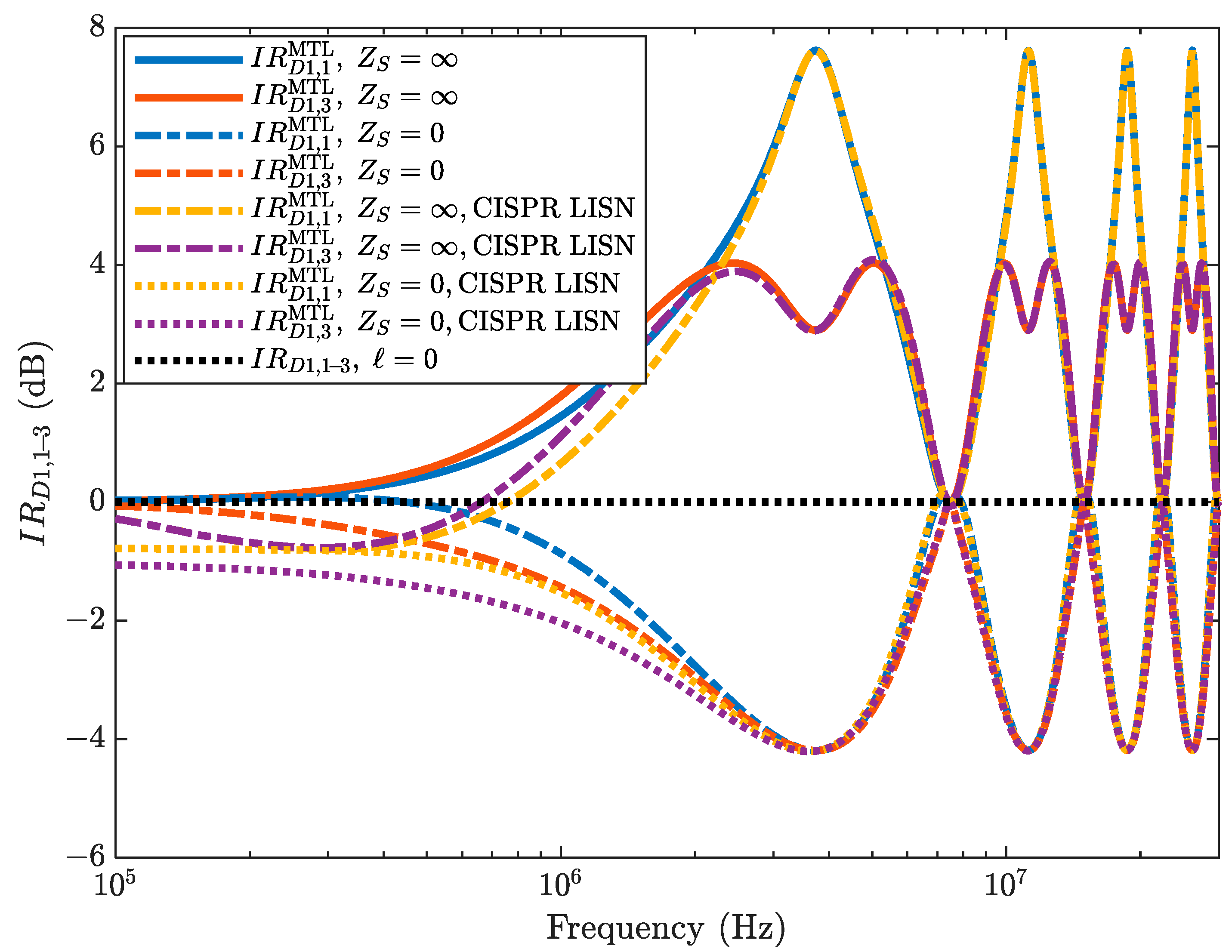
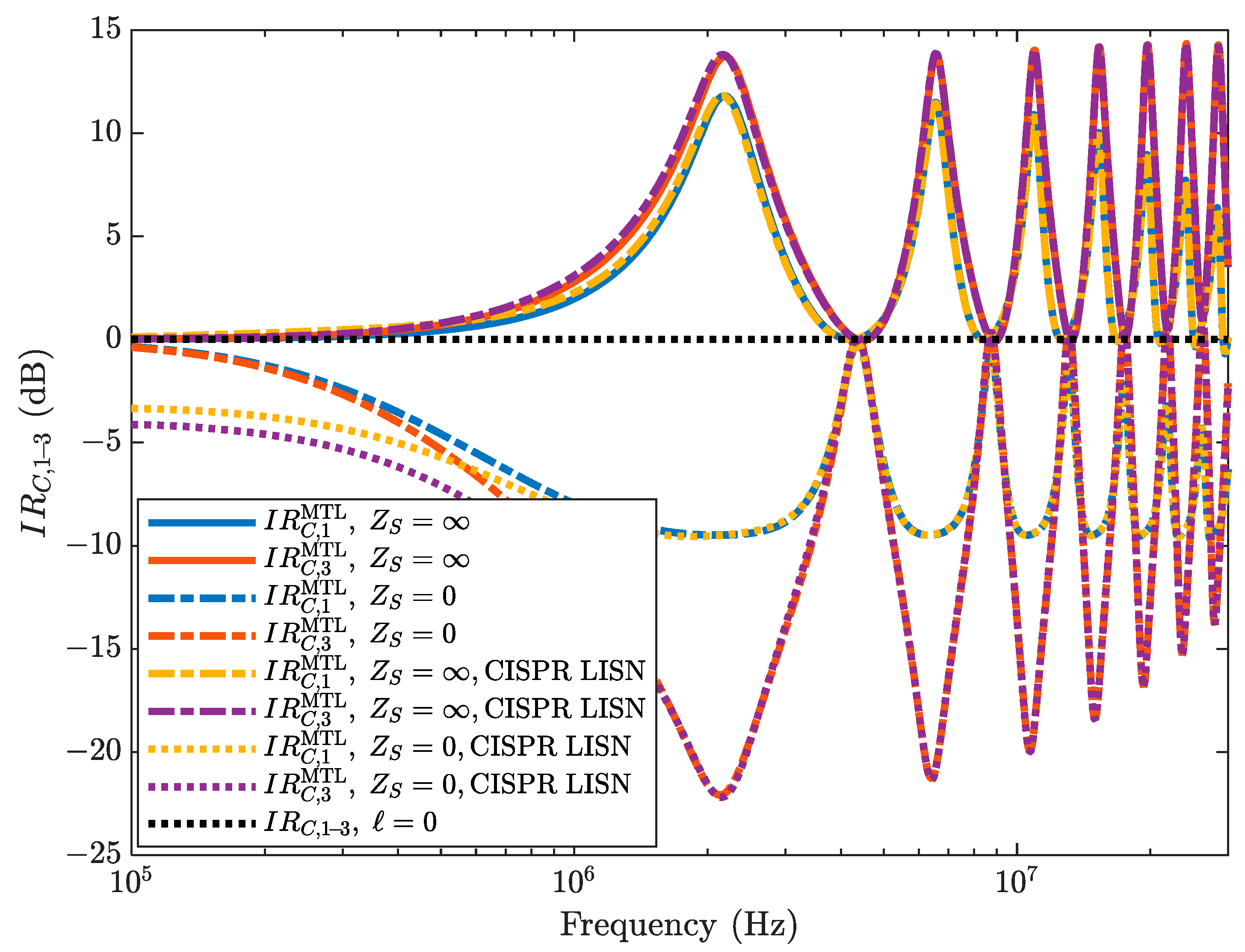
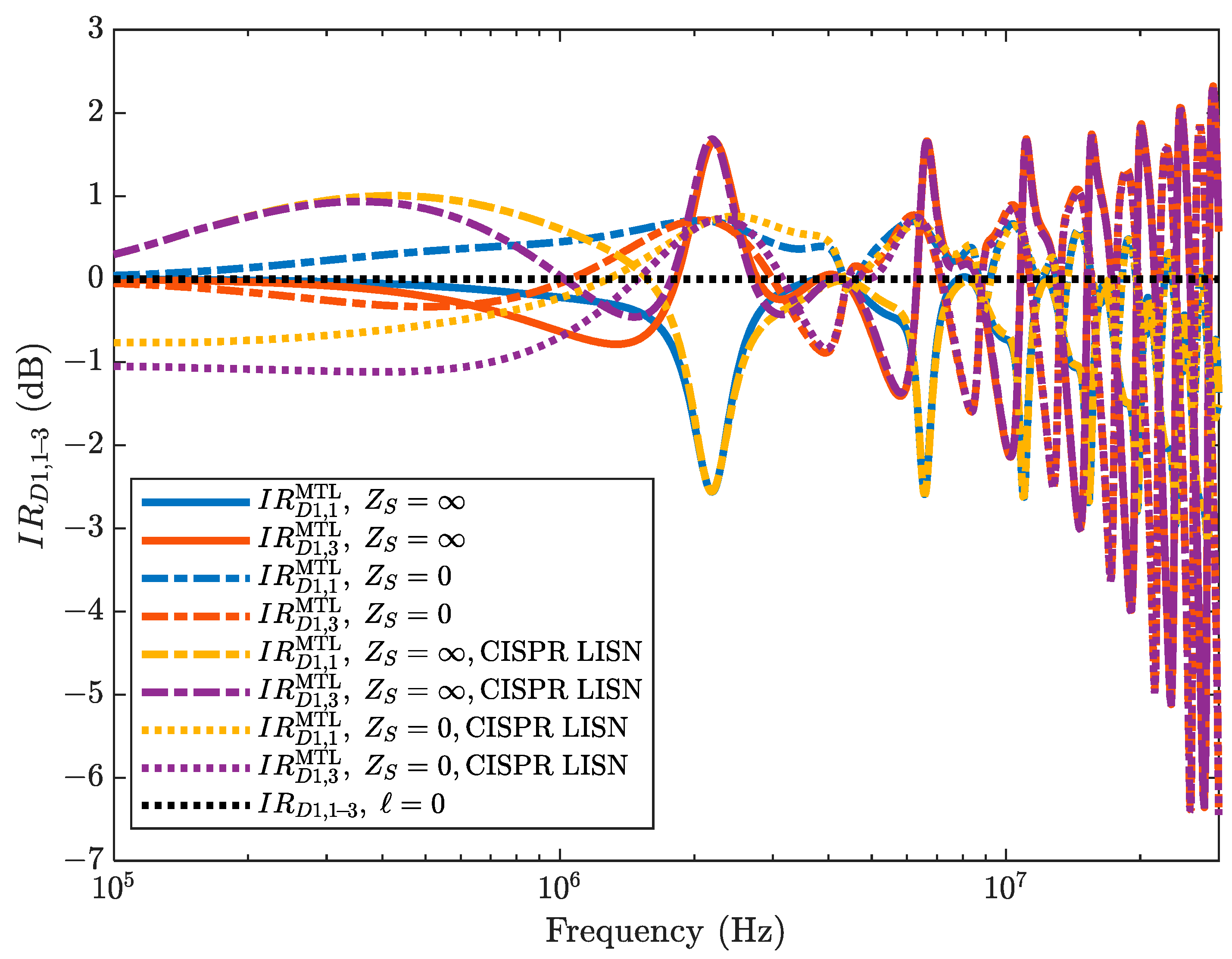
4.2. Representative Numerical Results
4.3. Results and Discussion
4.4. Comparison with Cyclic-Symmetric Geometry
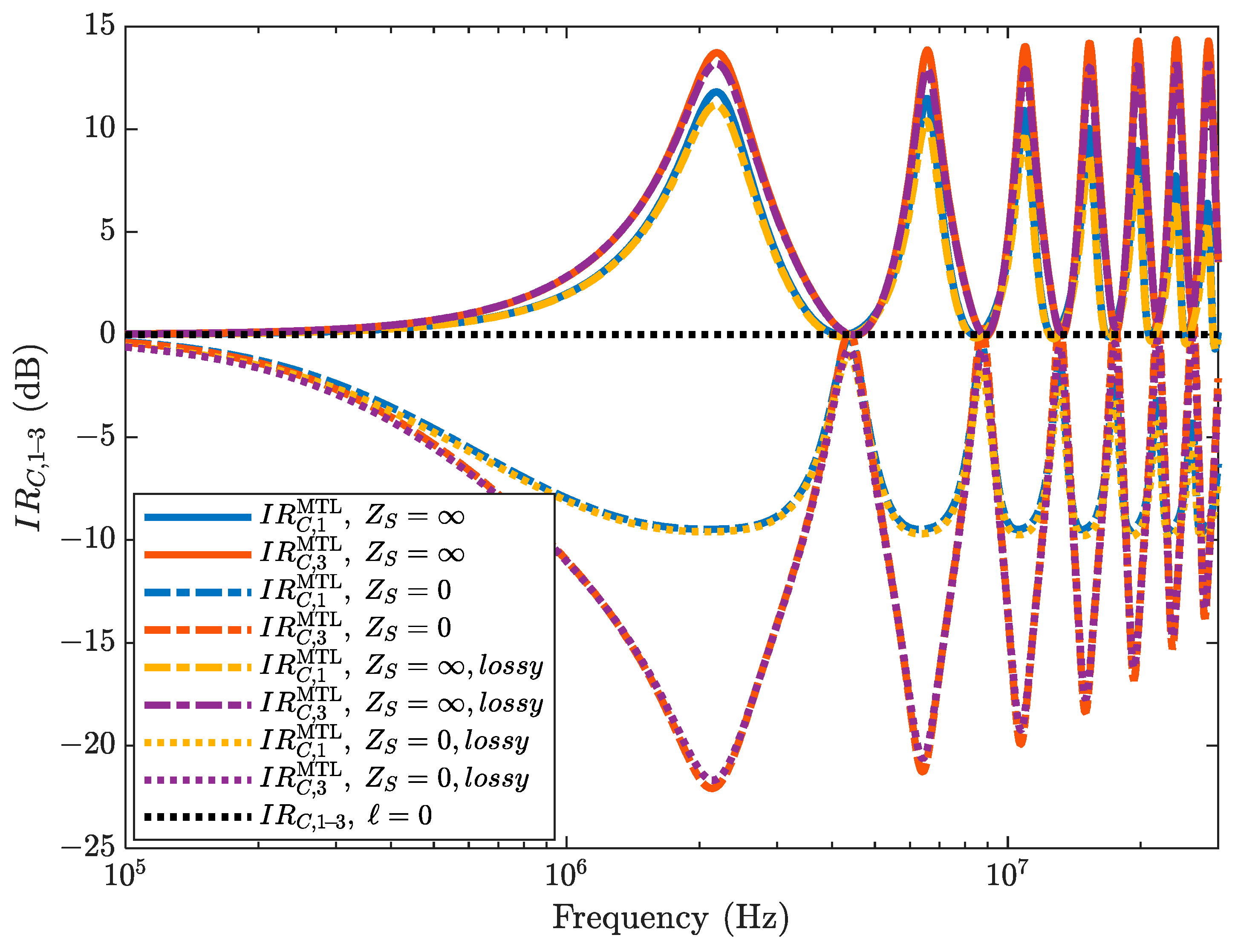
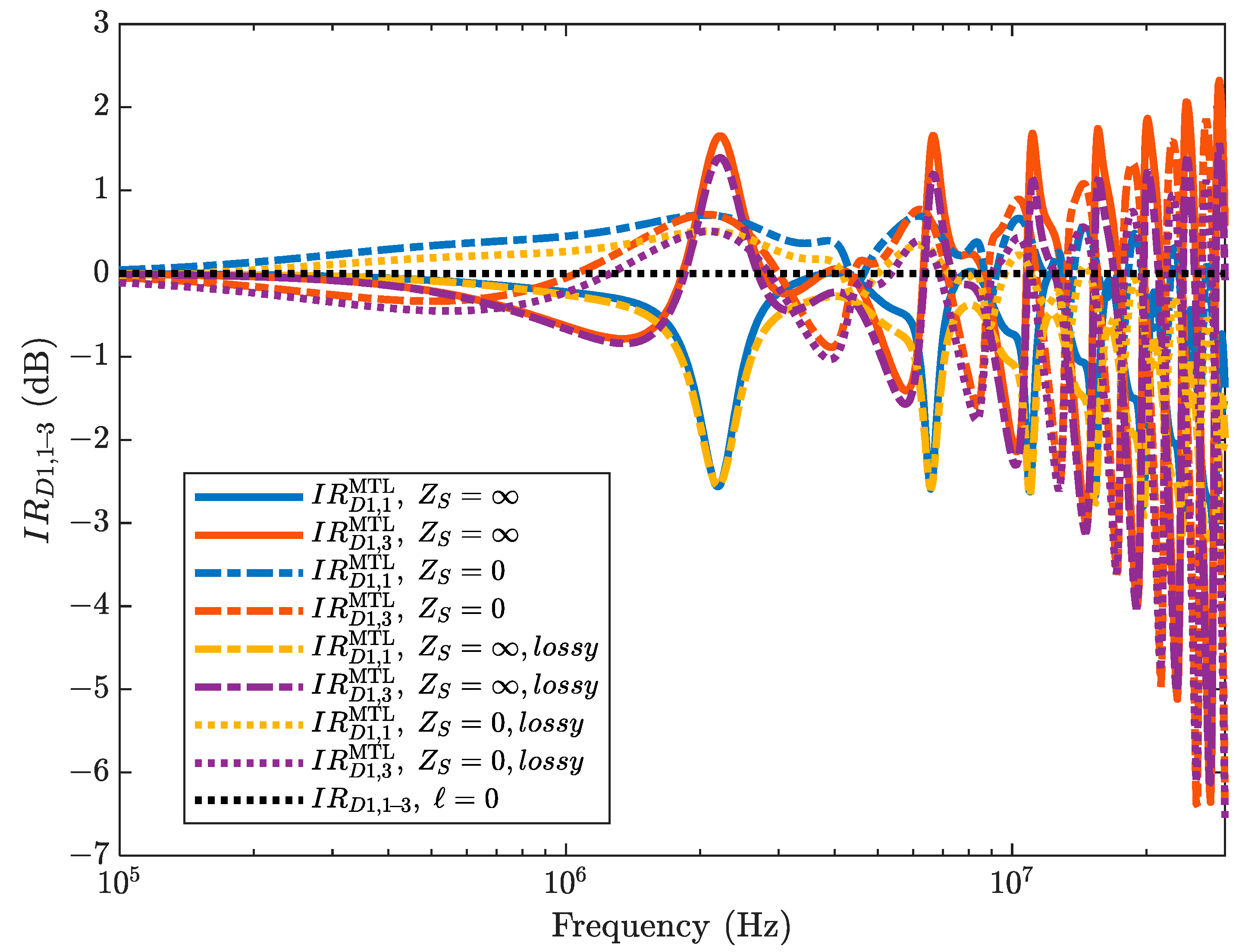
4.5. Inclusion of Losses
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Homogeneous Medium Characteristic Impedance Computation
Appendix A.2. Inhomogeneous Medium Characteristic Impedance and Propagation Constant Computations
References
- Skibinski, G.L.; Kerkman, R.J.; Schlegel, D. EMI Emissions of Modern PWM ac Drives. IEEE Ind. Appl. Mag. 1999, 5, 47–81. [Google Scholar] [CrossRef]
- Boglietti, A.; Carpaneto, E. Induction motor high frequency model. In Proceedings of the 1999 IEEE Industry Applications Conference, Phoenix, AZ, USA, 3–7 October 1999; Volume 3, pp. 1551–1558. [Google Scholar] [CrossRef]
- Widek, P.; Alaküla, M. Methods for the Investigation and Mitigation of Conducted Differential-Mode Electromagnetic Interference in Commercial Electrical Vehicles. Energies 2025, 18, 859. [Google Scholar] [CrossRef]
- Zhang, Z.; Hu, Y.; Chen, X.; Jewell, G.W.; Li, H. A Review on Conductive Common-Mode EMI Suppression Methods in Inverter Fed Motor Drives. IEEE Access 2021, 9, 18345–18360. [Google Scholar] [CrossRef]
- De Lima, A.C.S.; Dommel, H.W.; Stephan, R.M. Modeling adjustable-speed drives with long feeders. IEEE Trans. Ind. Electron. 2000, 47, 549–556. [Google Scholar] [CrossRef]
- Lee, K.; Zhang, Z. Conducted EMI Modeling and Analysis of Adjustable Speed Drive Systems with DC Chokes. In Proceedings of the 2024 IEEE Energy Conversion Congress and Exposition (ECCE), Chicago, IL, USA, 27–31 October 2024; pp. 7446–7452. [Google Scholar] [CrossRef]
- Zhai, L.; Lin, L.; Zhang, X.; Song, C. The Effect of Distributed Parameters on Conducted EMI from DC-Fed Motor Drive Systems in Electric Vehicles. Energies 2017, 10, 1. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Y.; Ali, M.S.; Chen, G.; Guerrero, J.M.; Vasquez, J.C. High-Frequency Modeling and Filter Design for PWM Drives with Long Cables. Energies 2021, 14, 1155. [Google Scholar] [CrossRef]
- Illiano, L.; Liu, X.; Wu, X.; Grassi, F.; Pignari, S.A. Signal Order Optimization of Interconnects Enabling High Electromagnetic Compatibility Performance in Modern Electrical Systems. Energies 2024, 17, 2786. [Google Scholar] [CrossRef]
- Orlandi, A.; Pignari, S. Modal Analysis of Conducted EMI in Three-Phase Power Drive Systems. In Proceedings of the 14th International Zurich Symposium and Technical Exposition on Electromagnetic Compatibility, Zurich, Switzerland, 20–22 February 2001; pp. 1–6. [Google Scholar] [CrossRef]
- Pignari, S.A.; Orlandi, A. Long-cable effects on conducted emissions levels. IEEE Trans. Electromagn. Compat. 2003, 45, 43–54. [Google Scholar] [CrossRef]
- Park, S.; Lee, E.; Noh, Y.-H.; Choi, D.-H.; Yook, J.-G. Accurate Modeling of CCS Combo Type 1 Cable and Its Communication Performance Analysis for High-Speed EV-EVSE Charging System. Energies 2023, 16, 5947. [Google Scholar] [CrossRef]
- Rezaei, H.; Sørensen, M.; Huang, W.; Beetner, D.G.; Pommerenke, D. Analyzing the Influence of Imbalanced Two- or Three-Wire VHF LISN on Radiated Emissions from AC Cables. IEEE Trans. Electromagn. Compat. 2022, 64, 327–337. [Google Scholar] [CrossRef]
- Rezaei, H.; Sørensen, M.; Jensen, K.; Pommerenke, D.; Beetner, D.G. Influence of Variations in Imbalanced LISN Termination Impedances on Radiated Emissions. IEEE Trans. Instrum. Meas. 2025, 74, 1001011. [Google Scholar] [CrossRef]
- Babu, P.; Tang, Z.; Peyghami, S.; Blaabjerg, F.; Christensen, N.; Davari, P. Systematic Approach for EMI Equivalent Model Derivation of Three Phase DC-Fed Motor Drives. In Proceedings of the 2024 International Conference on Electrical Machines (ICEM), Bari, Italy, 1–4 September 2024; pp. 1–7. [Google Scholar] [CrossRef]
- Jafari Roudposht, A.; Illiano, L.; Wu, X.; Grassi, F.; Pignari, S.A. Analysis and Circuit Modeling of Mode Conversion in Non-Ideal EMI Filters. In Proceedings of the EMC Europe 2025, Kraków, Poland, 1–5 September 2025. paper accepted for presentation. [Google Scholar]
- Grassi, F.; Pignari, S.A. Conducted Emissions Analysis in Four-Conductor Systems with Long Feeders. In Proceedings of the EMC Europe 2004, International Symposium on Electromagnetic Compatibility, Eindhoven, The Netherlands, 6–10 September 2004; pp. 1–6. [Google Scholar] [CrossRef]
- Xie, P.; Vakil, G.; Gerada, C. Electric drive systems with long feeder cables. IET Electr. Power Appl. 2020, 14, 16–30. [Google Scholar] [CrossRef]
- Wan, L.; Beshir, A.H.; Wu, X.; Liu, X.; Grassi, F.; Spadacini, G.; Pignari, S.A.; Zanoni, M.; Chiumeo, R.; Tenti, L. Cable Effects on Noise Propagation in Distribution Networks with Renewable Sources. In Proceedings of the 2022 20th International Conference on Harmonics & Quality of Power (ICHQP), Naples, Italy, 29 May–1 June 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Krim, A.; Lakrim, A.; Tahri, D. Two VHDL-AMS-based models of multi-conductor power cables for EMI simulations. Electr. Eng. 2021, 103, 647–661. [Google Scholar] [CrossRef]
- Kwak, H.; Hubing, T.H. Investigation of the Imbalance Difference Model and its Application to Various Circuit Board and Cable Geometries. In Proceedings of the 2012 IEEE International Symposium on Electromagnetic Compatibility, Pittsburgh, PA, USA, 5–10 August 2012; pp. 273–278. [Google Scholar] [CrossRef]
- Genc, S.; Muneeswaran, V.; Thomas, D.; Greedy, S.; Gundogdu, B.; Sarma, N.; Ozgonenel, O. The Effect of Conducted Emissions of Grid-Tied Three-Phase Adjustable Drives. Eng. Sci. Technol. Int. J. 2023, 46, 101505. [Google Scholar] [CrossRef]
- Niklaus, P.S.; Antivachis, M.M.; Bortis, D.; Kolar, J.W. Analysis of the Influence of Measurement Circuit Asymmetries on Three-Phase CM/DM Conducted EMI Separation. IEEE Trans. Power Electron. 2021, 36, 4066–4080. [Google Scholar] [CrossRef]
- Antivachis, M.; Niklaus, P.S.; Bortis, D.; Kolar, J.W. Input/output EMI filter design for three-phase ultra-high speed motor drive GaN inverter stage. CPSS Trans. Power Electron. Appl. 2021, 6, 74–92. [Google Scholar] [CrossRef]
- Paul, C.R. Analysis of Multiconductor Transmission Lines, 2nd ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2008. [Google Scholar]
- Illiano, L.; Wu, X.; Grassi, F.; Spadacini, G.; Pignari, S.A. Review of Mode Conversion and Modal Analysis in Electromagnetic Compatibility. IEEE Access 2024, 12, 65513–65529. [Google Scholar] [CrossRef]
- Paul, C.R.; Scully, R.C.; Steffka, M.A. Introduction to Electromagnetic Compatibility, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2022. [Google Scholar]
- CISPR 17:2011; Methods of Measurement of the Suppression Characteristics of Passive EMC Filtering Devices. IEC: Geneva, Switzerland, 2011.
- Tarateeraseth, V. Derivation of Insertion Loss Equations for EMI Filter Design. In Proceedings of the 2012 5th IASTED Asian Conference on Power and Energy Systems (AsiaPES 2012), Nakhon Nayok, Thailand, 2–4 April 2012. [Google Scholar]
- Luna, M.; La Tona, G.; Accetta, A.; Pucci, M.; Di Piazza, M.C. An Evolutionary EMI Filter Design Approach Based on In-Circuit Insertion Loss and Optimization of Power Density. Energies 2020, 13, 1957. [Google Scholar] [CrossRef]
- CISPR 16-1-2:2014/AMD 1:2017; Specification for Radio Disturbance and Immunity Measuring Apparatus and Methods—Part 1–2: Coupling Devices for Conducted Disturbance Measurements. IEC: Geneva, Switzerland, 2017; Amendment 1.
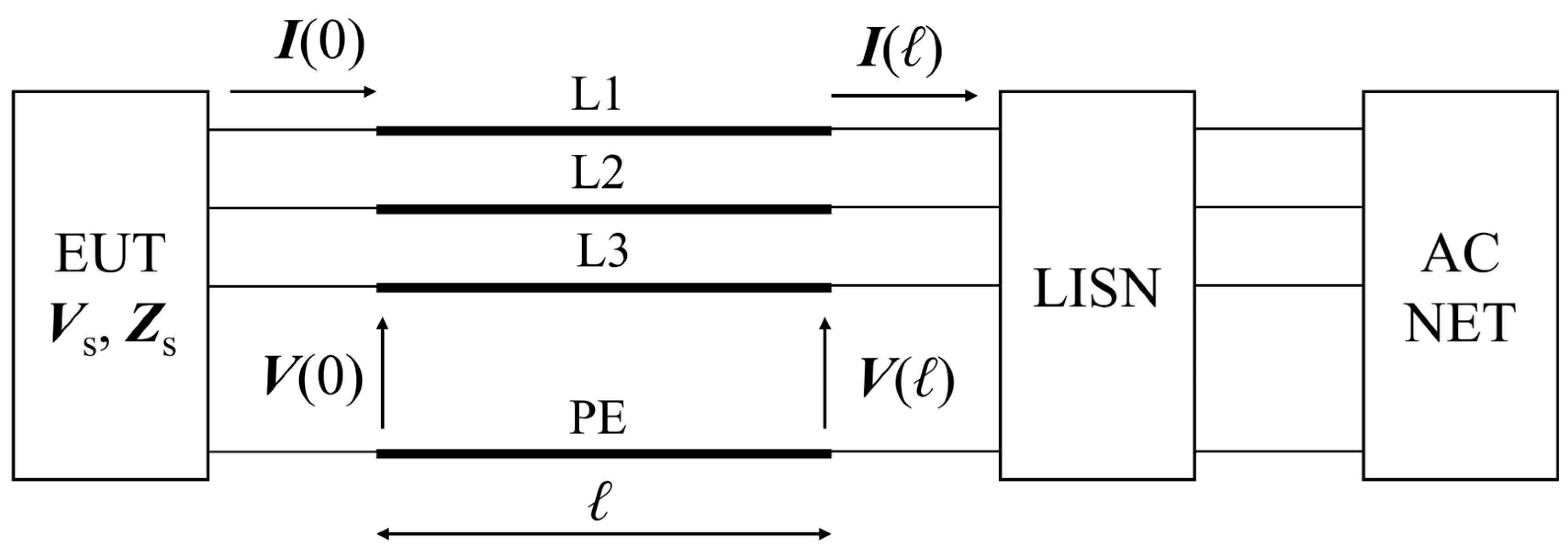
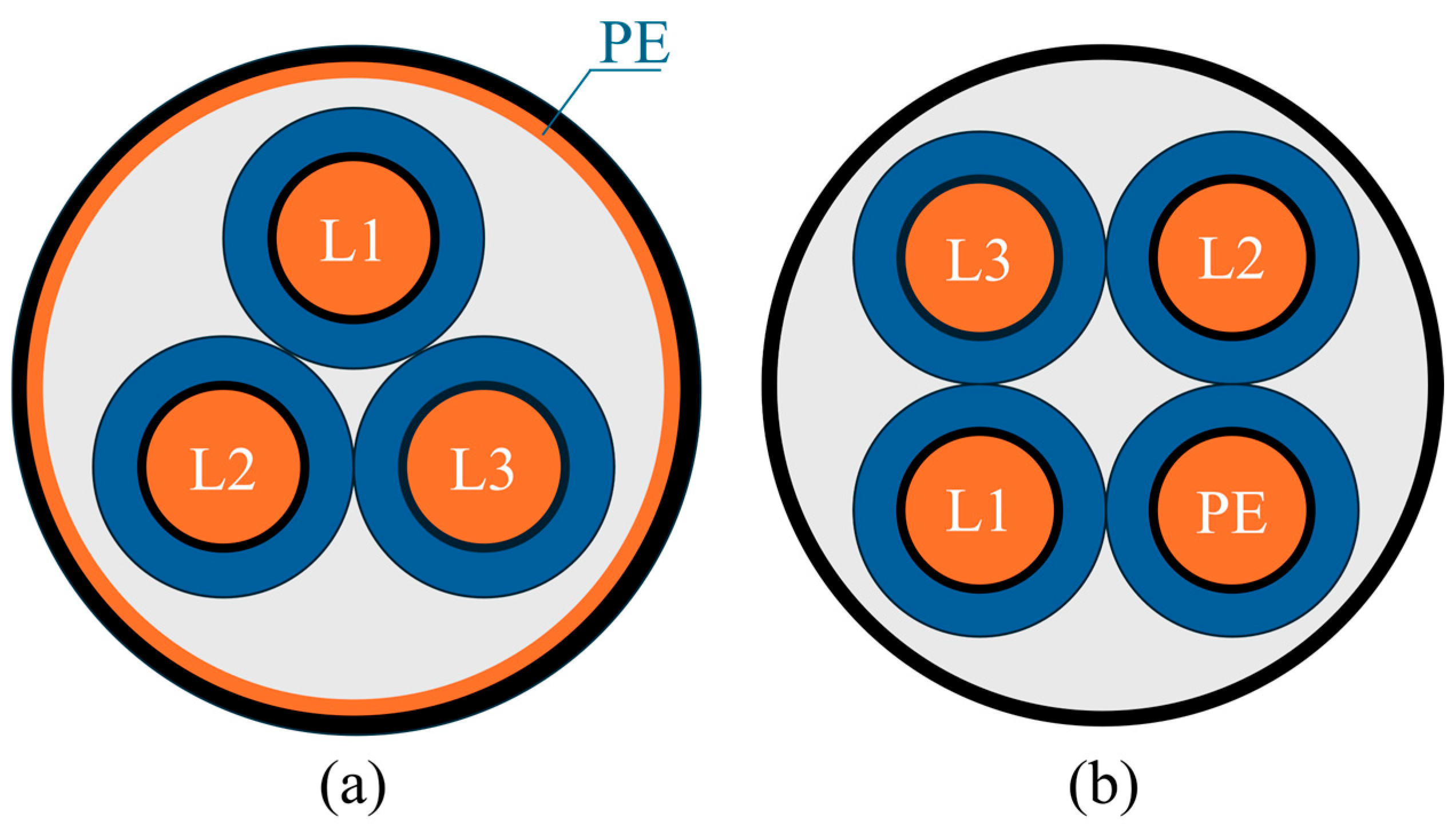
| Parameters | Symmetric Structure | Quadrilateral Structure |
|---|---|---|
| Wires inner radius, rw | 1.8 mm | 1.8 mm |
| Wires external radius, rw,ext | 4 mm | 4 mm |
| Distance between wires dw | 8 mm | 8 mm |
| Shield radius, rPE | 12 mm | / |
| Relative permittivity, εr | 3.5 | 3.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Illiano, L.; Wu, X.; Grassi, F.; Pignari, S.A. Influence of Asymmetric Three-Phase Cable Cross-Sections on Conducted Emission Measurements. Energies 2025, 18, 4720. https://doi.org/10.3390/en18174720
Illiano L, Wu X, Grassi F, Pignari SA. Influence of Asymmetric Three-Phase Cable Cross-Sections on Conducted Emission Measurements. Energies. 2025; 18(17):4720. https://doi.org/10.3390/en18174720
Chicago/Turabian StyleIlliano, Ludovica, Xinglong Wu, Flavia Grassi, and Sergio Amedeo Pignari. 2025. "Influence of Asymmetric Three-Phase Cable Cross-Sections on Conducted Emission Measurements" Energies 18, no. 17: 4720. https://doi.org/10.3390/en18174720
APA StyleIlliano, L., Wu, X., Grassi, F., & Pignari, S. A. (2025). Influence of Asymmetric Three-Phase Cable Cross-Sections on Conducted Emission Measurements. Energies, 18(17), 4720. https://doi.org/10.3390/en18174720








