An Adaptive Multi-Task Gaussian Process Regression Approach for Harmonic Modeling of Aggregated Loads in High-Voltage Substations
Abstract
1. Introduction
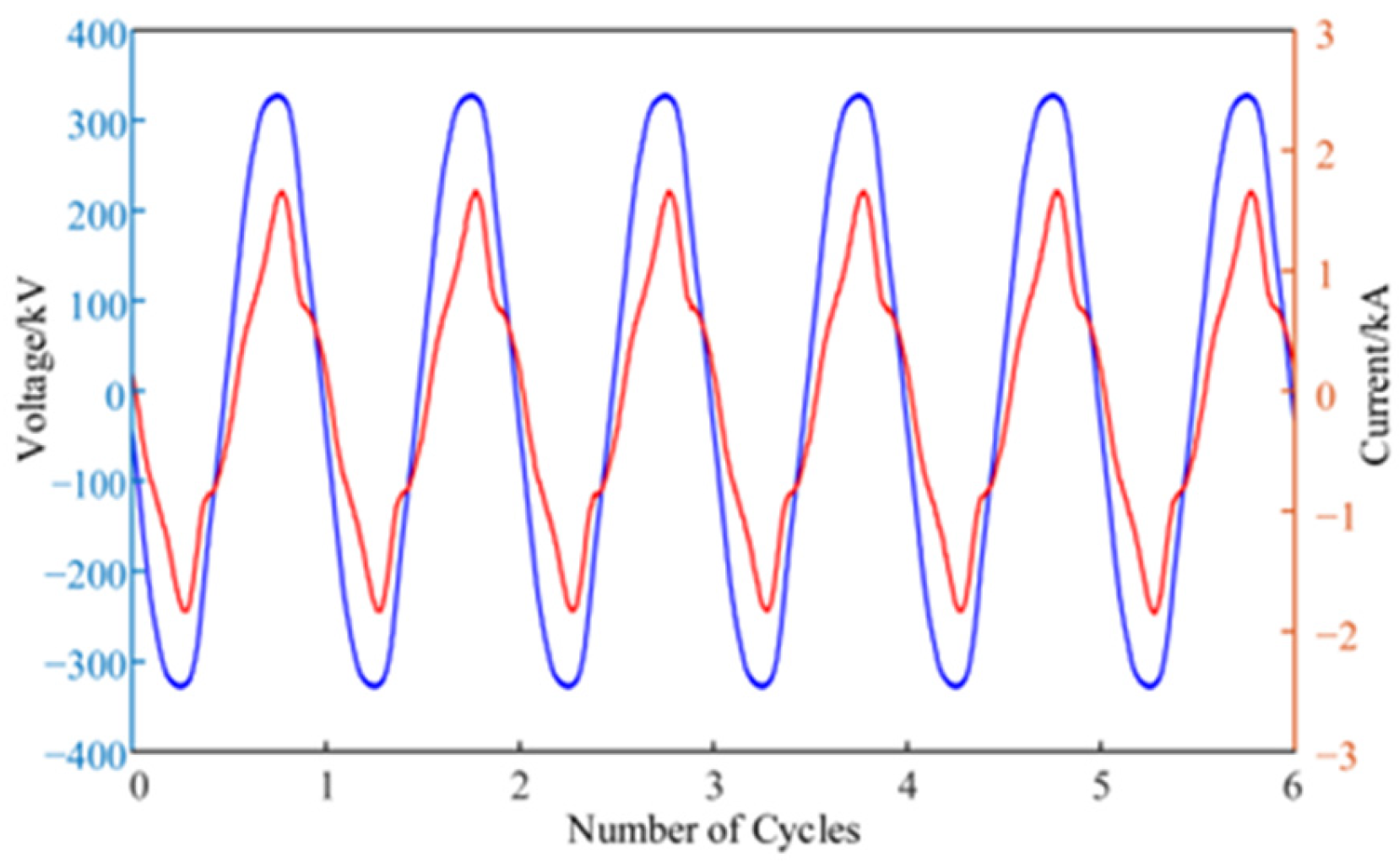
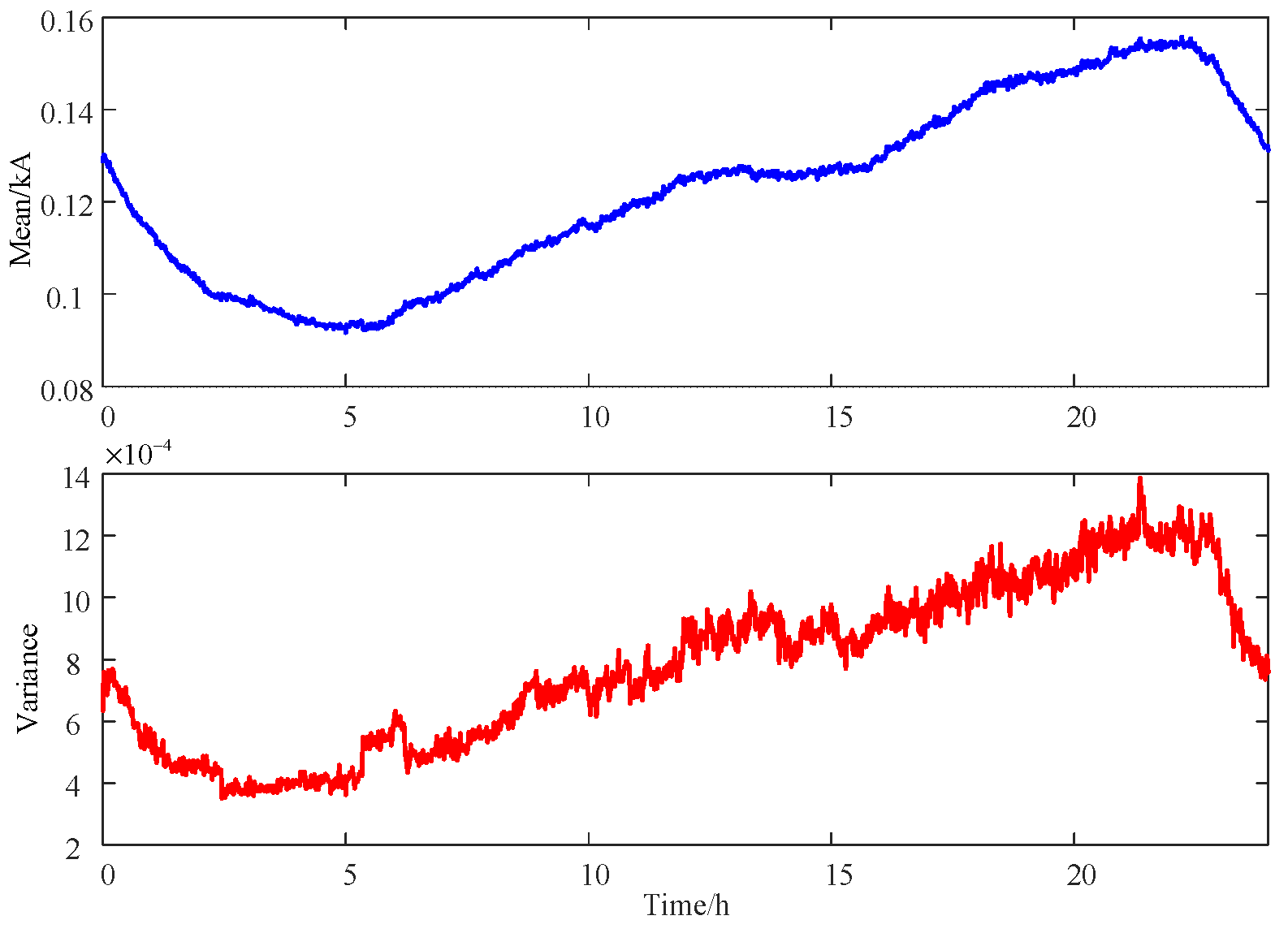
2. Measured Data Analysis
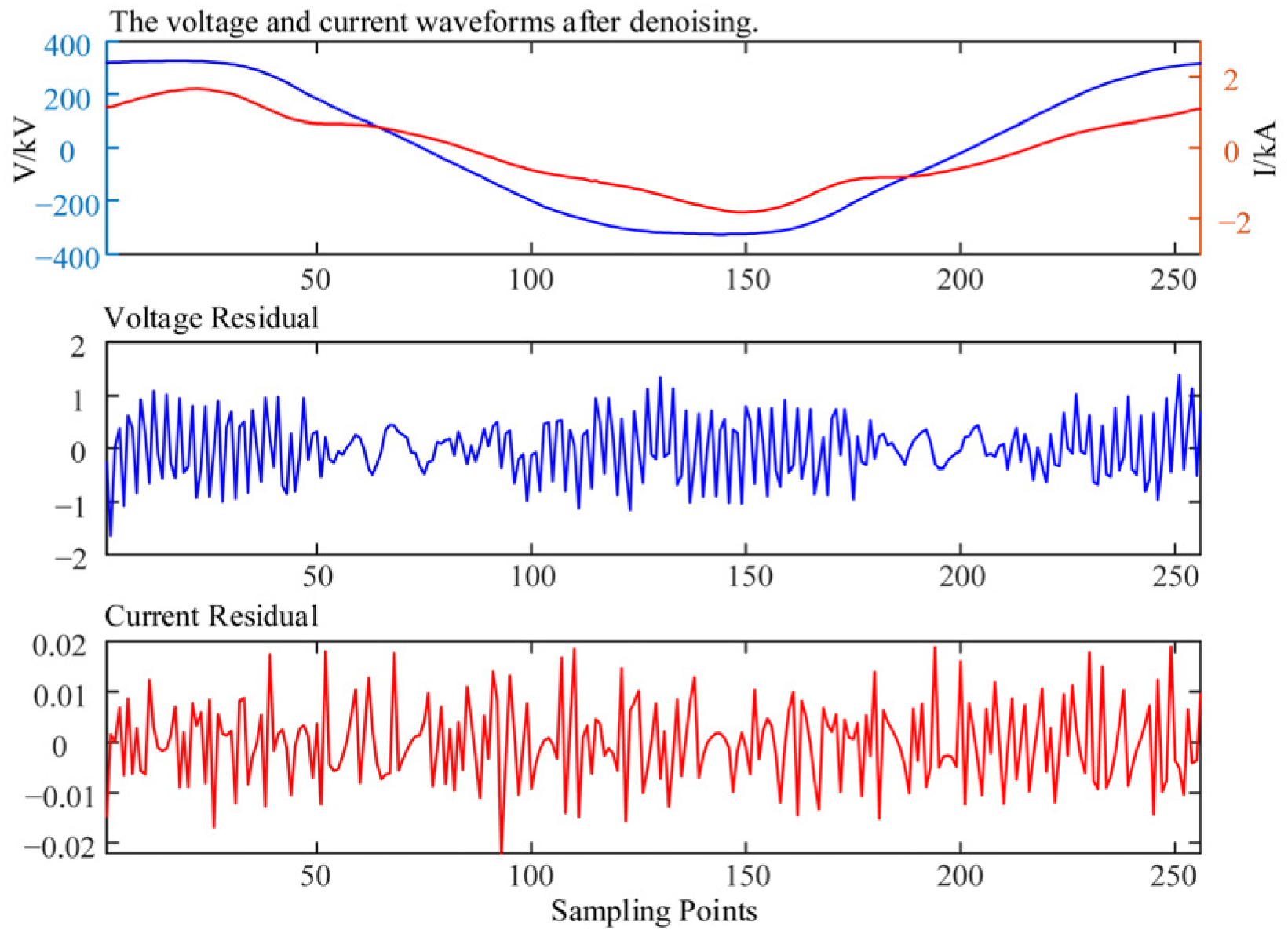
2.1. Denoising
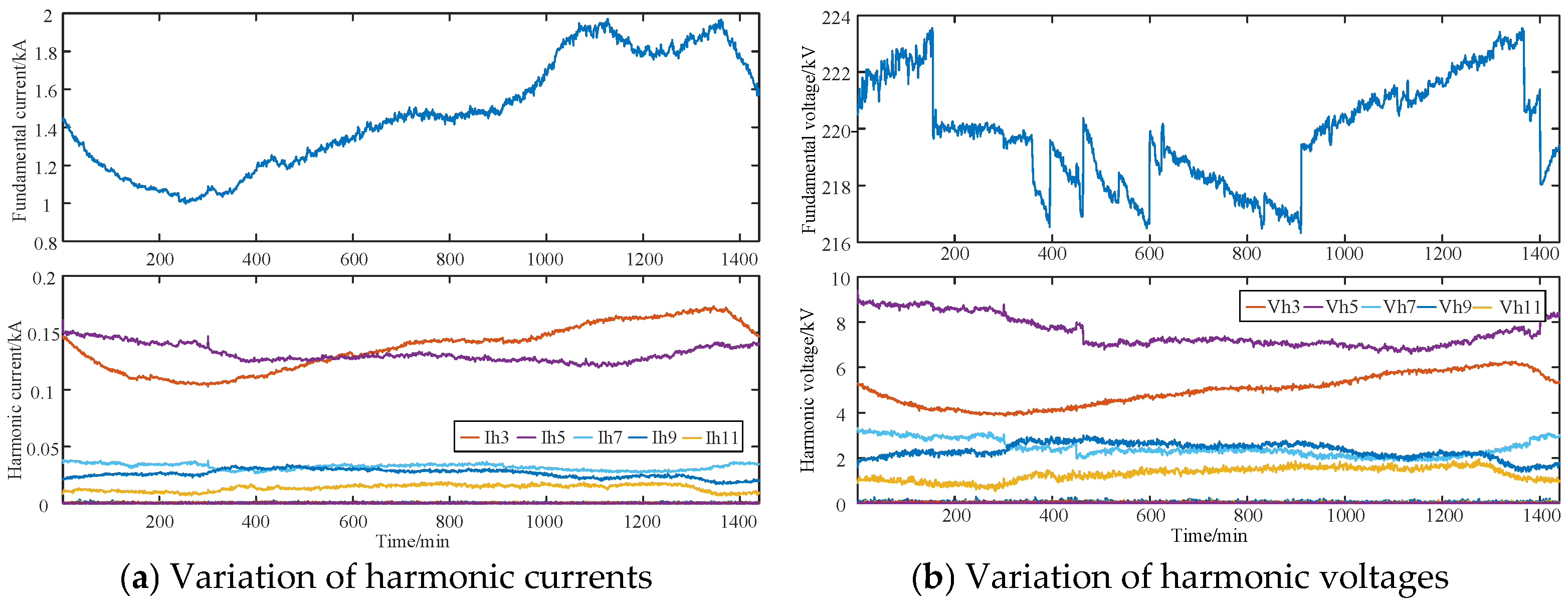
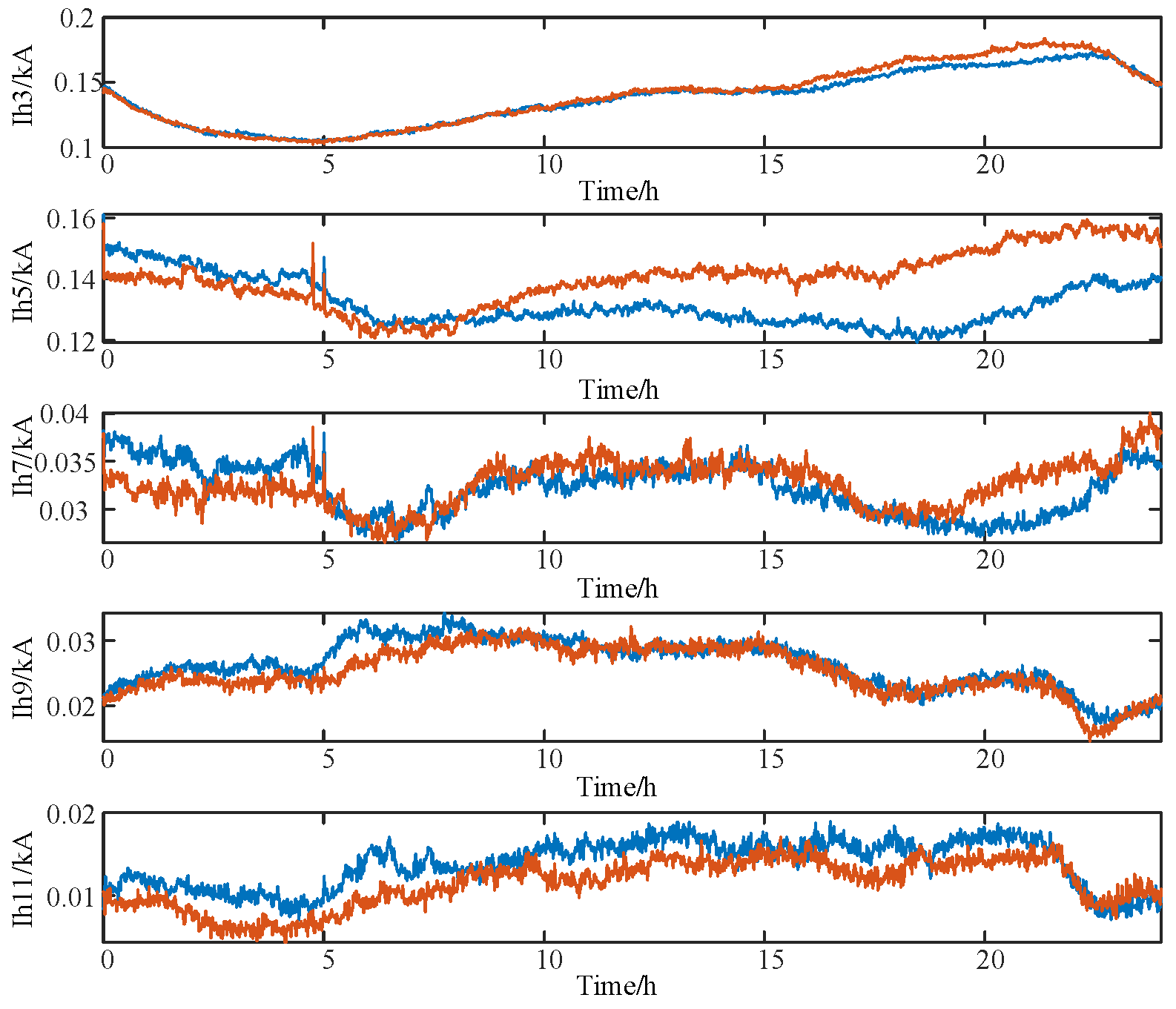
2.2. Harmonic Extraction
3. General Probabilistic Harmonic Model Based on Adaptive Multi-Task Gaussian Process Regression
3.1. Gaussian Process Regression
3.2. Multi-Task Gaussian Process Regression
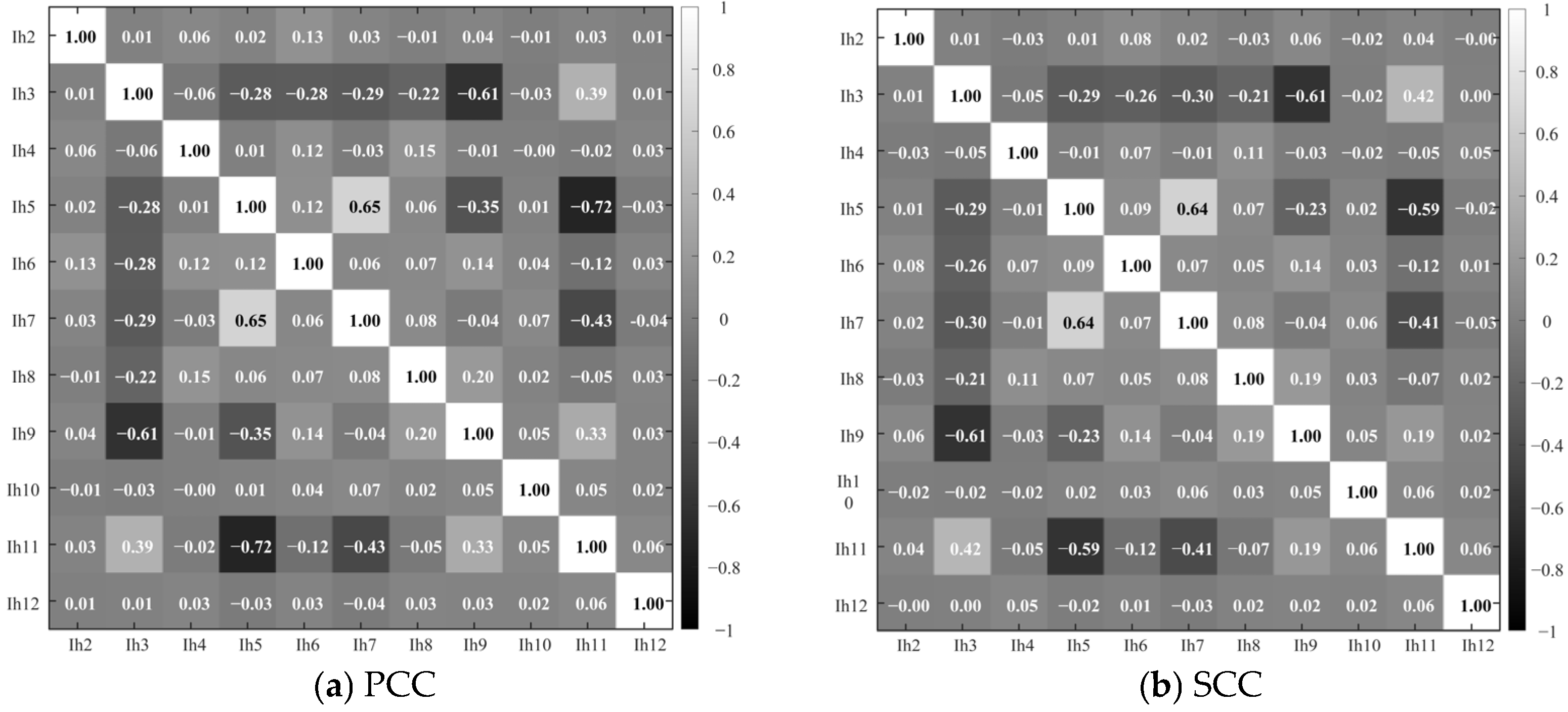
- Pearson Correlation Coefficient (PCC)
- Spearman Correlation Coefficient (SCC)
3.3. Adaptive Kernel Function Design
- Different feature scales—for instance, as demonstrated by the analysis in Figure 3, lower-order harmonic currents typically have larger magnitudes, while higher-order components are relatively smaller.
- Different data distributions—harmonic currents of different orders may follow distinct statistical patterns.
- Initial setting: During the definition of the model, initial parameters may be set to some predefined values.
- Optimization process: Parameters are adjusted through optimization algorithms. Specifically, first, the optimization algorithm adjusts the parameters based on the loss function (such as negative log-likelihood). Next, parameter updates occur, and in each iteration, the optimization algorithm computes the gradient of the loss function with respect to the parameters and adjusts the parameters accordingly.
3.4. Adaptive Multi-Task Gaussian Process Regression for General Probabilistic Harmonic Modeling
- Data Preparation: Preprocess the acquired harmonic signals, construct the multi-task output matrix, and partition the dataset into training and testing sets;
- Model Design: Select a covariance function suitable for multi-task modeling and adopt the adaptive Matern kernel to capture the smoothness and periodic characteristics of the harmonic signals;
- Hyperparameter Optimization: Optimize the task-specific length scales, covariance matrix parameters, and noise variances using maximum likelihood estimation or Bayesian optimization techniques;
- Model Training: Compute the covariance matrix of the training set and derive the posterior distribution based on Equations (16) and (17) to obtain the predictive mean and variance;
- Model Evaluation: Assess the prediction accuracy using test data, with performance metrics such as Mean Squared Error (MSE) and Mean Absolute Percentage Error (MAPE).
4. Case Study
4.1. Performance Analysis of the Improved Model
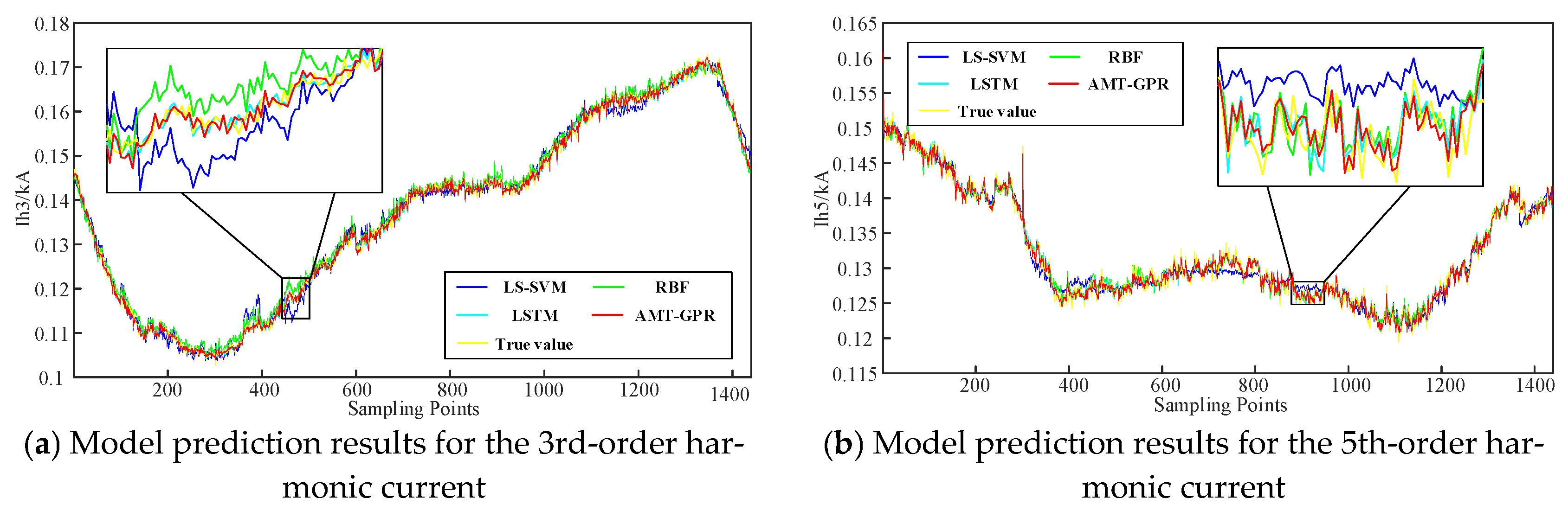
4.2. Comparison with Other Modeling Methods
4.3. Analysis of the Impact of Data Conditions on Model Performance
- Gaussian Process Regression (GPR) is a Bayesian non-parametric model that, unlike traditional machine learning methods such as neural networks, does not require a large amount of data to optimize parameters. Instead, GPR models the relationships between input data points through a kernel function. As a result, its predictions rely on data distribution rather than parameter fitting, allowing for reasonable prediction performance even with limited data.
- AMT-GPR is a multi-task learning method that models inter-task relationships by sharing the kernel function. This enables information sharing across tasks, so that even when the data for a single task is sparse, the model can leverage data from other tasks for auxiliary learning, thereby improving robustness.
- The introduction of an adaptive kernel function allows the model to maintain stable performance under varying data sizes, reducing its sensitivity to data quantity. The adaptive mechanism enables the model to reduce complexity and avoid overfitting with limited data, while enhancing accuracy and generalization capability when more data are available.
- From a statistical perspective, as the number of harmonic samples increases, the statistical characteristics of the sample (e.g., mean, variance) more closely approximate those of the population. This implies that larger datasets yield estimates that are closer to the true values, thereby reducing prediction errors;
- From the perspective of model training, expanding the dataset enhances the model’s capacity to capture harmonic characteristics, thereby improving prediction accuracy;
- In terms of generalization, increasing the sample size helps to mitigate overfitting and improves the model’s generalization ability.
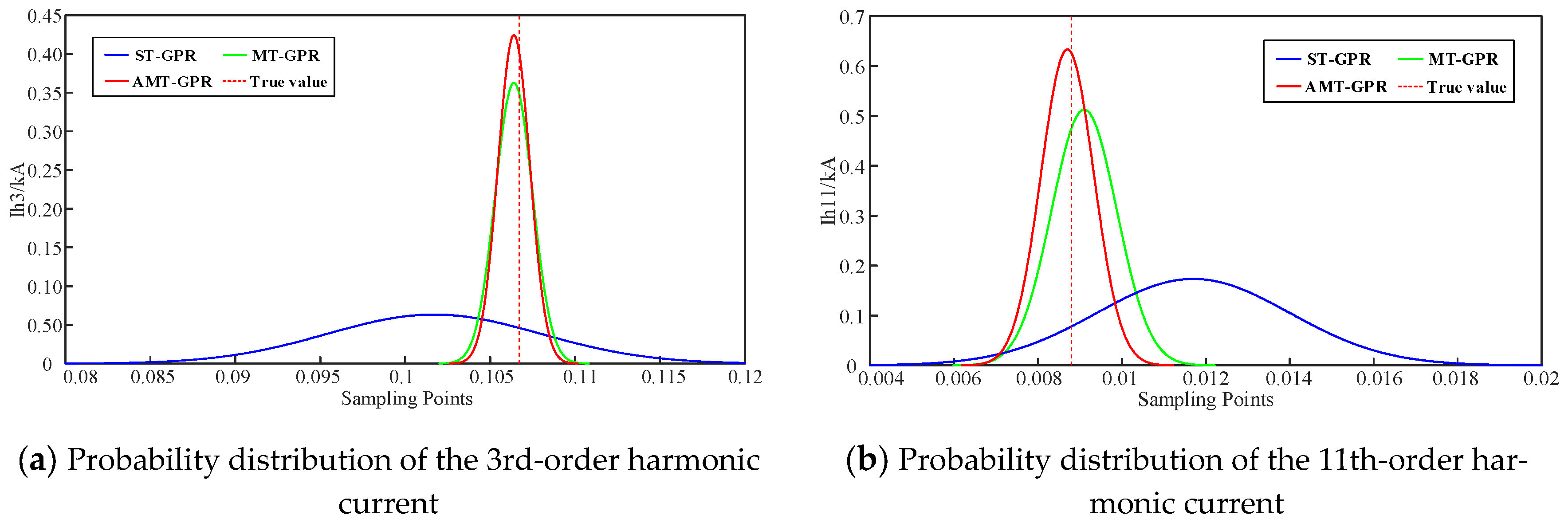
4.4. Probabilistic Modeling of Harmonic Sources
5. Conclusions
- Harmonic Characteristic Analysis: Based on measured data from a high-voltage substation, the time-varying characteristics of harmonics generated by aggregated loads are analyzed. The results reveal a strong correlation between harmonic currents and system load variations, providing a solid data foundation for harmonic modeling.
- Model Design: The proposed AMT-GPR method assigns independent and trainable length-scale parameters to each harmonic task, enabling adaptive feature scale learning. This design substantially improves model flexibility and adaptability across different harmonic orders.
- Performance Validation: Through comparative experiments with ST-GPR, MT-GPR, and other data-driven approaches (including LS-SVM, RBF, and LSTM), AMT-GPR demonstrates superior performance in prediction accuracy, uncertainty quantification, and computational efficiency. The results show that AMT-GPR performs well for both low- and high-order harmonics and exhibits strong robustness under small training datasets.
- Probabilistic Modeling: Based on the AMT-GPR prediction results, Gaussian probability distributions of harmonic currents are constructed, providing a reliable theoretical foundation for subsequent probabilistic harmonic power flow analysis.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shao, Z.; Xu, H.; Xiao, S.; Wu, G.; Zhang, Y. Harmonic problems in a new energy power grid. Power Syst. Prot. Control 2021, 49, 178–187. [Google Scholar] [CrossRef]
- Valavi, M.; Devillers, E.; Besnerais, J.L.; Nysveen, A.; Nilsen, R. Influence of converter topology and carrier frequency on airgap field harmonics, magnetic forces, and vibrations in converter-fed hydropower generator. IEEE Trans. Ind. Appl. 2018, 54, 2202–2214. [Google Scholar] [CrossRef]
- Domínguez-Crespo, M.A.; Rodríguez, E.; Torres-Huerta, A.M.; Soni-Castro, I.J.; Brachetti-Sibaja, S.B.; Narro-García, R.; López-Oyama, A.B. Production of BN nanostructures by pulsed laser ablation in liquids: Influence of the applied Nd: YAG harmonics on the structural, optical and photoluminescence properties. Ceram. Int. 2020, 46, 21667–21680. [Google Scholar] [CrossRef]
- Zhang, W.; Xiong, Y.; Li, C.; Yao, W.; Wen, J.; Gao, D. Continuous commutation failure suppression and coordinated recovery of multi-infeed DC system based on improved VDCOL. Power Syst. Prot. Control 2020, 48, 63–72. [Google Scholar] [CrossRef]
- Chen, L.; He, H.; Wang, L.; Chen, H. Fault isolation method of a hybrid HVDC system based on the coordination of a fault current limiter and a DC circuit breaker. Power Syst. Prot. Control 2020, 48, 119–127. [Google Scholar] [CrossRef]
- Hiyama, T.; Hammam, M.S.A.A.; Ortmeyer, T.H. Distribution system modeling with distributed harmonic sources. IEEE Trans. Power Deliv. 1992, 4, 1297–1304. [Google Scholar] [CrossRef]
- Salles, D.; Jiang, C.; Xu, W.; Freitas, W.; Mazin, H.E. Assessing the collective harmonic impact of modern residential loads—Part I: Methodology. IEEE Trans. Power Deliv. 2012, 27, 1937–1946. [Google Scholar] [CrossRef]
- Jiang, C.; Salles, D.; Xu, W.; Freitas, W. Assessing the collective harmonic impact of modern residential loads—Part II: Applications. IEEE Trans. Power Deliv. 2012, 27, 1937–1946. [Google Scholar] [CrossRef]
- Thunberg, E.; Soder, L. Norton approach to distribution network modeling for harmonic studies. IEEE Trans. Power Deliv. 1999, 14, 272–277. [Google Scholar] [CrossRef]
- Fauri, M. Harmonic modelling of non-linear load by means of crossed frequency admittance matrix. IEEE Trans. Power Syst. 1997, 12, 1632–1638. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, G.; Xu, W.; Mayordomo, J.G. A harmonically coupled admittance matrix model for AC/DC converters. IEEE Trans. Power Syst. 2007, 22, 1574–1582. [Google Scholar] [CrossRef]
- Sun, Y.; Li, J.; Yin, Z.; Wang, G. A frequency domain harmonic model for uncontrolled rectifier in AC/DC/AC converter. Proc. CSEE 2015, 35, 5483–5491. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, F.; Li, J.; Kun, Z. Unified harmonic models and operational mode determination for the three-phase uncontrolled voltage source converters. Proc. CSEE 2016, 36, 3413–3421+3360. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, L.; Xie, X.; Feng, Z.; Wang, S. The collective harmonic evaluation of residential load based on the harmonic coupling dominant component model. Proc. CSEE 2019, 39, 4775–4785+4979. [Google Scholar] [CrossRef]
- Xie, X.; Sun, Y.; Zhang, L.; He, J.; Zhang, Y. Self-adaptive harmonic modeling of the residential nonlinear load. Proc. CSEE 2020, 40, 2479–2489. [Google Scholar] [CrossRef]
- Liao, Y.; Hu, J.; Zhang, H. Time-varying parameter model of AC electrical arc furnace for power quality predictions and analysis. Electr. Eng. 2016, 17, 41–46. [Google Scholar]
- Wang, J.; Shu, H.; Lin, M.; Xueyun, C. Modeling and simulation of AC arc furnace for dynamic power quality studies. Trans. China Electrotech. Soc. 2003, 18, 53–58. [Google Scholar] [CrossRef]
- King, P.E.; Ochs, T.L.; Hartman, A.D. Chaotic response in electric arc furnaces. J. Appl. Phys. 1994, 76, 2059–2065. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, J. A novel chaotic model of AC electric arc furnace for power quality study. In Proceedings of the 2007 International Conference on Electrical Machines and Systems (ICEMS), Seoul, Republic of Korea, 8–11 October 2007; pp. 106–110. [Google Scholar]
- Lin, C.; Zhang, Y.; Shao, Z.; Lin, C.; Zhang, Y. An ultra-high-power electric arc furnace model for low-frequency non-stationary inter-harmonics studies. Electr. Power 2020, 53, 1–8. [Google Scholar]
- Nian, H.; Zhou, Q.; Wu, C.; Zhu, Q. The modeling and characteristic analysis of harmonic current of DFIG based wind turbine in grid-connected mode. Proc. CSEE 2019, 39, 5037–5048+5285. [Google Scholar] [CrossRef]
- Zhang, B. Research on Harmonic Dynamic Model and Resonance Analysis of Wind Parks. Ph.D. Thesis, Shandong University, Jinan, China, 2019. [Google Scholar]
- Tao, S.; Zhu, X.; Chen, H.; Xu, Y. Dead-time coupling harmonic source modeling of grid-connected Inverter. Proc. CSEE 2024, 1–14. [Google Scholar]
- Che, Q.; Yang, H. Assessing the harmonic emission level based on robust regression method. Proc. CSEE 2004, 24, 43–46+53. [Google Scholar]
- Ortega, J.M.M.; Exposito, A.G.; Garcia, A.L.T.; Payan, M.B. A state estimation approach to harmonic polluting load characterization in distribution systems. IEEE Trans. Power Syst. 2005, 20, 765–772. [Google Scholar]
- Huang, S.; Xu, Y. Assessing harmonic impedance and the harmonic emission level based on partial least-squares regression method. Proc. CSEE 2007, 27, 93–97. [Google Scholar]
- Feng, F.; Xie, X. Assessment of network harmonic emission level via enhanced partial least-squares regression method. Metrol. Meas. Tech. 2014, 41, 33–35. [Google Scholar]
- Hua, H.C.; Jia, X.F.; An, H.Q.; Zhang, S.G. Determining harmonic contributions based on complex least squares method. Proc. CSEE 2013, 33, 149–155. [Google Scholar] [CrossRef]
- Yongle, A.; Yudong, W.; Jingjing, D.; Wang, W. A method for assessing harmonic emission level based on robust regression of LTS initial value. Power Syst. Prot. Control 2015, 43, 99–105. [Google Scholar]
- Moreno, M.A.; Usaola, J. A new balanced harmonic load flow including nonlinear loads modeled with RBF networks. IEEE Trans. Power Deliv. 2004, 19, 686–693. [Google Scholar] [CrossRef]
- Yong, Z.; Haozhong, C.; Naicheng, G. Generalized growing and pruning RBF neural network based harmonic source modeling. Proc. CSEE 2005, 25, 42–46. [Google Scholar]
- Maciej, K.; Dariusz, G. Application of shallow neural networks in electric arc furnace modeling. IEEE Trans. Ind. Appl. 2022, 58, 6814–6823. [Google Scholar] [CrossRef]
- Xie, K.; Yang, H.; Zhang, Y. Harmonic source modeling based on generalized regression neural network. Adv. Technol. Electr. Eng. Energy 2012, 31, 64–67. [Google Scholar]
- Zhang, Y.; Ou, J.; Chen, S.; Jie, K.; Liu, S. A data-driven harmonic source modeling method based on joint time-frequency features extraction. Proc. CSEE 2025, 1–14. [Google Scholar]
- Lianqing, Z.; Ping, W.; Xiaolong, L. Application of least squares support vector machine to harmonic sources modeling based on genetic algorithm. Power Syst. Prot. Control 2011, 39, 52–56. [Google Scholar]
- Yang, P.; Wang, X.; Zhao, X. Research on harmonic prediction of the grid-connected photovoltaic system based on deep learning. Power Syst. Clean Energy 2022, 38, 71–80. [Google Scholar]


| Model | Harmonic Order | MPE (%) | MAPE (%) | MSE | CP (%) | AIW | Training Time (s) |
|---|---|---|---|---|---|---|---|
| ST-GPR | 3th | 7.16 | 1.45 | 2.45 | 96.0 | 10.09 | 21.7 |
| 5th | 11.35 | 1.08 | 1.86 | 87.4 | 7.32 | 22.6 | |
| 7th | 13.98 | 2.65 | 1.12 | 88.7 | 3.82 | 19.2 | |
| 9th | 14.29 | 1.83 | 0.61 | 99.4 | 3.50 | 25.6 | |
| 11th | 45.02 | 8.40 | 1.33 | 99.2 | 6.71 | 26.5 | |
| MT-GPR | 3th | 6.55 | 0.61 | 1.08 | 96.2 | 4.56 | 18.7 |
| 5th | 7.83 | 0.46 | 0.85 | 96.1 | 3.25 | ||
| 7th | 8.74 | 1.40 | 0.57 | 94.1 | 2.18 | ||
| 9th | 5.94 | 1.20 | 0.40 | 96.0 | 1.62 | ||
| 11th | 25.08 | 3.73 | 0.68 | 96.1 | 3.15 | ||
| AMT-GPR | 3th | 3.46 | 0.49 | 0.87 | 96.5 | 3.88 | 16.2 |
| 5th | 1.75 | 0.40 | 0.66 | 97.1 | 2.94 | ||
| 7th | 5.58 | 1.20 | 0.48 | 96.6 | 2.08 | ||
| 9th | 5.66 | 1.16 | 0.38 | 95.8 | 1.57 | ||
| 11th | 19.12 | 3.70 | 0.60 | 95.8 | 1.61 |
| Model | Harmonic Order | MPE (%) | MAPE (%) | MSE |
|---|---|---|---|---|
| LS-SVM | 3th | 6.28 | 1.00 | 1.76 |
| 5th | 5.68 | 0.69 | 1.18 | |
| 7th | 9.72 | 1.58 | 0.64 | |
| RBF | 3th | 4.01 | 0.73 | 1.54 |
| 5th | 2.36 | 0.46 | 0.81 | |
| 7th | 6.63 | 1.30 | 0.54 | |
| LSTM | 3th | 3.95 | 0.62 | 1.06 |
| 5th | 2.64 | 0.40 | 0.67 | |
| 7th | 6.31 | 1.20 | 0.49 | |
| AMT-GPR | 3th | 3.46 | 0.49 | 0.87 |
| 5th | 1.75 | 0.40 | 0.66 | |
| 7th | 5.58 | 1.20 | 0.48 |
| Model | Harmonic Order | MPE (%) | MAPE (%) | MSE |
|---|---|---|---|---|
| LS-SVM | 3th | 12.01 | 3.08 | 4.86 |
| 5th | 7.57 | 1.21 | 2.11 | |
| 7th | 16.86 | 2.93 | 1.25 | |
| RBF | 3th | 5.36 | 1.41 | 2.35 |
| 5th | 7.38 | 0.98 | 1.72 | |
| 7th | 13.89 | 2.61 | 1.08 | |
| LSTM | 3th | 5.10 | 0.78 | 1.38 |
| 5th | 6.45 | 0.57 | 1.03 | |
| 7th | 8.43 | 1.54 | 0.63 | |
| AMT-GPR | 3th | 3.77 | 0.59 | 1.02 |
| 5th | 5.74 | 0.44 | 0.85 | |
| 7th | 6.54 | 1.32 | 0.54 |
| Model | ST-GPR | MT-GPR | AMT-GPR | True Value |
|---|---|---|---|---|
| Ih3 | N (1.017 × 10−1, 6.3 × 10−3) | N (1.064 × 10−1, 1.1 × 10−3) | N (1.064 × 10−1, 9.4 × 10−4) | 1.067 × 10−1 |
| Ih5 | N (1.391 × 10−1, 4.7 × 10−3) | N (1.415 × 10−1, 7.7 × 10−4) | N (1.414 × 10−1, 7.1 × 10−4) | 1.412 × 10−1 |
| Ih7 | N (3.32 × 10−2, 2.0 × 10−3) | N (3.54 × 10−2, 5.29 × 10−4) | N (3.54 × 10−2, 5.04 × 10−4) | 3.55 × 10−2 |
| Ih9 | N (2.58 × 10−2, 1.9 × 10−3) | N (2.60 × 10−2, 4.05 × 10−4) | N (2.58 × 10−2, 3.91 × 10−4) | 2.65 × 10−2 |
| Ih11 | N (1.17 × 10−2, 2.3 × 10−3) | N (9.10 × 10−3, 7.78 × 10−4) | N (8.70 × 10−4, 6.30 × 10−4) | 8.80 × 10−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, J.; Song, K.; Duan, J.; Wang, Y. An Adaptive Multi-Task Gaussian Process Regression Approach for Harmonic Modeling of Aggregated Loads in High-Voltage Substations. Energies 2025, 18, 4670. https://doi.org/10.3390/en18174670
Zheng J, Song K, Duan J, Wang Y. An Adaptive Multi-Task Gaussian Process Regression Approach for Harmonic Modeling of Aggregated Loads in High-Voltage Substations. Energies. 2025; 18(17):4670. https://doi.org/10.3390/en18174670
Chicago/Turabian StyleZheng, Jiahui, Kun Song, Jiaqi Duan, and Yang Wang. 2025. "An Adaptive Multi-Task Gaussian Process Regression Approach for Harmonic Modeling of Aggregated Loads in High-Voltage Substations" Energies 18, no. 17: 4670. https://doi.org/10.3390/en18174670
APA StyleZheng, J., Song, K., Duan, J., & Wang, Y. (2025). An Adaptive Multi-Task Gaussian Process Regression Approach for Harmonic Modeling of Aggregated Loads in High-Voltage Substations. Energies, 18(17), 4670. https://doi.org/10.3390/en18174670





