Overview of Deadbeat Predictive Control Technology for Permanent Magnet Synchronous Motor System
Abstract
1. Introduction
2. Composition of PMSM Drive System Based on Deadbeat Predictive Control
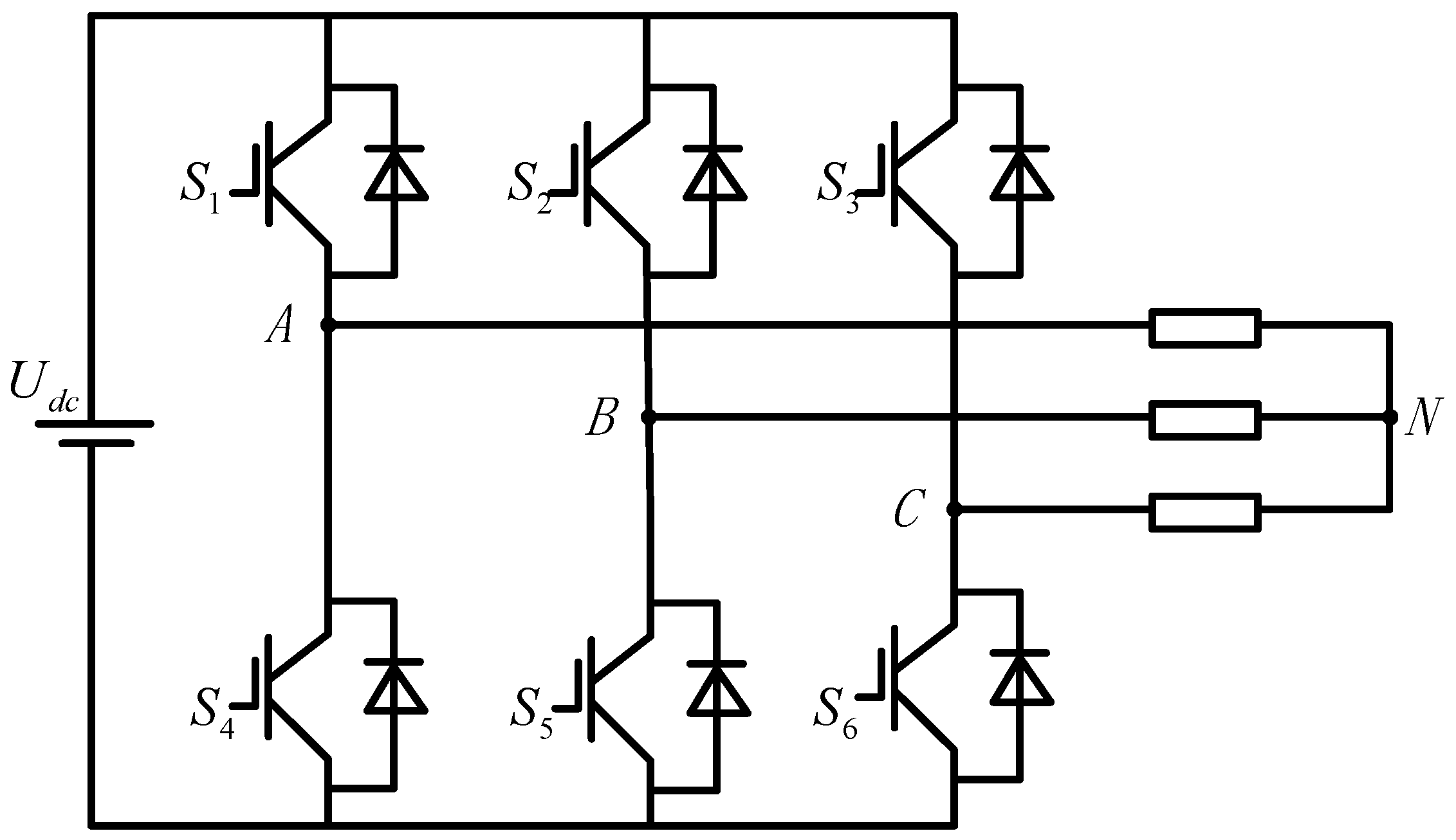
2.1. Composition of PMSM System
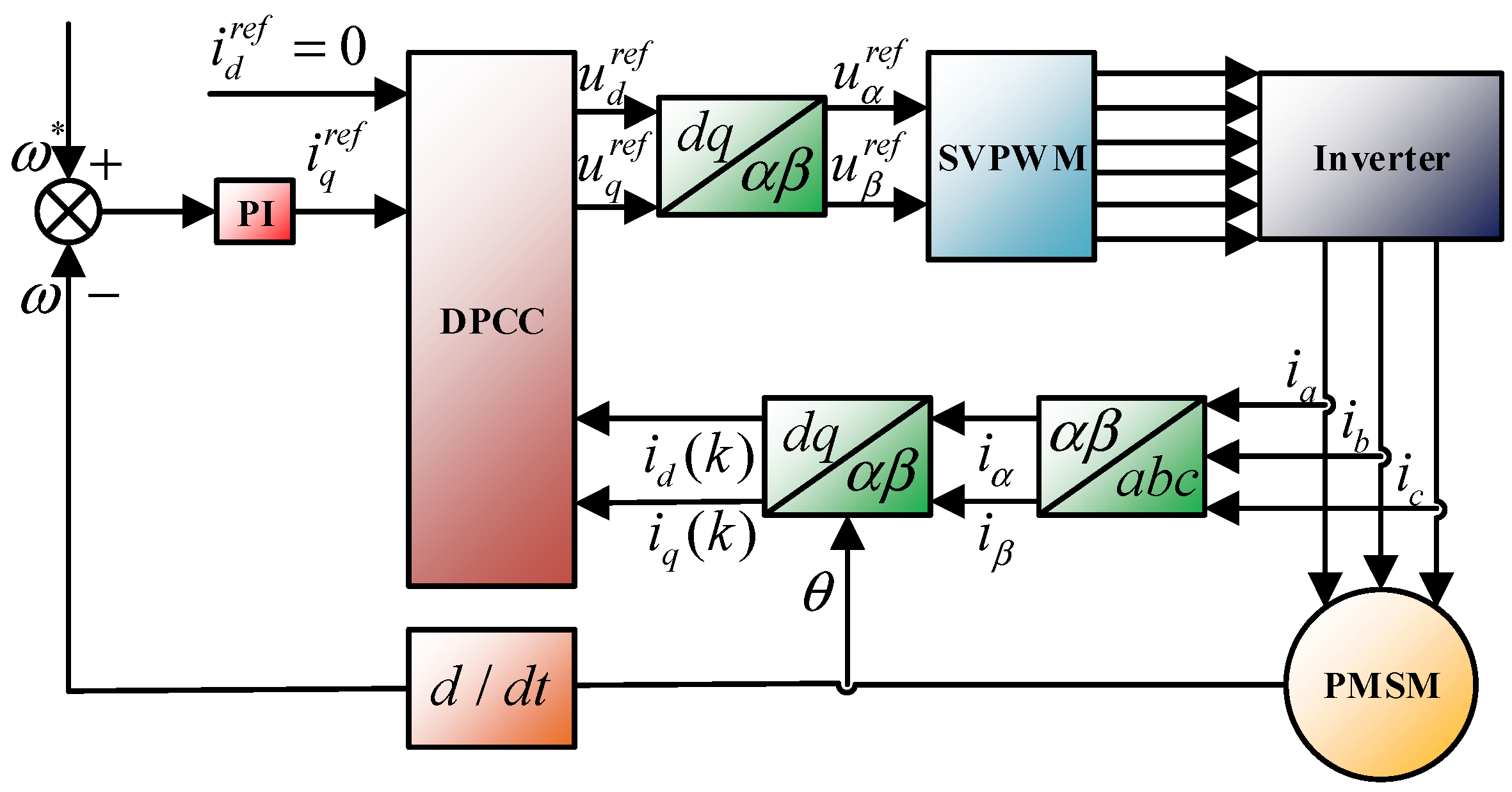
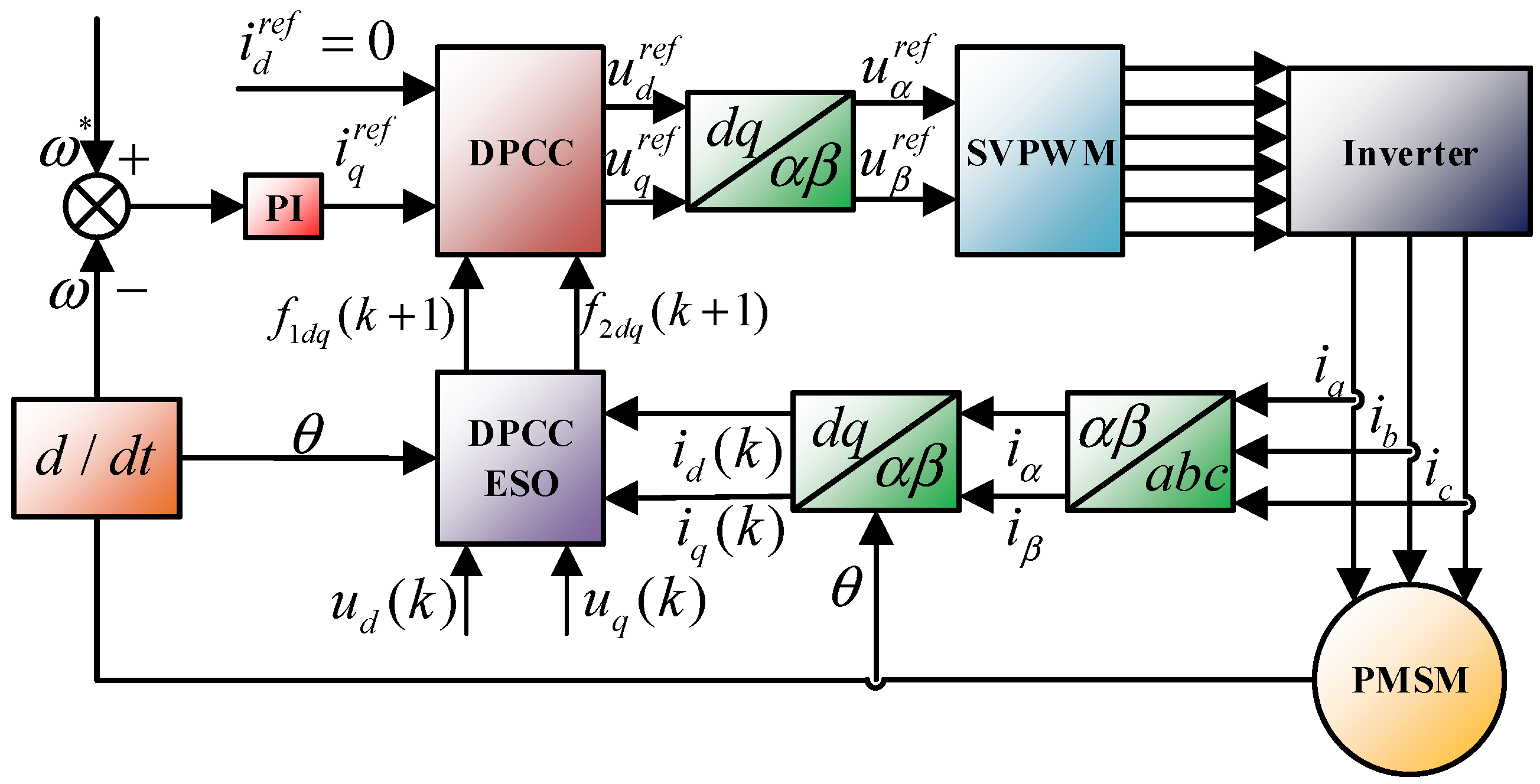
2.2. Conventional DPCC Model
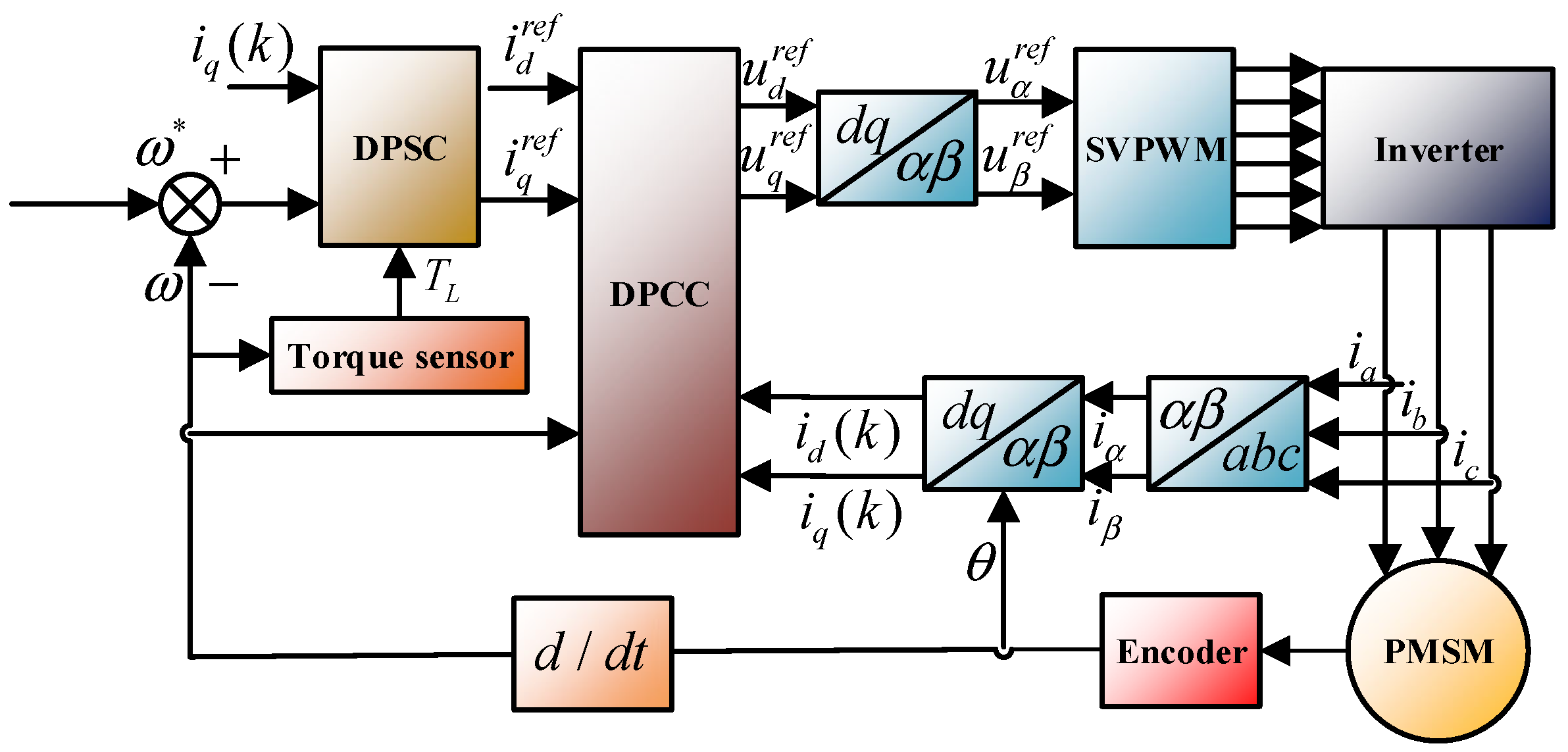
2.3. Conventional DPSC Model
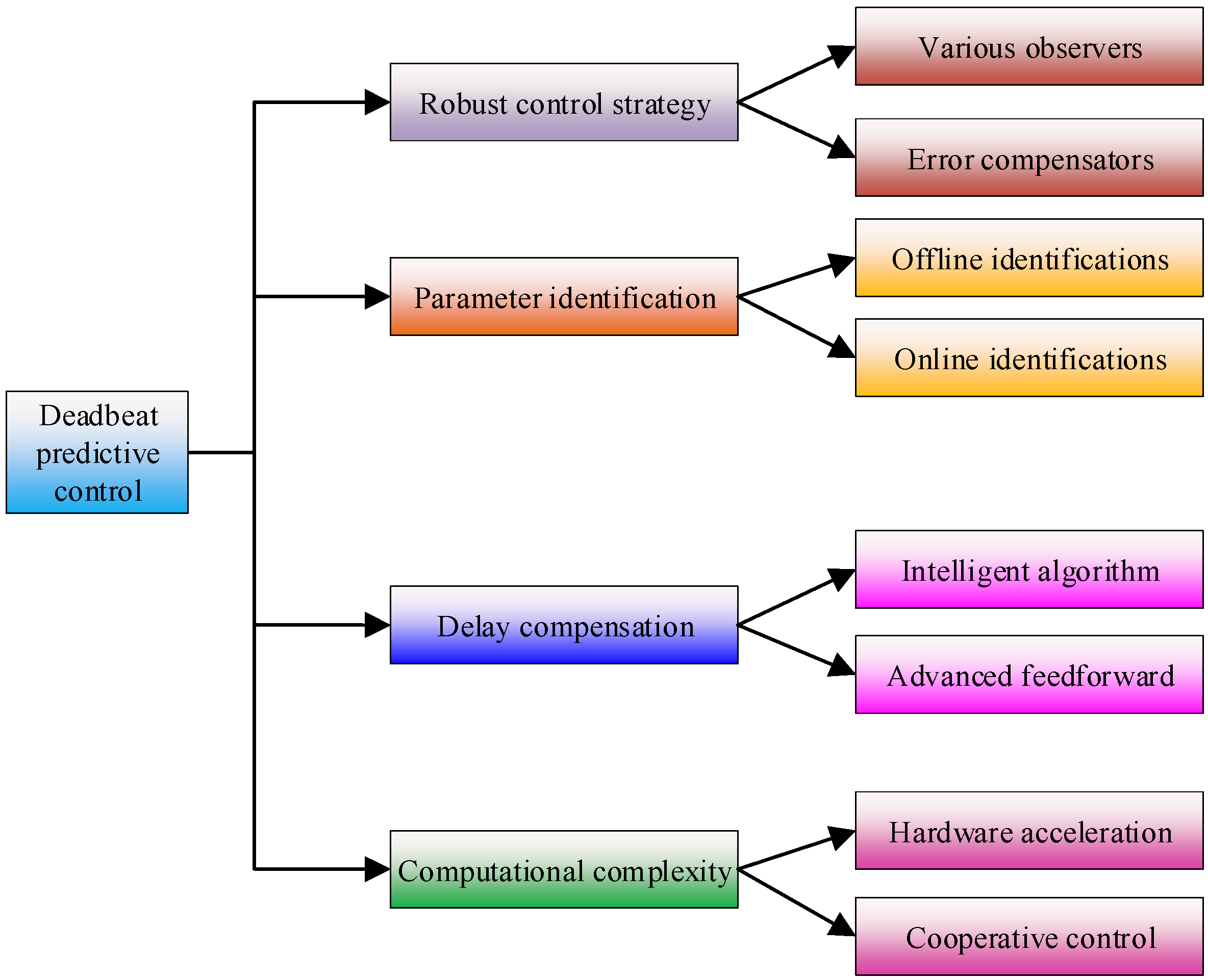
3. An Overview of the Recent Development for Deadbeat Predictive Control Methods of PMSM
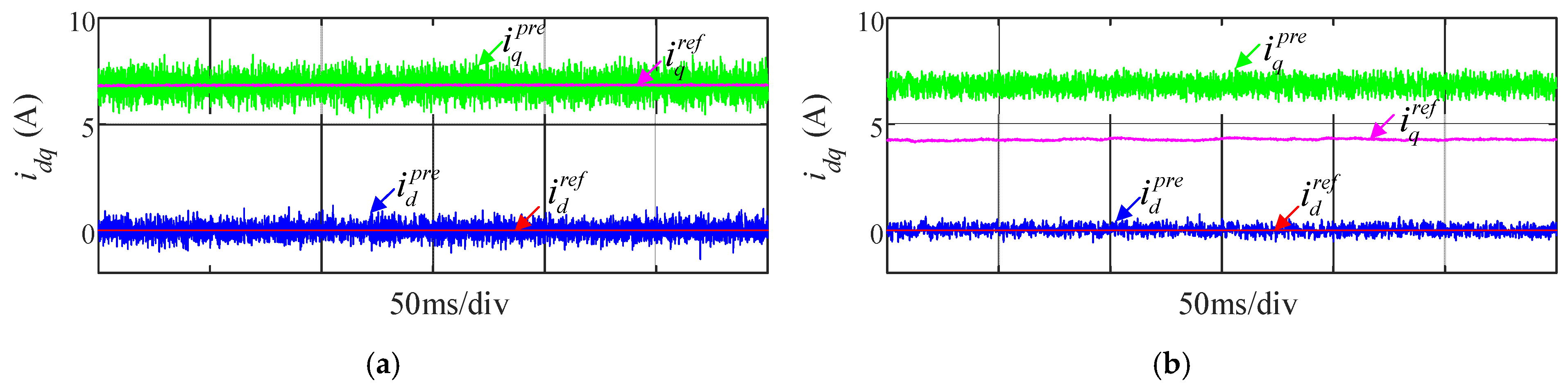
3.1. Deadbeat Predictive Current Control of PMSM
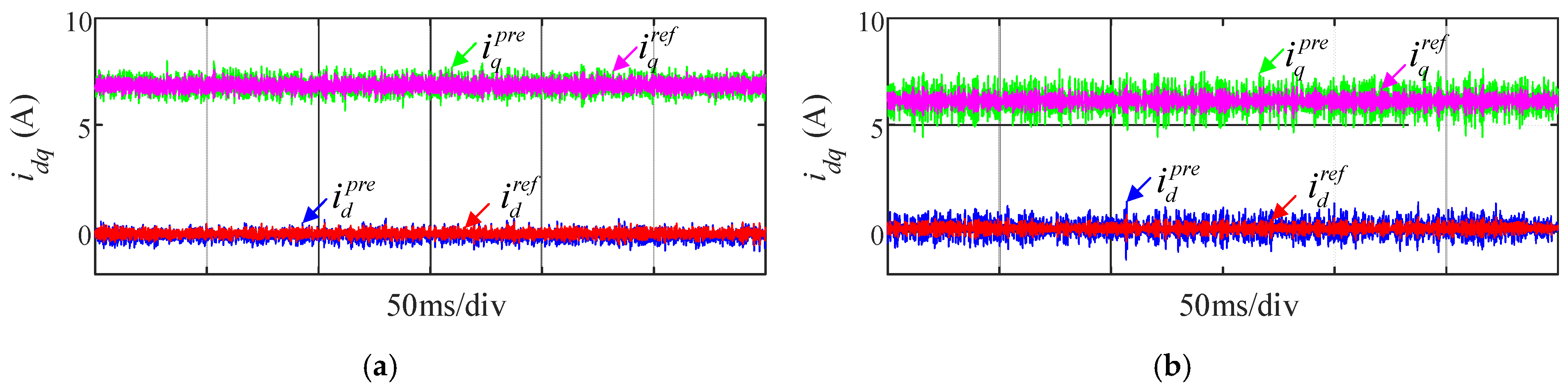
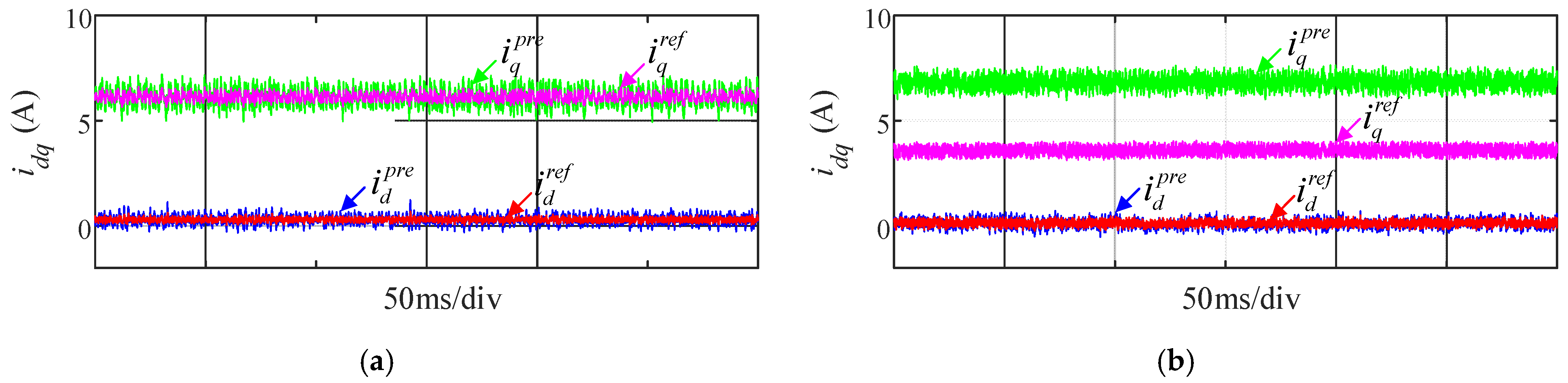
3.1.1. Robust Control Strategy
3.1.2. Delay Compensation
3.1.3. DPCC Based on Incremental Model
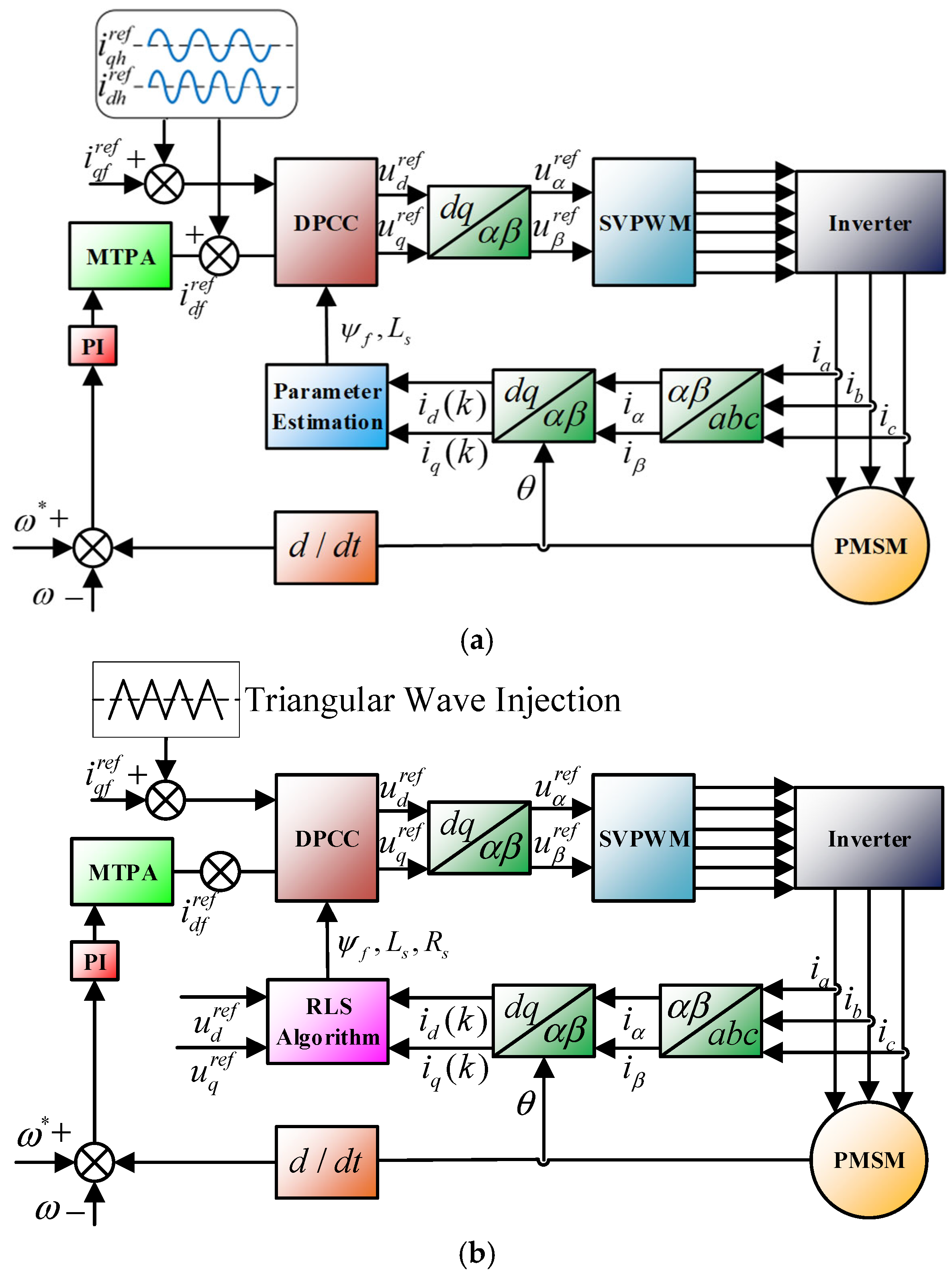
3.1.4. High Performance of DPSC
4. Future Directions
4.1. Enhancement of Robustness Against Model Uncertainties
4.2. Advanced Delay Compensation Techniques
4.3. Optimization and Improvement in Comprehensive Disturbance Observer
4.4. Multi-Objective Optimization Frameworks
4.5. Computationally Efficient Implementations
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
References
- Li, T.; Sun, X.; Lei, G.; Yang, Z.; Guo, Y.; Zhu, J. Finite-control-set model predictive control of permanent magnet synchronous motor drive systems—An overview. IEEE/CAA J. Autom. Sin. 2022, 9, 2087–2105. [Google Scholar] [CrossRef]
- Wu, G.; Huang, S.; Wu, Q.; Rong, F.; Zhang, C.; Liao, W. Robust predictive torque control of N*3-phase PMSM for high-power traction application. IEEE Trans. Power Electron. 2020, 35, 10799–10809. [Google Scholar] [CrossRef]
- Sun, X.; Xu, Z.; Pan, M.; Sun, C.; Lei, G. Medium-to-High Speed Range Sensorless Control of SRM Drives Based on Unaligned Rotor Position Estimation. IEEE Trans. Ind. Electron. 2025; early access. [Google Scholar] [CrossRef]
- Lei, G.; Zhu, J.G.; Guo, Y.G.; Liu, C.C.; Ma, B. A review of design optimization methods for electrical machines. Energies 2017, 10, 1962. [Google Scholar] [CrossRef]
- Sun, X.; Xu, Z.; Pan, M.; Cai, Y.; Jin, Z.; Tian, X. Driving-Style-Oriented Energy Management Strategy Based on Fuzzy Logic for Plug-in Hybrid Electric Buses. IEEE Trans. Ind. Electron. 2025; early access. [Google Scholar] [CrossRef]
- Yue, R.; Yao, M.; Zhang, T.; Shi, J.; Zhou, J.; Hu, J. Design and experiment of dual-row seedling Pick-Up device for High-Speed automatic transplanting machine. Agriculture 2024, 14, 942. [Google Scholar] [CrossRef]
- Niu, S.X.; Luo, Y.X.; Fu, W.N.; Zhang, X.D. An indirect reference vector-based model predictive control for a three-phase PMSM motor. IEEE Access 2020, 8, 29435–29445. [Google Scholar] [CrossRef]
- Jin, Z.; Sun, X.; Cai, Y.; Yao, M.; Tian, X. Simultaneous-Level Energy Management Optimization Considering Specific Urban Driving Cycles for PHEBs. IEEE/ASME Trans. Mechatron. 2024; early access. [Google Scholar] [CrossRef]
- Sun, X.; Xu, N.; Yao, M.; Cai, F.; Wu, M. Efficient feedback linearization control for an IPMSM of EVs based on improved firefly algorithm. ISA Trans. 2023, 134, 431–441. [Google Scholar] [CrossRef]
- Shao, L.; Hua, W.; Dai, N.; Tong, M.; Cheng, M. Mathematical Modeling of a 12-Phase Flux-Switching Permanent-Magnet Machine for Wind Power Generation. IEEE Trans. Ind. Electron. 2016, 63, 504–516. [Google Scholar] [CrossRef]
- Ding, X.F.; Guo, H.; Xiong, R.; Chen, F.D.; Zhang, D.H.; Gerada, C. A new strategy of efficiency enhancement for traction systems in electric vehicles. Appl. Energy 2017, 205, 880–891. [Google Scholar] [CrossRef]
- Hao, S.; Tang, Z.; Guo, S.; Ding, Z.; Su, Z. Model and method of fault signal diagnosis for blockage and slippage of rice threshing drum. Agriculture 2022, 12, 1968. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Y.; Ji, K.; Zhu, R. A Fault Diagnosis Method for a Differential Inverse Gearbox of a Crawler Combine Harvester Based on Order Analysis. Agriculture 2022, 12, 1300. [Google Scholar] [CrossRef]
- Trancho, E.; Ibarra, E.; Arias, A.; Kortabarria, I.; Prieto, P.; De Alegría, I.M.; Andreu, J.; López, I. Sensorless control strategy for light-duty EVs and efficiency loss evaluation of high frequency injection under standardized urban driving cycles. Appl. Energy 2018, 224, 647–658. [Google Scholar] [CrossRef]
- Shi, Z.; Sun, X.; Yang, Z.; Cai, Y.; Lei, G.; Zhu, J.; Lee, C.H.T. Design optimization of a spoke type axial-flux PM machine for in-wheel drive operation. IEEE Trans. Transp. Electrif. 2024, 10, 3770–3781. [Google Scholar] [CrossRef]
- Li, T.; Sun, X.; Su, Z.; Zha, X.; Dianov, A.; Prakht, V.; Demidova, G.; Ma, J. Model-Free Predictive Control for Harmonic Suppression of PMSMs Based on Adaptive Resonant Controller. IEEE Trans. Energy Convers. 2025; early access. [Google Scholar] [CrossRef]
- Wang, S. Nonlinear uncertainty estimator based robust control for PMSM servo mechanisms with prescribed performance. IEEE Trans. Transp. Electrific. 2023, 9, 2535–2543. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, G. Predictive DTC strategy with fault-tolerant function for six-phase and three-phase PMSM series-connected drive system. IEEE Trans. Ind. Electron. 2018, 65, 9101–9112. [Google Scholar] [CrossRef]
- Yang, S.; Zhai, C.; Gao, Y.; Dou, H.; Zhao, X.; He, Y.; Wang, X. Planting uniformity performance of motor-driven maize precision seeding systems. Int. J. Agric. Biol. Eng. 2022, 15, 101–108. [Google Scholar] [CrossRef]
- Yu, F.; Zhang, W.; Shen, Y.; Mao, J. A Nine-Phase Permanent Magnet Electric-Drive-Reconstructed Onboard Charger for Electric Vehicle. IEEE Trans. Energy Convers. 2018, 33, 2091–2101. [Google Scholar] [CrossRef]
- Hao, Z.; Zhu, H.; Cheng, Y.; Huang, L. Speed Control of Bearingless Permanent Magnet Synchronous Motor Based on Flux Strengthening and Voltage Regulation. IEEE Access 2018, 6, 72392–72401. [Google Scholar] [CrossRef]
- Hu, Y.; Li, Y.; Ma, X.; Li, X.; Huang, S. Flux-weakening control of dual three-phase PMSM based on vector space decomposition control. IEEE Trans. Power Electron. 2021, 36, 8428–8438. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, S.; An, X.; Su, Z.; Li, F. A robust DPCC and inductance identification method for SPMSM based on incremental model and current error compensation. IEEE Trans. Ind. Electron. 2025; early access. [Google Scholar] [CrossRef]
- Gu, M.; Wang, Z.; Xia, W.; Cheng, M. Analysis and Modeling of Switching Surges in PMSM Drives Due to Eddy-Current Reaction. IEEE Trans. Ind. Electron. 2025, 72, 5681–5692. [Google Scholar] [CrossRef]
- Yao, H.; Yan, Y.; Shi, T.; Zhang, G.; Wang, Z.; Xia, C. A novel SVPWM scheme for field-oriented vector-controlled PMSM drive system fed by cascaded H-bridge inverter. IEEE Trans. Power Electron. 2021, 36, 8988–9000. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, H.; Lin, X.; Su, Z.; Yao, M. Speed sensorless control based on model -free predictive controller for dual three-phase PMSMs. IEEE Trans. Ind. Electron. 2025; early access. [Google Scholar] [CrossRef]
- Han, J.; Wang, F. Design and testing of a small orchard tractor driven by a power battery. Eng. Agric. 2023, 43, e20220195. [Google Scholar] [CrossRef]
- Pang, Y.; Li, H.; Tang, P.; Chen, C. Irrigation scheduling of pressurized irrigation networks for minimizing energy consumption. Irrig. Drain. 2023, 72, 268–283. [Google Scholar] [CrossRef]
- Ping, Z.; Ma, Q.; Wang, T.; Huang, Y.; Lu, J.-G. Speed tracking control of permanent magnet synchronous motor by a novel two-step internal model control approach. Int. J. Control Autom. Syst. 2018, 16, 2754–2762. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, J.; Cheng, M.; Chau, K.T. Field-oriented control and direct torque control for paralleled VSIs fed PMSM drives with variable switching frequencies. IEEE Trans. Power Electron. 2016, 31, 2417–2428. [Google Scholar] [CrossRef]
- Lee, K. Fault-Tolerant Control for One-Phase Current Sensor Fault in Open-End Winding PMSM fed by Dual Inverter With a Common DC Bus. IEEE Trans. Power Electron. 2025, 40, 124–128. [Google Scholar] [CrossRef]
- Rubio, F.; Pereda, J.; Mora, A.; Rojas, F. Optimal Switching Sequence MPC of a Three- Port-Converter for Variable-Speed PMSM With Hybrid Energy Storage. IEEE Trans. Power Electron. 2025, 40, 5069–5079. [Google Scholar] [CrossRef]
- Zhang, Q.F.; Guo, H.H.; Guo, C.; Liu, Y.C.; Wang, D.; Lu, K.Y.; Zhang, Z.R.; Zhuang, X.Z.; Chen, D.Z. An adaptive proportionalintegral-resonant controller for speed ripple suppression of PMSM drive due to current measurement error. Int. J. Electr. Power Energy Syst. 2021, 129, 106866. [Google Scholar] [CrossRef]
- Casadei, D.; Profumo, F.; Serra, G.; Tani, A. FOC and DTC: Two viable schemes for induction motors torque control. IEEE Trans. Power Electron. 2002, 17, 779–787. [Google Scholar] [CrossRef]
- Xiang, Z.; Wei, J.; Zhu, X. Torque ripple suppression of a PM vernier machine from Perspective of time and space harmonic magnetic field. IEEE Trans. Ind. Electron. 2024, 71, 10150–10161. [Google Scholar] [CrossRef]
- Yu, Y.; Hao, S.; Guo, S.; Tang, Z.; Chen, S. Motor torque distribution strategy for different tillage modes of agricultural electric tractors. Agriculture 2022, 12, 1373. [Google Scholar] [CrossRef]
- Shinohara, A.; Inoue, Y.; Morimoto, S.; Sanada, M. Maximum Torque Per Ampere Control in Stator Flux Linkage Synchronous Frame for DTC-Based PMSM Drives Without Using q-Axis Inductance. IEEE Trans. Ind. Appl. 2017, 53, 3663–3671. [Google Scholar] [CrossRef]
- Ding, L.; Li, Y.W.; Zargari, N.R. Discrete-time SMO sensorless control of current source converter-fed PMSM drives with low switching frequency. IEEE Trans. Ind. Electron. 2021, 68, 2120–2129. [Google Scholar] [CrossRef]
- Wu, L.; Liu, J.; Vazquez, S.; Mazumder, S.K. Sliding mode control in power converters and drives: A review. IEEE/CAA J. Autom. Sin. 2022, 9, 392–406. [Google Scholar] [CrossRef]
- Lian, S.; Meng, W.; Lin, Z.; Shao, K.; Zheng, J.; Li, H.; Lu, R. Adaptive attitude control of a quadrotor using fast nonsingular terminal sliding mode. IEEE Trans. Ind. Electron. 2022, 69, 1597–1607. [Google Scholar] [CrossRef]
- Xu, W.; Junejo, A.K.; Liu, Y.; Hussien, M.G.; Zhu, J. An efficient antidisturbance sliding-mode speed control method for PMSM drive systems. IEEE Trans. Power Electron. 2021, 36, 6879–6891. [Google Scholar] [CrossRef]
- Wu, S.; Su, X.; Wang, K. Time-dependent global nonsingular fixed-time terminal sliding mode control-based speed tracking of permanent magnet synchronous motor. IEEE Access 2020, 8, 186408–186420. [Google Scholar] [CrossRef]
- Gou, L.; Wang, C.; Zhou, M.; You, X. Integral sliding mode control for starting speed sensorless controlled induction motor in the rotating condition. IEEE Trans. Power Electron. 2020, 35, 4105–4116. [Google Scholar] [CrossRef]
- Xu, P.L.; Zhu, Z.Q. Novel Carrier Signal Injection Method Using Zero-Sequence Voltage for Sensorless Control of PMSM Drives. IEEE Trans. Ind. Electron. 2016, 63, 2053–2061. [Google Scholar] [CrossRef]
- Verrelli, C.M.; Bifaretti, S.; Carfagna, E.; Lidozzi, A.; Solero, L.; Crescimbini, F.; Di Benedetto, M. Speed Sensor Fault Tolerant PMSM Machines: From Position-Sensorless to Sensorless Control. IEEE Trans. Ind. Appl. 2019, 55, 3946–3954. [Google Scholar] [CrossRef]
- Luo, B.; Yang, X.; Zhou, Y. Model-Free Predictive Current Control of Permanent Magnet Synchronous Motor Based on Estimation of Current Variations. IEEE Trans. Ind. Electron. 2024, 71, 8395–8405. [Google Scholar] [CrossRef]
- Sun, X.; Li, T.; Zhu, Z.; Lei, G.; Guo, Y.; Zhu, J. Speed sensorless model predictive current control based on finite position set for PMSHM Drives. IEEE Trans. Transport. Electrific. 2021, 7, 2743–2752. [Google Scholar] [CrossRef]
- Sun, X.; Cai, F.; Yang, Z.; Tian, X. Finite position control of interior permanent magnet synchronous motors at low speed. IEEE Trans. Power Electron. 2022, 37, 7729–7738. [Google Scholar] [CrossRef]
- Novak, Z. Confidence Weighted Learning Entropy for Fault-Tolerant Control of a PMSM With a High-Resolution Hall Encoder. IEEE Trans. Ind. Electron. 2024, 71, 5176–5186. [Google Scholar] [CrossRef]
- Zhang, H.; Ji, W.; Xu, B.; Yu, X. Optimizing contact force on an apple picking robot end-effector. Agriculture 2024, 14, 996. [Google Scholar] [CrossRef]
- Shi, J.; Hu, J.; Li, J.; Liu, W.; Yue, R.; Zhang, T.; Yao, M. Design and experiment of planting mechanism of automatic transplanter for densely planted vegetables. Agriculture 2024, 14, 1357. [Google Scholar] [CrossRef]
- Jin, L.; Mao, Y.; Wang, X.; Shi, P.; Lu, L.; Wang, Z. Optimization-Based Maximum-Torque Fault-Tolerant Control of Dual Three-Phase PMSM Drives Under Open-Phase Fault. IEEE Trans. Power Electron. 2023, 38, 3653–3663. [Google Scholar] [CrossRef]
- Wu, L.; Guo, Y.; Huang, X.; Fang, Y.; Liu, J. Harmonic Torque Suppression Methods for Single-Phase Open-Circuit Fault-Tolerant Operation of PMSM Considering Third Harmonic BEMF. IEEE Trans. Power Electron. 2021, 36, 1116–1129. [Google Scholar] [CrossRef]
- He, Y.; Zhu, Q.; Fu, W.; Luo, C.; Cong, Y.; Qin, W.; Meng, Z.; Chen, L.; Zhao, C.; Wu, G. Design and experiment of a control system for sweet potato seedling-feeding and planting device based on a pre-treatment seedling belt. J. Agric. Eng. 2022, 53, 1261. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, X.; Wang, X.; Zhang, T.; Wang, Z.; Mao, Y. Online Current Optimization Based Fault-Tolerant Control of Standard PMSM Drives. IEEE Trans. Ind. Electron. 2024, 71, 15521–15531. [Google Scholar] [CrossRef]
- Liu, S.; Liu, C.; Huang, Y.; Zhao, H. Model predictive two-target current control for OW-PMSM. IEEE Trans. Power Electron. 2021, 36, 3224–3235. [Google Scholar] [CrossRef]
- Li, X.; Tian, W.; Gao, X.; Yang, Q.; Kennel, R. A generalized observer-based robust predictive current control strategy for PMSM drive system. IEEE Trans. Ind. Electron. 2022, 69, 1322–1332. [Google Scholar] [CrossRef]
- Su, Z.; Sun, X.; Lei, G.; Yao, M. Model-free predictive current control for dual three-phase PMSM drives with an optimal modulation pattern. IEEE Trans. Ind. Electron. 2024, 71, 10140–10149. [Google Scholar] [CrossRef]
- Sun, X.; Huang, Z.; Yang, Z.; Lei, G.; Li, T. Improved Model-Free Predictive Current Control for Suppressing Inverter Nonlinearity and Parametric Time-Varying of PMSM Drive Systems. IEEE Trans. Ind. Electron. 2025; early access. [Google Scholar] [CrossRef]
- Lian, C.; Guo, L.; Xu, G.; Xiao, F.; Wang, R.; Gao, S.; Liu, J.; Zhang, W. Current Harmonic Minimum Pulse Width Modulation for Dual Three-Phase PMSM System With 3L-NPC Inverter and Output Filter. IEEE Trans. Power Electron. 2025, 40, 2847–2859. [Google Scholar] [CrossRef]
- Zhou, Z.; Xia, C.; Yan, Y.; Wang, Z.; Shi, T. Torque Ripple Minimization of Predictive Torque Control for PMSM With Extended Control Set. IEEE Trans. Ind. Electron. 2017, 64, 6930–6939. [Google Scholar] [CrossRef]
- Wang, X.; Fang, X.; Lin, S.; Lin, F.; Yang, Z. Predictive common-mode voltage suppression method based on current ripple for permanent magnet synchronous motors. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 946–955. [Google Scholar] [CrossRef]
- Li, T.; Sun, X.; Yao, M.; Guo, D.; Sun, Y. Improved Finite Control Set Model Predictive Current Control for Permanent Magnet Synchronous Motor with Sliding Mode Observer. IEEE Trans. Transp. Electrific. 2024, 10, 699–710. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, X.; Xiao, D.; Ma, D.; Yang, X.; Wang, Z. Model Predictive Control of Five-Level Open-End Winding PMSM Drives. IEEE Trans. Transp. Electrific. 2024, 10, 10115–10124. [Google Scholar] [CrossRef]
- Deng, J.; Ni, L.; Bai, X.; Jiang, H.; Xu, L. Simultaneous analysis of mildew degree and aflatoxin B1 of wheat by a multi-task deep learning strategy based on microwave detection technology. LWT 2023, 184, 115047. [Google Scholar] [CrossRef]
- Yao, C.; Ma, G.; Sun, Z.; Luo, J.; Ren, G.; Xu, S. Weighting Factors Optimization for FCS-MPC in PMSM Drives Using Aggregated Residual Network. IEEE Trans. Power Electron. 2024, 39, 1292–1307. [Google Scholar] [CrossRef]
- Xu, S.; Yao, C.; Ren, G.; Sun, Z.; Wu, S.; Ma, G. Weighting Factors Autotuning of FCS-MPC for Hybrid ANPC Inverter in PMSM Drives Based on Deep Residual Networks. IEEE Trans. Power Electron. 2024, 39, 16540–16552. [Google Scholar] [CrossRef]
- Jiang, X.; Yang, Y.; Fan, M.; Ji, A.; Xiao, Y.; Zhang, X.; Zhang, W.; Garcia, C.; Vazquez, S.; Rodriguez, J. An Improved Implicit Model Predictive Current Control with Continuous Control Set for PMSM Drives. IEEE Trans. Power Electron. 2022, 8, 2444–2455. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, X.; Hu, Q.; Li, Z.; Jiang, Z.; Yu, Y.; Chen, Z. A Modified Deadbeat Predictive Current Control for Improving Dynamic Performance of PMSM. IEEE Trans. Power Electron. 2022, 37, 14173–14185. [Google Scholar] [CrossRef]
- Ke, D.; Wang, F.; Yu, X.; Davari, S.A.; Kennel, R. Predictive Error Model-Based Enhanced Observer for PMSM Deadbeat Control Systems. IEEE Trans. Ind. Electron. 2024, 71, 2242–2252. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, C.; Liu, S.; Song, Z. A New Cascaded Adaptive Deadbeat Control Method for PMSM Drive. IEEE Trans. Ind. Electron. 2023, 70, 3384–3393. [Google Scholar] [CrossRef]
- Wang, W.; Liu, C.; Song, Z.; Dong, Z. Harmonic Current Suppression for Dual Three-Phase PMSM Based on Deadbeat Control and Disturbance Observer. IEEE Trans. Ind. Electron. 2023, 70, 3482–3492. [Google Scholar] [CrossRef]
- Li, X.; Yang, Y.; Sun, J.; Xiao, Y.; Fan, M.; Ni, K.; Hu, J.; Wen, H.; Yang, H.; Rodriguez, J. Multiple-Voltage-Vector Model-Free Predictive Deadbeat Control with Updated Reference Voltage Vector for PMSM Drive. IEEE Trans. Power Electron. 2025, 40, 6492–6505. [Google Scholar] [CrossRef]
- Chen, K.; Li, T.; Yan, T.; Xie, F.; Feng, Q.; Zhu, Q.; Zhao, C. A soft gripper design for apple harvesting with force feedback and fruit slip detection. Agriculture 2022, 12, 1802. [Google Scholar] [CrossRef]
- Huan, J.; Cao, W.; Liu, X. Technical note: A dissolved oxygen prediction method based on K-means clustering and the ELM neural network: A case study of the Changdang Lake. Appl. Eng. Agric. 2017, 33, 461–469. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Tran, H.N.; Nguyen, T.H.; Jeon, J.W. Recurrent Neural Network-Based Robust Adaptive Model Predictive Speed Control for PMSM With Parameter Mismatch. IEEE Trans. Ind. Electron. 2023, 70, 6219–6228. [Google Scholar] [CrossRef]
- Duan, J.; Cao, P.; Shu, T.; Zhou, B.; Xue, L.; Yang, L. Effects of Cellulosic Carbon Addition on Nitrogen Removal from Simulated Dry Land Drainage, and Its Environmental Effects. Agronomy 2023, 13, 3044. [Google Scholar] [CrossRef]
- Lin, X.; Liu, J.; Liu, Z.; Gao, Y.; Peretti, L.; Wu, L. Model-Free Current Predictive Control for PMSMs With Ultra local Model Employing Fixed-Time Observer and Extremum-Seeking Method. IEEE Trans. Power Electron. 2025, 40, 10682–10693. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, Y.; Gao, Q.; Yin, Z. A Wide-Speed Range Three-Vector-Based Model Predictive Flux Control with Improved Predictive Model for PMSM Drives. IEEE Trans. Transp. Electrific. 2024, 10, 2689–2700. [Google Scholar] [CrossRef]
- Wu, X.; Kang, J.; Yang, M.; Wu, T.; Huang, S. Model-Free Deadbeat Predictive Current Control for SPMSM Based on Adaptive Gain Extended State Observer. IEEE Trans. Transp. Electrific. 2025, 11, 536–543. [Google Scholar] [CrossRef]
- Cao, H.; Deng, Y.; Liu, J.; Zuo, Y.; Liu, X.; Wang, H.; Lee, C.H.T. Improved Deadbeat Predictive Current Control of PMSM Drives with Repetitive Control-Based Disturbance Correction Observer. IEEE Trans. Power Electron. 2025, 40, 801–812. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, S.; Zhang, C.; Zhou, Y. An Improved Deadbeat Predictive Current Control Based on Parameter Identification for PMSM. IEEE Trans. Transp. Electrific. 2024, 10, 2740–2753. [Google Scholar] [CrossRef]
- Xu, Q.; Fang, S. Robust Deadbeat Predictive Current Sensorless Control for Permanent Magnet Synchronous Motor. IEEE Trans. Power Electron. 2024, 39, 11441–11454. [Google Scholar] [CrossRef]
- Jin, Z.; Sun, X.; Cai, Y.; Tian, X. Robust collaborative optimization design of plug-in hybrid electric bus based on 6 Sigma theory. IEEE Trans. Transport. Electrific. 2024, 10, 10253–10261. [Google Scholar] [CrossRef]
- Hang, J.; Zhang, J.; Ding, S.; Huang, Y.; Wang, Q. A Model-Based Strategy with Robust Parameter Mismatch for Online HRC Diagnosis and Location in PMSM Drive System. IEEE Trans. Power Electron. 2020, 35, 10917–10929. [Google Scholar] [CrossRef]
- Zhou, J.; Yang, J.; Miao, H.; Fan, X.; Wang, Y.; Song, D. Shift-MRF Based Current Harmonics Compensation Decoupling Strategy in PMSM Considering Sampling Delay and Parameter Mismatch. IEEE Trans. Ind. Electron. 2025, 72, 5625–5635. [Google Scholar] [CrossRef]
- Layek, K.; Nair, S.V.; Krishnan, P.H.; Hatua, K. Voltage Angle-Based Torque Control of Dual Three-Phase Interior Permanent Magnet Synchronous Motor Considering Mismatch in Winding Parameters. IEEE Trans. Ind. Electron. 2024, 71, 10119–10129. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhu, Z.; Zhang, H.; Gao, Y.; Chen, L. Design of an electronically controlled fertilization system for an air-assisted side-deep fertilization machine. Agriculture 2023, 13, 2210. [Google Scholar] [CrossRef]
- Sun, X.; Lin, X.; Guo, D.; Lei, G.; Yao, M. Improved deadbeat predictive current control with extended state observer for dual three-phase PMSMs. IEEE Trans. Power Electron. 2024, 39, 6769–6782. [Google Scholar] [CrossRef]
- Dong, X.; Mao, J.; Yan, Y.; Zhang, C.; Yang, J. Generalized Dynamic Predictive Control for Nonlinear Systems Subject to Mismatched Disturbances with Application to PMSM Drives. IEEE Trans. Ind. Electron. 2024, 71, 954–964. [Google Scholar] [CrossRef]
- Li, X.; Zhang, S.; Zhang, C.; Zhou, Y.; Zhang, C. An Improved Deadbeat Predictive Current Control Scheme for Open-Winding Permanent Magnet Synchronous Motors Drives with Disturbance Observer. IEEE Trans. Power Electron. 2021, 36, 4622–4632. [Google Scholar] [CrossRef]
- Yang, F.; Zhao, X.; Jin, H.; Wang, X.; Liu, X. Improved Deadbeat Predictive Current Control with Embedded Resonant Polynomial and Disturbance Observer for PMSM Current Distortion Rejection. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 1934–1945. [Google Scholar] [CrossRef]
- Dai, S.; Wang, J.; Sun, Z.; Chong, E. Model Inaccuracy Analysis and Compensation of Stationary Frame-Based Deadbeat Predictive Current Control for High-Speed PMSM Drives. IEEE Trans. Transp. Electrific. 2022, 8, 2654–2666. [Google Scholar] [CrossRef]
- Zhang, Q.; Fan, Y.; Mao, C. A Gain Design Method for a Linear Extended State Observers to Improve Robustness of Deadbeat Control. IEEE Trans. Energy Convers. 2020, 35, 2231–2239. [Google Scholar] [CrossRef]
- Rovere, L.; Formentini, A.; Zanchetta, P. FPGA Implementation of a Novel Oversampling Deadbeat Controller for PMSM Drives. IEEE Trans. Ind. Electron. 2019, 66, 3731–3741. [Google Scholar] [CrossRef]
- Sun, J.; Nirere, A.; Dusabe, K.D.; Yuhao, Z.; Adrien, G. Rapid and nondestructive watermelon (Citrullus lanatus) seed viability detection based on visible near-infrared hyperspectral imaging technology and machine learning algorithms. J. Food Sci. 2024, 89, 4403–4418. [Google Scholar] [CrossRef]
- Huang, X.; Hu, Q.; Liu, Z.; Li, W.; Yang, G.; Li, Z. A Robust Deadbeat Predictive Current Control Method for IPMSM. IEEE Trans. Transp. Electrific. 2024, 10, 4722–4733. [Google Scholar] [CrossRef]
- Jiang, Y.; Xu, W.; Mu, C.; Liu, Y. Improved Deadbeat Predictive Current Control Combined Sliding Mode Strategy for PMSM Drive System. IEEE Trans. Veh. Technol. 2018, 67, 251–263. [Google Scholar] [CrossRef]
- Liu, Z.-H.; Wei, H.-L.; Li, X.-H.; Liu, K.; Zhong, Q.-C. Global Identification of Electrical and Mechanical Parameters in PMSM Drive Based on Dynamic Self-Learning PSO. IEEE Trans. Power Electron. 2018, 33, 10858–10871. [Google Scholar] [CrossRef]
- Inoue, Y.; Kawaguchi, Y.; Morimoto, S.; Sanada, M. Performance Improvement of Sensorless IPMSM Drives in a Low-Speed Region Using Online Parameter Identification. IEEE Trans. Ind. Appl. 2011, 47, 798–804. [Google Scholar] [CrossRef]
- Xie, C.; Zhang, S.; Li, X.; Zhou, Y.; Dong, Y. Parameter Identification for SPMSM With Deadbeat Predictive Current Control Using Online PSO. IEEE Trans. Transp. Electrific. 2024, 10, 4055–4064. [Google Scholar] [CrossRef]
- Xiang, D.; Yang, J.; Hao, Y.; Xu, G. Parallel-Cascaded Parameter Identification Scheme for PMSM-Driven Servo Systems During Self-Commission. IEEE Trans. Ind. Electron. 2025, 72, 1914–1924. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, M.; Zhang, C.; Shen, A.; Bing, L. Identification of PMSM Parameters with Time-Error Compensated Based on Contractile Factor Antipredator PSO. IEEE Trans. Transp. Electrific. 2024, 10, 4006–4017. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, S.; Hu, J.; Huang, D. Multiscenarios Parameter Optimization Method for Active Disturbance Rejection Control of PMSM Based on Deep Reinforcement Learning. IEEE Trans. Ind. Electron. 2023, 70, 10957–10968. [Google Scholar] [CrossRef]
- Liu, S.; Tang, Z.; Zhang, B.; Liang, Y.; Gu, X. Ergonomic design of cab structure for wheeled combine harvester. Eng. Agric. 2022, 42, e20220023. [Google Scholar] [CrossRef]
- Tang, Z.; Wang, H.; Jing, T.; Liu, S.; Shen, C. Centroid swinging property of a machine body undergoing longitudinal excitation in a straw compression baler. Eng. Agric. 2024, 44, e20230109. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, P.; Mao, H.; Gao, H.; Li, Q. Detection of the nutritional status of phosphorus in lettuce using THz time-domain spectroscopy. Eng. Agric. 2021, 41, 599–608. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; Yi, W.; Yang, Y.; Cao, K.; Luo, B. A Robust Model Predictive Current Closed-Loop Control with Parameter Estimation Strategy Based on Immune Chaotic Antipredator PSO for PMSM. IEEE Trans. Power Electron. 2025, 40, 1836–1848. [Google Scholar] [CrossRef]
- Liu, Z.-H.; Nie, J.; Wei, H.-L.; Chen, L.; Wu, F.-M.; Lv, M.-Y. Second-Order ESO-Based Current Sensor Fault-Tolerant Strategy for Sensorless Control of PMSM With B-Phase Current. IEEE/ASME Trans. Mechatron. 2022, 27, 5427–5438. [Google Scholar] [CrossRef]
- Su, Z.; Sun, X.; Lei, G.; Yao, M. Improved model-free predictive current control for SPMSM drives with adaptive prediction horizon strategy. IEEE Trans. Ind. Electron. 2025, 72, 5705–5715. [Google Scholar] [CrossRef]
- Sun, X.; Su, Z.; Lei, G.; Cai, Y.; Yao, M. Adaptive model-free predictive current control for SPMSM drives with optimal virtual vector modulation. IEEE/ASME Trans. Mechatron. 2024, 29, 2569–2578. [Google Scholar] [CrossRef]
- Xiong, J.; Fu, X. Extended Two-State Observer-Based Speed Control for PMSM With Uncertainties of Control Input Gain and Lumped Disturbance. IEEE Trans. Ind. Electron. 2024, 71, 6172–6182. [Google Scholar] [CrossRef]
- Hou, Q.; Xu, S.; Zuo, Y.; Wang, H.; Sun, J.; Lee, C.H.T.; Ding, S. Enhanced Active Disturbance Rejection Control with Measurement Noise Suppression for PMSM Drives via Augmented Nonlinear Extended State Observer. IEEE Trans. Energy Convers. 2024, 39, 287–299. [Google Scholar] [CrossRef]
- Song, J.; Wang, Y.-K.; Niu, Y.; Lam, H.-K.; He, S.; Liu, H. Periodic Event-Triggered Terminal Sliding Mode Speed Control for Networked PMSM System: A GA-Optimized Extended State Observer Approach. IEEE/ASME Trans. Mechatron. 2022, 27, 4153–4164. [Google Scholar] [CrossRef]
- Wang, B.; Wang, T.; Yu, Y.; Xu, D. Second-order terminal sliding mode speed controller for induction motor drives with nonlinear control gain. IEEE Trans. Ind. Electron. 2023, 70, 10923–10934. [Google Scholar] [CrossRef]
- Sun, Y.; Yang, M.; Wang, B.; Chen, Y.; Xu, D. Precise position control based on resonant controller and second-order sliding mode observer for PMSM-driven feed servo system. IEEE Trans. Transport. Electrific. 2023, 9, 196–209. [Google Scholar] [CrossRef]
- Sun, X.; Lin, X.; Han, S.; Wang, Y. An improved continuous-control-set model predictive control for dual three-phase PMSMs based on extended state observer. IEEE Trans. Ind. Electron. 2025, 72, 3449–3459. [Google Scholar] [CrossRef]
- Liang, Z.; Li, Y.; Xu, L.; Zhao, Z. Sensor for monitoring rice grain sieve losses in combine harvesters. Biosyst. Eng. 2016, 147, 51–66. [Google Scholar] [CrossRef]
- Guan, C.; Fu, J.; Xu, L.; Jiang, X.; Wang, S.; Cui, Z. Study on the reduction of soil adhesion and tillage force of bionic cutter teeth in secondary soil crushing. Biosyst. Eng. 2022, 213, 133–147. [Google Scholar] [CrossRef]
- Han, J.; Yan, X.; Tang, H. Method of controlling tillage depth for agricultural tractors considering engine load characteristics. Biosyst. Eng. 2023, 227, 95–106. [Google Scholar] [CrossRef]
- Ma, Z.; Wu, Z.; Li, Y.; Song, Z.; Yu, J.; Li, Y.; Xu, L. Study of the grain particle-conveying performance of a bionic non-smooth-structure screw conveyor. Biosyst. Eng. 2024, 238, 94–104. [Google Scholar] [CrossRef]
- Li, Z.; Zhou, S.; Xiao, Y.; Wang, L. Sensorless vector control of permanent magnet synchronous linear motor based on self-adaptive super-twisting sliding mode controller. IEEE Access 2019, 7, 44998–45011. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, J.; Huang, L. Model-Free Predictive Current Control of PMSM Drives Based on Extended State Observer Using Ultralocal Model. IEEE Trans. Ind. Electron. 2021, 68, 993–1003. [Google Scholar] [CrossRef]
- Zhang, Y.; Shen, W.; Yang, H. An Improved Deadbeat Predictive Current Control of PMSM Drives Based on the Ultra-local Model. Chin. J. Integr. Med. 2023, 9, 27–37. [Google Scholar] [CrossRef]
- Su, G.; Li, H.; Li, Z.; Zhou, Y. Model-Free Control of Permanent Magnet Synchronous Linear Motor Based on Ultra-local Model. Chin J Integr Med. 2024, 10, 73–82. [Google Scholar] [CrossRef]
- Safaei, A.; Mahyuddin, M.N. Adaptive Model-Free Control Based on an Ultra-Local Model With Model-Free Parameter Estimations for a Generic SISO System. IEEE Access 2018, 6, 4266–4275. [Google Scholar] [CrossRef]
- Chen, J.; Fan, Y.; Cheng, M.; Zhang, Q.; Chen, Q. Parameter-free ultralocal model-based deadbeat predictive current control for PMVMs using finite-time gradient method. IEEE Trans. Ind. Electron. 2023, 70, 5549–5559. [Google Scholar] [CrossRef]
- Yuan, X.; Zuo, Y.; Fan, Y.; Lee, C.H.T. Model-free predictive current control of SPMSM drives using extended state observer. IEEE Trans. Ind. Electron. 2022, 69, 6540–6550. [Google Scholar] [CrossRef]
- Long, J.; Yang, M.; Chen, Y.; Liu, K.; Xu, D. Current-Controller-Free Self-Commissioning Scheme for Deadbeat Predictive Control in Parametric Uncertain SPMSM. IEEE Access 2021, 9, 289–302. [Google Scholar] [CrossRef]
- Brosch, A.; Hanke, S.; Wallscheid, O.; Bocker, J. Data-Driven Recursive Least Squares Estimation for Model Predictive Current Control of Permanent Magnet Synchronous Motors. IEEE Trans. Power Electron. 2021, 36, 2179–2190. [Google Scholar] [CrossRef]
- Siami, M.; Khaburi, D.A.; Abbaszadeh, A.; Rodriguez, J. Robustness Improvement of Predictive Current Control Using Prediction Error Correction for Permanent-Magnet Synchronous Machines. IEEE Trans. Ind. Electron. 2016, 63, 3458–3466. [Google Scholar] [CrossRef]
- Akter, M.P.; Mekhilef, S.; Tan, N.M.L.; Akagi, H. Modified model predictive control of a bidirectional AC-DC converter based on Lyapunov function for energy storage systems. IEEE Trans. Ind. Electron. 2016, 67, 704–715. [Google Scholar] [CrossRef]
- Brosch, A.; Wallscheid, O.; Bocker, J. Long-Term Memory Recursive Least Squares Online Identification of Highly Utilized Permanent Magnet Synchronous Motors for Finite-Control-Set Model Predictive Control. IEEE Trans. Power Electron. 2023, 38, 1451–1467. [Google Scholar] [CrossRef]
- Sun, J.; Gong, J.; Chen, B.; Zha, X. Analysis and design of repetitive controller based on regeneration spectrum and sensitivity function in active power filter system. IET Power Electron. 2014, 67, 2133–2140. [Google Scholar] [CrossRef]
- Cao, G.Z.; Zhou, H.H.; Huang, S.D.; Hu, H.J.; He, J.B. Position Estimation Method of a Permanent Magnet Synchronous Motor Based on Moving Horizon Estimation EKF Algorithm. IEEE Trans. Magn. 2025, 61, 8201106. [Google Scholar] [CrossRef]
- Wang, Y.; Liao, W.; Huang, S.; Zhang, J.; Yang, M.; Li, C.; Huang, S. A Robust DPCC for IPMSM Based on a Full Parameter Identification Method. IEEE Trans. Ind. Electron. 2023, 70, 7695–7705. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, X.; Yang, P.; Hua, W.; Buja, G. Effects of Triangular Wave Injection and Current Differential Terms on Multiparameter Identification for PMSM. IEEE Trans. Power Electron. 2024, 39, 2943–2947. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, G.; Zhao, N.; Zhang, G.; Cui, Q.; Xu, D.G. An Impedance Model-Based Multiparameter Identification Method of PMSM for Both Offline and Online Conditions. IEEE Trans. Power Electron. 2021, 36, 727–738. [Google Scholar] [CrossRef]
- Zhang, Q.; Guo, H.; Liu, Y.; Guo, C.; Zhang, F.; Zhang, Z.; Li, G. A Novel Error-Injected Solution for Compensation of Current Measurement Errors in PMSM Drive. IEEE Trans. Ind. Electron. 2023, 70, 4608–4619. [Google Scholar] [CrossRef]
- Wang, F.; Ke, D.; Yu, X.; Huang, D. Enhanced predictive model based deadbeat control for PMSM drives using exponential extended state observer. IEEE Trans. Ind. Electron. 2022, 69, 2357–2369. [Google Scholar] [CrossRef]
- Wang, F.; Kong, W.; Qu, R. Model Parameter Self-Correcting Deadbeat Predictive Current Control for SPMSM Drives. IEEE Trans. Ind. Electron. 2025, 72, 2357–2368. [Google Scholar] [CrossRef]
- Sun, X.; Zhu, Y.; Cai, Y.; Yao, M.; Sun, Y.; Lei, G. Optimized-Sector-Based Model Predictive Torque Control With Sliding Mode Controller for Switched Reluctance Motor. IEEE Trans. Energy Convers. 2024, 39, 379–388. [Google Scholar] [CrossRef]
- Zhang, X.; Fang, S.; Zhang, H. Predictive Current Error Compensation Based Strong Robust Model Predictive Control for PMSM Drive Systems. IEEE Trans. Ind. Electron. 2024, 71, 15280–15289. [Google Scholar] [CrossRef]
- Zhang, X.; Cao, Y.; Zhang, C.; Niu, S. Model Predictive Control for PMSM Based on the Elimination of Current Prediction Errors. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 2651–2660. [Google Scholar] [CrossRef]
- Chen, P.; Ma, R.; Bai, H.; Chen, Z.; Song, S. Rotating High Frequency Voltage Injection Strategy Considering Time Delay for PMSM Based on Dual Heterodyne Method. IEEE Trans. Energy Convers. 2025, 40, 901–910. [Google Scholar] [CrossRef]
- Han, Y.; Gong, C.; Yan, L.; Wen, H.; Wang, Y.; Shen, K. Multiobjective Finite Control Set Model Predictive Control Using Novel Delay Compensation Technique for PMSM. IEEE Trans. Power Electron. 2020, 35, 11193–11204. [Google Scholar] [CrossRef]
- Wu, T.; Luo, D.; Wu, X.; Liu, K.; Huang, S.; Peng, X. Square-Wave Voltage Injection Based PMSM Sensorless Control Considering Time Delay at Low Switching Frequency. IEEE Trans. Ind. Electron. 2022, 69, 5525–5535. [Google Scholar] [CrossRef]
- Zhang, X.; Cheng, Y.; Zhao, Z.; Yan, K. Optimized model predictive control with dead-time voltage vector for PMSM drives. IEEE Trans. Power Electron. 2021, 36, 3149–3158. [Google Scholar] [CrossRef]
- Sun, X.; Cao, J.; Lei, G.; Guo, Y.; Zhu, J. A robust deadbeat predictive controller with delay compensation based on composite sliding mode observer for PMSMs. IEEE Trans. Power Electron. 2021, 36, 10742–10752. [Google Scholar] [CrossRef]
- Bouafia, A.; Gaubert, J.-P.; Krim, F. Predictive Direct Power Control of Three-Phase Pulsewidth Modulation (PWM) Rectifier Using Space-Vector Modulation (SVM). IEEE Trans. Power Electron. 2010, 25, 228–236. [Google Scholar] [CrossRef]
- Moon, H.-T.; Kim, H.-S.; Youn, M.-J. A discrete-time predictive current control for PMSM. IEEE Trans. Power Electron. 2003, 18, 464–472. [Google Scholar] [CrossRef]
- Sun, X.; Xu, Z.; Pan, M.; Sun, C.; Pan, W.; Lei, G. Sensorless Control Strategy for SRM Based on Flux Linkage in Medium to High-Speed Range. IEEE Trans. Ind. Electron. 2025; early access. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Z.; Zhao, Z.; Cheng, M. Model Predictive Voltage Control for SPMSM Drives with Parameter Robustness Optimization. IEEE Trans. Transp. Electrific. 2022, 8, 3151–3163. [Google Scholar] [CrossRef]
- Yang, M.; Lang, X.; Long, J.; Xu, D. Flux Immunity Robust Predictive Current Control with Incremental Model and Extended State Observer for PMSM Drive. IEEE Trans. Power Electron. 2017, 32, 9267–9279. [Google Scholar] [CrossRef]
- He, L.; Wang, F.; Wang, J.; Rodriguez, J. Zynq implemented Luenberger disturbance observer based predictive control scheme for PMSM drives. IEEE Trans. Power Electron. 2020, 35, 1770–1778. [Google Scholar] [CrossRef]
- Wang, H.; Gan, C.; Zhang, C.; Ren, H.; Qu, R. Parameter Robust Predictive Current Control for PMSM Drives Based on Self-Tuning Incremental Model and Voltage Constraint Compensation. IEEE Trans. Power Electron. 2025, 40, 11268–11282. [Google Scholar] [CrossRef]
- Sun, X.; Lin, X.; Zhang, L.; Yao, M.; Cai, Y. An improved torque enhancement strategy for dual three-phase PMSM based on model-free predictive current control. IEEE Trans. Transport. Electrific. 2025, 11, 176–187. [Google Scholar] [CrossRef]
- Fuentes, E.J.; Silva, C.A.; Yuz, J.I. Predictive Speed Control of a Two-Mass System Driven by a Permanent Magnet Synchronous Motor. IEEE Trans. Ind. Electron. 2012, 59, 2840–2848. [Google Scholar] [CrossRef]
- Gao, X.; Abdelrahem, M.; Hackl, C.M.; Zhang, Z.; Kennel, R. Direct Predictive Speed Control with a Sliding Manifold Term for PMSM Drives. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1258–1267. [Google Scholar] [CrossRef]
- Sun, X.; Su, Z.; Lei, G.; Yao, M. Robust predictive cascaded speed and current control for PMSM drives considering parameter variations. IEEE Trans. Ind. Electron. 2024, 71, 10235–10245. [Google Scholar] [CrossRef]
- Wang, T.; Luo, G.; Chen, Z.; Tu, W.; Liu, C. An improved robust model predictive speed control with inertia identification for PMSM drives in electro-hydrostatic actuator. IEEE Trans. Power Electron. 2023, 38, 13825–13841. [Google Scholar] [CrossRef]
- Li, T.; Sun, X.; Yang, Z.; Lei, G. Simplified two-step model predictive control with fast voltage vector search. IEEE Trans. Ind. Electron. 2025, 72, 3303–3312. [Google Scholar] [CrossRef]
- Li, R.; Huang, D.; Chen, Y.; Zhao, Q. Deadbeat Predictive Speed Control of PMSM via Enhanced Low-Gain Disturbance Observer Design and Inertia Identification. IEEE J. Emerg. Sel. Top. Power Electron. 2025, 13, 2524–2534. [Google Scholar] [CrossRef]
- Sun, J.; He, X.; Ge, X.; Wu, X.; Shen, J.; Song, Y. Detection of key organs in tomato based on deep migration learning in a complex background. Agriculture 2018, 8, 196. [Google Scholar] [CrossRef]
- Peng, Y.; Zhao, S.; Liu, J. Fused deep features-based grape varieties identification using support vector machine. Agriculture 2021, 11, 869. [Google Scholar] [CrossRef]
- Ji, K.; Li, Y.; Liang, Z.; Liu, Y.; Cheng, J.; Wang, H.; Zhu, R.; Xia, S.; Zheng, G. Device and method suitable for matching and adjusting reel speed and forward speed of multi-crop harvesting. Agriculture 2022, 12, 213. [Google Scholar] [CrossRef]
- Zhou, H.; Jia, W.; Li, Y.; Ou, M. Method for estimating canopy thickness using ultrasonic sensor technology. Agriculture 2021, 11, 1011. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, X.; Liang, R.; Wang, X.; Meng, H.; Kan, Z. Calibration and test of contact parameters between chopped cotton stalks using response surface methodology. Agriculture 2022, 12, 1851. [Google Scholar] [CrossRef]
- Qiu, S.; Yu, Y.; Feng, Y.; Tang, Z.; Cui, Q.; Yuan, X. Crushing characteristics of sorghum grains subjected to compression and impact loading at different moisture contents. Agriculture 2022, 12, 1422. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhang, H.; Zhu, Z.; Gao, Y.; Chen, L. Structural design and simulation of pneumatic conveying line for a paddy side-deep fertilisation system. Agriculture 2022, 12, 867. [Google Scholar] [CrossRef]
- Gao, J.; Zhang, J.; Lu, D. Design and atomization experiments of an ultrasonic atomizer with a levitation mechanism. Appl. Eng. Agric. 2016, 32, 353–360. [Google Scholar] [CrossRef]
- Kumi, F.; Mao, H.; Li, Q.; Luhua, H. Assessment of tomato seedling substrate-root quality using X-ray computed tomography and scanning electron microscopy. Appl. Eng. Agric. 2016, 32, 417–427. [Google Scholar] [CrossRef]
- Shi, Q.; Mao, H.; Guan, X. Numerical simulation and experimental verification of the deposition concentration of an unmanned aerial vehicle. Appl. Eng. Agric. 2019, 35, 367–376. [Google Scholar] [CrossRef]
- Fordjour, A.; Zhu, X.; Yuan, S.; Dwomoh, F.A.; Issaka, Z. Numerical simulation and experimental study on internal flow characteristic in the dynamic fluidic sprinkler. Appl. Eng. Agric. 2020, 36, 61–70. [Google Scholar] [CrossRef]
- Hua, L.; Li, H.; Jiang, Y. Axis-switching behavior of liquid jets issued from non-circular nozzles under low-intermediate pressure. Appl. Eng. Agric. 2021, 37, 367–378. [Google Scholar] [CrossRef]
- Sun, X.; Chen, Z.; Pan, M.; Cai, Y.; Jin, Z.; Lei, G.; Tian, X. Robust energy management optimization for PHEB considering driving uncertainties by using sequential Taguchi method. IEEE Trans. Transport. Electrific. 2025, 11, 5191–5200. [Google Scholar] [CrossRef]
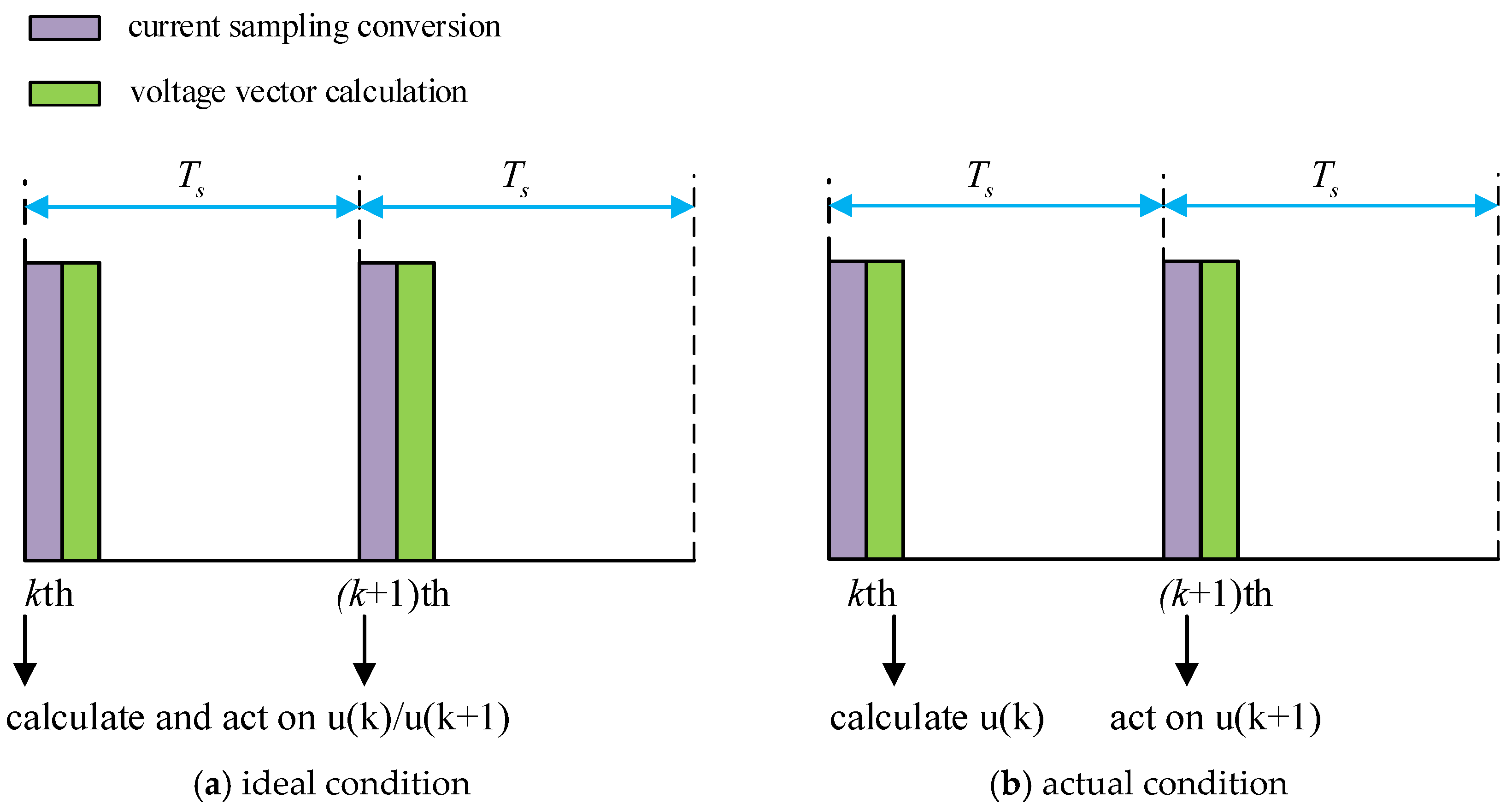
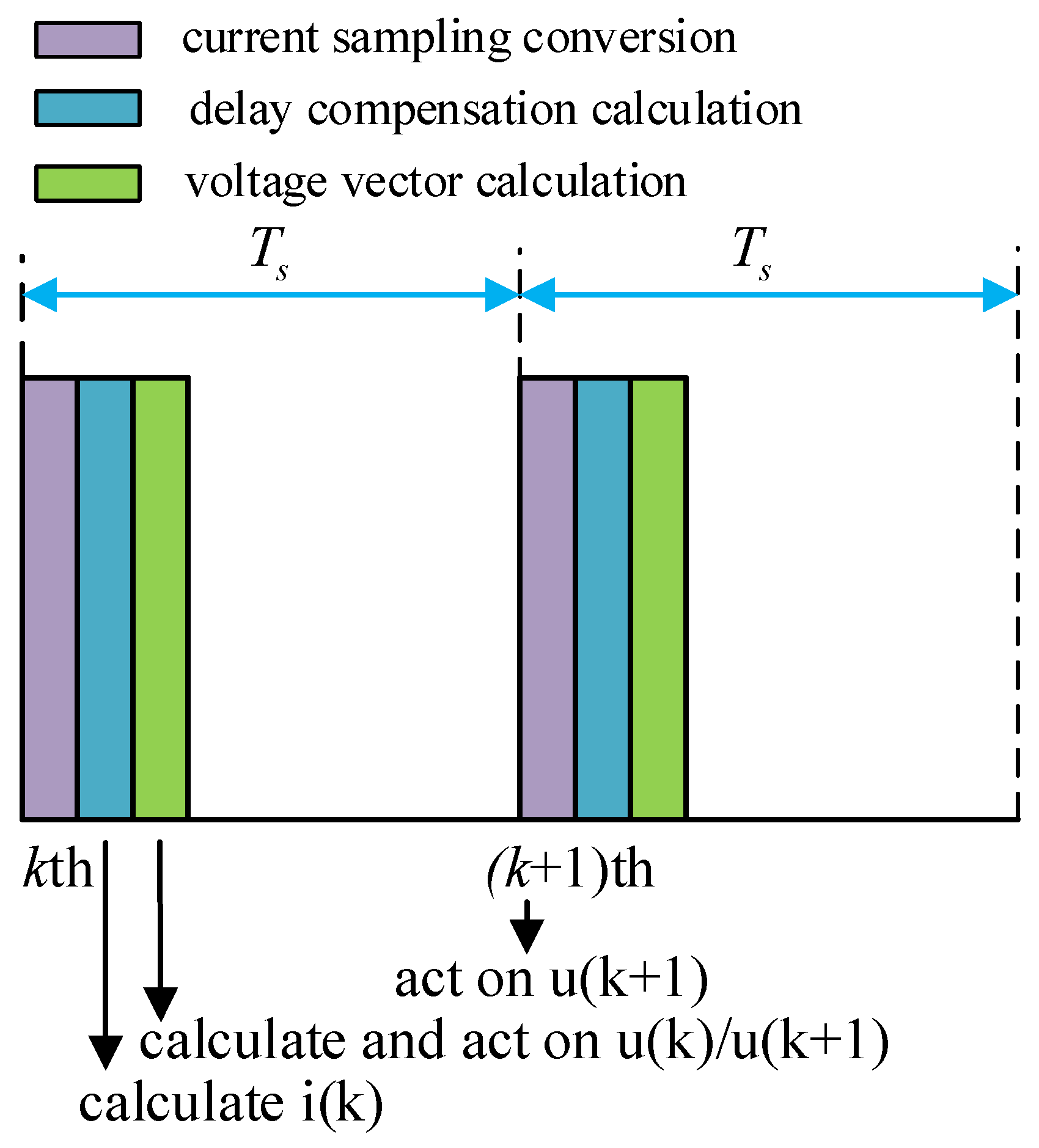
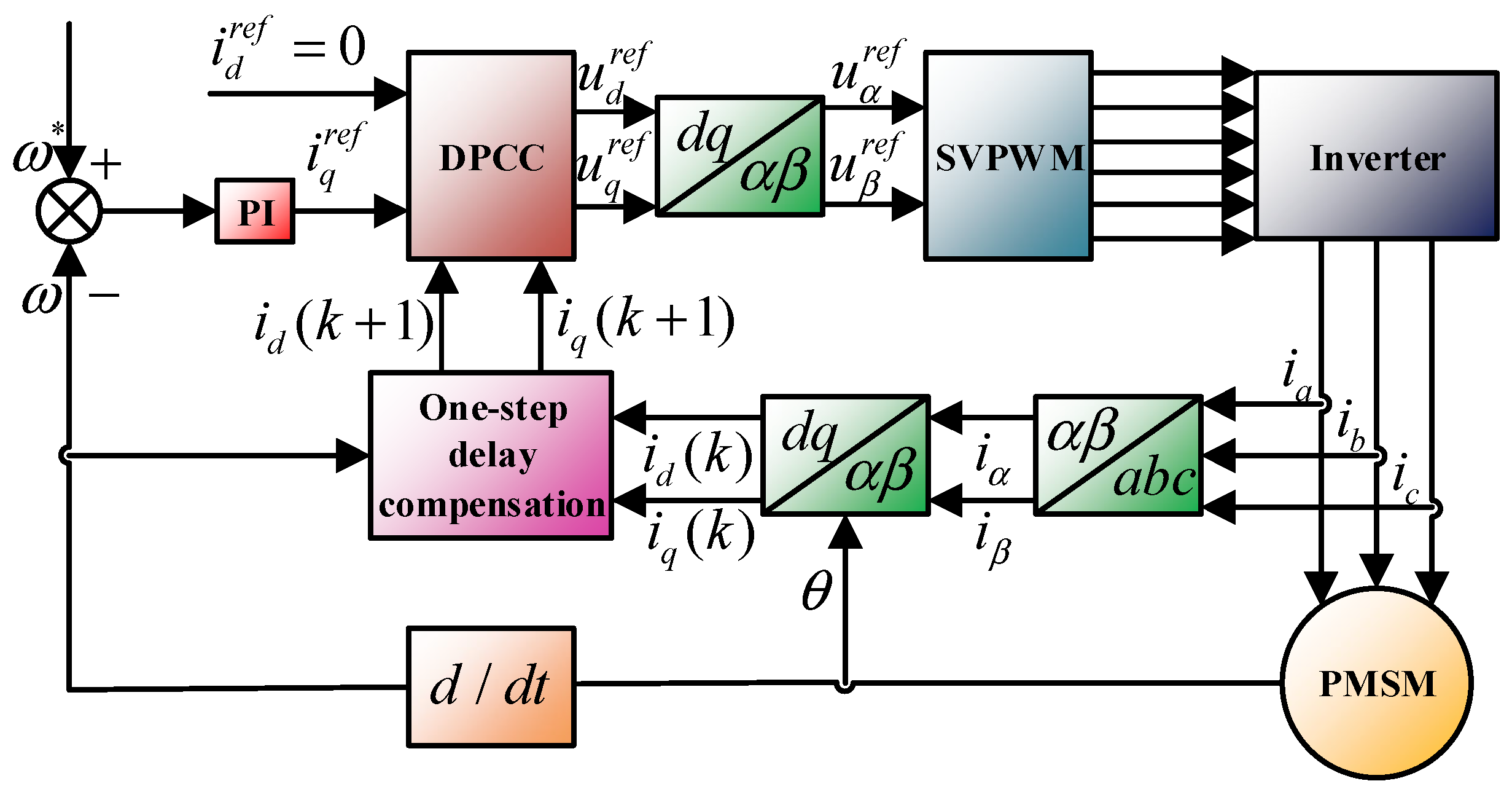
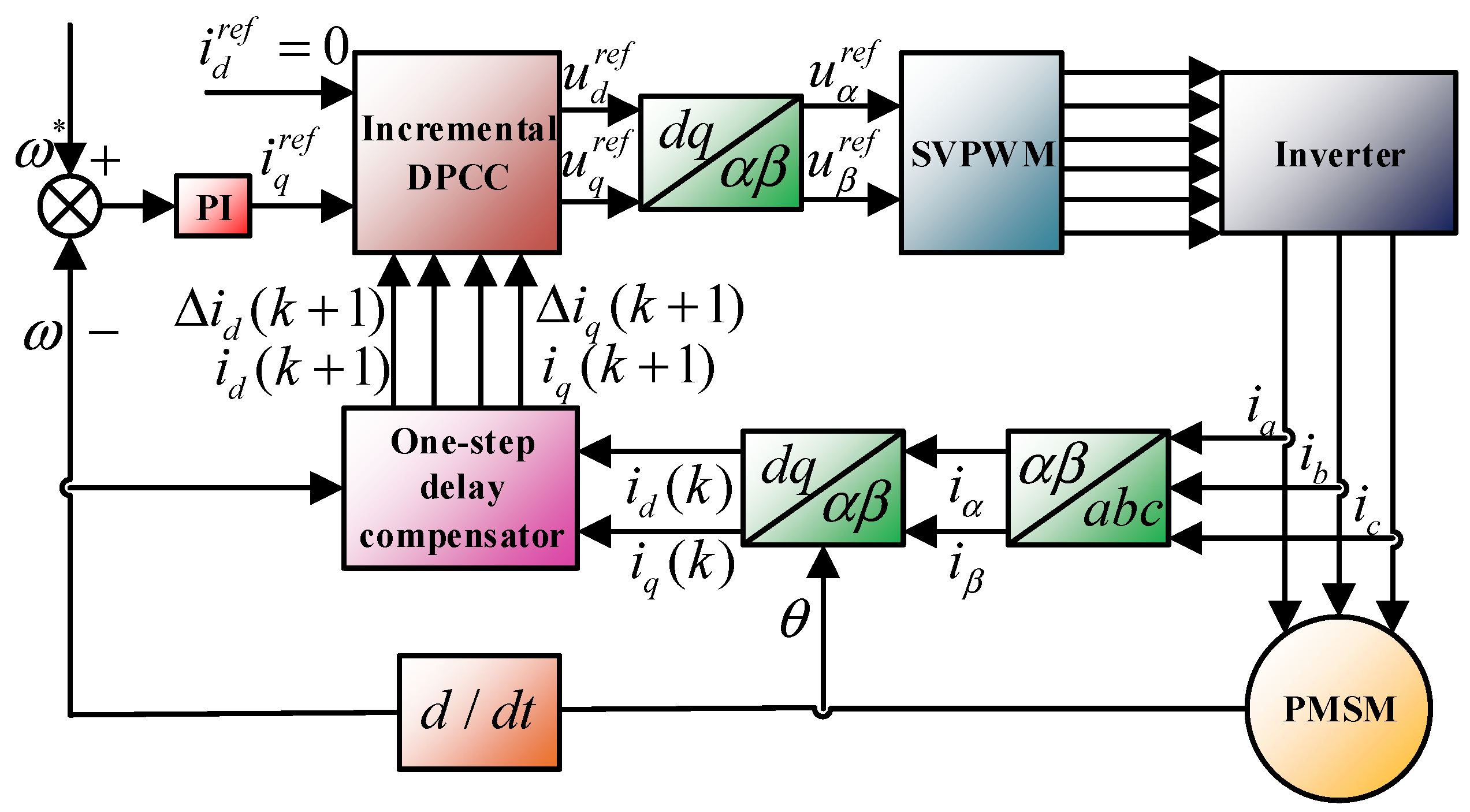
| Methods | Fixed Switching Rate | PWM Modulation Requirements | Algorithm Complexity | Whether Constraint Processing Is Required |
|---|---|---|---|---|
| Deadbeat Predictive Control | Yes | Yes | complicated | No |
| Continuous-set model predictive control | Yes | Yes | complicated | Yes |
| Finite-set model predictive control | No | No | normal | Yes |
| Methods | Advantage | Disadvantage | Complexity | Accuracy |
|---|---|---|---|---|
| RLS | Easy to implement | Low accuracy | High | Medium |
| EKF | Strong robustness to noise | Complex computations | High | High |
| MRAS | Wide speed range and easy to implement | Need additional conditions | Medium | Slightly High |
| Method | DPCC | DPCC-ESO | Method in [Ultra] | Method in [CEC] | Method in [Wang] |
|---|---|---|---|---|---|
| Clock period | 5466 | 5682 | 5548 | 6224 | 6118 |
| Algorithm execution time | 36.54 μs | 37.98 μs | 36.84 μs | 42.68 μs | 42.04 μs |
| Methods | PI-DPCC | DPCC-ESO | Method in [Robust Ca] | Method in [Zuihou] |
|---|---|---|---|---|
| Speed tracking (setting/rising time) | 140 ms/160 ms | 110 ms/250 ms | 112 ms/125 ms | 130 ms/144 ms |
| Load disturbance rejection (speed drop/recovery time) | 40 rpm/400 ms | 32 rpm/230 ms | 28 rpm/200 ms | 26 rpm/228 ms |
| Steady-state Performance (speed ripples/current ripples) | 2 rpm/0.1 A | 2 rpm/0.3 A | 2 rpm/0.5 A | 1.4 rpm/0.3 A |
| Methods | Features of Application |
|---|---|
| Parameter identification + DPCC | Parameter mismatch |
| Observers + DPCC | Disturbances and complex working conditions |
| Error compensation + DPCC | Parameter mismatch or complex working conditions |
| Delay compensation + DPC | Low computing power equipment and high-precision instrument |
| Observers + DPSC | Disturbances and quick response time conditions |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Zhang, S.; Yang, Y.; Wen, Y.; Sun, X.; Zhou, Z.; Li, Y. Overview of Deadbeat Predictive Control Technology for Permanent Magnet Synchronous Motor System. Energies 2025, 18, 4668. https://doi.org/10.3390/en18174668
Wang R, Zhang S, Yang Y, Wen Y, Sun X, Zhou Z, Li Y. Overview of Deadbeat Predictive Control Technology for Permanent Magnet Synchronous Motor System. Energies. 2025; 18(17):4668. https://doi.org/10.3390/en18174668
Chicago/Turabian StyleWang, Renzhong, Sunyang Zhang, Yifei Yang, Yifang Wen, Xiaodong Sun, Zhongzhuang Zhou, and Yuting Li. 2025. "Overview of Deadbeat Predictive Control Technology for Permanent Magnet Synchronous Motor System" Energies 18, no. 17: 4668. https://doi.org/10.3390/en18174668
APA StyleWang, R., Zhang, S., Yang, Y., Wen, Y., Sun, X., Zhou, Z., & Li, Y. (2025). Overview of Deadbeat Predictive Control Technology for Permanent Magnet Synchronous Motor System. Energies, 18(17), 4668. https://doi.org/10.3390/en18174668







