A Robust Collaborative Optimization of Multi-Microgrids and Shared Energy Storage in a Fraudulent Environment
Abstract
1. Introduction
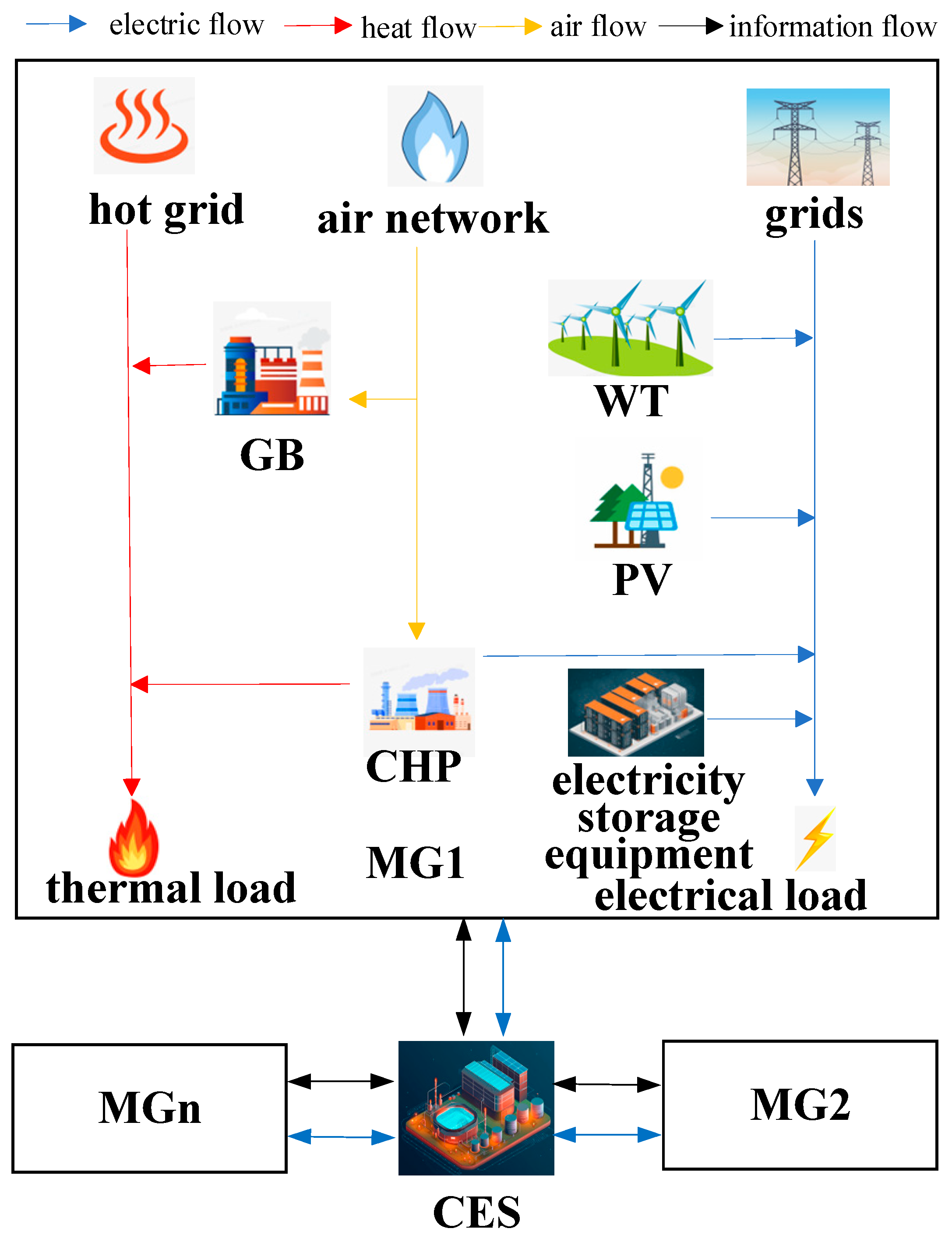
2. Multiple MG-CES Operating Modes and Operating Models for Each Entity
3. Consideration of Uncertainty in Multi-Microgrid—Shared Energy Storage System Coordinated Optimization Operation Model
3.1. Integrated Energy System Model
3.1.1. Gas Turbine Model
3.1.2. Gas Boiler (GB) Model
3.2. Electric Energy Storage Model
3.3. Interaction Model with Other Integrated Energy Systems
3.4. Power Balance Constraints3.5. Objective Function
3.5. Objective Function
3.6. Shared Energy Storage Model
3.7. Objective Function of Shared Energy Storage
3.8. Source-Load Output Uncertainty Model
3.9. Multi-Stage Robust Scheduling Model for MG Considering Multiple UncertaintMG
Compact Form of the Model
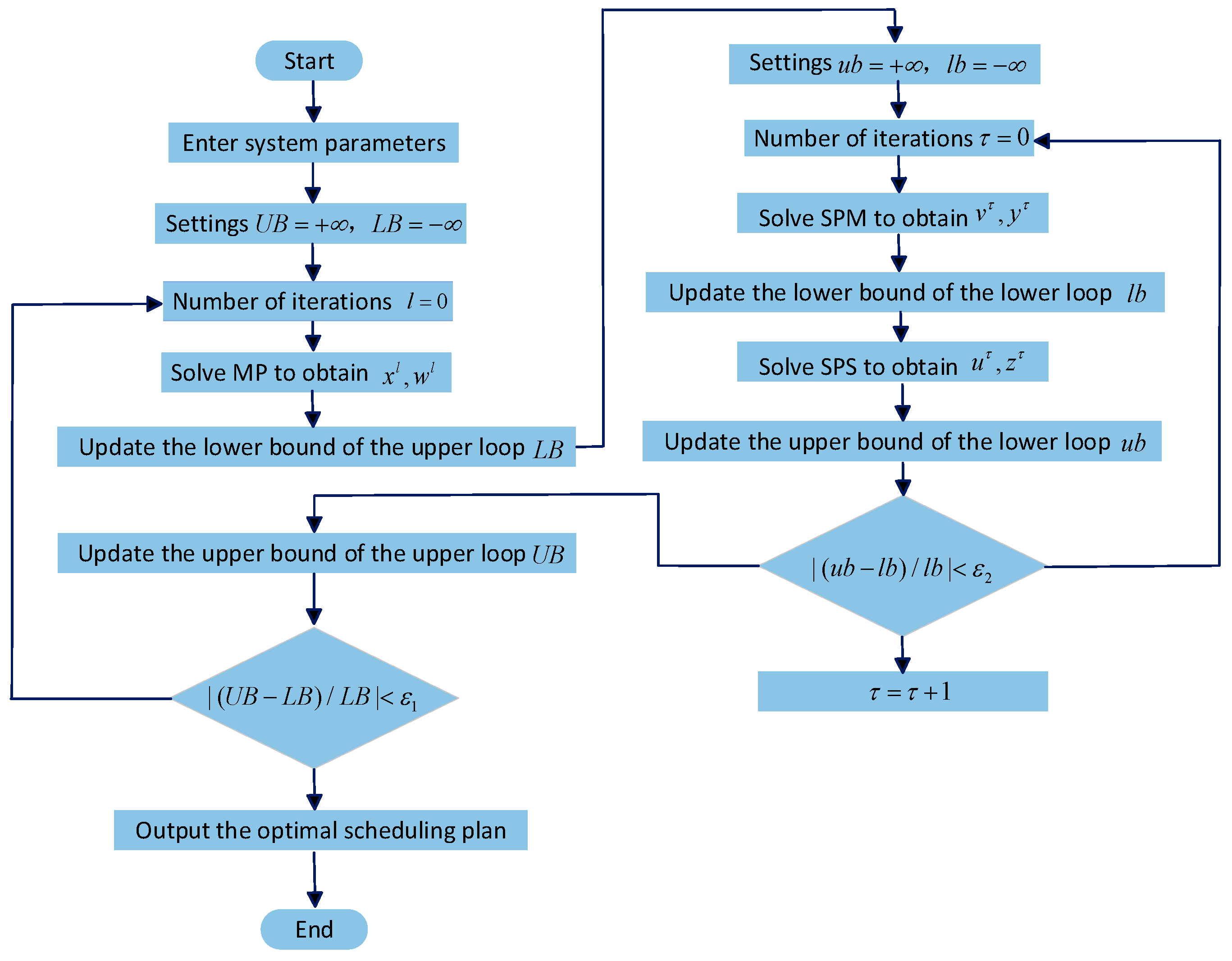
3.10. Parallelizable AOP-Looped C&CG Algorithm
3.11. Parallelizable Outer-Loop C&CG
- (1)
- Main Problem (MP)
- (2)
- Sub-Problem (SP)
- Parallelizable Inner-Loop C&CG
- 2.
- Pseudocode and Flowchart for Parallelizable Alternating Optimization Procedure(AOP)-Looped C&CG Algorithm
| Algorithm 1: Parallelizable Computation AOP-Looped C&CG Algorithm |
| 1: Parallelizable Computation Outer -Loop C&CG: Set the lower bound , the upper bound , the number of iterations , the convergence threshold , the seasonal scenario probability , the typical day scenario probability , the power purchase and sale price , and the wind-solar and electric-heat load . 2: repeat 3: Substitute into MP, optimize to get () and the objective function value , and update . 4: Parallelizable Computation Inner -Loop C&CG: Set the lower bound , the upper bound , the number of iterations , and the convergence threshold . 5: repeat 6: 7: repeat 8: Substitute () into SPM, optimize to get and the objective function value , and update . 9: Substitute into SPS, optimize to get and the objective function value , and update . 10: . 11: until , and return as to MP. 12: until 13: Substitute into , optimize to get and the objective function value , and return as to MP. 14: Substitute into , optimize to get and the objective function value , and return as to MP. 15: Update . 16: . 17: unti , and output the optimization result. |
| Algorithm 2: Progressive Hedging Distributed Algorithm (PH Algorithm) |
| 1. Initialize iteration count . Set the penalty factor for the algorithm and Convergence threshold |
| 6. end |
| 7. Adjust the discrete values of transaction prices based on the results of the initialization phase in each scenario. |
| 8. repeat |
| Adjusting penalty factors, such as making |
4. Multi-MG Energy Interaction Optimization Model Considering Electricity Price Uncertainty and Deceptive Behavior
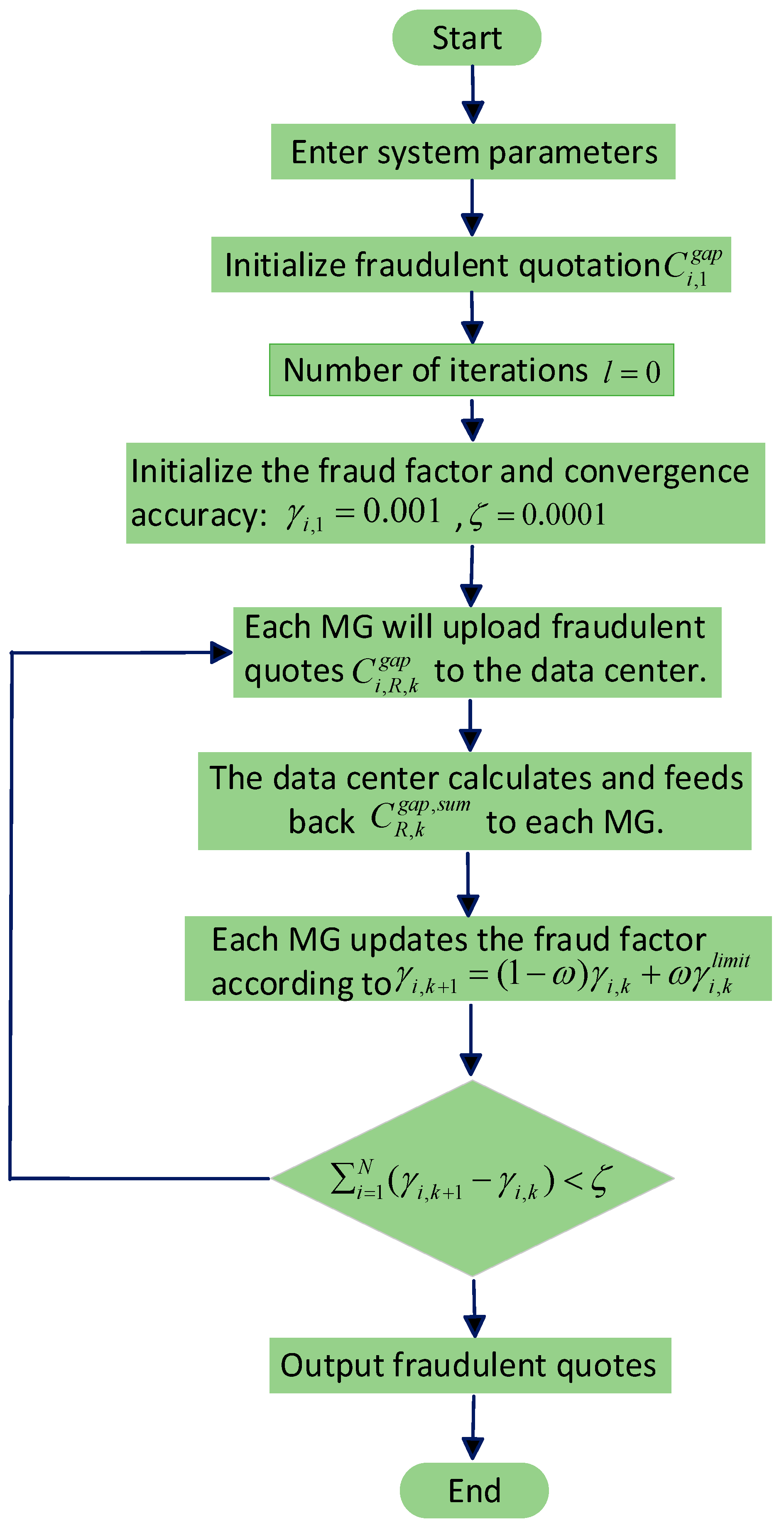
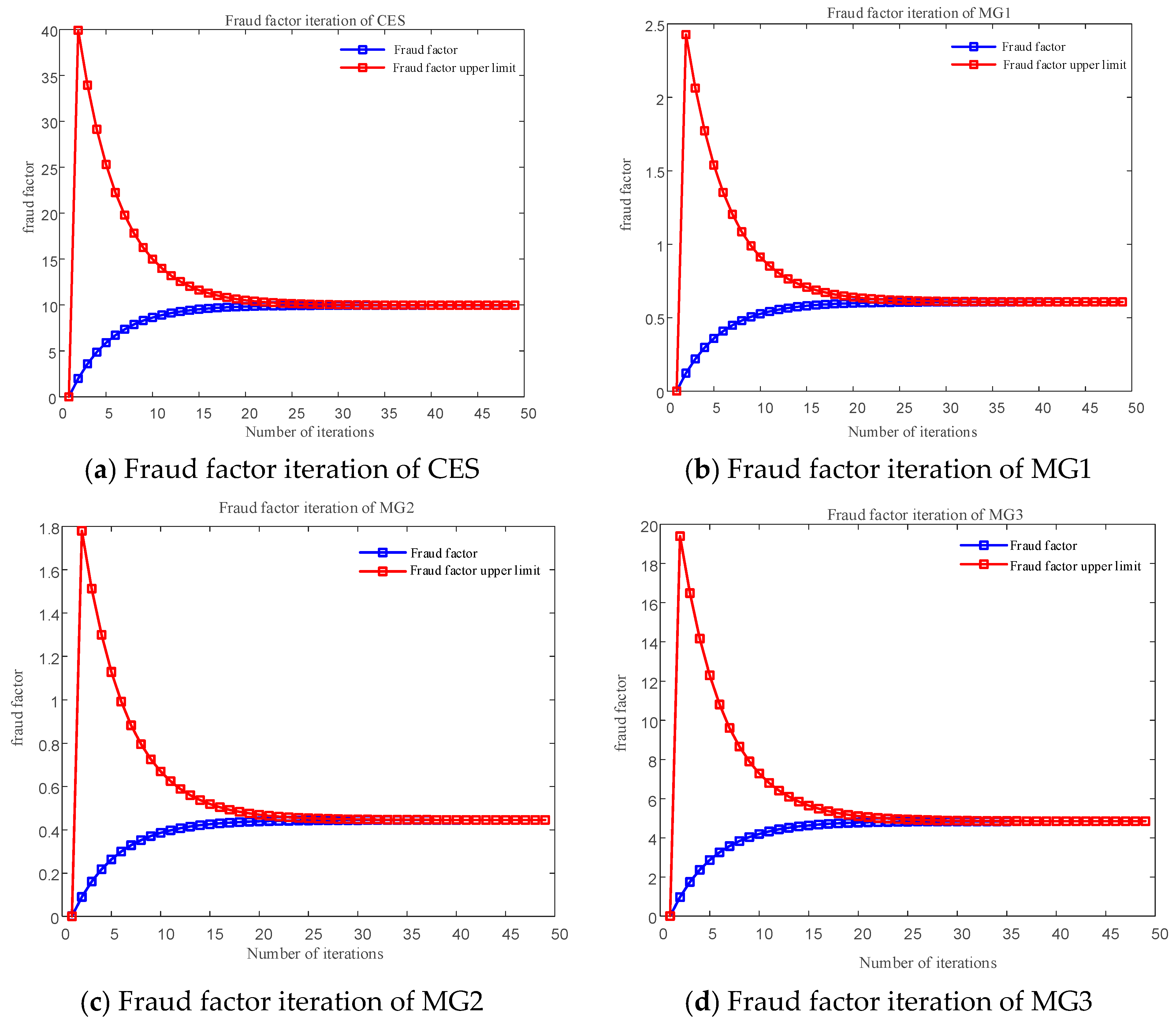
4.1. Multi-MG Energy Interaction Game Strategy Considering Electricity Price Uncertainty and Deceptive Behavior
- (1)
- Initialize the deceptive quotation for each MG, set the iteration count to k = 1, the deception factor to , and the convergence precision .
- (2)
- Each MG performs a deceptive quotation according to the formulaand uploads the deceptive quotation to the data center.
- (3)
- The data center calculatesand feeds back the sum of deceptive quotations to each MG.
- (4)
- Each MG updates the deception factor according to the formulawhereand is the relaxation coefficient with a value range of .
- (5)
- Check for convergence; if , output the deceptive quotation ; otherwise, set k = k + 1 and repeat steps (2) to (5).
4.2. Solution for the Multi-MG Energy Sharing Nash Bargaining Model
4.3. Solution Algorithm
- Distributed Algorithm for the Multi-MG Coalition Benefit Maximization Sub-problem
- (1)
- Set the maximum iteration count , convergence precision ζ = 0.1, penalty factor ρ = 0.01, initial iteration count k = 1, and initial inter-MG power exchange .
- (2)
- Solve the distributed optimization operation model for MG1. From MG2, receive the expected power transmission from MG2 to MG1; from MG3, receive the expected power transmission from MG3 to MG1. Obtain the expected power transmission from MG1 to MG2 and from MG1 to MG3.
- (3)
- Solve the distributed optimization operation model for MG2. From MG1, receive the expected power transmission from MG1 to MG2; from MG3, receive the expected power transmission from MG3 to MG2. Obtain the expected power transmission from MG2 to MG1 and from MG2 to MG3.
- (4)
- Solve the distributed optimization operation model for MG3. From MG1, receive the expected power transmission from MG1 to MG3; from MG2, receive the expected power transmission from MG2 to MG3. Obtain the expected power transmission from MG3 to MG1 and from MG3 to MG2.
- (5)
- Update the Lagrange multipliers:
- (6)
- Check the convergence of the algorithm. If equation (B2) is satisfied, terminate the iteration:
- (7)
- Otherwise, set k = k + 1 and repeat steps (2) to (6).
- Distributed Algorithm for the Electricity Trading Revenue Maximization Sub-problem
- (1)
- Set the maximum iteration count , convergence precision ζ = 0.1, penalty factor γ = 10, initial iteration count k = 1, and initial inter-MG trading price .
- (2)
- Solve the distributed optimization operation model for MG1. From MG2, receive the expected trading price from MG2 to MG1; from MG3, receive the expected trading price from MG3 to MG1. Obtain the expected trading prices from MG1 to MG2 and from MG1 to MG3.
- (3)
- Solve the distributed optimization operation model for MG2. From MG1, receive the expected trading price from MG1 to MG2; from MG3, receive the expected trading price from MG3 to MG2. Obtain the expected trading prices from MG2 to MG1 and from MG2 to MG3.
- (4)
- Solve the distributed optimization operation model for MG3. From MG1, receive the expected trading price from MG1 to MG3; from MG2, receive the expected trading price from MG2 to MG3. Obtain the expected trading prices from MG3 to MG1 and from MG3 to MG2.
- (5)
- Update the Lagrange multipliers:
- (6)
- Check the convergence of the algorithm:If the following condition is satisfied, terminate the iteration:
- (7)
- Otherwise, set k = k + 1, and repeat steps (2) to (5).
5. Case Study
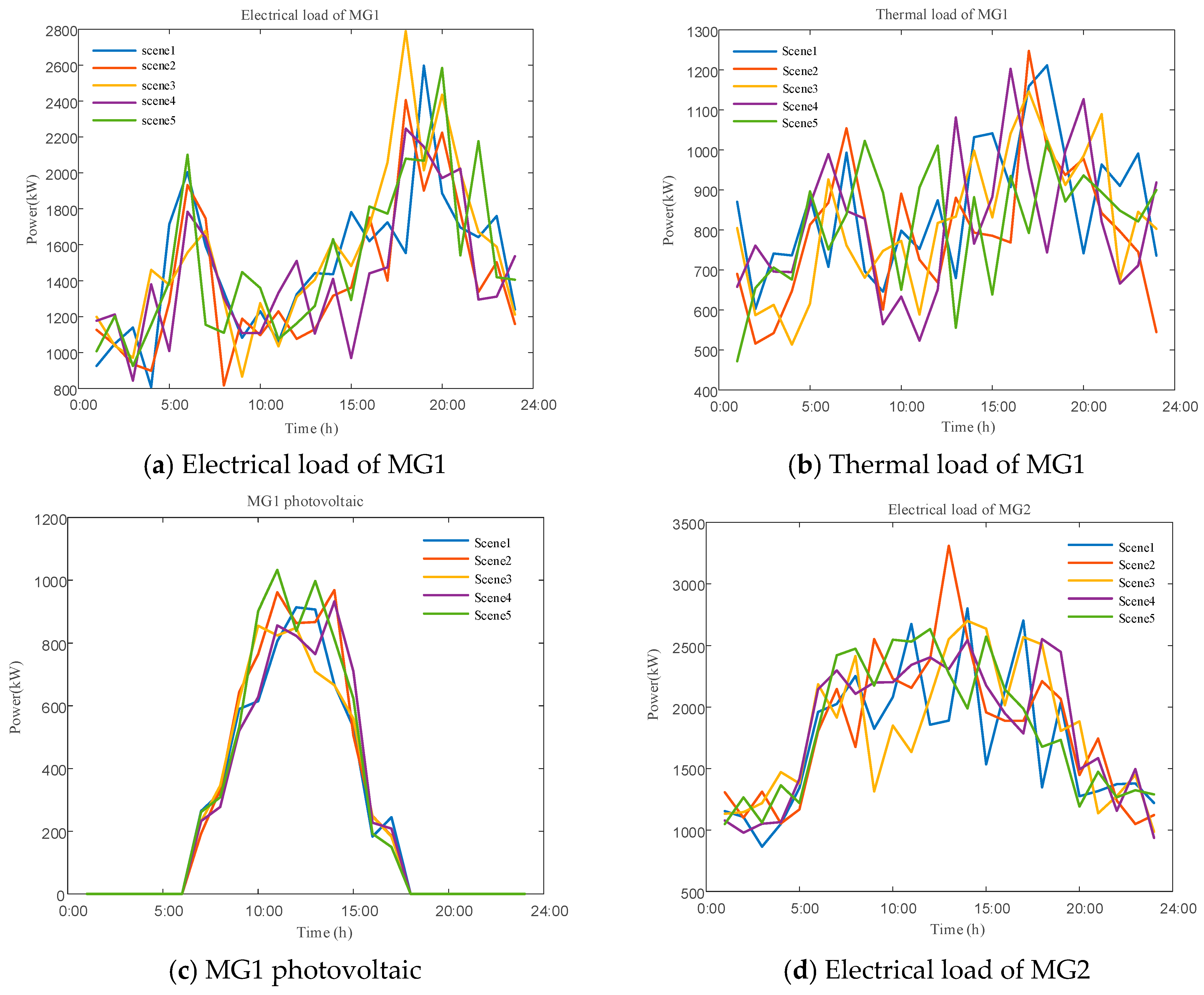
5.1. Basic Data and System Structure Description
5.2. Scheduling Plan
5.2.1. Convergence Analysis
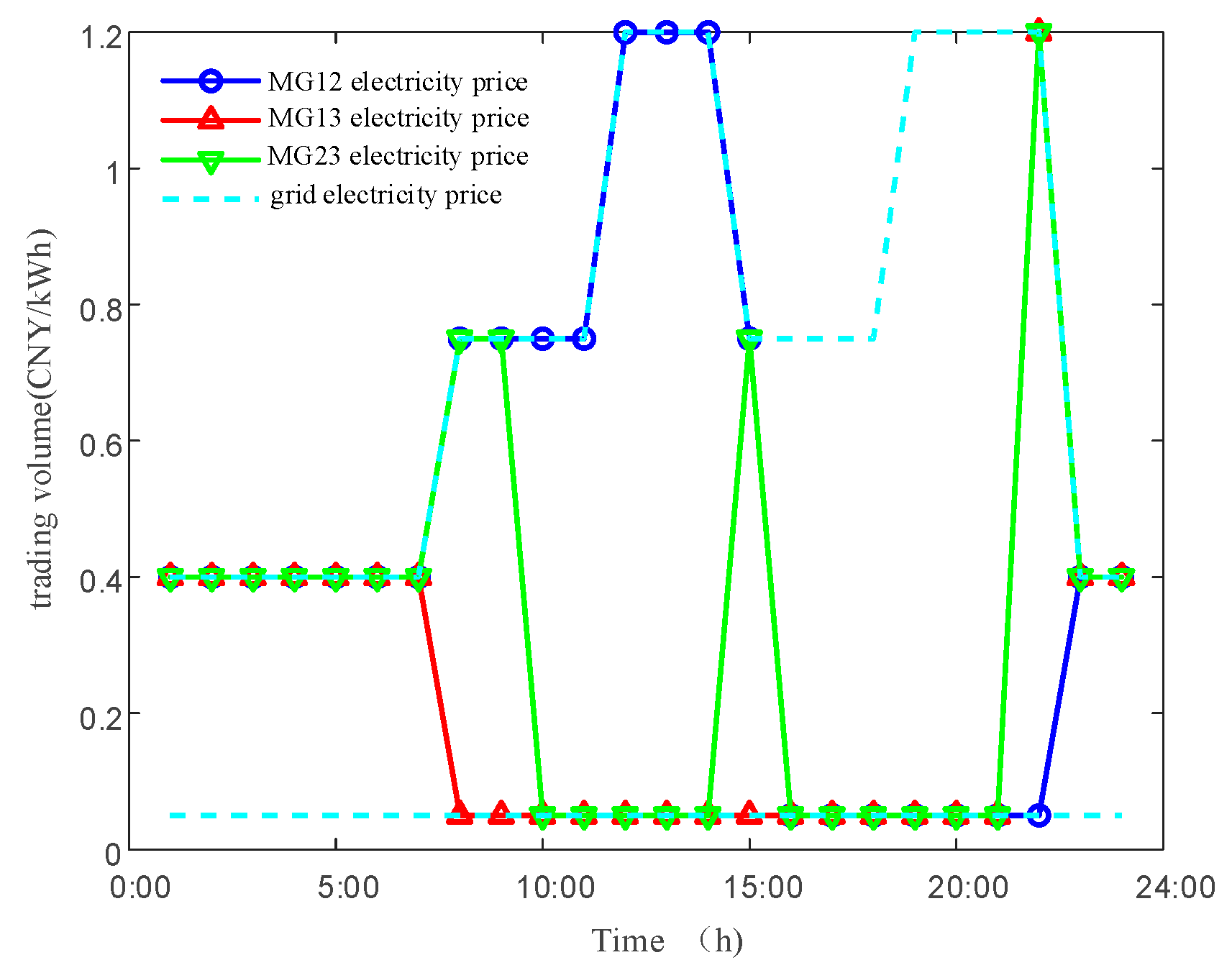
5.2.2. Analysis of Traded Electricity Volume and Traded Electricity Price
5.2.3. Worst-Case Scenario Analysis
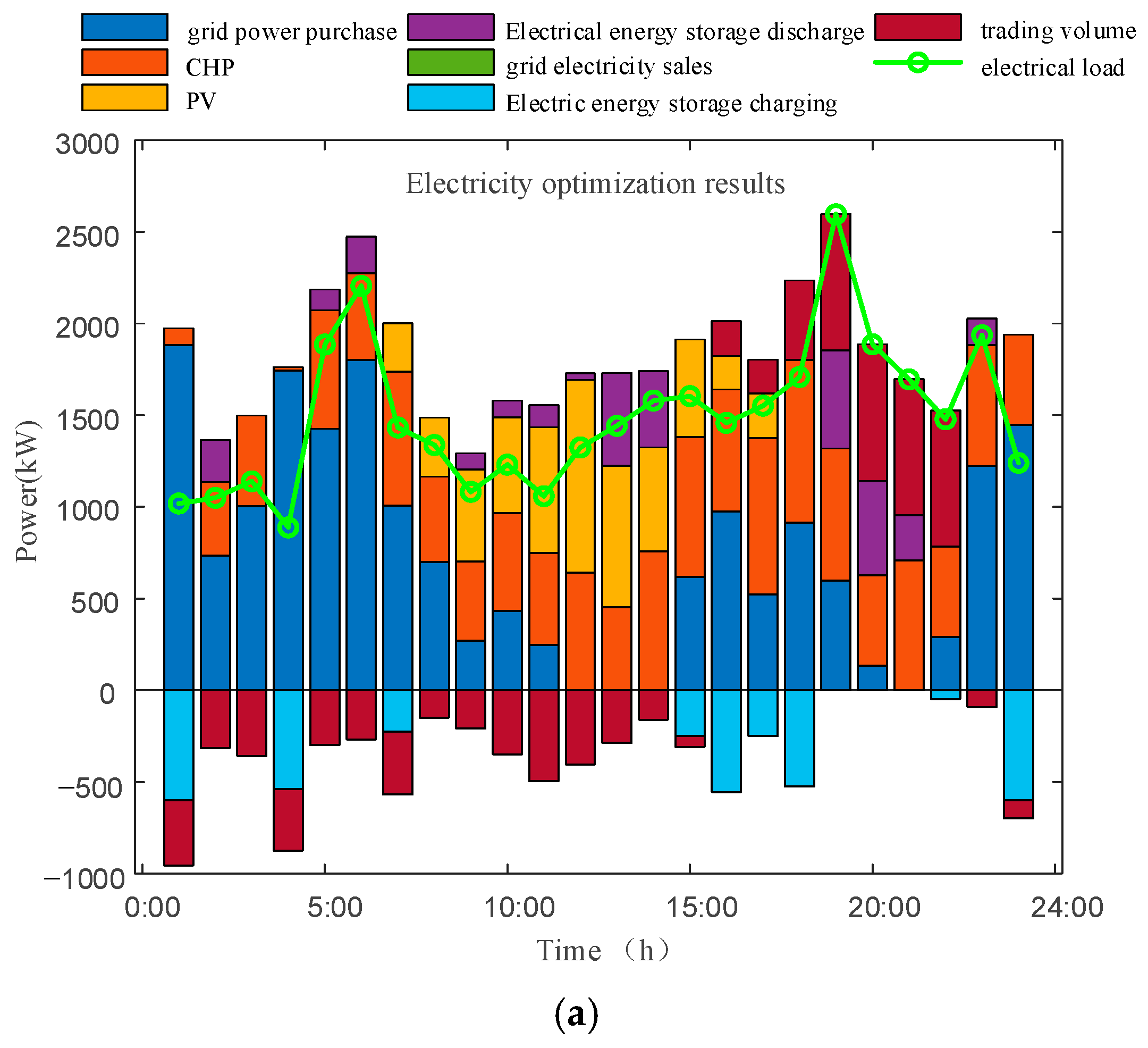
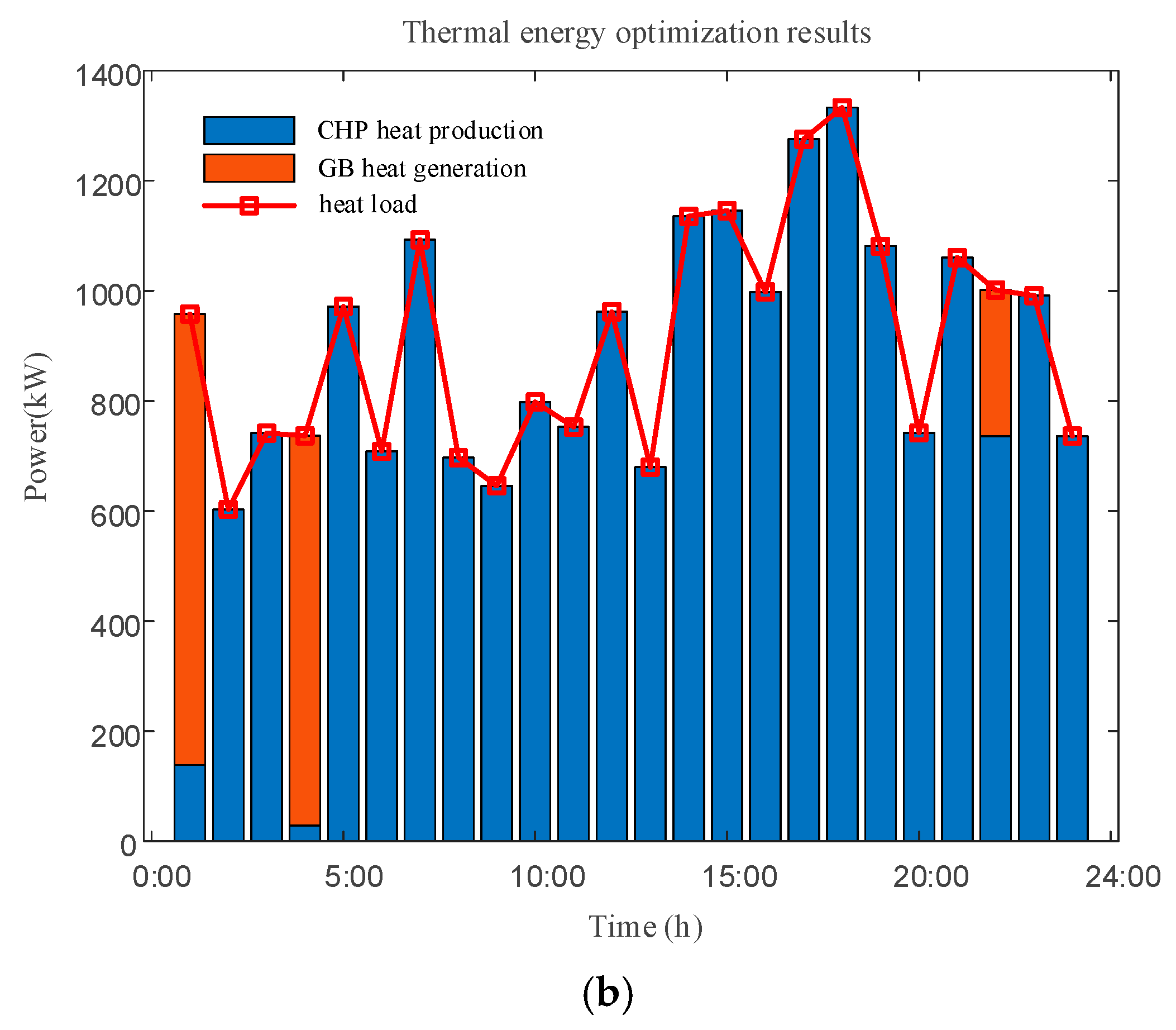
5.2.4. Scheduling Plan Analysis
5.3. Cost-Benefit Analysis
5.4. Uncertainty Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MG | microgrid |
| CES | community energy storage |
| BdC | bidirectional converters |
| DcUS | data-correlated uncertainty set |
| C&CG | Column-and-Constraint Generation |
| ADMM | Alternating Direction Method of Multipliers |
| MMG | multi-microgrid |
| DFIG | dynamics in doubly fed induction generators |
| P2P | peer-to-peer |
| MEMG | multi-energy microgrids |
| CHP | cogeneration of heat and power |
| GB | gas boiler |
References
- Ferrada, F.; Babonneau, F.; Homem-de-Mello, T.; Jalil-Vega, F. The role of hydrogen for deep decarbonization of energy systems: A Chilean case study. Energy Policy 2023, 177, 113536. [Google Scholar] [CrossRef]
- Khorramfar, R.; Mallapragada, D.; Amin, S. Electric-gas infrastructure planning for deep decarbonization of energy systems. Appl. Energy 2024, 354, 122176. [Google Scholar] [CrossRef]
- Abbasi, M.; Abbasi, E.; Li, L.; Aguilera, R.P.; Lu, D.; Wang, F. Review on the microgrid concept, structures, components, communication systems, and control methods. Energies 2023, 16, 484. [Google Scholar] [CrossRef]
- Tariq, A.H.; Kazmi, S.A.A.; Hassan, M.; Ali, S.M.; Anwar, M. Analysis of fuel cell integration with hybrid microgrid systems for clean energy: A comparative review. Int. J. Hydrogen Energy 2024, 52, 1005–1034. [Google Scholar] [CrossRef]
- Thirunavukkarasu, G.S.; Seyedmahmoudian, M.; Jamei, E.; Horan, B.; Mekhilef, S.; Stojcevski, A. Role of optimization techniques in microgrid energy management systems—A review. Energy Strategy Rev. 2022, 43, 100899. [Google Scholar] [CrossRef]
- Wang, Z.; Hou, H.; Wei, R.; Li, Z. A Distributed Market-Aided Restoration Approach of Multi-Energy Distribution Systems Considering Comprehensive Uncertainties from Typhoon Disaster. IEEE Trans. Smart Grid 2025, 16, 3743–3757. [Google Scholar] [CrossRef]
- Wu, X.; Li, S.; He, P.; Zhao, C.; Liu, M. Economic dispatch of multi-microgrids considering flexible load based on distributed consensus algorithm. Electr. Eng. 2025, 107, 4699–4710. [Google Scholar] [CrossRef]
- Tehrani, K.; Simde, D.; Fozing, J.; Jamshidi, M. (Eds.) A 3D design of small hybrid farm for microgrids. In Proceedings of the 2022 World Automation Congress (WAC), San Antonio, TX, USA, 11–15 October 2022. [Google Scholar]
- Lilliu, F.; Recupero, D.R. A cooperative game-theory approach for incentive systems in local energy communities. Sustain. Energy Grids Netw. 2024, 38, 101391. [Google Scholar] [CrossRef]
- Liu, X.; Ji, Z.; Sun, W.; He, Q. Robust game-theoretic optimization for energy management in community-based energy system. Electr. Power Syst. Res. 2023, 214, 108939. [Google Scholar] [CrossRef]
- Naji El Idrissi, R.; Ouassaid, M.; Maaroufi, M. Game theory approach for energy consumption scheduling of a community of smart grids. J. Electr. Eng. Technol. 2023, 18, 2695–2708. [Google Scholar] [CrossRef]
- Gao, X.; Zhang, X. Robust collaborative scheduling strategy for multi-microgrids of renewable energy based on a non-cooperative game and profit allocation mechanism. Energies 2024, 17, 519. [Google Scholar] [CrossRef]
- Dorahaki, S.; Muyeen, S.; Amjady, N. A Stackelberg Game Theory Model for Integrated Community Energy Storage Systems. IEEE Access 2024, 12, 152908–152920. [Google Scholar] [CrossRef]
- Wang, C.; Xu, H.; Guo, C.; Zhang, X.; Qiao, Y. Multi-stakeholder behavior analysis of shared energy storage market based on evolutionary game. CSEE J. Power Energy Syst. 2024, 1–2, early access. [Google Scholar]
- Liang, Z.; Chung, C.; Wang, Q.; Chen, H.; Yang, H.; Wu, C. Fortifying Renewable-Dominant Hybrid Microgrids: A Bi-Directional Converter Based Interconnection Planning Approach. Engineering 2025, 51, 130–143. [Google Scholar] [CrossRef]
- Hou, H.; Wang, Z.; Zhao, B.; Zhang, L.; Shi, Y.; Xie, C. Peer-to-peer energy trading among multiple microgrids considering risks over uncertainty and distribution network reconfiguration: A fully distributed optimization method. Int. J. Electr. Power Energy Syst. 2023, 153, 109316. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, Y.; Zou, Y.; Jiang, T.; Li, X. Privacy-Preserving Cooperative Optimal Operation for Reconfigurable Multimicrogrid Distribution Systems: A Noniterative Distributed Optimization Approach. IEEE Trans. Ind. Inform. 2025, 21, 5766–5776. [Google Scholar] [CrossRef]
- Zhong, J.; Li, Y.; Cao, Y.; Tan, Y.; Peng, Y.; Zhou, Y.; Nakanishi, Y.; Li, Z. Robust coordinated optimization with adaptive uncertainty set for a multi-energy microgrid. IEEE Trans. Sustain. Energy 2022, 14, 111–124. [Google Scholar] [CrossRef]
- Khaligh, V.; Ghezelbash, A.; Mazidi, M.; Liu, J.; Ryu, J.-H. P-robust energy management of a multi-energy microgrid enabled with energy conversions under various uncertainties. Energy 2023, 271, 127084. [Google Scholar] [CrossRef]
- Tan, B.; Lin, Z.; Zheng, X.; Xiao, F.; Wu, Q.; Yan, J. Distributionally robust energy management for multi-microgrids with grid-interactive EVs considering the multi-period coupling effect of user behaviors. Appl. Energy 2023, 350, 121770. [Google Scholar] [CrossRef]
- Yu, M.; Liao, M.; Du, M.; Chen, A. Cooperative Optimal Operation of Multi-Microgrids Based on Two-Staged Robustness. In Proceedings of the 2024 China Automation Congress (CAC), Qingdao, China, 1–3 November 2024. [Google Scholar]
- Zhang, S.; Hu, W.; Cao, X.; Du, J.; Zhao, Y.; Bai, C.; Liu, W.; Tang, M.; Zhan, W.; Chen, Z. A two-stage robust low-carbon operation strategy for interconnected distributed energy systems considering source-load uncertainty. Appl. Energy 2024, 368, 123457. [Google Scholar] [CrossRef]
- Liu, Y.; Li, X.; Liu, Y. A low-carbon and economic dispatch strategy for a multi-microgrid based on a meteorological classification to handle the uncertainty of wind power. Sensors 2023, 23, 5350. [Google Scholar] [CrossRef]
- Aminlou, A.; Hayati, M.; Zare, K. ADMM-based fully decentralized Peer to Peer energy trading considering a shared CAES in a local community. J. Energy Manag. Technol. 2024, 8, 141–147. [Google Scholar]
- Wang, J.; Li, Y.; Liu, J. Distributed coordinated planning for cross-border energy system: An ADMM-based decentralized approach. Electr. Power Syst. Res. 2023, 221, 109441. [Google Scholar] [CrossRef]
- Zhai, J.; Jiang, Y.; Shi, Y.; Jones, C.N.; Zhang, X.-P. Distributionally robust joint chance-constrained dispatch for integrated transmission-distribution systems via distributed optimization. IEEE Trans. Smart Grid 2022, 13, 2132–2147. [Google Scholar] [CrossRef]
- Lü, Y.; Zhao, X.; Shah, P. Robust optimal framework for doubly fed induction generator with uncertain dynamics. Prot. Control Mod. Power Syst. 2024, 9, 129–141. [Google Scholar] [CrossRef]
- Wang, Y.; Li, R.; Erofeev, A.; He, J. Benefit–cost model of microgrid integration based on Nash negotiation optimization algorithm. Electr. Eng. 2025, 1–12. [Google Scholar] [CrossRef]
- Fu, Y.; Sun, Q.; Wennersten, R.; Pang, X.; Liu, W. Interactive scheduling optimization of regional multi-agent integrated energy systems considering uncertainties based on game theory. J. Clean. Prod. 2024, 449, 141697. [Google Scholar] [CrossRef]
- Du, J.; Han, X.; Wang, J. Distributed cooperation optimization of multi-microgrids under grid tariff uncertainty: A nash bargaining game approach with cheating behaviors. Int. J. Electr. Power Energy Syst. 2024, 155, 109644. [Google Scholar] [CrossRef]
- Wang, Z.; Hou, H.; Zhao, B.; Zhang, L.; Shi, Y.; Xie, C. Risk-averse stochastic capacity planning and P2P trading collaborative optimization for multi-energy microgrids considering carbon emission limitations: An asymmetric Nash bargaining approach. Appl. Energy 2024, 357, 122505. [Google Scholar] [CrossRef]



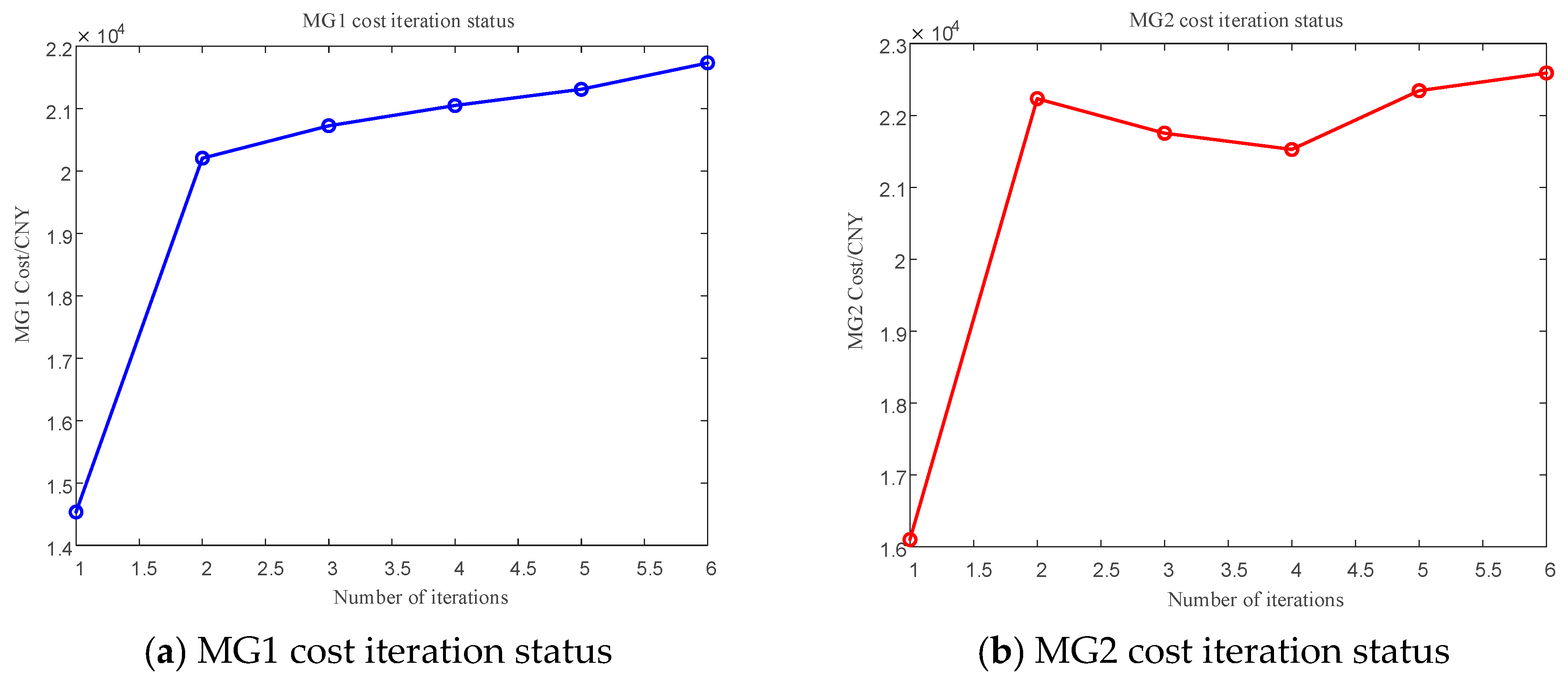

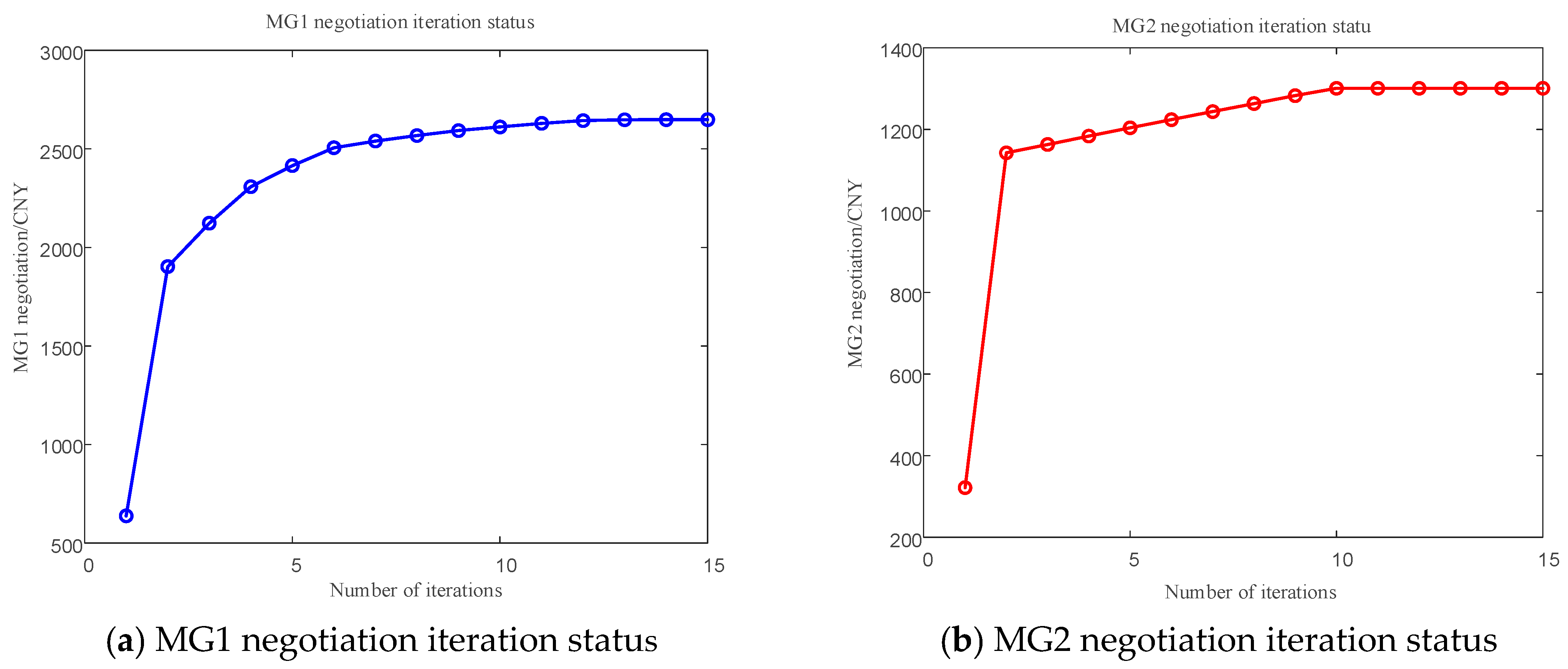
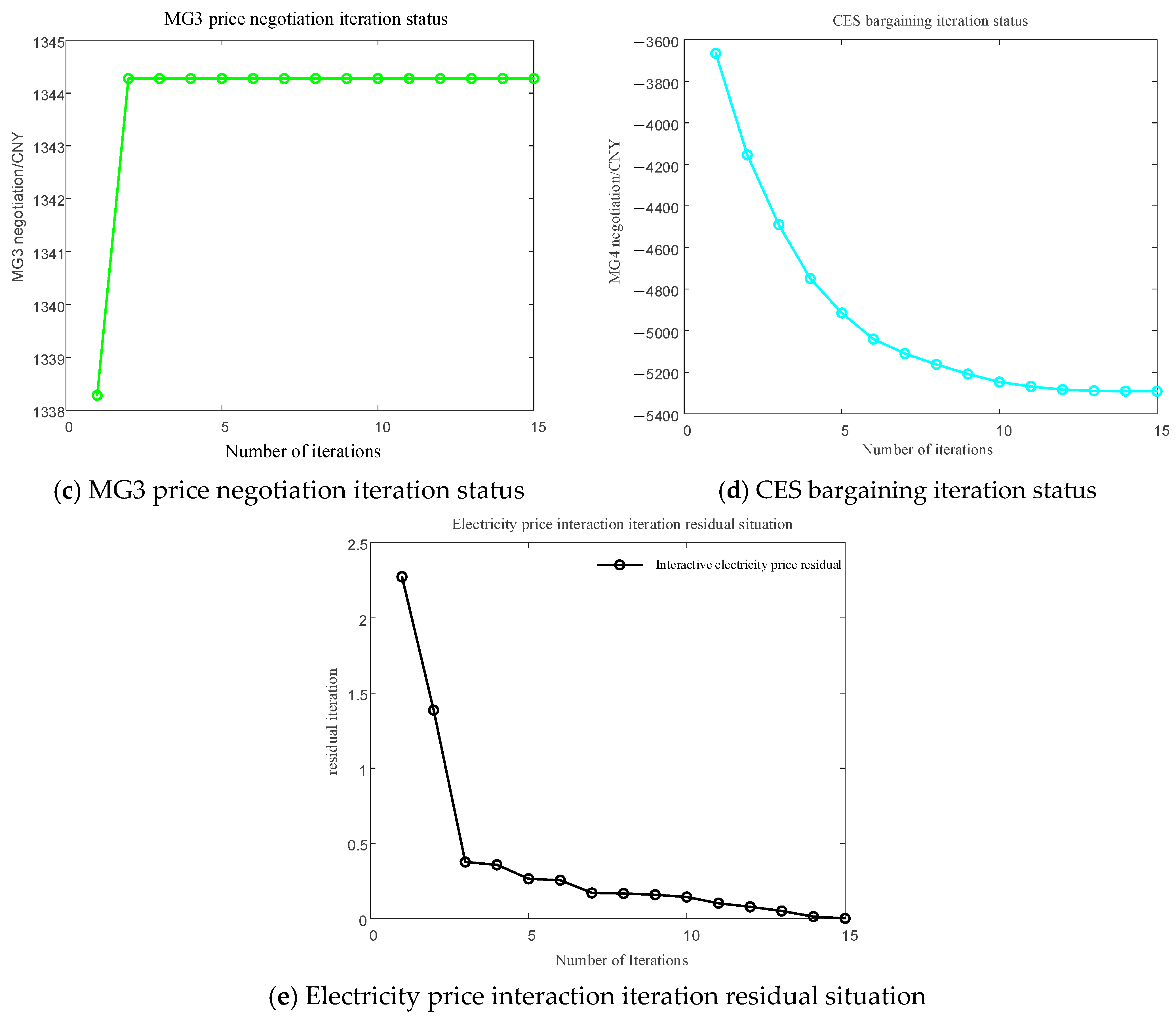
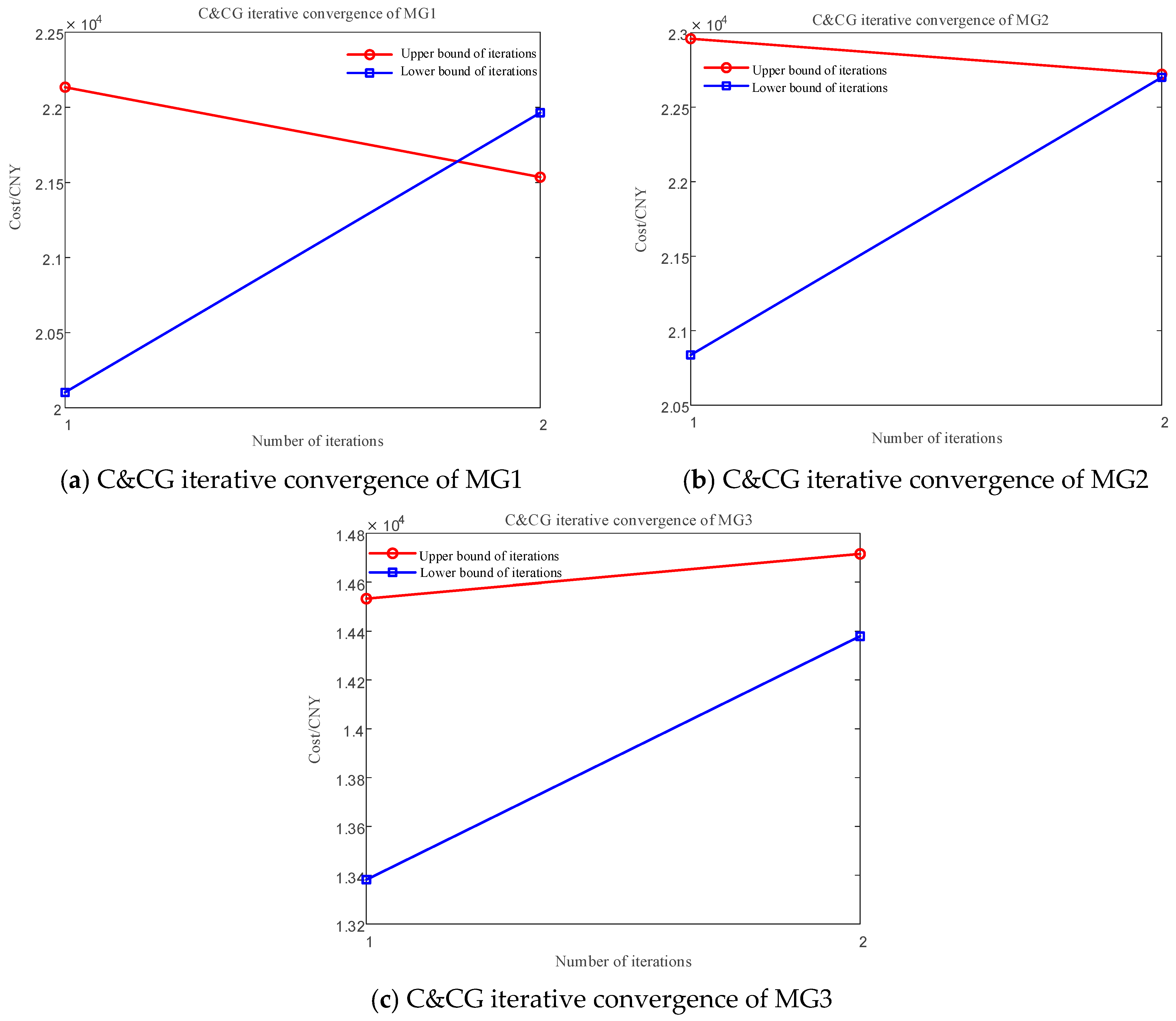




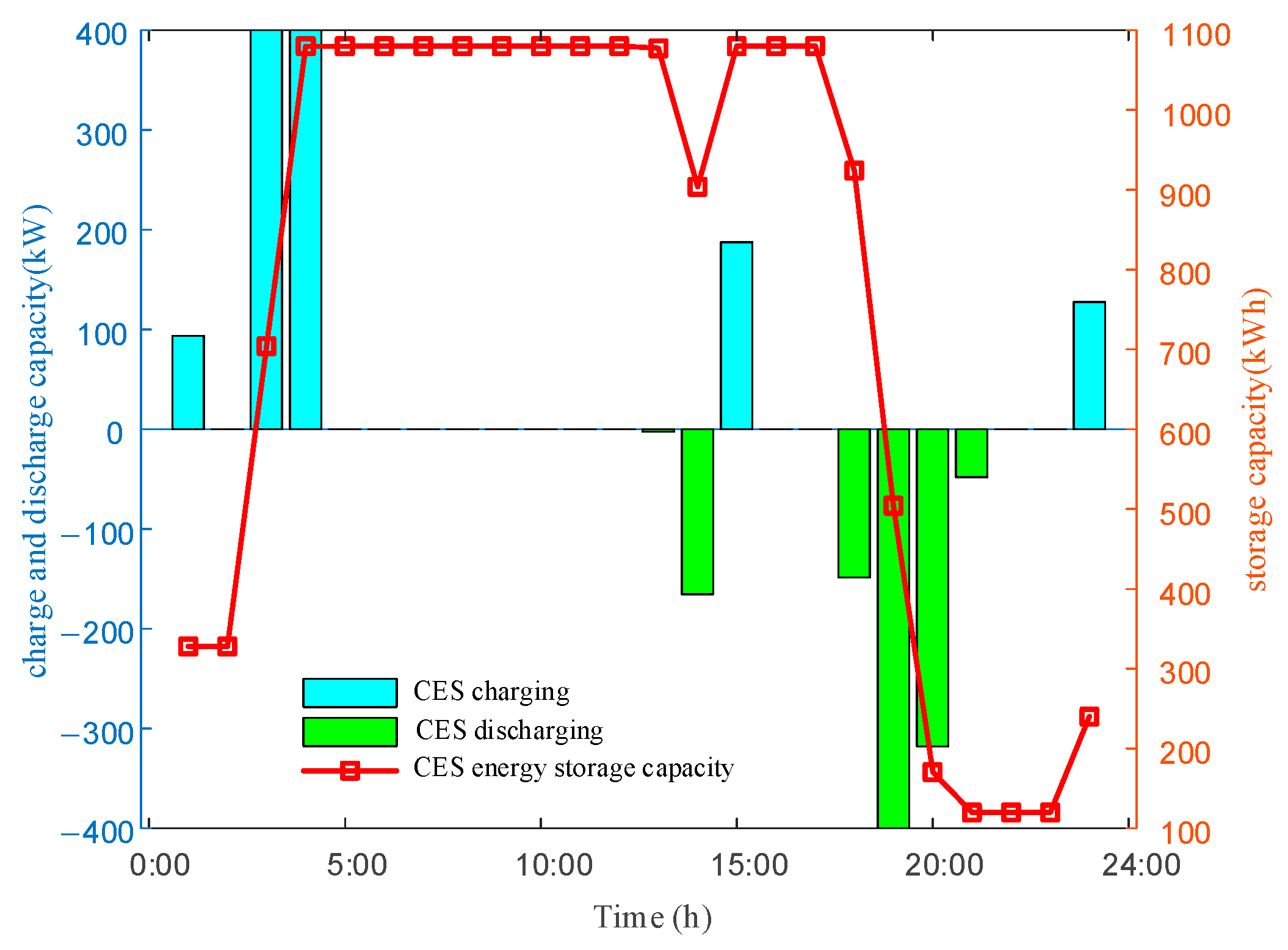
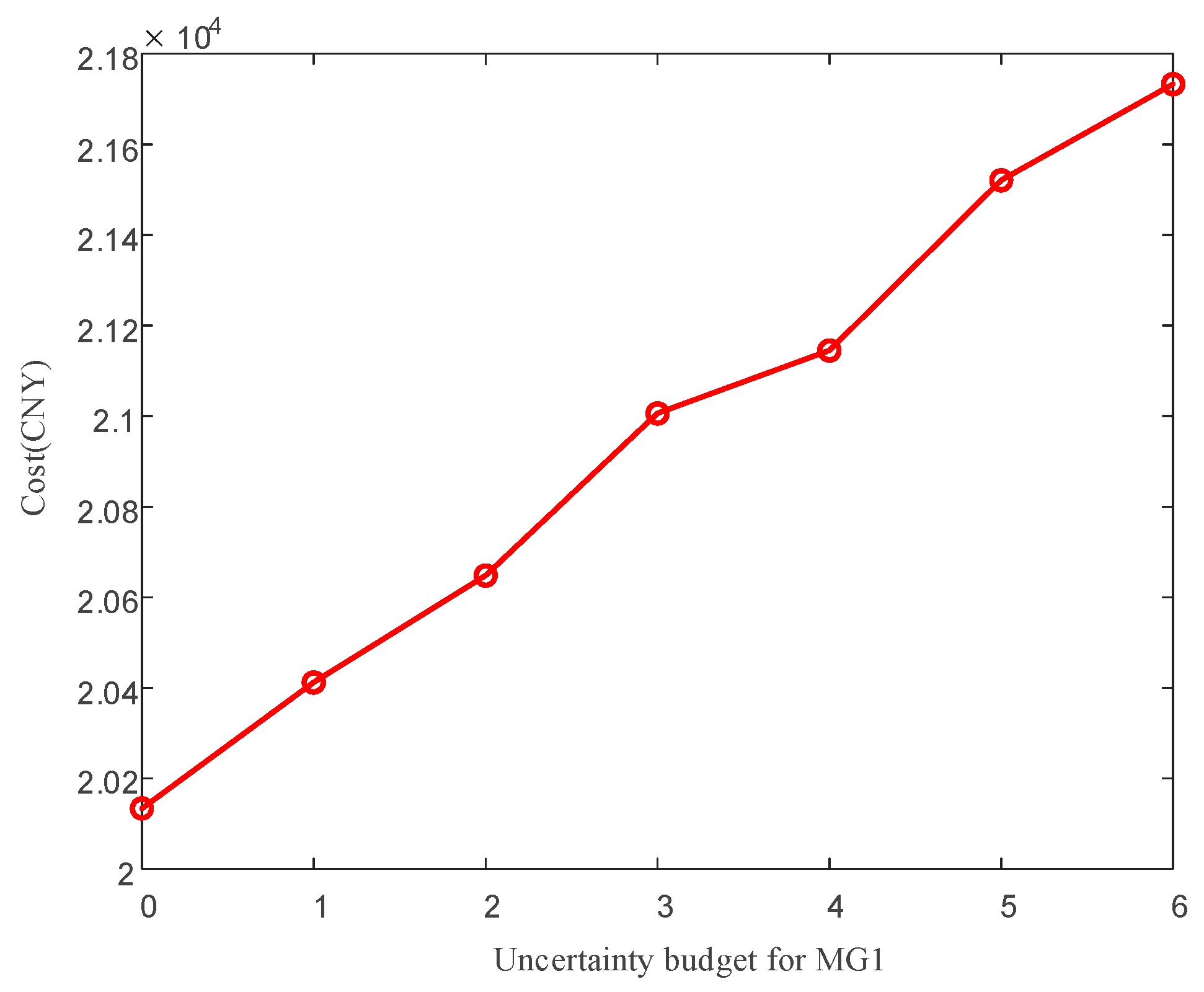
| Time Period Type | Time Period | Purchase Price (CNY/kWh) | Sale Price (CNY/kWh) | Gas Price (CNY/m3) |
|---|---|---|---|---|
| Peak time | 12:00−14:00, 19:00−22:00 | 1.20 | 0.60 | 2.5 |
| Off−peak time | 01:00−07:00, 23:00−24:00 | 0.40 | 0.20 | |
| Normal time | 08:00−11:00, 15:00−18:00 | 0.75 | 0.40 |
| Scene | MG1 | MG2 | MG3 |
|---|---|---|---|
| 1 | 0.12 | 0.17 | 0.17 |
| 2 | 0.38 | 0.15 | 0.38 |
| 3 | 0.15 | 0.11 | 0.14 |
| 4 | 0.13 | 0.35 | 0.16 |
| 5 | 0.22 | 0.22 | 0.15 |
| Optimization Part | Microgrid Scale | Iteration | Solution Time/s |
|---|---|---|---|
| Maximizing social welfare | 3 | 6 | 4278.3 |
| 4 | 12 | 5965.9 | |
| Distribution of benefits on Duowei Network | 3 | 15 | 27.1 |
| 4 | 23 | 33.2 |
| Algorithm | Microgrid | Iteration | Solution Time/s |
|---|---|---|---|
| Traditional C&CG | 1 | 2 | 423.21 |
| 2 | 3 | 76.19 | |
| 3 | 3 | 68.45 | |
| C&CG embedded with PH | 1 | 2 | 30.06 |
| 2 | 2 | 30.47 | |
| 3 | 2 | 30.53 |
| Cost | MG1 | MG2 | MG3 | CES | Alliance |
|---|---|---|---|---|---|
| Break-even point cost/CNY | 24,360.83 | 26,888.18 | 15,070.36 | 0 | 66,319.37 |
| Cooperation cost/CNY | 21,733.16 | 22,591.83 | 14,423.83 | 161.30 | 58,910.12 |
| Fraud cost/CNY | 1041.79 | 2007.84 | −1278.17 | −1771.28 | / |
| Negotiation conclusion cost/CNY | 23,618.23 | 25,818.26 | 13,618.96 | −5130.56 | 57,924.89 |
| Benefit increase value/CNY | 742.60 | 1069.92 | 1451.40 | 5130.56 | 8394.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bian, H.; Ji, K. A Robust Collaborative Optimization of Multi-Microgrids and Shared Energy Storage in a Fraudulent Environment. Energies 2025, 18, 4635. https://doi.org/10.3390/en18174635
Bian H, Ji K. A Robust Collaborative Optimization of Multi-Microgrids and Shared Energy Storage in a Fraudulent Environment. Energies. 2025; 18(17):4635. https://doi.org/10.3390/en18174635
Chicago/Turabian StyleBian, Haihong, and Kai Ji. 2025. "A Robust Collaborative Optimization of Multi-Microgrids and Shared Energy Storage in a Fraudulent Environment" Energies 18, no. 17: 4635. https://doi.org/10.3390/en18174635
APA StyleBian, H., & Ji, K. (2025). A Robust Collaborative Optimization of Multi-Microgrids and Shared Energy Storage in a Fraudulent Environment. Energies, 18(17), 4635. https://doi.org/10.3390/en18174635






