A Two-Stage Stochastic Unit Commitment Model for Sustainable Large-Scale Power System Planning Under Renewable and EV Variability

Abstract

The increasing integration of renewable energy sources and the widespread adoption of electric vehicles have introduced considerable uncertainty into the operation of large-scale power systems. Traditional deterministic unit commitment models are insufficient for managing such variability in a reliable and cost-effective manner. This study proposes a two-stage stochastic unit commitment model that captures uncertainties in solar photovoltaic generation, electric vehicle charging demand, and load fluctuations using a mixed-integer linear programming framework with recourse. The model is applied to Thailand’s national power system, comprising 171 generators across five regions, to assess its scalability for sustainable large-scale planning. Results indicate that the stochastic model significantly enhances system reliability across most demand profiles. Under the Winter Weekday group, the number of lacking scenarios decreases by 76.92 percent and the number of missing periods decreases by 78.57 percent, while the average and maximum lack percentages are reduced by 56.32 percent and 72.61 percent, respectively. Improvements are even greater under the Rainy Weekday group, where lacking scenarios and periods decline by more than 92 percent and the maximum lack percentage falls by over 98 percent, demonstrating the model’s robustness under volatile solar output and load conditions. Although minor anomalies are observed, such as slight increases in average and maximum lack percentages in the Summer Weekday group, these are minimal and likely attributable to randomness in scenario generation or boundary effects in optimization. Overall, the stochastic model provides substantial advantages in managing uncertainty, achieving notable improvements in reliability with only modest increases in operational cost and computational time. The findings confirm that the proposed approach offers a robust and practical framework for supporting sustainable and resilient power systems in regions with high variability in both generation and demand.

1. Introduction

Power systems worldwide are undergoing significant structural transformations due to the increasing integration of renewable energy sources and the rapid growth of electric vehicles (EVs). These advancements introduce substantial uncertainties in both power generation and consumption, thereby elevating the complexity of power system management. Conventional deterministic unit commitment (UC) models, which were initially designed under the premise of stable and predictable conditions, are now inadequate for contemporary power systems. Such models do not accurately capture the inherent variability and stochastic nature of renewable energy output and EV charging demands, resulting in suboptimal or potentially unreliable scheduling decisions [1,2]. The discrepancy between generation and demand heightens the risk of reserve shortages and undermines the economic efficiency of system operations. Therefore, sophisticated UC models capable of effectively managing uncertainty while guaranteeing operational reliability and cost-effectiveness have become indispensable.

Numerous studies have endeavored to address the limitations of deterministic unit commitment (UC) by integrating uncertainty through stochastic, fuzzy, or hybrid optimization methodologies. For instance, Trojani et al. developed a stochastic security-constrained UC model that encompasses flexible loads, energy storage systems, and electric vehicles within the scheduling framework [3]. Although their model enhanced dispatch efficiency under uncertain conditions, it did not comprehensively represent the complexities of power transmission constraints across regional zones. Ny and Jeenanunta proposed a fuzzy unit commitment framework aimed at improving system reliability and reducing carbon emissions by incorporating uncertainty stemming from renewable generation, electric vehicle demand, and energy storage [4]. However, this model necessitated precise parameter calibration and lacked detailed modeling of transmission networks. Langenmayr et al. extended UC models to include photovoltaic–battery systems by considering uncertainties in solar power generation, electric vehicle loads, and consumer demand [5]. Nevertheless, their model was specialized for microgrid configurations, thereby limiting its applicability to larger, national systems. Kamboj and Malik formulated a UC strategy that integrates plug-in electric vehicles and renewable energy sources [6]. However, their model primarily concentrated on cost optimization and did not explicitly address stochastic variations in load or generation. These investigations highlight ongoing efforts to incorporate uncertainty, although they reveal existing gaps concerning spatial resolution, transmission modeling, and adaptive responses of the system.

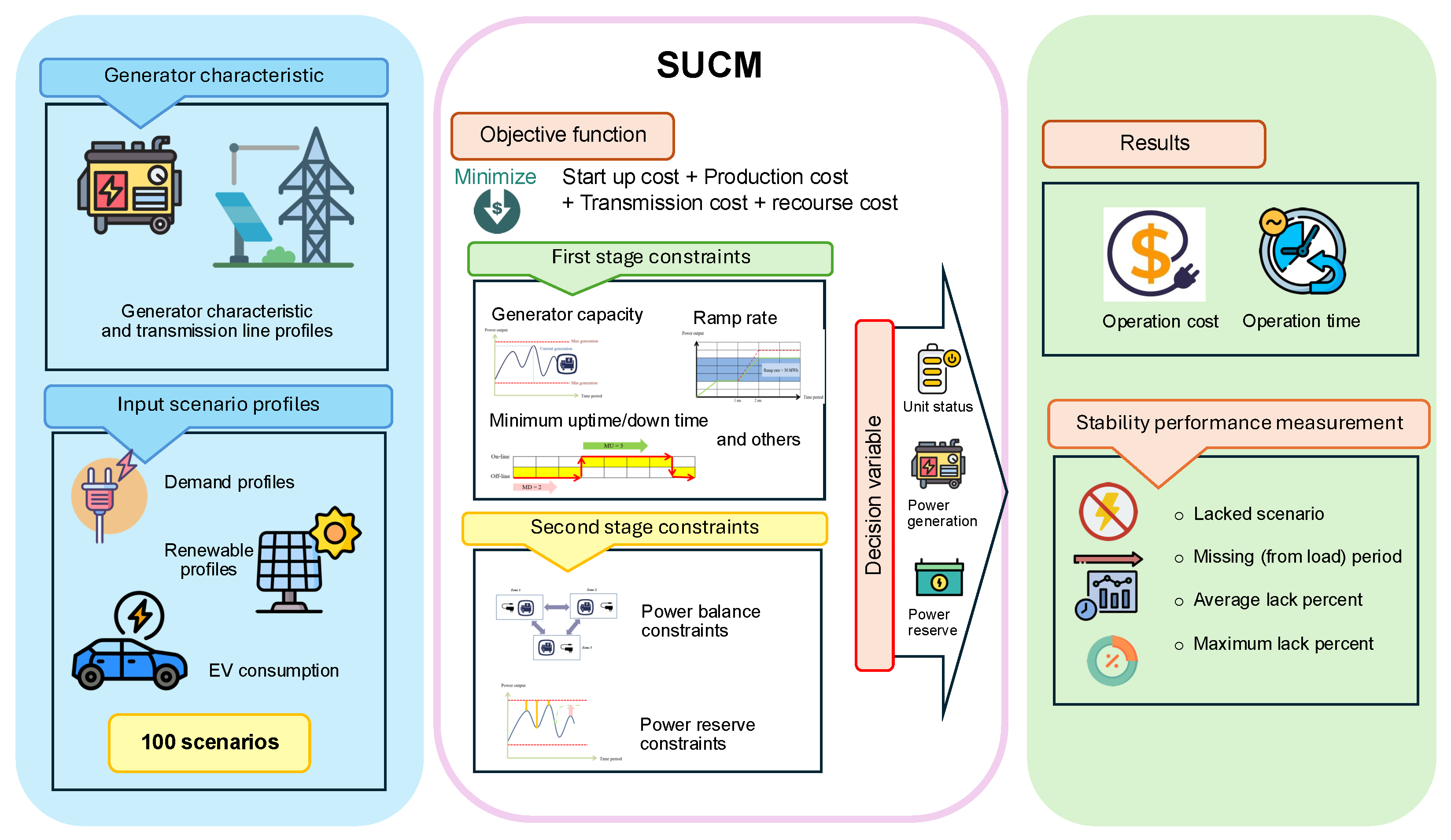
To address these limitations, this study proposes a two-stage stochastic unit commitment model with recourse, referred to as the SUCM, that integrates the variability of solar generation, stochastic electric vehicle charging demand, and zonal transmission constraints. The model represents system-wide uncertainty through multiple scenarios and enables adaptive decision-making by optimizing both first-stage commitment schedules and second-stage recourse variables. Unlike previous approaches that aggregate renewable output or neglect spatial dynamics, the proposed method evaluates solar generation at both zonal and plant-specific levels and accounts for power flows across regions. In addition, it introduces new performance indicators that measure system reliability under uncertainty, ensuring practical validation in large-scale systems. The primary innovation of this research lies in the combined treatment of renewable variability, electric vehicle demand, and transmission constraints within a unified stochastic framework, supported by extensive real-world validation using Thailand’s national power system. The overall framework of the proposed SUCM, together with its empirical evaluation, is presented in Figure 1.

The main contributions of this research are outlined as follows:

(1)

The introduction of a stochastic recourse-based unit commitment formulation that explicitly integrates uncertainties from renewable energy, electric vehicle charging, and load profiles, with detailed consideration of transmission constraints;

(2)

Application of the model to a large-scale national power system using real operational data from Thailand, thereby generating policy-relevant insights for system operators and planners;

(3)

Evaluation of the effects of spatial solar distribution and scenario resolution on system cost, computational requirements, and grid stability, highlighting the model’s robustness and adaptability.;

(4)

A comparative analysis with a deterministic model, demonstrating that the SUCM achieves significant improvements in system reliability and cost-effectiveness under conditions of high uncertainty while maintaining computational feasibility;

(5)

The development of performance indicators and scenario sensitivity assessments that provide a more comprehensive understanding of reliability outcomes and enhance the model’s applicability to future energy planning in different national contexts.

2. Literature Review

The integration of renewable energy and electric vehicle (EV) charging has introduced significant uncertainty into large-scale power system operations. Traditional deterministic unit commitment (UC) models, which assume perfect forecasts, often yield suboptimal or infeasible schedules under real-world variability in generation and demand [1,2]. To enhance reliability and economic efficiency amidst uncertainty, researchers have developed advanced UC frameworks that incorporate probabilistic and intelligent decision-making mechanisms [7]. Stochastic programming is a foundational approach in this context, modeling uncertainties in renewable output and load through multiple scenarios. For example, Liu et al. [8] proposed a scenario-based stochastic UC model to accommodate wind power variability alongside plug-in hybrid EV charging patterns. Zhao et al. [2] applied chance-constrained UC to improve wind utilization and mitigate reserve shortfalls. These stochastic models optimize expected operating costs across multiple potential outcomes and have demonstrated superior scheduling performance compared to deterministic methods. However, their application to large-scale systems faces computational challenges due to the exponential growth in the number of scenario combinations. Various techniques have been explored to manage this complexity. For instance, Quan et al. developed a comprehensive framework to integrate uncertainty in UC while reducing scenario count, improving tractability for larger systems [9]. Papavasiliou and Oren introduced one of the earliest stochastic UC models integrating renewable generation with demand response, showing that responsive loads can help meet reserve requirements under high renewable penetration [10]. Despite these innovations, scenario-based methods can become computationally intensive for national-scale systems.

Robust optimization offers an alternative by guaranteeing performance under worst-case uncertainty within predefined bounds. This approach ensures strong reliability but can lead to overly conservative and costly schedules. To reduce this conservatism, researchers have introduced hybrid methods. Zhou et al. [11] formulated a multistage robust UC model informed by probabilistic forecasts, striking a balance between robustness and cost-effectiveness. Such approaches maintain feasibility under uncertainty while avoiding extreme conservatism. Distributionally robust optimization further advances this idea by acknowledging ambiguity in probability distributions, yielding more balanced decisions between cost and reliability [7]. In addition, risk-aware formulations have been proposed. Asensio and Contreras integrated a Conditional Value-at-Risk (CVaR) criterion into a stochastic UC model for an islanded system, explicitly quantifying and limiting the risk of high-cost outcomes under renewable uncertainty [12]. This CVaR-based UC achieved a prudent trade-off between reliability and expected cost. Researchers have also unified stochastic and robust paradigms. Zhao and Guan proposed a unified stochastic–robust UC model that leverages both scenario-based and worst-case approaches to mitigate uncertainty [12]. Their unified framework reduces dispatch variability without the excessive conservatism of purely robust methods. Similarly, the seminal work of Bertsimas et al. on adaptive robust UC introduced dynamic uncertainty sets that adjust over the scheduling horizon, yielding robust schedules with minimal cost penalties [13]. More recent work by Lorca and Sun extended multistage robust UC to explicitly model the temporal evolution of uncertainty and the role of energy storage, improving reliability for systems with deep renewable penetration [14]. These robust and risk-averse approaches provide strong guarantees, though at the expense of increased computational complexity.

Artificial intelligence techniques have also been applied to address the stochastic unit commitment problem. Metaheuristic algorithms, including evolutionary computation and swarm intelligence, have demonstrated effectiveness in navigating the extensive solution space inherent in unit commitment problems. Kamboj and Malik proposed an enhanced scheduling strategy based on a chaotic zebra optimization algorithm for power systems with significant levels of renewable energy integration and electric vehicle charging demand [6]. Their approach improved the efficiency of identifying near-optimal scheduling solutions under uncertainty. Similarly, Jo and Kim developed an improved genetic algorithm that incorporates uncertainty directly into the unit commitment process, resulting in more resilient scheduling decisions under variable renewable energy conditions [15]. Concurrently, fuzzy logic has been employed as a means to manage uncertainty by representing imprecise parameters through linguistic variables. Ny and Jeenanunta implemented a fuzzy unit commitment model that accounts for renewable generation variability, electric vehicle charging behavior, and energy storage systems [4]. This method enhanced system reliability and contributed to reductions in carbon emissions. Nevertheless, fuzzy models require meticulous calibration of membership functions and may lack physical transparency. Despite these limitations, both metaheuristic and fuzzy approaches offer valuable tools for enhancing decision-making under uncertainty in sustainable power system planning.

Advances in machine learning have shown promise for complex, large-scale UC problems. Supervised learning techniques have been employed to predict unit commitment decisions, yielding satisfactory initial solutions and accelerating optimization. In particular, deep reinforcement learning (DRL) has been investigated for the derivation of near-optimal UC policies in dynamic environments. Zhang et al. reviewed applications of deep RL in power systems, highlighting its potential for operational decision-making under uncertainty [16]. Xu et al. [17] implemented a DRL-based model-free UC approach that learns to adaptively handle wind power fluctuations. These learning-based approaches can improve over time by learning from data rather than relying solely on explicit models. Nevertheless, challenges remain regarding the interpretability of their models, the enforcement of complex constraints, and the extensive data required for training [18]. To address such issues, hybrid methods that combine machine learning with mathematical optimization have emerged. Venkatesh et al. introduced a hybrid framework in which a machine learning module generates candidate UC solutions that are then refined via fuzzy optimization to ensure feasibility [19]. This approach capitalizes on the speed of learning algorithms while preserving the rigorous constraint satisfaction of optimization. Such hybrid techniques have proven effective for large-scale problems, demonstrating faster solution times and improved scalability. Overall, while pure AI methods are not yet widely deployed in real operations due to reliability concerns [18], they represent a growing area of research that complements traditional stochastic and robust UC methods.

The proliferation of electric vehicles introduces new flexibility, as well as new uncertainties, into power systems. When equipped with smart charging and vehicle-to-grid (V2G) capabilities, EVs can act as adjustable demand or distributed storage resources. Multiple studies have explored EV integration within UC frameworks to harness this flexibility. Mohanty et al. and Ravi and Aziz show that coordinated EV charging and V2G discharging can shave peak loads and provide ancillary services to the grid [20,21]. By optimally scheduling EV demand, these strategies mitigate the impact of large EV fleets on the system. In their optimal UC formulation, Kamboj and Malik demonstrated that jointly optimizing generation dispatch with EV charging schedules reduces operational costs and increases utilization of renewable energy [6]. In another work, Kumar et al. presented a stochastic profit-based UC model that explicitly includes renewable sources, battery storage, and plug-in EVs, achieving improvements in system profitability and resilience under uncertainty [22]. High renewable penetration, especially from solar and wind, has been a driving force for such integrated models. For instance, Langenmayr et al. extended the UC problem to a photovoltaic–battery microgrid, accounting for uncertainties in solar generation, EV charging, and load demand [5]. Their results confirmed that incorporating distributed batteries and flexible EV loads enhances local grid reliability, although their model was limited to the microgrid scale. Overall, these studies underscore that intelligently managed EVs and energy storage can help buffer the variability of renewables, contributing to a more reliable and economic unit commitment solution.

Many of the above studies simplify transmission network constraints or focus on isolated sub-systems, which can limit their practical applicability to real large-scale power grids. In reality, accurate modeling of network constraints (transmission limits and security requirements) is essential for UC solutions to be feasible in operation. Security-constrained UC formulations incorporate these network limits and have been shown to provide more realistic schedules at the cost of higher computational complexity [7]. In their recent review, Aharwar et al. emphasize that including transmission constraints and N-1 security in the UC problem greatly increases the solution complexity yet is crucial for ensuring operational feasibility in practice. Some researchers have begun to address this by extending uncertainty-based UC models to the multi-region grid level. Trojani et al. integrated stochastic UC with inter-zonal transmission constraints, flexible EV charging, and energy storage across multiple regions [3]. Their multi-zone model yielded more reliable and economic schedules compared to treating each area in isolation. Similarly, Dhawale et al. developed a security-constrained UC approach for a hybrid power system with renewable generation and EV fleets, demonstrating enhanced system stability and robustness when these resources are properly co-optimized [23]. These works highlight that a unified framework capturing uncertainty, spatial diversity, and network limitations is needed for large-scale systems. However, such comprehensive models inevitably face scalability challenges.

Despite extensive progress in stochastic, robust, and intelligent unit commitment models, important gaps remain. Most existing studies address uncertainty, scalability, or network constraints individually rather than in an integrated manner. Only a limited number of models incorporate renewable variability, electric vehicle demand, and transmission constraints simultaneously in a framework suitable for national-scale power systems. Furthermore, emerging machine learning approaches, although promising, have yet to be fully applied in practical unit commitment settings that require strict reliability and interpretability. To contribute to the scientific community, the present research proposes a two-stage stochastic unit commitment model that integrates renewable uncertainty, electric vehicle variability, and transmission network constraints into a single comprehensive framework. Unlike earlier studies that focused primarily on either renewable energy integration, electric vehicle flexibility, or robust security-constrained scheduling, this work combines all three aspects, with an explicit emphasis on large-scale applicability. Comparisons are added to both the methodology discussion and the literature review, highlighting the differences between the proposed stochastic unit commitment model and other approaches, such as the fuzzy and deterministic formulations. In particular, the stochastic model explicitly quantifies uncertainty through probabilistic scenarios, incorporates electric vehicle demand within a temporal and spatially resolved framework, and ensures regional applicability by modeling zonal and plant-level solar generation alongside inter-zonal transmission flows. The model is validated using Thailand’s national power grid, offering both methodological innovation and practical policy relevance. By balancing probabilistic scenario optimization with network security requirements and adaptive recourse actions, the proposed approach advances the existing literature by addressing reliability, cost efficiency, and computational tractability concurrently, thereby providing a novel and holistic framework for sustainable and resilient power system operation under uncertainty.

3. Research Methodology and Formulation of the Two-Stage Stochastic Unit Commitment Model

The stochastic unit commitment model is developed by incorporating a stochastic recourse framework into the traditional unit commitment structure. The proposed model considers power generation from both conventional generators and renewable energy sources while accounting for load demand that includes both original (base) consumption and new demand from EV charging.

The proposed stochastic model employs a two-stage approach. In the first stage, decisions are made for each time period under deterministic conditions, including the on/off commitment of conventional generators, the power output levels of committed units, and the transmission power flows between zones. In the second stage, once these first-stage decisions are made, recourse decisions adjust the operation to handle uncertainties, namely to balance power deviations due to renewable output variability, to allocate additional spinning reserve for reliability, and to accommodate fluctuations in EV charging demand. The mathematical formulation of the key model constraints is presented below.

Let $T, G, Z, L$, and S be a set of time periods, a set of unit generators, a set of service zones, a set of transmission lines, and a set of scenarios, respectively.

3.1. First-Stage Decision Constraints: Unit Commitment and Reserve Requirements

• Generator limit constraints: The power output of each generator must remain between its minimum and maximum generation limits when the unit is online.

  $$u_u^t{\underline{p}}_u\le p_u^t\le u_u^t{\overline{p}}_u,\forall u\in G,t\in T,$$

  (1)

  where
  ${\underline{p}}_u$ is the minimum power generation of unit u;
  ${\overline{p}}_u$ is the maximum power generation of unit u;
  $u_u^t$ is the unit status of unit u in time period t.
  The value of unit status will be one if the generator is online and will be zero if the generator is offline.
• Ramp-rate up/down constraints: The increase or decrease in a generator’s output between two consecutive periods must not exceed the unit’s ramp-up or ramp-down limits.

  $$p_u^{t+1}-p_u^t\le R{U}_u,\forall u\in G,t\in T,$$

  (2)

  $$p_u^t-p_u^{t+1}\le R{D}_u,\forall u\in G,t\in T.$$

  (3)

  where
  ${RU}_u$ is the ramp-up rate of unit u in the case in which power production is increased;
  ${RD}_u$ is the ramp-down rate of unit u in the case in which power production is decreased.
• Unit status constraints: These constraints link the on/off status of a unit between consecutive periods with its start-up and shut-down decisions.

  $$u_u^{t+1}-u_u^t\le y_u^{t+1},\forall u\in G,t\in T,$$

  (4)

  $$z_u^{t+1}=y_u^{t+1}+u_u^t-u_u^{t+1},\forall u\in G,t\in T,$$

  (5)

  where
  $x{y}_u^t$ is the startup status of unit u in time period t (one when the unit is in startup and zero otherwise);
  $z_u^t$ is the shutdown status of unit u in time period t (one when the unit is in shutdown and zero otherwise).
• Initial condition constraints: These constraints define the status of each unit in the first period based on its status at the end of the previous day. They ensure consistency of start-up and shut-down variables at the beginning of the scheduling horizon. For example, if a unit was already running at the end of the previous day, then in time period 1, it cannot be counted as a start-up, etc. The specific logical conditions are applied for each unit’s initial on/off state; for brevity, detailed equations are not expanded upon here.

  $$\mathrm{if}int{u}_u>0,\mathrm{then}{y}_u^1=0\mathrm{and}{z}_u^1+u_u^1=1,\forall u\in G,$$

  (6)

  $$\mathrm{if}int{u}_u=0,\mathrm{then}{z}_u^1=0\mathrm{and}{y}_u^1=u_u^1,\forall u\in G,$$

  (7)

  where
  $int{u}_u$ is the unit status of unit u during the last period in the previous day.
• Minimum up/downtime constraint: Once a unit is started, it must remain ON for at least its minimum up time, and once shut down, it must remain OFF for at least its minimum down time. These constraints enforce the required number of consecutive periods of operation or down time.

  $$\begin{array}{c}\hfill \mathrm{if}int{up}_u>0\mathrm{and}int{up}_u<{MU}_u,\mathrm{then}\\ \hfill \underset{m=1}{\sum ^{M{U}_u-int{up}_u}}{u}_u^m\le M{U}_u-int{up}_u,\forall u\in G,\end{array}$$

  (8)

  $$\begin{array}{c}\hfill \mathrm{if}int{dw}_u>0\mathrm{and}int{dw}_u<{MD}_u,\mathrm{then}\\ \hfill \underset{m=1}{\sum ^{M{D}_u-int{dw}_u}}{u}_u^m=0,\forall u\in G,\end{array}$$

  (9)

  $$\underset{m=t-M{U}_u+1}{\sum ^t}{y}_u^m\le u_u^t,\forall u\in G,t>M{U}_u,$$

  (10)

  $$\underset{m=t-M{D}_u+1}{\sum ^t}{z}_u^m\le 1-u_u^t,\forall u\in G,t>M{D}_u,$$

  (11)

  where
  $int{up}_u$ is the initial uptime number of unit u in the generator set;
  $int{down}_u$ is the initial downtime number of unit u in the generator set;
  $M{U}_u$ is the minimum up time of unit u, namely the maximum number of online periods in the generator set;
  $M{D}_u$ is the minimum down time of unit u, namely the maximum number of offline periods in the generator set.
• Transmission limit constraints: Power flows on each transmission line must not exceed the line’s capacity. Additionally, for each zone, the total power transmitted out of the zone cannot exceed the power generated in that zone (to prevent “exporting” more power than produced).

  $$T{R}_l^t\left(i,j\right)\le {\overline{TR}}_l^t\left(i,j\right),\forall l\in L,t\in T,i,j\in Z,$$

  (12)

  $$\sum _{i\in Z,i\ne j}\sum _{l\in L_j,}T{R}_l^t(i,j)\le \sum _{u\in G_j}{p}_u^t,\forall j\in Z,t\in T,$$

  (13)

  where
  ${\overline{TR}}_l^t\left(i,j\right)$ is the maximum capacity of transmission power from zone i to zone j with transmission line l.

After all the decisions in the first stage have been made, constraints in the second stage are considered, including the power balance constraints.

3.2. Second-Stage Recourse Constraints: Power Balance Under Uncertainty

• Power balance constraints: For each zone (j) in each scenario (s), the total power supply must meet the load demand. In the second stage, this supply includes conventional generation, net transmission, and any recourse power deployed (such as fast-ramping generation or load shedding).

  $$\begin{array}{cc}\hfill \sum _{u\in G_j}{p}_u^t& +\sum _{i\in Z,i\ne j}\sum _{l\in L_j,}T{R}_l^t(i,j)-\sum _{i\in Z,i\ne j}\sum _{l\in L_j}T{R}_l^t\left(j,i\right)\hfill \\ & +\sum _{p\in P}{\tau }_{s,p}^t{R}_p^t+{RL}_s^t\ge d_j^t,\forall t\in T,j\in Z,s\in S,\hfill \end{array}$$

  (14)

  where
  $R^t$ is the solar power output in time period t;
  ${\tau }_{s,p}^t$ is the binary parameter that represents the status of solar plant p in the scenario s in time period t.
  In this equation, $d_j^t$ is the demand in zone j at time t. The term ${\tau }_{s,p}^t$ is a binary parameter indicating the status of solar plant p in scenario s at time t (1 if the plant is producing normally and 0 if it is effectively offline in that scenario). $R_p^t$ is the potential output of solar plant p at time t (e.g., its forecasted generation capacity). Thus, ${\tau }_{s,p}^t{R}_p^t$ represents the actual solar generation from plant p in scenario s (it equals either $R_p^t$ if online or 0 if offline). $R{L}_s^t$ is a recourse term for scenario s at time t representing any additional power to cover load (for instance, dispatch of reserve generators or load shedding). This constraint ensures that in each scenario, the supply (from conventional generators, net imports, and recourse) meets the demand.
• Spinning reserve constraints: For each time (t) and scenario (s), the combination of conventional reserve capacity and any recourse reserve must meet the reserve requirement under the scenario’s conditions. In the model, the reserve requirement is increased by the amount of lost solar generation in that scenario (since if some solar plants are offline, more reserve is needed to compensate).

  $$\sum _{u\in G}({\overline{p}}_u{u}_u^t-p_u^t)+{RS}_s^t\ge {\beta }^t+\sum _{p\in P}{\tau }_{s,p}^t{R}_p^t,\forall t\in T,s\in S,$$

  (15)

  where $R{S}_s^t$ is a second-stage recourse variable representing additional spinning reserve in scenario s at time t. The right-hand side of the inequality is the base reserve requirement (${\beta }^t$) plus the total solar generation available in scenario s at time t (since ${\sum }_{p\in P}{\tau }_{s,p}^t{R}_p^t$ effectively subtracts the offline solar capacity from what would normally be available, requiring that much extra reserve). This constraint ensures that even in the worst case for each scenario (with certain renewables offline), there is sufficient reserve from conventional units and recourse options.
  In addition to the above, all first-stage constraints (generator limits, ramp rates, unit status, initial conditions, minimum up/down times, and transmission limits) are implicitly applied within each scenario in the second stage. In other words, even under the conditions of each scenario, the generator’s outputs and statuses must respect those operational constraints.

3.3. Objective Function: Minimizing Expected Total Operating Costs

The SUCM integrates solar power generation and electric vehicle charging scenarios, affecting the power balance constraint, spinning reserve constraint, and objective function. Recourse variables are implemented to enhance the constraints addressing these uncertainties. Consequently, these constraints must be revised to incorporate the uncertainty presented by the scenarios. The SUCM is mathematically formulated as follows:

The objective of the SUCM is to minimize the total cost, including the conventional production cost, transmission cost, and recourse cost, as shown below.

$$\mathrm{Minimize}z=\sum _{t\in T}\sum _{u\in G}{s}_u{y}_u^t+\sum _{t\in T}\sum _{u\in G}{c}_u{p}_u^t+\sum _{i,j\in Z}\sum _{t\in T}\sum _{l\in L}T{R}_l^t(i,j)+\phi \sum _{t\in T}\sum _{s\in S}{\pi }_s({RL}_s^t+{RS}_s^t)$$

(16)

where

• $S$ is the set of scenarios;
• $P$ is the set of considered solar PV plants;
• ${\pi }_s$ is the probability of scenario s;
• ${RL}_s^t$ is the recourse variable of the power balance constraint in scenarios s in time period t;
• ${RS}_s^t$ is the recourse variable of the spinning reserve constraint in scenarios s in time period t;
• $\phi$ is the penalty cost of the recourse power.

However, this model does not account for the fixed and variable costs of solar power generation, so these costs were not included in the objective function.

4. Results: Empirical Evaluation and Case Study Analysis

4.1. Impact of Solar Plant Spatial Distribution on Stochastic Unit Commitment: Comparative Analysis of Regional Aggregation and High-Resolution Modeling

This section investigates the influence of spatial resolution in solar photovoltaic modeling on the performance of stochastic unit commitment within a large-scale power system. The analysis compares two configurations of solar generation in Thailand’s national power grid. The first aggregates all solar capacity into five regional zones. The second distributes the same total capacity across 500 individually modeled solar plants. The optimization problem was solved using IBM ILOG CPLEX Optimization Studio version 12.6 on a computing platform equipped with an Intel Core i5 8300H processor and 16 gigabytes of memory.

Uncertainty scenarios were generated by grouping solar output profiles according to geographic location and seasonal characteristics. These clusters were derived using monthly photovoltaic production data from the Photovoltaic Geographical Information System for Thailand [24]. Groups of plants with similar monthly output patterns across regions and seasons were identified following the approach of Kaewpasuk et al. [25]. For each cluster, a representative daily solar generation profile was constructed using high-resolution hourly data from the System Advisor Model provided by the National Renewable Energy Laboratory [26]. To evaluate the sensitivity of results to the number of scenarios, the analysis began with a small set of five and progressively increased to one hundred. Scenarios were selected randomly from a normal distribution to ensure that the probability space was adequately represented, thereby capturing both common and extreme variations in solar availability.

In the regional aggregation configuration, the total solar capacity within each of the five zones, namely Metropolitan, Central, North, Northeast, and South, is represented by a single equivalent generator. In this case, scenario generation treats each zone’s output as one uncertain variable. In the high-resolution configuration, the same total solar capacity is distributed among five hundred plants. Each plant is assigned to a cluster based on its location and modeled individually within the scenario set. The operational status of each plant varies across scenarios, and the probability of each scenario is determined by the proportion of plants available in that configuration. Both configurations incorporate a projected electric vehicle charging load profile within the net demand to reflect anticipated changes in consumption behavior.

Table 1. Regional allocation of installed solar photovoltaic capacity under aggregated and disaggregated configurations.

Zone	Number of Solar Plants	Average Capacity Per Plant (MW)	Total Installation Capacity (MW)
Central	255	5.07	1292.250
Metropolitan	2	0.01	0.028
North	46	6.15	282.739
Northeast	117	3.76	439.940
South	80	3.94	315.575
Total			2330.532

presents the installed solar photovoltaic capacity by region, totaling 2330.532 megawatts. These figures are evaluated alongside Thailand’s conventional generation capacity of 24,223 megawatts from 171 thermal and hydroelectric units. In the Central region, for example, the total solar capacity of 1292.25 megawatts is represented in the high-resolution configuration by 255 individual plants, each contributing approximately 5 megawatts, based on official data from the national Energy Regulatory Commission [27]. This level of disaggregation allows the model to capture temporal smoothing effects, as variations in solar output at different sites partially offset one another, thereby reducing overall variability in power supply.

The SUCM is solved for both configurations across five scenario levels: 5, 10, 20, 50, and 100.

Table 2. Comparison of expected operating costs and computational times under different solar distribution scenarios.

Load Demand Groups	Operation Cost (Million THB)		Computational Time (Seconds)
	Case 1: Regional Aggregation	Case 2: High- Resolution Modeling	Case 1		Case 2
			Average	SD	Average	SD
5 scenarios	1115.78	1068.07	50	29	109	33
10 scenarios	1131.03	1066.39	61	28	139	32
20 scenarios	1136.73	1073.92	98	38	129	42
50 scenarios	1145.26	1184.57	86	19	312	53
100 scenarios	1177.11	1084.76	138	31	456	31

reports the expected total operating cost and computational time for each case. Results indicate that the disaggregated configuration yields superior or comparable economic performance. For example, with 5 scenarios, the expected operating cost for the high-resolution model is THB 1068.07 million, which is approximately THB 47 million lower than the aggregated case. Similar advantages persist at other scenario levels, except for 50 scenarios, where sampling variability may explain a marginal increase in cost for the disaggregated configuration.

However, this improvement in cost performance comes at the expense of higher computational complexity. The increased number of decision variables and constraints in the high-resolution model results in longer computational times. For example, the average computational time for 100 scenarios is approximately 456 s in the disaggregated case, compared to 138 s in the aggregated case. This pattern holds across all scenario levels and is statistically significant at higher scenario counts. Nonetheless, the maximum computational time remains within 10 min, which is acceptable for day-ahead operational planning, particularly when modern solvers and computational resources are available.

In conclusion, increasing the spatial resolution of solar generation enhances the fidelity of the SUCM, improving cost efficiency and mitigating the risks associated with renewable intermittency. While it introduces greater computational requirements, the trade-off remains manageable for practical applications. These findings underscore the importance of incorporating geographically resolved renewable data into operational planning models to support the reliable and sustainable integration of variable energy resources in modern power systems.

4.2. Sensitivity Analysis of Stochastic Unit Commitment Under Load Demand Variability

This section analyzes the performance of the SUCM under varying load demand conditions. Seven representative daily demand profiles from Thailand’s power system are evaluated: Winter Weekday, Winter Weekend, Summer Weekday, Summer Weekend, Rainy Weekday, Rainy Weekend, and Long Holiday. Each profile consists of forty-eight time intervals across a full day, capturing distinct seasonal and weekly consumption patterns.

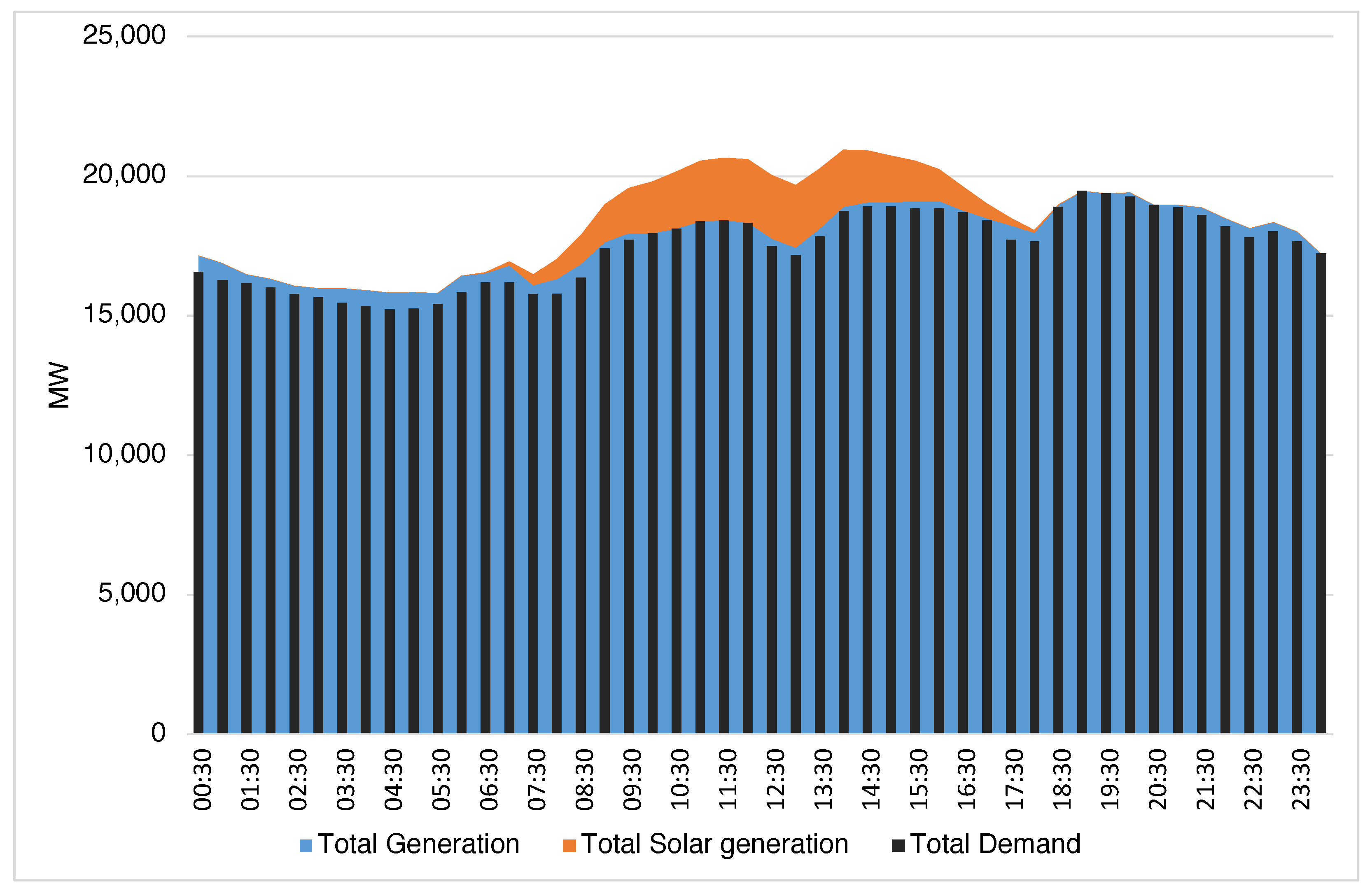
The analysis focuses on a configuration with spatially distributed solar photovoltaic generation, involving 500 solar plants. This setting is selected for its heightened sensitivity to uncertainty. The model is tested using five levels of scenario counts: 5, 10, 20, 50, and 100. Each scenario set incorporates fluctuations in both electricity demand and solar generation. An example of the daily planning results, including the total generation from both conventional sources and renewable solar power, together with the corresponding load demand in the Winter Weekday group, is presented in Figure 2.

Table 3. Expected operating costs in millions of THB across load demand profiles and scenario counts.

Demand Groups	Number of Scenarios
	5	10	20	50	100
Winter Weekday	999.06	1007.68	1005.00	1021.63	1036.67
Winter Weekend	834.05	839.89	846.06	843.89	874.36
Summer Weekday	1068.07	1066.39	1073.92	1184.57	1084.76
Summer Weekend	905.01	912.25	915.51	935.34	921.32
Rainy Weekday	1036.08	1062.73	1061.90	1048.68	1138.92
Rainy Weekend	1017.10	1025.92	1021.61	1038.50	1030.47
Long Holidays	508.99	510.37	509.52	510.33	509.79

presents the expected total operating costs in millions of THB across all demand categories and scenario levels. A general increase in cost is observed with higher scenario counts, reflecting more conservative commitments in response to uncertainty. For instance, the Summer Weekday profile shows costs rising from approximately THB 1068 million with 5 scenarios to THB 1185 million with 50 scenarios, followed by a decline to THB 1085 with 100 scenarios. This non-monotonic trend suggests diminishing returns or improved optimization with more granular scenario representation. Profiles such as Winter Weekend exhibit a gradual and consistent increase in cost. In contrast, the Long Holiday profile maintains the lowest cost across all scenario levels due to low demand and abundant reserve capacity. Across all profiles, the cost difference between the lowest and highest scenario counts typically remains within 5%, indicating limited economic benefit from excessive scenario expansion. As shown in

Table 4. Average computational time for scenario-based stochastic unit commitment across demand profiles.

Demand Groups	Number of Scenarios
	5		10		20		50		100
	Avg	SD	Avg	SD	Avg	SD	Avg	SD	Avg	SD
Winter Weekday	169	30	146	20	137	53	192	25	279	52
Winter Weekend	111	32	120	39	176	40	220	31	335	64
Summer Weekday	109	33	139	32	129	42	312	53	456	31
Summer Weekend	114	32	124	34	149	29	293	39	272	55
Rainy Weekday	52	31	66	19	75	39	136	32	239	34
Rainy Weekend	72	12	134	12	119	36	160	31	302	30
Long Holidays	55	27	35	24	45	31	62	53	141	56

, computational time increases substantially with the addition of more scenarios, highlighting a trade-off between model accuracy and efficiency.

To further assess system reliability, one hundred solar generation scenarios are simulated to evaluate commitment outcomes using four performance indicators. The first is the number of lacking scenarios, defined as those in which generation fails to meet the combined requirement of load and spinning reserve at any time. The second is the total number of time periods lacking across all scenarios. The third is the average lack percentage, representing the mean shortfall relative to the total required power in periods where shortages occur. The fourth is the maximum percentage of lack observed across all instances of power deficit.

Table 5. Average of system stability metrics under varying scenario counts: number of lacking scenarios, periods, and power deficits.

Performance Measurement	Number of Scenarios
	5	10	20	50	100
Number of lacking scenarios	38	26	11	24	9
Number of missing periods	53	29	12	26	9
Average lack percentage	0.81%	0.59%	0.58%	0.54%	0.34%
Maximum lack percentage	2.59%	1.90%	1.44%	1.50%	0.90%

summarizes these stability metrics. Results show that increasing the number of scenarios improves system reliability. The number of lacking scenarios decreases from thirty-eight with five scenarios to nine with one hundred. Similarly, the average lack percentage drops from 0.81 to 0.34. Although this improvement is not uniform across all scenario levels—for example, no consistent reduction is observed at fifty scenarios—the general trend confirms that more extensive scenario modeling enhances system robustness. This is particularly evident in profiles with higher variability, such as Summer Weekday and Rainy Weekday.

While increased scenario counts impose additional computational burden, the associated improvements in reliability and operational resilience justify this cost for daily planning. Overall, the proposed model demonstrates the ability to manage uncertainty effectively, supporting the development of a more reliable and sustainable power system under high renewable energy penetration.

4.3. Comparative Analysis of Deterministic and Stochastic Unit Commitment Models

This section presents a comparative assessment of the Deterministic Unit Commitment Model and the SUCM, examining two key dimensions: economic efficiency and system reliability. The analysis aims to evaluate the trade-offs between cost, computational requirements, and stability under different load demand profiles.

4.3.1. Economic Impact and Computational Feasibility of Unit Commitment Models

The first objective is to compare the operational cost and computational time associated with both models.

Table 6. Operational cost and computational time comparison of deterministic and stochastic unit commitment models.

Load Demand Groups	Operation Cost (THB)				Difference (%)
	DUCM *		SUCM **
Winter Weekday	979,219,219.00		1,016,971,588.78		3.78%
Winter Weekend	821,092,464.06		868,555,009.43		5.62%
Summer Weekday	1,047,922,497.98		1,048,252,764.38		0.03%
Summer Weekend	892,447,492.76		906,962,052.31		1.61%
Rainy Weekday	868,118,138.84		1,108,060,648.31		24.28%
Rainy Weekend	1,048,041,623.59		1,022,664,935.88		2.45%
Long Holidays	507,517,650.60		507,815,159.96		0.06%
Load Demand Groups	Computational Time (Seconds)				Difference (%)
	DUCM *		SUCM **
	Avg	SD	Avg	SD
Winter Weekday	175	23	279	69	59.43
Winter Weekend	104	17	335	55	222.12
Summer Weekday	91	21	456	49	401.10
Summer Weekend	104	25	272	68	161.54
Rainy Weekday	53	19	239	61	350.94
Rainy weekend	65	18	302	46	364.62
Long Holidays	49	14	141	38	187.76

* DUCM with mean solar power output. ** SUCM with 100 scenarios.

outlines the results for various demand groups.

The stochastic model incurs slightly higher operational costs in most cases, typically resulting in an increase of 5% or less. For instance, the Winter Weekday demand profile shows an increase of approximately 3.8% compared to the deterministic model. The highest cost difference appears under the Rainy Weekday group, where the stochastic model records a 24.3% increase. This rise is expected, as the stochastic approach considers uncertainty in renewable generation, leading to more conservative and reliability-focused decisions. The percentage difference values in this table were recalculated using the standard percent change formula. Each value represents the relative difference in operational cost between the SUCM and DUCM based on the DUMC value.

Despite higher costs in some cases, the stochastic model offers acceptable computational performance. The average computation time for the stochastic approach ranges from approximately 2 to 8 min, making it feasible for day-ahead planning. While the deterministic model performs faster, the gap is not prohibitive, given the increased robustness provided by the stochastic model.

4.3.2. Evaluation of Reliability and System Adequacy Under Uncertainty

The second objective addresses system stability.

Table 7. Comparison of performance metrics between the DUCM, FUCM, and SUCM in Thailand’s system.

Load Demand Groups	Number of Lacking Scenarios			%Change
	DUCM *	FUCM	SUCM **
Winter Weekday	39	59	9	51.28%
Winter Weekend	34	13	3	−61.76%
Summer Weekday	44	29	5	−34.09%
Summer Weekend	64	36	18	−43.75%
Rainy Weekday	46	41	3	−10.87%
Rainy Weekend	67	42	2	−37.31%
Long Holidays	0	0	0	0.00%
Load Demand Groups	Number of Missing Periods			%Change
	DUCM *	FUCM	SUCM **
Winter Weekday	42	87	9	107.14%
Winter Weekend	36	15	3	−58.33%
Summer Weekday	50	34	5	−32.00%
Summer Weekend	92	46	19	−50.00%
Rainy Weekday	62	51	3	−17.74%
Rainy Weekend	100	52	2	−48.00%
Long Holidays	0	0	0	0.00%
Load Demand Groups	Average Lack Percentage			%Change
	DUCM *	FUCM	SUCM **
Winter Weekday	0.87%	0.93%	0.38%	6.90%
Winter Weekend	0.94%	1.02%	0.82%	8.51%
Summer Weekday	0.66%	0.48%	0.84%	−27.27%
Summer Weekend	0.98%	0.90%	0.55%	−8.16%
Rainy Weekday	1.19%	0.89%	0.05%	−25.21%
Rainy Weekend	0.91%	0.86%	0.51%	−5.49%
Long Holidays	0.00%	0.00%	0.00%	0.00%
Load Demand Groups	Maximum Lack Percentage			%Change
	DUCM *	FUCM	SUCM **
Winter Weekday	2.52%	3.54%	0.69%	40.48%
Winter Weekend	3.03%	2.90%	0.88%	−4.29%
Summer Weekday	1.69%	1.91%	1.83%	13.02%
Summer Weekend	3.51%	3.09%	1.83%	−11.97%
Rainy Weekday	4.01%	2.99%	0.07%	−25.44%
Rainy Weekend	3.32%	2.71%	0.53%	−18.37%
Long Holidays	0.00%	0.00%	0.00%	0.00%

* DUCM with mean solar power output. ** SUCM with 100 scenarios.

presents four performance measures: the number of lacking scenarios, the number of missing periods, the average lack percentage, and the maximum lack percentage of the DUCM, FUCM [28], and SUCM.

Results indicate that the SUCM significantly enhances system reliability across most demand profiles. For instance, under the Winter Weekday group, the model reduces the number of lacking scenarios by 76.92% and the number of missing periods by 78.57%. It also reduces the average and maximum lack percentages by 56.32% and 72.61%, respectively. The improvements are even more pronounced in the Rainy Weekday group, where the number of lacking scenarios and periods decreases by over 92%. The maximum lack percentage drops by over 98%, underscoring the stochastic model’s ability to maintain system balance under volatile solar output and load conditions. While some anomalies are observed, such as a slight increase in the average and maximum lack percentages for the Summer Weekday group, these are minimal and may result from randomness in scenario generation or boundary effects in optimization.

In contrast to the fuzzy model, which addresses uncertainty through imprecise linguistic representations requiring careful calibration, the stochastic model explicitly quantifies uncertainties in solar generation and electric vehicle charging demand across a wide range of scenarios. This approach provides a more detailed and probabilistic representation of variability, improving robustness and operational adequacy. Furthermore, while the fuzzy model enhances system reliability primarily through the treatment of uncertain parameters, the stochastic model captures spatial resolution by incorporating regional solar distributions and inter-zonal transmission constraints, thereby ensuring greater applicability to large-scale systems. Both models account for electric vehicle behavior; however, the stochastic formulation offers improved flexibility by embedding vehicle charging demand within a probabilistic scenario framework that better reflects temporal and spatial demand fluctuations.

Overall, the SUCM demonstrates clear advantages in managing uncertainty, with only modest increases in operational cost and computational requirements. These findings support its adoption in power systems undergoing transitions toward renewable energy integration. The added robustness and reliability offered by the stochastic model justify the increased resource investment, especially in regions with high levels of variability in both generation and demand.

5. Conclusions and Discussion

This study addressed the limitations of traditional unit commitment models under increasing renewable energy penetration by developing a stochastic unit commitment framework that incorporates uncertainties in solar generation, electric vehicle charging, and load demand. Motivated by the need for more reliable and adaptive power system operations, the proposed model was formulated as a mixed-integer linear program and solved using scenario-based analysis.

Scenarios were generated using spatial and seasonal clustering of solar output data obtained from PVGIS and the NREL System Advisor Model, applied to both aggregated and high-resolution configurations of Thailand’s power system. Electric vehicle charging loads were also included to reflect evolving demand patterns.

The results demonstrate that high-resolution modeling improves cost efficiency and operational reliability, particularly under variable conditions. In the Winter Weekday group, lacking scenarios decreased by 76.92% and missing periods by 78.57%, while in the Rainy Weekday group, both measures improved by more than 92%, with the maximum lack percentage reduced by over 98%. Compared with deterministic models, the stochastic approach reduced power deficits and enhanced system stability, with only moderate increases in computational time and cost.

These findings emphasize the importance of integrating spatially resolved renewable data and comprehensive uncertainty modeling into unit commitment processes. The model prioritizes operational planning to ensure reliability and cost-effectiveness. Nevertheless, the analysis of carbon emissions is recognized as an important direction for future research, as it would further enhance the sustainability dimension of the proposed framework. Thus, the model supports sustainable system planning and operation and is particularly suited for future systems with high levels of renewable integration. A comparison with existing literature shows that the proposed SUCM achieves higher reliability improvements than previous fuzzy and deterministic models applied to similar contexts. The present study advances beyond these approaches by simultaneously modeling renewable variability, electric vehicle demand, and zonal transmission limits, resulting in more robust outcomes. The significant reductions in lacking scenarios and unmet demand periods observed in this study underscore its superior capacity for managing uncertainty in large-scale systems.

It is important to note that the results presented in this study may not be directly transferable to power systems with different load characteristics, renewable energy mixes, or network configurations. The effectiveness of the proposed approach in other contexts will depend on local conditions, data quality, and system design.

Future research could extend this work by incorporating additional forms of uncertainty such as wind generation, more detailed electric vehicle behavior modeling, and demand response mechanisms. Further enhancements may also be achieved by integrating real-time data streams and adaptive scenario generation techniques. Expanding the model to consider multi-regional transmission constraints and emission limits would further strengthen its applicability for broader policy and planning contexts.