A Two-Stage Cooperative Scheduling Model for Virtual Power Plants Accounting for Price Stochastic Perturbations

Abstract

With the increasing integration of renewable energy, virtual power plants (VPPs) have emerged as key market participants by aggregating distributed energy resources. However, their involvement in electricity markets is increasingly challenged by two major uncertainties: price volatility and the intermittency of renewable generation. This study presents the first application of Information Gap Decision Theory (IGDT) within a two-stage cooperative scheduling framework for VPPs. A novel bidding strategy model is proposed, incorporating both robust and opportunistic optimization methods to explicitly account for decision-making behaviors under different risk preferences. In the day-ahead stage, a risk-responsive bidding mechanism is designed to address price uncertainty. In the real-time stage, the coordinated dispatch of micro gas turbines, energy storage systems, and flexible loads is employed to minimize adjustment costs arising from wind and solar forecast deviations. A case study using spot market data from Shandong Province, China, shows that the proposed model not only achieves an effective balance between risk and return but also significantly improves renewable energy integration and system flexibility. This work introduces a new modeling paradigm and a practical optimization tool for precision trading under uncertainty, offering both theoretical and methodological contributions to the coordinated operation of flexible resources and the design of electricity market mechanisms.

1. Introduction

Amid escalating global climate change, energy shortages and environmental pollution have increasingly become major bottlenecks hindering sustainable socio-economic development. In response to the urgent need for energy system transformation, nations worldwide are accelerating the pace of energy reform and promoting the construction of a new electricity system centered on renewable energy. China has formally pledged to peak carbon emissions by 2030 and achieve carbon neutrality by 2060; this “dual-carbon” strategic commitment not only outlines a clear timeline for the country’s energy transition but also presents both unprecedented challenges and significant opportunities for advancing a decarbonized power infrastructure [1].

Given its role as the primary source of carbon emissions, the power industry is undergoing multiple challenges, including resource constraints, environmental pressures, and increasing system complexity, all while striving to meet the continuously rising demand for electricity. In this context, the traditional centralized power supply model, once the foundation of scheduling and operations, is increasingly unable to accommodate the high penetration of renewable energy into the grid, the integration of new types of loads, and the growing need for system flexibility to meet diverse energy demands. As a result, the development of a modern power system focused on renewable energy, enhanced flexibility in regulation, and greater market responsiveness has emerged as a crucial pathway for the power industry to achieve a green and low-carbon transformation [2].

To address the challenges of resource coordination and operational efficiency arising from the widespread integration of distributed energy, the virtual power plant (VPP) has emerged as a comprehensive smart coordination framework [3]. By integrating localized generation, energy storage solutions, and flexible demand-side devices, VPPs enable unified management, collaborative optimization, and flexible scheduling of decentralized resources, demonstrating notable advantages in improving resource utilization, enhancing system regulation capabilities, and promoting the consumption of clean energy. Externally, VVPs participate in electricity market operations as aggregators, strengthening the market competitiveness of distributed resources; internally, they facilitate intelligent coordination and responsive control, thereby enhancing the stability and controllability of resource operations. As such, VPPs serve as a critical hub linking generation, the power grid, loads, and storage across diverse actors [4].

In recent years, China’s power market reform has continued to deepen. Since the launch of a new reform phase in 2015, the development of a unified national electricity market has accelerated, with the market mechanism gradually shifting from centralized planning and dispatch to a dual-layered structure encompassing both medium- to long-term and spot markets, thereby making electricity increasingly commodified. In 2025, the National Development and Reform Commission and the National Energy Administration jointly issued the Guiding Opinions on Accelerating the Development of VPPs (NDRC Energy Regulation [2025] No. 357), which, for the first time at the national level, systematically defined the development objectives, market mechanisms, operational models, and regulatory frameworks for VPPs. The document set a clear target: by 2027, China aims to establish a VPP system that is market-oriented, operationally efficient, and both secure and controllable [5].

At the same time, the core technologies enabling VPPs have made continuous strides. Artificial intelligence-driven forecasting and optimization algorithms, blockchain-based secure trading mechanisms, fine-grained modeling of flexible resources, and high-resolution dispatch technologies are increasingly being integrated into VPP aggregation and operations. These advancements have significantly strengthened the capacity of VPPs to respond to real-time control requirements and to operate competitively within complex and uncertain market environments [6]. In addition, recent studies have introduced optimization frameworks based on Information Gap Decision Theory (IGDT), stochastic robust optimization, and distributed control architectures, effectively overcoming the limitations of traditional scheduling models in addressing multi-dimensional uncertainties and the challenges of multi-market coupling scenarios [7].

As shown in

Table 1. Comparative overview of representative studies on VPPs.

Reference	Focus Area	Technique	Advantages	Limitations
[14]	EV aggregation and storage coordination	Carbon trading mechanism; consumer behavior analysis	Balances economy and eco-performance	Focused on EV and carbon policy only
[15]	Multi-timescale economic dispatch for DLs	Clustering + aggregation/disaggregation modeling	Captures DL flexibility across timescales	May be complex for large-scale systems
[16]	Flexibility assessment with uncertainty	Chance-constrained + robust optimization	Explicit uncertainty handling for flexibility	Conservativeness from chanceconstraints
[17]	DIMS proactive aggregation model	Virtual generator/battery, polytope bounding	Robust across services, embedded in dispatch	Focuses on DIMS, not general VPP
[18]	Multi-market bidding (energy and peak)	Non-cooperative game theory, alliance modeling	Evaluates alliance competitiveness effectively	Lacks renewable uncertainty modeling
[19]	Electricity–carbon market co-optimization	Two-stage game-based bidding framework	Joint clearing and strategy coordination	Requires hierarchical data and coordination
[20]	Intraday dispatch with profit allocation	Enhanced Shapley value, marginal contribution	Fair revenue sharing, risk awareness	High computational burden for allocation
[21]	Day-ahead and real-time scheduling optimization	Enhanced metaheuristic (particle dynamics)	Accurate, dynamic output adjustment	Depends on metaheuristic tuning

, contemporary research on VPP systems primarily focuses on the modeling and optimization of VPP aggregation and scheduling capabilities [8,9,10,11,12], as well as the participation of VPPs in market mechanisms and bidding strategies [13,14,15,16]. In particular, with regard to aggregation and scheduling, the literature [17] further investigates the accessible capacity of virtualized storage resources for electric vehicle (EV) aggregation within VPPs, analyzing the spatiotemporal variation patterns of EV usage and consumer demand elasticity. It also explores viable approaches to balancing economic efficiency and environmental sustainability through the application of carbon trading mechanisms. These findings offer valuable guidance for VPP operators in designing effective user incentive schemes and coordinating energy storage system (ESS) operations, ultimately enhancing system flexibility and economic performance. The literature [18] proposes a multi-timescale economic dispatch strategy for VPPs participating in wholesale energy and reserve markets, with a particular emphasis on the aggregation and disaggregation of large-scale deferrable loads (DLs). To address the VPP’s multi-timescale scheduling challenges, including both day-ahead bidding and real-time operations, the authors develop a clustering-based DL aggregation model, an economic dispatch model that accounts for aggregated DLs, and a disaggregation model tailored to meet individual consumer demands. The literature [19] addresses the flexibility assessment problem by formulating it as a chance-constrained optimization model that incorporates the stochastic characteristics of renewable energy. To enhance computational tractability, system flexibility is modeled using a combination of a virtual generator and a virtual battery, with the virtual battery further decomposed through a robust optimization algorithm. A bounding contraction method based on high-dimensional polytopes is also introduced to estimate the parameters of both virtual components. The literature [20] presents a robust and proactive dynamic aggregation model for Distributed and Intelligent Multi-energy Systems (DIMSs), aimed at characterizing the maximum feasible operating region. This aggregation model integrates power, energy, and ramping constraints to effectively coordinate heterogeneous resources within DIMSs. Notably, the proposed generator-like and storage-like models are designed to function independently of ancillary service markets and can be directly embedded into standard power system economic dispatch frameworks.

Regarding the participation of VPPs in market mechanisms and bidding strategies, the literature [21] investigates VPP engagement across multiple markets, focusing on both day-ahead power energy markets and peak market trading strategies. The study introduces a non-cooperative game-theoretic trading approach, accounting for the presence of other market participants, and compares various types of VPP trading alliances. The findings reveal that new forms of VPP alliances exhibit stronger market competitiveness. The literature [22] explores VPP involvement in a joint operational environment encompassing both electricity and carbon markets, also using a non-cooperative game framework. The authors develop a two-stage stacked bidding architecture with upper- and lower-level interactions to optimize individual scheduling and enable joint market clearing. The literature [23] considers two VPP types, demand-side users and supply-side equipment, and proposes a dynamic intraday dispatch model aimed at minimizing deviation penalty costs. The model comprehensively addresses uncertainty levels and cumulative marginal contributions of each participant, applying a profit allocation mechanism that combines an enhanced Shapley value method with independent risk contribution theory to equitably distribute total VPP revenue. The literature [24] focuses on optimizing hourly scheduling strategies for VPPs to maximize economic gains from day-ahead market participation, utilizing an improved metaheuristic method based on particle dynamics. During the real-time phase, the VPP adjusts its output to minimize system imbalance penalties. Results indicate that the model effectively identifies optimal and precise scheduling solutions, offering a comprehensive management approach for interactive energy systems.

Although existing studies have laid a solid theoretical foundation and developed various modeling methodologies for the trading behavior of VPPs in electricity markets, several critical challenges and gaps remain. First, in the face of highly volatile power market clearing prices and complex multi-temporal market linkage mechanisms, current VPP bidding strategies still lack a systematic modeling framework and adaptive response mechanism to effectively manage price variability. Second, the coordination between day-ahead and real-time electricity markets remains insufficiently developed, making it difficult to optimize returns while effectively managing trading risks. Addressing the dual objective of maximizing revenue and minimizing transaction risk remains a pressing challenge for ongoing research in this field. In response to the aforementioned challenges, this study proposes an innovative multi-stage uncertainty modeling framework grounded in the principles of IGDT, offering a novel approach to addressing electricity price volatility. By systematically integrating multi-dimensional uncertainty scenarios, particularly those related to wind power output, into the bidding and dispatch decisions of VPPs, the study develops a coordinated day-ahead and real-time trading optimization model. This model addresses the limitations of existing methods, which often concentrate on isolated market stages or rely on static uncertainty assumptions. It enables integrated optimization of bidding strategies and resource scheduling within complex market environments and under diverse uncertainty sources. By jointly modeling electricity price fluctuations and renewable generation variability in a unified framework, the proposed approach significantly strengthens the VPP’s ability to manage operational risks and capitalize on revenue opportunities in dynamic spot markets, offering both theoretical advancements and practical tools for robust VPP operation in high-renewable power systems.

2. Two-Stage Trading Framework for VPPs

Currently, China’s power trading spot market primarily operates through a two-stage mechanism involving spot and real-time electricity trading. This system allocates the full volume of electricity, establishes time-based pricing, and implements a sequential day-ahead and real-time market structure to enable comprehensive power optimization. Contractual relationships are jointly established between power generation and consumption entities, while power trading institutions and dispatch centers share responsibility for organizing and operating the power market. As shown in Figure 1, this collaborative framework aims to achieve the optimal spatial and temporal allocation of power resources.

In the day-ahead phase, each trading entity determines, through centralized bidding, the unit startup combinations and power generation schedules for the following day. This process effectively establishes the operational status of generating units, formulates day-ahead time-based tariffs and nodal prices, and provides a basis for real-time adjustments. These adjustments include corrections to generation schedules, load curves, and deviations from medium- and long-term contract commitments, all aimed at maintaining power system balance within the day-ahead planning horizon.

In the real-time phase, deviations from the day-ahead output plan may arise due to the variability of wind and solar generation, inaccuracies in load forecasting, unexpected unit failures, and other unforeseen factors. Consequently, it becomes necessary to adjust electricity generation and consumption curves, as well as correct deviations from day-ahead forecasts, in alignment with the current grid operating conditions and ultra-short-term electricity market dynamics. The offer mechanism employed by VPP operators for various resource combinations plays a critical role in incentivizing diverse demand-side resources to actively participate in VPP trading mechanisms, thereby enhancing the overall operational efficiency and performance of VPPs.

Based on the forecasted clearing price and actual cost data, the boundary conditions for bidding offers can be established. This chapter proposes a two-stage day-ahead and real-time trading optimization model for VPPs. The upper-level model incorporates the inherent uncertainty of market clearing prices to generate a declared bidding plan for the portion of the VPP that secures market acceptance based on the actual clearing price. The lower-level model addresses deviations resulting from fluctuations in wind power output and adjusts the day-ahead declared plan accordingly to minimize deviation costs.3 Modeling of VPP aggregation units

To achieve unified scheduling and optimized operation of VPPs under conditions of multi-source integration and multi-scenario coordination, it is crucial to establish a systematic modeling framework for internally heterogeneous resources. A typical VPP comprises a diverse mix of components, including conventional dispatchable units, distributed generation systems, energy storage facilities, and flexible loads. These resources vary significantly in their physical attributes, operational dynamics, and response behaviors. As such, detailed and precise modeling is necessary to quantitatively define their controllable capacities, scheduling boundaries, and operational constraints. This modeling provides a standardized data foundation and computational interface essential for aggregated optimization and coordinated control across the VPP.

In terms of model structure, the dispatchable unit model captures the output capacity and startup/shutdown characteristics of conventional generation units, such as gas turbines. The distributed generation model represents the output patterns and inherent uncertainties of intermittent renewable sources like wind and solar power. The energy storage model defines the charging and discharging strategies, capacity limitations, and conversion efficiencies of storage systems. The flexible load model examines the response logic, availability windows, and user behavior constraints associated with adjustable loads. While these four models are structurally independent, they are integrated within a unified VPP scheduling framework through standardized control interfaces and coordinated response mechanisms, enabling holistic optimization and reliable operation.

From a data flow perspective, the inputs to each model include resource-specific parameters, such as capacity, efficiency, and operational time windows, along with forecasted information, including load demand, electricity prices, and renewable energy output. Additionally, dispatch commands and market signals are incorporated as dynamic inputs. The model outputs typically consist of operational boundaries, adjustment limits, and state variables, which serve as critical decision constraints and indicators of response capabilities for the upper-level scheduling model.

2.1. Controllable Output Modeling

Small gas turbine power generation operates based on the stroke cycle principle, converting the thermal energy produced by natural gas combustion into mechanical energy, which is then used to generate electricity. The power output is influenced by factors such as fuel combustion efficiency, mechanical energy conversion efficiency, and the temperature and pressure of the intake air. To simplify the model, compression-induced effects are not considered, and it is assumed that the fuel undergoes complete combustion. Under these assumptions, the output of the micro gas turbine is modeled as follows:

$$P_{MT}=m_f\cdot LHV\cdot \eta$$

(1)

where $P_{MT}$ is the electrical output of the micro gas turbine, $m_f$ is the fuel flow rate in kilograms per second (kg/s), $LHV$ is the lower calorific value of the fuel in joules per kilogram (J/kg), and $\eta$ is the combined operational efficiency of the system.

2.2. Photovoltaic Power Output Modeling

The performance of photovoltaic (PV) power generation is influenced by multiple factors, including the characteristics of the PV devices, solar irradiance, and other environmental conditions, introducing a significant degree of uncertainty. Solar irradiance varies throughout the day and is subject to seasonal and climatic randomness. Currently, the majority of experts and researchers model the stochastic nature of solar irradiance using a Beta distribution. Considering that PV units are typically equipped with a Maximum Power Point Tracking (MPPT) system, the corresponding PV power output is modeled as follows:

$$g_{PV,t}=[1-{\gamma }_T(T_{air}+{\displaystyle \frac{T_n-20}{800}}{R}_t-T_{ref})]{\eta }_{ref}{N}_{PV}{S}_{PV}{R}_t$$

(2)

where $g_{PV,t}$ denotes the output power of the PV device at time t; ${\gamma }_T$ is the thermal sensitivity coefficient of PV conversion efficiency; $T_{air}$ is the ambient temperature; $T_n$ is the nominal operating temperature; $R_t$ is the solar radiation intensity at time t; $T_{ref}$ represents the standard operating temperature; ${\eta }_{ref}$ is the rated efficiency under standard test conditions; $N_{PV}$ is the number of PV panels; and $S_{PV}$ is the module area per PV unit.

2.3. Wind Power Output Modeling

The output power extracted from wind by a turbine system primarily depends on wind speed. The turbine operates only when the actual wind speed falls within a defined range, bounded by the cut-in and cut-out thresholds. If the wind speed is below the cut-in threshold, the turbine remains inactive; if it exceeds the cut-out threshold, the turbine enters a shutdown protection mode to prevent mechanical damage. Wind speed is treated as a random variable, and its stochastic behavior is typically modeled using the Weibull distribution. Accordingly, the wind power output is represented as follows:

$$g_{wpp,t}=\left\{\begin{array}{cc}0& ,0\le v_t\le v_{in},v_t\ge v_{out}\\ 0.5C_{wpp}\rho S_{wpp}{v}_t^3& ,v_{in}\le v_t\le v_R\\ g_R& ,v_R\le v_t\le v_{out}\end{array}\right.$$

(3)

where $g_{wpp,t}$ denotes the power generation output of the wind power plant (WPP) at time t; $v_{in}$, $v_{out}$, $v_R$, and $v_t$ represent the characteristic wind speeds of the wind turbine generator (WTG), including cut-in speed, rated speed, cut-out speed, and the free-stream wind speed at time t, respectively; $C_{wpp}$ is the performance coefficient of the WTG; $\rho$ is the atmospheric air density; $S_{wpp}$ is the swept area of the WTG blades projected onto a plane perpendicular to the wind direction; and $g_R$ is the nameplate (rated) capacity of the WTG.

2.4. Decentralized Energy Storage Infrastructure Modeling

By injecting and absorbing power from the grid, the ESS plays a critical role in balancing supply and demand, alleviating operational stress on the power system during peak load periods, maintaining grid frequency stability, and avoiding or postponing the need for grid infrastructure upgrades. Additionally, by regulating the power fluctuations associated with clean energy sources such as wind and PV systems, the ESS enhances the penetration of renewable energy in grid-connected environments. Furthermore, it can function as a backup power source, providing rapid support in the event of failures or insufficient capacity from other generation resources within the grid.

The state of charge (SOC) in the modeling framework of the ESS is formulated as follows:

$$SOC(t)=SOC(t-1)+{\displaystyle \frac{{\eta }_{c,t}^{ESS}{P}_{c,t}^{ESS}}{En}}\cdot ∆t+{\displaystyle \frac{P_{d,t}^{ESS}}{{\eta }_{d,t}^{ESS}En}}\cdot ∆t$$

(4)

$$0\le {\eta }_{c,t}^{ESS}+{\eta }_{d,t}^{ESS}\le 1$$

(5)

where $SOC(t)$ is the instantaneous charge level of the energy storage unit at time t; $E_n$, ${\eta }_c$, and ${\eta }_d$ represent the rated capacity, charging efficiency, and discharging efficiency of the energy storage battery, respectively; and $P_{c,t}^{ESS}$ and $P_{d,t}^{ESS}$ denote the charging and discharging power of the energy storage unit at time t, respectively. Since the ESS cannot simultaneously operate in both charging and discharging modes, the corresponding binary variables ${\eta }_{c,t}^{ESS}$ and ${\eta }_{d,t}^{ESS}$ must be mutually exclusive 0-1 variables, such that they cannot both equal 1 at the same time.

2.5. Flexible Load Modeling

(1) EV clusters are integrated into the VPP, allowing users to actively regulate their power consumption in response to external signals based on electricity market price indicators and load demand. This dynamic participation enables users to reduce their electricity costs while also earning policy incentives for contributing to power plant scheduling and grid flexibility.

A binary integer variable is introduced to represent the two operational states of electric vehicles (EVs), where 0 indicates no charging and 1 indicates charging. Based on this, the electric load of the EV cluster is modeled as follows:

$${\mathrm{g}}_{\mathrm{EVC},\mathrm{t}}={\eta }_{EVC,t}{\mathrm{g}}_{\mathrm{EVC},\mathrm{r}}$$

(6)

where ${\mathrm{g}}_{\mathrm{EVC},\mathrm{t}}$ denotes the total electric power of the EV cluster at time t, ${\eta }_{EVC,t}$ represents the state of charge of the EV at time t, and ${\mathrm{g}}_{\mathrm{EVC},\mathrm{r}}$ is the rated electric power of the EV cluster.

The selection of charging time for EVs depends on the user’s travel behavior and power demand, and during the charging process, the vehicle must store enough energy to meet the user’s immediate travel needs, meaning that, before disconnecting from the grid, the vehicle must achieve a certain minimum state of charge. To ensure battery durability and extend its lifespan, overcharging and deep discharging must be avoided, which requires the battery’s state of charge to remain within a permissible range; accordingly, the dynamic progression of the battery’s state of charge within the EV cluster is modeled as follows:

$$SO{C}_{out,t}\ge SO{C}_{\exp }$$

(7)

where $SO{C}_{out,t}$ and $SO{C}_{\exp }$ are the battery charge state of the EV traveling at moment t and the expected charge state of the user traveling, respectively.

$$SO{C}_{EVC,t}=SO{C}_{EVC,t-1}-{\displaystyle \frac{g_{EVC,t}}{N_{ev,t}{Q}_{ev}}}-{\displaystyle \frac{\delta M{N}_{in,t}}{(N_{ev,t}+N_{in,t})Q_{ev}}}$$

(8)

where $SO{C}_{EVC,t}$ is the battery charge state of the EV cluster at time t, $Q_{ev}$ is the rated power of a single EV, $\delta$ represents the average power consumption per kilometer, $M$ is the average distance traveled by EVs entering the network for charging, and $N_{in,t}$ is the number of EVs accessing the network at time t.

$$SO{C}_{\min }^{EVC}\le SO{C}_{EVC,t}\le SO{C}_{\max }^{EVC}$$

(9)

where $SO{C}_{\min }^{EVC}$ and $SO{C}_{\min }^{EVC}$ are the SoC limits of the EV cluster, defined by its minimum and maximum charge thresholds.

(2) Some non-critical loads in the power system, such as water heaters and air conditioners, are relatively easier to control compared to electric vehicles, as their operational patterns can be adjusted based on demand; however, it is still essential to meet users’ electricity requirements. This section primarily focuses on the load modeling of typical air conditioners:

$${\mu }_{AC,t}{g}_{t,\min }^{AC}\le {\mu }_{AC,t}{g}_{AC,t}\le {\mu }_{AC,t}{g}_{t,\max }^{AC}$$

(10)

where ${\mu }_{AC,t}$ denotes the two operational states of the air conditioner (AC) at moment t, with 0 representing the off state and 1 representing the working state, and $g_{t,\min }^{AC}$ and $g_{t,\max }^{AC}$ denote the minimum and maximum electric loads of the AC at moment t, respectively.

3. Market Trading Modeling Under Multi-Dimensional Uncertainties

3.1. Day-Ahead Stage Trading Model Accounting for Tariff Uncertainty

When dealing with uncertain information, the IGDT method can tolerate a certain degree of data noise and imprecision, and does not require precise statistical distributions of uncertain inputs, only their possible ranges or bounds. Even in situations where data are limited or probabilistic characterization of uncertain parameters is difficult to obtain, IGDT can still offer valuable decision-making support. Its independence from detailed data also reduces the risk of model overfitting. In this paper, we establish a robust day-ahead phase trading optimization model that incorporates the IGDT approach to effectively address severe uncertainty and help market participants better manage the risks associated with electricity price fluctuations.

In the day-ahead phase, power producers must formulate an offer strategy based on their generation capacity and the market’s offer rules, aiming to maximize profits, and submit this strategy to the market operator in the form of an offer curve. This paper considers an aggregated energy resource system acting as a price taker in the market bidding process, under the assumption that its scale is small enough that its offer does not influence the market clearing price, and the winning bid is settled based on the declared price. A decision-making model is constructed within the IGDT framework, accounting for the uncertainty in the market clearing price of electricity, and a day-ahead trading model is developed with the objective of maximizing the revenue of the VPP aggregator.

(1)

Objective function

$$\max G={\displaystyle \sum _{t=1}^T{Q}_t{P}_t}$$

(11)

where $G$ is the revenue earned by the VPP aggregator in the electricity market at time t, $Q_t$ is the total declared electricity at time t, and $P_t$ is the offer price at time t.

(2)

Constraints

(1) Reporting constraints

$$\left\{\begin{array}{cc}{Q}_t=0,& P_t>{\lambda }_{\mathrm{t}}\\ Q_t=Q_t^{VPP},& P_{MIN}<P_t<{\lambda }_{\mathrm{t}}\\ Q_t=0,& P_{MIN}>{\lambda }_{\mathrm{t}}\end{array}\right.$$

(12)

where ${\lambda }_t$ is the market clearing price (tariff) at moment t. If the declared offer price is higher than the clearing price, the bid is not accepted, and the winning quantity is zero. In cases where the lower bound of the offer price exceeds the clearing price, i.e., the cost cannot be covered, the aggregator chooses not to participate in the bidding process. The VPP aggregator will only participate in the market and secure a winning bid if the declared price is both above its cost and lower than or equal to the clearing price. This ensures profitability while enabling participation in market transactions.

(2) The main operating constraints of a distributed micro gas turbine generator unit include start–stop limitations, output boundaries, and ramp rate (climb) restrictions. These constraints define the technical and operational conditions under which the micro gas turbine must function, ensuring stability, efficiency, and safe operation during generation scheduling and dispatch:

$$\left\{\begin{array}{c}(T_{on,t-1}-T_{\min on})({\mu }_{MT,t-1}-{\mu }_{MT,t})\ge 0\\ (T_{off,t-1}-T_{\min off})({\mu }_{MT,t}-{\mu }_{MT,t-1})\ge 0\\ g_{MT,\min }\le g_{MT,t}\le g_{MT,\max }\\ ∆g_{MT}^{-}\le g_{MT,t}-g_{MT,t-1}\le ∆g_{MT}^{+}\end{array}\right.$$

(13)

where ${\mu }_{MT,t}$ represents the commitment status of the unit at time t, with 0 indicating shutdown and 1 indicating startup; $T_{on,t-1}$ is the elapsed operating time of the unit at time t; $T_{\min on}$ denotes the minimum required startup duration; $T_{off,t-1}$ is the elapsed shutdown time at time t; and $T_{\min off}$ is the minimum duration the unit must remain offline once shut down. $g_{MT,t}$, $g_{MT,\min }$, and $g_{MT,\max }$ are the outputs of the unit corresponding to time t, and bounded by the unit’s permissible output range. $∆g_{MT}^{-}$ and $∆g_{MT}^{+}$ are the maximum allowable power increase and decrease rates of the unit, respectively.

(3) Scenery output constraint

$$\left\{\begin{array}{c}0\le {\mathrm{g}}_{pv,t}\le g_{pv,t}^{\max }\\ 0\le g_{wpp,t}\le g_{wpp,t}^{\max }\end{array}\right.$$

(14)

where $g_{pv,t}^{\max }$ and $g_{wpp,t}^{\max }$ represent the maximum generating capacity of PV and wind power at moment t, respectively.

(4) The primary constraints governing the participation of the energy storage component in VPP operations include limits on charging and discharging power, along with SoC boundaries, and are accordingly represented through a set of operational equations that ensure the system functions within its rated capacity and efficiency constraints:

$$\left\{\begin{array}{c}0\le g_{c,t}^{ESS}\le g_{cm\mathrm{ax},t}^{ESS}{\eta }_{c,t}^{ESS}\\ 0\le g_{d,t}^{ESS}\le g_{d\max ,t}^{ESS}{\eta }_{d,t}^{ESS}\\ SO{C}_{\min }^{ESS}\le SOC(t)\le SO{C}_{\max }^{ESS}\\ 0\le {\eta }_{c,t}^{ESS}+{\eta }_{d,t}^{ESS}\le 1\end{array}\right.$$

(15)

where $g_{c\max ,t}^{ESS}$ and $g_{d\max ,t}^{ESS}$ denote the maximum allowable power flow into and out of the ESS at time t, respectively, and $SO{C}_{\min }^{ESS}$ and $SO{C}_{\max }^{ESS}$ represent the lower and upper bounds of the required state of charge of the ESS.

(5) EV clusters and ACs participate in VPP scheduling by adjusting their operational modes to gain economic benefits, such as incentives or preferential tariffs. The primary constraints considered in their operation include the output capacity limitation and the constraint on the number of allowable responses, and these factors are incorporated into the operation constraint modeling accordingly:

$$\left\{\begin{array}{l}\begin{array}{c}0\le {\eta }_{EVC,t}{g}_{EVC,t}\le {\eta }_{EVC,t}{g}_{\max ,t}^{EVC}\\ 0\le {\mu }_{AC,t}{g}_{AC,t}\le {\mu }_{AC,t}{g}_{\max ,t}^{AC}\end{array}\\ {\displaystyle \sum _{t=1}^T{\eta }_{EVC,t}\le {\eta }_{\max }}\\ {\displaystyle \sum _{t=1}^T{\mu }_{AC,t}\le {\mu }_{\max }}\end{array}\right.$$

(16)

where $g_{EVC,t}$ and $g_{AC,t}$ represent the equivalent outputs that the EV cluster (EVQ) and AC can provide to the VPP stateofcharge (SoS) at moment t, $g_{\max ,t}^{EVC}$ and $g_{\max ,t}^{AC}$ denote their respective maximum equivalent outputs at moment t, and ${\eta }_{\max }$ and ${\mu }_{\max }$ are the maximum numbers of times the EVQ and AC are allowed to respond within the complete dispatch cycle, respectively.

(3)

Clearing the tariff uncertainty set

$$U({\alpha }_P,{\tilde{\lambda }}_{\mathrm{t}})=\left\{{\lambda }_t:(1-{\alpha }_P){\tilde{\lambda }}_{\mathrm{t}}\le {\lambda }_t\le (1+{\alpha }_P)\tilde{\lambda }\right\}$$

(17)

where ${\tilde{\lambda }}_{\mathrm{t}}$ is the predicted value of the market clearing tariff, ${\lambda }_t$ is the actual market clearing tariff, and ${\alpha }_P$ represents the fluctuation in the clearing tariff. Initially, the uncertainty in the clearing tariff is ignored, and the predicted value is substituted into the model to obtain a deterministic solution. The resulting outcome serves as the objective function’s reference value, i.e., the expected profit benchmark for subsequent decision-making periods. To address the uncertainty in actual clearing prices and their deviations from forecasted values, both robust optimization and opportunity-based optimization models are developed.

(4)

IGDT robust optimization model

Setting the robust deviation factor of revenue in the robust optimization model as $\beta$, the model solves for the maximum robustness such that the resulting revenue is not lower than $(1-\beta )G_b$ times the expected revenue under the predicted market conditions

$$\left\{\begin{array}{cc}\max a& \\ s.t.& \min G\ge G_{\exp }\\ & G_{\exp }=(1-\beta )G_b\\ & {\lambda }_{\mathrm{t}}\in U({\alpha }_P,{\tilde{\lambda }}_{\mathrm{t}})\\ & \begin{array}{l}(4-5)(4-6)(4-7)\\ (4-8)(4-9)\end{array}\end{array}\right.$$

(18)

(5)

IGDT chance optimization model

Setting the chance deviation factor of returns in the chance optimization model as $\delta$, the model solves for the minimum confidence level (chance degree) under which the returns are not less than $(1-\delta )G_b$.

3.2. Real-Time Deviation Balancing Model Taking into Account Wind and Solar Uncertainties

Due to stochastic fluctuations in wind speed and solar irradiance, the actual output of wind power generation can significantly deviate from forecasted values. Such deviations directly affect the accuracy of power market bids and disrupt the supply–demand balance within the power system. To effectively manage this uncertainty and ensure stable system operation along with optimal dispatch, generation plans can be dynamically adjusted during each dispatch cycle based on the latest wind power forecasts and real-time operational data. This adaptive approach mitigates the adverse effects of wind power variability, enhancing both the reliability and operational efficiency of electricity systems.

Considering the uncertainty of wind power, it is necessary to temporarily dispatch controllable units such as microgas turbines, ESSs, electric vehicles, and ACs to maximize adherence to the previously declared day-ahead plan by adjusting their operating status or power consumption behavior. Since changes to the day-ahead declaration plan by these controllable units incur adjustment costs, this section focuses on minimizing the system’s deviation adjustment cost as the objective function. This approach aims to align real-time execution as closely as possible with the day-ahead plan while avoiding high penalty costs associated with large deviations.

(1)

Objective function

$$\min C_t={\displaystyle \sum _{t=1}^{\mathrm{T}}(∆C_{MT,t}+∆C_{ESS,t}+∆C_{EVC,t}+∆C_{AC,t}+∆C_{grid,t})}$$

(19)

$$\left\{\begin{array}{c}∆C_{MT,t}=P_{MT,t}^{∆}∆g_{MT,t}\\ ∆C_{ESS,t}=P_{ESS,t}^{∆}∆g_{c,t}^{ESS}{\eta }_{c,t}^{∆}+P_{ESS,t}^{∆}∆g_{d,t}^{ESS}{\eta }_{d,t}^{∆}\\ ∆C_{EVC,t}=P_{EVC,t}^{∆}∆g_{EVC,t}\\ \begin{array}{l}∆C_{AC,t}=P_{AC,t}^{∆}∆g_{AC,t}\\ ∆C_{grid,t}=P_{grid,t}^{∆}∆g_{grid,t}\end{array}\end{array}\right.$$

(20)

where $C_t$ is the total imbalance mitigation cost of the VPP at time t, $∆C_{MT,t}$, $∆C_{ESS,t}$, $∆C_{EVC,t}$, $∆C_{AC,t}$, and $∆C_{grid,t}$ are the adjustment cost and deviation penalty cost of each unit of a heterogeneous resource portfolio comprising gas turbines, ESSs, EVs, and air conditioners, respectively, $P_{MT,t}^{∆}$, $P_{ESS,t}^{∆}$, $P_{EVC,t}^{∆}$, $P_{AC,t}^{∆}$, and $P_{grid,t}^{∆}$ are the unit adjustment costs of each unit, and $∆{\mathrm{g}}_{MT,t}$, $∆g_{c,t}^{ESS}$, $∆g_{d,t}^{ESS}$, $∆g_{EVC,t}$, $∆g_{AC,t}$, and $∆g_{grid,t}$ are the adjusted outputs of each unit, respectively.

(2)

Constraints

(1) Nodal power balance equations

$$∆g_{pv,t}+∆g_{wpp,t}=∆g_{MT,t}+∆g_{ESS,t}+∆g_{EVC,t}+∆g_{AC,t}+∆g_{grid,t}$$

(21)

where $∆g_{pv,t}$ and $∆g_{wpp,t}$ are the deviated outputs of PV and WPP; and $∆g_{MT,t}$, $∆g_{ESS,t}$, $∆g_{EVC,t}$, $∆g_{AC,t}$, and $∆g_{grid,t}$ denote the adjusted outputs of each unit at moment t, respectively.

(2) Controllable unit operation constraints

During the real-time dispatch phase, the output adjustment of the micro gas turbine is limited by its operational boundaries and ramping capabilities. Specifically, the output must remain within the unit’s rated upper and lower limits and adhere to its maximum allowable ramp-up and ramp-down rates at time t. The detailed operational constraints are formulated as follows:

$$\left\{\begin{array}{c}{g}_{MT,\min }\le g_{MT,t}+∆g_{MT,t}\le g_{MT,\max }\\ ∆g_{MT}^{-}\le ∆g_{MT,t}\le ∆g_{MT}^{+}\end{array}\right.$$

(22)

where $g_{MT,t}$ is the planned output of the unit at time t.

(3) ESS scheduling constraints

In the real-time phase, the operation of the ESS is continuously constrained by its SoS limits and power capacity restrictions. Additionally, the charge and discharge adjustments of the ESS are limited by the maximum allowable changes within the given time interval. The battery’s operating state must also remain consistent with the previous day’s scheduled plan. The specific constraints are detailed as follows:

$$\left\{\begin{array}{l}0<∆Q_{c,t}^{ESS}{\eta }_{c,t}^{∆}+∆Q_{d,t}^{ESS}{\eta }_{d,t}^{∆}<Q_{\max }^{ESS}\\ {\displaystyle \sum _{\mathrm{t}=1}^T(∆Q_{c,t}^{ESS}+∆Q_{d,t}^{ESS})=0}\end{array}\right.$$

(23)

where $Q_{\max }^{ESS}$ represents the maximum allowable adjustment of the ESS’s power output, and ${\eta }_{c,t}^{∆}$ and ${\eta }_{d,t}^{∆}$ are the binary state variables indicating charging and discharging status at time t, respectively.

(4) Flexible load constraints

EVs and air conditioners, as adjustable flexible loads, have inherent limitations in their real-time adjustment capabilities, restricting the magnitude of their adjustment range. The specific constraints are as follows:

$$\left\{\begin{array}{c}{\eta }_{EVC,t}{g}_{\min ,t}^{EVC}\le {\eta }_{EVC,t}∆g_{EVC,t}\le {\eta }_{EVC,t}{g}_{\max ,t}^{EVC}\\ {\mu }_{AC,t}{g}_{\min ,t}^{AC}\le {\mu }_{AC,t}∆g_{AC,t}\le {\mu }_{AC,t}{g}_{\max ,t}^{AC}\end{array}\right.$$

(24)

where ${\eta }_{EVC,t}$ and ${\mu }_{AC,t}$ are 0–1 state variables, where 0 indicates that the EV and AC outputs are not adjustable during the real-time stage, and 1 indicates that their outputs are adjustable. $g_{\max ,t}$ and $g_{\min ,t}$ represent the permissible ranges of output adjustment for the EV and AC, respectively.

3.3. Two-Stage Trading Optimization Model Solving

(1)

Upper-level model solving steps

Step 1: The deterministic model is optimized using the predicted market clearing price and the aggregated cost data of controllable units to obtain the optimal return value, which serves as the benchmark for subsequent decision-making and uncertainty analysis.

Step 2: By replacing the predicted clearing price with the actual clearing tariff and setting the robustness deviation factor and opportunity deviation factor based on the decision maker’s risk attitude, the model determines both the minimum expected return acceptable to the decision maker and the higher return value being pursued. Under these expectations, the model solves for the maximum robustness and the minimum opportunity degree to reflect the trade-off between risk aversion and potential gain.

Step 3: The IGDT-based robust optimization model under the conservative strategy and the opportunity optimization model under the speculative strategy are solved separately. For both models, the corresponding uncertainty tolerance levels, optimal unit generation schedules, and bidding strategies are derived.

(2)

Lower model solving steps

As shown in Figure 2, in the first step, the output deviation between the day-ahead declared plan and the real-time output of PV and WPP is calculated.

In the second step, the output plans of the micro gas turbine (MT), ESS EV cluster (EVC), AC, and other controllable units are adjusted based on the output deviation of PV and WPP, taking into account whether the output of each unit can fulfill the day-ahead declared plan to achieve deviation correction; if correction is achieved, the calculation ends; otherwise, the process proceeds to the third step.

In the third step, if the flexible units are still unable to meet the output deviation adjustment requirements after reaching their maximum regulation capacities, the VPP must bear the deviation penalty cost, which is incorporated into the overall deviation adjustment cost considered in this paper.

4. Calculated Case Analysis

4.1. Introduction to Basic Data

(1)

In the present work, a VPP composed of micro gas turbine units, PV units, wind turbines, ESSs, commercial buildings, and neighborhood users is selected for the case study analysis, assuming a 24 h operational cycle divided into 1 h time intervals.

To evaluate the applicability and flexibility of the proposed framework, a representative VPP test case is developed, consisting of a micro gas turbine (MT, 4 MW rated power), PV units (PV, 6 MW installed capacity), wind turbines (WPP, 4 MW rated power), an ESS (ESS), and commercial buildings alongside neighborhood users. A 24h scheduling horizon with 1h intervals is adopted, reflecting typical day-ahead market operations and capturing intraday fluctuations in load and renewable generation. The capacities of MT, PV, and WPP reflect realistic configurations commonly found in distribution-level integrated energy systems, ensuring a practical balance between dispatchable and renewable resources. The ESS is assumed to maintain energy neutrality over the cycle to emphasize its dual role in peak shaving and renewable smoothing via bidirectional power flow. Moreover, the curtailable outputs of EVs and ACs are treated as equivalent dispatchable resources, enabling unified optimization alongside supply-side units. Figure 3 illustrates the declarable power limits of each VPP component, serving as a visual reference for the bidding and scheduling constraints. This test configuration encapsulates the essential features of a “multi-energy complementarity + storage support + demand response” VPP model and offers a scalable benchmark for future extensions involving numerous heterogeneous units.

(2)

Offer cap data

The tariff data disclosed during the trial operation of the Shandong spot electricity market were selected for analysis. A preliminary inspection confirmed that the dataset contained no missing values. Time series forecasting was conducted using the ARIMA model within SPSS software (version 27). The original data were imported into the SPSS dataset, with appropriate definitions assigned for time and date variables. Subsequently, the data were transformed into a time series format to facilitate accurate modeling and prediction.

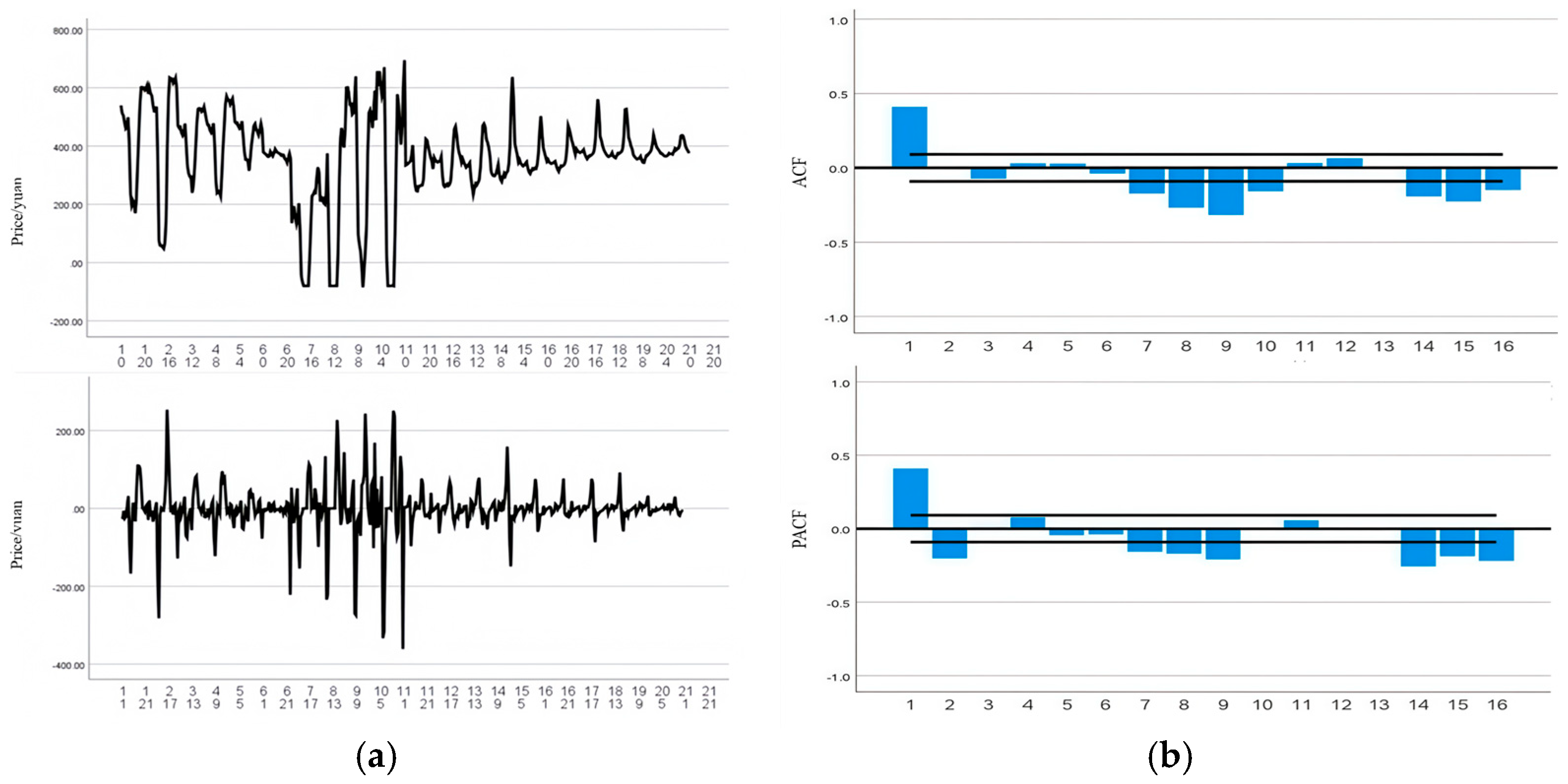
As observed in the time series plot of the original data (Figure 4a, top), the data exhibit non-stationary behavior, indicating the presence of trends or variability over time. To address this, first-order differencing was applied, and the resulting time series plot (Figure 4a, bottom) shows that the data have become approximately stationary. A comparison of the plots before and after differencing highlights the effectiveness of this preprocessing step in stabilizing time series.

The ACF plot and PACF are plotted, the truncated and tailing patterns are observed, and the p-value and q-value are determined. As shown in Figure 4b, the model parameters are initially set as ARIMA (1, 1, 2).

Upon examining the ACF plots of both the predicted values and residuals, the initial ARIMA (1, 1, 2) model exhibited suboptimal performance. To enhance the model fit without altering the dataset, the “Expert Modeler” function in SPSS was utilized, which recommended an ARIMA (1, 1, 8) model with improved fitting accuracy. This model achieved an R-squared value of 0.966, indicating strong explanatory power, and all AR and MA parameters were statistically significant, with p-values less than 0.001, thereby confirming the reliability of the parameter estimates. The model fitting results are presented in Figure 5.

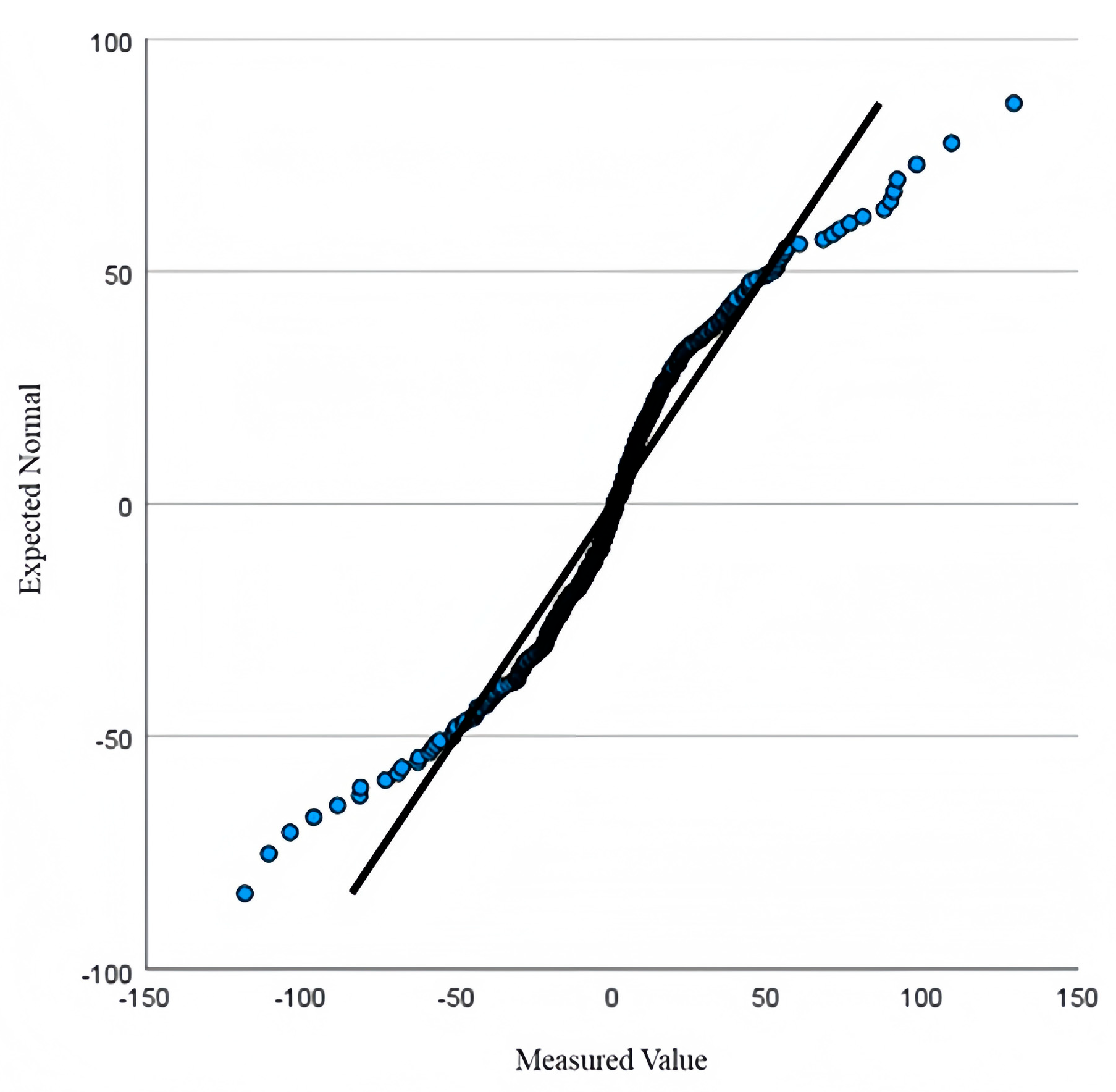
A diagnostic test was conducted to assess the adequacy of the fitted ARIMA (1, 1, 8) model by examining the residuals for autocorrelation and normality. The ACF and PACF plots of the residuals, shown in Figure 6, revealed no significant autocorrelation, indicating that the residuals behave as white noise. Furthermore, the Q-Q plot in Figure 7 demonstrated that the residuals approximately follow a normal distribution. These results confirm that the residuals pass the white noise test, and therefore, there is no need for further model refinement.

In summary, the tariff unit is CNY/MWh, and the predicted data for the clearing tariff are obtained, as shown in

Table 2. Clearance tariff forecast data.

Time	Price	Time	Price	Time	Price	Time	Price
1	377.32	7	373.45	13	376.88	19	411.5
2	369.84	8	369.53	14	380.82	20	399.71
3	365.23	9	368.54	15	381.1	21	386.23
4	366.48	10	366.54	16	390.42	22	379.56
5	369.1	11	373.48	17	412.08	23	375
6	370.97	12	380.82	18	413.5	24	369.55

.

(3)

Offer lower-limit data

The micro gas turbine offers flexible power output ranging from 0 MW to 2 MW depending on the time of day, demonstrating a high degree of controllability. PV units generate power between 0 MW and 6 MW during daylight hours but cease production at night. Wind turbines, influenced by fluctuations in wind speed, produce power in the range of 0 MW to 4 MW. ESSs exhibit varying charging and discharging capacities throughout the day, with a maximum bidirectional power of 2 MW. EV clusters contribute a maximum equivalent output of 1 MW. Additionally, different user types, including commercial buildings, residential neighborhoods, and factories, display diverse load and demand patterns over the course of a day. Through effective aggregation and demand-side management, it is feasible to ensure the availability of consumers willing to reduce air conditioning usage at any given time, offering a maximum equivalent output of 0.5 MW.

To ensure a certain profit threshold, a profit margin of 0.12 is applied. By integrating the internal unit output with the average power purchase price across multiple users, the minimum bidding price is calculated and expressed in CNY/MWh, as presented in

Table 3. Quotation floor data.

Time	Price	Time	Price	Time	Price	Time	Price
1	226.62	7	202.85	13	218.37	19	196.48
2	209.27	8	205.32	14	216.01	20	237.70
3	213.51	9	280.30	15	238.33	21	234.71
4	239.78	10	234.74	16	233.85	22	241.12
5	203.48	11	237.69	17	204.35	23	225.79
6	196.06	12	224.96	18	194.30	24	244.18

.

4.2. Analysis of VPP Trading Results

(1)

Analysis of trading results for the first day phase

Substituting the parameters into the deterministic model yields 14 winning time slots, resulting in a total gain of CNY30,677.7272; the VPP’s successful bids in the electric energy market for each time slot are shown in Figure 8.

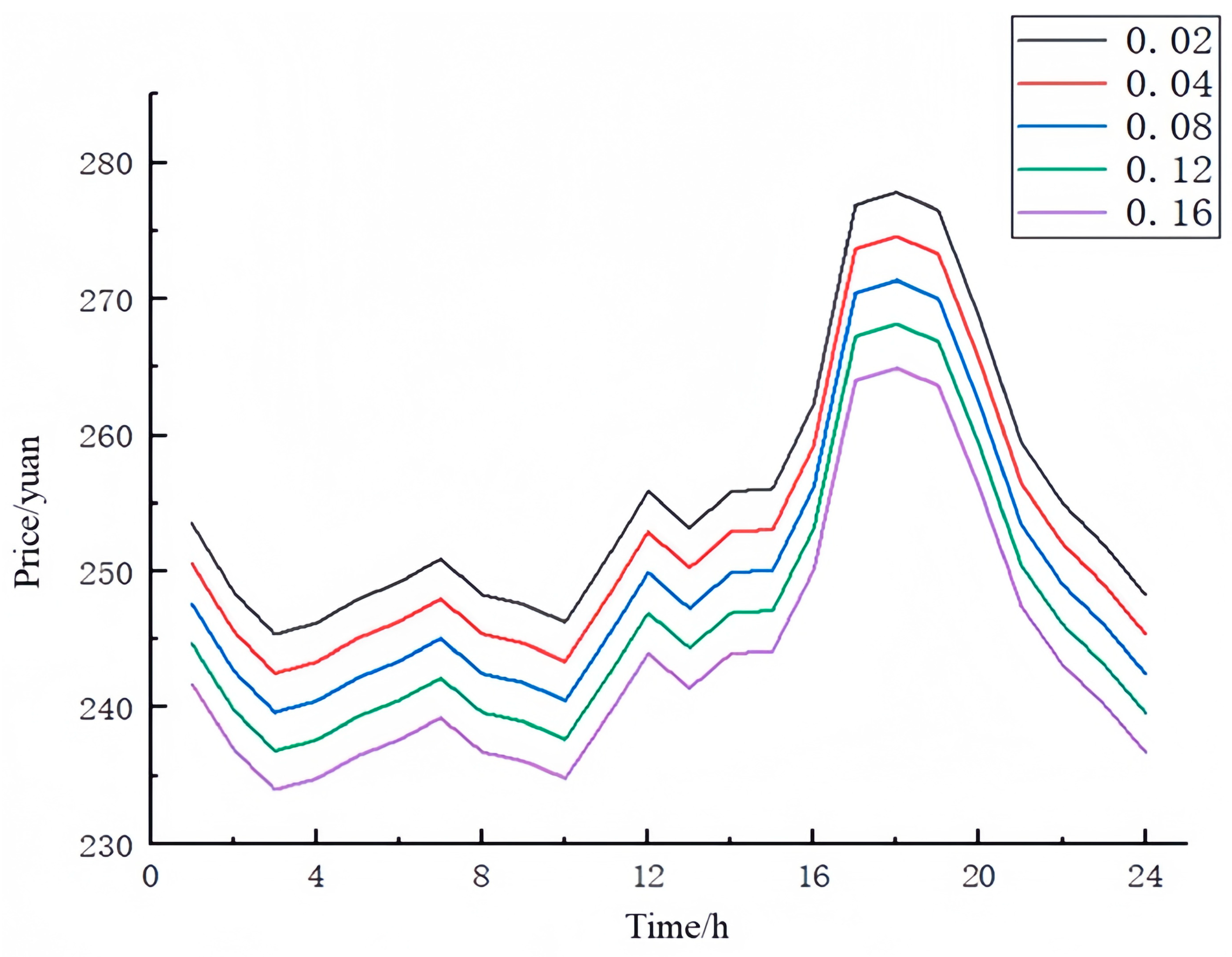
The range of the deviation factor of the robust optimization model is set to 0.02~0.16, i.e., the decision maker in the worst-case scenario.

A higher value indicates a lower risk tolerance on the part of the decision maker, reflecting a more conservative or risk-averse attitude toward uncertainty. Setting five different deviation factors, the variation in the final offer with adjustments to the robust deviation factor is shown in Figure 9, and the corresponding changes in robustness and the decision maker’s return with deviation factor fluctuations are shown in Figure 10.

From these two figures, it is evident that as the deviation factor gradually increases, the decision maker’s final offer decreases, leading to a decline in overall returns while robustness improves. This trend reflects the decision maker’s consideration of potential discrepancies between predicted tariffs and actual clearing prices. To enhance robustness, a more conservative bidding strategy is adopted, sacrificing higher returns in favor of a lower, more reliable offer. Although the deterministic model yields higher expected returns, this does not imply that its bidding strategy is superior. In adverse market conditions with significant fluctuations in clearing prices, the deterministic model’s offer scheme may fail to secure successful bids across multiple time slots, whereas the robust model maintains greater stability and feasibility under uncertainty.

The deviation factor range for the opportunity optimization model is set between 0.04 and 0.2, representing the decision maker’s expectation that favorable tariff fluctuations could result in a return increase of 4% to 20%. A higher deviation factor reflects a stronger inclination toward pursuing high returns and a more optimistic view of risk impacts. However, model results indicate that even under optimistic assumptions, the likelihood of achieving the decision maker’s expected minimum return is extremely low. Specifically, when the expected return increase is set to even a modest 2% (i.e., an opportunity deviation factor of 0.02), the corresponding opportunity degree remains as low as 0.00001. This suggests that, under actual market conditions, where upward tariff fluctuations are minimal, the speculative strategy of bidding high in anticipation of elevated clearing prices is ineffective. Consequently, such an approach results in fewer successful bids and a reduction in overall returns. This phenomenon is clearly illustrated in Figure 11.

4.3. Analysis of Real-Time Phase Trading Results

The results of the robust optimization model, obtained using a robustness deviation factor of 0.04, are selected to determine the winning bidding outcomes, as illustrated in Figure 12. These outcomes serve as parameter inputs for deviation correction during the real-time operation phase.

A total of 19 time slots are successfully cleared in the day-ahead phase, and during the real-time phase, deviations caused by the actual outputs of wind and PV units within these winning time slots must be corrected; by leveraging flexible response units to rapidly adjust capacity and align with the day-ahead scheduling plan, the deviation correction is achieved at a minimum cost of CNY3509.6, with the results illustrated in Figure 13.

As shown in the figure, during time periods 1–5, 9–11, and 17–19, where wind power exhibits a positive deviation, the MT reduces its output, the ESS either decreases discharging or increases charging, and the EVs and ACs respond by decreasing their power consumption to maximize wind power utilization. Conversely, in periods 8 and 12–16, when wind power shows a negative deviation, the MT increases output, the ESS increases discharging or reduces charging, and EVs and ACs increase power consumption to compensate for the wind power deficit. Despite the full adjustment of internal units, in time periods 4 and 17, wind generation exceeds the VPP’s self-consumption capacity, leading to surplus power, while in period 13, the wind power shortfall surpasses the VPP’s maximum responsive capacity, resulting in a power shortage. In the remaining 16 time slots, the VPP successfully implements deviation correction through the coordinated adjustment of internal flexibility response units.

5. Conclusions

This study addresses the dual challenges encountered by VPPs in participating in electricity markets amid price volatility and renewable generation uncertainty by proposing a two-stage decision-making framework that integrates electricity price forecasting, robust and opportunistic optimization strategies, and real-time deviation correction, thereby significantly enhancing both the resilience of bidding strategies and the operational flexibility of VPPs.

In the day-ahead stage, a market-clearing-oriented bidding interval is established by combining ARIMA-based electricity price forecasting with cost-based lower bound pricing, reflecting the aggregator role of VPPs. A set of robust and opportunity optimization models grounded in IGDT is developed to accommodate varying risk preferences of decisionmakers. Simulation results reveal that the robust model, with a deviation factor of 0.04, clears bids in 19 time intervals, ensuring high revenue stability. In contrast, the opportunity model fails to meet even modest return expectations under optimistic scenarios, due to infrequent favorable market conditions, thus highlighting the limited viability of speculative bidding strategies in practical applications. In the real-time stage, a deviation correction model is introduced to minimize adjustment costs stemming from forecast errors in wind and solar output. Results demonstrate that the coordinated flexibility of microturbines, ESSs, and responsive loads enables rapid mitigation of intra-hour imbalances, reducing the total deviation correction cost to CNY 3509.6. Among the 19 cleared intervals, 16 were successfully corrected, while a few remained constrained by internal resource limits, validating the effectiveness and operational resilience of the proposed flexibility coordination mechanism.

Methodologically, this work presents an integrated framework that combines price forecasting, risk-aware bidding, and real-time multi-resource coordination, addressing the modeling gap in VPP scheduling under high uncertainty and multi-market coupling. It offers a robust and extensible approach applicable across diverse scenarios, enabling VPPs to navigate volatile markets while ensuring operational efficiency. The framework is particularly well-suited for emerging applications such as multi-market coordination, regional integrated energy regulation, and demand-side resource aggregation, thereby supporting the development of intelligent, low-carbon, and resilient power systems.

The findings offer theoretical insight for market mechanism design, practical tools for VPP operators to formulate robust strategies, and a modeling reference for future research on flexible and market-driven energy systems.