Modeling and Validation of High-Pressure Hydrogen Joule-Thomson Effect for Enhanced Hydrogen Energy System Safety
Abstract
1. Introduction
2. The JT Effect
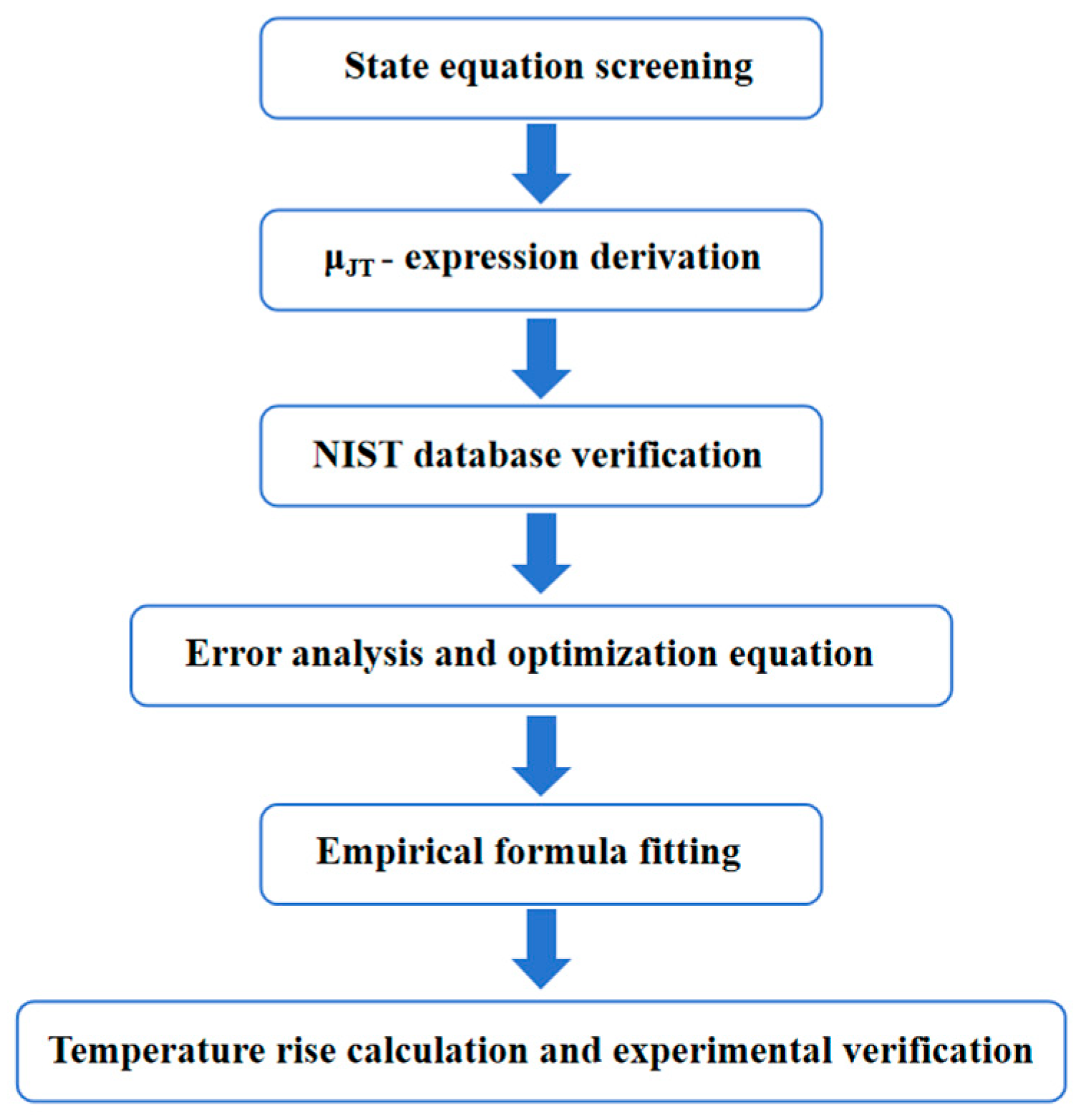
3. The Derivation of for Multiple State Equations
3.1. Multiple Expressions of State Equations
3.2. The Derivation of the
3.3. Calculation of Physical Parameters of Hydrogen
3.3.1. Calculation of Hydrogen Compression Factor and Specific Volume
3.3.2. The Actual Molar Specific Heat Capacity of Hydrogen at Constant Pressure
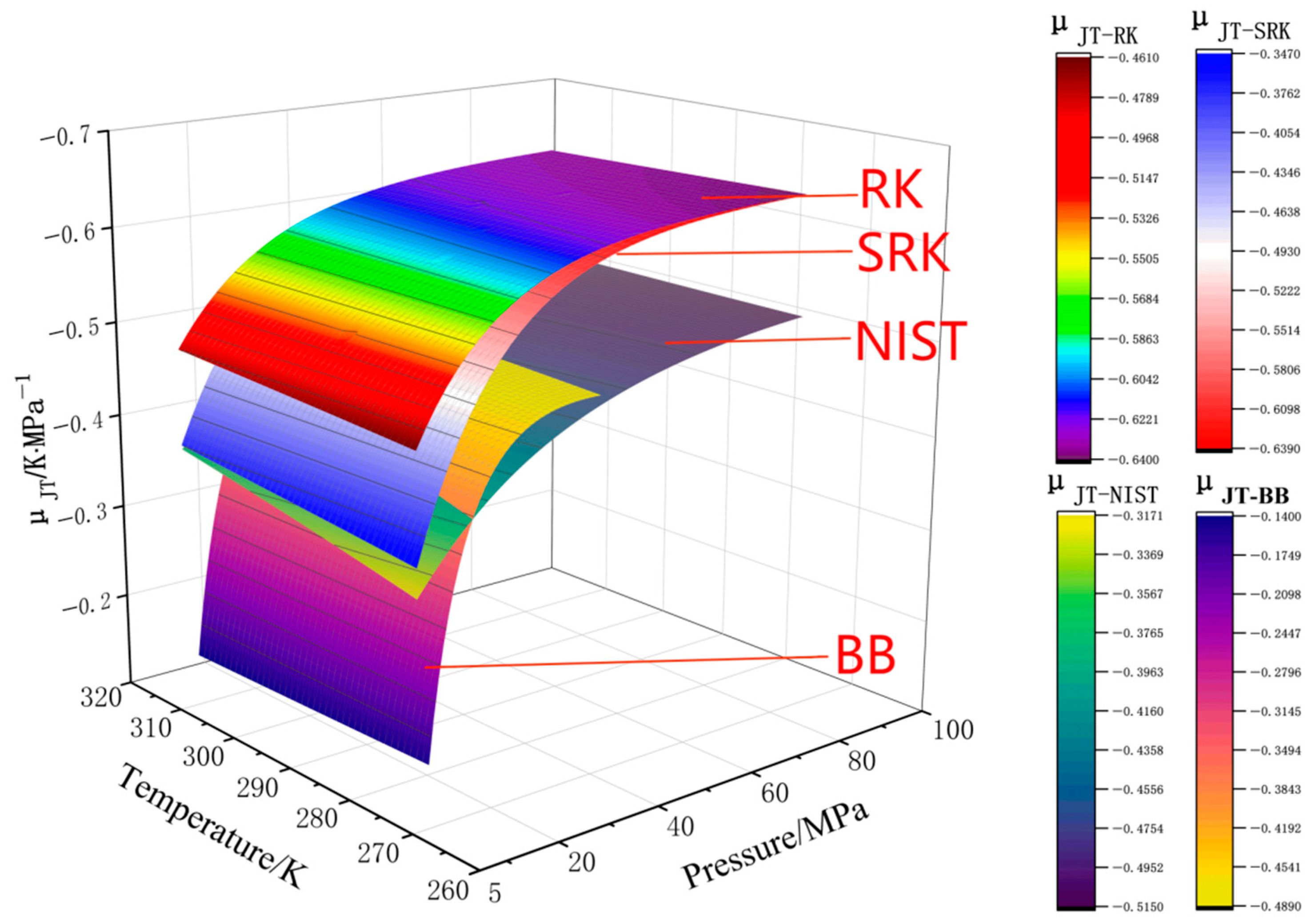
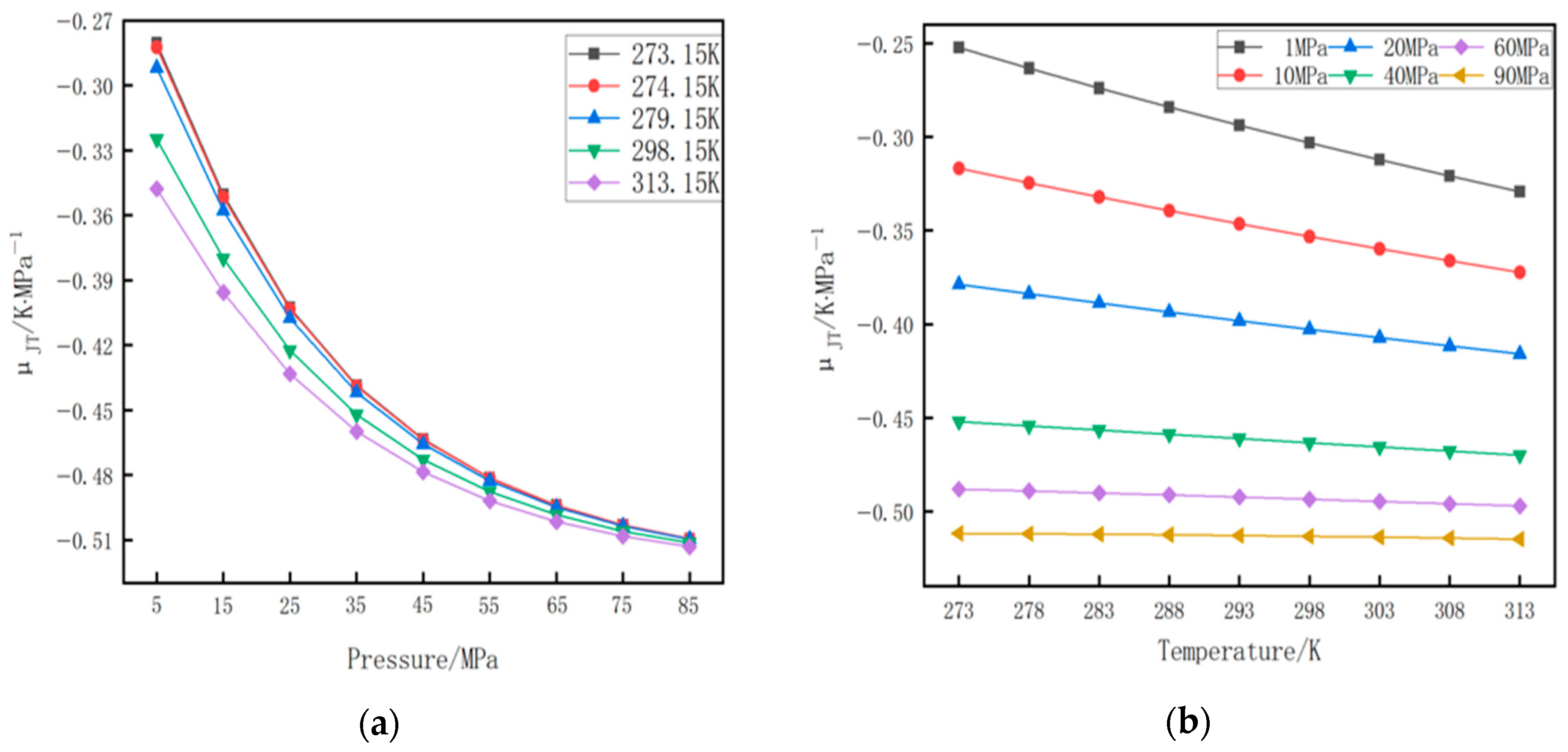
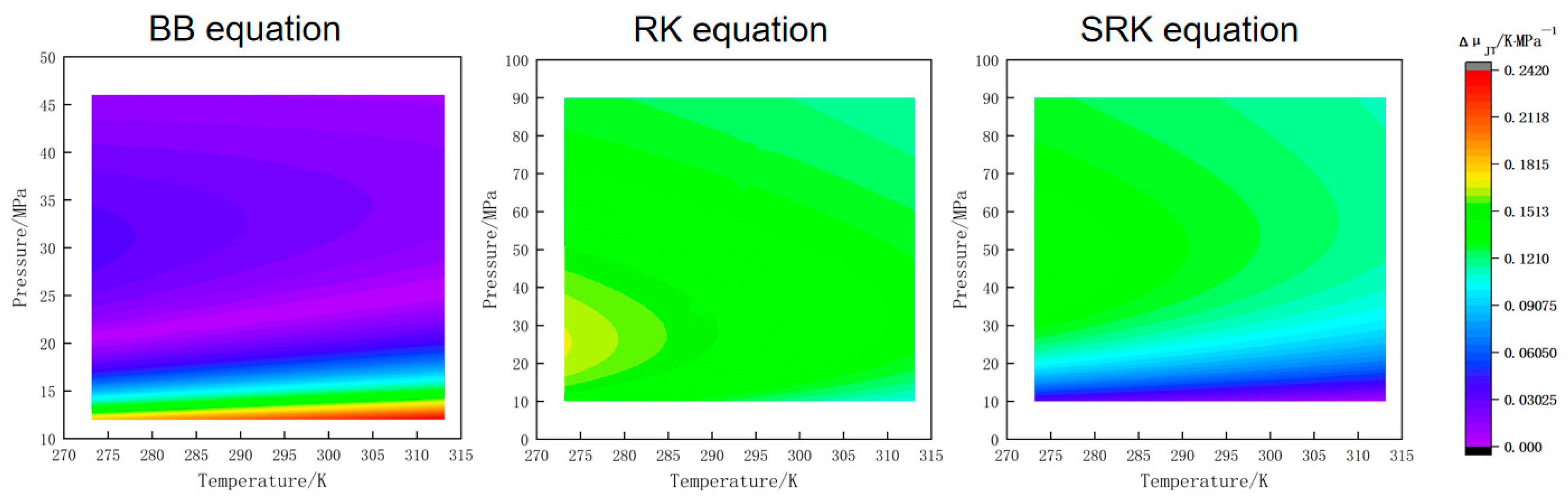
4. Results and Analysis
4.1. Analysis of Calculation Errors of Four State Equations
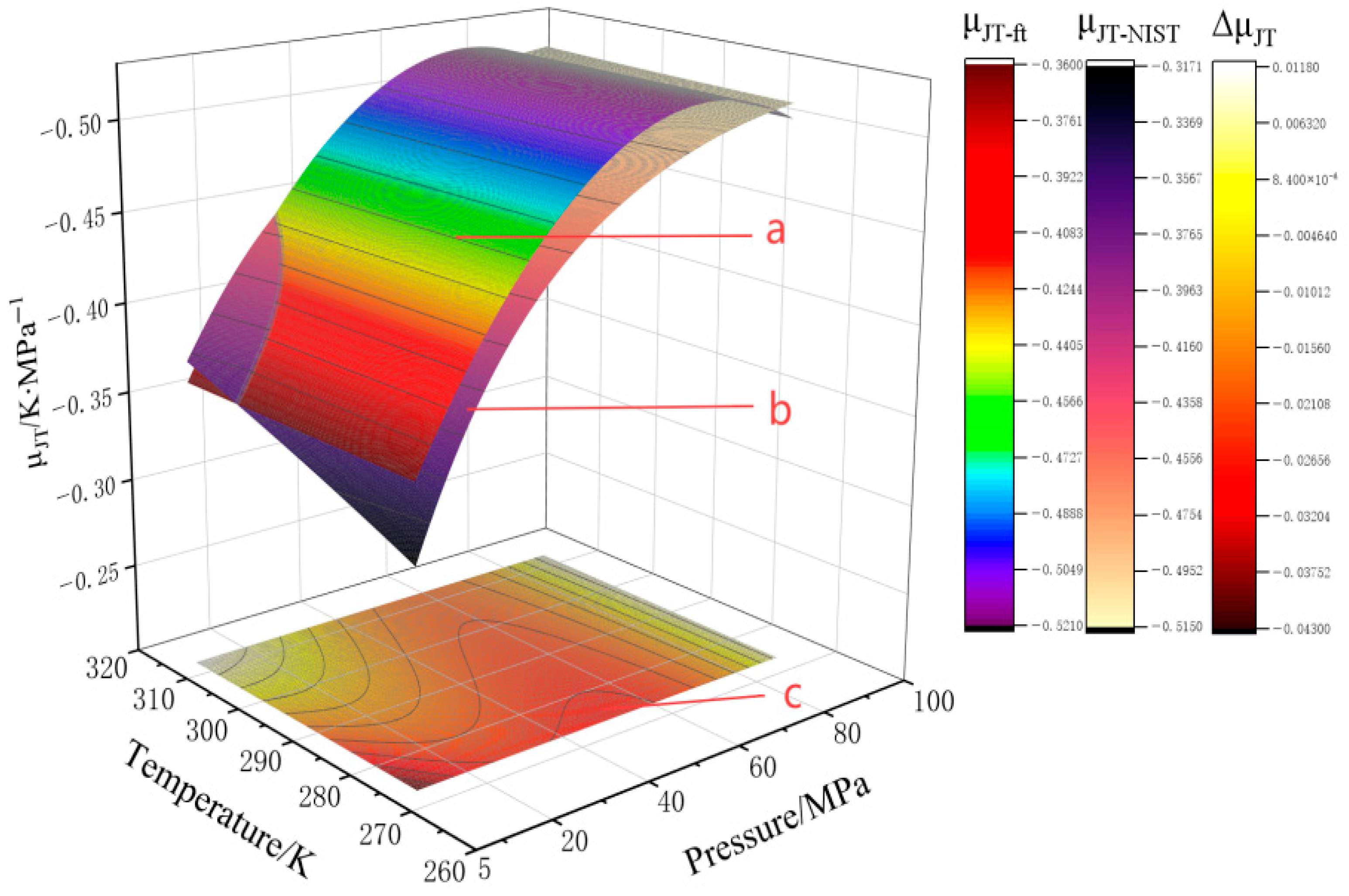
4.2. Derive the Empirical Expression About
4.3. Calculation of Throttling Temperature Rise
5. Conclusions
6. Future and Outlook
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Equation | a | b |
|---|---|---|
| VDW | ||
| RK | ||
| SRK | ||
| PR |
| GAS | |||||
|---|---|---|---|---|---|
| 20.0117 | −0.00506 | 0.02096 | −0.04359 | 504 |
References
- Naseem, K.; Khalid, F.; Fei, Q.; Suo, G.; Khan, A.A.; Jabeen, T.; Karamat, S.; Shah, B.A. Role of carbon-based materials to promote the hydrolysis performance of magnesium-based materials. Renew. Sustain. Energy Rev. 2025, 219, 115864. [Google Scholar] [CrossRef]
- Wang, J.; Cui, X.; Geng, H.; She, H.; Chang, Z. Performance prediction of a distributed Joule-Thomson effect cooler with pillars. Appl. Therm. Eng. 2023, 218, 119265. [Google Scholar] [CrossRef]
- Geng, H.; Cui, X.; Weng, J.; She, H.; Wang, W. Review of experimental research on Joule–Thomson cryogenic refrigeration system. Appl. Therm. Eng. 2019, 157, 113640. [Google Scholar] [CrossRef]
- Naseem, K.; Qin, F.; Suo, G.; Ahmed, S.; Hanif, M.; Gilani, N. Recent progress of mechanically activated Mg-based materials to promote hydrogen generation via hydrolysis. Fuel 2025, 391, 134783. [Google Scholar] [CrossRef]
- Su, Y.; Lv, H.; Liu, D.; Zhang, C. The effects of different hydrogen incident angles on the temperature rise of the Type IV tanks for fuel cell passenger cars. Process Saf. Environ. Prot. 2025, 199, 107285. [Google Scholar] [CrossRef]
- Li, J.Q.; Chen, Y.; Ma, Y.B.; Kwon, J.T.; Xu, H.; Li, J.C. A study on the Joule-Thomson effect of during filling hydrogen in high pressure tank. Case Stud. Therm. Eng. 2023, 41, 102678. [Google Scholar] [CrossRef]
- Kumar, N.; Singh, D.; Verma, S.; Paul, A.R.; Tolj, I. Numerical study of Joule-Thomson effect for high-pressure hydrogen injection. Int. J. Hydrog. Energy 2025, 138, 595–604. [Google Scholar] [CrossRef]
- Liu, C.; Xue, D.; Li, W.; Yu, L.-J.; Zhao, J.; Yang, J.-Y.; Jin, Z.-J.; Chen, D.-Y.; Qian, J.-Y. Dynamic behavior and Joule-Thomson characteristics analysis on flow limiter inside hydrogen On Tank Valve for hydrogen fuel cell vehicles. Int. J. Hydrogen Energy 2025, 123, 162–172. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, C.; Li, C.; Wu, X.; Xie, H.; Jiang, L. Thermodynamic evaluation of the effects of hydrogen blending on the Joule-Thomson characteristics of hydrogen-blended natural gas. J. Clean. Prod. 2023, 406, 137074. [Google Scholar] [CrossRef]
- Zhang, C.; Li, Z.; Li, C.; Wu, X.; Sun, L.; Chen, C. Insight into the effects of hydrogen on inside-valve flow and Joule-Thomson characteristics of hydrogen-blended natural gas: A numerical study. Int. J. Hydrogen Energy 2024, 49, 1056–1074. [Google Scholar] [CrossRef]
- Chen, J.; Veenstra, M.; Purewal, J.; Hobein, B.; Papasavva, S. Modeling a hydrogen pressure regulator in a fuel cell system with Joule–Thomson effect. Int. J. Hydrogen Energy 2019, 44, 1272–1287. [Google Scholar] [CrossRef]
- Tiuman, E.T.; Pereira, M.V.R.; Neto, M.A.M.; Bertoldi, D.; Morales, R.E.M. Predictions of the Joule-Thomson coefficients and inversion curves from the CPA equation of state. J. Supercrit. Fluids 2021, 168, 105077. [Google Scholar] [CrossRef]
- Pakravesh, A.; Zarei, H. Prediction of Joule–Thomson coefficients and inversion curves of natural gas by various equations of state. Cryogenics 2021, 118, 103350. [Google Scholar] [CrossRef]
- Rößler, J.; Antolović, I.; Stephan, S.; Vrabec, J. Assessment of thermodynamic models via Joule–Thomson inversion. Fluid Phase Equilibria 2022, 556, 113401. [Google Scholar] [CrossRef]
- Shoghl, S.N.; Naderifar, A.; Farhadi, F.; Pazuki, G. Comparing the predictive ability of two-and three-parameter cubic equations of state in calculating specific heat capacity, Joule–Thomson coefficient, inversion curve and outlet temperature from Joule–Thomson valve. Cryogenics 2021, 116, 103288. [Google Scholar] [CrossRef]
- Huang, H.; Li, J.; Sun, X.; Yu, B.; Wang, X.; Wang, N.; Ma, L. Adaptability Study of Gas Equations of State for the Calculation of Thermophysical Parameters of Hydrogen-Blended Natural Gas. J. Pipeline Sci. Eng. 2025, 100313. [Google Scholar] [CrossRef]
- Wang, J.; Ouyang, X.; Cheng, L.; Peng, S.; Wang, Z.; Wang, J. Investigation on adaptability of physical property state equation model for hydrogen-blended natural gas. Int. J. Hydrogen Energy 2024, 81, 1256–1277. [Google Scholar] [CrossRef]
- Alanazi, A.; Bawazeer, S.; Ali, M.; Keshavarz, A.; Hoteit, H. Thermodynamic modeling of hydrogen–water systems with gas impurity at various conditions using cubic and PC-SAFT equations of state. Energy Convers. Manag. X 2022, 15, 100257. [Google Scholar] [CrossRef]
- Wu, S.; Zhao, B.; Tan, J.; Zhao, Y.; Zhai, Y.; Xue, R.; Tan, H.; Ma, D.; Wu, D.; Dang, H. Thermodynamic study on throttling process of Joule-Thomson cooler to improve helium liquefaction performance between 2 K and 4 K. Energy 2023, 277, 127691. [Google Scholar] [CrossRef]
- Chen, S.; Qiu, C.; Shen, Y.; Tao, X.; Zhang, Z.; Wan, A.; Gan, Z. Experimental and dynamic simulation study of the Joule-Thomson cryocooler working at liquid hydrogen temperature. Appl. Therm. Eng. 2023, 235, 121285. [Google Scholar] [CrossRef]
- Ariadji, T.; Adisasmito, S.; Mucharam, L.; Abdassah, D. Improved Joule Thomson equation of supercritical CO2-rich natural gas in separation system. Nat. Gas Ind. B 2023, 10, 245–253. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, L.; Wang, Y.; Shang, X.; Bao, W.; Li, Z.; Shao, C.; Cui, Z. Cryogenic helium flow in adiabatic capillary tubes: Numerical insights into choked flow and superfluid behavior in Joule-Thomson cryocoolers. Cryogenics 2025, 147, 104043. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, Y.; Wang, H.; Gao, S.; Gong, M. Evaluation and analysis from pressure and component in the single-stage mixed-refrigerant Joule-Thomson cooler from 100 to 200 K. Energy 2025, 319, 135018. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, Y.; Sun, Y.; Wang, H.; Guo, H.; Gong, M. Optimization method for mixed refrigerants in Joule–Thomson refrigerators with fixed-temperature heat loads. Appl. Therm. Eng. 2023, 233, 121198. [Google Scholar] [CrossRef]
- Farzaneh-Gord, M.; Rahbari, H.R.; Zangeneh, J. Effects of natural gas compositions on its Joule–Thomson coefficients and Joule–Thomson inversion curves. Cryogenics 2020, 111, 103169. [Google Scholar] [CrossRef]
- Hosseini, A.; Khoshsima, A. Evaluation of translated-consistent equations of state compared for the prediction of the Joule–Thomson effect at high pressures and high temperatures. Fluid Phase Equilibria 2020, 523, 112775. [Google Scholar] [CrossRef]
- Tada, K. The full range Joule-Thomson inversion curve of helium-3. Int. J. Refrig. 2021, 127, 157–164. [Google Scholar] [CrossRef]
- Soave, G. Improvement of the van der Waals equation of state. Chem. Eng. Sci. 1984, 39, 357–369. [Google Scholar] [CrossRef]
- Redlich, O.; Kwong, J.N.S. On the thermodynamics of solutions. V. An equation of state. Fugacities of gaseous solutions. Chem. Rev. 1949, 44, 233–244. [Google Scholar] [CrossRef]
- Soave, G. Improving the Treatment of Heavy Hydrocarbons by the SRK EOS. Fluid Phase Equilibria 1993, 84, 339–342. [Google Scholar] [CrossRef]
- Cengel, Y.A.; Boles, M.A. Thermodynamics: An engineering approach. Sea 2002, 1000, 287–293. [Google Scholar]
- Li, Z.; Tian, Z. Research on Throttling Effect of High-Pressure Hydrogen. China Plant Eng. 2025, S1, 138–141. [Google Scholar]
- Deng, C.; Song, P.; Ma, A. Analysis of Joule-Thomson effect of real gas system sealed by dry gas. CIESC J. 2016, 67, 3833. [Google Scholar]
- Perry, R.H. Perry’s Chemical Engineers’ Handbook, 7th ed.; McGraw-Hill: New York, NY, USA, 1997; pp. 132–182. [Google Scholar]
| VDW | (7) | |
| RK | (8) | |
| SRK | (9) | |
| PR | (10) | |
| PT | (11) | |
| NB | (12) | |
| HK | (13) | |
| BB | (14) | |
| Virial | (15) | |
| BWR | (16) |
| State Equation | Expression | |
|---|---|---|
| VDW | (17) | |
| RK | (18) | |
| SRK | (19) | |
| PR | (20) | |
| PT | (21) | |
| NB | (22) | |
| HK | (23) | |
| BB | (24) | |
| Virial | (25) | |
| BWR | (26) | |
| j | |||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| i | 1 | 1.00018 | −0.0022546 | 0.01053 | −0.013205 |
| 2 | −0.00067291 | 0.028051 | −0.024126 | −0.0058663 | |
| 3 | 0.000010817 | −0.00012653 | 0.00019788 | 0.00085677 | |
| 4 | −1.4368 × 10−7 | 1.2171 × 10−6 | 7.7563 × 10−7 | −1.7418 × 10−5 | |
| 5 | 1.2441 × 10−9 | −8.965 × 10−9 | −1.6711 × 10−8 | 1.4697 × 10−7 | |
| 6 | −4.4709 × 10−12 | 3.0271 × 10−11 | 6.3329 × 10−11 | −4.6974 × 10−10 | |
| Gas | /K | /K | |||||
|---|---|---|---|---|---|---|---|
| 0.2762 | 0.0956 | 2.4660 | 0.0376 | 567.6 | 250 | 1500 |
| P/MPa | T/K | |||
|---|---|---|---|---|
| 0.1 | 298.15 | −0.24346 | −0.2994 | 0.05594 |
| 0.5 | 298.15 | −0.256743 | −0.30119 | 0.044447 |
| 1 | 298.15 | −0.273245 | −0.30354 | 0.030295 |
| 2 | 298.15 | −0.305945 | −0.30851 | 0.002565 |
| 4 | 298.15 | −0.36966 | −0.31927 | 0.05039 |
| 6 | 298.15 | −0.430465 | −0.33061 | 0.099855 |
| 8 | 298.15 | −0.487648 | −0.34209 | 0.145558 |
| 10 | 298.15 | −0.539488 | −0.35342 | 0.186068 |
| a | b | c | d | e |
|---|---|---|---|---|
| 6.67971 × 10−8 | 2.4358 × 10−5 | −5.774 × 10−5 |
|
Pressure Before Throttling p0/MPa | Temperature Before Throttling T0/K | Pressure After Throttling p1/MPa | Experimental Value T1/K | Calculated Value T1/K | Relative Error % | |
|---|---|---|---|---|---|---|
| 22 | 285.15 | 5 | 286.56 | 291.62908 | 6.47908 | 1.77% |
| 40 | 285.15 | 5 | 298.54 | 300.0838 | 14.9338 | 0.52% |
| 40 | 285.15 | 7.5 | 310.57 | 299.2323 | 14.0823 | −3.65% |
| 40 | 288.15 | 10 | 300.54 | 301.3464 | 13.1964 | 0.27% |
| 40 | 292.15 | 15 | 302.81 | 303.4673 | 11.3173 | 0.22% |
| 60 | 288.15 | 7.5 | 309.73 | 313.2137 | 25.0637 | 1.12% |
| 60 | 293.15 | 10 | 313.41 | 317.3307 | 24.1807 | 1.25% |
| 80 | 287.15 | 7.5 | 318.4 | 324.4826 | 37.3326 | 1.91% |
| 80 | 297.15 | 10 | 326.83 | 333.608 | 36.458 | 2.07% |
| 80 | 299.15 | 15 | 324.55 | 333.7285 | 34.5785 | 2.83% |
| 87.5 | 287.15 | 7.5 | 322.45 | 329.3371 | 42.1871 | 2.14% |
| 87.5 | 297.15 | 10 | 329.54 | 338.4638 | 41.3138 | 2.71% |
| 87.5 | 303.15 | 15 | 335.52 | 342.5897 | 39.4397 | 2.11% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, M.-Y.; Fang, Y.; Wang, Q.-H.; Dai, Y.-M.; Liu, Z.-H.; Li, J.-Q.; Kwon, J.-T. Modeling and Validation of High-Pressure Hydrogen Joule-Thomson Effect for Enhanced Hydrogen Energy System Safety. Energies 2025, 18, 4573. https://doi.org/10.3390/en18174573
Zhou M-Y, Fang Y, Wang Q-H, Dai Y-M, Liu Z-H, Li J-Q, Kwon J-T. Modeling and Validation of High-Pressure Hydrogen Joule-Thomson Effect for Enhanced Hydrogen Energy System Safety. Energies. 2025; 18(17):4573. https://doi.org/10.3390/en18174573
Chicago/Turabian StyleZhou, Mu-Yao, Yi Fang, Qian-Hua Wang, Yi-Ming Dai, Zhan-Hao Liu, Ji-Qiang Li, and Jeong-Tae Kwon. 2025. "Modeling and Validation of High-Pressure Hydrogen Joule-Thomson Effect for Enhanced Hydrogen Energy System Safety" Energies 18, no. 17: 4573. https://doi.org/10.3390/en18174573
APA StyleZhou, M.-Y., Fang, Y., Wang, Q.-H., Dai, Y.-M., Liu, Z.-H., Li, J.-Q., & Kwon, J.-T. (2025). Modeling and Validation of High-Pressure Hydrogen Joule-Thomson Effect for Enhanced Hydrogen Energy System Safety. Energies, 18(17), 4573. https://doi.org/10.3390/en18174573






