Investigation of the Influence of Gyroid Lattice Dimensions on Cooling
Abstract
1. Introduction
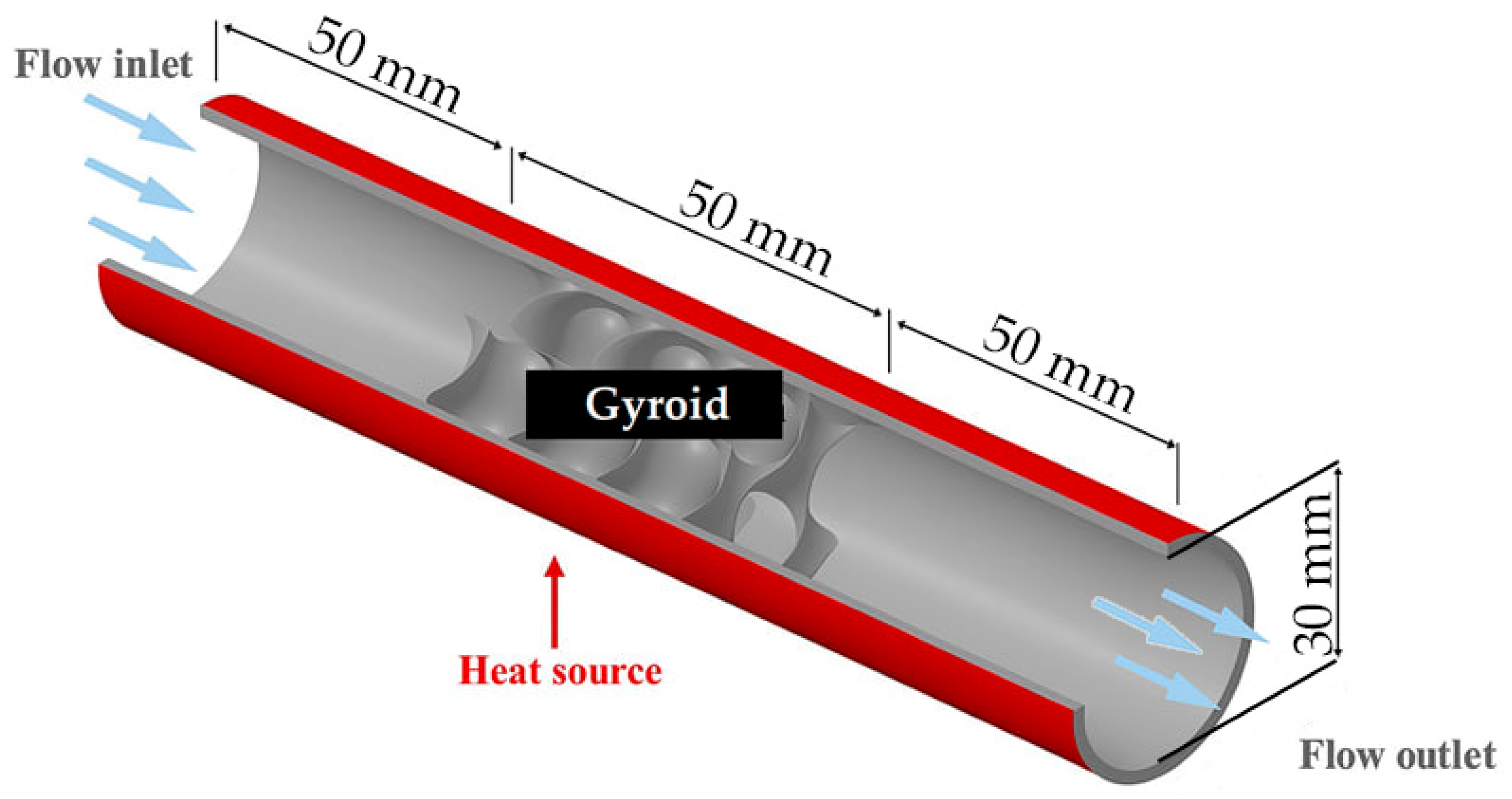
2. Materials and Methods
- Develop geometric models of channels with integrated lattice structures of varying periodicity and wall thickness;
- Perform numerical simulations of flow and heat transfer in the channels under different cooling flow regimes;
- Determine key thermophysical parameters: Nusselt number, cooling depth coefficient, and hydraulic drag coefficient;
- Conduct a comparative analysis of the performance of lattice structures relative to a smooth channel;
- Prepare and carry out experimental studies of channel flow for verification of the numerical results.
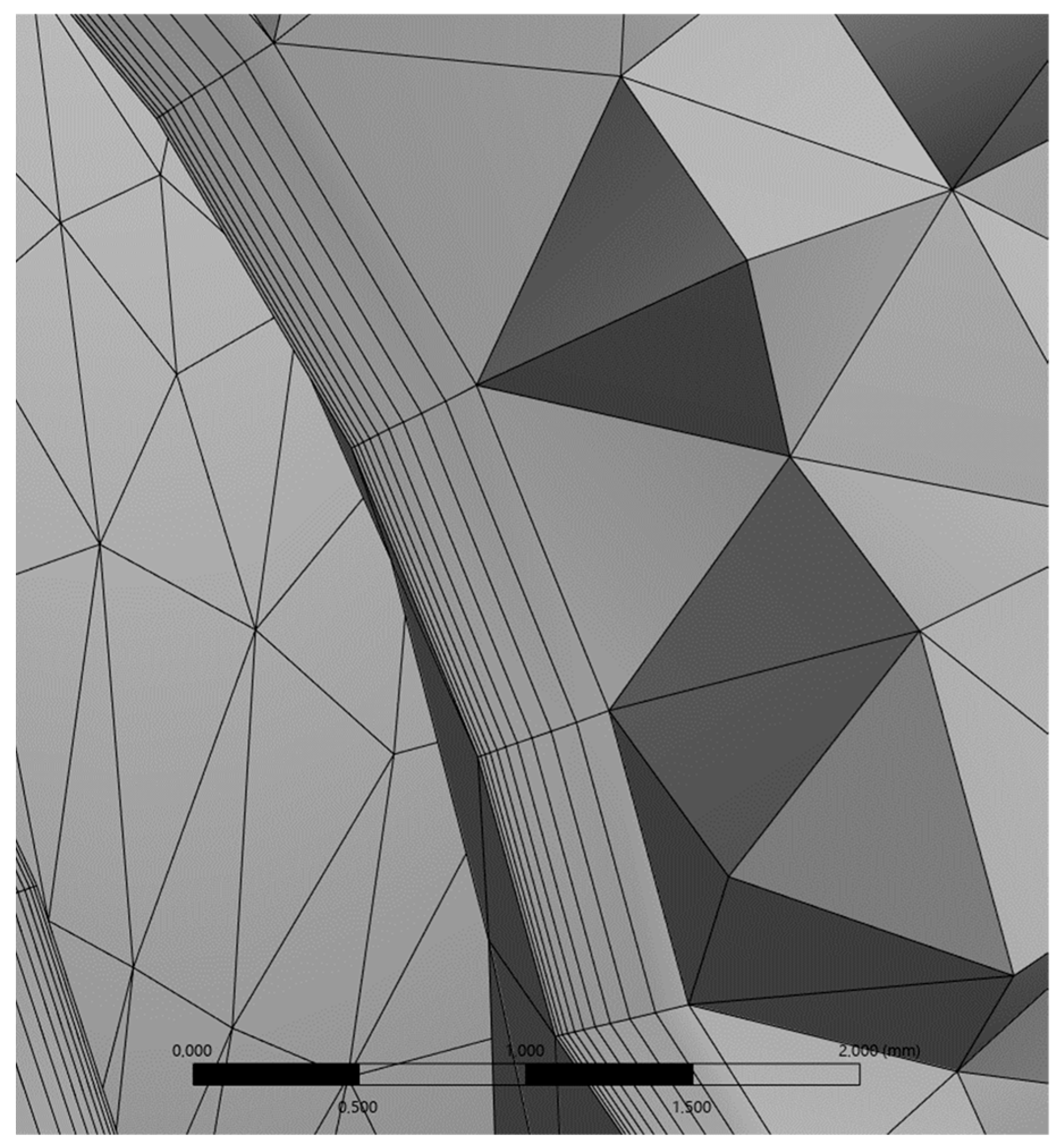
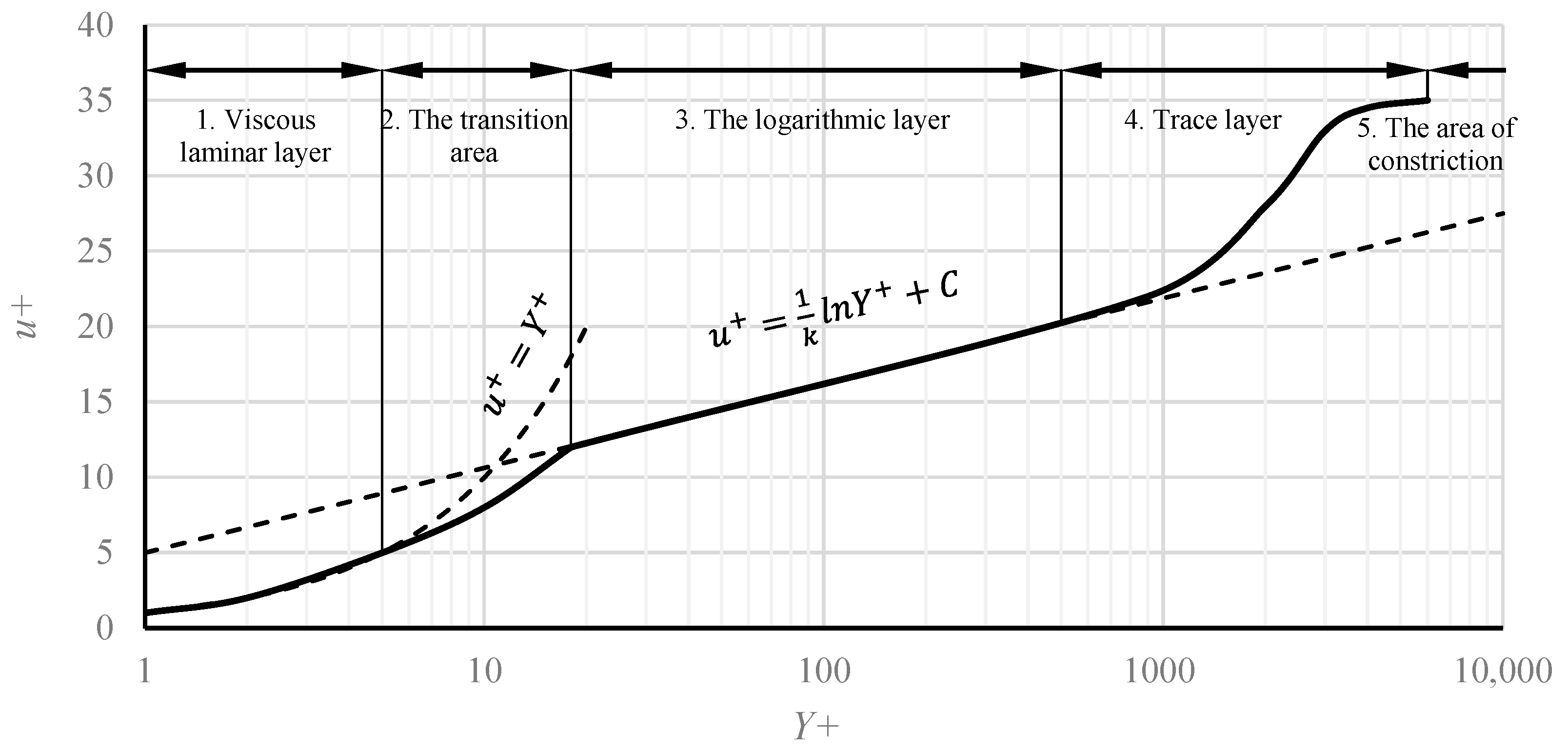
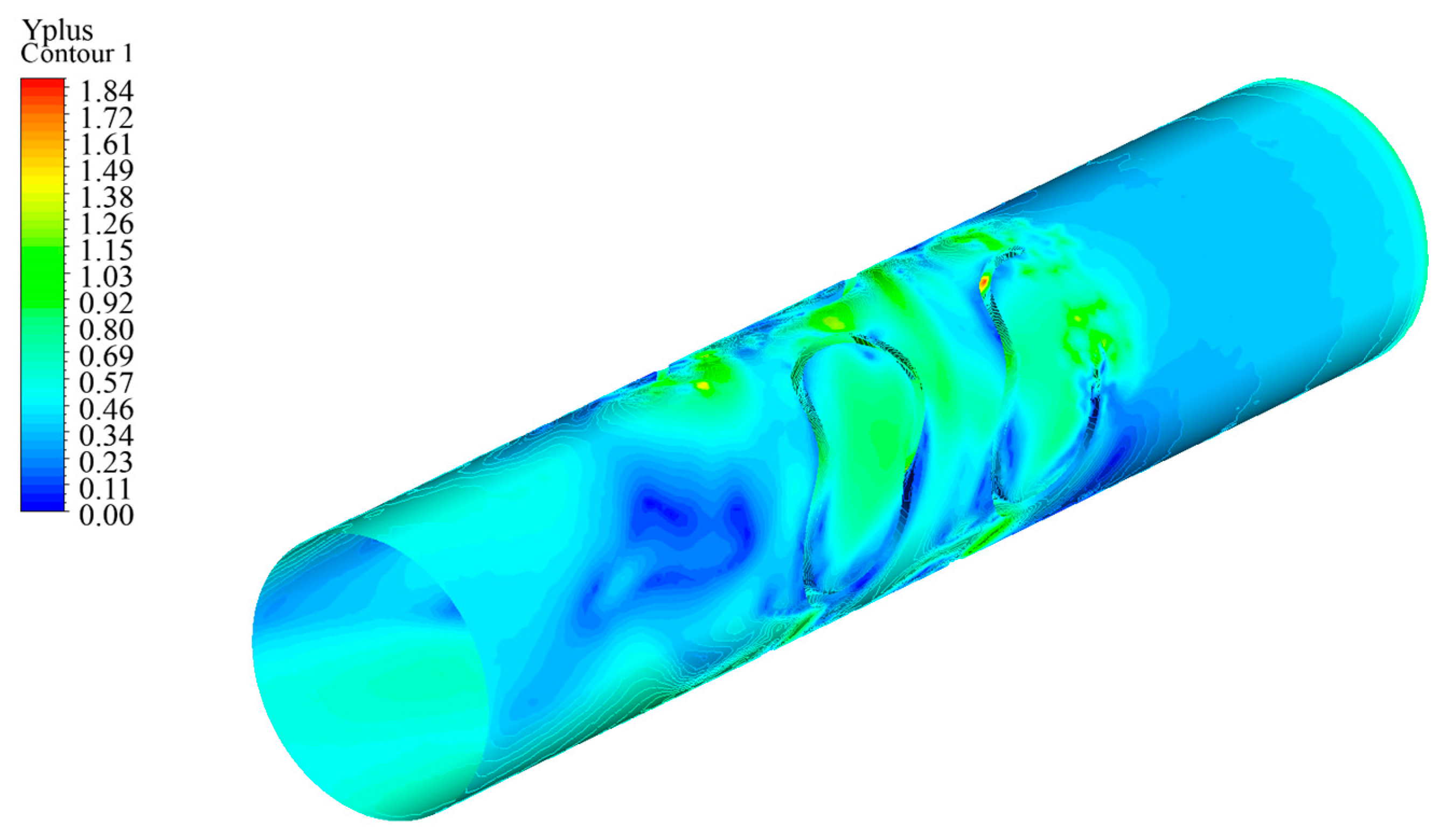
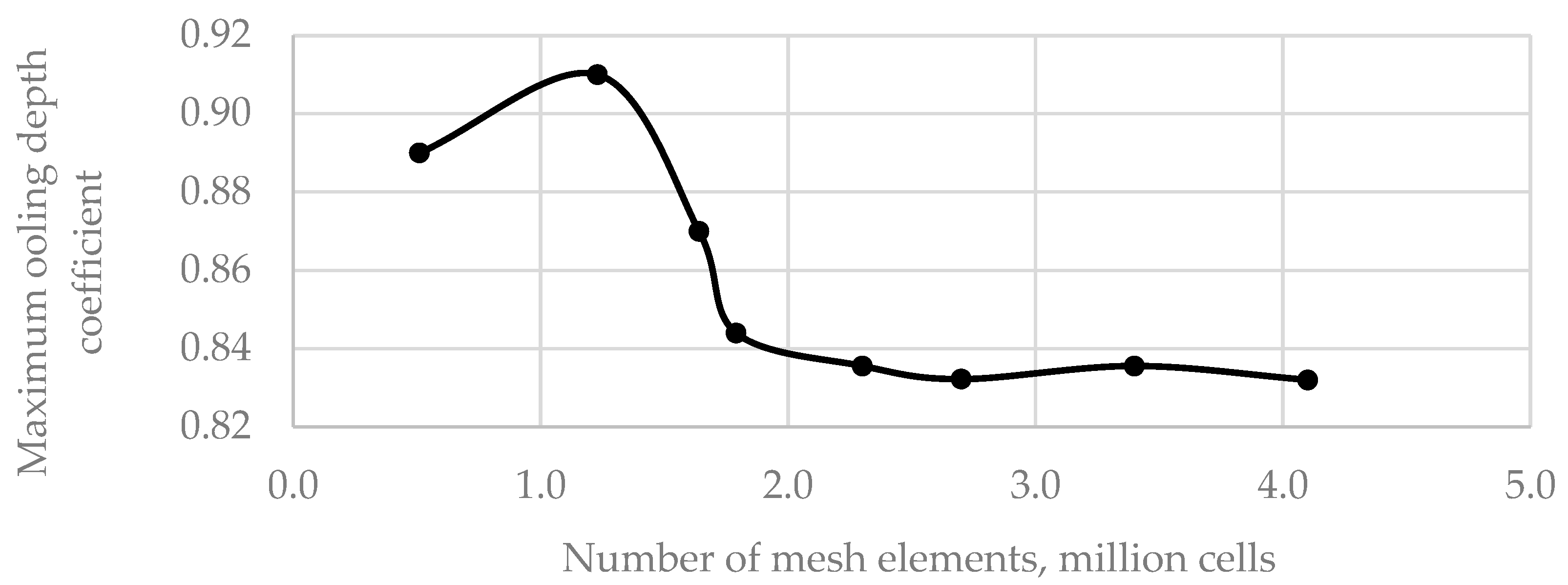
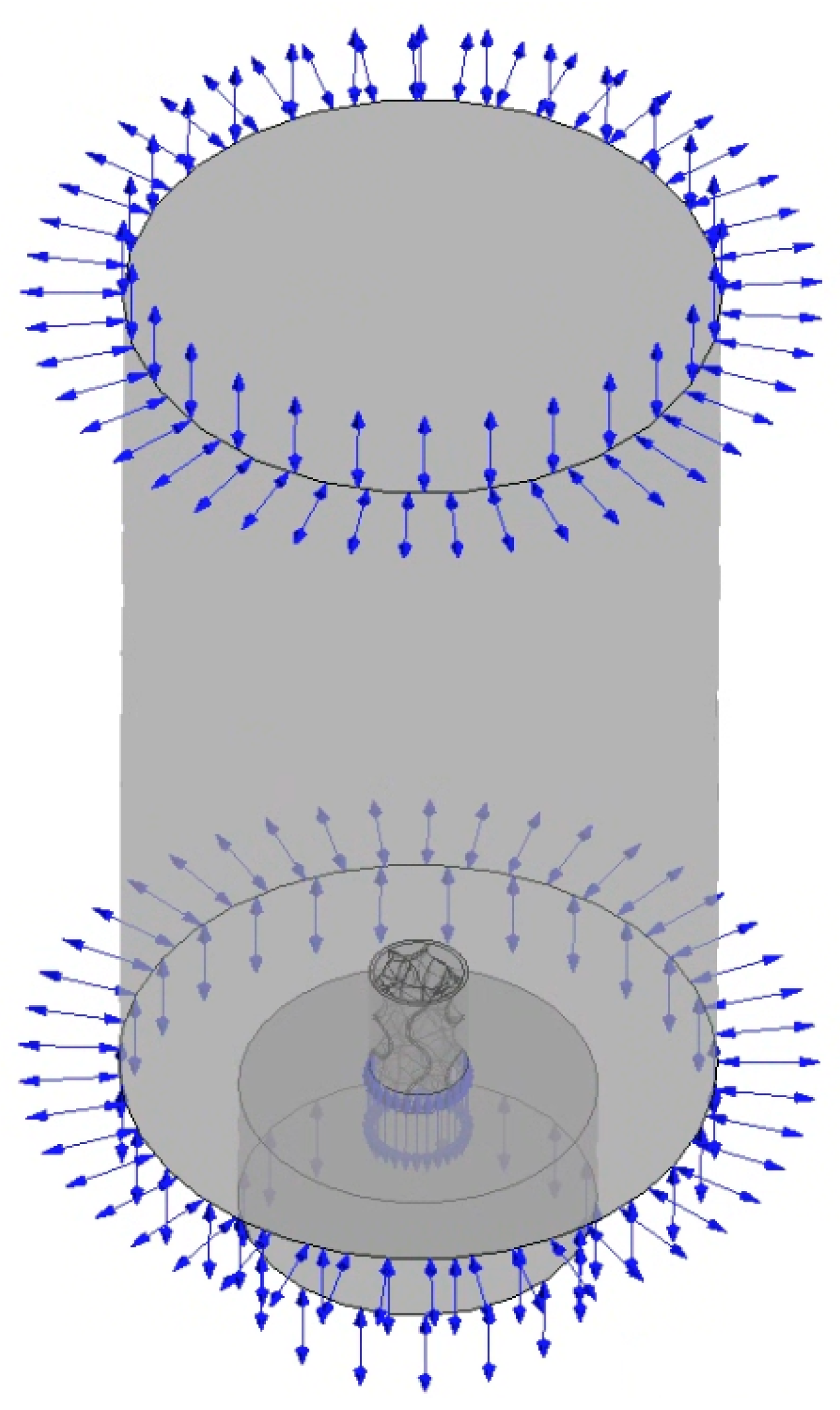
2.1. Numerical Simulation
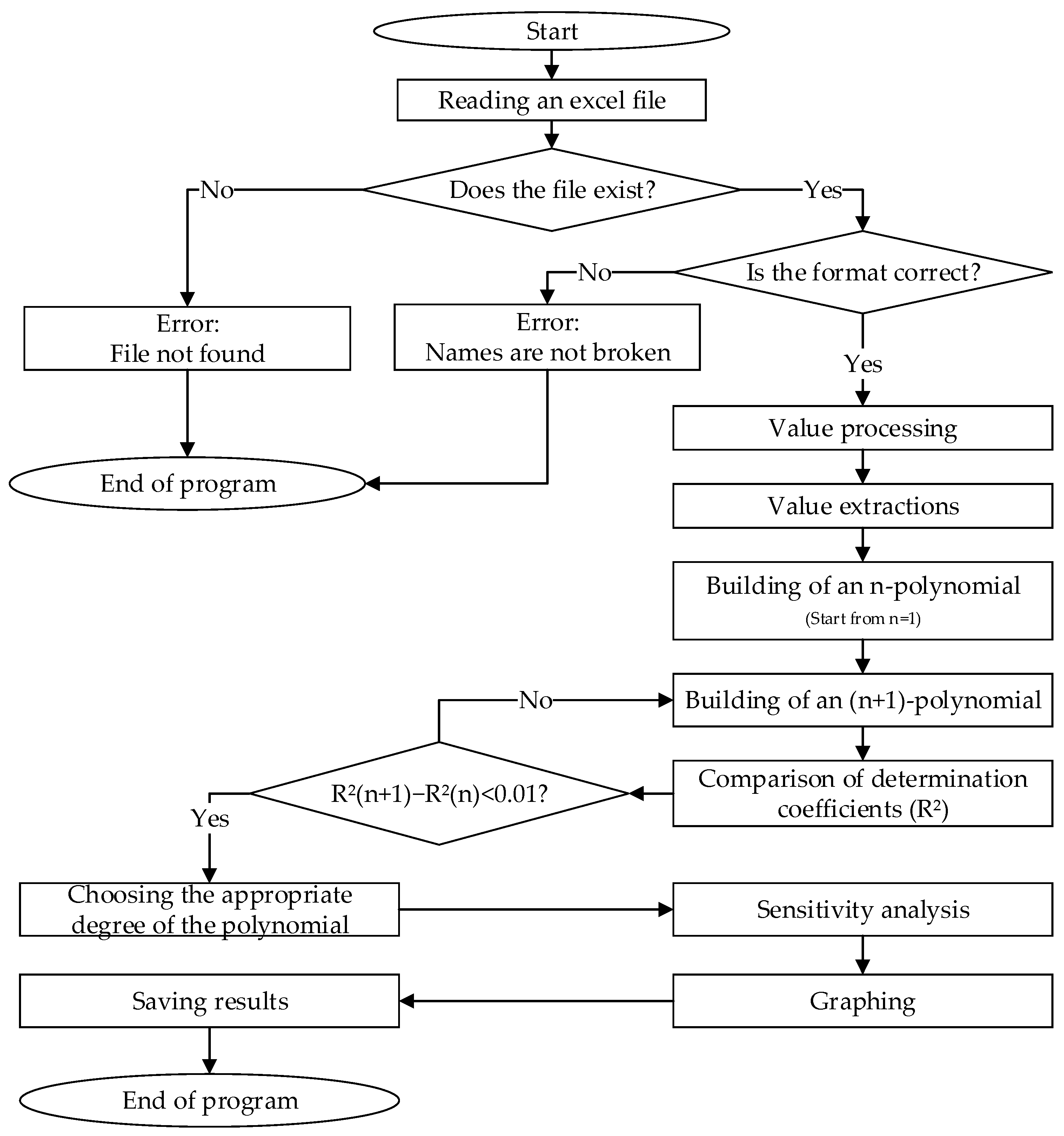
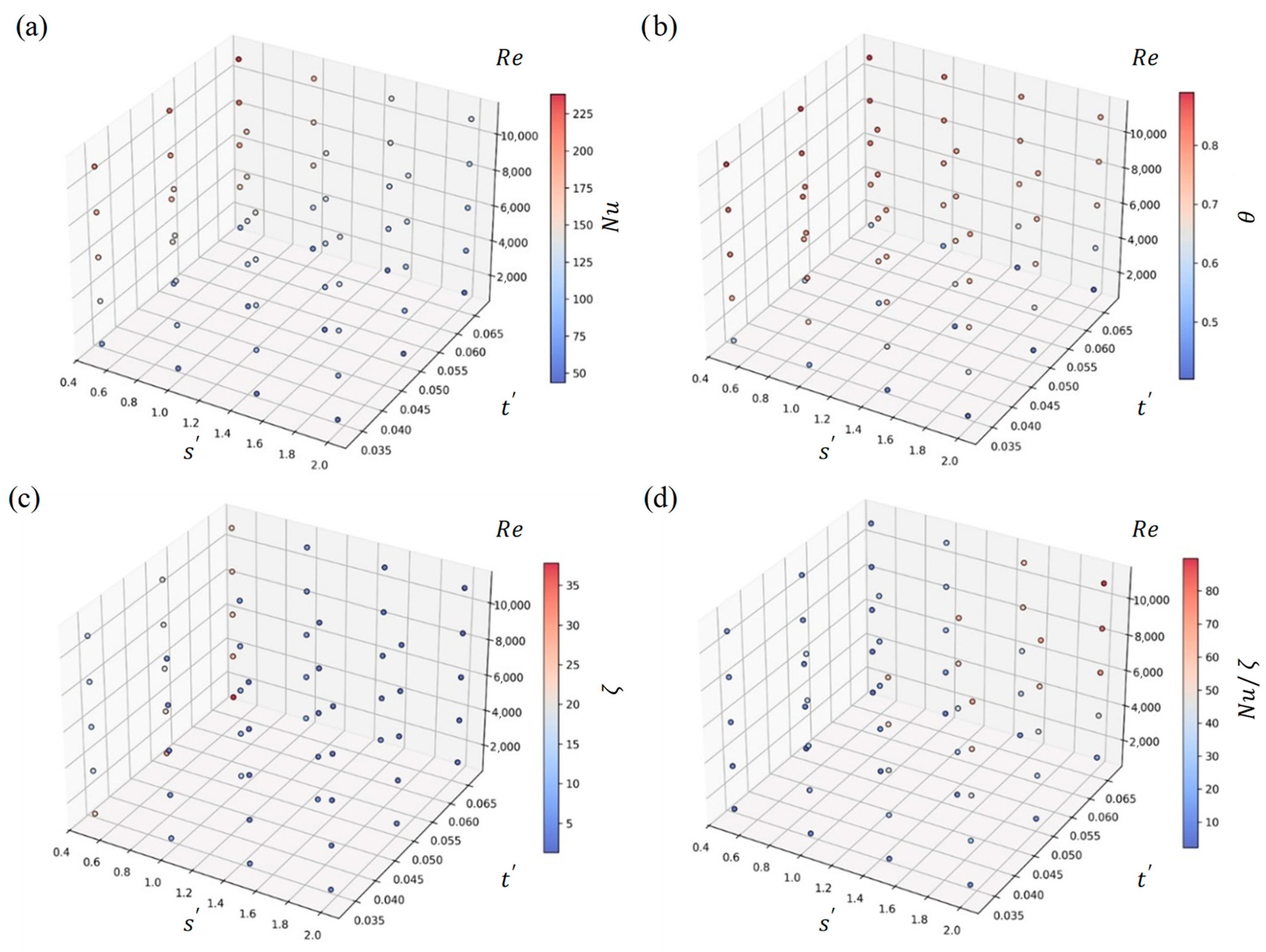
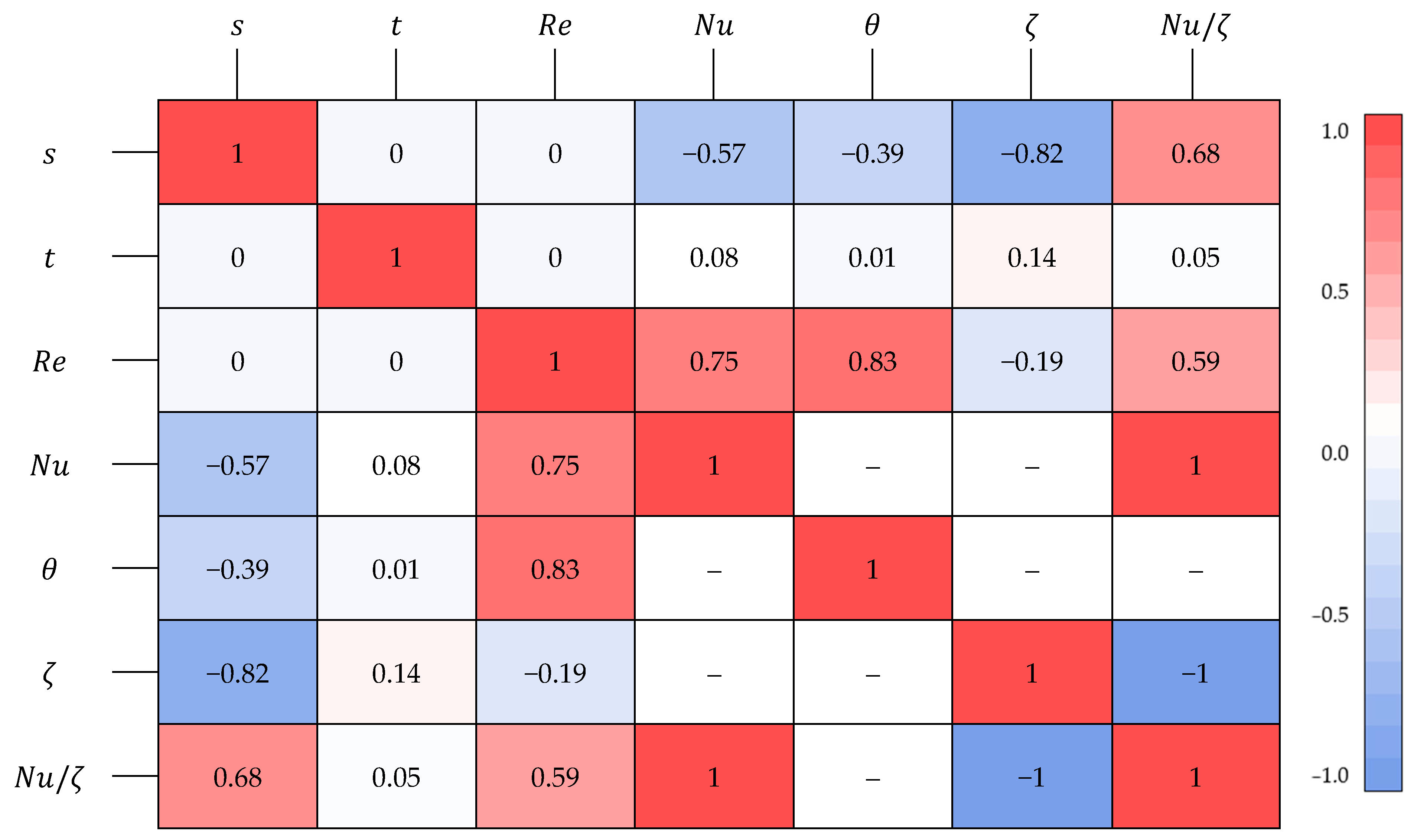
2.2. Analysis of the Influence of Geometric and Flow Parameters on Objective Functions
- Formation of the observation matrix. At this stage, the initial matrix is constructed from the dataset of flow regime parameters obtained during the three-dimensional CFD simulation. The final matrix has the following structure: the first column represents the intercept term of the matrix, and the second column contains the values of the dependent parameter.
- Formation of the response vector. At this stage, a matrix is constructed representing the values of the objective functions in the order in which they were computed. The resulting matrix has the following form: a single column containing the values of the objective functions.
- Transposition of the observation matrix. Matrix transposition is the process by which the rows of a matrix are converted into columns, and the columns into rows. The formation of the transposed matrix is a necessary step in the computation of the inverse matrix.
- Matrix multiplication. This step involves multiplying the observation matrix by its transposed counterpart. The resulting product provides important insights into the relationships between the variables.
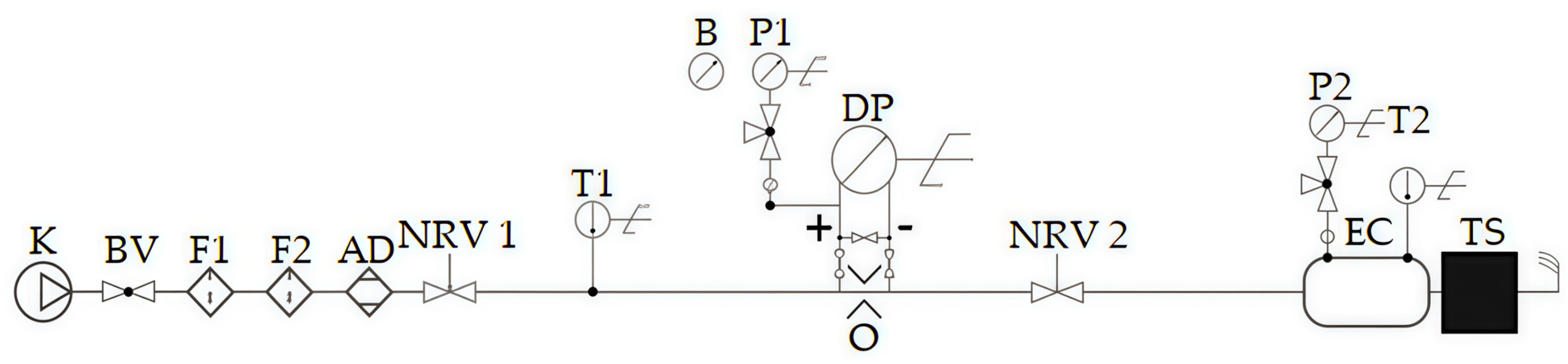
2.3. Experimental Hydraulic Investigation
2.4. Analysis of Experimental Investigation Results
2.5. Validation of Results Using Model Conditions and the Theory of Geometric and Dynamic Similarity
3. Results and Discussion
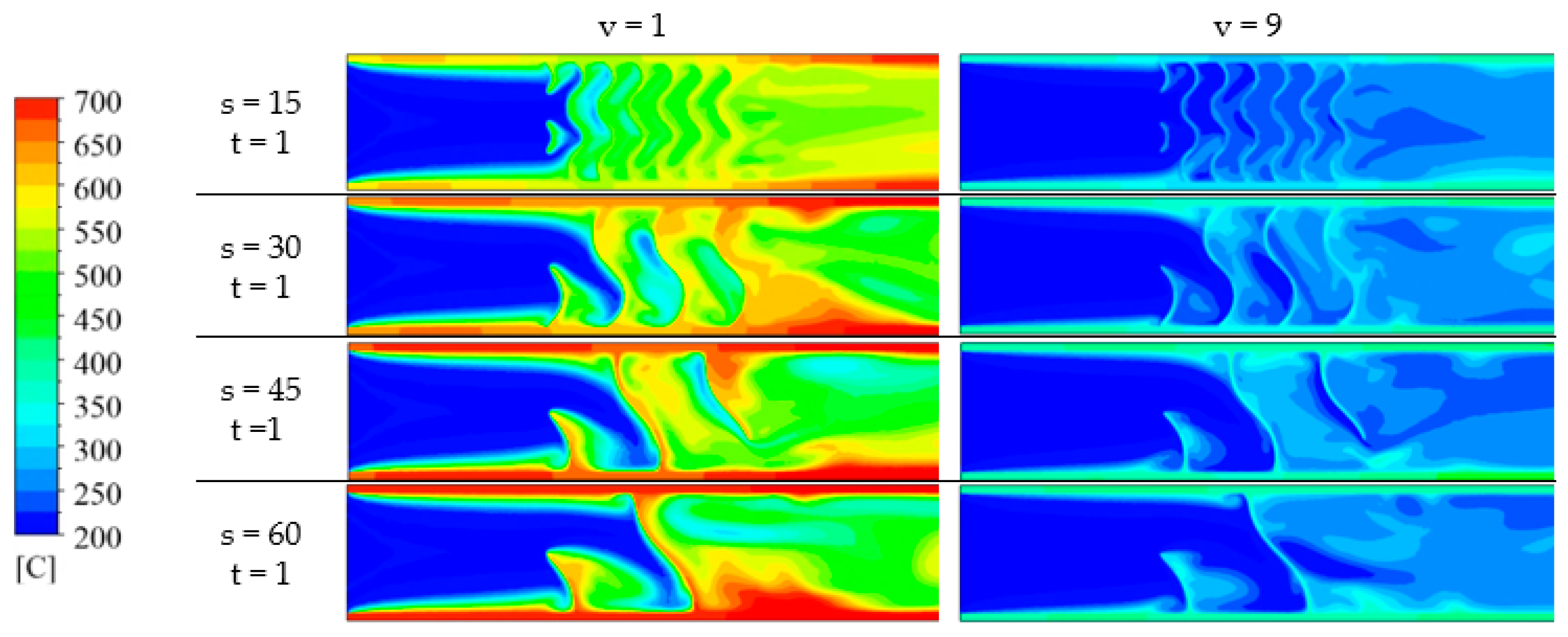
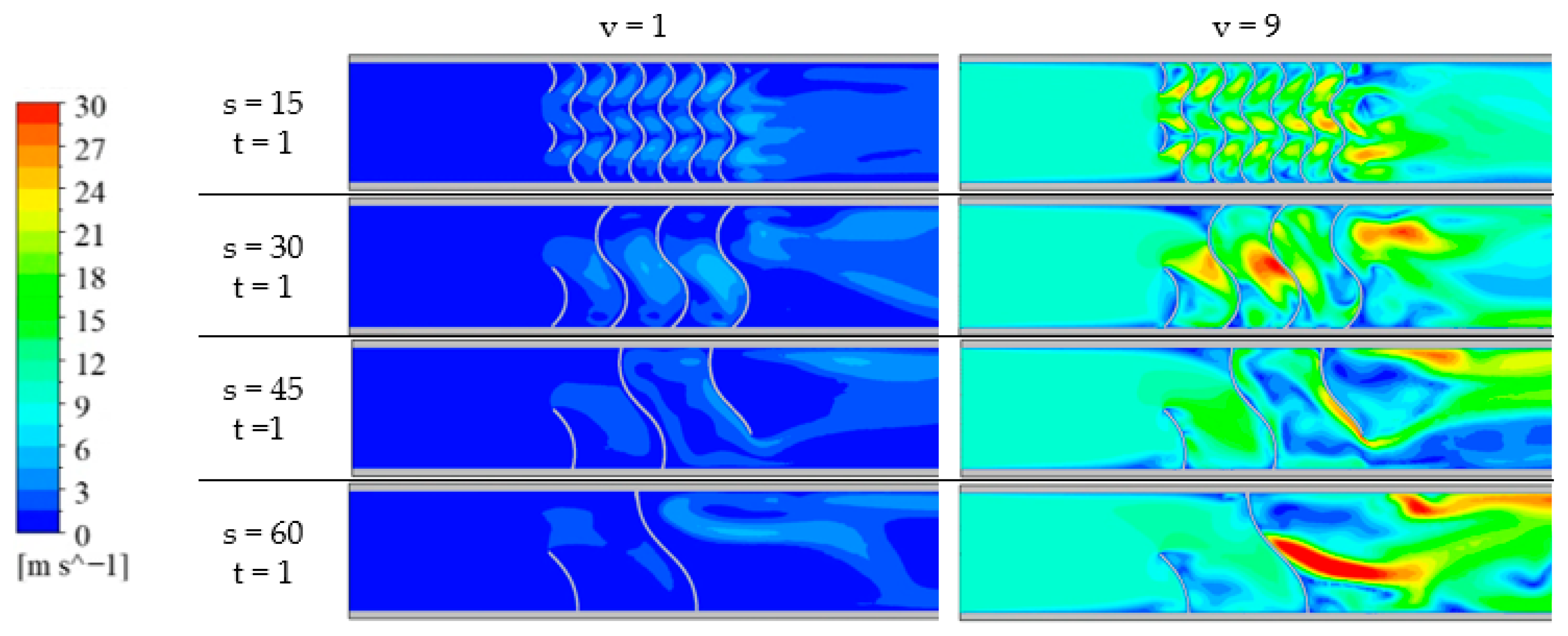
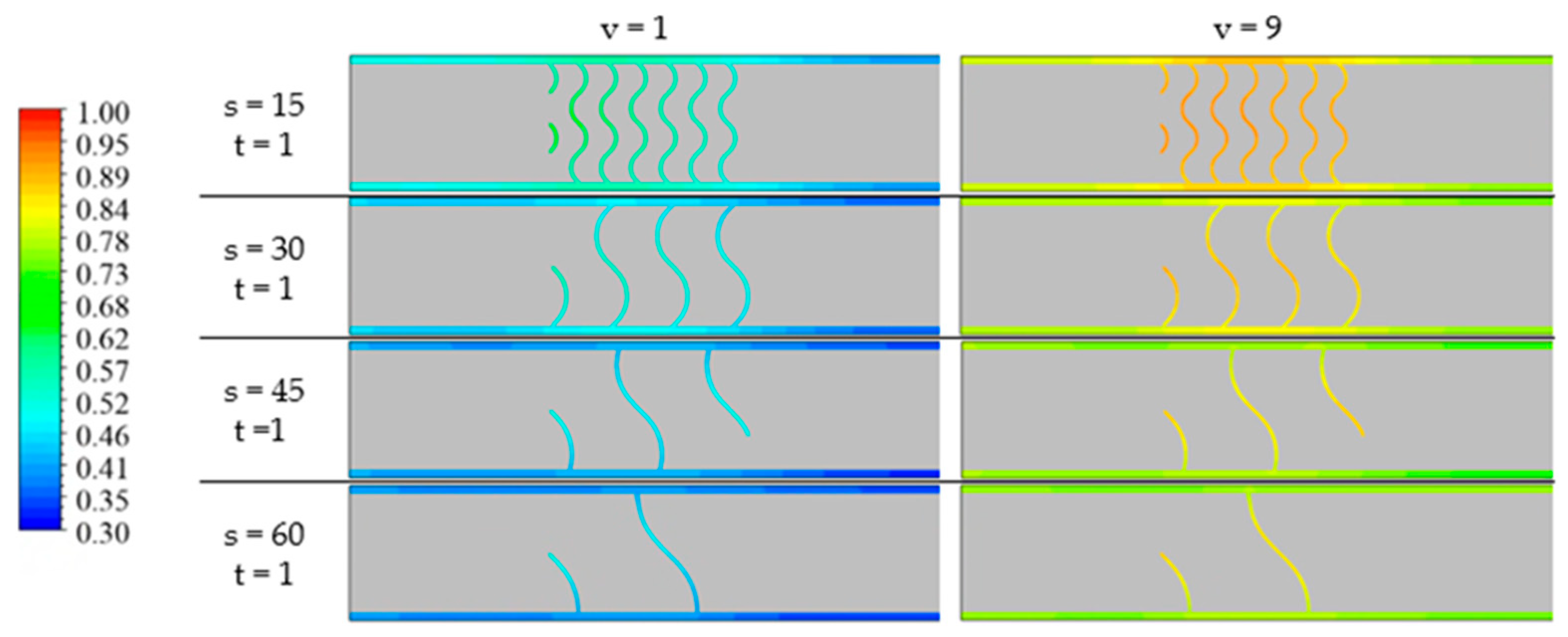
3.1. Results of Numerical Simulation
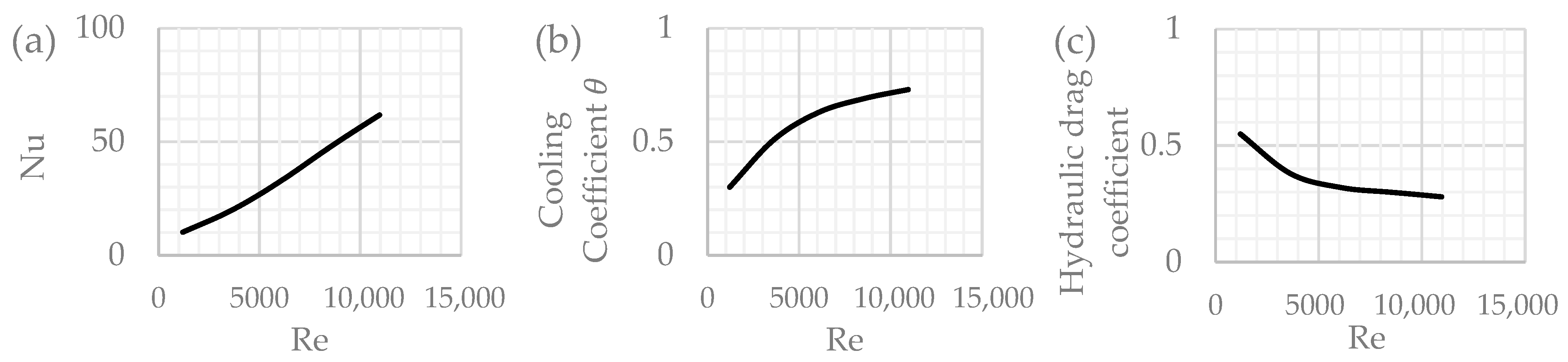
3.2. Results of the Influence of Geometric and Flow Parameters on Objective Functions
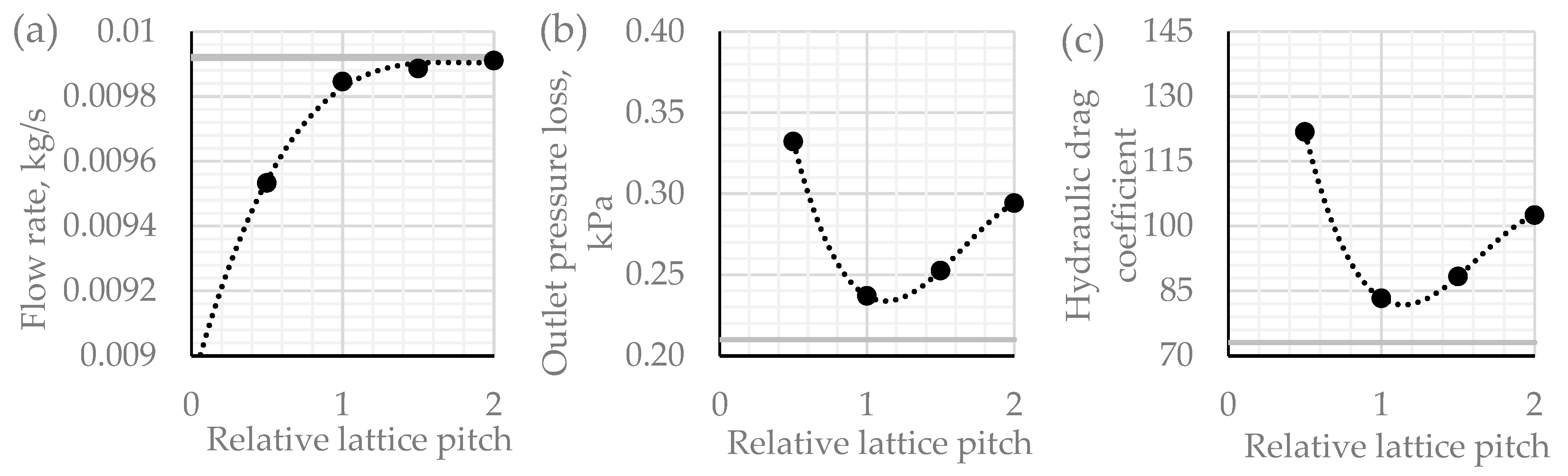
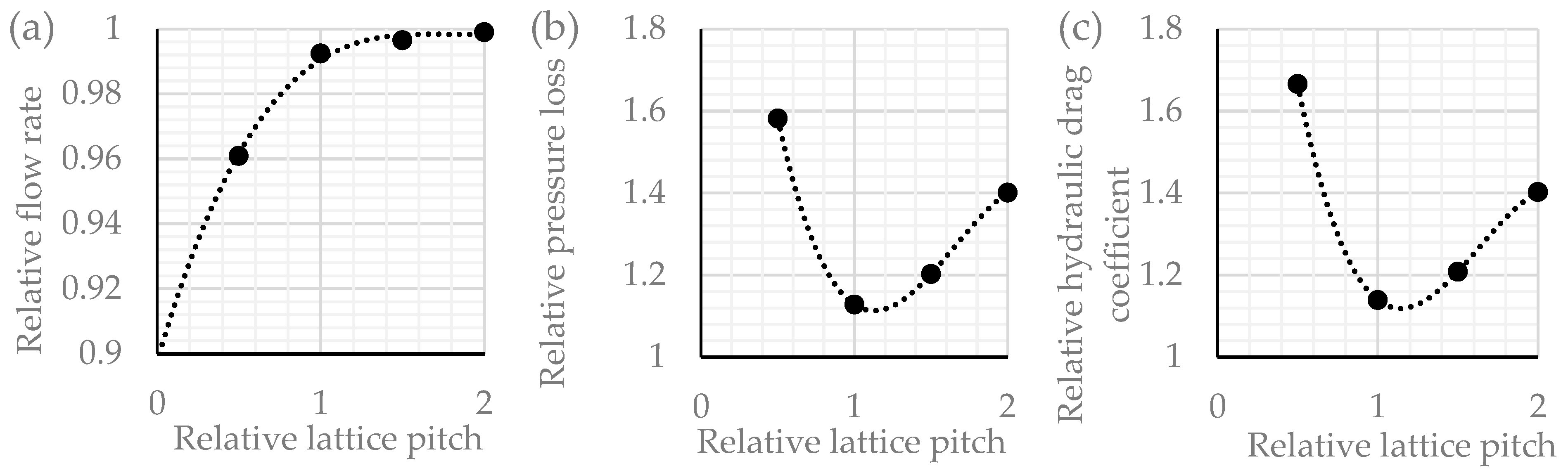
3.3. Results of the Experimental Hydraulic Investigation
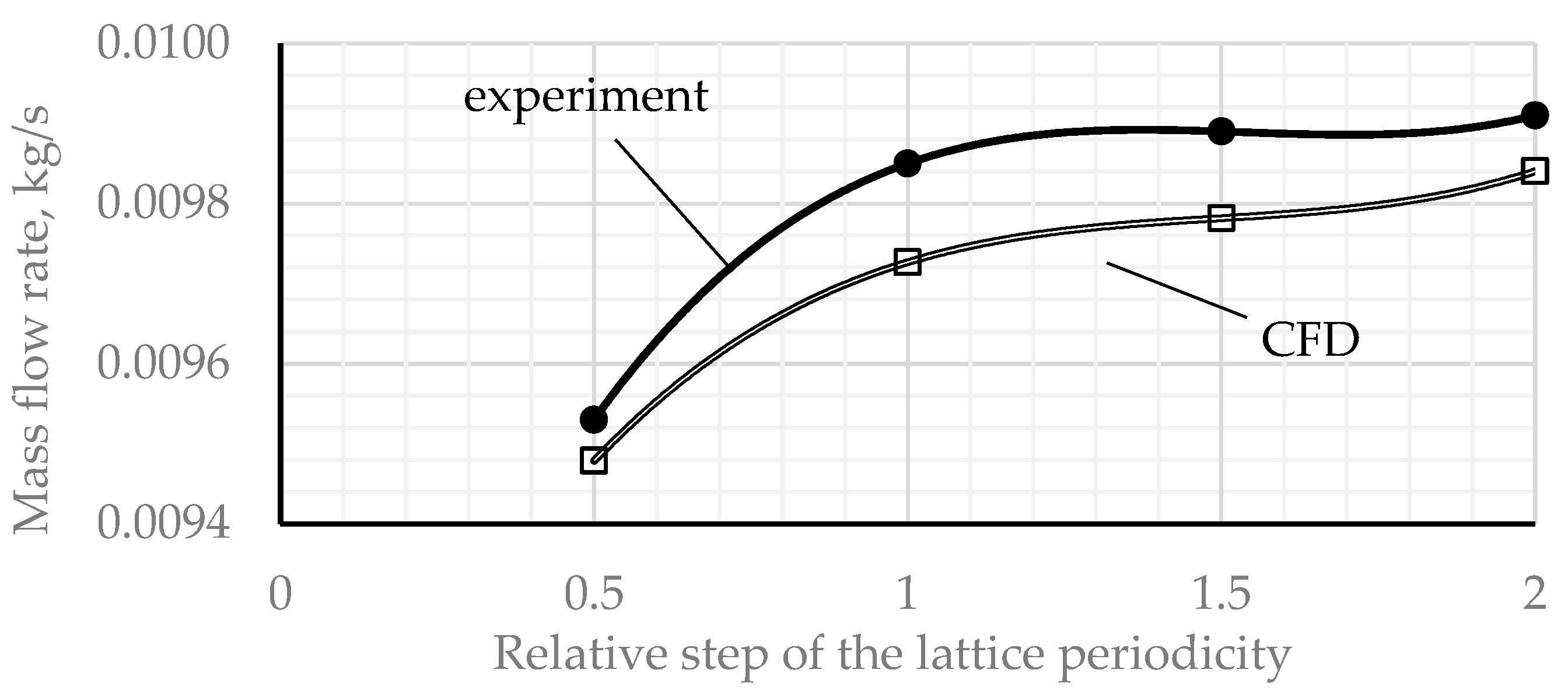
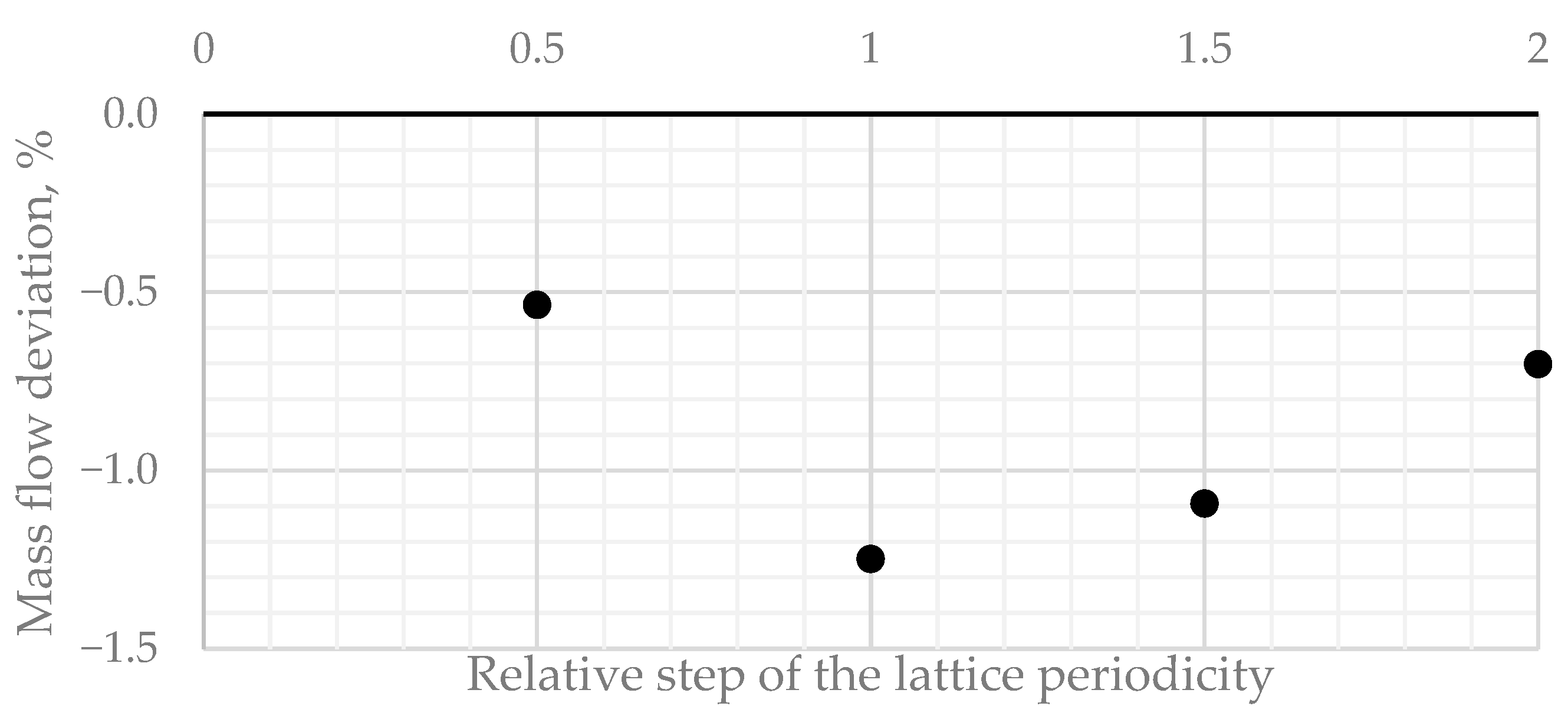
3.4. Results of Calculations Under Model Conditions of the Experimental Stand
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Takeishi, K. Evolution of Turbine Cooled Vanes and Blades Applied for Large Industrial Gas Turbines and Its Trend toward Carbon Neutrality. Energies 2022, 15, 8935. [Google Scholar] [CrossRef]
- Invernizzi, C.M.; Di Marcoberardino, G. An Overview of Real Gas Brayton Power Cycles: Working Fluids Selection and Thermodynamic Implications. Energies 2023, 16, 3989. [Google Scholar] [CrossRef]
- Xu, L.; Sun, Z.; Ruan, Q.; Xi, L.; Gao, J.; Li, Y. Development Trend of Cooling Technology for Turbine Blades at Super-High Temperature of above 2000 K. Energies 2023, 16, 668. [Google Scholar] [CrossRef]
- Chang, S.W.; Wu, P.-S.; Wan, T.-Y.; Cai, W.-L. A Review of Cooling Studies on Gas Turbine Rotor Blades with Rotation. Inventions 2023, 8, 21. [Google Scholar] [CrossRef]
- Zhu, S.; Li, Y.; Yan, J.; Zhang, C. Recent Advances in Cooling Technology for the Leading Edge of Gas Turbine Blades. Energies 2025, 18, 540. [Google Scholar] [CrossRef]
- Wee, S.; Do, J.; Kim, K.; Lee, C.; Seok, C.; Choi, B.-G.; Choi, Y.; Kim, W. Review on Mechanical Thermal Properties of Superalloys and Thermal Barrier Coating Used in Gas Turbines. Appl. Sci. 2020, 10, 5476. [Google Scholar] [CrossRef]
- Guo, X.; Li, X.; Ren, J. Evolution of Rotating Internal Channel for Heat Transfer Enhancement in a Gas Turbine Blade. Aerospace 2024, 11, 836. [Google Scholar] [CrossRef]
- Xu, L.; Bo, S.; Hongde, Y.; Lei, W. Evolution of Rolls-Royce Air-Cooled Turbine Blades and Feature Analysis. Procedia Eng. 2015, 99, 1482–1491. [Google Scholar] [CrossRef]
- Shuai, L.; Qingsong, W.; Zhang, D.; Kai, C.C. Microstructures and Texture of Inconel 718 Alloy Fabricated by Selective Laser Melting. In Proceedings of the 1st International Conference on Progress in Additive Manufacturing, Singapore, 17–19 May 2016. [Google Scholar] [CrossRef]
- Raju, R.; Duraiselvam, M.; Arun, G.; Petley, V.; Shweta, R.; Rajendran, R. Mechanical and Metallurgical Characterization of Laser Metal Deposited Aero-Engine Blade Materials; Tampere University of Technology: Tampere, Finland, 2014. [Google Scholar]
- Wang, W.; Yan, Y.; Zhou, Y.; Cui, J. Review of Advanced Effusive Cooling for Gas Turbine Blades. Energies 2022, 15, 8568. [Google Scholar] [CrossRef]
- Yang, H.; Shan, Z.; Wu, R.; Yan, D.; Shi, J.; Huang, J.; Shi, H.; Dong, S.; Fang, X.; Hu, T. Research Progress on Additive Manufacturing Technology and Equipment for the Vat Polymerization of Ceramic Cores of Aeroengine Blades. Addit. Manuf. Front. 2025, 4, 200204. [Google Scholar] [CrossRef]
- Yeranee, K.; Rao, Y. A Review of Recent Research on Flow and Heat Transfer Analysis in Additively Manufactured Transpiration Cooling for Gas Turbines. Energies 2025, 18, 3282. [Google Scholar] [CrossRef]
- Huang, G.; Zhu, Y.; Liao, Z.; Xu, R.; Jiang, P.-X. Biomimetic Self-Pumping Transpiration Cooling for Additive Manufactured Porous Module with Tree-like Micro-Channel. Int. J. Heat Mass Transf. 2019, 131, 403–410. [Google Scholar] [CrossRef]
- Du Plessis, A.; Broeckhoven, C.; Yadroitsava, I.; Yadroitsev, I.; Hands, C.H.; Kunju, R.; Bhate, D. Beautiful and Functional: A Review of Biomimetic Design in Additive Manufacturing. Addit. Manuf. 2019, 27, 408–427. [Google Scholar] [CrossRef]
- Gad-el-Hak, I. Fluid–Structure Interaction for Biomimetic Design of an Innovative Lightweight Turboexpander. Biomimetics 2019, 4, 27. [Google Scholar] [CrossRef]
- Li, J.; Li, M.; Koh, J.J.; Wang, J.; Lyu, Z. 3D-Printed Biomimetic Structures for Energy and Environmental Applications. DeCarbon 2024, 3, 100026. [Google Scholar] [CrossRef]
- Ren, F.; Zhang, C.; Liao, W.; Liu, T.; Li, D.; Shi, X.; Jiang, W.; Wang, C.; Qi, J.; Chen, Y. Transition Boundaries and Stiffness Optimal Design for Multi-TPMS Lattices. Mater. Des. 2021, 210, 110062. [Google Scholar] [CrossRef]
- Hussain, S.; Ghopa, W.A.W.; Singh, S.; Azman, A.H.; Abdullah, S. Experimental and Numerical Vibration Analysis of Octet-Truss-Lattice-Based Gas Turbine Blades. Metals 2022, 12, 340. [Google Scholar] [CrossRef]
- Ligrani, P. Heat Transfer Augmentation Technologies for Internal Cooling of Turbine Components of Gas Turbine Engines. Int. J. Rotating Mach. 2013, 2013, 275653. [Google Scholar] [CrossRef]
- Zhang, G.; Rui, Z.; Gongnan, X.; Shulei, L.; Sunden, B. Optimization of Cooling Structures in Gas Turbines: A Review. Chin. J. Aeronaut. 2022, 35, 18–46. [Google Scholar] [CrossRef]
- Yeranee, K.; Xu, C.; Rao, Y.; Chen, J.; Zhang, Y. Rotating Flow and Heat Transfer Characteristics of a Novel Cooling Channel for Gas Turbine Blade Trailing Edge with Diamond-Type TPMS Structures. ASME J. Heat Mass Transf. 2024, 146, 051002. [Google Scholar] [CrossRef]
- Yeranee, K.; Rao, Y.; Xu, C.; Zhang, Y.; Su, X. Turbulent Flow Heat Transfer and Thermal Stress Improvement of Gas Turbine Blade Trailing Edge Cooling with Diamond-Type TPMS Structure. Aerospace 2023, 11, 37. [Google Scholar] [CrossRef]
- Patil, A.Y.; Hegde, C.; Savanur, G.; Kanakmood, S.M.; Contractor, A.M.; Shirashyad, V.B.; Chivate, R.M.; Kotturshettar, B.B.; Mathad, S.N.; Patil, M.B. Biomimicking Nature-Inspired Design Structures—An Experimental and Simulation Approach Using Additive Manufacturing. Biomimetics 2022, 7, 186. [Google Scholar] [CrossRef] [PubMed]
- Olivas-Alanis, L.H.; Fraga-Martínez, A.A.; García-López, E.; Lopez-Botello, O.; Vazquez-Lepe, E.; Cuan-Urquizo, E.; Rodriguez, C.A. Mechanical Properties of AISI 316L Lattice Structures via Laser Powder Bed Fusion as a Function of Unit Cell Features. Materials 2023, 16, 1025. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, C.; Liu, W.; Liu, Z.; Bian, H.; Zhang, K. Advances in Triply Periodic Minimal Surface Structures for Thermal Management Systems: A Comprehensive Review. Appl. Therm. Eng. 2025, 279, 127481. [Google Scholar] [CrossRef]
- Pulin, A.; Laptev, M.; Alisov, K.; Barskov, V.; Rassokhin, V.; Gong, B.; Kotov, V.; Roshchenko, G.; Balakin, A.; Golubtsov, M. Heat Exchanger and the Influence of Lattice Structures on Its Strength. Mater. Phys. Mech. 2024, 52, 61–80. [Google Scholar] [CrossRef]
- Pulin, A.; Laptev, M.; Kortikov, N.; Barskov, V.; Roschenko, G.; Alisov, K.; Talabira, I.; Gong, B.; Rassokhin, V.; Popovich, A. Numerical Investigation of Heat Transfer Intensification Using Lattice Structures in Heat Exchangers. Energies 2024, 17, 3333. [Google Scholar] [CrossRef]
- Yeranee, K.; Rao, Y. A Review of Recent Investigations on Flow and Heat Transfer Enhancement in Cooling Channels Embedded with Triply Periodic Minimal Surfaces (TPMS). Energies 2022, 15, 8994. [Google Scholar] [CrossRef]
- Svoboda, D.G.; Zharkovskii, A.A.; Ivanov, E.A. Gidrodinamicheskoe Modelirovanie Techenii v Protochnoi Chasti Lopastnykh Nasosov s Ispol’zovaniem Programmnogo Paketa Ansys Fluent: Uchebnoe Posobie; SPbPU Press: St. Petersburg, Russia, 2022. (In Russian) [Google Scholar]
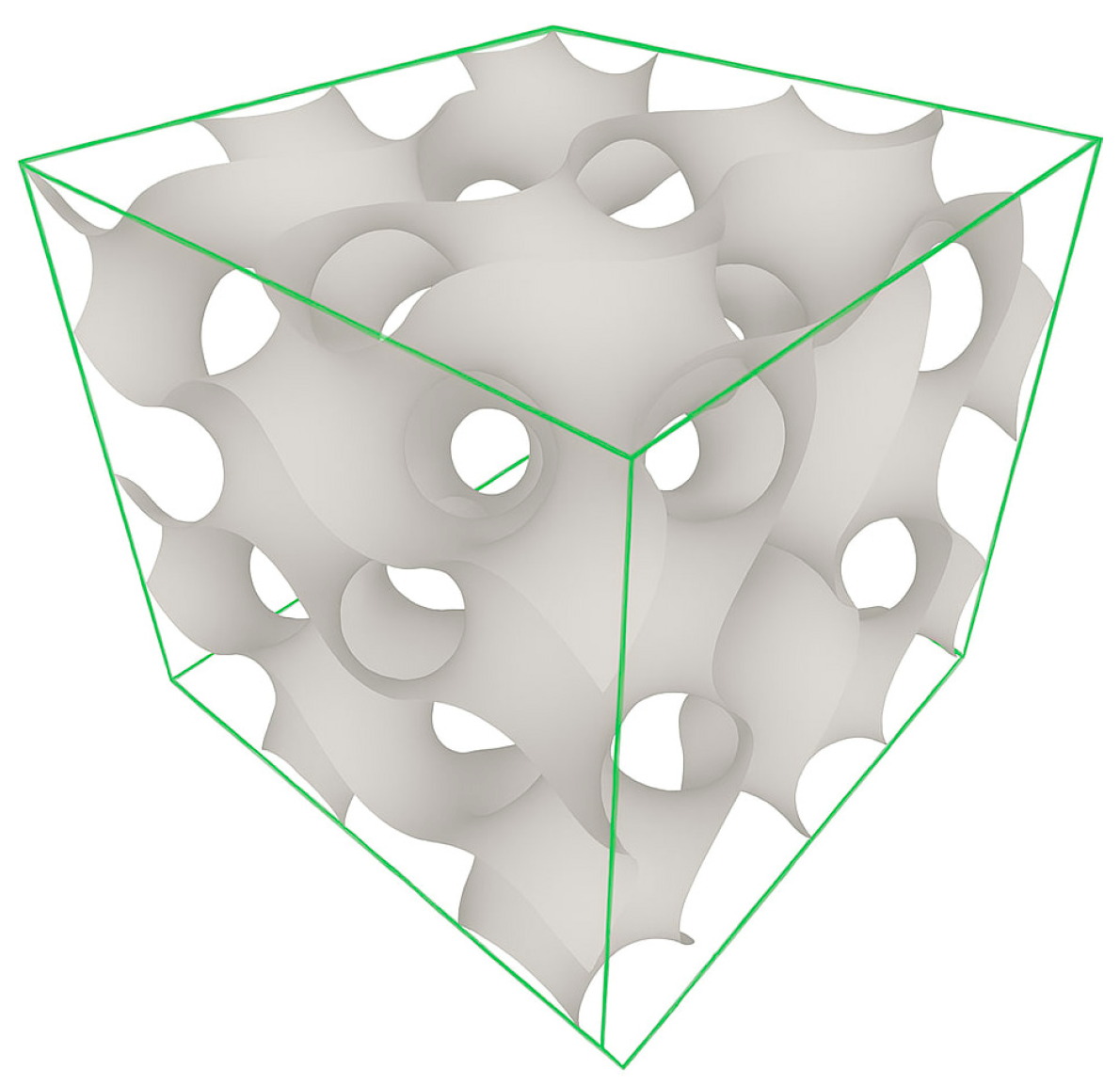





| Thickness, mm | Lattice Structure Periodicity, mm | |||
|---|---|---|---|---|
| 15 | 30 | 45 | 60 | |
| 1.0 |  |  |  |  |
| 1.5 |  |  |  |  |
| 2.0 |  |  |  |  |
| Parameter | Notation | Unit of Measurement | Value |
|---|---|---|---|
| Inlet coolant velocity | ν | 1–9 | |
| Inlet coolant temperature | °C | 200 | |
| Wall heater temperature | °C | 1000 | |
| Outlet pressure | atm. | 1 |
| Turbulizer | The Value of Nusselt Number | The Value of the Depth Coefficient of Cooling θ | The Value of the Coefficient of Hydraulic Resistance ζ | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Reynolds Number at Inlet | |||||||||||||||
| 1200 | 3635 | 6080 | 8540 | 11,000 | 1200 | 3635 | 6080 | 8540 | 11,000 | 1200 | 3635 | 6080 | 8540 | 11,000 | |
| Gyroid = 0.5; t = 1.0 mm | 76.85 | 139.61 | 169.83 | 191.04 | 208.96 | 0.570 | 0.771 | 0.831 | 0.861 | 0.882 | 23.16 | 16.24 | 14.67 | 14.53 | 14.57 |
| Gyroid = 0.5; t = 1.5 mm | 81.03 | 149.49 | 181.00 | 203.29 | 222.85 | 0.580 | 0.781 | 0.840 | 0.869 | 0.888 | 28.96 | 21.81 | 20.07 | 19.33 | 19.05 |
| Gyroid = 0.5; t = 2.0 mm | 84.46 | 159.05 | 192.76 | 217.12 | 238.31 | 0.580 | 0.780 | 0.840 | 0.870 | 0.890 | 37.80 | 27.47 | 24.81 | 23.76 | 23.88 |
| Gyroid = 1.0; t = 1.0 mm | 57.97 | 108.33 | 128.61 | 145.65 | 157.21 | 0.488 | 0.700 | 0.772 | 0.808 | 0.831 | 8.23 | 5.37 | 4.57 | 4.42 | 4.40 |
| Gyroid = 1.0; t = 1.5 mm | 63.10 | 109.71 | 132.00 | 152.13 | 166.90 | 0.534 | 0.723 | 0.783 | 0.82 | 0.838 | 13.37 | 8.93 | 7.63 | 7.43 | 6.13 |
| Gyroid = 1.0; t = 2.0 mm | 61.05 | 119.98 | 152.59 | 164.09 | 182.12 | 0.489 | 0.717 | 0.785 | 0.819 | 0.844 | 9.81 | 7.71 | 6.31 | 6.03 | 6.31 |
| Gyroid = 1.5; t = 1.0 mm | 46.95 | 88.09 | 110.63 | 126.82 | 139.78 | 0.425 | 0.637 | 0.718 | 0.760 | 0.787 | 4.82 | 3.27 | 2.68 | 2.34 | 2.24 |
| Gyroid = 1.5; t = 1.5 mm | 49.16 | 92.15 | 114.1 | 129.72 | 142.73 | 0.428 | 0.643 | 0.723 | 0.765 | 0.791 | 5.02 | 3.39 | 2.75 | 2.37 | 2.23 |
| Gyroid = 1.5; t = 2.0 mm | 51.47 | 94.32 | 116.72 | 132.76 | 145.43 | 0.435 | 0.645 | 0.724 | 0.766 | 0.794 | 5.09 | 3.28 | 2.87 | 2.4 | 2.32 |
| Gyroid = 2.0; t = 1.0 mm | 43.58 | 83.76 | 104.87 | 121.06 | 132.59 | 0.407 | 0.635 | 0.716 | 0.756 | 0.782 | 4.36 | 3.01 | 2.44 | 2.06 | 1.88 |
| Gyroid = 2.0; t = 1.5 mm | 44.92 | 83.65 | 101.98 | 115.33 | 125.76 | 0.417 | 0.629 | 0.707 | 0.749 | 0.774 | 3.79 | 2.84 | 2.35 | 2.01 | 1.81 |
| Gyroid = 2.0; t = 2.0 mm | 43.65 | 77.91 | 95.35 | 110.7 | 123.93 | 0.403 | 0.609 | 0.694 | 0.737 | 0.766 | 2.99 | 1.75 | 1.30 | 1.36 | 1.38 |
| Typical ribs | 21.54 | 43.73 | 50.32 | 64.77 | 77.4 | 0.341 | 0.572 | 0.670 | 0.710 | 0.739 | 1.46 | 0.94 | 0.73 | 0.71 | 0.69 |
| Typical pins | 28.34 | 44.96 | 51.05 | 66.10 | 79.94 | 0.370 | 0.621 | 0.727 | 0.751 | 0.780 | 1.77 | 1.63 | 1.61 | 1.58 | 1.48 |
| Smooth channel | 10.20 | 19.86 | 32.79 | 47.77 | 61.85 | 0.550 | 0.379 | 0.321 | 0.303 | 0.279 | 0.55 | 0.38 | 0.32 | 0.30 | 0.20 |
| Air Density | DP Pressure | Air Flow Rate | Temperature T1 | Temperature T2 | Pressure P1 | Pressure P2 | |
|---|---|---|---|---|---|---|---|
| – | kPa | °C | °C | kPa | kPa | ||
| 0.5 | 2.0837 | 22.2075 | 0.00953 | 27.06 | 21.76 | 78.476 | 0.3322 |
| 1 | 2.1316 | 23.1356 | 0.00985 | 27.51 | 22.08 | 82.666 | 0.2370 |
| 1.5 | 2.1374 | 23.2597 | 0.00989 | 27.70 | 22.25 | 83.186 | 0.2526 |
| 2 | 2.1409 | 23.3509 | 0.00991 | 27.69 | 22.33 | 83.562 | 0.2942 |
| Smooth | 2.1429 | 23.3826 | 0.00992 | 27.74 | 22.42 | 83.671 | 0.2100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pulin, A.; Talabira, I.; Konin, D.; Alisov, K.; Kanakin, M.; Laptev, M.; Komlev, E.; Barskov, V.; Popovich, A.; Starikov, K. Investigation of the Influence of Gyroid Lattice Dimensions on Cooling. Energies 2025, 18, 4552. https://doi.org/10.3390/en18174552
Pulin A, Talabira I, Konin D, Alisov K, Kanakin M, Laptev M, Komlev E, Barskov V, Popovich A, Starikov K. Investigation of the Influence of Gyroid Lattice Dimensions on Cooling. Energies. 2025; 18(17):4552. https://doi.org/10.3390/en18174552
Chicago/Turabian StylePulin, Anton, Ivan Talabira, Denis Konin, Kirill Alisov, Mikhail Kanakin, Mikhail Laptev, Evgenii Komlev, Viktor Barskov, Anatoliy Popovich, and Kirill Starikov. 2025. "Investigation of the Influence of Gyroid Lattice Dimensions on Cooling" Energies 18, no. 17: 4552. https://doi.org/10.3390/en18174552
APA StylePulin, A., Talabira, I., Konin, D., Alisov, K., Kanakin, M., Laptev, M., Komlev, E., Barskov, V., Popovich, A., & Starikov, K. (2025). Investigation of the Influence of Gyroid Lattice Dimensions on Cooling. Energies, 18(17), 4552. https://doi.org/10.3390/en18174552






