Optimization Scheduling Strategy for Coal Railway Integrated Energy Systems

Abstract

This paper proposes an optimal scheduling strategy for coal-dedicated railway integrated energy systems, leveraging coordinated electric boiler and thermal storage operation to enhance economic efficiency, improve wind power integration, and reduce carbon emissions. By decoupling the traditional “heat-led-electricity” constraint of combined heat and power (CHP) units, the approach increases operational flexibility and wind power accommodation capacity. A demand response model further optimizes demand-side dispatchability, while a tiered carbon trading mechanism systematically addresses emission costs. The resulting day-ahead scheduling model minimizes total costs—including electricity procurement, wind curtailment penalties, carbon trading, and maintenance expenses—demonstrating superior performance in case studies: a 12.5% reduction in carbon emissions, 56.8% lower operating costs versus conventional methods, and full (100%) wind power utilization.

1. Introduction

In recent years, the development of new energy has become a critical component in achieving a low-carbon economy [1]. Coal railways, as a vital means of traditional energy transportation, are gradually integrating new energy technologies into their operations, enhancing the overall operational efficiency and environmental performance of the coal railway system [2].

Wind power has undergone rapid growth in China due to its environmental, economic, and sustainability benefits, leading to a continuous expansion of installed wind power capacity [3]. However, the counter-peak nature of wind power generation, coupled with the operation of combined heat and power (CHP) units in a “heat-determined electricity” mode, which prioritizes heat load demands, has resulted in relatively low wind power utilization rates [4,5]. Furthermore, traditional CHP units emit significant amounts of harmful gases during operation, causing adverse environmental impacts [6]. Therefore, improving the utilization rate of wind power is essential to enhance both the economic and environmental performance of coal railway systems.

A substantial amount of research has been dedicated to enhancing wind power consumption, with thermoelectric decoupling emerging as a critical area of focus [7]. For instance, the role of electric boilers in improving the wind power consumption levels of CHP systems has been analyzed and evaluated in [8], aiming to enhance their economic and environmental performance. In [9], the integration of thermal storage devices on the CHP unit side has been shown to improve system wind power consumption levels by decoupling thermoelectric coupling characteristics. Researchers in [10] have explored the use of electric boilers and thermal storage tanks to increase the operational flexibility of CHP units, proposing a linear model for the comprehensive dispatch of integrated energy systems. In [11], a coordinated heating dispatch model for electric boilers and thermal storage devices has been established with the goal of minimizing system operational costs, accompanied by proposed control strategies. The effectiveness of these methods has been validated through comparative case studies. Furthermore, in an integrated cogeneration system comprising CHP units, wind farms, and condensing power plants, the incorporation of electricity and heat storage has successfully achieved thermal and electrical decoupling, enabling the comprehensive dispatch of cogeneration [12].

Recently, researchers have increasingly recognized the importance of demand response in facilitating wind power integration. By fully leveraging the potential of electricity and heat demand, it is possible to significantly enhance wind power consumption. For example, a joint optimization scheduling model has been proposed to integrate load-side time-of-use electricity pricing with cogeneration units equipped with thermal storage [13]. This strategy not only improves the system’s peak-shaving capabilities but also minimizes overall dispatch costs. In [14], an intelligent optimization algorithm has been employed to horizontally shift loads in response to fluctuations in wind power output, achieving effective dispatch of load resources through strategic management of electric thermal loads. In [15], demand elasticity has been incorporated into the system, with further analysis based on the unit commitment model. Simulation results demonstrate that considering demand elasticity can increase wind power utilization and reduce dispatch costs. As summarized in

Table 1. Comparison of integrated energy systems.

Feature	Conventional Methods	Recent Works
Thermoelectric decoupling	None	Electric boiler and TES [8,9,10,11,12]
Demand response (DR)	None	Time-of-use pricing, load shifting [13,14,15]
Wind curtailment mitigation	Limited	CHP flexibility [7,8,9]
Carbon trading mechanism	None	Basic carbon pricing [17,18]
Industrial application	Generic power systems	District heating, microgrids [12,13]

Note: TES = thermal energy storage.

, existing works predominantly focus on thermoelectric decoupling or demand response in isolation while neglecting the integration of carbon trading mechanisms [16] within industrial transportation systems.

In recent years, carbon trading mechanisms have been progressively incorporated into energy dispatch optimization. As seen in some examples shown in

Table 2. Some existing dispatch optimization works.

Reference	Application	Algorithm	Objective	Carbon Trading
Duan et al. [19]	Industrial park	MILP	Operational cost minimization	Stepped trading
Nie et al. [20]	Multi-microgrid	Multi-agent deep RL	Cost + emission minimization	Multi-phase carbon cost
Frison et al. [21]	District heating	Nonlinear MPC	Accommodation maximization	None
Xiong et al. [22]	Port microgrid	Distributed optimization	Operating cost minimization	None
Gao et al. [23]	Integrated energy system	Multi-timescale optimization	Low-carbon dispatch	Stepped trading
Zhang et al. [24]	Power system	Stochastic optimization	Cost + emission minimization	ToU + ladder carbon trading

, existing studies have explored carbon-aware scheduling in steel industrial parks, multi-microgrids, and district heating systems, employing diverse optimization approaches. For instance, Duan et al. implemented a stepped carbon trading mechanism in steel production processes using MILP to minimize operational costs under ToU pricing. Nie et al. developed a multi-agent deep reinforcement learning framework for multi-microgrid coordination, integrating carbon flux tracing and multi-phase carbon cost mechanisms to concurrently reduce operational costs and emissions. Conversely, Frison et al. focused on renewable maximization in district heating via nonlinear MPC, but notably omitted carbon trading considerations. However, critical gaps persist: (1) most studies focus on stationary industrial systems [19,20,21], neglecting mobile transportation scenarios such as ports and railways [22]; (2) only a few implement progressive carbon mechanisms despite their emission reduction efficacy [23,24]; and (3) no work simultaneously integrates thermoelectric decoupling, multi-type demand response, and tiered carbon trading in transportation energy systems.

Based on the aforementioned discussions, this paper extends previous research by incorporating carbon emission rights as a dispatchable resource and introducing a carbon trading system. A day-ahead dispatch strategy is proposed for coal-dedicated railway energy systems, integrating electricity–heat decoupling, demand response, and carbon trading mechanisms. The effectiveness of the proposed strategy is validated through comparative case studies. The main contributions of this paper are summarized as follows:

• By integrating electric boilers and heat storage coordination devices into the comprehensive energy system of coal transportation railways, thermal and electrical energy have been effectively decoupled, thereby improving the overall energy utilization efficiency.
• In addition to the implementation of electric boilers and coordinated heat storage systems, this study incorporates a carbon trading mechanism, significantly reducing the system’s carbon emissions.
• Demand response is introduced to optimize the temporal distribution of electricity and heat loads, effectively reducing peak-to-valley differences and lowering overall costs. Furthermore, it minimizes wind power curtailment, achieving full utilization of wind energy.

The remainder of this paper is organized as follows. Section 2 details the model of the integrated energy system, including energy system models, the carbon emission trading mechanism, and energy dispatch optimization. Section 3 presents a case study for energy dispatch optimization in a coal railway integrated energy system. Finally, Section 4 concludes the paper and discusses potential directions for future research.

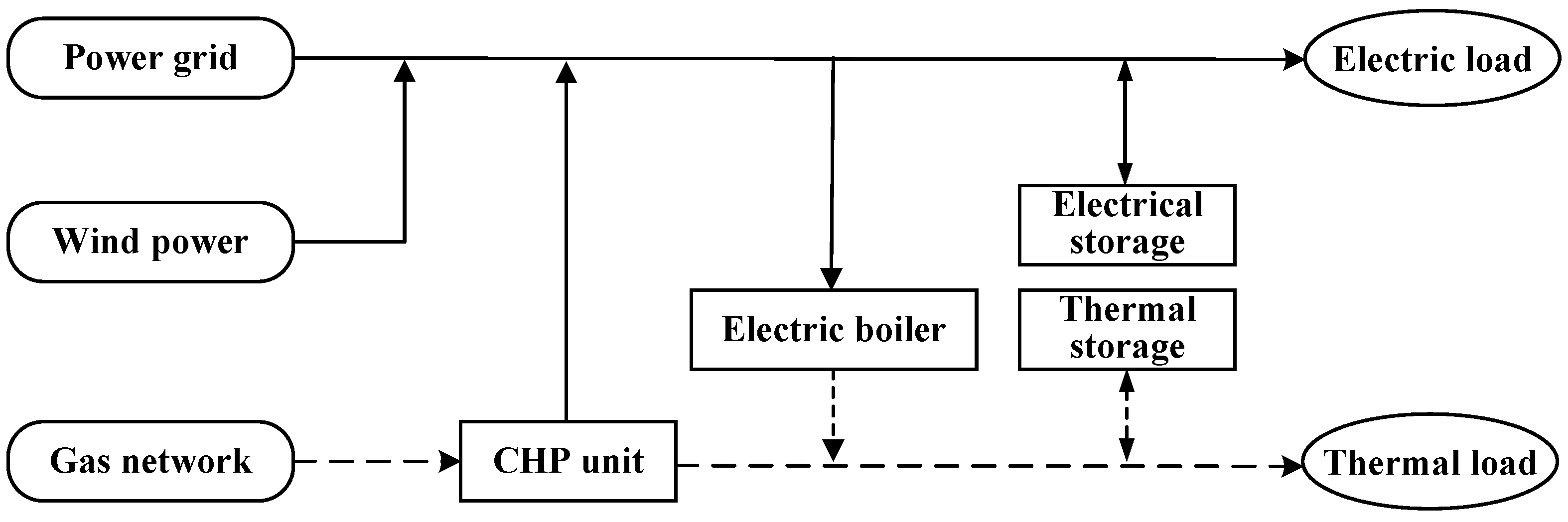
2. Model of the Integrated Energy System

2.1. Energy System Models

The structure of the integrated energy system discussed in this paper is illustrated in Figure 1. The system’s electricity is supplied by wind power generation, the power grid, and CHP units, while thermal energy is provided by CHP units and electric boilers. The demand side encompasses both electric and thermal loads. The energy storage system is an electric–thermal hybrid storage device. The CHP units operate in a thermoelectric decoupling mode, allowing the system to adapt to diverse operating conditions. In the following section, we present the models of the electric boiler, thermal energy storage, and electric energy storage.

2.1.1. Model of Electric Boiler

In the integrated energy system, the electric boiler serves as a combined unit for energy transformation, utilizing electrical components to generate heat. Unlike traditional boilers, it does not involve combustion-related chemical reactions and therefore emits no waste products such as black smoke, sulfur dioxide, or carbon dioxide. The heating efficiency of an electric boiler can exceed 95%, and it is characterized by a high level of automation, ensuring safe and reliable operation. By utilizing surplus wind power to supply heat to a thermal storage electric boiler, the local electricity load can be effectively increased [25]. The output model of the electric boiler is expressed as follows:

$$H_{eb}\left(t\right)={\eta }_{ah}{P}_{eb}\left(t\right),$$

(1)

where $P_{eb}\left(t\right)$ and $H_{eb}\left(t\right)$ represent the electricity consumption and heating power of the electric boiler at time t, respectively; ${\eta }_{ah}$ denotes the efficiency of the electric–thermal conversion of the electric boiler.

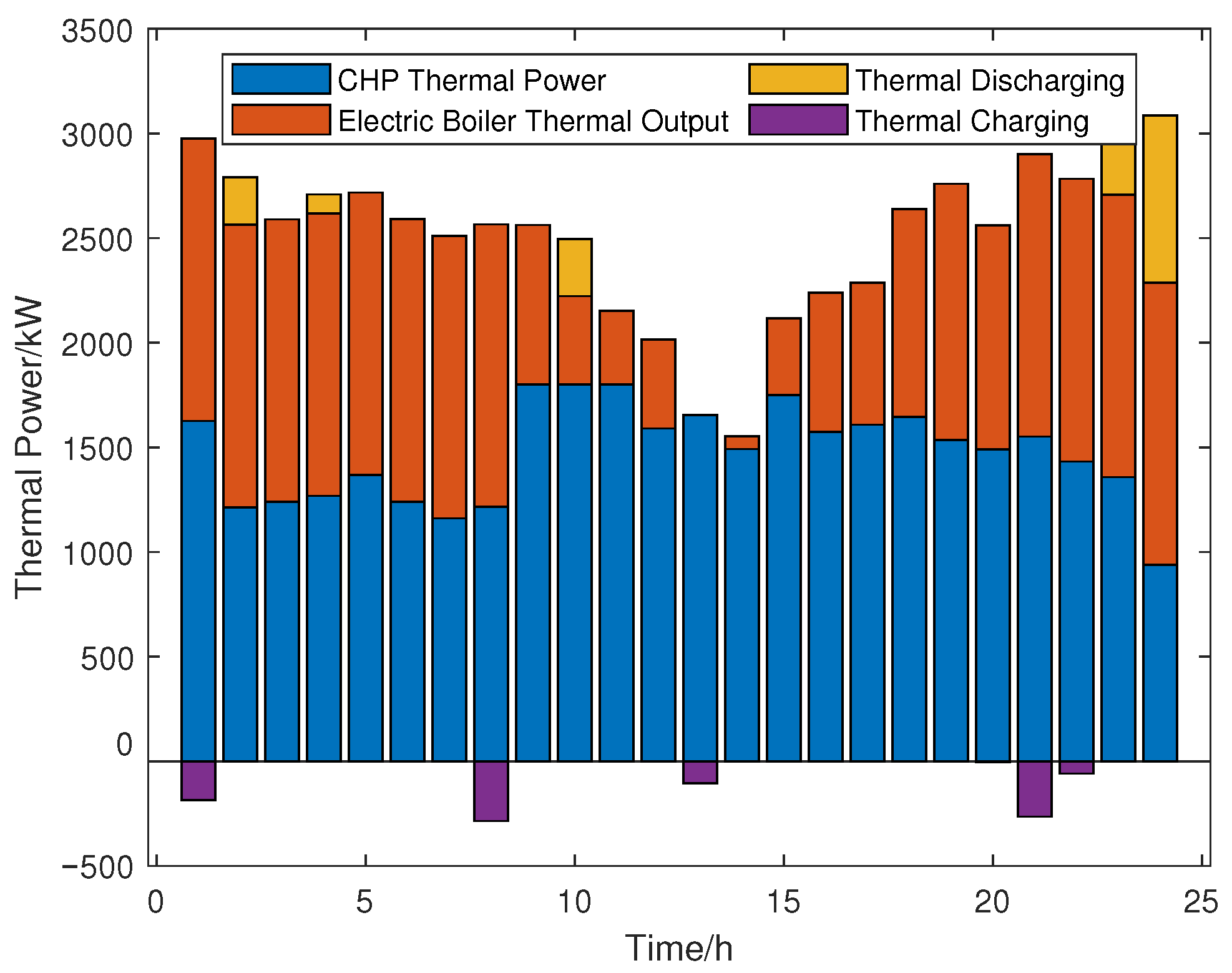
2.1.2. Model of Thermal Energy Storage

To date, thermal energy storage is primarily achieved through three methods: sensible heat storage, latent heat storage, and thermochemical storage. However, thermochemical storage has not yet been widely adopted. Compared to sensible heat storage, latent heat storage is distinguished by its high energy density and smaller physical size [26]. Therefore, this paper focuses on latent heat storage as the thermal energy storage medium, and its model is detailed as follows:

$$S_{hs}\left(t\right)=(1-\mu )S_{hs}(t-1)+\left({\lambda }_{in}{H}_{in}\left(t\right)-{\displaystyle \frac{H_{out}\left(t\right)}{{\lambda }_{out}}}\right)\mathrm{\Delta }t,$$

(2)

where $S_{hs}\left(t\right)$ and $S_{hs}(t-1)$ represent the thermal energy storage capacity at time t and $t-1$, respectively; $H_{in}\left(t\right)$ and $H_{out}\left(t\right)$ denote the heat storage power and heat release power at time t, respectively; ${\lambda }_{in}$ and ${\lambda }_{out}$ are the thermal storage efficiency and heat release efficiency, respectively; $\mu$ represents the heat loss coefficient of the thermal energy storage system; and $\mathrm{\Delta }t$ is the sampling interval.

2.1.3. Model of Electrical Energy Storage

Electrical energy storage is achieved through the conversion between chemical and electrical energy. Its model is described as follows [27]:

$$S_{bat}\left(t\right)=S_{bat}(t-1)+\left({\eta }_{ch}{P}_{ch}\left(t\right)-{\displaystyle \frac{1}{{\eta }_{dis}}}{P}_{dis}\left(t\right)\right)\mathrm{\Delta }t,$$

(3)

where $S_{bat}\left(t\right)$ denotes the energy stored in the energy storage device at time t; ${\eta }_{ch}$ and ${\eta }_{dis}$ represent the charging efficiency and discharging efficiency of the energy storage device, respectively; and $P_{ch}\left(t\right)$ and $P_{dis}\left(t\right)$ denote the charging power and discharging power of the energy storage device at time t, respectively.

2.2. Carbon Emission Trading Mechanism

Under China’s dual-carbon strategy, the carbon emission trading mechanism is being systematically implemented and expanded. The government or relevant regulatory authorities allocate free carbon emission quotas to each carbon emission source. If a producer’s actual carbon emissions exceed the government-allocated quotas, they must purchase additional carbon emission allowances to offset the excess [17]. In the following section, we present the models for carbon emissions, carbon quotas, and carbon trading costs.

2.2.1. Model of Carbon Emission

The carbon emissions associated with obtaining electricity from the primary power grid can be expressed as [18]:

$$E_{C{O}_2,g}=\sum _{t=1}^T{\mu }_g{P}_{ebuy}\left(t\right),$$

(4)

where $E_{C{O}_2,g}$ denotes the carbon emissions generated from purchasing electricity; ${\mu }_g$ represents the carbon emission intensity per unit of electricity; and $P_{ebuy}\left(t\right)$ indicates the amount of electricity purchased by the system at time t.

The carbon emission calculation for the CHP unit can be expressed as follows:

$$\left\{\begin{array}{cc}\hfill & E_{C{O}_2,c}=\sum _{t=1}^T\sum _{i=1}^N{\mu }_{ci}{P}_{ci}\left(t\right)\hfill \\ \hfill & P_{ci}\left(t\right)=P_{cei}\left(t\right)+c_h{H}_{ci}\left(t\right)\hfill \end{array}\right.$$

(5)

where $E_{C{O}_2,c}$ denotes the carbon emissions of the thermal power unit; ${\mu }_{ci}$ represents the carbon emission intensity per unit output of the i-th thermal power unit; $P_{ci}\left(t\right)$ indicates the electrical output of the i-th CHP unit at time t under condensing conditions; $P_{cei}\left(t\right)$ and $H_{ci}\left(t\right)$ represent the net electrical output and thermal power of the i-th CHP unit at time t, respectively; $c_h$ is the thermoelectric ratio of the extraction-type CHP unit; N is the number of CHP units; and T is the scheduling cycle.

2.2.2. Model of Carbon Quota

In this paper, the allocation of carbon quotas for the system’s power sources is implemented using a free distribution method based on generation capacity [28], which can be expressed as follows:

$$\left\{\begin{array}{cc}\hfill & E_{f,g}=\sum _{t=1}^T{\sigma }_g{P}_{ebuy}\left(t\right)\hfill \\ \hfill & E_{f,c}=\sum _{t=1}^T\sum _{i=1}^N{\sigma }_g{P}_{ci}\left(t\right)\hfill \end{array}\right.$$

(6)

where $E_{f,g}$ and $E_{f,c}$ denote the free carbon quotas allocated for purchasing electricity from the power grid and the CHP units, respectively; and ${\sigma }_g$ represents the carbon emission allocation per unit of electricity.

2.2.3. Model of Carbon Trading Cost

Traditional carbon trading calculates the cost of carbon transactions using a single formula. Within a specified period, if an economic entity’s carbon emissions are below the benchmark emissions, it can earn corresponding credit quotas for trading; conversely, if the entity’s carbon emissions exceed the benchmark, it must purchase additional emission credit quotas.

To further control total carbon emissions, this paper proposes a tiered carbon trading cost calculation model. Based on the allocated carbon emission quotas, several emission quantity intervals are established, with higher carbon trading prices assigned to intervals with larger emission volumes. The carbon trading cost model can be expressed as follows [29]:

$$C_{C{O}_2}=\left\{\begin{array}{cc}\lambda E_{C{O}_2}& 0⩽E_{C{O}_2}<L\\ \lambda (1+\beta )(E_{C{O}_2}-L)+\lambda L& L⩽E_{C{O}_2}<2L\\ \lambda (1+2\beta )(E_{C{O}_2}-2L)+\lambda (2+\beta )L& 2L⩽E_{C{O}_2}<3L\\ \lambda (1+3\beta )(E_{C{O}_2}-3L)+\lambda (3+3\beta )L& 3L⩽E_{C{O}_2}<4L\\ \lambda (1+4\beta )(E_{C{O}_2}-4L)+\lambda (4+6\beta )L& 4L⩽E_{C{O}_2}<\infty \end{array}\right.$$

(7)

where $C_{C{O}_2}$ represents the cost of tiered carbon trading; $E_{C{O}_2}$ denotes the system’s trading share in the carbon market within a trading cycle, expressed as $E_{C{O}_2}={\sum }_{i\in \{g,c\}}{E}_{C{O}_2,i}-E_{f,i}$; $\lambda$ stands for the base price of carbon trading; $\beta$ is the rate of price increase for tiered carbon trading; and L signifies the interval length of carbon emissions.

2.3. Energy Dispatch Optimization

2.3.1. Optimization Algorithm

The proposed optimization problem, formulated as a Mixed-Integer Linear Programming (MILP) problem after piecewise linearization, is solved using CPLEX—a high-performance mathematical optimization solver. CPLEX combines branch-and-cut algorithms with advanced heuristics and simplex methods to efficiently handle large-scale linear and integer programming problems [30]. This approach guarantees globally optimal solutions for convex problems while accommodating the complex constraints of our integrated system (thermoelectric decoupling, tiered carbon trading, and multi-phase demand response.

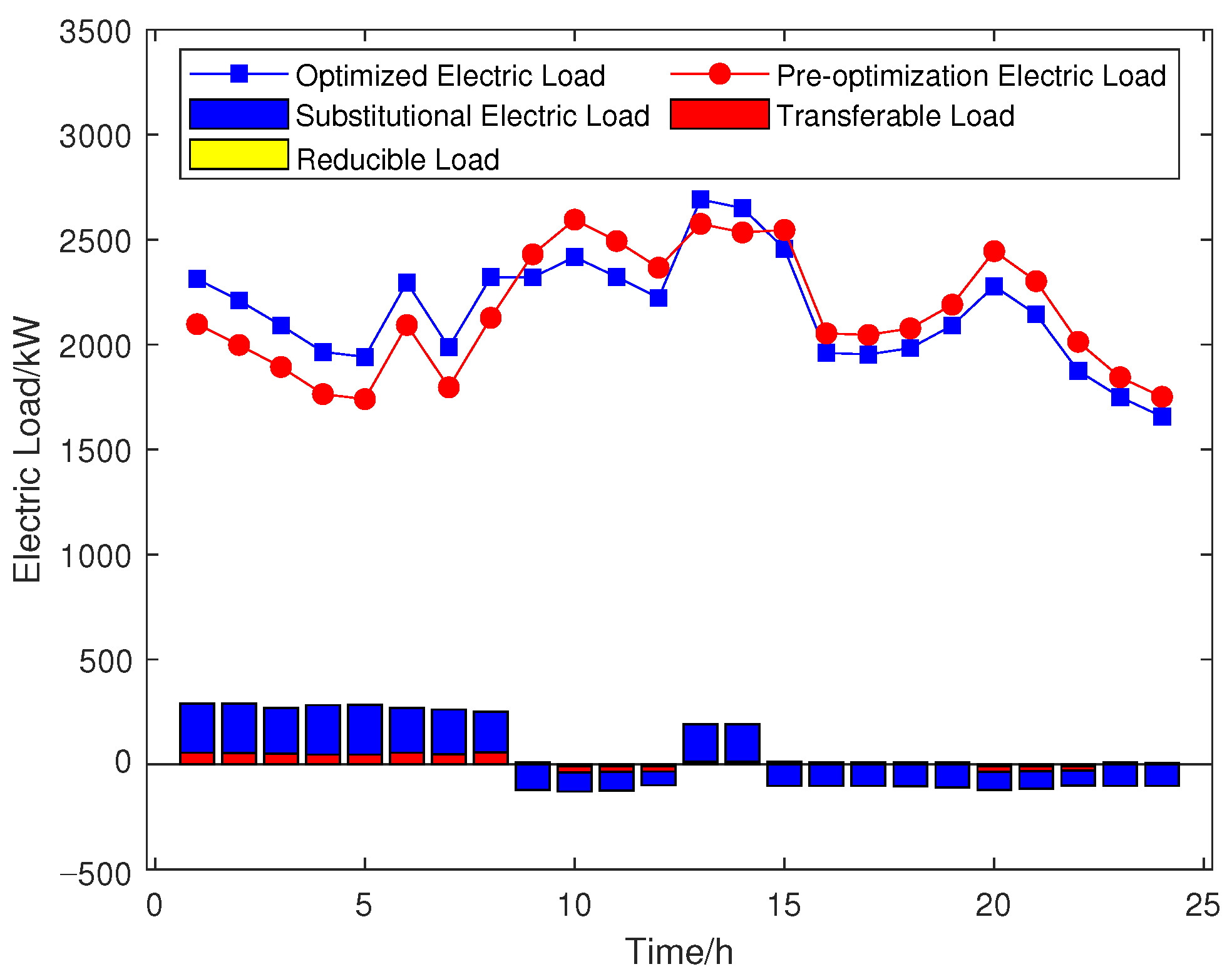
2.3.2. Demand Response Model

Demand response (DR) refers to the adjustment of energy consumption patterns by users in response to electricity prices or incentive mechanisms, enabling active participation in grid operations to optimize load profiles and enhance the overall efficiency of the system. Demand response loads include reducible loads, transferable loads, and substitutable loads, while fixed loads do not participate in demand response [31]. The demand response model can be expressed as follows:

$$\left\{\begin{array}{cc}\hfill & P_{lk}\left(t\right)=L_{lk}\left(t\right)+P_{lk}^c\left(t\right)+P_{lk}^s\left(t\right)+P_{lk}^r\left(t\right)\hfill \\ \hfill & P_{lk}^c\left(t\right)=P_{lk}^{c*}\left(t\right)+\mathrm{\Delta }{P}_{lk}^c\left(t\right)\hfill \\ \hfill & P_{lk}^s\left(t\right)=P_{lk}^{s*}\left(t\right)+\mathrm{\Delta }{P}_{lk}^s\left(t\right)\hfill \\ \hfill & P_{lk}^r\left(t\right)=P_{lk}^{r*}\left(t\right)+\mathrm{\Delta }{P}_{lk}^r\left(t\right)\hfill \end{array}\right.$$

(8)

where k denotes the type of load, whether electrical or thermal; $P_{lk}\left(t\right)$ represents the power of the k-th load at time t; $L_{lk}$ signifies the power of the k-th fixed load at time t; $P_{lk}^c\left(t\right)$, $P_{lk}^s\left(t\right)$, and $P_{lk}^r\left(t\right)$ indicate the power values of the reducible, transferable, and substitutable loads, respectively, for the k-th load after participating in demand response during time period t; $P_{lk}^{c*}\left(t\right)$, $P_{lk}^{s*}\left(t\right)$, and $P_{lk}^{r*}\left(t\right)$ represent the power of the reducible, transferable, and substitutable loads, respectively, for the k-th load before participating in demand response during time period t; $\mathrm{\Delta }{P}_{lk}^c\left(t\right)$, $\mathrm{\Delta }{P}_{lk}^s\left(t\right)$, and $\mathrm{\Delta }{P}_{lk}^r\left(t\right)$ denote the power changes of the reducible, transferable, and substitutable loads, respectively, when participating in demand response.

2.3.3. Objective Function

The objective function includes energy procurement costs, carbon trading costs, wind curtailment costs, and the operational and maintenance costs of various equipment. The objective function employed in this study is as follows:

$$C_{total}=C_{buy}+C_{C{O}_2}+C_{op}+C_{loss},$$

(9)

where the energy purchase cost is detailed as follows:

$$C_{buy}=\sum _{t=1}^T{\alpha }_t{P}_{ebuy}\left(t\right),$$

(10)

where T represents one operational cycle and ${\alpha }_t$ denotes the electricity purchase price at time t.

The operational and maintenance cost is expressed as:

$$C_{op}=\sum _{t=1}^T\sum _{n=1}^N{\omega }_n{P}_n\left(t\right),$$

(11)

where N denotes the total number of maintenance equipment; $P_n\left(t\right)$ and ${\omega }_n$ represent the output power during time period t and the maintenance price of the n-th equipment, respectively.

The wind curtailment cost is expressed as follows:

$$C_{loss}=\sum _{t=1}^T{c}_{loss}(P_{w,max}\left(t\right)-P_w\left(t\right)),$$

(12)

where $c_{loss}$ represents the unit loss for wind curtailment; $P_{w,max}\left(t\right)$ and $P_w\left(t\right)$ denote the rated maximum wind power and grid-connected wind power at time t, respectively.

2.3.4. Constraints

In this paper, we consider several constraints for the optimal scheduling of the integrated energy system, including wind power output constraints, electric boiler output constraints, CHP unit constraints, energy storage constraints, energy balance constraints, and user satisfaction constraints. The wind power output constraint is expressed as follows:

$$0⩽P_w\left(t\right)⩽P_{w,max},$$

(13)

where $P_{w,max}$ is the rated maximum wind power.

The electric boiler output constraint is expressed as follows:

$$0⩽P_{eb}\left(t\right)⩽P_{eb,max},$$

(14)

where $P_{eb,max}$ represents the rated maximum electric power of the electric boiler.

The CHP unit constraint is expressed as follows:

$$\left\{\begin{array}{cc}\hfill & P_{cei}\left(t\right)⩽min\left\{c_{mi}{H}_{ci}\left(t\right)+K_{ci}{P}_{ci,min}-c_h{H}_{ci}\left(t\right)\right\}\hfill \\ \hfill & P_{cei}⩽P_{ci,max}-c_h{H}_{ci}\left(t\right)\hfill \\ \hfill & 0⩽H_{ci}\left(t\right)⩽H_{ci,max}\hfill \\ \hfill & P_{cei}\left(t\right)=Q_{ci}^g\left(t\right){ϵ}_c^e{v}_g\hfill \\ \hfill & H_{ci}\left(t\right)=Q_c^g\left(t\right){ϵ}_c^h{v}_g\hfill \end{array}\right.$$

(15)

where $P_{ci,min}$ and $P_{ci,max}$ denote the minimum and maximum electric power of the i-th unit under condensing conditions, respectively; $c_{mi}$ and $K_{ci}$ are operational parameters; $H_{ci,max}$ represents the upper limit of thermal output for the unit; $Q_{ci}^g\left(t\right)$ is the gas consumption of the i-th CHP unit; ${ϵ}_c^e$ and ${ϵ}_c^h$ are the gas-to-electricity and gas-to-heat efficiency of the CHP unit, respectively; and $v_g$ is the calorific value of natural gas, taken as $9.88 \mathrm{kWh}/{\mathrm{m}}^3$.

The electric and thermal energy storage models are similar, with the following constraints:

$$\left\{\begin{array}{cc}\hfill & 0⩽P_{Sj}^{ch}\left(t\right)⩽P_{Sj}^{max}\hfill \\ \hfill & 0⩽P_{Sj}^{dis}\left(t\right)⩽P_{Sj}^{max}\hfill \\ \hfill & S_j\left(t\right)=S_j\left(0\right)+{\int }_0^t{P}_{Sj}^{ch}\left(t\right){\eta }_{Sj}^{ch}-P_{Sj}^{dis}\left(t\right)/{\eta }_{Sj}^{dis}\hfill \\ \hfill & S_j\left(1\right)=S_j\left(T\right)\hfill \\ \hfill & S_j^{min}⩽S_j\left(t\right)⩽S_j^{max}\hfill \end{array}\right.$$

(16)

where $P_{S,j}^{ch}\left(t\right)$ and $P_{S,j}^{dis}\left(t\right)$ ($j\in h,e$) represent, respectively, the input and output power of the j-th energy storage device at time t; ${\eta }_{S,j}^{ch}$ and ${\eta }_{S,j}^{dis}$ denote the charging and discharging efficiency of the j-th energy storage device, respectively; $S_i\left(t\right)$ represents the capacity of the j-th energy storage device at time t; and $S_j^{min}$ and $S_j^{max}$ indicate the upper and lower limits of the capacity of the j-th energy storage device, respectively.

The railway energy system in this paper simultaneously considers the flow of electrical energy and thermal energy, both of which must satisfy the energy balance constraints. The specific expressions are as follows:

$$\left\{\begin{array}{cc}\hfill & P_{eb}\left(t\right)+P_{el}\left(t\right)+P_{ch}\left(t\right)=P_{ebuy}\left(t\right)+\sum _{i=1}^N{P}_{cei}\left(t\right)+P_{dis}\left(t\right)+P_w\left(t\right)\hfill \\ \hfill & P_{hl}\left(t\right)+H_{in}\left(t\right)=H_{eb}\left(t\right)+\sum _{i=1}^N{H}_{ci}\left(t\right)+H_{out}\left(t\right)\hfill \end{array}\right.$$

(17)

where $P_{el}\left(t\right)$ represents the electrical load at time t, and $P_{hl}\left(t\right)$ represents the thermal load at time t.

The willingness of users to participate in demand response is closely tied to their actual experience with changes in electricity usage. Therefore, when designing and implementing demand response strategies, it is crucial to fully consider and incorporate user satisfaction constraints related to electricity usage habits. The constraint is expressed as follows:

$$s=1-{\displaystyle \frac{{\sum }_{t\in T}|P_{el}^{*}\left(t\right)+\mathrm{\Delta }{P}_{el}^c\left(t\right)+\mathrm{\Delta }{P}_{el}^s\left(t\right)+\mathrm{\Delta }{P}_{el}^r\left(t\right)|}{{\sum }_{t\in T}{P}_{el}^{*}\left(t\right)}}⩾s_{min}$$

(18)

where $s_{min}$ and s represent the minimum and actual satisfaction levels of users with their electricity usage patterns, respectively; $P_{el}^{*}\left(t\right)$ represents the electrical load before demand response at time t.

3. Case Study—Energy Dispatch Optimization in Coal Railway Integrated Energy System

This study selects a coal transportation railway station in northern China as the research object, with a 24-h operational cycle and a unit operational time of 1 h. The carbon emission quota per unit of electricity generated in the system is $0.798 \mathrm{kg}/\mathrm{kWh}$. The length of the tiered carbon emission interval L is 2 tons, the price increase rate $\beta$ is $0.25$, and the base price of carbon trading $\lambda$ is 250 yuan/ton. The time-of-use electricity prices are referenced from the literature [32]. On the demand side, transferable loads account for 10% of the total load, while reducible loads and substitutable loads each account for 5% of the total load. The aforementioned low-carbon optimal dispatch model is piecewise linearized into a linear model, and the CPLEX solver in MATLAB R2023b is used to optimize and solve the model.

As shown in Figure 2, the composition of electrical load includes reducible load, transferable load, and substitutable load. Reducible load is achieved by cutting a portion of the load during high-price periods (10:00–12:00, 20:00–22:00). Transferable load shifts part of the load from high-price periods to low-price periods (00:00–07:00), reducing load during high-price periods and increasing it during low-price periods, thereby narrowing the peak–valley difference in the load curve. Substitutable load converts part of the electrical load into thermal load during high-price periods and reverses the process during low-price periods. The coordinated action of these three demand response methods smooths the load curve, achieving peak shaving and valley filling.

The operational status of the system equipment is shown in Figure 3 and Figure 4. During the off-peak period, when electricity prices are at their lowest and wind power generation is at its peak, the total electrical load is supplied by wind power, CHP units, and grid purchases, while the thermal load is mainly met by electric boilers and CHP units. During the flat and peak periods, when electricity prices are relatively higher compared to gas prices, CHP units increase their electrical output, and the electrical load is supported by CHP units and wind power. Since some intervals during the peak and flat periods coincide with low wind power generation, electric boilers reduce their output, and CHP units increase their thermal output. Additionally, electrical energy storage charges during low-price periods and discharges during high-price periods, while thermal energy storage operates in the opposite manner, charging during high-price periods and discharging during low-price periods, thereby significantly enhancing the system’s operational flexibility.

This study systematically validates the proposed model’s optimization effects on carbon emissions and wind power utilization in the power system by designing three comparative cases. The specific case settings are as follows:

• Case I (Baseline): We adopt the traditional scheduling mode, which neither considers the carbon trading mechanism nor introduces demand response strategies. The system is not equipped with electric boilers or thermal storage devices, serving as the benchmark scenario.
• Case II (Carbon Trading Mode): On the basis of Case I, we introduce a carbon trading mechanism to quantify carbon emission costs. The system is equipped with electric boilers and thermal storage devices to investigate the impact of the carbon trading mechanism on system scheduling.
• Case III (Comprehensive Optimization Mode): Based on Case II, a synergistic optimization mode of carbon trading and demand response is built up by further incorporating a demand response mechanism. The comprehensive benefits of the proposed model are thoroughly evaluated.

According to the comparative analysis results in

Table 3. Scheduling result.

Item	Case 1	Case 2	Case 3
Total cost (yuan)	78,436	35,260	33,884
Energy purchase cost (yuan)	28,035	7453	7539
Carbon emission cost (yuan)	36,401	22,717	22,705
Wind/solar curtailment cost (yuan)	10,300	450	0
Actual carbon emission (ton)	66.2	57.9	57.8

, Case II achieved a reduction of 13,684 yuan in carbon emission costs compared to Case I, with actual carbon emissions decreasing by 8.3 tons, a reduction of 12.5%. Meanwhile, the wind power utilization cost was also reduced by 9850 yuan. This significant improvement is primarily attributed to the introduction of the carbon trading mechanism in Case II. The system effectively offset part of the carbon emission costs through initial carbon emission allowances, while Case I had to bear the full cost of actual carbon emissions. Additionally, the electric boilers and thermal storage devices configured in Case II optimized the thermoelectric coupling characteristics of the system, not only enhancing wind power utilization capacity but also reducing energy procurement costs by 20,582 yuan.

Furthermore, Case III introduced a demand response mechanism on the basis of Case II. By considering time-of-use electricity prices and the temporal distribution of wind power output, Case III achieved efficient substitution of thermal and electrical energy on the user side through horizontal load shifting and partial load curtailment, effectively narrowing the peak-to-valley load difference. This optimization allowed the system to choose more economical and low-carbon operating modes based on the procurement costs of electricity and natural gas and the output capacity of equipment during different time periods. Ultimately, Case III achieved full utilization of wind power while outperforming Case II in all operational costs, successfully balancing the goals of operational economy and low-carbon performance.

4. Conclusions

This study focuses on the optimal scheduling of coal railway electric–heat integrated energy systems, innovatively combining a tiered carbon trading mechanism with demand response strategies. An optimal scheduling model for the system is constructed, and three typical case studies are designed for comparative analysis. The following key conclusions are drawn:

Firstly, the introduction of a tiered carbon trading mechanism in a system equipped with electric boilers and heat storage devices can significantly reduce system carbon emissions by up to 12.5%. This optimization is primarily attributed to the effective improvement of the system’s thermoelectric coupling characteristics by electric boilers and heat storage devices, which not only reduce wind curtailment but also significantly enhance the competitiveness of wind power in the integrated energy system.

Secondly, the introduction of demand response strategies under the framework of the tiered carbon trading mechanism achieves an optimized temporal distribution of electric and thermal loads. The results show that this strategy effectively narrows the peak-to-valley load difference and reduces the total operating costs of the system. Simultaneously, through an effective complementary substitution mechanism between electric and thermal energy on the user side, wind energy waste is further reduced. Additionally, by flexibly selecting energy purchasing methods, the pressure on energy supply is alleviated, achieving a dynamic balance between economic efficiency and low-carbon operation of the system.

This study assumes deterministic renewable generation and load profiles, which aligns with the stable operational patterns of industrial energy systems. In future work, we will incorporate stochastic optimization for more volatile environments.