Abstract
Using high-frequency financial data, this study investigates volatility spillovers between five renewable energy subsectors (wind, solar, geothermal, bioenergy, and fuel cells), five conventional energy markets (oil, gas, coal, uranium, and gasoline), and carbon emissions for five industrial sectors (power, industry, ground transportation, domestic aviation, and residential) based on a Diebold–Yilmaz VAR-based spillover framework. The results document that the industry and power sectors are the key players in the transmission effects of carbon shocks. In contrast, the reverse is true for the residential and aviation sectors. For renewable energy, fuel cells, and geothermal power, strong forward linkages appear to significantly reduce carbon emissions, while reverse linkages that increase carbon emissions in response to shocks in clean-energy and carbon-intensive industries are relatively high for coal and oil. We also find that the total volatility connectedness exceeds 84%, indicating significant systemic risk transmission. The clean-energy subsectors, particularly wind and solar, now compete in fossil-fuel markets during geopolitical crises. Applying the DCC-GARCH t-copula method to assess portfolio hedging strategies, we find that fuel cell and geothermal assets are the most effective in hedging against volatility in fossil-fuel prices. In contrast, nuclear and gas assets provide benefits from diversification. These results underscore the growing strategic importance of clean energy in mitigating sector-specific emission risks and fostering resilient energy systems in alignment with the United States’ net-zero carbon goals.
1. Introduction
Countries, companies, and individuals must drastically reduce their greenhouse gas emissions to achieve net-zero emissions through various measures, such as switching to sustainable energy sources, enacting energy-saving laws, and utilizing carbon capture and storage technology [1,2]. To mitigate the most severe consequences of climate change and to maintain global warming within a threshold of 1.5 degrees Celsius above pre-industrial averages, numerous nations, including the United States, have pledged to reach net-zero emissions by the midpoint of the 21st century [3]. However, extraordinary global events, such as the COVID-19 pandemic and the Russia–Ukraine War (RUW), present potential obstacles to achieving these net-zero objectives. Specifically, the onset of the COVID-19 pandemic prompted a realignment of priorities among governments and communities, with a heightened emphasis on curbing the proliferation of the virus, diverting attention and resources from climate change initiatives [4,5]. The ripple effects of the RUW might cast a shadow over the clean-energy landscape in the United States, as it is intricately linked to the ebbs and flows of transmission returns. The crux of the issue lies in the European Union’s (EU) dependency on Russian natural gas, which is a linchpin in its energy matrix [6]. This reliance breeds apprehensions about energy supply continuity and security, given the tumultuous backdrop. This scenario could pose a conundrum for the clean-energy crusade in the USA: elevated energy prices might temporarily dim the allure of clean energy, giving fossil fuels an edge in the affordability arena.
As the world races towards net-zero emissions, decarbonization is not a one-size-fits-all solution. Emission abatement paths for the industrial, transport, electricity, and residential sectors vary substantially in terms of technological requirements, policy frameworks, and cost profiles [7,8,9]. For example, although the power sector is quickly adopting renewables, sectors such as transportation and heavy industry still rely heavily on fossil fuels [10]. The complexity becomes even more complicated at home when political changes, such as Trump’s relaxation of environmental rules, destabilize what should be a consistent climate commitment and commitment to clean energy [11,12]. At the same time, rising geopolitical tensions, such as the conflict in the Red Sea, are threatening global energy security and adding another layer of volatility to the fossil-fuels market, impacting the clean versus brown energy transition [13]. However, the clean-energy sector in the USA has demonstrated enviable resilience to market fluctuations. Case in point, during the COVID-19 pandemic, when energy demand plummeted, the US experienced an increase in Renewable Energy (RENE) installations. This surge was fueled by a combination of factors, including the US economy’s bolstering of self-reliance in clean-energy production, notably wind and solar, which acts as a bulwark against the unpredictability of external energy supplies [14]. This strategic shift not only mitigates the impact of market volatility but also guides the country toward a more self-sufficient and sustainable energy future.
Based on the above, this study aims to investigate the volatility spillovers between five RENE subsectors (wind, solar, geothermal, bioenergy, and fuel cells), five conventional energy markets (oil, gas, coal, uranium, and gasoline), and carbon emissions for five industrial sectors (power, industry, ground transportation, domestic aviation, and residential). We also aim to present three key observations based on the facts and literature reviewed in this field. First, since the USA is expected to be the second-largest emitter of carbon emissions after China in 2021, very few studies have examined the return and volatility connectedness from the USA’s perspective. Second, none of the studies have addressed different subsectors within the economy. We aim to address this gap in our research by utilizing Carbon Monitor data that encompass the following five key subsectors: power, industry, aviation, transportation, and residential. Further, very few studies have taken daily data for their volatility connectedness analysis. The empirical analysis focuses on the extreme market conditions, particularly post-COVID-19 and since the onset of the RUW, including the 2021–2022 period, when the Carbon Monitor project provided, for the first time, scientifically sound daily estimates of subsector CO2 emissions. To the best of our knowledge, this is one of the earliest attempts to investigate the short-term relationship between energy price variation and CO2 emissions using high-frequency data. The analysis includes information for five subsectors of clean energy, namely, NOMXS, NOMXW, NOMXG, NOMXFC, and NOMXB, as well as the following five conventional energy sources: WTI (crude oil), natural gas, nuclear energy, coal, and traditional gasoline from New York Harbor. The sectoral CO2 emissions are partitioned into the following five relevant industrial sectors: power (POW), industry (IND), ground transportation (GT), domestic aviation (DA), and residential (RE). Using the vector autoregressive (VAR) settings in [15,16], we add to the literature on cross-market return spillovers and dynamic connectivities between green and brown energy sectors under global stress conditions. This paper also assesses the determinants of dynamic connectedness between energy subsectors and finite CO2 emissions within the overarching context of net-zero transition objectives. Furthermore, this research can inform portfolio management practices by examining the optimal weights of portfolios and the hedging effectiveness of clean-energy assets as part of hedging against risks in traditional energy markets. Third, the impact of geopolitical risk, such as the Ukraine crisis and global shocks like COVID-19, is still evolving and under evaluation. Adopting a focused approach and utilizing data enable us to examine the volatility and connectedness across subsectors resulting from shocks that could not have been anticipated. Although studies on clean- and non-clean-energy returns are available during the Pandemic, we believe this is the first study to capture the return connectedness purely across subsectors in a single-country analysis using daily data. We utilize both renewable and non-renewable subsectors to capture the return transmission currently missing in the literature.
2. Review of Literature
In simpler terms, volatility connectedness refers to the spillover of external shocks into the share of volatilities in other markets [17,18]. Regardless of the volatility transmission in the energy markets, Apergis et al. [19] find that asymmetries in the volatility transmission are due to both good and bad volatility. Although volatility connectedness changes over time, negative spillovers do not strictly dominate positive spillovers. The asymmetry can be attributed to market power exercised by generators across different regions in the Australian electricity market. Similar connections exist between Ireland’s and Great Britain’s electricity markets. An asymmetric analysis suggests that good volatility connectedness is marginally larger than bad. Okorie and Lin [20] studied connectedness and hedging strategies between WTI and ten cryptocurrencies. The authors demonstrated bidirectional volatility between the oil market and BitCapitalVendor, from the crude WTI to the Bitcoin Cash market. Asadi et al. [21] investigated volatility connectedness across the US’s and China’s natural gas, crude oil, coal, stock, and currency markets. Daily data from December 2008 to December 2020 revealed that total connectedness among energy, stock, and currency markets is not high. Furthermore, total volatility connectedness outperforms it in the long run compared to the short run. The Global Financial Crisis saw a significant increase in total spillover, indicating a notable transfer of volatility between WTI and logistics company stocks. With a total volatility spillover of 47%, the authors argue for the existence of interdependencies between oil and logistics. Farid et al. [22] studied the impact of the worldwide pandemic on quantile connectedness across energy, agricultural commodities, and metals. Evidence suggests robust transmission across these sectors due to the global pandemic. The return shocks are only prevalent in the energy commodity group. Concerned about the volatility during the COVID-19 pandemic, Ghosh et al. [23] show asymmetric quantile dependence among markets with a sharp increase in connectedness during the pandemic. Since the onset of the global pandemic, a connection has been established between metals and energy sources, regardless of whether the energy source is environmentally friendly. Tiwari et al. [24] examined the conditional volatility spread during the pre-pandemic and pandemic periods using the rolling-window-based quantile VAR. The evidence from the analysis suggests systematic risk spillovers during extreme market movements. The results show significant variation in volatility spillovers across markets before and during the global pandemic.
In recent years, the clean-energy sector has experienced substantial growth, prompting numerous studies to investigate the risks and market dynamics of clean-energy stocks compared to conventional energy and carbon. A key area of research is the intersection between clean-energy markets and traditional fossil-fuel energy markets. Notably, in [25] the interplay among green energy stocks, carbon, and conventional energy prices was analyzed. Their results suggest that increases in conventional energy prices heighten the systemic risk for clean-energy companies, potentially impacting carbon markets. In [26], the causal link between the returns and volatility of oil markets and five green energy stock indices was studied using the non-parametric causality across quantiles. Surprisingly, no statistical evidence suggested a causal link between oil price volatility and RENE stocks during the global pandemic. Furthermore, adopting a carbon price floor will reduce volatility in Irish electricity markets.
More recently, Wang et al. [27] investigated the volatility links between clean-energy markets and fossil fuels, particularly during the recent pandemic. Their research reveals a relatively weak connection between the volatility of clean-energy stocks and fossil-fuel markets. References [28,29] discuss how the global economy is sensitive to energy price changes, including clean energy, emphasizing the need for stable policies during COVID-19 and Ukraine’s conflict, in which the geopolitical situation has raised net-zero challenges. Temporary price increases prompted by political uncertainty can be detrimental to the real economy. In addition to the need for clean energy as a response to climate change in the context of both SDGs 7 and 13, such a transition reflects the policy of sustainable development in the energy sector. Although this type of conversion supports economic development and growth, it also brings about some environmental improvements. However, the Sustainable Development Goals Report 2022 reveals that achieving this goal is very challenging even in the most developed economies, such as those in the OECD. These concerns were reiterated at the COP26 Summit and also aligned with previous observations in the 2017 OECD report, “Investing in Climate, Investing in Growth”. In light of the net-zero ambitions, Pham et al. The impact of environmental policy on US eco-conscious firms’ (ECS) stock performance, volatility, trading volume, and return connectedness was investigated by Kim et al. Their findings reflect the mixed response of green stocks, particularly to significant climate policy events such as the signing of the Paris Agreement and US presidential elections.
While numerous studies have explored volatility connectedness and spillover effects in energy and financial markets, key gaps remain in their scope and methodological rigor. In terms of research subjects, most prior work has focused on aggregated sectoral indices or global-level carbon markets (e.g., renewable indices vs. oil benchmarks), neglecting disaggregated sectoral emissions such as GT, DA, and RE. This aggregation masks heterogeneity in sector-specific risk transmission, which is critical for understanding climate-financial feedback in large, decentralized economies like the US. Regarding research approaches, many studies rely on static or symmetric models, such as traditional VAR or rolling-window-based spillover indices, which fail to capture crisis-driven asymmetries or nonlinear interactions under extreme shocks like COVID-19 or the RUW. Additionally, earlier studies often overlook clean-energy interaction channels and fail to explicitly integrate high-frequency policy risk metrics, such as the EPU and OVX, into their transmission frameworks. Finally, concerning research models, prior studies have typically employed bivariate and trivariate GARCH-type models, which overlook the multivariate and time-varying nature of connectedness across emission sectors and macro-financial variables. In contrast, this study addresses these gaps by employing a high-frequency, multivariate framework using DCC-GARCH- and GFEVD (generalized forecast error variance decomposition)-based dynamic connectedness measures across five CO2-intensive sectors, clean-energy indices, and policy risk variables. The inclusion of disaggregated US sectoral emissions as decision-making units allows us to uncover sector-specific spillover dynamics with greater granularity. Moreover, by combining time-varying connectedness with a robustness-validated regression model, we provide a more comprehensive picture of volatility transmission during systemic crises. This approach represents a methodological and empirical advance that directly addresses the limitations in the existing literature.
3. Materials and Methods
3.1. Data and Basic Model
Financial variables typically respond to external shocks quickly and symmetrically, particularly during times of economic instability. We base our empirical analysis on a heterogeneous sample that includes RE-exposed market indices, as well as conventional energy market indices, as proposed in [30]. Moreover, CO2 emission data were obtained from Carbon Monitor, providing high-frequency, daily estimates and exclusive coverage for the US, the second-largest emitter in the world in 2021, responsible for more than 13% of global CO2 emissions [31]. US emissions increased by nearly 6% in 2021 and rose by another 1.8% in 2022 [32]. Daily CO2 monitoring, now made possible through Carbon Monitor, aligns with the European Green Deal, the 2030 Agenda for Sustainable Development, and COP26 [33].
Emissions data for five sectors—power (POW), industry (IND), ground transportation (GT), domestic aviation (DA), and residential (RE)—were generated from the Carbon Monitor database between 1 January and 30 September 2022 (at https://eu.carbonmonitor.org/). Although Carbon Monitor provides a critical, regular dataset at the highest sustainability level, cross-sectoral distinctions in dimensional precision, as well as coverage lags, especially between residential and industrial sources, could influence the other CO2 emissions rates. Product emissions from point-source industrial and power sectors can be measured more accurately. Still, residential and transportation data are often estimated indirectly, resulting in greater uncertainty and discrepancies in sectoral emissions. Moreover, immediate or near-immediate data reporting communication latencies could introduce robust difficulties in continuous tracking, especially when faced with rapidly changing market and policy variables. This dataset provides a means to compare CO2-emission increases relative to some of the most significant global disruptions of the past few years, including COVID-19, post-pandemic recovery, and the RUW. To compare the RENE market’s outperformance, we utilize five RENE subindices (NOMXS, NOMXW, NOMXG, NOMXFC, and NOMXB) from Yahoo Finance [34,35,36]. This methodology is similar to those of previous studies, which have used indices such as the WilderHill Clean Energy Index and MSCI Global Green Bonds [37,38]. Conventional energy markets are represented by the following five fossil-fuel references, obtained from the EIA: WTI crude oil, New York Harbor conventional gasoline (HGG), uranium (URA), coal (COAL), and natural gas (GASN). For methodological reasons, price volatility is visible in market spikes. Table 1 and Figure 1 represent the data sources and trends, respectively. We measure performance via a volatility proxy, which can be described as follows:
where the following definitions apply:

Table 1.
Descriptive variables and sources.
Figure 1.
Data return trends.
: volatility index at time t;
: volatility index at time t − 1;
: index volatility at the time.
3.2. Methodology
3.2.1. VAR Spillover Method
Building upon the recent literature, the VAR-based Diebold and Yilmaz framework is used to measure the extent of interdependence and network of connections across the time series [39,40,41]. Networked approaches can also provide advantages over standard conditional heteroscedasticity models. This involves mapping the strength and directionality of information spillovers, identifying key transmitters and receivers in the system, and calculating measures of connectivity. While we acknowledge the growing application of advanced models, such as quantile VAR (QVAR) and TVP-VAR frameworks, our choice of the Diebold–Yilmaz VAR-based spillover framework was deliberate and aligned with the objective of this study. Specifically, the VAR model is highly effective in detecting and quantifying dynamic return and volatility connectedness across multiple asset classes, especially under extreme market conditions such as COVID-19 and the RUW [42]. Unlike QVAR, which captures distributional asymmetries at different quantiles, the VAR-based connectedness approach provides a clear network representation of directional spillovers, enabling us to measure systemic-risk transmission paths during crises. These two methods utilize generalized forecast error variance decomposition (FEVDs) to address the identification issues. Along this line, assuming the stationarity of the series, a VAR(p) is a model defined as follows:
where y and depict a vector with a k*1 dimension. Vector has a K*1-dimension conditional mean vector. has a variance–covariance metric with a k*k-dimension VAR.
In [15,16], the GFEVD is the following:
where the following apply:
Finally, the difference between TO and FROM results in a net spillover, as follows:
3.2.2. Portfolio and Hedging Strategies Using DCC GARCH t-Copula
The dynamic conditional correlation (DCC) model is an extension of the generalized autoregressive conditional heteroskedasticity (GARCH) model [43], which followed the R. F. ARCH model [44]. Its primary objective is to calculate the product of the standard deviations to deduce the time-varying variance–covariance matrix. Denoting the time-varying variance–covariance matrix by Ht, it is defined by the following:
where Rt is the time matrix of the time-varying correlations, and Dt is a diagonal matrix composed of conditional variances obtained from any univariate GARCH process. We tested whether this was a constant conditional correlation (CCC) model by assuming Rt to be constant over time; however, we rejected the null hypothesis of constant correlation. The Rt matrix is obtained through a GARCH-type parameterization of a Qt matrix obtained as follows:
where the sum of a and b must be strictly less than one to ensure the stationarity of the process, and Q bar is the unconditional matrix of the standard errors, z, obtained through the following transformation:
where is the result of a mean conditional process, E[rt|It−1] = + . The correlation matrix is then the product of a quadratic form of the Qt matrix defined above, as follows:
The DCC-GARCH model has been proposed several times, and its advantages include the ability to successfully handle a large number of returns and volatility while examining the portfolio’s dependence structure. This extremely adaptable model enables the modeling of dependencies between random variables from various perspectives. The standardized residuals, designated as var epsilon in [45], follow a multivariate Student’s t-distribution with eta degrees of freedom. Theory connects copula functions to joint distribution functions of random variables. Reference [46] showed that copulas can be built using conditional distributions, which we used in our evaluation of the DCC-GARCH t-copula system. GARCH models have several advantages over stochastic volatility (SV) models. These advantages encompass econometric simplicity, enhanced short-term forecasting accuracy, explicit financial interpretability, and adaptability through the incorporation of diverse forms, such as EGARCH and TGARCH, which enable the capture of distinctive data characteristics [47].
Nevertheless, the selection of a volatility model, such as the GARCH specification, can have a substantial impact on the outcomes. Various models emphasize distinct data characteristics, and the specifications of these models, such as lag lengths and the specific form of the GARCH model, can introduce biases. When comparing the DCC-GARCH model with the BEKK model (Baba, Engle, Kraft, and Kroner’s ) GARCH, it is noteworthy that the DCC-GARCH model exhibits a notable characteristic of parameter parsimony.
After calculating the DCC conditional correlation matrix, we used the hedge effectiveness (HE) ratio suggested in [48]. We first introduced Kroner [49] and dynamic hedge ratio [50] optimum portfolio weights. Hedge ratios are used to determine the costs of hedging a USD-1-long position in variable I with a USD xi short position in variable j; xi can be calculated using the following equation by the conditional covariance of variables i and j approximated by the DCC model:
We compute dynamic portfolio weights and the hedging effectiveness (HE) according to the hedged and unhedged positions [51].
4. Main Results
4.1. Summary Statistics
Table 2 reflects the summary statistics of the entire time series of asset returns. The mean values across variables are near-zero, and the median values closely converge with the means, indicating a low probability of outliers that could affect the estimation process, a crucial requirement for VAR model estimation. The standard deviations are minor, suggesting that returns are not widely dispersed from their means. The results from the skewness analysis show a combination of distributional asymmetry. In most conventional and RENE markets, we observe right-skewed distributions, whereas our carbon-emission series is left-skewed, and wind power returns are almost symmetric (skewness close to 0.05). Conventional energy variables have higher moments of skewness. These results indicate non-normal return distribution characteristics. For most variables, the kurtosis values are greater than three, meaning that there are large tails and a leptokurtic distribution. The null hypothesis of normality is rejected for all series by the Jarque–Bera test, indicating that the distributions of returns do not follow the Gaussian assumption.

Table 2.
Descriptive statistics for panel variables.
4.2. Total Connectedness of the Volatility
The dynamic connectedness and pairwise links between CO2 sector emissions and energy markets are examined in Table 2. To facilitate the interpretation of the SPI-LOVER matrix presented in Table 3, we summarize the key net transmitters and receivers of volatility using the net SPI-LOVER index (TO–FROM). The industry (IND) and power (POW) sectors emerge as the strongest net transmitters of volatility shocks, while clean-energy subsectors, such as solar and wind, act more as net receivers. Among fossil-fuel markets, uranium (URA) exhibits high bidirectional spillover. These directional insights provide a more nuanced understanding of sectoral vulnerability and resilience under stress conditions, enabling policymakers to identify priority sectors for risk mitigation and energy diversification. The total connectedness measure for volatility has remained high, at 84%, suggesting significant spillover effects among the three groups (clean energy, conventional energy, and Carbon Monitor). When the spillover values in each volatility variable are compared, it is discovered that carbon emissions by industry have the greatest transmission of shock to others, followed by clean-energy markets. Furthermore, the spillover effects from fossil energy to carbon monitoring are significant in the US and conventional energy markets, especially in the uranium market. External variables influenced the relative price volatility of oil and solar energy in traditional energy markets more than internal return dynamics.

Table 3.
Total connectedness index.
The self-system on volatility decreases, driving the shock in the carbon monitoring, US sectors, and clean-energy markets. The volatility spillover patterns depend on H-step-ahead prediction (10-step) and rolling windows (40 days). These results are linked to the specific characteristics of the conventional energy market, which COVID-19 and the RUW have induced, such as reasonable supply adjustments, management reserves, exposure, and price caps.
The network of volatility connectedness reflects the spillover effects between clean- and non-clean-energy markets and the carbon-emission industry, as shown in Figure 2. Nodes represent individual energy sectors or CO2-emitting sectors, with the node size proportional to total connectedness (TO + FROM). Edge thickness indicates the magnitude of directional spillover, derived from the GFEVD, which is represented by yellow for the net receivers and blue for the net transmitters. The node highlights key transmitters (larger nodes with thicker outgoing edges) and recipients (nodes with predominantly incoming edges), offering a visual representation of systemic risk flow in the energy-carbon system. Carbon Monitor is the most important transmitter of volatility shocks to other markets in the industry sector. In contrast, fuel cell, geothermal, bio, and uranium markets lead in driving volatility in the conventional energy market. In the United States, solar continues to be the most vulnerable to carbon-emission-related disruptions. The coal and WTI markets are also heavily impacted by shocks and pressures from clean energy and carbon emissions, primarily due to the COVID-19 pandemic and the military involvement in Ukraine. These findings suggest that the energy and carbon-emission markets are highly interdependent and that shocks in one market can have substantial spillover effects on the others. The finding that the industrial and power sectors are the strongest volatility transmitters is consistent with the US economy’s reliance on energy-intensive industries, particularly chemicals, steel, and manufacturing, which remain heavily dependent on fossil fuels. In contrast, wind and solar subsectors emerge as receivers of volatility, reflecting their rapid but policy-driven expansion under frameworks such as the Inflation Reduction Act (IRA). The high connectedness index (84%) underscores the systemic risk in the US energy system, where the absence of a nationwide carbon price and fragmented regulatory regimes amplify spillovers across sectors.
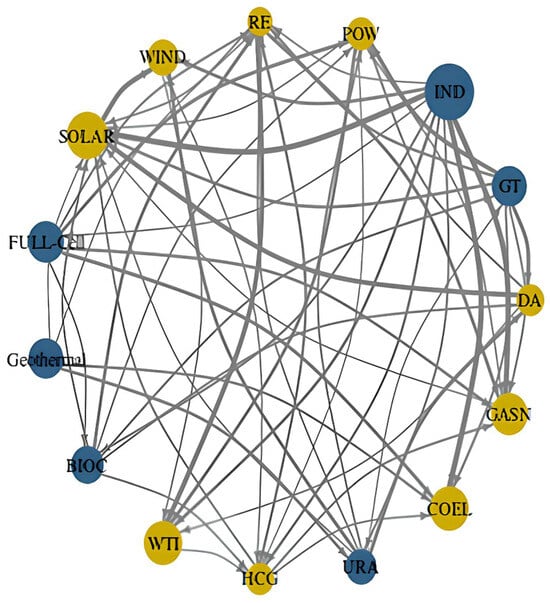
Figure 2.
The network of volatility connectedness.
4.3. Robustness Test
In this section, we conducted experiments using varying window lengths to examine the resilience of our model, explicitly utilizing a 70-day window length and forecasting boundaries of 30 steps. These variations were used to assess the overall spillover and its decomposition, as presented in Table 4. As the dynamic connectedness and network spillover exhibit similar time-varying properties, our findings remain robust to window width. They forecast horizon changes, consistently reflecting the effects discussed in the tables and figures above.

Table 4.
Total connectedness index on the volatility of the robustness test.
To determine the continued presence of previously identified sources and recipients of volatility within the initial group, it is crucial to analyze their functions when a subsequent dataset is introduced. The incorporation of a new time series, such as the Mont Belvieu propane data from Texas, into econometric or financial analyses has the potential to yield nuanced interpretations and necessitate adjustments to the study’s outcomes and theoretical foundations. The utilization of the MontBelvieu propane data, which represents a conventional energy variable, highlights the prominence of carbon metrics and specific RENE sources like geothermal and fuel cells, which serve as the primary channels for transmitting shocks. In contrast, propane primarily serves as a recipient of information in conjunction with traditional energy sources, corroborating previous findings, as shown in Figure 3. The robustness of the spillover patterns across alternative windows emphasizes that systemic risk transmission in US energy markets is structurally persistent. This persistence is linked to socio-economic realities such as the country’s high reliance on private vehicles and aviation for mobility, where fuel demand remains inelastic. These structural dependencies limit the extent to which short-term shocks can be absorbed, explaining why volatility spillovers remain elevated across specifications.
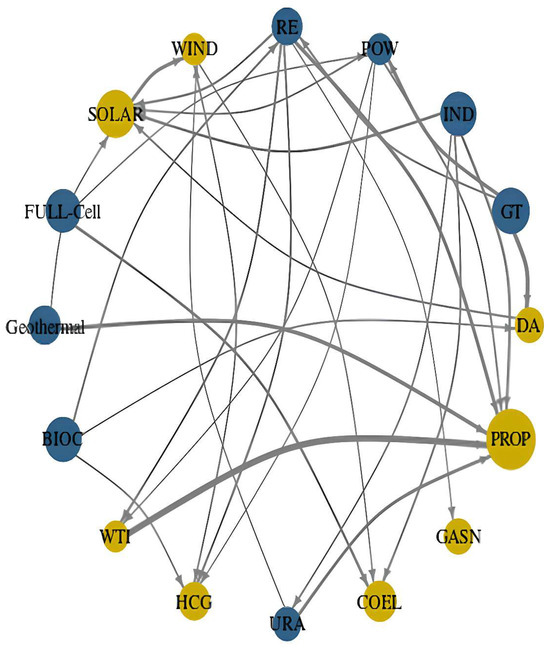
Figure 3.
Network of volatility connectedness after adding further time series.
4.4. Regression Results on the TCI
The remainder of this section will investigate factors influencing the dynamic interconnection between RENE subsectors, traditional energy markets, and carbon-emission-related assets in the presence of net-zero carbon policy targets. To identify the main determinants of the TCI, a linear regression model was applied (Table 5). The model setup we adopt is similar to recent works [52,53,54] and involves the use of macroeconomic and financial variables, among them the EPU index and OVX index, as independent variables. The identification of these drivers is of potential use to policymakers and investors seeking to manage systemic risk and capitalize on cross-market spillovers. The financial variables analyzed include carbon emissions futures (CF), tradeable contracts that allow companies to mitigate their emissions based on the price of future CO2 emissions. These contracts, also known as carbon credits, are traded on markets, including those operated by the Intercontinental Exchange (ICE), and represent the right to emit a specific amount of greenhouse gases. Governments or governing organizations generate these credits. We also include the NASDAQ Clean Edge Green Energy Index (NTI), which measures the performance of businesses in the clean-energy sector, such as solar, wind, and other RENE sources. The SPI and SPT represent the S&P Select Industry and S&P Select Transport, respectively. We adopted the EPU measure [55] as our uncertainty indicator. This information was obtained from the Federal Reserve Bank of St. Louis.

Table 5.
Regression results on the TCI.
Meanwhile, we received the S&P Index and CF data from Yahoo Finance. Furthermore, the CBOE has been publishing the OVX, a critical instrument for gauging oil price volatility, since mid-2007. We can also write this Eq. as follows:
The initial results suggest that the industry sector represented by the S&P had a significant negative impact on the TCI during the COVID-19 pandemic, primarily due to supply-chain disruptions and decreased investment. As a result, as the world strives for a more sustainable future, there is an increasing focus on the importance of investing in zero-carbon [56,57]. At the same time, the transport market is positive, while green technology has a negative effect, but it is insignificant [58]. The CF has a negative impact on the TCI, consistent with previous research indicating that environmental regulations and initiatives aimed at improving carbon efficiency and energy transitions can harm carbon emissions [59,60]. The findings illustrate that the EPU has a positive impact on the TCI, which is consistent with prior research that has identified the EPU in the United States as a significant factor driving the interdependence of the carbon market. Finally, the OVX is positive but insignificant, contradicting the study [61], which found that volatility in oil prices drives volatility spillover in new energy in the long term, including net-zero carbon. The significant adverse effect of the industrial sector highlights the fragility of US supply chains during the COVID-19 pandemic, which exposed vulnerabilities in just-in-time production and reliance on imported inputs. The positive effect of the EPU is consistent with US political polarization, where shifts between Republican and Democratic administrations generate large swings in environmental regulations and market expectations. The insignificant role of the OVX suggests a partial decoupling of renewable subsectors from oil shocks, reflecting the structural transformation of the US energy mix, where domestic shale production and renewable investments have reduced the direct transmission of oil price volatility. Although the regression yields moderate explanatory power, this is consistent with prior high-frequency volatility studies, which often find that market-wide spillovers are driven by unforeseen shocks that observable macro-financial variables cannot fully explain. Thus, the results should be interpreted as capturing the directional influence of uncertainty and sectoral factors on connectedness, rather than as a full decomposition of variance.
Furthermore, we evaluated the reliability of our regression model using a variance inflation factor (VIF) multicollinearity check, as shown in Table 6. The VIF values for all variables were greater than 5 (with a maximum VIF of 1.66), indicating that collinearity is not a significant issue within our model. This ensures that the explanatory variables do not exhibit collinearity, allowing us to interpret the estimated coefficients safely.

Table 6.
Multicollinearity results.
4.5. Portfolio Implications
Following the current literature, this section examines the impact of our connectedness results on portfolio management, utilizing asset portfolio weights that account for their interconnectedness with other variables [62,63]. Table 7 shows the portfolio weights for short positions, long positions, and hedge efficacy between conventional and unconventional energy assets. The mean hedge-ratio values between a long position in clean energy and a short position in the implied return of the traditional range of energy from USD 51:71 cents for the wind to USD 44:63 cents for solar, USD 22:71 cents for fuel cell, USD 48:65 cents for geothermal, and USD 0.49:0.72 cents for bio, indicating that the hedge for a USD 1 position in clean energy is obtained with traditional energy by USD 49 cents. WTI is the least pricey hedge market (USD 42.8 cents), while gas is the costliest (USD 58.4 cents). Nuclear energy has an insignificant p-value, suggesting it cannot be used as a hedge for short or long positions. Despite hedging clean-energy assets with conventional energy, the average hedge ratio in a conventional and non-conventional energy-asset portfolio is USD 0.49, implying that USD 51 cents should be invested in traditional energy markets.

Table 7.
Portfolio implications.
In comparison, USD 19 and USD 78 should be invested in green energy markets in short and long positions, respectively. WTI is the most expensive hedge market (USD 57.2 cents), while GASN is the cheapest (USD 37.4 cents). This implies that uranium is the least-effective index for hedging against RE, with clean energy providing the cheapest hedge for a USD 1 position in URN (USD 9 cents). According to Table 5, the optimum hedge ratios do not remain constant over time, as demonstrated by the standard deviation of 0.15. The uranium asset exhibits the lowest volatility compared to other assets, while COEL with clean energy shows the highest observed volatility. This finding emphasizes the time-varying nature of optimal hedge ratios, implying that investors should employ dynamic hedging strategies rather than static ones. The results demonstrate the sensitivity of green energy to hedge portfolios against conventional energy, achieving a hedging effectiveness of over 42%.
FUEL-CELL/WTI has the highest hedging efficacy, about 78%, while the lowest connection is BIOC/GASN. The findings presented in Table 5 indicate that investing in non-conventional energy is always less profitable than hedging positions through a dynamic hedge ratio and effective hedge strategies. The highest level of effectiveness is observed in the FULL-Cell/WTI connection, which is approximately 78%, while the lowest level of effectiveness is observed in the BIOC/GASN pair. These results demonstrate that the most optimal strategies employ the cheapest hedges, which is typically the most effective hedging strategy. Our findings align with prior studies [37,64]. In addition to the points above, the dynamic optimal hedging weights and ratios are illustrated in Figure 4. The presented visualization provides further evidence, highlighting the significant ability of clean energy to mitigate risks compared to traditional energy markets. The evident correlation between clean energy and its capacity to serve as a reliable safeguard against conventional energy sectors is underscored in the illustrated patterns, strengthening the strategic importance of incorporating clean-energy assets into diversified portfolios.
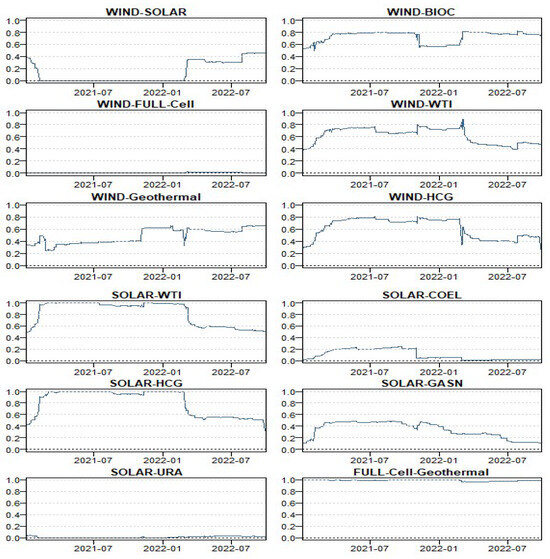
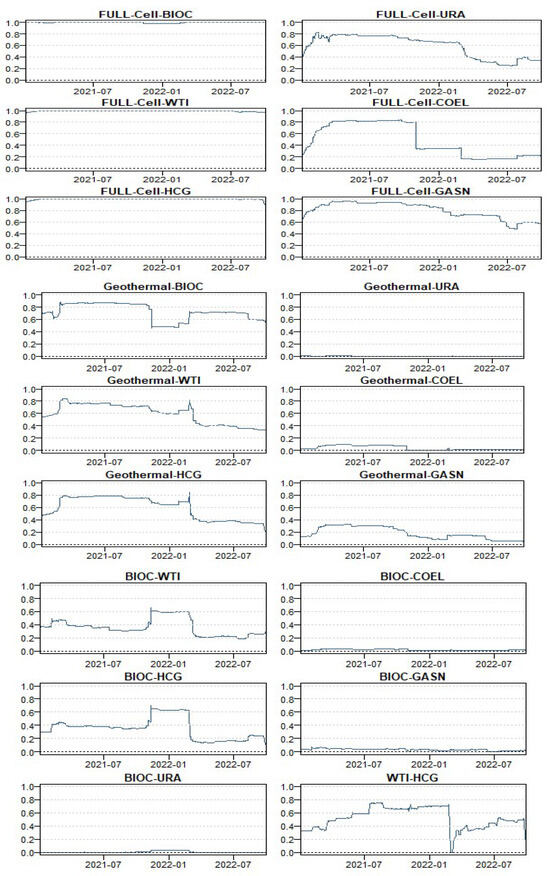
Figure 4.
Dynamic hedge weights.
4.6. Findings Discussion
The findings are largely consistent with those of the complete sample, revealing volatility and return links between the energy markets and carbon emissions. The outcome indicates high cross-market risk transmission, exceeding 80% during and after the COVID-19 pandemic, suggesting that the shock of the pandemic and Russia’s confrontation with Ukraine have intensified the link between carbon emissions and clean- and non-clean-energy markets. Meanwhile, we discovered significant volatility in connectivity among intergroup variables [65]. The system exhibits virtually immediate symmetric behavior in response to shocks, supporting [66], in which it was demonstrated how financial variables become more interconnected during times of crisis. Also, these results align with the work in [67], which reported the vital link between energy and carbon emissions during the crisis. Nuclear, as the only conventional energy market, transmits the shock in the network system. Still, the node size appears smaller than that of the main transmitter in the carbon monitoring sector and the clean-energy market. The findings demonstrate the limited significance of conventional energy in transferring shocks, including oil prices, to clean energy. This result extends the reasoning in [64,68,69], which contend that oil price shocks have a minimal impact on the volatility of clean-energy equities.
On the contrary, during the recent geopolitical and COVID-19 crises, clean energy has sent shockwaves through the traditional energy markets in the USA. The findings indicate that wind and geothermal markets have a small node, separated from the other variables, regarding return and volatility spillovers. The implications of the recent findings regarding the effectiveness of RENE in mitigating risks associated with traditional energy markets are manifold. From a policy standpoint, this supports the argument favoring the maintenance of a diversified energy portfolio, with a particular emphasis on RENE sources. This approach is justified not only on environmental sustainability but also due to its potential to contribute to economic stability. Regulatory authorities are encouraged to guide financial institutions on the potential use of hedging strategies in the context of RENE sources. This encouragement includes promoting transparent reporting practices and ensuring compliance with relevant regulations. At a global level, these findings have the potential to be applied in various energy markets, prompting nations to reassess their investment strategies. This study emphasizes the dual function of RE, serving both as a crucial environmental necessity and a strategic mechanism for mitigating risks within energy portfolios. Also, this result aligns with prior studies [70]. Due to the involvement of various sectors, carbon monitors in the US play a significant role in shaping the energy market.
Unique American socio-economic and structural factors strongly influence the differences across industries in our spillover analysis. One prominent aspect is the transportation structure, which in the United States is overwhelmingly dominated by private automobiles and domestic air travel. More than three-quarters of Americans commute by personal car, at 76%, while only about 11% use public transit, a stark contrast to Europe’s more multimodal transit mix. This heavy reliance on private vehicles—alongside the extensive use of domestic aviation (US aircraft operations contribute roughly 24% of global aviation CO2 emissions) amplifies the ripple effects of fuel price shocks and disruptions in the transport sector. Lacking robust nationwide public transportation or high-speed rail alternatives, ground transportation and domestic aviation in the US remain highly vulnerable to oil price volatility and geopolitical events, which accentuates the system-wide interconnectedness of energy markets. Our finding that the transportation sector (especially ground transportation) emerged as a significant source of volatility is consistent with this structural reality. In contrast, sectors like residential energy use naturally showed more limited spillover influence—yet even those sectors cannot escape indirect effects in such a tightly coupled energy system. Other key dimensions are the industrial sector’s energy intensity and fossil-fuel dependence, which help to explain its outsized role in volatility connectedness. The US industrial sector accounts for approximately one-third of the nation’s energy consumption. This high energy usage makes manufacturing and heavy industry particularly sensitive to fluctuations in input costs and supply-chain stresses. Notably, the fragility of global supply chains, exposed during crises like COVID-19, can exacerbate volatility for energy-intensive industries. Sudden interruptions in the supply of critical materials or fuels cause disproportionate shocks. For instance, pandemic-related disruptions in logistics and production led to dramatic swings in energy prices and availability. Our results, indeed, highlight the industry sector as a central node of volatility spillovers (consistent with its large carbon footprint and energy needs), which can be attributed to the combination of high energy demand, dependency on fossil-fuel inputs, and vulnerability to supply disruptions in US manufacturing. These structural factors underscore why shocks originating from the industrial and transportation sectors tend to spread broadly across other markets in the American context. In contrast, lower-energy sectors have a more contained impact. In addition to these structural drivers, the policy environment and market psychology in the US shape the patterns of volatility connectedness. The political polarization surrounding energy and climate policy has introduced substantial uncertainty into the system. Policy swings—for example, the rollback of environmental regulations under the Trump administration versus the ambitious clean energy push under the Biden administration—create an unstable investment climate.
5. Conclusions
5.1. Key Research Findings
This study examines the impact of five green energy subsectors and five conventional energy sources on carbon emissions across five sectors, including the power sector. CO2 emissions decreased and then increased during the COVID-19 pandemic and since the RUW. The VAR connectedness framework showed that cross-market risk transmission exceeded 80% during and after the COVID-19 pandemic. Carbon emissions and clean- and non-clean-energy markets are more closely linked due to the COVID-19 shock and the RUW.
5.2. Policy Implications
This study offers a high-frequency, sectoral-level view of connectedness dynamics, supplementing the burgeoning literature on climate–finance interactions. The results of this research provide significant insights for major stakeholders, particularly in the fluctuations of carbon-intensive and clean-energy sectors. The high levels of and significant differences in connectedness across the sectors signal that sector-specific decarbonization policies are essential for policymakers to address climate change. The central volatility generators—transportation and industry—need strong regulation through zero-emission vehicle mandates, industrial incentives for electrification, and carbon-adjusted tax structures. Moreover, anchoring the EPU via predictable, transparent environmental regulations (encompassing, for example, long-run clean-energy subsidies or cap-and-trade coverage) would lower the passage of uncertainty shocks across markets. During crises, higher TCI levels signal to investment/fund managers that they must consider systemic spillover risk during the portfolio-construction process. During periods of elevated volatility, diversification strategies should account for sectoral spillover intensity and HE to maximize risk-adjusted returns. The strong effects of the OVX and CF also suggest introducing signals based on macro-volatility indicators and carbon-pricing mechanisms into asset-allocation frameworks. The two-way relationship between clean-energy indices and emissions-intensive sectors also serves as a stark reminder to stakeholders in the energy market, including utilities, investors, and firms associated with clean tech, of the critical importance of resilience-building in operational and financial planning. Grid stability, storage investments, and the feasibility of decentralized, de-risked systems are essential to offset negative externalities and enhance resilience during periods of geopolitical or macroeconomic turmoil. Taken together, these suggestions will help to fortify timely and adaptive decision making for sustainable, low-carbon economic transitions.
5.3. Limitations and Future Research
Our manuscript has a few limitations, which can serve as a foundation for future research. First, although our results are robust within the US context, we acknowledge that they may not be generalizable to other developing economies due to differences in energy infrastructure, regulatory environments, and exposure to shocks. Compared to emerging markets, which have lower RENE penetration, more dispersed carbon-pricing mechanisms, and greater vulnerability to external shocks such as political threats or commodity price fluctuations, the volatility and connectedness reported in this study may not fully represent countries that are transitioning from steam-regulated energy systems to clean energy with limited institutional capacity. We look forward to future research that expands this framework across a broader range of emerging economies, thereby enhancing the global applicability of the results and providing insights into more inclusive net-zero policy strategies. Second, although our analysis builds on the Diebold–Yilmaz VAR-based framework for its clarity and dominance in the spillover literature, we recognize the value of more advanced methodologies, such as TVP-VAR, QVAR, and machine learning-based nonlinear connectedness frameworks. These alternatives are better equipped to capture crisis-induced structural breaks or regime-switching behavior, which we aim to consider in future work. Our current choice enables straightforward interpretation and benchmarking against the existing literature while maintaining consistency with high-frequency data dynamics. Third, our paper examines the 2021–2022 period, characterized by a confluence of the following particularly acerbic crisis states: the COVID-19 pandemic and the RUW. This provides a context for studying extreme volatility dynamics, which, however, may not be general enough for the research conclusions to be scalable to calmer periods or future crises, unlike the present. Similarly, the temporal extent of daily high-frequency sectoral CO2 data that have become available globally is relatively limited compared to the complete archive of emissions tracking. Fourth, while integrated into the TCI as a third determinant factor, it is also valuable to note that the EPU can be endogenously influenced by market volatility and macroeconomic shocks themselves, especially during crisis states. This timing may introduce endogeneity, and, thus, the estimated coefficients on policy risk may be inflated as a result. The incorporation of these endogeneity issues addressed this by semi-logarithmically transforming the variables; however, future extensions could incorporate best instrumental variable approaches and structural VAR methods. We should note that ESG signals, specifically firm-level or sectoral ESG scores and sustainability metrics, are excluded from the current analysis due to a lack of high-frequency data on these factors. However, ESG behavior could powerfully mediate the transmission of volatility, particularly in clean-energy sectors, which generally attract investor sentiment that tilts towards ESG. Future high-frequency connectedness-based works may be even more explanatory and useful for sustainable finance issues if we incorporate ESG factors into their models. Finally, a key limitation of our regression analysis is the relatively modest explanatory power (R2 = 0.65). While this aligns with other high-frequency volatility studies, it highlights the presence of unobserved factors—such as geopolitical shocks, sudden policy changes, or investor sentiment—that influence systemic connectedness but are not captured by our set of regressors. As a result, the coefficients should be understood as indicative of directional relationships rather than precise measures of explanatory strength. Future research could incorporate additional macroeconomic and climate risk indicators to enhance explanatory power.
Author Contributions
Conceptualization, H.A. and K.S.M.; Methodology, H.A.; Validation, K.S.M.; Formal Analysis, H.A.; Data Curation, K.S.M.; Writing—Original Draft Preparation, H.A.; Writing—Review and Editing, K.S.M.; Supervision, K.S.M. All authors have read and agreed to the published version of the manuscript.
Funding
The authors extend their appreciation to the Deanship of Scientific Research and Libraries in Princess Nourah bint Abdulrahman University for funding this research work through the Research Group project, Grant No. (RG-2025-04).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors upon request.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| VAR | Vector Autoregressive |
| GFEVD | Generalized Forecast Error Variance Decomposition |
| DCC-GARCH | Dynamic Conditional Correlation Generalized Autoregressive Conditional Heteroskedasticity |
| BEKK | Baba, Engle, Kraft, and Kroner’s |
| HE | Hedge Effectiveness |
| TCI | Total Connectedness Index |
| INC.OWN | Including Own Forecast Variance |
| RUW | Russia–Ukraine War |
| RENE | Renewable Energy |
| CO2 | Carbon Dioxide |
| ESG | Environmental, Social, and Governance |
| EPU | Economic Policy Uncertainty |
| OVX | Oil Volatility Index |
| CF | Carbon Emissions Futures |
| SPI | S&P Select Industry Index |
| SPT | S&P Select Transport Index |
| NTI | NASDAQ Clean Edge Green Energy Index |
| NOMXS | Nasdaq OMX Bioenergy Subindex |
| NOMXW | Nasdaq OMX Wind Energy Subindex |
| NOMXG | Nasdaq OMX Geothermal Energy Subindex |
| NOMXFC | Nasdaq OMX Fuel Cell Subindex |
| NOMXB | Nasdaq OMX Solar Energy Subindex |
| POW | Power Sector |
| IND | Industrial Sector |
| GT | Ground Transportation Sector |
| DA | Domestic Aviation Sector |
| Res | Residential Sector |
| WTI | West Texas Intermediate (Crude Oil Benchmark) |
| HCG | Harbor Conventional Gasoline (New York) |
| URA | Uranium Market Index |
| COAL | Coal Price Index |
| GASN | Natural Gas Index |
| BIOC | Bioenergy Sector Index |
References
- Borowski, P.F. Economic and Technological Challenges in Zero-Emission Strategies for Energy Companies. Energies 2025, 18, 898. [Google Scholar] [CrossRef]
- Bistline, J.E.T.; Binsted, M.; Blanford, G.; Boyd, G.; Browning, M.; Cai, Y.; Edmonds, J.; Fawcett, A.A.; Fuhrman, J.; Gao, R.; et al. Policy implications of net-zero emissions: A multi-model analysis of United States emissions and energy system impacts. Energy Clim. Change 2025, 6, 100191. [Google Scholar] [CrossRef]
- Chen, L.; Li, X.; Zhu, J. Carbon peak control for achieving net-zero renewable-based smart cities: Digital twin modeling and simulation. Sustain. Energy Technol. Assess. 2024, 65, 103792. [Google Scholar] [CrossRef]
- Ongoma, V.; Epule, T.E.; Brouziyne, Y.; Tanarhte, M.; Chehbouni, A. COVID-19 response in Africa: Impacts and lessons for environmental management and climate change adaptation. Environ. Dev. Sustain. 2024, 26, 5537–5559. [Google Scholar] [CrossRef]
- Al-Maadid, A.; Ben Ali, M.S.; Si Mohammed, K. The effect of climate risk on the human development index using the panel time-varying interactive fixed effects. Environ. Sustain. Indic. 2025, 27, 100757. [Google Scholar] [CrossRef]
- Bakkar, Y.; Ben Jabeur, S.; Si Mohammed, K.; Ben Arfi, W. Environmental transition dynamics under external conflict risk: New evidence from European countries. J. Clean. Prod. 2024, 472, 143510. [Google Scholar] [CrossRef]
- Van Heerden, R.; Edelenbosch, O.Y.; Daioglou, V.; Le Gallic, T.; Baptista, L.B.; Di Bella, A.; Colelli, F.P.; Emmerling, J.; Fragkos, P.; Hasse, R.; et al. Demand-side strategies enable rapid and deep cuts in buildings and transport emissions to 2050. Nat. Energy 2025, 10, 380–394. [Google Scholar] [CrossRef]
- Monjardino, J.; Dias, L.; Fortes, P.; Tente, H.; Ferreira, F.; Seixas, J. Carbon neutrality pathways effects on air pollutant emissions: The Portuguese case. Atmosphere 2021, 12, 324. [Google Scholar] [CrossRef]
- Mohammed, K.S.; Magdalena, R.; Alofaysan, H.; Hagiu, A. The Impact of Green and Energy Investments on Environmental Sustainability in China: A Technological and Financial Development Perspectives. Environ. Model. Assess. 2025, 1–21. [Google Scholar] [CrossRef]
- Strielkowski, W.; Tarkhanova, E.; Tvaronavičienė, M.; Petrenko, Y. Renewable Energy in the Sustainable Development of Electrical. Energies 2021, 14, 8240. [Google Scholar] [CrossRef]
- Elder, M.; Zusman, E.; Hengesbaugh, M. Why the Second Trump Administration Could Struggle to Undermine Domestic Climate Policies: Obstacles to Backsliding; Institute for Global Environmental Strategies: Kanagawa, Japan, 2025; pp. 1–24. [Google Scholar]
- Hu, L.; Chen, S.; Zhang, C.; Zhou, L.; Li, A. Understanding the heterogeneous roles of China’s sectors under the shock of second Trump administration’s new tariffs: A novel method of shock-based input-output data envelopment analysis. Energy 2025, 324, 135687. [Google Scholar] [CrossRef]
- Ali, A.H.; Abdalla, M. Energy transitions era: Geopolitical characteristics and connotations in the Arab Gulf States. Sustain. Futur. 2025, 10, 100808. [Google Scholar] [CrossRef]
- International Energy Agency (IEA). Renewable Energy Market: Update Outlook for 2020 and 2021; IEA Report; International Energy Agency: Paris, France, 2020; p. 63. [Google Scholar]
- Diebold, F.X.; Yilmaz, K. On the network topology of variance decompositions: Measuring the connectedness of financial firms. J. Econom. 2014, 182, 119–134. [Google Scholar] [CrossRef]
- Diebold, F.X.; Yilmaz, K. Better to give than to receive: Predictive directional measurement of volatility spillovers. Int. J. Forecast. 2012, 28, 57–66. [Google Scholar] [CrossRef]
- Gupta, R.; Pierdzioch, C. Do US economic conditions at the state level predict the realized volatility of oil-price returns? A quantile machine-learning approach. Financ. Innov. 2023, 9, 24. [Google Scholar] [CrossRef] [PubMed]
- Alshammari, S.; Andriosopoulos, K.; Kaabia, O.; Si Mohamed, K.; Urom, C. The interplay among corporate bonds, geopolitical risks, equity market, and economic uncertainties. Int. Rev. Financ. Anal. 2024, 95, 103350. [Google Scholar] [CrossRef]
- Apergis, N.; Payne, J.E.; Menyah, K.; Wolde-Rufael, Y. On the causal dynamics between emissions, nuclear energy, renewable energy, and economic growth. Ecol. Econ. 2010, 69, 2255–2260. [Google Scholar] [CrossRef]
- Okorie, D.I.; Lin, B. Crude oil price and cryptocurrencies: Evidence of volatility connectedness and hedging strategy. Energy Econ. 2020, 87, 104703. [Google Scholar] [CrossRef]
- Asadi, M.; Roubaud, D.; Tiwari, A.K. Volatility spillovers amid crude oil, natural gas, coal, stock, and currency markets in the US and China based on time and frequency domain connectedness. Energy Econ. 2022, 109, 105961. [Google Scholar] [CrossRef]
- Farid, S.; Naeem, M.A.; Paltrinieri, A.; Nepal, R. Impact of COVID-19 on the quantile connectedness between energy, metals and agriculture commodities. Energy Econ. 2022, 109, 105962. [Google Scholar] [CrossRef]
- Ghosh, B.; Pham, L.; Teplova, T.; Umar, Z. COVID-19 and the quantile connectedness between energy and metal markets. Energy Econ. 2023, 117, 106420. [Google Scholar] [CrossRef]
- Alshammari, S.; Serret, V.; Tiwari, S.; Si Mohammed, K. Industry 4.0 and AI amid economic uncertainty: Implications for sustainable markets. Res. Int. Bus. Financ. 2025, 75, 102773. [Google Scholar] [CrossRef]
- Kumar, S.; Managi, S.; Matsuda, A. Stock prices of clean energy firms, oil and carbon markets: A vector autoregressive analysis. Energy Econ. 2012, 34, 215–226. [Google Scholar] [CrossRef]
- Zhao, X.; Si Mohammed, K.; Wang, Y.; Stępień, P.; Mentel, G. Effect of geopolitical risk and economic uncertainty indices on renewable energy. Geosci. Front. 2024, 15, 101655. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, X.; Zhou, C.; Zhang, Y.; Wei, Y. Examining the quantile cross-coherence between fossil energy and clean energy: Is the dependence structure changing with the COVID-19 outbreak? Int. Rev. Financ. Anal. 2024, 94, 103266. [Google Scholar] [CrossRef]
- Udeagha, M.C.; Breitenbach, M.C. Revisiting the nexus between fiscal decentralization and CO2 emissions in South Africa: Fresh policy insights. Financ. Innov. 2023, 9, 50. [Google Scholar] [CrossRef]
- Arnell, L.; Engström, E.; Uddin, G.S.; Hasan, M.B.; Kang, S.H. Volatility spillovers, structural breaks and uncertainty in technology sector markets. Financ. Innov. 2023, 9, 106. [Google Scholar] [CrossRef]
- Ferreira, P.; Almeida, D.; Dionísio, A.; Bouri, E.; Quintino, D. Energy markets–Who are the influencers? Energy 2022, 239, 121962. [Google Scholar] [CrossRef]
- US Environmental Protection Agency. Sources of Greenhouse Gas Emissions; US Environmental Protection Agency: Washington, DC, USA, 2022. [Google Scholar]
- Energy Information Administration (EIA). Short-Term Energy Outlook; US Department of Energy: Washington, DC, USA, 2022; pp. 4–6. [Google Scholar]
- Liu, Z.; Deng, Z.; Davis, S.J.; Giron, C.; Ciais, P. Monitoring global carbon emissions in 2021. Nat. Rev. Earth Environ. 2022, 3, 217–219. [Google Scholar] [CrossRef] [PubMed]
- Yadav, M.; Mishra, N.; Ashok, S. Dynamic connectedness of green bond with financial markets of European countries under OECD economies. Econ. Change Restruct. 2023, 56, 609–631. [Google Scholar] [CrossRef]
- Liu, T.; Nakajima, T.; Hamori, S. The impact of economic uncertainty caused by COVID-19 on renewable energy stocks. Empir. Econ. 2022, 62, 1495–1515. [Google Scholar] [CrossRef] [PubMed]
- Naeem, M.A.; Karim, S.; Tiwari, A.K. Risk Connectedness Between Green and Conventional Assets with Portfolio Implications. Comput. Econ. 2023, 62, 609–637. [Google Scholar] [CrossRef]
- Mohammed, K.S.; Usman, M.; Ahmad, P.; Bulgamaa, U. Do all renewable energy stocks react to the war in Ukraine? Russo-Ukrainian conflict perspective. Environ. Sci. Pollut. Res. 2023, 30, 36782–36793. [Google Scholar] [CrossRef]
- Hossain, M.R.; Ben Jabeur, S.; Si Mohammed, K.; Shahzad, U. Time-varying relatedness and structural changes among green growth, clean energy innovation, and carbon market amid exogenous shocks: A quantile VAR approach. Technol. Forecast. Soc. Change 2024, 208, 123705. [Google Scholar] [CrossRef]
- Xu, C.; Chen, Z.; Zhu, W.; Zhi, J.; Yu, Y.; Shi, C. Time-frequency spillover and early warning of climate risk in international energy markets and carbon markets: From the perspective of complex network and machine learning. Energy 2025, 318, 134857. [Google Scholar] [CrossRef]
- Attarzadeh, A.; Balcilar, M. On the Dynamic Connectedness of the Stock, Oil, Clean Energy, and Technology Markets. Energies 2022, 15, 1893. [Google Scholar] [CrossRef]
- Dong, F.; Li, Z.; Huang, Z.; Liu, Y. Extreme weather, policy uncertainty, and risk spillovers between energy, financial, and carbon markets. Energy Econ. 2024, 137, 107761. [Google Scholar] [CrossRef]
- Ben Jabeur, S.; Gozgor, G.; Rezgui, H.; Mohammed, K.S. Dynamic dependence between quantum computing stocks and Bitcoin: Portfolio strategies for a new era of asset classes. Int. Rev. Financ. Anal. 2024, 95, 103478. [Google Scholar] [CrossRef]
- Bollerslev, T. A generalized least absolute deviation method for parameter estimation of autoregressive signals. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- Engle, R.F. Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica 1982, 50, 987. [Google Scholar] [CrossRef]
- Antonakakis, N.; Chatziantoniou, I.; Floros, C.; Gabauer, D. The dynamic connectedness of UK regional property returns. Urban Stud. 2018, 55, 3110–3134. [Google Scholar] [CrossRef]
- Patton, A.J. Modelling asymmetric exchange rate dependence. Int. Econ. Rev. 2006, 47, 527–556. [Google Scholar] [CrossRef]
- Emenogu, N.G.; Adenomon, M.O.; Nweze, N.O. On the volatility of daily stock returns of Total Nigeria Plc: Evidence from GARCH models, value-at-risk and backtesting. Financ. Innov. 2020, 6, 18. [Google Scholar] [CrossRef]
- Antonakakis, N.; Cunado, J.; Filis, G.; Gabauer, D.; Gracia, F.P. De Oil volatility, oil and gas firms and portfolio diversification. Energy Econ. 2018, 70, 499–515. [Google Scholar] [CrossRef]
- Kroner, K.F.; Jahangir, S. Time-Varying Distributions and Dynamic Hedging with Foreign Currency Futures. J. Financ. Quant. Anal. 1993, 28, 535–551. [Google Scholar] [CrossRef]
- Roner, K.F.; Ng, V.K. Modeling Asymmetric Comovements of Asset Returns, Review of. Rev. Financ. Stud. 1998, 11, 817–844. [Google Scholar]
- EDERINGTON, L.H. The Hedging Performance of the New Futures Markets. J. Financ. 1979, 34, 157–170. [Google Scholar] [CrossRef]
- Charfeddine, L.; Benlagha, N.; Khediri, K. Ben An intra-cryptocurrency analysis of volatility connectedness and its determinants: Evidence from mining coins, non-mining coins and tokens. Res. Int. Bus. Financ. 2022, 62, 101699. [Google Scholar] [CrossRef]
- Balcilar, M.; Cakan, E.; Gupta, R. Does US news impact Asian emerging markets? Evidence from nonparametric causality-in-quantiles test. N. Am. J. Econ. Financ. 2017, 41, 32–43. [Google Scholar] [CrossRef]
- Ji, Q.; Bouri, E.; Lau, C.K.M.; Roubaud, D. Dynamic connectedness and integration in cryptocurrency markets. Int. Rev. Financ. Anal. 2019, 63, 257–272. [Google Scholar] [CrossRef]
- Baker Nicholas Bloom Steven J Davis, S.R.; Jorring, A.; Kost, K.; Al-Kuwari, A.; Biffar, S.; Boehnke, J.; Dashkeyev, V.; Deriy, O.; Dinh, E.; Ezure, Y.; et al. Measuring Economic Policy Uncertainty. Q. J. Econ. 2016, 131, 1593–1636. [Google Scholar] [CrossRef]
- Shahzad, U.; Si Mohammed, K.; Schneider, N.; Faggioni, F.; Papa, A. Technological Forecasting & Social Change GDP responses to supply chain disruptions in a post-pandemic era: Combination of DL and ANN outputs based on Google Trends. Technol. Forecast. Soc. Change 2023, 192, 122512. [Google Scholar] [CrossRef]
- Vats, G.; Mathur, R. A net-zero emissions energy system in India by 2050: An exploration. J. Clean. Prod. 2022, 352, 131417. [Google Scholar] [CrossRef]
- Raza, S.A.; Shah, N.; Sharif, A. Time frequency relationship between energy consumption, economic growth and environmental degradation in the United States: Evidence from transportation sector. Energy 2019, 173, 706–720. [Google Scholar] [CrossRef]
- Xu, H.; Pan, X.; Li, J.; Feng, S.; Guo, S. Comparing the impacts of carbon tax and carbon emission trading, which regulation is more effective? J. Environ. Manag. 2023, 330, 117156. [Google Scholar] [CrossRef]
- Li, S.; Cifuentes-Faura, J.; Talbi, B.; Sadiq, M.; Si Mohammed, K.; Bashir, M.F. Dynamic correlated effects of electricity prices, biomass energy, and technological innovation in Tunisia’s energy transition. Util. Policy 2023, 82, 101521. [Google Scholar] [CrossRef]
- Qu, F.; Chen, Y.; Zheng, B. Is new energy driven by crude oil, high-tech sector or low-carbon notion? New evidence from high-frequency data. Energy 2021, 230, 120770. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Aikins Abakah, E.J.; Gabauer, D.; Dwumfour, R.A. Dynamic spillover effects among green bond, renewable energy stocks and carbon markets during COVID-19 pandemic: Implications for hedging and investments strategies. Glob. Financ. J. 2022, 51, 100692. [Google Scholar] [CrossRef]
- Pham, L.; Hao, M.; Truong, H.; Trinh, H.H. The Impact of Climate Policy on U.S. Clean Energy Firms: A Firm-Level Examination of Stock Return, Volume, Volatility, and Connectedness. SSRN Electron. J. 2022. [Google Scholar] [CrossRef]
- Umar, M.; Farid, S.; Naeem, M.A. Time-frequency connectedness among clean-energy stocks and fossil fuel markets: Comparison between financial, oil and pandemic crisis. Energy 2022, 240, 122702. [Google Scholar] [CrossRef]
- Shahzad, U.; Si, K.; Tiwari, S.; Nakonieczny, J.; Nesterowicz, R. Connectedness between geopolitical risk, financial instability indices and precious metals markets: Novel findings from Russia Ukraine conflict perspective. Resour. Policy 2023, 80, 103190. [Google Scholar] [CrossRef]
- Bossman, A.; Umar, Z.; Agyei, S.K.; Junior, P.O. A new ICEEMDAN-based transfer entropy quantifying information flow between real estate and policy uncertainty. Res. Econ. 2022, 76, 189–205. [Google Scholar] [CrossRef]
- Umar, M.; Mirza, N.; Hasnaoui, J.A.; Rochoń, M.P. The nexus of carbon emissions, oil price volatility, and human capital efficiency. Resour. Policy 2022, 78, 17–22. [Google Scholar] [CrossRef]
- Sadorsky, P. Correlations and volatility spillovers between oil prices and the stock prices of clean energy and technology companies. Energy Econ. 2012, 34, 248–255. [Google Scholar] [CrossRef]
- Kang, S.; Hernandez, J.A.; Sadorsky, P.; McIver, R. Frequency spillovers, connectedness, and the hedging effectiveness of oil and gold for US sector ETFs. Energy Econ. 2021, 99, 105278. [Google Scholar] [CrossRef]
- Kuang, Z.; Chen, Q.; Yu, Y. Assessing the CO2-emission risk due to wind-energy uncertainty. Appl. Energy 2022, 310, 118615. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).