Applicability Evaluation of an Online Parameter Identification Method: From Lithium-Ion to Lithium–Sulfur Batteries
Abstract
1. Introduction
2. Methodology
2.1. Battery Cell Modeling
2.2. FFRLS Algorithm
| Algorithm 1 FFRLS |
| Input:
, , , 1: Prediction errors: 2: Gain: 3: Covariance matrix update: 4: Parameter vector update: Output: |
2.3. Fisher Information Matrix
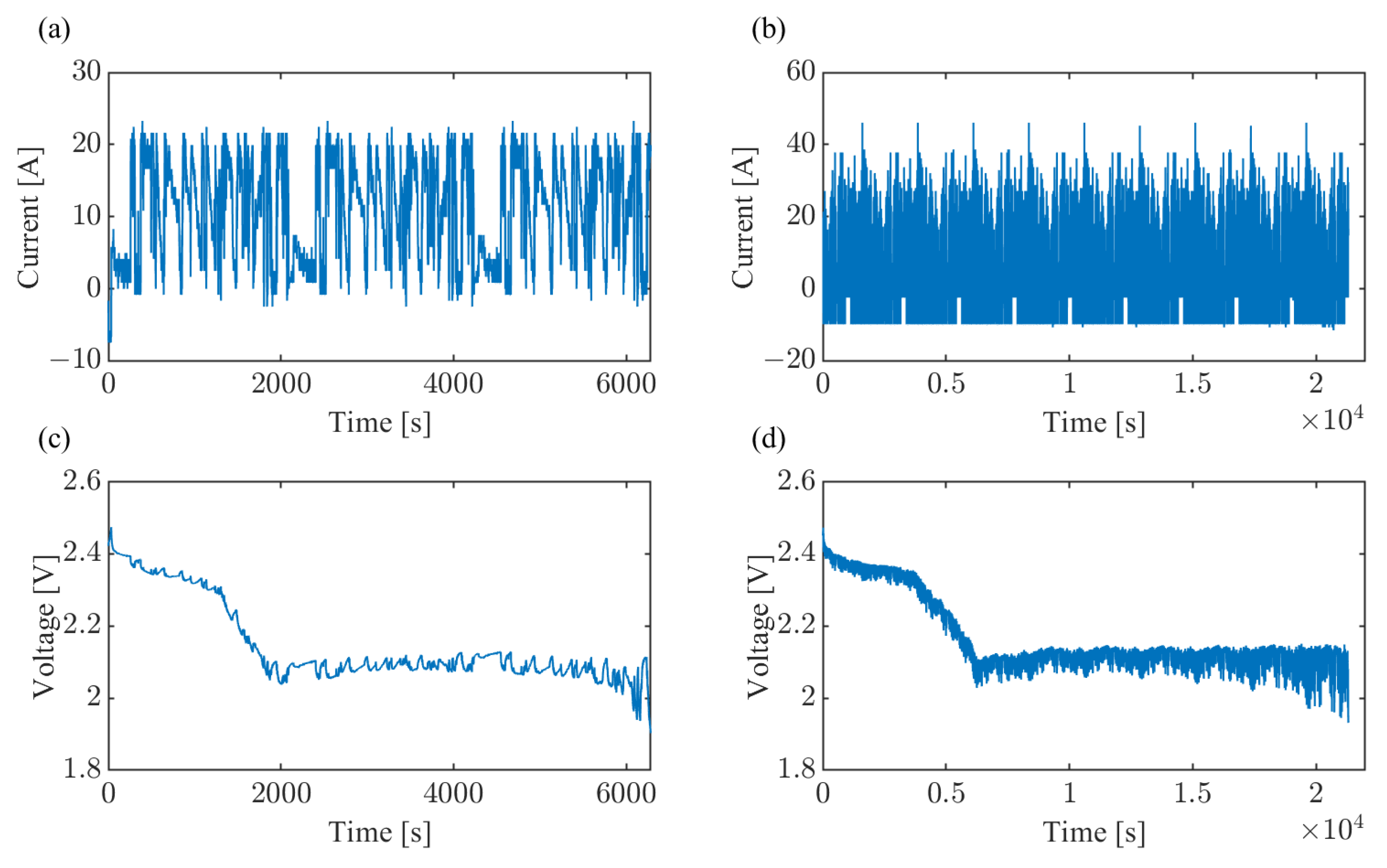
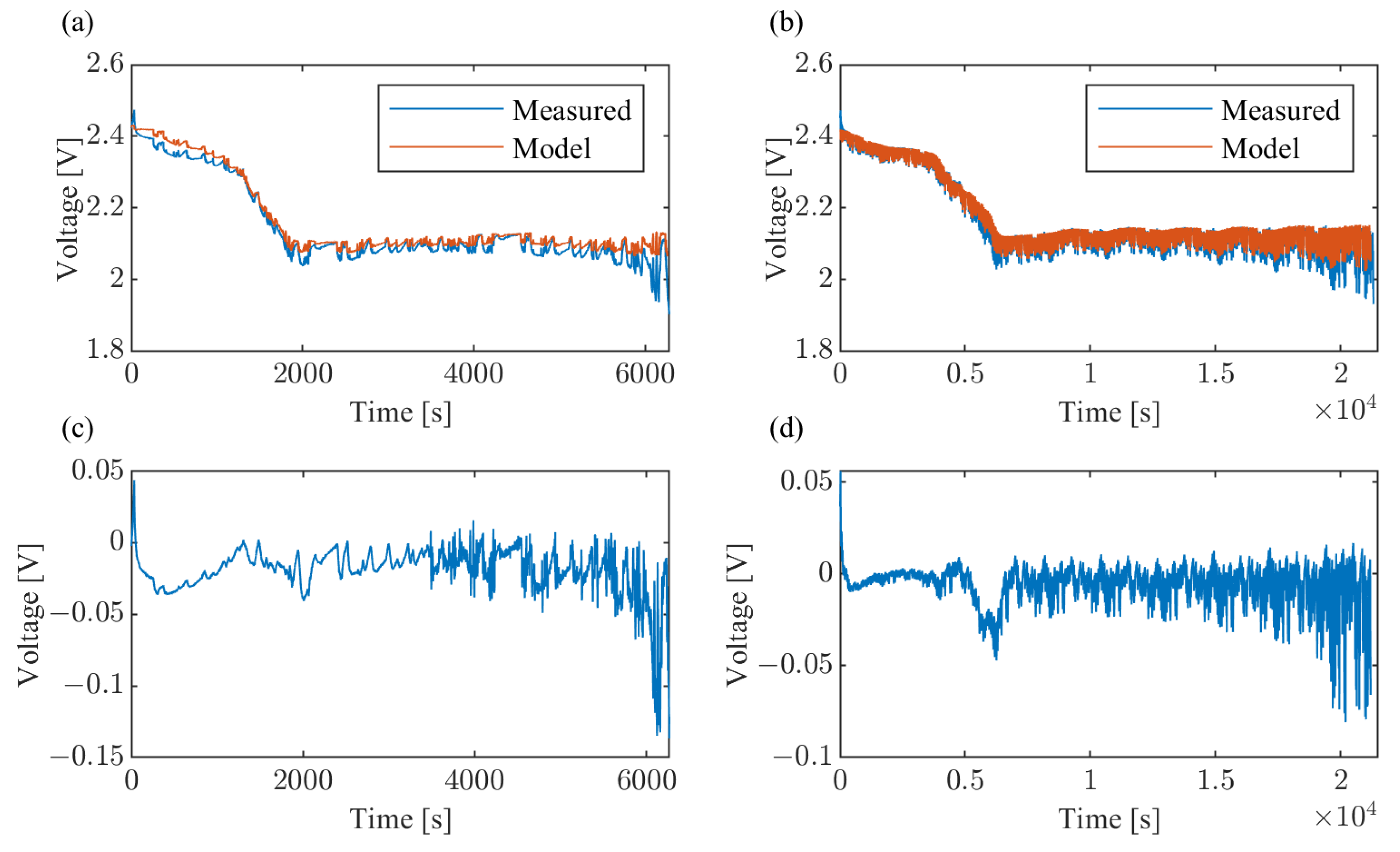
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Li-S | Lithium–sulfur |
| ECN | Equivalent circuit network |
| RMSE | Root mean square error |
| BMS | Battery management system |
| Li-ion | Lithium-ion |
| SOC | State of charge |
| SOH | State of health |
| OCV | Open-circuit voltage |
| SISO | Single input–single output |
| DP | Dual polarization |
| RC | Resistor–capacitor |
| FF | Forgetting factor |
| FFRLS | Forgetting factor recursive least square |
| CRB | Cramér–Rao lower bound |
References
- Fotouhi, A.; Auger, D.J.; Propp, K.; Longo, S.; Wild, M. A review on electric vehicle battery modelling: From Lithium-ion toward Lithium–Sulphur. Renew. Sustain. Energy Rev. 2016, 56, 1008–1021. [Google Scholar] [CrossRef]
- Fotouhi, A.; Auger, D.J.; O’Neill, L.; Cleaver, T.; Walus, S. Lithium-sulfur battery technology readiness and applications—A review. Energies 2017, 10, 1937. [Google Scholar] [CrossRef]
- Dörfler, S.; Walus, S.; Locke, J.; Fotouhi, A.; Auger, D.J.; Shateri, N.; Abendroth, T.; Härtel, P.; Althues, H.; Kaskel, S. Recent progress and emerging application areas for lithium–sulfur battery technology. Energy Technol. 2021, 9, 2000694. [Google Scholar] [CrossRef]
- Sun, Z.; Guo, Y.; Zhang, C.; Whitehouse, J.; Zhou, Q.; Xu, H.; Wang, C. Experimental study of battery passive thermal management system using copper foam-based phase change materials. Int. J. Thermofluids 2023, 17, 100255. [Google Scholar] [CrossRef]
- Zhao, M.; Li, B.Q.; Zhang, X.Q.; Huang, J.Q.; Zhang, Q. A perspective toward practical lithium–sulfur batteries. ACS Cent. Sci. 2020, 6, 1095–1104. [Google Scholar] [CrossRef]
- Zhou, G.; Chen, H.; Cui, Y. Formulating energy density for designing practical lithium–sulfur batteries. Nat. Energy 2022, 7, 312–319. [Google Scholar] [CrossRef]
- Urbonaite, S.; Poux, T.; Novák, P. Progress towards commercially viable Li–S battery cells. Adv. Energy Mater. 2015, 5, 1500118. [Google Scholar] [CrossRef]
- Shi, C.; Yu, M. Flexible solid-state lithium-sulfur batteries based on structural designs. Energy Storage Mater. 2023, 57, 429–459. [Google Scholar] [CrossRef]
- Shateri, N.; Shi, Z.; Auger, D.J.; Fotouhi, A. Lithium-sulfur cell state of charge estimation using a classification technique. IEEE Trans. Veh. Technol. 2020, 70, 212–224. [Google Scholar] [CrossRef]
- Li, G.; Chen, Z.; Lu, J. Lithium-sulfur batteries for commercial applications. Chem 2018, 4, 3–7. [Google Scholar] [CrossRef]
- Sun, Z.; Guo, Y.; Zhang, C.; Zhou, Q.; Xu, H.; Wang, C. Algorithm-driven optimization of lithium-ion battery thermal modeling. J. Energy Storage 2023, 65, 107388. [Google Scholar] [CrossRef]
- Gong, Y.; Auger, D.J.; Fotouhi, A.; Hale, C.J. A new topology for electric all-terrain vehicle hybrid battery systems using low-frequency discrete cell switching. IEEE Trans. Transp. Electrif. 2022, 9, 609–621. [Google Scholar] [CrossRef]
- Zhang, T.; Marinescu, M.; Walus, S.; Offer, G.J. Modelling transport-limited discharge capacity of lithium-sulfur cells. Electrochim. Acta 2016, 219, 502–508. [Google Scholar] [CrossRef]
- Shateri, N.; Auger, D.J.; Fotouhi, A.; Brighton, J. Charging characterization of a high-capacity lithium-sulfur pouch cell for state estimation: An experimental approach. Energy Storage 2023, 5, e412. [Google Scholar] [CrossRef]
- Cai, C.; Gong, Y.; Fotouhi, A.; Auger, D.J. A novel hybrid electrochemical equivalent circuit model for online battery management systems. J. Energy Storage 2024, 99, 113142. [Google Scholar] [CrossRef]
- Sun, Z.; Guo, Y.; Zhang, C.; Xu, H.; Zhou, Q.; Wang, C. A novel hybrid battery thermal management system for prevention of thermal runaway propagation. IEEE Trans. Transp. Electrif. 2022, 9, 5028–5038. [Google Scholar] [CrossRef]
- Propp, K.; Auger, D.J.; Fotouhi, A.; Longo, S.; Knap, V. Kalman-variant estimators for state of charge in lithium-sulfur batteries. J. Power Sources 2017, 343, 254–267. [Google Scholar] [CrossRef]
- Meng, J.; Luo, G.; Ricco, M.; Swierczynski, M.; Stroe, D.I.; Teodorescu, R. Overview of lithium-ion battery modeling methods for state-of-charge estimation in electrical vehicles. Appl. Sci. 2018, 8, 659. [Google Scholar] [CrossRef]
- Zheng, Y.; Gao, W.; Han, X.; Ouyang, M.; Lu, L.; Guo, D. An accurate parameters extraction method for a novel on-board battery model considering electrochemical properties. J. Energy Storage 2019, 24, 100745. [Google Scholar] [CrossRef]
- Ouyang, M.; Liu, G.; Lu, L.; Li, J.; Han, X. Enhancing the estimation accuracy in low state-of-charge area: A novel onboard battery model through surface state of charge determination. J. Power Sources 2014, 270, 221–237. [Google Scholar] [CrossRef]
- Rotas, R.; Iliadis, P.; Nikolopoulos, N.; Rakopoulos, D.; Tomboulides, A. Dynamic battery modeling for electric vehicle applications. Batteries 2024, 10, 188. [Google Scholar] [CrossRef]
- Tran, M.K.; Mathew, M.; Janhunen, S.; Panchal, S.; Raahemifar, K.; Fraser, R.; Fowler, M. A comprehensive equivalent circuit model for lithium-ion batteries, incorporating the effects of state of health, state of charge, and temperature on model parameters. J. Energy Storage 2021, 43, 103252. [Google Scholar] [CrossRef]
- Nejad, S.; Gladwin, D.; Stone, D. A systematic review of lumped-parameter equivalent circuit models for real-time estimation of lithium-ion battery states. J. Power Sources 2016, 316, 183–196. [Google Scholar] [CrossRef]
- Jiang, C.; Wang, S.; Wu, B.; Etse-Dabu, B.; Xiong, X. A novel adaptive extended Kalman filtering and electrochemical-circuit combined modeling method for the online ternary battery state-of-charge estimation. Int. J. Electrochem. Sci. 2020, 15, 9720–9733. [Google Scholar] [CrossRef]
- Tran, M.K.; Mevawalla, A.; Aziz, A.; Panchal, S.; Xie, Y.; Fowler, M. A review of lithium-ion battery thermal runaway modeling and diagnosis approaches. Processes 2022, 10, 1192. [Google Scholar] [CrossRef]
- Sun, Z.; Read, E.; Chen, Y.; Dai, Y.; Marco, J.; Shearing, P.R. Numerical and experimental characterization of nail penetration induced thermal runaway propagation in 21700 lithium-ion batteries: Exploring the role of interstitial thermal barrier materials. J. Energy Chem. 2025, 109, 576–589. [Google Scholar] [CrossRef]
- Wang, Q.; Ping, P.; Zhao, X.; Chu, G.; Sun, J.; Chen, C. Thermal runaway caused fire and explosion of lithium ion battery. J. Power Sources 2012, 208, 210–224. [Google Scholar] [CrossRef]
- Naseri, F.; Schaltz, E.; Stroe, D.I.; Gismero, A.; Farjah, E. An enhanced equivalent circuit model with real-time parameter identification for battery state-of-charge estimation. IEEE Trans. Ind. Electron. 2021, 69, 3743–3751. [Google Scholar] [CrossRef]
- Fotouhi, A.; Auger, D.J.; Propp, K.; Longo, S. Lithium–sulfur battery state-of-charge observability analysis and estimation. IEEE Trans. Power Electron. 2017, 33, 5847–5859. [Google Scholar] [CrossRef]
- Fotouhi, A.; Auger, D.J.; Propp, K.; Longo, S. Electric vehicle battery parameter identification and SOC observability analysis: NiMH and Li-S case studies. IET Power Electron. 2017, 10, 1289–1297. [Google Scholar] [CrossRef]
- Zhang, Q.; Shang, Y.; Li, Y.; Cui, N.; Duan, B.; Zhang, C. A novel fractional variable-order equivalent circuit model and parameter identification of electric vehicle Li-ion batteries. ISA Trans. 2020, 97, 448–457. [Google Scholar] [CrossRef] [PubMed]
- He, H.; Xiong, R.; Guo, H.; Li, S. Comparison study on the battery models used for the energy management of batteries in electric vehicles. Energy Convers. Manag. 2012, 64, 113–121. [Google Scholar] [CrossRef]
- Hu, X.; Sun, F.; Zou, Y.; Peng, H. Online estimation of an electric vehicle lithium-ion battery using recursive least squares with forgetting. In Proceedings of the 2011 American Control Conference, San Francisco, CA, USA, 29 June–1 July 2011; pp. 935–940. [Google Scholar]
- He, H.; Zhang, X.; Xiong, R.; Xu, Y.; Guo, H. Online model-based estimation of state-of-charge and open-circuit voltage of lithium-ion batteries in electric vehicles. Energy 2012, 39, 310–318. [Google Scholar] [CrossRef]
- Lao, Z.; Xia, B.; Wang, W.; Sun, W.; Lai, Y.; Wang, M. A novel method for lithium-ion battery online parameter identification based on variable forgetting factor recursive least squares. Energies 2018, 11, 1358. [Google Scholar] [CrossRef]
- Sharma, A.; Fathy, H.K. Fisher identifiability analysis for a periodically-excited equivalent-circuit lithium-ion battery model. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 274–280. [Google Scholar]
- Schmidt, A.P.; Bitzer, M.; Imre, Á.W.; Guzzella, L. Experiment-driven electrochemical modeling and systematic parameterization for a lithium-ion battery cell. J. Power Sources 2010, 195, 5071–5080. [Google Scholar] [CrossRef]
- Lin, X.; Stefanopoulou, A.G. Analytic bound on accuracy of battery state and parameter estimation. J. Electrochem. Soc. 2015, 162, A1879. [Google Scholar] [CrossRef]
- Rothenberger, M.J.; Anstrom, J.; Brennan, S.; Fathy, H.K. Maximizing parameter identifiability of an equivalent-circuit battery model using optimal periodic input shaping. In Proceedings of the Dynamic Systems and Control Conference, American Society of Mechanical Engineers, San Antonio, TX, USA, 22–24 October 2014; Volume 46186, p. V001T19A004. [Google Scholar]
- Cai, C.; Auger, D.J.; Perinpanayagam, S. Enhanced online identification of battery models exploiting data richness. In Proceedings of the 2023 IEEE International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Venice, Italy, 28–31 March 2023; pp. 1–6. [Google Scholar]
- Xiong, R.; Wang, S.; Yu, C.; Xia, L. An estimation method for lithium-ion battery SOC of special robots based on Thevenin model and improved extended Kalman. Energy Storage Sci. Technol. 2021, 10, 695. [Google Scholar]
- Shateri, N.; Auger, D.J.; Fotouhi, A.; Brighton, J.; Du, W.; Owen, R.E.; Brett, D.J.; Shearing, P.R. Investigation of the effect of temperature on lithium-sulfur cell cycle life performance using system identification and x-ray tomography. Batter. Supercaps 2022, 5, e202200035. [Google Scholar] [CrossRef]




| Parameter | Value |
|---|---|
| Package format | Pouch |
| Capacity | 19 Ah |
| Maximum voltage | 2.6 V |
| Minimum voltage | 1.9 V |
| Nominal voltage | 2.15 V |
| Maximum discharge rate | 3 C-rate (57 A) |
| Maximum charge rate | 0.25 C-rate (4.75 A) |
| Cell mass | 141 g |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, N.; Gong, Y.; Yang, X.; Yang, D.; Yang, Y.; Wang, B.; Long, H. Applicability Evaluation of an Online Parameter Identification Method: From Lithium-Ion to Lithium–Sulfur Batteries. Energies 2025, 18, 4493. https://doi.org/10.3390/en18174493
Gao N, Gong Y, Yang X, Yang D, Yang Y, Wang B, Long H. Applicability Evaluation of an Online Parameter Identification Method: From Lithium-Ion to Lithium–Sulfur Batteries. Energies. 2025; 18(17):4493. https://doi.org/10.3390/en18174493
Chicago/Turabian StyleGao, Ning, You Gong, Xiaobei Yang, Disai Yang, Yao Yang, Bingyu Wang, and Haifei Long. 2025. "Applicability Evaluation of an Online Parameter Identification Method: From Lithium-Ion to Lithium–Sulfur Batteries" Energies 18, no. 17: 4493. https://doi.org/10.3390/en18174493
APA StyleGao, N., Gong, Y., Yang, X., Yang, D., Yang, Y., Wang, B., & Long, H. (2025). Applicability Evaluation of an Online Parameter Identification Method: From Lithium-Ion to Lithium–Sulfur Batteries. Energies, 18(17), 4493. https://doi.org/10.3390/en18174493






