A Review of State-of-the-Art AI and Data-Driven Techniques for Load Forecasting
Abstract
1. Introduction
- (I)
- Load Spatial Scale: Among 140 identified papers (the rest of the papers did not specify the spatial scale clearly), there are 47 papers (accounting for about 33.6%) related to city-/region-scale forecasting, 39 papers related to building-scale forecasting (such as residential, commercial, and educational buildings and so on), 30 papers related to station-scale forecasting, and 24 papers related to national-grid-scale forecasting. The statistic chart is shown in Figure 2.
- (II)
- Forecasting Time Scale: According to the time scale, LF can be categorized into short-term, medium-term, and long-term forecasting. Figure 3 provides the proportions of three time scales based on the survey of 154 papers (rest of the papers did not specify the time scale clearly). There are 128 papers (accounting for about 83.1%) focusing on short-term forecasting, 16 papers focusing on medium-term forecasting, and 10 papers focusing on long-term forecasting. It is observed that studies prefer short-term LF scales, which can provide more detailed and accurate forecasting results.
2. Data Preprocessing Methods
2.1. Basic Preprocessing Methods
- (I)
- Feature extraction
- (II)
- Data decomposition
- (III)
- Combined preprocessing
2.2. Advanced Data Preprocessing Methods
- (I)
- Feature extraction based on deep learning
- (II)
- Feature/sample selection based on reinforcement learning
- (III)
- Feature extraction based on attention mechanism
2.3. Comparison and Summary
3. Advanced AI-Based Forecasting Models
3.1. Deep Learning-Based Models
- (I)
- Deep ResNet
- (II)
- TCN
- (III)
- Transformer with attention mechanism
3.2. Reinforcement Learning-Based Models
- (I)
- Direct forecasting
- (II)
- Parameter optimization
- (III)
- Construction or integration of base learners
3.3. Transfer Learning-Based Models
- (I)
- Model transfer
- (II)
- Instance transfer
- (III)
- Feature transfer
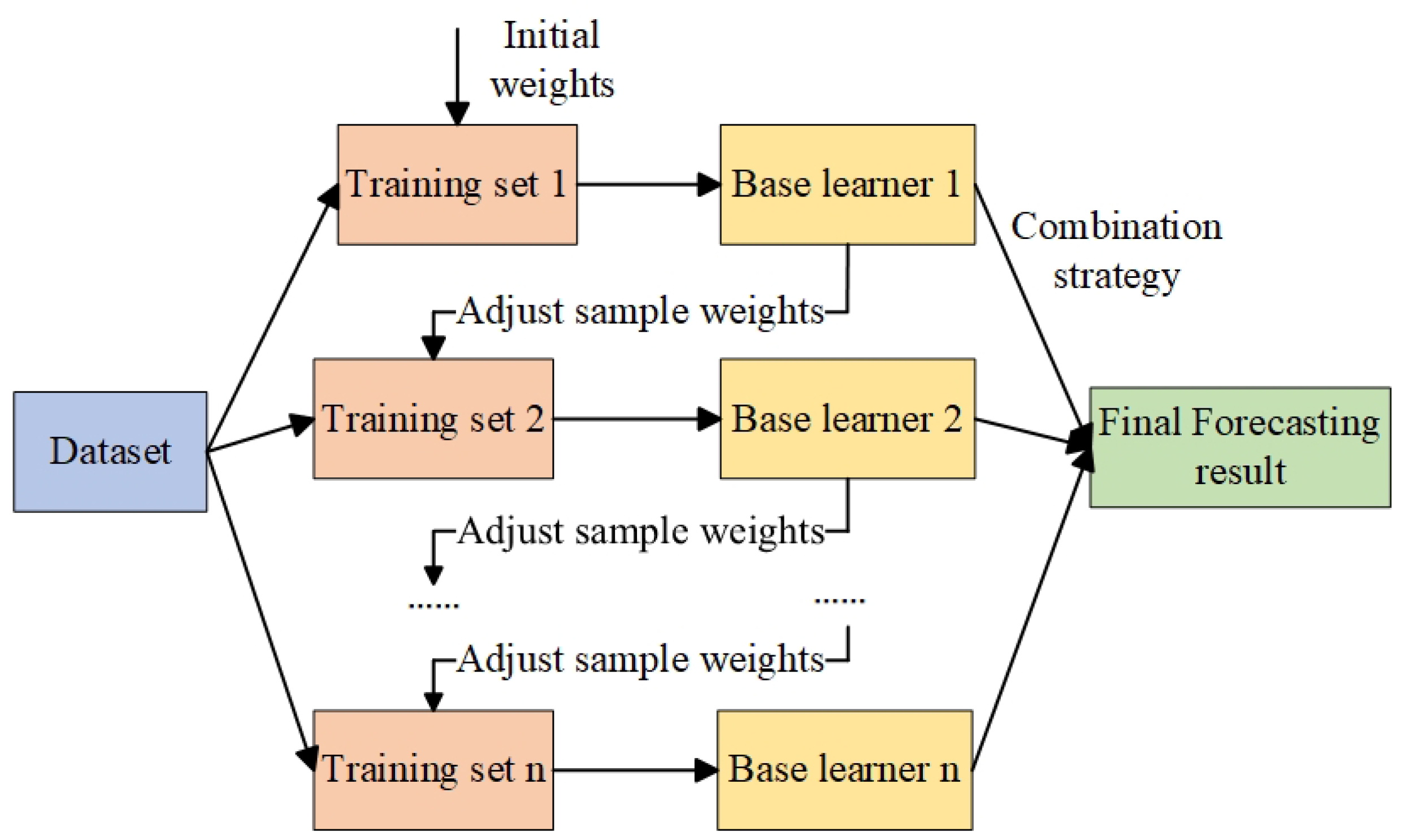
3.4. Ensemble Learning-Based Models
3.4.1. Parallel Ensemble Model
3.4.2. Serial Ensemble Model
3.5. Comparison and Summary
4. Discussion
- (I)
- Data Perspective: Sample Scarcity Problem.Supported by big data technologies, machine learning and deep learning have achieved success in the field of LF. From the perspective of data, using high-quality load characteristics as data inputs is the key to ensuring the efficiency and accuracy of these self-learning models. However, in practical scenarios, such as insufficient historical data span, differences in device operating modes, improper handling of outliers, etc., LF often faces the problem of scarce samples or limited available data. How to achieve accurate LF using a small number of samples has become one of the main challenges.
- (II)
- Technical Perspective: Generalization Modeling Problem.Traditional LF models for single forecasting tasks are not suitable for the requirements of new distributed energy supply–demand forecasting. From the perspective of techniques, it is quite difficult to develop a single AI model that performs the best for all forecasting scenarios. Considering the coupling and complementary relationship between distributed new energy and multiple loads, how to improve the generalization performance of the model in different forecasting scenarios has become a research trend.
- (III)
- Operational Perspective: Model Adaptability Problem.Current LF generally adopts the method of “offline training, online forecasting”. From the perspective of operations, the trained model lacks the ability to dynamically and adaptively adjust to the environment. Therefore, when the environment and operation parameters are significantly different from those utilized for training, accuracy of the forecasting model may decrease obviously. How to improve the environmental adaptability of a model is quite important in practical applications.
4.1. Data Perspective: Small-Sample Forecasting
4.2. Technical Perspective: Generalization Modeling in Different Scenarios
4.3. Operational Perspective: Online Adaptive Forecasting
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, X.; Wang, H.; Bhandari, B.; Cheng, L. AI-empowered methods for smart energy consumption: A review of load forecasting, anomaly detection and demand response. Int. J. Precis. Eng. Manuf. Green Technol. 2024, 11, 963–993. [Google Scholar] [CrossRef]
- Mishra, S.K.; Gupta, V.K.; Kumar, R.; Swain, S.K.; Mohanta, D.K. Multi-objective optimization of economic emission load dispatch incorporating load forecasting and solar photovoltaic sources for carbon neutrality. Electr. Power Syst. Res. 2023, 223, 109700. [Google Scholar] [CrossRef]
- Gu, L.; Wang, J.; Liu, J. A combined system based on data preprocessing and optimization algorithm for electricity load forecasting. Comput. Ind. Eng. 2024, 191, 110114. [Google Scholar] [CrossRef]
- Eren, Y.; Küçükdemiral, İ. A comprehensive review on deep learning approaches for short-term load forecasting. Renew. Sustain. Energy Rev. 2024, 189, 114031. [Google Scholar] [CrossRef]
- Xu, H.; Hu, F.; Liang, X.; Zhao, G.; Abugunmi, M. A framework for electricity load forecasting based on attention mechanism time series depthwise separable convolutional neural network. Energy 2024, 299, 131258. [Google Scholar] [CrossRef]
- Mathumitha, R.; Rathika, P.; Manimala, K. Intelligent deep learning techniques for energy consumption forecasting in smart buildings: A review. Artif. Intell. Rev. 2024, 57, 35. [Google Scholar] [CrossRef]
- Zhu, J.; Dong, H.; Zheng, W.; Li, S.; Huang, Y.; Xi, L. Review and prospect of data-driven techniques for load forecasting in integrated energy systems. Appl. Energy 2022, 321, 119269. [Google Scholar] [CrossRef]
- Xu, H.; Fan, G.; Kuang, G.; Song, Y. Construction and application of short-term and mid-term power system load forecasting model based on hybrid deep learning. IEEE Access 2023, 11, 37494–37507. [Google Scholar] [CrossRef]
- Lin, J.; Ma, J.; Zhu, J.; Cui, Y. Short-term load forecasting based on LSTM networks considering attention mechanism. Int. J. Electr. Power Energy Syst. 2022, 137, 107818. [Google Scholar] [CrossRef]
- Nunekpeku, X.; Zhang, W.; Gao, J.; Adade, S.Y.S.S.; Li, H.; Chen, Q. Gel strength prediction in ultrasonicated chicken mince: Fusing near-infrared and Raman spectroscopy coupled with deep learning LSTM algorithm. Food Control 2025, 168, 110916. [Google Scholar] [CrossRef]
- Li, K.; Xue, W.; Tan, G.; Denzer, A.S. A state of the art review on the prediction of building energy consumption using data-driven technique and evolutionary algorithms. Build. Serv. Eng. Res. Technol. 2020, 41, 108–127. [Google Scholar] [CrossRef]
- Zhou, X.; Zhao, C.; Sun, J.; Cao, Y.; Yao, K.; Xu, M. A deep learning method for predicting lead content in oilseed rape leaves using fluorescence hyperspectral imaging. Food Chem. 2023, 409, 135251. [Google Scholar] [CrossRef]
- Deng, J.; Ni, L.; Bai, X.; Jiang, H.; Xu, L. Simultaneous analysis of mildew degree and aflatoxin B1 of wheat by a multi-task deep learning strategy based on microwave detection technology. LWT 2023, 184, 115047. [Google Scholar] [CrossRef]
- Chang, X.; Huang, X.; Xu, W.; Tian, X.; Wang, C.; Wang, L.; Yu, S. Monitoring of dough fermentation during Chinese steamed bread processing by near-infrared spectroscopy combined with spectra selection and supervised learning algorithm. J. Food Process Eng. 2021, 44, e13783. [Google Scholar] [CrossRef]
- Elbeltagi, A.; Srivastava, A.; Deng, J.; Li, Z.; Raza, A.; Khadke, L.; Yu, Z.; El-Rawy, M. Forecasting vapor pressure deficit for agricultural water management using machine learning in semi-arid environments. Agric. Water Manag. 2023, 283, 108302. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, X.; Lin, Z.; Lu, M.; Yang, W.; Sun, X.; Battino, M.; Shi, J.; Huang, X.; Shi, B.; et al. Nondestructive detection of pungent and numbing compounds in spicy hotpot seasoning with hyperspectral imaging and machine learning. Food Chem. 2025, 469, 142593. [Google Scholar] [CrossRef]
- Zhang, D.; Lin, Z.; Xuan, L.; Lu, M.; Shi, B.; Shi, J.; He, F.; Battino, M.; Zhao, L.; Zou, X. Rapid determination of geographical authenticity and pungency intensity of the red Sichuan pepper (Zanthoxylum bungeanum) using differential pulse voltammetry and machine learning algorithms. Food Chem. 2024, 439, 137978. [Google Scholar] [CrossRef]
- Chen, C.; Zhu, W.; Steibel, J.; Siegford, J.; Han, J.; Norton, T. Classification of drinking and drinker-playing in pigs by a video-based deep learning method. Biosyst. Eng. 2020, 196, 1–14. [Google Scholar] [CrossRef]
- Liu, J.; Abbas, I.; Noor, R.S. Development of deep learning-based variable rate agrochemical spraying system for targeted weeds control in strawberry crop. Agronomy 2021, 11, 1480. [Google Scholar] [CrossRef]
- Wang, J.; Gao, Z.; Zhang, Y.; Zhou, J.; Wu, J.; Li, P. Real-time detection and location of potted flowers based on a ZED camera and a YOLO V4-tiny deep learning algorithm. Horticulturae 2021, 8, 21. [Google Scholar] [CrossRef]
- Zhao, S.; Adade, S.Y.S.S.; Wang, Z.; Jiao, T.; Ouyang, Q.; Li, H.; Chen, Q. Deep learning and feature reconstruction assisted vis-NIR calibration method for on-line monitoring of key growth indicators during kombucha production. Food Chem. 2025, 463, 141411. [Google Scholar] [CrossRef]
- Zhang, Z.; Lu, Y.; Yang, M.; Wang, G.; Zhao, Y.; Hu, Y. Optimal training strategy for high-performance detection model of multi-cultivar tea shoots based on deep learning methods. Sci. Hortic. 2024, 328, 112949. [Google Scholar] [CrossRef]
- Piotrowski, P.; Baczyński, D.; Kopyt, M.; Gulczyński, T. Advanced ensemble methods using machine learning and deep learning for one-day-ahead forecasts of electric energy production in wind farms. Energies 2022, 15, 1252. [Google Scholar] [CrossRef]
- Jeon, B.K.; Kim, E.J. Solar irradiance prediction using reinforcement learning pre-trained with limited historical data. Energy Rep. 2023, 10, 2513–2524. [Google Scholar] [CrossRef]
- Jagait, R.K.; Fekri, M.N.; Grolinger, K.; Mir, S. Load forecasting under concept drift: Online ensemble learning with recurrent neural network and ARIMA. IEEE Access 2021, 9, 98992–99008. [Google Scholar] [CrossRef]
- Zhu, Q.; Li, J.; Qiao, J.; Shi, M.; Wang, C. Application and Prospect of Artificial Intelligence Technology in Renewable Energy Forecasting. Proc. CSEE 2023, 43, 3027–3048. [Google Scholar]
- Ramokone, A.; Popoola, O.; Awelewa, A.; Temitope, A. A review on behavioural propensity for building load and energy profile development—Model inadequacy and improved approach. Sustain. Energy Technol. Assessments 2021, 45, 101235. [Google Scholar] [CrossRef]
- Patsakos, I.; Vrochidou, E.; Papakostas, G.A. A survey on deep learning for building load forecasting. Math. Probl. Eng. 2022, 2022, 1008491. [Google Scholar] [CrossRef]
- Khalil, M.; McGough, A.S.; Pourmirza, Z.; Pazhoohesh, M.; Walker, S. Machine Learning, Deep Learning and Statistical Analysis for forecasting building energy consumption—A systematic review. Eng. Appl. Artif. Intell. 2022, 115, 105287. [Google Scholar] [CrossRef]
- Han, F.; Wang, X.; Qiao, J.; Shi, M.; Pu, T. Review on artificial intelligence based load forecasting research for the new-type power system. Proc. CSEE 2023, 43, 8569–8591. [Google Scholar]
- Abdel-Jaber, F.; Dirks, K.N. A review of cooling and heating loads predictions of residential buildings using data-driven techniques. Buildings 2024, 14, 752. [Google Scholar] [CrossRef]
- Ma, H.; Yuan, A.; Wang, B.; Yang, C.; Dong, X.; Chen, L. Review and prospect of load forecasting based on deep learning. High Volt. Eng. 2025, 51, 1233–1250. [Google Scholar]
- Liu, C.; Yu, H.; Liu, Y.; Zhang, L.; Li, D.; Zhang, J.; Li, X.; Sui, Y. Prediction of Anthocyanin Content in Purple-Leaf Lettuce Based on Spectral Features and Optimized Extreme Learning Machine Algorithm. Agronomy 2024, 14, 2915. [Google Scholar] [CrossRef]
- Ahmed, N.; Assadi, M.; Zhang, Q. Investigating the impact of borehole field data’s input parameters on the forecasting accuracy of multivariate hybrid deep learning models for heating and cooling. Energy Build. 2023, 301, 113706. [Google Scholar] [CrossRef]
- Oprea, S.V.; Bâra, A. A stacked ensemble forecast for photovoltaic power plants combining deterministic and stochastic methods. Appl. Soft Comput. 2023, 147, 110781. [Google Scholar] [CrossRef]
- Li, K.; Zhang, J.; Chen, X.; Xue, W. Building’s hourly electrical load prediction based on data clustering and ensemble learning strategy. Energy Build. 2022, 261, 111943. [Google Scholar] [CrossRef]
- Ibrahim, I.A.; Hossain, M. Short-term multivariate time series load data forecasting at low-voltage level using optimised deep-ensemble learning-based models. Energy Convers. Manag. 2023, 296, 117663. [Google Scholar] [CrossRef]
- Jalali, S.M.J.; Osório, G.J.; Ahmadian, S.; Lotfi, M.; Campos, V.M.; Shafie-khah, M.; Khosravi, A.; Catalão, J.P. New hybrid deep neural architectural search-based ensemble reinforcement learning strategy for wind power forecasting. IEEE Trans. Ind. Appl. 2021, 58, 15–27. [Google Scholar] [CrossRef]
- You, W.; Guo, D.; Wu, Y.; Li, W. Multiple Load Forecasting of Integrated Energy System Based on Sequential-Parallel Hybrid Ensemble Learning. Energies 2023, 16, 3268. [Google Scholar] [CrossRef]
- Jalali, S.M.J.; Ahmadian, S.; Nakisa, B.; Khodayar, M.; Khosravi, A.; Nahavandi, S.; Islam, S.M.S.; Shafie-khah, M.; Catalão, J.P. Solar irradiance forecasting using a novel hybrid deep ensemble reinforcement learning algorithm. Sustain. Energy Grids Netw. 2022, 32, 100903. [Google Scholar] [CrossRef]
- Lu, S.; Xu, Q.; Jiang, C.; Liu, Y.; Kusiak, A. Probabilistic load forecasting with a non-crossing sparse-group Lasso-quantile regression deep neural network. Energy 2022, 242, 122955. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhou, M.; Hu, F.; Wang, S.; Ma, J.; Gao, B.; Bian, K.; Lai, W. A day-ahead industrial load forecasting model using load change rate features and combining FA-ELM and the AdaBoost algorithm. Energy Rep. 2023, 9, 971–981. [Google Scholar] [CrossRef]
- Li, C.; Li, G.; Wang, K.; Han, B. A multi-energy load forecasting method based on parallel architecture CNN-GRU and transfer learning for data deficient integrated energy systems. Energy 2022, 259, 124967. [Google Scholar] [CrossRef]
- Shi, H.; Wang, L.; Scherer, R.; Woźniak, M.; Zhang, P.; Wei, W. Short-term load forecasting based on adabelief optimized temporal convolutional network and gated recurrent unit hybrid neural network. IEEE Access 2021, 9, 66965–66981. [Google Scholar] [CrossRef]
- Liu, R.; Chen, T.; Sun, G.; Muyeen, S.; Lin, S.; Mi, Y. Short-term probabilistic building load forecasting based on feature integrated artificial intelligent approach. Electric Power Syst. Res. 2022, 206, 107802. [Google Scholar] [CrossRef]
- Pirbazari, A.M.; Sharma, E.; Chakravorty, A.; Elmenreich, W.; Rong, C. An ensemble approach for multi-step ahead energy forecasting of household communities. IEEE Access 2021, 9, 36218–36240. [Google Scholar] [CrossRef]
- Dai, Y.; Yu, W.; Leng, M. A hybrid ensemble optimized BiGRU method for short-term photovoltaic generation forecasting. Energy 2024, 299, 131458. [Google Scholar] [CrossRef]
- Dong, Z.; Liu, J.; Liu, B.; Li, K.; Li, X. Hourly energy consumption prediction of an office building based on ensemble learning and energy consumption pattern classification. Energy Build. 2021, 241, 110929. [Google Scholar] [CrossRef]
- Lu, J.; Liu, J.; Luo, Y.; Zeng, J. Small sample load forecasting method considering characteristic distribution similarity based on improved WGAN. Control Theory Appl. 2024, 41, 597–608. [Google Scholar]
- Zhang, X.; Chau, T.K.; Chow, Y.H.; Fernando, T.; Iu, H.H.C. A novel sequence to sequence data modelling based CNN-LSTM algorithm for three years ahead monthly peak load forecasting. IEEE Trans. Power Syst. 2023, 39, 1932–1947. [Google Scholar] [CrossRef]
- Chandrasekar, A.; Ajeya, K.; Vinatha, U. InFLuCs: Irradiance Forecasting Through Reinforcement Learning Tuned Cascaded Regressors. IEEE Trans. Ind. Inform. 2024, 20, 10912–10921. [Google Scholar] [CrossRef]
- Hou, G.; Wang, J.; Fan, Y. Multistep short-term wind power forecasting model based on secondary decomposition, the kernel principal component analysis, an enhanced arithmetic optimization algorithm, and error correction. Energy 2024, 286, 129640. [Google Scholar] [CrossRef]
- Yuan, Y.; Yang, Q.; Ren, J.; Mu, X.; Wang, Z.; Shen, Q.; Li, Y. Short-term power load forecasting based on SKDR hybrid model. Electr. Eng. 2024, 107, 5769–5785. [Google Scholar] [CrossRef]
- Moon, J.; Park, S.; Rho, S.; Hwang, E. Robust building energy consumption forecasting using an online learning approach with R ranger. J. Build. Eng. 2022, 47, 103851. [Google Scholar] [CrossRef]
- Zhao, M.; Guo, G.; Fan, L.; Han, L.; Yu, Q.; Wang, Z. Short-term natural gas load forecasting based on EL-VMD-Transformer-ResLSTM. Sci. Rep. 2024, 14, 20343. [Google Scholar]
- Liu, H.; Chen, C. Data processing strategies in wind energy forecasting models and applications: A comprehensive review. Appl. Energy 2019, 249, 392–408. [Google Scholar] [CrossRef]
- Zhao, Z.; Yun, S.; Jia, L.; Guo, J.; Meng, Y.; He, N.; Li, X.; Shi, J.; Yang, L. Hybrid VMD-CNN-GRU-based model for short-term forecasting of wind power considering spatio-temporal features. Eng. Appl. Artif. Intell. 2023, 121, 105982. [Google Scholar] [CrossRef]
- Junior, M.Y.; Freire, R.Z.; Seman, L.O.; Stefenon, S.F.; Mariani, V.C.; dos Santos Coelho, L. Optimized hybrid ensemble learning approaches applied to very short-term load forecasting. Int. J. Electr. Power Energy Syst. 2024, 155, 109579. [Google Scholar]
- Heo, S.; Nam, K.; Loy-Benitez, J.; Yoo, C. Data-driven hybrid model for forecasting wastewater influent loads based on multimodal and ensemble deep learning. IEEE Trans. Ind. Inform. 2020, 17, 6925–6934. [Google Scholar] [CrossRef]
- Junliang, L.; Runhai, J.; Shuangkun, W.; Hui, H. An ensemble load forecasting model based on online error updating. Proc. CSEE 2022, 43, 1402–1412. [Google Scholar]
- Zhang, Z.; Zhang, C.; Dong, Y.; Hong, W.C. Bi-directional gated recurrent unit enhanced twin support vector regression with seasonal mechanism for electric load forecasting. Knowl.-Based Syst. 2025, 310, 112943. [Google Scholar] [CrossRef]
- Tian, Z.; Liu, W.; Jiang, W.; Wu, C. Cnns-transformer based day-ahead probabilistic load forecasting for weekends with limited data availability. Energy 2024, 293, 130666. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, J.; Ma, Y.; Li, G.; Ma, J.; Wang, C. Short-term load forecasting method with variational mode decomposition and stacking model fusion. Sustain. Energy Grids Netw. 2022, 30, 100622. [Google Scholar] [CrossRef]
- Cao, Z.; Wang, J.; Xia, Y. Combined electricity load-forecasting system based on weighted fuzzy time series and deep neural networks. Eng. Appl. Artif. Intell. 2024, 132, 108375. [Google Scholar] [CrossRef]
- Wang, J.; Liu, H.; Zheng, G.; Li, Y.; Yin, S. Short-Term Load Forecasting Based on Outlier Correction, Decomposition, and Ensemble Reinforcement Learning. Energies 2023, 16, 4401. [Google Scholar] [CrossRef]
- Yang, D.; Guo, J.E.; Sun, S.; Han, J.; Wang, S. An interval decomposition-ensemble approach with data-characteristic-driven reconstruction for short-term load forecasting. Appl. Energy 2022, 306, 117992. [Google Scholar] [CrossRef]
- Memarzadeh, G.; Keynia, F. Short-term electricity load and price forecasting by a new optimal LSTM-NN based prediction algorithm. Electr. Power Syst. Res. 2021, 192, 106995. [Google Scholar] [CrossRef]
- Liu, H.; Yu, C.; Wu, H.; Duan, Z.; Yan, G. A new hybrid ensemble deep reinforcement learning model for wind speed short term forecasting. Energy 2020, 202, 117794. [Google Scholar] [CrossRef]
- Malhan, P.; Mittal, M. A novel ensemble model for long-term forecasting of wind and hydro power generation. Energy Convers. Manag. 2022, 251, 114983. [Google Scholar] [CrossRef]
- Ribeiro, M.H.D.M.; da Silva, R.G.; Moreno, S.R.; Mariani, V.C.; dos Santos Coelho, L. Efficient bootstrap stacking ensemble learning model applied to wind power generation forecasting. Int. J. Electr. Power Energy Syst. 2022, 136, 107712. [Google Scholar] [CrossRef]
- Liu, H.; Yu, C.; Yu, C. A new hybrid model based on secondary decomposition, reinforcement learning and SRU network for wind turbine gearbox oil temperature forecasting. Measurement 2021, 178, 109347. [Google Scholar] [CrossRef]
- Ye, L.; Li, Y.; Pei, M.; Zhao, Y.; Li, Z.; Lu, P. A novel integrated method for short-term wind power forecasting based on fluctuation clustering and history matching. Appl. Energy 2022, 327, 120131. [Google Scholar] [CrossRef]
- Ribeiro, M.H.D.M.; da Silva, R.G.; Ribeiro, G.T.; Mariani, V.C.; dos Santos Coelho, L. Cooperative ensemble learning model improves electric short-term load forecasting. Chaos Solitons Fractals 2023, 166, 112982. [Google Scholar] [CrossRef]
- Zhou, S.; Li, Y.; Guo, Y.; Yang, X.; Shahidehpour, M.; Deng, W.; Mei, Y.; Ren, L.; Liu, Y.; Kang, T.; et al. A Load Forecasting Framework Considering Hybrid Ensemble Deep Learning with Two-Stage Load Decomposition. IEEE Trans. Ind. Appl. 2024, 60, 4568–4582. [Google Scholar] [CrossRef]
- Zhang, M.; Xiao, G.; Lu, J.; Liu, Y.; Chen, H.; Yang, N. Robust load feature extraction based secondary VMD novel short-term load demand forecasting framework. Electric Power Syst. Res. 2025, 239, 111198. [Google Scholar] [CrossRef]
- Sibtain, M.; Li, X.; Saleem, S.; Asad, M.S.; Tahir, T.; Apaydin, H. A multistage hybrid model ICEEMDAN-SE-VMD-RDPG for a multivariate solar irradiance forecasting. IEEE Access 2021, 9, 37334–37363. [Google Scholar] [CrossRef]
- Zhao, X.; Sun, B.; Geng, R. A new distributed decomposition–reconstruction–ensemble learning paradigm for short-term wind power prediction. J. Clean. Prod. 2023, 423, 138676. [Google Scholar] [CrossRef]
- Li, F.; Zheng, H.; Li, X.; Yang, F. Day-ahead city natural gas load forecasting based on decomposition-fusion technique and diversified ensemble learning model. Appl. Energy 2021, 303, 117623. [Google Scholar] [CrossRef]
- Tian, J.; Li, K.; Xue, W. An adaptive ensemble predictive strategy for multiple scale electrical energy usages forecasting. Sustain. Cities Soc. 2021, 66, 102654. [Google Scholar] [CrossRef]
- Yan, Q.; Lu, Z.; Liu, H.; He, X.; Zhang, X.; Guo, J. Short-term prediction of integrated energy load aggregation using a bi-directional simple recurrent unit network with feature-temporal attention mechanism ensemble learning model. Appl. Energy 2024, 355, 122159. [Google Scholar] [CrossRef]
- Lin, Z.; Lin, T.; Li, J.; Li, C. A novel short-term multi-energy load forecasting method for integrated energy system based on two-layer joint modal decomposition and dynamic optimal ensemble learning. Appl. Energy 2025, 378, 124798. [Google Scholar] [CrossRef]
- Sun, X.; Li, J.; Zeng, B.; Gong, D.; Lian, Z. Small-sample day-ahead power load forecasting of integrated energy system based on feature transfer learning. Control Theory Appl. 2021, 38, 63–72. [Google Scholar]
- Wu, D.; Hur, K.; Xiao, Z. A GAN-enhanced ensemble model for energy consumption forecasting in large commercial buildings. IEEE Access 2021, 9, 158820–158830. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, R.; Cao, J.; Tan, J. A CNN and LSTM-based multi-task learning architecture for short and medium-term electricity load forecasting. Electr. Power Syst. Res. 2023, 222, 109507. [Google Scholar] [CrossRef]
- Ye, W.; Yang, D.; Tang, C.; Wang, W.; Liu, G. Combined prediction of wind power in extreme weather based on time series adversarial generation networks. IEEE Access 2024, 12, 102660–102669. [Google Scholar] [CrossRef]
- Liu, L.; Fu, Q.; Lu, Y.; Wang, Y.; Wu, H.; Chen, J. CorrDQN-FS: A two-stage feature selection method for energy consumption prediction via deep reinforcement learning. J. Build. Eng. 2023, 80, 108044. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, J.; Liu, L. Physics-informed reinforcement learning for probabilistic wind power forecasting under extreme events. Appl. Energy 2024, 376, 124068. [Google Scholar] [CrossRef]
- Wang, X.; Wang, H.; Li, S.; Jin, H. A reinforcement learning-based online learning strategy for real-time short-term load forecasting. Energy 2024, 305, 132344. [Google Scholar] [CrossRef]
- Li, A.; Xiao, F.; Zhang, C.; Fan, C. Attention-based interpretable neural network for building cooling load prediction. Appl. Energy 2021, 299, 117238. [Google Scholar] [CrossRef]
- Yu, C.; Yan, G.; Yu, C.; Zhang, Y.; Mi, X. A multi-factor driven spatiotemporal wind power prediction model based on ensemble deep graph attention reinforcement learning networks. Energy 2023, 263, 126034. [Google Scholar]
- Yao, H.; Qu, P.; Qin, H.; Lou, Z.; Wei, X.; Song, H. Multidimensional electric power parameter time series forecasting and anomaly fluctuation analysis based on the AFFC-GLDA-RL method. Energy 2024, 313, 134180. [Google Scholar] [CrossRef]
- Zhou, X.; Sun, J.; Tian, Y.; Lu, B.; Hang, Y.; Chen, Q. Hyperspectral technique combined with deep learning algorithm for detection of compound heavy metals in lettuce. Food Chem. 2020, 321, 126503. [Google Scholar] [CrossRef]
- Tian, Y.; Sun, J.; Zhou, X.; Yao, K.; Tang, N. Detection of soluble solid content in apples based on hyperspectral technology combined with deep learning algorithm. J. Food Process. Preserv. 2022, 46, e16414. [Google Scholar] [CrossRef]
- Rafi, S.H.; Deeba, S.R.; Hossain, E. A short-term load forecasting method using integrated CNN and LSTM network. IEEE Access 2021, 9, 32436–32448. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, Z.; Han, Z.; Sun, W.; He, L. A decision-making system for cotton irrigation based on reinforcement learning strategy. Agronomy 2023, 14, 11. [Google Scholar] [CrossRef]
- Xue, W.; Jia, N.; Zhao, M. Multi-agent deep reinforcement learning based HVAC control for multi-zone buildings considering zone-energy-allocation optimization. Energy Build. 2025, 329, 115241. [Google Scholar] [CrossRef]
- Niu, D.; Yu, M.; Sun, L.; Gao, T.; Wang, K. Short-term multi-energy load forecasting for integrated energy systems based on CNN-BiGRU optimized by attention mechanism. Appl. Energy 2022, 313, 118801. [Google Scholar] [CrossRef]
- Moreno, S.R.; Mariani, V.C.; dos Santos Coelho, L. Hybrid multi-stage decomposition with parametric model applied to wind speed forecasting in Brazilian Northeast. Renew. Energy 2021, 164, 1508–1526. [Google Scholar] [CrossRef]
- Yang, G.; Zheng, H.; Zhang, H.; Jia, R. Short-term load forecasting based on Holt-Winters exponential smoothing and temporal convolutional network. Autom. Electr. Power Syst. 2022, 46, 73–82. [Google Scholar]
- Fan, G.F.; Zhang, L.Z.; Yu, M.; Hong, W.C.; Dong, S.Q. Applications of random forest in multivariable response surface for short-term load forecasting. Int. J. Electr. Power Energy Syst. 2022, 139, 108073. [Google Scholar] [CrossRef]
- Pinto, T.; Praça, I.; Vale, Z.; Silva, J. Ensemble learning for electricity consumption forecasting in office buildings. Neurocomputing 2021, 423, 747–755. [Google Scholar] [CrossRef]
- Ge, Q.; Guo, C.; Jiang, H.; Lu, Z.; Yao, G.; Zhang, J.; Hua, Q. Industrial power load forecasting method based on reinforcement learning and PSO-LSSVM. IEEE Trans. Cybern. 2022, 52, 1112–1124. [Google Scholar] [CrossRef]
- Zhang, T.; Tang, Z.; Wu, J.; Du, X.; Chen, K. Short term electricity price forecasting using a new hybrid model based on two-layer decomposition technique and ensemble learning. Electric Power Syst. Res. 2022, 205, 107762. [Google Scholar] [CrossRef]
- Li, H.; Sheng, W.; Adade, S.Y.S.S.; Nunekpeku, X.; Chen, Q. Investigation of heat-induced pork batter quality detection and change mechanisms using Raman spectroscopy coupled with deep learning algorithms. Food Chem. 2024, 461, 140798. [Google Scholar] [CrossRef]
- Xu, M.; Sun, J.; Cheng, J.; Yao, K.; Wu, X.; Zhou, X. Non-destructive prediction of total soluble solids and titratable acidity in Kyoho grape using hyperspectral imaging and deep learning algorithm. Int. J. Food Sci. Technol. 2023, 58, 9–21. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, Y.; Wang, X.; Gao, X.X.; Hou, Z. Low-cost livestock sorting information management system based on deep learning. Artif. Intell. Agric. 2023, 9, 110–126. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, P.; Wang, P.; Lee, W.J. Transfer learning featured short-term combining forecasting model for residential loads with small sample sets. IEEE Trans. Ind. Appl. 2022, 58, 4279–4288. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, W.; Zhu, K.; Zhou, D.; Dai, H.; Wu, Q. A novel trilinear deep residual network with self-adaptive Dropout method for short-term load forecasting. Expert Syst. Appl. 2021, 182, 115272. [Google Scholar] [CrossRef]
- Hua, H.; Liu, M.; Li, Y.; Deng, S.; Wang, Q. An ensemble framework for short-term load forecasting based on parallel CNN and GRU with improved ResNet. Electr. Power Syst. Res. 2023, 216, 109057. [Google Scholar] [CrossRef]
- Su, H.Y.; Lai, C.C. Towards Improved Load Forecasting in Smart Grids: A Robust Deep Ensemble Learning Framework. IEEE Trans. Smart Grid 2024, 15, 4292–4296. [Google Scholar] [CrossRef]
- Zheng, G.q.; Kong, L.r.; Su, Z.e.; Hu, M.s.; Wang, G.d. Approach for short-term power load prediction utilizing the ICEEMDAN–LSTM–TCN–bagging model. J. Electr. Eng. Technol. 2025, 20, 231–243. [Google Scholar] [CrossRef]
- Gao, S.; Liu, Y.; Wang, J.; Wang, Z.; Wenjun, X.; Yue, R.; Cui, R.; Liu, Y.; Fan, X. Short-term residential load forecasting via transfer learning and multi-attention fusion for EVs’ coordinated charging. Int. J. Electr. Power Energy Syst. 2025, 164, 110349. [Google Scholar] [CrossRef]
- Xie, F.; Guo, Z.; Li, T.; Feng, Q.; Zhao, C. Dynamic Task Planning for Multi-Arm Harvesting Robots Under Multiple Constraints Using Deep Reinforcement Learning. Horticulturae 2025, 11. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, M.; Yu, Z.; Sun, W.; Fu, W.; He, L. Enhancing cotton irrigation with distributional actor—critic reinforcement learning. Agric. Water Manag. 2025, 307, 109194. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, Q.; Yan, J.; Zhang, S.; Xu, J. A novel asynchronous deep reinforcement learning model with adaptive early forecasting method and reward incentive mechanism for short-term load forecasting. Energy 2021, 236, 121492. [Google Scholar] [CrossRef]
- Fu, Q.; Li, K.; Chen, J.; Wang, J.; Lu, Y.; Wang, Y. Building energy consumption prediction using a deep-forest-based DQN method. Buildings 2022, 12, 131. [Google Scholar] [CrossRef]
- Zhou, X.; Lin, W.; Kumar, R.; Cui, P.; Ma, Z. A data-driven strategy using long short term memory models and reinforcement learning to predict building electricity consumption. Appl. Energy 2022, 306, 118078. [Google Scholar] [CrossRef]
- He, X.; Zhao, W.; Gao, Z.; Zhang, L.; Zhang, Q.; Li, X. Short-term load forecasting by GRU neural network and DDPG algorithm for adaptive optimization of hyperparameters. Electr. Power Syst. Res. 2025, 238, 111119. [Google Scholar] [CrossRef]
- Kosana, V.; Teeparthi, K.; Madasthu, S.; Kumar, S. A novel reinforced online model selection using Q-learning technique for wind speed prediction. Sustain. Energy Technol. Assessments 2022, 49, 101780. [Google Scholar] [CrossRef]
- Sun, J.; Gong, M.; Zhao, Y.; Han, C.; Jing, L.; Yang, P. A hybrid deep reinforcement learning ensemble optimization model for heat load energy-saving prediction. J. Build. Eng. 2022, 58, 105031. [Google Scholar] [CrossRef]
- Wang, J.; Fu, J.; Chen, B. Multi-model fusion photovoltaic power generation prediction method based on reinforcement learning. Acta Energiae Solaris Sin. 2024, 45, 382–388. [Google Scholar]
- Ren, X.; Tian, X.; Wang, K.; Yang, S.; Chen, W.; Wang, J. Enhanced load forecasting for distributed multi-energy system: A stacking ensemble learning method with deep reinforcement learning and model fusion. Energy 2025, 319, 135031. [Google Scholar] [CrossRef]
- Liu, T.; Tan, Z.; Xu, C.; Chen, H.; Li, Z. Study on deep reinforcement learning techniques for building energy consumption forecasting. Energy Build. 2020, 208, 109675. [Google Scholar] [CrossRef]
- Nguyen, N.A.; Dang, T.D.; Verdú, E.; Kumar Solanki, V. Short-term forecasting electricity load by long short-term memory and reinforcement learning for optimization of hyper-parameters. Evol. Intell. 2023, 16, 1729–1746. [Google Scholar] [CrossRef]
- Li, Z.; Xu, B.; Zhang, J.; Yang, J.; Guo, Y. Short-term load optimal weighted forecasting strategy based on TD3 variable length time window. Electr. Power Constr. 2024, 45, 140–148. [Google Scholar]
- Dabbaghjamanesh, M.; Moeini, A.; Kavousi-Fard, A. Reinforcement learning-based load forecasting of electric vehicle charging station using Q-learning technique. IEEE Trans. Ind. Inform. 2020, 17, 4229–4237. [Google Scholar] [CrossRef]
- Yin, S.; Liu, H. Wind power prediction based on outlier correction, ensemble reinforcement learning, and residual correction. Energy 2022, 250, 123857. [Google Scholar] [CrossRef]
- Pannakkong, W.; Vinh, V.T.; Tuyen, N.N.M.; Buddhakulsomsiri, J. A Reinforcement Learning Approach for Ensemble Machine Learning Models in Peak Electricity Forecasting. Energies 2023, 16, 5099. [Google Scholar] [CrossRef]
- Wei, B.; Li, K.; Zhou, S.; Xue, W.; Tan, G. An instance based multi-source transfer learning strategy for building’s short-term electricity loads prediction under sparse data scenarios. J. Build. Eng. 2024, 85, 108713. [Google Scholar] [CrossRef]
- Yang, F.; Sun, J.; Cheng, J.; Fu, L.; Wang, S.; Xu, M. Detection of starch in minced chicken meat based on hyperspectral imaging technique and transfer learning. J. Food Process Eng. 2023, 46, e14304. [Google Scholar] [CrossRef]
- Wu, D.; Xu, Y.T.; Jenkin, M.; Wang, J.; Li, H.; Liu, X.; Dudek, G. Short-term load forecasting with deep boosting transfer regression. In Proceedings of the ICC 2022—IEEE International Conference on Communications, Seoul, Republic of Korea, 16–20 May 2022; pp. 5530–5536. [Google Scholar]
- Lu, Y.; Wang, G.; Huang, S. A short-term load forecasting model based on mixup and transfer learning. Electr. Power Syst. Res. 2022, 207, 107837. [Google Scholar] [CrossRef]
- Zhou, Z.; Xu, Y.; Ren, C. A transfer learning method for forecasting masked-load with behind-the-meter distributed energy resources. IEEE Trans. Smart Grid 2022, 13, 4961–4964. [Google Scholar] [CrossRef]
- Peng, C.; Tao, Y.; Chen, Z.; Zhang, Y.; Sun, X. Multi-source transfer learning guided ensemble LSTM for building multi-load forecasting. Expert Syst. Appl. 2022, 202, 117194. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, J. Transfer learning based multi-layer extreme learning machine for probabilistic wind power forecasting. Appl. Energy 2022, 312, 118729. [Google Scholar] [CrossRef]
- Yang, Q.; Lin, Y.; Kuang, S.; Wang, D. A novel short-term load forecasting approach for data-poor areas based on K-MIFS-XGBoost and transfer-learning. Electr. Power Syst. Res. 2024, 229, 110151. [Google Scholar] [CrossRef]
- Xiao, L.; Bai, Q.; Wang, B. A dynamic multi-model transfer based short-term load forecasting. Appl. Soft Comput. 2024, 159, 111627. [Google Scholar] [CrossRef]
- Wei, N.; Yin, C.; Yin, L.; Tan, J.; Liu, J.; Wang, S.; Qiao, W.; Zeng, F. Short-term load forecasting based on WM algorithm and transfer learning model. Appl. Energy 2024, 353, 122087. [Google Scholar] [CrossRef]
- Cheng, M.; Zhai, J.; Ma, J.; Lu, L.; Jin, E. Transfer learning based CNN-GRU short-term power load forecasting method. Eng. J. Wuhan Univ. 2024, 57, 812–820. [Google Scholar]
- Li, K.; Liu, Y.; Chen, L.; Xue, W. Data efficient indoor thermal comfort prediction using instance based transfer learning method. Energy Build. 2024, 306, 113920. [Google Scholar] [CrossRef]
- Li, K.; Chen, L.; Luo, Y.; He, X. An ensemble strategy for transfer learning based human thermal comfort prediction: Field experimental study. Energy Build. 2025, 330, 115344. [Google Scholar] [CrossRef]
- Cheng, J.; Sun, J.; Yao, K.; Xu, M.; Wang, S.; Fu, L. Hyperspectral technique combined with stacking and blending ensemble learning method for detection of cadmium content in oilseed rape leaves. J. Sci. Food Agric. 2023, 103, 2690–2699. [Google Scholar] [CrossRef]
- Yu, J.; Zhangzhong, L.; Lan, R.; Zhang, X.; Xu, L.; Li, J. Ensemble Learning Simulation Method for Hydraulic Characteristic Parameters of Emitters Driven by Limited Data. Agronomy 2023, 13, 986. [Google Scholar] [CrossRef]
- Raza, A.; Hu, Y.; Lu, Y. Improving carbon flux estimation in tea plantation ecosystems: A machine learning ensemble approach. Eur. J. Agron. 2024, 160, 127297. [Google Scholar] [CrossRef]
- Jin, H.; Li, Y.; Wang, B.; Yang, B.; Jin, H.; Cao, Y. Adaptive forecasting of wind power based on selective ensemble of offline global and online local learning. Energy Convers. Manag. 2022, 271, 116296. [Google Scholar] [CrossRef]
- Shi, J.; Li, C.; Yan, X. Artificial intelligence for load forecasting: A stacking learning approach based on ensemble diversity regularization. Energy 2023, 262, 125295. [Google Scholar] [CrossRef]
- Hu, Y.; Qu, B.; Wang, J.; Liang, J.; Wang, Y.; Yu, K.; Li, Y.; Qiao, K. Short-term load forecasting using multimodal evolutionary algorithm and random vector functional link network based ensemble learning. Appl. Energy 2021, 285, 116415. [Google Scholar] [CrossRef]
- Sun, F.; Jin, T. A hybrid approach to multi-step, short-term wind speed forecasting using correlated features. Renew. Energy 2022, 186, 742–754. [Google Scholar] [CrossRef]
- Yang, Q.; Tian, Z. A hybrid load forecasting system based on data augmentation and ensemble learning under limited feature availability. Expert Syst. Appl. 2025, 261, 125567. [Google Scholar] [CrossRef]
- Che, J.; Yuan, F.; Zhu, S.; Yang, Y. An adaptive ensemble framework with representative subset based weight correction for short-term forecast of peak power load. Appl. Energy 2022, 328, 120156. [Google Scholar] [CrossRef]
- Hadjout, D.; Torres, J.; Troncoso, A.; Sebaa, A.; Martínez-Álvarez, F. Electricity consumption forecasting based on ensemble deep learning with application to the Algerian market. Energy 2022, 243, 123060. [Google Scholar] [CrossRef]
- Von Krannichfeldt, L.; Wang, Y.; Zufferey, T.; Hug, G. Online ensemble approach for probabilistic wind power forecasting. IEEE Trans. Sustain. Energy 2021, 13, 1221–1233. [Google Scholar] [CrossRef]
- Massaoudi, M.; Abu-Rub, H.; Refaat, S.S.; Trabelsi, M.; Chihi, I.; Oueslati, F.S. Enhanced deep belief network based on ensemble learning and tree-structured of Parzen estimators: An optimal photovoltaic power forecasting method. IEEE Access 2021, 9, 150330–150344. [Google Scholar] [CrossRef]
- Fan, C.; Li, Y.; Yi, L.; Xiao, L.; Qu, X.; Ai, Z. Multi-objective LSTM ensemble model for household short-term load forecasting. Memetic Comput. 2022, 14, 115–132. [Google Scholar] [CrossRef]
- He, Y.; Xiao, J.; An, X.; Cao, C.; Xiao, J. Short-term power load probability density forecasting based on GLRQ-Stacking ensemble learning method. Int. J. Electr. Power Energy Syst. 2022, 142, 108243. [Google Scholar] [CrossRef]
- He, Y.; Zhang, H.; Dong, Y.; Wang, C.; Ma, P. Residential net load interval prediction based on stacking ensemble learning. Energy 2024, 296, 131134. [Google Scholar] [CrossRef]
- Li, K.; Tian, J.; Xue, W.; Tan, G. Short-term electricity consumption prediction for buildings using data-driven swarm intelligence based ensemble model. Energy Build. 2021, 231, 110558. [Google Scholar] [CrossRef]
- Shuyin, C.; Xinjie, W. Multivariate load forecasting in integrated energy system based on maximal information coefficient and multi-objective Stacking ensemble learning. Electr. Power Autom. Equip. 2022, 42, 32–39. [Google Scholar]
- Li, Y.; Zhang, S.; Hu, R.; Lu, N. A meta-learning based distribution system load forecasting model selection framework. Appl. Energy 2021, 294, 116991. [Google Scholar] [CrossRef]
- Shen, Q.; Mo, L.; Liu, G.; Zhou, J.; Zhang, Y.; Ren, P. Short-term load forecasting based on multi-scale ensemble deep learning neural network. IEEE Access 2023. [Google Scholar] [CrossRef]
- Massaoudi, M.; Refaat, S.S.; Chihi, I.; Trabelsi, M.; Oueslati, F.S.; Abu-Rub, H. A novel stacked generalization ensemble-based hybrid LGBM-XGB-MLP model for Short-Term Load Forecasting. Energy 2021, 214, 118874. [Google Scholar] [CrossRef]
- Shojaei, T.; Mokhtar, A. Forecasting energy consumption with a novel ensemble deep learning framework. J. Build. Eng. 2024, 96, 110452. [Google Scholar] [CrossRef]
- Gong, J.; Qu, Z.; Zhu, Z.; Xu, H.; Yang, Q. Ensemble models of TCN-LSTM-LightGBM based on ensemble learning methods for short-term electrical load forecasting. Energy 2025, 318, 134757. [Google Scholar] [CrossRef]
- Meng, H.; Han, L.; Hou, L. An ensemble learning-based short-term load forecasting on small datasets. In Proceedings of the 2022 IEEE 33rd Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Online, 12–15 September 2022; pp. 346–350. [Google Scholar]
- Ma, C.; Pan, S.; Cui, T.; Liu, Y.; Cui, Y.; Wang, H.; Wan, T. Energy Consumption Prediction for Office Buildings: Performance Evaluation and Application of Ensemble Machine Learning Techniques. J. Build. Eng. 2025, 102, 112021. [Google Scholar] [CrossRef]
- Zhao, P.; Cao, D.; Wang, Y.; Chen, Z.; Hu, W. Gaussian process-aided transfer learning for probabilistic load forecasting against anomalous events. IEEE Trans. Power Syst. 2023, 38, 2962–2965. [Google Scholar] [CrossRef]
- Ye, L.; Dai, B.; Li, Z.; Pei, M.; Zhao, Y.; Lu, P. An ensemble method for short-term wind power prediction considering error correction strategy. Appl. Energy 2022, 322, 119475. [Google Scholar] [CrossRef]
- Zhao, P.; Hu, W.; Cao, D.; Zhang, Z.; Huang, Y.; Dai, L.; Chen, Z. Probabilistic multienergy load forecasting based on hybrid attention-enabled transformer network and gaussian process-aided residual learning. IEEE Trans. Ind. Inform. 2024, 20, 8379–8393. [Google Scholar] [CrossRef]
- Fan, C.; Nie, S.; Xiao, L.; Yi, L.; Wu, Y.; Li, G. A multi-stage ensemble model for power load forecasting based on decomposition, error factors, and multi-objective optimization algorithm. Int. J. Electr. Power Energy Syst. 2024, 155, 109620. [Google Scholar] [CrossRef]
- Fan, C.; Nie, S.; Xiao, L.; Yi, L.; Li, G. Short-term industrial load forecasting based on error correction and hybrid ensemble learning. Energy Build. 2024, 313, 114261. [Google Scholar] [CrossRef]
- Qian, F.; Ruan, Y.; Lu, H.; Meng, H.; Xu, T. Enhancing source domain availability through data and feature transfer learning for building power load forecasting. In Building Simulation; Springer: Berlin/Heidelberg, Germany, 2024; Volume 17, pp. 625–638. [Google Scholar]
- Moghadam, S.T.; Delmastro, C.; Corgnati, S.P.; Lombardi, P. Urban energy planning procedure for sustainable development in the built environment: A review of available spatial approaches. J. Clean. Prod. 2017, 165, 811–827. [Google Scholar] [CrossRef]
- Tardioli, G.; Kerrigan, R.; Oates, M.; O’Donnell, J.; Finn, D.P. Identification of representative buildings and building groups in urban datasets using a novel pre-processing, classification, clustering and predictive modelling approach. Build. Environ. 2018, 140, 90–106. [Google Scholar] [CrossRef]
- Feng, C.; Cui, M.; Hodge, B.M.; Zhang, J. A data-driven multi-model methodology with deep feature selection for short-term wind forecasting. Appl. Energy 2017, 190, 1245–1257. [Google Scholar] [CrossRef]
- Carneiro, T.C.; Rocha, P.A.; Carvalho, P.C.; Fernández-Ramírez, L.M. Ridge regression ensemble of machine learning models applied to solar and wind forecasting in Brazil and Spain. Appl. Energy 2022, 314, 118936. [Google Scholar] [CrossRef]
- Lu, S.; Bao, T. Short-term electricity load forecasting based on NeuralProphet and CNN-LSTM. IEEE Access 2024, 12, 76870–76879. [Google Scholar] [CrossRef]
- Fan, C.; Xiao, F.; Wang, S. Development of prediction models for next-day building energy consumption and peak power demand using data mining techniques. Appl. Energy 2014, 127, 1–10. [Google Scholar] [CrossRef]
- Wang, Z.; Liang, Z.; Zeng, R.; Yuan, H.; Srinivasan, R.S. Identifying the optimal heterogeneous ensemble learning model for building energy prediction using the exhaustive search method. Energy Build. 2023, 281, 112763. [Google Scholar] [CrossRef]
- Zhang, Y.; Wen, H.; Wu, Q.; Ai, Q. Optimal adaptive prediction intervals for electricity load forecasting in distribution systems via reinforcement learning. IEEE Trans. Smart Grid 2022, 14, 3259–3270. [Google Scholar] [CrossRef]
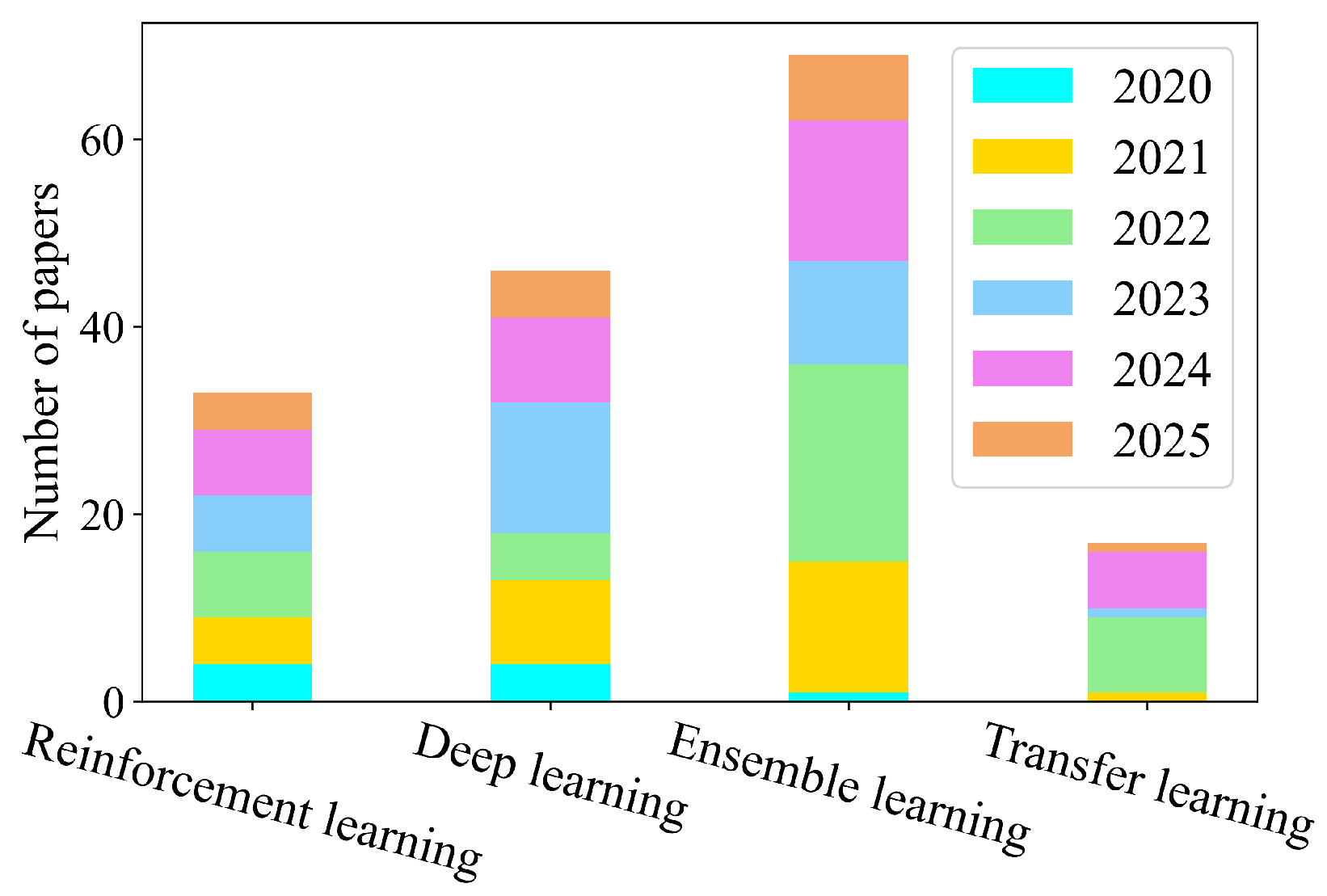
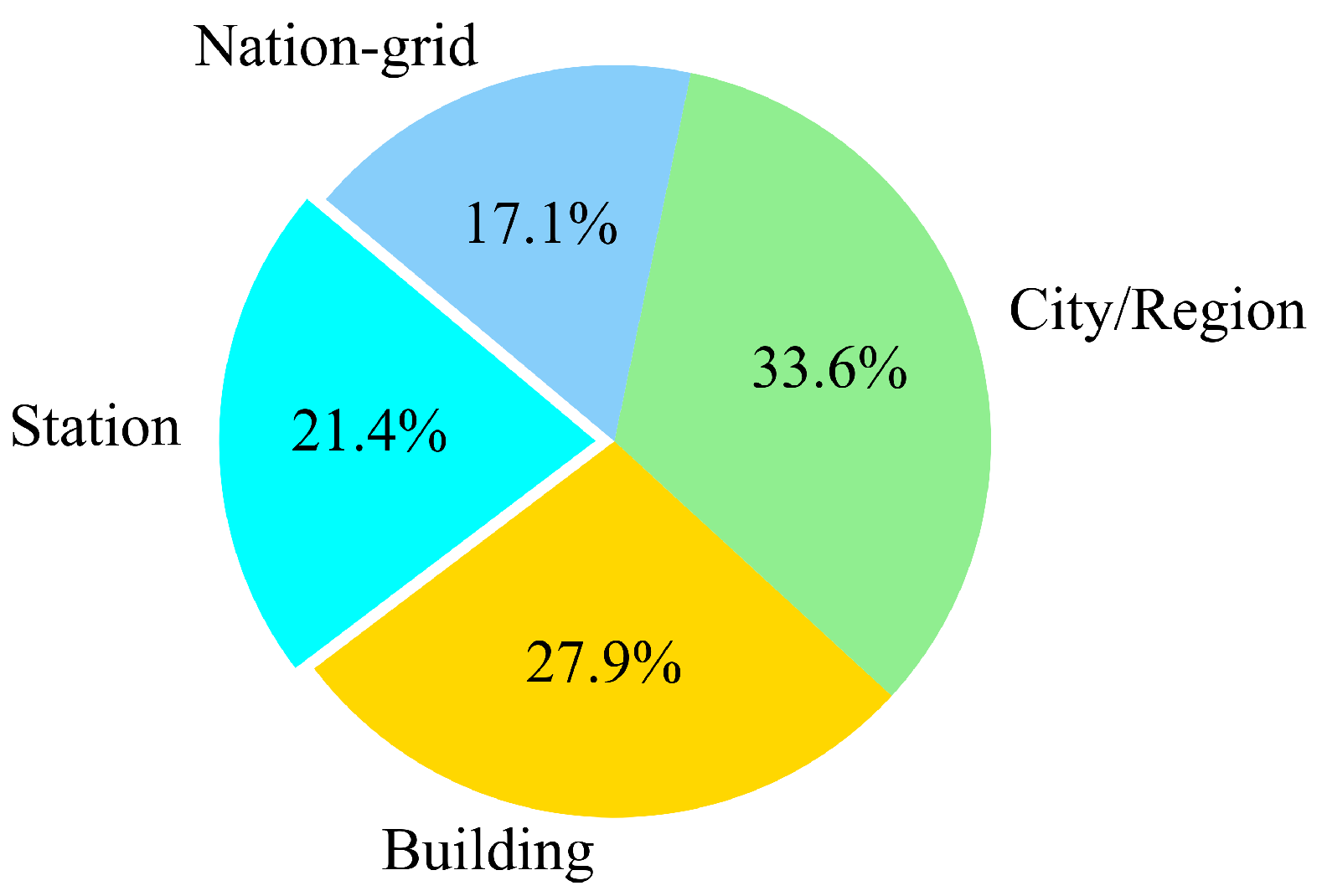
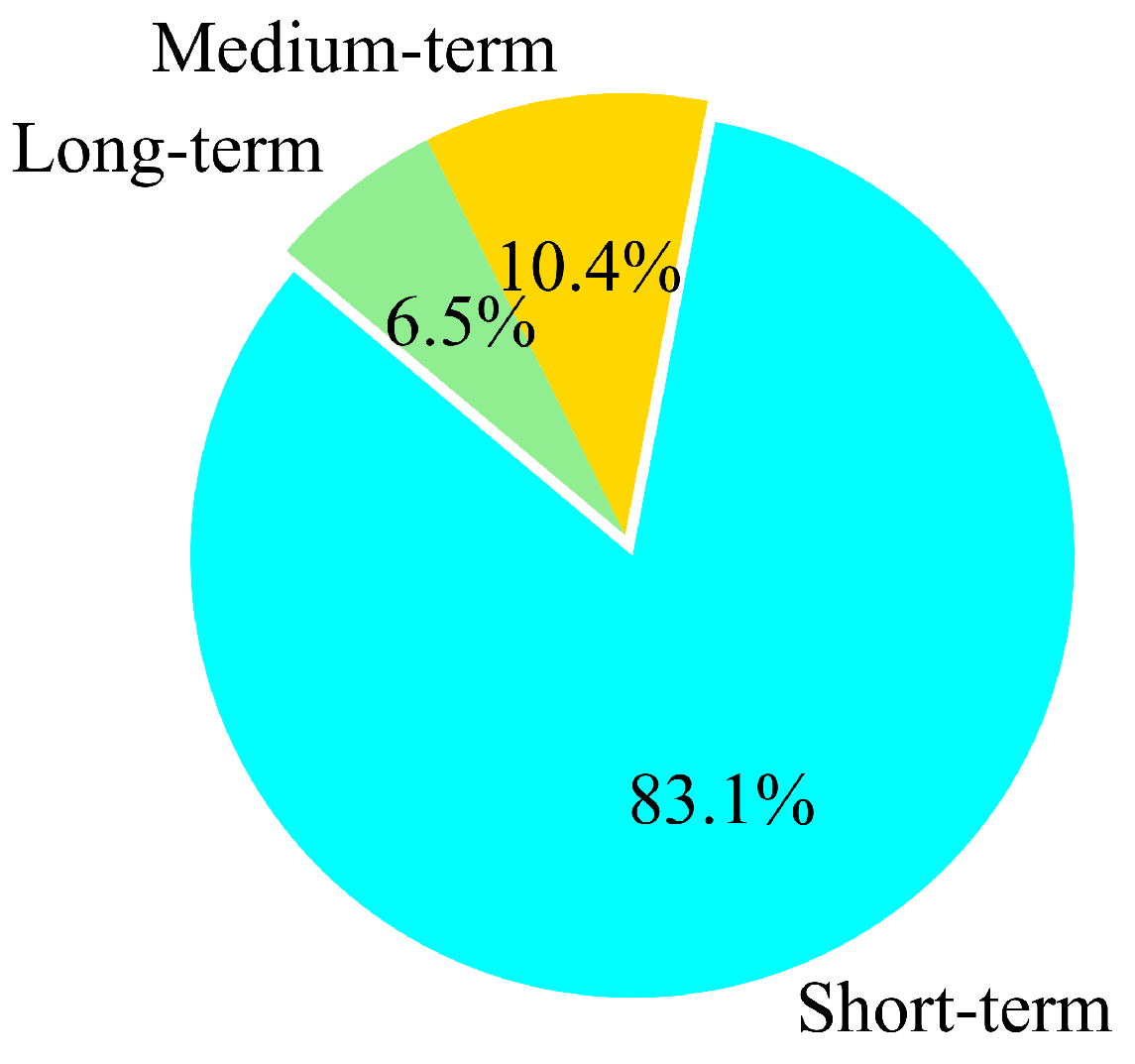
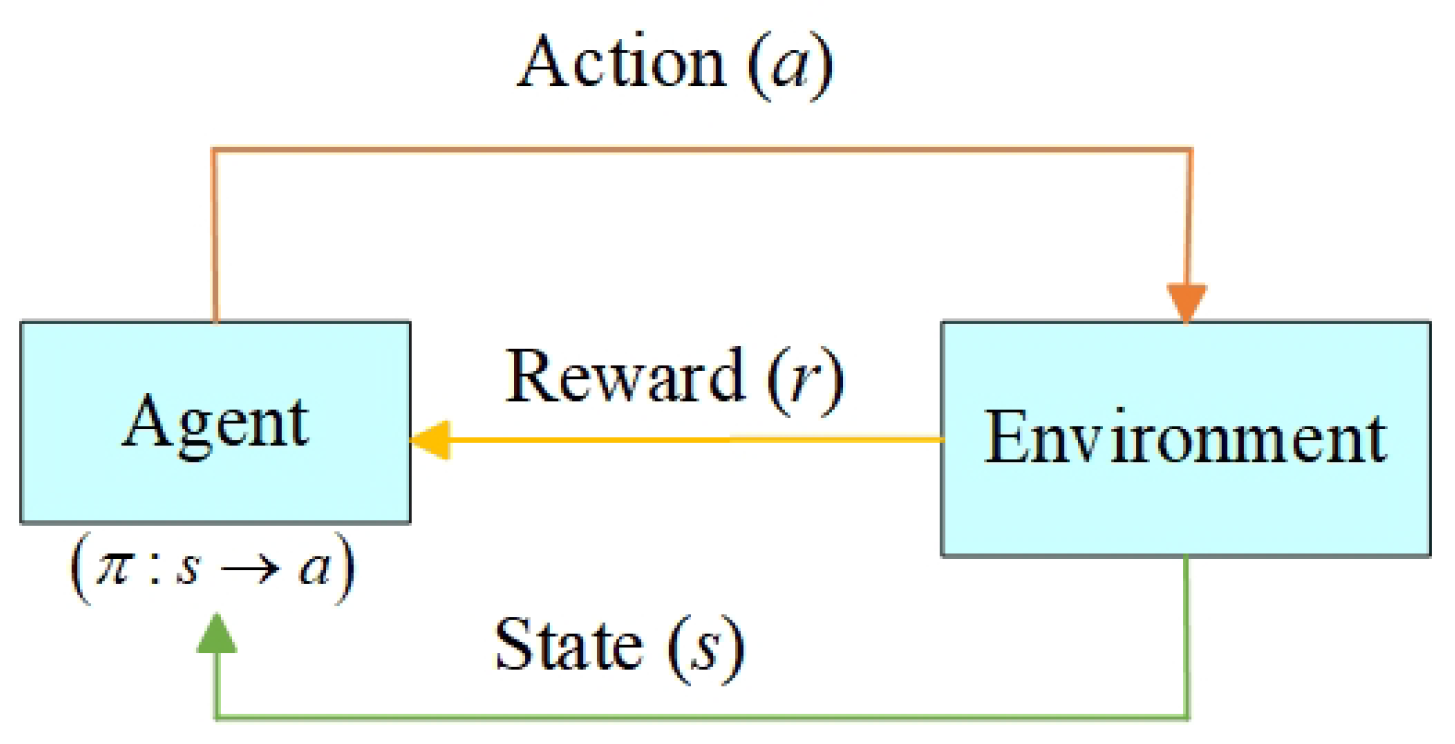


| Model | Modeling Difficulty | Applicability of Time Scale | Parameter Acquisition | Interpretability |
|---|---|---|---|---|
| Time-series model | Easy (the principle is simple) | Short term or medium to long term | Model training with a small amount of data (easy) | Relatively strong |
| AI model | Easy (various universal models and mature toolkits can be used) | Short term or medium to long term | Model training with a large amount of data (relatively easy) | Weak |
| Physical model | Difficult (high level of multidisciplinary expertise is required) | Short term | Experimental testing or product manuals (difficult) | Strong |
| Contents | [27] (2021) | [28] (2022) | [7] (2022) | [29] (2022) | [30] (2023) | [31] (2024) | [32] (2025) |
|---|---|---|---|---|---|---|---|
| Spatial-/temporal-scale statistics | × | ✓ | ✓ | ✓ | × | × | ✓ |
| Basic preprocessing | × | × | × | ✓ | × | × | ✓ |
| Advanced preprocessing | × | × | ✓ | ✓ | × | × | × |
| Deep learning models | × | ✓ | ✓ | ✓ | ✓ | × | ✓ |
| Reinforcement learning models | × | × | × | × | × | × | × |
| Transfer learning models | × | × | ✓ | ✓ | × | × | ✓ |
| Ensemble learning models | ✓ | × | × | ✓ | ✓ | ✓ | × |
| Preprocessing Method | Literature (Year) | Network/Algorithm/Mechanism | Benefits of Preprocessing |
|---|---|---|---|
| Deep learning-based feature extraction | [82] (2021) | GRU | RMSE decrease: 30.52% |
| [83] (2021) | GAN | RMSE decrease: 1.63% | |
| [44] (2021) | TCN | RMSE decrease: 41.20%; training time decrease: 11.32% | |
| [84] (2023) | CNN | increase: 3.85% | |
| [85] (2024) | GAN | RMSE decrease: 16.46% | |
| Reinforcement learning-based feature selection | [71] (2021) | Sarsa | RMSE decrease: 0.96–10.08% |
| [86] (2023) | DQN | RMSE decrease: 17.00% | |
| [87] (2024) | DDPG | Reliability improvement: 22.42% | |
| [88] (2024) | Actor–critic | RMSE decrease: 34.07% | |
| Attention mechanism-based feature extraction | [89] (2021) | RNN, cross-attention | RMSE decrease: 18.5% |
| [90] (2023) | GNN, hierarchical Attention | RMSE decrease: 6.82% | |
| [91] (2024) | CNN, global–local attention | RMSE decrease: 25.71% |
| Classification | Method | Interpretability | Complexity | Application Scenarios | Performance Improvement |
|---|---|---|---|---|---|
| Basic methods | Statistic-/information-based feature selection | High | Low to medium | Linear/monotonic relationships between features and targets | Overfitting reduction, training acceleration |
| ML-based feature selection | Medium | Medium to high | Complex coupling/nonlinear relationships between features | Training acceleration, improved generalization | |
| Data-dimension reduction | Low to medium | Medium to high | Feature redundancy | Noise reduction, training acceleration | |
| Feature enhancement | Low | Medium to high | Strong nonlinear data | Robustness improvement | |
| Mode decomposition | Medium to high | Low to medium | Series with fluctuations and multiple frequencies | Accuracy improvement, noise reduction | |
| Wavelet decomposition | Medium | Medium | Series with transient events or sudden changes | Noise reduction | |
| STL | High | Low | Series with seasonality and trend fluctuations | Robustness improvement | |
| Advanced methods | DL-based feature extraction | Low | Very high | Big data, complex features | Accuracy improvement |
| RL-based feature selection | Low | Very high | Dynamic feature selection | Adaptability improvement | |
| AM-based feature extraction | Medium to high | Very high | Deep/dynamic feature selection | Adaptability improvement, overfitting reduction |
| Application | Literature (Year) | Reinforcement Learning Algorithm | State | Action |
|---|---|---|---|---|
| Direct forecasting | [115] (2021) | ADDPG | A sequence of load data | Forecasted load |
| [116] (2022) | DQN | State class probabilities and historical energy consumption data | Discrete forecasted energy consumption | |
| Parameter optimization | [117] (2022) | DDPG | MAPE | Learning rate of LSTM |
| [51] (2024) | REINFORCE | Hyperparameters and kernel operators for two models | Model hyperparameter values | |
| [118] (2025) | DDPG | Absolute value of error | Hyperparameters of GRU | |
| Integration of base learners | [40] (2022) | Q-learning | Optimal learner label sequence in current step, absolute value of error | Optimal learner label sequence in next step |
| [119] (2022) | Q-learning | Optimal learner label sequence in current step | Optimal learner label sequence in next step | |
| [120] (2022) | DDPG | Weights of base learners | Weight increments | |
| [90] (2023) | DDPG | Weights of base learners | Weight increments | |
| [121] (2024) | Q-learning | Weights of base learners in current step | Weights of base learners in next step | |
| [122] (2025) | DDPG | Predicted loads of base learners | LF value |
| Literature (Year) | Transfer Algorithm | Transfer Method | Similarity Measurement |
|---|---|---|---|
| [131] (2022) | LSTM | Model transfer | / |
| [132] (2022) | LSTM | Instance transfer, model transfer | MIC |
| [43] (2022) | CNN-GRU | Model transfer | MMD, PCC |
| [133] (2022) | DANN | Feature transfer | / |
| [134] (2022) | MTE-LSTM | Model transfer | TSS-DC |
| [135] (2022) | ELM | Model transfer, feature transfer | / |
| [136] (2024) | K-MIFS-XGBoost | Instance transfer, model transfer | PCC |
| [129] (2024) | iTrAdaBoost-LSTM | Instance transfer | WD, NNS |
| [137] (2024) | BP, ELM, ENN, RBF, LSTM, GRU | Model transfer | PCC |
| [49] (2024) | CNN-LSTM | Feature transfer | MIC |
| [138] (2024) | DSSFA-LSTM | Model transfer | WM |
| [139] (2024) | CNN-GRU | Model transfer | MD |
| Literature (Year) | Basic Framework | Base Learner | Combination of Base Learners |
|---|---|---|---|
| [151] (2022) | Stacking | GRU, LSTM, TCN | Weight searching |
| [160] (2023) | Stacking | LSTM, GRU, TCN | Weight optimization (DE) |
| [64] (2024) | Stacking | TCN, ISSA-WFTS, BiLSTM-Attention | Weight optimization (ISSA) |
| [81] (2025) | Stacking | GRU, LSTM, BiLSTM, TCN | Weight optimization (MLP) |
| [46] (2021) | Stacking | BiLSTM | Meta-learner (GBDT) |
| [161] (2021) | Stacking | PSO, SA, ES, RS, BO-XGBoost, LGBM | Meta-learner (MLP) |
| [37] (2023) | Bagging | RNN, LSTM, GRU, BiLSTM | Weight optimization |
| [47] (2024) | Bagging | Attention-CNN-BiGRU | Average |
| [162] (2024) | Stacking | RNN, LSTM, GRU, BiLSTM, CNN | Meta-learner (KNN) |
| [163] (2025) | Stacking | TCN-LSTM, LightGBM | Meta-learner (MLR) |
| Literature (Year) | Boosting Algorithm or Correction Model | Base Learner |
|---|---|---|
| [129] (2024) | TrAdaBoost | LSTM |
| [166] (2023) | GP-based error correction | ResNet |
| [168] (2024) | GP-based error correction | Transformer |
| [169] (2024) | GRU-based error correction | GRU |
| [170] (2024) | GE-based error correction | RR |
| [85] (2024) | SVR-based similar day error correction | XGBoost |
| Advanced Model | Computational Cost | Interpretability | Generalization Capability | MAPE | Application Scenarios |
|---|---|---|---|---|---|
| Deep ResNet | High | Low to medium | Strong | 1.447% [108] | High-resolution spatiotemporal data forecasting |
| TCN | Medium to high | Low to medium | Strong | 1.123% [64] | Sequence with long-term dependency |
| Transformer | Very high | Medium | Very strong | 1.113% [75] | Complex feature extraction, sequence with long-term dependency |
| DDPG-based model | Very high | Low | Medium | 1.102% [122] | Sequence with sudden fluctuations or transient events |
| TL-based model | Medium | Low to medium | Strong | 1.88% [129] | Small-sample forecasting |
| Parallel ensemble model | High | Low to medium | Strong | 1.099% [163] | Generalized forecasting |
| Serial ensemble model | Medium to high | Low to medium | Strong | 1.010% [52] | Non-stationary sequence |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; He, X.; Li, K.; Xue, W. A Review of State-of-the-Art AI and Data-Driven Techniques for Load Forecasting. Energies 2025, 18, 4408. https://doi.org/10.3390/en18164408
Liu J, He X, Li K, Xue W. A Review of State-of-the-Art AI and Data-Driven Techniques for Load Forecasting. Energies. 2025; 18(16):4408. https://doi.org/10.3390/en18164408
Chicago/Turabian StyleLiu, Jian, Xiaotian He, Kangji Li, and Wenping Xue. 2025. "A Review of State-of-the-Art AI and Data-Driven Techniques for Load Forecasting" Energies 18, no. 16: 4408. https://doi.org/10.3390/en18164408
APA StyleLiu, J., He, X., Li, K., & Xue, W. (2025). A Review of State-of-the-Art AI and Data-Driven Techniques for Load Forecasting. Energies, 18(16), 4408. https://doi.org/10.3390/en18164408







