Abstract
Aiming at the incentive effect of real-time electricity prices on load demand response in the context of the electricity market, this paper proposed a dual layer optimization operation method for regional energy storage considering dynamic electricity prices and battery capacity degradation. The innovation of the proposed method lies in introducing user satisfaction and establishing real-time electricity price models based on fuzzy theory and consumer satisfaction, making dynamic electricity prices more realistic. At the same time, the proposed dual layer optimization operation model for regional energy storage has modeled the capacity degradation performance of energy storage batteries, which more accurately reflects the practicality of energy storage batteries. Finally, the particle swarm optimization (PSO) algorithm is utilized to efficiently optimize charging/discharging strategies, balancing economic benefits with battery longevity. The correctness of the proposed method is verified through simulation examples using MATLAB. Simulation results demonstrate that real-time electricity prices based on consumer satisfaction increase load demand response resources, resulting in stronger absorption of new energy sources, improving by 73.7%, albeit with reduced economic efficiency by 11.27%. While the real-time electricity prices based on fuzzy theory exhibit weaker absorption of new energy sources improving by only 36.4%, but achieve the best overall economic performance.
1. Introduction
With the widespread adoption of smart metering devices and the rapid advancement of energy storage technologies, the ability of end-users to participate in power system regulation has significantly improved. How to leverage dynamic electricity price signals to guide user consumption behavior and achieve deep coordination between flexible resources such as energy storage and grid operations has become a critical issue for ensuring stable power system operation and enhancing overall benefits. Therefore, conducting research on dynamic electricity pricing and exploring corresponding optimal operation strategies for energy systems holds significant practical importance and research value [1,2].
Foreign research on dynamic pricing was initiated relatively early. In the 1980s, Professor F. C. Schweppe proposed the concept of real-time pricing [3]. Some studies have established models from the perspective of marginal cost. Although this approach has certain rationality, the calculation of marginal cost is cumbersome and does not fully consider consumer demand flexibility. Moreover, due to the numerous factors influencing consumer purchasing decisions, the prediction accuracy remains limited, and further exploration is needed to develop reasonable pricing strategies tailored to different consumer needs. Machine learning algorithms can uncover patterns from large datasets to improve model accuracy [4], but they require substantial data and lack strong explanatory power. Significant progress has also been made in domestic research on this topic. Although existing studies have attempted to apply these models to electricity markets, accurately predicting power output under these models and formulating reasonable electricity prices based on such predictions remains a challenging issue in the field. Additionally, considering the safety and reliability of power systems, some researchers have proposed incorporating constraints into power systems to ensure their safe and stable operation [5]. However, obtaining and updating these constraints, as well as developing optimal solution methods for them, have consistently been focal points of attention [6].
Centralized and decentralized energy storage optimization are the main research directions of foreign scholars. Centralized optimization treats the power network as a whole and executes scheduling in a unified manner by establishing an overall optimization model, thereby maximizing the benefits of the power network. However, centralized optimization requires extensive computation and communication, resulting in high computational load and information security risks. Decentralized optimization divides the power system into several subsystems, where each subsystem makes independent decisions and then collaboratively solves the problem, which is flexible and scalable, aligning with the decentralized trend of power systems. However, it faces challenges in information coordination among subsystems and is prone to falling into local optimal solutions. Additionally, many optimization algorithms have been studied under different environments and constraints. For example, the Dynamic Programming Method can optimize charging and discharging schedules, but it suffers from the “curse of dimensionality” and exhibits very low computational efficiency [7].
Domestic research should be conducted in accordance with the actual conditions and development needs of China’s power system [8,9]. In response to the large-scale integration of new energy sources, many researchers have proposed coordinated optimization and scheduling methods for energy storage and new energy [10,11]. By establishing coordinated scheduling models between energy storage and new energy, these methods aim to improve the utilization of new energy and the stability of the power grid [12,13,14]. However, the uncertain characteristics of energy storage and new energy determine that such coordinated scheduling methods still require further improvement [15]. Some researchers have also explored the trading strategies of energy storage power generation enterprises participating in the market from an economic perspective by establishing optimal models [16,17,18,19]. They argue that energy storage power generation enterprises can achieve maximum profits by establishing optimal models. However, these enterprises face complex market rules, market uncertainties, and barriers to market entry. Moreover, the policies and mechanisms for energy storage power generation enterprises also need further improvement [20,21].
To address the limitations of existing research, this paper proposes a two-layer optimization operation model for regional energy storage considering the capacity degradation characteristics of energy storage batteries and dynamic electricity pricing. The key innovations are as follows: (1) introduces user satisfaction levels and establishes a real-time electricity pricing model based on fuzzy theory and consumer satisfaction metrics, making dynamic pricing more aligned with practical scenarios; (2) incorporates a battery capacity degradation model that accurately reflects the practical utility of energy storage batteries, addressing performance decay under complex charge/discharge cycles. Finally, the particle swarm optimization (PSO) algorithm is utilized to efficiently optimize charging/discharging strategies, balancing economic benefits with battery longevity. The correctness of the proposed method is verified through simulation examples using MATLAB R2023b.
2. Dynamic Electricity Price Model
The variation in electricity demand is closely related to changes in electricity prices, while electricity price fluctuations are influenced by numerous factors. From an economic perspective, changes in electricity prices significantly impact consumer electricity usage behavior, exhibiting a clear negative correlation between the two—a fundamental reflection of the electricity supply–demand relationship.
Large industrial consumers exhibit high dependence on electricity, strong demand elasticity, and sensitivity to price changes. They adjust their production schedules in response to price fluctuations. Meanwhile, commercial consumers’ electricity usage is affected by factors such as working hours. When electricity prices are high, they reduce costs by adjusting work schedules; conversely, when prices are low, they increase promotional activities to lower expenses.
2.1. Real-Time Electricity Price Model Based on Fuzzy Theory
Fuzzy mathematics is a novel approach based on fuzzy theory, utilizing the concept of fuzzy membership functions to describe the relationships between fuzzy elements and fuzzy sets within a system. In the electricity market environment, the prices during peak, valley, and flat periods exhibit uncertain characteristics, making them suitable for the application of fuzzy theory. By introducing the membership relationships of peak, off-peak, and flat periods into the real-time pricing model of power systems, this paper defines membership functions for each time point across these three periods and quantifies their respective affiliations [20].
Specifically, we define three membership functions: μpeak(t) represents the degree of membership of time, t, in the peak period, μvalley(t) represents the degree of membership of time, t, in the off-peak period, and μflat(t) represents the degree of membership of time, t, in the flat period. The values of these three membership functions all lie within the range [0, 1], and they satisfy the constraint: μpeak(t) + μvalley(t) + μflat(t) = 1, meaning that each time point must belong-to some extent-to one or more of these three periods.
The determination of membership functions is a critical step in establishing a real-time electricity pricing model based on fuzzy theory. In this paper, triangular membership functions are adopted. The shape of these functions is determined based on historical load data, electricity consumption patterns, and expert experience. For the peak period membership function μpeak(t), the degree of membership is set to 1 at the center of the peak period and gradually decreases as time moves away from the center toward the boundaries of the peak period, where the membership drops to 0. The specific mathematical expression can be written as:
Here, tpeak1 and tpeak4 represent the start and end times of the peak period, respectively, while tpeak2 and tpeak3 are two critical time points within the peak period used to determine the shape of the membership function. Similarly, the membership functions for the off-peak period (μvalley(t)) and the flat period (μflat(t)) can be defined in the same manner.
The real-time electricity pricing method has been improved based on the peak–valley–flat membership degrees. In the traditional Time-of-Use (TOU) pricing model, the electricity price remains fixed for each time period. In contrast, the peak–valley–flat membership-based pricing model determines the electricity price for each time period according to users’ membership degrees. Assuming the electricity prices for the peak, off-peak, and flat periods are ppeak, pvalley, and pflat, respectively, the real-time electricity price at time, t, denoted as p(t), can be calculated using the following formula:
2.2. Real-Time Electricity Pricing Model Based on Consumer Satisfaction
To conduct an in-depth analysis of the relationship between electricity demand and electricity prices, we can establish a mathematical model for quantitative research. Assuming the electricity demand function is D(p), where p represents the electricity price, the demand elasticity coefficient can be expressed as:
where ΔD represents the change in electricity demand, Δp represents the change in electricity price. The demand elasticity coefficient reflects the sensitivity of electricity demand to changes in electricity prices. When , it indicates that electricity demand is highly sensitive to price changes—a small price adjustment can lead to a significant change in demand, meaning the demand is elastic. When , it suggests that electricity demand is relatively insensitive to price changes—a price variation has minimal impact on demand, meaning the demand is inelastic. When , The percentage change in electricity demand is proportionally equal to the percentage change in electricity price, indicating unitary price elasticity of demand.
The Least Squares Method (LSM) is a cornerstone of statistical modeling and data fitting, widely adopted across disciplines like economics, engineering, and data science. For the estimation of the electricity demand function D(p), historical data on electricity demand and prices from multiple users in the power system can be collected. By applying the Least Squares Method (LSM) and other curve-fitting techniques, a functional relationship D(p) = a + bp can be established between the electricity demand and prices of multiple users in the power system. Given a set of historical data points , according to the principle of the Least Squares Method, the objective is to minimize the sum of squared errors between the observed values Di and the predicted values Dpi from the function.
By solving the above optimization problem, we can obtain estimates for parameters a and b, thereby determining the load requirement as a function of electricity price. Based on this, a new electricity market pricing model has been developed, with the primary objective of guiding consumer electricity usage behavior through rational pricing to achieve optimal power allocation.
Under the conditions of total system load demand D and generation cost C(D), the model aims to minimize generation costs while meeting load requirements, thereby achieving economic operation. Simultaneously, considering consumer responses to electricity prices, a utility function U(D, p) is established, where U represents consumer satisfaction with both electricity price and demand quantity U(D, p) quantifies this satisfaction level.
Taking into account both power generation costs and consumer utility, the following real-time pricing model is established:
Users aim to maximize their utility under the constraint of limited budget.
3. Battery Capacity Fade Model
Over time, the capacity of energy storage batteries gradually declines, which adversely affects the performance and service life of the energy storage system. Key factors influencing battery performance include the number of charge–discharge cycles, charge–discharge rates, and operating temperature. As the number of cycles increases, the rate of battery degradation accelerates. High charge and discharge rates not only reduce battery capacity but may also pose safety risks due to elevated charge rates. Higher temperatures accelerate self-discharge, damage the battery’s internal structure, while lower temperatures reduce the available capacity and accelerate aging.
The calculation formula for energy storage battery capacity fade Cdeg(%) is:
where represents the cycle degradation cost coefficient, represents the calendar degradation rate, represents the rated capacity (kWh), T represents the operating days, Δt is the charging and discharging time interval (h).
represents the time degradation coefficient, and the temperature correction formula is given by:
4. Regional Energy Storage Bi-Level Optimization Operation Model
The upper-level optimization objective of the regional energy storage system considering real-time electricity prices is to maximize: (1) peak-shaving and valley-filling benefits; (2) renewable energy accommodation benefits; and (3) operating profits from low-price storage and high-price dispatch. The lower-level optimization objective is to minimize: (1) battery capacity fade in the regional energy storage system and (2) capacity fade-related costs.
where represents the accommodation benefit of renewable energy, represents the operational profit from low-price storage and high-price dispatch of energy storage, represents the benefits of peak shaving and valley filling, represents the cost of capacity fade.
Based on economic value weights, dynamically adjusting the weight coefficient ω according to the revenue proportion:
where α = 0.15 (electricity price sensitivity) and β = 0.08 (subsidy sensitivity).
4.1. Objective Function
The calculation formula for the benefits of renewable energy accommodation is:
where represents the incremental accommodation (kWh), represents the on-grid electricity price (¥/kWh), represents the per-kilowatt-hour subsidy.
The calculation formula for the operational profit from low-price storage and high-price dispatch of energy storage is:
where represents the real-time electricity price (¥/kWh), represents the charging/discharging power (kW), represents the charging/discharging efficiency.
By utilizing demand response from loads and energy storage systems, the demand curve can be effectively adjusted to reduce peak loads. While ensuring power supply reliability and power quality, this approach delays investments in power system equipment. The peak-shaving and valley-filling benefits can be expressed as:
The calculation formula for capacity charge savings is:
The revenue from transferred electricity is the difference between peak-period discharge and off-peak charging quantities. represents the capacity tariff (¥/kW), represents the average electricity price (¥/kWh).
The calculation of capacity degradation at the lower level is performed according to Equation (6).
4.2. The Coordinated Interaction Relationship Between Energy Storage and Source-Load Systems
In summary, the coordinated interaction between energy storage and source-load systems achieves power balance, enabling peak shaving and valley filling while facilitating new energy integration. The calculation formula for the dynamic supply–demand balance equation is:
represents the output of renewable energy sources (kW), denotes the charging/discharging power of the energy storage system (kW), indicates the electricity consumption of the load (kW). When , it represents surplus renewable energy absorbed by charging; When , it represents deficit compensated by discharging.
The dynamic equation governing the State of Charge (SOC) of the energy storage system is expressed as:
where represents charging/discharging efficiency.
4.3. Constraints
When the energy storage device is in the charging state and its charging power is consumed by the electrical system, the power generated from the alternative power source must satisfy the sum of the load demand and the energy storage device’s charging power at a specific moment. When the energy storage system operates in discharge mode, its discharged power supplies electricity to the power grid, thereby reducing the generation requirement from other power sources. Specifically, the power balance limit can be expressed as:
where represents the power generation output of alternative power sources at time, t, (kW), denotes the discharging power of the energy storage system at time, t, (kW), indicates the cumulative charged energy stored in the energy storage system up to time, t, (kW).
To ensure the safe and stable operation of the energy storage system, its State of Charge (SOC) must be maintained within specific operational limits:
where and represents the lower limit and upper limit of the energy storage system’s State of Charge (SOC), SOC(t) indicates the State of Charge of the energy storage system at time—t.
To ensure the safe and smooth operation of the energy storage system, it is necessary to limit the charge/discharge rate. The charge/discharge rate limits can be expressed as follows:
where and respectively represents the maximum charging power and the maximum discharging power of the energy storage system. These limiting parameters are determined based on the technical specifications and safety requirements of the energy storage system. During actual operation, the charging and discharging power of the energy storage system must remain within this range to ensure normal operation and extend service life.
Battery aging occurs progressively during charge/discharge processes, with accelerated capacity and performance degradation under high utilization conditions. For enhanced battery longevity, the depth of discharge (DOD) and charge/discharge frequency must be constrained within specified limits. Consequently, the system’s operational constraints for battery lifespan are defined as:
where is the permitted maximum depth of charge/discharge (DOD). DOD(t) represents the depth of discharge of the energy storage system at time—t. By limiting the charge and discharge depths, the degradation rate of the battery can be effectively reduced, thereby achieving longer battery lifespan and lower operational costs for the energy storage system.
4.4. Solving Process
The Particle Swarm Optimization (PSO) algorithm formulates the solution of optimization problems as a swarm of particles characterized by their movement velocity and position. The trajectory of each particle represents a potential solution to the problem, while the velocity of the particle indicates its movement direction and step size. In this method, particles move along specific trajectories, with each particle adjusting its velocity and position iteratively to converge toward the optimal solution [22,23]. This study employs the PSO algorithm to solve the bi-level optimization model for regional energy storage operation. During the optimization process, each particle memorizes the best position it has encountered individually (personal best, pbest) and is aware of the best position discovered by the entire swarm (global best, gbest). The velocity and position of particles are updated according to the following equations:
where represents the velocity of particle i in dimension d at the t-th iteration; ω is the inertia weight, which controls the degree to which a particle inherits its previous velocity.
A larger ω value favors global search, while a smaller ω value favors local search; c1 and c2 are learning factors (also called acceleration constants); r1 and r2 are two random numbers in the range [0, 1], introduced to enhance the randomness of the algorithm; is the personal best position of particle i at the t-th iteration; is the global best position of the entire swarm at the t-th iteration; is the position of particle i in dimension d at the t-th iteration; and respectively represent the position and velocity of particle i in dimension d at the (t + 1)-th iteration.
During each iteration, particles adjust their movement equations based on their current displacement and velocity, progressively converging toward their personal best and global best positions throughout the optimization process. Through iterative refinement, the particle swarm continuously approaches the optimal solution, ultimately yielding the optimized operational strategy for regional energy storage.
5. Case Study
This paper validates the proposed bi-level optimization operation method for regional energy storage considering dynamic electricity prices through practical case studies on a regional distribution network. Different optimal operation schemes for energy storage under various pricing models are developed. The designed scenarios include: Scenario 1: real-time electricity price based on fuzzy theory; and Scenario 2: real-time electricity price model considering consumer satisfaction.
The case study is conducted on the IEEE 33-node distribution network system, where Wind farms are connected to nodes 28 and 23; Photovoltaic units are connected to nodes 3 and 13; The energy storage system is connected to nodes 10 and 27, with an installed power of 447.23 kW and installed capacity 1282.44 kWh. The simulation parameters are set as follows: Installed capacity of wind turbines and PV units: 300 kW; Minimum/maximum grid power exchange: Pgrid,min = 1000 kW, Pgrid,max = 1400 kW; State of Charge (SOC) constraints: SOCmin = 0.2, SOCmax = 0.98. The dynamic electricity price curves for the two scenarios are shown in Figure 1 and Figure 2, respectively. For PSO, population size is 300, number of iterations is 100, acceleration factor c1 = 0.5, c2 = 1, convergence criteria: Error less than 1%. The data is sourced from the commercial and industrial load data of Shanghai Changxing Island Fishing Port Co., Ltd. (Shanghai, China), but the proposed dual layer optimization operation method for regional energy storage considering dynamic electricity prices are not in practical application.

Figure 1.
Real-time electricity price curve based on fuzzy theory.

Figure 2.
Consumer satisfaction-oriented real-time electricity pricing model.
As shown in Figure 1 and Figure 2, the real-time electricity price curve based on fuzzy theory better reflects the demand characteristics of the power market; whereas the consumer satisfaction-based real-time pricing model is more effective in guiding power consumption behavior, achieving peak shaving and valley filling in the power market, as well as energy conservation and emission reduction.
5.1. Optimal Operation Schemes Under Different Scenarios
Figure 3 presents the contour plot illustrating the dynamic electricity price–time–load demand response relationship under Scenario 1.

Figure 3.
Relationship between electricity price and load response under Scenario 1.
It is apparent that the fuzzy-theory-based real-time pricing curve exhibits superior capability in capturing the dynamic demand patterns of the power market. Consequently, a scenario-specific bi-level optimization strategy for regional energy storage systems is formulated, as demonstrated in Figure 4. Furthermore, Figure 5 showcases the intricate power operational dynamics of the regional distribution network under Scenario 1.

Figure 4.
Bi-level optimal operation scheme for regional energy storage under Scenario 1.
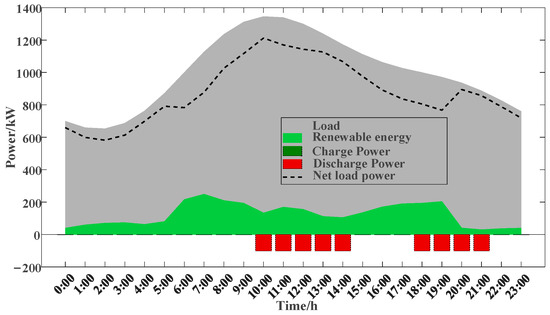
Figure 5.
Operational power of the regional distribution network under Scenario 1.
As depicted in Figure 4, the energy storage system adopts a 2-charge and 2-discharge strategy within a single day. The principle of “charging during low electricity prices and discharging during high electricity prices” enables energy storage systems to achieve greater profits. This strategy, known as “peak–valley arbitrage”, leverages electricity price differentials to maximize revenue by storing energy when costs are minimal and releasing it during high-demand, high-price periods. Specifically, it charges from 0:30 to 3:00 and from 16:30 to 17:30. This charging behavior is primarily due to the low electricity prices and relatively low load demand during these periods. Conversely, the energy storage discharges from 9:30 to 13:30, from 17:30 to 18:30, and from 22:30 to 23:30. These discharging periods align with higher electricity prices and increased load demand. Figure 5 illustrates that, due to the limited penetration of new energy sources within the regional network, the energy storage system and interconnection lines effectively absorb the available renewable energy. Figure 6 presents the benefits of the regional network over the course of one week under Scenario 1. In Figure 6, we selected a 7-day scenario for Daily Economic Benefit Analysis and Figure 5 is the Monday in Figure 6.

Figure 6.
Daily Economic Benefit Analysis and Benefit Composition Under Scenario 1.
As illustrated in Figure 6, the energy storage system achieves maximum benefits through low-storage–high-generation strategies, followed by benefits from new energy absorption, with peak shaving and valley filling providing the least benefits. Under Scenario 2, the real-time electricity price model incorporates consumer satisfaction, thereby enhancing the system’s load demand response capabilities. Following the introduction of consumer satisfaction, the net load power of the regional grid is depicted in Figure 7. It is evident that the regional network exhibits stronger load regulation capabilities. The bi-level optimal operation scheme for regional energy storage under Scenario 2 is shown in Figure 8.

Figure 7.
Net Load Power of the Regional Grid Considering Consumer Satisfaction.

Figure 8.
Bi-level Optimal Operation Scheme for Regional Energy Storage Under Scenario 2.
Figure 9: Assessment of Economic Performance and Battery Degradation Characteristics for Regional Energy Storage Systems Under Scenario 2.

Figure 9.
Economic Performance of Bi-level Optimal Operation Scheme for Regional Energy Storage Under Scenario 2.
Under Scenario 2, the charging and discharging power of energy storage significantly decreases, primarily due to the introduction of load demand response, which reduces the need for energy storage. Compared to Scenario 1, the economic efficiency of Scenario 2 is lower, which is also attributable to the reduced usage of energy storage. Correspondingly, the capacity degradation of the energy storage is also less pronounced.
5.2. Comparative Analysis
To evaluate the impact of dynamic electricity prices on the optimal operation scheme of regional energy storage, a comparative analysis of the regional energy storage optimization under Scenario 1 and Scenario 2 is conducted from the perspectives of regional network economic benefits, profit growth rate, payback period, and renewable energy absorption rate. The analysis of economic benefits, profit growth rate, and payback period of regional energy storage under different electricity pricing models is illustrated in Figure 10. The research of TOU price is the previous study in Reference [24]. We compare the real-time electricity prices based on fuzzy theory and real-time electricity prices based on consumer satisfaction with the TOU price.

Figure 10.
Analysis of Economic Benefits, Profit Growth Rate, and Payback Period of Regional Energy Storage under Different Electricity Pricing Models.
As shown in Figure 10, the implementation of real-time electricity prices based on fuzzy theory and consumer satisfaction models significantly enhances the economic benefits of the regional distribution network, achieving increases of 32% and 15%, respectively. Correspondingly, the payback period is shortened from 10 years to 6–8 years.
Figure 11: Analysis of Renewable Energy Absorption Rates for Regional Energy Storage Under Different Electricity Pricing Models. Evidently, the implementation of real-time electricity prices based on fuzzy theory and consumer satisfaction models significantly enhances the absorption rates of wind and solar energy by the regional distribution network, improving by 36.4% and 73.7%, respectively. If grid policy wants to achieve higher consumption of new energy, more reasonable electricity prices should be developed. Due to the inclusion of load demand response resources in the consumer satisfaction-based real-time pricing model, its capacity to absorb new energy is stronger, albeit with reduced economic efficiency.

Figure 11.
Analysis of Wind and Solar Energy Absorption Rates for Regional Energy Storage Under Different Electricity Pricing Models.
Upon comparing Figure 10 and Figure 11, it can be observed that the real-time electricity pricing model based on consumer satisfaction achieves a higher renewable energy absorption rate. However, its economic efficiency is not as high. This is primarily because the introduction of load demand response reduces the benefits of energy storage in peak shaving and valley filling. In contrast, the real-time electricity pricing model based on fuzzy theory yields greater economic benefits. This is mainly due to the substantial earnings from both peak shaving and valley filling, as well as low-storage–high-generation strategies of the energy storage system. Nevertheless, the renewable energy absorption rate under this pricing model is relatively low, primarily because only the energy storage system is capable of absorbing renewable energy.
6. Conclusions
In response to the incentive effects of real-time electricity prices on load demand response within the electricity market environment, this paper investigates a bi-level optimal operation method for regional energy storage that considers dynamic pricing. By integrating energy storage systems to absorb new energy sources, the study aims to enhance the reliability of power supply in the grid. Simulation case studies demonstrate that: (1) under different dynamic pricing models, the operational schemes for regional energy storage vary significantly, and the impact of battery capacity degradation on these operational schemes is substantial; (2) real-time electricity prices based on consumer satisfaction increase load demand response resources, resulting in stronger absorption of new energy sources, improving by 73.7%, albeit with reduced economic efficiency by 11.27%; (3) real-time electricity prices based on fuzzy theory exhibit weaker absorption of new energy sources improving by only 36.4%, but achieve the best overall economic performance. It should be noted that real-time electricity prices based on fuzzy theory and real-time electricity prices based on consumer satisfaction are only just a rough modeling of electricity market prices, more uncertainty methods are needed for the accurate modeling of electricity prices.
Author Contributions
Methodology, Z.Y.; Software, J.J.; Validation, Y.F.; Data curation, C.Z. and J.L.; Writing—original draft, W.Z.; Writing—review & editing, Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Science and Technology Project of Zhejiang Electric Power Company (891500Q202408084).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Authors Weilin Zhang, Zengxiang Yang, Yong Feng, Jie Jin, and Chenmu Zhou were employed by the State Grid Wenling Power Supply Company. Authors Liang Yongwei and Jiazhi Lei were employed by the State Grid Taizhou Power Supply Company. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Zheng, Y.; Song, Y.; Huang, A.; Hill, D.J. Hierarchical Optimal Allocation of Battery Energy Storage Systems for Multiple Services in Distribution Systems. IEEE Trans. Sustain. Energy 2020, 11, 1911–1921. [Google Scholar] [CrossRef]
- Qifeng, S.; Jiazhi, L.; Zhao, L. Optimal allocation of vanadium redox flow battery energy storage systems in active distribution networks considering multiple operation strategies. Int. J. Energy Res. 2022, 46, 18225–18238. [Google Scholar] [CrossRef]
- Yuan, Z.; Wang, W.; Wang, H.; Yildizbasi, A. Allocation and sizing of battery energy storage system for primary frequency control based on bio-inspired methods: A case study. Int. J. Hydrogen Energy 2020, 45, 19455–19464. [Google Scholar] [CrossRef]
- Alarfaj, F.K.; Malik, I.; Khan, H.U.; Almusallam, N.; Ramzan, M.; Ahmed, M. Credit Card Fraud Detection Using State-of-the-Art Machine Learning and Deep Learning Algorithms. IEEE Access 2022, 10, 39700–39715. [Google Scholar] [CrossRef]
- Li, X.; Xie, K.; Shao, C.; Hu, B. A Region-Based Approach for the Operational Reliability Evaluation of Power Systems with Renewable Energy Integration. IEEE Trans. Power Syst. 2024, 39, 3389–3400. [Google Scholar] [CrossRef]
- Pontes, L.R.B.; Rodriguez, Y.P.M.; Kuong, J.L.; Espinoza, H.R. Optimal Allocation of Energy Storage System in Distribution Systems with Intermittent Renewable Energy. IEEE Lat. Am. Trans. 2021, 19, 288–296. [Google Scholar] [CrossRef]
- Liu, G. Optimal power distribution method for energy storage system based on available capacity. Int. J. Low-Carbon Technol. 2021, 16, 45–49. [Google Scholar]
- Zheng, Y.; Dong, Z.; Huang, S.; Meng, K.; Luo, F.; Huang, J.; Hill, D. Optimal integration of mobile battery energy storage in distribution system with renewables. J. Mod. Power Syst. Clean Energy 2015, 3, 589–596. [Google Scholar] [CrossRef]
- Hannan, M.A.; Wali, S.B.; Ker, P.J.; Abd Rahman, M.S.; Mansor, M.; Ramachandaramurthy, V.K.; Muttaqi, K.M.; Mahlia, T.M.I.; Dong, Z.Y. Battery energy-storage system: A review of technologies, optimization objectives, constraints, approaches, and outstanding issues. J. Energy Storage 2021, 42, 103023. [Google Scholar] [CrossRef]
- Wang, D.; Zhi, Y.; Yu, B.; Chen, Z.; An, Q.; Cheng, L.; Fan, M. Optimal Coordination Control Strategy of Hybrid Energy Storage Systems for Tie-line Smoothing Services in Integrated Community Energy Systems. CSEE J. Power Energy Syst. 2018, 4, 408–416. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, C.; Dong, Z.Y.; Li, X. Improving Hosting Capacity of Unbalanced Distribution Networks via Robust Allocation of Battery Energy Storage Systems. IEEE Trans. Power Syst. 2021, 36, 2174–2185. [Google Scholar] [CrossRef]
- Zhang, D.; Shafiullah, G.M.; Das, C.K.; Wong, K.W. Optimal allocation of battery energy storage systems to improve system reliability and voltage and frequency stability in weak grids. Appl. Energy 2025, 377, 124541. [Google Scholar] [CrossRef]
- Elseify, M.A.; SeyyedAbbasi, A.; Domínguez-García, J.L.; Kamel, S. Probabilistic optimal planning of multiple photovoltaics and battery energy storage systems in distribution networks: A boosted equilibrium optimizer with time-variant load models. J. Energy Storage 2023, 73, 108986. [Google Scholar] [CrossRef]
- Yu, Y.; Jicheng, L. Collaborative decision-making model for capacity allocation of photovoltaics energy storage system under Energy Internet in China. J. Energy Storage 2023, 66, 107456. [Google Scholar] [CrossRef]
- Pawan, S.; Lata, G. An environmental based techno-economic assessment for battery energy storage system allocation in distribution system using new node voltage deviation sensitivity approach. Int. J. Electr. Power Energy Syst. 2021, 128, 106665. [Google Scholar] [CrossRef]
- Li, J.; Zou, W.; Yang, Q.; Yi, F.; Bai, Y.; Wei, Z.; He, H. Size optimization and power allocation of a hybrid energy storage system for frequency service. Int. J. Electr. Power Energy Syst. 2022, 141, 108165. [Google Scholar] [CrossRef]
- Zhang, T.; Qiu, W.; Zhang, Z.; Lin, Z.; Ding, Y.; Wang, Y.; Wang, L.; Yang, L. Optimal bidding strategy and profit allocation method for shared energy storage-assisted VPP in joint energy and regulation markets. Appl. Energy 2022, 329, 120158. [Google Scholar] [CrossRef]
- Ibrahim, N.N.; Jamian, J.J.; Rasid, M.M. Optimal multi-objective sizing of renewable energy sources and battery energy storage systems for formation of a multi-microgrid system considering diverse load patterns. Energy 2024, 304, 131921. [Google Scholar] [CrossRef]
- Al Ahmad, A.K.; Verayiah, R.; Shareef, H. Long-term optimal planning for renewable based distributed generators and battery energy storage systems toward enhancement of green energy penetration. J. Energy Storage 2024, 90, 111868. [Google Scholar] [CrossRef]
- Zhao, L.; Xueyi, W.; Jiazhi, L. A nested bi-level method for battery energy storage system optimized operation in active distribution networks considering differences of dynamic electricity prices. J. Energy Storage 2024, 85, 111099. [Google Scholar] [CrossRef]
- He, D.; Lin, W.; Liu, N.; Harley, R.G.; Habetler, T.G. Incorporating Non-Intrusive Load Monitoring into Building Level Demand Response. IEEE Trans. Smart Grid 2023, 4, 1870–1877. [Google Scholar]
- Sadiqa, J.; Yung-Cheol, B. AI-driven state of power prediction in battery systems: A PSO-optimized deep learning approach with XAI. Energy 2025, 331, 136764. [Google Scholar]
- Kariman, H.; Hoseinzadeh, S.; Khiadani, M.; Nazarieh, M. 3D-CFD analysing of tidal Hunter turbine to enhance the power coefficient by changing the stroke angle of blades and incorporation of winglets. Ocean Eng. 2023, 287, 115713. [Google Scholar] [CrossRef]
- Liu, H.; Liu, S.; Gai, X.; Liu, Y.; Yan, Y.; Sun, L. Optimal Allocation of Distributed Generators in Active Distribution Network considering TOU Price. Int. J. Antennas Propag. 2023, 10, 7471214. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).