Calculation of the Natural Fracture Distribution in a Buried Hill Reservoir Using the Continuum Damage Mechanics Method
Abstract
1. Introduction
2. Materials and Methods
2.1. Principles of the Calculation and Workflow
- Load/boundary condition parameters of the finite element model;
- Plastic damage material model parameters of rocks.
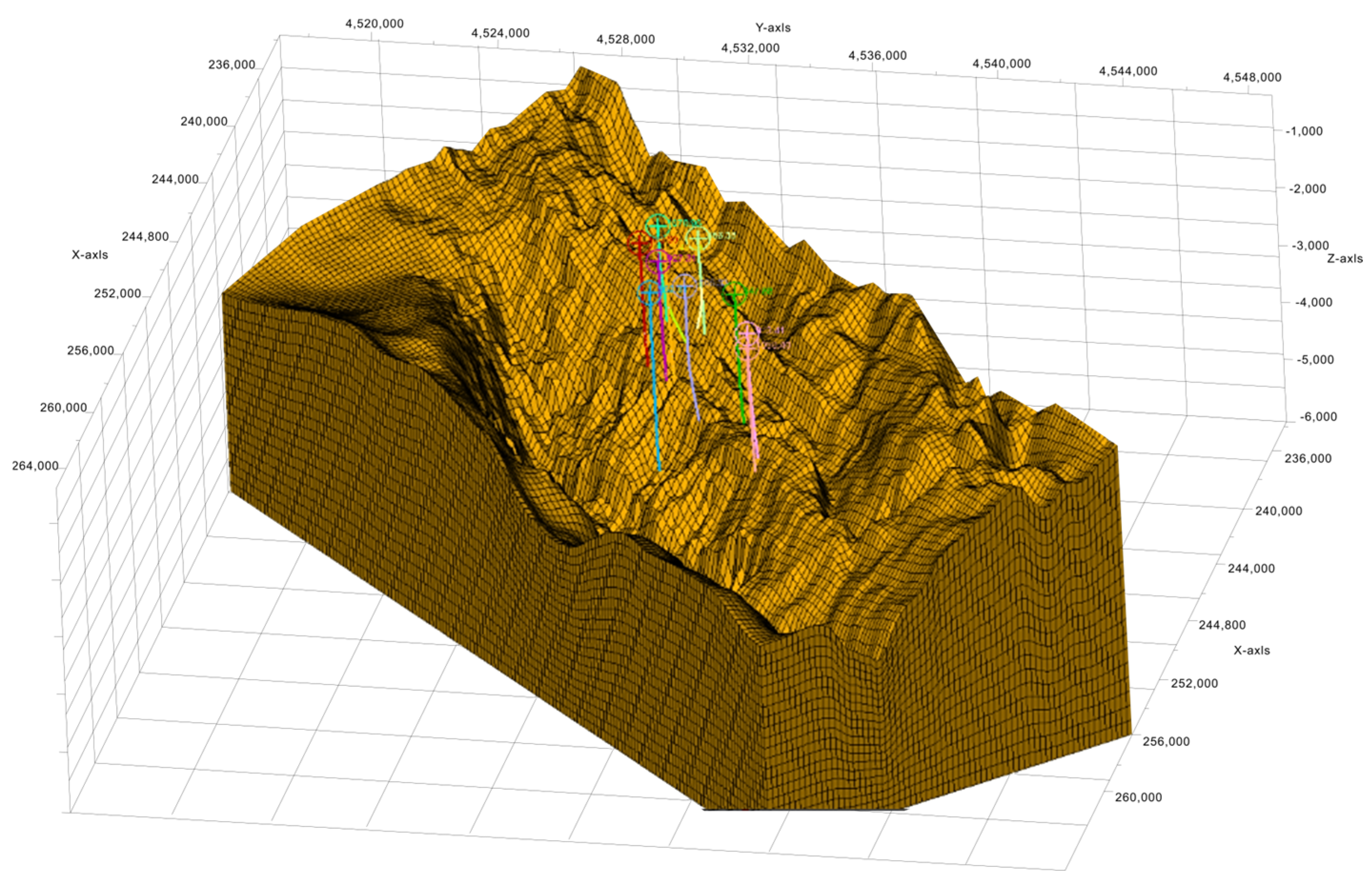
2.2. Geological Model
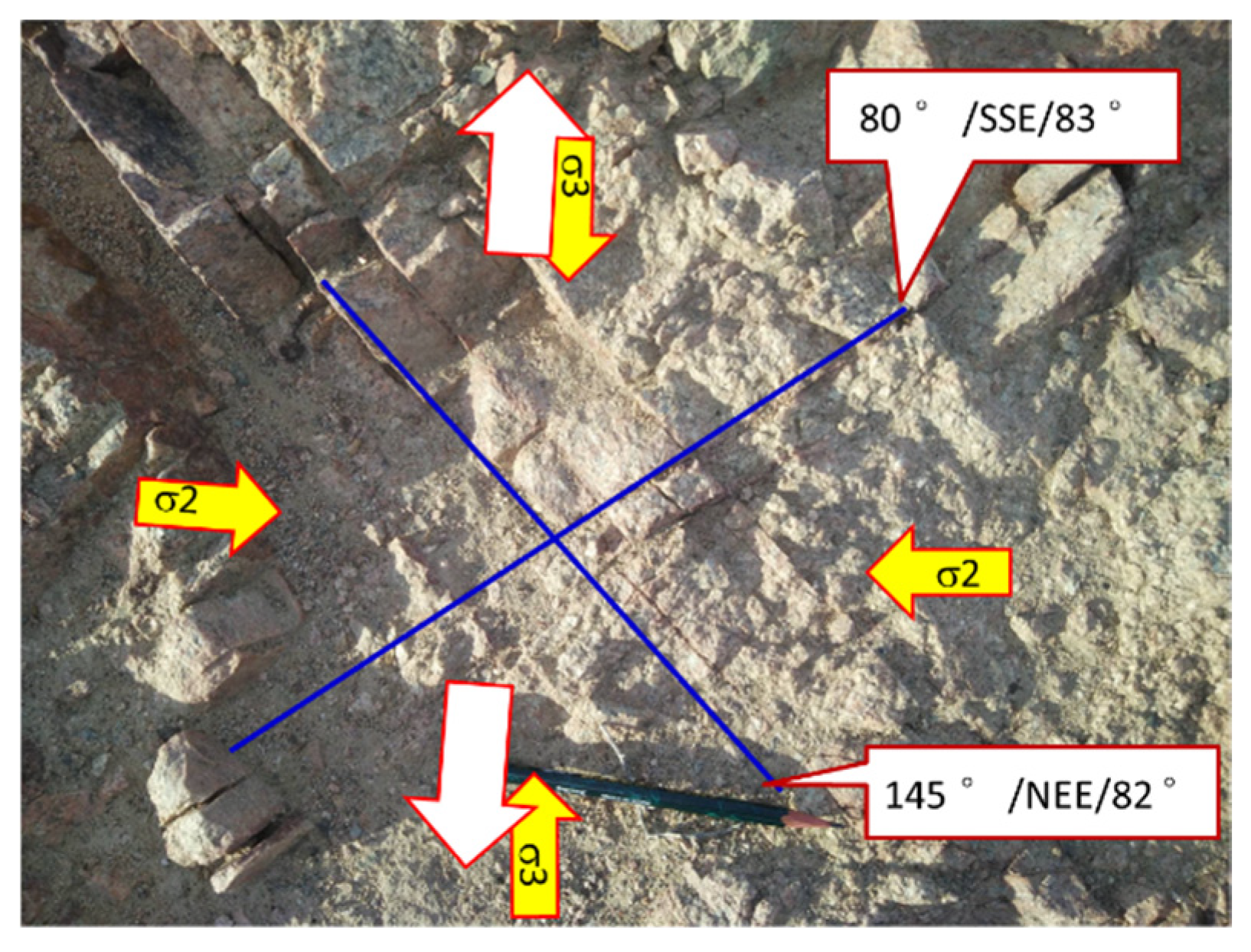
2.3. Orogenic Movements
- (1)
- Late Triassic Mesozoic extensional rifting.
- (2)
- Mid-Late Cretaceous compressional tectonism.
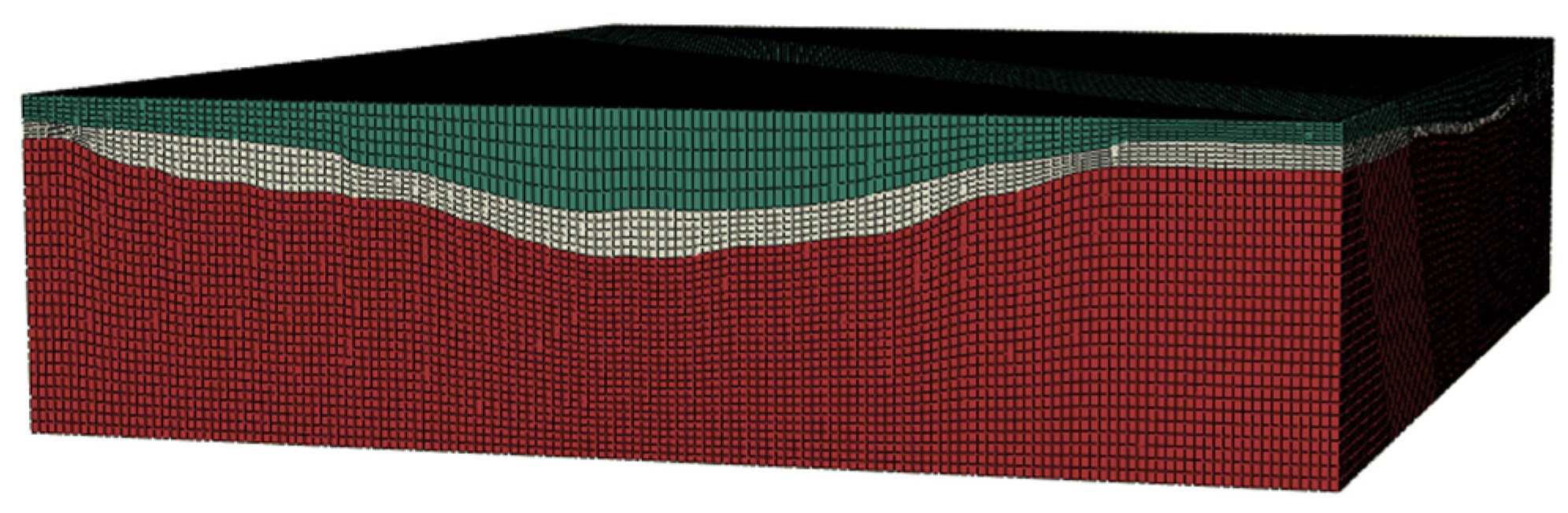
2.4. Finite Element Model
- (1)
- Top layer (green);
- (2)
- Cretaceous K1b Formation (gray-white);
- (3)
- Buried hill reservoir (reddish-brown).
- (1)
- K1b Formation: 5 sublayers.
- (2)
- Buried hill reservoir: 25 sublayers.
- (3)
- Top layer: 5 sublayers.
2.5. The Plastic Damage Model for the Rock of the Target Formation
3. Results
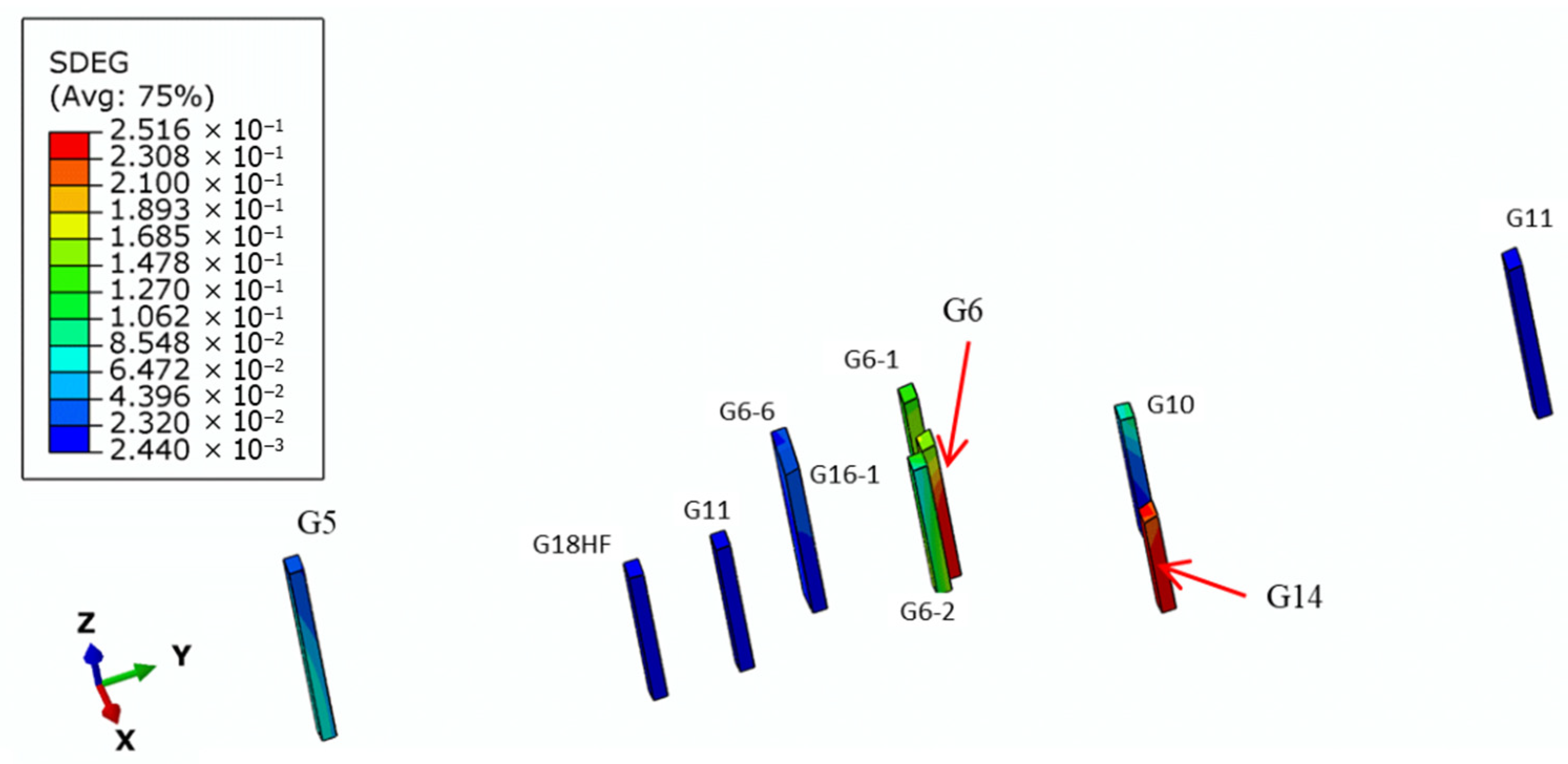
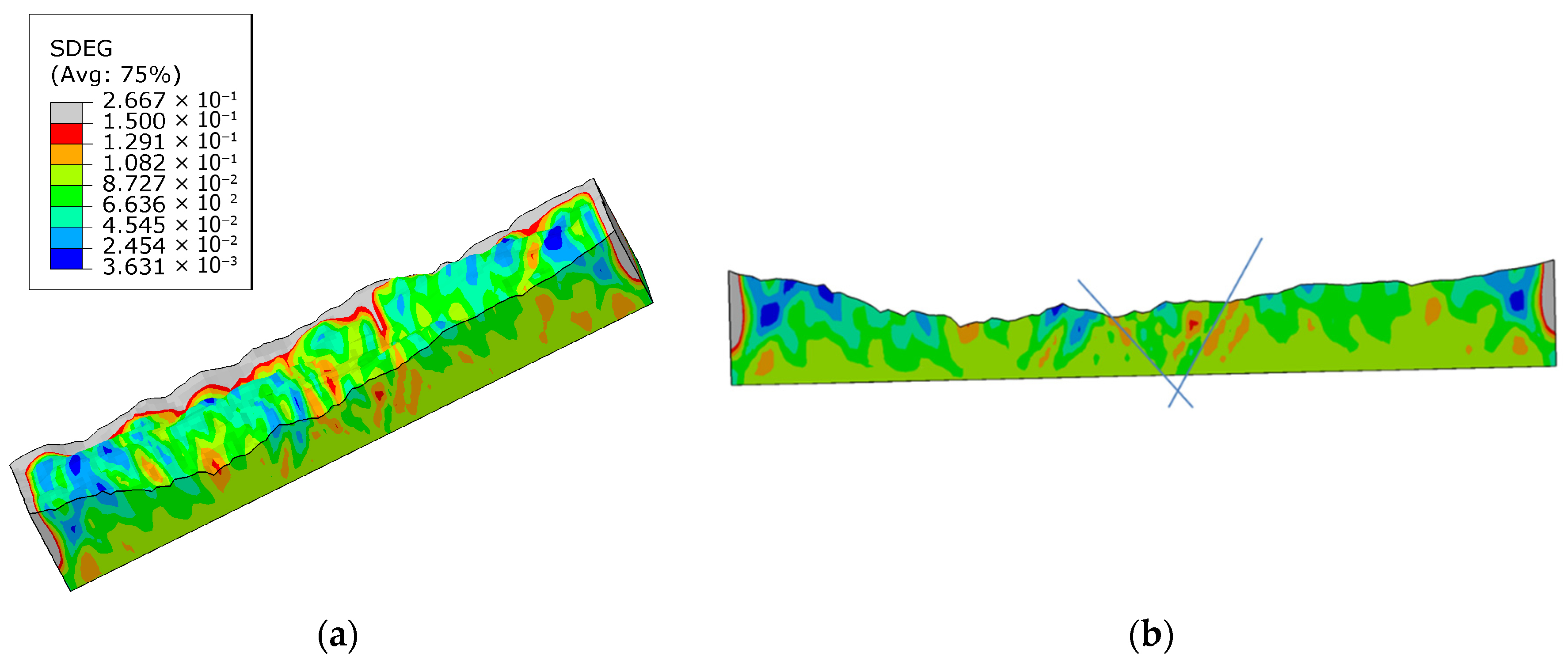
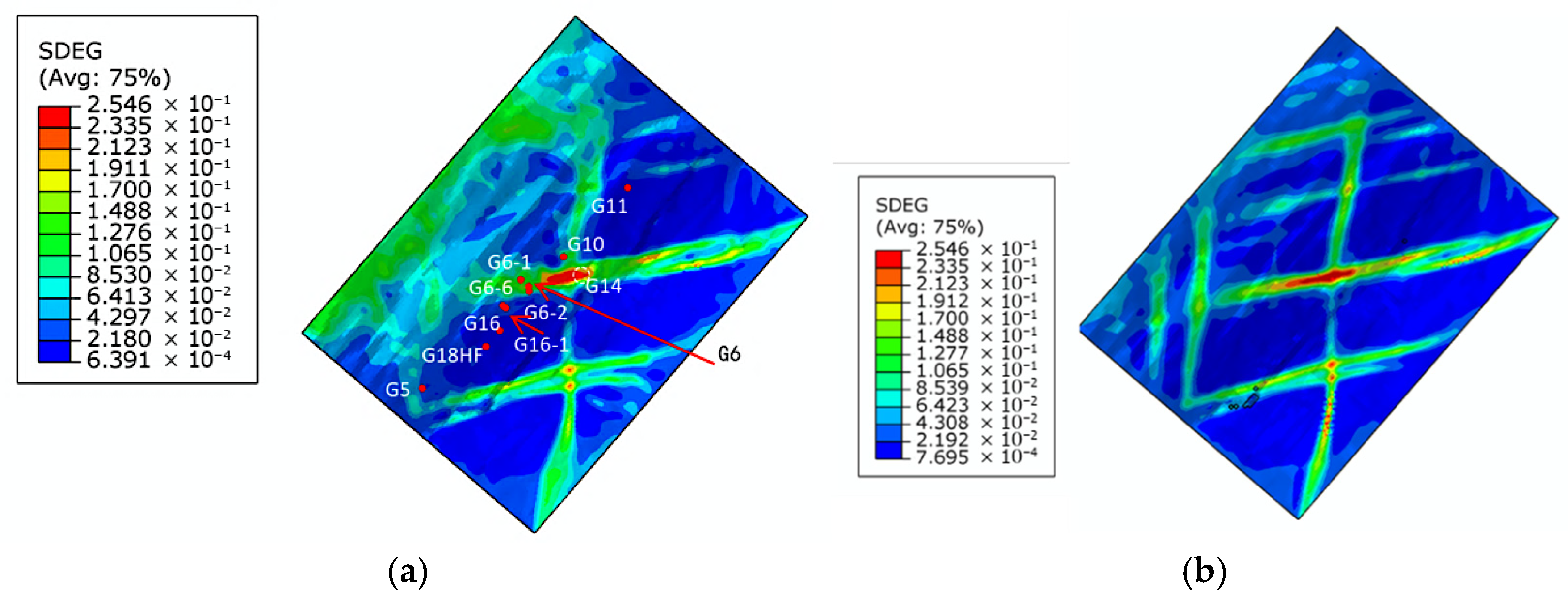
3.1. Numerical Results of the Distribution of Damage Variables Within the Reservoir
- (1)
- Three primary damage zones are identified on the buried hill surface: two E–W trending zones and one N–S trending zone.
- (2)
- Well G14 is situated at the intersection of the N–S and E–W damage zones, exhibiting the highest fracture intensity (SDEG > 0.25).
- (3)
- Favorable fracture development occurs at Wells G6, G14, and G5, with moderate fracturing observed at Wells G6-1, G6-2, and G10. Other wells show limited fracture connectivity.
3.2. Comparison Between the Numerical Results and the Well Logging Analysis Results of Natural Fractures
- (1)
- Damage value < 0.05: Natural fractures are underdeveloped.
- (2)
- 0.05 ≤ Damage value ≤ 0.1: Natural fractures exhibit moderate development.
- (3)
- 0.1 < Damage value ≤ 0.15: Natural fractures show good development.
- (4)
- Damage value > 0.15: Natural fractures are highly developed.
- (1)
- If there are ≤1 segments of Class III fracture or no fractures, natural fractures are underdeveloped;
- (2)
- If there are 3–5 segments of Class III fractures or the presence of Class II fractures, natural fractures exhibit moderate development;
- (3)
- If there are 5–10 segments of Class III fractures or the presence of Class II fractures, natural fractures show good development;
- (4)
- If there are >10 segments of Class III fractures, natural fractures are well developed.
- Sonic logging, compensated neutron log (CNL), deep laterolog resistivity (LLD), and deep induction resistivity (ILD);
- The four kinds of resultant petrophysical parameters are oil saturation, formation porosity, permeability, and clay content;
- This is achieved through a cross-plot matrix approach where each parameter is calculated using weighted combinations of multiple logging responses.
- Category I: φf ≥ 0.15 (major fractures);
- Category II: 0.1 ≤ φf < 0.15 (moderate fractures);
- Category III: 0.05 <φf < 0.1.
4. Discussion
- (1)
- Three major zones of natural fracture are identified on the buried hill surface, comprising two east–west trending zones and one north–south trending zone.
- (2)
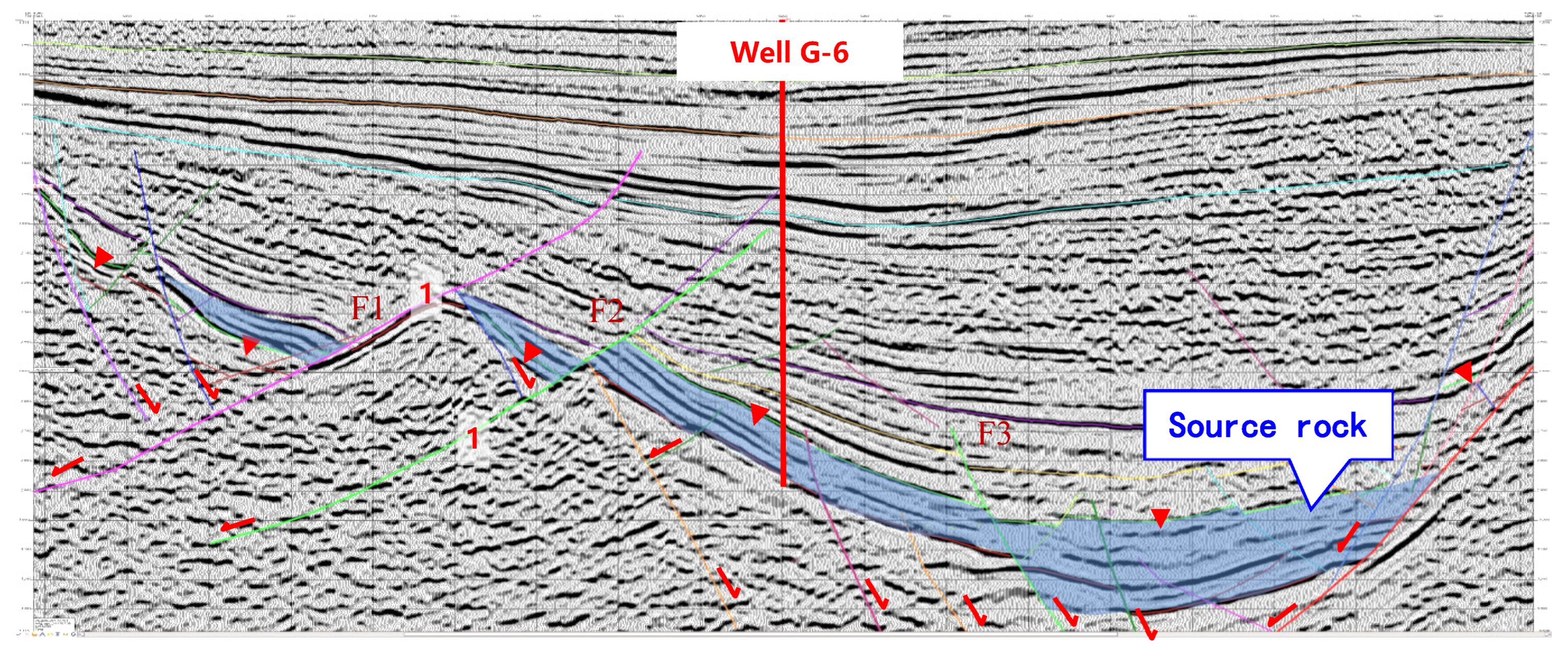
- Well G14 is situated at the intersection of the north–south and east–west fracture zones, exhibiting the highest degree of fracturing at this location. The well G6 situated at the place is only the slope close to the well G14.
- (3)
- Substantial natural fracture development is observed in wells G6, G14, and G5. Moderate fracture distribution occurs in wells G6-1, G6-2, and G10, while other wells demonstrate limited natural fracture development.
- (1)
- Azimuthal orientations of fracture zones;
- (2)
- Fracture zone widths;
- (3)
- Fault fragmentation intensity;
- (4)
- Vertical connectivity characteristics.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, J.; Peng, G.R.; Zhang, L.L. Genetic mechanisms and classification of paleo-buried hills in the inherited continental margin setting of Baiyun Sag, northern South China Sea. Earth Sci. 2025, 50, 405–418. (In Chinese) [Google Scholar]
- Wang, Y.; Wang, B.J.; Deng, H. Structural evolution and genetic mechanisms of buried hills in southern Liaoning area, Bohai Bay Basin. Geotecton. Metallog. 2025, 49, 1–10. (In Chinese) [Google Scholar]
- Gao, Z.L.; Li, H.B.; Zhang, L.L. Application of finite element numerical simulation technology to quantitative prediction of buried hill fractures: A case study of Huizhou 26 structure in Huizhou Sag, Pearl River Mouth Basin. Geol. Rev. 2023, 69, 591–602. (In Chinese) [Google Scholar]
- Guo, Z.N. Seismic attribute response and fracture prediction in metamorphic rock buried hills. Sci. Technol. Innov. 2021, 27, 142–143. (In Chinese) [Google Scholar]
- Li, X.G.; Guo, Y.M.; Cai, G.G.; Zhao, L.M.; Wang, G.W. Reservoir formation conditions and exploration of subtle buried hills in Damintun Sag. Pet. Explor. Dev. 2007, 02, 135–141. (In Chinese) [Google Scholar]
- Yi, J.; Li, H.; Shan, X.L.; Hao, G.L.; Yang, H.F.; Wang, Q.B.; Xu, P.; Ren, S. Division and identification of vertical reservoir units n Archaeozoic metamorphic buried hill of Bozhong Sag, Bohai Bay Basin, East China. Petroleum. Explor. Dev. 2022, 49, 1282–1294. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, K.; Cheng, Y.H.; Wu, Q.H. Identification and evaluation of fault-fracture reservoirs in buried hills of the Lower Paleozoic, Chengdao area, China. Energy Geosci. 2023, 4, 100183. [Google Scholar] [CrossRef]
- Zhang, X.N.; Yao, Y.B.; Zhang, G.B.; Ma, R.Y.; Wang, Z.F. Natural fractures in a metamorphic buried hill reservoir, Bozhong 19–6 area, Bohai Bay Basin, China. Mar. Pet. Geol. 2023, 155, 106402. [Google Scholar] [CrossRef]
- Jin, F.M.; Wang, X.; Li, H.J.; Wu, X.S.; Fu, L.X.; Lou, D.; Zhang, J.N.; Feng, J.Y. Formation of the primary petroleum reservoir in Wumaying inner buried-hill of Huanghua Depression, Bohai Bay Basin, China. Petroleum. Explor. Dev. 2019, 46, 543–552. [Google Scholar] [CrossRef]
- Wang, S.; Wang, G.; Lai, J.; Li, D.; Liu, S.C.; Chen, X.; Yang, K.F.; Song, L.T. Logging identification and evaluation of vertical zonation of buried hill in Cambrian dolomite reservoir: A study of Yingmai-Yaha buried hill structural belt, northern Tarim basin. J. Pet. Sci. Eng. 2020, 195, 107758. [Google Scholar] [CrossRef]
- Xie, Y.H.; Luo, X.P.; Wang, D.Y.; Xu, C.Q.; Xu, Y.L.; Hou, M.C.; Chen, A.Q. Hydrocarbon accumulation of composite-buried hill reservoirs in the western subsag of Bozhong sag, Bohai Bay Basin. Nat. Gas Ind. B 2019, 6, 546–555. [Google Scholar] [CrossRef]
- Xu, C.G.; Yang, H.F.; Wang, F.L.; Peng, I.S. Formation conditions of deep to ultra-deep large composite buried-hill hydrocarbon reservoirs in offshore Bohai Bay Basin, China. Pet. Explor. Dev. 2024, 51, 1421–1434. [Google Scholar] [CrossRef]
- Xu, C.G.; Wang, Q.B.; Zhu, H.T.; Liu, X.J.; Feng, C.; Hu, B.; Li, H.; Hao, Y.W.; Jin, X.Y.; Jia, Y. Hydrothermal alteration mechanisms of an Archaean metamorphic buried hill and the models for reservoir zonation, Bozhong depression, Bohai Bay Basin, China. Mar. Pet. Geol. 2024, 164, 106843. [Google Scholar] [CrossRef]
- Veeningen, R.; Fall, A.; Böttcher, M.E.; Eichhubl, E.; Decker, K.; Grasemann, B. Deformation and fluid flow history of a fractured basement hydrocarbon reservoir below the Sab’atayn Basin, Habban Field. Yemen. Mar. Pet. Geol. 2024, 169, 107082. [Google Scholar] [CrossRef]
- Son, L.N.; Trung, P.N.; Masuda, Y.; Murata, S.; Nguyen, T.D.; Takagi, S.; Ghassemi, A. Development of a method for adjusting rock compaction parameters and aquifer size from production data and its application to Nam-Su fractured basement reservoir of Vietnam. J. Pet. Sci. Eng. 2022, 210, 109894. [Google Scholar] [CrossRef]
- Valencia-Gómez, J.C.; Cardona, A.; Zapata, S.; Monsalve, G.; Marín, D.; Rodríguez-Cuevas, M.; Sobel, E.R.; Parra, M.; Glodny, J. Fracture analysis and low-temperature thermochronology of faulted Jurassic igneous rocks in the Southern Colombian Andes: Reservoir and tectonic implications. Mar. Pet. Geol. 2024, 165, 106850. [Google Scholar] [CrossRef]
- Pantaleone, S.; Bhattacharya, S. Hydrologic and geomechanical characterization of deep sedimentary rocks and basement for safe carbon sequestration in the Cook Inlet Basin, Alaska. Int. J. Greenh. Gas Control. 2021, 106, 103243. [Google Scholar] [CrossRef]
- Ziaie, M.; Takmili, A.; Sadeghnejad, S.; Hakimzadeh, M. Integrated geomechanical analysis of shear failure wellbore instability in abnormal and normal pore pressure zones using diverse input data: A case study. Ore Energy Resour. Geol. 2025, 18, 100093. [Google Scholar] [CrossRef]
- Cao, Y.L.; Feng, B.; Cui, Z.P.; Duan, X.F.; Zhao, L.C. Numerical simulation study of segmented hydraulic fracturing in horizontal wells of fractured hot dry rocks, at the U.S. FORGE site. Geoenergy Sci. Eng. 2025, 249, 213790. [Google Scholar] [CrossRef]
- Vazic, E.C.; Bryant, K.C.B. Single objective optimization for modeling elastoplastic damage of rock. Int. J. Rock Mech. Min. Sci. 2025, 186, 106034. [Google Scholar] [CrossRef]
- Shen, X.P.; Yang, L. Concrete Damage Theory and Experiments, 1st ed.; Science Press: Beijing, China, 2009. [Google Scholar]
- Dassault Systèmes Simulia Corp. Abaqus user’s manual, 2: Analysis, Version 6.10; Dassault Systems: Vélizy-Villacoublay, France, 2010. [Google Scholar]
- Lee, J.; Fenves, G.L. Plastic-damage model for cyclic loading of concrete structures. ASCE J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]

| Formation Type | Young’s Modulus/GPa | Poisson’s Ratio |
|---|---|---|
| Top layer | 15 | 0.21 |
| cretaceous K1b Formation | 20 | 0.23 |
| Buried hill reservoir | 25 | 0.22 |
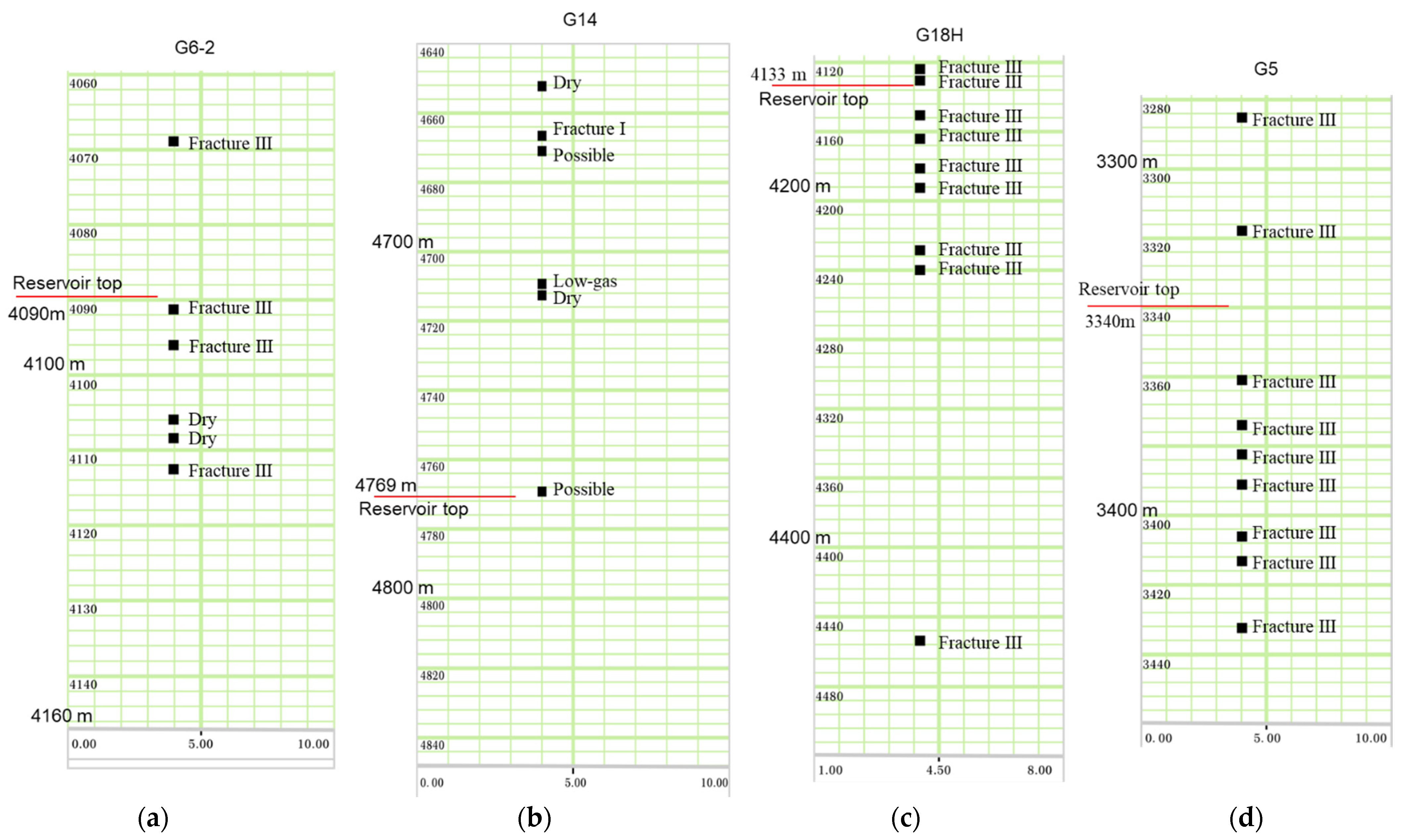
| Well G6-2 | Well G14 | Well G18H | Well G5 | |
|---|---|---|---|---|
| Numerical Solution | SDEG value ≈ 0.07: Natural fractures are moderately underdeveloped. | SDEG value reaches 0.17: Natural fractures are well developed. | Maximum value of SDEG = 0.04: Natural fractures are underdeveloped. | Maximum SDEG value = 0.2: Natural fractures are highly developed. |
| Well Interpretation Results | Below 4090 m, only two Class III fractures exist in the buried hill reservoir; below 4140 m, all layers are dry. Fracture density is moderately low. | Well-developed Class I fractures near 4660 m. The buried hill reservoir lies below 4769 m. Logging interpretation shows possible oil existence, representing a potential oil reservoir with good natural fracture development. | Upper section (4133–4240 m): Six natural fractures identified; fractures are well developed. Lower section: Only one Class III natural fracture near 4450 m; other intervals are dry, indicating underdeveloped natural fractures. | Nine sets of Class III natural fractures have been identified below 3340 m, demonstrating good natural fracture development |
| Compliance | Good compliance | Good compliance | 50% compliance (upper section non-compliant, lower section compliant). | Good compliance |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, Y.; Shen, X.; Gao, P.; Huang, W.; Ren, J. Calculation of the Natural Fracture Distribution in a Buried Hill Reservoir Using the Continuum Damage Mechanics Method. Energies 2025, 18, 4369. https://doi.org/10.3390/en18164369
Jia Y, Shen X, Gao P, Huang W, Ren J. Calculation of the Natural Fracture Distribution in a Buried Hill Reservoir Using the Continuum Damage Mechanics Method. Energies. 2025; 18(16):4369. https://doi.org/10.3390/en18164369
Chicago/Turabian StyleJia, Yunchao, Xinpu Shen, Peng Gao, Wenjun Huang, and Jinwei Ren. 2025. "Calculation of the Natural Fracture Distribution in a Buried Hill Reservoir Using the Continuum Damage Mechanics Method" Energies 18, no. 16: 4369. https://doi.org/10.3390/en18164369
APA StyleJia, Y., Shen, X., Gao, P., Huang, W., & Ren, J. (2025). Calculation of the Natural Fracture Distribution in a Buried Hill Reservoir Using the Continuum Damage Mechanics Method. Energies, 18(16), 4369. https://doi.org/10.3390/en18164369






