SOC Estimation for Lithium-Ion Batteries Based on Weighted Multi-Innovation Sage–Husa Adaptive EKF

Abstract

In lithium-ion battery management systems (BMSs), accurate state of charge (SOC) estimation is essential for the stable operation of BMSs. Furthermore, the accuracy of SOC estimation is significantly influenced by the precision of battery model parameters. To improve the SOC estimation accuracy, this paper focuses on the second-order RC equivalent circuit model, firstly designs a simple and reliable improved adaptive forgetting factor (IAFF) regulation mechanism, and proposes the improved adaptive forgetting factor recursive least squares (IAFFRLS) algorithm, which not only improves the accuracy of parameter identification, but also exhibits excellent performance in anti-interference. Secondly, based on the identified model, a weighted multi-innovation improved Sage–Husa adaptive extended Kalman filter (WMISAEKF) algorithm is proposed to solve the problem of filter divergence caused by noise covariance updating. It fully utilizes historical innovations to reasonably allocate innovation weights to achieve accurate SOC estimation. Compared with the VFFRLS algorithm and AFFRLS algorithm, the IAFFRLS algorithm reduces the root mean square error (RMSE) by 29.30% and 19.29%, respectively, and the RMSE under noise interference is decreased by 82.37% and 78.59%, respectively. Based on the identified model for SOC estimation, the WMISAEKF algorithm reduces the RMSE by 77.78%, compared to the EKF algorithm. Furthermore, the WMISAEKF algorithm could still converge under different levels of noise interference and incorrect initial SOC values, which proves that the proposed algorithm has good stability and robustness. Simulation results verify that the parameter identification algorithm proposed in this paper demonstrates higher identification accuracy and anti-interference performance. The proposed SOC estimation algorithm has higher estimation accuracy and good robustness, which provides a new practical support for extending battery life.

1. Introduction

Against the backdrop of the global shift in energy structure in recent years, countries worldwide are accelerating their transition to green and low-carbon energy, establishing it as the dominant trend. Products such as electric vehicles and lithium-ion batteries, serving as the primary carriers of green energy, are advancing rapidly in the related industrial technologies. This progress contributes significantly to the ongoing promotion of high-efficiency and high-quality development in the green energy industry [1,2]. Lithium-ion batteries, which serve as the primary power source for electric vehicles, are characterized by high energy density, long service life, and excellent power performance. In BMSs, SOC represents the remaining available energy of the battery and is a key indicator of the BMS. Accurate SOC estimation plays a vital role in ensuring battery safety, enhancing overall performance, and extending the lifespan of the batteries [3,4]. There are inherent dynamic nonlinear characteristics in lithium-ion batteries due to the complex operating environments and the intricate electrochemical reaction mechanisms during charging and discharging cycles. Consequently, direct measurement of the SOC through external means is impractical. Therefore, the uses of model-based method and other methods are necessary for estimation and prediction to indirectly obtain SOC [5,6,7]. The prerequisite for SOC prediction is based on accurate battery model parameters [8]. Therefore, SOC estimation should comprehensively consider improving the identification of battery model parameters and enhancing the accuracy of SOC estimation.

Currently, the primary methods for SOC estimation include the ampere-hour integral method, the open-circuit voltage method, the data-driven method, and the model-based method [9,10]. The ampere-hour integral method is a simple calculation process, but it is prone to causing large cumulative errors [11]. The open-circuit voltage method requires extended idle periods for batteries and imposes stringent environmental conditions; therefore, it is unsuitable for real-time estimation of dynamic working conditions. Furthermore, it is significantly affected by factors such as temperature and aging, resulting in a limited scope of application [12]. The data-driven method relies on extensive datasets to establish mapping relationships. While theoretically capable of handling lithium batteries’ complex nonlinear characteristics using voltage and current data, the practical implementation faces significant limitations: data dependency, high computational load, poor generalization capability, substantial hardware requirements, and challenges to the real-time performance of algorithms [13]. The model-based method simulates the dynamic characteristics of battery by establishing a robust battery model and uses a reliable state estimation algorithm for SOC estimation. The model-based method not only ensures the accuracy of battery estimation but also effectively mitigates the effects of measurement noise on the estimation process. Among the aforementioned methods, the model-based method has become the dominant technical means for SOC estimation due to its inherent advantages [14,15,16]. The battery models utilized in the model-based method are mainly categorized into electrochemical models and equivalent circuit models [17]. Electrochemical models elucidate the electrochemical reaction mechanisms of the battery through coupled partial differential equations. Although the electrochemical models provide high accuracy, they are computationally complex and exhibit limited engineering practicality [18]. In contrast, equivalent circuit models emulate battery polarization behavior using networks of passive components, simulating external characteristics for real-time applications. Owing to their straightforward structure, computational efficiency, robust scalability, and ease of implementation in engineering, equivalent circuit models are extensively used [19,20,21].

Parameter identification and optimization of the SOC estimation algorithm represent the primary technical methods for enhancing the SOC estimation accuracy of batteries. Parameter identification is the foundation for SOC estimation, with commonly used algorithms including circuit analysis, the particle swarm optimization algorithm, and least squares, along with its derivative algorithms. Chen et al. used circuit analysis as the foundation for battery parameter identification [22]. While this method is conceptually simple, it is an offline identification approach with limited real-time performance. Guo et al. employed circuit analysis to isolate the internal resistance of the battery within a second-order RC equivalent circuit model and then applied the least squares algorithm to identify and calculate other parameters. However, the internal resistance derived from the circuit analysis exhibits significant errors, which adversely affects the accuracy of the SOC estimation to a certain extent [23]. Ren et al. employed the particle swarm optimization (PSO) algorithm for offline parameter identification coupled with real-time adjustment of online estimation [24], and Zhu et al. proposed a dual particle swarm cooperative optimization method for parameters identification based on an adaptive dynamic sliding window [25]. While these approaches demonstrated a relative improvement in identification accuracy, the correction process and particle sampling significantly increased the calculation time, leading to a slow overall processing speed. Literature [26,27] proposed integrating the PSO algorithm with the least squares algorithm to address challenges such as particle degeneracy and resampling. However, this hybrid approach also results in algorithmic complexity. Compared to the other two algorithms, the least squares algorithm maintains a core principle: minimizing the sum of squared errors. It is an online identification method with low algorithmic complexity and rapid convergence speed. Lim et al. employed a recursive least squares algorithm for battery parameter identification to achieve a relatively high parameter accuracy that enables effective state estimation of lithium-ion batteries [28]. However, this method exhibits susceptibility to data saturation when applied to the estimation of slowly time-varying battery parameters. Therefore, some literature has proposed incorporating the forgetting factor to enhance research outcomes. Literature [29,30] proposed the forgetting factor recursive least squares algorithm for parameter identification calculations in the equivalent circuit model of lithium-ion batteries. However, fixed forgetting factors undermine the simultaneous optimization of parameter identification stability and accuracy. Furthermore, excessively low forgetting factor values may induce unstable fluctuations in identified parameters. Then, scholars proposed the variable forgetting factor least squares algorithm for parameter identification. Ge et al. introduced a forgetting factor recursive least squares algorithm based on the means and standard deviations of the innovations [31]. However, continuous computation of means and standard deviations during iterations significantly degraded algorithmic efficiency due to computational overhead. Literature [32,33] proposed a variable forgetting factor strategy that is adjusted in time with the change in errors in order to improve the accuracy of the parameter identification algorithm. However, the coefficient adjustment mechanism of the strategy has a significant impact on the error tracking ability of the algorithm. Improper design of the adaptation mechanism may trigger excessive parameter fluctuations, degrading identification accuracy and potentially inducing algorithm divergence. Furthermore, an improper coefficient adjustment mechanism can also critically compromise the anti-interference ability of the algorithm.

Currently, the primary model-based SOC estimation methods include the Kalman filter algorithm, the H∞ algorithm, and the sliding mode observer algorithm [34]. The H∞ algorithm demonstrates strong robustness against noise distribution uncertainty yet incurs significant computational burden. Furthermore, its emphasis of robustness may lead to a reduction in estimation accuracy [35,36,37]. The sliding film observer method has good robustness, but the problem of output jitter is an obvious drawback of this method [38,39,40]. In the field of battery SOC estimation, numerous improved algorithms derived from Kalman filter (KF) theory have been extensively utilized [41]. These improved KF algorithms, designed to address the nonlinear characteristics of lithium-ion batteries, primarily include the extended Kalman filter (EKF), untraceable Kalman filter (UKF), and cubature Kalman filter (CKF). Among them, the EKF algorithm has become a research hotspot in SOC estimation due to its advantages, such as low computational complexity, high stability, good real-time performance, and strong robustness [42,43]. In response to the need for improving SOC estimation accuracy, scholars have optimized the traditional EKF method in various aspects. Literature [44,45] proposed an adaptive EKF (AEKF) algorithm that leverages statistical characteristics of residual sequences for SOC estimation in lithium-ion batteries. Li et al. proposed incorporating the multi-innovation theory into the EKF algorithm to form the multi-innovation EKF (MIEKF) for SOC estimation [46]. Meanwhile, other researchers have proposed combining parameter identification techniques with the SOC estimation algorithm to enhance SOC estimation accuracy in lithium-ion batteries. He et al. proposed a study of SOC estimation based on the variable forgetting factor recursive least squares algorithm for first-order RC circuit parameter identification combined with the AEKF algorithm [47], but the accuracy of parameter identification in this method is inadequate, which directly degrades the SOC estimation accuracy. Tian et al. proposed AEKF based on second-order equivalent circuit parameter identification for SOC estimation to improve the tracking of the algorithm [48]. Wu et al. proposed combining the multi-innovation least squares algorithm for parameter identification with the multi-innovation EKF(MIEKF) algorithm for SOC estimation to enhance the accuracy of SOC estimation in lithium-ion batteries [49]. Nevertheless, the allocation of innovation weights is not sufficiently reasonable, which adversely impacts SOC estimation accuracy. Dong et al. implemented the multi-innovation least squares algorithm with heterogeneous forgetting factors, enabling independent adaptation rates for distinct parameters to mitigate errors in the battery model [50]. This approach improves the model estimation accuracy; it is combined with EKF for SOC estimation. However, this algorithm necessitates decoupling the covariance matrix and gain matrix of the least squares algorithm for computation, which increases the computational workload, while the robustness of the algorithm is generally moderate.

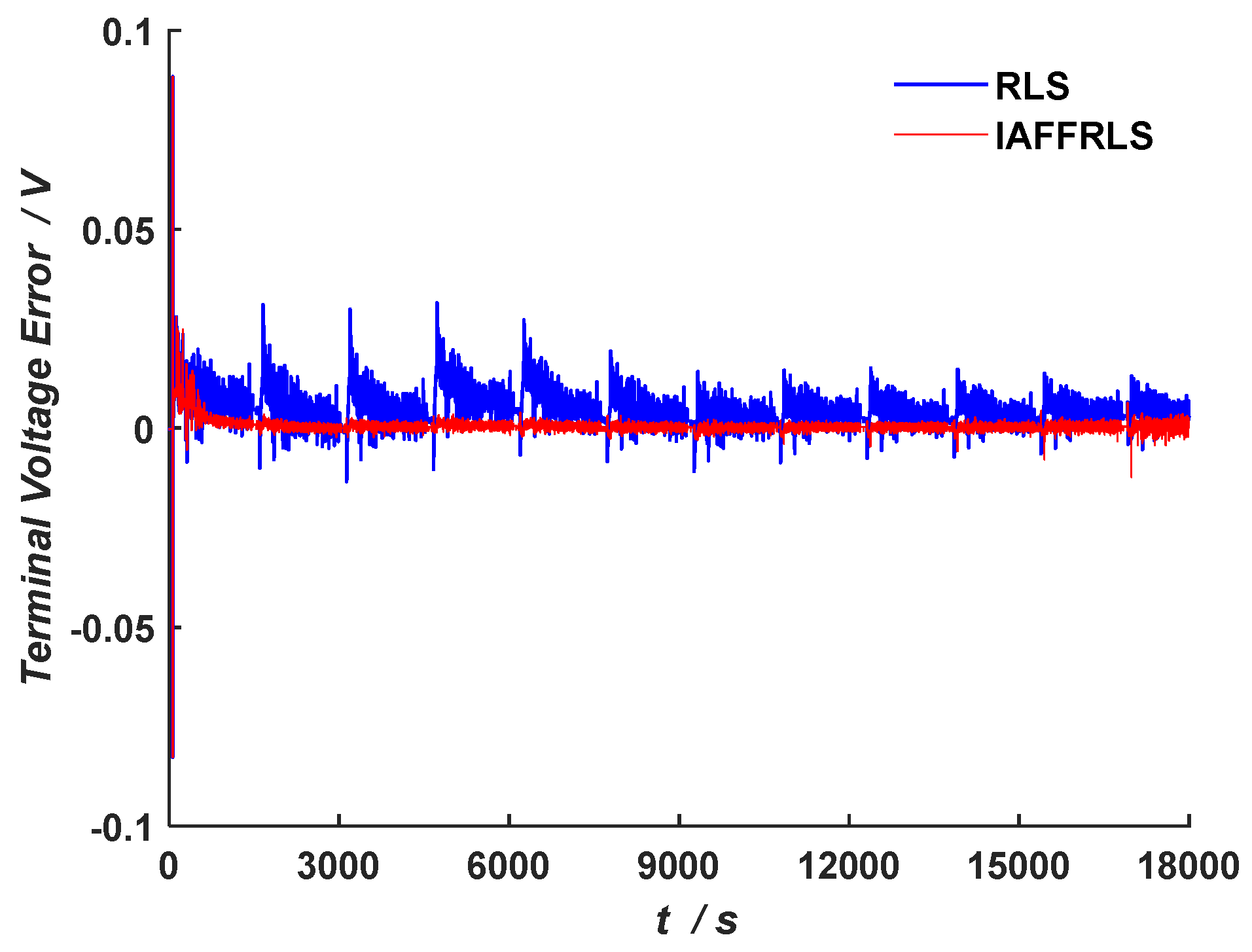
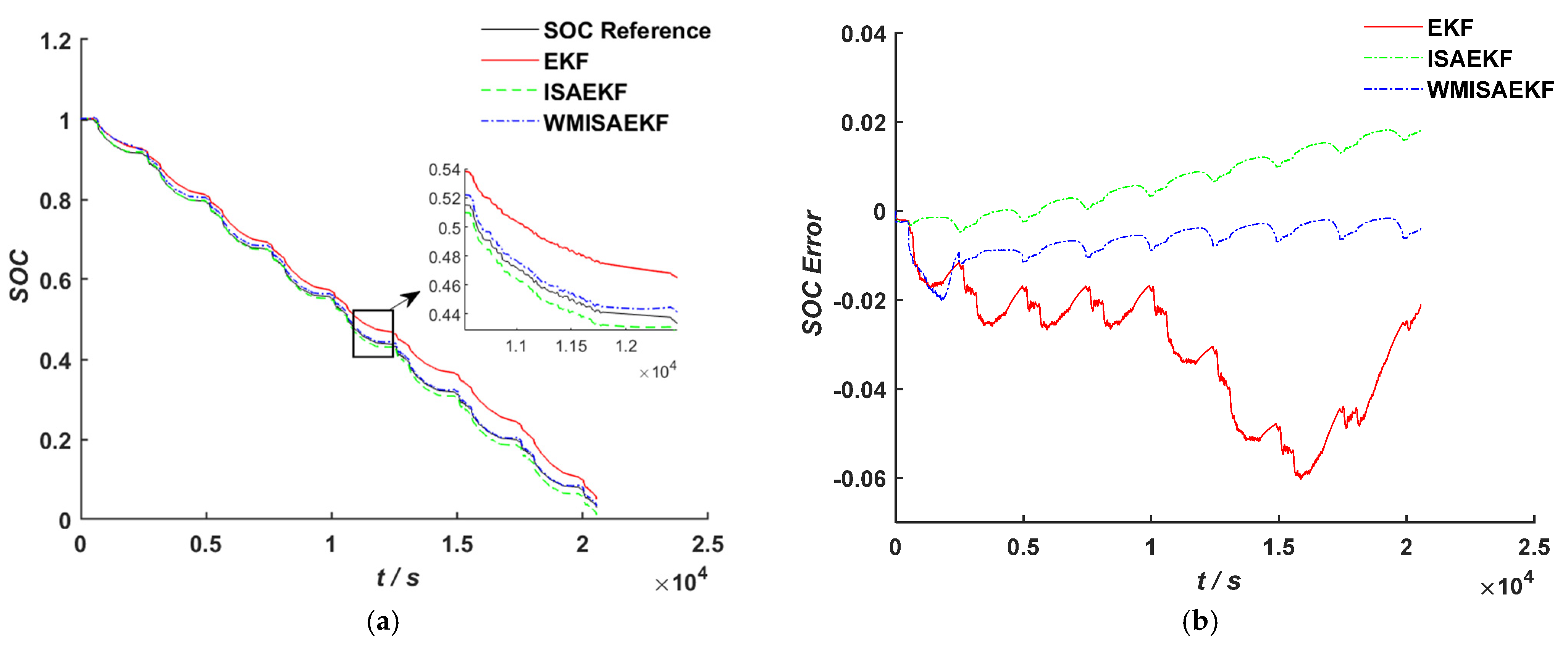
The RLS algorithm and its improved algorithms demonstrated strong dynamic tracking capabilities in lithium-ion battery parameter identification, and the EKF and its improved algorithms showed notable advances in SOC estimation. The aforementioned studies predominantly employed adaptive forgetting factors for RLS enhancement, while the accuracy and anti-interference ability of parameter identification were limited. It is particularly difficult to maintain consistent parameter accuracy under noise interference. When used for SOC estimation, EKF-based algorithms are susceptible to diverging in cases of strong model nonlinearity or large initial errors. In addition, while the MIEKF incorporates historical observation innovations, the traditional weight allocation methods inadequately assign weights to the historical innovation values, especially ignoring the critical impact of observation error magnitude on innovation values, leading to issues such as reduced accuracy and overcorrection in the iterative process, thereby constraining the enhancement of SOC estimation.

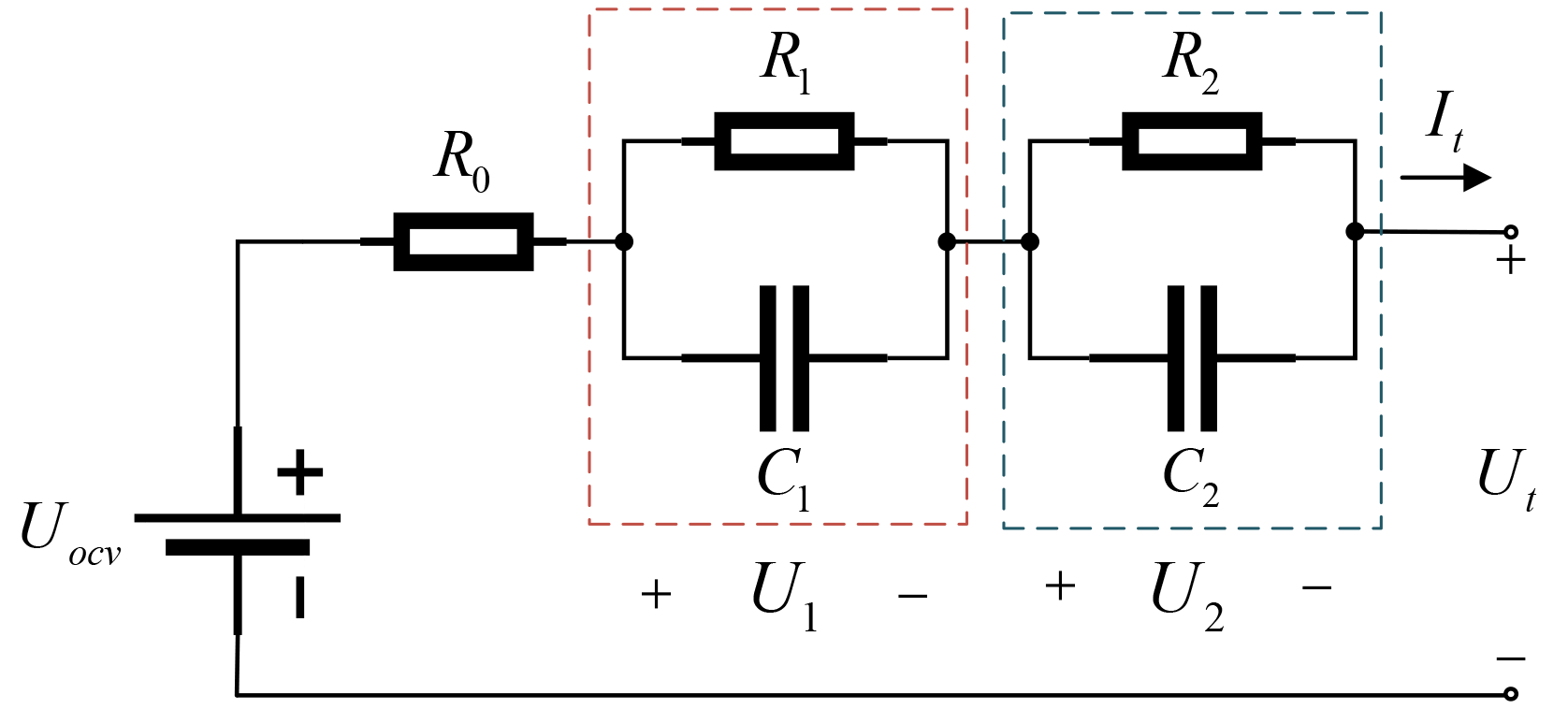
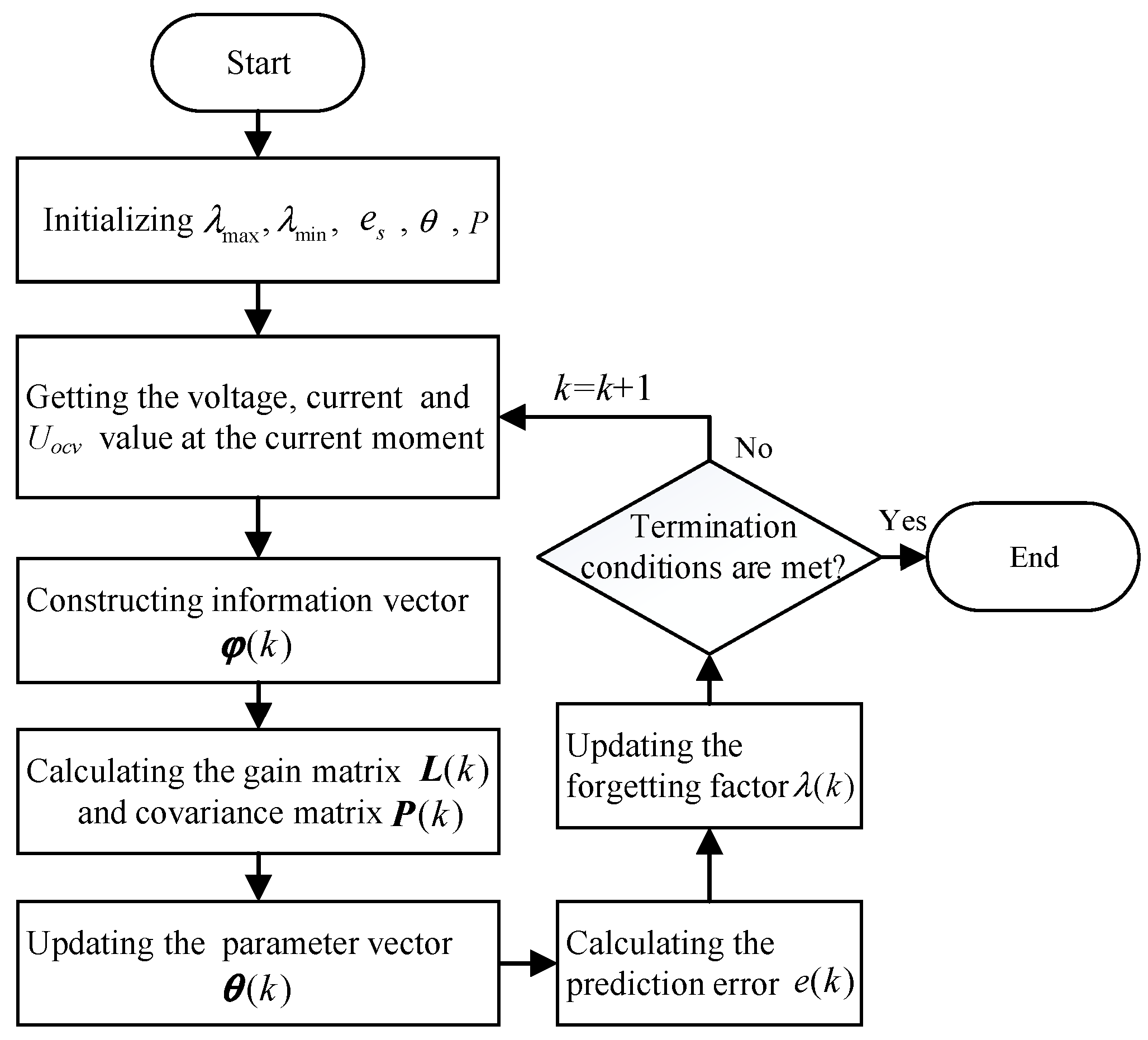
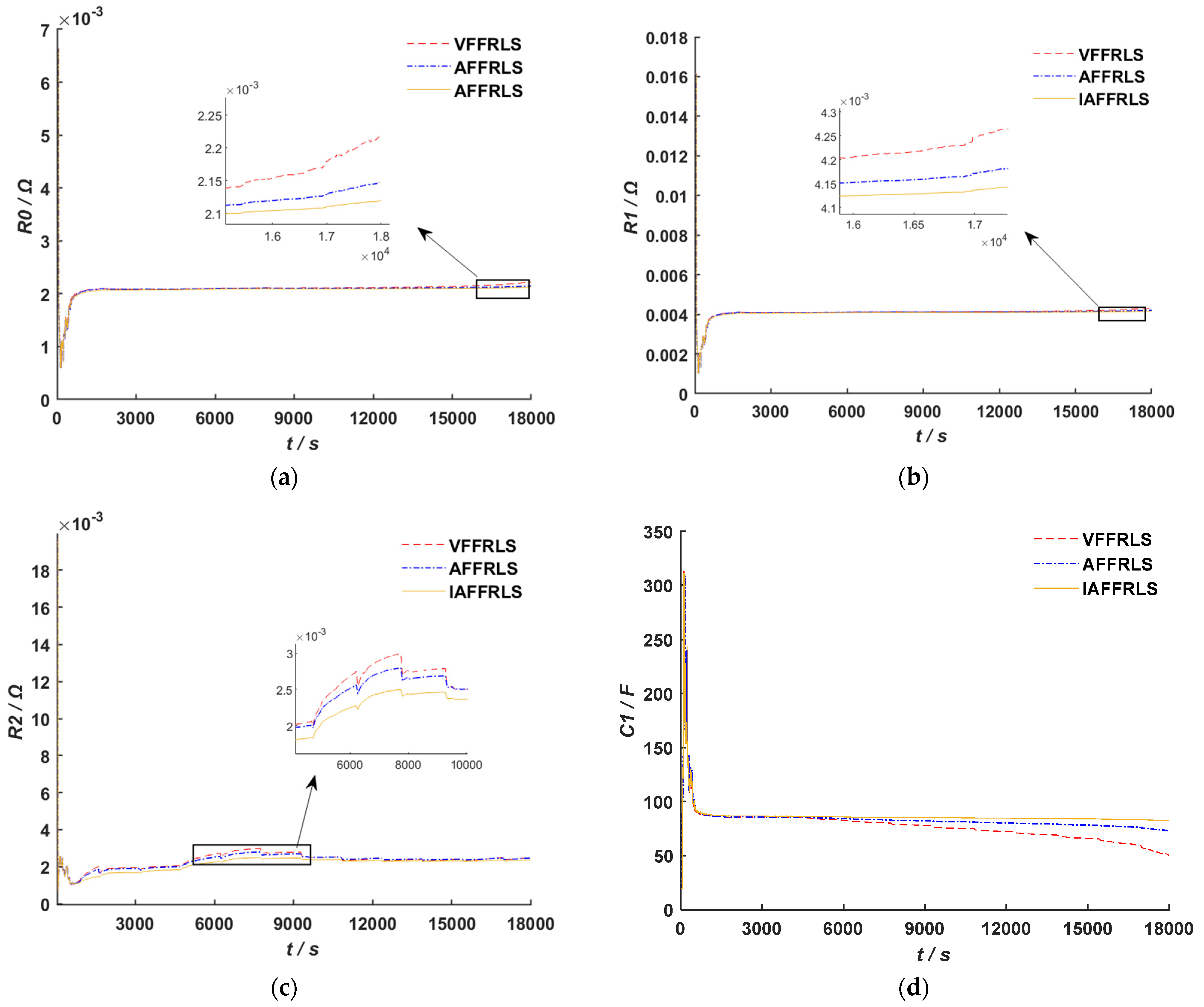
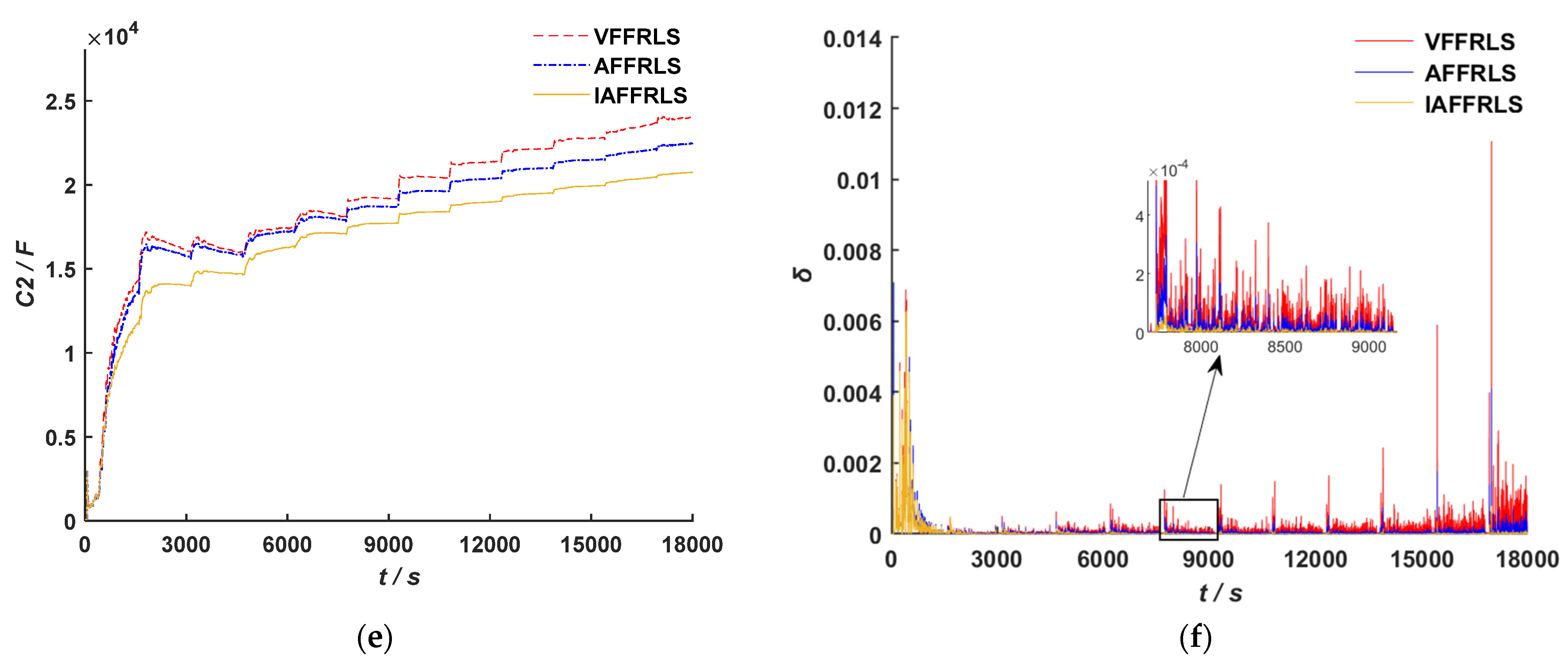
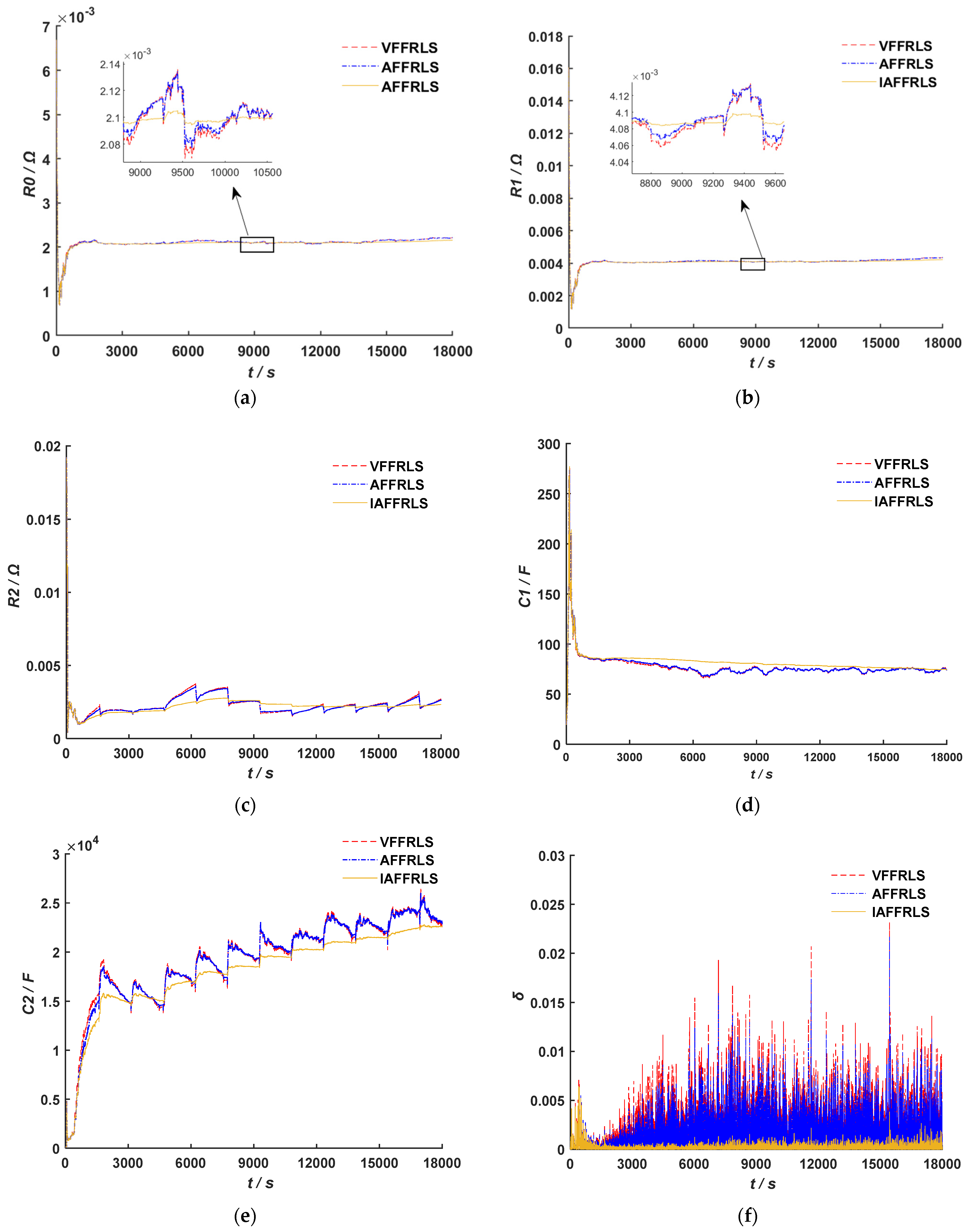
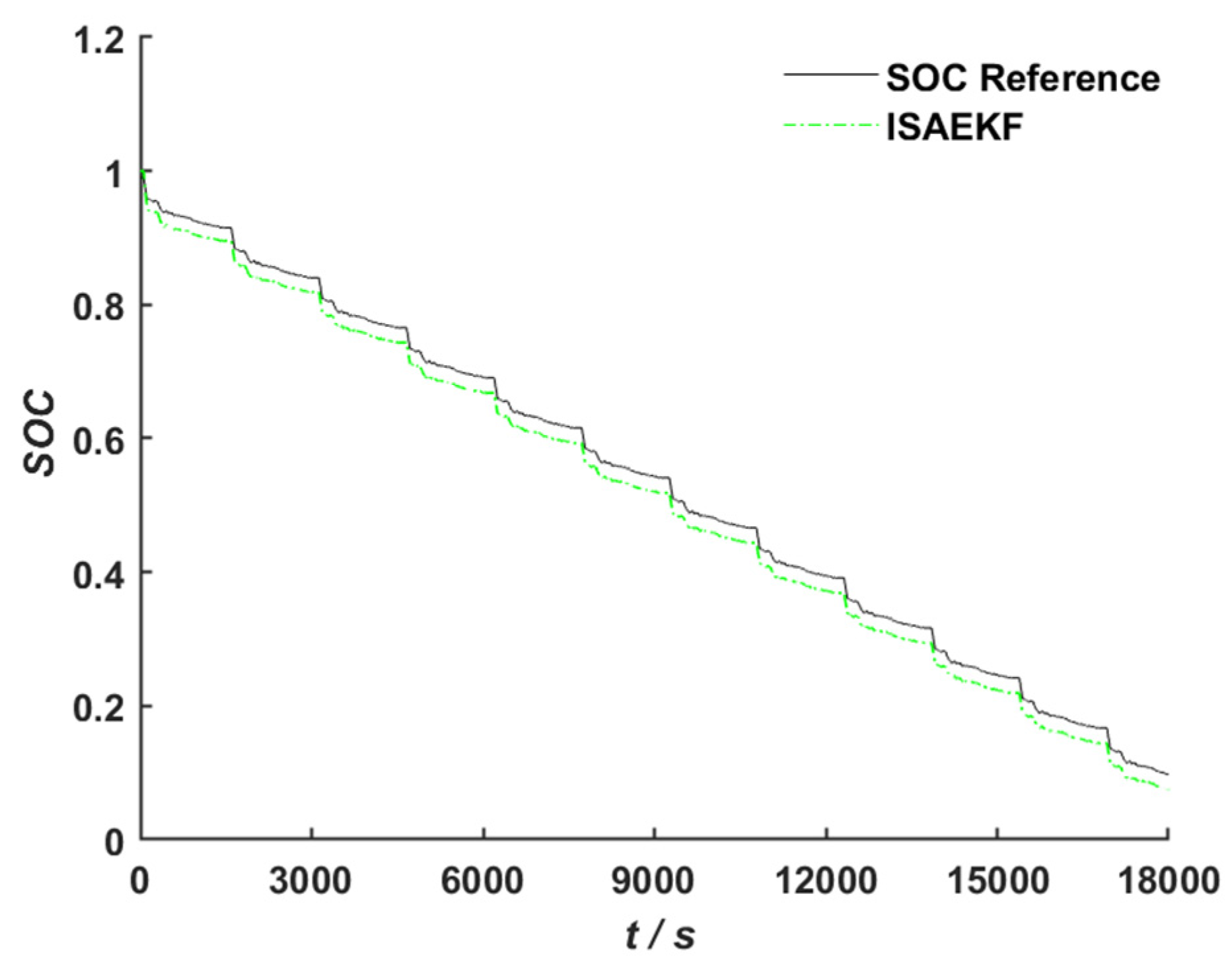
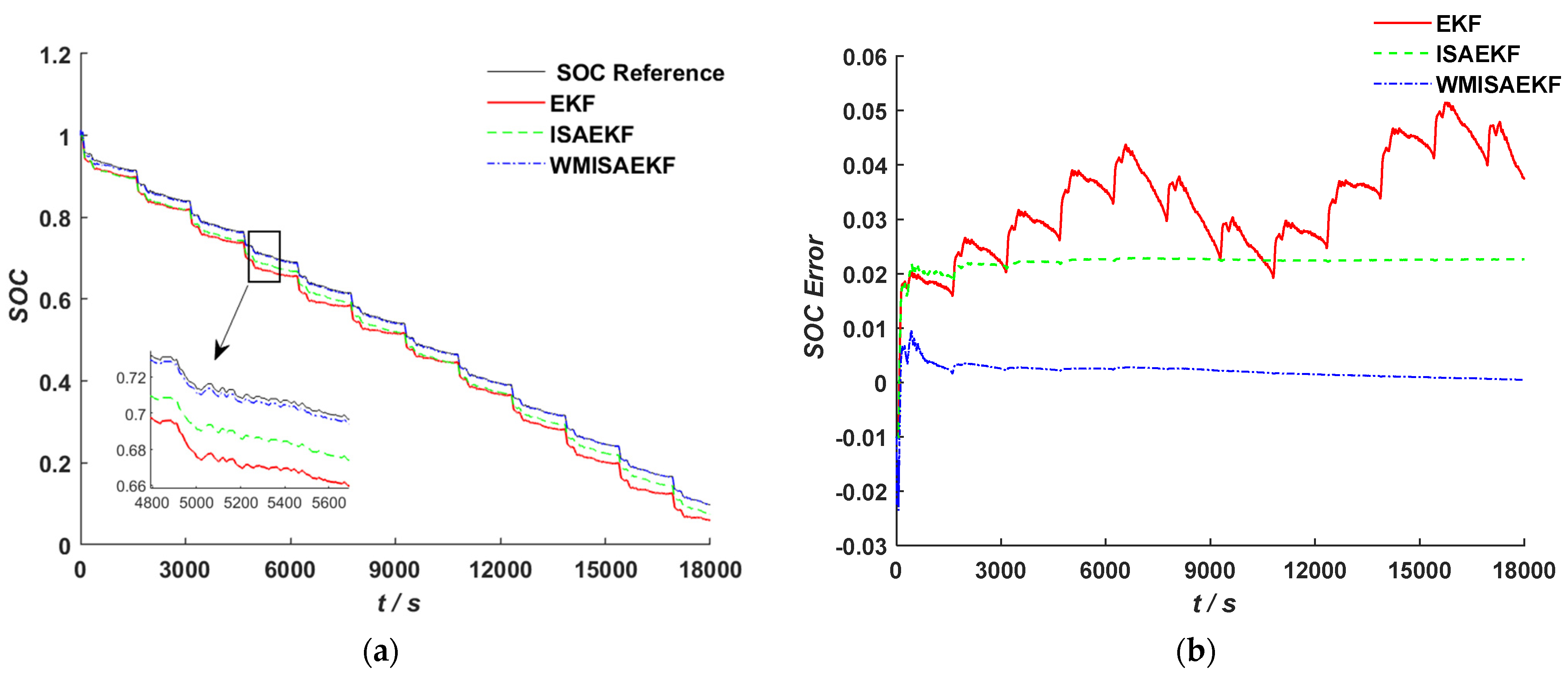
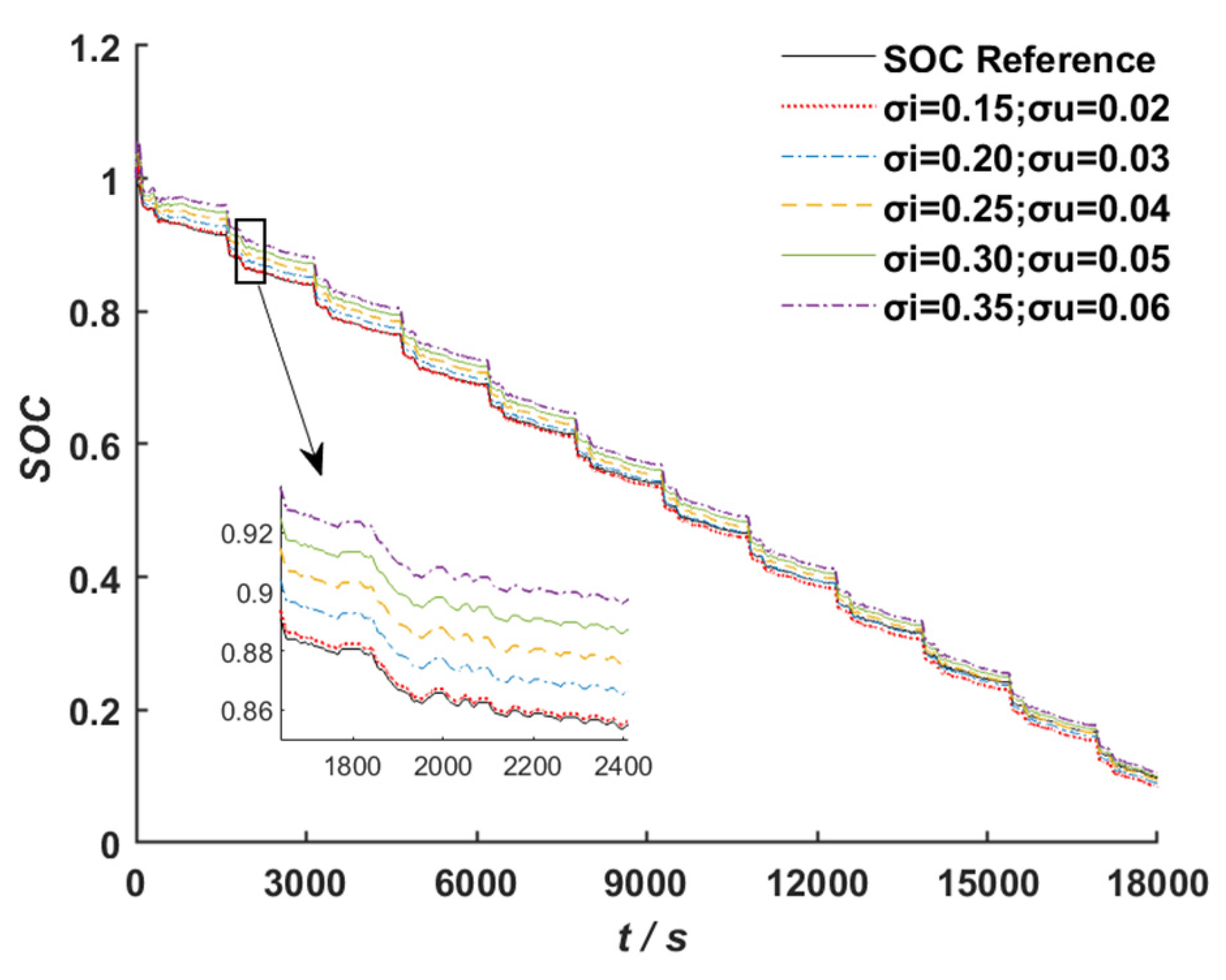
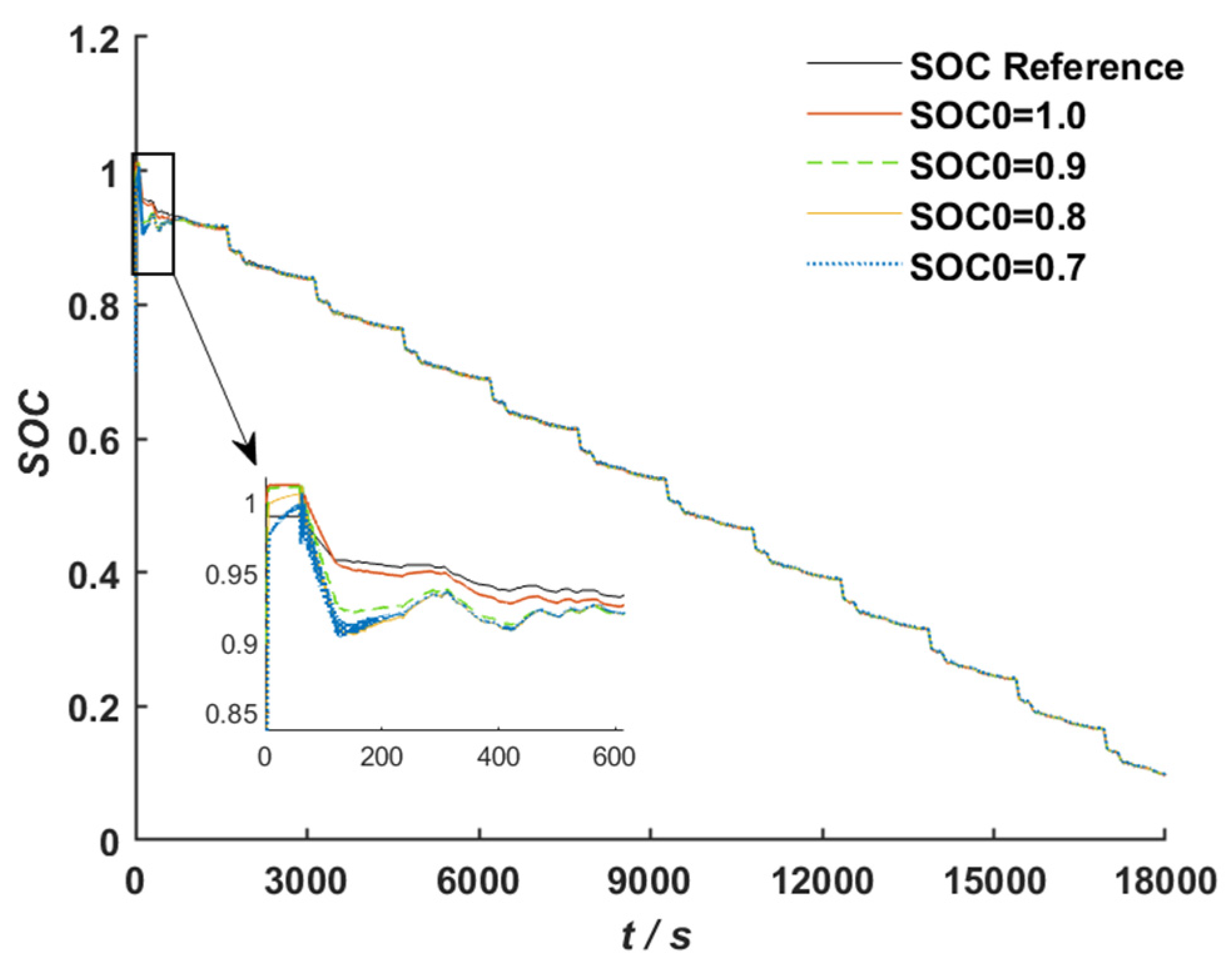
According to the studies presented above, we propose a SOC estimation approach for lithium-ion batteries based on a second-order RC equivalent circuit model and design an improved adaptive variable forgetting factor regulation mechanism (IAFF) with wide applicability. An improved adaptive variable forgetting factor recursive least squares algorithm (IAFFRLS) is proposed for model parameter identification. This algorithm not only improves the accuracy of parameter identification but also demonstrates excellent anti-interference capabilities. On this basis, an improved method of the extended Kalman filter algorithm based on Sage–Husa adaptive filtering is proposed to solve the problem of filter divergence. Furthermore, a novel weight calculation method is designed based on multi-innovation theory, which assigns larger weight factors to innovations that are closer to the current time and have larger observation errors. This method is used to calculate the innovation weights for the improved Sage–Husa multi-innovation EKF algorithm, thereby resolving issues such as low precision and over-correction during iterations in the MIEKF. This approach not only improves SOC estimation accuracy, but also has strong robustness.

2. Model Structure and Parameter Identification of Lithium-Ion Batteries

2.1. Equivalent Circuit Model for Lithium-Ion Batteries

Lithium-ion batteries demonstrate significant nonlinearity during operations. The circuit network constructed by electronic components, such as resistors and capacitors, can effectively simulate the charging and discharging progresses, thereby enabling accurate characterization of the battery working status. In relevant research, literature [34,51] elaborated on multiple equivalent circuit models applicable to lithium-ion batteries, such as the Rint model, Thevenin model, PNGV model, and GNL model. Among them, the Rint model, despite its simple structure and low computational complexity, has significant drawbacks, notably the failure to consider the polarization effect of the battery, which results in low model accuracy [41]. The Thevenin model addresses the shortcomings of the Rint model by incorporating a parallel RC circuit network to simulate the battery’s polarization phenomenon [50]. The PNGV model, an improved circuit network structure based on the Thevenin model, introduces a capacitor in series with the RC network to describe voltage changes caused by current. This model offers higher accuracy than the Thevenin model, but the additional series capacitor introduces circuit losses that are not fully considered [10]. The GNL model circuit structure is highly complex. Although it can simulate the charging–discharging characteristics of battery relatively accurately, its overly complex structure leads to high computational complexity, long processing times, and poor real-time performance [34]. Combining the characteristics of the aforementioned four equivalent circuit models, the Davinen equivalent circuit model based on the RC structure can simulate the battery operation mechanism using the parallel network of resistors and capacitors. As the number of RC parallel loops increases, the accuracy of the model can be improved. However, an excessive number of RC parallel loops leads to significant increases in computational complexity, greater difficulty in parameter identification, and diminishing marginal effects of accuracy improvement, among other limitations [51]. Considering the balance between model accuracy and practicality, this study adopts the second-order RC equivalent circuit model for investigation, with the equivalent circuit illustrated in Figure 1.

The circuit equation is constructed from Kirchhoff’s voltage law and Kirchhoff’s current law as follows:

$$\left\{\begin{array}{l}{U}_{ocv}-U_t=I_t{R}_0+U_1+U_2\\ U_1=I_t{R}_1-R_1{C}_1{\displaystyle \frac{d{U}_1}{dt}}\\ U_2=I_t{R}_2-R_2{C}_2{\displaystyle \frac{d{U}_2}{dt}}\end{array}\right.$$

(1)

where $R_0$ is the internal ohmic resistance; $R_1$ and $R_2$ are the polarization resistances; $C_{ 1}$ and $C_{ 2}$ are the polarized capacitors; and $U_{ocv}$, $U_t$, and $I_t$ denote the open-circuit voltage (OCV), terminal voltage, and current, respectively. $U_{ 1}$ and $U_{ 2}$ are the polarization voltages of $R_1$$C_1$ and $R_2$$C_2$, respectively.

Laplace transformation is used in Equation (1), and the equation is written as follows:

$$U_{ocv}(s)-U_t(s)=I_t(s)\cdot \left(R_0+{\displaystyle \frac{R_1}{1+{\tau }_{1}s}}+{\displaystyle \frac{R_2}{1+{\tau }_{2}s}}\right)$$

(2)

where the time constants are defined as: ${\tau }_1=R_1{C}_1$, ${\tau }_2=R_2{C}_2$. The transfer function form of Equation (2) is expressed as follows:

$$G(s)={\displaystyle \frac{U_{ocv}(s)-U_t(s)}{I_t(s)}}={\displaystyle \frac{R_0{s}^2+\frac{1}{{\tau }_1{\tau }_2}\left(R_0{\tau }_1+R_0{\tau }_2+R_1{\tau }_2+R_2{\tau }_1\right)s+\frac{(R_0+R_1+R_2)}{{\tau }_1{\tau }_2}}{s^2+\frac{\left({\tau }_1+{\tau }_2\right)}{{\tau }_1{\tau }_2}s+\frac{1}{{\tau }_1{\tau }_2}}}$$

(3)

To make the transfer function applicable to the discrete system, it is essential to convert the system transfer function from s-domain to $z$-domain. Based on the bilinear transformation $s=2\left(1-z^{-1}\right)/\left[T\left(1+z^{-1}\right)\right]$, the discrete state-space equation of the system can be obtained as follows:

$$G(z^{-1})={\displaystyle \frac{b_1+b_2{z}^{-1}+b_3{z}^{-2}}{1-a_1{z}^{-1}-a_2{z}^{-2}}}$$

(4)

where $z$ is the $z$-domain operator, and $a_1,a_2,b_1,b_2,b_3$ are the parameters to be identified.

The parameter vector for the lithium-ion battery RC model is defined as $\mathit{\beta }={[R_0,R_1,R_2,C_1,C_2]}^{\mathrm{T}}$; thus, the relationship between the RC circuit model parameters from vector $\mathit{\beta }$ and $a_1,a_2,b_1,b_2,b_3$ can be obtained from Equations (3) and (4) as follows:

$$\left\{\begin{array}{l}{R}_0={\displaystyle \frac{b_1-b_2+b_3}{1+a_1-a_2}}\\ R_0+R_1+R_2={\displaystyle \frac{b_1+b_2+b_3}{1-a_1-a_2}}\\ R_0{\tau }_1+R_0{\tau }_2+R_1{\tau }_2+R_2{\tau }_1={\displaystyle \frac{T(b_1-b_3)}{1-a_1-a_2}}\\ {\tau }_1+{\tau }_2={\displaystyle \frac{T(1+a_2)}{1-a_1-a_2}}\\ {\tau }_1{\tau }_2={\displaystyle \frac{T^2(1+a_1-a_2)}{4(1-a_1-a_2)}}\end{array}\right.$$

(5)

The following equation can be obtained:

$$y(k)=U_{ocv}(k)-U_t(k)$$

(6)

To maintain generality, a white noise signal $v(k)$ is introduced. Then, the difference equation of Equation (2) in the discrete domain can be expressed as follows:

$$y(k)=a_{1}y(k-1)+a_{2}y(k-2)+b_1{I}_t(k)+b_2{I}_t(k-1)+b_3{I}_t(k-3)+v(k)$$

(7)

where $y(k)$ is the system output, $I_t(k)$ is the system input, and $z(k)$ is random interference with white noise. The information vector $\mathit{\phi }(k)$ and parameter vector $\mathit{\theta }$ of the identified model can be defined as follows:

$$\left\{\begin{array}{l}\mathit{\phi }(k)={\left[y(k-1),y(k-2),I_{\mathrm{T}}(k),I_{\mathrm{T}}(k-1),I_{\mathrm{T}}(k-2)\right]}^{\mathrm{T}}\\ \mathit{\theta }={\left[a_1,a_2,b_1,b_2,b_3\right]}^{\mathrm{T}}\end{array}\right.$$

(8)

Thus, the model of the unidentified system is expressed by Equation (9):

$$y(k)=\mathit{\phi }{(k)}^{\mathrm{T}}\mathit{\theta }+z(k)$$

(9)

2.2. The Relationship Between Open-Circuit Voltage and SOC for Lithium-Ion Batteries

There is a direct one-to-one correspondence between open-circuit voltage ($U_{ocv}$) and the SOC of lithium-ion batteries. However, the $U_{ocv}$ cannot be measured during dynamic operation, necessitating pre-calibration of the $U_{ocv}$–SOC relationship as a foundational prerequisite for both parameter identification and SOC estimation. During battery operations, the internal complex and variable electrochemical mechanism result in nonlinearity in the $U_{ocv}$–SOC relationship. Accurate $U_{ocv}$–SOC characterization necessitates discrete-step discharge testing with measurements at incremental SOC levels, ensuring that the battery terminal voltage stabilizes fully after resting. The resulting equilibrium voltages can represent $U_{ocv}$ values [52]. After obtaining the $U_{ocv}$ values at different SOCs, a polynomial fitting method is employed to establish the $U_{ocv}$–SOC relationship curve.

2.3. Parameter Identification Algorithm

The internal electrochemical mechanism of lithium-ion battery during charging and discharging processes are complex, which compromise the parameter identification accuracy. Additionally, the working environment of lithium-ion battery, along with factors such as degradation, further challenge online parameter identification. To simultaneously enhance identification accuracy, noise immunity, and self-adaptation of parameters, this paper develops the VFFRLS framework for online estimation of parameter identification with a novel IAFF adjustment mechanism designed, yielding the IAFFRLS algorithm. This method not only enhances the parameter identification accuracy, but also demonstrates outstanding advantages in anti-interference capability.

Applying the forgetting factor least squares identification principle to the model represented by Equation (9) allows for the estimation of the parameter vector $\mathit{\theta }$ by using the observed data $\{y(k),\mathit{\phi }(k)\}$. We define the quadratic criterion function as follows:

$$J(\theta ):={\displaystyle \sum _{k=1}^{\mathit{L}}{\left[y(k)-{\mathit{\phi }}^{\mathrm{T}}(k)\mathit{\theta }\right]}^2}={\left(y-{\mathit{\phi }}^{\mathrm{T}}\mathit{\theta }\right)}^{\mathrm{T}}\left(y-{\mathit{\phi }}^{\mathrm{T}}\mathit{\theta }\right)$$

(10)

Minimizing the quadratic criterion function and introducing a variable forgetting factor $\lambda (k)$, we can derive an expression for the variable forgetting factor recursive least squares algorithm (VFFRLS) pertaining to the parameter vector $\mathit{\theta }$:

$$\left\{\begin{array}{l}\hat{\mathit{\theta }}(k)=\hat{\mathit{\theta }}(k-1)+\mathit{L}(k)[y(k)-{\mathit{\phi }}^{\mathrm{T}}(k)\hat{\mathit{\theta }}(k-1)]\\ \mathit{L}(k)=\mathit{P}(k-1)\mathit{\phi }(k){[\lambda (k)+{\mathit{\phi }}^{\mathrm{T}}(k)\mathit{P}(k-1)\mathit{\phi }(k)]}^{-1}\\ \mathit{P}(k)={\displaystyle \frac{1}{\lambda (k)}}[\mathit{I}-\mathit{L}(k){\mathit{\phi }}^{\mathrm{T}}(k)]\mathit{P}(k-1)\end{array}\right.$$

(11)

where $\mathit{L}(k)$ is the gain matrix, $\mathit{P}(k)$ is the covariance matrix, I is the unit matrix, $\lambda (k)$ is the forgetting factor, and the general value range is 0.90–1. When $\lambda (k)$ is large, the algorithm is relatively stable with small parameter estimation errors, but the convergence of the algorithm is slow. When $\lambda (k)$ is small, the algorithm is capable of tracking and adjusting the data. Nevertheless, the parameter estimation tends to fluctuate more.

In the VFFRLS algorithm proposed in reference [32], the updated expression of the forgetting factor $\lambda (k)$ is given as follows:

$$\left\{\begin{array}{l}\alpha (k)=2^{\rho {\delta }^2(k)}\\ \lambda (k)={\lambda }_{\min }+{(1-{\lambda }_{\min })}^{\alpha (k)}\end{array}\right.$$

(12)

where $\delta (k)$ is the error, ${\lambda }_{\min }$ is the minimum value of the forgetting factor, and $\rho \in [{10}^4,5\times {10}^4]$. When the error approaches 0, $\lambda (k)$ tends to 1; when the error is large, $\lambda (k)$ tends to ${\lambda }_{\min }$. The variable forgetting factor strategy enables adaptive adjustment of the forgetting factor $\lambda (k)$. However, in Equation (12), the update adjustment of $\lambda (k)$ is affected by the changing rate of parameter $\rho$. Unreasonable values of $\rho$ not only degrade the identification accuracy, but also severely impact the anti-interference capability of the algorithm. On this basis, in order to ensure the convergence speed of the algorithm, reduce the parameter estimation errors, and enhance the anti-interference ability, this paper proposes an IAFF adjustment mechanism:

$$\left\{\begin{array}{l}\lambda (k)={\lambda }_{\min }+({\lambda }_{\max }-{\lambda }_{\min })\mathrm{arccot}(\alpha (k))\cdot 2/\pi \\ \alpha (k)=\mathrm{N}\mathrm{I}\mathrm{N}\mathrm{T}\left({\left|{\displaystyle \frac{e(k)}{e_s}}\right|}^n\right)\end{array}\right.$$

(13)

where $e(k)=y(k)-{\phi }^{\mathrm{T}}(k)\hat{\mathit{\theta }}(k-1)$ is the prediction error; $e_s$ is the datum error; ${\lambda }_{\max }$, ${\lambda }_{\min }$, and $n$ are fixed values; ${\lambda }_{\max }$ is the maximum value of the forgetting factor; ${\lambda }_{\min }$ is the minimum value of the forgetting factor, with the value being $0.90\le {\lambda }_{\min }\le {\lambda }_{\max }\le 1$; $n$ is an integer with values $2\le n\le 6$; and $\mathrm{N}\mathrm{I}\mathrm{N}\mathrm{T}(\cdot )$ is the closest integer to $(\cdot )$. From the modification function, it can be seen that the forgetting factor $\lambda (k)$ is regulated by $e(k)$. The gradual adjustment is managed by the inverse cotangent function to address the inadequate tracking performance of the algorithm caused by rapid changes in $\lambda (k)$. When $e(k)>e_s$, the ratio of $e(k)$ and $e_s$ is amplified by the $n$-th power, resulting in a larger $\alpha (k)$. $\lambda (k)$ needs to be reduced to quickly adjust the parameter responsiveness and improve the accuracy of the algorithm. When $e(k)<e_s$, $\alpha (k)$ is smaller, and $\lambda (k)$ needs to be increased to ensure the stability of the parameter estimate. From the analysis mentioned above, it is evident that the forgetting factor $\lambda (k)$ can be adaptively adjusted with the observed errors during the identification process. In the parameter estimation, timely adjustment of the forgetting factor $\lambda (k)$ in accordance with the dynamics of the prediction error $e(k)$ is the basis for effectively improving the accuracy of the algorithm and optimizing the speed of data tracking.

The combination of Equations (11) and (13) is the IAFFRLS algorithm expression. In Equations (11) and (13) of the IAFFRLS algorithm:

(1) If $\lambda (k)$ is constant, the algorithm morphs into the forgetting factor recursive least squares algorithm (FFRLS);

(2) If ${\lambda }_{\max }={\lambda }_{\min }=1$, the algorithm degenerates into the recursive least squares algorithm (RLS).

Based on the IAFFRLS algorithm, the parameter vector $\mathit{\theta }$ can be identified, allowing for further estimations of the parameter vector $\mathit{\beta }$ in the second-order circuit model of the lithium-ion battery. The flow chart of IAFFRLS is shown in Figure 2.

3. SOC Estimation Algorithm Based on WMISAEKF

3.1. Extended Kalman Filter

The extended Kalman filter (EKF) is one of the SOC estimation methods for lithium-ion batteries. Unlike the traditional Kalman filter (KF), which is effective for linear systems, EKF is more suitable in the SOC estimation of lithium-ion batteries with complex charging and discharging characteristics. The core idea of EKF is to expand the nonlinear system function into a Taylor series based on the current filtered estimate and omit the higher-order terms to simplify computation so as to obtain an approximate linearized model, which is subsequently combined with standard Kalman filtering to complete the state estimation of the system.

For the nonlinear system model of lithium-ion batteries, the discrete state-space and observation equations are as follows:

$$\left\{\begin{array}{l}x(k)=f\left[x(k-1),u(k-1)\right]+\omega (k-1)\\ y(k)=g\left[x(k),u(k)\right]+v(k)\end{array}\right.$$

(14)

where $x$ is the state quantity; $y$ is the observation quantity; $u$ is the input quantity; $f(\cdot )$ is the coefficient matrix of the process equation; $g(\cdot )$ is the coefficient matrix of the measurement equation; $\omega$ is the process noise with zero mean, and its variance is Q; and $v$ is the observation noise with zero mean, and its variance is R. Meanwhile, $\omega$ and $v$ are independent from each other.

The process of the EKF linearizes the nonlinear system by expanding the process equation $f[x(k-1),u(k-1)]$ and the nonlinear measurement equation $g[x(k),u(k)]$ into a Taylor series. By omitting higher-order terms and retaining only the primary terms, an approximate linear system can be derived as follows:

$$\left\{\begin{array}{l}\hat{x}(k)=A(k)x(k-1)+B(k)u(k-1)+E\cdot \omega (k-1)\\ y(k)=C(k)x(k)+D(k)u(k)+v(k)\end{array}\right.$$

(15)

among them, A is the transfer matrix, B is the control matrix, C is the observation matrix, D is the observed state matrix, and E is the noise-driven unit matrix. Based on the previous analysis, combined with the second-order RC equivalent circuit model, the EKF algorithm is applied to estimate the SOC of lithium-ion batteries using the operating current $I_t$ as the input and the terminal voltage $U_t$ as the output observation. The following equations can be obtained:

$$\left\{\begin{array}{l}\mathit{x}={[SOC U_1 U_2]}^{\mathrm{T}}\\ y=U_t=U_{ocv}-U_1-U_2-I{R}_0\end{array}\right.$$

(16)

The discretized state equation and observation equation can be obtained as Equations (17) and (18):

$$\left[\begin{array}{l}SOC (k)\\ U_1 (k)\\ U_2 (k)\end{array}\right]=\left[\begin{array}{l}1 0 0\\ 0 1-{\displaystyle \frac{T}{{\tau }_1}} 0\\ 0 0 1-{\displaystyle \frac{T}{{\tau }_2}}\end{array}\right]\left[\begin{array}{l}SOC (k-1)\\ U_1 (k-1)\\ U_2 (k-1)\end{array}\right]+\left[\begin{array}{l}{\displaystyle \frac{\eta T}{C_n}}\\ {\displaystyle \frac{T}{C_1}}\\ {\displaystyle \frac{T}{C_2}}\end{array}\right]I(k-1)$$

(17)

$$U_t(k)=U_{ocv}(k-1)-U_1(k-1)-U_2(k-1)-I(k-1)R_0$$

(18)

where $C_n$ is the battery capacity. $\eta$ is the charging and discharging efficiency. Combining Equations (17) and (18), the coefficient matrices can be obtained as follows:

$$A(k)=\left[\begin{array}{l}1 0 0\\ 0 e^{-{\displaystyle \frac{T}{{\tau }_1}}} 0\\ 0 0 e^{-{\displaystyle \frac{T}{{\tau }_2}}}\end{array}\right]$$

(19)

$$B(k)=\left[\begin{array}{l} {\displaystyle \frac{\eta T}{C_n}}\\ R_1\left(1-e^{-{\displaystyle \frac{T}{{\tau }_1}}}\right)\\ R_2\left(1-e^{-{\displaystyle \frac{T}{{\tau }_2}}}\right)\end{array}\right]$$

(20)

$$C(k)=\left[{\displaystyle \frac{\mathsf{\partial }{U}_{OCV}}{\mathsf{\partial }SOC}} - 1 - 1\right]$$

(21)

$$D(k)=-R_0$$

(22)

From the above equations, the coefficient matrices of the state equation and the observation equation are related to the system identification parameters at moment $k$. Therefore, the system identification parameters can update the coefficient matrices in real time. The updated coefficient matrices $A(k)$, $B(k)$, $C(k)$, and $D(k)$ are incorporated into the EKF algorithm to refine the predicted estimates at time step $k+1$. The EKF recursive formulas are shown as Equations (23)–(27):

$$\hat{\mathit{x}}(k)=A(k-1)\mathit{x}(k-1)+B(k-1)I_t(k-1)$$

(23)

$$\hat{P}(k)=A(k-1)P(k-1)A{(k-1)}^{\mathrm{T}}+\mathit{Q}$$

(24)

$$K(k)=\hat{P}(k)C{(k)}^{\mathrm{T}}{(C(k)\hat{P}(k)C{(k)}^{\mathrm{T}}+\mathit{R})}^{-1}$$

(25)

$$\mathit{x}(k)=\hat{\mathit{x}}(k)+K(k)(y(k)-C(k)\hat{\mathit{x}}(k)-D{I}_t(k))$$

(26)

$$P(k)=\hat{P}(k)-K(k)C(k)\hat{P}(k)$$

(27)

where $K\in R^{3\times 1}$ is the Kalman gain matrix, $P\in R^{3\times 3}$ is the error covariance matrix, $\mathit{Q}\in R^{3\times 3}$ is the covariance of process noise, and $\mathit{R}\in R$ is the covariance of observation noise.

3.2. Improved Sage–Husa Adaptive Extended Kalman Filter Algorithm

Lithium-ion batteries are influenced by various factors during actual operation, including sensor sampling rate, environmental conditions, and temperature. In the EKF algorithm, the process noise and observation noise are not involved in the iterative update calculation of the algorithm, which is not fully consistent with the complex and variable working conditions of the batteries in practice. Maintaining algorithm stability under actual battery operating conditions necessitates adaptive noise covariance updating synchronized with estimated parameter changing during iterative estimation. The Sage–Husa adaptive filtering algorithm is introduced in this paper [53]. The proposed algorithm dynamically adapts both process and observation noise covariance matrices through real-time estimation, enabling iterative correction that reduces model error, suppresses filter divergence, and improves the accuracy of the algorithm.

In the recursive formulation of the EKF, the system prediction error is defined as the innovation value, which represents the difference between the observed and predicted values of the terminal voltage. This can be expressed mathematically as follows:

$$e(k)=y(k)-\mathbf{C}(k)\hat{\mathit{x}}(k)-D(k)I_t(k)$$

(28)

According to the Sage–Husa adaptive filtering algorithm, the noise correction formula is as follows:

$$\left\{\begin{array}{l}d(k-1)=(1-b)/(1-b^k)\\ \mathit{Q}(k)=(1-d(k-1))\mathit{Q}(k-1)\\ +d(k-1)[\mathbf{K}(k)e(k)e{(k)}^{\mathrm{T}}\mathbf{K}{(k)}^{\mathrm{T}}+\mathbf{P}(k)\\ -\mathbf{A}(k-1)\mathbf{P}(k-1)\mathbf{A}{(k-1)}^{\mathrm{T}}]\\ \mathit{R}(k)=(1-d(k-1))\mathit{R}(k-1)\\ +d(k-1)[e(k)e{(k)}^{\mathrm{T}}-\mathbf{C}(k)\mathbf{P}(k)\mathbf{C}{(k)}^{\mathrm{T}}]\end{array}\right.$$

(29)

Among them, $b$ is the correction factor. Typically, the value range of $b$ is $0.95\le b<1$.

The Sage–Husa adaptive filtering algorithm can obtain the noise covariance matrices Q and R by combining the EKF algorithm and the above formulas in the presence of noise uncertainty. However, as can be observed from Equation (29), the calculations of Q and R may yield non-positive values due to the presence of subtraction. It is difficult to guarantee the positive definiteness of system process noise covariance and measurement noise covariance matrices, leading to the failure of the EKF algorithm to continue iteration, resulting in filter divergence. Therefore, it is necessary to improve the Sage–Husa adaptive algorithm, according to the observation noise correction formula in Equation (28), in order to ensure the positive characterization of the noise covariance matrices Q and R. This paper adopts the biased estimation approach for the adaptive updating of the noise covariance matrices Q and R. Therefore, the improved Sage-Husa adaptive extended Kalman filter algorithm (ISAEKF) for time-varying noise estimation can be described as Equation (30):

$$\left\{\begin{array}{l}d(k-1)=(1-b)/(1-b^k)\\ \mathit{Q}(k)=(1-d(k-1))\mathit{Q}(k-1)\\ +d(k-1)\left(\mathbf{K}(k)e(k)e{(k)}^{\mathrm{T}}\mathbf{K}{(k)}^{\mathrm{T}}\right)\\ \mathit{R}(k)=(1-d(k-1))\mathit{R}(k-1)+d(k-1)(e(k)e{(k)}^{\mathrm{T}})\end{array}\right.$$

(30)

3.3. Weighted Multi-Innovation Improved Sage–Husa Adaptive Extended Kalman Filter

In the ISAEKF algorithm, the iterative update process relies solely on the state of the previous moment to estimate the current state, and all the data beforehand are lost. If a series of relevant information before the current moment can be effectively used, the estimation accuracy will be greatly improved. The multi-innovation theory is proposed to extend the scalar single-innovation value in the algorithm to the multi-innovation vector. This means that the state estimation at the current moment is correlated with the useful information from the previous moment, thereby improving the accuracy and stability of the algorithm. The multi-innovation error vector is defined as follows:

$$\mathit{E}(p,k)=\left[\begin{array}{l} e(k)\\ e(k-1)\\ ⋮\\ e(k-p+1)\end{array}\right]$$

(31)

where $k$ is the current moment, and $p$ is the length of historical innovation.

Correspondingly, the gain matrix of the Kalman filter also needs to be extended to the multi-innovation gain matrix:

$$G(p,k)=\left[ K(k) K(k-1) ··· K(k-p+1)\right]$$

(32)

In literature [54], a multi-innovation EKF algorithm was constructed to incorporate a forgetting factor, which weakened the cumulative interference problem associated with stale data. However, the forgetting factor defined in that literature assigns the same weight factor to the historical innovation, and its rationality remains to be studied. In practical applications, terminal voltage errors in lithium-ion batteries are random, meaning that the innovation values in the algorithm are irregular [32,55,56]. The continuous irregular variations in innovation values can further reflect battery-specific factors, leading to dispersion in SOC estimation results among individual cells [57]. If the innovation value of the update iteration is large, whereas the weight factor remains small, the algorithm exhibits poor robustness during the update iteration. In order to solve the above problems, this paper proposes a multi-innovation weight factor calculation method, that is, the larger value of the innovation gives a larger weight factor, and the value closer to the current moment of innovation is more important for the update and is also assigned a larger weight. The matrices of weight factors are defined as follows:

$$\left\{\begin{array}{l}{w}_{t,i}=e^{-{\displaystyle \frac{{(i-k)}^2}{2}}}\\ w_{e,i}=e^{-{\displaystyle \frac{{(e_i-\max (E_{p,k}))}^2}{2}}}\\ w={\displaystyle \sum _{i=k-p+1}^k{w}_{t,i}\cdot w_{e,i}}\\ {\mathit{W}}_{t,p}=diag\left[w_{t,k} w_{t,k-1} ··· w_{t,k-p+1}\right]\\ {\mathit{W}}_{e,p}=diag\left[w_{e,k} w_{e,k-1} ··· {\mathit{w}}_{e,k-p+1}\right]\end{array}\right.$$

(33)

where $w_{t,i}$ is the innovation weight related to current moment; $w_{e,i}$ is the innovation weight related to the error; ${\mathit{W}}_{t,p}$ is the diagonal matrix of innovation weight related to current moment; ${\mathit{W}}_{e,p}$ is the diagonal matrix of the innovation weight related to the error; and $w$ is the weighted value.

Correspondingly, the gain matrix is defined as follows:

$$\mathit{\Gamma }(p,k)={\displaystyle \frac{p}{w}}\left[K(k) K(k-1) ··· K(k-p+1)\right]$$

(34)

The improved update state equation is as follows:

$$x(k)=\hat{x}(k)+\mathit{\Gamma }(p,k){\mathit{W}}_{t,p}{\mathit{W}}_{e,p}E(p,k)$$

(35)

This study presents an improvement of the weighted multi-innovation improved Sage–Husa adaptive extended Kalman filter algorithm (WMIASEKF) in SOC estimation. The specific processes involved in the algorithm are shown in Figure 3.

As demonstrated by the aforementioned recursive computation process, the WMISAEKF algorithm retains the advantages of the EKF algorithm, which employs a continuous ‘estimation + correction’ process, whereby the state estimation at time $k$ is recursively derived from the state estimation and observation at time $k-1$. By integrating the multi-innovation theory with an improved adaptive filtering method, the weight matrix is constructed, and the noise covariance matrices are updated, enabling the WMISAEKF algorithm to exhibit superior performance compared to EKF. In the SOC estimation and calculation of lithium-ion batteries, the parameters identified by the model correct the SOC estimation by altering the coefficients of the state equation and the observation equation.

4. Results and Discussion

In practical applications, lithium-ion batteries discharge according to vehicle driving profiles. The Urban Dynamometer Driving Schedule (UDDS) provides standardized emulation of urban driving patterns. Through the UDDS condition, the effectiveness of the SOC estimation for batteries can be evaluated [58]. To verify the effectiveness of the IAFFRLS online parameter identification algorithm and the reliability and robustness of the SOC estimation algorithm proposed in this paper, UDDS data are adopted as the verification benchmark. The experimental environment is strictly controlled at a constant temperature of 25 °C. The accuracy of the battery testing system meets the following specifications: voltage detection error ±0.05%, current detection error ±0.05%, and temperature error ±1 °C. The research subject is a ternary lithium battery with a nominal capacity of 33 Ah. The data sampling interval is 1 s. The relevant parameters of the battery and the testing equipment are shown in

Table 1. Related parameters of battery and test equipment.

Parameter	Specification
Capacity	33 Ah
Charge/Discharge cut-off voltage	4.2 V/3.0 V
Temperature	−15–50 °C
Life cycle	>2000
Brand	ATL
Battery test system	Neware CE6008a (Neware Technology Co., Shenzhen, China)

. When the battery health state was 100%, the UDDS condition test was conducted on the battery for 300 min, with approximately 11 cycles. Figure 4 shows the terminal voltage and current curves collected by the research object under the UDDS condition.

4.1. Parameter Identification Verification Based on IAFFRLS

The acquisition of the $U_{ocv}$–SOC curve for lithium-ion batteries is crucial for parameter identification. The dataset utilized in this study employs the intermittent discharge rest method for $U_{ocv}$ testing. At various SOCs, the terminal voltage of the battery, which stabilizes after an adequate resting period, is regarded as the $U_{ocv}$ value [52,54]. The $U_{ocv}$–SOC curve was obtained by applying polynomial fitting to the test data, with the residual sum of squares (RSS), the coefficient of determination (R2), and the adjusted coefficient of determination (adj. R2) as the fitting evaluation criteria. The statistics of polynomial fittings are shown in

Table 2. Parameter comparison of polynomial fitting.

Order	SSE	R2	adj.R2
3	0.0021	0.9965	0.9951
4	0.0019	0.9969	0.9948
5	0.0004	0.9993	0.9987
6	0.0002	0.9996	0.9990
7	0.0001	0.9998	0.9993
8	0.0001	0.9999	0.9993

. Analysis of Table 2 reveals that the 7th-order polynomial fitting performs well, while the 8th-order polynomial exhibits overfitting. Considering the fitting effect comprehensively, the 7th-degree polynomial was selected to fit the curve, and the obtained $U_{ocv}$–SOC curve is shown in Figure 5.

In the parameter identification verification of the proposed IAFFRLS algorithm, considering the influence of different ${\lambda }_{\max }$ and ${\lambda }_{\min }$ on the online parameter identification results, ${\lambda }_{\max }$ is set to 1 to ensure the stability of parameter identification. To verify the boundary performance of ${\lambda }_{\min }$, three metrics—mean absolute error (MAE), root mean square error (RMSE), and maximum absolute error (MAXE)—are used to quantitatively analyze the systematic error variation with ${\lambda }_{\min }$. The systematic error variation with ${\lambda }_{\min }$ is shown in

Table 3. Quantitative analysis table of λ_min and systematic errors.

λmin	δMAE	δRMSE	δMAXE
0.90	8.9273 × 10−5	6.7893 × 10−4	0.0265
0.93	8.1759 × 10−5	5.4860 × 10−4	0.0298
0.95	7.4885 × 10−5	4.6769 × 10−4	0.0336
0.96	7.0405 × 10−5	4.3699 × 10−4	0.0379
0.97	7.1034 × 10−5	3.4636 × 10−4	0.0246
0.98	6.7422 × 10−5	2.9657 × 10−4	0.0089
0.985	6.1002 × 10−5	1.7805 × 10−4	0.0040
0.99	6.1002 × 10−5	1.7805 × 10−4	0.0040

. From Table 3, it can be observed that the MAE metric gradually decreases as ${\lambda }_{\min }$ increases within the range of ${\lambda }_{\min }$ ∈ [0.90,0.96]. When ${\lambda }_{\min }$ = 0.97, the MAE metric slightly increases, and within ${\lambda }_{\min }$ ∈ [0.97,0.985], the MAE metric gradually decreases as ${\lambda }_{\min }$ increases. When λmin ≥ 0.985, the error metric remains unchanged. The RMSE metric gradually decreases as λmin increases, and when λmin ≥ 0.985, the RMSE metric remains unchanged. The MAXE metric gradually increases as ${\lambda }_{\min }$ increases within the range of ${\lambda }_{\min }$ ∈ [0.90,0.96], rapidly decreases within ${\lambda }_{\min }$ ∈ [0.96,0.985], and remains unchanged when ${\lambda }_{\min }$ ≥ 0.985. Based on the above analysis, to ensure the superiority of the algorithm, the IAFFRLS algorithm in this paper selects ${\lambda }_{\min }$ = 0.985 for parameter identification verification.

In order to verify the accuracy of the parameter identification results of the IAFFRLS algorithm proposed in this paper, the terminal voltage errors obtained by the online estimation of the IAFFRLS algorithm and the traditional RLS algorithm are compared and analyzed. The terminal voltage estimates obtained by the two algorithms are shown in Figure 6. The comparison of terminal voltage errors of the two algorithms is shown in Figure 7.

As illustrated in Figure 6 and Figure 7, the IAFFRLS algorithm demonstrates a reduced voltage prediction error compared to the traditional RLS algorithm. To facilitate a more intuitive comparison between the two identification algorithms, the two algorithms are quantitatively analyzed by MAE, RMSE, and MAXE, three key metrics. The quantitative evaluation of terminal voltage prediction errors for the various algorithms is presented in

Table 4. Quantitative evaluation of terminal voltage prediction errors for different identifications.

Identification Algorithm	UMAE/V	URMSE/V	UMAXE/V
RLS	0.0029	0.0041	0.0871
IAFFRLS	7.8626 × 10−4	0.0019	0.0878

. Through quantitative and comparative analysis, it is evident that the IAFFRLS identification algorithm significantly outperforms the RLS algorithm in terms of MAE and RMSE, with improvements of 72.89% and 53.66%, respectively. Regarding the MAXE index, the values for both algorithms are comparable, primarily due to the substantial initial identification error caused by the selection of initial values in the identification algorithm, which results in a high MAXE index. Overall, the IAFFRLS algorithm demonstrates clear advantages over the RLS algorithm, effectively enhancing the accuracy of model parameter identification and improving the terminal voltage fitting accuracy of the second-order identification model for lithium-ion batteries.

In order to further verify the accuracy of the identification algorithm, the model parameter identification IAFFRLS algorithm proposed in this paper is compared with the VFFRLS algorithm proposed in literature [32] and the AFFRLS algorithm proposed in literature [33] to perform a horizontal comparison and analysis of the recognition parameters. Figure 8a–e illustrates the comparison of each parameter for the second-order RC model, as obtained from the parameter identification conducted by the three algorithms mentioned above. Figure 8f shows the results of systematic errors in parameter identification of the three algorithms.

The fluctuations of identification parameters reflect the time-varying property of model parameters as input and output change. The identification results of battery parameters can be analyzed. As illustrated in Figure 8a–e, the VFFRLS algorithm has the largest fluctuation range of identification parameters, followed by the AFFRLS algorithm, whereas the IAFFRLS algorithm demonstrates the smallest fluctuation and the best stability. As can be seen from Figure 8f, the parameter estimation errors of the VFFRLS algorithm proposed in literature [32] and AFFRLS algorithm proposed in literature [33] are large, especially in the latter half of identification, and the VFFRLS algorithm has the largest error. The systematic errors of the above three algorithms are measured by three indicators: MAE, RMSE, and MAXE. The quantitative error analysis of the three algorithms is shown in

Table 5. Quantitative evaluation analysis of systematic errors for the three algorithms.

Identification Algorithm	δMAE	δRMSE	δMAXE
VFFRLS	1.1045 × 10−4	3.4188 × 10−4	0.0110
AFFRLS	8.4287 × 10−5	3.0372 × 10−4	0.0077
IAFFRLS	5.3601 × 10−5	2.4513 × 10−4	0.0063

. It can be obtained from Table 5 that the IAFFRLS algorithm has the highest precision and the best stability. In summary, it can be concluded that among the three algorithms, the IAFFRLS algorithm proposed in this paper has the smallest error, the highest identification accuracy, and the best stability for model parameter identification of lithium-ion batteries.

To validate the anti-interference capabilities of the algorithms, simulations of model parameter identification are performed by introducing zero-mean white noise interference into the terminal current and voltage. The parameter identification effectiveness of the three algorithms is then evaluated under these noise-contaminated conditions. The results are shown in Figure 9, where Figure 9a–e presents the parameter identification results of the three algorithms, and Figure 9f displays the system errors of the three algorithms.

The results indicate that when the input and output data of the identification model are disturbed, the identification results obtained by the VFFRLS algorithm proposed in literature [32] and AFFRLS algorithm proposed in literature [33] are significantly affected. Comparing the identification parameter results before and after the disturbance, the superiority of the AFFRLS algorithm over the VFFRLS algorithm is no longer evident, as both algorithms exhibit similar performance in parameter identification and system error metrics. However, the IAFFRLS algorithm proposed in this paper maintains relatively stable identification results, even after disturbances in the input and output, demonstrating its strong anti-interference capability. Moreover, the system error remains absolutely superior compared to the other two algorithms. The systematic errors of the three algorithms are quantitatively analyzed from the three indexes of MAE, RMSE, and MAXE, and the analysis results are shown in

Table 6. Quantitative evaluation analysis of systematic errors for the three algorithms with noise.

Identification Algorithm	δMAE	δRMSE	δMAXE
VFFRLS	0.0012	0.0017	0.0239
AFFRLS	9.5717 × 10−4	0.0014	0.0206
IAFFRLS	1.5613 × 10−4	2.9975 × 10−4	0.0063

. As can be seen from Table 6, the quantization error values of the IAFFRLS algorithm proposed in this paper are all the minimums.

Based on the above analysis, the IAFFRLS algorithm proposed in this paper demonstrates superior characteristics in the parameter identification research of lithium-ion batteries when compared to the various parameter identification algorithms discussed previously. Specifically, it exhibits high identification accuracy, good stability, and strong anti-interference capability.

4.2. SOC Estimation Verification Based on WMISAEKF

In response to the issue that the noise covariance matrix does not participate in the system update when EKF is used for SOC estimation, this paper proposes the ISAEKF algorithm for SOC estimation, ensuring the convergence of the filtering algorithm. When the system noise and measurement noise of Equation (21) are substituted into the EKF algorithm for iterative updates, the filter diverges, as shown in Figure 10. When the improved noise algorithm of Equation (22) is iterated in the EKF, the filtering of the ISAEKF algorithm converges, as illustrated in Figure 11. Combined with the above analysis, the ISAEKF algorithm proposed in this paper solves the problem of non-positive definite noise covariance matrix, thereby preventing filter divergence.

The parameters obtained from the parameter identification algorithm are brought into the SOC estimation algorithm to update the state equation and observation equation, so the system state variables are predicted and updated in each iteration to obtain the SOC estimation. Figure 12a shows the comparison between the true value of SOC and the estimated SOC by the EKF algorithm, ISAEKF algorithm, and the WMISAEKF algorithm proposed in this paper. Figure 12b shows the errors of the three SOC estimation algorithms. The maximum errors of EKF, ISAEKF, and WMISAEKF algorithms are 5.21%, 2.24%, and 2.12%, respectively. It is obvious from the figure that the error of WMISAEKF is stable and at the lowest level among the three algorithms. To provide a more intuitive comparison of the estimation performance of the algorithms, the MAE, RMSE, and MAXE of the aforementioned three algorithms are selected as the quantitative evaluation metrics for estimation. The quantitative error analysis of the three algorithms is shown in

Table 7. SOC estimation quantitative error analysis of different algorithms under the UDDS condition.

SOC Estimation Algorithms	SOCMAE	SOCRMSE	SOCMAXE
EKF	0.0074	0.0090	0.0521
ISAEKF	0.0018	0.0034	0.0284
WMISAEKF	0.0006	0.0021	0.0226

. From SOC quantitative error analysis, it can be concluded that each error index of WMISAEKF is the minimum value among the three algorithms.

Although the three indicators of MAE, RMSE, and MAXE have already demonstrated the superiority of the WMISAEKF algorithm in estimation accuracy, the safety decision-making of BMS requires more attention to the uncertainty bounds of the estimation results. To quantitatively analyze the reliability differences among the three algorithms, this study further calculated the variance and 95% confidence interval (CI) of the SOC estimations.

Table 8. Variance and confidence intervals of the three methods.

Indicator	MAE			RMSE			MAXE
	EKF	ISAEKF	WMISAEKF	EKF	ISAEKF	WMISAEKF	EKF	ISAEKF	WMISAEKF
Variance	2.176 × 10−6	1.292 × 10−7	7.402 × 10−8	5.685 × 10−6	2.994 × 10−6	1.152 × 10−6	0.0036	0.0033	0.0024
95% CI	[0.0061, 0.0082]	[0.0008, 0.0023]	[0.0003, 0.0010]	[0.0074, 0.0108]	[0.0032, 0.0056]	[0.0016, 0.0032]	[0.0473, 0.1328]	[0.0165, 0.1291]	[0.0180, 0.1166]

summarizes the key indicators of variance and CI for the three methods. As shown in Table 8, the CI boundary of the EKF algorithm is the widest, whereas the WMISAEKF algorithm not only provides more accurate CIs but also ensures that the SOC values fall into the prediction interval with a higher probability, demonstrating more significant stability and accuracy.

In the evaluation of the SOC estimation algorithm, we compared the computing times of the three algorithms. The computer configuration used for the calculation is an Intel Core(TM) i9-13900H processor with 32 GB of memory, and the execution time calculated is performed in Matlab R2020a software. Since the algorithm computation time is influenced by factors such as the current CPU and memory of the system, even on the same computer, the computation time may slightly vary when the same calculation method is executed at different times. To accurately evaluate the computation time of the algorithms, each of the three algorithms was run 10 times in Matlab, and the statistical information of the computation time is shown in

Table 9. The average computing times of the three algorithms.

SOC Estimation Algorithm	Average Computing Time (s)
EKF	0.984245
ISAEKF	0.539685
WMISAEKF	0.638925

. As can be seen from Table 9, among the three algorithms, the ISAEKF algorithm has the shortest computation time. The increase in computation time of the WMISAEKF algorithm proposed in this paper compared to the ISAEKF algorithm is mainly due to the matrix computation in the WMISAEKF algorithm; however, compared to the EKF algorithm, the WMISAEKF algorithm reduces the computation time by 35.09%, showing a significant advantage.

Considering that the collection of voltage and current signals in the actual operation of lithium-ion batteries may be affected by various interference factors, to verify the robustness of the algorithm proposed in this paper, white noise interference with zero mean and ${\sigma }_u$ variance was added to the terminal voltage of the lithium-ion battery, and white noise interference with zero mean and ${\sigma }_i$ variance was added to the current. The interference convergence of the WMISAEKF algorithm was validated under noise interference conditions, and the results are shown in Figure 13. As can be seen from Figure 13, the WMISAEKF algorithm can still converge under different levels of noise interference, even in the case of ${\sigma }_i$ = 0.35 and ${\sigma }_u$ = 0.06. The steady-state error remains within 4.5%, verifying that the algorithm maintains convergence, even when the data are subject to noise interference.

In practical SOC estimation, it is often difficult to obtain the initial SOC value accurately, whereas the erroneous initial value will significantly affect SOC estimation and even deviate from the true SOC value. For this purpose, the WMISAEKF algorithm is validated for robustness by setting different initial values of SOC. The results are shown in Figure 14. The figures illustrate that the algorithm is capable of rapidly converging to the correct SOC estimation, even when provided with an incorrect initial SOC value. This demonstrates that the algorithm not only has good robustness but also maintains high accuracy.

To verify the applicability of the algorithm proposed in this paper under different working conditions, the algorithm was used for SOC estimation verification under the FTP-75 condition of INR18650-25R lithium-ion battery. Under a constant temperature of 25 °C, the rated capacity of the test object was 2500 mAh. The measured condition data were used to verify the SOC estimation in the algorithm proposed in this paper. Figure 15 shows the SOC estimation results and estimation errors of EKF, ISAEKF, and WMISAEKF algorithms. The quantization error analysis of the three algorithms is shown in

Table 10. SOC estimation quantitative error analysis of different algorithms under the FTP-75 condition.

SOC Estimation Algorithm	SOCMAE	SOCRMSE	SOCMAXE
EKF	0.0123	0.0144	0.0305
ISAEKF	0.0059	0.0067	0.0121
WMISAEKF	0.0030	0.0039	0.0135

. As can be seen from Figure 15 and Table 10, the WMISAEKF algorithm demonstrates superior overall estimation stability despite a marginally higher MAXE relative to ISAEKF. While Figure 15b indicates initial error fluctuation in WMISAEKF, it exhibits rapid convergence to a stable, high-precision operating regime. Conversely, the ISAEKF’s lower MAXE masks the characteristics of monotonically increasing error and progressive accuracy degradation. Under the FTP-75 condition, compared with the EKF algorithm, the MAE, RMSE, and MAXE of WMISAEKF are decreased by 75.61%, 72.92%, and 55.74%, respectively. Among the three algorithms, the WMISAEKF algorithm has the best stability and the highest estimation accuracy. Comprehensively, compared with the other two algorithms, the WMISAEKF algorithm proposed in this paper effectively improves the SOC estimation accuracy for lithium-ion batteries.

5. Conclusions

In this paper, we study the problems of low identification accuracy and inadequate anti-interference ability of parameter identification by the RLS algorithm for lithium-ion batteries. We propose a new forgetting factor adjustment mechanism and introduce the IAFFRLS algorithm to accurately identify the parameters of the second-order equivalent circuit model. The effectiveness of the IAFFRLS algorithm is verified by simulation. On this basis, in order to improve the accuracy of SOC estimation, the WMISAEKF algorithm is proposed to solve the problem of the filter divergence caused by the noise covariance updating, and a more reasonable weighted calculation method is designed to improve the SOC estimation accuracy. The simulation results show that the WMISAEKF has high estimation accuracy. Furthermore, in the presence of an incorrect initial SOC value, the algorithm is capable of rapidly correcting the influence caused by the incorrect initial value, thereby demonstrating strong robustness. However, it is necessary to clarify the limitations of this study to avoid over-generalization of the conclusion: validation was exclusively conducted under laboratory conditions using simulated UDDS and FTP-75 profiles at a constant temperature. Performance generalization to real operational environments, particularly under extreme thermal cycling and nonlinear degradation states, remains unverified and needs further verification.

In BMSs, the state of health (SOH) for batteries is an important indicator to evaluate the battery performance. Lithium-ion batteries may not continue to maintain the factory-rated capacity after a period of use under complex operating conditions, which can also affect the SOC estimation results. Therefore, the co-estimation of SOC and SOH for lithium-ion batteries is considered in the subsequent work to provide a technical guarantee for the stable operation of lithium-ion batteries.