DNS Study of Freely Propagating Turbulent Lean-Premixed Flames with Low-Temperature Chemistry in the Broken Reaction Zone Regime
Abstract
1. Introduction
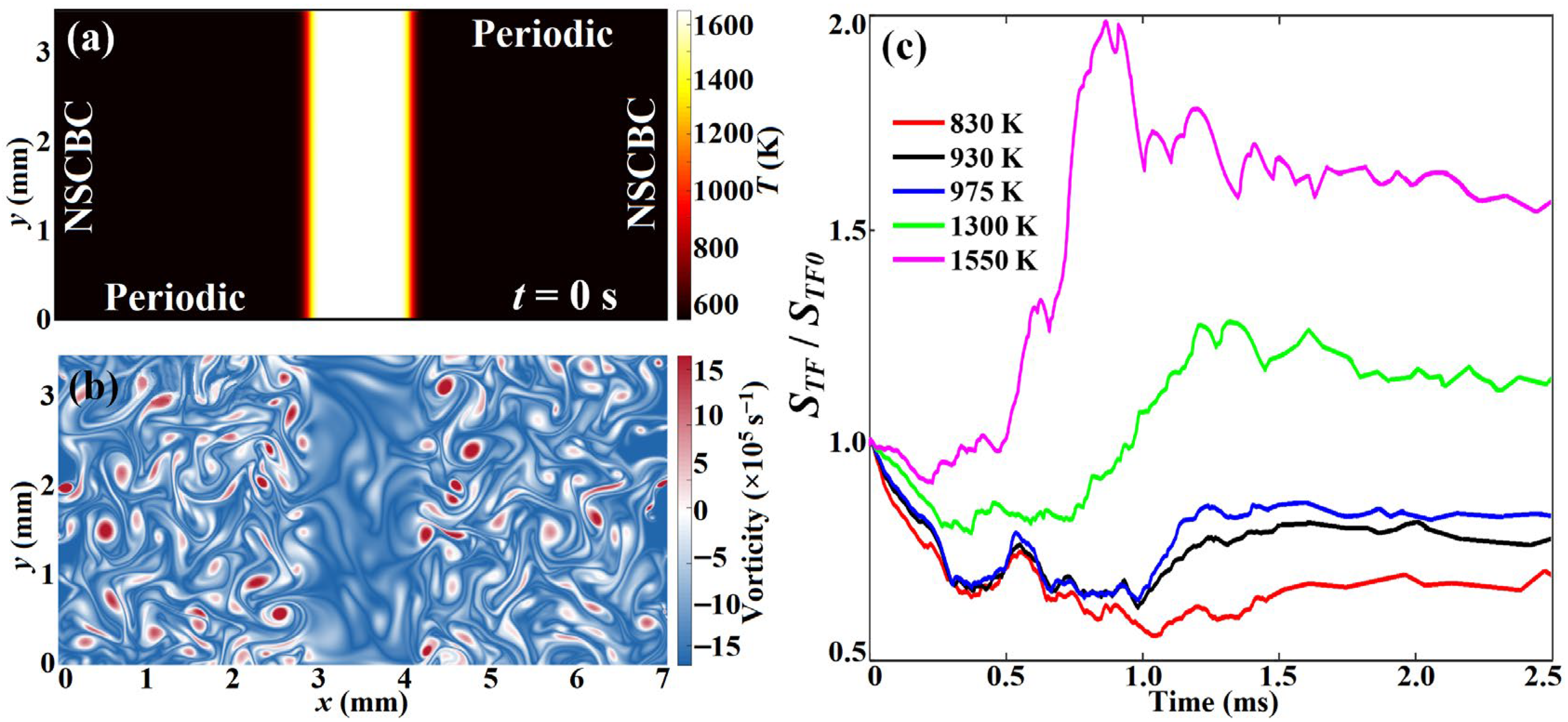
2. Flame Configuration and Numerical Methods for the DNSs
3. Results and Discussion
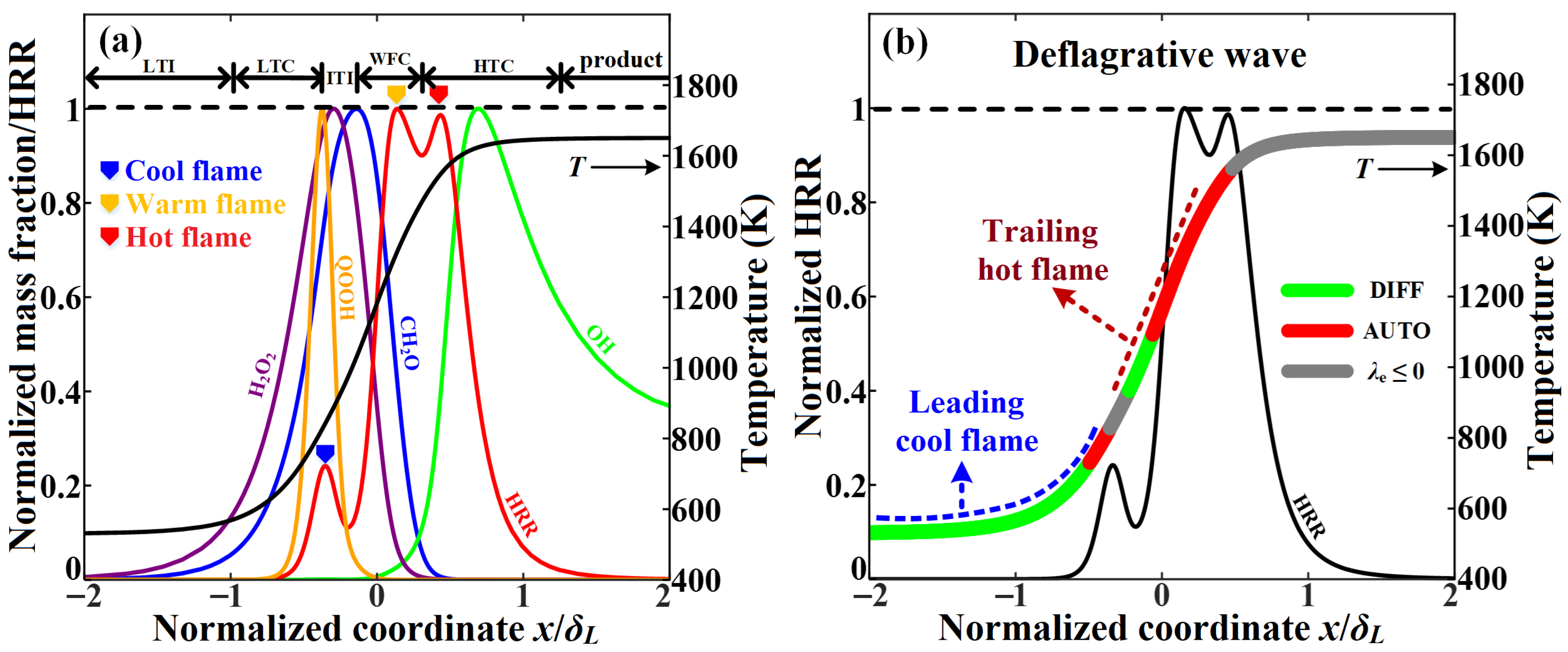
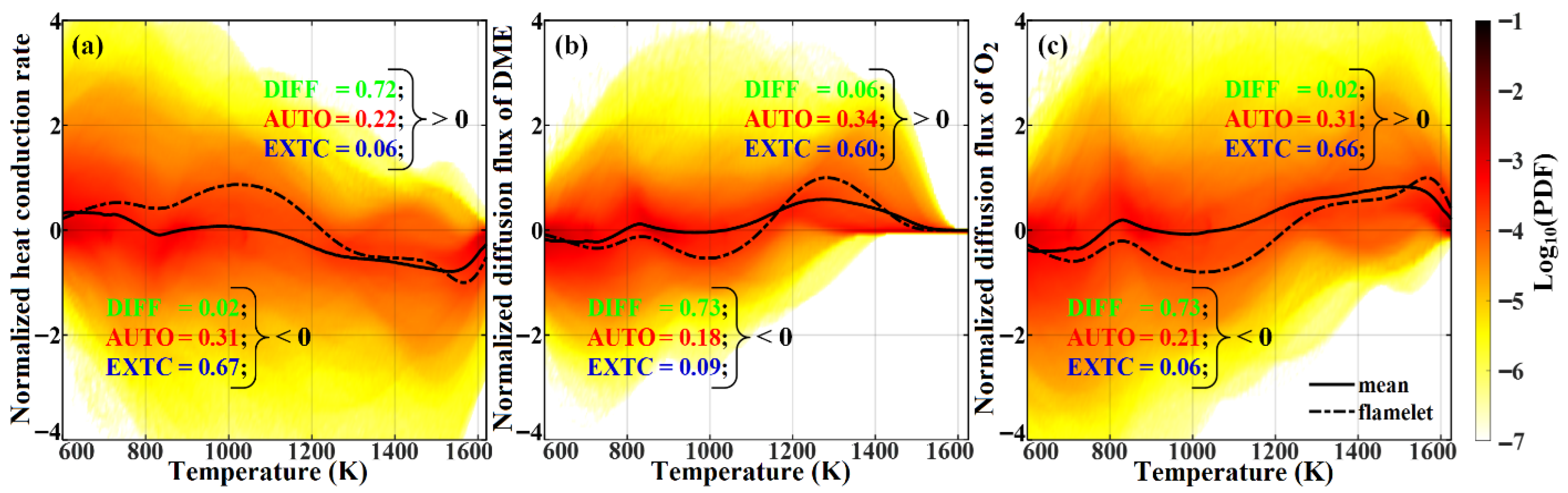
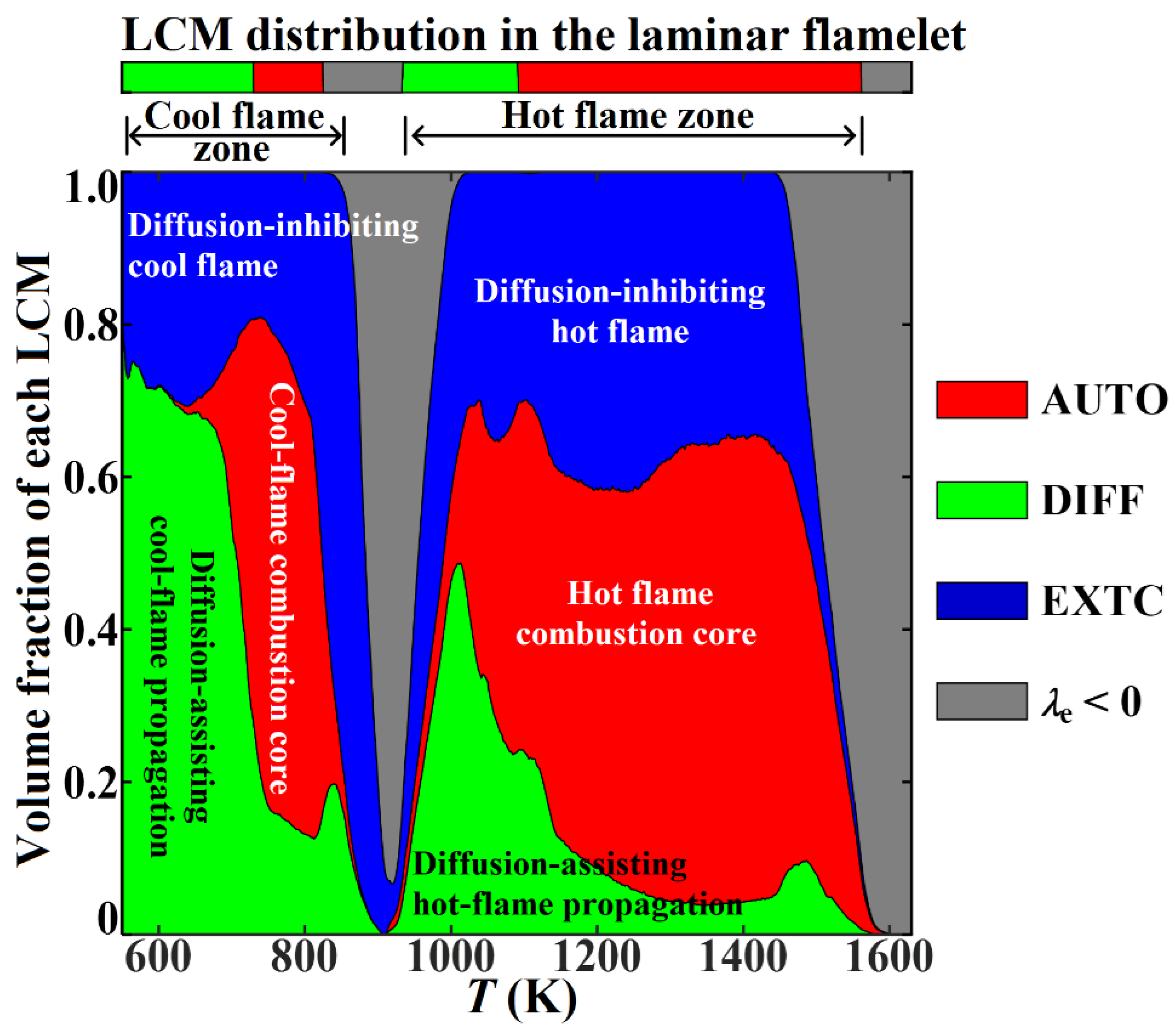
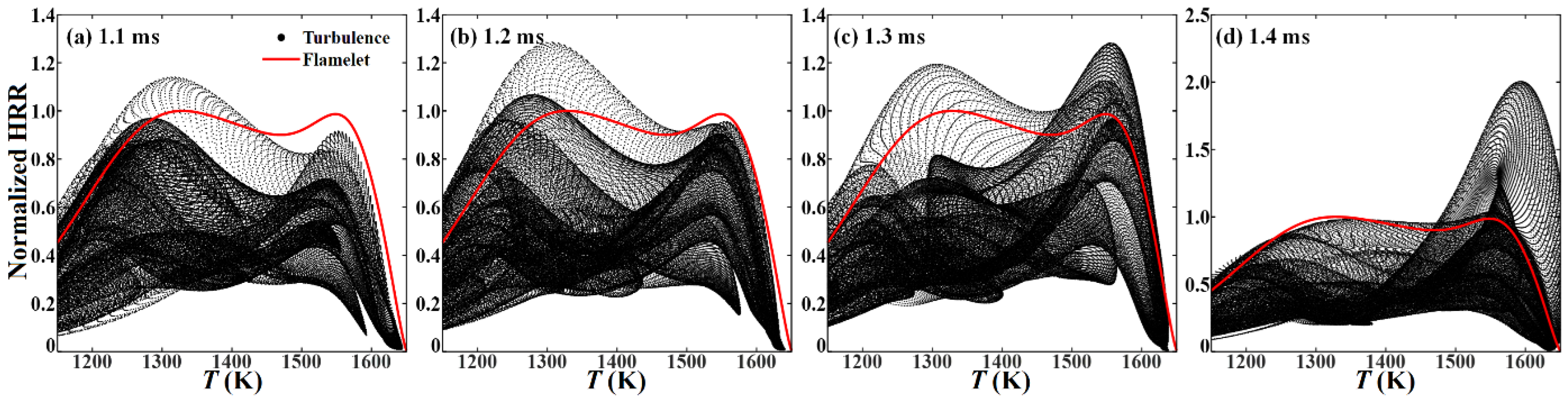
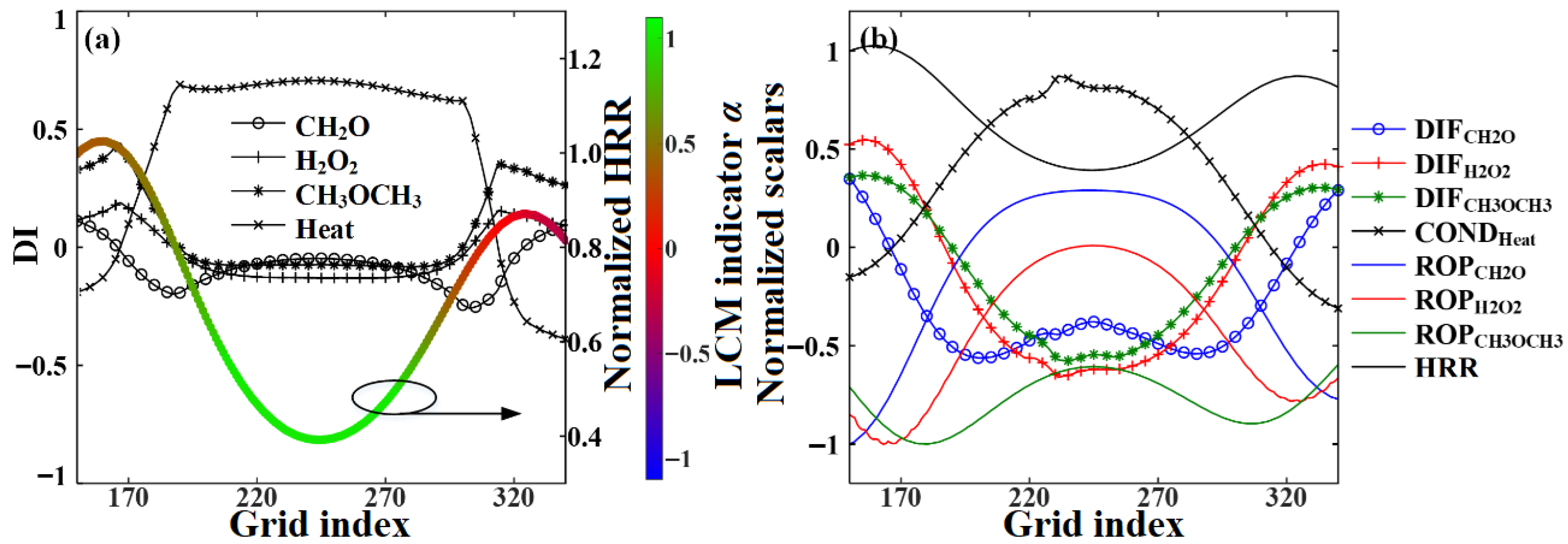
3.1. Flame Structure and Local Combustion Modes in the Laminar Premixed Flamelet
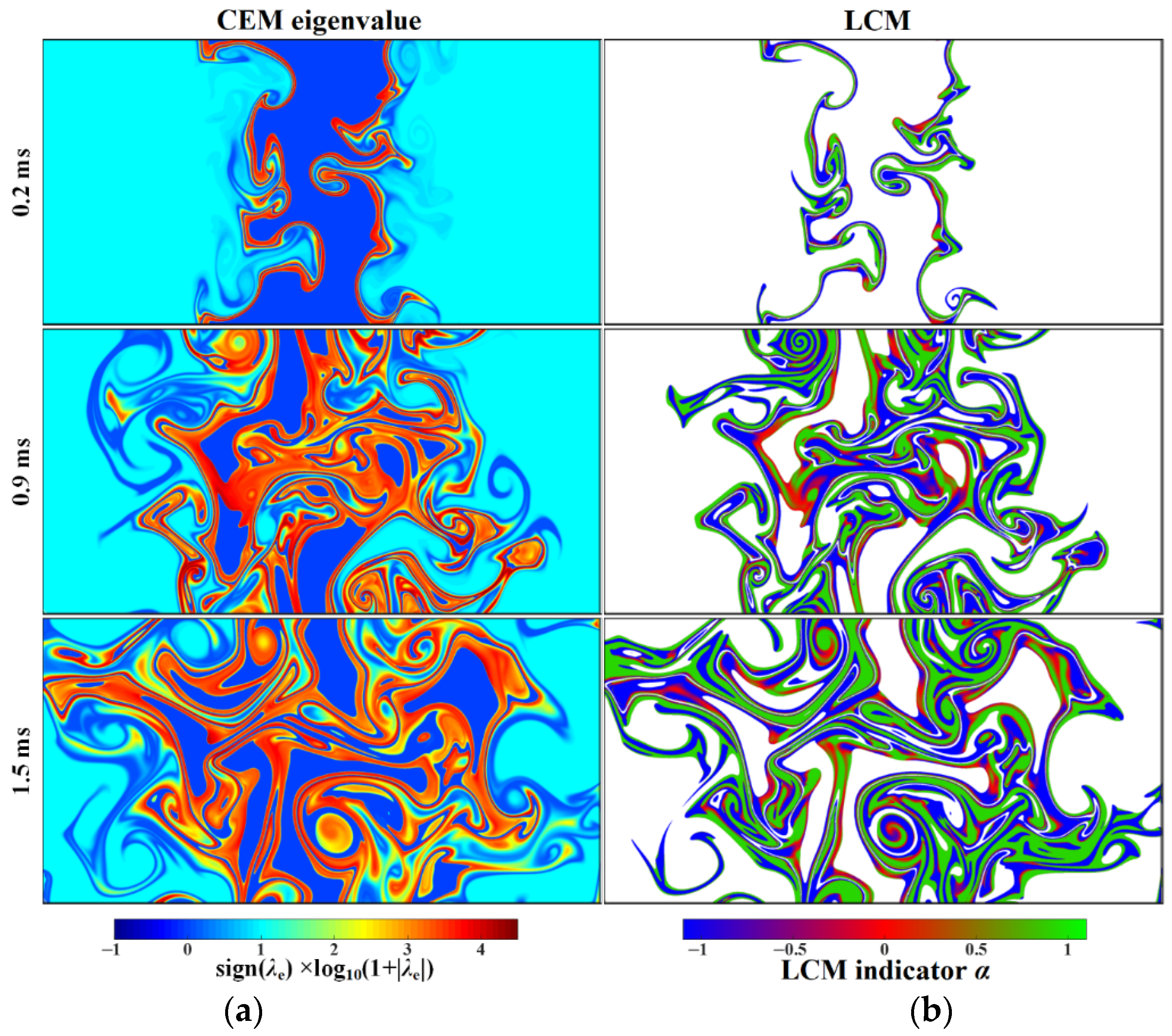
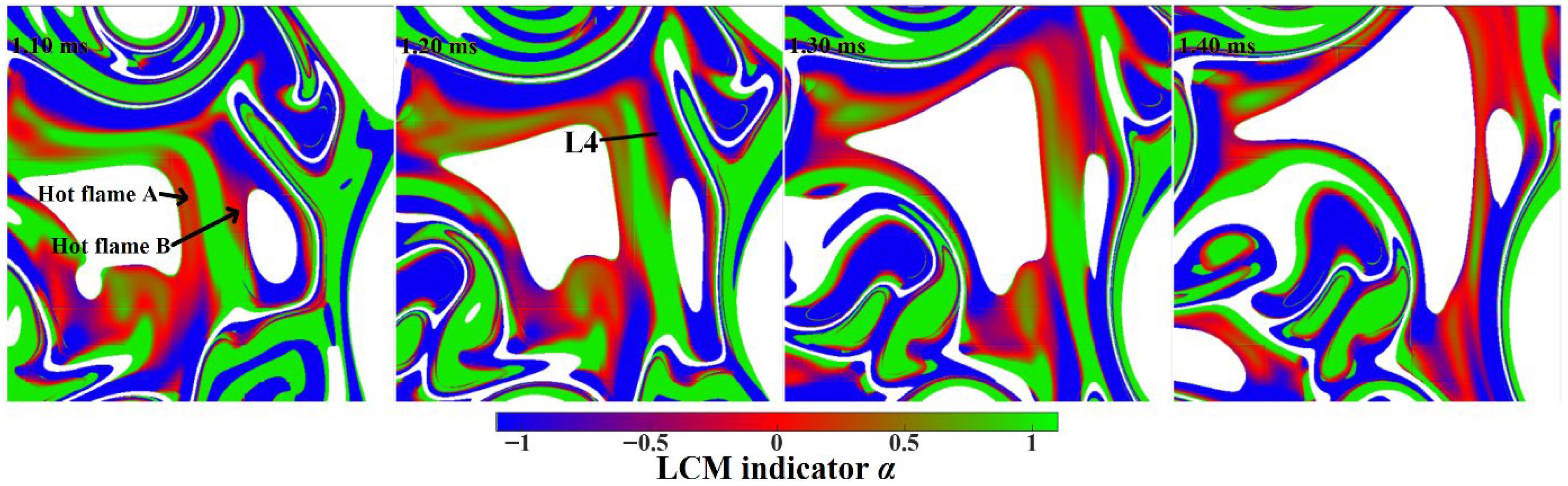
3.2. Flame Surface Topology and Development in the Broken Reaction Zone Regime
- (1)
- Continuous flamelet mode stage (0~0.6 ms): the flame surface kept still connected and retained the basic behaviors of laminar premixed flamelet, although partial segments of the flame surfaces had shown a tendency to be thickened. By 0.3 ms, flame wrinkling/folding generated a few isolated hot pockets that propagated independently in the domain.
- (2)
- Combustion mode transition stage (0.6~0.9 ms): the flame changed from the laminar flamelet structure to the segmented reaction zone regime, and the phenomena of flame folding and surface thickening with generations of isolated propagating pockets became more ubiquitous.
- (3)
- Broken reaction zone mode stage (after 0.9 ms): the flame completely entered the broken reaction zone regime, with distributed flame segments, a remarkably thickened reaction zone, and obvious separation of the cool- and hot-flame fronts, especially at the instances of 1.2 and 1.5 ms.
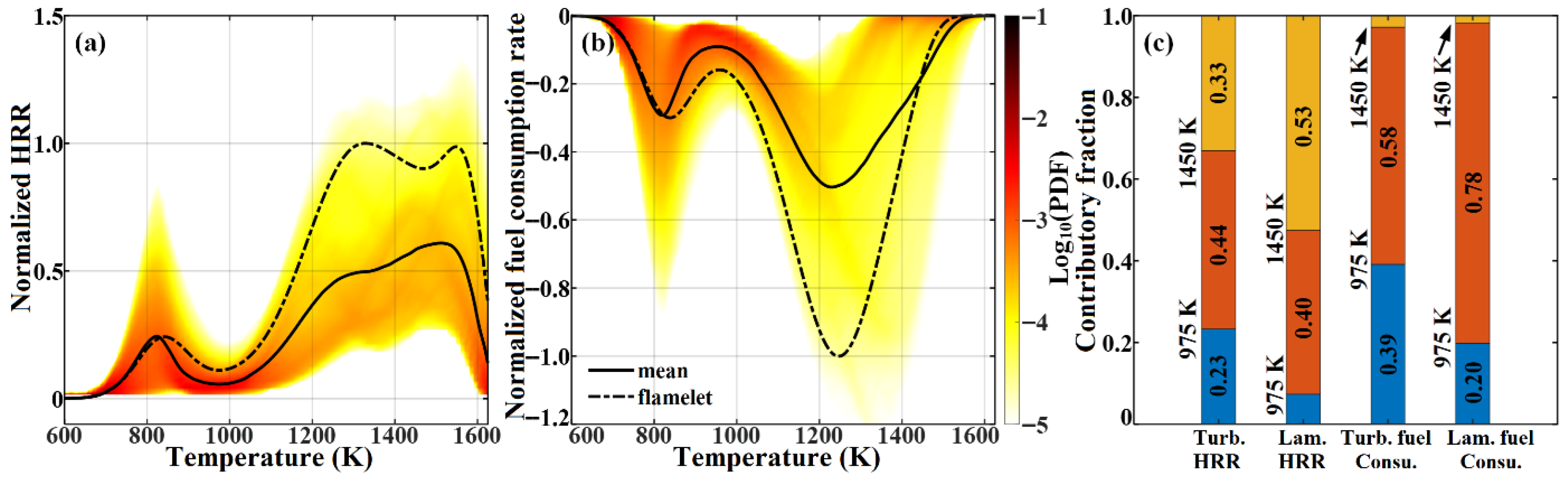
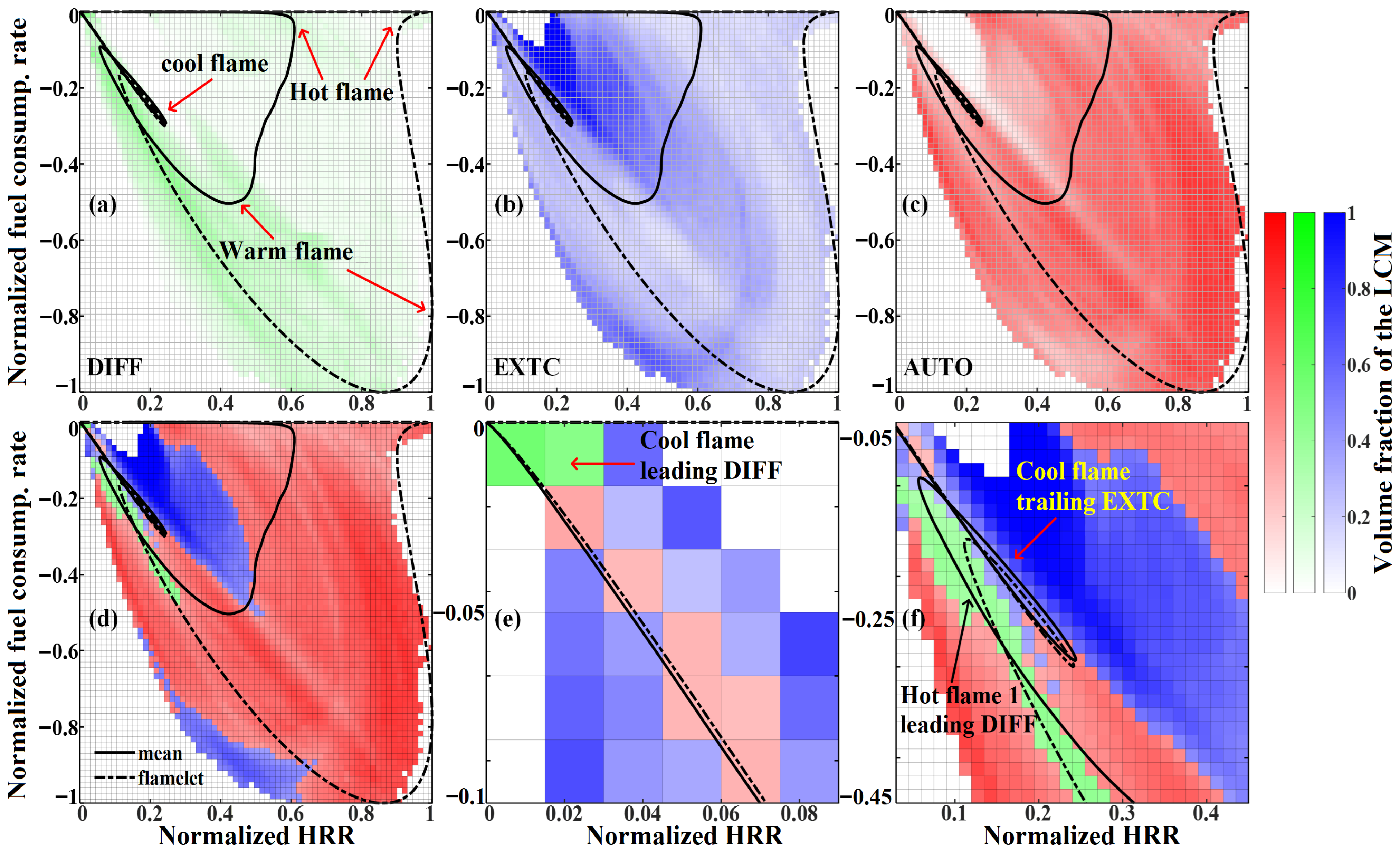
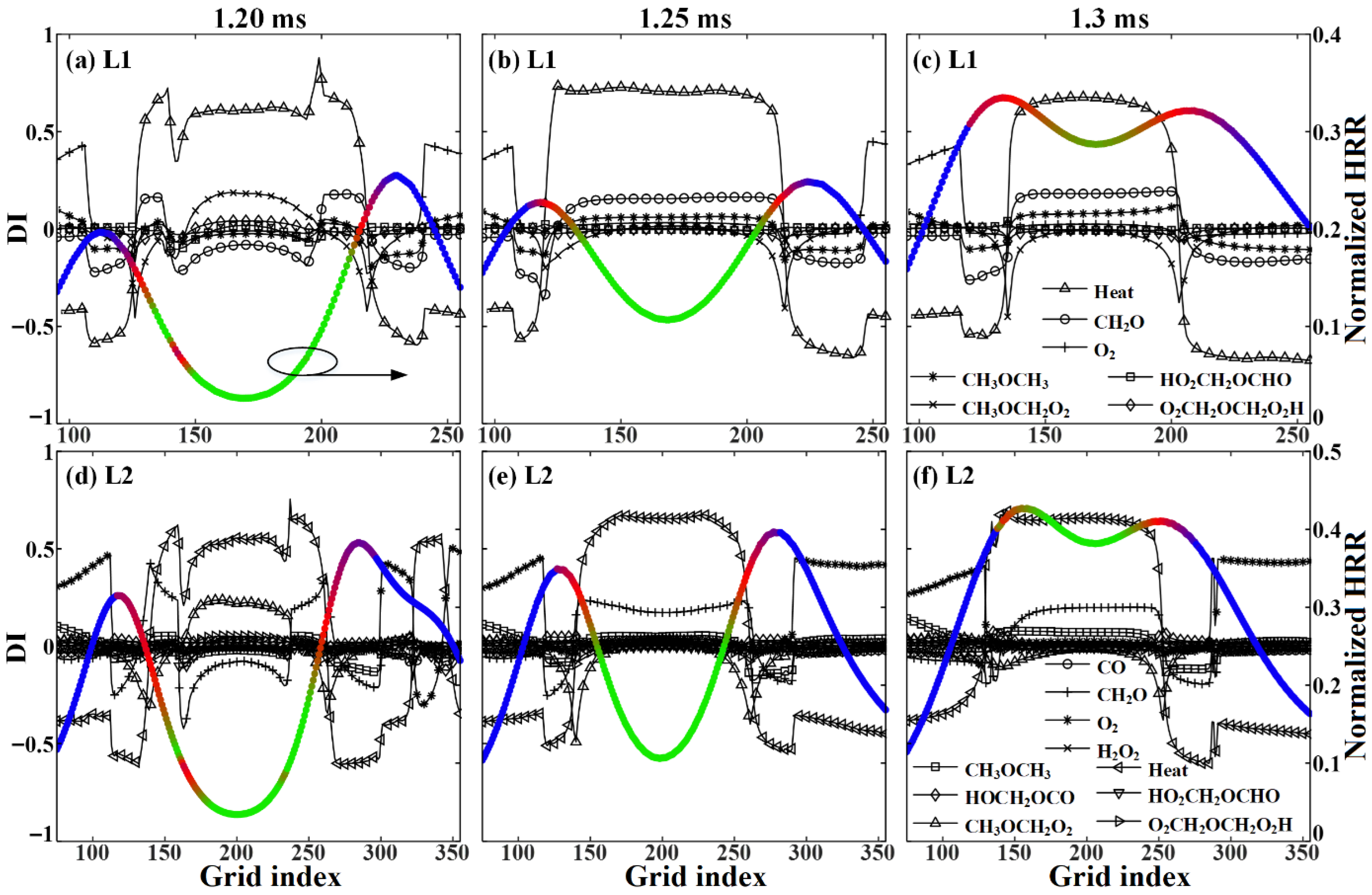
3.3. Local Combustion Modes and Conditional Statistics in the Broken Reaction Zone Regime
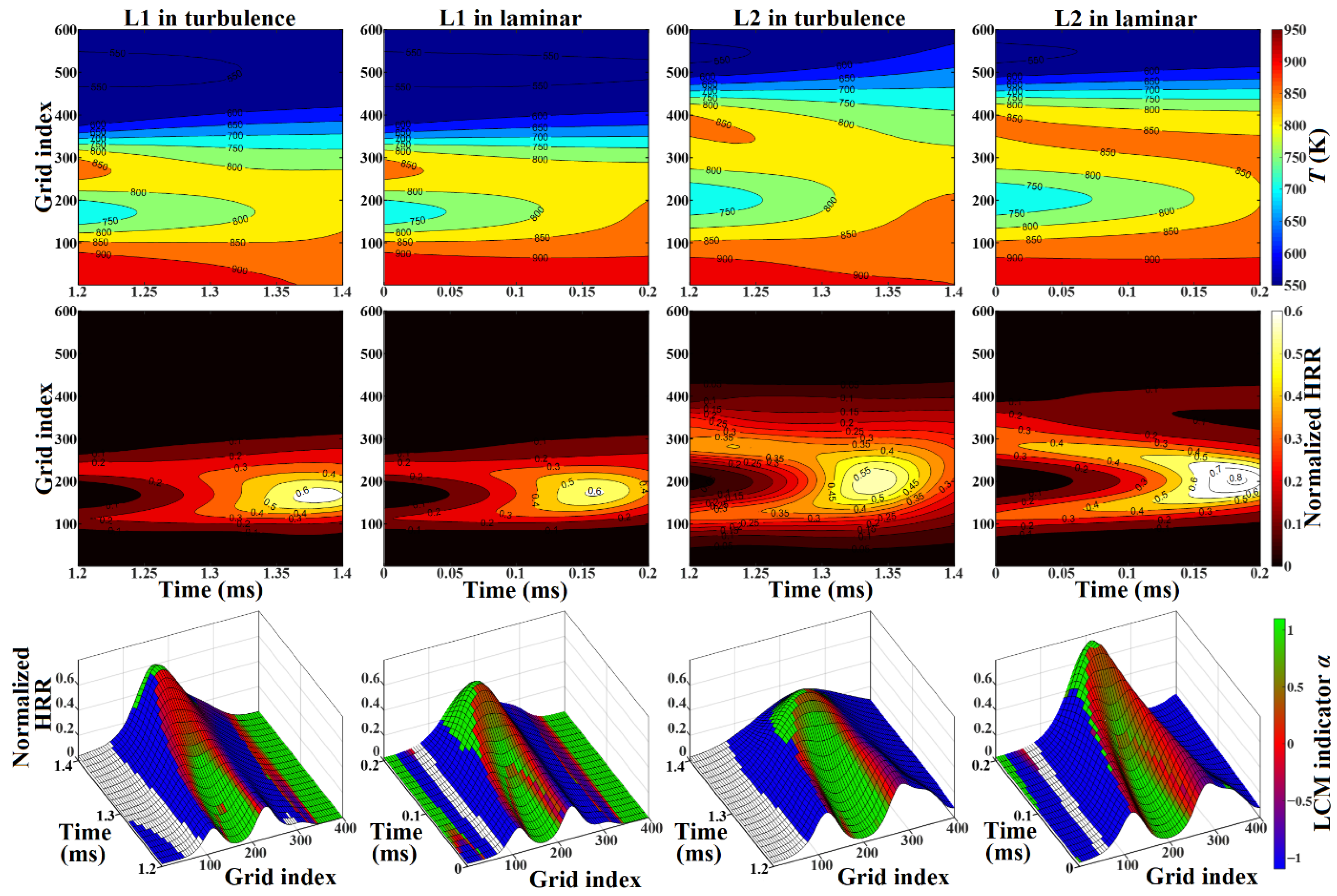
3.4. Dynamical Processes and Diffusive Transport Mechanism in the Broken Reaction Zone Regime
3.4.1. Cool Flame Reaction Enhancement in the Turbulence


| Reaction Index | Chemical Equation | Note |
|---|---|---|
| R9 | H + O2 (+M) = HO2 (+M) | |
| R14 | HO2 + HO2 = H2O2 + O2 | Duplicate reaction |
| R15 | HO2 + HO2 = H2O2 + O2 | Duplicate reaction |
| R27 | HCO + O2 = CO + HO2 | |
| R40 | CH2O + OH = HCO + H2O | |
| R132 | CH3OCH3 + OH = CH3OCH2 + H2O | |
| R151 | CH3OCH2 + O2 = CH3OCH2O2 | |
| R156 | CH3OCH2O2 = CH2OCH2O2H | |
| R157 | CH2OCH2O2H = OH + CH2O + CH2O | |
| R158 | CH2OCH2O2H + O2 = O2CH2OCH2O2H | |
| R159 | O2CH2OCH2O2H = HO2CH2OCHO + OH | |
| R160 | HO2CH2OCHO = OCH2OCHO + OH | |
| R162 | HOCH2OCO = HOCH2O + CO |
3.4.2. Hot Flame Zone Thickening in Turbulence
4. Conclusions
- (1)
- The three-staged combustion, including cool-flame, warm-flame, and hot-flame fronts, is a unique behavior of DME flame under the elevated-pressure, lean-premixed condition. Compared with the laminar flamelet, in the broken reaction zone regime the reacting front structure as well as its inner diffusion processes has changed significantly. The reaction zone thickness increases remarkably, and the HRR and fuel consumption rate in the cool-flame zone are increased by 16% and 19%, respectively. The diffusion effect not only enhances flame propagation, but also suppresses local HRR and fuel consumption.
- (2)
- The strong turbulence interplaying with diffusive transports is the underlying physics for the enhancements in cool- and hot-flame fronts. In the turbulence field with strong flame folding and eddy mixing, it created intermixed reacting fronts with varying progress variables; the heat/radical diffusions, on the other hand, are the intrinsic mechanisms for the formation of flame intensification and thickening phenomenon.
- (3)
- For the cool-flame front, diffusive transports of heat, CH2O, CH3OCH2O2, and CH3OCH3 are of the governing significances for the flame thickening and combustion enhancement. For the hot-flame front, heat conductivity is most dominant, and the diffusions of CH2O, H2O2, and CH3OCH3 are of less importance with an inhabitation impact.
- (4)
- The extreme turbulence transport would induce the separation of cool and hot flame fronts, and evolve to independent freely propagating cool-flame fronts. The strong low-temperature chemistry of DME is responsible for the formation of self-sustaining cool flames, which is supported by diffusions of low-temperature species and heat.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Steinberg, A.M.; Hamlington, P.E.; Zhao, X.Y. Structure and dynamics of highly turbulent premixed combustion. Prog. Energy Combust. Sci. 2021, 85, 100900. [Google Scholar] [CrossRef]
- Skiba, A.W.; Carter, C.D.; Hammack, S.D.; Driscoll, J.F. Premixed flames subjected to extreme levels of turbulence part II: Surface characteristics and scalar dissipation rates. Combust. Flame 2022, 239, 111703. [Google Scholar] [CrossRef]
- Skiba, A.W.; Wabel, T.M.; Carter, C.D.; Hammack, S.D.; Temme, J.E.; Driscoll, J.F. Premixed flames subjected to extreme levels of turbulence part I: Flame structure and a new measured regime diagram. Combust. Flame 2018, 189, 407–432. [Google Scholar] [CrossRef]
- Yuen, F.T.C.; Gülder Ö, L. Turbulent premixed flame front dynamics and implications for limits of flamelet hypothesis. Proc. Combust. Inst. 2013, 34, 1393–1400. [Google Scholar] [CrossRef]
- Tamadonfar, P.; Gülder Ö, L. Experimental investigation of the inner structure of premixed turbulent methane/air flames in the thin reaction zones regime. Combust. Flame 2015, 162, 115–128. [Google Scholar] [CrossRef]
- Seffrin, F.; Fuest, F.; Geyer, D.; Dreizler, A. Flow field studies of a new series of turbulent premixed stratified flames. Combust. Flame 2010, 157, 384–396. [Google Scholar] [CrossRef]
- Schneider, C.; Dreizler, A.; Janicka, J. Fluid dynamical analysis of atmospheric reacting and isothermal swirling flows. Flow Turbul. Combust. 2005, 74, 103–127. [Google Scholar] [CrossRef]
- Li, Z.S.; Li, B.; Sun, Z.W.; Bai, X.S.; Aldén, M. Turbulence and combustion interaction: High resolution local flame front structure visualization using simultaneous single-shot PLIF imaging of CH, OH, and CH2O in a piloted premixed jet flame. Combust. Flame 2010, 157, 1087–1096. [Google Scholar] [CrossRef]
- Zhou, B.; Brackmann, C.; Wang, Z.; Li, Z.; Richter, M.; Aldén, M.; Bai, X.S. Thin reaction zone and distributed reaction zone regimes in turbulent premixed methane/air flames: Scalar distributions and correlations. Combust. Flame 2017, 175, 220–236. [Google Scholar] [CrossRef]
- Zhou, B.; Brackmann, C.; Li, Q.; Wang, Z.; Petersson, P.; Li, Z.; Aldén, M.; Bai, X.S. Distributed reactions in highly turbulent premixed methane/air flames: Part, I. Flame structure characterization. Combust. Flame 2015, 162, 2937–2953. [Google Scholar] [CrossRef]
- Zhou, B.; Brackmann, C.; Li, Z.; Aldén, M.; Bai, X.S. Simultaneous multi-species and temperature visualization of premixed flames in the distributed reaction zone regime. Proc. Combust. Inst. 2015, 35, 1409–1416. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, B.; Yu, S.; Brackmann, C.; Li, Z.; Richter, M.; Aldén, M.; Bai, X.S. Structure and burning velocity of turbulent premixed methane/air jet flames in thin-reaction zone and distributed reaction zone regimes. Proc. Combust. Inst. 2019, 37, 2537–2544. [Google Scholar] [CrossRef]
- Fan, Q.; Liu, X.; Cai, X.; Brackmann, C.; Alden, M.; Bai, X.S.; Li, Z. Structure and scalar correlation of ammonia/air turbulent premixed flames in the distributed reaction zone regime. Combust. Flame 2022, 241, 112090. [Google Scholar] [CrossRef]
- Chen, J.H.; Choudhary, A.; De Supinski, B.; DeVries, M.; Hawkes, E.R.; Klasky, S.; Liao, W.K.; Ma, K.L.; Mellor-Crummey, J.; Podhorszki, N.; et al. Terascale direct numerical simulations of turbulent combustion using S3D. Comput. Sci. Discov. 2009, 2, 015001. [Google Scholar] [CrossRef]
- Lu, T.F.; Yoo, C.S.; Chen, J.H.; Law, C.K. Three-dimensional direct numerical simulation of a turbulent lifted hydrogen jet flame in heated coflow: A chemical explosive mode analysis. J. Fluid Mech. 2010, 652, 45–64. [Google Scholar] [CrossRef]
- Yoo, C.S.; Lu, T.; Chen, J.H.; Law, C.K. Direct numerical simulations of ignition of a lean n-heptane/air mixture with temperature inhomogeneities at constant volume: Parametric study. Combust. Flame 2011, 158, 1727–1741. [Google Scholar] [CrossRef]
- Luong, M.B.; Luo, Z.; Lu, T.; Chung, S.H.; Yoo, C.S. Direct numerical simulations of the ignition of lean primary reference fuel/air mixtures with temperature inhomogeneities. Combust. Flame 2013, 160, 2038–2047. [Google Scholar] [CrossRef]
- Lecoustre, V.R.; Arias, P.G.; Roy, S.P.; Luo, Z.; Haworth, D.C.; Im, H.G.; Lu, T.F.; Trouvé, A. Direct numerical simulations of non-premixed ethylene–air flames: Local flame extinction criterion. Combust. Flame 2014, 161, 2933–2950. [Google Scholar] [CrossRef][Green Version]
- Krisman, A.; Hawkes, E.R.; Talei, M.; Bhagatwala, A.; Chen, J.H. Characterisation of twostage ignition in diesel engine-relevant thermochemical conditions using direct numerical simulation. Combust. Flame 2016, 172, 326–341. [Google Scholar] [CrossRef]
- Krisman, A.; Hawkes, E.R.; Talei, M.; Bhagatwala, A.; Chen, J.H. A direct numerical simulation of cool-flame affected autoignition in diesel engine-relevant conditions. Proc. Combust. Inst. 2017, 36, 3567–3575. [Google Scholar] [CrossRef]
- Aspden, A.J.; Day, M.S.; Bell, J.B. Turbulence-flame interactions in lean premixed hydrogen: Transition to the distributed burning regime. J. Fluid Mech. 2011, 680, 287–320. [Google Scholar] [CrossRef]
- Aspden, A.J.; Day, M.S.; Bell, J.B. Lewis number effects in distributed flames. Proc. Combust. Inst. 2011, 33, 1473–1480. [Google Scholar] [CrossRef]
- Xu, C.; Poludnenko, A.Y.; Zhao, X.; Wang, H.; Lu, T. Structure of strongly turbulent premixed n-dodecane–air flames: Direct numerical simulations and chemical explosive mode analysis. Combust. Flame 2019, 209, 27–40. [Google Scholar] [CrossRef]
- Xu, C.; Park, J.W.; Yoo, C.S.; Chen, J.H.; Lu, T. Identification of premixed flame propagation modes using chemical explosive mode analysis. Proc. Combust. Inst. 2019, 37, 2407–2415. [Google Scholar] [CrossRef]
- Poludnenko, A.Y.; Oran, E.S. The interaction of high-speed turbulence with flames: Turbulent flame speed. Combust. Flame 2011, 158, 301–326. [Google Scholar] [CrossRef]
- Poludnenko, A.Y.; Oran, E.S. The interaction of high-speed turbulence with flames: Global properties and internal flame structure. Combust. Flame 2010, 157, 995–1011. [Google Scholar] [CrossRef]
- Bhagatwala, A.; Luo, Z.; Shen, H.; Sutton, J.A.; Lu, T.; Chen, J.H. Numerical and experimental investigation of turbulent DME jet flames. Proc. Combust. Inst. 2015, 35, 1157–1166. [Google Scholar] [CrossRef]
- Zhao, Z.; Chaos, M.; Kazakov, A.; Dryer, F.L. Thermal decomposition reaction and a comprehensive kinetic model of dimethyl ether. Int. J. Chem. Kinet. 2008, 40, 1–18. [Google Scholar] [CrossRef]
- Lu, T.F.; Law, C.K. On the applicability of directed relation graphs to the reduction of reaction mechanisms. Combust. Flame 2006, 146, 472–483. [Google Scholar] [CrossRef]
- Su, L.; Zhang, M.; Wang, J.; Huang, Z. Direct numerical simulation of DME auto-ignition with temperature and composition stratification under HCCI engine conditions. Fuel 2021, 285, 119073. [Google Scholar] [CrossRef]
- Minamoto, Y.; Chen, J.H. DNS of a turbulent lifted DME jet flame. Combust. Flame 2016, 169, 38–50. [Google Scholar] [CrossRef]
- Kang, Y.; Xu, X.; Tan, L.; Huang, X.; Zhang, Y.; Zeng, T.; Luo, J.; Lu, X. Combustion mechanism of ammonia and ammonia-hydrogen mixtures in the intensely turbulent jet mixing layer under the spontaneous ignition condition. Int. J. Hydrogen Energy 2024, 59, 1335–1351. [Google Scholar] [CrossRef]
- Driscoll, J.F.; Chen, J.H.; Skiba, A.W.; Carter, C.D.; Hawkes, E.R.; Wang, H. Premixed flames subjected to extreme turbulence: Some questions and recent answers. Prog. Energy Combust. Sci. 2020, 76, 100802. [Google Scholar] [CrossRef]
- Ju, Y.G. Understanding cool flames and warm flames. Proc. Combust. Inst. 2021, 38, 83–119. [Google Scholar] [CrossRef]
- Ju, Y.; Reuter, C.B.; Yehia, O.R.; Farouk, T.I.; Won, S.H. Dynamics of cool flames. Prog. Energy Combust. Sci. 2019, 75, 100787. [Google Scholar] [CrossRef]
- Cheatham, S.; Matalon, M. A general asymptotic theory of diffusion flames with application to cellular instability. J. Fluid Mech. 2000, 414, 105–144. [Google Scholar] [CrossRef]
- Hamlington, P.E.; Darragh, R.; Briner, C.A.; Towery, C.A.; Taylor, B.D.; Poludnenko, A.Y. Lagrangian analysis of high-speed turbulent premixed reacting flows: Thermochemical trajectories in hydrogen–air flames. Combust. Flame 2017, 186, 193–207. [Google Scholar] [CrossRef]
- Zhang, Y.; Kang, Y.H.; Lu, X.F.; Wang, Q.H. Numerical study on oscillatory propagation dynamics and physics near the limits of planar freely propagating premixed flames. Phys. Fluids 2021, 33, 083602. [Google Scholar] [CrossRef]
- Pitz, R.W.; Hu, S.; Wang, P. Tubular premixed and diffusion flames: Effect of stretch and curvature. Prog. Energy Combust. Sci. 2014, 42, 1–34. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Kang, Y.; Huang, X.; Zhang, P.; Tang, X. DNS Study of Freely Propagating Turbulent Lean-Premixed Flames with Low-Temperature Chemistry in the Broken Reaction Zone Regime. Energies 2025, 18, 4357. https://doi.org/10.3390/en18164357
Zhang Y, Kang Y, Huang X, Zhang P, Tang X. DNS Study of Freely Propagating Turbulent Lean-Premixed Flames with Low-Temperature Chemistry in the Broken Reaction Zone Regime. Energies. 2025; 18(16):4357. https://doi.org/10.3390/en18164357
Chicago/Turabian StyleZhang, Yi, Yinhu Kang, Xiaomei Huang, Pengyuan Zhang, and Xiaolin Tang. 2025. "DNS Study of Freely Propagating Turbulent Lean-Premixed Flames with Low-Temperature Chemistry in the Broken Reaction Zone Regime" Energies 18, no. 16: 4357. https://doi.org/10.3390/en18164357
APA StyleZhang, Y., Kang, Y., Huang, X., Zhang, P., & Tang, X. (2025). DNS Study of Freely Propagating Turbulent Lean-Premixed Flames with Low-Temperature Chemistry in the Broken Reaction Zone Regime. Energies, 18(16), 4357. https://doi.org/10.3390/en18164357








