Numerical Study on Hydrodynamic Performances of Novel Dual-Layer Flower-Shaped Heave Plates of a Floating Offshore Wind Turbine
Abstract
1. Introduction
2. Methodologies
2.1. Governing Equations
2.2. Forced Oscillation and Overset Mesh Technique
2.3. Hydrodynamic Coefficients
3. Computational Settings
3.1. Computational Domain and Boundary Conditions
3.2. Mesh Generation
4. Verification and Validation Studies
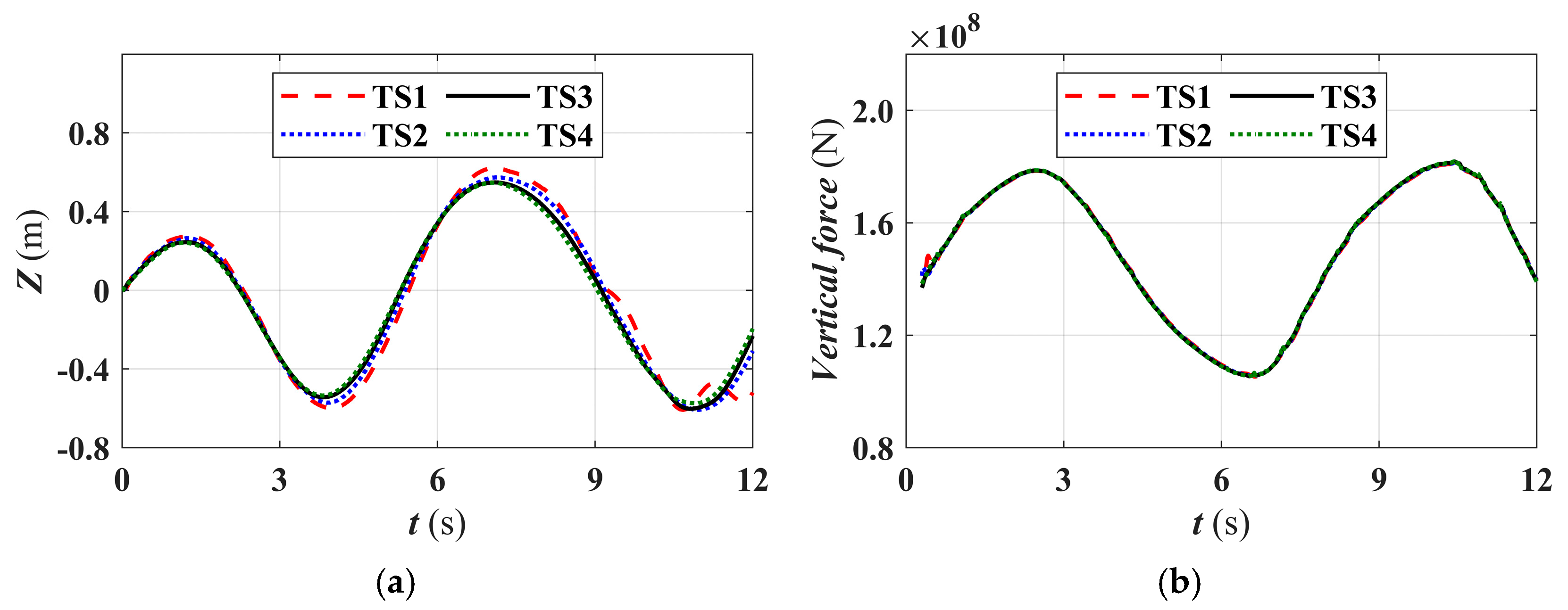
4.1. Mesh and Time Step Sensitivity Studies
4.2. Validation Studies
5. Results and Discussions
5.1. Vertical Force and Hydrodynamic Coefficients
5.2. Radiated Waves Due to Heave Motion
5.3. Local Flow Fields Adjacent to Heave Plates
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- GWEC. Global Wind Report 2023; GWEC: Brussels, Belgium, 2023. [Google Scholar]
- Zhang, J.H.; Wang, H. Development of offshore wind power and foundation technology for offshore wind turbines in China. Ocean Eng. 2022, 266, 113256. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, W.; Li, D.; Li, X.; Duan, Y.; Verma, A.S. A novel framework for modeling floating offshore wind turbines based on the vector form intrinsic finite element (VFIFE) method. Ocean Eng. 2022, 262, 112221. [Google Scholar] [CrossRef]
- Jiang, H.-R.; Bai, X.-L.; Vaz, M.A. Aero-hydrodynamic coupled dynamic characteristics of semi-submersible floating offshore wind turbines under inflow turbulence. China Ocean Eng. 2023, 37, 660–672. [Google Scholar] [CrossRef]
- Han, Y.-Q.; Le, C.-H.; Zhang, P.-Y.; Dang, L.; Fan, Q.-L. Stochastic analysis of short-term structural responses and fatigue damages of a submerged tension leg platform wind turbine in wind and waves. China Ocean Eng. 2021, 35, 566–577. [Google Scholar] [CrossRef]
- Meng, L.; He, Y.-P.; Zhao, Y.-S.; Yang, J.; Yang, H.; Han, Z.-L.; Yu, L.; Mao, W.-G.; Du, W.-K. Dynamic response of 6MW spar type floating offshore wind turbine by experiment and numerical analyses. China Ocean Eng. 2020, 34, 608–620. [Google Scholar] [CrossRef]
- Liu, Q.-S.; Miao, W.-P.; Yue, M.-N.; Li, C.; Wang, B.; Ding, Q. Dynamic response of offshore wind turbine on 3×3 barge array floating platform under extreme sea conditions. China Ocean Eng. 2021, 35, 186–200. [Google Scholar] [CrossRef]
- Chen, X.; Jiang, Z.; Li, Q.; Li, Y.; Ren, N. Extended environmental contour methods for long-term extreme response analysis of offshore wind turbines. J. Offshore Mech. Arct. Eng. 2020, 142, 052003. [Google Scholar] [CrossRef]
- Mello, P.C.; Malta, E.B.; da Silva, R.O.P.; Candido, M.H.O.; Carmo, L.H.S.D.; Alberto, I.F.; Franzini, G.R.; Simos, A.N.; Suzuki, H.; Gonçalves, R.T. Influence of heave plates on the dynamics of a floating offshore wind turbine in waves. J. Mar. Sci. Technol. 2021, 26, 190–200. [Google Scholar] [CrossRef]
- Tao, L.B.; Dray, D. Hydrodynamic performance of solid and porous heave plates. Ocean Eng. 2008, 35, 1006–1014. [Google Scholar] [CrossRef]
- Li, J.; Liu, S.; Zhao, M.; Teng, B. Experimental investigation of the hydrodynamic characteristics of heave plates using forced oscillation. Ocean Eng. 2013, 66, 82–91. [Google Scholar] [CrossRef]
- Thiagarajan, K.; Moreno, J. Wave induced effects on the hydrodynamic coefficients of an oscillating heave plate in offshore wind turbines. J. Mar. Sci. Eng. 2020, 8, 622. [Google Scholar] [CrossRef]
- Ezoji, M.; Shabakhty, N.; Tao, L.B. Hydrodynamic damping of solid and perforated heave plates oscillating at low KC number based on experimental data: A review. Ocean Eng. 2022, 253, 111247. [Google Scholar] [CrossRef]
- Tao, L.; Molin, B.; Scolan, Y.-M.; Thiagarajan, K. Spacing effects on hydrodynamics of heave plates on offshore structures. J. Fluids Struct. 2007, 23, 1119–1136. [Google Scholar] [CrossRef]
- Garrido-Mendoza, C.A.; Thiagarajan, K.P.; Souto-Iglesias, A.; Colagrossi, A.; Bouscasse, B. Computation of flow features and hydrodynamic coefficients around heave plates oscillating near a seabed. J. Fluids Struct. 2015, 59, 406–431. [Google Scholar] [CrossRef]
- Wang, B.; Xu, Z.; Li, C.; Wang, D.; Ding, Q. Hydrodynamic characteristics of forced oscillation of heave plate with fractal characteristics based on floating wind turbine platform. Ocean Eng. 2020, 212, 107621. [Google Scholar] [CrossRef]
- Zhang, S.N.; Ishihara, T. Numerical study of distributed hydrodynamic forces on a circular heave plate by large-eddy simulations with volume of fluid method. Ships Offshore Struct. 2020, 15, 574–586. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, C.; Jia, P.; Lu, Z.; Xie, Y. Numerical simulation and experimental study on perforated heave plate of a DeepCwind floating wind turbine platform. Ships Offshore Struct. 2023, 18, 438–449. [Google Scholar] [CrossRef]
- Shen, W.-J.; Tang, Y.-G.; Liu, L.-Q. Research on the hydrodynamic characteristics of heave plate structure with different form edges of a Spar platform. China Ocean Eng. 2012, 26, 177–184. [Google Scholar] [CrossRef]
- Tian, X.; Yang, J.; Li, X.; Peng, T. Experimental investigations on the hydrodynamic characteristics of heave plate. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Nantes, France, 9–14 June 2013; p. 10437. [Google Scholar]
- Tian, X.L.; Tao, L.; Li, X.; Yang, J. Hydrodynamic coefficients of oscillating flat plates at 0.15 ≤KC≤3.15. J. Mar. Sci. Technol. 2017, 22, 101–113. [Google Scholar] [CrossRef]
- Rusch, C.J.; Hartman, A.R.; Maurer, B.D.; Polagye, B.L. Influence of heave plate topology on reaction force. Ocean Eng. 2021, 241, 110054. [Google Scholar] [CrossRef]
- Zhang, L.; Shi, W.; Zeng, Y.; Michailides, C.; Zheng, S.; Li, Y. Experimental investigation on the hydrodynamic effects of heave plates used in floating offshore wind turbines. Ocean Eng. 2023, 267, 113103. [Google Scholar] [CrossRef]
- Chen, J.H.; Yin, Z.W.; Zhu, R.K.; Ma, Z.; Jing, X.; Li, Y. Design and research on damping structure of floating offshore wind turbine platform. South. Energy Constr. 2021, 8, 18–25. [Google Scholar]
- Manuel, A.M.; Vera, E.B.; Saettone, S.; Calderon-Sanchez, J.; Bulian, G.; Souto-Iglesias, A. Hydrodynamic coefficients from forced and decay heave motion tests of a scaled model of a column of a floating wind turbine equipped with a heave plate. Ocean. Eng. 2022, 252, 110985. [Google Scholar] [CrossRef]
- Saettone, S.; Fernandez, E.M.; Gomez, C.S.; Ynocente, L.A.S.; Campayo, D.D.; Souto-Iglesias, A.; Loureiro, A.M. A particle image velocimetry investigation of the flow field close to a heave plate for models of different scales. Appl. Ocean Res. 2022, 129, 103387. [Google Scholar] [CrossRef]
- Hegde, P.; Nallayarasu, S. Investigation of heave damping characteristics of buoy form spar with heave plate near the free surface using CFD validated by experiments. Ships Offshore Struct. 2023, 18, 1650–1667. [Google Scholar] [CrossRef]
- Philip, N.T.; Nallayarasu, S.; Bhattacharyya, S.K. Experimental investigation and CFD simulation of heave damping effects due to circular plates attached to spar hull. Ships Offshore Struct. 2019, 14, 396–411. [Google Scholar] [CrossRef]
- Jiang, Y.C.; Hu, G.Q.; Zong, Z.; Zou, L.; Jin, G. Influence of an integral heave plate on the dynamic response of floating offshore wind turbine under operational and storm conditions. Energies 2020, 13, 6122. [Google Scholar] [CrossRef]
- Robertson, A.; Jonkman, J.; Masciola, M.; Song, H.; Goupee, A.; Coulling, A.; Luan, C. Definition of the Semisubmersible Floating System for Phase II of OC4[R/OL]; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2014. [Google Scholar]
- Rao, M.J.; Nallayarasu, S.; Bhattacharyya, S.K. Numerical and experimental studies of heave damping and added mass of spar with heave plates using forced oscillation. Appl. Ocean Res. 2021, 111, 102667. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Pinguet, R.; Benoit, M.; Molin, B.; Rezende, F. CFD analysis of added mass, damping and induced flow of isolated and cylinder-mounted heave plates at various submergence depths using an overset mesh method. J. Fluids Struct. 2022, 109, 103442. [Google Scholar] [CrossRef]
- Chen, J.H. Study on the Rigid-Flexible Coupled Multi-Body Dynamics and the Characteristics of Floating Offshore Wind Turbines; Shanghai Jiao Tong University: Shanghai, China, 2018. [Google Scholar]
- Subbulakshmi, A.; Sundaravadivelu, R. Heave damping of spar platform for offshore wind turbine with heave plate. Ocean Eng. 2016, 121, 24–36. [Google Scholar] [CrossRef]















| Time Step | (m) | |
|---|---|---|
| TS1 | 0.6223 | - |
| TS2 | 0.5741 | 7.735% |
| TS3 | 0.5486 | 4.450% |
| TS4 | 0.5471 | 0.003% |
| Type of the Motion | Damping Coefficient |
|---|---|
| Free decay (STAR-CCM+) | 0.0440 |
| Free decay (DARwind) | 0.0389 |
| Forced oscillation (STAR-CCM+) | 0.0400 |
| Types of Heave Plates | Number of Petals | Spacing of the Two Layers (m) | |
|---|---|---|---|
| Without heave plates | - | - | 20.69° |
| Circular type | - | 0.3 | 28.63° |
| Flower-shaped Aligned type | 3 | 0.3 | 26.56° |
| Flower-shaped Aligned type | 6 | 0.3 | 25.21° |
| Flower-shaped Aligned type | 9 | 0.3 | 26.00° |
| Flower-shaped Staggered type | 3 | 0.3 | 29.82° |
| Flower-shaped Staggered type | 6 | 0.3 | 31.43° |
| Flower-shaped Staggered type | 9 | 0.3 | 31.19° |
| Flower-shaped Staggered type | 3 | 5.9 | 29.82° |
| Types of Heave Plates | Number of Petals | Spacing of the Two Layers (m) | ||
|---|---|---|---|---|
| Without heave plates | - | - | 3.5027 × 106 | 1.1074 × 107 |
| Circular type | - | 0.3 | 1.0388 × 107 | 2.2719 × 107 |
| Flower-shaped Aligned type | 3 | 0.3 | 9.3816 × 106 | 2.2405 × 107 |
| Flower-shaped Aligned type | 6 | 0.3 | 8.6621 × 106 | 2.1974 × 107 |
| Flower-shaped Aligned type | 9 | 0.3 | 8.8397 × 106 | 2.1639 × 107 |
| Flower-shaped Staggered type | 3 | 0.3 | 1.3557 × 107 | 2.8231 × 107 |
| Flower-shaped Staggered type | 6 | 0.3 | 1.3156 × 107 | 2.5699 × 107 |
| Flower-shaped Staggered type | 9 | 0.3 | 1.2498 × 107 | 2.4646 × 107 |
| Flower-shaped Staggered type | 3 | 5.9 | 1.3796 × 107 | 3.1857 × 107 |
| Types of Heave Plates (Spacing = 0.3 m) | Number of Petals | Amplitude (m/s) |
|---|---|---|
| Circular type | - | 1.3232 |
| Flower-shaped Aligned type | 3 | 1.3222 |
| Flower-shaped Aligned type | 6 | 1.3155 |
| Flower-shaped Aligned type | 9 | 1.3174 |
| Flower-shaped Staggered type | 3 | 1.3948 |
| Flower-shaped Staggered type | 6 | 1.4101 |
| Flower-shaped Staggered type | 9 | 1.4282 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zha, R.; Liang, J.; Chen, J.; Wu, X.; Li, X.; Liang, Z. Numerical Study on Hydrodynamic Performances of Novel Dual-Layer Flower-Shaped Heave Plates of a Floating Offshore Wind Turbine. Energies 2025, 18, 4304. https://doi.org/10.3390/en18164304
Zha R, Liang J, Chen J, Wu X, Li X, Liang Z. Numerical Study on Hydrodynamic Performances of Novel Dual-Layer Flower-Shaped Heave Plates of a Floating Offshore Wind Turbine. Energies. 2025; 18(16):4304. https://doi.org/10.3390/en18164304
Chicago/Turabian StyleZha, Ruosi, Junwen Liang, Jiahao Chen, Xiaodi Wu, Xiaotian Li, and Zebin Liang. 2025. "Numerical Study on Hydrodynamic Performances of Novel Dual-Layer Flower-Shaped Heave Plates of a Floating Offshore Wind Turbine" Energies 18, no. 16: 4304. https://doi.org/10.3390/en18164304
APA StyleZha, R., Liang, J., Chen, J., Wu, X., Li, X., & Liang, Z. (2025). Numerical Study on Hydrodynamic Performances of Novel Dual-Layer Flower-Shaped Heave Plates of a Floating Offshore Wind Turbine. Energies, 18(16), 4304. https://doi.org/10.3390/en18164304







