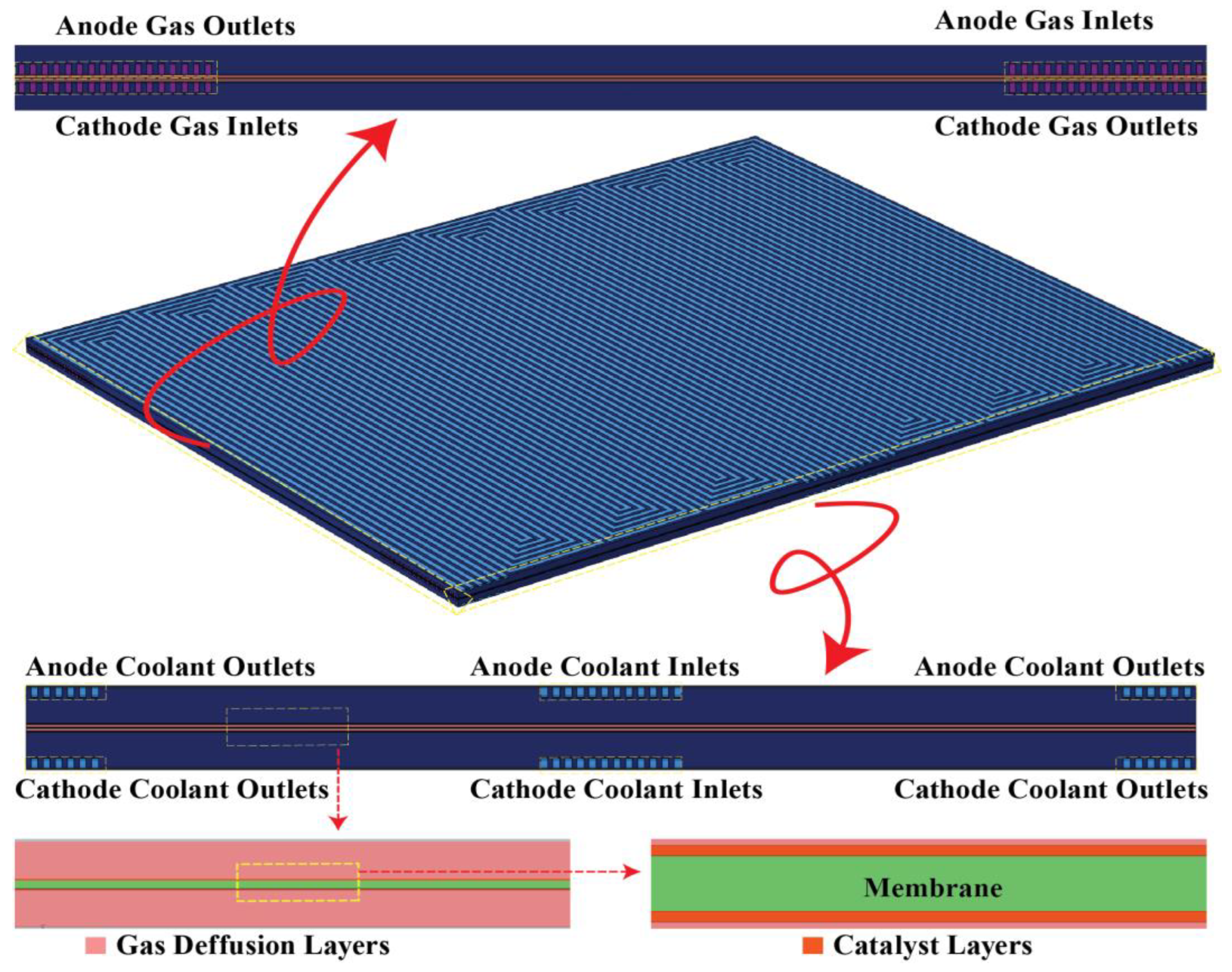
1. Introduction and Literature Review
Global demographic expansion, exponentially increasing energy demands, and anthropogenic climate challenges, including rising emissions and air pollution, demand a paradigm shift from carbon-intensive energy systems to clean, green, and sustainable energy solutions. As the global population is expected to surpass 8.9 billion by 2035, this will require additional energy resources to meet the needs of almost 720 million more individuals [
1]. The current power generation system is the biggest contributor to global pollution, as the share of renewable energy in the electrical sector is only 30%. However, it remains challenging to expand the scope of renewable energy in other sectors, such as heating and transportation [
2]. Therefore, this emphasizes the need for a clean, green, and sustainable energy solution to not only meet increasing energy demands but also contribute to achieving the goal of net-zero emissions by the middle of the century, set by the major economies of the world.
In recent years, PEMFCs have emerged as a highly promising and sustainable technology for clean energy generation as they offer a much higher energy density than conventional energy resources (gasoline/diesel) and even traditional renewable energy resources (solar and wind), which makes them particularly suitable for transportation applications. Furthermore, low-temperature PEMFCs offer many other benefits, including their quick startup, continuous operation, quick refueling, low operating temperatures, and minimal environmental impact as they primarily produce only water as a byproduct. Their scalability, versatility, and compact nature make them a promising solution for the decarbonization of the transportation sector [
3]. Therefore, the adaptation of PEMFCs can play a pivotal role in bridging the renewable energy adaptation gap, particularly in heating and, especially, in the transportation sector, due to their compact size and high energy density.
A PEMFC is an electrochemical device that converts the chemical energy of reactants (hydrogen and oxygen) directly into electricity after a reaction and produces only heat and water as byproducts [
4]. When operating, the fuel (hydrogen) and the oxidizer (oxygen) are supplied externally, and the system involves an exchange of both energy and matter with the environment, as hydrogen fuel must be replenished, and the byproducts (water) must be discharged. In principle, as long as the necessary reactants are continuously supplied and the reaction products are effectively removed, the FC can generate power without interruption, making it a highly efficient and sustainable energy solution [
5,
6].
The choice of a low-temperature PEMFC is due to its various advantages, which make it suitable for automotive, portable, and backup power applications. Its low operating temperature (60 to 80 °C) offers several benefits, including quick startup, as it is easy to reach this operating temperature in cold regions, typically taking from seconds to minutes. Another benefit is its rapid response to changing power demands. Further, the use of a solid polymer electrolyte membrane (PEM) and a compact catalyst layer enables very compact stack designs, which results in a high power density [
7,
8].
The smooth operation of a PEMFC is affiliated with the proper thermal management of the system. For a single cell, the overall heat generation rate (W/cm
2) is given by the following equation:
where
refers to the thermal voltage (which gives the hypothetical voltage of the FC when the change in enthalpy is converted into electricity),
shows the current density (A/cm
2), and
is the operating voltage. Therefore, the rate of heat generation is directly proportional to the current density and cell voltage, as given in Equation (1). As a result, the heat generation exceeds the power generation at higher current densities in PEMFCs. This causes critical challenges in thermal management, especially for vehicle applications in which a higher current density is required.
The performance of the stack is greatly impacted by temperature. When the stack temperature is low, the chemical reaction’s activation energy inside the cell is larger, and the activation loss increases. Lower temperatures also lead to lower conductivity and increased ohmic polarization. At the same time, the expansion rate of the gas decreases at low temperatures, and the concentration polarization increases. Similarly, at very high temperatures, the water content of the proton-exchange membrane (PEM) decreases, and the conductivity and transport characteristics of the membrane decrease, which increases the ohmic loss and concentration loss and decreases the output performance of the stack [
9,
10,
11,
12].
Furthermore, excessively high temperatures can dry out the membrane, and over time, this may lead to damage in both the membrane and the catalyst layers [
13]. Very low temperatures can reduce catalyst activity and increase the risk of water buildup, leading to flooding inside the cell [
14,
15]. Temperature impacts nearly all the transport properties of an FC, and studies suggest that thermal management systems can account for up to 8% of the total stack design in some cases [
16,
17]. Therefore, the proper thermal management of PEMFCs is necessary, and the main objective of thermal management is to maintain PEMFCs within an optimal temperature range (70–80 °C) to ensure maximum efficiency [
18].
However, effectively cooling a PEMFC stack in real-world applications is quite challenging. In practice, multiple single cells are combined to form a stack, which makes uniform temperature control even more difficult [
19]. As a result, the temperature across the cells in the stack can become uneven. Addressing thermal management is the key to improving PEMFC stack performance and durability [
20]. Various thermal management techniques can be used, such as edge cooling, separate airflow cooling, air cooling, cooling with the cathode air supply, phase change cooling, and liquid cooling. Each method has its own advantages and limitations, making the choice dependent on specific system requirements [
18]. Due to its high heat removal capability and simple operation, liquid cooling is preferred in all FC electric vehicles (FCEVs). Typically, coolant channels are engraved in the bipolar plates, and the coolant is circulated in those coolant channels with the help of liquid pumps [
21]. Serpentine designs are widely recognized as the industry standard because of their excellent performance and their ability to maintain a uniform thermal distribution. They are often used as a benchmark when evaluating or developing new flow field configurations [
22,
23].
Despite significant advancements in the design and analysis of SFFs for PEMFCs’ thermal management, there remain critical gaps in our understanding of the interplay between the impact of varying channel counts and channel widths of multi-path serpentine flow fields (MPSFFs). Previous studies have predominantly focused on limited configurations and simplified geometries, often neglecting the combined effects of varying channel counts and channel widths on the fluid dynamics and heat transfer efficiency of SFFs. Existing studies often isolate design parameters (e.g., varying channel counts, varying channel widths, or comparing different types of FFs). A few research studies have considered the combined effect of varying channel counts and widths by holistically addressing their coupled impact on thermo-electrochemical performance. For instance, prior works typically explored fixed channel widths while varying channel counts (or vice versa).
For instance, Yihong Gu et al. [
24] demonstrated that coupling LBM-LES effectively models high-speed gear lubrication with baffles, revealing optimal baffle designs that enhance fluid enthalpy and vorticity while maintaining stable oil film formation at radial speeds of 8 m/s. This approach provides insights into turbulence control and energy dissipation, which are critical for aerospace and industrial applications. Similarly, Yunfeng Tan et al. [
25] reviewed advancements in SAF, highlighting the integration of ultrasonic and magnetic fields to enhance turbulence and abrasive particle kinetics. Techniques like CFD-DEM coupling and PIV measurements have elucidated particle–wall interactions and cavitation effects, improving surface finish uniformity and efficiency. For example, gas–liquid–solid three-phase flows with microbubbles were shown to increase fluid velocity by 20%, significantly boosting polishing performance for hard materials like optical glass and silicon wafers.
S.M. Rahgoshay et al. [
10] analyzed the index of uniform temperature (IUT), pressure drops, and temperature gradients of two different types of flow fields (SFF and Parallel FF) and found that SFF outperformed Parallel FF by 24%. Yang Wang et al. [
26] investigated six different PEMFC models by integrating six different CFFs (single serpentine channel, triple serpentine channels, quintuple serpentine channels, and two configurations with mixed serpentine channels (I–V and V–I)) to obtain a better temperature distribution and found that V–I yielded the best performance. Xin Xu et al. [
27] compared two novel CFFs (A and B) with the traditional SFF through numerical modelling. They found the A novel CFF was the best CFF in terms of cooling performance.
Xuanyu Liu et al. [
28] compared three different CFFs (parallel flow field (PFF), parallel serpentine flow field (PSFF) along the
Y-axis, and PSFF along the
X-axis) in terms of thermal performance and found that the PSFF along the
X-axis contributes to the effective thermal management of PEMFCs. Similarly, Ben Chen et al. [
29] analyzed the impact of the different coolant directions and found that when the coolant flow direction is the same as that of the reactants, an improved IUT is achieved and the coolant temperature difference is less than 6 K. Zhang et al. [
30] also analyzed a metallic PEMFC structure by integration with a wavy flow field. Their study demonstrated that the thermal distribution is more uniform when the CFF is has the same direction as that of the cathode.
Moreover, while the remarkable advantages of SFFs are well documented, the pressure drop remains a significant challenge. Numerous researchers have attempted to address this issue using various techniques, but there remains a research gap. The study by Xuanyu Liu et al. [
28] highlighted an important observation regarding pressure drops in their research, in which they found that while the PSFF along the
X-axis provided improved thermal management, it also resulted in a pressure loss that was consistently 1.06 times higher than that of the PFF. This emphasizes the challenge of optimizing the trade-off between cooling efficiency and pressure loss in MPSFFs. Specifically, the research indicated that while reducing the number of channels in a manifold is beneficial for enhancing the uniformity of flow, it inevitably leads to an increase in the pressure drop within the CFFs. This underscores the need for further analyses to balance improved cooling performance and acceptable pressure losses.
Seung Man Baek et al. [
31] also assessed the performance of parallel MPSFFs in designing a flow field for a larger cooling plate measuring 18 cm × 18 cm. Their findings indicated that parallel MPSFFs demonstrated a superior cooling efficiency compared to conventional parallel SFFs, while the pressure drop characteristics remained similar when the number of parallel channels was unchanged. The study attributed the improved temperature uniformity in parallel MPSFFs to their highly intertwined structure.
Similarly, G Amarnath et al. [
32] conducted a CFD analysis of a PEMFC using ANSYS Fluent 17.2, comparing two different flow configurations: the dual serpentine flow field (DSFF) and the split serpentine counter flow field (SSCFF). The DSFF consisted of two distinct single serpentine flow fields within the active region of the FC, whereas the SSCFF was designed with a counterflow arrangement to enhance thermal management. The study revealed that the SSCFF configuration demonstrated a superior performance in terms of temperature regulation and uniformity across the FC system compared to the DSFF.
Extensive research on the thermal performance of PEMFCs has provided a thorough evaluation of various coolant flow field (CFF) configurations, particularly serpentine flow fields (SFFs) used with bipolar plates or cooling plates. These studies have rigorously examined aspects such as temperature distribution, heat dissipation efficiency, and overall thermal behavior and have proposed that the SFFs greatly enhance all these parameters. Variations in SFFs’ design configurations can augment the effective coolant fluid distribution and could help in keeping PEMFCs under an ideal operating temperature [
2]. While these investigations emphasize the importance of effective thermal regulation, they also consistently highlight the often overlooked need to address pressure drops.
To bridge this gap, the present study focuses on advanced computational fluid dynamics (CFD) modeling of multi-pass serpentine flow fields (MPSFFs). It aims to systematically analyze channel geometry to both optimize thermal management and minimize pressure losses within the flow field. This dual optimization is expected to significantly enhance the efficiency and operational performance of PEMFC systems.
While existing studies have explored various aspects of CFFs, few have investigated the impact of geometric variations in MPSFFs, particularly the number of channels. Increasing the number of channels has shown promise in improving both the thermal uniformity and reducing pressure drops. He Lu et al. [
33] studied the impact of increasing the number of channels on the reactant distribution in PEMCs and indicated that increasing the number of channels of SFFs makes the length of individual channels shorter, which improves the fluid supply capacity and distribution uniformity. Further, they concluded that the increased number of channels has a shunt-like effect on the fluid, which significantly minimizes the pressure drop.
However, the effectiveness of SFFs in maintaining a uniform thermal distribution and reliable coolant flow has led to them being a widely adopted design in proton-exchange membrane fuel cells (PEMFCs). Despite their popularity, recent studies have highlighted the potential for further performance improvements through careful geometric optimization of the flow field. Specifically, variations in the number of the channels can significantly enhance the thermal distribution and reduce pressure drops within the flow path. Existing research has demonstrated that even modest adjustments to the channel geometry can lead to better heat management and more efficient coolant flow. By systematically evaluating the impact of the number of channels, it is possible to optimize the thermal profile and minimize the pressure drop, which are the two critical factors that directly influence the efficiency and longevity of PEMFCs. Given the limitations of traditional SFFs and the significant gap in the literature regarding geometric optimization, this study focuses on the dual optimization of multi-pass serpentine flow fields (MPSFFs). The aim is to enhance thermal management while simultaneously reducing pressure drops, addressing these key challenges to improve the overall performance of PEMFCs.
Furthermore, the most compelling aspects of geometric variation in MPSFFs are their simplicity and cost-effectiveness. Unlike complex multi-material or multi-layer designs, adjusting the number and width of channels is a straightforward modification that can be implemented without the need for expensive materials or intricate manufacturing processes. This makes it an attractive approach for improving PEMFC performance, especially in commercial applications for which cost and efficiency are critical factors.
This study uses numerical simulations to evaluate the cooling efficacy and pressure drop of CFFs based on MPSFFs in a PEMFC. For this purpose, six three-dimensional (3D) computational models were developed using COMSOL Multiphysics 6.2. This investigation aimed to optimize the cooling capabilities of MPSFFs and to minimize the pressure drop, which plays a critical role in maintaining the operating temperature of PEMFCs within an ideal range. The novelty of this study is the dual optimization of the coolant flow field (CFF) configuration based on a multi-path serpentine flow field (MPSFF) strategy to enhance the thermal distribution uniformity while minimizing the pressure drop in PEMFCs and the proposed geometrical designs, which are not only structurally effective but also inherently simple, making them highly practical and cost-efficient for real-world manufacturing and integration.
3. Results and Discussion
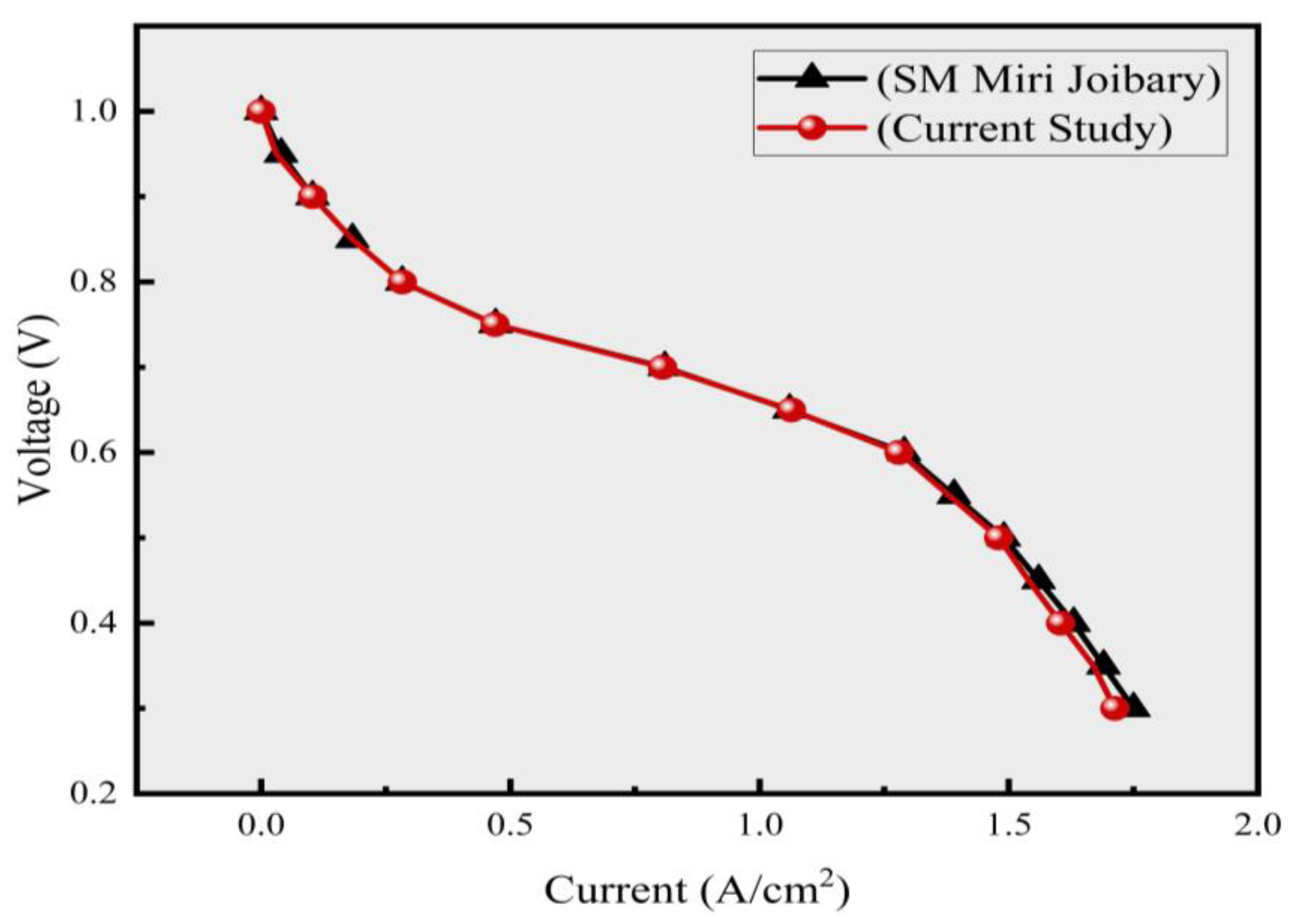
The efficiency of a PEMFC is influenced by various factors, such as the operating temperature, species concentration in the GDL, catalyst layer (CL), membrane, membrane hydration, and the risk of drying out. All these factors could be controlled by effective thermal management. In this study, the thermal performance of MPSFFs is evaluated by varying the number of channels across various configurations, ranging from 2 to 12, while maintaining the channel width constant at 1.5 mm. All the models were evaluated to assess the impact of channel variations on the temperature distribution in CFFs and the overall efficiency of PEMFCs. Cell performance was analyzed for voltages ranging from 0.3 V to 1 V; however, the results were reported at 0.6 V to maintain consistency with comparable studies.
3.1. Thermal Distribution
The primary objective of this study was to improve the thermal management capability of MPSFFs in PEMFC applications. To achieve this goal, a comprehensive thermal analysis of the critical components of PEMFC, like anode coolant channels, the membrane midplane, and cathode coolant channels, was conducted. This approach is widely regarded as best practice for thermal optimization studies of PEMFC systems. Therefore, temperature plots were extracted at the above-mentioned locations from the computed models. As liquid coolant channels were utilized to enhance the performance of the FC, the heat distribution in the coolant channels could effectively reflect the cooling performance of CFFs.
This study is based on varying the number of channels of MPSFFs, and it is a fact that increasing the number of channels results in a decreased length of the channels, which ultimately shortens the distance covered by the fluid from the inlet to outlet.
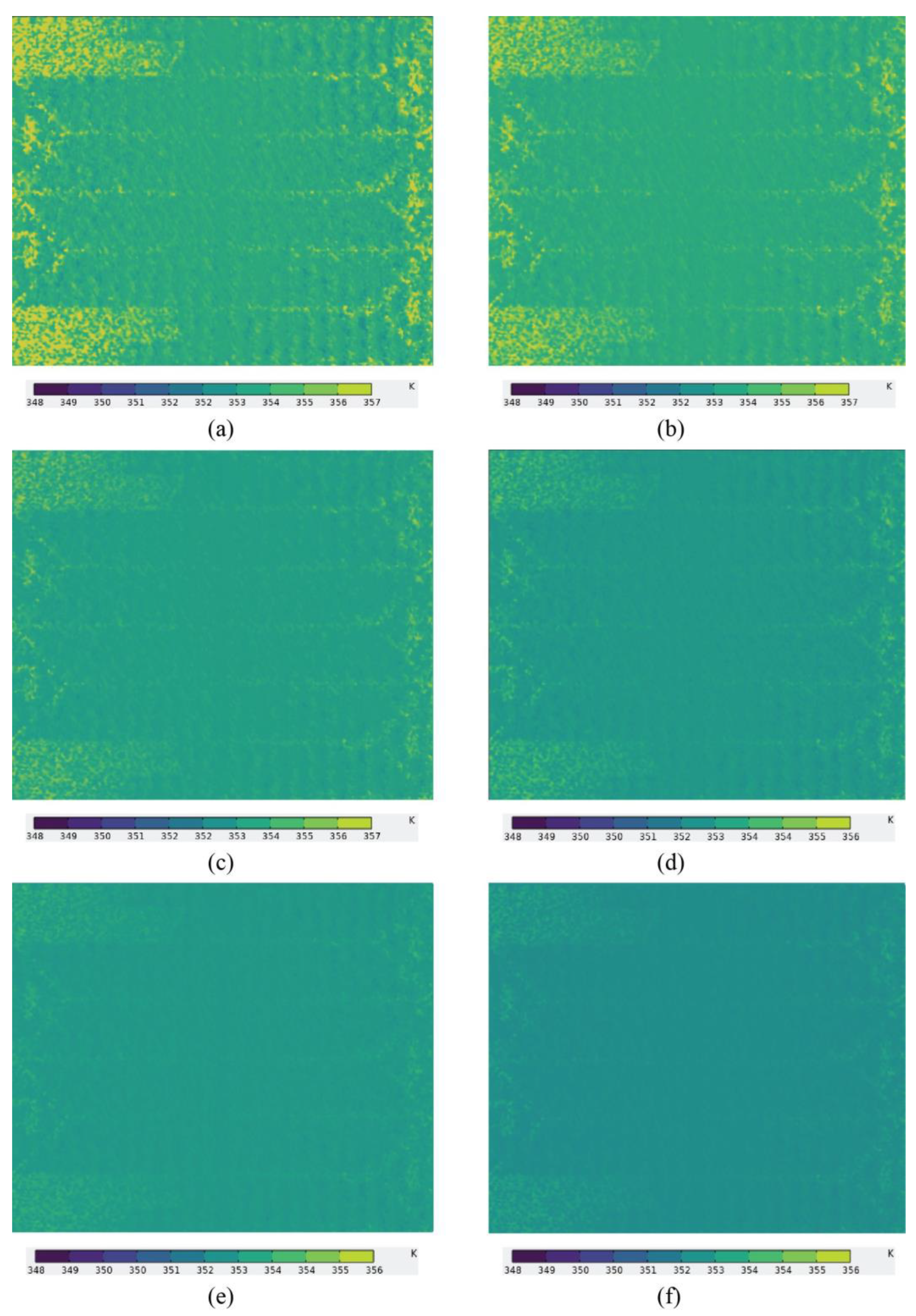
Figure 6 shows the temperature distribution on the membrane midplane, where it is evident that as the number of channels increases from two to twelve, the average temperature of the plane is reduced sufficiently. The temperature at the membrane midplane in geometries with two- to six-paths yields a large number of hotspots, which shows a nonuniform temperature distribution. This uneven temperature distribution in the models with two-, four-, and six-path CFFs could be attributed to the greater number of serpentine curves in the channels, which hinders the coolant in these FFs. Planes with eight to twelve paths yielded a much better thermal performance as fewer and less intense hotspots could be seen in planes with these geometries. This is due to the shorter channel length and fewer serpentine curves. The highest thermal uniformity was observed in the membrane midplane with twelve-path CFF geometry.
It is clearly noticeable in
Figure 7 and
Figure 8 that the temperature varies from the inlet to outlet in the cathode and anode coolant channels. Considering the overall performance of the coolant channels, it is observed that the FFs with more serpentine turns and a greater number of curves (two- to six-path FFs) experience higher temperatures near the outlets. It is also observed that these FFs failed to extract uniform heat from the system and yielded more hotspots, which could be attributed to their longer channels and the greater number of serpentine curves. In contrast, geometries with a higher number of channels (six to twelve) presented a better cooling performance, as fewer hotspots were observed in these FFs, and the thermal extraction by these FFs was remarkable. The 12-path FF geometry was observed to have the best cooling performance in terms of its uniform heat distribution throughout.
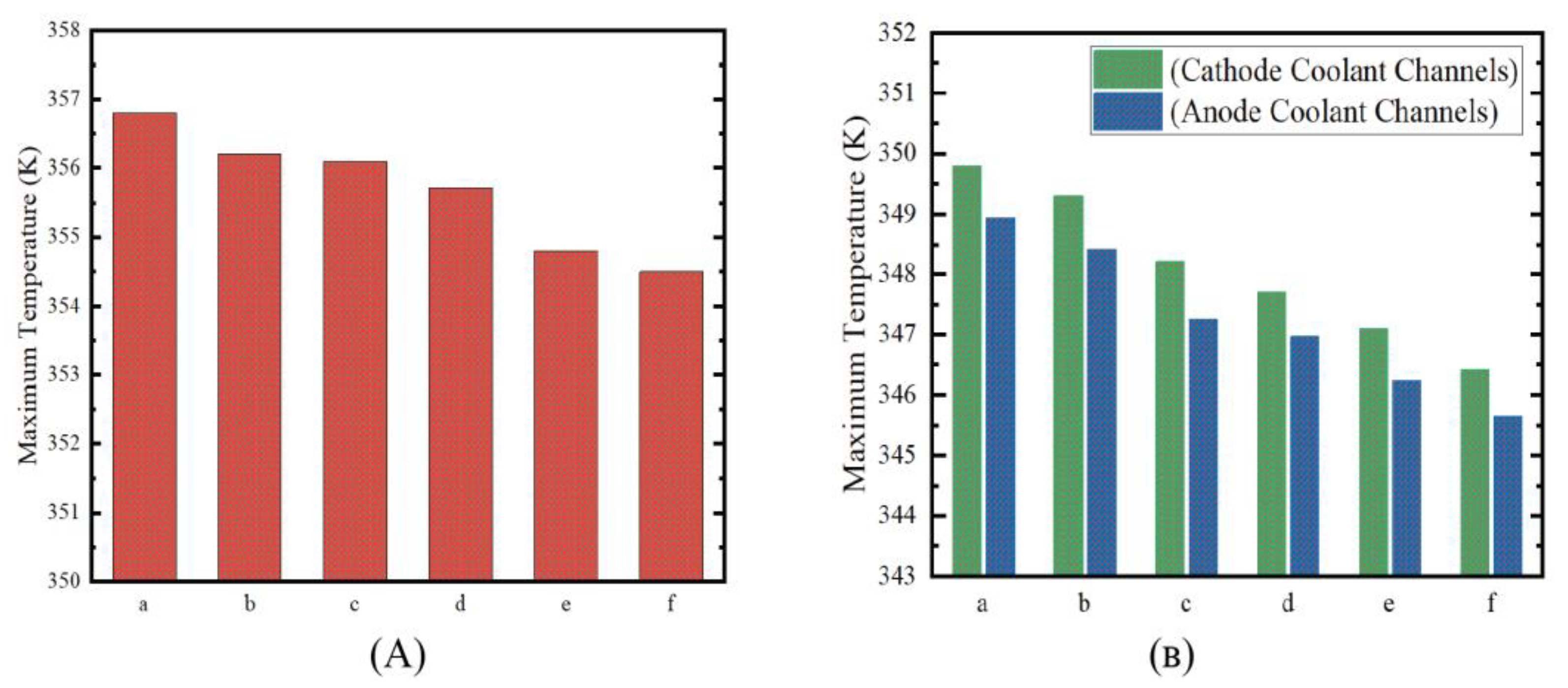
Figure 9 represents the average temperature distribution at the membrane midplane, anode coolant channel, and cathode coolant channels of various models. The highest average temperature was observed in the two-path CFF, whereas the lowest average temperature was observed in the 12-path FF. Further, a consistent temperature differential of nearly 1 K was measured between the anode- and cathode-side CFFs across all tested models, with the cathode side exhibiting elevated temperatures compared to the anode side. This thermal asymmetry can be linked to the distinct electrochemical reactions occurring at each electrode, in which exothermic processes at the cathode dominate, while the anode experiences comparatively lower levels of heat generation. The primary source of heat generation in PEMFCs is the oxygen reduction reaction (ORR), which releases heat as the oxygen molecules are reduced to water. Further, the average temperature difference of the membrane midplane of the models is interesting: the temperature difference between two-, four-, and six-path FFs is less than one degree, whereas as the number of channels increases from six to twelve, the temperature of the membrane midplane drops with a difference of more than one degree, which shows the 10- and 12-path FFs have a better thermal performance.
The maximum temperature measurements also serve as a crucial indicator of the inefficiency or inadequacy of a flow channel design. It is evident in
Figure 10 that the two-path CFF exhibits the maximum temperature, reaching approximately 350 K at the cathode-side channels and around 349 K at the anode-side channels. In contrast, the 12-path CFF demonstrates the lowest maximum temperature. This temperature disparity can be attributed to several factors inherent to the channel design. The two-path CFF exhibits the highest temperature because it has fewer paths, resulting in a longer coolant residence time in each channel. Longer channels with more serpentine curves and turns allow the coolant to remain inside the channels longer. Consequently, this extended flow time allows the coolant to absorb more heat from the FC system, resulting in a higher temperature near turns. Additionally, the longer path means that the fluid has more time to equilibrate with the temperature of the FC, leading to greater thermal transfer during the fluid’s passage through the system.
However, a lower maximum temperature was observed in the 12-path CFF. This does not indicate a failure in heat extraction, but it is due to the balanced heat distribution inside the cell. It has also been discussed above that improved thermal management was achieved by the twelve-path CFF, followed by the eight-path and six-path CFF. The twelve-path configuration resulted in more balanced heat exchange, ensuring that the coolant can distribute the extracted heat more evenly across the system. The eight-, ten-, and twelve-path CFFs allow for more temperature uniformity, leading to more balanced thermal profiles, ensuring that the system operates within an optimal temperature range. It is crucial to emphasize that the role of the CFFs in PEMFC applications is not to extract the maximum possible heat from the system, but to keep the FC temperature within an appropriate operational range, typically between 70 °C and 80 °C. As highlighted in the literature, temperature uniformity is just as important, if not more so, than heat extraction efficiency. Maintaining a stable thermal distribution ensures that the FC operates efficiently, minimizes the risk of thermal stresses on the components, and contributes to the longevity and reliability of the system. Therefore, the 12-path CFF in this study offers the best overall thermal performance not necessarily by extracting more heat, but by ensuring an optimal heat distribution and maintaining the system within its ideal temperature range.
The temperature distribution in the membrane is the most critical issue as it directly influences the performance and durability of the FC. The maximum temperature in the membrane midplane refers to the highest recorded temperature in the membrane midplane. This is an important parameter that shows the localized hotspots in the membrane.
Figure 10 reflects the maximum temperature at the membrane midplanes of various models. The maximum temperature in this region is offered by the two-path FF, followed by four and six-path configurations. These FFs reflect the most critical behavior at the membrane midplane. This critical thermal behavior greatly influences the current density in the membrane midplane. Moreover, this thermal pattern also affects the temperature uniformity index in these models. The 12-path geometry depicts the appropriate maximum temperature patterns, followed by the ten- and eight-path geometries.
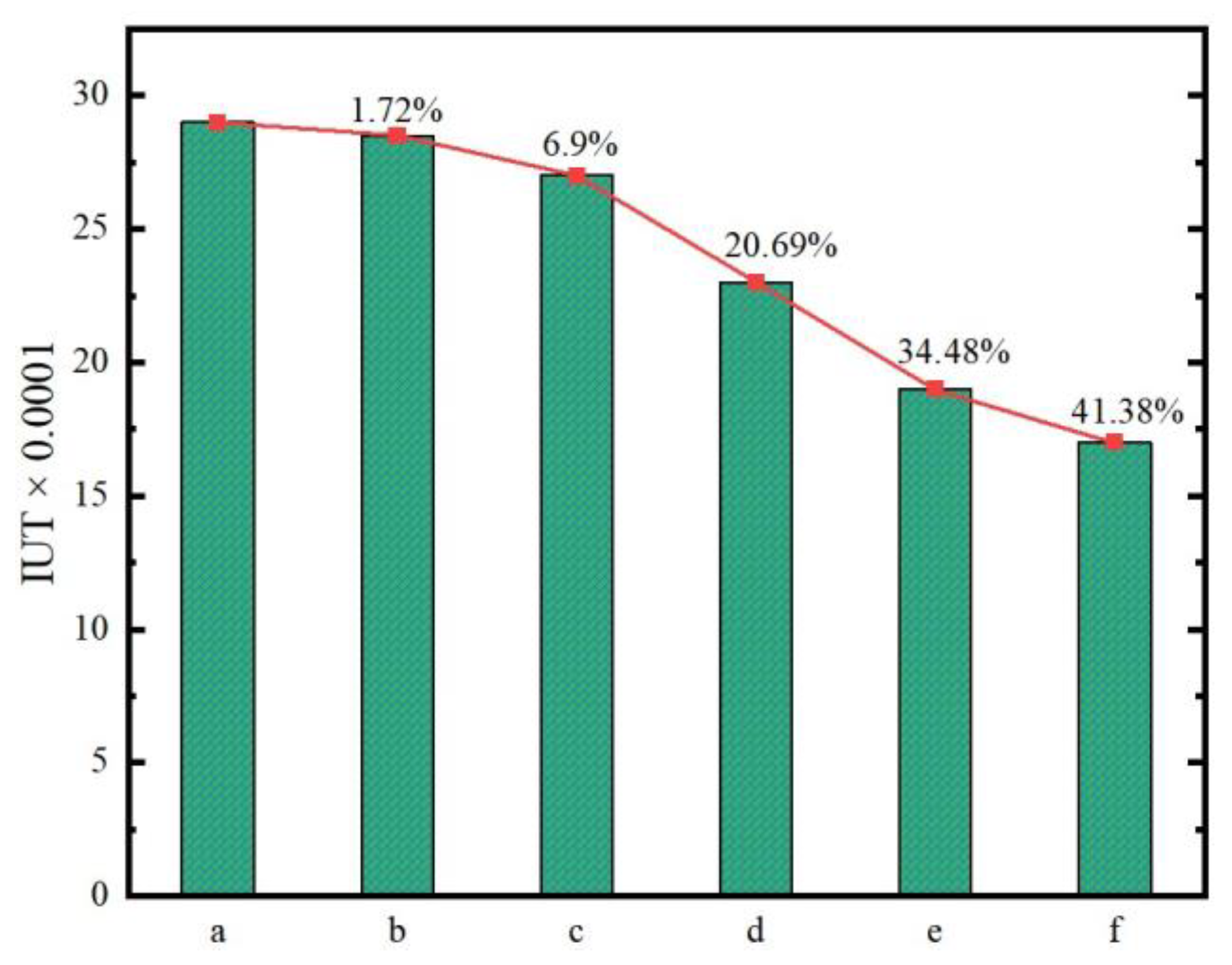
3.2. Temperature Uniformity Index
The IUT quantifies the degree of temperature variation across the FC, which directly impacts several performance aspects. Areas with excessive heat (hot spots) may experience an overconsumption of hydrogen, while cooler regions may face fuel starvation. A high IUT indicates that these imbalances are present, leading to inefficient energy production and a reduction in performance. Monitoring the IUT helps to maintain stable operating conditions and avoid thermal imbalance during operation. Similarly the IUTs of membrane midplanes in various models were calculated and are reflected in
Figure 11. The highest temperature uniformity was achieved with the twelve-path CFF geometry, followed by the ten-path and eight-path geometries. Overall, in all the models, the IUT was noted as being in the acceptable range, reflecting the proper thermal distribution capability of MPSFF. This is because the cooling fluid starts the cooling process at the center of the FC, which is crucial. After all, this area often experiences higher temperatures due to the concentration of electrochemical reactions. This geometrical arrangement ensures that the most critical regions receive adequate thermal management by initiating cooling at the center. Similarly, as the cooling fluid reaches the outlets towards the edges, it enhances the reaction rates in areas with high hydrogen and oxygen mass ratios. This is because optimal temperatures facilitate faster electrochemical reactions, leading to the increased efficiency and performance of the FC.
This approach promotes efficient thermal management by ensuring that the regions with higher reaction rates (typically where the hydrogen and oxygen mass ratios are the greatest) are adequately cooled. By optimizing cooling in these areas, reaction rates increase, leading to better fuel utilization and improved performance. As the chemical species are consumed more effectively in the well-cooled regions, the temperature becomes more uniform across the FC. This uniformity results from the more balanced reaction rates throughout the FC, where the energy input and reaction output are harmonized. With a more even temperature distribution, less cooling is required in regions further from the inlet, as these areas operate at more stable, lower temperatures. Consequently, this efficient cooling strategy not only optimizes the overall FC performance but also reduces the cooling energy consumption, making the system more energy-efficient and enhancing its operational stability over time.
3.3. Hydrogen Concentrations
The concentration of hydrogen in the membrane midplane plays a crucial role in examining the overall performance of PEMFCs. It refers to how evenly the hydrogen is distributed across the membrane. Since the membrane is responsible for transporting the protons from the anode to the cathode, a uniform hydrogen distribution is key for the uniform transportation of protons across the membrane. This critical factor influences multiple aspects of the FC, including reaction kinetics, proton conductivity, membrane hydration, temperature distribution, and overall efficiency. Areas with excessive hydrogen result in oversaturation.
In contrast, areas with a lower hydrogen concentration would suffer from the underutilization of the electrochemical sites; both factors contribute to reducing the overall current density and power output. All these phenomena are greatly affected by the uneven temperature distribution, as hotter regions would cause a faster hydrogen flow, while cooler regions may result in fuel starvation. Further, poor cooling would cause water evaporation (drying out the membrane), whereas excessive cooling would cause water accumulation (flooding). Therefore, effective thermal management not only prevents fuel starvation and overconsumption but also keeps the membrane in an optimally hydrated state, which helps to safeguard it from both drying out and flooding.
The hydrogen distribution at the membrane midplane is depicted in
Figure 12. It could be observed that the hydrogen concentration is highest at the inlet regions (e.g., edges or entry zones of the channels), consistent with the depletion of the reactant as the hydrogen flows toward the center. This concentration reduction toward the FC center is caused by the interplay of flow dynamics, reactant consumption, and electrochemical reaction distribution, as different patterns were observed in different models. A clear relation between temperature and hydrogen concentration was observed. The variation in concentration patterns across different models suggests that the geometry of CFFs plays a significant role in the hydrogen distribution. The clear relationship between temperature and hydrogen concentration likely indicates that higher temperatures result in a reduced hydrogen concentration gradient. This phenomenon resulted from the enhanced hydrogen diffusion and accelerated reaction kinetics at elevated temperatures, promoting a more uniform hydrogen distribution across the membrane.
3.4. Pressure Drop
In serpentine coolant flow channels for PEMFC applications, a pressure drop is an important factor that influences the overall performance of the FC, as the serpentine channels have a series of serpentine turns that offer remarkable resistance to the fluid. The length of the SFF also plays a critical role in pressure reduction. Longer channels result in a greater level of resistance to the flow and, thus, a greater pressure drop. There are many other factors affecting the pressure, but in this study, the effect of channel geometry was considered as a prime factor. Considering that the pressure drop is also influenced by the number of paths in the serpentine design, various models with different numbers of paths were produced. As it is also the fact that having fewer number of passes, increases the length of the channel, leading to a higher resistance to fluid. Therefore, this study has evaluated various models with different numbers of passes to investigate the impact of varying the number of channels.
The total pressure drop in the coolant flow field is reflected in
Figure 13. The pressure drops in CFFs follows the normal trend of SFFs and significant reduction in the pressure drop was observed with increasing number of channels. This optimization in the pressure drop could be attributed to the reduced length and serpentine turns of channels, as increasing the number of channels results in a reduced length and fewer serpentine turns of channels, ultimately minimizing the residence period of the coolant inside the CFF. This shorter residence time of the coolant inside the CFF facilitates the extraction of a balanced amount of heat from the cell, ultimately increasing the thermal uniformity. Similarly, the maximum pressure drop was observed in the FF with the maximum length and the highest number of serpentine turns. In contrast, the minimum pressure drop was reported in the FF with the fewest serpentine turns and the minimum length. Therefore, this increased pressure drop results in the increased residence of the coolant inside the CFF, which also ultimately increases the heat extraction by the coolant near turns, causing a non-uniform temperature distribution, as seen in
Figure 7a–c and
Figure 8a–c. Evaluating the overall pressure drop in the CFF, the 12-path CFF offered the lowest pressure drop of the fluid.
The key mechanisms influencing the thermal and flow behavior in PEMFCs with MPSFF are the convective heat transfer, pressure drop, and the distribution of the flow within the channels. These factors interact in complex ways to influence the temperature distribution, coolant flow dynamics, and ultimately, the performance of the fuel cell.
3.5. Key Mechanisms Influencing Thermal and Flow Behaviors
3.5.1. Convective Heat Transfer
The increase in the number of channels generally improves the convective heat transfer by increasing the surface area available for heat exchange. This effect is particularly important for larger active areas, as a higher channel count leads to a more efficient thermal distribution, helping to avoid the formation of localized hot spots. The path length also plays a significant role, as longer channels promote a more uniform heat distribution, which reduces the thermal gradient across the membrane.
3.5.2. Flow Distribution and Pressure Drop
Path length and channel geometry impact the flow distribution, with longer channels typically resulting in a more uniform flow, while shorter paths may lead to higher velocity fluctuations and potential areas of stagnant flow. This has a direct effect on heat dissipation, as uneven flow can cause localized heating or a reduced cooling efficiency. Additionally, the pressure drop in the flow field increases with longer channels, which can affect the overall fuel cell efficiency by requiring greater pumping power.
3.5.3. Membrane Water Management
The temperature distribution across the membrane is also closely tied to membrane hydration levels, which affect ionic conductivity. As the coolant flow is adjusted, both the channel count and path length can influence water removal and hydration at different locations within the membrane. Effective temperature management, therefore, not only minimizes thermal stress but also helps in maintaining optimal hydration levels for ionic conduction.
4. Conclusions and Future Recommendations
This study investigated the impact of MPSFF on the thermal management and pressure drop of PEMFCs. It was concluded that introducing a coolant at the center led to effective thermal management, preventing hotspots, maintaining optimal temperatures, and ensuring peak reaction rates. As the reaction concentration is usually high at the center, effective cooling in high-reactant-concentration regions prevents thermal inhibition, stabilizing temperatures to maintain efficient charge transfer, reactant utilization, and an enhanced power output.
This study systematically analyzed the thermal behavior of coolant channels with two- to twelve-paths, while maintaining a constant channel width of 1.5 mm. Models with two-to-six-path CFFs demonstrated notable high-temperature hotspots, primarily caused by the extended length of the cooling channels and the excessive number of serpentine bends. However, models with eight-to-twelve-path CFFs had fewer hotspots and a uniform temperature distribution. At the membrane midplane, the highest average temperature was observed for the model with the two-path CFF, having an average membrane temperature around 356 K. In contrast, the model with 12-path CFFs reflected the 0.98% lowest average temperature (352.1) in the region. Similarly, a temperature difference of up to 1 K was observed between the anode and cathode CFFs, which could be due to the ORR on the cathode side. The highest maximum temperature was also observed in two-path CFFs, which could be attributed to the extended coolant residence time inside the FF due to longer channels with the maximum number of serpentine turns. In contrast, the value of the maximum temperature observed in the 12-path CFF was 0.81% lower, which outperformed all other CFF configurations, which could be due to the same reason that the maximum temperature in the two-path CFF is elevated.
The study concluded that the minimum number of coolant channels (i.e., two paths) causes longer channel lengths and a greater number of serpentine turns, resulting in the maximum number of hot spots around turns, whereas maximizing the number of channels (12 paths) results in the shorter length of the channels, causing a uniform thermal distribution. In addition, the maximum uniformity of the thermal distribution was reflected in 12-path CFFs with the lowest average temperature of around 352.3 K at the membrane midplane. However, this investigation is constrained by fixed channel dimensions, static operational parameters, and limited material variations. To advance this research, future work should incorporate dynamic operating conditions, such as modulated coolant flow rates, and evaluate advanced cooling media, e.g., nanofluids. Additionally, conventional CFD tools face computational limitations in exhaustively exploring geometric design spaces. Thus, a data-driven approach leveraging machine learning models, trained on high-fidelity CFD datasets, is proposed to efficiently predict optimized CFF architectures.
Building on the current findings, the optimized CFF configuration warrants further investigation through parametric variations in channel width and height, guided by a systematic evaluation of hydraulic diameter and aspect ratio. Such an approach could refine the trade-off between thermal uniformity and pressure drops. A future work will specifically examine width-adjusted channel designs derived from the present optimized geometry, targeting enhanced pressure loss mitigation. This methodology holds significant potential to redefine thermal–fluid performance boundaries in MPSFFs, enabling next-generation designs that harmonize thermal regulation and hydrodynamic efficiency.