Co-Adaptive Inertia–Damping Control of Grid-Forming Energy Storage Inverters for Suppressing Active Power Overshoot and Frequency Deviation
Abstract
1. Introduction
- (1)
- Compared to single-parameter adaptive control: Most existing studies focus on the adaptive regulation of either virtual inertia or damping, neglecting their synergistic effects. The control strategy proposed in this paper is capable of simultaneously adjusting both virtual inertia and damping coefficients, achieving bidirectional optimization of the system’s dynamic performance, thereby addressing the balance between rate of change in frequency and frequency deviation.
- (2)
- Compared to linear algorithms: In existing research, many methods use linear algorithms to regulate virtual inertia and damping coefficients, but these methods often fail to provide sufficiently fine adjustments. This paper uses an RBF neural network to regulate virtual inertia, which, compared to linear algorithms, offers more granular control, thereby improving the system’s response accuracy to frequency variations.
- (3)
- Compared to neural-network-based methods: Although the application of neural networks in control systems is increasing, their high computational demands and training complexity limit their implementation in real-time control. The method proposed in this paper uses a neural network only for virtual inertia regulation, while the damping coefficient is adjusted using a linear algorithm. This effectively reduces computational requirements and training complexity, making the control strategy suitable for real-time digital control systems and overcoming the issues of high computational demand and long training times present in existing methods.
- (1)
- The proposed coordinated adaptive control strategy for virtual inertia and damping provides a more balanced and refined solution to the problem of controlling the rate of change in frequency and frequency deviation.
- (2)
- An efficient implementation method is provided by optimizing the computational structure, where the neural network is used solely for inertia regulation and damping is adjusted using a linear algorithm. This significantly reduces the computational complexity, making the method suitable for real-time applications.
- (3)
- By comparing with existing methods, the proposed approach has been validated to offer advantages in system dynamic response, frequency stability, and power overshoot, demonstrating its great potential for practical applications.
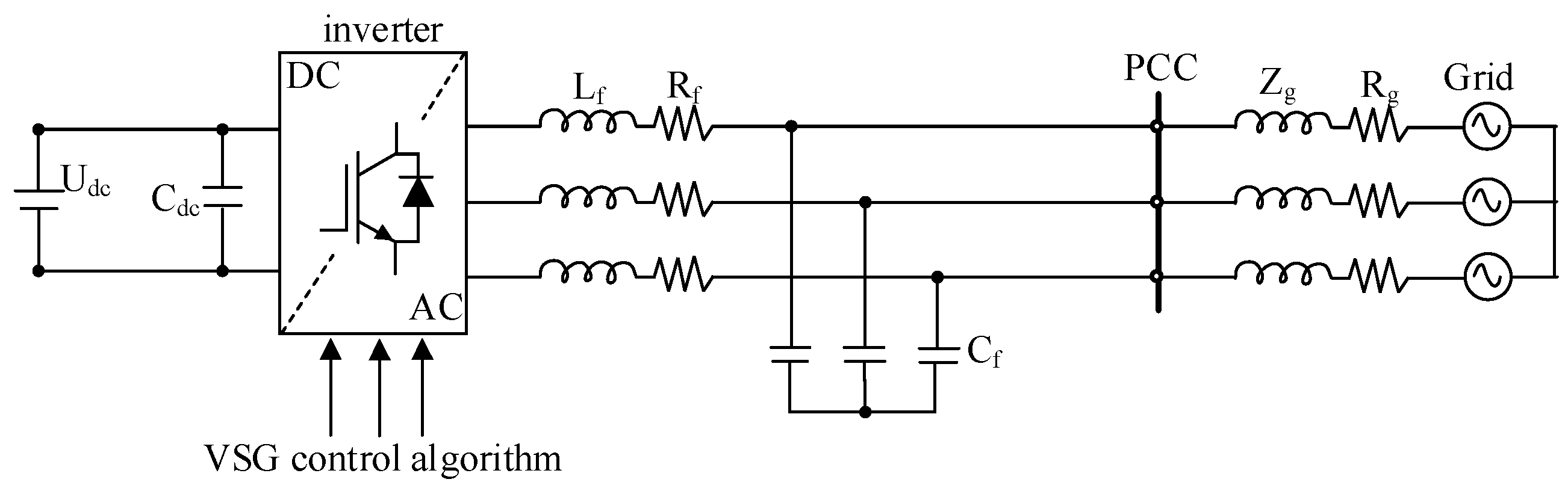
2. Mechanism Analysis of the Impact of Inertia and Damping on the Stability of VSG Systems
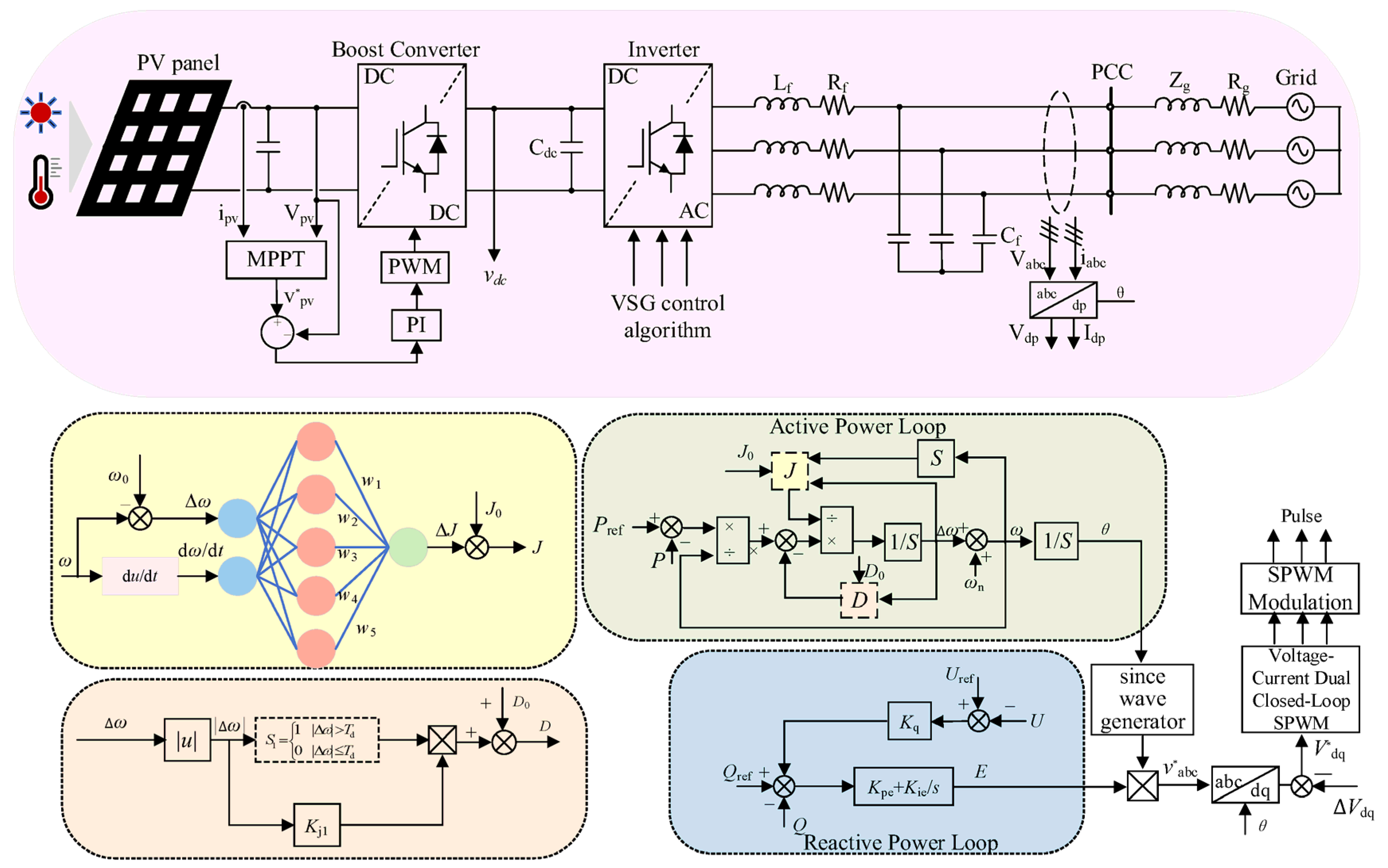
2.1. Active Power Control Principle of VSG
2.2. Effect of J and D on Frequency Response
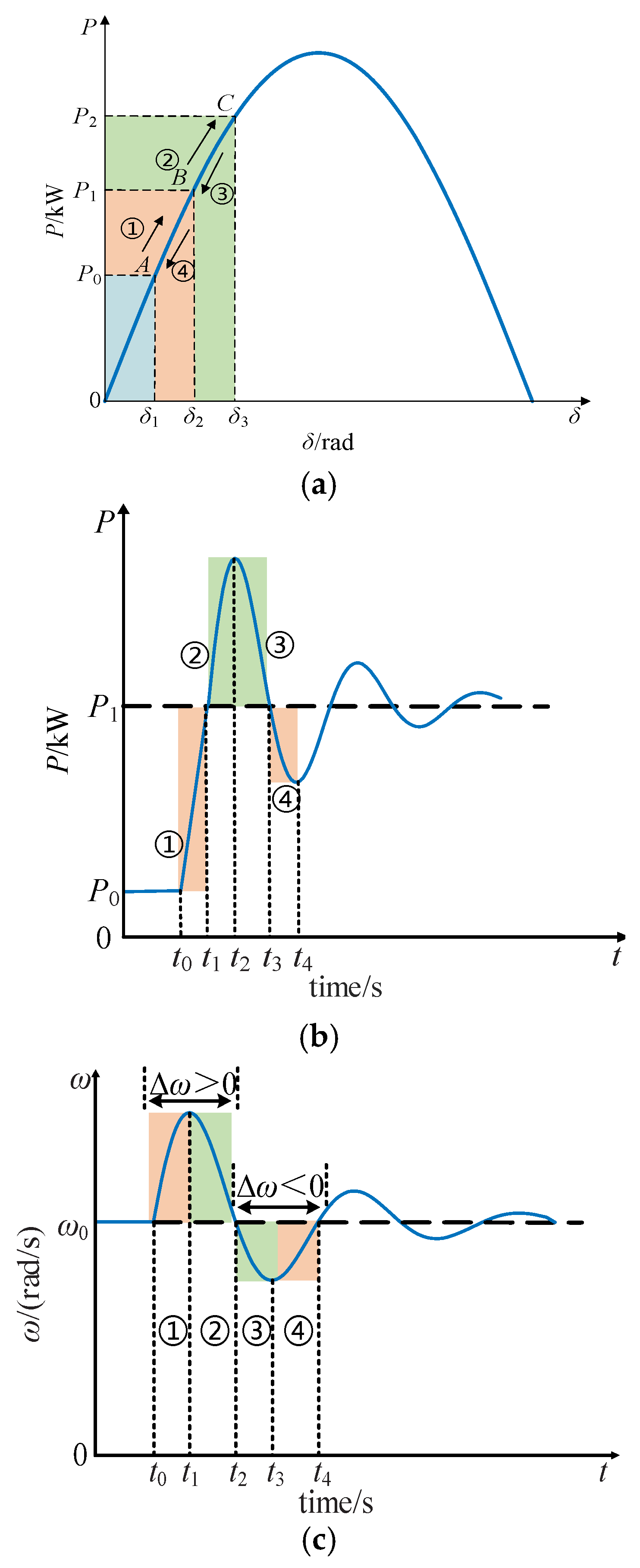
2.3. Impact of J and D on Active Power Response
3. Adaptive Control Method for Virtual Inertia
3.1. Principle of Adaptive Inertia Control
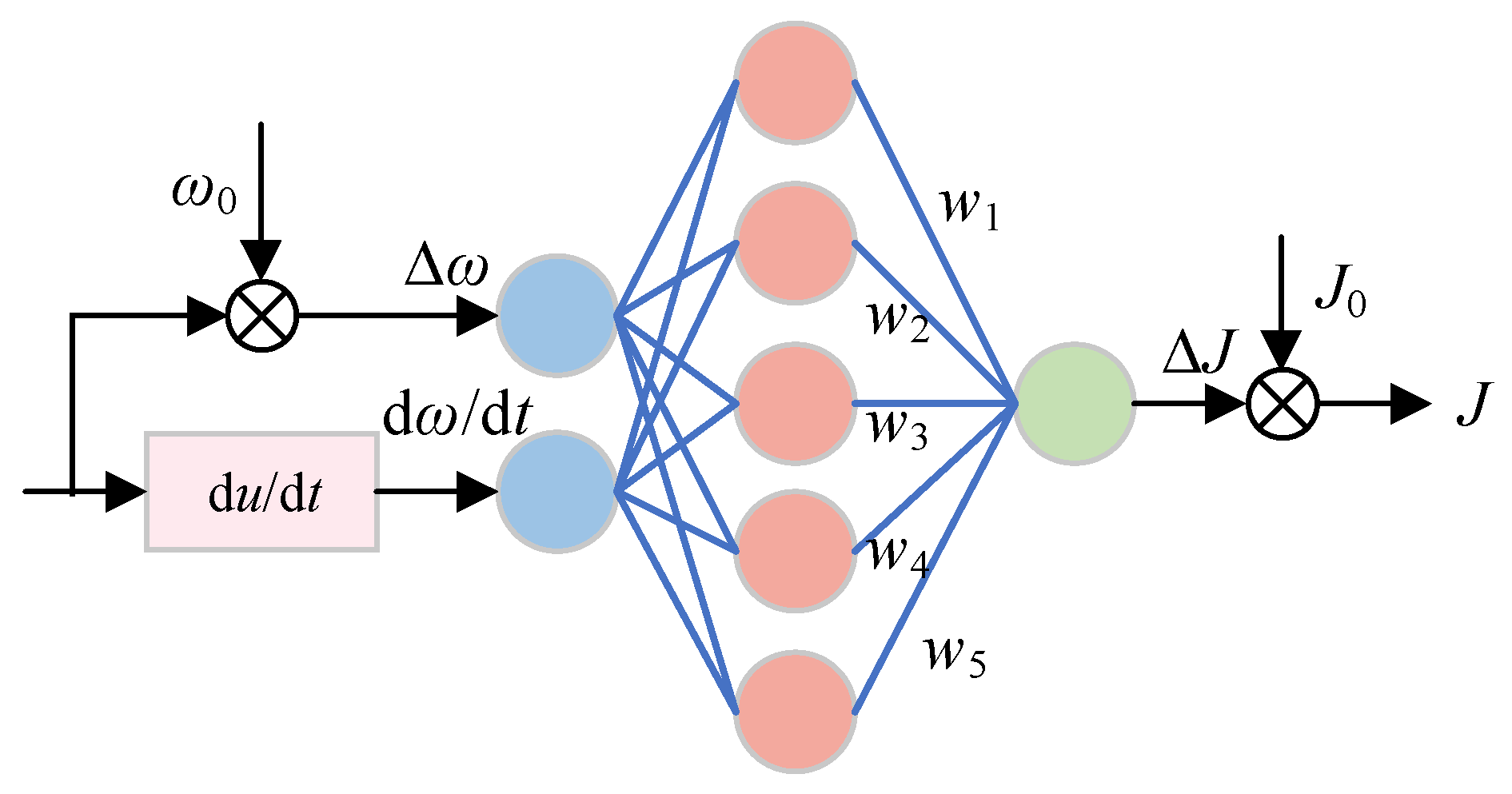
3.2. Inertia Adaptive Adjustment Based on RBF Neural Network
4. Analysis of Damping Adjustment Mechanisms and Adaptive Techniques
4.1. Analysis of the Damping Adjustment Mechanism
- (1)
- The interval t0–t1 is defined as Stage 1. During this stage, the reference power of the VSG is greater than the actual output power, resulting in an increase in angular velocity. To suppress the frequency deviation and mitigate the sudden rise in the frequency ramp rate, the damping coefficient should be adaptively increased, thereby slowing down the deviation of angular velocity from its nominal value.
- (2)
- The interval t1–t2 is defined as Stage 2. In this stage, the reference power of the VSG is lower than the actual output power, causing the angular velocity to gradually decrease. However, the angular velocity deviation remains positive. To reduce this deviation, the damping coefficient should be adaptively increased.
- (3)
- The interval t2–t3 is defined as Stage 3. During this stage, the power difference ΔP is negative, and the angular frequency deviates from its nominal value in the negative direction. To suppress the rate of change in angular velocity and reduce the deviation, the damping coefficient should be adaptively increased.
- (4)
- The interval t3–t4 is defined as Stage 4. In this stage, the power difference ΔP becomes positive, leading to an increase in angular velocity, which gradually approaches its nominal value. At this point, the damping coefficient should be appropriately increased to reduce the angular frequency deviation and enhance the frequency ramp rate, thereby accelerating the restoration of angular frequency to its nominal value.
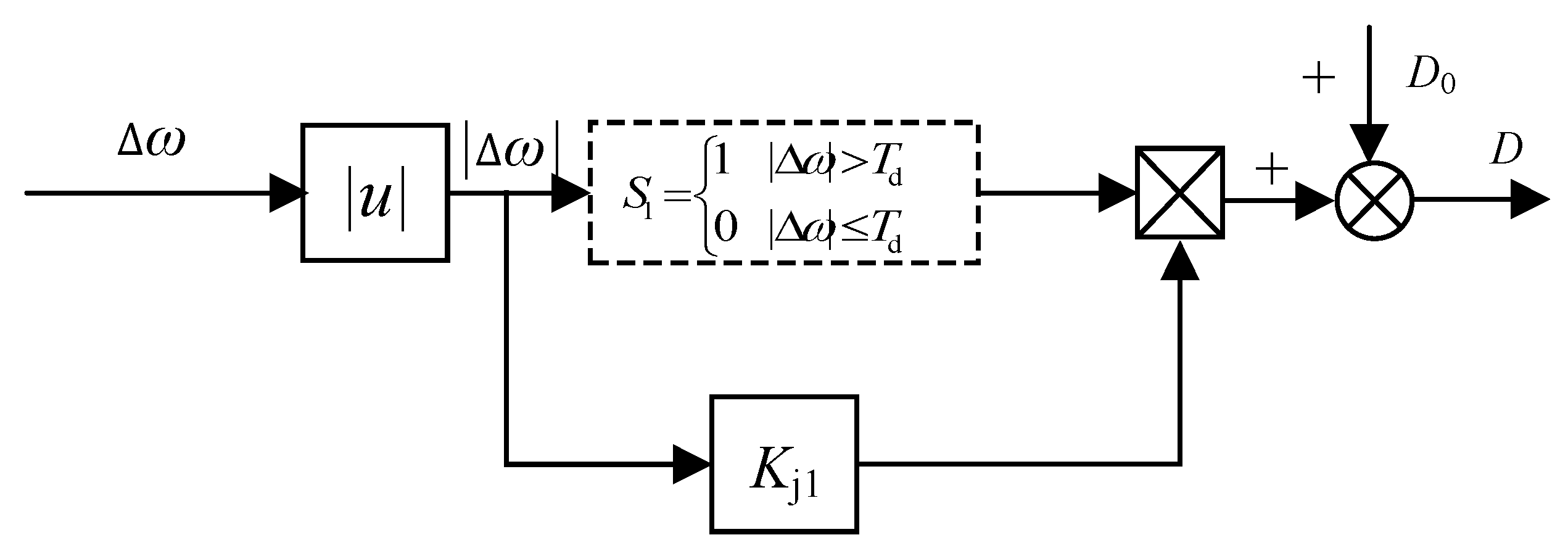
4.2. Adaptive Adjustment Method for the Damping Coefficient
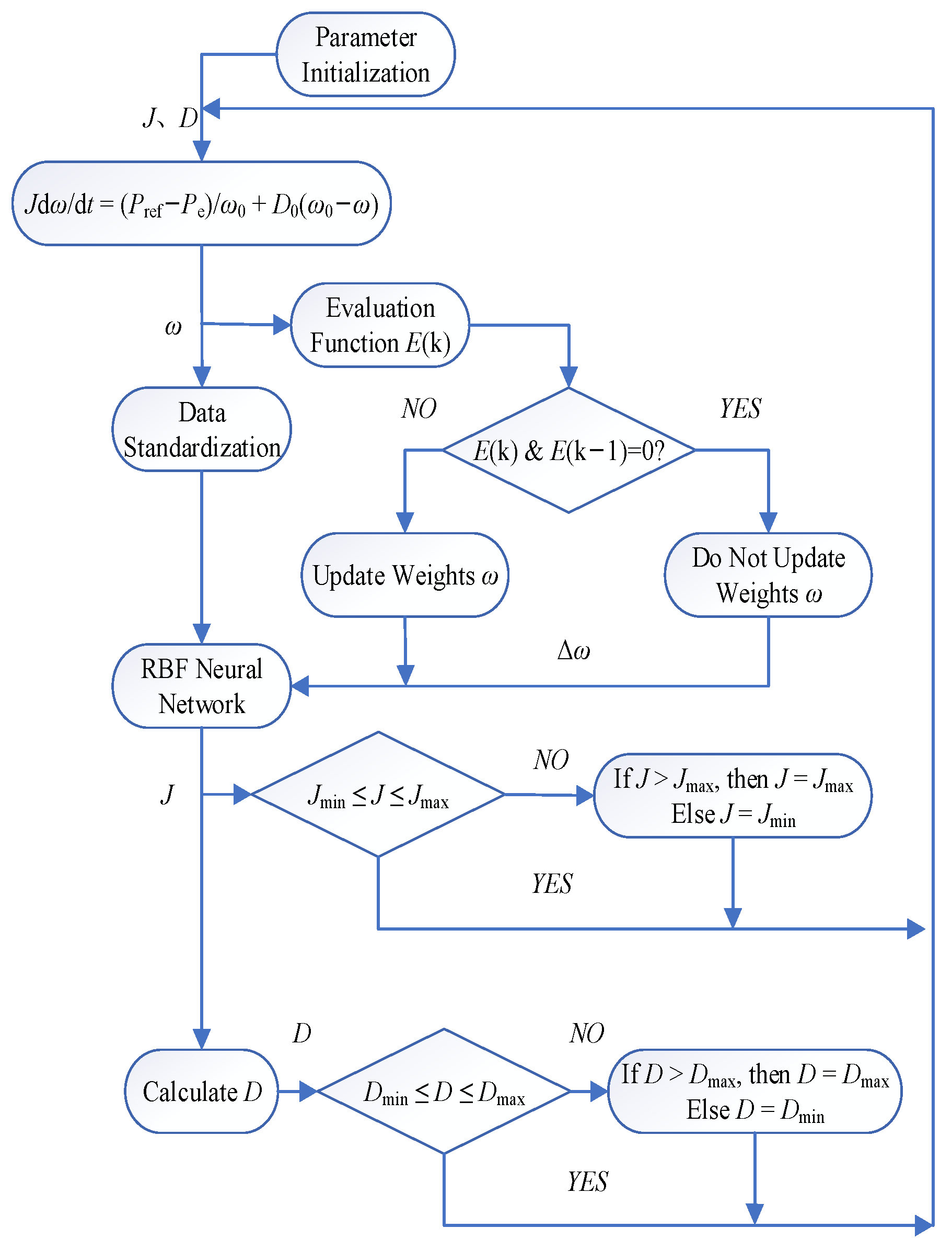
5. Coordinated Adaptive Adjustment Method for Inertia and Damping
5.1. Overall Control Block Diagram and Control Algorithm Flowchart
- (1)
- Real-time state sensing: In each control cycle, the controller continuously monitors the system’s frequency deviation (Δω) and its rate of change (dω/dt). These two signals, which best reflect the system’s dynamic characteristics, serve as the inputs for the coordinated adjustment.
- (2)
- Intelligent inertia regulation: The signals Δω and dω/dt are fed into the RBF neural network. Leveraging its powerful nonlinear mapping capability, the network intelligently calculates the optimal virtual inertia J for the current moment. This part is primarily responsible for the “fast response,” i.e., strongly suppressing the rate of change in frequency by increasing inertia during the initial phase of a disturbance.
- (3)
- Precise damping compensation: Simultaneously, the controller calculates a damping increment ΔD using a simple linear algorithm based on the magnitude of the frequency deviation Δω. This part is mainly in charge of “stable suppression,” i.e., providing just-right damping throughout the oscillation process to effectively mitigate frequency overshoot and accelerate the system’s return to stability.
- (4)
- Coordinated output: Finally, the adaptively adjusted inertia J and damping D are simultaneously applied to the VSG’s swing equation, jointly determining the system’s dynamics for the next time step.
5.2. Discussion on Computational Complexity and Real-Time Implementation
- (1)
- Computational load of RBF network forward propagation: In each forward propagation, the system inputs (Δω, dω/dt) are used to calculate the Euclidean distance between the input data and the center vectors of the h neurons in the hidden layer, followed by processing through the Gaussian activation function. The computational load of this process is proportional to the number of neurons, h, and is fixed and predictable. Therefore, even in larger systems, the computational load of forward propagation remains controllable.
- (2)
- Online update of RBF network parameters (gradient descent): The computational load during the gradient descent process is proportional to the number of hidden layer neurons, h, and the input dimension. Compared to traditional control methods, the computational load of this process is slightly higher; however, it does not significantly impact real-time performance.
- (3)
- Adaptive damping calculation: the calculation of adaptive damping involves only one absolute value calculation, one multiplication, and one addition, making its computational load negligible.
6. Parameter Tuning and System Stability Analysis
6.1. Parameter Tuning for Kd and Td
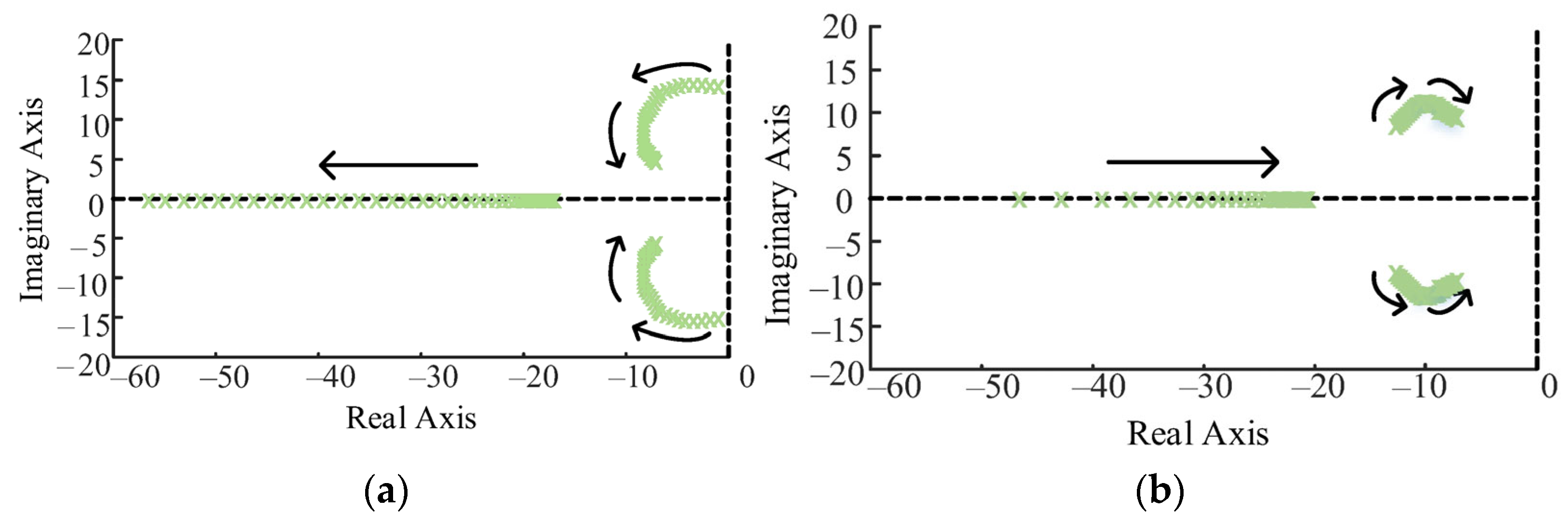
6.2. System Stability Analysis
7. Simulation and Results Analysis
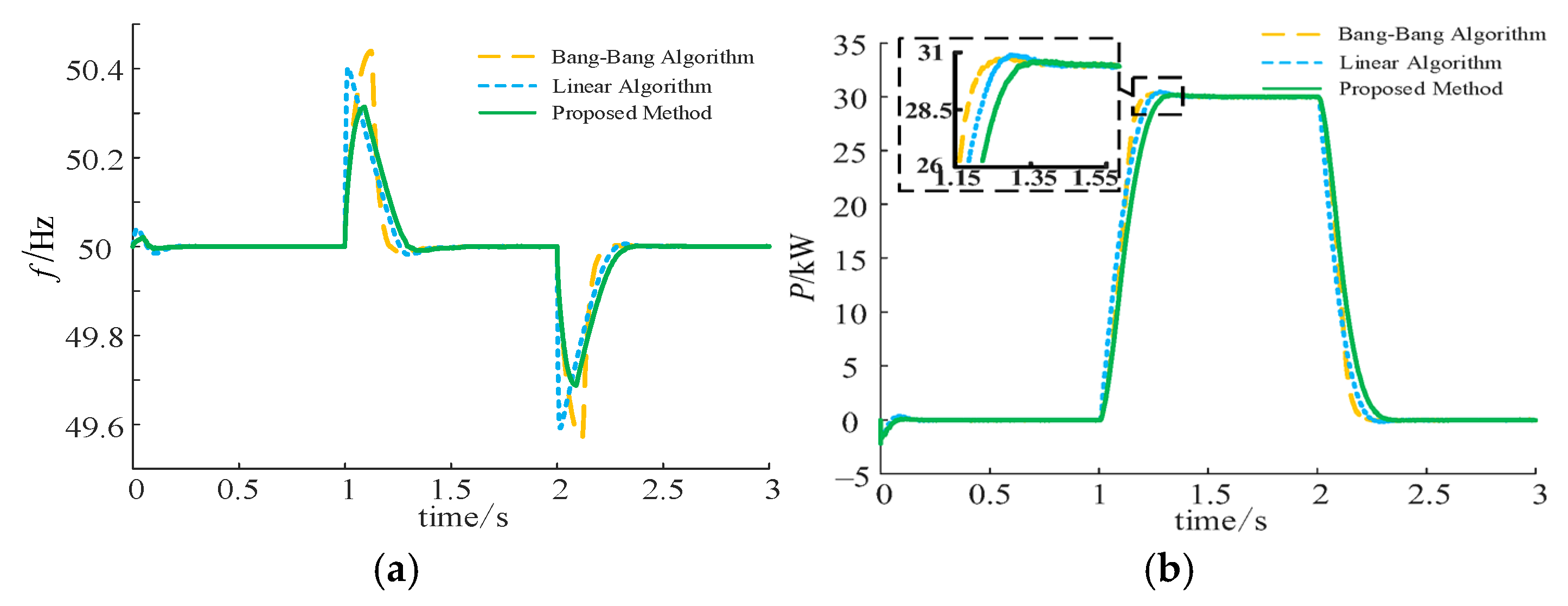
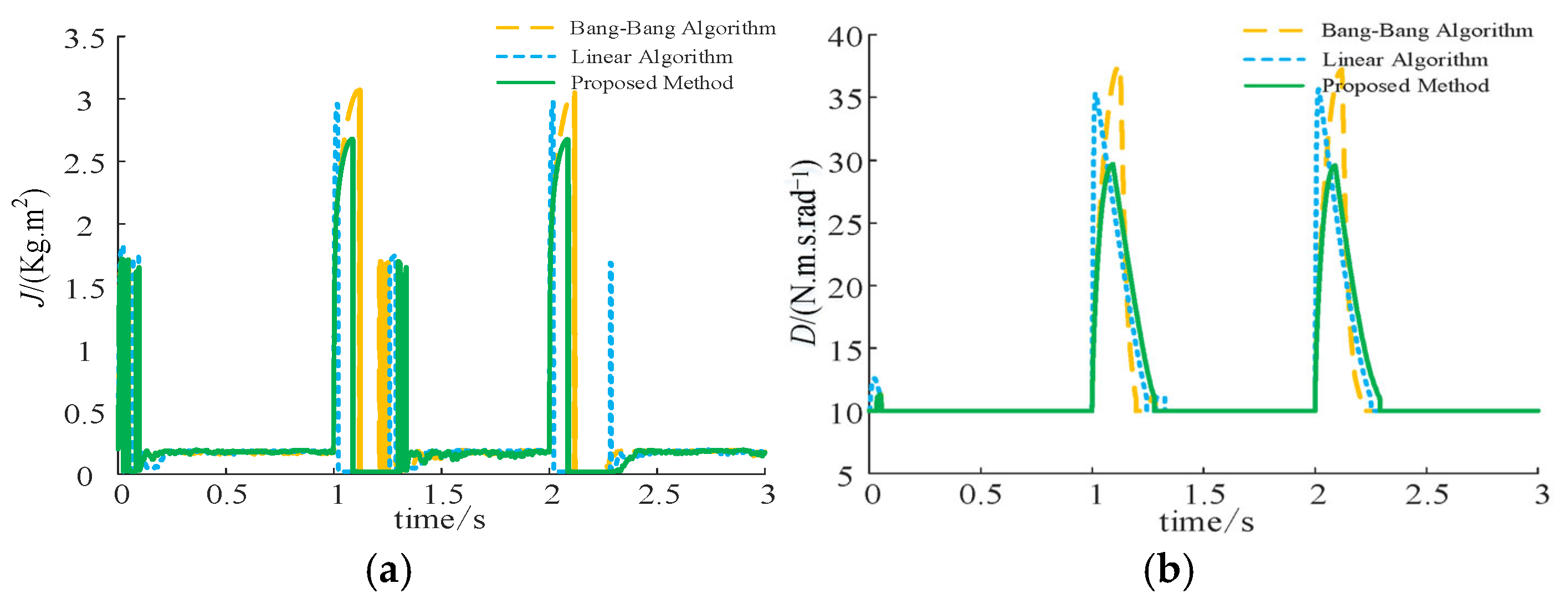
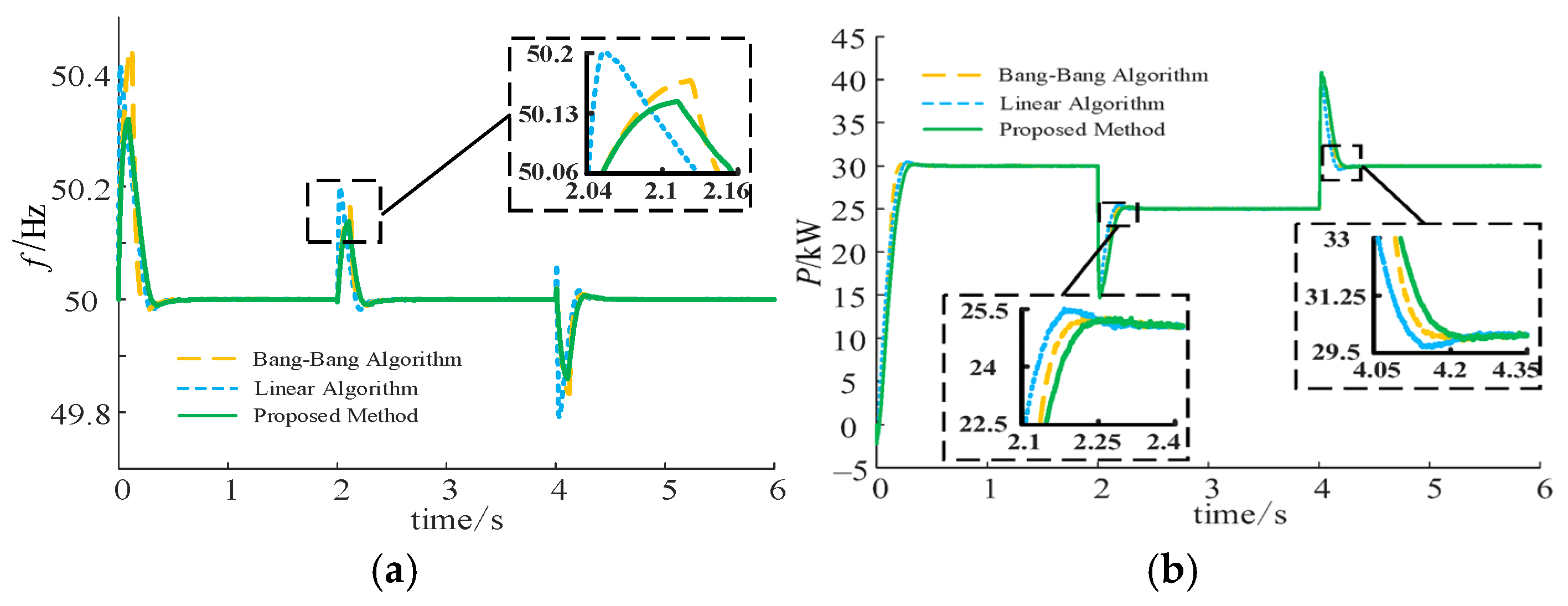
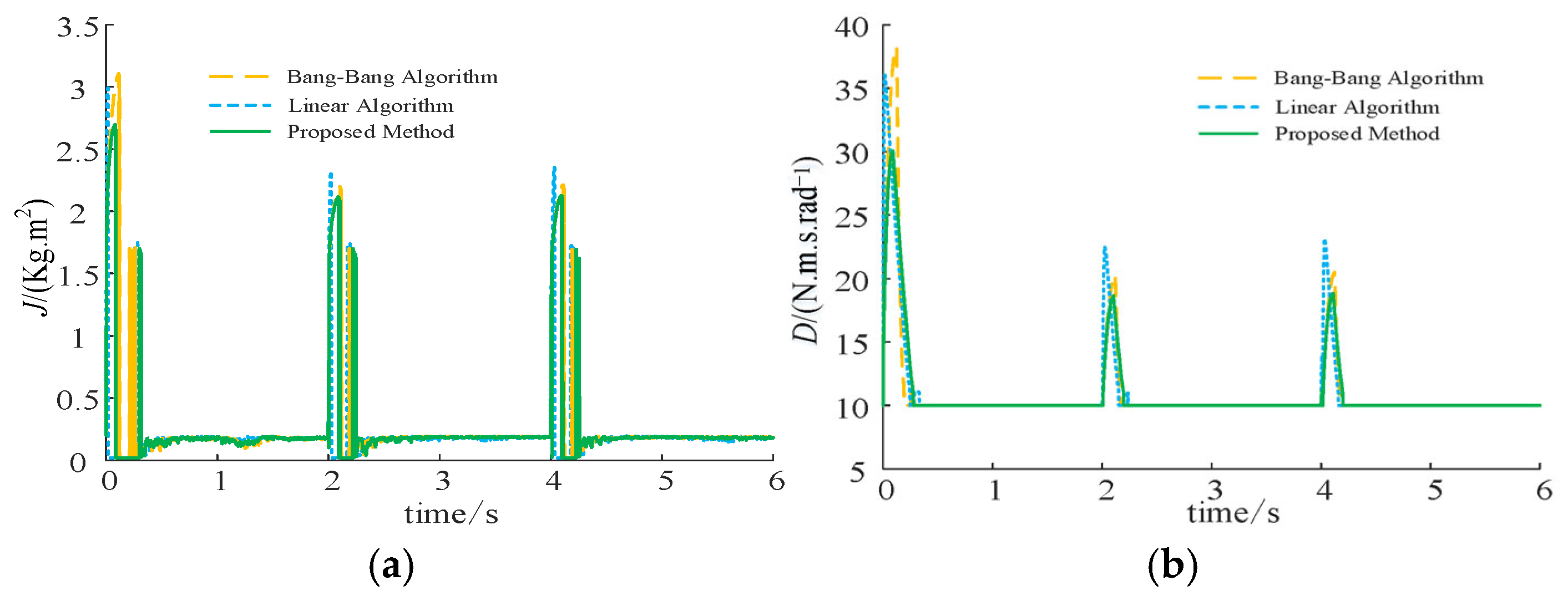
7.1. Validation of the Control Strategy Effectiveness Under Active Power Reference Variation
7.2. Validation of the Control Strategy Effectiveness Under Load Step Change
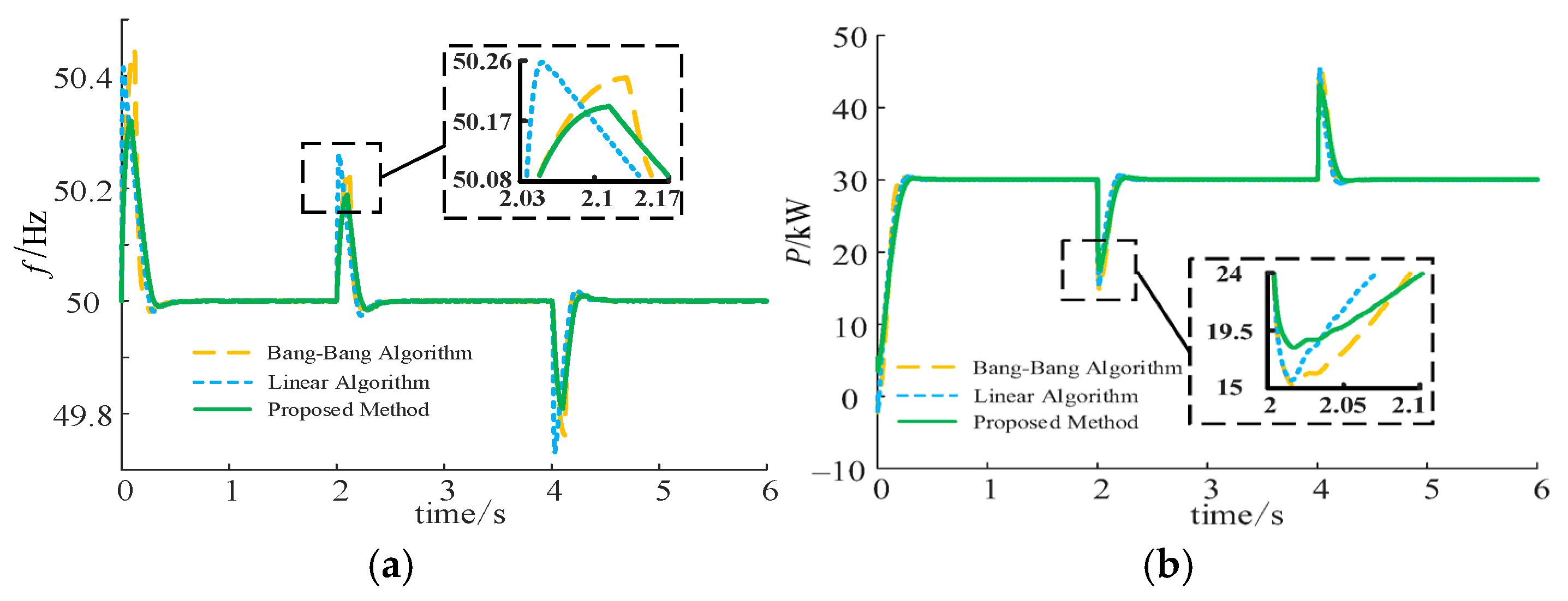
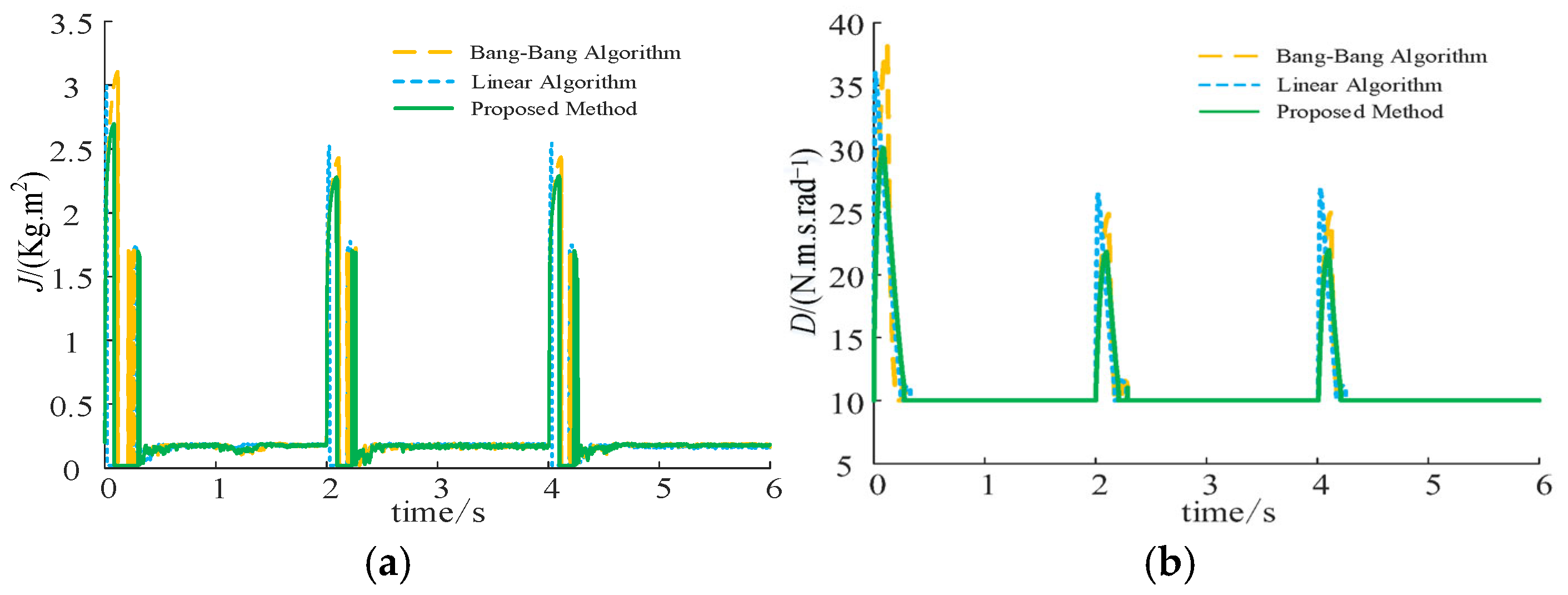
7.3. Validation of the Control Strategy Effectiveness Under Combined Disturbance Variation
8. Conclusions
- (1)
- Revealing the inherent coordinated mechanism of inertia–damping control: This paper confirms that virtual inertia primarily governs the system’s initial response to disturbances, while virtual damping plays a dominant role in suppressing oscillations and steady-state deviations. This study further reveals a coupled interaction between these two parameters during dynamic processes, and adjusting either parameter alone does not achieve optimal control. This provides a solid theoretical foundation for the coordinated regulation strategy.
- (2)
- Proposing a coordinated control framework that balances speed and stability: The proposed strategy optimizes the system’s dynamic response through decoupled control. Specifically, adaptive inertia regulation based on the RBF neural network intelligently manages the rate of change in frequency, while adaptive damping compensation, which is linearly related to frequency deviation, effectively suppresses overshoot. This coordinated mechanism allows the controller to perform optimally during different disturbance phases, ensuring stable system operation under various disturbance conditions.
- (3)
- Significant performance improvements validated through simulations: Under typical power step disturbances, the proposed strategy reduces the maximum frequency deviation by over 65% and active power overshoot by approximately 66.7%. Additionally, under load variation and composite disturbance conditions, frequency overshoot and power response are optimized by approximately 3.6% and 23.3%, respectively. These quantitative results demonstrate that the proposed coordinated control strategy offers significant advantages in enhancing system dynamic response, frequency stability, and power overshoot suppression.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Variable | Description |
| G(s) | Transfer function representing the relationship between system output and input. |
| P(s) | System output signal. |
| Pref(s) | Reference or target input signal for the system. |
| E, U | Input to the system (e.g., voltage, power). |
| ω0 | Natural frequency of the system, related to its inherent oscillatory properties. |
| Z | Impedance of the system, describing the relationship between current and voltage. |
| J | Moment of inertia of the system, determining its resistance to rotational movement. |
| D | Damping coefficient, affecting the system’s oscillatory behavior. |
| K | Gain constant, influencing the system response speed. |
| s | Complex frequency variable used in system analysis. |
| Vpv | Output voltage of the PV panel. |
| Ipv | Current from the PV panel. |
| Vdc | DC voltage in the system. |
| Cdc | DC voltage capacitor used for smoothing. |
| Lr | Inductor in the inverter. |
| Rr | Resistor in the inverter. |
| PCC | Point of Common Coupling, where the system connects to the grid. |
| Zr | Impedance of the grid. |
| Δω | Frequency deviation between the system and the grid. |
| dω/dt | Rate of frequency change. |
| J0 | Equivalent moment of inertia for the system. |
| w1, w2, w3, w4, w5 | Neural network weights used for system control. |
| p | Active power of the system. |
| ω | Angular velocity of the system. |
| S | Impedance of the system. |
| e | Error signal used for feedback control. |
| Uf | Reactive power loop voltage. |
| Kp | Proportional gain constant in the control loop. |
| Kd | Differential gain constant in the control loop. |
| E | Control error signal for adjustment. |
| SPWM | Sine wave pulse-width modulation for controlling inverter output. |
| ΔVud | Voltage error signal used to adjust output voltage. |
| Δg | Change in current. |
| * | Per unit value |
References
- Grover, H.; Sharma, S.; Verma, A.; Singh, B.; Mishra, S. Adaptive parameter tuning strategy of VSG-based islanded microgrid under uncertainties. Electr. Power Syst. Res. 2024, 235, 1108–1119. [Google Scholar] [CrossRef]
- Lu, S.; Zhu, Y.; Dong, L.H.; Li, J.; Wang, L.; Wang, Z. Small-signal stability research of grid-connected virtual synchronous generators. Energies 2022, 15, 7158. [Google Scholar] [CrossRef]
- Guo, L.; Xu, Z.; Jin, N.; Wang, Y.; Chen, H.; Liu, Y. A weighted voltage model predictive control method for a virtual synchronous generator with enhanced parameter robustness. Prot. Control Mod. Power Syst. 2021, 6, 482–492. [Google Scholar] [CrossRef]
- Wang, Z.; Meng, F.; Zhang, Y.; Wang, W.; Li, G.; Ge, J. Cooperative Adaptive Control of Multi-Parameter Based on Dual-Parallel Virtual Synchronous Generators System. IEEE Trans. Energy Convers. 2023, 38, 2396–2408. [Google Scholar] [CrossRef]
- Hou, X.; Sun, Y.; Zhang, X.; Lu, J.; Wang, P.; Guerrero, J.M. Improvement of Frequency Regulation in VSG-Based AC Microgrid Via Adaptive Virtual Inertia. IEEE Trans. Power Electron. 2020, 35, 1589–1602. [Google Scholar] [CrossRef]
- Karimi, A.; Khayat, Y.; Naderi, M.; Dragičević, T.; Mirzaei, R.; Blaabjerg, F.; Bevrani, H. Inertia response improvement in AC microgrids: A fuzzy-based virtual synchronous generator control. IEEE Trans. Power Electron. 2020, 35, 4321–4331. [Google Scholar] [CrossRef]
- Wang, Y.; Wai, R. Adaptive fuzzy-neural-network power decoupling strategy for virtual synchronous generator in micro-grid. IEEE Trans. Power Electron. 2022, 37, 3878–3891. [Google Scholar] [CrossRef]
- Chen, Y.; Hesse, R.; Turschner, D.; Beck, H.-P. Improving the grid power quality using virtual synchronous machines. In Proceedings of the 2011 IEEE 8th International Conference on Power Electronics and ECCE Asia (ICPE & ECCE), Jeju, Republic of Korea, 30 May–3 June 2011; pp. 1058–1065. [Google Scholar]
- Liu, C.; Li, B.; Zhang, Y.; Jiang, Q.; Liu, T. The LCC type DC grids forming method and fault ride-through strategy based on fault current limiters. Int. J. Electr. Power Energy Syst. 2025, 170, 110843. [Google Scholar] [CrossRef]
- Alipour, J.; Miura, Y.; Ise, T. Power system stabilization using virtual synchronous generator with alternating moment of inertia. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 451–458. [Google Scholar] [CrossRef]
- Zhao, H.; Dong, Y.; Sun, K. Data-driven virtual inertia control based on neural networks for microgrid frequency stability. Appl. Energy 2020, 275, 115353. [Google Scholar]
- Xiong, R.; Ma, Y.; He, H. An improved neural-network-based adaptive control method for grid-connected inverters in low-inertia power systems. Energy Rep. 2021, 7, 6452–6460. [Google Scholar]
- Liu, J.; Liu, X.; Liu, J.; Li, X.; Wang, J. Adaptive-Droop-Coefficient VSG Control for Cost-Efficient Grid Frequency Support. IEEE Trans. Power Syst. 2024, 39, 6768–6771. [Google Scholar] [CrossRef]
- Jain, A.; Pathak, M.K.; Padhy, N.P. Modified VSG Control for Enhancing Its Numerical Stability and Reducing the Impact on ULFO of System. IEEE Trans. Power Syst. 2025, 40, 1320–1334. [Google Scholar] [CrossRef]
- Utkarsha, P.; Naidu, N.K.S.; Sivaprasad, B.; Singh, K.A. A Flexible Virtual Inertia and Damping Control Strategy for Virtual Synchronous Generator for Effective Utilization of Energy Storage. IEEE Access 2023, 11, 124068–124080. [Google Scholar] [CrossRef]
- Li, L.; Zhou, K.; Tian, P. A Decentralized Control with Adaptive Virtual Inertia and Damping Combination for Islanded Cascaded-Type VSG Systems. IEEE Access 2023, 11, 139272–139283. [Google Scholar] [CrossRef]
- Li, C.; Yang, Y.; Cao, Y.; Aleshina, A.; Xu, J.; Blaabjerg, F. Grid Inertia and Damping Support Enabled by Proposed Virtual Inductance Control for Grid-Forming Virtual Synchronous Generator. IEEE Trans. Power Electron. 2023, 38, 294–303. [Google Scholar] [CrossRef]
- Jiang, K.; Su, H.; Lin, H.; He, K.; Zeng, H.; Che, Y. A Practical Secondary Frequency Control Strategy for Virtual Synchronous Generator. IEEE Trans. Smart Grid 2020, 11, 2734–2736. [Google Scholar] [CrossRef]
- Chen, S.; Sun, Y.; Han, H.; Shi, G.; Guan, Y.; Guerrero, J.M. Dynamic Frequency Performance Analysis and Improvement for Parallel VSG Systems Considering Virtual Inertia and Damping Coefficient. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 478–489. [Google Scholar] [CrossRef]
- Tao, L.; Zha, X.; Tian, Z.; Sun, J. Optimal Virtual Inertia Design for VSG-Based Motor Starting Systems to Improve Motor Loading Capacity. IEEE Trans. Energy Convers. 2022, 37, 1726–1738. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, Y.; Li, X.; Xu, Y.; Luo, C.; Li, Q. Active Power Oscillation Suppression Based on Decentralized Transient Damping Control for Parallel Virtual Synchronous Generators. IEEE Trans. Smart Grid 2023, 14, 2582–2592. [Google Scholar] [CrossRef]
- Fu, S.; Sun, Y.; Li, L.; Liu, Z.; Han, H.; Su, M. Power Oscillation Suppression of Multi-VSG Grid via Decentralized Mutual Damping Control. IEEE Trans. Ind. Electron. 2022, 69, 10202–10214. [Google Scholar] [CrossRef]
- Rathnayake, D.B.; Me, S.P.; Razzaghi, R.; Bahrani, B. H∞-Based Control Design for Grid-Forming Inverters with Enhanced Damping and Virtual Inertia. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 2311–2325. [Google Scholar] [CrossRef]
- Xiong, X.; Li, X.; Luo, B.; Huang, M.; Zhao, C.; Blaabjerg, F. An Additional Damping Torque Method for Low-Frequency Stability Enhancement of Virtual Synchronous Generators. IEEE Trans. Power Electron. 2024, 39, 15858–15869. [Google Scholar] [CrossRef]
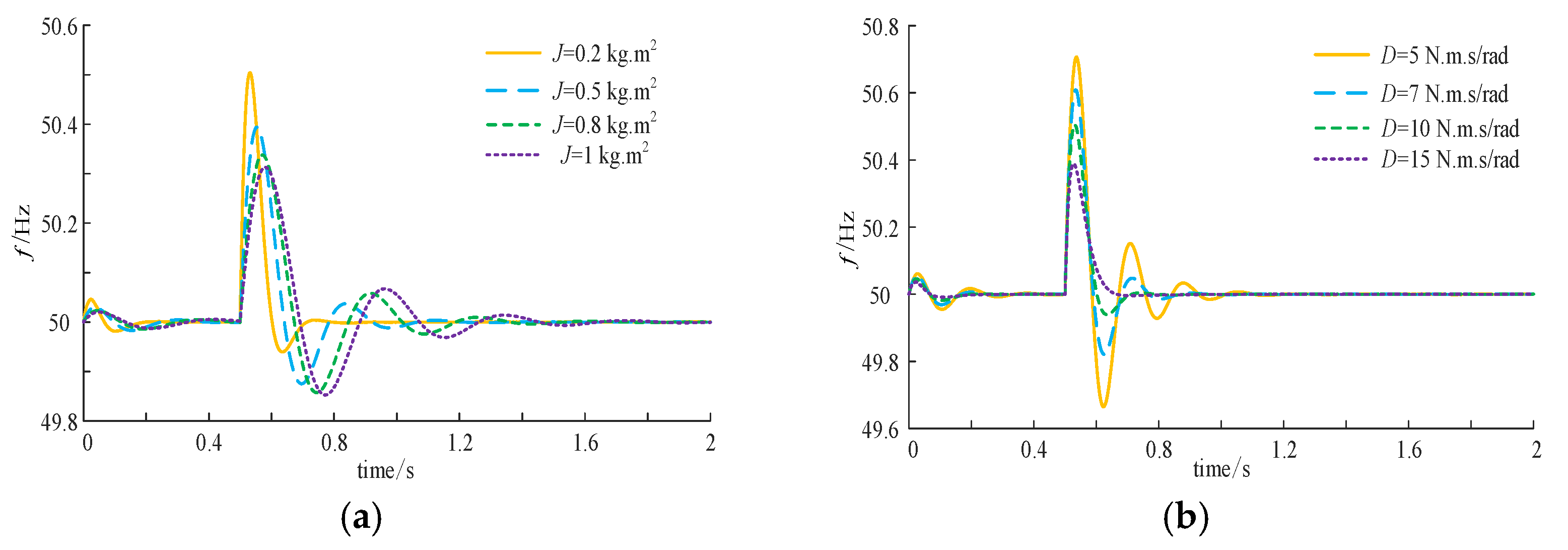

| Method | Inertia Adjustment | Damping Adjustment | Computational Complexity | Real-Time Applicability | Adjustment Accuracy |
|---|---|---|---|---|---|
| Fixed Parameters [6,7,8] | × | × | √ | × | × |
| Single-Parameter Adaptive Method [9] | √ | × | √ | × | × |
| Neural-Network-Based Adaptive Method [10,11,12,13] | √ | √ | × | × | √ |
| Linear-Algorithm-Based Adaptive Control [14,15] | √ | √ | √ | √ | × |
| Proposed Method | √ | √ | √ | √ | √ |
| Parameter | Value |
|---|---|
| DC Voltage Udc/V | 800 |
| Grid-Side Voltage U/V | 380 |
| Rated Frequency f/Hz | 50 |
| Inverter-Side Inductance L1/mH | 0.7 |
| Grid-Side Inductance L2/mH | 1.5 |
| Capacitor C/μF | 1500 |
| Rated Angular Frequency ω0/(rad·s−1) | 314 |
| Performance Metric | Bang–Bang Control | Linear Control | Proposed Method |
|---|---|---|---|
| Peak Frequency (Hz) | 49.59 | 50.31 | 49.88 |
| Maximum Frequency Deviation (Hz) | 0.41 | 0.48 | 0.12 |
| Peak Power (kW) | 30.32 | 30.48 | 30.18 |
| Power Overload (%) | 1.07 | 1.6 | 0.6 |
| Performance Metric | Bang–Bang Control | Linear Control | Proposed Method |
|---|---|---|---|
| Peak Frequency (Hz) | 50.24 | 50.26 | 50.19 |
| Maximum Frequency Deviation (Hz) | 0.24 | 0.26 | 0.19 |
| Power Response (kW) | 14.5 | 15 | 18.5 |
| Performance Metric | Bang–Bang Control | Linear Control | Proposed Method |
|---|---|---|---|
| Peak Frequency (Hz) | 50.16 | 50.2 | 50.13 |
| Maximum Frequency Deviation (Hz) | 0.16 | 0.2 | 0.13 |
| Power Response (kW) | −14.5 | −15 | −18.5 |
| Minimum Frequency (Hz) | −49.83 | −49.79 | −49.86 |
| Maximum Frequency Deviation (Hz) | 0.17 | 0.21 | 0.14 |
| Power Response (kW) | −14.5 | −15 | −18.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, H.; Ma, B.; Cheng, X.; Cui, Y.; Bo, L. Co-Adaptive Inertia–Damping Control of Grid-Forming Energy Storage Inverters for Suppressing Active Power Overshoot and Frequency Deviation. Energies 2025, 18, 4255. https://doi.org/10.3390/en18164255
Zheng H, Ma B, Cheng X, Cui Y, Bo L. Co-Adaptive Inertia–Damping Control of Grid-Forming Energy Storage Inverters for Suppressing Active Power Overshoot and Frequency Deviation. Energies. 2025; 18(16):4255. https://doi.org/10.3390/en18164255
Chicago/Turabian StyleZheng, Huiping, Boyu Ma, Xueting Cheng, Yang Cui, and Liming Bo. 2025. "Co-Adaptive Inertia–Damping Control of Grid-Forming Energy Storage Inverters for Suppressing Active Power Overshoot and Frequency Deviation" Energies 18, no. 16: 4255. https://doi.org/10.3390/en18164255
APA StyleZheng, H., Ma, B., Cheng, X., Cui, Y., & Bo, L. (2025). Co-Adaptive Inertia–Damping Control of Grid-Forming Energy Storage Inverters for Suppressing Active Power Overshoot and Frequency Deviation. Energies, 18(16), 4255. https://doi.org/10.3390/en18164255





