Fault Diagnosis of Rolling Bearings Under Variable Speed for Energy Conversion Systems: An ACMD and SP-DPS Clustering Approach with Traction Motor Validation

Abstract

Rolling bearing failures in rotating machinery essential to energy systems (e.g., motors, generators, or turbines) can cause downtime, energy inefficiency, and safety hazards—especially under variable speed conditions common in traction drives. Traditional diagnosis methods struggle with nonstationary signals from speed variations. In response, there is a growing trend toward unsupervised and adaptive signal processing techniques, which offer better generalization in complex operating scenarios. This paper proposes an intelligent fault diagnosis framework combining Adaptive Chirp Mode Decomposition (ACMD)-based order tracking with a novel Shortest Paths Density Peak Search (SP-DPS) clustering algorithm. ACMD is chosen for its proven ability to extract instantaneous speed profiles from nonstationary signals, enabling angular domain resampling and quasi-stationary signal representation. SP-DPS enhances clustering robustness by incorporating global structure awareness into the analysis of statistical features in both the time and frequency domains. The method is validated using both a public bearing dataset and a custom-built metro traction motor test bench, representative of electric traction systems. The results show over 96% diagnostic accuracy under significant speed fluctuations, outperforming several state-of-the-art clustering approaches. This study presents a scalable and accurate unsupervised solution for bearing fault diagnosis, with strong potential to improve reliability, reduce maintenance costs, and prevent energy losses in critical energy conversion machinery.

1. Introduction

With the accelerating urbanization and increasing demand for efficient public transportation, metro systems have become the backbone of modern cities. At the heart of these systems, traction motors serve as critical energy conversion units [1], directly influencing urban rail transit’s efficiency, reliability, and safety. Rolling bearings [2], indispensable components within traction motors, play a pivotal role in supporting mechanical loads and ensuring smooth operation. However, bearing faults can severely degrade energy conversion efficiency [3], reduce system reliability, and escalate operational costs due to unexpected downtime and maintenance requirements. Given the essential function of traction motors in energy systems, the accurate and intelligent diagnosis of rolling bearing faults is paramount for ensuring the reliable operation of energy conversion equipment and improving energy utilization efficiency [4]. Many fault diagnosis techniques have achieved notable success under constant speed conditions [5,6,7]. However, in practical applications such as metro systems, variable speed conditions are frequent due to fluctuating load demands and complex driving patterns. These conditions introduce nonlinear and nonstationary behaviors into vibration signals, complicating the fault diagnosis and potentially obscuring early-stage fault signatures [8]. The fault bearing of the motor runs at a variable speed, which leads to lower energy conversion efficiency and further increases energy waste, and there are also safety risks [9].

Order tracking techniques have been developed to address these issues and transform the time domain vibration signal into the order domain, which is invariant to speed fluctuations [10]. Order tracking (OT) technology can be classified into three main categories: hardware order tracking (HOT), computed order tracking (COT), and tacho-less order tracking (TLOT) [11]. HOT utilizes specialized analog hardware to sample data at a rate proportional to shaft speed [12], whereas COT employs constant-rate sampling followed by software-based resampling at fixed angular increments [13]. In contrast, TLOT estimates rotational speed indirectly from other signals, eliminating the need for tachometers [14]. These approaches typically resample signals into the angular domain, transforming them into cyclostationary signals before denoising, thereby enhancing fault detection in time-varying speed conditions. Adaptive Chirp Mode Decomposition (ACMD) has emerged as a promising method due to its capability to extract intrinsic mode functions with time-varying frequency characteristics [15]. Compared with traditional time-frequency analysis methods such as variational mode decomposition [16] or synchrosqueezing transform [17], ACMD provides better adaptability in tracking fast-varying fault-related components. Beyond traction motors, ACMD and related order tracking techniques have also been applied to various types of rotating machinery in energy and industrial domains. For instance, ACMD-based approaches have been used for fault diagnosis in wind turbine bearings, where speed fluctuations due to wind variation pose similar challenges [18]. In gas turbines and centrifugal pumps, adaptive order tracking techniques are applied to monitor critical components under load transients [19]. These studies demonstrate the generalizability of adaptive signal decomposition and tracking strategies across different energy-related technical systems.

Recent studies have attempted to integrate ACMD with order tracking to enhance fault feature extraction. For instance, some works employ resampling-based preprocessing followed by ACMD to decompose order-aligned signals [20]. Furthermore, a novel method based on particle swarm optimization (PSO) and ACMD, called parameter-adaptive ACMD [21], is exploited. To overcome the challenges of requiring prior knowledge of multivariate signal modes, a novel adaptive multivariate chirp mode decomposition (AMCMD) is proposed [22]. According to the vibration characteristics, active power and root mean square values based on an ACMD approach are developed [23]. To address sensitive input control parameter issues, a novel method called bandwidth-aware ACMD (BA-ACMD) is proposed based on ACMD in this article [24]. The above method has achieved outstanding results. However, it typically lacks a unified strategy for preserving order coherence during decomposition, which affects diagnosis robustness. The signal obtained by ACMD decomposition is still a non-stationary signal, and it is tough to perform intelligent fault diagnosis on this signal directly in the case of variable speed, which affects the diagnosis accuracy.

In addition, intelligent clustering methods play a vital role in the postprocessing stage of fault diagnosis by grouping similar features and identifying fault patterns without prior labeling [25]. The density peak clustering (DPC) algorithm has recently demonstrated strong potential due to its non-parametric and unsupervised nature [26]; for example, a novel diagnosis method for rolling bearing combined with the adaptive symmetrized dot pattern and density-based spatial clustering of applications with noise [27]. An optimized DPC method is proposed to realize online diagnosis solved by an improved BSO algorithm [28]. Meanwhile, an adaptive tensor density peaks search (ATDPS) clustering algorithm is proposed for the HS division of rolling bearing [29]. Such intelligent clustering methods have also been explored in other technical contexts. For example, enhanced DPC variants have been applied to detect bearing faults in aero-engines [30], gear wear in wind turbine gearboxes [31], and imbalance faults in industrial pumps [32], all of which share the characteristics of noisy, nonlinear, and nonstationary signal environments. These applications reinforce the importance and versatility of unsupervised clustering in fault diagnosis across a wide range of machinery. Nevertheless, its performance is often limited by sensitivity to parameter selection and density estimation in high-dimensional spaces [33].

Inspired by the successful application of ACMD and intelligent clustering across diverse rotating systems, this paper proposes an intelligent fault diagnosis framework for rolling bearings operating under variable speeds to address these limitations in energy-critical systems like metro traction motors. The framework integrates ACMD-based order tracking with a novel clustering strategy, Shortest Paths Density Peak Search (SP-DPS) [34]. ACMD enables adaptive extraction of fault-related order components, while SP-DPS improves clustering precision by considering global sample relationships. This combination enhances diagnostic reliability and enables timely maintenance decisions, ultimately contributing to metro traction systems’ improved energy efficiency and operational safety.

The main contributions of this study are summarized as follows:

(1)

An ACMD-based order tracking method is developed to enhance fault feature extraction under variable speed conditions.

(2)

A robust diagnosis framework combining ACMD and SP-DPS is proposed, tailored to the energy-critical scenario of traction systems.

(3)

Experiments on variable speed bearing datasets validate the proposed method’s effectiveness and practical applicability.

The remainder of this paper is organized as follows: Section 2 describes the related methodology in detail. Section 3 shows the proposed intelligent fault diagnosis framework. Section 4 presents experimental validations. Section 5 concludes the study and future directions for research.

2. Related Methodologies

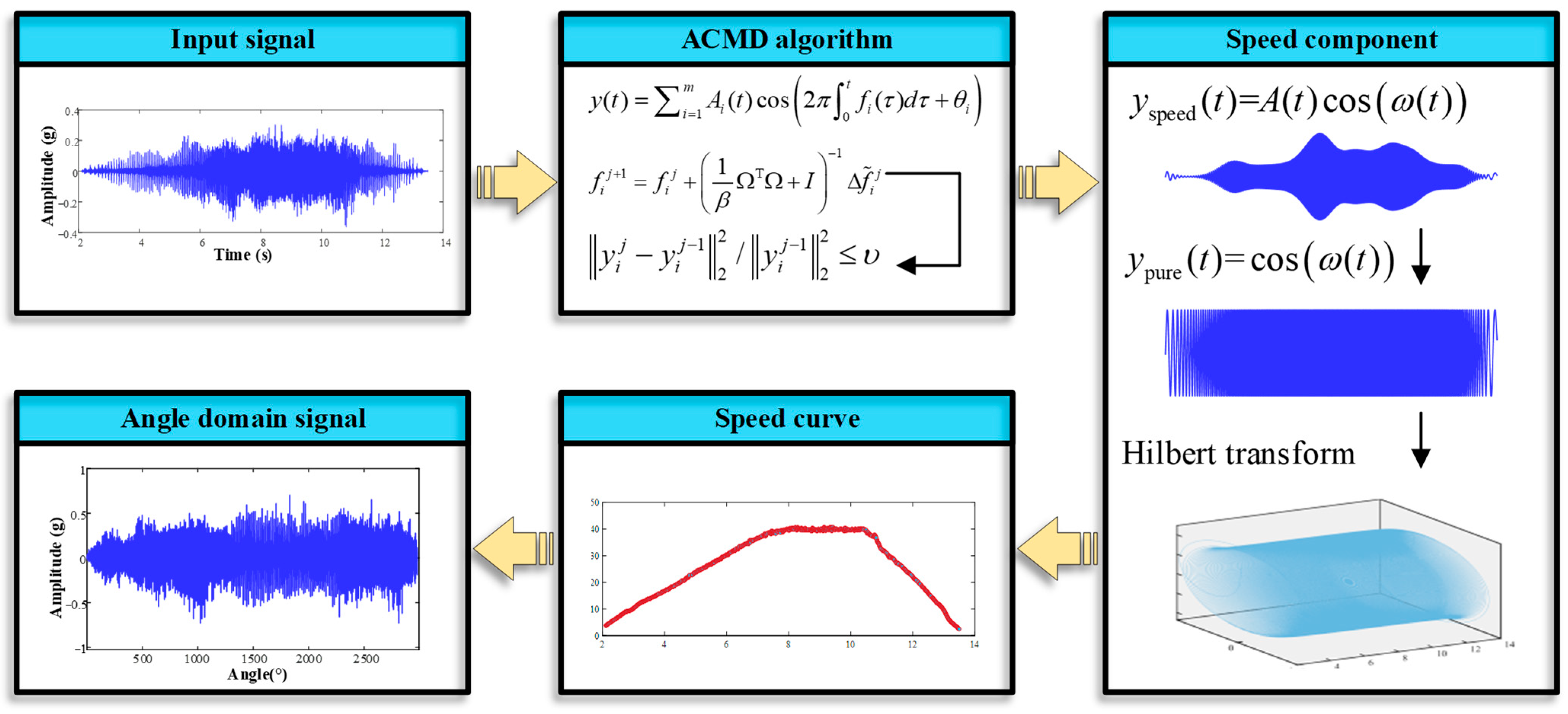
2.1. ACMD-Based Order Tracking Method

2.1.1. Review of the ACMD Algorithm

To extract mechanical fault signals with time-varying frequencies, Chen et al. proposed Variational Nonlinear Chirp Mode Decomposition (VNCMD) [35]. VNCMD aims to optimally recover the observed signal by simultaneously estimating multiple intrinsic modes, each characterized by a narrowband structure after being demodulated to baseband using their respective instantaneous frequency estimates. However, a key limitation of VNCMD lies in its requirement that the number of signal components, denoted by K, must be known a priori, along with initial estimates of the instantaneous frequencies for all K components. This joint optimization framework for simultaneously extracting all components can be impractical, particularly under strong interference conditions [15].

To address this limitation, Chen et al. developed an improved method called Adaptive Chirp Mode Decomposition (ACMD) [15], which builds upon the VNCMD framework. The notable advantage of ACMD is its use of a greedy algorithm, akin to the matching pursuit strategy, to extract signal components one at a time iteratively. This recursive extraction process alleviates the need to specify the number of components and their initial frequency estimates beforehand. ACMD isolates each target mode by solving the following constrained optimization problem:

$$\left\{\begin{array}{c}\underset{p_i(t),q_i(t),f_i(t)}{\min }\left\{{‖p_i^{″}(t)‖}_2^2+{‖q_i^{″}(t)‖}_2^2+\alpha {‖y(t)-y_i(t)‖}_2^2\right\}\\ s.t.y_i(t)=p_i(t)\cos \left(2\pi {\displaystyle {\int }_0^t{f}_i(t)dt}\right)+q_i(t)\sin \left(2\pi {\displaystyle {\int }_0^t{f}_i(t)dt}\right)\end{array}\right.$$

(1)

where $t$ denotes the duration of the signal, $y(t)-y_i(t)$ represents the residual energy, and $\alpha$ is the weighting factor. The function $f_i(t)$ denotes the instantaneous frequency. Furthermore, $p_i$ and $q_i$ are two de-chirped signals used to reconstruct the instantaneous amplitude of the i-th component. In practical applications, the signal is observed in discrete time. The discrete form of Equation (1) can thus be expressed as:

$$\underset{\left\{u_i\right\},\left\{f_i\right\}}{\min }\{{\Vert \Theta u_i\Vert }_2^2\}+\alpha {\Vert y-G_i{u}_i\Vert }_2^2$$

(2)

where $\Theta =\mathrm{Diag}(\Omega ,\Omega )$ is a second-order difference matrix. Furthermore:

$$\left\{\begin{array}{c}{u}_i={[p_i^T{q}_i^T]}^T\\ p_i={\left[\begin{array}{c}{p}_i(t_0),\dots ,p_i(t_N-1)\end{array}\right]}^T\\ q_i={\left[\begin{array}{c}{q}_i(t_0),\dots ,q_i(t_N-1)\end{array}\right]}^T\\ y={\left[\begin{array}{c}y(t_0),\dots ,y(t_N-1)\end{array}\right]}^T\end{array}\right.$$

(3)

Meanwhile, the $G_i$ in Equation (2) can be written as:

$$G_i=\left[\begin{array}{c}{C}_i,S_i\end{array}\right]$$

(4)

where $C_i=\mathrm{Diag}[\cos ({\phi }_i(t_0)),\dots ,\cos ({\phi }_i(t_{N-1}))]$, $S_i=\mathrm{Diag}[\sin ({\phi }_i(t_0)),\dots ,\sin ({\phi }_i(t_{N-1}))]$. Furthermore:

$${\phi }_i(t)=2\mathsf{\pi }{\displaystyle {\int }_0^t{f}_i}(\tau )d\tau$$

(5)

As shown in Equation (2), given the frequency function $f_i(\tau )$, the vector $u_i$ can be estimated by solving the $l_2$-regularized least-squares problem. Specifically, at the j-th iteration, $u_i$ is updated as:

$$u_i^j=\left[\begin{array}{c}{p}_i^j\\ q_i^j\end{array}\right]=arg \underset{\left\{u_i\right\}}{\min }\{{\Vert \Theta u_i\Vert }_2^2\}+\alpha {\Vert y-G_i^j{u}_i\Vert }_2^2$$

(6)

where $G_i^j$ consists of the frequency function $f_i\mathbf{(}\tau \mathbf{)}$, then the j-th iteration can be written as:

$$y_i^j=G_i^j{u}_i^j$$

(7)

The demodulated signals from Equations (6) and (7) are used to calculate the frequency increment as follows:

$$\Delta f_i^j(t)=-{\displaystyle \frac{1}{2\mathsf{\pi }}}{\displaystyle \frac{d}{dt}}\left({\displaystyle \frac{p_i^j(t)}{q_i^j(t)}}\right)$$

(8)

A low-pass filter is used to preprocess the frequency increment to reduce the noise interference in the actual working state. The instantaneous frequency can be finally updated as follows:

$$f_i^{j+1}=f_i^j+{\left({\displaystyle \frac{1}{\beta }}{\Omega }^T\Omega +I\right)}^{-1}\Delta f_i^j$$

(9)

where $I$ is the identity matrix. Here, a modal difference ${\nu }^j$ in the iteration process is defined as the termination condition of the iteration:

$${\nu }^j={\displaystyle \frac{\Vert f_i^j-f_i^{j-1}{\Vert }_2^2}{\Vert f_i^j{\Vert }_2^2}}$$

(10)

The operation of ACMD requires the input of an estimated frequency as the initial function. However, the signal obtained by ACMD decomposition is still a non-stationary signal, and it is tough to perform intelligent fault diagnosis on this signal directly. In the case of variable speed, the distribution of the signal will have a “long-tail effect,” which affects the diagnosis accuracy.

2.1.2. ACMD-Based Order Tracking

To overcome the limitations of traditional ACMD algorithms and better meet the demands of high-efficiency and reliable energy systems, we integrate ACMD with order-tracking techniques. Extracting the rotational speed component through ACMD and conducting post-processing on the original vibration signal effectively converts the non-stationary time domain signal—typical of variable speed operating conditions—into a stationary angular domain representation. This transformation enhances the clarity and stability of fault-related features, enabling more accurate and intelligent fault diagnosis. The proposed ACMD-based order tracking method improves diagnostic precision, enhances energy conversion efficiency, reduces system downtime, and lowers maintenance costs in critical applications such as metro traction motors. The five main steps of this method are illustrated in Figure 1.

(1)

Signal Acquisition: The original vibration signal is acquired from an acceleration sensor.

(2)

ACMD Decomposition: The acquired signal is processed using the ACMD algorithm. Following the procedure described in Section 2.1.1, the rotational speed component and several Amplitude Modulation–Frequency Modulation (AM–FM) signal components are extracted. Suppose the obtained AM–FM signal is as follows:

$$y(t)=A(t)\cos (wt)$$

(11)

(3)

FM Signal Conversion and Hilbert Transform: The AM–FM component corresponding to the rotational speed is converted into a purely frequency-modulated (FM) signal. This FM signal is subsequently processed using the Hilbert transform to obtain its analytic form. Suppose the obtained FM signal is as follows:

$$y(t)=\cos (wt)$$

(12)

Then, applying the Hilbert transform to Equation (11):

$$\widehat{y}(t)=y(t){\displaystyle \frac{1}{\pi t}}$$

(13)

(4)

Instantaneous Frequency Extraction: The instantaneous phase of the analytic signal is differentiated to obtain the instantaneous frequency, representing the rotational speed curve.

(5)

Angular Domain Resampling: Finally, the derived speed curve is used to resample the original vibration signal, thereby converting it into an angular domain signal suitable for further analysis. The key premise of angular domain resampling is to determine the resampling time. In this study, the resampling time is obtained by solving the integral equation of the speed curve:

$$2\mathsf{\pi }{\displaystyle {\int }_{T_0}^{T_n}{f}_i}(t)dt=n\cdot \Delta \theta$$

(14)

After the above five steps, we can convert the original signal into the angular domain signal, and the subsequent intelligent diagnosis processing can be carried out in the angular domain signal.

To enhance the clarity and reproducibility of the proposed signal processing framework, we present the detailed steps of the order tracking procedure in

Table 1. Detailed steps of the order tracking procedure.

Step	Description
Input	Time domain vibration signal $x(t)$; instantaneous rotational speed signal $\Omega (t)$ (or angular signal $\theta (t)$);
1	Apply ACMD to $x(t)$ to extract the dominant mode(s) representing the fault-related signal component;
2	Estimate the instantaneous angular position $\theta (t)={\displaystyle {\int }_0^t\omega (\tau )d\tau }$ (if only $\Omega (t)$ is available);
3	Define a uniform angular grid ${\theta }_i=i\cdot \Delta \theta ,i=1,\dots ,N$ over $[0,{\theta }_{\max }]$;
4	Interpolate the extracted signal $x(t)$ from the time domain to the angular domain: Use $\theta (t)$ and $x(t)$ to obtain $x(\theta )$ via interpolation;
5	Perform spectral analysis (e.g., FFT) on $x(\theta )$ to extract order components or construct an order spectrum;
Output	Angular domain signal $x(\theta )$; order spectrum or features for subsequent fault diagnosis.

. This procedure is integrated with the ACMD-based decomposition to convert the time domain signal into the angular domain, enabling effective extraction of order-related fault features under variable speed conditions. The pseudocode outlines the key steps, including angular position estimation, resampling, and subsequent spectral analysis. This structured representation serves as a practical guide for readers to understand and implement the order tracking module as part of the overall fault diagnosis pipeline.

2.2. Shortest Paths Density Peak Search

The DPS algorithm [36] operates based on two key assumptions. First, cluster centers are typically surrounded by neighboring data points with lower local densities. Second, cluster centers are located relatively far from other points with higher local densities. Based on these assumptions, DPS defines two indicators for each data point: (1) the local density $\rho$, which reflects the density around the current sample point, and (2) the distance $\delta$, which measures the distance from the current point to the nearest point with a higher density.

$${\rho }_i={\sum }_{j\in I_s\backslash \left\{i\right\}}{\mathrm{e}}^{-(d_{ij}/d_c)}$$

(15)

$${\delta }_i=\left\{\begin{array}{c}\min (d_{ij}),{\rho }_j>{\rho }_i\\ \max (d_{ij}),{\rho }_j<{\rho }_i\end{array}\right.$$

(16)

The Shortest Path Density Peak Clustering algorithm (SP-DPS) [34] questions the assignment strategy of the remaining points in the original DPS algorithm. It argues that such assignments should be based on global optimality rather than local decisions. In the DPS algorithm, the remaining points are assigned to the same cluster as the nearest point with a higher density. However, if a high-density point is misclassified, this error can propagate to its surrounding lower-density points, resulting in incorrect cluster assignments.

To address the assignment issue of the remaining points, the SP-DPS algorithm proposes a globally optimal strategy [34]. Point assignments should be based on the shortest path approach, where each remaining point is assigned to the cluster center that reaches it via the shortest path. Specifically, the algorithm introduces a virtual node s, which is connected to all cluster centers with zero distance. The goal is to compute the single-source shortest paths from node s to all other points, effectively constructing a minimum spanning tree rooted at s. A weighted path cost function is then defined as follows:

$${\xi }_p(\mathsf{\Gamma })={{\displaystyle \sum _{i,j\in \mathsf{\Gamma }}\left({\left|d_{i,j}\right|}^p\right)}}^{{\displaystyle \frac{1}{p}}}$$

(17)

when $P>1$, the path cost function ${\xi }_p(\mathsf{\Gamma })$ penalizes high-cost (i.e., long-distance) edges. As the value of $P$ increases, paths containing larger edge distances contribute more significantly to the overall path cost. At the limit, as $P$ approaches positive infinity, the path cost approximates the maximum single-edge distance along the path.

The SP-DPS algorithm argues that it is necessary to penalize such long-distance paths by assigning them larger weights, thereby preventing them from being included in the shortest path. The rationale is to prefer assembling a route composed of multiple short segments—even if the total path length is longer—over selecting a path that contains a single long edge, even if its total distance is shorter. This strategy helps avoid local clustering errors caused by interference from chain-like distributions. Since the single-source shortest path algorithm must compute the weighted shortest distance for all nodes in each iteration, its average time complexity is $O(n^2)$. A schematic diagram of the SP-DPS algorithm is shown in Figure 2.

Since the SP-DPS algorithm excels at identifying patterns in data with long-tail or skewed distributions, it is particularly effective for recognizing fault features under variable speed conditions—common in energy conversion systems such as metro traction motors. By accurately clustering these complex feature distributions, SP-DPS enhances the robustness of the diagnostic process. Therefore, this study integrates the intelligent fault diagnosis framework, with SP-DPS as the final stage, to ensure reliable identification of bearing faults. It supports timely maintenance decisions and helps minimize energy losses, improve operational reliability, and reduce the overall lifecycle cost of energy-critical equipment.

To facilitate a more precise understanding and practical implementation of the proposed method, the core steps of the SP-DPS (Shortest Path from Density Peaks with Trainable Path Cost) algorithm are summarized in pseudocode form in

Table 2. Pseudocode for the SP-DPS algorithm.

Step	Description
Input	Data points set X; distance function $dis{t}_{ij}$; estimated density ${\rho }_i$; density peak thresholds $t_r$, $t_d$; path cost function $Pat{h}_{cost}$ (e.g., minimax);
1	Construct a graph $G=(V,E,w)$ where $V=X$ and edge weights $w(i,j)=dis{t}_{ij}$ (fully connected or k-nearest neighbors);
2	Estimate the density ${\rho }_i$ for each point $i\in V$ (e.g., using a Gaussian kernel or neighborhood count);
3	For each point $i$, compute $\delta (i)=\min (dis{t}_{ij})\left|{\rho }_j>\right.{\rho }_i$;
4	Identify the set of density peaks: $P_t=i\left|\rho (i)>t_r\wedge \delta (i)>\right.t_d$;
5	Add a virtual source node s and connect it to each density peak $p\in P_t$ with a negligible edge cost D;
6	Apply Dijkstra’s single-source shortest path (SSSP) algorithm from s to all other nodes:Use $Pat{h}_{cost}$ to evaluate the path from s to each node x: For minimax cost: use the maximum edge weight in the path; For a trainable classifier: extract a fixed-length path fragment and evaluate it using a trained path classifier;
7	Assign each node x to the cluster associated with the density peak that its shortest path passes through;
8	Noise handling: if the path cost to a point exceeds a threshold (e.g., Otsu-based), mark it as noise;
Output	Cluster labels for all data points in X.

. This pseudocode outlines the entire clustering pipeline, including graph construction, density peak detection, and global association via Dijkstra’s algorithm using either a generic minimax path cost or a learned classifier-based cost function. The pseudocode provides a concise and systematic representation of the algorithm, serving as a practical reference for readers interested in reproducing or extending this work. In addition to this pseudocode, the official implementation of the SP-DPS algorithm, along with demo scripts for both the generic and trainable versions, can be found in Reference [29], which contains the MATLAB R2023a source code provided by the original authors.

Regarding computational complexity, the algorithm primarily relies on Dijkstra’s single-source shortest path (SSSP) algorithm, which has a time complexity of O(|E| + |V|\log|V|) when implemented using a Fibonacci heap for sparse graphs. Since the graph can be constructed with limited connectivity (e.g., k-nearest neighbors), the complexity remains tractable even for large datasets. The cost evaluation strategy further influences the overall complexity: the minimax formulation has constant-time path extension, while the trainable version may incur additional overhead due to fragment-based classification. Nevertheless, both versions maintain reasonable performance and scalability for medium- to large-scale clustering tasks.

To ensure scalability, especially for large datasets, a k-nearest neighbor (k-NN) graph can be employed in place of a fully connected graph. This reduces the number of edges to |E| = O(k|V|), keeping the computational cost nearly linear concerning the number of data points. For the generic (minimax) version of SP-DPS, each path extension involves only a simple comparison of edge weights, thus keeping the per-step cost low. For the trainable version, which uses a path fragment classifier, the cost per path extension depends on the evaluation of fixed-length path segments. This additional cost remains constant per step and does not affect the overall order of complexity. Overall, the SP-DPS algorithm remains computationally feasible for medium-to-large datasets and can be further optimized for real-time or large-scale scenarios through graph sparsification, precomputation of density peaks, and parallelization of path evaluations.

3. The Proposed Intelligent Fault Diagnosis Framework

Based on the computational procedures described in Section 2, the proposed framework—an intelligent fault diagnosis method for rolling bearings under variable speed conditions, integrating ACMD-based order tracking and shortest path density peak search (SP-DPS) clustering—is illustrated in the flowchart shown in Figure 3. This framework is designed to enhance the operational reliability and energy efficiency of critical systems such as metro traction motors, where bearing failures can lead to increased energy losses, unscheduled maintenance, and substantial economic impact. It consists of three main stages:

(1)

Data Acquisition: Vibration signals are directly collected from machinery operating under variable speed conditions, such as traction motors. These raw signals reflect the dynamic load and speed fluctuations typical of real-world energy conversion environments, making them valuable for fault detection.

(2)

Signal Processing: The collected vibration signals are processed using the proposed ACMD-based order tracking technique to improve diagnostic precision under these complex conditions. Specifically, the Adaptive Chirp Mode Decomposition (ACMD) algorithm extracts instantaneous speed information, which is then applied in the order tracking process to transform non-stationary time domain signals into stationary angular domain signals. This transformation enhances feature stability and provides a more informative representation for subsequent diagnosis, enabling better support for proactive maintenance and operational decision-making.

(3)

Fault Identification: In the final stage, discriminative features are extracted from the stationary signals in both the time and frequency domains, recognizing that bearing faults can exhibit multi-domain signatures.

These features, summarized in

Table 3. Time domain statistical features (TF_i).

Feature	Expression	Feature	Expression
$T{F}_1$	${\displaystyle \sum _1^{N}x(n)}/N$	$T{F}_6$	${\displaystyle \sum _1^N{(x\left(n\right)-T{F}_1)}^3}/\left(N-1\right)T{F}_2^3$
$T{F}_2$	$\sqrt{{\displaystyle \sum _1^N{(x\left(n\right)-T{F}_1)}^2}/N-1}$	$T{F}_7$	${\displaystyle \sum _1^N{(x\left(n\right)-T{F}_1)}^4}/\left(N-1\right)T{F}_2^4$
$T{F}_3$	${\left({\displaystyle \sum _1^N\sqrt{\left|x(N)\right|}}/N\right)}^2$	$T{F}_8$	$T{F}_5/T{F}_4$
$T{F}_4$	$\sqrt{{\displaystyle \sum _1^{N}x{(n)}^2}/N}$	$T{F}_9$	$T{F}_5/T{F}_3$
$T{F}_5$	$\max \left|x(n)\right|$	$T{F}_{10}$	$N\cdot T{F}_5/{\displaystyle \sum _1^N\left|x(n)\right|}$

and

Table 4. Frequency domain statistical features (FF_i).

Feature	Expression	Feature	Expression
$F{F}_1$	${\displaystyle \sum _1^{\Theta }s(\theta )}/\Theta$	$F{F}_7$	$\sqrt{{\displaystyle \sum _1^{\Theta }{f}_{\theta }^{2}s(\theta )}/{\displaystyle \sum _1^{K}s(\theta )}}$
$F{F}_2$	${\displaystyle \sum _1^{\Theta }{(s\left(\theta \right)-F{F}_1)}^2}/\Theta -1$	$F{F}_8$	$\sqrt{{\displaystyle \sum _1^{\Theta }{f}_{\theta }^{4}s(\theta )}/{\displaystyle \sum _1^K{f}_{\theta }^{2}s(\theta )}}$
$F{F}_3$	${\displaystyle \sum _1^{\Theta }{(s\left(\theta \right)-F{F}_1)}^3}/\Theta {(\sqrt{F{F}_2})}^3$	$F{F}_9$	${\displaystyle \sum _1^{\Theta }{f}_{\theta }^{2}s(\theta )}/\sqrt{{\displaystyle \sum _1^{K}s(\theta ){\displaystyle \sum _1^K{f}_{\theta }^{4}s(\theta )}}}$
$F{F}_4$	${\displaystyle \sum _1^{\Theta }{(s\left(\theta \right)-F{F}_1)}^4}/\Theta F{F}_2^2$	$F{F}_{10}$	$F{F}_6/F{F}_5$
$F{F}_5$	${\displaystyle \sum _1^{\Theta }{f}_{\theta }s(\theta )}/{\displaystyle \sum _1^{\Theta }s(\theta )}$	$F{F}_{11}$	${\displaystyle \sum _1^{\Theta }{\left(f_{\theta }-F{F}_5\right)}^{3}s(\theta )}/\Theta F{F}_6^3$
$F{F}_6$	$\sqrt{{\displaystyle \sum _1^K{\left(f_{\theta }-F{F}_5\right)}^{2}s(\theta )}/\Theta }$	$F{F}_{12}$	${\displaystyle \sum _1^{\Theta }{\left(f_{\theta }-F{F}_5\right)}^{4}s(\theta )/\Theta F{F}_6^4}$

, serve as inputs to the SP-DPS clustering algorithm, which performs unsupervised pattern identification. It is acknowledged that certain time domain features, such as kurtosis (TF6), can be sensitive to impulsive outliers unrelated to bearing faults (e.g., external impacts) when analyzed in raw vibration signals [37]. However, within the proposed framework, the ACMD-based order tracking process (Section 2.1.2) significantly mitigates this concern. By transforming the signal into the angular domain, non-synchronous impulsive events are attenuated, allowing features like kurtosis to more reliably reflect fault-induced impulses synchronized with shaft rotation. Furthermore, the robustness of the SP-DPS clustering algorithm (Section 2.2) to potential feature noise and outliers provides additional resilience. With its ability to handle complex data structures and skewed distributions, SP-DPS ensures robust classification of fault types. It directly minimizes diagnostic uncertainty, improves system reliability, and optimizes the effectiveness of maintenance strategies in energy-critical applications. The SP-DPS algorithm is primarily evaluated in the subsequent experiments by comparing it with five other state-of-the-art (SOAT) methods.

4. Experimental Verification

4.1. Experiment 1: Bearing Fault Under Variable Speed Without Load

To validate the proposed method’s effectiveness in improving the operational reliability and energy efficiency of critical rotating equipment, this study employs a widely used and publicly available bearing fault dataset [38], which has become a benchmark in condition monitoring and intelligent fault diagnosis research. The test bench used in Experiment 1 with the faulty bearing is displayed in Figure 4.

As shown in Figure 4b, the experimental platform consists of three main components: a variable speed motor, a shaft-mounted rotor, and an adjustable mechanical load that simulates realistic operating conditions typical of energy conversion systems such as metro traction drives. Vibration signals were collected using a high-sensitivity piezoelectric accelerometer mounted above the drive-end bearing via a magnetic base, ensuring firm contact and minimizing signal distortion. The drive end, subject to higher mechanical stress and thermal variation in real-world systems, is often the most failure-prone point in traction motors. The data acquisition was performed using the CoCo80 system, a high-performance and portable data recorder capable of capturing high-frequency signals. The sampling rate is 25.6 kHz to ensure acceptable temporal resolution and accurate capture of transient fault signatures that may impact energy transmission efficiency and equipment health. The bearings tested were of type NSK6203, with the faulty bearing deliberately located at the drive end of the motor to emulate fault-prone conditions in energy-critical machinery. Six fault scenarios were introduced, including inner race faults (IF) and outer race faults (OF), each with three progressive severity levels. These defects were precisely manufactured using controlled machining techniques to represent typical degradation patterns in service. Figure 4a illustrates the geometry and severity of the faults. By validating the proposed diagnostic framework under such controlled yet representative conditions, this experiment demonstrates its capability to accurately identify faults under variable speed conditions and support preventive maintenance strategies. The experimentation is vital for improving system uptime, reducing unplanned energy losses, and lowering the long-term operational costs of key energy conversion equipment in applications such as urban rail transit and industrial drives. The fault type and fault severity are presented in

Table 5. The type of fault and its damage.

Type of Fault	Area of Failure (mm2)	Depth of Damage (mm)
IF	4	0.5
IF	8	4
IF	12	2
OF	4	4
OF	8	8
OF	12	12

.

The control strategy for the variable speed condition is implemented as follows: the variable speed condition is linearly accelerated from the static state to the rated speed of 3000 rpm, and a constant speed is maintained for 5 s before undergoing linear deceleration to complete rest. Its normal signal sample and variable speed curve are shown in Figure 5.

The vibration signals corresponding to these six fault categories were collected using the aforementioned setup and are presented in Figure 6. These signals serve as the basis for evaluating the effectiveness of this study’s proposed signal denoising and fault feature extraction techniques.

After acquiring the data, the signal is processed using the ACMD algorithm according to the flowchart shown in Figure 3, and the rotational speed curve is extracted. Based on this curve, order tracking is performed to convert the signal in Figure 6 into an angular domain signal. The resulting angular domain signals for the six fault types are shown in Figure 7.

As shown in the flowchart in Figure 3, feature extraction is required first in the fault diagnosis process. The data is divided into multiple fault data samples based on the obtained angular domain signals. Each angular domain signal segment used for feature calculation contains 2000 points, resulting in 50 samples for each fault category and 350 samples.

In order to show the changes of time domain features and frequency domain features in the process of variable speed, TF4 of time domain features and FF4 of frequency domain features are extracted and plotted in Figure 8. From Figure 8, it can be observed that the time domain features and frequency domain features will change with the change of speed.

Figure 9 shows the feature distributions obtained using the original time domain and angular domain signals, respectively. The x-axis and y-axis represent the feature dimensions obtained through the T-SNE dimensionality reduction method. As presented in Figure 9, although the feature space after ACMD and order tracking processing is still not optimally distributed, it visually demonstrates clear separability.

To further validate the performance of the SP-DPS method for bearing fault diagnosis under variable speed conditions, we compared it with four relatively novel clustering methods of the same category and the original DPS clustering method. The comparison was conducted by inputting the processed features (i.e., those in Figure 9b) into six different clustering algorithms and obtaining their final clustering results.

It is essential to clarify that Figure 9b represents the T-SNE visualization of the extracted features after angular domain transformation and serves as the standard input for all subsequent clustering algorithms, including SP-DPS. In contrast, Figure 10 presents the clustering results obtained by applying different clustering methods to these same features. Thus, while the distributions in the subfigures of Figure 10 appear visually similar to Figure 9b, their underlying meaning differs: Figure 9b reflects pre-clustering feature space, and Figure 10 shows post-clustering label assignments.

Furthermore, to evaluate the quality of feature separability, the Silhouette Average Value (Sav) [39] is used as a quantitative indicator. A higher Sav indicates better feature distribution for clustering. The comparison between Figure 9a (raw signal) and Figure 9b (angular domain signal) shows that the proposed method significantly improves Sav, validating its superiority in feature extraction and transformation.

The methods used for comparison include DAP clustering [36], ATDPS clustering [29], K-medoids clustering [40], and DBSCAN clustering [41]. The clustering results obtained by all methods are shown in Figure 10. For a further comparison, the quantified statistics are shown in

Table 6. Experimental results obtained by different methods.

Experiment	Approach	Correct/Total	Accuracy	Real Fault/Identified
Experiment 1	SP-DPS	342/350	97.7%	7/7
	DPS	252/350	72.0%	7/12
	ATDPS	211/350	60.3%	7/14
	K-medoids	205/350	58.5%	7/7
	DAP	209/350	59.7%	7/17
	DBSCAN	266/350	76.0%	7/5
Experiment 2	SP-DPS	311/320	97.2%	4/4
	DPS	198/320	61.9%	4/8
	ATDPS	204/320	63.7%	4/14
	K-medoids	254/320	79.4%	4/4
	DAP	237/320	74.1%	4/14
	DBSCAN	262/320	81.8%	4/4

.

These results confirm the superior fault discrimination capability of SP-DPS in complex, nonstationary environments. Specifically, SP-DPS achieved an accuracy of 97.7%, substantially outperforming DPS (72.0%) and ATDPS (60.3%), which often misclassified samples due to local density errors or sensitivity to parameter choices. The key advantage of SP-DPS lies in its global optimization strategy for point assignment, which considers the shortest path from density peaks rather than relying solely on local proximity. This design reduces the risk of error propagation, particularly in cases involving long-tailed or overlapping sample distributions. Furthermore, SP-DPS effectively captures the actual cluster structure in high-dimensional feature spaces, enhancing the diagnostic resolution without requiring prior labeling or extensive hyperparameter tuning. These findings validate the practical value of the proposed method for diagnosing variable speed bearings in critical energy systems.

4.2. Experiment 2: Bearing Fault Under Variable Speed with Load

To further demonstrate the proposed method’s practical applicability and engineering value in real-world energy systems, a second experiment was conducted using a metro traction motor bearing test platform. As displayed in Figure 11, this experimental setup is specifically designed to emulate the operational conditions of metro train traction systems, where bearing faults can lead to reduced energy efficiency, increased maintenance costs, and even safety risks in urban rail transport.

The test bearing, a cylindrical roller bearing (SKF-NU216), is mounted on the right side of the platform, representing a typical load-bearing position in traction motors. During the experiment, analog vibration signals are collected and converted into digital form using a high-fidelity data acquisition device and then transmitted to a PC-based monitoring system for real-time processing. Three piezoelectric accelerometers are strategically positioned on the bearing housing—covering horizontal, vertical, and axial (parallel) directions—to capture multidimensional vibration characteristics that reflect complex fault dynamics under variable speed operation. Each channel is sampled at 20 kHz to capture high-frequency fault components accurately. The experimental procedure includes a complete variable speed profile: initial acceleration, steady-state running, and final deceleration to a complete stop. This dynamic operation replicates the actual load cycles experienced by traction motors in metro systems, making it ideal for validating diagnostic algorithms aimed at energy-critical applications.

In the experiment, the speed change simulates the train accelerating from 0 to 80 km/h and then decelerating to 0, as displayed in Figure 12. The curves of its speed change and the normal bearing vibration signal are shown in Figure 1. In Experiment 2, we used the magnetic powder brake to load the 1 (horsepower, HP) on the traction motor, causing it to run with a load. This is also to draw a contrast with running without a load in Experiment 1. It is worth noting that the load remained unchanged in Experiment 2. This paper primarily analyzed the speed change, so it did not consider whether the load changed or not. In future studies, we will consider the case where speed and load are changed simultaneously.

This experiment tests the proposed ACMD-based order tracking and SP-DPS clustering framework under conditions that closely mirror those in service environments. The results highlight the method’s ability to identify early-stage bearing degradation amid speed fluctuations and signal interference. The experiment supports predictive maintenance and fault prevention. It contributes to improved energy utilization, enhanced operational reliability, and extended service life of traction equipment—key goals in pursuing efficient and sustainable urban rail transport systems. Three types of bearing faults were introduced in the experiment: outer ring fault, inner ring fault, and rolling element fault. The corresponding fault signals are presented in Figure 13.

As follows in the flowchart in Figure 3, the raw vibration signal, which is inherently non-stationary due to the varying rotational speed, is first subjected to ACMD. This algorithm is particularly well-suited for analyzing non-stationary signals, as it adaptively extracts intrinsic mode functions that reflect the underlying time-varying frequency components. This study employs the ACMD algorithm to isolate the dominant component associated with the shaft’s rotational speed. This extracted speed profile is then utilized to perform order tracking, transforming the time domain signal into the angular domain, thereby eliminating the influence of speed fluctuations and enabling a more consistent analysis of fault characteristics.

Figure 14 illustrates the angular domain signal obtained through this order-tracking process. It clearly observes that the originally non-stationary raw signal, which contains frequency modulation due to speed variation, has been successfully converted into a quasi-stationary signal in the angular domain. This transformation facilitates the identification of repetitive patterns associated with bearing faults, which are otherwise obscured in the time domain.

In this experiment, each angular domain signal segment used for feature calculation contains 2048 points, resulting in 80 samples for each fault category and a total of 320 samples. Furthermore, in order to show the changes of time domain features and frequency domain features in the process of variable speed, TF4 of time domain features and FF4 of frequency domain features are extracted and plotted in Figure 15. From Figure 15, it can be observed that the time domain features and frequency domain features will change with the change of speed. This is similar to Experiment 1.

To quantitatively assess the effect of this transformation on downstream tasks, feature extraction was performed on both the raw time domain signal and the angular domain signal. A consistent feature set was employed for both signals, including time domain statistical features, frequency domain descriptors, and time–frequency representations.

The extracted features are visualized in Figure 16 using a dimensionality reduction method for clarity. As illustrated in Figure 16, the feature samples derived from the angular domain signal demonstrate a more compact and well-separated distribution than those from the raw signal. This improved clustering tendency indicates a higher inter-class separability and lower intra-class variance, desirable properties for subsequent classification or clustering tasks. Moreover, a quantitative comparison based on the Sav index reveals that the angular domain features yield a significantly higher Sav score, confirming their superior clustering performance. This validates the effectiveness of combining ACMD and order tracking as a preprocessing pipeline for bearing fault diagnosis under varying speed conditions.

This experiment adopts an identical comparison strategy to ensure consistency with the evaluation framework established in Experiment 1 and further to verify the effectiveness and generalizability of the proposed method. Specifically, five representative clustering algorithms from the same category are selected for benchmarking. These include the proposed SP-DPS method and four existing methods—DPS, ATDPS, K-medoids, and DAP—alongside the widely used density-based algorithm DBSCAN. The clustering results obtained from all methods are visualized in Figure 17 for comparative analysis. For a further parameter comparison in Figure 17, we have quantified the statistics in Table 6.

As illustrated, SP-DPS maintains excellent performance under more challenging operational conditions with variable loads, achieving an accuracy of 96.0%. The method exhibits consistent precision across multiple fault types and shows improved resilience to the noise and nonstationary signal introduced by realistic metro traction motor operation. Compared to traditional clustering methods, SP-DPS’s shortest-path-based assignment and density-aware clustering mechanism enable it to better adapt to non-ideal data distributions, reducing intra-class dispersion and enhancing inter-class separation. Importantly, SP-DPS was able to identify all real fault categories correctly (4/4). At the same time, other methods, such as DAP and ATDPS, introduced excessive or erroneous clusters due to their sensitivity to outliers or density thresholds. These results support the practical scalability and generalization of the proposed framework, making it well-suited to early fault detection and predictive maintenance in mission-critical transportation and industrial systems.

The outcomes demonstrate the superior performance of the proposed SP-DPS algorithm, particularly in environments characterized by nonstationary signals and variable speed operating conditions—conditions common in energy-critical systems such as traction motors and other industrial drives. These operating regimes often challenge conventional clustering algorithms, which exhibit poor reliability due to their sensitivity to irregular data distributions and complex feature geometries. In contrast, SP-DPS shows marked robustness and adaptability, enabling accurate fault pattern recognition even when signal characteristics deviate significantly from ideal assumptions. This advantage stems from its path-guided clustering strategy, which captures long-tailed or nonlinearly separable data’s intrinsic topological structure and continuity. By preserving global relationships among data samples, SP-DPS avoids local misclassification and ensures more stable diagnostic results. Thereby, SP-DPS supports proactive maintenance, reducing unplanned downtime, and enhancing key equipment’s overall operational efficiency and energy performance within modern transportation and industrial energy systems.

By integrating this path-based strategy, SP-DPS is better equipped to preserve local neighborhood relationships and identify meaningful cluster boundaries, even in cases involving significant speed fluctuations or transient dynamics. The proposed method is well-suited for real-world applications involving nonuniform rotational profiles, such as fault diagnosis in rotating machinery operating under variable speed or start–stop conditions. These results further underscore the practical value and scalability of SP-DPS in data-driven condition monitoring tasks.

5. Conclusions

This study proposes an intelligent fault diagnosis framework tailored for rolling bearings operating under variable speed conditions. It integrates ACMD-based order tracking with the SP-DPS clustering algorithm. Beyond methodological innovation, the proposed approach is positioned as a practical solution to the pressing challenges of energy efficiency, system reliability, and maintenance cost in critical energy conversion equipment such as traction motors used in metro systems and industrial drives. The following key conclusions can be drawn:

(1)

Reliable signal transformation for energy-critical systems: The ACMD-based order tracking method effectively transforms nonstationary time domain signals into stationary angular domain signals, providing a robust foundation for fault feature extraction even under fluctuating speed conditions. This enhances the reliability of condition monitoring in dynamic operating environments, contributing to improved energy efficiency and reduced unexpected failures.

(2)

Enhanced diagnostic robustness: By leveraging a global path-guided clustering mechanism, the SP-DPS algorithm overcomes the limitations of traditional clustering methods, particularly in handling complex, long-tailed, and nonlinearly separable fault features. The higher fault identification precision, which supports earlier and more accurate maintenance decisions critical for reducing downtime and lowering operational costs in high-demand energy applications.

(3)

Validated performance in realistic energy scenarios: Experimental validation across two platforms—including a metro traction motor bearing testbed—demonstrates that the proposed method consistently delivers superior diagnostic accuracy (up to 97.3% and 96.0%, respectively). These results affirm the framework’s effectiveness in safeguarding the reliability and safety of energy systems.

In summary, the proposed method is a technically sound diagnostic tool and a valuable enabler for enhancing the energy utilization efficiency and operational stability of critical rotating machinery. In future work, the proposed method will be further extended and validated for other types of rotating machinery, including wind turbines, pumps, and gas turbines. These applications will help assess the generalization capability of the algorithm under diverse working conditions, fault modes, and sensor configurations. Additionally, issues such as noise robustness, sensor placement sensitivity, and adaptability to unseen fault types will be systematically investigated. Furthermore, in research with a practical application, the running efficiency of the algorithm, the memory consumption of the hardware, and the energy consumption of the overall operation are mainly considered. Only when the speed and accuracy reach a certain level is the method used in this paper applicable in practice.