Learning Residual Distributions with Diffusion Models for Probabilistic Wind Power Forecasting

Abstract

Accurate and uncertainty-aware wind power forecasting is essential for reliable and cost-effective power system operations. This paper presents a novel probabilistic forecasting framework based on diffusion probabilistic models. We adopted a two-stage modeling strategy—a deterministic predictor first generates baseline forecasts, and a conditional diffusion model then learns the distribution of residual errors. Such a two-stage decoupling strategy improves learning efficiency and sharpens uncertainty estimation. We employed the elucidated diffusion model (EDM) to enable flexible noise control and enhance calibration, stability, and expressiveness. For the generative backbone, we introduced a time-series-specific diffusion Transformer (TimeDiT) that incorporates modular conditioning to separately fuse numerical weather prediction (NWP) inputs, noise, and temporal features. The proposed method was evaluated using the public database from ten wind farms in the Global Energy Forecasting Competition 2014 (GEFCom2014). We further compared our approach with two popular baseline models, i.e., a distribution parameter regression model and a generative adversarial network (GAN)-based model. Results showed that our method consistently achieves superior performance in both deterministic metrics and probabilistic accuracy, offering better forecast calibration and sharper distributions.

1. Introduction

Wind power forecasting is essential for maintaining the reliability and economic efficiency of power systems with high shares of renewable energy [1]. It supports key operations such as grid stability, market participation, and reserve scheduling [2]. While deterministic forecasting methods provide single-point estimates of future wind power output, they often fail to account for the inherent uncertainty in wind behavior and limitations of numerical weather prediction (NWP) models [3]. This lack of uncertainty representation restricts their value in risk-sensitive applications like real-time dispatch or energy trading [4].

Probabilistic forecasting addresses this limitation by offering a full distribution of potential outcomes rather than a single estimate [5]. This enables power system operators and market participants to assess forecast confidence, quantify operational risks, and make more robust decisions under uncertainty [6]. In practice, probabilistic forecasts are particularly valuable in applications such as reserve allocation and energy bidding, where understanding both expected outcomes and associated uncertainties is crucial [7]. As the share of wind energy increases, the need for such uncertainty-aware forecasting becomes even more critical to ensure secure and cost-effective system operation [8].

Probabilistic wind power forecasting (PWPF) can be categorized by prediction horizons, with short-term forecasting—typically covering the next 24 h—being the most directly applicable to real-time operations [9]. Short-term PWPF often relies on NWP data as major inputs to model the relationship between weather conditions and future power output [10]. Due to the dynamic variability in atmospheric conditions and the evolving state of the power system, modeling this relationship remains a complex yet impactful research problem. Moreover, short-term PWPF holds distinct engineering value by balancing forecast accuracy and uncertainty quantification, aligning well with operational timescales for power system planning and decision-making [11]. Given its high practical relevance and technical challenges, short-term PWPF forms the core focus of this study.

In response to the limitations of traditional statistical methods (i.e., quantile regression [5], kernel density estimation [12], and Gaussian process regression [13]), machine learning (ML)-based approaches have become the dominant paradigm in PWPF. These data-driven methods are capable of modeling nonlinear relationships, capturing high-dimensional spatiotemporal features from NWP inputs, and scaling to large datasets in operational environments. Within this modern framework, three major model categories have emerged: (1) distribution-based approaches that predict parameters of assumed probability distributions [14], (2) generative adversarial network (GAN)-based methods that approximate the conditional distribution via adversarial training [15], and (3) diffusion probabilistic models that generate forecast samples through a learned reverse stochastic process [16]. These categories reflect different trade-offs in modeling assumptions, generative flexibility, and computational behavior, as compared in

Table 1. Comparison of three typical categories of PWPF methods.

Category	Distribution-Based	GAN-Based	Diffusion-Based
Distribution assumption	Explicit (e.g., Gaussian, Beta)	N/A	N/A
Expressiveness	Low (limited by fixed form)	Moderate (theoretically flexible)	High (naturally multimodal)
Training stability	High (easy to train)	Low (unstable training)	High (stable convergence)
Uncertainty modeling	Weak (fail with skewed or multimodal patterns)	Moderate (usually poorly calibrated)	High (well-calibrated outputs)
Sampling efficiency	High (closed form)	High (single pass)	Moderate (multi-step)
Limitations	Rigid assumptions, limited flexibility	Mode collapse, temporal inconsistency	Slower sampling, higher inference cost

.

The first category (i.e., distribution-based methods) assumes that future wind power outputs follow a predefined probability distribution—commonly Gaussian, Beta, Gamma, Weibull, or a mixture of Gaussians. A neural network is trained to predict the parameters (e.g., mean and variance) of the chosen distribution based on historical and NWP-derived features. Sampling from the resulting distribution yields the probabilistic forecast. While this approach is conceptually simple and computationally efficient, its performance is inherently limited by the correctness of the distributional assumption. Moreover, such models often struggle to represent complex, multimodal, or skewed uncertainty patterns that frequently arise in real-world wind power scenarios.

The second category (GAN-based methods [17]) avoids explicit distributional assumptions by learning to model the entire conditional data distribution. A generator takes both known inputs and injected noise to produce plausible future power sequences, while a discriminator distinguishes real from generated sequences. Through adversarial training, the generator learns to produce outputs that closely resemble the true data distribution. Once trained, the generator enables probabilistic forecasting by sampling multiple trajectories from different noise inputs. Despite their theoretical flexibility, GAN-based models suffer from practical challenges, including mode collapse, unstable optimization, and difficulties in capturing temporal consistency and calibrated uncertainty, limiting their robustness in high-stakes forecasting tasks.

The third and increasingly prominent category involves diffusion probabilistic models, which offer a new framework for generative modeling by learning to reverse a multi-step stochastic corruption process [18]. In this setup, a forward process gradually adds noise to training data, while a neural network is trained to learn the reverse denoising process. For wind power forecasting, diffusion models generate future trajectories conditioned on past observations and NWP features by progressively transforming noise into realistic outputs. Unlike previous approaches, diffusion models do not rely on restrictive distributional assumptions and naturally support flexible, multimodal generation. They also exhibit stable training dynamics and produce well-calibrated outputs across forecast horizons [19]. These advantages make diffusion models especially suited for representing the diverse and uncertain nature of short-term wind power evolution.

Diffusion-based generative modeling has progressed rapidly in recent years. The denoising diffusion probabilistic model (DDPM) [19] brought diffusion models into the spotlight by framing data generation as a progressive denoising process. Although effective, the DDPM requires hundreds or even thousands of sampling steps due to its discrete-time formulation, resulting in significant computational overhead. Concurrently, score-based models [20] adopted Langevin dynamics to guide the denoising process using learned gradients of the data distribution. While these models improved sample quality, they remained bound to inefficient discrete-time sampling. To alleviate this issue, subsequent work formulated diffusion in the continuous-time domain using stochastic differential equations (SDEs) [18], enabling the integration of high-order ordinary differential equation (ODE)/SDE solvers to accelerate inference without compromising generation quality. Building on this, the flow-matching [21] framework proposed to model the transformation from prior to data distribution as a continuous velocity field, bypassing score estimation altogether and offering a new perspective rooted in probability transport.

A major milestone was the introduction of the elucidated diffusion model (EDM) [22], which systematically unified the above approaches under a general theoretical framework. The EDM demonstrated that prior methods could be interpreted through a common lens based on noise scaling and training objectives, thereby clarifying their implicit connections. On top of this unified view, the EDM proposed a simplified and highly effective parameterization of the diffusion trajectory, yielding improved stability, faster convergence, and better sample fidelity. It has since become a leading approach in diffusion-based modeling, delivering state-of-the-art results across multiple domains while significantly reducing sampling steps [23]. This makes the EDM not only theoretically elegant but also practically advantageous for real-world applications that demand both accuracy and efficiency—such as probabilistic forecasting in energy systems.

This study introduces ResD-PWPF, a novel residual diffusion-based probabilistic wind power forecasting framework. Built upon EDM, ResD-PWPF brings key improvements over existing approaches in terms of modeling formulation, diffusion strategy, and architectural design. Specifically, our approach differs from prior work in three main aspects:

(1) Modeling strategy: Rather than directly predicting the probability distribution of future wind power values, we adopt a two-stage approach that decouples the forecasting task into deterministic prediction and probabilistic error modeling. A deterministic model first produces the baseline forecast, and a conditional diffusion model is then used to estimate the distribution of the residual error between the prediction and the ground truth. This strategy allows the diffusion model to focus solely on modeling uncertainty, leading to more efficient learning, sharper uncertainty characterization, and improved interpretability [24].

(2) Diffusion framework: We adopt the EDM [22] in place of the more commonly used DDPM [19]. The EDM offers continuous noise scale control, improved conditioning via $\sigma$-parameterization, and a more stable training process. These features enhance sampling quality, enable better calibration of forecast distributions, and allow for more expressive modeling of complex uncertainty structures—attributes that are particularly beneficial for short-term wind power forecasting.

(3) Architecture design: For the conditional generation network, we adopt the time diffusion Transformer (TimeDiT) [25,26], a recent architecture designed for time-series generative modeling. Unlike conventional methods that fuse known features, noise, and timestep embeddings via simple concatenation, TimeDiT introduces a modular conditioning mechanism. Specifically, known inputs, noise vectors, and temporal encodings are separately processed through modulation networks, which inject scale and shift parameters into different Transformer layers. This structured integration improves the network’s ability to hierarchically fuse diverse information sources, leading to more accurate and calibrated probabilistic forecasts.

To validate the effectiveness of the proposed ResD-PWPF, we perform extensive experiments on open-source data from ten wind farms provided by the Global Energy Forecasting Competition 2014 [27] (GEFCom2014). The proposed ResD-PWPF is compared against two baseline approaches: a parameter-prediction model based on predefined distributional assumptions, and a GAN-based generative model. For the deterministic component of the forecast, we evaluate mean value prediction accuracy using root mean square error (RMSE) and mean absolute error (MAE). For probabilistic forecasts, we use the continuous ranked probability score (CRPS), which measures the quality of the predicted distribution by jointly assessing calibration (how well the predicted probabilities reflect observed frequencies) and sharpness (the concentration of the distribution). To further examine whether the observed performance differences between models are statistically meaningful, we apply the Wilcoxon signed-rank test (WSRT), a non-parametric test that evaluates paired differences without assuming a specific distribution. Experimental results show that the proposed ResD-PWPF consistently outperforms both baselines across all evaluation metrics, confirming its superior ability to capture both the central tendency and the uncertainty of future wind power outputs.

The remainder of this paper is structured as follows. Section 2 outlines the overall workflow of the proposed ResD-PWPF framework. Section 3 elaborates on the EDM-based diffusion formulation tailored for time-series applications. Section 4 describes the architecture of the TimeDiT model and its design principles. Section 5 presents the experimental setup and case study results based on the GEFCom2014 dataset. Section 6 concludes the paper and discuss the future perspectives for advancing the field.

2. Workflow of the ResD-PWPF

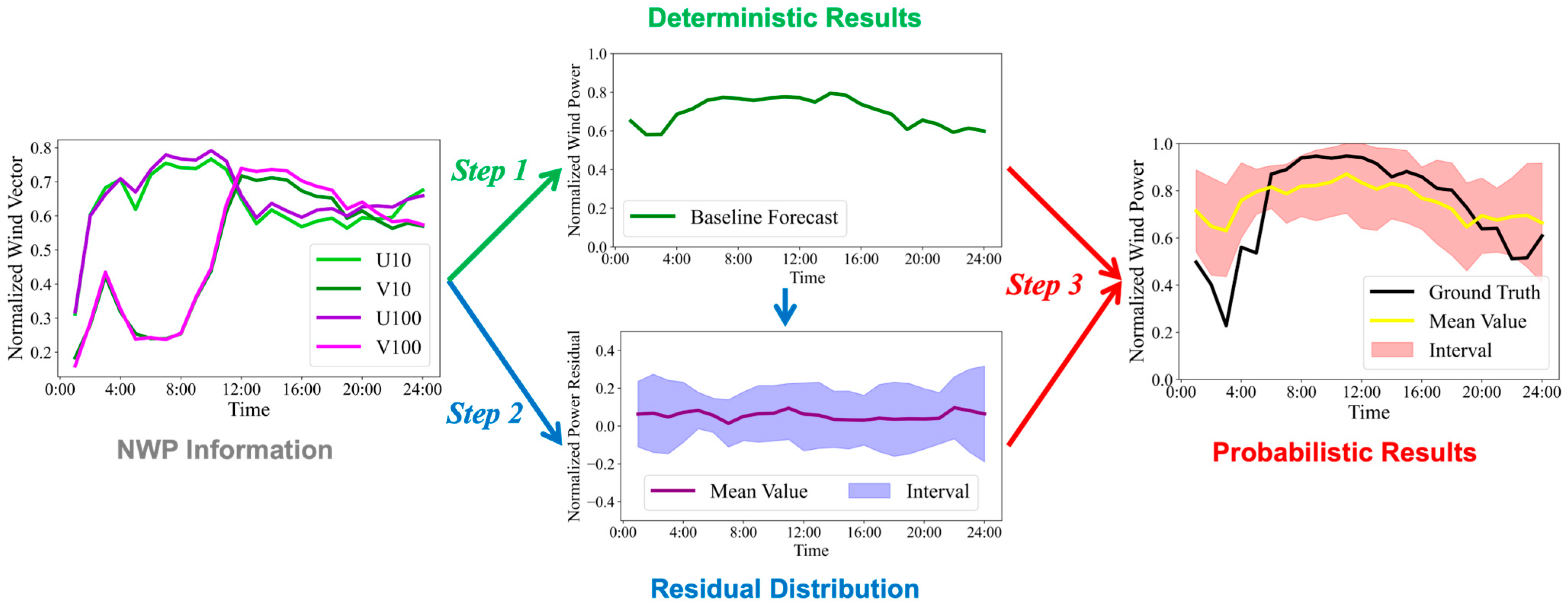
The overall workflow of the proposed ResD-PWPF framework is illustrated in Figure 1, which consists of three steps to generate the final PWPF results.

• Step 1: A deterministic power forecasting model is first applied to generate point forecasts based on NWP inputs. This process is formulated as Equation (1), where ${\mathcal{F}}_{DP}$ denotes the deterministic predictor, $\mathit{n}\mathit{w}\mathit{p}\in {\mathbb{R}}^{\mathrm{S}\times {\mathrm{C}}_{nwp}}$ represents the NWP input sequence ($\mathrm{S}$ represents the overall length of the sequence, while ${\mathrm{C}}_{nwp}$ indicates the dimensionality of the features), and ${\tilde{\mathit{y}}}_{DP}\in {\mathbb{R}}^{\mathrm{S}\times 1}$ denotes the resulting deterministic wind power forecasting results.

$${\tilde{\mathit{y}}}_{DP}={\mathcal{F}}_{DP}\left(\mathit{n}\mathit{w}\mathit{p}\right)$$

(1)

• Step 2: This step models the error uncertainty in the deterministic predictions. Specifically, given both the NWP inputs and the deterministic forecasts, a residual modeling module learns the distribution of forecasting errors at each time step. As shown in Equation (2), ${\mathcal{F}}_{PP}$ refers to the probabilistic residual prediction model, while ${\tilde{\mathit{\mu }}}_{PP}\in {\mathbb{R}}^{\mathrm{S}\times 1}$ and ${\tilde{\mathit{\sigma }}}_{PP}\in {\mathbb{R}}^{\mathrm{S}\times 1}$ represent the mean and standard deviation of the residual distribution, respectively.

$$[{\tilde{\mathit{\mu }}}_{PP}, {\tilde{\mathit{\sigma }}}_{PP}]={\mathcal{F}}_{PP}(\mathit{n}\mathit{w}\mathit{p},{\tilde{\mathit{y}}}_{DP})$$

(2)

• Step 3: The deterministic forecasts are combined with the estimated residual distributions to obtain the full probabilistic forecasts. The average value of the resulting predictive distribution ${\tilde{\mathit{y}}}_{PP}\in {\mathbb{R}}^{\mathrm{S}\times 1}$ is given by Equation (3), and its standard deviation directly corresponds to the residual uncertainty estimated in Step 2.

$${\tilde{\mathit{y}}}_{PP}={\tilde{\mathit{y}}}_{DP}+{\tilde{\mathit{\mu }}}_{PP}$$

(3)

As shown in the workflow above, Step 3 simply combines the deterministic forecasts and the estimated residual distributions to produce the final probabilistic prediction. Therefore, the core modeling efforts of this study are concentrated in the first two stages, corresponding to deterministic modeling and uncertainty (residual) modeling, respectively. In this study, in Step 1—deterministic modeling—we adopt one of the most widely used and effective strategies for short-term wind power forecasting: using a Transformer [28] encoder to map NWP sequences to wind power series. The model is configured with a hidden dimension of 128 and consists of two encoder layers. Each layer uses the GELU activation function and employs 8 self-attention heads. During training, the Adam optimizer is used with mean squared error (MSE) as the loss function. Step 2 is centered on two key aspects: the training and inference strategy of the diffusion model (i.e., EDM), and the architectural design of the model itself (i.e., TimeDiT), which are discussed in detail in Section 3 and Section 4.

The proposed two-stage decomposition strategy—comprising an initial point prediction model followed by residual modeling—is theoretically justified even when the residuals are not purely stochastic. In real-world forecasting tasks, especially in complex systems such as wind power, the initial model may fail to capture all temporal dependencies, nonlinearities, or regime-specific behaviors, leaving behind structured and learnable residual patterns. In such cases, the residual component is not merely noise but also contains additional predictive signals.

This decomposition aligns with the principle of functional approximation, where a complex mapping is incrementally approximated by simpler components. The first-stage model captures the dominant signal, while the second-stage model acts as a corrective mechanism to refine prediction accuracy. Furthermore, from a statistical perspective, the two-stage approach can be interpreted through bias-variance decomposition [24]: the first stage aims to reduce bias, and the residual stage reduces variance by modeling finer deviations. This layered refinement strategy enhances both expressiveness and generalization, especially when modeling uncertainty or adapting to distributional shifts.

3. Training and Inference Formulation Using EDM

Figure 2 illustrates the basic principle of applying diffusion models to time-series forecasting. The framework consists of two main stages: the forward diffusion process and the reverse denoising process. In the forward process, the original time series ${\mathit{x}}_{\mathbf{0}}$ is gradually perturbed by adding Gaussian noise, eventually becoming a noisy version ${\mathit{x}}_{\mathit{T}}$ that approximately follows an isotropic Gaussian distribution. In the reverse process, we start by sampling an initial noisy sequence ${\tilde{\mathit{x}}}_{\mathit{T}}$ from the Gaussian distribution. This sequence is then progressively denoised using a trained diffusion model to generate a predicted sequence ${\tilde{\mathit{x}}}_{\mathbf{0}}$. In this study, ${\mathit{x}}_{\mathbf{0}}$ specifically represents the residual between the deterministic forecast and the actual wind power output.

Since the initial noise ${\tilde{\mathit{x}}}_{\mathit{T}}$ is sampled stochastically, each denoising trajectory can lead to a different outcome ${\tilde{\mathit{x}}}_{\mathbf{0}}$. By generating multiple predictions with different noise samples, we can estimate the distribution of future sequences, thereby achieving probabilistic time-series forecasting.

A central focus in the design of diffusion models lies in formulating an effective forward noise schedule and enhancing the model’s ability to learn the reverse denoising process. In this work, we adopt the EDM [22] as the core framework. Compared to conventional diffusion models, the EDM offers a more flexible noise scaling mechanism, enabling stable training across a wide range of noise levels. It also improves the precision and expressiveness of the output generated. Furthermore, the EDM demonstrates superior sampling efficiency and numerical robustness, making it particularly well-suited for PWPF.

3.1. Modeling Training in EDM

During training, the EDM abandons the discrete time-step-based noise scheduling in the traditional DDPM and instead samples a continuous noise level, enabling a more flexible and generalized forward diffusion strategy. Given a clean data sample ${\mathit{x}}_{\mathbf{0}}$, the noisy input ${\mathit{x}}_{\mathit{\sigma }}$ is generated as in Equation (4) [22]. Here, $\sigma$ represents the noise scale, sampled from a log-uniform distribution that spans a broad range from low to high noise. $\mathit{ϵ}$ is standard Gaussian noise with the same shape as ${\mathit{x}}_{\mathbf{0}}$.

$${\mathit{x}}_{\mathit{\sigma }}={\mathit{x}}_{\mathbf{0}}+\sigma ·\mathit{ϵ}$$

(4)

The EDM aims to train a denoising model ${\mathit{F}}_{\mathit{\theta }}$, which is going to predict the original sequence ${\tilde{\mathit{x}}}_{\mathbf{0}}$ based on the current noisy sequence ${\mathit{x}}_{\mathit{\sigma }}$ and the corresponding noise level $\sigma$, as illustrated in Equation (5) [22].

$${\tilde{\mathit{x}}}_{\mathbf{0}}={\mathit{F}}_{\mathit{\theta }}({\mathit{x}}_{\mathit{\sigma }},\sigma )$$

(5)

During model training, this study employs the MSE as a loss function to encourage the predicted original sequence ${\tilde{\mathit{x}}}_{\mathbf{0}}$ to be as close as possible to the ground truth ${\mathit{x}}_{\mathbf{0}}$. The model parameters are optimized using the Adam optimizer to ensure efficient and stable convergence.

To enhance prediction stability across varying noise levels, the EDM does not directly use the raw output of the neural network as the final prediction. Instead, it introduces three scale coefficients during training and inference [22]: skip scale factor $c_{skip}\left(\sigma \right)$, input scale factor $c_{in}\left(\sigma \right)$, and output scale factor $c_{out}\left(\sigma \right),$ which are used to rescale the input and output before combining them. Assuming the original neural network is denoted as ${\mathit{f}}_{\mathit{\theta }}$, the expression for ${\mathit{F}}_{\mathit{\theta }}$ is given in Equation (6). The three scaling coefficients are computed as shown in Equations (7)–(9), where ${\sigma }_{data}$ represents the standard deviation of the dataset. To further stabilize training across different noise levels, the EDM also incorporates a loss weighting coefficient $\lambda \left(\sigma \right)$, which adjusts the contribution of each training sample based on its noise scale. The weight coefficient is defined as in Equation (10).

$${\mathit{F}}_{\mathit{\theta }}\left({\mathit{x}}_{\mathit{\sigma }},\mathit{\sigma }\right)=c_{skip}\left(\sigma \right)·{\mathit{x}}_{\mathit{\sigma }}+c_{out}\left(\sigma \right)·{\mathit{f}}_{\mathit{\theta }}\mathbf{\left[}{\mathit{c}}_{\mathit{i}\mathit{n}}\mathbf{\left(}\mathit{\sigma }\mathbf{\right)}·{\mathit{x}}_{\mathit{\sigma }},\mathit{\sigma }\mathbf{\right]}$$

(6)

$$c_{skip}\left(\sigma \right)={\displaystyle \frac{{{\sigma }_{data}}^2}{{\sigma }^2+{{\sigma }_{data}}^2}}$$

(7)

$$c_{in}\left(\sigma \right)={\displaystyle \frac{1}{\sqrt{{\sigma }^2+{{\sigma }_{data}}^2}}}$$

(8)

$$c_{out}\left(\sigma \right)={\displaystyle \frac{\sigma ·{\sigma }_{data}}{\sqrt{{\sigma }^2+{{\sigma }_{data}}^2}}}$$

(9)

$$\lambda (\sigma )={\displaystyle \frac{{\sigma }^2+{{\sigma }_{data}}^2}{{\left(\sigma ·{\sigma }_{data}\right)}^2}}$$

(10)

3.2. Sample Inference in EDM

In the inference phase, the EDM supports two types of sampling strategies: ODE inference and SDE inference [22]. In the context of the current PWPF task, the performance difference between these two approaches is negligible. Therefore, this study adopts ODE-based inference as the prediction strategy, specifically implemented using Heun’s 2nd method, and the corresponding pseudocode is presented in

Table 2. Pseudocode of ODE-based inference implemented with Heun’s 2nd method.

1.	Sample ${\tilde{\mathit{x}}}_N~\mathcal{N}(0, {{\sigma }_{max}}^2\mathrm{I})$
2.	For $i\in \left\{N, N-1,\dots ,1\right\}$ do
3.	${\mathit{d}}_i\leftarrow {\displaystyle \frac{1}{{\sigma }_i}}\left[{\tilde{\mathit{x}}}_i-{\mathit{F}}_{\mathit{\theta }}\left({\tilde{\mathit{x}}}_i,{\sigma }_i\right)\right]$
4.	${\tilde{\mathit{x}}}_{i-1}\leftarrow {\tilde{\mathit{x}}}_i+({\sigma }_{i-1}-{\sigma }_i)·{\mathit{d}}_i$
5.	If $i\ne 1$ then
6.	${\tilde{\mathit{d}}}_{i-1}\leftarrow {\displaystyle \frac{1}{{\sigma }_{i-1}}}\left[{\tilde{\mathit{x}}}_{i-1}-{\mathit{F}}_{\mathit{\theta }}\left({\tilde{\mathit{x}}}_{i-1},{\sigma }_{i-1}\right)\right]$
7.	${\tilde{\mathit{x}}}_{i-1}\leftarrow {\tilde{\mathit{x}}}_i+{\displaystyle \frac{\left({\sigma }_{i-1}-{\sigma }_i\right)}{2}}·({\mathit{d}}_i+{\tilde{\mathit{d}}}_{i-1})$
8.	Return ${\tilde{\mathit{x}}}_{\mathbf{0}}$

[22]. Here, $N$ denotes the number of sampling steps, which is set to 10 in this case. The noise level ${\sigma }_i$ used at each sampling step is determined according to Equation (11), where the parameters ${\sigma }_{max}$, ${\sigma }_{min}$, and $\rho$ are set to 80, 0.002, and 7, respectively.

$${\sigma }_i={\left[{{\sigma }_{max}}^{{\displaystyle \frac{1}{\rho }}}+{\displaystyle \frac{N-i}{N-1}}({{\sigma }_{min}}^{{\displaystyle \frac{1}{\rho }}}-{{\sigma }_{max}}^{{\displaystyle \frac{1}{\rho }}})\right]}^{\rho }$$

(11)

To generate probabilistic forecasts, the EDM begins by sampling an initial random noise sequence from a standard Gaussian distribution. This noise is then transformed through the ODE-based denoising process, ultimately producing a single trajectory representing the forecast error curve for wind power at each time step. By repeating this process with multiple independently sampled noise inputs, the model generates an ensemble of error trajectories. Statistical aggregation of these trajectories—specifically, computing the mean and standard deviation at each time point—yields a time-dependent probabilistic distribution of wind power forecasting errors.

While Heun’s second-order method provides a good trade-off between stability and computational cost, it is not necessarily optimal across all settings. First-order solvers like Euler [18] are simpler but often require more steps to maintain fidelity, whereas higher-order methods such as fourth-order Runge–Kutta [18] or DPM-Solver [29] can achieve comparable quality with fewer evaluations, albeit at higher per-step cost and implementation complexity. The effectiveness of different solvers can also vary depending on the noise schedule, data distribution, and conditioning structure. A more comprehensive evaluation of solver selection, including adaptive step-size control or learned solver strategies, remains a promising direction for future work.

To better justify the adoption of the EDM in this study for PWPF, a structured comparative analysis between the DDPM and the EDM is presented, with a focus on four key aspects: time domain formulation, forward diffusion process, optimization objective, and reverse denoising dynamics (details see Appendix A).

4. Architecture of TimeDiT

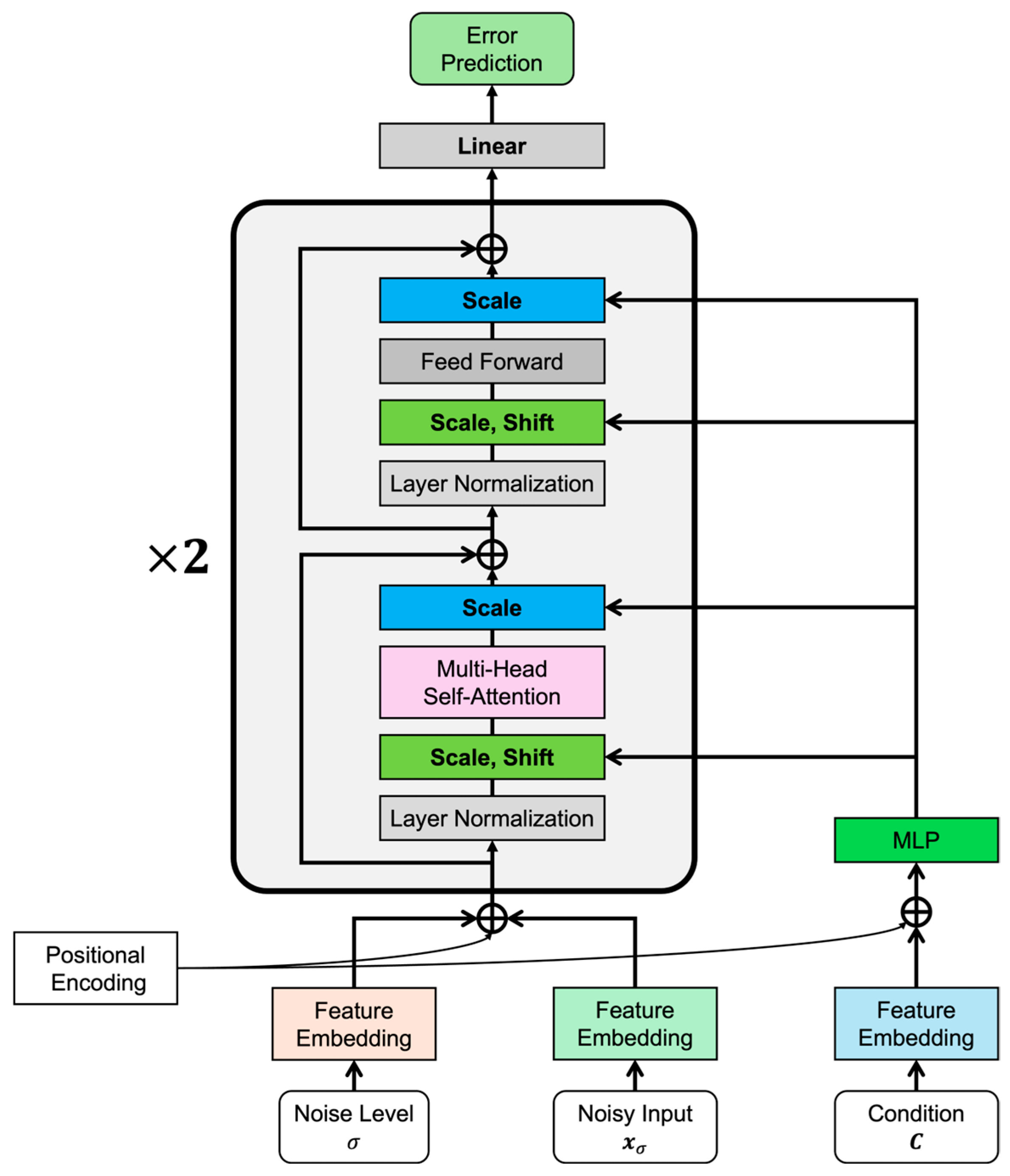
The network architecture of TimeDiT [26] is illustrated in Figure 3. The overall design is based on the Transformer encoder framework, with several tailored modifications to support multi-source probabilistic modeling. The model takes as input three types of information: the current noise level $\sigma$, the noise-corrupted sequence ${\mathit{x}}_{\mathit{\sigma }}$, and the conditional context $\mathit{C}$ at prediction time. These components are encoded separately using different feature encoders suited to their nature. Specifically, the noise level $\sigma$ is encoded using the sinusoidal timestep encoding adopted from the DDPM [19], the sequence ${\mathit{x}}_{\mathit{\sigma }}$ is processed through a one-dimensional convolutional neural network, and the conditional context $\mathit{C}$ is encoded via a linear projection layer. In this study, the conditional input $\mathit{C}$ is formed by concatenating the NWP sequence $\mathit{n}\mathit{w}\mathit{p}$ with the deterministic forecasting result ${\tilde{\mathit{y}}}_{DP}$ along the feature dimension.

After encoding, the features of $\sigma$ and ${\mathit{x}}_{\mathit{\sigma }}$ are elementwise added to positional encodings and then passed into the encoder. The encoder consists of two identical stacked blocks. A key architectural distinction between TimeDiT and the original Transformer encoder lies in its use of conditional modulation. Prior to each encoder block, the conditional embedding is passed through a multi-layer perceptron (MLP) to generate a pair of modulation coefficients: a scale-used one and a shift-used one.

The modulation procedure for a single encoder layer is detailed as follows. Let ${\mathit{h}}_{\mathbf{0}}$ denote the input tensor to an encoder layer and $\mathcal{C}$ denote the corresponding conditional vector. A lightweight MLP first transforms $\mathcal{C}$ into six parameter vectors: ${\mathit{c}}_{scale}^1$, ${\mathit{c}}_{shift}^1$, ${\mathit{c}}_{scale}^2$, ${\mathit{c}}_{scale}^3$, ${\mathit{c}}_{shift}^3$, ${\mathit{c}}_{scale}^4$, with each having the same dimensionality as $\mathcal{C}$. These parameters are then used to inject conditional information through a series of scale and shift operations embedded within the encoder layer.

First, ${\mathit{h}}_{\mathbf{0}}$ undergoes layer normalization to produce ${\mathit{h}}_{\mathbf{1}}$, which is then modulated using a scale-and-shift transformation, as given in Equation (12).

$${\tilde{\mathit{h}}}_{\mathbf{1}}={\mathit{c}}_{scale}^1\odot {\mathit{h}}_{\mathbf{1}}+{\mathit{c}}_{shift}^1$$

(12)

The modulated tensor ${\tilde{\mathit{h}}}_{\mathbf{1}}$ is passed through a multi-head self-attention block to obtain ${\mathit{h}}_2$, followed by a scaling operation, as shown in Equation (13).

$${\tilde{\mathit{h}}}_{\mathbf{2}}={\mathit{c}}_{scale}^2\odot {\mathit{h}}_{\mathbf{2}}$$

(13)

After residual connection and layer normalization, the output becomes ${\mathit{h}}_{\mathbf{3}}$, which is then subjected to a second scale-and-shift modulation, as shown in Equation (14).

$${\tilde{\mathit{h}}}_{\mathbf{3}}={\mathit{c}}_{scale}^3\odot {\mathit{h}}_{\mathbf{3}}+{\mathit{c}}_{shift}^3$$

(14)

Subsequently, ${\tilde{\mathit{h}}}_{\mathbf{3}}$ is passed through a feedforward network to produce ${\mathit{h}}_{\mathbf{4}}$, followed by the final scaling step, as shown in Equation (15).

$${\tilde{\mathit{h}}}_{\mathbf{4}}={\mathit{c}}_{scale}^4\odot {\mathit{h}}_{\mathbf{4}}$$

(15)

where ${\tilde{\mathit{h}}}_{\mathbf{4}}$ is either used as input to the next encoder layer or transformed via a linear projection to forecast the error output. In the above equations, the symbol $\odot$ represents the Hadamard product, applied component-wise between tensors of identical dimensions. Overall, TimeDiT demonstrates a highly modular and effective design for multi-source information fusion. By decoupling the encoding of different input types and injecting conditional knowledge directly into the model’s core computations via modulation, it enables flexible and fine-grained control over the prediction process while preserving the architectural integrity of the Transformer backbone.

5. Case Study

5.1. Dataset Description

To validate the effectiveness of the proposed ResD-PWPF framework, we conduct extensive experiments on open-source data from ten wind farms provided by the GEFCom2014 [27]. For clarity and consistency throughout the study, these wind farms are sequentially labeled WF1 to WF10. The wind power data for each site is pre-normalized, with values scaled between 0 and 1. The NWP inputs include four features: the U and V wind components are 10 m and 100 m above ground level. The forecast horizon spans from 1:00 to 24:00 of the following day. For each NWP feature, min–max normalization is applied based on its historical range. The dataset has an hourly resolution and covers a two-year period from 1 January 2012 to 31 December 2013. We split the data chronologically along the time axis into training, validation, and test sets with a ratio of 7:1:2. During model training, early stopping is employed based on performance on the validation set to prevent overfitting and determine the optimal stopping point.

5.2. Evaluation Metrics for PWPF

To evaluate the quality of PWPF, this study adopts CRPS, a widely used metric for assessing the accuracy of predictive distributions, defined as in Equation (16).

$$\mathrm{C}\mathrm{P}\mathrm{R}\mathrm{S}\left(F,y\right)={\int }_{-\infty }^{+\infty }({F\left(z\right)-\mathbb{l}\{z\ge y\})}^2 dz$$

(16)

where $F\left(z\right)$ denotes the cumulative distribution function (CDF) of the forecast, $y$ is the observed ground-truth value, and $\mathbb{l}\{z\ge y\}$ is an indicator function that equals 1 when $z\ge y$. Intuitively, CRPS measures the squared difference between the predicted CDF and the empirical step function at the true value, integrated over the entire range of outcomes. It can be viewed as a probabilistic extension of the mean absolute error (MAE), capturing both the sharpness and calibration of the predictive distribution.

When the forecast is assumed to follow a Gaussian distribution with mean $\mu$ and standard deviation $\sigma$, the CRPS has a closed-form expression, as in Equation (17). $\mathsf{\Phi }\left(·\right)$ and $\varnothing \left(·\right)$ represent the cumulative distribution function and probability density function of the standard normal distribution, respectively.

$$\mathrm{C}\mathrm{P}\mathrm{R}\mathrm{S}\left(\mu ,\sigma ,y\right)=\sigma \left[{\displaystyle \frac{y-\mu }{\sigma }}\left(2\mathsf{\Phi }\left({\displaystyle \frac{y-\mu }{\sigma }}\right)-1\right)+2\varnothing \left({\displaystyle \frac{y-\mu }{\sigma }}\right)-{\displaystyle \frac{1}{\sqrt{\pi }}}\right]$$

(17)

In addition to CRPS, we also evaluate the accuracy of the mean prediction using two deterministic metrics: MAE and RMSE. These metrics are widely used in forecasting literature and are not elaborated on here due to their well-established definitions. Together, CRPS, MAE, and RMSE provide a comprehensive assessment of both the distributional quality and the central tendency accuracy of the proposed probabilistic forecasting model.

In addition to the standard error-based metrics—MAE, RMSE, and CRPS—which evaluate the average prediction accuracy, we introduce WSRT to assess the statistical significance of performance differences between models. Unlike simple averaging, which can be sensitive to outliers, this non-parametric test evaluates whether one method consistently outperforms another across paired samples, without assuming normality. Specifically, we collect daily metric values for each wind farm in the test set and perform the WSRT test by comparing the paired errors between the proposed method and each baseline. Since lower metric values indicate better performance, the null hypothesis assumes that the baseline method is not worse than the proposed method. A small $p$-value implies strong evidence against this assumption (e.g., <0.05), indicating that the proposed method significantly outperforms the baseline across the test set.

5.3. Baseline Comparison Methods

To validate the effectiveness of the proposed method, we compare it against two representative probabilistic forecasting baselines: DeepAR and GAN-BERT.

• DeepAR is an autoregressive forecasting model that estimates the parameters of a predefined probability distribution at each time step. It is built on a long short-term memory architecture and optimized using the negative log-likelihood loss. While widely used in time-series forecasting, it assumes a fixed distribution form and may struggle to model complex uncertainty patterns.
• GAN-BERT adopts a generative adversarial training framework, where both the generator and discriminator are based on Transformer encoders. The generator takes NWP sequences and Gaussian noise as input and outputs wind power predictions. The discriminator receives NWP features along with either real or generated power sequences and learns to distinguish between them. This adversarial setup encourages the generator to produce realistic and diverse probabilistic forecasts.

5.4. Results and Discussion

Table 3. Performance comparison of three PWPF methods across 10 wind farms.

Sites	MAE			RMSE			CPRS
	DeepAR	GAN-BERT	ResD-PWPF	DeepAR	GAN-BERT	ResD-PWPF	DeepAR	GAN-BERT	ResD-PWPF
WF1	0.1355	0.1255	0.1246	0.1672	0.1589	0.1584	0.0959	0.1253	0.0916
WF2	0.1238	0.1262	0.1221	0.1502	0.1533	0.1494	0.0919	0.1214	0.0937
WF3	0.1253	0.1278	0.1209	0.1547	0.1582	0.1522	0.0902	0.1165	0.0920
WF4	0.1256	0.1192	0.1121	0.1644	0.1599	0.1507	0.0904	0.1117	0.0816
WF5	0.1311	0.1327	0.1190	0.1668	0.1675	0.1546	0.0939	0.1230	0.0865
WF6	0.1355	0.1320	0.1242	0.1729	0.1671	0.1586	0.0990	0.1278	0.0914
WF7	0.1104	0.1016	0.0961	0.1380	0.1270	0.1210	0.0778	0.0941	0.0696
WF8	0.1339	0.1333	0.1296	0.1676	0.1645	0.1603	0.0965	0.1252	0.0938
WF9	0.1190	0.1157	0.1067	0.1525	0.1472	0.1385	0.0862	0.1108	0.0782
WF10	0.1570	0.1565	0.1482	0.1922	0.1951	0.1851	0.1113	0.1473	0.1064
AVERAGE	0.1297	0.1271	0.1204	0.1626	0.1599	0.1529	0.0933	0.1203	0.0885

presents the forecasting performance of three probabilistic models—DeepAR, GAN-BERT, and the proposed ResD-PWPF—on ten wind farms (WF1~WF10) using three evaluation metrics: MAE, RMSE, and CRPS. Across all metrics, ResD-PWPF consistently outperforms both baselines.

In terms of MAE, ResD-PWPF achieves the lowest average error of 0.1204, compared to 0.1271 for GAN-BERT and 0.1297 for DeepAR. Similar trends are observed for RMSE, where ResD-PWPF reports the lowest average of 0.1529, while GAN-BERT and DeepAR reach 0.1599 and 0.1626, respectively. These results indicate that ResD-PWPF provides more accurate mean predictions across all sites. Most notably, ResD-PWPF achieves the best performance in CRPS, a metric that captures both the calibration and the sharpness of probabilistic forecasts. With an average CRPS of 0.0885, ResD-PWPF outperforms GAN-BERT (0.1203) and DeepAR (0.0933) by a significant margin, suggesting superior ability to represent forecast uncertainty. This advantage is especially evident at sites such as WF7 and WF9, where ResD-PWPF shows substantial reductions in CRPS.

Table 4. Statistical comparison of three PWPF methods across 10 wind farms.

Sites	MAE		RMSE		CPRS
	ResD-PWPF > DeepAR	ResD-PWPF > GAN-BERT	ResD-PWPF > DeepAR	ResD-PWPF > GAN-BERT	ResD-PWPF > DeepAR	ResD-PWPF > GAN-BERT
WF1	$3\times {10}^{-6}$	$4\times {10}^{-2}$	$8\times {10}^{-4}$	$1\times {10}^{-1}$	$2\times {10}^{-4}$	$1\times {10}^{-17}$
WF2	$3\times {10}^{-1}$	$9\times {10}^{-3}$	$5\times {10}^{-1}$	$3\times {10}^{-2}$	$6\times {10}^{-1}$	$1\times {10}^{-22}$
WF3	$1\times {10}^{-2}$	$3\times {10}^{-3}$	$8\times {10}^{-2}$	$3\times {10}^{-3}$	$7\times {10}^{-1}$	$4\times {10}^{-17}$
WF4	$4\times {10}^{-9}$	$7\times {10}^{-5}$	$3\times {10}^{-7}$	$6\times {10}^{-5}$	$1\times {10}^{-8}$	$1\times {10}^{-22}$
WF5	$6\times {10}^{-6}$	$4\times {10}^{-9}$	$8\times {10}^{-5}$	$7\times {10}^{-7}$	$9\times {10}^{-6}$	$2\times {10}^{-23}$
WF6	$5\times {10}^{-6}$	$5\times {10}^{-5}$	$4\times {10}^{-6}$	$2\times {10}^{-4}$	$4\times {10}^{-6}$	$2\times {10}^{-23}$
WF7	$1\times {10}^{-11}$	$1\times {10}^{-3}$	$1\times {10}^{-10}$	$3\times {10}^{-3}$	$6\times {10}^{-9}$	$1\times {10}^{-20}$
WF8	$3\times {10}^{-3}$	$1\times {10}^{-3}$	$7\times {10}^{-4}$	$5\times {10}^{-3}$	$8\times {10}^{-3}$	$6\times {10}^{-23}$
WF9	$3\times {10}^{-6}$	$3\times {10}^{-5}$	$2\times {10}^{-5}$	$7\times {10}^{-4}$	$8\times {10}^{-6}$	$2\times {10}^{-23}$
WF10	$5\times {10}^{-3}$	$3\times {10}^{-4}$	$3\times {10}^{-2}$	$2\times {10}^{-4}$	$2\times {10}^{-2}$	$9\times {10}^{-24}$

presents the results of the WSRT comparing the proposed ResD-PWPF method against two baselines—DeepAR and GAN-BERT—across 10 wind farms, using three evaluation metrics: MAE, RMSE, and CRPS. Each cell shows the p-value computed from daily prediction results over the test set. Underlined entries indicate $p$-values greater than 0.05, suggesting that the difference between ResD-PWPF and the baseline is not statistically significant at the 95% confidence level.

The results demonstrate that ResD-PWPF consistently outperforms both DeepAR and GAN-BERT, with high statistical significance. In particular, for the CRPS metric, all p-values are below 0.05, often reaching extremely small magnitudes (e.g., 1 × 10⁻²²), reflecting strong probabilistic calibration across all sites. For MAE and RMSE, statistical superiority is observed in most cases, with only a small number of exceptions (e.g., WF2), possibly due to site-specific variability or noise. These findings confirm that ResD-PWPF provides more accurate and better-calibrated probabilistic forecasts, with improvements that are statistically significant and robust under diverse wind farm conditions.

5.5. Scenario Generalizability Analysis

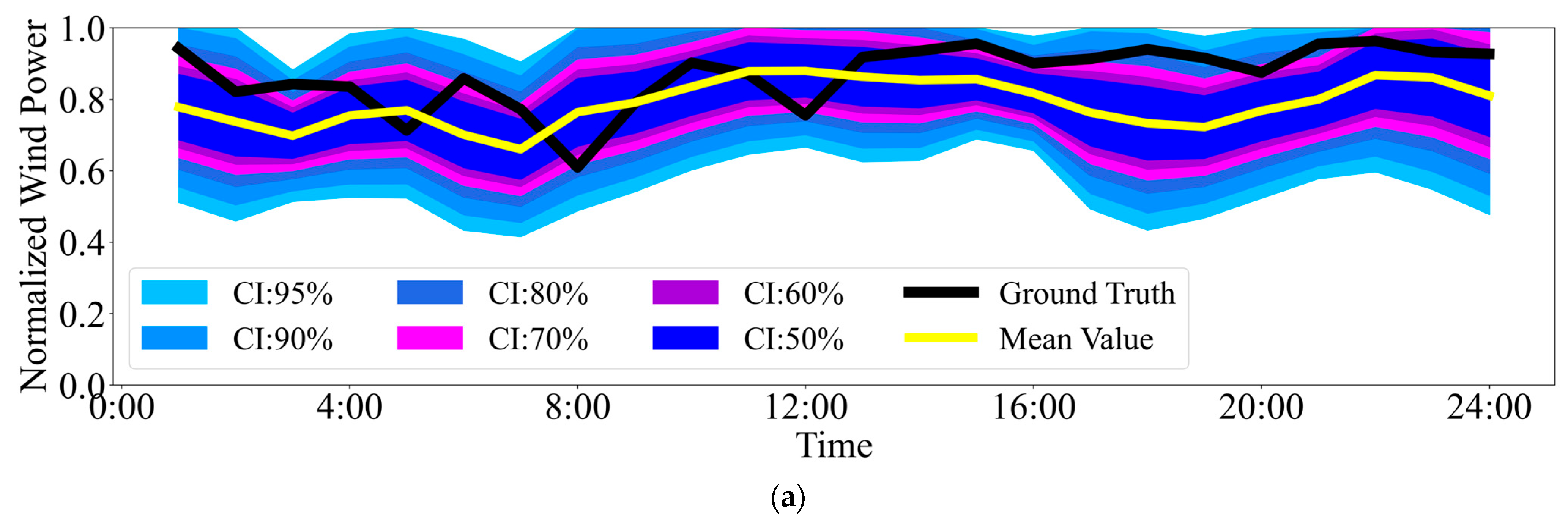
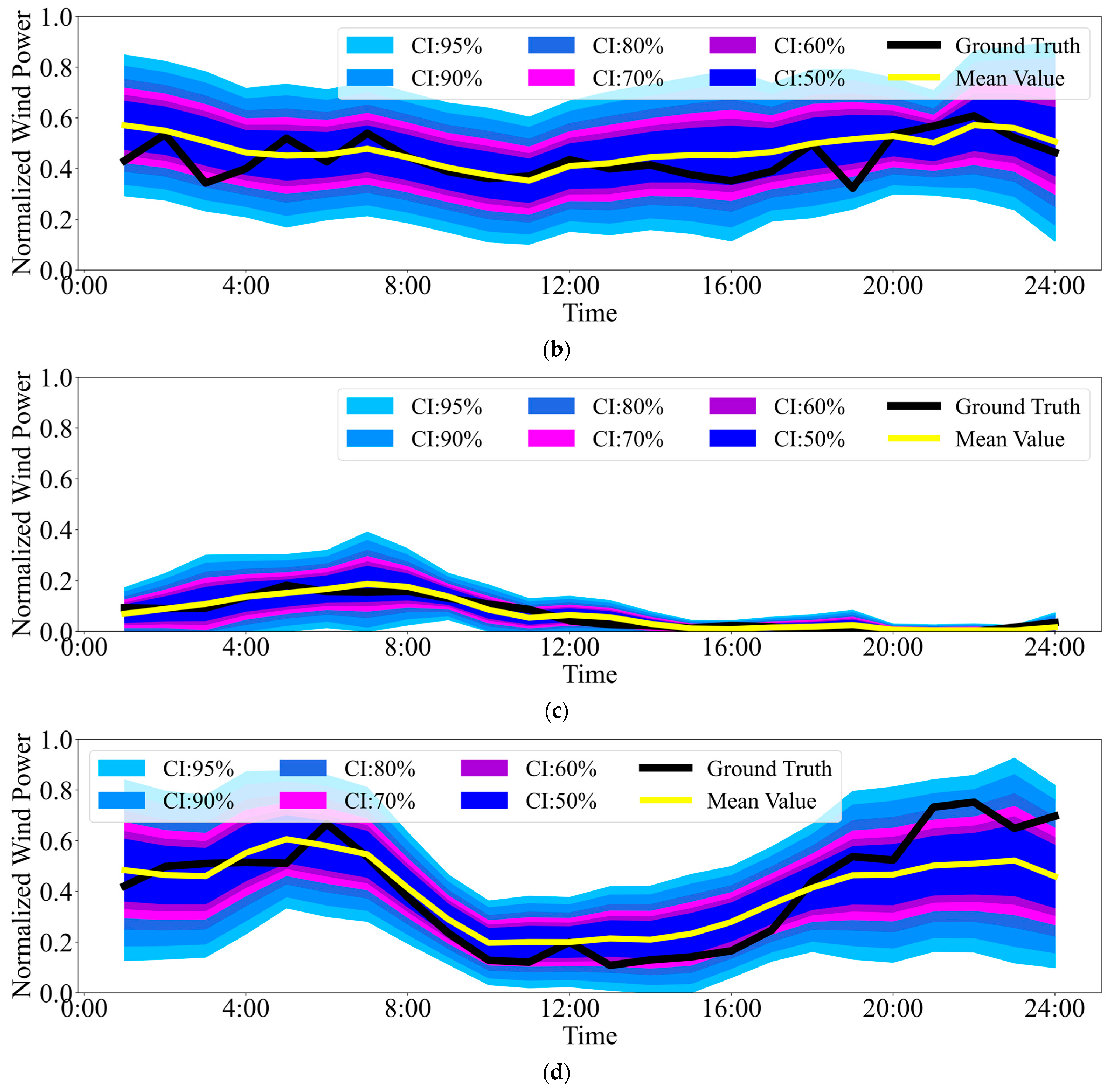
To evaluate the generalization and robustness of the proposed ResD-PWPF framework under varying operational conditions, four representative wind power output scenarios are selected: high output, low output, medium output, and high fluctuation. The probabilistic forecasting results under each scenario are visualized in Figure 4 using multiple confidence intervals (CIs) and the corresponding mean forecasts.

Across all scenarios, the proposed method demonstrates strong generalization ability, with predictive distributions that closely follow the ground truth trajectories. In the high-output and medium-output scenarios (Figure 4a,b), the forecast mean values remain consistently close to the observed curves, and the uncertainty bands tightly capture the variations. This suggests that the model effectively learns from historical NWP features and produces well-calibrated forecasts in steady operating conditions. In the low-output scenario in Figure 4c, the method maintains narrow prediction intervals around low values, avoiding overestimation while preserving calibration. The ability to predict near-zero output while keeping confidence intervals consistent reflects good robustness to sparse information and weak wind signals. In the high-fluctuation scenario in Figure 4d, the model still provides smooth, continuous probabilistic bands that encompass most ground truth values. However, it can be observed that the ground truth occasionally falls near or just outside the 70%~90% confidence intervals, indicating a slight underestimation of uncertainty during rapidly changing conditions. This highlights a potential limitation of the model in extreme weather or abrupt transitions, where uncertainty quantification may benefit from incorporating higher-order temporal features or more dynamic noise modeling. The proposed method exhibits strong generalization across different output levels and resilience to noise and fluctuations, while showing room for improvement in capturing highly volatile transitions.

5.6. Computational Configuration and Efficiency

The experiments were conducted on a MacBook Pro equipped with an Apple M3 Max chip. All models were implemented using the PyTorch 2.7.1 framework, and training and inference were accelerated using the on-device Graphics Processing Unit (GPU). In the deterministic modeling stage, early stopping was applied to dynamically determine whether to continue or terminate training for each wind farm. Across 10 wind farms, the average training time for the deterministic model was approximately 20 min. During inference, the deterministic model required less than 0.1 s to generate a 24 h advance power forecast.

In the probabilistic modeling stage, model training was conducted with a batch size of 64 for a total of 50,000 epochs. The TimeDiT model consists of two encoder layers with a hidden dimension of 128 and 8 attention heads, resulting in a total of 73,065 trainable parameters. For a single wind farm, the average training time was approximately 106 min. During probabilistic inference, the number of diffusion steps $N$ was set to 10, and 100 samples of initial random noise were generated to form an ensemble forecast. The time required for a single 24 h advance probabilistic power forecast for one wind farm was approximately 5 s. Once the models are trained and deployed, the proposed method can produce a probabilistic power forecast for a single wind farm in under 6 s. This satisfies the time constraints of real-world engineering applications and demonstrates the practical feasibility of the approach.

6. Conclusions

This study presents ResD-PWPF, a novel residual diffusion-based PWPF framework that integrates deterministic prediction with conditional diffusion modeling. A baseline predictor first produces the mean wind power forecast, and a conditional diffusion model is then employed to learn the distribution of residual errors conditioned on both the forecast and the external features. To enable flexible and expressive modeling of uncertainty, we build the diffusion process upon the EDM, which provides continuous noise-level control, enhanced conditioning mechanisms, and improved training stability over conventional diffusion frameworks. For the denoising network, we introduce TimeDiT, a diffusion Transformer-based architecture tailored for time-series generation. TimeDiT incorporates modular feature encoders and conditional modulation through scale-and-shift transformations. Together, these design choices enable accurate, uncertainty-aware wind power forecasting under diverse operational scenarios.

Extensive experiments were conducted on ten wind farms from the GEFCom2014 dataset. The results demonstrate that ResD-PWPF consistently outperforms strong baselines such as DeepAR and GAN-BERT in terms of both point prediction metrics (MAE, RMSE) and probabilistic calibration (CRPS). Further case studies across four typical wind power output scenarios—high output, low output, medium output, and high fluctuation—validate the model’s strong generalization ability and robustness under diverse operating conditions. The method effectively captures uncertainty and remains well calibrated in most cases, although slight underestimation may occur in highly volatile scenarios. Such underestimation tends to arise when the wind power time series exhibits abrupt, large-magnitude transitions that fall outside the statistical patterns seen during training. In such cases, the baseline deterministic predictor may fail to provide sufficiently accurate forecasts, limiting the effectiveness of residual-based diffusion modeling. Moreover, the conditional diffusion model, while expressive, may struggle to represent multi-modal or long-tailed residual distributions under sparse data regimes or rare extreme weather events. We also caution readers regarding the use of a fixed conditioning structure: When external features such as NWP inputs are misaligned, delayed, or contain systematic biases, the model’s probabilistic outputs can become poorly calibrated. This issue is particularly pronounced under rapidly evolving meteorological conditions or sensor degradation and may be mitigated through strategies such as dynamic feature selection, hierarchical conditioning, or adaptive residual modeling.

For future work, several avenues can be explored to further improve performance and extend applicability. Incorporating spatial correlations among wind farms and leveraging multi-site joint modeling may enhance forecast consistency across different geographic regions. Additionally, the integration of online learning or real-time recalibration mechanisms could enable the model to better improve responsiveness to sudden environmental changes.