Evaluation System of AC/DC Strong–Weak Balance Relationship and Stability Enhancement Strategy for the Receiving-End Power Grid
Abstract
1. Introduction
2. Multidimensional Evaluation Indicator System for the AC/DC Strong–Weak Balance of the Receiving-End Power Grid
2.1. Grid Strength Evaluation
2.1.1. Voltage Support Capability Evaluation Indicator
2.1.2. Frequency Support Capability Evaluation Indicator
- (1)
- System inertia level
- (2)
- System primary frequency regulation indicator
2.1.3. AC Channel Utilization Ratio Indicator
2.2. Operational Security and Reliability Assessment
2.2.1. N-1 Power Flow Transfer Resilience Indicator
2.2.2. Short-Circuit Current Margin Indicator
2.2.3. Frequency Stability Margin Indicator
2.2.4. Rotor Angle Stability Indicator
2.2.5. Large-Scale Blackout Risk Indicator
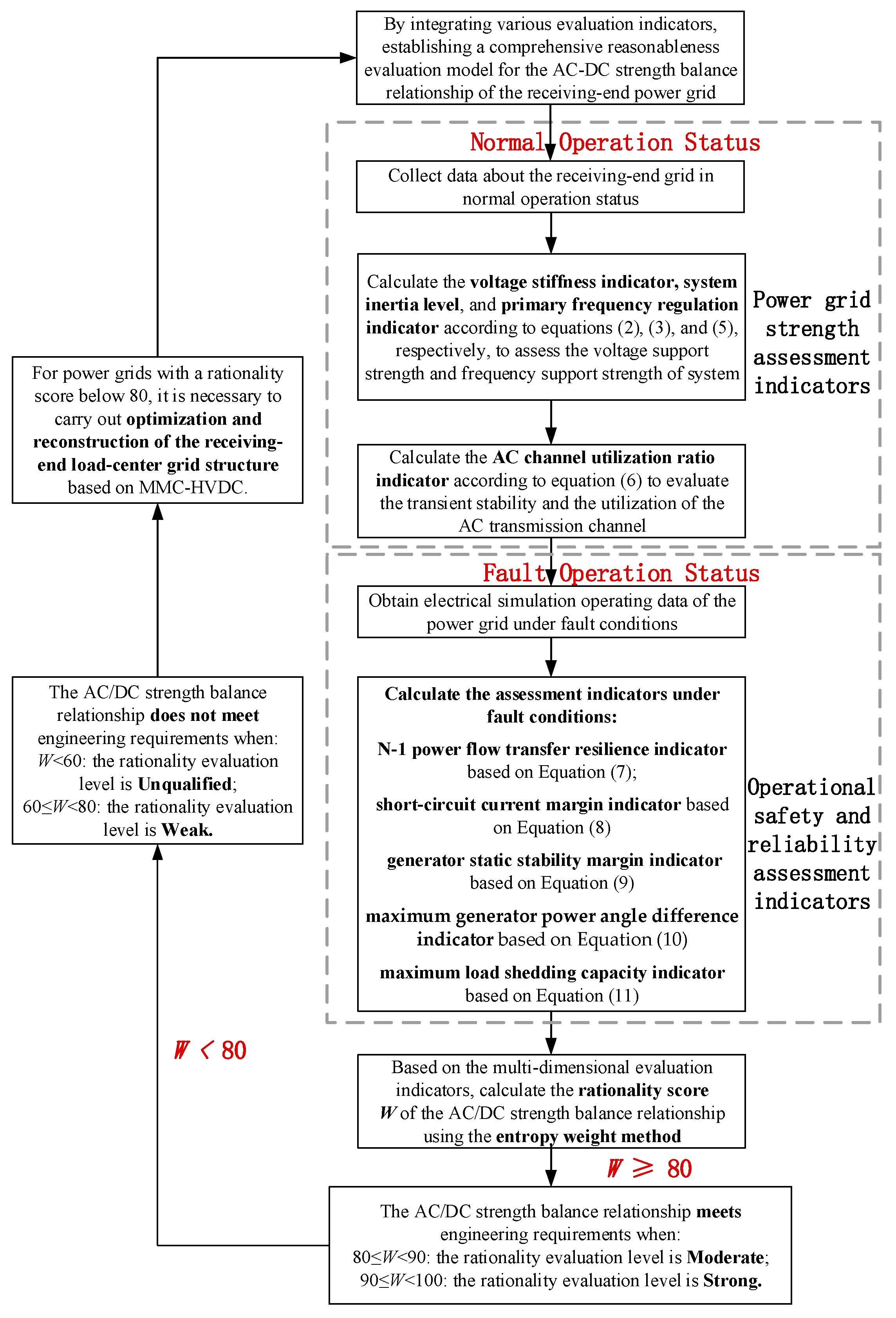
3. Evaluation Process for the Rationality of AC/DC Strong–Weak Balance Relationship in the Receiving-End Grid
3.1. Rationality Evaluation Model for the AC/DC Strength Balance Relationship
3.1.1. Indicator Membership Function Classification
3.1.2. Comprehensive Scoring Model
3.1.3. Sensitivity Analysis
3.2. Evaluation Scheme for the Rationality of AC/DC Strength Balance Relationship
- (1)
- Taking into comprehensive consideration the various evaluation indicators of grid strength and operational security and reliability, establish a complete reasonableness evaluation model for the AC-DC strength balance relationship of the receiving-end power grid.
- (2)
- Collect data AC-DC hybrid network topology, AC and DC transmission channel capacities and actual power flows, generator output statuses, operating characteristics of non-synchronous power sources, short-circuit currents, and other relevant information of the receiving-end grid, and sequentially calculate the values of each evaluation indicator.
- (3)
- First, calculate the voltage stiffness indicator, system inertia level, and primary frequency regulation indicator separately to assess the voltage support strength and frequency support strength of power system. When the voltage stiffness indicator is below 0.95, the grid is considered to have weak voltage support strength; similarly, when the inertia level is low, the grid is considered to have weak frequency support strength.
- (4)
- Calculate the AC channel utilization ratio indicator to evaluate the transient stability and the utilization rate of the AC channel in grid. When the indicator is less than 0.33, it is considered that the transient stability is poor under single-circuit channel blocking conditions, and the channel utilization is low, indicating resource waste.
- (5)
- Next, simulate and calculate various operational security and reliability indicators of the grid under fault conditions. Specifically, calculate the N-1 power flow transfer resilience indicator, short-circuit current margin indicator, generator static stability margin indicator, maximum rotor angle difference indicator, and maximum load shedding capacity indicator, and evaluate whether they meet engineering safety requirements.
- (6)
- For the above indicators, calculate the rationality score of the AC/DC strength balance relationship in the grid based on the entropy weight method. For grids with a score below 80, optimization and reconstruction of the receiving-end load center grid structure are required.
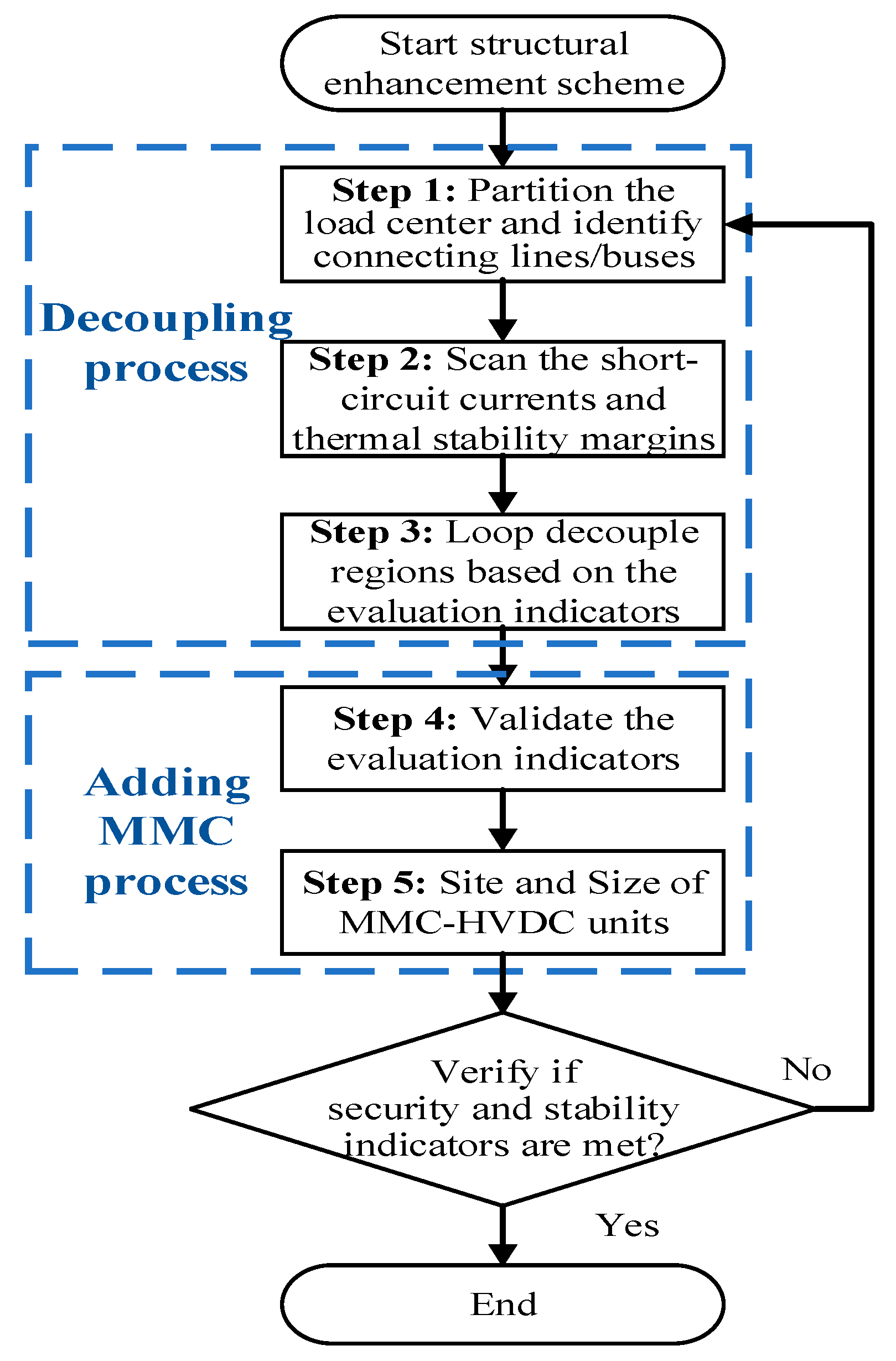
4. Structural Enhancement Method for the Receiving-End Power Grid Based on MMC–HVDC
4.1. Role of MMC–HVDC in Improving the Security and Stability of Load Center Grid
- (1)
- Security Enhancement
- (2)
- Stability Enhancement
4.2. Enhancement Method of the Load Center Grid
- (1)
- Based on the partitioning structure of the load center, evaluate the short-circuit current margin at all buses in the grid, and identify key buses with a high risk of short-circuit current exceeding the limit.
- (2)
- Decouple the identified key buses with high short-circuit current risk from other partitions, reducing the short-circuit current level at the load center of the receiving grid to within the safety limits allowed by engineering standards.
- (3)
- Assess the operational stability of the grid after decoupling by scanning the generator static stability margin and the large-scale blackout risk indicators and identify areas with higher stability risks.
- (4)
- Determine the location of MMC–HVDC units and add MMC–HVDC lines at key buses between areas with high blackout risk and nearby areas with stronger grid strength.
- (5)
- Determine the capacity of the MMC–HVDC units to reduce the large-scale blackout risk and improve generator static stability margin to within engineering-acceptable ranges. The units should be designed with a certain long-term overload capability to adapt to various operating conditions.
- (6)
- Assess the operational security of the load center by scanning the short-circuit current margin indicator and assess the operational stability by scanning both the large-scale blackout risk and generator static stability margin indicators. If all indicators meet engineering requirements, the proposed grid reinforcement scheme is deemed reasonable; otherwise, return to previous steps for re-planning.
5. Case Analysis
6. Conclusions
- (1)
- A quantitative method for the strength balance relationship of the receiving-end power grid in AC/DC hybrid grids is proposed, evaluating both grid strength under normal operation and operational safety and reliability under fault conditions, thereby establishing a multidimensional indicator evaluation system for the AC/DC strong–weak balance relationship.
- (2)
- By integrating the multidimensional indicator evaluation system with electrical parameters under different grid operating conditions, a rationality evaluation model for the AC/DC strength balance relationship based on the entropy weight method is developed, along with a complete evaluation process for assessing the rationality of the AC/DC strength balance relationship in the receiving-end power grid.
- (3)
- To address the issue of an unreasonable AC/DC strong–weak balance relationship and common problems in AC/DC power grids such as excessive short-circuit current and uncontrollable power flow, this paper proposes a power grid stability enhancement strategy that combines network decoupling technology with Modular Multilevel Converter HVDC (MMC–HVDC). This strategy leverages the advantages of network decoupling to reduce short-circuit current and prevent overloads, alongside the flexible active and reactive power regulation capabilities of MMC–HVDC, forming a MMC–HVDC-based structural optimization method for the receiving-end power grid, thereby providing stability assurance for the grid. The simulation of a typical test power grid system confirms that this enhancement approach effectively optimizes power flow behavior and stability, thereby enhancing the grid’s operational safety and efficiency.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Papadis, E.; Tsatsaronis, G. Challenges in the decarbonization of the energy sector. Energy 2020, 205, 118025. [Google Scholar] [CrossRef]
- Impram, S.; Nese, S.V.; Oral, B. Challenges of renewable energy penetration on power system flexibility: A survey. Energy Strategy Rev. 2020, 31, 100539. [Google Scholar] [CrossRef]
- Liang, X.; Abbasipour, M. HVDC transmission and its potential application in remote communities: Current practice and future trend. IEEE Trans. Ind. Appl. 2022, 58, 1706–1719. [Google Scholar] [CrossRef]
- Yuan, S.; Chen, D.; Chen, T.; Tang, W.; Ma, S.; Luo, Y.; Song, Y.; Ren, J.; Zi, P.; Wang, Q.; et al. Coordinated control of multi-HVDC participating in three defense line at the receiving end of the power system with strong DC and weak AC. Electr. Power 2018, 51, 72–79. [Google Scholar]
- Majidi-Qadikolai, M.; Baldick, R. Stochastic transmission capacity expansion planning with special scenario selection for integrating N-1 contingency analysis. IEEE Trans. Power Syst. 2016, 31, 4901–4912. [Google Scholar] [CrossRef]
- Liu, B.; Wang, W.; Zhang, J.; Cheng, J.; Dong, Z.; Xu, Z. Active Power Coordination Control Method of Converter Stations of MMCDC System and UPFC in Jiangsu Power Grid Interconnected with the LargeScale Wind Power. South. Power Syst. Technol. 2024, 18, 138–145. [Google Scholar] [CrossRef]
- Lin, S.; Yang, Y.; Liu, M.; Xie, Y.; Lu, Y. Static voltage stability margin calculation of power systems with high wind power penetration based on the interval optimisation method. IET Renew. Power Gener. 2020, 14, 1728–1737. [Google Scholar] [CrossRef]
- Saha, S.; Saleem, M.I.; Roy, T.K. Impact of high penetration of renewable energy sources on grid frequency behaviour. Int. J. Electr. Power Energy Syst. 2023, 145, 108701. [Google Scholar] [CrossRef]
- Liu, Y.; Song, Y.; Wang, Z.; Shen, C. Optimal emergency frequency control based on coordinated droop in multi-infeed hybrid AC-DC system. IEEE Trans. Power Syst. 2021, 36, 3305–3316. [Google Scholar] [CrossRef]
- Bai, E.; Xu, J. Hierarchical Frequency Modulation Control Strategy for Large-Capacity AC/DC Hybrid Power System. J. Electr. Eng. Technol. 2024, 19, 2149–2158. [Google Scholar] [CrossRef]
- Jose, K.; Joseph, T.; Liang, J.; Ugalde-Loo, C.E. Auxiliary dead-band controller for the coordination of fast frequency support from multi-terminal HVDC grids and offshore wind farms. IET Renew. Power Gener. 2018, 12, 1444–1452. [Google Scholar] [CrossRef]
- Sun, S.; Zhou, G.; Song, Y.; Tang, X.; Zhou, Y.; Yuan, Z. Research on Measures to Limit Short-Circuit Current by Changing the Structure of the Power Grid. Energies 2025, 18, 2098. [Google Scholar] [CrossRef]
- Zhang, W.; Guo, R.; Shi, Y.; Tang, Y.; Lin, Y. A Power Grid Partitioning Method for Short-Circuit Current Considering Multi-Scenario Security with an Improved Direct Current Model. Energies 2023, 16, 7332. [Google Scholar] [CrossRef]
- Akbarzadeh Aghdam, P.; Khoshkhoo, H. Voltage stability assessment algorithm to predict power system loadability margin. IET Gener. Transm. Distrib. 2020, 14, 1816–1828. [Google Scholar] [CrossRef]
- Sau-Bassols, J.; Prieto-Araujo, E.; Gomis-Bellmunt, O.; Hassan, F. Series interline DC/DC current flow controller for meshed HVDC grids. IEEE Trans. Power Deliv. 2017, 33, 881–891. [Google Scholar] [CrossRef]
- Zhong, X.; Zhu, M.; Chi, Y.; Liu, S.; Cai, X. Composite DC power flow controller. IEEE Trans. Power Electron. 2019, 35, 3530–3542. [Google Scholar] [CrossRef]
- Lotfjou, A.; Fu, Y.; Shahidehpour, M. Hybrid AC/DC transmission expansion planning. IEEE Trans. Power Deliv. 2012, 27, 1620–1628. [Google Scholar] [CrossRef]
- Xin, H.; Zhang, F.; Yu, Y.; Gan, D.; Xu, Q. Generalized short circuit ratio for multi-infeed DC systems: Definition and theoretical analysis. Proc. CSEE 2016, 36, 633–647. [Google Scholar] [CrossRef]
- Lee, D.H.A. Voltage stability assessment using equivalent nodal analysis. IEEE Trans. Power Syst. 2015, 31, 454–463. [Google Scholar] [CrossRef]
- Lee, D.H.A.; Andersson, G. An equivalent single-infeed model of multi-infeed HVDC systems for voltage and power stability analysis. IEEE Trans. Power Deliv. 2015, 31, 303–312. [Google Scholar] [CrossRef]
- Shao, Y.; Tang, Y. Analysis of influencing factors of multi-infeed HVDC system interaction factor. Power Syst. Technol 2013, 37, 794–799. [Google Scholar] [CrossRef]
- Wu, X.; Lan, Q.; Li, Z.; Zhuang, K.; Miao, Y.; Li, W. Frequency characteristics of East China Power Grid after bipolar locking of ultra-high voltage direct current (UHVDC). J. Eng. 2017, 2017, 1237–1241. [Google Scholar] [CrossRef]
- Dai, Z.; Wang, J.; Pan, X.; Teng, Z.; Qin, L. A comprehensive power flow evaluation method for a transmission section with UHVAC/DC integration. Power Syst. Prot. Control 2020, 48, 65–72. [Google Scholar] [CrossRef]
- Xu, Z. Reasonable definition and calculation method of power grid strength under the background of new type power systems. High Volt. Eng. 2022, 48, 3805–3819. [Google Scholar] [CrossRef]
- Dong, H.; Xu, Z.; Qian, Y.; Si, D.; Song, P.; Xing, F. General Principle of Asynchronous Segment for AC/DC Synchronous Power Systems. High Volt. Eng. 2017, 43, 2167–2174. [Google Scholar] [CrossRef]
- Cai, H.; Yan, M.; Gao, S.; Zhou, T.; Wang, G.; Huang, Y. Coupling Characteristic Analysis and Coordinated Planning Strategies for AC/DC Hybrid Transmission Systems with Multi-Infeed HVDC. Electronics 2025, 14, 2294. [Google Scholar] [CrossRef]
- Nami, A.; Liang, J.; Dijkhuizen, F.; Demetriades, G.D. Modular multilevel converters for HVDC applications: Review on converter cells and functionalities. IEEE Trans. Power Electron. 2014, 30, 18–36. [Google Scholar] [CrossRef]
- Li, H.; Shi, Y. Distributed model predictive control of constrained nonlinear systems with communication delays. Syst. Control Lett. 2013, 62, 819–826. [Google Scholar] [CrossRef]


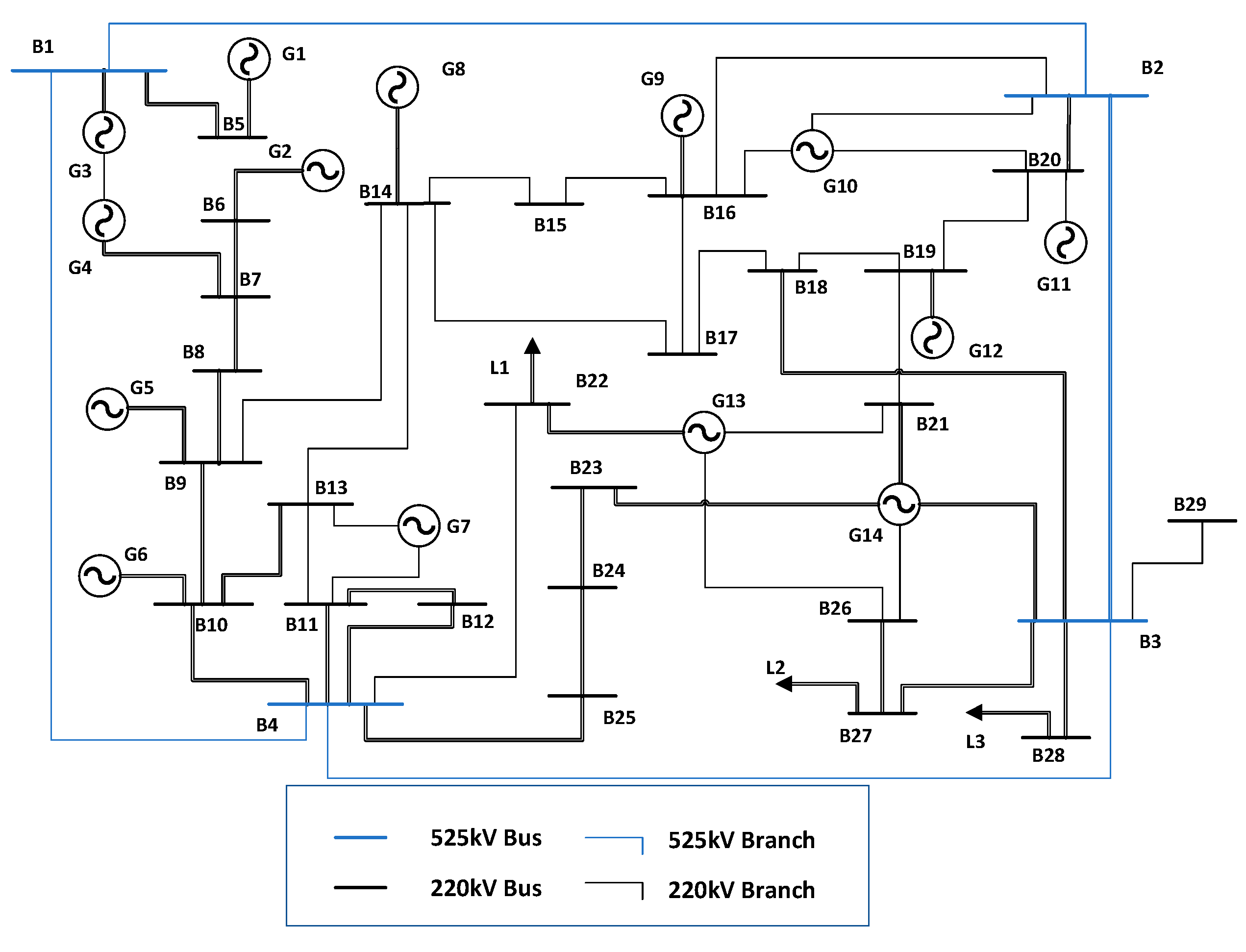
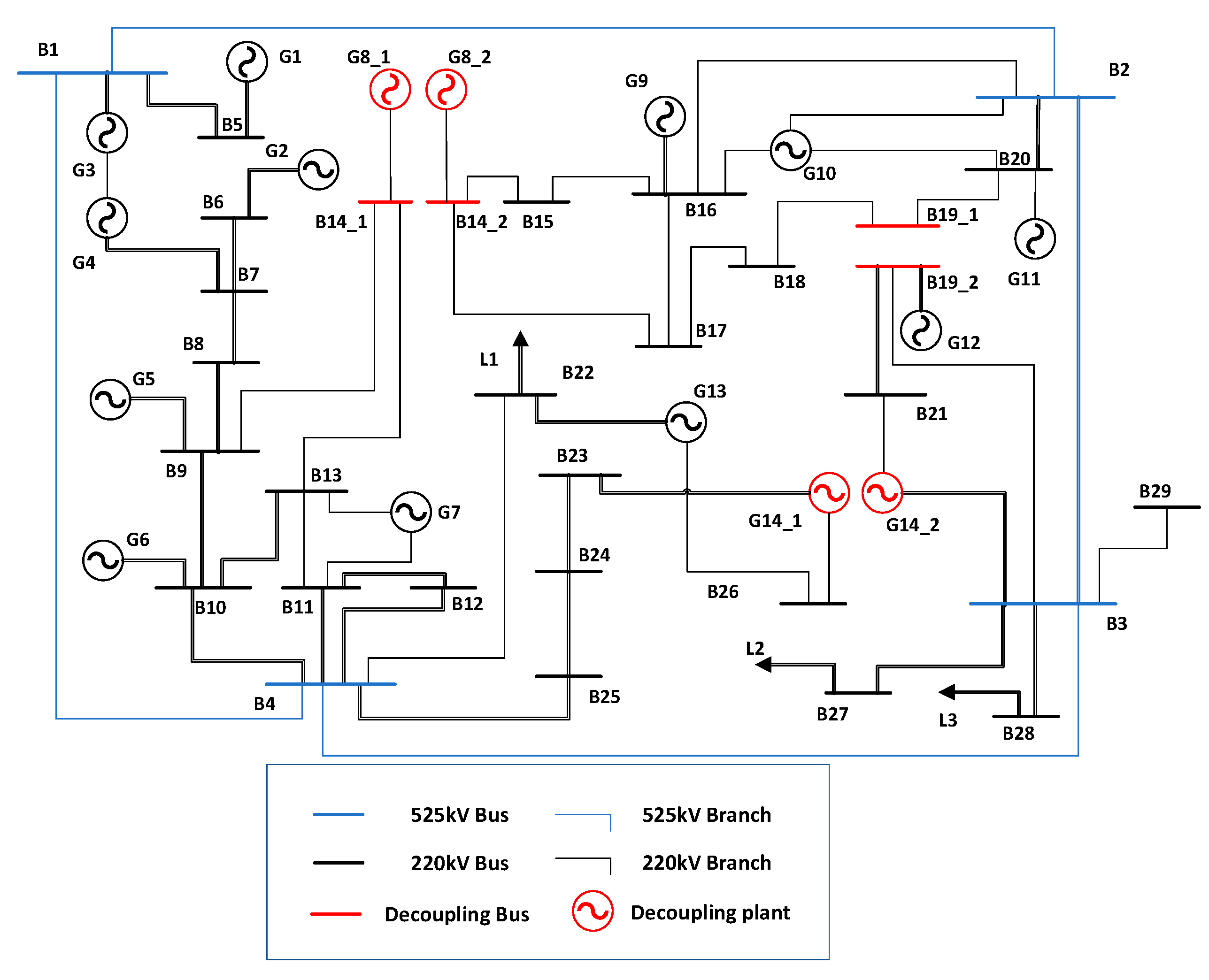
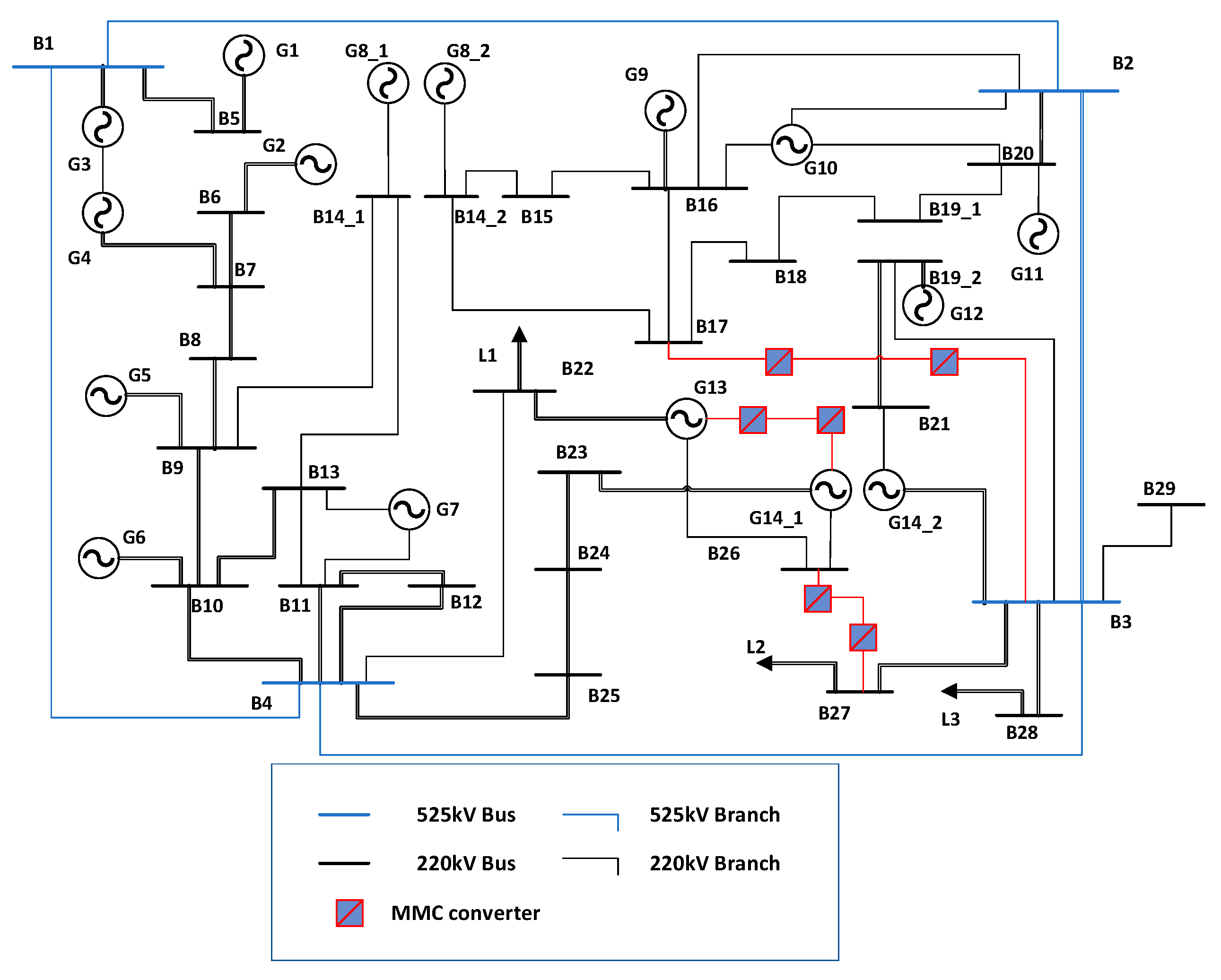
| Bus ID | Voltage Level/kV | Short-Circuit Current Margin Indicator/% |
|---|---|---|
| B19 | 220 | −11.42 |
| B3 | 525 | −16.56 |
| G14 | 220 | −22.84 |
| B16 | 220 | −33.14 |
| B3 | 220 | −89.08 |
| MMC–HVDC Units Number | Locations | Voltage Level/kV | Rated Capacity/MVA |
|---|---|---|---|
| 1 | B17-B3 | 320 | 600 |
| 2 | G13-G14_1 | 320 | 300 |
| 3 | B26-B27 | 320 | 600 |
| Bus Name | Voltage Level (kV) | Short-Circuit Current Margin Indicator Before Enhancement/% | Short-Circuit Current Margin Indicator After Enhancement/% |
|---|---|---|---|
| B19 | 220 | −11.42 | 28.17 |
| B3 | 525 | −16.56 | 29.82 |
| G14 | 220 | −22.84 | 31.88 |
| B16 | 220 | −33.14 | 25.54 |
| B3 | 220 | −89.08 | 8.53 |
| Region Name | Blackout Risk Indicator Before Adding MMC–HVDC/MW | Blackout Risk Indicator After Adding MMC–HVDC/MW |
|---|---|---|
| Region 2 | 1040.8 | 120.8 |
| Region 4 | 640.1 | 0 |
| Evaluation Indicators | Original Operating Condition | 1.2 Times Load Condition | 1.5 Times Load Condition |
|---|---|---|---|
| Short-Circuit Current Margin Indicator/% | −89.08→8.53 (B3) | −102.60→8.40 (B3) | −142.60→5.82 (B3) |
| Blackout Risk Indicator/MW | 1040.8→120.8 (Region 2) | 1250.5→150.2 (Region 2) | 1650.3→210.7 (Region 2) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, H.; Yan, M.; Han, X.; Wang, G.; Wang, Q.; Huang, Y. Evaluation System of AC/DC Strong–Weak Balance Relationship and Stability Enhancement Strategy for the Receiving-End Power Grid. Energies 2025, 18, 4216. https://doi.org/10.3390/en18164216
Cai H, Yan M, Han X, Wang G, Wang Q, Huang Y. Evaluation System of AC/DC Strong–Weak Balance Relationship and Stability Enhancement Strategy for the Receiving-End Power Grid. Energies. 2025; 18(16):4216. https://doi.org/10.3390/en18164216
Chicago/Turabian StyleCai, Hui, Mingxin Yan, Xingning Han, Guoteng Wang, Quanquan Wang, and Ying Huang. 2025. "Evaluation System of AC/DC Strong–Weak Balance Relationship and Stability Enhancement Strategy for the Receiving-End Power Grid" Energies 18, no. 16: 4216. https://doi.org/10.3390/en18164216
APA StyleCai, H., Yan, M., Han, X., Wang, G., Wang, Q., & Huang, Y. (2025). Evaluation System of AC/DC Strong–Weak Balance Relationship and Stability Enhancement Strategy for the Receiving-End Power Grid. Energies, 18(16), 4216. https://doi.org/10.3390/en18164216






