Construction of Analogy Indicator System and Machine-Learning-Based Optimization of Analogy Methods for Oilfield Development Projects

Abstract

Oil and gas development is characterized by high technical complexity, strong interdisciplinarity, long investment cycles, and significant uncertainty. To meet the need for quick evaluation of overseas oilfield projects with limited data and experience, this study develops an analogy indicator system and tests multiple machine-learning algorithms on two analogy tasks to identify the optimal method. Using an initial set of basic indicators and a database of 1436 oilfield samples, a combined subjective–objective weighting strategy that integrates statistical methods with expert judgment is used to select, classify, and assign weights to the indicators. This process results in 26 key indicators for practical analogy analysis. Single-indicator and whole-asset analogy experiments are then performed with five standard machine-learning algorithms—support vector machine (SVM), random forest (RF), backpropagation neural network (BP), k-nearest neighbor (KNN), and decision tree (DT). Results show that SVM achieves classification accuracies of 86% and 95% in medium-high permeability sandstone oilfields, respectively, greatly surpassing other methods. These results demonstrate the effectiveness of the proposed indicator system and methodology, providing efficient and objective technical support for evaluating and making decisions on overseas oilfield development projects.

1. Introduction

The complex process of oil and gas development involves high technical demands, strong interdisciplinarity, lengthy investment cycles, significant uncertainty, and substantial capital commitments [1]. Assessing potential development projects is further complicated by various project types, limited data availability, and tight decision-making timelines [2,3,4,5,6].

The reservoir analogy, which derives the potential of a new project from the experience of developed fields, plays a crucial role in reducing geological risk, optimizing development plans, and speeding up decision-making. It is particularly helpful during pre-development and early production stages and is most effective when used with newly discovered reservoirs within or near mature oil and gas fields. In the evaluation of new oilfield development projects, especially those overseas lacking operational experience or enough data, reservoir analogy offers guidance for reserves estimation, production forecasting, and strategy development. Both the U.S. Securities and Exchange Commission (SEC) regulations and the Society of Petroleum Engineers’ (SPE) Petroleum Resources Management System (PRMS) standard explicitly support using reliable analogies for reserves assessment when direct data are limited [7,8].

Analogy methods have been proposed or applied in reservoir characterization [9], seismic attribute analysis [10], and resource assessment [11]. With the widespread use of machine learning in petroleum engineering and its strong modeling ability and potential for generalization in reservoir identification, parameter prediction, and development scheme optimization, an increasing number of studies have used machine-learning techniques for analogy and prediction of various oilfield indicators [12,13,14,15,16,17,18]. Bai et al. [19] developed productivity prediction models using linear regression (LR), random forest regression (RF), support vector regression (SVR), backpropagation neural networks (BP), extreme gradient boosting (XGBoost), and LightGBM, demonstrating the role of machine learning in oilfield analogy and production forecasting. Guo et al. [20] introduced a new analogy and machine-learning approach for predicting reservoir permeability. Mahdaviara et al. [21] created a tool using statistical and machine-learning methods to evaluate and screen enhanced oil recovery (EOR) scenarios for low-permeability reservoirs. Rahimi and Riahi [22] classified offshore reservoir facies based on logging data with the RF method.

However, limitations remain in the current analogy practices used in oilfield development. The choice of analogy processes and parameters still heavily depends on expert knowledge and subjective judgment, lacking a systematic and objective evaluation framework. Oilfield projects involve numerous parameters, including geological, reservoir, fluid, reserves, and development factors. Because of the complexity in evaluating multiple parameters, many analogy studies focus on only a limited subset or a single category of parameters for similarity assessment, leading to the absence of a comprehensive and systematic indicator framework [23,24,25,26,27,28]. The weighting of analogy indicators is traditionally based on expert scoring or the Analytic Hierarchy Process (AHP). These methods, being highly subjective and poorly standardized, often produce significant discrepancies among different technical personnel, thus reducing comparability and reproducibility. Additionally, most existing studies on analogy methods concentrate on individual oilfield indicators, while research on analogy at the level of whole asset evaluation remains limited.

To address these challenges, this study aims to develop a comprehensive analogy indicator system specifically designed for overseas oilfield development projects and to optimize analogy methods using multiple machine-learning algorithms. First, raw indicators are extracted and categorized from commercial databases and representative development projects. Next, a set of key analogy indicators is generated through screening, classification, and weighting processes. Five commonly used machine-learning algorithms are then employed to model these key indicators and conduct both single-indicator and whole-asset analogy experiments, with performance evaluated based on adaptability and predictive accuracy. The experimental results validate the effectiveness of the proposed indicator system and identify support vector machine (SVM) as the most appropriate algorithm for this application.

The main contributions of this study are as follows:

• A range of statistical techniques, including the correlation coefficient, systematic clustering, and principal component analysis, are used to screen the original set of indicators and identify key analogy indicators. A classification scheme is then created for the selected key indicators based on probability statistics analysis and expert judgment, ensuring both representativeness and engineering relevance.
• A combined subjective–objective weighting method is proposed for key indicators. Subjective weights are assigned using direct expert scoring, while objective weights are derived from the averaged results of the entropy method and the coefficient of variation method. This approach ensures that the weighting reflects both expert experience and data characteristics.
• Through screening, classification, and weighting, a comprehensive analogy indicator system is developed. It combines static and dynamic parameters from geological, petrophysical, and development aspects, integrating both subjective and objective views to support similarity evaluation between target and candidate oilfields.
• Five machine-learning methods—support vector machine (SVM), random forest (RF), backpropagation neural network (BP), k-nearest neighbor (KNN), and decision tree (DT)—are used to perform both single indicator and whole analogy experiments. The adaptability and prediction accuracy of each method are evaluated under different reservoir conditions, such as medium-to-high permeability sandstone and low-permeability sandstone, leading to the identification of the optimal algorithm.

The paper is organized as follows. Section 2 provides a detailed discussion of the methodology and procedures for constructing the analogy indicator system and selecting analogy methods for oilfield development projects. Section 3 presents and analyzes the application of the proposed analogy indicator system and the selection of analogy methods, using real data from oilfield projects. Finally, Section 4 summarizes the main findings of the study.

2. Materials and Methods

Focusing on analogy analysis for oilfield development projects, the study includes two main components: the construction of analogy indicators and the optimization of analogy methods, as shown in Figure 1.

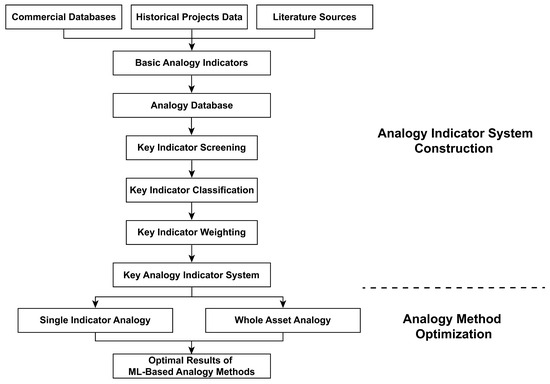
Figure 1. Indicator analogy process for oilfield development projects.

In the indicator construction component, technical indicators and representative oilfield data were first categorized and organized to create a base indicator system and database tailored to the characteristics of overseas oilfield development projects. Based on the requirements of the analogy task, key analogy indicators were then identified through a series of steps, including indicator screening, classification, and weighting, to prepare for subsequent analogy procedures. In the analogy method component, machine-learning algorithms were applied to perform both single-indicator and whole-asset analogy experiments for new oilfield development projects, to identify the most suitable method to meet the needs of such projects.

2.1. Analogy Indicator System for Oilfield Development Projects

The initial process for selecting basic analogy indicators involved several steps. First, relevant data were collected from multiple sources, including commercial databases like the C&C Reservoir database (http://www.ccreservoirs.com, accessed on 27 June 2025), the IHS Markit Energy Portal (https://energyportal.ci.spglobal.com, accessed on 27 June 2025), and the Wood Mackenzie database (https://www.woodmac.com, accessed on 27 June 2025), as well as historical project records and reviewed literature. Second, the objective analysis method was used to identify key factors that influence project evaluation, ensuring the indicators were comprehensive, complete, and easily interpretable. Third, the key factors were grouped into different indicator sets based on their technical features. Finally, expert consultation was conducted to validate the results, resulting in the basic analogy indicators.

A total of 36 basic analogy indicators were initially chosen, covering both static and development parameters. The static parameters include reservoir properties, trap and structural characteristics, fluid properties, and reserve parameters. Among these, eight are qualitative indicators (highlighted in blue), and twenty-eight are quantitative indicators (shown in black), as shown in Figure 2.

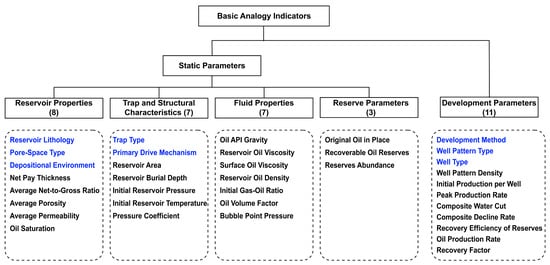
Figure 2. Basic analogy indicators for oilfield development projects. Qualitative indicators are highlighted in blue, and quantitative indicators are shown in black.

Among the 36 selected indicators, static parameters directly represent key geophysical and petrophysical attributes that govern reservoir performance. Reservoir properties such as lithology, average porosity, and permeability quantify storage capacity, while trap and structural characteristics define the reservoir framework. Fluid properties control fluid mobility and drive mechanisms, and reserve parameters measure volumetric resource potential [29]. Development parameters directly reflect production-process performance and reservoir drive characteristics. By integrating static and development parameters, the basic analogy indicators are firmly grounded in reservoir characteristics and field production performance, thus providing a comprehensive and reliable basis for analogy in oilfield development projects.

Using these 36 indicators, data from various oilfields were compiled and screened to build a basic analogy indicator database for different oilfield types. This database includes data from 1436 oilfields, categorized by region (onshore and offshore) and lithology (sandstone and carbonate).

Among the thirty-six basic analogy indicators, eight qualitative indicators—derived from oilfield classification standards or expert judgment—have clear categorical distinctions and classification functions. As categorical variables, they are not suitable for quantitative analysis and were therefore directly included in the construction of the analogy indicator system. For the remaining 28 quantitative indicators, statistical methods were used for screening, classification, and weight calculation to establish a more scientifically based key analogy indicator system. This system provides parameters and a foundation for future research on analogy methods for oilfield development projects. The flowchart for constructing the key analogy indicator system is shown in Figure 3.

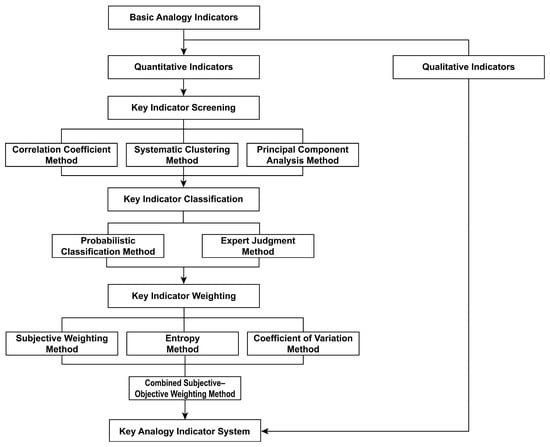
Figure 3. Flowchart for the construction of the key analogy indicator system in oilfield development projects.

2.1.1. Key Indicator Screening

The initially selected basic analogy indicators aimed to comprehensively capture all key factors characterizing oilfield development projects and influencing project evaluation. However, practical issues may arise with these indicators, such as overlapping or correlated parameters, parameters that do not clearly reflect evaluation-relevant features, and the need to clarify each parameter’s relative importance. Therefore, a secondary screening of the basic indicators is necessary to reduce redundancy and correlation among them and to identify the key indicators for analogy analysis.

In this study, three statistical methods were used for key indicator screening: the correlation coefficient method, the systematic clustering method, and the principal component analysis method.

Correlation Coefficient Method

The correlation coefficient is a statistical metric used to measure the strength of the relationship between two variables. It is calculated using the product-moment method, which is based on the deviations of each variable from its respective mean. The degree of correlation between the two variables is reflected by the product of these deviations.

Given two variables, $x=\left(x_1,x_2,{\dots ,x}_k,\dots x_n\right)$, $y=\left(y_1,y_2,{\dots ,y}_k,\dots y_n\right)$, the correlation coefficient $r_{xy}$ is calculated using the following formula:

$$\begin{array}{c}{r}_{xy}={\displaystyle \frac{{\sum }_{k=1}^n\left(x_k-\overline{x}\right)\left(y_k-\overline{y}\right)}{\sqrt{{\sum }_{k=1}^n\sum {\left(x_k-\overline{x}\right)}^2{\sum }_{k=1}^n\sum {\left(y_k-\overline{y}\right)}^2}}}\end{array},$$

(1)

where $\overline{x}$ and $\overline{y}$ represent the mean values of variables $x$ and $y$, respectively. The absolute value of the correlation coefficient $\left|r_{xy}\right|$ reflects the degree of similarity between the two variables.

Systematic Clustering Method

Cluster analysis groups sample data based on individual characteristics of the research objects according to predefined classification criteria. Systematic clustering is a hierarchical classification method based on distance metrics, with the core idea of iteratively merging similar objects to form hierarchical groupings from fine to coarse levels. In this method, each sample or variable is initially treated as an individual class. The algorithm then repeatedly calculates inter-class distances and merges the two closest classes until all objects are grouped into a single cluster. This process can be visually represented by a dendrogram, allowing researchers to select an appropriate distance threshold based on practical needs to determine the final clustering scheme. Systematic clustering does not require a predefined number of clusters and can naturally reveal the data’s hierarchical structure. However, its computational complexity increases significantly with the number of samples, making it more suitable for exploratory analysis of small to medium-sized datasets.

In variable clustering studies, the systematic clustering method is often combined with the correlation coefficient to identify groups of key indicators with similar variation patterns. For clustering analysis, the correlation coefficient was converted into a distance metric as follows:

$$d_{xy}=1-\left|r_{xy}\right|,$$

(2)

where $d_{xy}$ denotes the distance between variables x and y, calculated as one minus the absolute value of their correlation coefficient $\left|r_{xy}\right|$. A smaller value of $d_{xy}$ indicates a higher similarity between variables x and y, and such variables should be clustered together with higher priority.

Systematic clustering groups data by iteratively merging similar classes, with its core process being the definition of inter-class distances. This study adopts the Single Linkage method. The specific steps are as follows:

• Each sample or variable is initially treated as an independent class, denoted as G₁, G₂, …, Gₙ. All pairwise distances are calculated to form the initial distance matrix D⁽⁰⁾, where the element D_ij = d_xy represents the distance between variables.
• The minimum distance element in the current matrix is selected as D_pq = min {D_ij}, and the corresponding classes G_p and G_q are merged to form a new class G_s.
• The distance matrix is updated by calculating the distance between the new class G_s and any other class G_k as D_sk = min {D_pk, D_qk}, where D_pk and D_qk are the distances between the original classes G_p, G_q, and class G_k.
• The above steps are repeated until all classes are merged into a single class. The entire clustering process can be visualized using a dendrogram, and researchers can determine the final classification scheme by selecting an appropriate distance threshold based on practical needs.

Principal Component Analysis Method

Factor analysis is a multivariate dimensionality reduction method aimed at extracting a small number of latent, unobservable common factors from a set of correlated observed variables. The goal is to simplify the data structure and reveal the intrinsic relationships among variables while retaining as much original information as possible. Factor analysis explains most of the variation in the original observed variables through common factors. It assumes that the original variables $X_1,X_2,{\dots ,X}_p$ can be expressed as a linear combination of k latent factors $F_1,F_2,{\dots ,F}_k$ (where $k\ll p$), along with a unique error term ${\epsilon }_i$ associated with each variable. The mathematical model of factor analysis can thus be expressed as:

$$X_i=a_{i1}{F}_1+a_{i2}{F}_2+{\dots +a}_{ik}{F}_k+{\epsilon }_i,\hspace{1em}\hspace{1em}i=1,2,\dots ,p.$$

(3)

It can also be expressed in matrix form as:

$$X=AF+\epsilon ,$$

(4)

where $A=\left[a_{ij}\right]$ is the factor loading matrix, representing the degree of correlation between the original variables and the extracted factors.

We extract principal components using principal component analysis and employ them as factor inputs in the subsequent modeling. The specific steps for determining factor variables using principal component analysis in this study are as follows:

• Standardize the original variables to zero mean and unit variance in order to eliminate the influence of differing units and scales.
• Construct the correlation matrix R for the original variables.
• Perform eigenvalue decomposition on the correlation matrix R. Let $U$ be the matrix composed of the top $k$ principal eigenvectors, and $\Lambda$ be the diagonal matrix of the corresponding eigenvalues. The factor loading matrix $A$ can then be computed as:

$$A=U{\Lambda }^{1/2}$$

(5)

where $a_{ij}=u_{ij}\sqrt{{\mathsf{\lambda }}_j}$, representing the loading of variable $X_i$ on factor $F_j$, i.e., the degree to which factor $F_j$ explains the variance of variable $X_i$.

4.

Determine the number of factors k based on the cumulative variance contribution rate, choosing the smallest k such that the cumulative explained variance is at least 90%.

5.

Linearly transform the original variables into factor scores to be used as inputs for subsequent modeling. Let wⱼᵢ denote the weight of variable Xᵢ on factor Fⱼ, and the factor score, which is a weighted sum of all variables on a given factor, can be calculated as follows:

$$F_j=w_{j1}{X}_1+w_{j2}{X}_2+{\dots +w}_{jp}{X}_p.$$

(6)

2.1.2. Key Indicators Classification

After identifying the key analogy indicators, it is necessary to further classify and assign weights to them to support both single indicator and whole asset analogy tasks. In this study, quantitative indicators were classified using both probability distribution curves and expert knowledge, ensuring a balance between objective data features and subjective domain experience. This method improves the credibility of the classification results by considering both expert insights and variability from random sampling.

Based on the probabilistic analysis of key quantitative indicators, the distribution patterns were categorized into the following types:

1.

Normal distribution type: This includes indicators such as Average Porosity, Reservoir Burial Depth, Initial Reservoir Pressure, Oil API Gravity, Original Oil in Place, and Recovery Factor.

For normally distributed indicators, the classification thresholds were calculated based on the mean ($\mu$) and standard deviation ($\sigma$), using the values: $\mu -\sigma ,\mu -\sigma /2,\mu +\sigma /2,\mu +\sigma$.

2.

Exponential distribution type: This category includes Net Pay Thickness, Average Permeability, Oil Volume Factor, Bubble Point Pressure, Reserves Abundance, Well Pattern Density, Initial Production per Well, Peak Production Rate, and Oil Production Rate.

For exponentially distributed indicators, the classification thresholds were determined based on the characteristic quantiles extracted from the cumulative distribution function (CDF) at probability levels of 15%, 30%, 70%, and 85%.

3.

Uniform distribution type: This category includes Average Net-to-Gross Ratio and Recovery Efficiency of Reserves.

For uniformly distributed indicators, the classification thresholds were defined by the characteristic quantiles extracted from the CDF at probability levels of 20%, 40%, 60%, and 80%.

2.1.3. Key Indicator Weighting

In analogy-based evaluation of new oilfield development projects, different analogy objectives relate to various key influencing factors and their associated weights. The weight assigned to each key indicator indicates its relative contribution to the final evaluation result. Common weighting methods are divided into three categories: subjective methods (such as analytic hierarchy process, expert scoring), objective methods (such as entropy method, coefficient of variation method), and combined subjective–objective methods.

Subjective methods reflect the preferences and judgments of decision-makers, but they often lack objectivity. Objective methods depend on the inherent structure of the data but may miss the practical significance of indicators. To balance expert opinions with data-driven insights, this study uses a combined subjective–objective weighting approach. For the subjective part, expert scoring was used, where domain specialists assigned scores to each indicator based on engineering experience and the analogy objective, producing the subjective weights. For the objective part, both the entropy method and the coefficient of variation method were applied to calculate the objective weights, and their average was used as the final objective value.

Entropy Method

The entropy method is an objective weighting technique based on information entropy theory. Entropy measures uncertainty, with an indicator’s entropy value indicating its degree of dispersion. The lower the entropy value, the higher the dispersion and the greater the impact of that indicator on the overall evaluation. The steps for calculating the entropy method are as follows:

1.

Normalize the data. Let $i$ denote the sample index and $j$ denote the indicator index. Let $X_{ij}$ represent the original value of the $j$-th indicator for the $i$-th sample. Denote the minimum and maximum values of all samples for the $j$-th indicator as $min\left\{X_j\right\}$ and $max\left\{X_j\right\}$, respectively. Each $X_{ij}$ is linearly mapped to the interval [0, 1], resulting in the normalized value $X_{ij}^{\prime }$.

For a positive indicator, the normalization is computed as follows:

$$X_{ij}^{\prime }={\displaystyle \frac{X_{ij}-min\left\{X_j\right\}}{max\left\{X_j\right\}-min\left\{X_j\right\}}}.$$

(7)

For a negative indicator, the normalization is computed as follows:

$$X_{ij}^{\prime }={\displaystyle \frac{max\left\{X_j\right\}-X_{ij}}{max\left\{X_j\right\}-min\left\{X_j\right\}}}.$$

(8)

2.

Calculate the proportion of the $j$-th indicator in the $i$-th sample, denoted as $Y_{ij}$, using the following formula:

$$Y_{ij}={\displaystyle \frac{X_{ij}^{\prime }}{{\sum }_{i=1}^m{X}_{ij}^{\prime }}}.$$

(9)

3.

Compute the entropy value of the $j$-th indicator. Let $m$ be the total number of samples and $k={\displaystyle \frac{1}{\ln m}}$ be the normalization constant. The entropy value $e_j$ is calculated as follows:

$$e_j=-k\sum _{i=1}^m{Y}_{ij}\ln Y_{ij}.$$

(10)

4.

Compute the redundancy $d_j$ and derive the weight of each indicator. The redundancy is given by $d_j=1-e_j$, and the final weight $w_j^{ent}$ is calculated as follows:

$$w_j^{ent}={\displaystyle \frac{d_j}{{\sum }_{j=1}^n{d}_j}}.$$

(11)

Coefficient of Variation Method

The coefficient of variation method is an objective weighting approach based on the degree of variability of indicator data. The coefficient of variation is a relative measure of data dispersion, calculated as the standard deviation divided by the mean. This method removes the effects of units and magnitude. Because of its properties, the coefficient of variation measures how much an indicator varies relative to others. A higher coefficient indicates more dispersion, meaning the indicator has a greater influence on the overall evaluation.

Let the mean and standard deviation of the $j$-th indicator across all samples be denoted as $\overline{x_j}$ and $s_j$, respectively. The coefficient of variation ${\sigma }_j$ is calculated using the following formula:

$${\sigma }_j={\displaystyle \frac{s_j}{\overline{x_j}}}.$$

(12)

The weight of indicator $j$ based on the coefficient of variation method, denoted as $w_j^{cv}$, is calculated using the following formula:

$$w_j^{cv}={\displaystyle \frac{{\sigma }_j}{{\sum }_{j=1}^n{\sigma }_j}}.$$

(13)

Combined Subjective–Objective Weighting Method

This study adopts a linear weighting approach to combine subjective and objective methods. Let $b_j$ denote the subjective weight of indicator $j$, obtained using the expert direct rating method. Let $\alpha$, $\beta$, and $\gamma$ represent the weight coefficients for the subjective method, entropy method, and coefficient of variation method, respectively. The final weight $W_j$ for each indicator is calculated by linearly combining the subjective weight and the two objective weights, as shown below:

$$W_j=\alpha b_j+\beta w_j^{ent}+\gamma w_j^{cv}.$$

(14)

In this study, the coefficients are set as $\alpha =0.5$, $\beta =\gamma =0.25.$

2.2. Analogy Methods for Oilfield Development Projects

Analogy, also referred to as analogical reasoning, is a method of inference that deduces the presence of certain properties in a target entity based on the known existence of similar properties in a comparable reference. The validity of such inference must be empirically verified, and the more attributes the two entities share, the more reliable the analogical conclusion becomes.

In oilfield development projects, analogy involves selecting similar reference projects to evaluate a new development project through comparison and inference, thereby enabling rapid screening and evaluation. In this study, two analogy approaches are employed: (1) single indicator analogy, which supplies reference values for missing indicators in the target asset, and (2) whole asset analogy, which qualitatively evaluates the overall potential and value of the target project. Both approaches are implemented using five machine-learning algorithms: support vector machine (SVM), random forest (RF), backpropagation neural network (BP), k-nearest neighbor (KNN), and decision tree (DT). The workflow of the analogy method is shown in Figure 4.

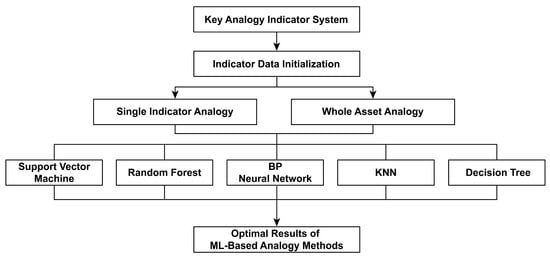
Figure 4. Flowchart for machine-learning-based optimization of analogy methods for oilfield development projects.

2.2.1. Machine-Learning Methods

Machine learning is an interdisciplinary field that combines statistics, artificial intelligence, and computer science. It is also called predictive analytics or statistical learning. Machine-learning algorithms find patterns and features directly from data using computational methods, without depending on predetermined equations. As the number of training samples grows, these algorithms can improve their performance adaptively. The main idea is to train models to discover the underlying patterns and key rules of a phenomenon, ultimately enabling prediction or decision-making.

This study builds on the previously established key analogy indicator system and uses five machine-learning methods to predict key indicators and assess the whole asset level of oilfield development projects. A comparative overview of the characteristics of these methods is shown in Table 1.

Table 1. Comparison of machine-learning methods.

Method	Advantages	Disadvantages	Applicable Scenarios	Algorithm Principle
Support Vector Machine (SVM)	Performs well on high-dimensional, nonlinearly separable data; good generalization.	Lacks interpretability; decision process not intuitive.	Suitable for relatively small samples with high feature dimensionality.	Maps inputs via kernel functions into a high-dimensional space and finds the hyperplane that maximizes class margin.
Random Forest (RF)	Strong noise robustness; resistant to overfitting.	High memory footprint; computationally expensive for training and inference.	Works well on high-dimensional or very large datasets.	Ensembles multiple decision trees trained on bootstrapped samples and random feature subsets; predictions by majority vote or averaging.
Backpropagation Neural Network (BP)	Flexible architecture; capable of modeling complex nonlinear mappings.	Black-box model; internal workings hard to interpret.	Well suited for large datasets and complex nonlinear tasks.	Multi-layer feedforward network trained by backpropagation using gradient descent to minimize prediction error.
K-Nearest Neighbors (KNN)	Simple to implement; intuitive prediction by neighbors.	High storage and computation cost, especially for large datasets.	Suitable for low-dimensional problems with modest sample sizes.	Instance-based learning: finds k-nearest neighbors by distance in feature space; predicts by majority vote or averaging.
Decision Tree (DT)	Easy to understand; highly interpretable.	Prone to overfitting; may generalize poorly.	Suits problems with few classes and clear feature semantics.	Recursively partitions the feature space by selecting splits that maximize information gain or minimize Gini impurity.

2.2.2. Single Indicator Analogy

According to oilfield classification, the key indicator system was used to comprehensively include both reservoir static parameters and development parameters. Machine-learning methods were then applied to predict the target indicator. In this study, experiments were carried out separately for two types of oilfields: onshore medium-to-high permeability sandstone reservoirs and onshore low-permeability sandstone reservoirs [30].

Before the analogy process, data preprocessing was performed on the key indicator set. Indicators with more than 70% sample coverage were chosen as feature variables. Using the recovery factor as the target variable for the analogy, seven key indicators were selected as features: well pattern density, oil API gravity, original oil in place, reserves abundance, average porosity, net pay thickness, and reservoir burial depth. After removing outliers, imputing missing values with the median, and normalizing the data, 663 samples from medium-to-high permeability sandstone oilfields and 157 samples from low-permeability oilfields were retained.

2.2.3. Whole Asset Analogy

Using conventionally classified oilfield asset categories as the reference standard and incorporating the selected key indicators, machine-learning methods were applied to classify asset levels for onshore medium-to-high permeability sandstone oilfields, with a total of 663 samples. Based on oilfield characteristics, development potential, and economic benefits, the assets were divided into five levels, with Level 1 representing the highest priority. Compared to the limited sample size of low-permeability oilfields, the larger dataset of medium-to-high permeability oilfields is more suitable for training and optimizing machine-learning models, making it ideal for whole asset analogy and selection.

In the analogy indicator system for oilfield development projects, nine features were chosen: well pattern density, oil API gravity, original oil in place, reserves abundance, average porosity, average permeability, net pay thickness, reservoir burial depth, and recovery factor. These were used as inputs for the five machine-learning methods mentioned earlier to classify and prioritize target oilfield assets.

In the conventional empirical classification, asset categories are determined via a linear weighted scoring procedure applied to the n selected key quantitative indicators, comprising the following steps:

1.

Construct the evaluation matrix by arranging the $n$ indicators as columns and the 663 oilfields as rows.

2.

Normalize each indicator to the [0, 1] range and multiply by its obtained key-indicator weight.

3.

Compute each oilfield’s analogy score $S$ by summing the weighted, normalized scores.

4.

Plot the score histogram and, based on empirical distribution characteristics, divide S into five intervals to define the asset levels.

The histogram of analogy scores for the 663 medium-to-high permeability sandstone oilfields is shown in Figure 5. According to conventional empirical classification, the five asset levels are defined as Level 1 for $S$ ≥ 0.58, Level 2 for 0.53 ≤ $S$ < 0.58, Level 3 for 0.43 ≤ $S$ < 0.53, Level 4 for 0.38 ≤ $S$ < 0.43, and Level 5 for $S$ < 0.38.

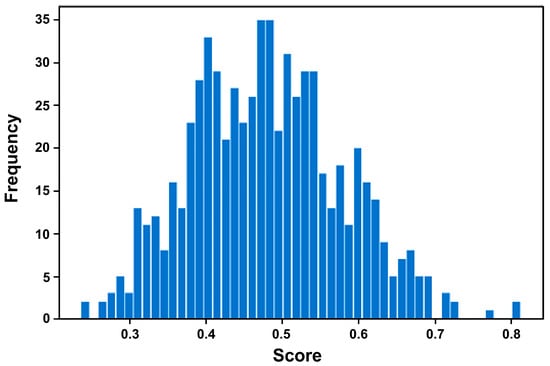
Figure 5. Histogram of composite analogy scores for 663 medium-to-high permeability sandstone oilfields.

All analyses were conducted in Python 3.8, using NumPy, pandas, and SciPy for data handling and statistical computations, scikit-learn for machine-learning tasks, and Matplotlib 3.3.2 for visualization.

3. Results and Analysis

3.1. Construction of the Analogy Indicator System

3.1.1. Results of Key Indicator Screening

Correlation Coefficient Method

Among the twenty-eight basic quantitative indicators, three indicators—pressure coefficient, reservoir oil density, and surface oil viscosity—had a high proportion of missing data in the collected dataset and were therefore excluded from the correlation analysis. The remaining 25 indicators were divided into two categories: static parameters and development parameters. Correlation analysis was conducted separately for each category. The correlation coefficient matrix of static parameters is shown in Table 2, and that of development parameters is shown in Table 3.

Table 2. Correlation matrix of static parameters. Correlation coefficients greater than or equal to 0.6 are highlighted in bold to indicate relatively strong associations.

Parameter	Net Pay Thickness	Average Net-to-Gross Ratio	Average Porosity	Average Permeability	Oil Saturation	Reservoir Area	Reservoir Burial Depth	Initial Reservoir Pressure	Initial Reservoir Temperature	Oil API Gravity	Reservoir Oil Viscosity	Initial Gas–Oil Ratio	Oil Volume Factor	Bubble Point Pressure	Original Oil in Place	Recoverable Oil Reserves	Reserves Abundance
Net Pay Thickness	1.00	0.21	−0.16	−0.13	0.08	−0.10	0.29	0.47	0.27	0.05	−0.08	0.23	0.24	0.50	0.01	0.05	0.34
Average Net-to-Gross Ratio	0.21	1.00	0.11	0.25	0.21	0.03	0.01	0.06	0.13	−0.12	0.27	−0.02	0.00	0.14	0.18	0.06	0.24
Average Porosity	−0.16	0.11	1.00	0.51	−0.03	0.00	−0.36	−0.44	−0.44	−0.50	0.29	−0.50	−0.53	−0.36	0.16	0.19	0.28
Average Permeability	−0.13	0.25	0.51	1.00	0.19	0.14	−0.23	−0.25	−0.23	−0.54	0.45	−0.29	−0.31	−0.22	0.17	0.15	−0.05
Oil Saturation	0.08	0.21	−0.03	0.19	1.00	0.15	−0.02	0.13	0.05	0.01	0.05	0.14	0.15	0.17	0.16	0.17	−0.01
Reservoir Area	−0.10	0.03	0.00	0.14	0.15	1.00	0.01	0.08	−0.07	−0.11	0.11	−0.10	−0.08	−0.06	0.80	0.72	−0.06
Reservoir Burial Depth	0.29	0.01	−0.36	−0.23	−0.02	0.01	1.00	0.79	0.82	0.16	−0.15	0.38	0.46	0.61	0.10	0.01	−0.10
Initial Reservoir Pressure	0.47	0.06	−0.44	−0.25	0.13	0.08	0.79	1.00	0.73	0.22	−0.17	0.37	0.44	0.59	0.12	0.05	0.04
Initial Reservoir Temperature	0.27	0.13	−0.44	−0.23	0.05	−0.07	0.82	0.73	1.00	0.30	−0.18	0.48	0.58	0.58	0.02	−0.07	−0.11
Oil API Gravity	0.05	−0.12	−0.60	−0.54	0.01	−0.11	0.16	0.22	0.30	1.00	−0.54	0.49	0.55	0.26	−0.28	−0.16	−0.31
Reservoir Oil Viscosity	−0.08	0.27	−0.29	0.71	0.05	0.11	−0.15	−0.17	−0.18	−0.54	1.00	−0.22	−0.24	−0.24	0.20	0.00	0.05
Initial Gas–Oil Ratio	0.23	−0.02	−0.50	−0.29	0.14	−0.10	0.38	0.37	0.48	0.49	−0.22	1.00	0.93	0.73	−0.12	−0.11	−0.11
Oil Volume Factor	0.24	0.00	−0.53	−0.31	0.15	−0.08	0.46	0.44	0.58	0.55	−0.24	0.93	1.00	0.70	−0.10	−0.11	−0.12
Bubble Point Pressure	0.50	0.14	−0.36	−0.22	0.17	−0.06	0.61	0.59	0.58	0.26	−0.24	0.73	0.70	1.00	−0.03	−0.02	0.02
Original Oil in Place	0.01	0.18	0.16	0.17	0.16	0.80	0.10	0.12	0.02	−0.28	0.20	−0.12	−0.10	−0.03	1.00	0.86	0.16
Recoverable Oil Reserves	0.05	0.06	0.19	0.15	0.17	0.72	0.01	0.05	−0.07	−0.16	0.00	−0.11	−0.11	−0.02	0.86	1.00	0.14
Reserves Abundance	0.34	0.24	0.28	−0.05	−0.01	−0.06	−0.10	0.04	−0.11	−0.31	0.05	−0.11	−0.12	0.02	0.16	0.14	1.00

Table 3. Correlation matrix of development parameters.

Parameter	Well Pattern Density	Initial Production per Well	Peak Production Rate	Composite Water Cut	Composite Decline Rate	Recovery Efficiency of Reserves	Oil Production Rate	Recovery Factor
Well Pattern Density	1.00	0.47	0.08	−0.46	0.18	0.00	0.47	0.08
Initial Production per Well	0.47	1.00	0.10	−0.26	0.13	−0.08	0.31	0.08
Peak Production Rate	0.08	0.10	1.00	0.12	−0.10	0.04	−0.06	0.09
Composite Water Cut	−0.46	−0.26	0.12	1.00	−0.10	0.21	−0.19	0.21
Composite Decline Rate	0.18	0.13	−0.10	−0.10	1.00	0.09	0.20	−0.17
Recovery Efficiency of Reserves	0.00	−0.08	0.04	0.21	0.09	1.00	0.26	0.20
Oil Production Rate	0.47	0.31	−0.06	−0.19	0.20	0.26	1.00	0.36
Recovery Factor	0.08	0.08	0.09	0.21	−0.17	0.20	0.36	1.00

The correlation coefficient is used to assess the degree of linear association between two variables. When 0 < $\left|r_{xy}\right|$ < 1, it indicates that a certain degree of linear correlation exists between the two variables. The closer $\left|r_{xy}\right|$ is to 1, the stronger the linear relationship between them. Conversely, the closer $\left|r_{xy}\right|$ is to 0, the weaker the linear correlation. In general, the correlation coefficient is interpreted in three levels: $\left|r_{xy}\right|$ < 0.4 indicates low linear correlation, 0.4 ≤ $\left|r_{xy}\right|$ < 0.7 indicates significant correlation, and 0.7 ≤ $\left|r_{xy}\right|$ < 1 indicates high linear correlation.

However, due to differences in sample size, the number of variables, their characteristics, and the relationships among them, the threshold values used to determine the degree of correlation may vary in different situations. In some cases, a correlation coefficient greater than 0.5 is regarded as indicating good correlation, whereas in others, a threshold of 0.8 or even higher is required. We selected a threshold of 0.6. This choice balances the need for strong internal consistency within each indicator group against the requirement for clear separation between groups. Preliminary grouping experiments on our dataset showed that using a threshold of 0.6 produced stable clusters with high repeatability and minimal cross-group correlation.

In this study, based on the correlation coefficient (0.6 ≤ $\left|r_{xy}\right|$ < 1), the static parameter indicators were classified into three groups. Within each group, indicators show strong internal correlation, while the correlation between groups is relatively weak. The first group includes Reservoir Burial Depth, Initial Reservoir Pressure, and Initial Reservoir Temperature. The second group consists of Initial Gas–Oil Ratio, Oil Volume Factor, and Bubble Point Pressure. The third group includes Reservoir Area, Original Oil in Place, and Recoverable Oil Reserves. The remaining eight static parameters were treated as independent indicators. The pairwise correlation coefficients of these eight development parameters were below 0.6, indicating no significant correlation, and they were therefore treated as independent indicators. The detailed classification of parameters is shown in Table 4.

Table 4. Classification statistics of static and development parameters based on the correlation coefficient method.

Correlation Coefficient Threshold	Static Parameters (11 Categories)	Development Parameters (8 Categories)
0.6	1. Reservoir Burial Depth, Initial Reservoir Pressure, Initial Reservoir Temperature; 2. Initial Gas–Oil Ratio, Oil Volume Factor, Bubble Point Pressure; 3. Reservoir Area, Original Oil in Place, Recoverable Oil Reserves; 4. Average Permeability; 5. Reservoir Oil Viscosity; 6. Reserves Abundance; 7. Net Pay Thickness; 8. Average Net-to-Gross Ratio; 9. Average Porosity; 10. Oil Saturation; 11. Oil API Gravity.	Well Pattern Density; Initial Production per Well; Peak Production Rate; Composite Water Cut; Composite Decline Rate; Recovery Efficiency of Reserves; Oil Production Rate; Recovery Factor.

Systematic Clustering Method

Systematic clustering using the Single Linkage method was performed separately for static and development parameters, and the corresponding dendrograms are shown in Figure 6 and Figure 7. In the dendrogram, a smaller distance indicates a higher tendency for variables to cluster together, and indicators within the same cluster tend to have strong internal correlation and redundancy. The clustering results for both static and development parameters are summarized with cluster thresholds ranging from 2 to 5. Indicators grouped in the same cluster are enclosed in parentheses, while those without parentheses are considered independent indicators, as shown in Table 5 and Table 6.

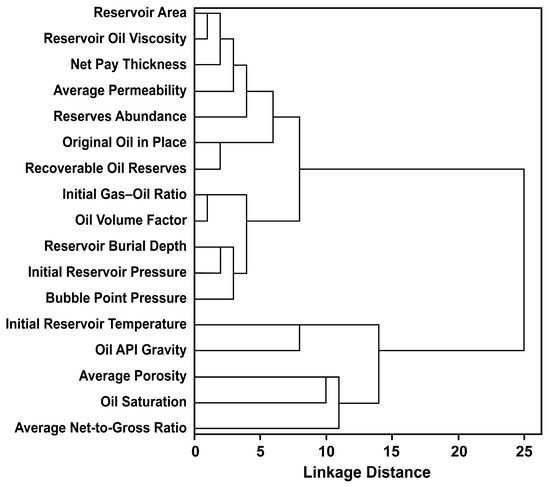
Figure 6. Hierarchical clustering dendrogram of static parameters.

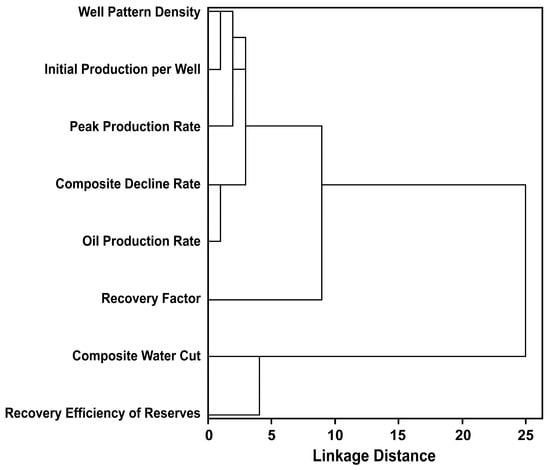
Figure 7. Hierarchical clustering dendrogram of development parameters.

Table 5. Classification of static parameters under different clustering distance thresholds. Grouped parameters are indicated within parentheses, while ungrouped entries represent individual indicators.

Clustering Distance Threshold	Number of Categories	Static Parameter Groups
5	8	(Reservoir Area, Reservoir Oil Viscosity, Net Pay Thickness, Average Permeability, Reserves Abundance); (Original Oil in Place, Recoverable Oil Reserves); (Initial Gas–Oil Ratio, Oil Volume Factor, Reservoir Burial Depth, Initial Reservoir Pressure, Bubble Point Pressure); Initial Reservoir Temperature; Oil API Gravity; Average Porosity; Oil Saturation; Average Net-to-Gross Ratio.
4	10	(Reservoir Area, Reservoir Oil Viscosity, Net Pay Thickness, Average Permeability); (Original Oil in Place, Recoverable Oil Reserves); (Initial Gas–Oil Ratio, Oil Volume Factor); (Reservoir Burial Depth, Initial Reservoir Pressure, Bubble Point Pressure); Reserves Abundance; Initial Reservoir Temperature; Oil API Gravity; Average Porosity; Oil Saturation; Average Net-to-Gross Ratio.
3	12	(Reservoir Area, Reservoir Oil Viscosity, Net Pay Thickness); (Original Oil in Place, Recoverable Oil Reserves); (Initial Gas–Oil Ratio, Oil Volume Factor); (Reservoir Burial Depth, Initial Reservoir Pressure); Average Permeability; Reserves Abundance; Bubble Point Pressure; Initial Reservoir Temperature; Oil API Gravity; Average Porosity; Oil Saturation; Average Net-to-Gross Ratio.
2	15	(Reservoir Area, Reservoir Oil Viscosity); (Initial Gas–Oil Ratio, Oil Volume Factor); Net Pay Thickness; Average Permeability; Reserves Abundance; Original Oil in Place; Recoverable Oil Reserves; Bubble Point Pressure; Reservoir Burial Depth; Initial Reservoir Pressure; Initial Reservoir Temperature; Oil API Gravity; Average Porosity; Oil Saturation; Average Net-to-Gross Ratio.

Table 6. Classification of development parameters under different clustering distance thresholds. Grouped parameters are indicated within parentheses, while ungrouped entries represent individual indicators.

Clustering Distance Threshold	Number of Categories	Development Parameter Groups
5	3	(Well Pattern Density, Initial Production per Well, Peak Production Rate, Composite Decline Rate, Oil Production Rate); (Composite Water Cut, Recovery Efficiency of Reserves); Recovery Factor.
4	4	(Well Pattern Density, Initial Production per Well, Peak Production Rate, Composite Decline Rate, Oil Production Rate); Composite Water Cut; Recovery Efficiency of Reserves; Recovery Factor.
3	5	(Well Pattern Density, Initial Production per Well, Peak Production Rate); (Composite Decline Rate, Oil Production Rate); Composite Water Cut; Recovery Efficiency of Reserves; Recovery Factor.
2	6	(Well Pattern Density, Initial Production per Well); (Composite Decline Rate, Oil Production Rate); Peak Production Rate; Composite Water Cut; Recovery Efficiency of Reserves; Recovery Factor.

According to the statistical results, a smaller clustering distance threshold leads to fewer merged clusters and more independent indicators, while a larger threshold results in more integrated clusters and fewer independent indicators. In this study, we consider the threshold value of 3 to be appropriate, as the resulting indicator sets are well suited for project evaluation requirements.

These results align with the engineering significance of oilfield attributes. Static parameters were divided into 12 categories: Reservoir Area, Reservoir Oil Viscosity, and Net Pay Thickness form one group, reflecting the fundamental storage space and flow characteristics of the reservoir. Original Oil in Place and Recoverable Oil Reserves form another group, highlighting the dominant role of reserve volume in oilfield assessment. Initial Gas–Oil Ratio and Oil Volume Factor form a group, indicating how fluid properties affect drive efficiency and sustain production. Reservoir Burial Depth and Initial Reservoir Pressure form a further group, demonstrating the critical role of reservoir pressure in maintaining production energy. Development parameters were divided into five categories: Well Pattern Density, Initial Production per Well, and Peak Production Rate form one group, characterizing the decisive influence of well spacing and initial output on production capacity. Composite Decline Rate and Oil Production Rate form another group, illustrating production decline behavior and long-term performance stability. The remaining indicators each form individual groups, underscoring their independent value in evaluation.

Principal Component Analysis Method

To evaluate the explanatory power of each factor and the contribution of variables, a scree plot was used to visualize the importance of factors. The number of factors was determined by finding the inflection point of the eigenvalue curve. According to this method, calculations were performed separately for the static parameters and development parameters, and the results were displayed using scree plots, as shown in Figure 8 and Figure 9.

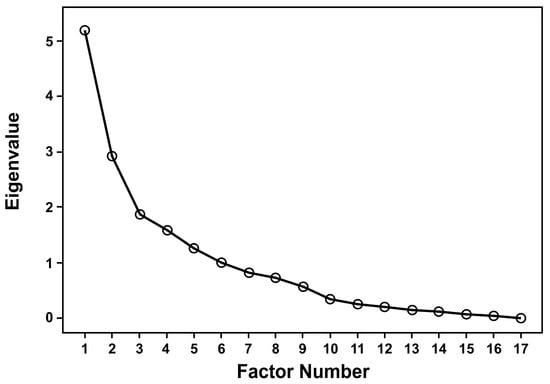
Figure 8. Scree plot of static parameters.

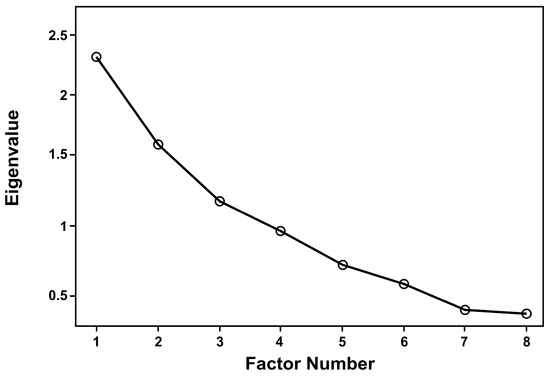
Figure 9. Scree plot of development parameters.

In the scree plot, a smaller eigenvalue indicates a larger number of extracted factors, a higher cumulative contribution rate, and better retention of the original information. The number of factors and the corresponding cumulative variance explained for various eigenvalue thresholds are shown in Table 7 and Table 8.

Table 7. Explained variance of factors for static parameters.

Factor Number	Eigenvalue	Explained Variance (%)	Cumulative Explained Variance (%)
1	5.193	30.208	30.208
2	2.935	17.076	47.284
3	1.876	10.916	58.200
4	1.578	9.181	67.381
5	1.267	7.369	74.750
6	1.005	5.845	80.596
7	0.816	4.744	85.340
8	0.733	4.265	89.605
9	0.566	3.292	92.897
10	0.344	2.003	94.899
11	0.262	1.527	96.426
12	0.205	1.193	97.619
13	0.158	0.919	98.538
14	0.122	0.709	99.247
15	0.078	0.451	99.698
16	0.052	0.302	100
17	0	0	100

Table 8. Explained variance of factors for development parameters.

Factor Number	Eigenvalue	Explained Variance (%)	Cumulative Explained Variance (%)
1	2.197	27.466	27.466
2	1.572	19.646	47.112
3	1.173	14.658	61.769
4	0.962	12.027	73.796
5	0.723	9.037	82.833
6	0.589	7.363	90.197
7	0.405	5.058	95.255
8	0.380	4.745	100

In this study, the number of factors was determined based on a cumulative variance explained threshold of 90%. For the static parameters, nine factors were extracted, meaning that the 17 indicators were grouped into nine factor categories. For the development parameters, six factors were extracted, corresponding to six categories for the eight development indicators.

Based on the number of factors corresponding to the 90% cumulative contribution rate, the rotated factor loading matrices were calculated, as shown in Table 9 and Table 10.

Table 9. Static parameter rotated factor loadings. The bold values represent the loading with the greatest absolute magnitude for each parameter, indicating its primary associated factor.

Parameter	Factor 1	Factor 2	Factor 3	Factor 4	Factor 5	Factor 6	Factor 7	Factor 8	Factor 9
Initial Gas–Oil Ratio	−0.931	0.065	−0.115	0.027	0.058	−0.194	−0.179	−0.024	−0.055
Oil Volume Factor	−0.881	0.053	−0.152	0.046	0.070	−0.236	−0.274	0.020	−0.027
Bubble Point Pressure	−0.688	0.017	−0.094	−0.016	0.082	0.003	−0.464	0.057	−0.375
Original Oil in Place	0.052	−0.937	0.130	−0.131	0.039	0.073	−0.104	0.093	0.038
Recoverable Oil Reserves	0.027	−0.921	−0.035	−0.056	0.070	0.133	0.028	−0.003	−0.081
Reservoir Area	0.052	−0.909	0.067	0.119	0.059	−0.074	0.010	−0.021	0.054
Average Permeability	0.083	−0.091	0.746	0.218	0.146	0.506	0.141	0.154	0.007
Reservoir Oil Viscosity	0.126	−0.056	0.983	−0.043	0.003	−0.224	0.096	0.124	0.041
Oil API Gravity	−0.343	0.118	−0.596	0.330	0.025	−0.533	−0.001	0.089	−0.013
Reserves Abundance	0.044	−0.055	0.003	−0.936	−0.011	0.122	0.057	0.132	−0.189
Oil Saturation	−0.104	−0.113	0.051	0.011	0.979	0.008	−0.013	0.094	−0.029
Average Porosity	0.294	−0.075	−0.097	−0.127	−0.003	0.931	0.251	0.071	0.060
Reservoir Burial Depth	−0.216	−0.045	−0.052	0.048	−0.068	−0.064	−0.924	−0.035	−0.080
Initial Reservoir Temperature	−0.316	0.042	−0.100	0.065	−0.001	−0.146	−0.851	0.154	0.006
Initial Reservoir Pressure	−0.144	−0.090	−0.097	−0.046	0.121	−0.213	−0.827	−0.017	−0.306
Average Net-to-Gross Ratio	−0.013	−0.052	0.166	−0.119	0.102	0.064	−0.054	0.955	−0.096
Net Pay Thickness	−0.135	0.015	−0.037	−0.196	0.027	−0.056	−0.211	0.105	−0.921

Table 10. Development parameter rotated factor loadings. The bold values represent the loading with the greatest absolute magnitude for each parameter, indicating its primary associated factor.

Parameter	Factor 1	Factor 2	Factor 3	Factor 4	Factor 5	Factor 6
Well Pattern Density	−0.711	−0.214	0.158	0.143	0.053	−0.406
Composite Water Cut	0.884	−0.173	0.006	0.115	0.160	0.081
Recovery Factor	0.144	−0.914	−0.158	0.064	0.057	−0.032
Oil Production Rate	−0.418	−0.632	0.253	−0.103	0.298	−0.218
Composite Decline Rate	−0.049	0.066	0.980	−0.051	0.042	−0.062
Peak Production Rate	0.032	−0.022	−0.050	0.989	0.020	−0.050
Recovery Efficiency of Reserves	0.080	−0.098	0.041	0.023	0.979	0.044
Initial Production per Well	−0.156	−0.062	0.058	0.047	−0.046	−0.972

Based on the results of the factor loading matrices, the classification of static and development parameters was summarized in Table 11.

Table 11. Classification statistics of static and development parameters based on the principal component analysis method.

Eigenvalue Threshold	Static Parameters (9 Categories)	Eigenvalue Threshold	Development Parameters (6 Categories)
0.566	Reservoir Burial Depth, Initial Reservoir Pressure, Initial Reservoir Temperature; Initial Gas–Oil Ratio, Oil Volume Factor, Bubble Point Pressure; Reservoir Area, Original Oil in Place, Recoverable Oil Reserves; Average Permeability, Reservoir Oil Viscosity, Oil API Gravity; Reserves Abundance; Net Pay Thickness; Average Net-to-Gross Ratio; Average Porosity; Oil Saturation.	0.589	Well Pattern Density, Composite Water Cut; Recovery Factor, Oil Production Rate; Composite Decline Rate; Peak Production Rate; Recovery Efficiency of Reserves; Initial Production per Well.

These classification results align with the engineering significance of oilfield attributes. Static parameters were divided into nine categories: Reservoir Burial Depth, Initial Reservoir Pressure, and Initial Reservoir Temperature form one group, reflecting the subsurface pressure–temperature conditions that govern drive energy. Initial Gas–Oil Ratio, Oil Volume Factor, and Bubble Point Pressure form another group, indicating how fluid phase behavior and volumetric expansion potential control recovery efficiency. Reservoir Area, Original Oil in Place, and Recoverable Oil Reserves form a group, highlighting the volumetric capacity that underpins overall field value; Average Permeability, Reservoir Oil Viscosity, and Oil API Gravity group together, capturing the combined effects of reservoir permeability and fluid mobility on deliverability. Development parameters were divided into six categories: Well Pattern Density and Composite Water Cut form a group, characterizing development intensity and waterflooding performance. Recovery Factor and Oil Production Rate form another group, illustrating overall production capacity. The remaining indicators each form individual groups, underscoring their independent value in evaluation.

Correlation coefficient analysis, systematic clustering, and principal component analysis were used to classify both static and development parameters. The classification results from the three methods are summarized in Table 12 and Table 13. Indicators marked with the same color in the tables belong to the same category, while uncolored indicators are considered independent, meaning they are not grouped with any other indicators.

Table 12. Summary of static parameter indicator classification results by three screening methods. Indicators marked in the same color belong to the same category; those left unshaded are treated as individual indicators.

Method	Number of Categories	Reservoir Properties					Trap and Structural Characteristics				Fluid Properties					Reserve Parameters
		Net Pay Thickness	Average Net-to-Gross Ratio	Average Porosity	Average Permeability	Oil Saturation	Reservoir Area	Reservoir Burial Depth	Initial Reservoir Pressure	Initial Reservoir Temperature	Oil API Gravity	Reservoir Oil Viscosity	Initial Gas–Oil Ratio	Bubble Point Pressure	Oil Volume Factor	Original Oil in Place	Recoverable Oil Reserves	Reserves Abundance
Correlation Analysis	11
Systematic Clustering	12
Principal Component Analysis	9

Table 13. Summary of development parameter indicator classification results by three screening methods. Indicators marked in the same color belong to the same category; those left unshaded are treated as individual indicators.

Method	Number of Categories	Development Parameters
		Well Pattern Density	Initial Production per Well	Peak Production Rate	Composite Water Cut	Composite Decline Rate	Recovery Efficiency of Reserves	Oil Production Rate	Recovery Factor
Correlation Analysis	8
Systematic Clustering	5
Principal Component Analysis	6

As shown in the tables above, the classification results of static parameters obtained by the three methods are generally consistent. For development parameters, the correlation coefficient method does not reduce the number of indicators, while the other two approaches yield alternative classification patterns. It is important to note that all three methods rely solely on statistical analysis and do not consider the geological or reservoir engineering significance of the indicators. Therefore, based on practical reservoir engineering needs and through expert discussion and validation, a comprehensive evaluation was performed to select the key indicators. In the end, twelve indicators were chosen from the seventeen static parameters and six from the eight development parameters. These eighteen quantitative indicators, combined with eight qualitative indicators, form a total of twenty-six key analogy indicators for oilfield development projects, as shown in Figure 10.

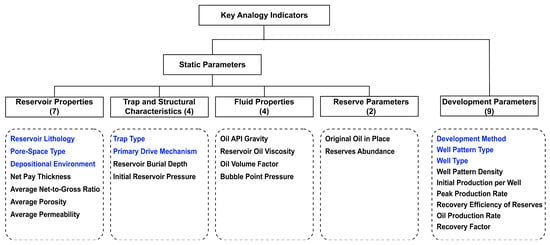
Figure 10. Key analogy indicators for oilfield development projects. Qualitative indicators are highlighted in blue, and quantitative indicators are shown in black.

3.1.2. Results of Key Indicators Classification

Following the procedure outlined in Section 2.1.2, the probability distribution of each key quantitative indicator was calculated based on the grading criteria, and the results are summarized in Table 14. For the three parameters with existing industry-standard classification systems (porosity, permeability, and formation oil viscosity), we primarily used the established industry criteria. By systematically incorporating expert knowledge, the classification thresholds for all key quantitative indicators were optimized and calibrated, with the final classification standards shown in Table 15.

Table 14. Threshold values for classifying indicators by distribution types.

Indicator	Unit	μ − σ	μ − σ/2	μ + σ/2	μ + σ	Distribution Type
Average Porosity	%	13.3	17	25.94	30	Normal distribution
Reservoir Burial Depth	m	1250	1700	2900	3500
Initial Reservoir Pressure	MPa	9.82	16.3	27.6	34.3
Oil API Gravity	°	25	30	38	41.98
Original Oil in Place	MMbbl	50.9	121.5	691	1650
Recovery Factor	%	11.98	19	30	39.84
Indicator	Unit	15%	30%	70%	85%	Distribution Type
Net Pay Thickness	m	7.5	14.1	50	85	Exponential distribution
Average Permeability	mD	29.7	110	1152.67	2187
Oil Volume Factor	-	1.08	1.13	1.34	1.5
Bubble Point Pressure	MPa	4.67	8.92	19.1	27.5
Reserves Abundance	MMbbl	1.4	3.83	17.17	33.33
Well Pattern Density	MMbbl/km2	0.12	0.27	1.38	3.04
Initial Production per Well	km2/well	3.56	10.51	85.63	269.27
Peak Production Rate	bbl/d	1.6	5.15	34.44	84.6
Oil Production Rate	%	0.6	1.24	3.62	5.71
Indicator	Unit	20%	40%	60%	80%	Distribution Type
Average Net-to-Gross	-	0.2	0.4	0.6	0.8	Uniform distribution
Recovery Efficiency of Reserves	%	37.34	70.2	100	100

Table 15. Classification standards for key quantitative indicators.

Indicator Name	Unit	Level 1	Level 2	Level 3	Level 4	Level 5	Distribution Type
Net Pay Thickness	m	≥80	50–80	15–50	5–15	<5	Exponential distribution
Average Net-to-Gross Ratio	-	≥0.8	0.6–0.8	0.4–0.6	0.2–0.4	<0.2	Uniform distribution
Average Porosity	%	≥30	25–30	15–25	10–15	<10	Industry Standard
Average Permeability	mD	≥2000	500–2000	50–500	10–50	<10	Industry Standard
Reservoir Burial Depth	m	<1000	1000–1500	1500–3000	3000–3500	≥3500	Normal distribution
Initial Reservoir Pressure	MPa	<10	10–20	20–30	30–40	≥40	Normal distribution
Oil API Gravity	°	≥43	38–43	30–38	20–30	<20	Normal distribution
Reservoir Oil Viscosity	mPa·s	<1	1–5	5–20	20–50	≥50	Industry Standard
Oil Volume Factor	-	≥1.5	1.34–1.5	1.13–1.34	1.08–1.13	<1.08	Exponential distribution
Bubble Point Pressure	MPa	<5	5–10	10–20	20–30	≥30	Exponential distribution
Original Oil in Place	MMbbl	≥1600	700–1600	120–700	50–120	<50	Log-normal distribution
Reserves Abundance	MMbbl/km2	≥32	16–32	4–16	2–4	<2	Exponential distribution
Well Pattern Density	km2/well	≥1.2	0.6–1.2	0.25–0.6	0.1–0.25	<0.1	Exponential distribution
Initial Production per Well	bbl/d	≥250	100–250	50–100	10–50	<10	Exponential distribution
Peak Production Rate	kb/d	≥85	35–85	5–35	2–5	<2	Exponential distribution
Recovery Efficiency of Reserves	%	≥80	60–80	40–60	20–40	<20	Exponential distribution
Oil Production Rate	%	≥5	3.5–5	1.5–3.5	1–1.5	<1	Exponential distribution
Recovery Factor	%	≥40	30–40	20–30	10–20	<10	Normal distribution

3.1.3. Results of Key Indicator Weighting

For the two categories of key quantitative indicators—static parameters and development parameters—we calculated objective weights using the entropy method and the coefficient of variation method. We assigned reasonable subjective weights based on expert judgment and then used the combined subjective–objective weighting formula to determine the comprehensive weight for each indicator. The results are shown in Table 16 and Table 17.

Table 16. Key indicator weights for static parameters.

Weighting Method	Static Parameters
	Net Pay Thickness	Average Net-to-Gross Ratio	Average Porosity	Average Permeability	Reservoir Burial Depth	Initial Reservoir Pressure	Oil API Gravity	Reservoir Oil Viscosity	Oil Volume Factor	Bubble Point Pressure	Original Oil in Place	Reserves Abundance
Subjective Weighting Method	0.11	0.04	0.12	0.13	0.05	0.06	0.12	0.08	0.05	0.02	0.08	0.14
Entropy Method	0.084	0.015	0.038	0.125	0.037	0.032	0.185	0.095	0.048	0.033	0.185	0.123
Coefficient of Variation Method	0.081	0.018	0.046	0.096	0.038	0.041	0.17	0.087	0.068	0.042	0.165	0.148
Combined Subjective–Objective Method	0.096	0.028	0.085	0.121	0.043	0.048	0.148	0.084	0.054	0.028	0.127	0.138

Table 17. Key indicator weights for development parameters.

Weighting Method	Development Parameters
	Well Pattern Density	Initial Production per Well	Peak Production Rate	Recovery Efficiency of Reserves	Oil Production Rate	Recovery Factor
Subjective Weighting Method	0.16	0.18	0.15	0.16	0.15	0.2
Entropy Method	0.203	0.195	0.175	0.093	0.152	0.182
Coefficient of Variation Method	0.193	0.235	0.143	0.114	0.136	0.178
Combined Subjective–Objective Method	0.179	0.198	0.159	0.117	0.152	0.195

3.2. Analogy Method Optimization

Based on a systematic review of prior studies and algorithms, we selected five classical machine-learning methods—support vector machine (SVM), random forest (RF), backpropagation neural network (BP), k-nearest neighbors (KNN), and decision tree (DT)—for comparative analysis. These methods span linear and nonlinear, parametric and nonparametric, model-based and distance-based paradigms, enabling a comprehensive evaluation of the proposed analogy indicator system. Their interpretability and ease of implementation also satisfy the reproducibility and engineering requirements of oilfield development decision-making. Although recent work has applied next-generation ensemble methods such as extreme gradient boosting (XGBoost) and LightGBM to production forecasting [19], those algorithms typically demand large sample sizes and extensive hyperparameter tuning, which risks overfitting under our sample conditions. In contrast, the five selected classical algorithms achieve robust performance without complex tuning, enhancing the generalizability of our findings and providing a valuable reference for future research.

3.2.1. Results of Single Indicator Analogy

A dataset of 663 onshore medium-to-high permeability sandstone oilfields was used for single indicator analogy. Machine-learning models were trained on 80% of the samples and tested on the remaining 20%. Test-set fitting accuracy was calculated to assess each method’s predictive performance. Table 18 shows that SVM and RF achieved accuracies of 85.81% and 74.1%, respectively, both meeting engineering requirements. The BP neural network, KNN, and DT showed lower accuracies.

Table 18. Test set accuracy (%) of five machine-learning methods for recovery factor prediction in medium-high permeability sandstone oilfields.

Method	SVM	RF	BP	KNN	DT
Test Set Accuracy (%)	85.81	74.1	68.75	67.8	39.01

Figure 11 presents predicted versus actual recovery values for each method. Green points denote training-data predictions, and red points denote test-data predictions. In the SVM plot, both green and red points cluster tightly along the 45° line, indicating an excellent fit on the training data and strong generalization to unseen cases. RF also aligns densely around the diagonal, although test-data points show slightly greater scatter, indicating robust performance with limited variance. By contrast, the BP neural network achieves a near-perfect fit on the training data but exhibits marked dispersion on the test data, signaling mild overfitting. KNN yields a broadly dispersed point cloud for both sets, revealing underfitting due to its local-averaging nature. Finally, DT displays a staircase pattern in the training data, characteristic of overfitting, and notable scatter in the test data, reflecting poor generalization. These observations confirm that only support vector machine and random forest achieve an optimal balance between bias and variance that meets engineering requirements.

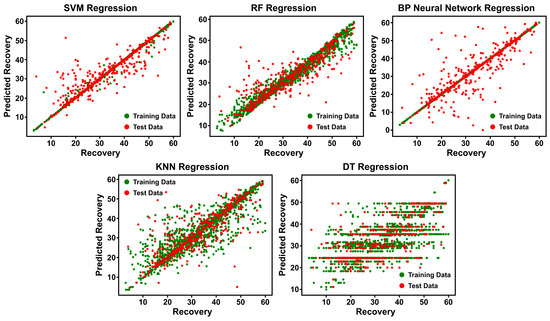
Figure 11. Comparison of predicted versus actual recovery values for medium-high permeability sandstone oilfields computed by five machine-learning methods.

Therefore, support vector machine and random forest were selected for recovery factor prediction.

A total of 157 onshore low-permeability sandstone oilfields were analyzed similarly, with 80% of samples used for training and 20% for testing. Test set accuracy was calculated to evaluate the predictive performance of each method. As shown in Table 19, the small sample size resulted in poor outcomes across all five machine-learning methods, with the highest accuracy below 70%. This indicates that when the sample size is small (n < 200), the ability of conventional machine-learning algorithms to generalize is severely limited, making it difficult to attain high-precision predictions in oilfield development.

Table 19. Test set accuracy (%) of five machine-learning methods for recovery factor prediction in low-permeability sandstone oilfields.

Method	SVM	RF	BP	KNN	DT
Test Set Accuracy (%)	69.29	63.18	61.27	44.89	18.7

Figure 12, which presents the low-permeability dataset, shows that the training-data points follow similar trends as in the medium-high permeability case, while the test-data points are substantially more dispersed, indicating markedly poorer generalization when the sample size is small.

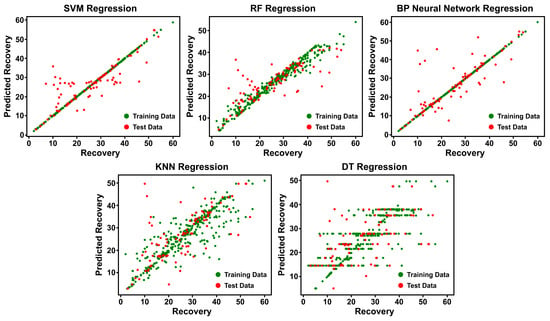
Figure 12. Comparison of predicted versus actual recovery values for low-permeability sandstone oilfields computed by five machine-learning methods.

3.2.2. Results of Whole Asset Analogy

SVM, RF, BP neural network, KNN, and DT methods were used to perform whole asset analogy on 663 onshore medium-to-high permeability sandstone oilfields. The dataset comprises five asset levels with approximately equal numbers of oilfields in each level, indicating a balanced multi-class dataset. Twenty oilfields were set aside for testing, and the predicted asset categories were compared with the conventional empirical classification categories. The results are shown in Table 20.

Table 20. Whole asset analogy results and test set accuracy (%) of five machine-learning methods.

Oilfield	Conventional Empirical Classification	SVM	RF	BP	KNN	DT
M	1	1	1	1	1	1
WC	1	1	2	1	1	1
X	1	1	1	3	1	5
KR	2	2	3	2	2	5
SA	2	2	2	2	2	5
LP	2	2	2	3	3	2
D	2	2	3	3	2	5
D2	3	3	3	1	3	1
BA	3	3	3	3	4	5
L	3	3	3	3	4	5
WS	3	3	3	3	3	5
QSF	3	4	3	4	4	5
BA2	3	3	3	3	4	5
M2	4	4	3	3	4	5
S	4	4	3	3	3	5
C	4	4	3	2	2	5
GPF	4	4	4	4	4	5
R	4	4	1	2	1	1
M3	5	5	5	2	5	5
HP	5	5	2	2	2	5
Test Set Accuracy (%)		95	70	55	55	25

DT achieved an accuracy of 25%, KNN 55%, and BP neural network 55%, indicating unsatisfactory performance. RF reached 70% accuracy, while SVM achieved 95%, both of which meet engineering requirements. SVM’s superior performance reflects its ability, through kernel-based high-dimensional mappings, to capture the complex nonlinear relationships among oilfield parameters even with limited training samples, making it particularly suitable for asset-level classification of medium-to-high permeability sandstone oilfields. With 95% accuracy, SVM can effectively replace traditional empirical classification methods, improving the objectivity and efficiency of oilfield evaluation.

4. Conclusions

This study addresses the need for quick evaluation of overseas oilfield development projects facing complex processes, limited data, and scarce experience by developing a systematic analogy indicator system and testing related machine-learning-based analogy methods.

A database of 1436 oilfields was compiled, and 36 original indicators were systematically screened using correlation coefficient analysis, systematic clustering, and principal component analysis. The selected indicators were then classified based on probability distribution curves and expert judgment and weighted with a combined approach that integrates expert scoring with entropy and coefficient of variation methods. The outcome is a set of 26 key analogy indicators covering reservoir properties, trap and structural characteristics, fluid properties, reserve parameters, and development parameters. This indicator system balances static and dynamic features, as well as subjective and objective information, providing a strong foundation for further research using the analogy method.

Five machine-learning algorithms—support vector machine (SVM), random forest (RF), backpropagation neural network (BP), k-nearest neighbors (KNN), and decision tree (DT)—were used for both single-indicator and whole-asset analogy tasks on actual oilfield data. For the 663 onshore medium-to-high permeability sandstone samples, SVM and RF achieved accuracies above 70%, meeting engineering requirements. SVM performed the best, with 86% accuracy in recovery factor prediction and 95% accuracy in whole-asset classification. Conversely, for the 157 low-permeability sandstone samples, all methods scored below 70%, showing that traditional machine-learning algorithms are not practical when the sample size is small.

The developed methodology provides a standardized, programmatic workflow for the quick evaluation of new overseas oilfield development projects. Using the key analogy indicator system along with the SVM-based analogy method enables rapid screening of multiple candidate fields, boosting evaluation efficiency and reducing investment risks caused by inconsistent judgments or limited experience. Future work could involve iterative refinement and reweighting of the indicator system as development technologies progress, as well as incorporating and comparing additional advanced algorithms to further enhance the accuracy and reliability of quick project screening and assessment.