Total Internal Reflection End-Pumped Solar Laser with the Solar-to-Laser Conversion Efficiency of 6.09%
Abstract
1. Introduction
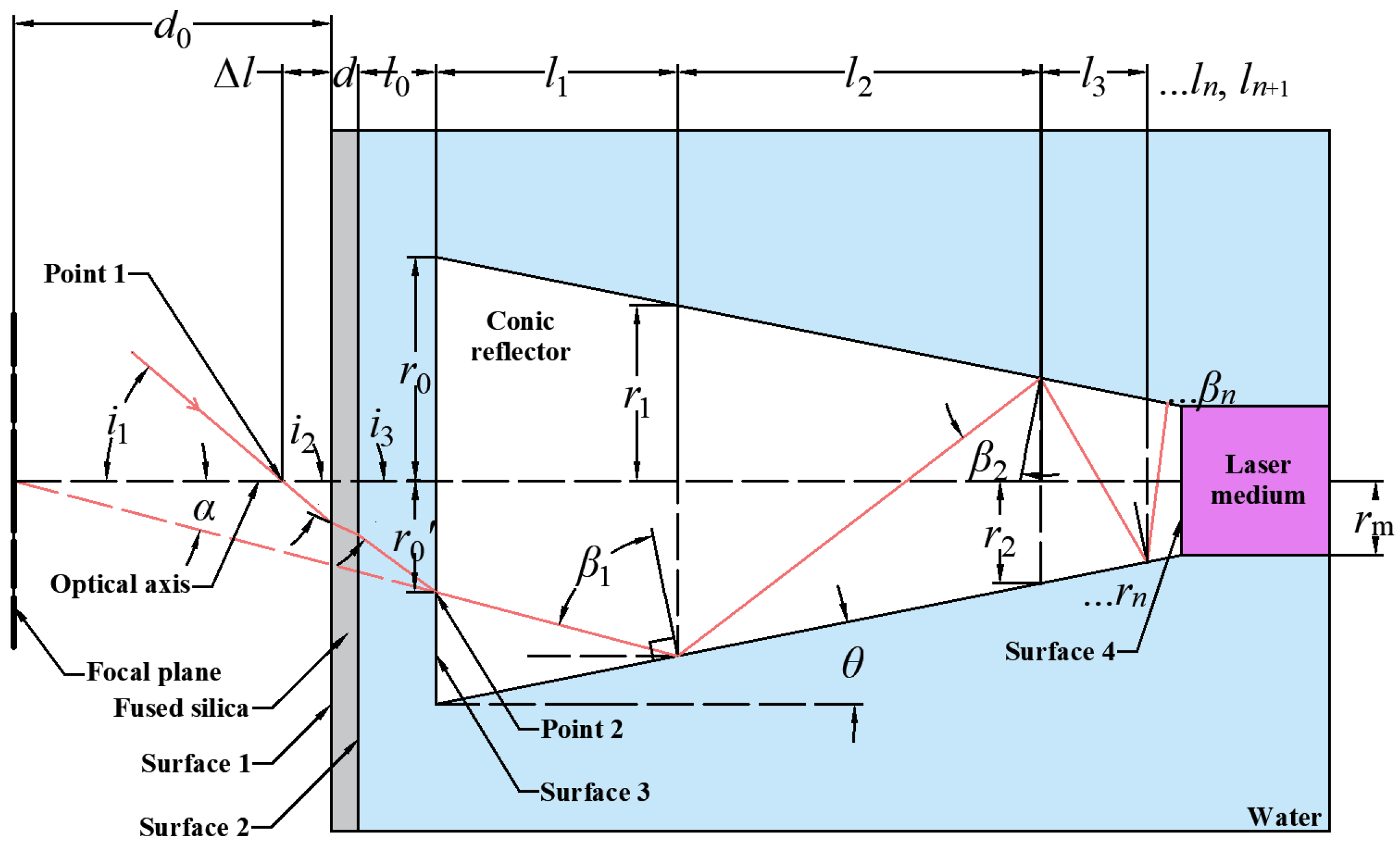
2. Conical Reflector
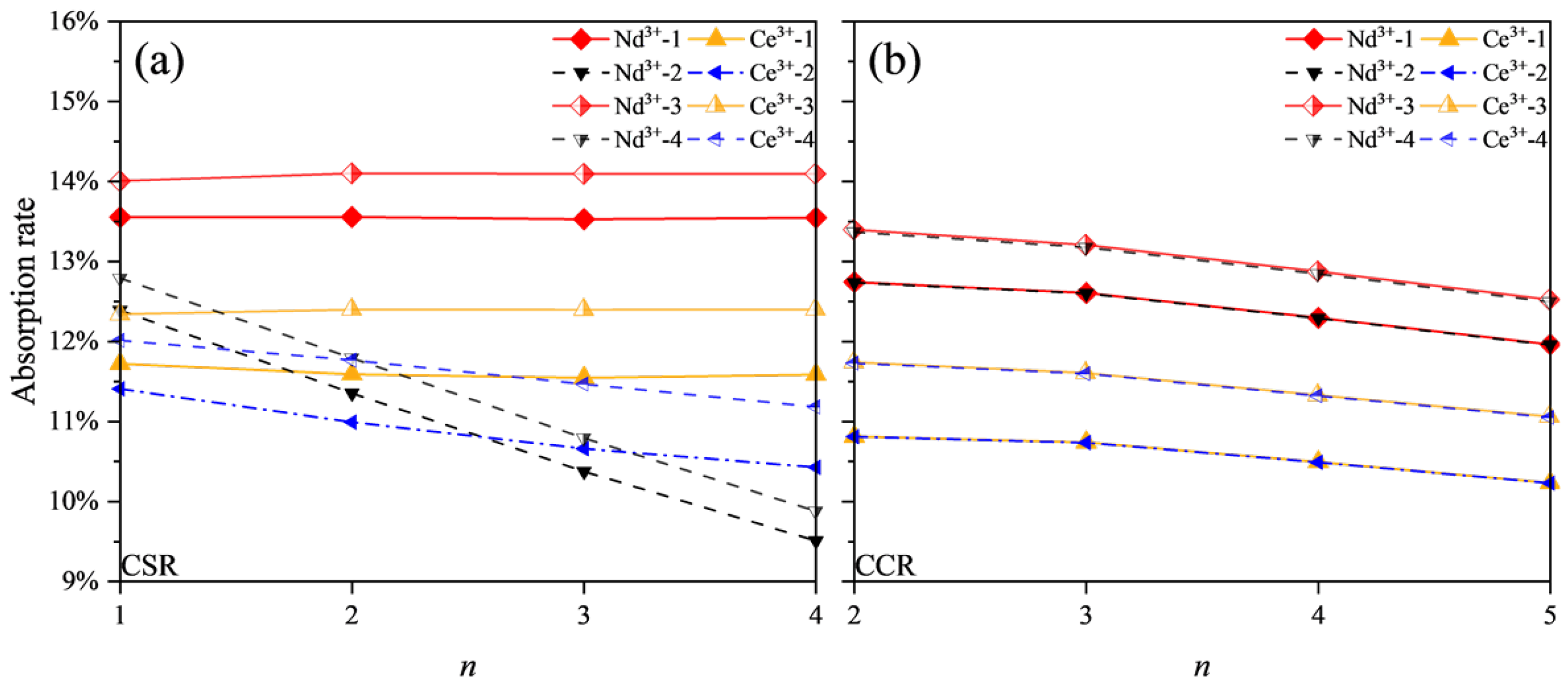
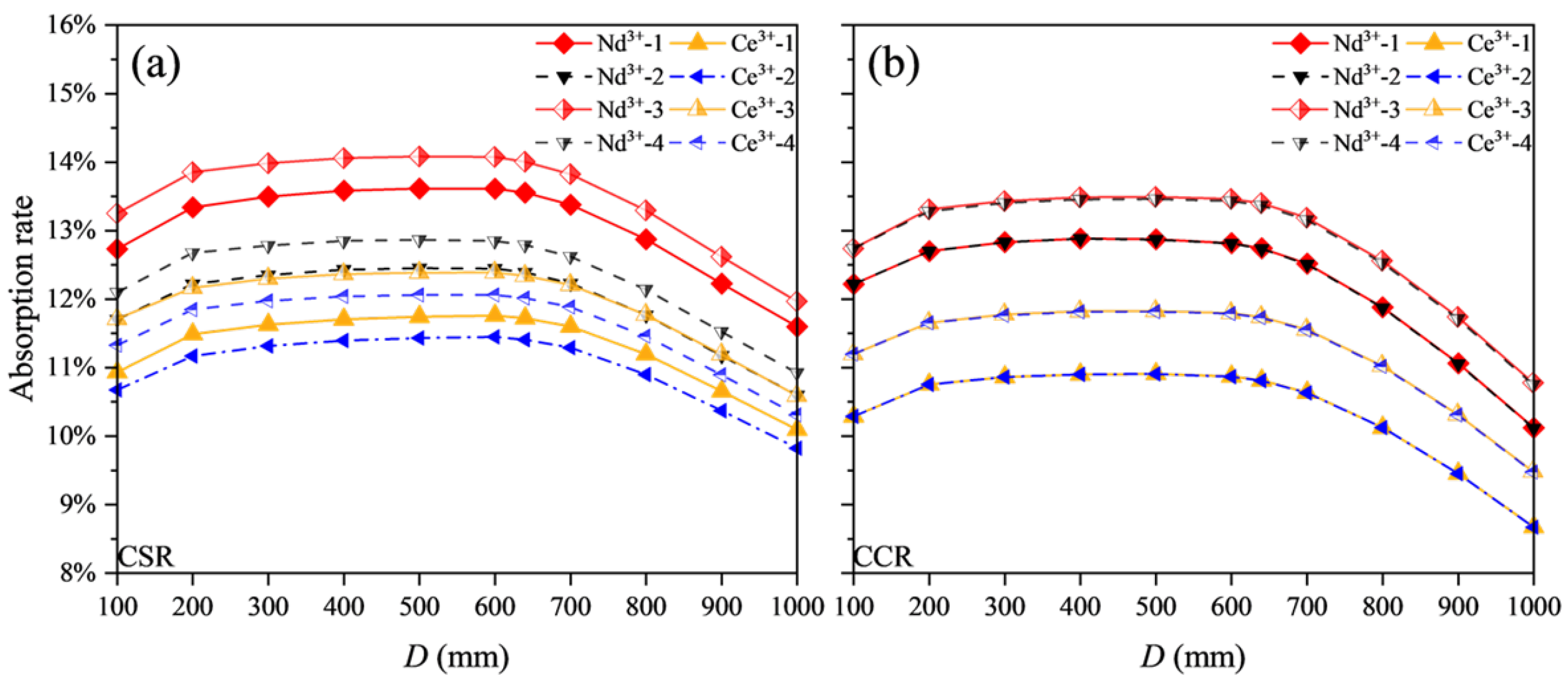
2.1. CSR
2.2. CCR
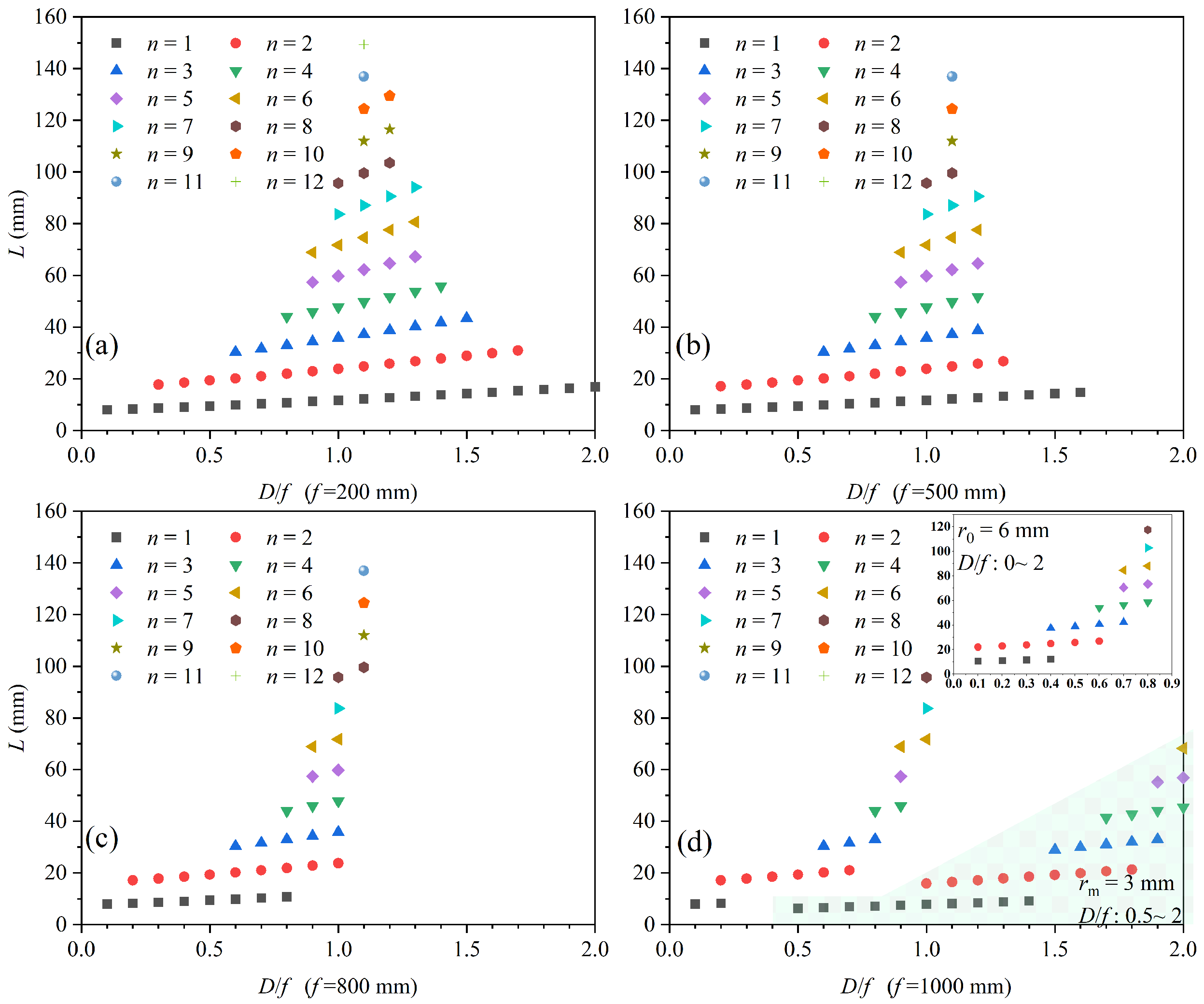
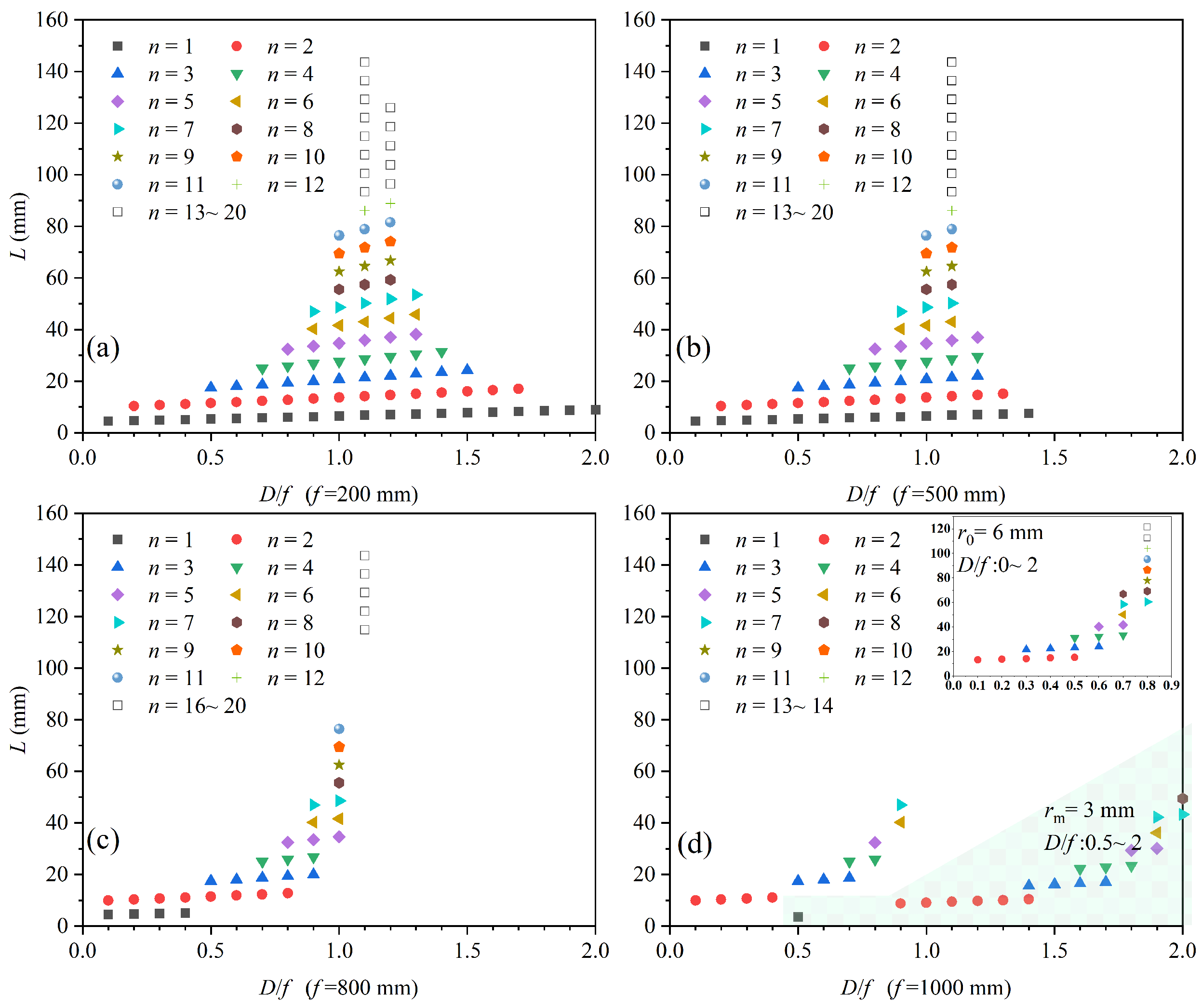
2.3. Calculation Results
2.4. TracePro Analysis
3. TIRSPL
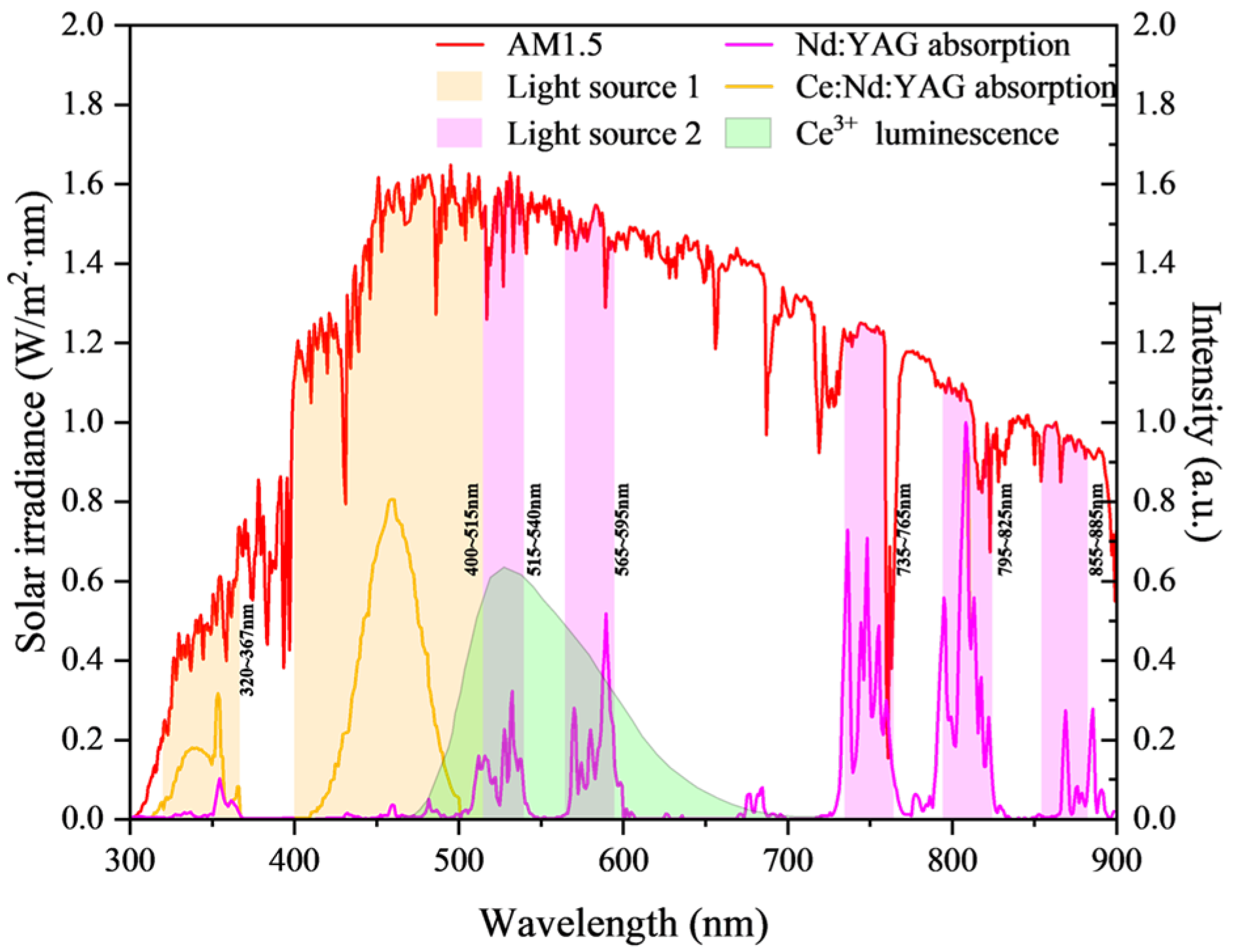
3.1. Theory of Laser
3.2. ALSD Simulation
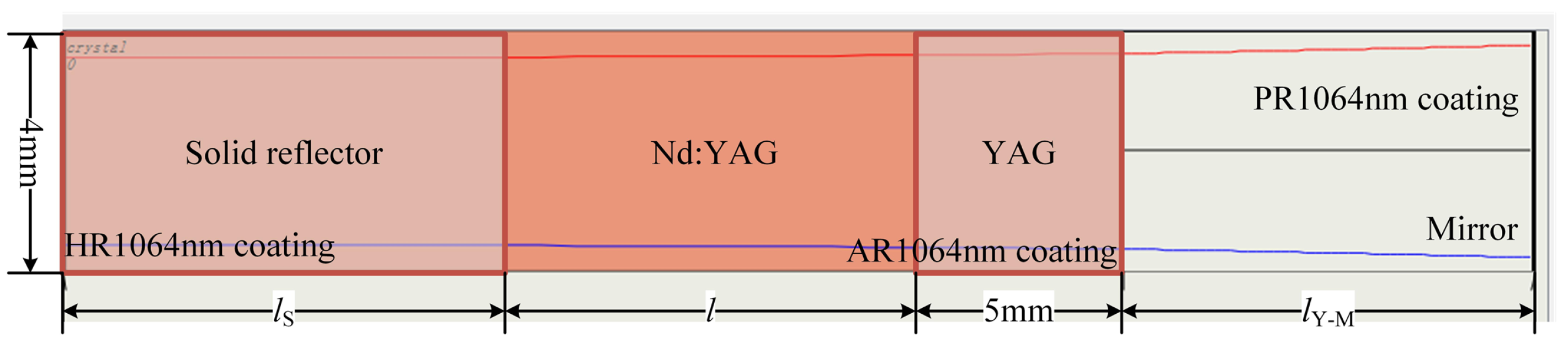
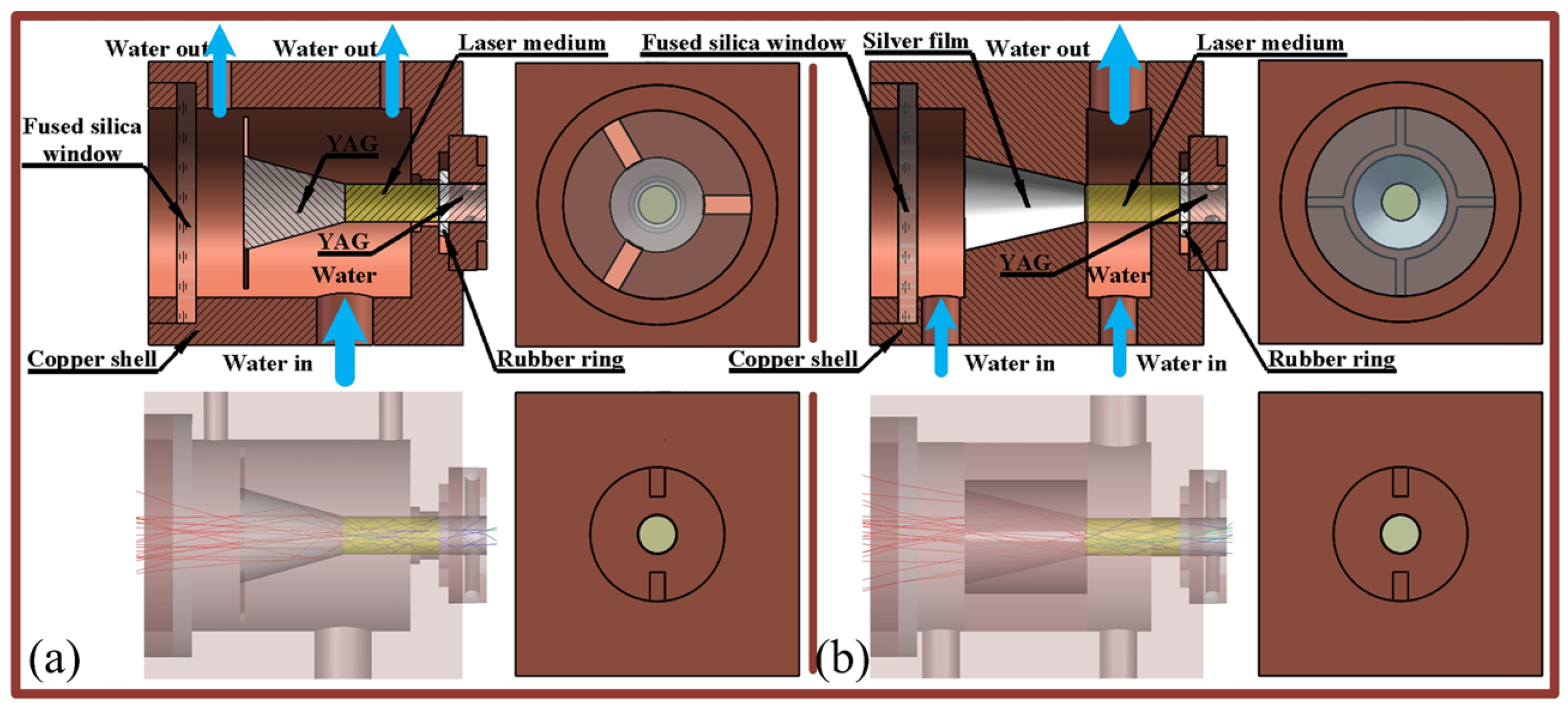
3.3. Structure
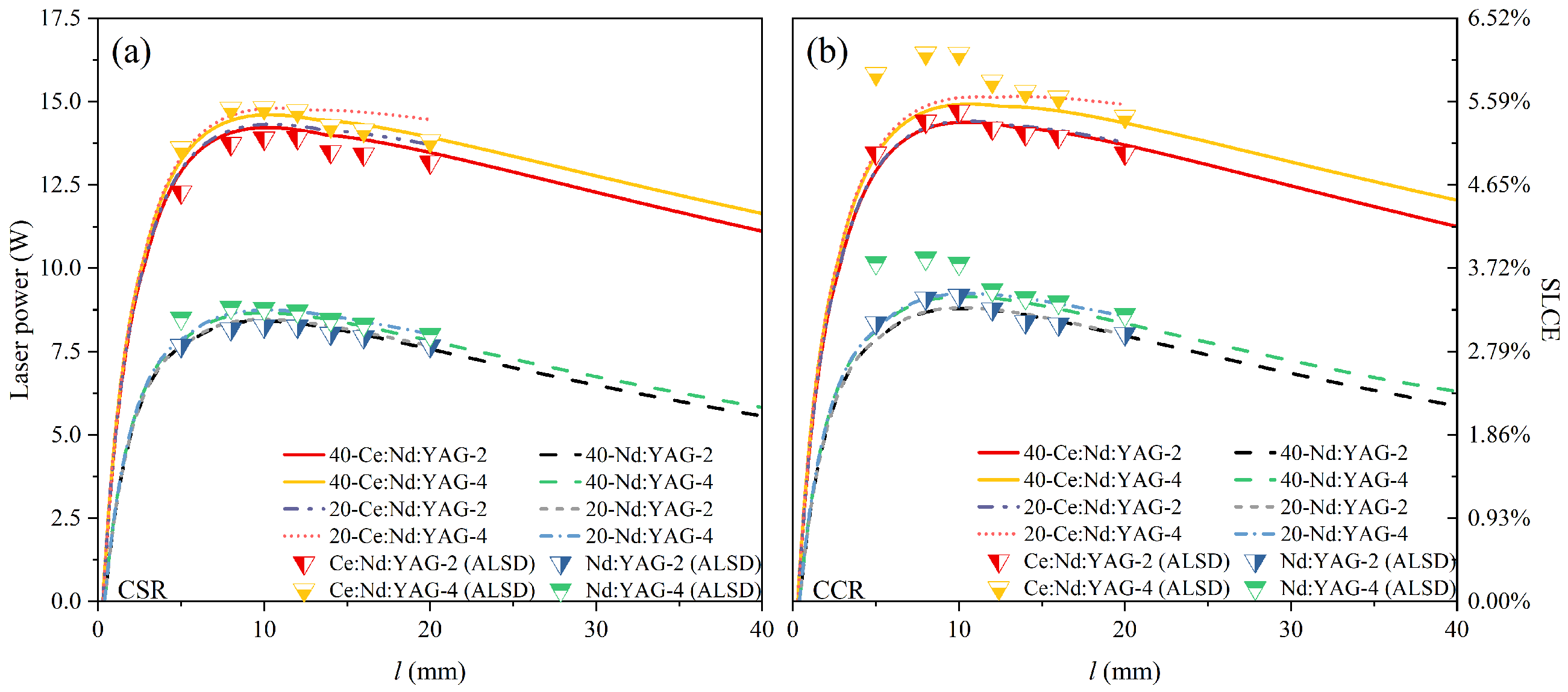
3.4. Model Comparison
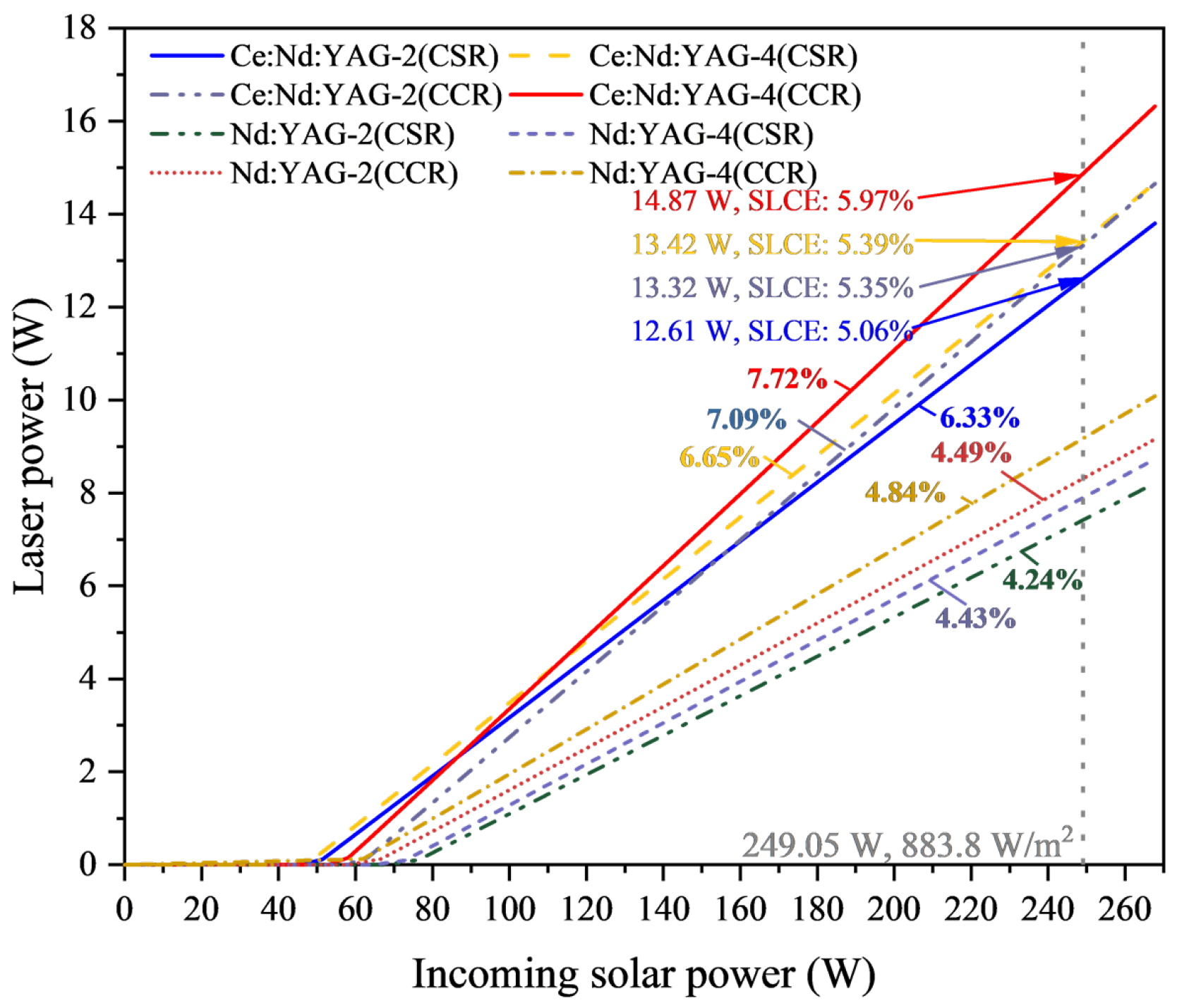
3.5. Laser Output
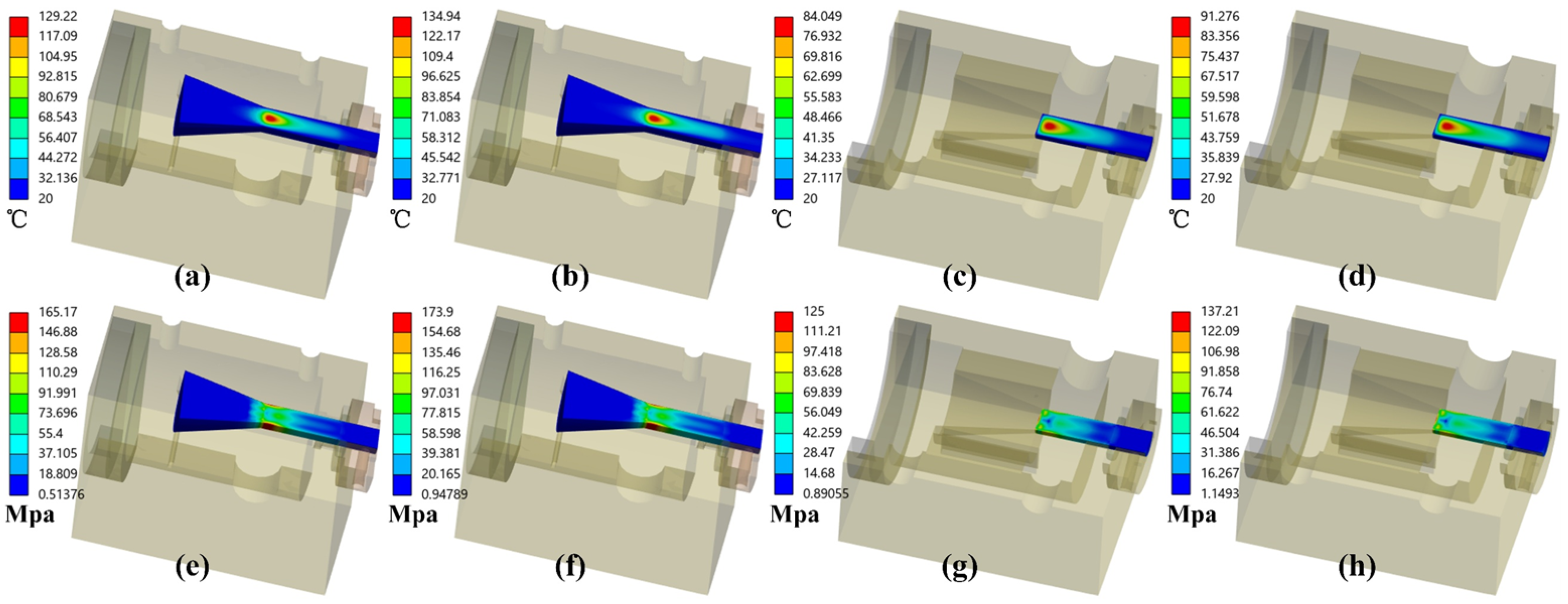
3.6. Thermal Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guan, Z.; Zhao, C.M.; Yang, S.H.; Wang, Y.; Ke, J.Y.; Zhang, H.Y. Demonstration of a Free-Space Optical Communication System Using a Solar-Pumped Laser as Signal Transmitter. Laser Phys. Lett. 2017, 14, 055804. [Google Scholar] [CrossRef]
- Mori, M.; Kagawa, H.; Saito, Y. Summary of Studies on Space Solar Power Systems of Japan Aerospace Exploration Agency (JAXA). Acta Astronaut. 2006, 59, 132–138. [Google Scholar] [CrossRef]
- Takeda, Y.; Iizuka, H.; Mizuno, S.; Hasegawa, K.; Ichikawa, T.; Ito, H.; Kajino, T.; Ichiki, A.; Motohiro, T. Silicon Photovoltaic Cells Coupled with Solar-Pumped Fiber Lasers Emitting at 1064 Nm. J. Appl. Phys. 2014, 116, 014501. [Google Scholar] [CrossRef]
- Kiss, Z.J.; Lewis, H.R.; Duncan, R.C. Sun Pumped Continuous Optical Maser. Appl. Phys. Lett. 1963, 2, 93–94. [Google Scholar] [CrossRef]
- Young, C.G. A Sun-Pumped Cw One-Watt Laser. Appl. Opt. 1966, 5, 993–997. [Google Scholar] [CrossRef]
- Lando, M.; Kagan, J.; Linyekin, B.; Dobrusin, V. A Solar-Pumped Nd:YAG Laser in the High Collection Efficiency Regime. Opt. Commun. 2003, 222, 371–381. [Google Scholar] [CrossRef]
- Yabe, T.; Ohkubo, T.; Uchida, S.; Yoshida, K.; Nakatsuka, M.; Funatsu, T.; Mabuti, A.; Oyama, A.; Nakagawa, K.; Oishi, T.; et al. High-Efficiency and Economical Solar-Energy-Pumped Laser with Fresnel Lens and Chromium Codoped Laser Medium. Appl. Phys. Lett. 2007, 90, 261120. [Google Scholar] [CrossRef]
- Liang, D.; Almeida, J. Highly Efficient Solar-Pumped Nd:YAG Laser. Opt. Express 2011, 19, 26399–26405. [Google Scholar] [CrossRef]
- Dinh, T.H.; Ohkubo, T.; Yabe, T.; Kuboyama, H. 120 watt continuous wave solar-pumped laser with a liquid light-guide lens and an Nd:YAG rod. Opt. Lett. 2012, 37, 2670. [Google Scholar] [CrossRef]
- Liang, D.; Almeida, J.; Vistas, C.R.; Guillot, E. Solar-Pumped Nd:YAG Laser with 31.5 W/M2 Multimode and 7.9 W/M2 TEM00-Mode Collection Efficiencies. Sol. Energy Mater. Sol. Cells 2017, 159, 435–439. [Google Scholar] [CrossRef]
- Liang, D.; Vistas, C.R.; Tibúrcio, B.D.; Almeida, J. Solar-Pumped Cr:Nd:YAG Ceramic Laser with 6.7% Slope Efficiency. Sol. Energy Mater. Sol. Cells 2018, 185, 75–79. [Google Scholar] [CrossRef]
- Guan, Z.; Zhao, C.; Li, J.; He, D.; Zhang, H. 32.1 W/M2 Continuous Wave Solar-Pumped Laser with a Bonding Nd:YAG/YAG Rod and a Fresnel Lens. Opt. Laser Technol. 2018, 107, 158–161. [Google Scholar] [CrossRef]
- Vistas, C.R.; Liang, D.; Garcia, D.; Almeida, J.; Tibúrcio, B.D.; Guillot, E. Ce:Nd:YAG Continuous-Wave Solar-Pumped Laser. Optik 2020, 207, 163795. [Google Scholar] [CrossRef]
- Yamaga, M.; Oda, Y.; Uno, H.; Hasegawa, K.; Ito, H.; Mizuno, S. Energy transfer from Ce to Nd in Y3Al5O12 ceramics. In Proceedings of the Physica Status Solidi C: Current Topics in Solid State Physics; Naito, H., Tanabe, S., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; Volume 9, pp. 2300–2303. [Google Scholar] [CrossRef]
- Tai, Y.; Zheng, G.; Wang, H.; Bai, J. Near-infrared quantum cutting of Ce3+–Nd3+ co-doped Y3Al5O12 crystal for crystalline silicon solar cells. J. Photochem. Photobiol. A Chem. 2015, 303–304, 80–85. [Google Scholar] [CrossRef]
- Payziyev, S.; Sherniyozov, A.; Bakhramov, S.; Zikrillayev, K.; Khalikov, G.; Makhmudov, K.; Ismailov, M.; Payziyeva, D. Luminescence sensitization properties of Ce:Nd:YAG materials for solar pumped lasers. Opt. Commun. 2021, 499, 127283. [Google Scholar] [CrossRef]
- Vistas, C.R.; Liang, D.; Almeida, J.; Tibúrcio, B.D.; Garcia, D.; Catela, M.; Costa, H.; Guillot, E. Ce:Nd:YAG Side-Pumped Solar Laser. J. Photonics Energy 2021, 11, 018001. [Google Scholar] [CrossRef]
- Garcia, D.; Liang, D.; Vistas, C.R.; Costa, H.; Catela, M.; Tiburcio, B.D.; Almeida, J. Ce:Nd:YAG Solar Laser with 4.5% Solar-to-Laser Conversion Efficiency. Energies 2022, 15, 5292. [Google Scholar] [CrossRef]
- Liang, D.; Vistas, C.R.; Gracia, D.; Tiburcio, B.D.; Catela, M.; Costa, H.; Guillot, E.; Almeida, J. Most Efficient Simultaneous Solar Laser Emissions from Three Ce:Nd:YAG Rods within a Single Pump Cavity. Sol. Energy Mater. Sol. Cells 2022, 246, 111921. [Google Scholar] [CrossRef]
- Cai, Z.; Zhao, C.; Zhao, Z.; Zhang, J.; Zhang, Z.; Zhang, H. Efficient 38.8 W/m2 solar pumped laser with a Ce:Nd:YAG crystal and a Fresnel lens. Opt. Express 2023, 31, 1340–1353. [Google Scholar] [CrossRef]
- Costa, H.; Liang, D.; Almeida, J.; Tiburcio, B.D.; Vistas, C.R. Four-Ce:Nd:YAG-rod Solar Laser with 4.49% Conversion Efficiency through Fresnel Lens. Sci. Rep. 2025, 15, 13354. [Google Scholar] [CrossRef]
- Mizuno, S.; Ito, H.; Hasegawa, K.; Suzuki, T.; Ohishi, Y. Laser Emission from a Solar-Pumped Fiber. Opt. Express 2012, 20, 5891–5895. [Google Scholar] [CrossRef]
- ASTM G173-03(2012); Tables for Reference Solar Spectral Irradiances: Direct Normal and Hemispherical on 37 Tilted Surface. ASTM: West Conshohocken, PA, USA, 2012. [CrossRef]
- Samuel, P.; Yanagitani, T.; Yagi, H.; Nakao, H.; Ueda, K.I.; Babu, S.M. Efficient energy transfer between Ce3+ and Nd3+ in cerium codoped Nd: YAG laser quality transparent ceramics. J. Alloys Compd. 2010, 507, 475–478. [Google Scholar] [CrossRef]
- AB AR Coating Data. Available online: https://www.thorlabs.com/newgrouppage9.cfm?objectgroup_id=12767&pn=AC127-019-AB#12796 (accessed on 22 July 2025).
- E02 Reflection Data. Available online: https://www.thorlabs.com/newgrouppage9.cfm?objectgroup_id=139&pn=BB03-E02#11967 (accessed on 22 July 2025).
- Slack, G.A.; Oliver, D.W.; Chrenko, R.M.; Roberts, S. Optical Absorption of Y3Al5O12 from 10- to 55000- cm−1 Wave Numbers. Phys. Rev. 1969, 177, 1308–1314. [Google Scholar] [CrossRef]
- Koechner, W. Solid-State Laser Engineering; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar] [CrossRef]
- Weksler, M.; Shwartz, J. Solar-Pumped Solid-State Lasers. IEEE J. Quantum Electron. 1988, 24, 1222–1228. [Google Scholar] [CrossRef]
- Liang, D.; Almeida, J.; Vistas, C.; Tibúrcio, B.; Garcia, D. Solar-Pumped Lasers: With Examples of Numerical Analysis of Solid-State Lasers; Green Energy and Technology; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar] [CrossRef]
- Axicon Lenses. Available online: https://www.thorlabs.com/newgrouppage9.cfm?objectgroup_id=16616 (accessed on 22 July 2025).



| Parameter | Garcia (2022) [18] | Liang (2022) [19] | Costa (2025) [21] | The CSR Structure | The CCR Structure |
|---|---|---|---|---|---|
| Concentrator | Parabolic mirror | Parabolic mirror | Fresnel lens | Parabolic mirror | Parabolic mirror |
| Effective area () | 0.293 | 0.4 | 0.617 | 0.2818 | 0.2818 |
| Irradiance () | 850 | 890 | 860 | 950 | 950 |
| Number of laser medium | 1 | 3 | 4 | 1 | 1 |
| Laser power (W) | 11.2 | 16.5 | 22.46 | 14.67 | 16.32 |
| Incoming solar power (W) | 249.05 | 356 | 530 | 267.71 | 267.71 |
| Collection efficiency () | 38.22 | 41.25 | 36.4 | 52.03 | 57.9 |
| SLCE | 4.50% | 4.64% | 4.49% | 5.48% | 6.09% |
| Slope efficiency | 6.80% | 7.64% | 6.33% | 6.65% | 7.72% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Zhang, H.; Garcia, D.; Xu, W.; Zhao, C.; Guo, A. Total Internal Reflection End-Pumped Solar Laser with the Solar-to-Laser Conversion Efficiency of 6.09%. Energies 2025, 18, 4033. https://doi.org/10.3390/en18154033
Wang L, Zhang H, Garcia D, Xu W, Zhao C, Guo A. Total Internal Reflection End-Pumped Solar Laser with the Solar-to-Laser Conversion Efficiency of 6.09%. Energies. 2025; 18(15):4033. https://doi.org/10.3390/en18154033
Chicago/Turabian StyleWang, Lin, Haiyang Zhang, Dário Garcia, Weichen Xu, Changming Zhao, and Anran Guo. 2025. "Total Internal Reflection End-Pumped Solar Laser with the Solar-to-Laser Conversion Efficiency of 6.09%" Energies 18, no. 15: 4033. https://doi.org/10.3390/en18154033
APA StyleWang, L., Zhang, H., Garcia, D., Xu, W., Zhao, C., & Guo, A. (2025). Total Internal Reflection End-Pumped Solar Laser with the Solar-to-Laser Conversion Efficiency of 6.09%. Energies, 18(15), 4033. https://doi.org/10.3390/en18154033






