Integrating Dimensional Analysis and Machine Learning for Predictive Maintenance of Francis Turbines in Sediment-Laden Flow
Abstract
1. Introduction
2. Materials and Methods
2.1. Dimensional Analysis
2.2. Relationship Between Parameters and Non-Dimensional Groups:
2.3. Water Quality and Material in a Dimensional Analysis
2.4. Data Analysis
2.5. Regression Model
2.6. Evaluation Metrics
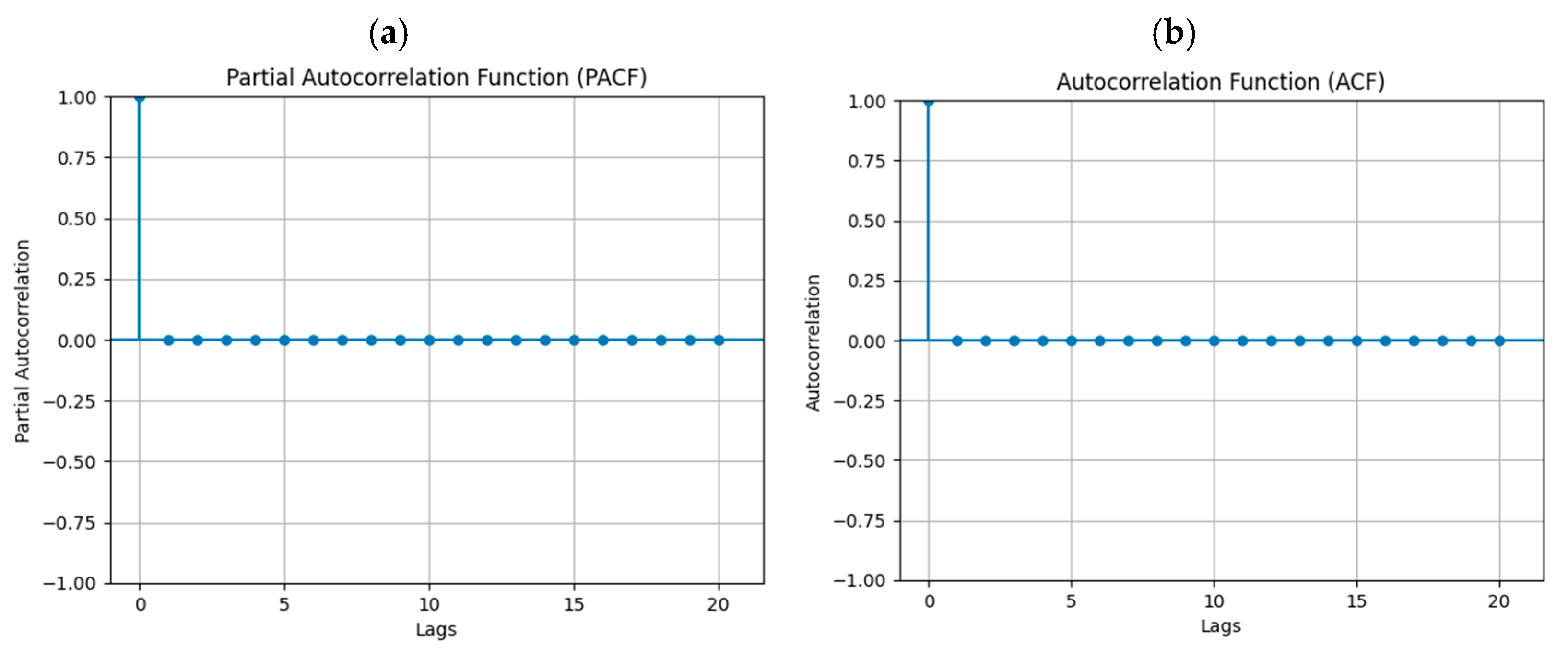
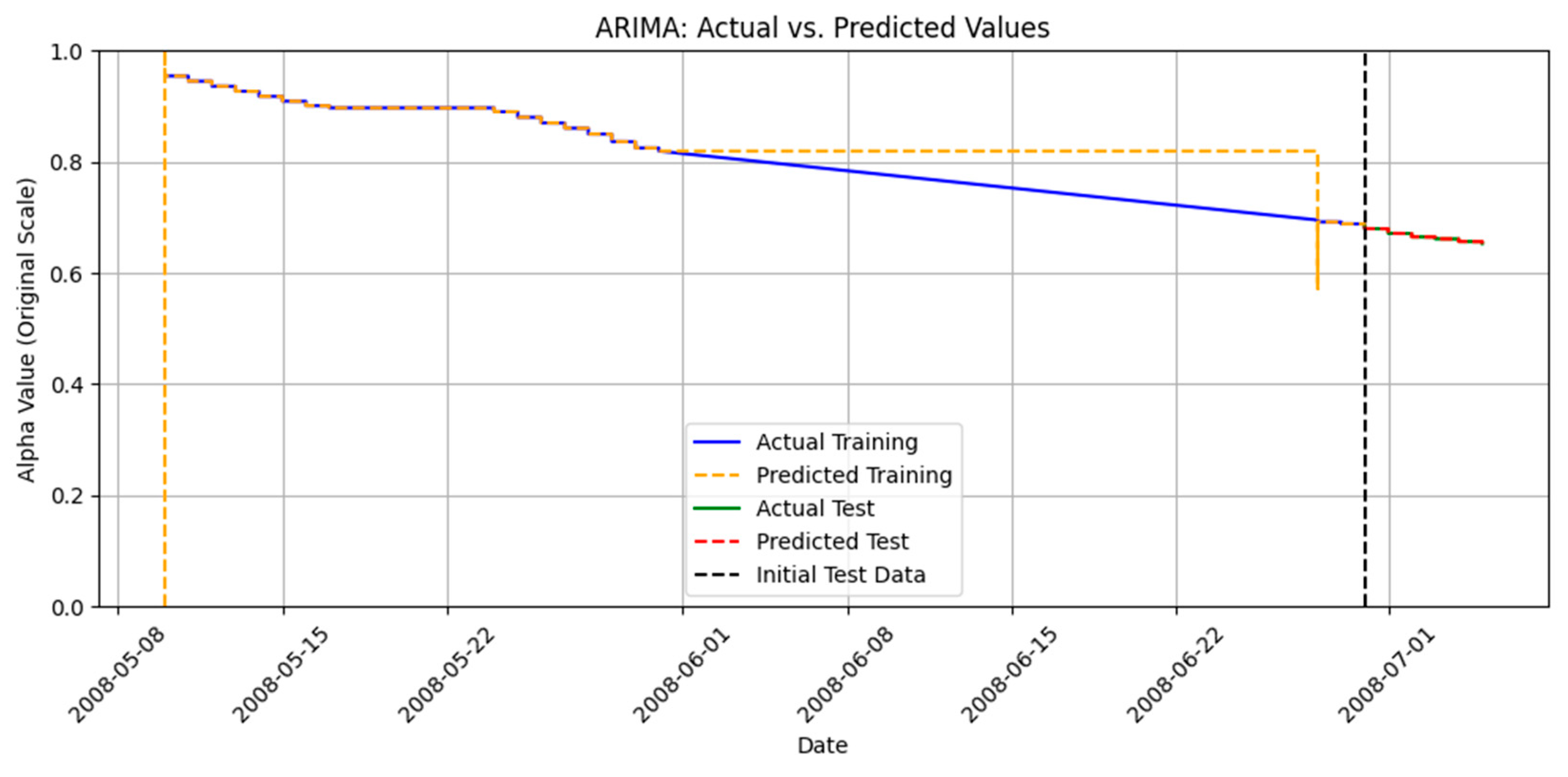
2.7. Methodology for Time Series with ARIMA
- Yt is the original time series.
- Wt is the differenced (stationary) series.
- p is the order of the autoregressive (AR) component, indicating the number of lagged observations of the series included in the model.
- d is the order of differencing required to make the series stationary. The first difference is ∇Yt = Yt − Yt−1, and the second difference is∇2Yt = ∇Yt –∇Yt−1.
- q is the order of the moving average (MA) component, indicating the number of lagged forecast errors included in the model.
- are the parameters for the AR terms.
- are the parameters for the MA terms.
- c is a constant or intercept.
- is the white noise error term at time t, assumed to be independently and identically distributed with a mean of zero and constant variance.
3. Results
Data Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ríos, E.H.; Guzmán, J.D.; Ribadeneira, R.; Bailón-García, E.; Acevedo, E.R.; Vélez, F.; Franco, C.A.; Riazi, M.; Cortes, F.B. Effect of the oil content on green hydrogen production from produced water using carbon quantum dots as a disruptive nanolectrolyte. Int. J. Hydrogen Energy 2024, 76, 353–362. [Google Scholar] [CrossRef]
- Paraschiv, L.S.; Paraschiv, S. Contribution of renewable energy (hydro, wind, solar and biomass) to decarbonization and transformation of the electricity generation sector for sustainable development. Energy Rep. 2023, 9, 535–544. [Google Scholar] [CrossRef]
- Oyebanji, M.O.; Kirikkaleli, D. Green technology, green electricity, and environmental sustainability in Western European countries. Environ. Sci. Pollut. Res. 2023, 30, 38525–38534. [Google Scholar] [CrossRef]
- Ohler, A.; Fetters, I. The causal relationship between renewable electricity generation and GDP growth: A study of energy sources. Energy Econ. 2014, 43, 125–139. [Google Scholar] [CrossRef]
- Sayed, E.T.; Wilberforce, T.; Elsaid, K.; Rabaia, M.K.H.; Abdelkareem, M.A.; Chae, K.-J.; Olabi, A. A critical review on environmental impacts of renewable energy systems and mitigation strategies: Wind, hydro, biomass and geothermal. Sci. Total Environ. 2021, 766, 144505. [Google Scholar] [CrossRef] [PubMed]
- Fierro, J.J.; Escudero-Atehortua, A.; Nieto-Londoño, C.; Giraldo, M.; Jouhara, H.; Wrobel, L.C. Evaluation of waste heat recovery technologies for the cement industry. Int. J. Thermofluids 2020, 7, 100040. [Google Scholar] [CrossRef]
- Brough, D.; Jouhara, H. The aluminium industry: A review on state-of-the-art technologies, environmental impacts and possibilities for waste heat recovery. Int. J. Thermofluids 2020, 1, 100007. [Google Scholar] [CrossRef]
- Mohan, C.; Robinson, J.; Lal, C.; Jammala, A.P.N.; Meena, P.L.; Kumari, N. Sustainable Energy Solutions for Environmental Pollution Control. In Proceedings of the E3S Web of Conferences, Les Mureaux, France, 21–22 November 2024; EDP Sciences: Les Ulis, France; Volume 511, p. 01023. [Google Scholar]
- Morales, S.; Álvarez, C.; Acevedo, C.; Diaz, C.; Rodriguez, M.; Pacheco, L. An overview of small hydropower plants in Colombia: Status, potential, barriers and perspectives. Renew. Sustain. Energy Rev. 2015, 50, 1650–1657. [Google Scholar] [CrossRef]
- Barnard, P.L.; Short, A.D.; Harley, M.D.; Splinter, K.D.; Vitousek, S.; Turner, I.L.; Allan, J.; Banno, M.; Bryan, K.R.; Doria, A.; et al. Coastal vulnerability across the Pacific dominated by El Niño/Southern Oscillation. Nat. Geosci. 2015, 8, 801–807. [Google Scholar] [CrossRef]
- McPhaden, M.J. El Niño and La Niña: Causes and global consequences. Encycl. Glob. Environ. Chang. 2002, 1, 353–370. [Google Scholar]
- Rosenzweig, C.; Hillel, D. Climate Variability and the Global Harvest: Impacts of El Niño and Other Oscillations on Agro-Ecosystems; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- González, O.N.; González, A.N.; Flores, S.M.; Vilchez, F.F. Influence of ENSO and the urban heat island on climate variation in a growing city of the western Mexico. One Ecosyst. 2024, 9, e125302. [Google Scholar] [CrossRef]
- Thakur, R.; Kumar, A.; Khurana, S.; Sethi, M. Correlation development for erosive wear rate on pelton turbine buckets. Int. J. Mech. Prod. Eng. Res. Dev. 2017, 7, 259–274. [Google Scholar] [CrossRef]
- Sangal, S.; Singhal, M.K.; Saini, R.P.; Tomar, G.S. Hydro-abrasive erosion modelling in Francis turbine at different silt conditions. Sustain. Energy Technol. Assess. 2022, 53, 102616. [Google Scholar] [CrossRef]
- Wei, X.-Y.; Pei, J.; Wang, W.-Q.; Yu, Z.-F. Numerical study on sediment erosion characteristics of Francis turbine runner. Eng. Fail. Anal. 2024, 161, 108270. [Google Scholar] [CrossRef]
- Eltvik, M. Sediment Erosion in Francis Turbines; Institutt for Energi-Og Prosessteknikk: Trondheim, Norwegia, 2009. [Google Scholar]
- Cruzatty, C.; Jimenez, D.; Valencia, E.; Zambrano, I.; Mora, C.; Luo, X.; Cando, E. A case study: Sediment erosion in francis turbines operated at the san francisco hydropower plant in ecuador. Energies 2021, 15, 8. [Google Scholar] [CrossRef]
- Thapa, B.S.; Dahlhaug, O.G.; Thapa, B. Sediment erosion in hydro turbines and its effect on the flow around guide vanes of Francis turbine. Renew. Sustain. Energy Rev. 2015, 49, 1100–1113. [Google Scholar] [CrossRef]
- Khurana, S.; Goel, V. Effect of jet diameter on erosion of turgo impulse turbine runner. J. Mech. Sci. Technol. 2014, 28, 4539–4546. [Google Scholar] [CrossRef]
- Chitrakar, S.; Neopane, H.P.; Dahlhaug, O.G. Study of the simultaneous effects of secondary flow and sediment erosion in Francis turbines. Renew. Energy 2016, 97, 881–891. [Google Scholar] [CrossRef]
- Seidel, U.; Mende, C.; Hübner, B.; Weber, W.; Otto, A. Dynamic loads in Francis runners and their impact on fatigue life. IOP Conf. Ser. Earth Environ. Sci. 2014, 22, 032054. [Google Scholar] [CrossRef]
- Iliev, I.; Trivedi, C.; Dahlhaug, O.G. Variable-speed operation of Francis turbines: A review of the perspectives and challenges. Renew. Sustain. Energy Rev. 2019, 103, 109–121. [Google Scholar] [CrossRef]
- Tong, D. Cavitation and wear on hydraulic machines. Int. Water Power Dam Constr. 1981, 2, 30–40. [Google Scholar]
- Masoodi, J.H.; Harmain, G. A methodology for assessment of erosive wear on a Francis turbine runner. Energy 2017, 118, 644–657. [Google Scholar] [CrossRef]
- Chitrakar, S. FSI Analysis of Francis Turbines Exposed to Sediment Erosion. Ph.D. Thesis, Kathmandu University, Dhulikhel, Nepal, 2013. [Google Scholar]
- Quaranta, E. Optimal rotational speed of Kaplan and Francis turbines with focus on low-head hydropower applications and dataset collection. J. Hydraul. Eng. 2019, 145, 04019043. [Google Scholar] [CrossRef]
- Thapa, B.S.; Thapa, B.; Dahlhaug, O.G. Empirical modelling of sediment erosion in Francis turbines. Energy 2012, 41, 386–391. [Google Scholar] [CrossRef]
- Alrayess, H.; Gharbia, S.; Beden, N.; Keskin, A.U. Using machine learning techniques and deep learning in forecasting the hydroelectric power generation in almus dam, turkey. Safety 2018, 72, 635–647. [Google Scholar]
- Sapitang, M.; Ridwan, W.M.; Kushiar, K.F.; Ahmed, A.N.; El-Shafie, A. Machine learning application in reservoir water level forecasting for sustainable hydropower generation strategy. Sustainability 2020, 12, 6121. [Google Scholar] [CrossRef]
- Condemi, C.; Casillas-Pérez, D.; Mastroeni, L.; Jiménez-Fernández, S.; Salcedo-Sanz, S. Hydro-power production capacity prediction based on machine learning regression techniques. Knowl.-Based Syst. 2021, 222, 107012. [Google Scholar] [CrossRef]
- Di Grande, S.; Berlotti, M.; Cavalieri, S.; Gueli, R. A Machine Learning Approach to Forecasting Hydropower Generation. Energies 2024, 17, 5163. [Google Scholar] [CrossRef]
- Essenfelder, A.H.; Larosa, F.; Mazzoli, P.; Bagli, S.; Broccoli, D.; Luzzi, V.; Mysiak, J.; Mercogliano, P.; Valle, F.D. Smart climate hydropower tool: A machine-learning seasonal forecasting climate service to support cost–benefit analysis of reservoir management. Atmosphere 2020, 11, 1305. [Google Scholar] [CrossRef]
- Ekanayake, P.; Wickramasinghe, L.; Jayasinghe, J.M.J.W.; Rathnayake, U.; Hong, T.-P. Regression-Based Prediction of Power Generation at Samanalawewa Hydropower Plant in Sri Lanka Using Machine Learning. Math. Probl. Eng. 2021, 2021, 4913824. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, D.; Peng, Q.; Lin, J.; Jin, T.; Yang, T.; Sorooshian, S.; Liu, Y. Prediction of the outflow temperature of large-scale hydropower using theory-guided machine learning surrogate models of a high-fidelity hydrodynamics model. J. Hydrol. 2022, 606, 127427. [Google Scholar] [CrossRef]
- de Souza, J.C.S.; Júnior, O.H.; Filho, G.L.T.; Carpinteiro, O.A.S.; Júnior, H.S.D.B.; dos Santos, I.F.S. Application of machine learning models in predictive maintenance of Francis hydraulic turbines. RBRH 2024, 29, e48. [Google Scholar] [CrossRef]
- Amini, A.; Pacot, O.; Voide, D.; Hasmatuchi, V.; Roduit, P.; Münch-Alligné, C. Development of a novel cavitation monitoring system for hydro turbines based on machine learning algorithms. IOP Conf. Ser. Earth Environ. Sci. 2022, 1079, 012015. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, J.; Infield, D.; Liu, Y.; Lien, F.-S. Short-term forecasting and uncertainty analysis of wind turbine power based on long short-term memory network and Gaussian mixture model. Appl. Energy 2019, 241, 229–244. [Google Scholar] [CrossRef]
- De Castro-Cros, M.; Velasco, M.; Angulo, C. Machine-learning-based condition assessment of gas turbines—A review. Energies 2021, 14, 8468. [Google Scholar] [CrossRef]
- Duan, R.; Liu, J.; Zhou, J.; Liu, Y.; Wang, P.; Niu, X. Study on performance evaluation and prediction of francis turbine units considering low-quality data and variable operating conditions. Appl. Sci. 2022, 12, 4866. [Google Scholar] [CrossRef]
- Srivastava, T.; Vedanshu; Tripathi, M.M. Predictive analysis of RNN, GBM and LSTM network for short-term wind power forecasting. J. Stat. Manag. Syst. 2020, 23, 33–47. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, D.; Wang, X.; Zhang, Y. Prediction of wind turbine-grid interaction based on a principal component analysis-long short term memory model. Energies 2018, 11, 3221. [Google Scholar] [CrossRef]
- Xiao, X.; Liu, J.; Liu, D.; Tang, Y.; Zhang, F. Condition monitoring of wind turbine main bearing based on multivariate time series forecasting. Energies 2022, 15, 1951. [Google Scholar] [CrossRef]
- Xiong, L.; Liu, J.; Song, B.; Dang, J.; Yang, F.; Lin, H. Deep learning compound trend prediction model for hydraulic turbine time series. Int. J. Low-Carbon Technol. 2021, 16, 725–731. [Google Scholar] [CrossRef]
- Truscott, G. A literature survey on abrasive wear in hydraulic machinery. Wear 1972, 20, 29–50. [Google Scholar] [CrossRef]
- Nozaki, T.; Takayanagi, T. Estimation of repair cycle of turbine due to abrasion caused by suspended sand and determination of capacity and cross section of desilting basin. Dengen Kaihatsu KK Chosa Shiryo 1987, 81, 68–98. [Google Scholar]
- Chen, J.-F.; Wang, W.-M.; Huang, C.-M. Analysis of an adaptive time-series autoregressive moving-average (ARMA) model for short-term load forecasting. Electr. Power Syst. Res. 1995, 34, 187–196. [Google Scholar] [CrossRef]
- Rojas, I.; Valenzuela, O.; Rojas, F.; Guillen, A.; Herrera, L.; Pomares, H.; Marquez, L.; Pasadas, M. Soft-computing techniques and ARMA model for time series prediction. Neurocomputing 2008, 71, 519–537. [Google Scholar] [CrossRef]
- Shumway, R.H.; Stoffer, D.S.; Shumway, R.H.; Stoffer, D.S. ARIMA models. In Time Series Analysis and Its Applications: With R Examples; Springer: Berlin/Heidelberg, Germany, 2017; pp. 75–163. [Google Scholar]
- Valipour, M.; Banihabib, M.E.; Behbahani, S.M.R. Comparison of the ARMA, ARIMA, and the autoregressive artificial neural network models in forecasting the monthly inflow of Dez dam reservoir. J. Hydrol. 2013, 476, 433–441. [Google Scholar] [CrossRef]
- Friede, M.; Ehlert, S.; Grimme, S.; Mewes, J.-M. Do Optimally tuned range-separated hybrid functionals require a reparametrization of the dispersion correction? It Depends. J. Chem. Theory Comput. 2023, 19, 8097–8107. [Google Scholar] [CrossRef]
- Cheng, Q.; Liu, P.; Xia, J.; Ming, B.; Cheng, L.; Chen, J.; Xie, K.; Liu, Z.; Li, X. Contribution of complementary operation in adapting to climate change impacts on a large-scale wind–solar–hydro system: A case study in the Yalong River Basin, China. Appl. Energy 2022, 325, 119809. [Google Scholar] [CrossRef]


| Parameter | Symbol | Dimension |
|---|---|---|
| Discharge | Q | |
| Pressure change | ρgH | ML−1 T−2 |
| Power | P | ML2 T−3 |
| Energy and work | E | ML2 T−2 |
| Speed | N | T−1 |
| Rotor Diameter | D | L |
| Fluid density | ρ | ML−3 |
| Fluid Viscosity | μ | ML−1 T−1 |
| Constant | N_Constant | D and N Varying |
|---|---|---|
| Q α D | Q α D3 | Q α ND3 |
| H α N2 | H α D2 | H α N2D2 |
| P α N3 | P α D5 | P α N3D5 |
| E α N2 | E α D5 | E α N2D5 |
| Non-Dimensional Group | Description |
|---|---|
| Flow Coefficient: This term can be understood as the volume or flow rate through a turbomachine or a specific runner diameter operating at a specific speed. | |
| Head Coefficient: It is a measure of the relationship between the fluid’s potential energy (height column H) and the fluid’s kinetic energy as it moves at the rotational speed of the runner U. We could establish that | |
| Power Coefficient: This term represents the relationship between power, fluid density, velocity, and the runner diameter. For a given turbomachine, the power is directly proportional to the cube of the velocity. |
| Parameter | Description |
|---|---|
| Turbine coefficient in the eroded area | |
| Sediment concentration in suspension | |
| Coefficient for average grain size _base (0.05 mm) | |
| Relative velocity | |
| Particle shape coefficient | |
| Material hardness coefficient | |
| Material abrasion resistance coefficient | |
| Exponent for concentration, approximately equal to 1 | |
| Exponent for grain size coefficient, approximately equal to 1 | |
| Exponent for velocity, usually 3 for Francis turbines |
| Parameter | Value |
|---|---|
| Net head [m] | 222 |
| Average density [kg m−3] | 1.005 |
| Gravity [m s−2] | 9.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ospina, Á.; Herrera Ríos, E.; Jaramillo, J.; Franco, C.A.; Taborda, E.A.; Cortes, F.B. Integrating Dimensional Analysis and Machine Learning for Predictive Maintenance of Francis Turbines in Sediment-Laden Flow. Energies 2025, 18, 4023. https://doi.org/10.3390/en18154023
Ospina Á, Herrera Ríos E, Jaramillo J, Franco CA, Taborda EA, Cortes FB. Integrating Dimensional Analysis and Machine Learning for Predictive Maintenance of Francis Turbines in Sediment-Laden Flow. Energies. 2025; 18(15):4023. https://doi.org/10.3390/en18154023
Chicago/Turabian StyleOspina, Álvaro, Ever Herrera Ríos, Jaime Jaramillo, Camilo A. Franco, Esteban A. Taborda, and Farid B. Cortes. 2025. "Integrating Dimensional Analysis and Machine Learning for Predictive Maintenance of Francis Turbines in Sediment-Laden Flow" Energies 18, no. 15: 4023. https://doi.org/10.3390/en18154023
APA StyleOspina, Á., Herrera Ríos, E., Jaramillo, J., Franco, C. A., Taborda, E. A., & Cortes, F. B. (2025). Integrating Dimensional Analysis and Machine Learning for Predictive Maintenance of Francis Turbines in Sediment-Laden Flow. Energies, 18(15), 4023. https://doi.org/10.3390/en18154023








