Battery SOH Estimation Based on Dual-View Voltage Signal Features and Enhanced LSTM
Abstract
1. Introduction
- (1)
- To address the issue of limited information, this paper proposes an SOH prediction method that relies exclusively on readily available voltage-domain signals containing electrochemical reaction mechanism information. This approach offers a novel perspective for battery lifespan prediction when current and temperature data are unavailable. Since only voltage signals are required, this method is straightforward to deploy.
- (2)
- Based on the electrochemical degradation mechanism, four kinetic features and two aggregated features are extracted to distill aging information, and their significant correlations with SOH are validated using the Pearson correlation coefficient. The resulting feature set is then fed into a neural network for prediction.
- (3)
- Owing to the constrained-signal scenario, higher demands are placed on the network’s ability to learn from the available features. In this study, the LSTM output mechanism is reexamined by discarding the conventional practice of using only the last hidden state. Instead, all historical hidden states are treated as the key and value matrices in a scaled dot-product attention mechanism. A learnable parameter is employed to dynamically generate the query matrix, which significantly enhances the model’s expressive capacity and thus yields superior prediction performance.
- (4)
- An SOH prediction framework is constructed by combining dual-view features extracted solely from voltage-domain signals with the improved LSTM network, thus obviating the need for current, temperature, or other sensor inputs. High prediction accuracy is achieved using only a small amount of easily obtainable information. Ablation analyses are conducted on the NASA battery dataset, and comparisons with conventional methods demonstrate the framework’s effectiveness.
2. Methods
2.1. Feature Engineering
2.1.1. Dataset Description
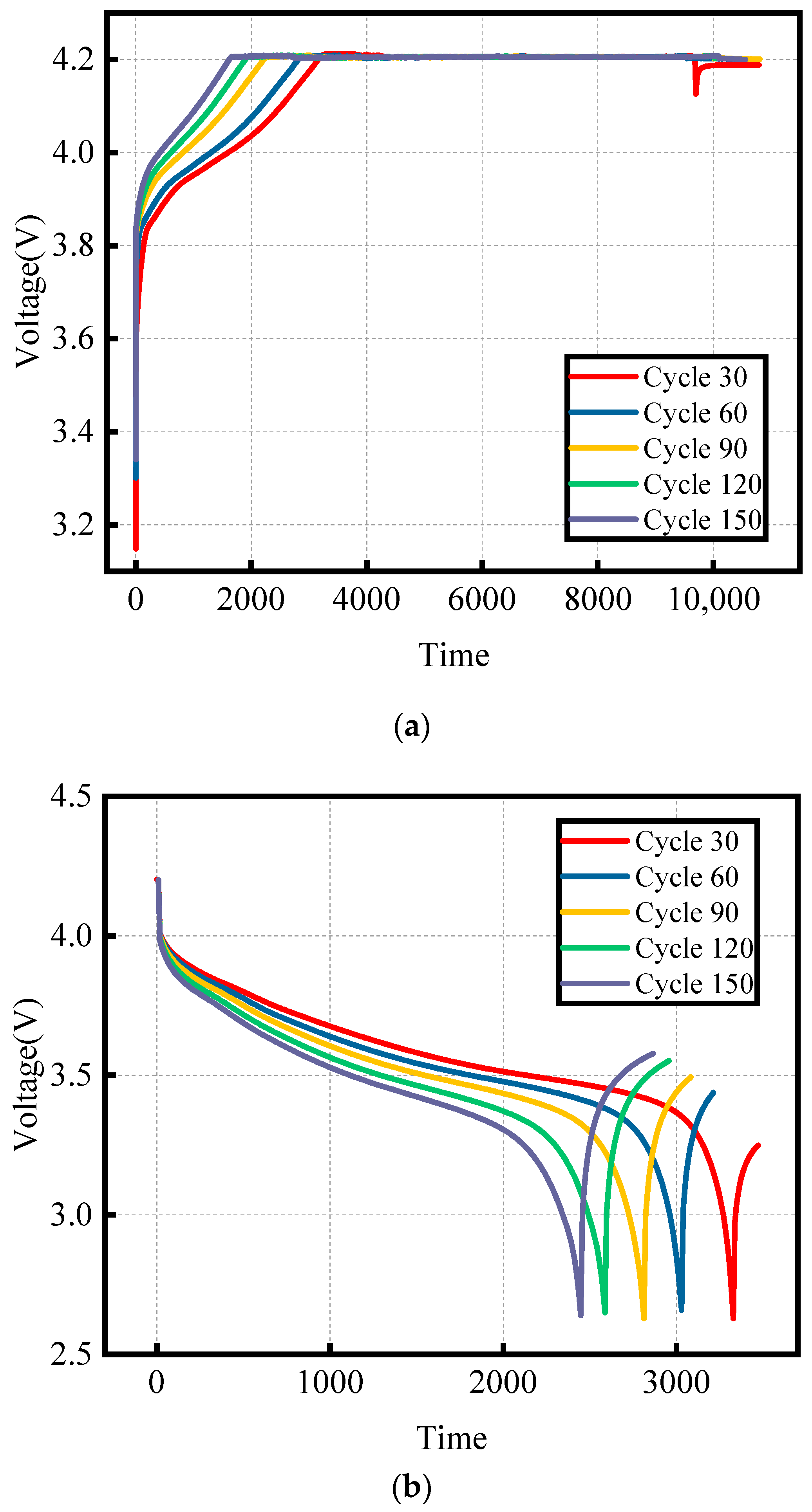
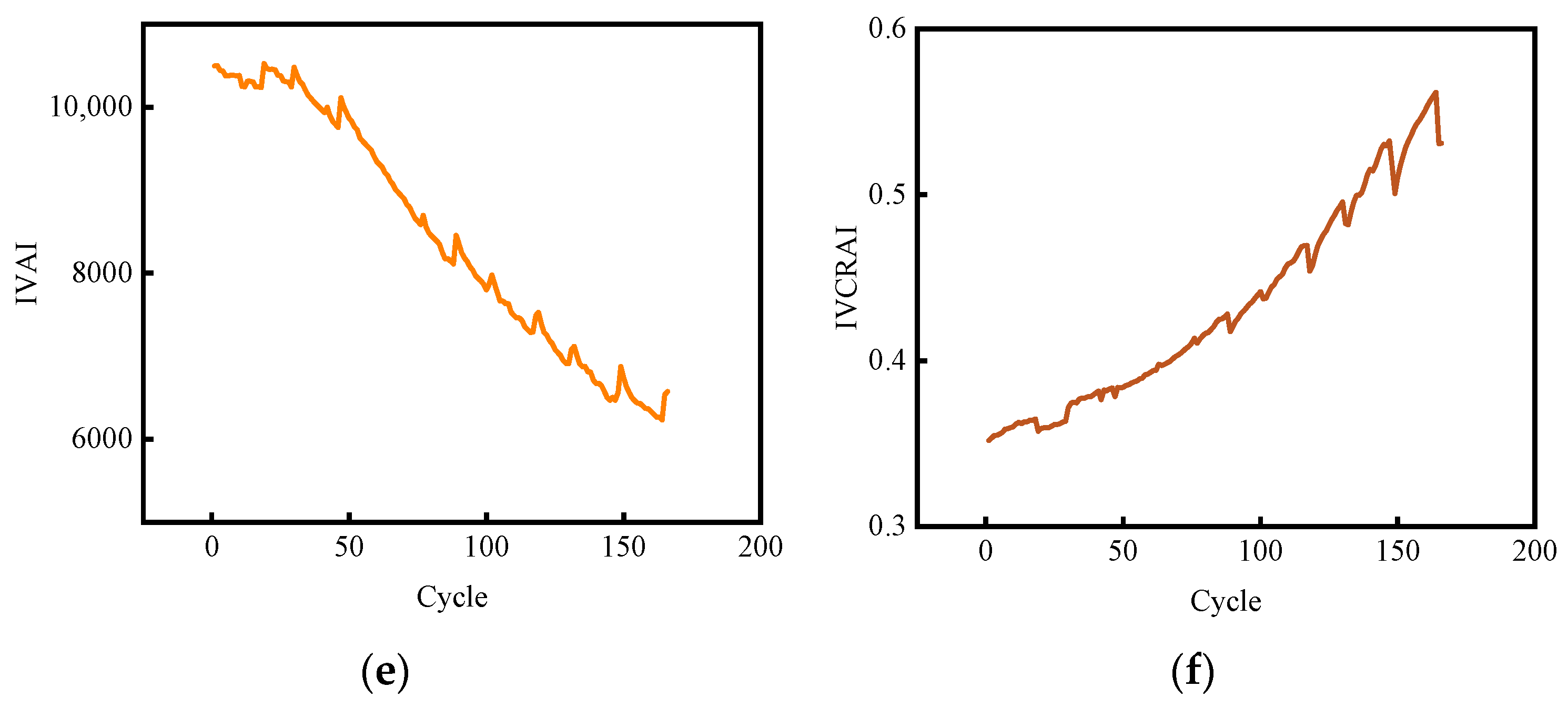
2.1.2. Dual-View Feature Extraction and Analysis of Voltage Signals
2.2. Neural Network
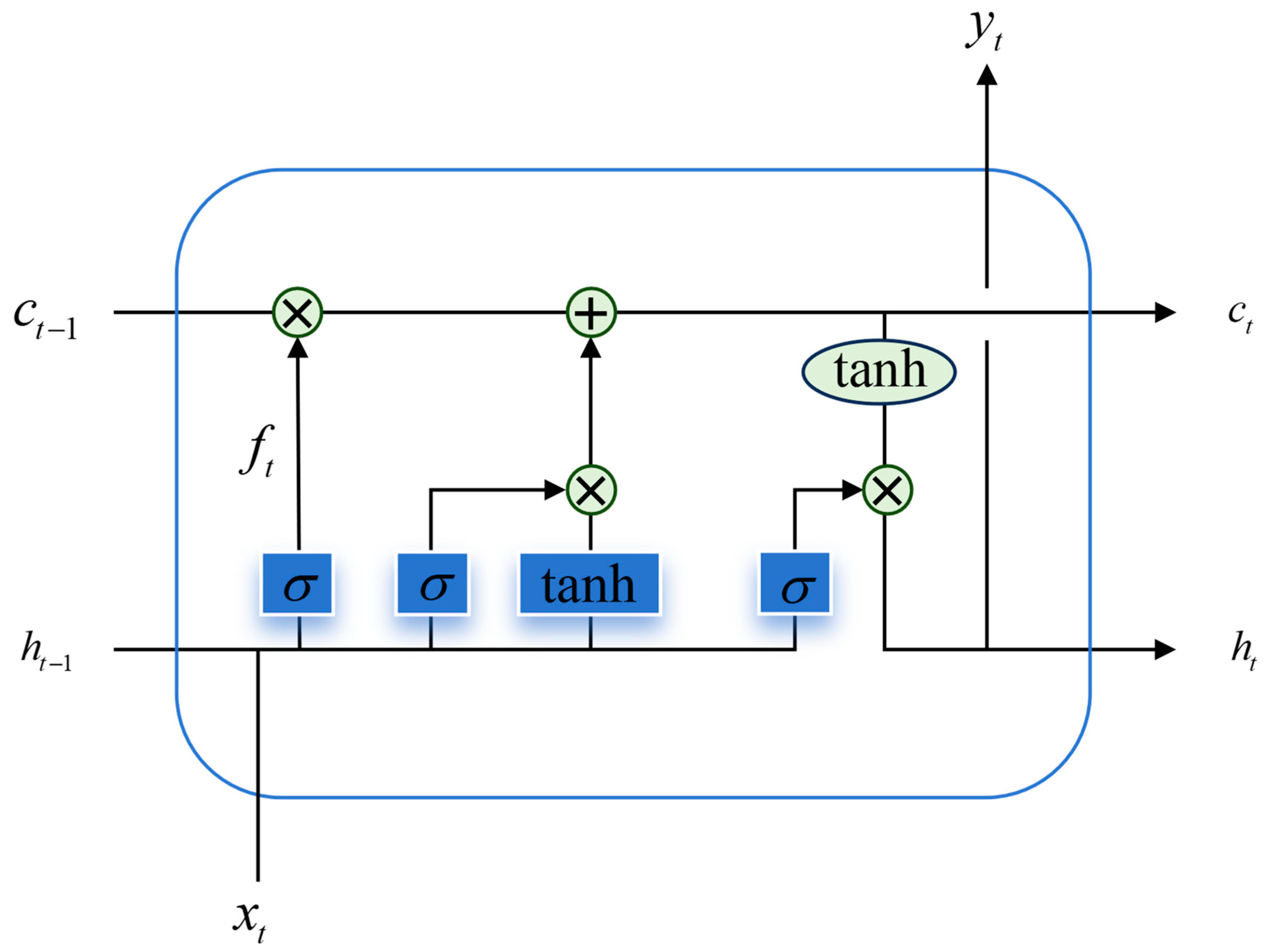
2.2.1. Long Short-Term Memory Neural Network
2.2.2. Scaled Dot-Product Attention Mechanism
2.2.3. Long Short-Term Memory Network with Scaled Dot-Product Attention
3. Results and Discussion
3.1. Evaluation Metrics
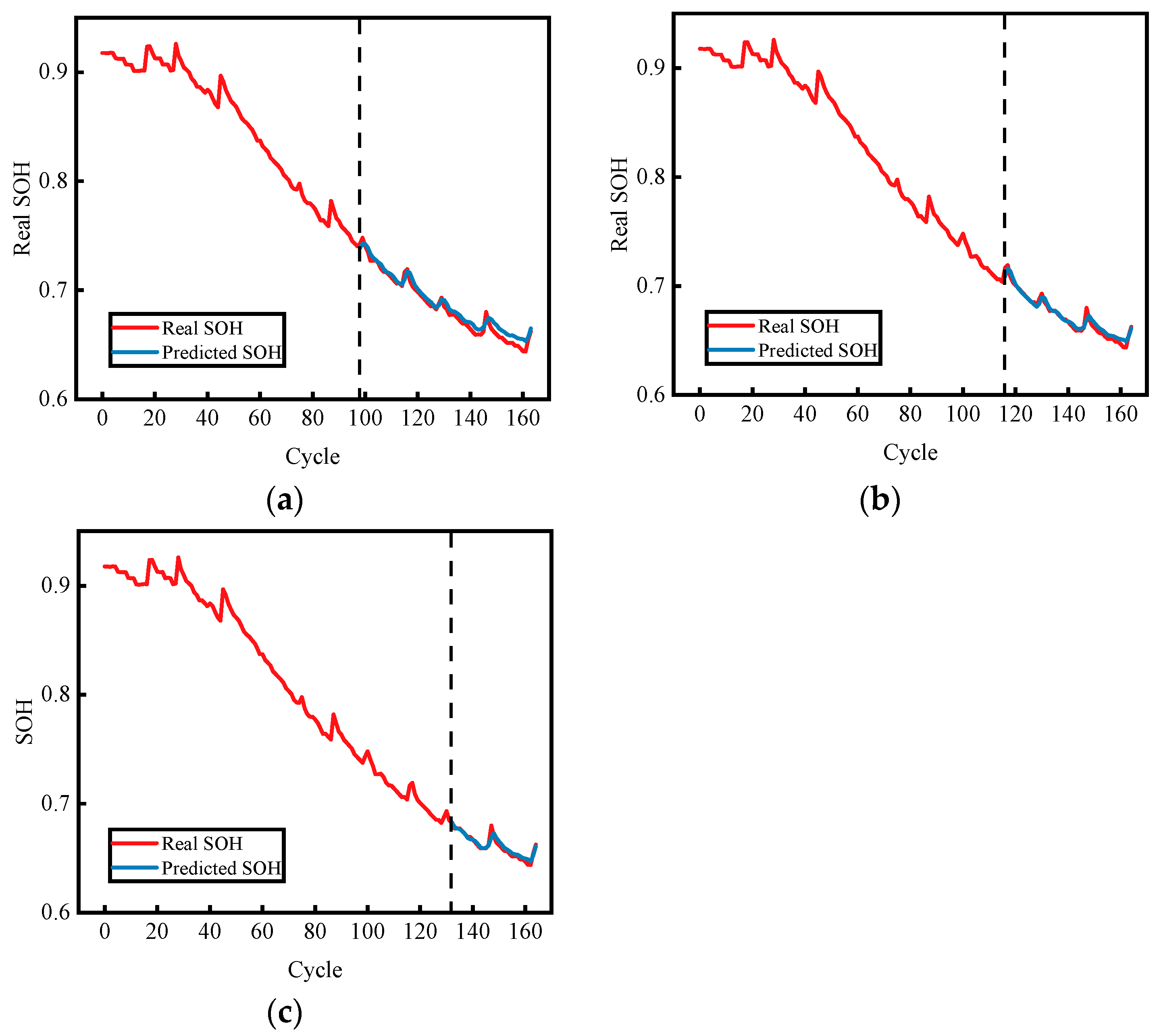
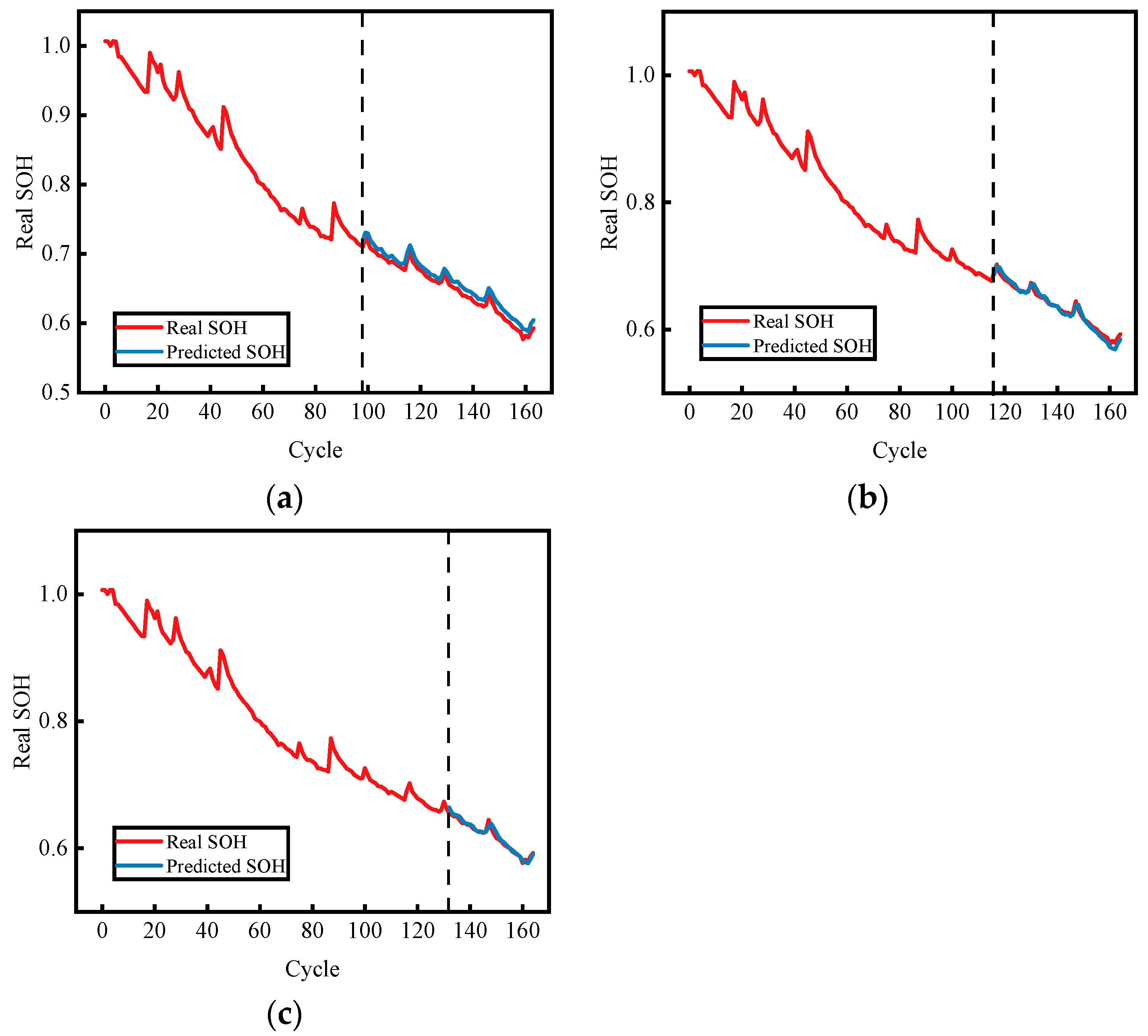
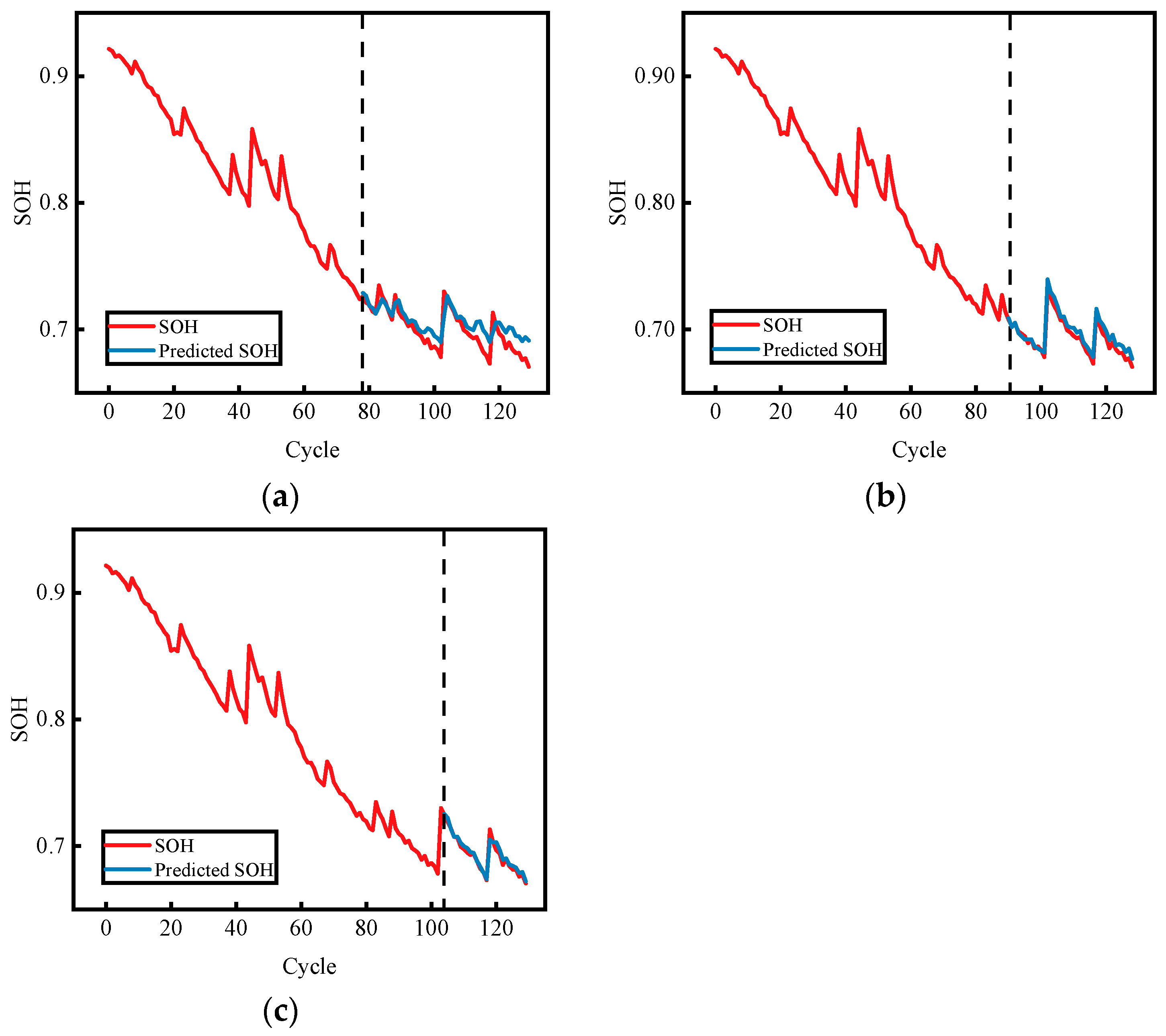
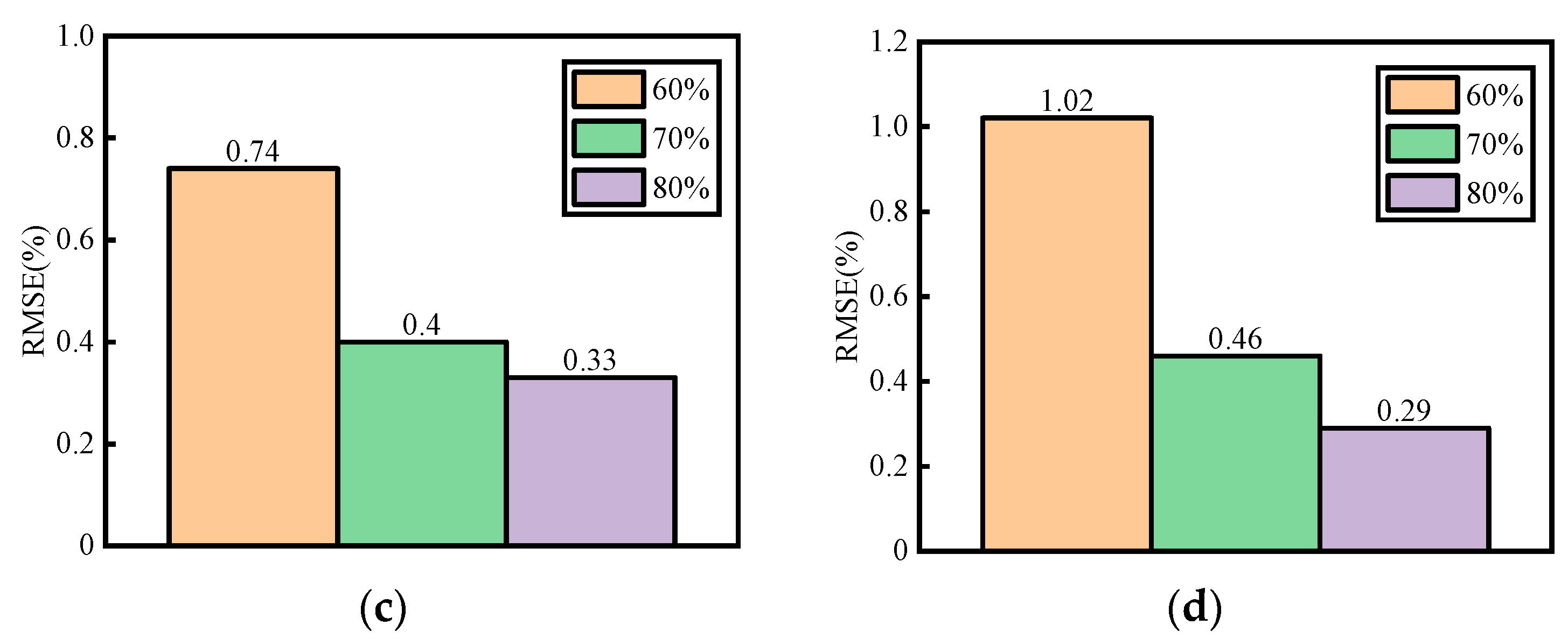
3.2. Study of Different Split Ratios
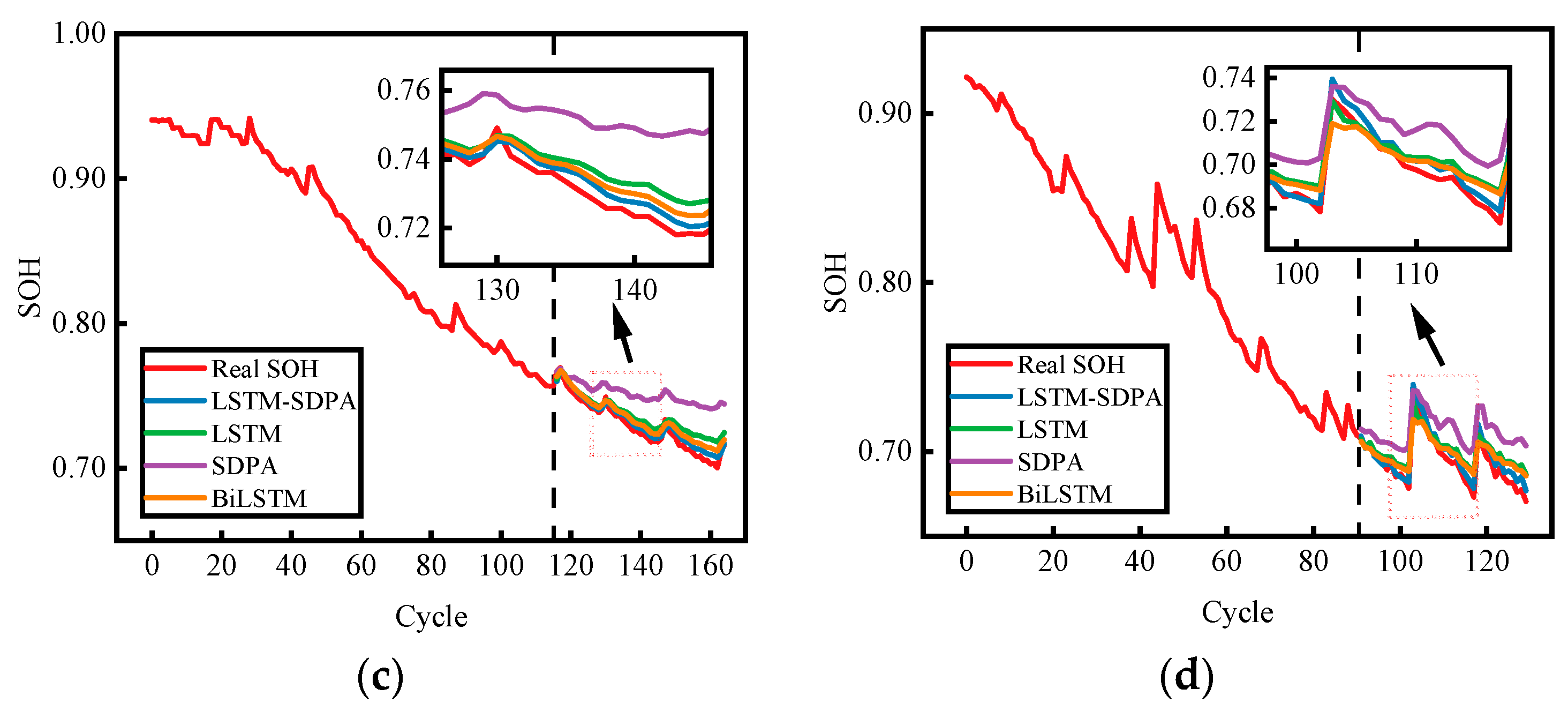
3.3. Structural Ablation Study
3.4. Comparison with Previous Studies
3.5. Practical Deployment Considerations
4. Conclusions
- (1)
- To address SOH prediction under constrained information, such as limited access to temperature or current data, this work leverages easily accessible voltage measurements, significantly lowering hardware requirements. Voltage data do not require additional sampling channels, making the method cost-effective and providing a high-accuracy SOH prediction solution even when current or temperature sensors fail or drift.
- (2)
- To fully exploit only the voltage signal, four kinetic features and two aggregated features were extracted based on electrochemical principles, comprehensively constructing a feature information network from dual perspectives. Correlation analysis verifies the importance of these features: each extracted feature shows high correlation with SOH, with the aggregated features exhibiting correlation exceeding 94%, thereby laying a solid foundation for subsequent prediction.
- (3)
- Relying solely on voltage information demands a stronger capability to learn aging-related patterns. To prevent conventional LSTM from overlooking intermediate key information when using only the final hidden state, all hidden states generated during the LSTM’s operation are preserved. A scaled dot-product attention mechanism scores these hidden states and dynamically assigns weights, with the query vector defined by a learnable parameter so the model can adaptively focus on critical time steps.
- (4)
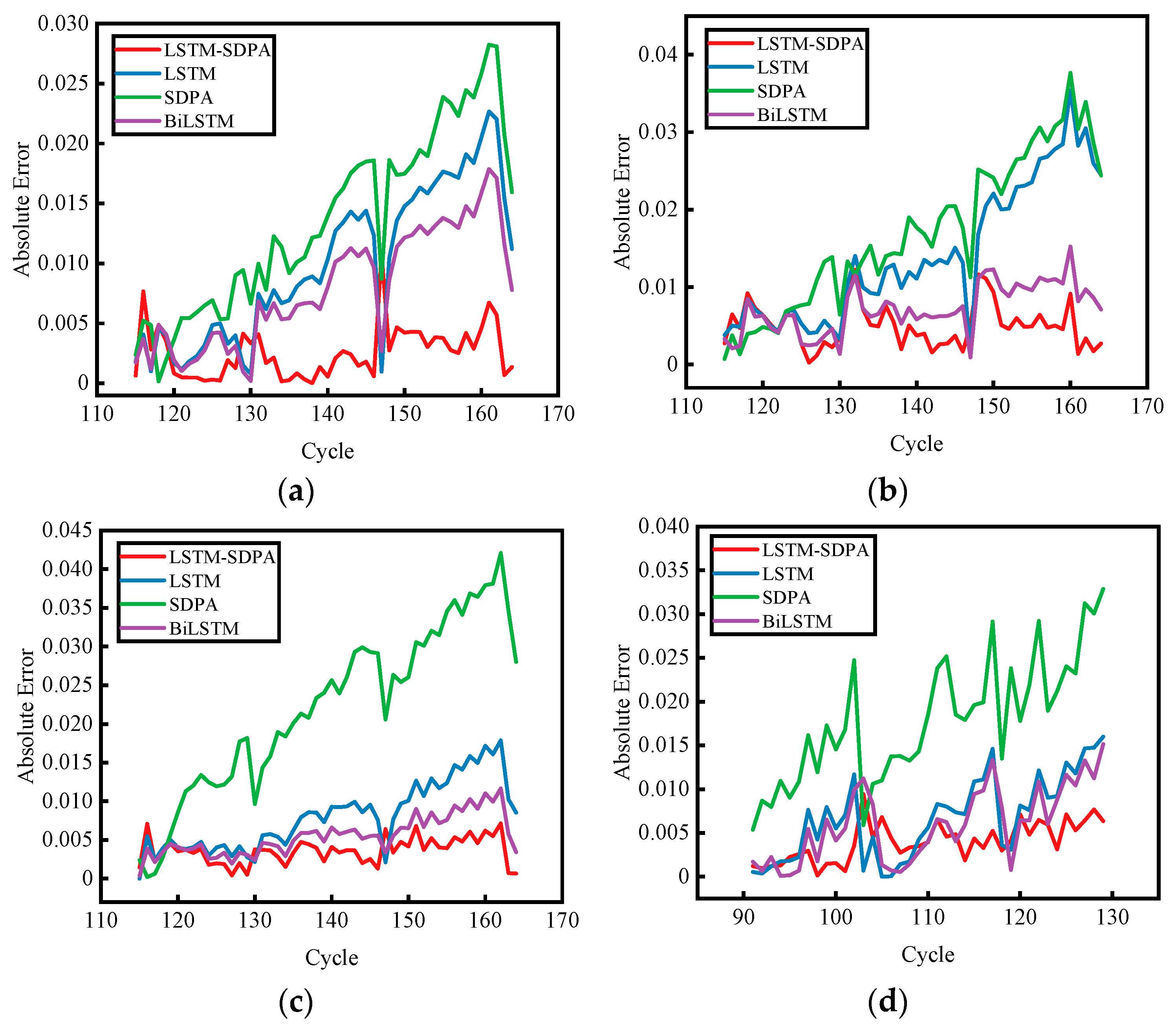
- Comparisons among LSTM, SDPA, Bi-LSTM, and the combined LSTM-SDPA model show that the proposed modification enhances performance. The ablation results demonstrate this improvement. The LSTM-SDPA model achieves an RMSE below 0.58%, and error-distribution plots indicate a narrower error range. Comparisons with other models confirm that this approach attains high prediction accuracy.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Yu, Y.; Ma, Y.; Shi, J. Lithium-ion battery health state estimation based on improved snow ablation optimization algorithm-deep hybrid kernel extreme learning machine. Energy 2025, 323, 135772. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, Y.; Li, Z.; Zhang, Z.; Nazir, M.S.; Peng, T. Enhancing state of charge and state of energy estimation in Lithium-ion batteries based on a TimesNet model with Gaussian data augmentation and error correction. Appl. Energy 2024, 359, 122669. [Google Scholar] [CrossRef]
- Khan, F.N.U.; Rasul, M.G.; Sayem, A.; Mandal, N.K. Design and optimization of lithium-ion battery as an efficient energy storage device for electric vehicles: A comprehensive review. J. Energy Storage 2023, 71, 108033. [Google Scholar] [CrossRef]
- Xu, J.; Cai, X.; Cai, S.; Shao, Y.; Hu, C.; Lu, S.; Ding, S. High-energy lithium-ion batteries: Recent progress and a promising future in applications. Energy Environ. Mater. 2023, 6, e12450. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H. Wavelet attention-powered neural network framework with hierarchical dynamic frequency learning for lithium-ion battery state of health prediction. J. Energy Storage 2023, 61, 106697. [Google Scholar] [CrossRef]
- Yao, L.; Xu, S.; Tang, A.; Zhou, F.; Hou, J.; Xiao, Y.; Fu, Z. A review of lithium-ion battery state of health estimation and prediction methods. World Electr. Veh. J. 2021, 12, 113. [Google Scholar] [CrossRef]
- Wang, M.; Wu, S.; Chen, Y.; Wang, S.; Chen, H.; Luan, W. Quantitative safety assessment of lithium-ion batteries: Integrating abuse risks and intrinsic safety. J. Power Sources 2025, 640, 236789. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, X.; He, Y.; Zhang, S.; Cai, Y. Edge–cloud collaborative estimation lithium-ion battery SOH based on MEWOA-VMD and Transformer. J. Energy Storage 2024, 99, 113388. [Google Scholar] [CrossRef]
- Li, X.; Ju, L.; Geng, G.; Jiang, Q. Data-driven state-of-health estimation for lithium-ion battery based on aging features. Energy 2023, 274, 127378. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, S.; Li, E.; Wang, Z.; Gu, F.; Ball, A.D. A hybrid intelligent model using the distribution of relaxation time analysis of electrochemical impedance spectroscopy for lithium-ion battery state of health estimation. J. Energy Storage 2024, 84, 110814. [Google Scholar] [CrossRef]
- Pang, Z.; Yang, K.; Song, Z.; Niu, P.; Chen, G.; Meng, J. A new method for determining SOH of lithium batteries using the real-part ratio of EIS specific frequency impedance. J. Energy Storage 2023, 72, 108693. [Google Scholar] [CrossRef]
- Zhang, S.; Zhu, H.; Wu, J.; Chen, Z. Voltage relaxation-based state-of-health estimation of lithium-ion batteries using convolutional neural networks and transfer learning. J. Energy Storage 2023, 73, 108579. [Google Scholar] [CrossRef]
- Lin, M.; Wu, D.; Meng, J.; Wang, W.; Wu, J. Health prognosis for lithium-ion battery with multi-feature optimization. Energy 2023, 264, 126307. [Google Scholar] [CrossRef]
- Li, X.; Yuan, C.; Wang, Z.; He, J.; Yu, S. Lithium battery state-of-health estimation and remaining useful lifetime prediction based on non-parametric aging model and particle filter algorithm. eTransportation 2022, 11, 100156. [Google Scholar] [CrossRef]
- Ge, D.; Jin, G.; Wang, J.; Zhang, Z. A novel data-driven IBA-ELM model for SOH/SOC estimation of lithium-ion batteries. Energy 2024, 305, 132395. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell. J. Electrochem. Soc. 1993, 140, 1526. [Google Scholar] [CrossRef]
- Huang, Z.; Best, M.; Knowles, J.; Fly, A. Adaptive piecewise equivalent circuit model with SOC/SOH estimation based on extended Kalman filter. IEEE Trans. Energy Convers. 2022, 38, 959–970. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, J.; Lund, P.D.; Zhang, Y. Co-estimating the state of charge and health of lithium batteries through combining a minimalist electrochemical model and an equivalent circuit model. Energy 2022, 240, 122815. [Google Scholar] [CrossRef]
- Obregon, J.; Han, Y.-R.; Ho, C.W.; Mouraliraman, D.; Lee, C.W.; Jung, J.-Y. Convolutional autoencoder-based SOH estimation of lithium-ion batteries using electrochemical impedance spectroscopy. J. Energy Storage 2023, 60, 106680. [Google Scholar] [CrossRef]
- Jorge, I.; Mesbahi, T.; Samet, A.; Boné, R. Time series feature extraction for lithium-ion batteries state-of-health prediction. J. Energy Storage 2023, 59, 106436. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, S.; Cao, W.; Xie, Y.; Fernandez, C. State of health prediction of lithium-ion batteries based on SSA optimized hybrid neural network model. Electrochim. Acta 2024, 487, 144146. [Google Scholar] [CrossRef]
- Ge, D.; Jin, G.; Wang, J.; Zhang, Z. A novel BA-ABC-ELM model for estimating state of health of lithium-ion batteries. Energy Rep. 2025, 13, 465–476. [Google Scholar] [CrossRef]
- Fan, Y.; Yang, H.; Ye, C.; Yang, W.; Panchal, S.; Fraser, R.; Fowler, M.; Dong, H. State of health estimation of lithium-ion batteries based on the fusion of aging feature extraction and SSA-ELM machine learning algorithms. Ionics 2025, 31, 7897–7915. [Google Scholar] [CrossRef]
- An, J.; Guo, W.; Lv, T.; Zhao, Z.; He, C.; Zhao, H. Joint prediction of the state of charge and the state of health of lithium-ion batteries based on the PSO-XGBoost algorithm. Energies 2023, 16, 4243. [Google Scholar] [CrossRef]
- Sun, J.; Fan, C.; Yan, H. SOH estimation of lithium-ion batteries based on multi-feature deep fusion and XGBoost. Energy 2024, 306, 132429. [Google Scholar] [CrossRef]
- Lin, C.; Wu, L.; Tuo, X.; Liu, C.; Zhang, W.; Huang, Z.; Zhang, G. A lightweight two-stage physics-informed neural network for SOH estimation of lithium-ion batteries with different chemistries. J. Energy Chem. 2025, 105, 261–279. [Google Scholar] [CrossRef]
- Dai, Y.; Yu, A. Combined CNN-LSTM and GRU based health feature parameters for lithium-ion batteries SOH estimation. Energy Storage Sci. Technol. 2022, 11, 1641. [Google Scholar]
- Zhao, F.-M.; Gao, D.-X.; Cheng, Y.-M.; Yang, Q. Estimation of lithium-ion battery health state using MHATTCN network with multi-health indicators inputs. Sci. Rep. 2024, 14, 18391. [Google Scholar] [CrossRef]
- Lin, M.; Zeng, X.; Wu, J. State of health estimation of lithium-ion battery based on an adaptive tunable hybrid radial basis function network. J. Power Sources 2021, 504, 230063. [Google Scholar] [CrossRef]
- Wang, X.; Dai, K.; Hu, M.; Ni, N. Lithium-ion battery health state and remaining useful life prediction based on hybrid model MFE-GRU-TCA. J. Energy Storage 2024, 95, 112442. [Google Scholar] [CrossRef]
- Zhang, L.; Ji, T.; Yu, S.; Liu, G. Accurate prediction approach of SOH for lithium-ion batteries based on LSTM method. Batteries 2023, 9, 177. [Google Scholar] [CrossRef]
- Zhao, S.; Luo, L.; Jiang, S.; Zhang, C. Lithium-Ion Battery State-of-Health Estimation Method Using Isobaric Energy Analysis and PSO-LSTM. J. Electr. Comput. Eng. 2023, 2023, 5566965. [Google Scholar] [CrossRef]
- Yayan, U.; Arslan, A.T.; Yucel, H. A novel method for SoH prediction of batteries based on stacked LSTM with quick charge data. Appl. Artif. Intell. 2021, 35, 421–439. [Google Scholar] [CrossRef]
- Peng, S.; Wang, Y.; Tang, A.; Jiang, Y.; Kan, J.; Pecht, M. State of health estimation joint improved grey wolf optimization algorithm and LSTM using partial discharging health features for lithium-ion batteries. Energy 2025, 315, 134293. [Google Scholar] [CrossRef]
- Vakharia, V.; Shah, M.; Nair, P.; Borade, H.; Sahlot, P.; Wankhede, V. Estimation of lithium-ion battery discharge capacity by integrating optimized explainable-AI and stacked LSTM model. Batteries 2023, 9, 125. [Google Scholar] [CrossRef]
- Saha, B. Battery Data Set. In NASA AMES Progmostics Data Repository; NASA Ames Research Center: Moffett Field, CA, USA, 2007. [Google Scholar]
- Tang, R.; Zhang, P.; Ning, S.; Zhang, Y. Prediction of battery SOH and RUL based on cooperative characteristics in voltage-temperature-time dimensions. J. Electrochem. Soc. 2023, 170, 060535. [Google Scholar] [CrossRef]
- Gu, X.; See, K.W.; Li, P.; Shan, K.; Wang, Y.; Zhao, L.; Lim, K.C.; Zhang, N. A novel state-of-health estimation for the lithium-ion battery using a convolutional neural network and transformer model. Energy 2023, 262, 125501. [Google Scholar] [CrossRef]
- Vaswani, A. Attention is all you need. In Advances in Neural Information Processing Systems; Neural Information Processing Systems Foundation: South Lake Tahoe, NV, USA, 2017. [Google Scholar]
- Carion, N.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-end object detection with transformers. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 213–229. [Google Scholar]
- Xu, H.; Wu, L.; Xiong, S.; Li, W.; Garg, A.; Gao, L. An improved CNN-LSTM model-based state-of-health estimation approach for lithium-ion batteries. Energy 2023, 276, 127585. [Google Scholar] [CrossRef]
- Fan, Y.; Xiao, F.; Li, C.; Yang, G.; Tang, X. A novel deep learning framework for state of health estimation of lithium-ion battery. J. Energy Storage 2020, 32, 101741. [Google Scholar] [CrossRef]
- Wu, J.; Fang, L.; Dong, G.; Lin, M. State of health estimation of lithium-ion battery with improved radial basis function neural network. Energy 2023, 262, 125380. [Google Scholar] [CrossRef]
- Chen, L.; Xie, S.; Lopes, A.M.; Bao, X. A vision transformer-based deep neural network for state of health estimation of lithium-ion batteries. Int. J. Electr. Power Energy Syst. 2023, 152, 109233. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, F.; Cai, Z.; Xu, L.; Shen, S.; Yu, P. State of health estimation of lithium-ion batteries based on interval voltage features. J. Energy Storage 2024, 102, 114112. [Google Scholar] [CrossRef]
- Lu, J.; Wu, S.; Qin, Z.; Yang, G. Frequency-Aware Attention-LSTM for PM2.5 Time Series Forecasting. arXiv 2025, arXiv:2503.24043. [Google Scholar]
- Ren, M.; Wei, J.; Qin, J.; Guo, X.; Wang, H.; Li, S. Attention based LSTM framework for robust UWB and INS integration in NLOS environments. Sci. Rep. 2025, 15, 21637. [Google Scholar] [CrossRef]







| CIKRT | DIKRT | CTPKT | MTPST | IVAI | IVCRAI | |
|---|---|---|---|---|---|---|
| B0005 | 0.9947 | 0.9714 | 0.9980 | −0.9135 | 0.9994 | −0.9669 |
| B0006 | 0.9929 | 0.9668 | 0.9948 | −0.9397 | 0.9974 | −0.9448 |
| B0007 | 0.9886 | 0.9785 | 0.9980 | −0.8845 | 0.9994 | −0.9877 |
| B0018 | 0.9887 | 0.9482 | 0.9821 | −0.7402 | 0.9982 | −0.9808 |
| Parameter | Setting |
|---|---|
| Number of LSTM layers | 2 |
| LSTM hidden size 1 | 32 |
| LSTM hidden size 2 | 32 |
| Attention heads | 2 |
| Optimizer | Adam |
| Loss function | MSE |
| Batch size | 4 |
| Learning rate | 0.0007 |
| Epoch | 200 |
| Model | Battery | MAE (%) | RMSE (%) |
|---|---|---|---|
| LSTM-SDPA | B0005 | 0.26 | 0.34 |
| B0006 | 0.51 | 0.58 | |
| B0007 | 0.37 | 0.40 | |
| B0018 | 0.40 | 0.46 | |
| LSTM | B0005 | 1.00 | 1.18 |
| B0006 | 1.43 | 1.67 | |
| B0007 | 0.82 | 0.92 | |
| B0018 | 0.67 | 0.82 | |
| SDPA | B0005 | 1.37 | 1.56 |
| B0006 | 1.73 | 1.97 | |
| B0007 | 2.25 | 2.48 | |
| B0018 | 1.79 | 1.92 | |
| Bi-LSTM | B0005 | 0.80 | 0.93 |
| B0006 | 0.73 | 0.79 | |
| B0007 | 0.56 | 0.61 | |
| B0018 | 0.60 | 0.73 |
| Model | Battery | MAE (%) | RMSE (%) |
|---|---|---|---|
| LSTM-SDPA | B0005 | 0.26 | 0.34 |
| B0006 | 0.51 | 0.58 | |
| B0007 | 0.37 | 0.40 | |
| B0018 | 0.40 | 0.46 | |
| TCN | B0005 | 0.60 | 0.66 |
| B0006 | 1.27 | 1.42 | |
| B0007 | 0.72 | 0.75 | |
| B0018 | 0.69 | 0.78 | |
| ESN | B0005 | 1.21 | 1.34 |
| B0006 | 1.38 | 1.82 | |
| B0007 | 0.96 | 1.07 | |
| B0018 | 0.90 | 1.04 |
| Model | Battery | MAE (%) | RMSE (%) |
|---|---|---|---|
| LSTM-SDPA | B0005 | 0.26 | 0.34 |
| B0006 | 0.51 | 0.58 | |
| B0007 | 0.37 | 0.40 | |
| B0018 | 0.40 | 0.46 | |
| [42] | B0005 | 2.53 | 2.71 |
| B0006 | 0.74 | 0.88 | |
| B0007 | 0.74 | 0.97 | |
| B0018 | 0.56 | 0.71 | |
| [43] | B0005 | 0.36 | 0.52 |
| B0006 | 0.74 | 0.93 | |
| B0007 | 0.44 | 0.59 | |
| B0018 | - | - | |
| [44] | B0005 | 0.31 | 0.43 |
| B0006 | 0.40 | 0.51 | |
| B0007 | 0.30 | 0.39 | |
| B0018 | 0.43 | 0.54 | |
| [45] | B0005 | 0.70 | 0.82 |
| B0006 | 1.19 | 1.69 | |
| B0007 | 0.41 | 0.52 | |
| B0018 | 0.69 | 0.79 |
| Battery | MAE (%) | RMSE (%) | |
|---|---|---|---|
| Without Noise | B0005 | 0.26 | 0.34 |
| B0006 | 0.51 | 0.58 | |
| B0007 | 0.37 | 0.40 | |
| B0018 | 0.40 | 0.46 | |
| With Noise | B0005 | 0.35 | 0.47 |
| B0006 | 0.75 | 0.90 | |
| B0007 | 0.56 | 0.64 | |
| B0018 | 0.59 | 0.73 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; He, Y.; Hu, H. Battery SOH Estimation Based on Dual-View Voltage Signal Features and Enhanced LSTM. Energies 2025, 18, 4016. https://doi.org/10.3390/en18154016
Wang S, He Y, Hu H. Battery SOH Estimation Based on Dual-View Voltage Signal Features and Enhanced LSTM. Energies. 2025; 18(15):4016. https://doi.org/10.3390/en18154016
Chicago/Turabian StyleWang, Shunchang, Yaolong He, and Hongjiu Hu. 2025. "Battery SOH Estimation Based on Dual-View Voltage Signal Features and Enhanced LSTM" Energies 18, no. 15: 4016. https://doi.org/10.3390/en18154016
APA StyleWang, S., He, Y., & Hu, H. (2025). Battery SOH Estimation Based on Dual-View Voltage Signal Features and Enhanced LSTM. Energies, 18(15), 4016. https://doi.org/10.3390/en18154016







