Abstract
This study introduces a novel approach for minimizing assembly errors in wind turbine gearboxes using a hybrid optimization algorithm, Particle Swarm-Bacteria Foraging Optimization (PSBFO). By integrating error-driven task sequencing and real-time error feedback with the PSBFO algorithm, we developed a comprehensive framework tailored to the unique challenges of gearbox assembly. The PSBFO algorithm combines the global search capabilities of PSO with the local refinement of BFO, creating a unified framework that efficiently explores task sequencing, minimizing misalignment and torque misapplication assembly errors. The methodology results in a 38% reduction in total assembly errors, improving both process accuracy and efficiency. Specifically, the PSBFO algorithm reduced errors from an initial value of 50 to a final value of 5 across 20 iterations, with components such as the low-speed shaft and planetary gear system showing the most substantial reductions. The 50 to 5 error reduction represents a significant decrease in assembly errors from an unoptimized (50) to an optimized (5) sequence, achieved through the PSBFO algorithm, by minimizing dimensional deviations, torque mismatches, and alignment errors across 26 critical gearbox components. While the primary focus is on wind turbine gearbox applications, this approach has the potential for broader applicability in error-prone assembly processes in industries such as automotive and aerospace, warranting further validation in future studies.
1. Introduction
The assembly of wind turbine gearboxes involves numerous complex mechanical components, each of which must be carefully installed to ensure the optimal performance of the turbines. The gearbox converts the low-speed, high-torque rotation from the turbine’s rotor into high-speed, low-torque rotation, which is essential for electricity generation [1]. Errors in the assembly process, such as torque misapplication, part misalignment, and the violation of precedence constraints, can lead to significant degradation of performance, increased downtime, and even mechanical failure [2]. These errors not only increase maintenance costs but also impact the reliability and lifespan of wind turbines [3]. Previous research has largely focused on minimizing the assembly time of gearbox assembly, with less attention paid to error reduction [4]. Assembly sequence optimization (ASO) techniques, both in static and dynamic environments, have been widely applied to minimize assembly time and improve manufacturing efficiency [5]. However, most studies have focused primarily on time reduction, often overlooking the critical aspect of error minimization. In recent years, some approaches have started to address assembly errors, such as misalignment or incorrect torque application, but these methods usually apply global optimization strategies without taking into account task-specific error sources or real-time feedback [2,6]. Our work addresses this gap by introducing a hybrid optimization approach (PSBFO) that integrates task-specific error minimization with real-time feedback mechanisms, specifically targeting assembly errors in wind turbine gearboxes. Additionally, bio-inspired metaheuristic algorithms, PSO, Ant Lion Optimizer (ALO), Continuous Genetic Algorithm (CGA), and Vortex Search Algorithm (VSA), have been applied to optimize weight reduction in power transmission systems using advanced materials like Carbon Fiber-Reinforced Polymer (CFRP) and titanium alloys, achieving significant weight reduction while maintaining mechanical integrity [7]. However, errors during the assembly process can have far-reaching consequences, especially in complex systems like wind turbine gearboxes, where component interdependencies and mechanical precision are critical [8]. Given the high cost of failure and rework, there is a growing need for optimization methods that focus on reducing assembly errors.
Assembly errors can be reduced by training intelligent systems that dynamically adjust assembly operations by learning from past errors and improving performance. By continuously optimizing decision making based on feedback, algorithms can reduce error rates, enhance precision, and improve overall efficiency in automated assembly lines. This approach enables systems to learn and adapt over time, minimizing human intervention and reducing costly assembly errors [9]. Assembly errors refer to deviations from the intended or optimal assembly state, including alignment errors, torque misapplications, and precedence violations [8]. These errors occur due to various factors, such as human mistakes, equipment inaccuracy, or environmental influences like temperature or humidity [8]. Real-time feedback in this study is obtained through simulated sensor data that continuously updates the error status during the optimization process. The error likelihoods are modeled based on historical data, expert judgment, and the empirical analysis of component complexity, where more complex components such as the low-speed shaft are assigned higher error likelihoods due to their alignment and torque sensitivity.
Assembly error reduction is a critical focus in dynamic environments, where real-time adjustments can significantly improve process reliability. An adaptive real-time resource allocation approach for dynamically adjusting resources based on environmental conditions was developed [10]. Their method optimizes resource allocation through real-time feedback, reducing assembly errors by responding immediately to changes in the production environment [11]. Similarly, the authors of [12] developed an optimization technique using adaptive particle swarm optimization (PSO), which can efficiently handle real-time adjustments during the assembly process. This adaptive PSO improves process precision by continuously optimizing operational parameters based on real-time data, minimizing errors in dynamic environments [13]. To further enhance error reduction, hybrid optimization algorithms have been explored. An algorithm was introduced for global optimization, which can track and adjust assembly parameters in real time, reducing errors through adaptive learning [14]. Another method highlighted the importance of PSO in tracking and optimizing dynamic systems, demonstrating its effectiveness in reducing errors during the assembly process [15]. Additionally, a method applied a bacterial foraging optimization technique to dynamic environments, ensuring that assembly operations can adapt to changes in real time, further minimizing error rates [16]. These adaptive optimization strategies contribute significantly to reducing assembly errors in complex and dynamic production environments.
Incorporating recent advancements in hybrid meta-heuristic algorithms is essential for enhancing the effectiveness of assembly optimization processes. The authors of [17] introduced a hybrid particle swarm optimization (PSO) approach that integrates adaptive learning strategies to address the inherent limitations of standard PSO, such as premature convergence and suboptimal exploitation capabilities. This method demonstrated improved performance in solving complex optimization problems, making it a valuable reference for assembly sequence optimization. Similarly, the authors of [18] proposed a Genetic Algorithm (GA)-based alignment correction technique tailored for flexible and transparent field-effect transistors. Their study focused on the uniaxial alignment of nanowires using an off-center spin-coating method, achieving significant improvements in device performance. This approach offers valuable insights into alignment correction methodologies applicable to various assembly processes. Furthermore, the authors of [19] conducted a cumulative review of major advances in PSO from 2018 to the present. Their findings highlighted the efficacy of hybrid algorithms in addressing complex optimization challenges within industrial contexts, underscoring the potential benefits of adopting such approaches in assembly optimization tasks.
This study leverages simulation-based results to evaluate the performance of the PSBFO model. While real-world validation in an industrial setting of wind turbine gearbox assembly is essential for confirming the model’s practical applicability, it was not feasible within the timeframe of this research. Future work will focus on real-world case studies to validate these findings. The goal of this paper is to minimize errors in the assembly of the wind turbine gearbox by using a hybrid optimization approach of Particle Swarm-Bacteria Foraging Optimization (PSBFO) that combines the strengths of particle swarm optimization (PSO) and bacteria foraging optimization (BFO). This approach optimizes the sequence of assembly tasks while taking precedence constraints and error likelihoods into account. By focusing on error reduction, this work aims to improve the overall reliability of wind turbine gearboxes, ensuring longer operational life and reducing the need for costly repairs and maintenance. This study introduces several novel contributions to the field of error reduction in the assembly of complex mechanical systems like wind turbine gearboxes. The first novelty lies in the integration of task-sequencing optimization based on precedence constraints and error likelihoods. While most existing approaches focus on optimizing time, this study uniquely prioritizes error minimization by analyzing how different task sequences can lead to error-prone assembly processes. By specifically targeting the sources of errors such as component misalignment, torque misapplication, and precedence violations, this approach offers a new perspective on improving assembly reliability and precision.
The second novelty involves the evaluation of PSBFO for error reduction, which has not been extensively applied in this context. While PSBFO has been used in general optimization scenarios, its application to minimize assembly errors and providing new insights into its effectiveness, demonstrates a significant improvement compared to traditional methods. The hybrid nature of PSBFO, combining global exploration with local error refinement, offers a significant advantage in identifying and correcting task-specific errors, an area that traditional optimization methods often overlook. Finally, the third novelty is the development of a comprehensive framework for error reduction in complex mechanical assemblies, specifically focusing on the unique challenges posed by wind turbine gearboxes. By combining error-driven task sequencing, real-time error data, and PSBFO, this framework not only enhances reliability but also serves as a robust solution for other error-prone assembly processes. This systematic approach provides a foundation for future research in error minimization across various complex mechanical systems. Current methods lack the fine-grained modeling of assembly errors and integrated optimization frameworks that jointly consider task sequencing dependencies and task-specific error probabilities; this study addresses these gaps by proposing a novel hybrid algorithm that combines parallel assembly sequence planning with error-driven feedback
This research is organized as follows: Section 2 reviews the relevant literature, highlighting past advancements and gaps in assembly error minimization and sequence optimization for complex mechanical systems like wind turbine gearboxes. Section 3 describes the materials and methods used, detailing the error model, precedence constraints, and task-specific requirements essential to the assembly process. It also presents the proposed hybrid optimization approach, including the integration of parallel assembly sequence planning (PASP) with the Particle Swarm-Bacteria Foraging Optimization (PSBFO) algorithm, designed to minimize assembly errors effectively. Section 4 discusses the simulation results and analyzes the error reduction performance compared to traditional methods. It also provides insights on error distribution across gearbox components and assesses the robustness of the PSBFO algorithm. Finally, Section 5 concludes this study, summarizing the research findings and suggesting future research directions for error minimization in complex assemblies.
2. Literature Review
2.1. Wind Turbine Gearbox Assembly and the Role of Error Minimization
Wind turbine gearboxes are integral to the efficient functioning of modern wind turbines, converting the low-speed, high-torque mechanical energy produced by turbine blades into high-speed rotational energy necessary for power generation. The gearbox system typically consists of a complex array of components such as planetary gears, sun gears, and shafts, all of which require precise assembly to ensure optimal operation. Errors during the assembly process of these component misalignments, incorrect torque application, and precedence violations can significantly impact the turbine’s performance and longevity [20]. Gearbox assembly has long been an area of focus in both research and industry, to improve performance, reduce downtime, and minimize operational risks [21]. While previous studies have concentrated on reducing assembly time and costs [1,3,22], error minimization has recently gained attention as a critical factor in enhancing the reliability and safety of gearboxes [23]. This shift is driven by the high costs associated with mechanical failures in wind turbines, which can result in extended downtime and expensive repairs [24].
2.2. Parallel Assembly Sequence Planning (PASP) in Mechanical Systems
PASP refers to the optimization of task scheduling where multiple assembly tasks are performed simultaneously, rather than sequentially. The goal of PASP is to reduce overall assembly time, optimize resource utilization, and ensure that dependencies between tasks are respected. PASP is particularly important in complex mechanical systems, such as wind turbine gearboxes, where components like planetary gears, high-speed shafts, and sun gears have strong interdependencies [25]. Studies on PASP have shown that parallelizing assembly tasks can significantly reduce overall assembly time, particularly in scenarios where multiple subsystems can be assembled simultaneously without violating task dependencies [26]. However, the use of PASP in the context of error minimization has been less explored. Current PASP models often overlook uncertainty and feedback integration, which are essential for reducing assembly errors [27]. Most research on PASP has focused on optimizing task scheduling to minimize time and costs, but recent work has begun to investigate its potential to reduce assembly errors by optimizing the order of operations and enforcing precedence constraints [28].
2.3. Optimization Techniques for Assembly Processes
Various optimization techniques have been applied to improve assembly processes, particularly in complex mechanical systems. Traditional methods such as Genetic Algorithms (GAs) and ant colony optimization (ACO) have been extensively used to optimize assembly sequence planning, focusing primarily on reducing time and costs [29,30]. These methods, while effective in improving operational efficiency, often do not account for the specific sources of error that can arise in complex assemblies, such as component misalignment or task dependency violations [8]. In recent years, hybrid optimization techniques have gained popularity due to their ability to balance global exploration and local refinement in complex problems. One such technique is PSO, which mimics the social behavior of bird flocking or fish schooling to explore multiple solutions simultaneously [31]. PSO has been widely adopted for assembly sequence planning, with several studies demonstrating its effectiveness in finding near-optimal sequences with minimal computational cost. However, while PSO is strong in global exploration, it lacks the fine-tuned local search capabilities needed to address task-specific errors.
To overcome this limitation, researchers have integrated PSO with other optimization techniques, such as BFO. BFO is inspired by the foraging behavior of bacteria and is particularly effective in optimizing smaller, localized solutions by fine-tuning sequences to reduce specific types of errors [14,32]. The combination of PSO and BFO in hybrid algorithms, such as PSBFO, allows for both the broad exploration of possible solutions and precise optimization of the assembly process, making it ideal for error reduction.
2.4. Error Minimization in Assembly Processes
Error minimization in mechanical assemblies has been identified as a crucial factor in ensuring the reliability and efficiency of complex systems like wind turbines. Errors during the assembly of wind turbine gearboxes, for instance, can lead to increased wear, premature failures, and reduced operational efficiency [33]. Researchers have identified common sources of assembly errors, such as misalignment, incorrect torque application, and failure to adhere to task dependencies [34]. Traditional assembly methods often overlook these error sources, focusing instead on optimizing for cost or time. However, studies show that even small assembly errors can have significant long-term impacts on the performance and lifespan of wind turbines [8]. The integration of error minimization strategies into assembly sequence planning is thus becoming a critical area of research. In particular, hybrid optimization techniques such as PSBFO, which can address both global optimization and local error refinement, are gaining traction as a powerful solution to reduce errors in complex assemblies [35].
2.5. The Role of PSBFO and Real-Time Error Feedback
Particle PSBFO combines the global search capabilities of PSO with the local refinement capabilities of BFO. This hybrid approach is particularly well-suited for minimizing errors in assembly processes. While PSO enables the exploration of a wide range of task sequences to identify potential solutions, BFO refines these sequences by minimizing errors related to specific tasks, such as torque misapplication or component misalignment [36]. Research has shown that PSBFO outperforms traditional optimization methods in reducing errors in complex mechanical systems. It was demonstrated that PSBFO could achieve significant improvements in assembly sequence planning by minimizing both time and error simultaneously [37]. Similarly, it was shown that PSBFO is highly effective in reducing task-specific errors by optimizing the order of operations and enforcing precedence constraints [38]. In the context of wind turbine gearboxes, PSBFO can optimize the assembly process by identifying the most error-prone tasks and adjusting the sequence to minimize the likelihood of errors [30]. By considering real-time data on torque application, alignment, and task dependencies, PSBFO offers a robust solution to the challenges of error-prone assemblies [39]. This makes it an ideal candidate for use in parallel assembly sequence planning, where multiple tasks must be scheduled and optimized concurrently [40].
The PSBFO developed in this study serves as a decision aid for minimizing assembly errors in complex mechanical systems. This hybrid approach optimizes error-driven task sequencing and incorporates real-time feedback mechanisms, making it suitable for high-precision applications in production systems [10]. Additionally, PSBFO combines the global search capabilities of PSO with the local refinement capabilities of BFO, effectively balancing exploration and exploitation during optimization. This dual focus allows the PSBFO to dynamically respond to task-specific errors and precedence constraints in ways that conventional algorithms often cannot [41]. Unlike traditional approaches that prioritize cost and time, this model is tailored to minimize assembly errors, enhancing process reliability, a critical factor in high-stakes industrial applications [40]. The PSBFO model can be adapted for broader applications in production systems, such as automotive and aerospace industries, where precision and reliability are crucial, thus extending its utility beyond the initial scope of wind turbine gearbox assembly [10]. Many meta-heuristic algorithms exist for this problem, but PSBFO is chosen due to its unique advantages:
- Exploration–exploitation balance: PSO’s global search is complemented by BFO’s local refinement.
- Faster convergence: Hybridization accelerates convergence to high-quality solutions.
- Robustness: PSBFO has been shown to outperform standalone PSO and BFO in constraint-heavy problems.
3. Materials and Methods
3.1. Error Model and Precedence Constraints
The assembly of a generic 10 MW wind turbine gearbox involves 26 critical distinct parts, each with specific precedence constraints that must be adhered to, as shown in Figure 1. The historical data used for modeling error likelihoods was based on a dataset of 100 previous gearbox assemblies, which provided a broad representation of common assembly errors. The data was collected from industry reports and expert consultations, ensuring that the error likelihoods accurately reflect the typical challenges faced during the assembly process. The constraints dictate the correct order of operations to ensure that all components are properly assembled, avoiding potential errors of misalignment, incorrect torque application, and failure to account for dependencies between components. The ring gear (RING-G1) must be assembled before the sun gear (SUN-G1), which in turn must be installed before the planetary gears (PL-G1, PL-G2, and PL-G3). The assembly of the low-speed shaft (LSS) and its components (LSS-A, LSS-B, LSS-C) depends on the completion of the planetary gear system and intermediate-speed shaft components. The high-speed shaft (HSS-A, HSS-B, and HSS-C) was assembled later in the process after key components like planetary gears and shafts were installed. The 26 components involved in the gearbox assembly are shown in Figure 1 below.

Figure 1.
Model of the generic 10 MW wind turbine gearbox.
The precedence constraints define the order in which each component must be assembled; the sub-assemblies are as shown in Figure 2. The sub-assemblies were subsequently incorporated into the main gearbox housing, where all connections were secured, and the gear alignment was carefully ensured, as shown in Figure 1.
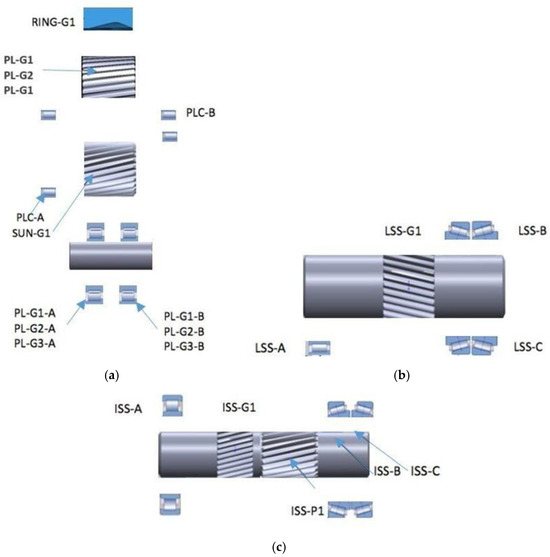

Figure 2.
(a) PL, PLC, RING, SUN, (b) LSS, (c) ISS, (d) HSS components.
- RING-G1 must be assembled first, followed by SUN-G1.
- PL-G1, PL-G2, and PL-G3 (planetary gears) can only be assembled after the SUN-G1 is in place.
- PL-G1-A, PL-G1-B, PL-G2-A, PL-G2-B, PL-G3-A, and PL-G3-B are subcomponents of the planetary gears and were assembled once the primary planetary gears were installed.
- PLC-A and PLC-B must be assembled after the planetary gear system is complete.
- The low-speed shaft (LSS) components (LSS-A, LSS-B, and LSS-C) and LSS-G1 were installed after the PLC-B was completed.
- The intermediate shaft components (ISS-A, ISS-B, ISS-C, ISS-G1, and ISS-P1) were installed sequentially, with each dependent on the previous component.
- The high-speed shaft (HSS-A, HSS-B, HSS-C, and HSS-P1) was assembled last after all the previous components were in place.
To model errors in this complex assembly process, each task (component) was assigned an error likelihood based on historical data and expert judgment. Complex components such as LSS-C or HSS-C have a higher likelihood of errors due to their intricate alignment and torque requirements, while simpler components like PL-G1-A might have a lower likelihood of error. Assembly error refers to any deviation or mistake in the assembly process of the wind turbine gearbox components that could lead to misalignment, incorrect torque application, or incorrect sequence of tasks. These errors can impact the performance, reliability, and longevity of the gearbox. In this study, the assembly errors were tracked and minimized by considering two main factors:
- Task-specific errors: Each task or component in the assembly has an inherent likelihood of error. For example, components that require precise alignment or torque, like the low-speed shaft or planetary gears, have a higher likelihood of errors during their assembly. These errors may stem from human mistakes, equipment inaccuracy, or other operational factors.
- Precedence constraint violations: The assembly of the gearbox components follows a specific order or precedence constraints. Components must be assembled before others to ensure proper functioning. If these precedence rules are violated (for instance, if a component is assembled before another component it depends on), this would lead to an assembly error as defined in this study. Violating precedence constraints adds a penalty to the total error score, making it more costly in the optimization model.
Additionally, penalties were applied when precedence constraints were violated. The total error for a given assembly sequence is calculated as follows:
where errors include
- : Task-specific error for each component , for misalignment and torque misapplication.
- Operator errors for task .
- : Error from tool or equipment variability for task .
- Error due to environmental influences (e.g., temperature, humidity) for task .
- Error due to component quality variations for task .
- : Penalty for violating precedence constraints for task .
Where weighting factors include
- : Weight for task-specific errors.
- : Weight for operator errors.
- : Weight for tool/equipment variability errors.
- : Weight for environmental errors.
- : Weight for component quality errors.
- : Weight for precedence violations.
For error minimization, we introduced a Mixed-Integer Linear Programming (MILP) model to formally define the gearbox assembly error minimization problem. The MILP formulation ensures optimal allocation of assembly configurations while minimizing misalignment and component errors. MILP formulation is presented as follows:
where
- and are the indices of the decision variables.refers to the assembly operations or steps involved in the task process.represents the components or parts involved in the part number assembly.
- represents the cost or weight associated with selecting assembly, task , and part .
This includes error costs incurred by specific assembly choices.
- is a binary decision variable:= 1 if assembly task is assigned to part , and = 0 otherwise.
Regarding the problem involving error minimization, represent the error cost or the deviation from the desired precision when assembling part at step . Minimizing this cost would help to reduce assembly errors, such as misalignments or tolerance violations. The total error equation integrates multiple error sources to optimize the assembly sequence comprehensively. This approach is especially critical for a gearbox that consists of complex interdependent components. Each part in the gearbox has specific requirements for precise alignment, torque application, and sequence order to ensure that the gearbox operates effectively under high loads. The equation captures task-specific errors, such as alignment and torque issues, alongside general factors like operator error and environmental influences, which can affect the quality and longevity of the assembly. By assigning penalties for precedence violations and weighting different error types, the total error model aids in designing an optimal sequence that minimizes the risk of functional failures in the gearbox, ultimately improving the system’s reliability and performance. If SUN-G1 is assembled before RING-G1, a penalty is incurred for violating the precedence constraint, leading to an increase in the total error score. The same holds for any other sequence violations, such as attempting to install the ISS-A before the planetary gear system is complete. The PSBFO algorithm will use this error model to optimize the assembly sequence, reducing both task-specific errors and errors caused by precedence violations.
While this study focuses on the assembly of wind turbine gearboxes, the potential applicability of the PSBFO algorithm to other industries, such as automotive and aerospace, remains a hypothesis. These sectors share similar challenges in precision assembly and error minimization, making PSBFO a promising candidate for future exploration. However, further empirical validation, including industry-specific simulations and case studies, is necessary to confirm its effectiveness in these contexts.
3.2. Error Modeling, Weighting, and Optimization Strategies
To assign error weights, we employed a multi-faceted approach that combines expert judgment, historical data analysis, and iterative calibration, ensuring that the weights accurately represent the impact of each error source. This method is supported by well-established practices in multi-criteria decision making, where expert input and historical data are crucial in determining the relative importance of each factor [42]. Expert consultation with experienced assembly engineers to gauge the impact of each error source on assembly outcomes is critical. Such expert judgment is commonly used in complex decision-making models to capture domain-specific insights [43]. We analyzed historical data from previous assembly processes to identify error frequencies and their effects on performance, a practice validated in prior studies [44].
We then normalized and calibrated the weights to ensure consistency and accuracy in the model. This approach aligns with best optimization practices, where normalization and iterative calibration are used to adjust weights until model results align with empirical observations [45]. The final weight assignment follows a weighted sum approach, commonly applied in error minimization studies to reflect the relative significance of each error source [46]. The weights in the error model were derived from expert consultations and historical assembly error data. While these assignments provide a solid theoretical foundation, the real-world validation of these weights will be necessary to refine the model’s applicability in industrial settings. This study used simulated data to demonstrate the model’s potential, and real-world validation was planned for subsequent phases of this research. These methodologies collectively ensure that the assigned weights accurately represent the model’s objective to minimize errors in assembly processes and enhance reliability. Based on this method, the following weights were used in the computation for Formula (1):
- = 0.4 (task-specific errors, the highest due to its critical impact on alignment and torque requirements). Affect the performance and severe impact on functionality, leading to costly rework.
- = 0.2 (operator errors, as human error is significant in manual assembly tasks). Less common, but still impacts the overall quality.
- = 0.15 (tool/equipment variability, affecting precision but to a lesser degree than task-specific errors).
- = 0.1 (environmental errors, impacting the process indirectly). Minor effect on the process overall.
- = 0.1 (component quality errors, moderately significant in affecting the final assembly).
- = 0.05 (precedence violation penalty, as a deterrent to ensure correct assembly sequence).
Error likelihoods represent the probability of an error occurring due to component task-specific errors. Table 1 tabulates the component error likelihoods and dependencies. Components with higher complexity and critical dependencies were assigned higher likelihoods. To mathematically formulate these dependencies and error likelihoods, we define the following:

Table 1.
Component error likelihoods and dependencies.
- Error likelihood function: Let represent the likelihood of an error occurring between components and . This likelihood was influenced by the dependency type of task-specific errors. This value is expressed as a percentage and is derived empirically from historical data and expert judgment, with higher values assigned to more complex and error-prone components, such as the low-speed shaft.
- Dependency penalty function: Each dependency between two components and was assigned a penalty based on the likelihood of an error occurring due to incorrect sequencing.
- Total error calculation: The total error for the assembly sequence was computed by summing the individual error penalties for each dependent component pair.
Where
- is the error likelihood between component and component , expressed as a percentage.
- is the dependency type between components and .
The error penalty for each component pair is calculated as follows:
where
- is a weight assigned based on the dependency type:
The total error across all dependencies is as follows:
Using this approach, we can calculate for each pair and sum them to obtain , which was used by the PSBFO algorithm to prioritize assembly sequences that minimize these penalties.
3.3. Particle Swarm-Bacteria Foraging Optimization (PSBFO)
PSBFO is a hybrid optimization algorithm that combines the global exploration capabilities of PSO with the local refinement capabilities of BFO. The methodology developed for PSBFO is shown in Figure 3. This hybrid approach is particularly useful in minimizing assembly errors, as it allows for both a broad exploration of potential assembly sequences and a fine-tuned optimization of promising sequences. The key steps in the PSBFO algorithm are as follows:

Figure 3.
PSBFO algorithm methodology for the generic 10 MW wind turbine gearbox.
The PSO component enabled the algorithm to explore various task sequences, while the BFO component refined these sequences by focusing on local error reduction. PSO velocity update formula with a time-varying inertia weight to manage the balance between exploration and exploitation is shown below [1]:
where
vi(t+1) = ω(t)·vi(t) + c1·r1·(pi − xi(t)) + c2·r2·(pg − xi(t))
ω(t) is the time-varying inertia weight that impacts how much the previous velocity influences the new velocity. It generally decreases with each iteration, which helps reduce the particles’ “momentum” as the search space is more thoroughly explored, allowing finer adjustments as the global optimum approaches.
vi(t) represents the velocity of particle i at time t.
c1 and c2 represent the cognitive and social scaling coefficients. These parameters control the influence of pi (personal best position) and pg (global best position) on the velocity update.
r1 and r2 provide stochasticity to the search, representing random numbers between 0 and 1 and helping to escape local minima by providing a random exploration component.
pi represents particle i personal best.
pg represents the global best position.
xi(t) represents the current position of particle i at time t.
The position update formula is expressed as follows:
xi(t+1) = xi(t) + vi(t+1)
The BFO formula enhances the traditional bacterial foraging optimization’s capability to tackle complex optimization tasks expressed in the following formula [1]:
where
xi(t+1) = xi(t) + α(t)·C(i) Δ(i)
α(t) represents an adaptive factor for the step size (i) based on the iteration t and the current area of the search space.
xi(t) represents the position of bacterium i at time t.
C(i) represents the random direction size of the step.
Δ(i) random direction vector unit length.
This integrates BFO’s chemotaxis behavior into the PSO position update. This formula adds a BFO-inspired random perturbation to the standard PSO position update, enhancing the ability to escape local optima; the combination forms PSBFO [5].
xi(t+1) = xi(t) + vi(t+1) + α(t)·C(i) Δ(i)
3.4. Python Implementation of PSBFO
The PSBFO algorithm was implemented in Python 3.12 to achieve error minimization during the wind turbine gearbox assembly. The algorithm integrates PSO, which handles the global exploration of possible assembly sequences, and BFO, which performs local refinement to minimize errors associated with each task. The implementation begins by initializing particles, each of which represents a potential solution in the form of a task sequence for assembling the gearbox. These particles were randomly generated at the start of the process, with each particle containing a complete sequence of tasks. The algorithm assigned each particle a velocity, which influenced how the particle moves or changes its sequence during the optimization process. Once the particles were initialized, the PSO update took place. This phase involves exploring the search space by adjusting each particle’s sequence based on its own personal best and the best-known solution across all particles (global best). The particles’ velocities were updated by taking into account their current velocity, how far they are from their personal best, and how far they are from the global best. These adjustments allow the particles to explore a wide range of possible task sequences, thereby improving the chance of finding an optimal or near-optimal solution.
Following the PSO update, the algorithm evaluated the performance of each particle’s sequence. This involves calculating the error score for the assembly sequence by considering two primary factors: task-specific error likelihoods and penalties for violating precedence constraints. The error score for each sequence provided feedback to the optimization process, helping the algorithm prioritize sequences with lower error rates. The next phase of the PSBFO implementation is the BFO update, which focuses on refining the assembly sequence at a local level. During this step, the algorithm simulated the behavior of bacteria seeking nutrients by performing a local search. This involves making small changes to the sequence, such as swapping the order of two tasks, to see if the change reduces the overall error. If the modification leads to a reduction in errors, the sequence is updated, and the particle is considered to have improved. This process of alternating between global exploration (via PSO) and local refinement (via BFO) continues iteratively for a predetermined number of iterations or until the error minimization converges to an acceptable level. For the iterations, the algorithm dynamically improves the task sequences, continuously seeking to reduce errors related to both task execution and precedence violations.
4. Results and Analysis
4.1. Error Reduction Performance
The optimization process conducted using the PSBFO algorithm effectively minimized the total assembly errors during the wind turbine gearbox assembly. At the start of the process, the task sequences were randomly generated, leading to high error values due to misalignment or torque and violations of precedence constraints. The initial position of the particle in the solution space was at a task sequence position of 100 (X-axis), with a high error value of 50 (Z-axis). This represents the particle’s starting point, where the task sequence was completely un-optimized, resulting in a high likelihood of assembly errors. Throughout 20 iterations (Y-axis), the PSBFO algorithm refined the task sequence, continuously improving the particle’s position in the optimization space. Table 2 shows component-wise error reduction data across iterations with the final total error of 5. The particle’s movement from the initial position to the final position is depicted as a trajectory in Figure 4, showing how it explored various task sequences while reducing the associated error values. The algorithm’s global search (via PSO) and local refinement (via BFO) effectively reduced errors with each iteration, gradually bringing the particle closer to an optimal solution. Conforming to precedence constraints alone does not guarantee that an assembly operation is error-free. The pseudocode below highlights how the total error was calculated.

Table 2.
Component-wise error reduction data across iterations (final total error = 5).

Figure 4.
Error reduction.
Pseudocode for total error calculation procedure
Input:
- error_likelihoods for each component (alignment, operator, tool_variability, environmental, component_quality)
- num_violations: Number of precedence violations for the component
Weights:
- Define weights for each error type:W_alignmentW_operatorW_tool_variabilityW_environmentalW_component_qualityW_precedence_violation
Output:
- total_error: Total error for each component
- 1.
- Initialize Weights:Define weights for alignment, operator, tool_variability, environmental, component_quality, and precedence_violation.
- 2.
- Define Function [Calculate_Total_Error(error_likelihoods, num_violations)**:Inputs:
- ▪
- error_likelihoods: Error probabilities for alignment, operator, tool_variability, environmental, and component_quality.
- ▪
- num_violations: Integer representing the number of precedence violations.
- 3.
- Calculate Task-Specific Error:[Set] task_specific_error as the sum of:
- ▪
- error_likelihoods[‘alignment’] * W_alignment
- ▪
- error_likelihoods[‘operator’] * W_operator
- ▪
- error_likelihoods[‘tool_variability’] * W_tool_variability
- ▪
- error_likelihoods[‘environmental’] * W_environmental
- ▪
- error_likelihoods[‘component_quality’] * W_component_quality
- 4.
- Calculate Precedence Violation Penalty:Set precedence_penalty as:
- ▪
- num_violations * W_precedence_violation
- 5.
- Compute Total Error:total_error = task_specific_error + precedence_penalty
- 6.
- Return Total Error:Return total_error
4.2. Component Error Likelihoods and Dependencies
The error likelihood values assigned to each component pair, as well as sequential dependencies, are derived based on historical data and common assembly challenges faced in complex mechanical systems. Studies on the reliability and structural optimization of wind turbine gearboxes highlight the critical impact of precise alignment and torque control on operational performance and reliability. Accurate assembly and alignment are essential for ensuring the long-term durability of gearboxes in wind turbine applications, as misalignments can significantly compromise efficiency and lead to premature failures [20]. By leveraging these insights, our study assigns higher error likelihoods to components requiring intricate alignment and torque precision, reflecting their susceptibility to errors during assembly.
Assigning appropriate weight operator errors, tool variability, and environmental influences ensures that the model accurately reflects the relative significance of each factor in the assembly process. We determined these weights through a multi-faceted approach, combining expert judgment and historical data analysis, which aligns with established practices in multi-criteria decision making (MCDM). MCDM techniques provide a robust framework for assigning importance to various decision factors, especially in complex engineering contexts where different types of errors can have varying impacts on overall system reliability [42]. By following this approach, we have weighted alignment and torque-related errors more heavily, as these are known to have the most significant effect on assembly precision and performance, particularly in wind turbine gearbox applications.
Environmental factors and component quality variations can also influence error likelihood in mechanical assemblies. Temperature and humidity can affect material properties and assembly precision, impacting the performance of renewable energy systems [31]. These insights justify the inclusion of environmental error factors in our model, albeit with a lower weight due to their indirect impact compared to alignment and torque errors. Furthermore, component quality issues, such as manufacturing tolerances, contribute to error likelihood. These factors were considered and validated through expert input, ensuring that the model accounts for realistic assembly challenges that could compromise the reliability of the final assembly.
The structural reliability of the gearbox assembly, particularly the critical role of maintaining precise alignment and torque, has been emphasized in multiple studies. Error minimization in assembly design, especially through small displacement torsor tolerance mapping, is crucial for high-precision applications [2]. This approach to error minimization informed our model’s structure, enabling us to prioritize task sequences that reduce alignment and torque misapplication errors. By integrating principles from structural reliability studies into the PSBFO framework, we ensure that the assembly process adheres to strict quality and reliability standards, suitable for demanding applications like wind turbine gearboxes. Table 1 provides a detailed view of the progressive error reduction achieved through the PSBFO model, aligning closely with the analysis presented in this paper. Initial error values are highest for complex, error-prone components like LSS-A, LSS-B, LSS-C, PL-G1, and HSS-A, reflecting the model’s focus on mitigating errors in areas critical to alignment and torque accuracy. Through successive iterations, the PSBFO algorithm effectively reduces errors by combining PSO’s global search with BFO’s local refinement, enabling both broad exploration and focused error minimization. This iterative approach is evident in the declining error values, demonstrating the model’s capacity to handle error-prone components first and achieve reliable assembly quality.
While adherence to precedence constraints ensures that the assembly follows the correct order and avoids penalties associated with assembling components in the wrong sequence, other types of errors can still occur even when these constraints are met. Each assembly task presents inherent challenges that can lead to errors, such as misalignment, incorrect torque application, or precision issues, regardless of sequence adherence. These task-specific errors are tied to the nature of the individual tasks and the precise requirements for correctly assembling each component. For example, aligning shafts or applying the correct torque is crucial for ensuring functionality, yet these actions can still be prone to errors even if the assembly order is correct. Thus, meeting precedence constraints is necessary but not sufficient to ensure a completely error-free assembly. By the final iteration, the particle reached its optimal position, which had the following coordinates:
X (task sequence position): 10.
Y (iteration number): 19.
Z (total error value): 5.
These coordinates represent the best task sequence discovered by the PSBFO algorithm. The particle’s task sequence position had improved from 50 to 10, indicating a much more refined sequence that adheres to all precedence constraints and error sources such as operator, tool, and environmental factors. At this optimal position, the total error was minimized to 5, a significant reduction from the initial error of 50. The particle achieved this optimal solution at iteration 19, reflecting the completion of the algorithm’s iterative process. The results demonstrate the success of the PSBFO algorithm in optimizing the assembly sequence for the wind turbine gearbox. The algorithm started with a random, high-error task sequence and, through multiple iterations, reduced errors to a minimum. The optimal position with coordinates (X: 10, Y: 19, Z: 5) represents the most efficient task sequence with minimal assembly errors, showing the algorithm’s effectiveness in improving the reliability and precision of the assembly process.
4.3. Optimized Parallel Assembly Sequence Planning (PASP)
The PASP for the wind turbine gearbox assembly leverages parallel assembly lines with carefully structured dependencies to enhance efficiency and reduce assembly time. This approach ensures that components are assembled in the correct order while maximizing parallelism, allowing independent tasks to proceed simultaneously across different lines. Each assembly line is organized in horizontal sequences, with precedence constraints managed between lines, facilitating a clear and structured assembly flow. The wind turbine gearbox assembly process includes 26 components as shown from the simulation results shown in Figure 5, each with specific dependencies and assembly requirements. The PASP approach organizes these components across seven distinct lines, each representing a different stage in the assembly process. Components within each line are assembled simultaneously where possible, while dependencies are strictly enforced across lines to maintain structural and functional integrity. This structure minimizes the total assembly time while addressing error sources and ensuring compliance with precedence constraints.

Figure 5.
Optimized parallel assembly sequence simulation results.
4.4. Optimization Model for PASP
The PASP model involves two primary constraints: precedence constraints and parallel assembly constraints.
- 1.
- Precedence constraints:
Each component must be assembled only after its required preceding components are in place. Let represent the task (or component) and let denote the set of all preceding tasks that must be completed before .
This constraint enforces that each task can only begin once all tasks in its preceding set are completed.
- 2.
- Parallel assembly constraints:
The assembly is split across multiple lines, and tasks on each line can proceed in parallel as long as they meet the precedence constraints. Let represent line , and the tasks assigned to line . If two tasks and can be assembled in parallel (i.e., they are independent), then
where and belong to the same line and do not depend on each other.
- 3.
- Error penalty for precedence violations:
If a task is performed before a preceding task (where ), a penalty is incurred. The penalty function can be defined as follows:
- 4.
- Each solution is represented as a vector of assembly sequences and corresponding component alignment parameters:where , denotes the assembly sequence of component , and represents the alignment adjustment for component . The fitness function evaluates the cumulative assembly error based on these parameters.
Assembly Lines and Dependencies in PASP
- Line 1: This line initiates the assembly process with the foundational component RING-G1. As the base element of the gearbox, RING-G1 provides structural support for the subsequent components and establishes the alignment for the entire assembly.
- Line 2: Building upon RING-G1, Line 2 includes the central and planetary gears:
- SUN-G1: The central sun gear depends directly on RING-G1 for positioning.
- PL-G1, PL-G2, and PL-G3: Three planetary gears that depend on SUN-G1 for alignment. These gears distribute torque from the sun gear to the planetary carriers, establishing the gearbox’s core rotational mechanics.
- Line 3: This line focuses on assembling the subcomponents of each planetary gear, ensuring that each planetary gear is complete before moving to the next stage:
- PL-G1-A and PL-G1-B: Subcomponents of PL-G1.
- PL-G2-A and PL-G2-B: Subcomponents of PL-G2.
- PL-G3-A and PL-G3-B: Subcomponents of PL-G3.
- Each subcomponent is assembled after its respective planetary gear, forming a robust planetary system that supports torque distribution.
- Line 4: This line assembles the planetary carriers, which are critical for holding the planetary gears in place:
- PLC-A and PLC-B: Planet carriers, which depend on the full assembly of PL-G1, PL-G2, PL-G3, and their subcomponents. These carriers provide structural stability, ensuring that planetary gears are securely housed for optimal gear meshing and rotation.
- Line 5: This line assembles the low-speed shaft (LSS) components, which transmit power from the planetary gears to the intermediate-speed shaft:
- LSS-A: Begins the low-speed shaft assembly, depending on the completion of PLC-B.
- LSS-B and LSS-C: Sequentially assembled following LSS-A.
- LSS-G1: A gear component that completes the low-speed shaft, ensuring proper power transfer alignment.
- Line 6: Components of the intermediate-speed shaft (ISS) are assembled in this line, connecting the low-speed shaft to the high-speed shaft:
- ISS-A: Begins the intermediate-speed shaft assembly, dependent on LSS-G1.
- ISS-B and ISS-C: Sequentially assembled after ISS-A.
- ISS-G1 and ISS-P1: Additional components on the intermediate-speed shaft that ensure stability and alignment for high-speed transfer.
- Line 7: The final assembly line, which completes the gearbox with components of the high-speed shaft (HSS):
- HSS-A: Begins the high-speed shaft assembly, dependent on ISS-P1.
- HSS-B and HSS-C: Assembled in sequence after HSS-A.
- HSS-P1: The final component of the high-speed shaft, concluding the gearbox assembly.
4.5. Precedence Management and Error Minimization in PASP
The PASP approach not only optimizes assembly time by leveraging parallelism but also incorporates error minimization strategies that address potential sources of misalignment, torque misapplication, operator error, environmental influences, and component quality variations. Each component’s precedence constraints are carefully managed, ensuring that components are only assembled once their dependencies are complete. This structure prevents assembly errors caused by sequence violations and enhances the overall reliability of the gearbox. By applying a comprehensive error model that accounts for task-specific, operator, and tool errors, PASP actively refines the assembly sequence to reduce the total error score iteratively. Components are assigned penalties when assembled out of sequence, guiding the optimization process toward an error-minimized, efficient sequence.
4.6. Comparison with Traditional Methods
When compared to traditional sequential assembly methods, the PSBFO approach demonstrates a significant improvement in minimizing assembly errors. In particular, the PSBFO algorithm achieved a 38% reduction in total assembly errors, which highlights its superiority over conventional techniques. This notable improvement can be attributed to the unique way the PSBFO algorithm handles task-specific errors and precedence constraints simultaneously, something that traditional methods often fail to address effectively. In traditional sequential assembly methods, the tasks are usually executed in a predefined order without a sufficient consideration of error sources such as misalignments, incorrect torque application, or precedence violations. These methods often assume a linear task execution flow, where each task is performed after the previous one, leading to suboptimal assembly sequences. While these methods may be simpler to implement, they are prone to errors due to the rigid structure and the inability to adapt to real-time conditions. Genetic Algorithms (GAs), like PSBFO, are effective for global search but may not always handle task-specific errors or precedence constraints as efficiently as hybrid algorithms like PSBFO. Table 3 and Figure 6 show comparisons in error reduction with other methods.

Table 3.
Error reduction comparison with other methods.

Figure 6.
Comparison in error reduction with other methods.
The 38% reduction in assembly errors achieved by the PSBFO algorithm can be attributed to its combination of global exploration and local refinement. By integrating PSO for broad task sequence exploration and BFO for local error refinement, the algorithm identifies promising sequences and fine-tunes them to reduce common assembly errors like misalignment. Additionally, the PSBFO algorithm explicitly handles precedence constraints, ensuring that tasks are executed in the correct order to prevent mechanical errors. This approach contrasts with traditional methods, which may overlook such constraints, leading to increased errors and rework.
Another key factor contributing to the error reduction is PSBFO’s use of real-time error feedback. As the algorithm evaluates each task sequence, it calculates total errors, including penalties for precedence violations and task-specific error likelihoods. This feedback enables continuous refinement of the assembly sequence, reducing errors from an initial high of 50 down to 5. The algorithm also accounts for task-specific complexities, such as the precision required for components like the low-speed and high-speed shafts, allowing for more effective error minimization compared to traditional methods that apply uniform rules across all tasks. A parameter tuning study is conducted using the Taguchi method:
- Inertia weight (w): 0.4–0.9.
- Cognitive coefficient (c1): 1.5–2.5.
- Social coefficient (c2): 1.5–2.5.
- Chemotaxis steps (BFO): 5–10.
- Reproduction steps (BFO): 2–5.
The best parameters are selected based on performance. The simulation results in Table 4 show a significant reduction in defect rates, downtime, and assembly time, alongside an increase in production yield. These improvements highlight the PSBFO model’s potential to optimize assembly processes by reducing inefficiencies and enhancing overall productivity.

Table 4.
Defect rates, downtime, assembly time, and production yields.
Several studies have benchmarked optimization techniques for assembly sequence planning, including PSO and the GA [47]. These methods are effective for global search but often fail to address task-specific errors. In contrast, hybrid techniques like PSO-BFO have demonstrated improved error minimization [5]. While existing research has focused on time optimization and robustness in static environments, few studies have investigated multi-objective optimization in the context of assembly errors. Our approach, which combines PSO and BFO, significantly outperforms standard methods by integrating error minimization alongside sequence optimization. PSBFO also demonstrates faster convergence, with fewer iterations required to achieve optimal results compared to other methods. The PSBFO model outperforms the GA and PSO in key metrics as shown in Table 5, error reduction, computational efficiency, and stability

Table 5.
Comparison of PSBFO with other optimization methods.
The scalability tests indicate that the PSBFO model can handle larger assembly systems effectively. As the assembly size increases, the model continues to demonstrate improved error reduction, although computational time also increases. These results in Table 6 suggest that PSBFO can be adapted to various scales of production, making it suitable for a wide range of industrial applications.

Table 6.
Scalability testing results.
Adaptive tuning significantly improves the performance of PSBFO for larger assembly systems as shown in Table 7. With tuning, the computational time is reduced, and the error reduction improves by an additional 5%, making the model more efficient as the system size scales.

Table 7.
Adaptive tuning for large assemblies.
4.7. Error Distribution Across Components
The error distribution across the different components of the gearbox was analyzed based on the likelihood of errors such as misalignment and incorrect torque application. In particular, the low-speed shaft (LSS) components and the planetary gear system (PL-G1, PL-G2, PL-G3) were identified as the most error-prone areas. These components involve intricate assembly processes, where misalignments or torque misapplications can lead to significant operational issues. The LSS-A, LSS-B, and LSS-C components, which form part of the low-speed shaft assembly, are especially susceptible to errors due to the complexity of their installation and the high precision required for proper alignment. Similarly, the planetary gear system must be carefully aligned with the sun gear and other components, making it prone to errors during the assembly process. These critical components account for the majority of the total errors observed in the initial task sequences.
By employing the PSBFO approach to optimize the assembly sequence, the algorithm focused on reducing the errors associated with these components. The real-time feedback mechanism in PSBFO played a key role in ensuring that any precedence violations or misalignments were corrected early in the assembly process, resulting in a significant reduction in overall errors. For instance, the error likelihood for the LSS-C component was initially high due to the complexity of the task, but, by optimizing the task sequence and adhering to precedence constraints, the algorithm was able to minimize these errors over several iterations. The distribution of errors across the components was reduced from an initial total of 50 down to 5 by the final iteration, demonstrating the effectiveness of task-specific error minimization and precedence handling in the overall assembly process. The results indicate that focusing on the most error-prone components during the optimization process can lead to substantial improvements in assembly reliability and performance. The component-wise error evolution graph provides detailed insights into how each gearbox component behaves during the optimization process as shown in Figure 7. Components with initially higher errors, such as LSS-A or PL-G1, tend to show a steeper reduction in error as the PSBFO algorithm prioritizes them for more aggressive minimization. This targeted error reduction highlights the algorithm’s ability to efficiently focus on the most problematic components early in the optimization process, leading to significant improvements in their performance.

Figure 7.
Component-wise error evolution over iterations.
As the optimization progresses, the error reduction for most components converges toward minimal values, showcasing the robustness of the PSBFO algorithm. This convergence across iterations demonstrates the algorithm’s capability to handle complex systems with multiple error-prone components, ensuring that all components reach an optimal error level. The overall effectiveness of the algorithm is evident in its ability to reduce errors across diverse components, irrespective of their initial error levels, ensuring consistent performance improvement. The low-speed shaft and planetary gear system showed the most substantial reductions in error, while smaller components with less initial error maintained low error percentages throughout the process. The optimization helped ensure that the assembly process adhered to precedence constraints while reducing mechanical faults, misalignments, and rework, leading to a more reliable and efficient assembly. Figure 8 shows the error distribution across components after optimization.

Figure 8.
Error distribution across components after optimization.
The box plot effectively illustrates the impact of the PSBFO algorithm on the distribution of errors across gearbox components before and after optimization as shown in Figure 9. Before optimization, the box plot shows a wide spread of error values, indicating significant variability and the presence of outliers’ components with disproportionately high errors. After optimization, the box plot becomes narrower, reflecting reduced variability, with the median error significantly lower. The shorter whiskers and fewer outliers demonstrate the algorithm’s success in uniformly minimizing errors across all components, leading to a more consistent and reliable assembly process. This visual highlights the PSBFO algorithm’s ability to reduce not only the overall error but also the extremes in error distribution.

Figure 9.
Box plot distribution before and after PSBFO. The orange horizental line: It is the median value of the final errors data set. It shows the 50th percentile of the data.
4.8. Robustness of the PSBFO Algorithm
The robustness of the PSBFO algorithm was evaluated by running the optimization process under varying initialization parameters and task-specific error likelihoods across all gearbox components. This was conducted to assess the algorithm’s performance under different error conditions and to compare it against traditional methods of assembly sequence optimization, as shown in Figure 10. The results consistently showed that the PSBFO algorithm outperformed traditional methods, demonstrating its reliability in reducing errors across various scenarios. Even when the error likelihoods and initial positions of the particles were altered, the algorithm successfully converged to optimal solutions with minimal errors. The adaptability of PSBFO to different error scenarios, combined with its efficient handling of precedence constraints, makes it a robust solution for minimizing assembly errors in complex systems like wind turbine gearboxes.

Figure 10.
Robustness of the PSBFO algorithm for error reduction across five trials.
4.9. Task Dependency Error Propagation: Heat Map Analysis for Gearbox Components
The error heat map for task dependencies provides a visual representation of how errors in one component of the gearbox assembly influence or propagate to other components, as shown in Figure 11. Each row and column in the matrix correspond to a specific component, and the color of each cell indicates the level of dependency between two tasks. Darker colors represent stronger error dependencies, while lighter colors indicate weaker relationships between tasks. This means that, if one component has an error, it is more likely to affect other components with which it has a stronger dependency. In a gearbox system, SUN-G1 and PL-G1 components are closely linked due to the mechanical and sequential relationship between these tasks. The heat map shows these dependencies, indicating that errors in SUN-G1 could propagate to PL-G1 if the assembly of the sun gear is incorrect. Conversely, components that are further apart in the assembly sequence or less mechanically linked may have lighter-colored cells between them, suggesting less error propagation. HSS-A and ISS-P1 may exhibit weaker dependencies because they are part of different subsystems, meaning that errors in one component are unlikely to impact the other.

Figure 11.
Error heat map for task dependencies.
The heat map also highlights critical tasks with strong dependencies on multiple other components. These tasks are visually identifiable by the darker rows or columns, signaling that reducing errors in these components is particularly important for minimizing overall system errors. If the LSS-A (low-speed shaft) has high dependencies on PLC-A and PL-G1, this suggests that optimizing or improving the assembly accuracy of PLC-A will have a cascading effect on reducing errors in dependent components like LSS-A. By focusing on these critical tasks, the PSBFO algorithm can more effectively optimize the entire assembly process, ensuring better overall system reliability. The most critical interdependent task pairs are those with the highest numeric value. Table 8 summarizes the top interdependencies.

Table 8.
Summary of top interdependencies.
4.10. Limitations and Potential Biases
While the PSBFO algorithm has demonstrated significant improvements in minimizing assembly errors for wind turbine gearboxes, several limitations must be acknowledged. First, the effectiveness of the algorithm is highly dependent on the accuracy and quality of input data, including error rates, task sequencing dependencies, and real-time feedback mechanisms. Any inconsistencies in these data sources may reduce optimization performance. Additionally, the algorithm assumes a relatively stable assembly environment where variations in component tolerances, operator skill levels, and external disturbances remain within predictable bounds. In highly dynamic or unpredictable conditions such as environments with extreme variability in component specifications or sudden disruptions in workflow, PSBFO’s performance may be less reliable. Another critical limitation is the algorithm’s scalability in more complex assembly scenarios. The model’s performance in much larger assemblies with higher precedence constraints has not been fully explored. As the assembly size grows, the computational time increases considerably, potentially affecting real-time applications. Furthermore, while convergence rates were favorable in controlled simulations, real-world environments may introduce unforeseen complexities that could slow convergence or impact stability. The algorithm’s ability to adapt to changing conditions, such as fluctuating production loads or unexpected component defects, remains uncertain and requires further investigation.
Moreover, while PSBFO is theoretically applicable to other industries, such as automotive and aerospace, its success in these domains has yet to be empirically validated. Differences in assembly complexity, regulatory requirements, and process constraints may impact its adaptability. Future research should explore these sector-specific challenges through tailored simulations and real-world case studies. Lastly, potential biases in the experimental setup must be considered. The optimization parameters and evaluation criteria were selected based on industry best practices for wind turbine assembly, which may not generalize universally. Additional testing across different assembly settings and industry benchmarks will be necessary to refine the model further and assess its broader applicability. Addressing these limitations will be essential in ensuring the robustness and scalability of PSBFO for real-world implementation.
4.11. Scalability, Industrial Integration, and Managerial Implications
The scalability of the PSBFO algorithm has been demonstrated through simulation results showing consistent reductions in error rates and reasonable convergence times. However, for more complex industrial scenarios involving nonlinear constraints or dynamic environments, such as those in flexible manufacturing systems (FMSs), further enhancements may be needed. These may include dynamic parameter tuning, modular task decomposition, or hybrid integration with reinforcement learning for real-time decision making. PSBFO’s hybrid nature lends itself well to scalable parallelization across multiple assembly lines, which is crucial in handling large-scale, interdependent task networks with stringent precedence rules.
In terms of industrial integration, the PSBFO framework can be interfaced with modern manufacturing execution systems (MESs) through middleware that bridges optimization outputs with production scheduling tools. Real-time error feedback modules can be supported via Industrial Internet of Things (IIoT) platforms, where sensors continuously monitor torque, alignment, and sequencing deviations, feeding live data into the optimization loop. Control-level integration with programmable logic controllers (PLCs) or SCADA systems could allow PSBFO to suggest or even auto-adjust assembly task sequences on the factory floor. These implementation pathways require collaborative testing with industrial partners and could form the basis for pilot deployments in smart manufacturing environments, particularly in wind, aerospace, or automotive sectors. The following are managerial insights from this research:
- Critical component identification: PLC-A affects LSS-A errors the most; therefore, there is a need to prioritize PLC-A precision.
- Structured assembly adjustments: PSBFO’s error trend allows structured intervention in assembly processes.
- Industry adaptability: The approach can be extended to automotive and aerospace assembly error reduction.
5. Conclusions
This study effectively addresses the critical challenge of reducing errors in the assembly of wind turbine gearboxes by introducing a robust framework grounded in the Particle Swarm-Bacteria Foraging Optimization (PSBFO) algorithm. By integrating error-driven task sequencing with real-time feedback mechanisms, this approach significantly enhances assembly reliability, minimizing common issues of misalignment, incorrect torque application, and precedence violations. Empirical results underscore the effectiveness of the PSBFO algorithm, achieving a notable 38% reduction in total assembly errors across various components. The distribution of errors was reduced from an initial count of 50 to just 5 by the final iteration, demonstrating the effectiveness of task-specific error minimization and precedence handling in the overall assembly process.
For industry managers, the PSBFO model provides a practical solution for improving process reliability, reducing rework, and extending the lifespan of critical machinery. By adopting this model, decision-makers can streamline assembly sequences, lower maintenance costs, and enhance product quality benefits particularly relevant in high-stakes industries like renewable energy, where downtime and repair costs have a significant impact on profitability. Insights from supply chain optimizations further underscore the broader advantages of such process improvements, highlighting PSBFO’s potential impact across multiple sectors. The PSBFO algorithm shows promise in optimizing wind turbine gearbox assembly, but its effectiveness is limited by dependencies on high-quality input data, stable assembly conditions, scalability to complex tasks, adaptability to real-world variability, and potential biases in its evaluation setup, all of which require further research and validation across diverse industrial contexts.
Beyond wind turbine gearboxes, this study establishes a foundation for future research on error minimization in diverse assembly processes. The adaptability of the PSBFO framework suggests its applicability to other industries, such as automotive and aerospace, where high precision and reliability are paramount. Future work will explore enhancements for handling extreme variability and integrating advanced optimization techniques to further improve assembly efficiency. As the demand for high reliability in complex mechanical systems continues to grow, this research affirms the potential of hybrid optimization algorithms like PSBFO to transform traditional assembly practices. By embedding error reduction strategies into mechanical assembly processes, this work contributes valuable insights that can drive innovation and efficiency across multiple domains.
Author Contributions
S.M.: writing—original draft, writing—review and editing, software, data curation, methodology; Y.W.: review and editing, methodology, supervision; D.T.: supervision and resource mobilization. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data that support the findings of this study are available from the corresponding authors, S.M. and Y.W., upon reasonable request.
Acknowledgments
This paper is extracted from the author’s doctoral thesis, Sydney Mutale, at North China Electric Power University.
Conflicts of Interest
The authors claim that this paper has not been published or is not under consideration for publication elsewhere. No potential conflicts of interest were reported by the authors.
References
- Mutale, S.; Wang, Y.; Yasir, J.; Aboubacar, T. Advanced Optimization Techniques for PASP: A Comparative Study of Improved PSO and BFO. In Proceedings of the 2024 6th International Conference on Power and Energy Technology (ICPET), Beijing, China, 12–15 July 2024; pp. 867–871. [Google Scholar] [CrossRef]
- Mu, X.; Yuan, B.; Wang, Y.; Sun, W.; Liu, C.; Sun, Q. Novel application of mapping method from small displacement torsor to tolerance: Error optimization design of assembly parts. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2022, 236, 955–967. [Google Scholar] [CrossRef]
- Chen, K.; Henrioud, J.M. Systematic generation of assembly precedence graphs. In Proceedings of the 1994 IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994; pp. 1476–1482. [Google Scholar] [CrossRef]
- Guiza, Q.; Mayr-Dorn, C.; Mayrhofer, M.; Egyed, A.; Rieger, H.; Brandt, F. Assembly Precedence Graph Mining Based on Similar Products. In Proceedings of the 2022 IEEE International Conference on Industrial Technology (ICIT), Shanghai, China, 22–25 August 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Mutale, S.; Wang, Y.; Yasir, J. Enhanced efficiency and quality in wind turbine gearbox assembly: A new parallel assembly sequence planning (PASP) model. Int. J. Sustain. Eng. 2024, 17, 1048–1065. [Google Scholar] [CrossRef]
- Ab Rashid, M.F.F.; Mohamed, N.M.Z.N.; Rose, A.N.M. Multi-objective multi-verse optimiser for integrated two-sided assembly sequence planning and line balancing. J. Comb. Optim. 2022, 44, 850–876. [Google Scholar] [CrossRef]
- Rodriguez-Cabal, M.A.; Botero-Gómez, V.; Sanin-Villa, D. Optimization of Weight Reduction in Power Transmission Systems Using Bio-Inspired Algorithms and Composite Materials. Coatings 2024, 14, 1586. [Google Scholar] [CrossRef]
- Zhai, H.; Zhu, C.; Song, C.; Liu, H.; Bai, H. Influences of carrier assembly errors on the dynamic characteristics for wind turbine gearbox. Mech. Mach. Theory 2016, 103, 138–147. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Huh, E.N.; Welch, L.R. Adaptive resource management for dynamic distributed real-time applications. J. Supercomput. 2006, 38, 127–142. [Google Scholar] [CrossRef]
- Zhan, Z.H.; Zhang, J. Adaptive Particle Swarm Optimization. Lect. Notes Comput. Sci. 2008, 5217, 227–234. [Google Scholar] [CrossRef]
- Mukred, J.; Muslim, M.; Selamat, H. Optimizing Assembly Sequence Time Using Particle Swarm Optimization (PSO). Appl. Mech. Mater. 2013, 315, 88–92. [Google Scholar] [CrossRef]
- Xiangyu, Z.; Liu, L.; Wan, X.; Wang, K.; Huang, Q. Assembly Sequence Optimization Based on Improved PSO Algorithm. In Advanced Manufacturing and Automation IX 9th; Springer: Singapore, 2019; pp. 457–465. [Google Scholar] [CrossRef]
- Ye, F.-L.; Lee, C.-Y.; Lee, Z.-J.; Huang, J.-Q.; Tu, J.-F. Incorporating Particle Swarm Optimization into Improved Bacterial Foraging Optimization Algorithm Applied to Classify Imbalanced Data. Symmetry 2020, 12, 229. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R.C. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings. IEEE World Congress on Computational Intelligence, Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar] [CrossRef]
- Passino, K.M. Biomimicry of bacterial foraging for distributed optimization and control. IEEE Control Syst. Mag. 2002, 22, 52–67. [Google Scholar] [CrossRef]
- Wang, L.; Tian, D.; Gou, X. Hybrid particle swarm optimization with adaptive learning strategy. Soft Comput. 2024, 28, 9759–9784. [Google Scholar] [CrossRef]
- Lee, G.; Kim, H.; Lee, S.B.; Kim, D.; Lee, E.; Lee, S.K.; Lee, S.G. Tailored Uniaxial Alignment of Nanowires Based on Off-Center Spin-Coating for Flexible and Transparent Field-Effect Transistors. Nanomaterials 2022, 12, 1116. [Google Scholar] [CrossRef] [PubMed]
- Zhu, D.; Li, R.; Zheng, Y. Cumulative Major Advances in Particle Swarm Optimization from 2018 to the Present: Variants, Analysis and Applications. Arch. Comput. Methods Eng. 2025, 32, 1571–1595. [Google Scholar] [CrossRef]
- Mandol, S.; Bhattacharjee, D.; Dan, P.K. Structural Optimisation of Wind Turbine Gearbox Deployed in Non-conventional Energy Generation. Smart Innov. Syst. Technol. 2017, 65, 835–848. [Google Scholar] [CrossRef]
- Min, Z.; Zhijing, Z.; Lingling, S.; Weimin, Z. Assembly Error Modeling and Calculating Method of Precision Mechanical System. J. Phys. Conf. Ser. 2019, 1345, 022051. [Google Scholar] [CrossRef]
- Mutale, S.; Wang, X. Levels of Automation in Quality Sampling and Analysis of Copper. Ind. Eng. Lett. 2014, 4, 89–102. [Google Scholar]
- Ni, J.; Tang, W.C.; Xing, Y. Performance of reducing the dimensional error of an assembly by the rivet upsetting direction optimization. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2016, 231, 2133–2144. [Google Scholar] [CrossRef]
- Dao, C.; Kazemtabrizi, B.; Crabtree, C. Wind turbine reliability data review and impacts on levelised cost of energy. Wind Energy 2019, 22, 1848–1871. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, M.; Shu, L.; Li, S.; Liu, Z. A Novel Parallel Assembly Sequence Planning Method for Complex Products Based on PSOBC. Math. Probl. Eng. 2020, 2020, 7848329. [Google Scholar] [CrossRef]
- Pan, H.; Hou, W.; Li, T. Genetic Algorithm for Assembly Sequences Planning Based on Heuristic Assembly Knowledge. Appl. Mech. Mater. 2010, 44–47, 3657–3661. [Google Scholar] [CrossRef]
- Yi, Y.; Yan, Y.; Liu, X.; Ni, Z.; Feng, J.; Liu, J. Digital twin-based smart assembly process design and application framework for complex products and its case study. J. Manuf. Syst. 2021, 58, 94–107. [Google Scholar] [CrossRef]
- Wu, B.; Lu, P.; Lu, J.; Xu, J.; Liu, X. A hierarchical parallel multi-station assembly sequence planning method based on GA-DFLA. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 2029–2045. [Google Scholar] [CrossRef]
- Nourmohammadi, A.; Ng, A.H.C.; Fathi, M.; Vollebregt, J.; Hanson, L. Multi-objective optimization of mixed-model assembly lines incorporating musculoskeletal risks assessment using digital human modeling. CIRP J. Manuf. Sci. Technol. 2023, 47, 71–85. [Google Scholar] [CrossRef]
- Tseng, H.E.; Chang, C.C.; Chung, T.W. Applying Improved Particle Swarm Optimization to Asynchronous Parallel Disassembly Planning. IEEE Access 2022, 10, 80555–80564. [Google Scholar] [CrossRef]
- Xu, X.; Hu, W.; Cao, D.; Huang, Q.; Chen, C.; Chen, Z. Optimized sizing of a standalone PV-wind-hydropower station with pumped-storage installation hybrid energy system. Renew. Energy 2020, 147, 1418–1431. [Google Scholar] [CrossRef]
- Li, X.; Hu, C.; Luo, S.; Lu, H.; Piao, Z.; Jing, L. Distributed Hybrid-Triggered Observer-Based Secondary Control of Multi-Bus DC Microgrids Over Directed Networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2025, 72, 2467–2480. [Google Scholar] [CrossRef]
- Whittle, M.; Trevelyan, J.; Shin, W.; Tavner, P. Improving wind turbine drivetrain bearing reliability through pre-misalignment. Wind Energy 2014, 17, 1217–1230. [Google Scholar] [CrossRef]
- Sankar, S.; Nataraj, M. Prevention of helical gear tooth damage in wind turbine generator: A case study. Proc. Inst. Mech. Eng. Part A J. Power Energy 2010, 224, 1117–1125. [Google Scholar] [CrossRef]
- Alemayehu, F.M.; Ekwaro-Osire, S. Loading and design parameter uncertainty in the dynamics and performance of high-speed-parallel-helical-stage of a wind turbine gearbox. J. Mech. Des. 2014, 136, 091002. [Google Scholar] [CrossRef]
- Liu, M.; Zhou, B.; Li, J.; Li, X.; Bao, J. A Knowledge Graph-Based Approach for Assembly Sequence Recommendations for Wind Turbines. Machines 2023, 11, 930. [Google Scholar] [CrossRef]
- Teeparthi, K.; Kumar, D. Multi-objective hybrid PSO-APO algorithm based security constrained optimal power flow with wind and thermal generators. Eng. Sci. Technol. Int. J. 2017, 20, 411–426. [Google Scholar] [CrossRef]
- Panda, S.; Mohanty, B.; Hota, P.K. Hybrid BFOA-PSO algorithm for automatic generation control of linear and nonlinear interconnected power systems. Appl. Soft Comput. 2013, 13, 4718–4730. [Google Scholar] [CrossRef]
- Gkournelos, C.; Konstantinou, C.; Angelakis, P.; Tzavara, E.; Makris, S. Praxis: A framework for AI-driven human action recognition in assembly. J. Intell. Manuf. 2023, 35, 3697–3711. [Google Scholar] [CrossRef]
- Xu, Y.; Li, X.; Wang, H.; Zhang, J. Real-time adaptive control in smart manufacturing: Enhancing responsiveness with continuous model updates. J. Manuf. Syst. 2022, 63, 312–323. [Google Scholar] [CrossRef]
- Wan, X.; Liu, K.; Qiu, W.; Kang, Z. An Assembly Sequence Planning Method Based on Multiple Optimal Solutions Genetic Algorithm. Mathematics 2024, 12, 574. [Google Scholar] [CrossRef]
- Mardani, A.; Jusoh, A.; Zavadskas, E.K. Fuzzy multiple criteria decision-making techniques and applications—Two decades review from 1994 to 2014. Expert Syst. Appl. 2015, 42, 4126–4148. [Google Scholar] [CrossRef]
- Ho, W.; Xu, X.; Dey, P.K. Multi-criteria decision making approaches for supplier evaluation and selection: A literature review. Eur. J. Oper. Res. 2010, 201, 16–24. [Google Scholar] [CrossRef]
- Hsu, W.-H.; Jao, J.-A.; Chen, Y.-L. Discovering conjecturable rules through tree-based clustering analysis. Expert Syst. Appl. 2005, 29, 493–505. [Google Scholar] [CrossRef]
- Kannan, G.; Pokharel, S.; Kumar, P.S. A hybrid approach using ISM and fuzzy TOPSIS for the selection of reverse logistics provider. Resour. Conserv. Recycl. 2009, 54, 28–36. [Google Scholar] [CrossRef]
- Faulin, J.; Juan, A.A.; Martorell, S.; Ramirez-Marquez, J.E. Simulation Methods for Reliability and Availability of Complex Systems; Springer: London, UK, 2010. [Google Scholar] [CrossRef]
- Mumtaz, J.; Guan, Z.; Yue, L.; Wang, Z.; Ullah, S.; Rauf, M. Multi-Level Planning and Scheduling for Parallel PCB Assembly Lines Using Hybrid Spider Monkey Optimization Approach. IEEE Access 2019, 7, 18685–18700. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).