Optimization Scheduling of Multi-Regional Systems Considering Secondary Frequency Drop
Abstract
1. Introduction
2. Analysis and Modeling of Power Dip Phenomena
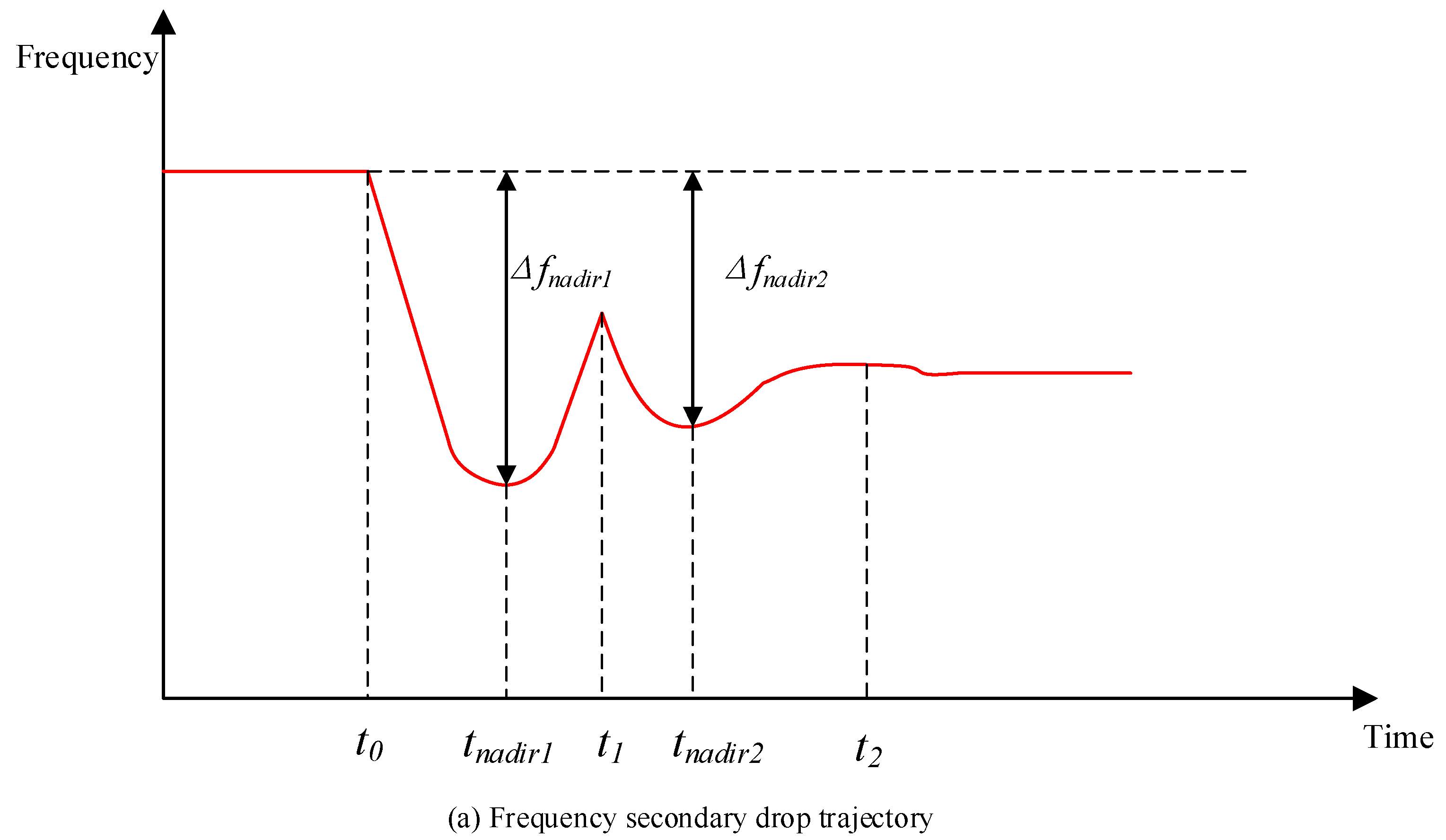
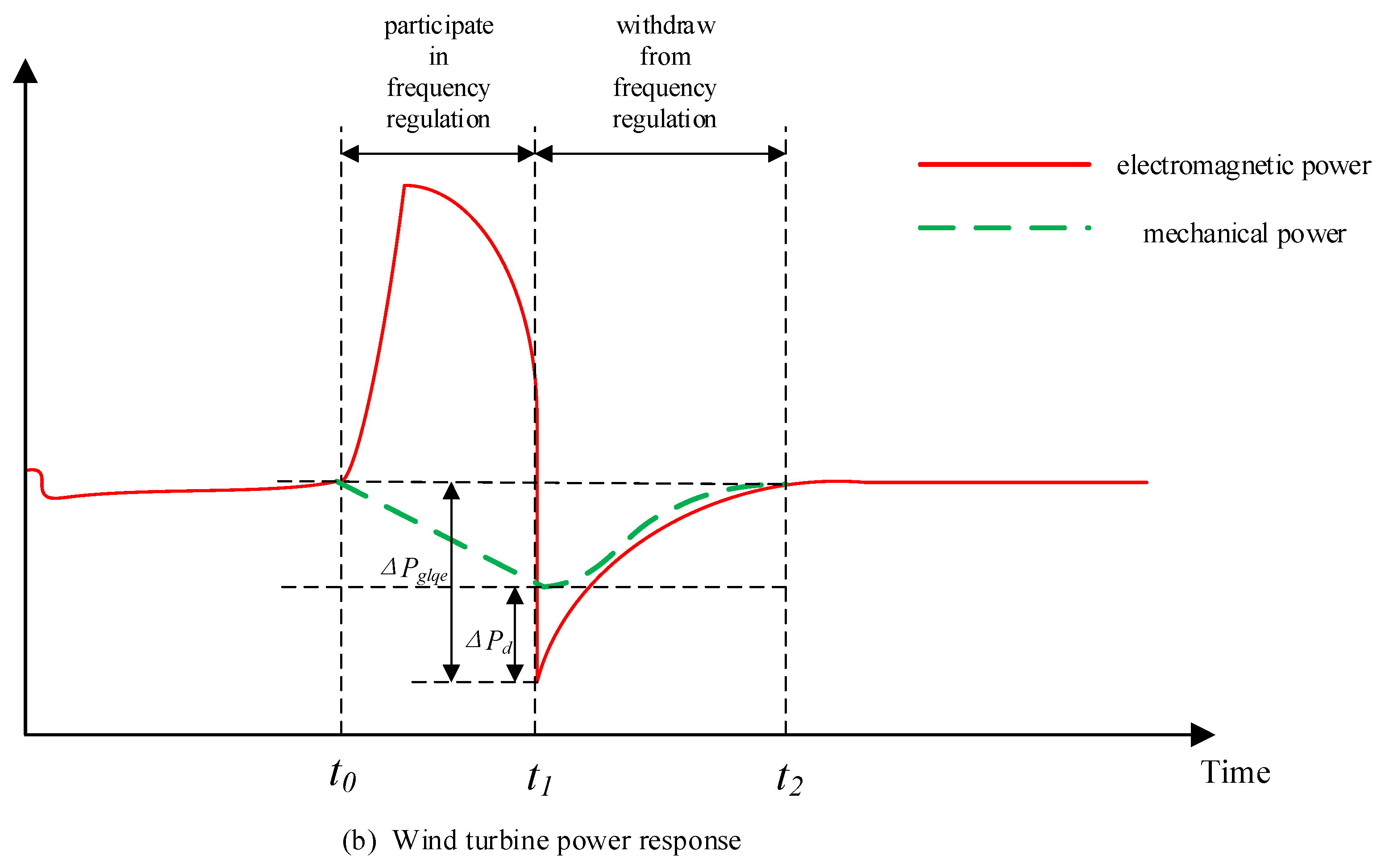
2.1. Analysis of Power Dip Phenomenon
2.2. Quantification of Secondary Frequency Drop
- Step 1: Obtain the unified structural parameters of the system.
- Step 2: Determine key settings such as the wind power disconnection time and the magnitude of the power deficiency disturbance.
- Step 3: Substitute these values into Equations (4) and (5) to calculate the intermediate parameters: , , , .
- Step 4: Insert the obtained parameters into Equations (2) and (3) to derive the time of the secondary frequency dip and the corresponding frequency nadir.
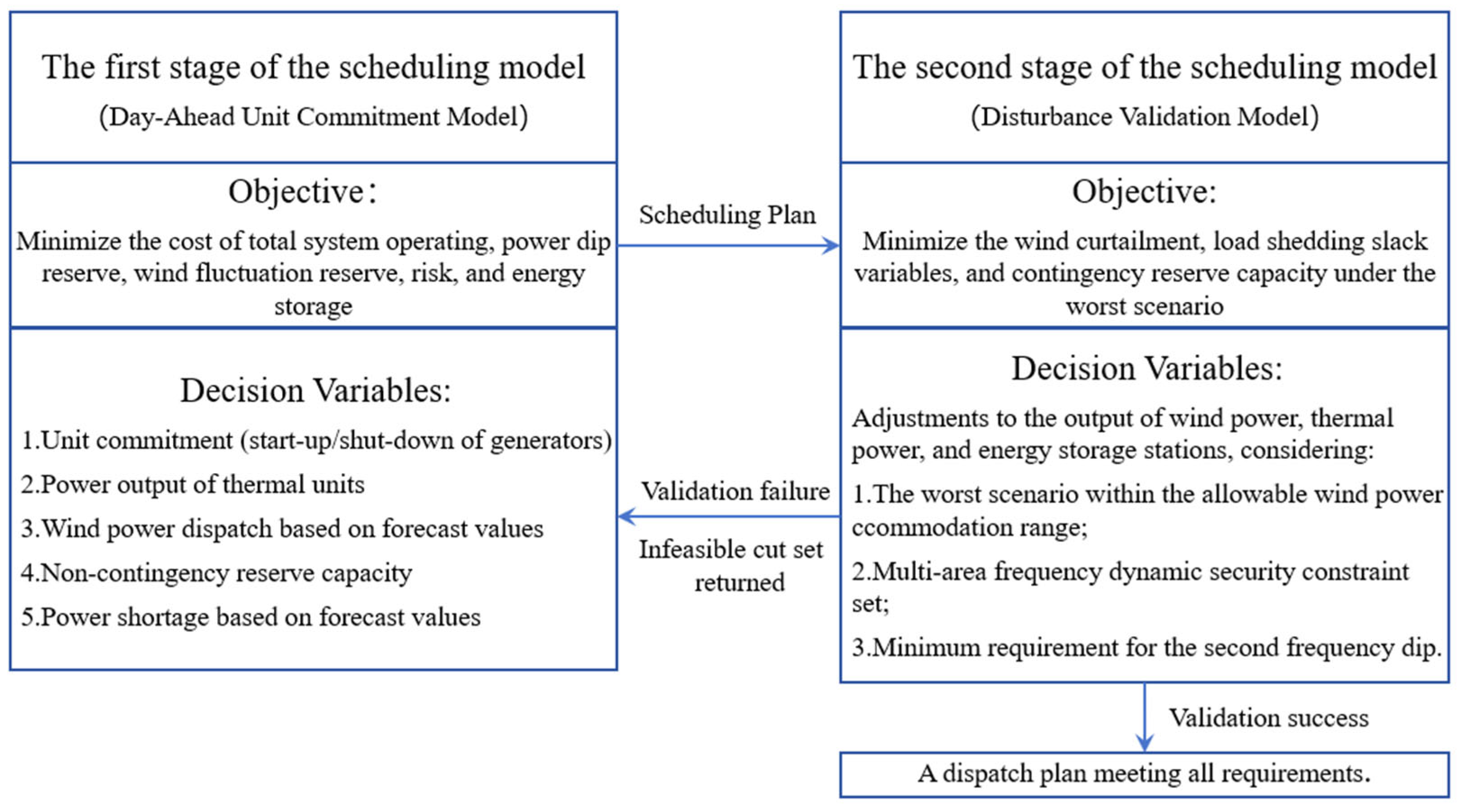
3. Two-Stage Scheduling Model
3.1. Overall Framework of the Scheduling Model
3.2. First-Stage Scheduling
3.2.1. Objective Function for the First-Stage Scheduling
3.2.2. First-Stage Scheduling Constraints
- (1)
- Generation capacity limits of thermal power units
- (2)
- Ramping constraints for thermal power units
- (3)
- Wind power fluctuation reserve and power dip reserve constraints
- (4)
- Constraints on wind power generation output
- (5)
- Active power balance constraint
- (6)
- DC power flow constraints for the sending-end and receiving-end grids
- (7)
- Tie-line transmission power constraint
3.3. Second-Stage Scheduling
3.3.1. Objective Function for the Second-Stage Scheduling
3.3.2. Second-Stage Scheduling Constraints
- (1)
- Power balance constraint
- (2)
- DC power flow constraints
- (3)
- Thermal unit output adjustment constraints
- (4)
- Tie-line power transfer adjustment constraints
- (5)
- Slack variable constraints for wind curtailment and load shedding
- (6)
- Uncertainty set of wind power output
- (7)
- Secondary frequency dip security constraint
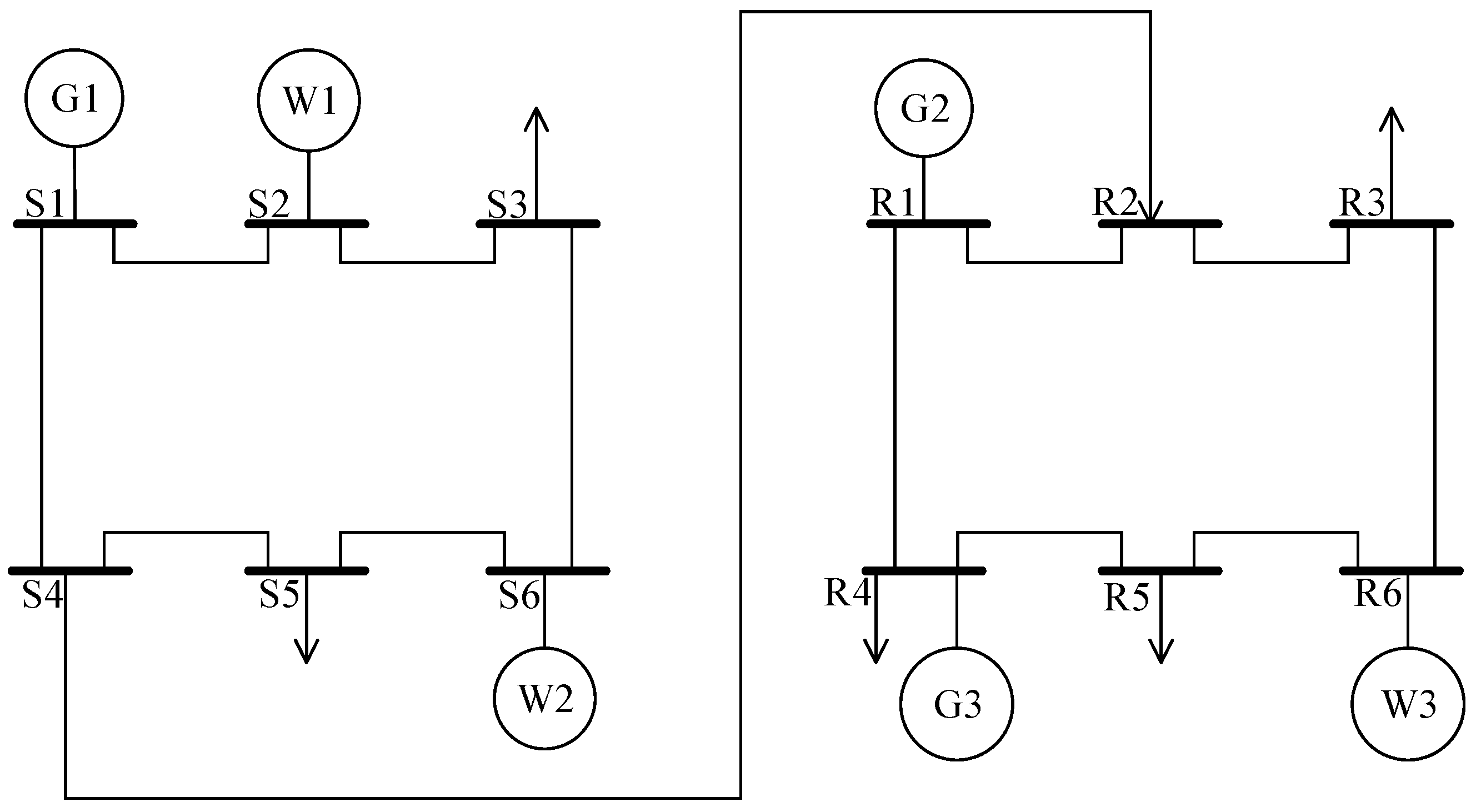
4. Case Study
4.1. Economic Impact of Scheduling in Multi-Area Systems
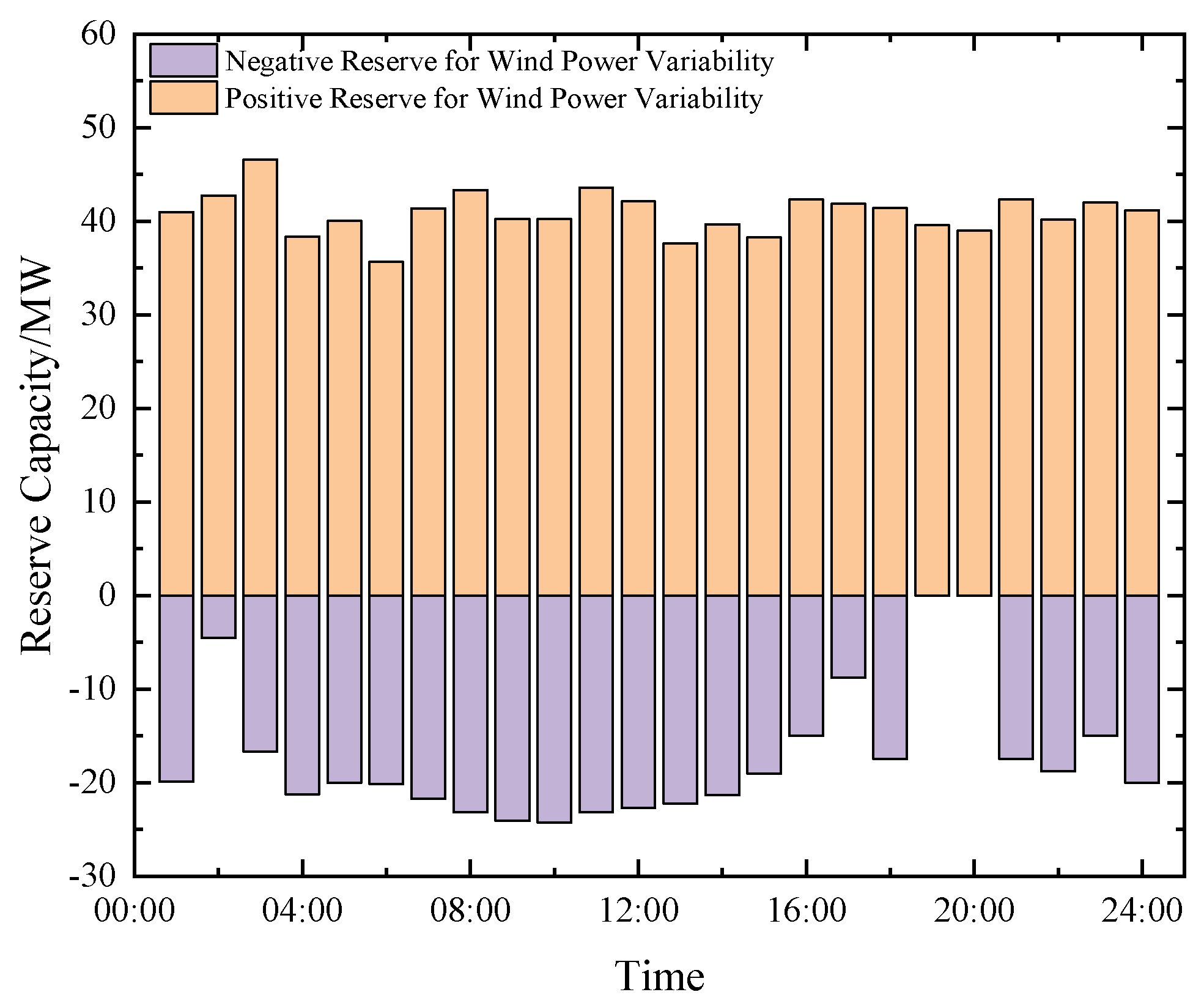
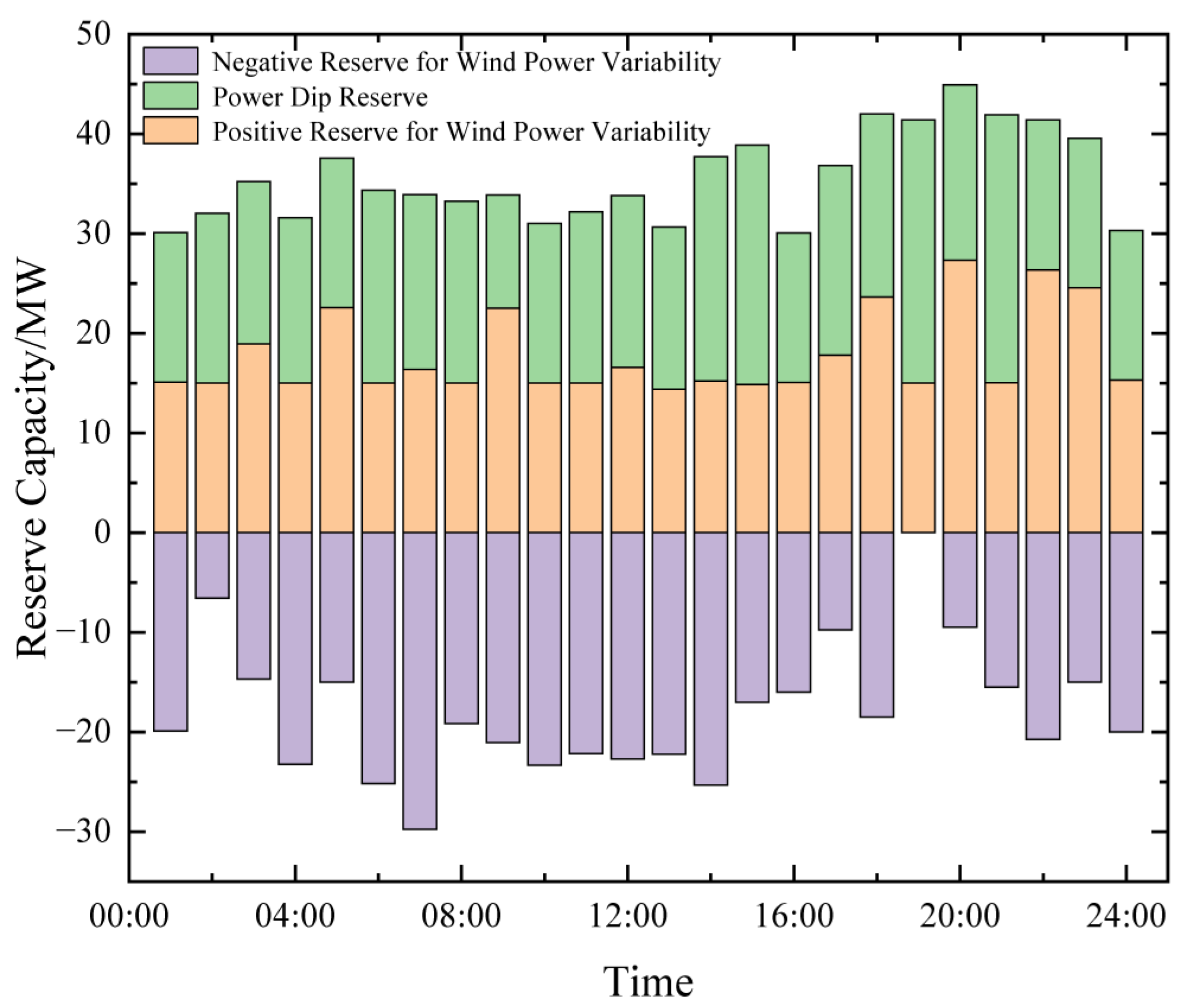
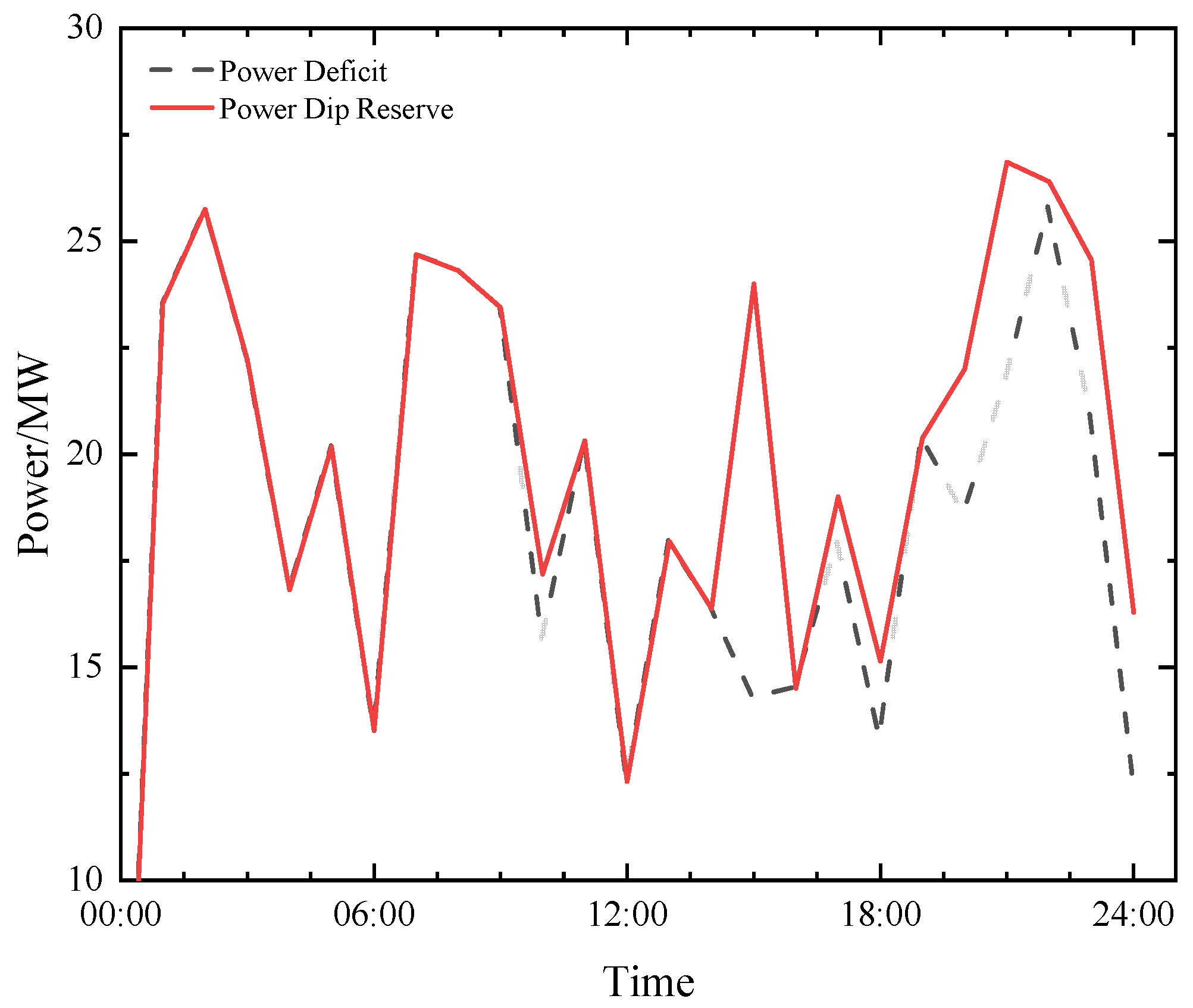
4.2. Impact of Scheduling Strategies on Reserve Capacity Allocation
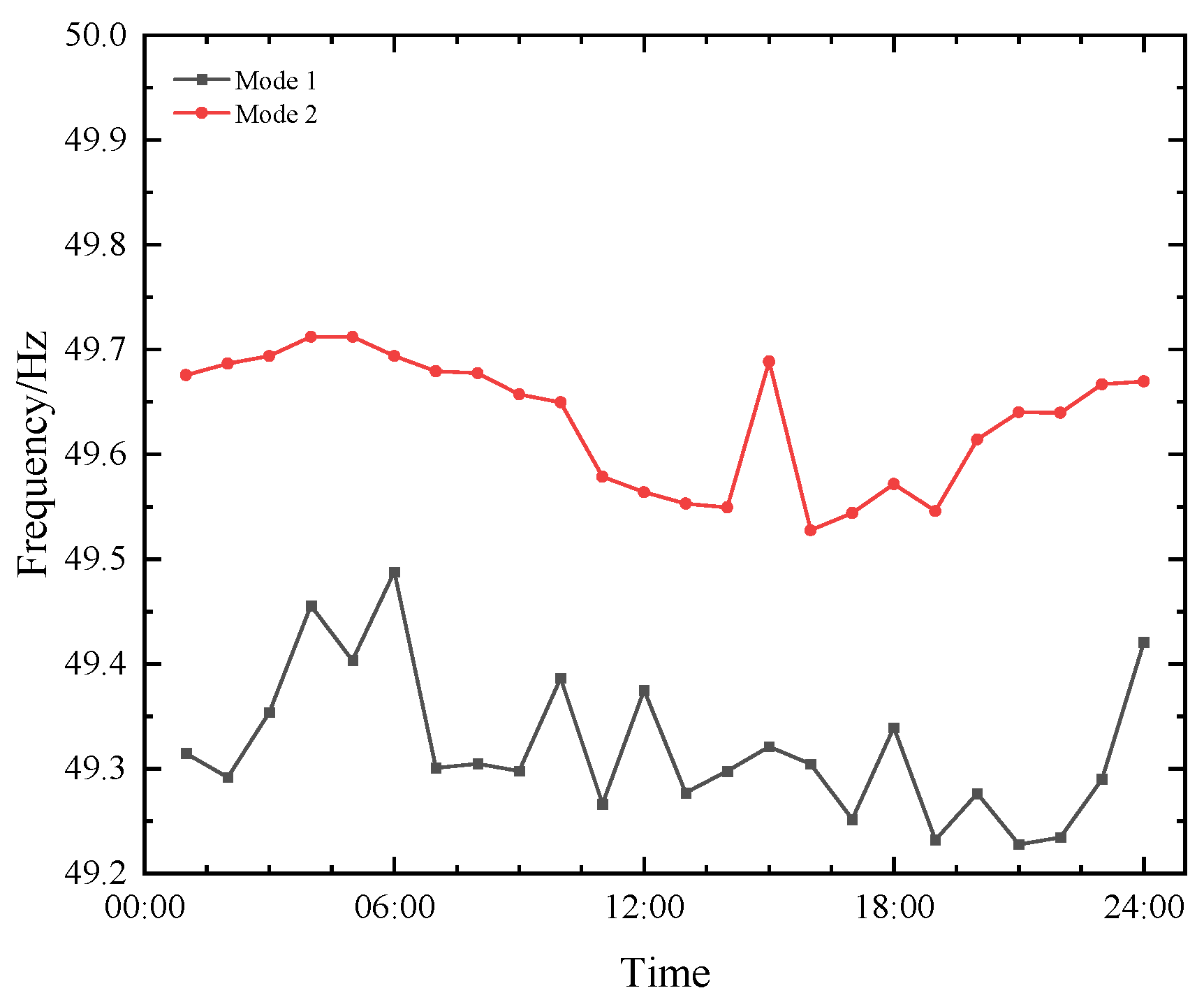
4.3. Impact of Scheduling Strategies on the Nadir of Secondary Frequency Drop
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kang, C.; Yao, L. Key Scientific Issues and Theoretical Research Framework for Power Systems with High Proportion of Renewable Energy. Autom. Electr. Power Syst. 2017, 41, 2–11. [Google Scholar]
- Zheng, Y.; Li, Z.; Chai, J. Progress and prospects of international carbon peaking and carbon neutral research—Based on bibliometric analysis (1991–2022). Front. Energy Res. 2023, 11, 1121639. [Google Scholar] [CrossRef]
- Ma, R.; Zhan, M.; Jiang, K.; Liu, D.; Hu, P.; Cheng, S. Transient Stability Assessment of Renewable Dominated Power Systems by the Method of Hyperplanes. IEEE Trans. Power Deliv. 2023, 38, 3455–3468. [Google Scholar] [CrossRef]
- Janusz, B. What does the GB power outage on 9 August 2019 tell us about the current state of decarbonised power systems? Energy Policy 2020, 146, 111821. [Google Scholar] [CrossRef]
- Yan, R.; Al Masood, N.; Kumar Saha, T.; Bai, F.; Gu, H. The Anatomy of the 2016 South Australia Blackout: A Catastrophic Event in a High Renewable Network. IEEE Trans. Power Syst. 2018, 33, 5374–5388. [Google Scholar] [CrossRef]
- Zhou, D.; Zou, Z.; Dan, Y.; Wang, C.; Teng, C.; Zhu, Y. An Integrated Strategy for Hybrid Energy Storage Systems to Stabilize the Frequency of the Power Grid Through Primary Frequency Regulation. Energies 2025, 18, 246. [Google Scholar] [CrossRef]
- Ratnam, K.S.; Palanisamy, K.; Yang, G. Future low-inertia power systems: Requirements, issues, and solutions—A review. Renew. Sustain. Energy Rev. 2020, 124, 109773. [Google Scholar] [CrossRef]
- Zou, S.; Zong, X.; Chen, Q.; Zhang, W.; Zhou, H. Optimization Scheduling of Integrated Energy Systems Considering Power Flow Constraints. Energies 2025, 18, 2442. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, Y.; Zhang, X.; Wang, Y.; Mi, R.; Song, J.; Hao, Z.; Xu, C. A Two-Stage Robust Optimization Strategy for Long-Term Energy Storage and Cascaded Utilization of Cold and Heat Energy in Peer-to-Peer Electricity Energy Trading. Energies 2025, 18, 323. [Google Scholar] [CrossRef]
- Jin, W.; Wang, P.; Yuan, J. Key Role and Optimization Dispatch Research of Technical Virtual Power Plants in the New Energy Era. Energies 2024, 17, 5796. [Google Scholar] [CrossRef]
- Zeng, B.; Zhao, L. Solving two-stage robust optimization problems using a column-and-constraint generation method. Oper. Res. Lett. 2013, 41, 457–461. [Google Scholar] [CrossRef]
- Tsang, M.Y.; Shehadeh, K.S.; Curtis, F.E. An inexact column-and-constraint generation method to solve two-stage robust optimization problems. Oper. Res. Lett. 2023, 51, 92–98. [Google Scholar] [CrossRef]
- Roald, L.A.; Pozo, D.; Papavasiliou, A.; Molzahn, D.K.; Kazempour, J.; Conejo, A. Power systems optimization under uncertainty: A review of methods and applications. Electr. Power Syst. Res. 2023, 214, 108725. [Google Scholar] [CrossRef]
- Guan, Y.; Wang, J. Uncertainty sets for robust unit commitment. IEEE Trans. Power Syst. 2014, 29, 1439–1440. [Google Scholar] [CrossRef]
- Wu, W.; Wang, K.; Li, G.; Ge, Y. Modeling ellipsoidal uncertainty set considering conditional correlation of wind power generation. Proc. CSEE 2017, 37, 2500–2507. [Google Scholar]
- Wu, Z.; Chen, C.; Xu, D.; Guan, L. Frequency-Constrained Economic Dispatch of Microgrids Considering Frequency Response Performance. Energies 2025, 18, 2014. [Google Scholar] [CrossRef]
- Teng, F.; Trovato, V.; Strbac, G. Stochastic scheduling with inertia-dependent fast frequency response requirements. IEEE Trans. Power Syst. 2016, 31, 1557–1566. [Google Scholar] [CrossRef]
- Zhou, Z.; Wang, Z.; Zhang, Y.; Wang, X. Nash Bargaining-Based Coordinated Frequency-Constrained Dispatch for Distribution Networks and Microgrids. Energies 2024, 17, 5661. [Google Scholar] [CrossRef]
- Badesa, L.; Teng, F.; Strbac, G. Simultaneous scheduling of multiple frequency services in stochastic unit commitment. IEEE Trans. Power Syst. 2019, 34, 3858–3868. [Google Scholar] [CrossRef]
- Badesa, L.; Teng, F.; Strbac, G. Conditions for Regional Frequency Stability in Power System Scheduling—Part I: Theory. IEEE Trans. Power Syst. 2021, 36, 5558–5566. [Google Scholar] [CrossRef]
- Badesa, L.; Teng, F.; Strbac, G. Conditions for Regional Frequency Stability in Power System Scheduling—Part II: Application to Unit Commitment. IEEE Trans. Power Syst. 2021, 36, 5567–5577. [Google Scholar] [CrossRef]
- Qian, M.; Wang, J.; Yang, D.; Yin, H.; Zhang, J. An Optimization Strategy for Unit Commitment in High Wind Power Penetration Power Systems Considering Demand Response and Frequency Stability Constraints. Energies 2024, 17, 5725. [Google Scholar] [CrossRef]
- Zhang, G.; Ela, E.; Wang, Q. Market Scheduling and Pricing for Primary and Secondary Frequency Reserve. IEEE Trans. Power Syst. 2019, 34, 2914–2924. [Google Scholar] [CrossRef]
- Xin, X.; Wang, T.; Gu, X.; Bai, Y.; Fan, H. Unit Commitment and Risk Dispatch Considering Multi-Regional Frequency Dynamic Security Under Large-Scale Wind Power Access. Proc. CSEE 2023, 43, 5824–5839. [Google Scholar]
- Wu, S.; Mu, R.; Zhang, Y.; Song, H.; Zhao, W.; Huang, K.; Zhu, B. Study of Power Pit in System Frequency Modulation of Doubly-Fed Induction Generator. Electr. Power Sci. Eng. 2021, 37, 1–11. [Google Scholar]
- Zhang, W.; Wu, C.; Huang, W.; Gao, H.; Cheng, M.; Xin, H. Evaluation of System Frequency Characteristic and Parameter Setting of Frequency Regulation for Wind Power Considering Secondary Frequency Drop. Autom. Electr. Power Syst. 2022, 46, 11–19. [Google Scholar]
- Liu, K.; Qu, Y.; Kim, H.-M.; Song, H. Avoiding Frequency Second Dip in Power Unreserved Control During Wind Power Rotational Speed Recovery. IEEE Trans. Power Syst. 2018, 33, 3097–3106. [Google Scholar] [CrossRef]
- Li, D.; Wan, R.; Xu, B.; Yao, Y.; Dong, N.; Zhang, X. Optimal Capacity Configuration of the Wind-Storage Combined Frequency Regulation System Considering Secondary Frequency Drop. Front. Energy Res. 2023, 11, 1037587. [Google Scholar] [CrossRef]
- Cheng, Y.; Sun, H.; Zhang, Y.; Xu, S.; Zhao, B.; Vorobev, P.; Terzija, V. A consecutive power dispatch in wind farms to mitigate secondary frequency dips. Int. J. Electr. Power Energy Syst. 2024, 158, 109939. [Google Scholar] [CrossRef]
| Parameters | G1 | G2 | G3 | WT1 | WT2 | WT3 |
|---|---|---|---|---|---|---|
| Jul | 13.94 | 13.94 | 19.91 | 12.6 | 12.6 | 12.6 |
| Dul | 11.46 | 11.46 | 17.19 | 17.93 | 17.93 | 17.93 |
| 1/Kul | 12.36 | 12.36 | 18.54 | −3.1 | −3.1 | −3.1 |
| T0 | 5 | 5 | 5 | 5 | 5 | 5 |
| Mode | Operating Cost/USD | Cost of Reserves for Wind Power Variability/USD | Power Dip Reserve Cost/USD | Wind Curtailment and Load Shedding Risk/USD | Total Cost/USD |
|---|---|---|---|---|---|
| 1 | 104,620 | 9849 | 0 | 1354 | 115,823 |
| 2 | 105,817 | 6423 | 4058 | 1862 | 118,160 |
| Mode | Operating Cost in Sending Region/USD | Operating Cost in Receiving Region/USD | Total Reserve Cost in the Sending Region/USD | Total Reserve Cost in the Receiving Region/USD |
|---|---|---|---|---|
| 1 | 49,217 | 55,403 | 6575 | 3274 |
| 2 | 48,997 | 56,820 | 8339 | 2142 |
| Mode | Total Cost/USD | The Lowest Value of Frequency Secondary Drop/Hz | Frequency Secondary Drop Time/s |
|---|---|---|---|
| 1 | 115,823 | 49.23 | 7.52 |
| 2 | 118,160 | 49.57 | 7.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Hua, X.; Cheng, L.; Wang, T.; Su, Y. Optimization Scheduling of Multi-Regional Systems Considering Secondary Frequency Drop. Energies 2025, 18, 3926. https://doi.org/10.3390/en18153926
Yang X, Hua X, Cheng L, Wang T, Su Y. Optimization Scheduling of Multi-Regional Systems Considering Secondary Frequency Drop. Energies. 2025; 18(15):3926. https://doi.org/10.3390/en18153926
Chicago/Turabian StyleYang, Xiaodong, Xiaotong Hua, Lun Cheng, Tao Wang, and Yujing Su. 2025. "Optimization Scheduling of Multi-Regional Systems Considering Secondary Frequency Drop" Energies 18, no. 15: 3926. https://doi.org/10.3390/en18153926
APA StyleYang, X., Hua, X., Cheng, L., Wang, T., & Su, Y. (2025). Optimization Scheduling of Multi-Regional Systems Considering Secondary Frequency Drop. Energies, 18(15), 3926. https://doi.org/10.3390/en18153926





