Abstract
The totem-pole bridgeless power factor correction (PFC) circuit based on the triangular current mode (TCM) in the front-end PFC of a switching power supply has the advantage of realizing zero-voltage switching (ZVS) in the full working range. However, the TCM control based on the critical conduction mode (CRM) further increases the inductance current ripple, and the traditional input voltage AC sampling circuit increases the circuit complexity and device cost. Therefore, this paper studies the corresponding improvement technology from two dimensions. Firstly, the coordinated interleaved parallel technology is employed to design the system’s overall control-improvement strategy. This approach not only achieves full working-range ZVS but also reduces both the inductor current ripple and power device stress. Simultaneously, an optimized input voltage sampling circuit is designed to accommodate varying voltage requirements of control chip pins. This circuit demonstrates strong synchronization in both voltage and phase sampling, and the structural characteristics of the optocoupler can also suppress electrical signal interference. Finally, a 600 W totem-pole bridgeless PFC prototype is developed. The experimental results demonstrate the effectiveness of the proposed improved method. The prototype efficiency peak reaches 97.3%.
1. Introduction
A switching mode power supply (SMPS) is a power supply device that converts input power into stable output power through the rapid on and off of high-frequency switching devices. Its core principle involves regulating the duty cycle of switching devices, followed by energy transfer and filtering through inductive and capacitive energy-storage elements, thereby enabling efficient power conversion.
SMPSs have emerged as the predominant power supply solution for modern electronic devices, finding widespread applications in communication systems, renewable energy systems, and consumer electronics, as illustrated in Figure 1 [1,2].

Figure 1.
Main application fields of SMPSs.
Figure 2 shows the typical structure of an SMPS, consisting of a former AC/DC stage followed by a latter DC/DC stage. The front stage converts the AC to high-voltage DC and dynamically adjusts the input current waveform to make the PF close to 1 to achieve power factor correction (PFC). DC/DC converts the high-voltage DC of the previous stage to isolated and stable low-voltage DC. This design takes into account high efficiency, power factor correction and stable output [3,4].
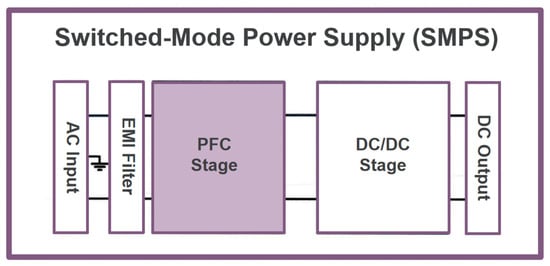
Figure 2.
Traditional two-level architecture switching mode power supply.
With the popularity of power electronic equipment, the problem of harmonic pollution in a power grid has become serious [5,6]. To enhance power system stability through improved power quality, numerous countries and international organizations have established various standards, including IEC 61000-3-2, GB/T 14549-1993, and IEEE 519 [7,8,9].
These standards strictly limit the harmonics contained in the input current of power electronic equipment when connected to the grid. As a core technology in modern power electronic system, PFC circuits play an irreplaceable role in power factor improvement, harmonic reduction, and energy efficiency enhancement. Currently, active PFC topologies have become the industry standard solution. The dynamic current waveform control is realized by introducing MOSFET, IGBT, and other high-frequency switching devices [10].
Table 1 provides a comprehensive comparison of various boost PFC rectifier topologies. The totem-pole bridgeless PFC circuit has become a popular topology due to its simple topology, low conduction loss, and common mode interference, which is conducive to achieving higher efficiency and power density [3,11,12,13,14,15].
The performance characteristics of totem-pole bridgeless PFC converters are strongly dependent on their inductor current modulation strategies. Based on the characteristic state of the inductor current during switching cycles, the operation modes can be classified into continuous conduction mode (CCM), discontinuous conduction mode (DCM), and critical conduction mode (CRM). Table 2 presents a comparison of these three operating modes.
Under CCM, the inductor current remains non-zero throughout the entire switching cycle, and the switching devices operate with continuous current flow. This mode exhibits low total harmonic distortion (THD) and reduced current ripple characteristics. However, the Si MOSFET has severe defects of diode reverse recovery characteristics, which makes the circuit difficult to operate stably. Hard switching loss is positively correlated with the switching frequency, which limits the maximum operating frequency of CCM. Compared with CCM, critical conduction mode (CRM) can reduce the inductance current to zero, realize zero-voltage switching (ZVS) through resonance, and reduce the switching loss. Under DCM, the inductor current decays to zero within each switching cycle, achieving natural zero-current switching (ZCS) turn-off. This inherent characteristic eliminates diode reverse recovery issues, thereby maintaining reliable operation even with conventional silicon-based devices. But DCM input current is intermittent, leading to increased harmonic distortion and a reduced power factor. And the inductance current ripple is significant, which adds difficulty to the filter design. Compared with DCM, CRM has better harmonic performance and a higher PF value. Therefore, CRM totem-pole bridgeless PFC converters have emerged as the predominant solution for high-efficiency, high-power-density applications.
However, CRM has inherent constraints: the converter operates with variable switching frequency control, resulting in relatively complex control-methodology implementation. ZVS is achievable when Uin ≤ 0.5Uo. However, for Uin > 0.5Uo, only the valley switching (VS) operation is possible, indicating that full-range ZVS cannot be realized [16,17,18].

Table 1.
Comparison of different boost PFC rectifier topologies [18].
Table 1.
Comparison of different boost PFC rectifier topologies [18].
| Topology | SD | M | FD | L | Co | Tot. Num |
|---|---|---|---|---|---|---|
| Conventional single switch | 4 | 1 | 1 | 1 | 1 | 8 |
| Dual boost bridgeless | 2 | 2 | 2 | 2 | 1 | 9 |
| Bi-directional bridgeless | 2 | 2 | 2 | 1 | 1 | 8 |
| totem-pole bridgeless | 2 | 2 | 0 | 1 | 1 | 6 |
SD: slow diodes; M: MOSFETs; FD: fast diodes; L: input inductors; Co: output capacitors.

Table 2.
Comparison of CCM, CRM, and DCM operation modes.
Table 2.
Comparison of CCM, CRM, and DCM operation modes.
| Comparative Elements | CCM | CRM | DCM |
|---|---|---|---|
| Inductor current | Continuous | Critical conduction | Discontinuous |
| Control methodology | Fixed frequency | Variable frequency | Fixed frequency/Variable frequency |
| Current ripple | Small | Relatively large | Large |
| Peak current | Small | Medium | Large |
| RMS current | Small | Medium | Large |
| Switching state | Hard switching | Soft switching | Soft switching |
To further enhance the efficiency and power factor of totem-pole PFC converters, numerous domestic and international scholars have conducted extensive research and improvements based on these three fundamental modulation modes.
The advent of wide-bandgap (WBG) devices has expanded the applications of totem-pole PFC topologies and facilitated innovative integration with modulation schemes. Ref. [19] implemented a CCM totem-pole bridgeless PFC rectifier using SiC devices, achieving a peak efficiency of 98.6%. Ref. [20] presents a complete 6.6 kW on-board charger (OBC) system utilizing hybrid SiC/GaN power devices, achieving a power density of 37 W/in3 with >96% peak efficiency. Ref. [21] proposed a 6.6 kW bidirectional SiC-based LLC charger featuring an interleaved CCM totem-pole bridgeless PFC front-end and a wide-ZVS-range, magnetically integrated 300 kHz LLC converter, achieving 96% peak discharge efficiency at full load. Ref. [13] developed an 800 W GaN-based CCM bridgeless totem-pole PFC prototype with 98% efficiency.
Control-strategy optimization has also emerged as a key research focus. Ref. [22] introduced interleaving techniques into a GaN HEMT-based CRM totem-pole bridgeless PFC circuit, realizing a 1.2 kW interleaved boost PFC converter prototype with 97.9% peak efficiency. Building upon CRM operation, Ref. [18] proposed a ZVS range-extension method termed triangular current mode (TCM) control. When Uin > 0.5Uo, the rectifier switch remains conducting after the inductor current reaches zero, extending its on-time to ensure sufficient energy storage for complete MOSFET junction capacitance discharge, thereby achieving full-range ZVS without auxiliary circuits. To improve the wide-load-range efficiency in high-frequency SiC-based boost converters, Ref. [23] developed a hybrid TCM–DCM current mode. At the rated load, TCM enables zero-voltage switching. At the same time, light-load conditions employ a TCM–DCM hybrid operation where TCM current pulses are generated during DCM zero-current intervals, simultaneously achieving ZVS and current ripple reduction for maintained high efficiency across load variations.
However, TCM control still has some deficiencies:
- The inductance current ripple is larger in CRM, and the TCM control makes the inductance current ripple further increase;
- Power devices bear higher current stress, and inductors need to adopt larger core sizes to avoid saturation and power density reduction.
Therefore, Ref. [16] integrated the TCM control with interleaving technology, achieving full-range ZVS while further reducing the inductor current ripple, with a peak efficiency of 96.9%. However, this approach requires coordinated control between a DSP and FPGA. Similarly, even for single-phase TCM control, the implementation in ref. [17] necessitates combined DSP and CPLD control. Furthermore, the control scheme in ref. [24] requires additional sampling of the actual inductor current value, which increases system complexity in terms of current sensing.
In addition, the 220 VAC input voltage sampling circuit mainly samples its phase and numerical information. It is necessary to construct the sampling circuit separately, which increases the structural complexity. Furthermore, to meet the requirements of the input voltage threshold range of the analog-to-digital converter (ADC) pin of the control chip, the additional bias voltage of the sampling circuit is required, which increases the workload of the auxiliary power supply design.
To address these challenges, this paper proposes an improved TCM-based control strategy for totem-pole bridgeless PFC circuits that incorporate interleaving technology while utilizing only a single STC32F12K54 control chip. The proposed approach eliminates the need for precise inductor current sampling while achieving ZVS across the entire operating range and significantly reducing inductor current ripple. An optimized AC voltage sampling circuit is designed to concurrently perform two critical functions: precise measurement of both the input voltage amplitude and phase, and the optocoupler structure incorporated optocoupler architecture provides inherent immunity to electrical interference. The design principle of the sampling optimization circuit is universal and can meet the requirements of different control chips for pin input voltage.
This paper is organized as follows: Section 2 analyzes the topology and working mode of the TCM totem-pole bridgeless PFC circuit, studies the two-phase interleaving technology, and constructs the overall improved control architecture of the circuit. Section 3 details the optimized AC voltage sampling circuit design, with a theoretical analysis of its working principles and performance benefits. Section 4 carries out a simulation test on and experimental verification of the circuit to verify the correctness of the improved control method. Section 5 summarizes the research work and results.
2. Research on Improvement Technology of Circuit Control Strategy
2.1. Working Principle of Circuit Based on TCM
Figure 3 shows the topology of the totem-pole bridgeless PFC. Uin denotes the input voltage; L represents the boost inductance; D1 and D2 are the body diodes of the high-frequency switches S1 and S2, respectively; and Coss1 and Coss2 (where Coss1 = Coss2 = Coss) are the junction capacitance of S1 and S2, respectively. S3 and S4 are power frequency switches, Co is the output filter capacitance, and RL is the load resistance. Figure 3 shows the operation mode of the circuit in a high-frequency switching cycle with a positive power frequency half cycle. Figure 4 shows the corresponding characteristic waveform.
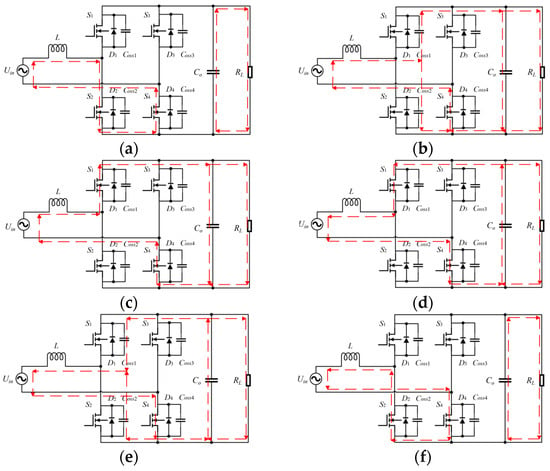
Figure 3.
Working mode of totem-pole bridgeless PFC circuit: (a) Stage I [t0, t1]; (b) Stage II [t1, t2]; (c) Stage III [t2, t3]; (d) Stage IV [t3, t4]; (e) Stage V [t4, t5]; (f) Stage VI [t5, t6].
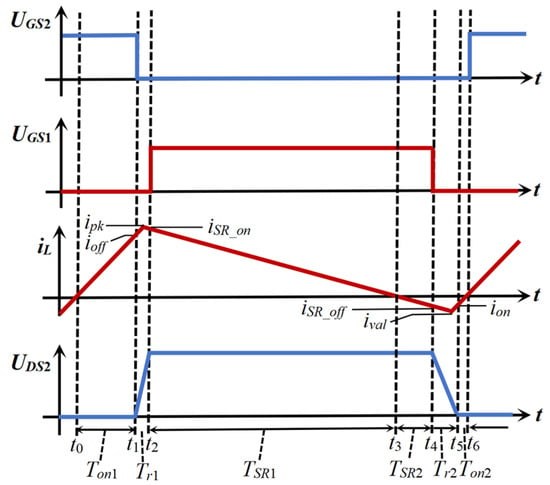
Figure 4.
Waveform diagram of switch tube voltage and inductor current.
A detailed analysis of the circuit’s operational modes and associated waveforms is presented below:
Stage I [t0, t1]: Positive energy storage stage. At t0, the voltage at S2 end of the main control switch tube is zero, driving S2 to realize zero-voltage turn-on. Uin is applied to L, and the inductance current iL rises linearly. Once the current ioff or the conduction time Ton of S2 is reached, S2 is turned off, marking the end of this stage.
Stage II [t1, t2]: Positive resonance stage. At t1, S2 is turned off, and L resonates with the junction capacitors Coss1 and Coss2 of S1 and S2. During resonance, the inductive current flows continuously through the synchronous rectifier S1. The inductive current charges Coss2 and discharges Coss1. Until t2, the voltage at both ends of Coss2 is Uo, and this stage ends.
Stage III [t2, t3]: Follow-up stage. At t2, the voltage at both ends of Coss1 drops to 0 and S1 turns on in reverse. iL flows continuously through S1, iL decreases linearly until t3, and iL drops to zero. This mode ends.
Stage IV [t3, t4]: Reverse recovery stage. At t3, S1 is conducting in the forward direction and iL is conducting in the reverse direction under the control of the drive signal.
When Uin ≤ 0.5Uo, S2 can be ZVS even if it does not go through this stage. Therefore, S1 is turned off immediately at t3.
When Uin > 0.5Uo, iL is 0 at t3, and S1 needs to be turned on for an additional period under certain conditions. At this time, iL increases negatively, storing energy in the reverse direction.
Stage V [t4, t5]: Reverse resonance stage.
If Uin ≤ 0.5Uo, S1 is turned off at t3, Coss1 and Coss2 are resonant with L, Coss1 is charged, and Coss2 is discharged. At t5, the voltage UDS2 at both ends of Coss2 drops to 0, and ZVS can be realized.
If Uin > 0.5Uo, under conventional control, S1 does not prolong its conduction period and turns off precisely at t3. Following resonance among Coss1, Coss2, and inductance L, UDS2(t5) = 2Uin – Uo, unable to drop to 0, and S2 can only achieve valley switching at t5.
Under the control of TCM, S1 remains conducting for an additional period. At t4, the auxiliary tube S1 is turned off, and resonance initiates among Coss1, Coss2, and L. The inductor has enough energy to charge Coss1 and discharge Coss2. Until t5, the voltage at both ends of Coss1 rises to bus voltage, UDS2 at both ends of Coss2 drops to zero, and this mode ends. It ensures that S2 can realize ZVS.
This mode is similar to that in the forward resonant phase, except that the polarity of the inductance current is opposite.
Stage VI [t5, t6]: Body diode freewheeling stage. At t5, the voltage at both ends of S2 is zero. At this time, iL(t) passes through the body diode D2 of S2, and the current increases. During this period, ZVS can be realized by turning on S2 before the inductance current increases to 0. End this mode at t6 and enter the next switching cycle.
The planar trajectory diagram of the iLZn-UDS2 phase at Uin > 0.5Uo and Uin ≤ 0.5Uo obtained through time domain modal analysis and theoretical model derivation is shown in Figure 5. This curve can more intuitively show the working states in the switching cycle.
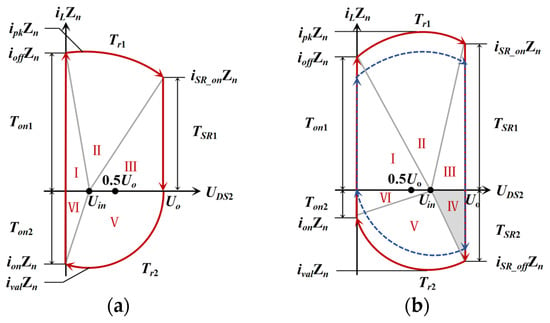
Figure 5.
iLZn-UDS2 state plane trajectory curve: (a) iLZn-UDS2 state plane trajectory curve when Uin ≤ 0.5Uo; (b) iLZn-UDS2 state plane trajectory curve when Uin > 0.5Uo.
When Uin ≤ 0.5Uo, as shown in Figure 5a, in stages I, III, and VI, the homogeneity of the inductance current increases or decreases. During stages II and V, the inductance resonates with the switch junction capacitance. This resonance reduces UDS2 to 0, enabling natural ZVS of the power switch. When Uin > 0.5Uo, an additional TCM-controlled stage IV must be incorporated, as illustrated in Figure 5b, to achieve full-range ZVS operation. The red arrow trajectories in this figure represent the normal operating paths under respective conditions, while the blue arrow trajectory in Figure 5b indicates the critical path that just achieves ZVS in TCM.
From the iLZn-UDS2 state plane trajectory diagram in Figure 5, Ton1 and iSR_off are set as unknown quantities, and the inductive current and time interval of the totem-pole PFC circuit at each stage can be deduced.
When Uin > 0.5Uo and Uin ≤ 0.5Uo, the derivation process of stages I~III is the same.
The inductance current ioff at the turn-off time of the main switch is as follows:
The arc radius rII in the resonance process of stage II is as follows:
where characteristic impedance .
The peak inductance current ipk in stage II is as follows:
The resonance time Tr1 of stage II can be obtained:
where θII is the center angle of the circular arc during stage II resonance, and the resonant angular frequency .
The inductance current iSR_on when the boost rectifier is turned on is as follows:
According to the principle of the voltage second balance of iL, the conduction time TSR1 of the boost rectifier in stage III can be calculated:
When Uin > 0.5Uo, the additional conduction time TSR2 of the boost rectifier in stage IV is as follows:
Obtain the reverse resonance time Tr2 of stage V:
where θV is the center angle of the stage V resonance process.
The inductance valley current ival in stage V is as follows:
Calculate the opening time of the main switch, and the inductance current ion is as follows:
Same as formula (6), the duration Ton2 of the reverse conduction phase of the main switch in stage VI is derived.
Under TCM control, the iSR_off and Ton1 formulas are further derived. In the positive half cycle of Uin, the turn-off current iSR_off of the synchronous rectifier only needs to meet one condition:
When Uin ≤ 0.5Uo, iSR_off = 0, the rectifier tube does not need additional conduction. When Uin > 0.5Uo, the required additional conduction time TSR2_min is as follows:
In a switching cycle, the inductance charge per unit time is the average value of inductance current iL_avg, assuming that the power factor PF = 1 and the overall efficiency is 1, then iL_avg is as follows:
where ωline = 2fline, fline is the input voltage frequency, taking the power frequency of 50 Hz.
The peak value ipk of inductance current is as follows:
The inductance current ioff when the main switch S2 is turned off is as follows:
From the characteristic impedance and the inductance current when the main switch S2 is turned off, the S2 conduction time Ton1 is obtained as follows:
This section verifies the effectiveness of TCM control through a comprehensive analysis of the circuit’s operational principles, stage-by-stage waveforms, and corresponding phase-plane trajectory curves. And the main parameter formulas such as the time and current are derived. This lays the foundation for the subsequent control loop calculation.
2.2. Two-Phase Interleaved Parallel Control
The increased current ripple based on TCM control makes the power devices in the circuit bear higher instantaneous current stress. The inductor needs to adopt a larger core size to avoid saturation, which directly leads to the reduction of power density. Filter capacitors also need to handle larger ripple currents, increasing the volume and cost of capacitors [25,26]. Therefore, this paper will study the two-phase interleaved parallel technology in this section and introduce the circuit to reduce the inductance current ripple.
Figure 6 shows the topology of two-phase interleaved totem-pole bridgeless PFC. L1 and switches S1 and S2 constitute boost module 1, while L2 and switches S3 and S4 constitute boost module 2. The two modules present a 180° phase difference, and the current peaks and valleys of the two inductors alternate, so that the current ripple can partially offset each other and reduce the total inductance current ripple. When the power level is the same, each module bears half of the total power, reducing the inductance volume and the current stress borne by each device to achieve higher power density [27].
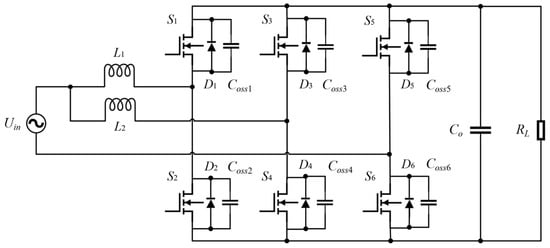
Figure 6.
Two-phase interleaved totem-pole bridgeless PFC circuit.
The waveforms of the switch voltage signal and inductance current of each interleaved parallel branch when duty cycle D ≤ 0.5 and D > 0.5 are shown in Figure 7. The voltages and driving signals of the two modules exhibit a half-cycle phase difference during the positive half-cycle period. The two inductive currents also have a phase difference of half a switching cycle. By superimposing two groups of inductive currents, the total inductive current iL is obtained. From the figure, the total current ripple value ΔiL is significantly reduced.
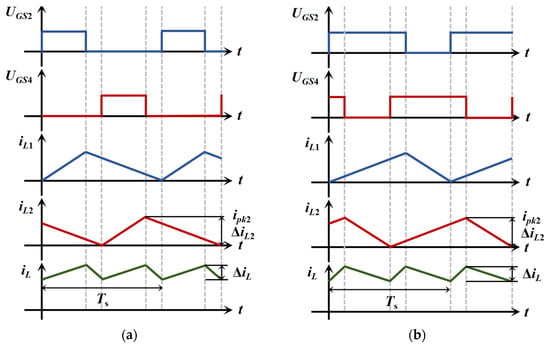
Figure 7.
Waveforms of switch tube voltage and inductor current in interleaved parallel circuit: (a) relevant waveform when D ≤ 0.5; (b) correlation waveform when D > 0.5.
Both the main-phase and slave-phase bridge arms share equal power distribution, with each bearing half of the total power. Based on this, the current ripple ΔiL1 and ΔiL2 of each phase inductance are the same as the current peak ipk1 and ipk2, including the following:
In the formula, D represents the duty cycle of the corresponding main switch, and L1 represents the inductance of one phase bridge arm. The inductance of two-phase bridge arm L1 = L2.
When D > 0.5, the duration of the rise in the current uniformity of the two inductors is (D − 0.5)TS, and the total inductance current ripple ΔiL is as follows:
When D ≤ 0.5, the duration of the decrease in the current uniformity of the two inductors is (0.5−D)TS. The total inductor current ripple ΔiL is as follows:
Suppose the transformation ratio k = ΔiL/ΔiL2, which is used to describe the quantitative relationship between the total inductance current ripple and the single-phase inductance current ripple under the condition of a two-phase interleaved parallel, then k is as follows:
Figure 8 shows the ripple curve. Combining Equation (21) and Figure 7, by implementing the interleaved parallel control, the total inductance current ripple of the system is lower than the value of the inductance current ripple of any phase in the entire duty cycle variation range.
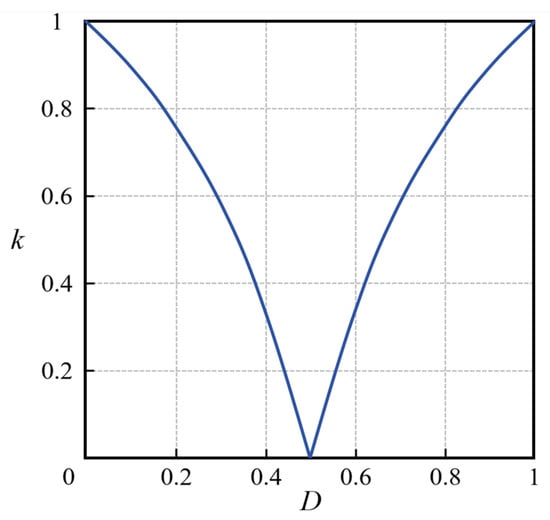
Figure 8.
The current ripple relationship between total inductance and single-phase inductance.
2.3. Control Implementation Strategy
The overall control idea of the system is to calculate the on signal Ton_ac and off signal Toff_ac of the main control switch S2 and the on signal Ton_sr and off signal Toff_sr of the synchronous rectifier S1 in combination with the corresponding time length of each mode deduced above. Then, the zero crossing detector (ZCD) signal is used as the reference trigger signal of each switch cycle, and the control is carried out according to the calculated opening and closing time of each switch tube.
Figure 9 shows the relationship between the inductance current and control signal in a switching cycle. Each control signal is as follows:
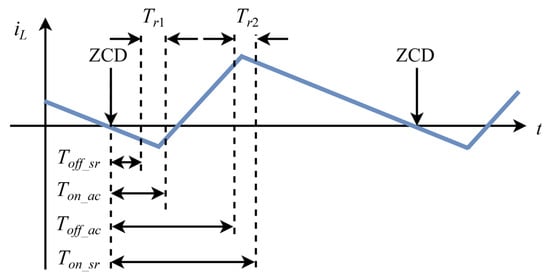
Figure 9.
Control signal corresponding to inductor current within one switching cycle.
Figure 10 is the overall control block diagram of the totem-pole bridgeless PFC circuit under improved control. The output voltage Uo of the circuit is different from the reference voltage Uref, where Uref = 400 V. The error voltage is multiplied by the output signal of the PI regulator and the phase signal of Uin to obtain the inductance current reference current iref, that is, the average inductance current iL_avg. iref undergoes real-time computation using the sampled Uin and Uo to generate switching signals for both the high-frequency main control switch and rectifier. These signals can control the opening and closing of the main-phase high-frequency switches S1 and S2 at the specific time calculated in real time based on the ZCD signal. Since the switching period of the main phase continuously changes with the power frequency period, it is necessary to accurately determine the switching period TS of the main-phase bridge arm tube through real-time sampling and calculation. The working process of the main phase is started by the ZCD signal ZCD-M of the main phase, while the slave phase begins operation after a time delay of TS/2 relative to the main-phase turn-on instant.
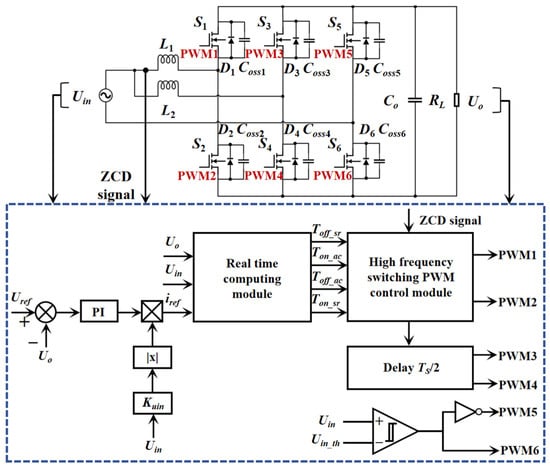
Figure 10.
Overall control block diagram of totem-pole bridgeless PFC circuit based on collaborative optimization control strategy.
The determination of the TS/2 delay time depends on the previous switching cycle value of the main phase. After 1/2 switch cycle delay, the main circuit drive signal is synchronized with the slave circuit drive signal, and the specific control time of the opening and closing of the slave phase high-frequency switches S3 and S4 is equal to that of the main circuit. The sampling input voltage Uin numerical signal is combined with the Uin phase signal to control the opening and closing of power frequency switches S5 and S6. Finally, the PWM module in the microcontroller unit (MCU) is configured to generate the corresponding drive signal to control the opening and closing of switches.
3. Optimal Design of AC Input Voltage Sampling Circuit
PFC monitors the input voltage signal in real time for subsequent loop calculation and maintains the circuit operation. In addition, the control chip needs to detect whether the input voltage exceeds the limit through the input voltage sampling circuit, trigger the protection circuit to turn off the PWM, and prevent subsequent DC/DC and load damage. Therefore, a 220 VAC input voltage sampling circuit is the key link of system stability and performance optimization [28,29,30].
The traditional 220 VAC input voltage sampling circuit often needs to build a positive and negative half-cycle phase-detection circuit and a digital differential sampling circuit, which has a complex circuit structure. In addition, the external reference voltage of the control chip may fluctuate, and the signal sampling will introduce errors due to the change in the power supply voltage. Therefore, this paper selects the internal 1.19 V reference source of the control chip STC32F12K54 as the reference voltage. The output voltage range of the numerical sampling circuit should be strictly constrained to 0~1.19 V, which requires the auxiliary power supply to provide the additional offset voltage of the sampling circuit and offset the negative voltage to the positive voltage to meet the processing requirements of the processor. The auxiliary power supply is mainly responsible for converting the high voltage of the system into the stable low-voltage DC power required by the controller, sampling circuit, switch driver circuit, and other peripheral circuits. It needs to continuously supply power to the peripheral circuits when the equipment is working. Therefore, too many offset voltages with different values will increase the workload of the auxiliary power supply design [31,32,33].
To address these challenges, this paper proposes an optocoupler-based input voltage sampling circuit optimization. As illustrated in Figure 11, the designed circuit can simultaneously realize two sampling functions of the input voltage value and phase and has higher synchronization. The optimization scheme has multiple advantages:
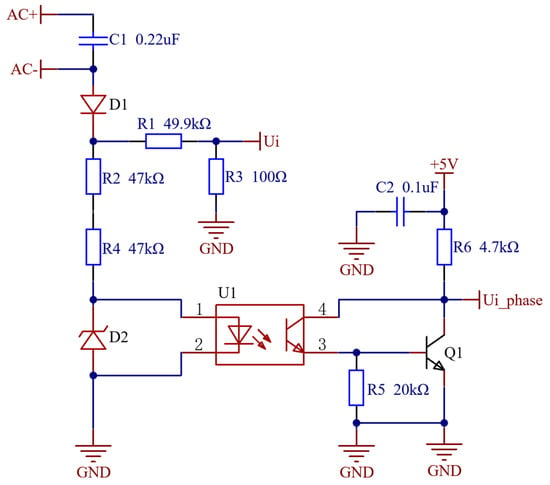
Figure 11.
Input voltage sampling optimization circuit.
- There is no electrical connection between the input and output of the optocoupler through optical signal transmission. The isolation voltage of the optocoupler is generally 1~5 kV to achieve electrical isolation, which can isolate the common ground interference between the high-voltage side of input sampling and the low-voltage side of signal processing, as well as a series of signal interference such as grid fluctuation, motor interference, and other common mode noise that may exist;
- The optimized circuit enhances the synchronization of the voltage value and phase signal, reduces the number of components, and reduces the material cost;
- This design greatly simplifies the design requirements for auxiliary power supply, and only a single +5 V power supply is required to meet all sampling requirements [34,35].
In the specific implementation, the digital sampling part of the input-voltage-sampling-optimization circuit adopts the resistance voltage division mode, and the sampling voltage AC− is connected to the ADC input pin of the MCU after proportional attenuation through the resistance voltage division circuit. Taking the selected control chip STC32F12K54 as an example, the voltage range at the input ADC pin can be set according to its ADC part external reference voltage source value or MCU internal reference voltage source value. This circuit selects the internal 1.19 V reference source as the reference voltage, so that the output amplitude of the numerical detection is strictly limited to the intermittent sinusoidal steamed bread wave within the range of 0~1.19 V.
In the phase-detection part, the sampling voltage AC is grounded through the diode, resistance and reverse diode, the reverse diode is connected in parallel to the optocoupler, the optocoupler output is connected to the triode, and its collector is connected to the +5 V voltage through the resistance. This collector output connects directly to the MCU’s ADC pin, utilizing the optocoupler’s switching characteristics to convert the AC voltage into a processed input signal via the diode rectifier network. The output end of the optocoupler adopts a common emitter triode circuit to convert the signal into a square wave signal with an amplitude of +5 V, which can be directly connected to the ADC pin of the MCU for phase identification.
The corresponding relationship of voltage waveforms of power frequency input voltage Uin, optocoupler input terminal voltage U1, and optocoupler output terminal voltage Uin_phase is shown in Figure 12. The light-emitting tube at the input side of the optocoupler has a certain conduction threshold, such as the optocoupler PC817C used in the figure, which has a conduction threshold of about 1.2 V. Consequently, the optocoupler-extracted waveform information does not initiate from the zero level. However, when processing the 220 V RMS input voltage, the threshold voltage effect becomes negligible, enabling the accurate extraction of both period and phase information. Observing the U1 and Uin_phase waveforms, the input and output of the optocoupler are reversed, that is; the rising edge of the output waveform is driven by the falling section of the input voltage. Because the collector is connected to the +5 V voltage through resistance, the top of the Uin_phase waveform is limited by the voltage, forming a flat top with an amplitude of 5 V [36].
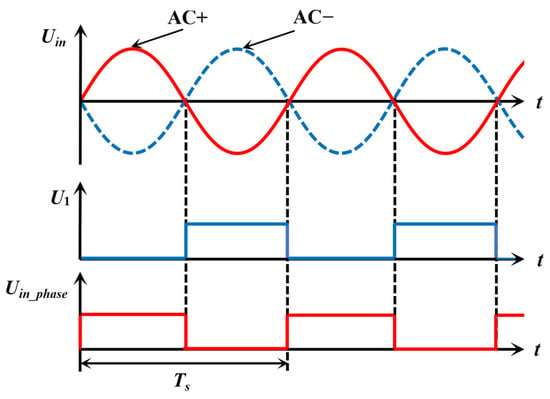
Figure 12.
Voltage waveforms of power frequency input, optocoupler input, and optocoupler output terminals.
The output waveform forms regular square wave characteristics, which is convenient for the MCU to accurately capture zero crossing and phase information. The phase detection only needs to detect the rising/falling edge of the level, which can be directly connected to the ADC pin of the MCU for extracting the phase and period information through the level or jump.
The key parameters of the optocoupler PC817C selected for this study are summarized in Table 3. All parameter values were obtained from the component datasheet. As evident from Table 3, the voltage rise and fall times of the optocoupler are significantly faster compared to the 0.02 s period of the line-frequency input voltage. Furthermore, the relatively low forward voltage drop setting will not adversely affect the overall voltage sampling accuracy.

Table 3.
Key specifications of PC817C optocoupler.
4. Experiment and Discussion
Building upon the theoretical analysis of circuit-improvement techniques, this section validates the effectiveness of the improved control strategy and the proposed AC input voltage sampling circuit through comprehensive simulation and experimental verification.
The medium-power segment has strong adaptability. It can cover a variety of application requirements through parallel or derating use, reduce the R&D cost, and is conducive to the balance between efficiency and cost. The design parameters used in both simulation and experiments are identical, and Table 4 shows the main design parameters of the circuit.

Table 4.
Main design parameters of circuit.
4.1. Simulation Analysis
To validate the proposed control optimization strategy, a complete system model is developed in MATLAB 2021a/Simulink based on the overall control framework presented in Figure 9, followed by a comprehensive analysis of the test results.
Figure 13 shows the overall waveform of a single inductor current at full load. The current envelope follows the sinusoidal variation of the Uin, showing the working characteristics of CRM.
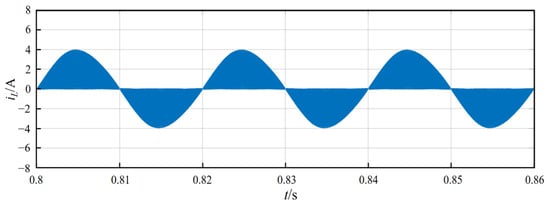
Figure 13.
Single-phase inductance current waveform.
Figure 14 shows the input voltage Uin, output voltage Uo, single inductance current amplification waveform, and the switching waveform UGS2 and terminal voltage UDS2 of the main switch S2. The drain-source voltage UDS2 of S2 is the terminal voltage at both ends of S2. The gate-source voltage UGS2 of S2 indicates the switching condition of S2. There are differences between the simulation environment and the actual experiment. The actual threshold voltage of the switch driver needs to refer to the specific datasheet. In the simulation, UGS2 is 1 V, indicating that a 1 V voltage is applied to the S2 grid to drive S2 on, and UGS2 is 0 V, indicating that S2 is in the off state. As shown in the figure, when either Uin > 0.5Uo or Uin ≤ 0.5Uo, UGS2 rises from 0 V to 1 V only after UDS2 drops to 0 V. This verifies that the TCM method achieves ZVS across the entire operating range, thereby reducing switching losses.
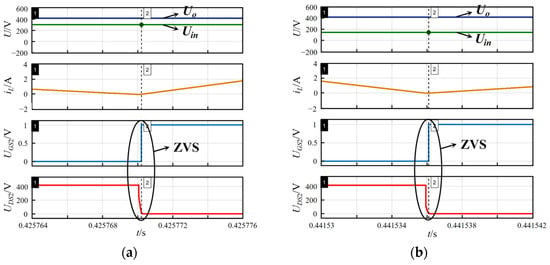
Figure 14.
Main control tube realizes the full working-range ZVS: (a) when Uin > 0.5Uo, the main control switch tube realizes ZVS; (b) when Uin ≤ 0.5Uo, the main control switch tube realizes ZVS.
Figure 15 is the output voltage waveform. The Uo is stable at 400 V, and the voltage ripple is within 5%. Figure 16 shows the waveform of input voltage and current. The input voltage and input current have the same phase and a high sinusoidal degree, indicating that the system can effectively achieve power factor correction.
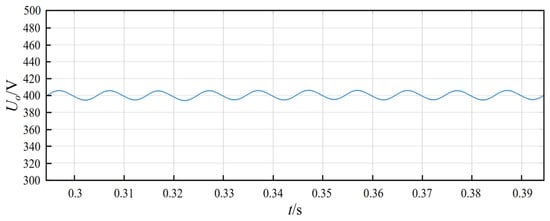
Figure 15.
Output voltage waveform diagram.
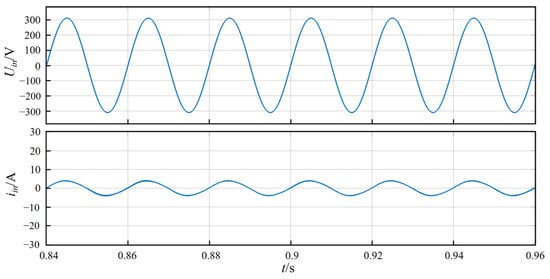
Figure 16.
Waveform diagram of input voltage and current.
Figure 17a,b are the overall and amplified waveforms of the inductance current of the main phase and the slave phase, respectively. The inductance current waveforms of the two branches are presented in a staggered manner based on the same phase of the outer contour. The phase difference is half of the switching cycle, and the waveform characteristics maintain good consistency.
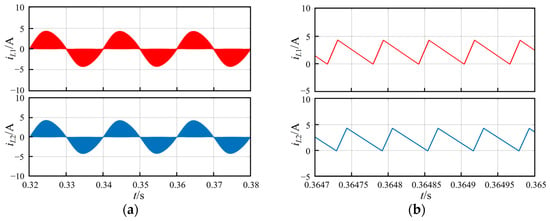
Figure 17.
Two-phase inductor current waveform: (a) overall waveform of inductance current of two branches; (b) two-branch inductance current amplification waveform.
Figure 18 shows the waveforms of the branch current and total inductance current of two inductors. The branch inductor current exhibits a period of approximately 19.077 μs, with an intercurrent phase difference of about 9.522 μs, corresponding to half the current period. The ripple of the iL is about 1 A, and the ripple of the one-phase inductance current is about 1.5 A. It can be seen that the ripple of the total inductance current after interleaving control is less than that of the inductance current of any branch, which thoroughly verifies the ripple-cancellation effect of the interleaving parallel technology based on TCM and proves the effective integration of the improved control technology.
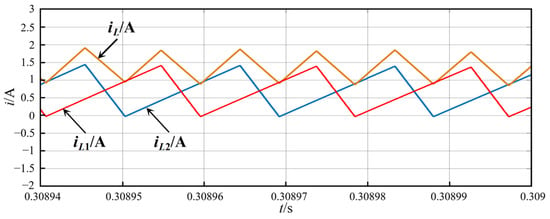
Figure 18.
Two-phase inductor branch current and total current waveform.
4.2. Empirical Test
Figure 19 is the prototype of the designed totem-pole bridgeless PFC. Based on the system control framework constructed in Figure 10, the overall program flow chart of digital control software for the circuit is shown in Figure 20. The main program is mainly responsible for initializing and setting the system, peripherals, and variables. After completing the configuration, initialize all modules, activate the timer, and wait for interruption.

Figure 19.
Experimental prototype.
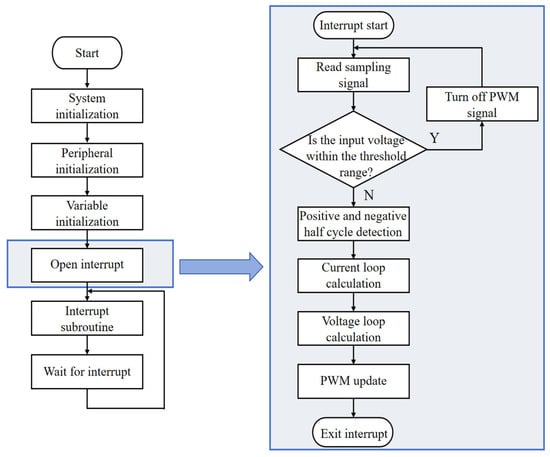
Figure 20.
Overall program flow chart of control chip.
After the system triggers the interrupt, first read the sampling signal to determine whether the input voltage value is within the set dead band threshold. If it is, turn off the switch. If it is not, further determine the positive and negative half cycles of the input voltage. Next, the loop calculation is carried out to calculate the opening and closing time and switching cycle of the main switch tube and the synchronous rectifier tube, update the PWM output, and finally exit the interrupt and run the interrupt program once. To avoid the influence of signal jitter on the accuracy of level reading in the process of sampling signal extraction, the MCU can read several times and take most of the results as the reading results to eliminate jitter. The fast interruption of each switching cycle is triggered by the ZCD signal.
Figure 21a shows the measured input voltage and current waveforms. The iin filtered by the LC circuit is sinusoidal and in phase with the Uin, realizing the power-factor-correction function of the circuit. Figure 21b shows the measured output voltage waveform at full load at 220 VAC. To better visualize the ripple characteristics of Uo, the oscilloscope’s central axis was calibrated to represent a 300 V DC offset voltage reference during measurements. The Uo is stable at 400 V, and the voltage ripple is ≤5% Uo, which is 20 V.
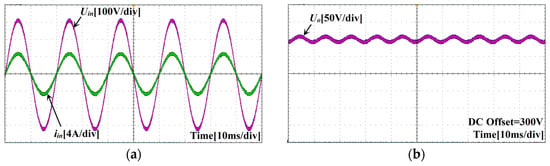
Figure 21.
System input and output waveforms: (a) input voltage and input current test waveforms; (b) output voltage test waveform.
According to the plane trajectory curve of the iLZn-UDS2 state in Figure 5, TCM control is not necessary when Uin ≤ 0.5Uo. When the inductance current drops to 0, the rectifier tube is not required to extend the conduction time, and the system can realize ZVS naturally. Therefore, it is essential to test the implementation of ZVS with TCM control when Uin > 0.5Uo. If ZVS can still be realized in this case, it can be further considered that the circuit can realize ZVS in the full operating range.
Figure 22 presents the measured waveforms under 220 VAC input conditions with Uin > 0.5Uo, showing the single-phase inductor current iL1 along with the gate-source voltage UGS2 of the main control switch S2 and the drain-source voltage UDS2 of the main control switch S2. After the inductance current passes 0, the synchronous rectifier S1 is extended and turned off, so that the voltage resonance at the junction capacitor Coss2 end of S2 is 0. After the voltage UDS2 at S2 end is reduced to 0, S2 is turned on again, and ZVS is realized.
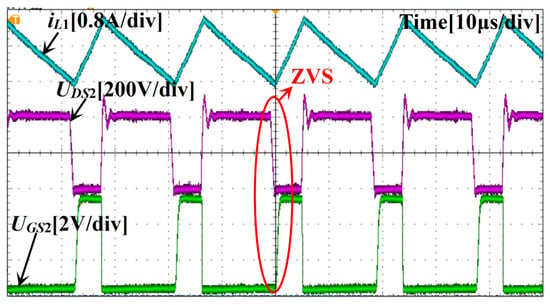
Figure 22.
When Uin > 0.5Uo, the main control switch S2 achieves ZVS.
The waveforms of input voltage Uin and two-phase inductive currents iL1 and iL2 are shown in Figure 23a. Under the interleaving control, the current envelope of the two-phase inductors is sinusoidal, the phase is consistent with the input voltage, and the value is uniform. Figure 23b shows the two-phase inductance current amplification waveform. The inductor currents in both branches exhibit a period of approximately 28.9 μs, with a phase difference of about 14.5 μs between them—corresponding to half of the current period. By employing 180° interleaved phase control, the system achieves a significant reduction in the total inductor current ripple.
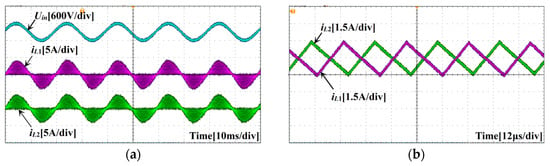
Figure 23.
Interleaved parallel control-related waveform: (a) experimental waveforms of input voltage and two-phase inductive current; (b) enlarged waveform of two-phase inductive current experiment.
The input voltage and current were connected as one channel pair, while the output voltage and current were connected as another channel pair to the power analyzer, enabling direct measurement of input power Pin, output power Po, and apparent power S. These measurements allowed the subsequent calculation of both the circuit efficiency η and power factor PF. Figure 24a shows the efficiency η of the prototype. The peak efficiency is 97.3%, and the efficiency at full load is 97.1%. Figure 24b shows the PF of the circuit. Under rated operating conditions, the converter maintains a PF above 0.99, thereby achieving power factor correction functionality.
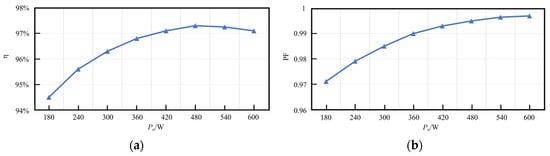
Figure 24.
Efficiency and power factor curves of the circuit under different output powers Po: (a) circuit efficiency test curve; (b) circuit power factor test curve.
The test results verify the effectiveness and synergy of the improved strategy, and the test waveform can be presented correctly. At the same time, it also shows the correctness of the optimization design principle of the Uin sampling circuit.
Table 5 provides a comparison between the proposed improved control approach and existing control strategies for TCM totem-pole bridgeless PFC converters. The converter topologies presented in [17,18,24] are restricted to single-phase configurations with [24] further requiring dedicated inductor current sensing and those in [16,17] employing complex dual-controller coordination schemes; the proposed converter architecture offers advantages through its single-controller implementation, elimination of current sampling requirements, and inherent current ripple-reduction capability enabled by interleaved parallel operation.

Table 5.
Comparisons of the proposed method and existing methods.
5. Conclusions
This paper mainly studies the defects of the totem-pole bridgeless PFC circuit based on TCM mode and makes a systematic improvement to research from the two dimensions of integrating interleaving technology and input AC voltage sampling optimization. Aiming at the problem that the TCM control based on CRM mode further increases the current ripple of the inductor, which leads to the increase in the stress of the power device and the increase in the size of the inductor, the interleaving parallel technology is integrated to solve the proposed defects based on realizing the full-working-range ZVS. Furthermore, addressing the limitation of conventional AC input voltage sampling circuits that require separate phase and magnitude sampling circuits, this paper designed an optimized sampling circuit that adapts to various control chip pin voltage requirements. This improved design enhances synchronization between the voltage phase and magnitude measurements while reducing the component count, with the incorporated optocoupler providing additional electrical isolation. The experimental results show that the improved method can effectively reduce the inductance current ripple based on the full-operating-range ZVS, and the effectiveness of the results can also verify the correctness of the design principle of the sampling optimization circuit.
However, the characteristic parameters of the proposed optocoupler-based input voltage sampling circuit—including response time, noise immunity, and phase error—are of critical importance, yet experimental testing of these parameters has not been conducted in the current study. We will address this limitation in our subsequent work by performing comprehensive experimental characterization of the proposed circuit.
Author Contributions
Conceptualization, P.N. and Z.G.; methodology, S.G.; software, J.G.; validation, P.N., J.G., Z.G., J.Y. and S.G.; formal analysis, S.G.; investigation, J.Y.; resources, P.N.; data curation, J.Y.; writing—original draft preparation, J.G.; writing—review and editing, J.G.; visualization, J.Y.; supervision, Z.G.; project administration, P.N.; funding acquisition, P.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Key R&D Program of China, grant number 2024YFB3613202.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
Author Zhigang Gao was employed by the company Tianjin Expansion Technology Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PFC | Power Factor Correction |
| SMPS | Switching Mode Power Supply |
| TCM | Triangular Current Mode |
| CRM | Critical Conduction Mode |
| CCM | Continuous Current Mode |
| DCM | Discontinuous Current Mode |
| WBG | Wide-Bandgap |
| OBC | On-Board Charger |
| ZVS | Zero-Voltage Switching |
| VS | Valley Switching |
| ZCS | Zero-Current Switching |
| MCU | Microcontroller Unit |
| ZCD | Zero Crossing Detector |
| ADC | Analog-to-Digital Converter |
References
- Asa, E.; Xue, L.; Mohammad, M. A 1MHz Oak Ridge AC/DC Converter for UAV Contactless Charger Implementation. In Proceedings of the 2022 IEEE Applied Power Electronics Conference and Exposition (APEC), Houston, TX, USA, 20–24 March 2022. [Google Scholar] [CrossRef]
- Son, W.-J.; Lee, B.K. Design and Analysis of High Power Density On-Board Charger with Active Power Decoupling Circuit for Electric Vehicles. Energies 2023, 16, 7450. [Google Scholar] [CrossRef]
- Shahzad, D.; Farooq, M.; Pervaiz, S. A High-Power-Density High-Efficiency Soft-Switched Single-Phase Universal Input to 28-V Isolated AC-DC Converter Module Designed for Paralleled Operation. IEEE Trans. Power Electron. 2022, 37, 8262–8280. [Google Scholar] [CrossRef]
- Zhou, K.; Chen, S.-M.; Jin, N.-Z.; Sun, D.-Y. Research on Single-Phase and Three-Phase Compatible Isolated On-Board Charger and Control Technology. Energies 2022, 15, 6445. [Google Scholar] [CrossRef]
- Singh, B.; Singh, B.N.; Chandra, A.; Al-Haddad, K.; Pandey, A.; Kothari, D.P. A review of single-phase improved power quality AC-DC converters. IEEE Trans. Ind. Electron. 2003, 50, 962–981. [Google Scholar] [CrossRef]
- García, O.; Cobos, J.A.; Prieto, R. Single phase power factor correction: A survey. IEEE Trans. Power Electron. 2003, 18, 749–755. [Google Scholar] [CrossRef]
- IEC 61000-3-2. Consolidated Version. Available online: https://webstore.iec.ch/en/publication/18726 (accessed on 14 June 2025).
- GB/T 14549-1993. Quality of Electric Energy Supply-Harmonics Inpublic Supply. Available online: https://openstd.samr.gov.cn/bzgk/gb/newGbInfo?hcno=10A576E61901DA59E9A6AC555C2BAFD1 (accessed on 14 June 2025).
- IEEE 519-2014. IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems. Available online: https://standards.ieee.org/ieee/519/3710/ (accessed on 14 June 2025).
- Chen, F.-Z.; Maksimović, D. Digital control for improved efficiency and reduced harmonic distortion over wide load range in boost PFC rectifiers. IEEE Trans. Power Electron. 2010, 25, 2683–2692. [Google Scholar] [CrossRef]
- Lee, Y.-D.; Kim, C.-E.; Baek, J.-I.; Kim, D.-K.; Moon, G.-W. A Zero-Voltage-Switching Totem-pole Bridgeless Boost Power Factor Correction Rectifier having Minimized Conduction Losses. In Proceedings of the 2018 International Power Electronics Conference (IPEC-Niigata 2018-ECCE Asia), Niigata, Japan, 20–24 May 2018. [Google Scholar] [CrossRef]
- Li, B.; Zhang, R.; Zhao, N. GaN HEMT Driving Scheme of Totem-Pole Bridgeless PFC Converter. In Proceedings of the IEEE International Power Electronics and Application Conference and Exposition (IEEE PEAC), Shenzhen, China, 4–7 November 2018. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, S.; Li, B. Totem-pole Bridgeless Boost PFC Converter Based on GaN HEMT for Air Conditioning Applications. In Proceedings of the 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 20–22 October 2018. [Google Scholar] [CrossRef]
- Shi, K.; Shoyama, M.; Tomioka, S. Common mode noise reduction in totem-pole bridgeless PFC converter. In Proceedings of the 2014 International Power Electronics and Application Conference and Exposition, Shanghai, China, 5–8 November 2014. [Google Scholar] [CrossRef]
- Han, J.-K. Efficiency and PF Improving Techniques with a Digital Control for Totem-Pole Bridgeless CRM Boost PFC Converters. Energies 2024, 17, 369. [Google Scholar] [CrossRef]
- Marxgut, C.; Biela, J.; Kolar, J.W. Interleaved triangular current mode (TCM) resonant transition, single phase PFC rectifier with high efficiency and high power density. In Proceedings of the IEEE International Power Electronics Conference (ECCE-Asia), Sapporo, Japan, 21–24 June 2010. [Google Scholar] [CrossRef]
- Biela, J.; Hassler, D.; Miniböck, J. Optimal design of a 5kW/dm3/98.3% efficient TCM resonant transition single-phase PFC rectifier. In Proceedings of the IEEE International Power Electronics Conference (ECCE-Asia), Sapporo, Japan, 21–24 June 2010. [Google Scholar] [CrossRef]
- Su, B.; Zhang, J.; Lu, Z. Totem-Pole Boost Bridgeless PFC Rectifier with Simple Zero- Current Detection and Full-Range ZVS Operating at the Boundary of DCM/CCM. IEEE Trans. Power Electron. 2011, 26, 427–435. [Google Scholar] [CrossRef]
- Zhu, K.; O’Grady, M.; Dodge, J. 1.5 kW single phase CCM totem-pole PFC using 650V SiC cascodes. In Proceedings of the 2016 IEEE 4th Workshop on Wide Bandgap Power Devices and Applications (WiPDA), Fayetteville, AR, USA, 7–9 November 2016. [Google Scholar] [CrossRef]
- Liu, Z.; Li, B.; Lee, F.C. Design of CRM AC/DC converter for very high-frequency high-density WBG-based 6.6 kW bidirectional on-board battery charger. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Z.; Wang, S. A 300-kHz 6.6-kW SiC Bidirectional LLC Onboard Charger. IEEE Trans. Ind. Electron. 2020, 67, 1435–1445. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, X.; Mu, M. Design and evaluation of GaN-based dual-phase interleaved MHz critical mode PFC converter. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014. [Google Scholar] [CrossRef]
- Le, H.N.; Itoh, J.-I. Wide-Load-Range Efficiency Improvement for High-Frequency SiC-Based Boost Converter with Hybrid Discontinuous Current Mode. IEEE Trans. Power Electron. 2018, 33, 1843–1854. [Google Scholar] [CrossRef]
- Huang, Q.; Yu, R.; Ma, Q. Predictive ZVS Control with Improved ZVS Time Margin and Limited Variable Frequency Range for a 99% Efficient, 130-W/in3 MHz GaN Totem-Pole PFC Rectifier. IEEE Trans. Power Electron. 2019, 34, 7079–7091. [Google Scholar] [CrossRef]
- Tang, Y.; Ding, W.; Khaligh, A. A bridgeless totem-pole interleaved PFC converter for plug-in electric vehicles. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016. [Google Scholar] [CrossRef]
- Cho, J.-H.; Kim, D.-K.; Bae, H.-H. A Fully Integrated Multi-Phase Buck Converter with On-Chip Capacitor Dynamic Re-Allocation and Fine-Grained Phase-Shedding Techniques. IEEE J. Solid-State Circuits 2022, 57, 3840–3852. [Google Scholar] [CrossRef]
- Dudak, A.T.; Bakan, A.F. A Digital Iterative Learning Based Peak Current Mode Control for Interleaved totem-pole PFC Circuit. Energies 2024, 17, 5026. [Google Scholar] [CrossRef]
- Ye, Z.; Zhu, D.; Yang, H. Totem-Pole PFC Reliability and Performance Improvement with Advanced Controls. IEEE Power Electron. Mag. 2022, 9, 37–44. [Google Scholar] [CrossRef]
- Wen, Y.; Ruan, L. Stability analysis of voltage sampling circuits applied to switching mode power supply with fully-immersed evaporative cooling. In Proceedings of the 2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, NSW, Australia, 11–14 August 2017. [Google Scholar] [CrossRef]
- Yang, C.; Zheng, S.; Feng, R. Design and Implementation of the Anti-noise High Precision Voltage/Current Data Acquisition System. In Proceedings of the 2020 15th IEEE Conference on Industrial Electronics and Applications (ICIEA), Kristiansand, Norway, 9–13 November 2020. [Google Scholar] [CrossRef]
- Motahari, M.; Daneshvar, A.R.; Tahami, F. A Comparative Analysis of the Reliability of Auxiliary Power Supplies. In Proceedings of the 2025 16th Power Electronics, Drive Systems, and Technologies Conference (PEDSTC), Tabriz, Iran, 4–6 February 2025. [Google Scholar] [CrossRef]
- Kaunkid, S.; Aurasopon, A.; Khamsen, W.; Takeang, C.; Piladaeng, N.; Lloret, J. Resistive Measurement Method for MQ Sensors Based on ADCs of Microcontrollers. IEEE Access 2024, 12, 144364–144376. [Google Scholar] [CrossRef]
- Li, Y.; Chen, H. Design Optimization of Low-Power Microelectronic Circuits Based on CMOS Technology. In Proceedings of the 2025 5th International Conference on Consumer Electronics and Computer Engineering (ICCECE), Dongguan, China, 28 February–2 March 2025. [Google Scholar] [CrossRef]
- Ali, F.B.; Dahman, H.; El Mir, L. Design and Realization of a Temperature Measurement and Control System Adapted to Gas Nanosensors. In Proceedings of the 2025 IEEE 22nd International Multi-Conference on Systems, Signals & Devices (SSD), Monastir, Tunisia, 17–20 February 2025. [Google Scholar] [CrossRef]
- Mikulka, J.; Dušek, J.; Dědková, J.; Pařilková, J.; Műnsterová, Z. A Fast and Low-cost Measuring System for Electrical Impedance Tomography. In Proceedings of the 2019 PhotonIcs & Electromagnetics Research Symposium-Spring (PIERS-Spring), Rome, Italy, 17–20 June 2019. [Google Scholar] [CrossRef]
- Jing, B.; Liu, F.; Li, G.; Xiong, G. Development of a low-power switching signal acquisition device. In Proceedings of the 2023 10th International Forum on Electrical Engineering and Automation (IFEEA), Nanjing, China, 3–5 November 2023. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).