Improved Segmented Control Strategy for Continuous Fault Ride-Through of Doubly-Fed Wind Turbines
Abstract
1. Introduction
2. Analysis of the Principle of Continuous Voltage Ride-Through in Wind Farms
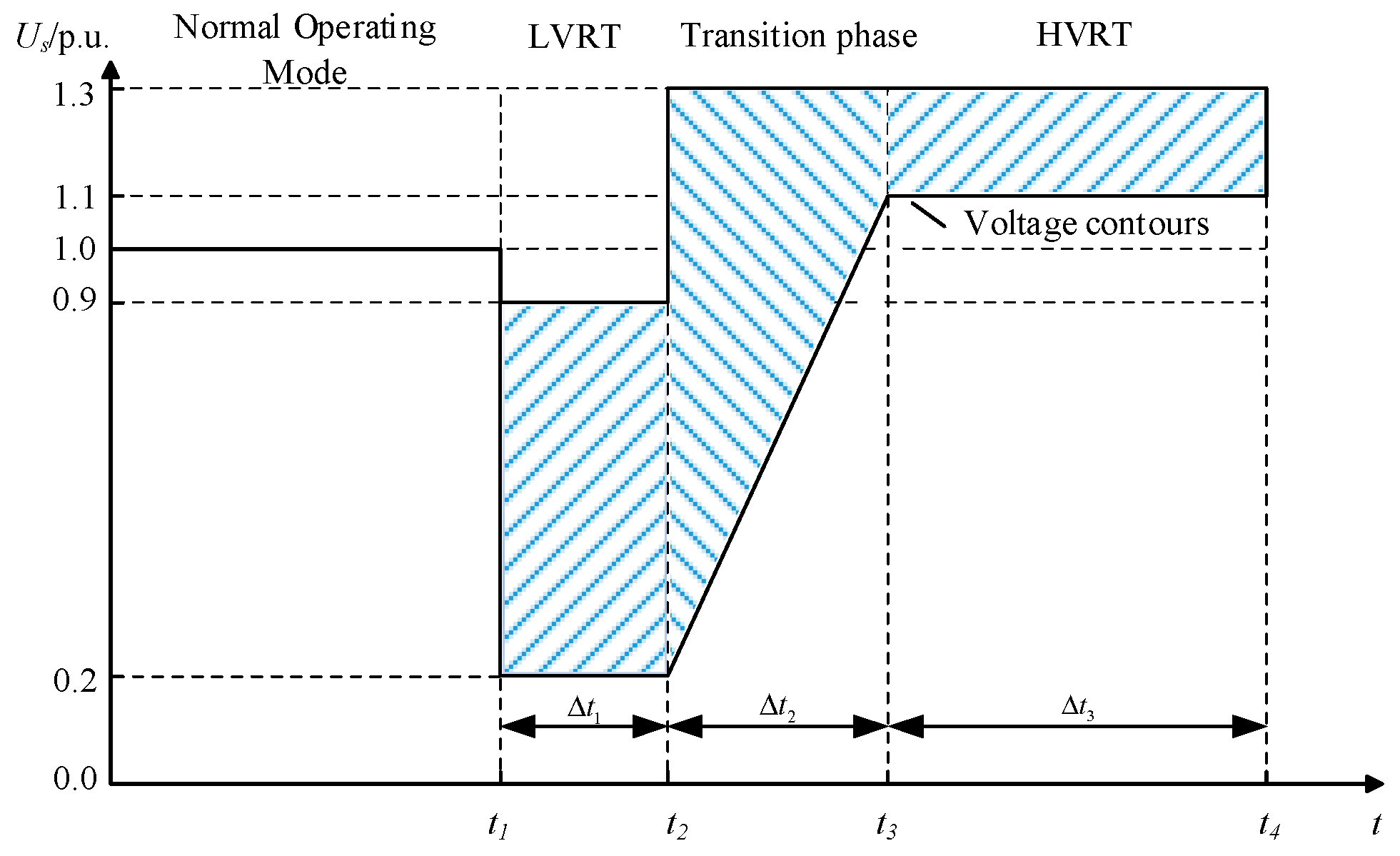
2.1. Requirements for Wind Farm Voltage Continuous Ride-Through
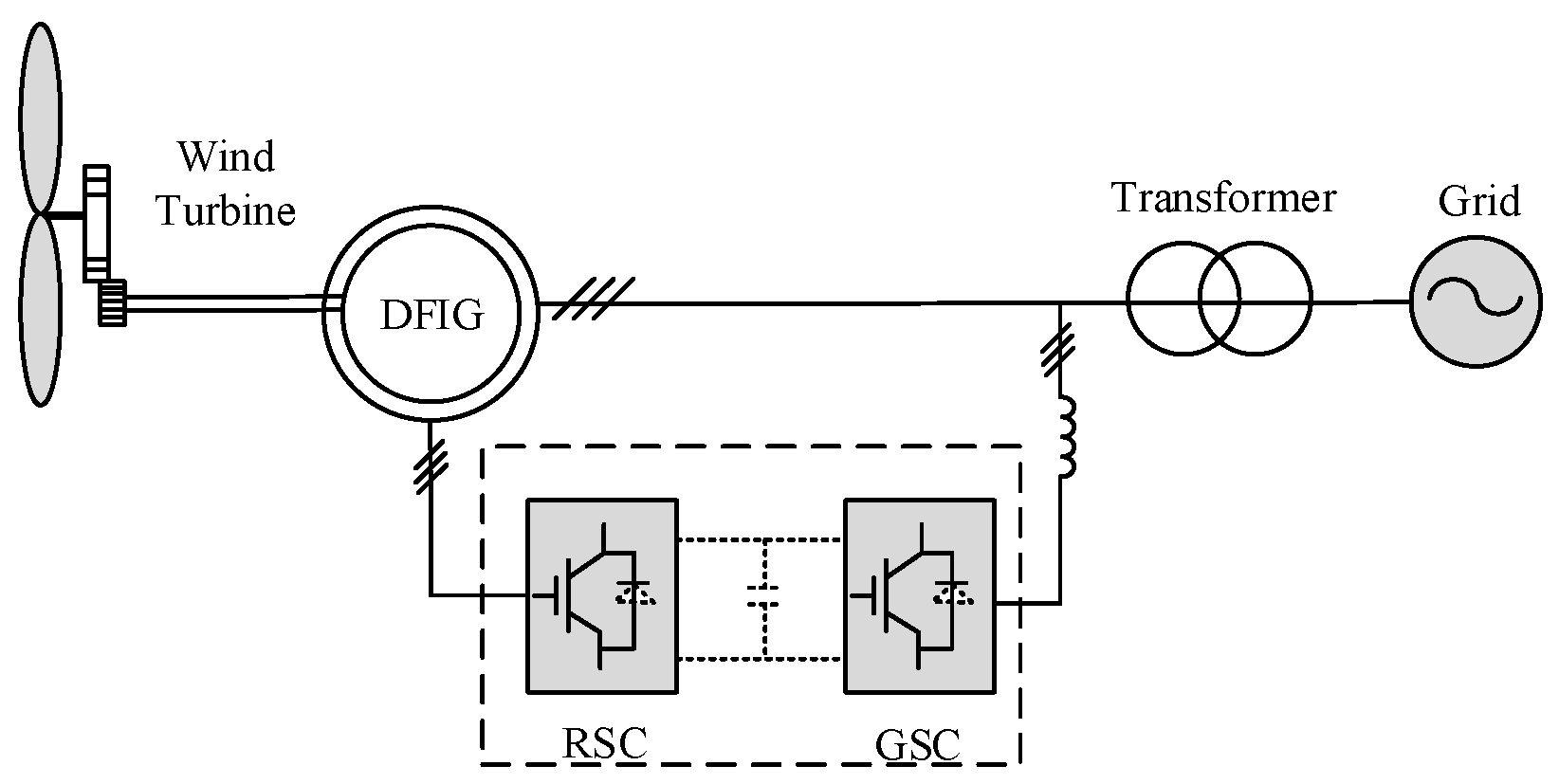
2.2. Transient Modeling of Doubly-Fed Wind Turbines
3. Control Strategy
3.1. Design Principle of Feed-Forward Based on Stator Current Transient Component
3.1.1. Continuous Ride-Through Transient Characteristics
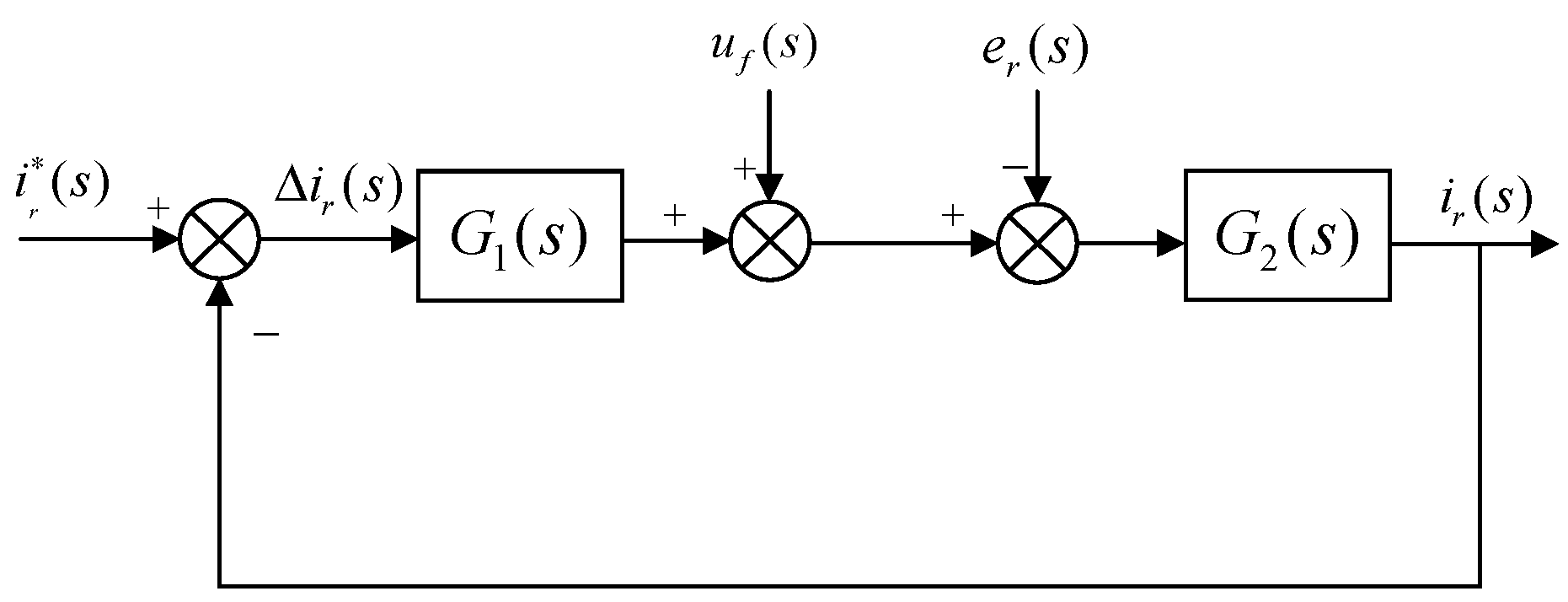
3.1.2. DFIG Rotor Current Loop
3.2. Control Strategy Based on Virtual Resistance
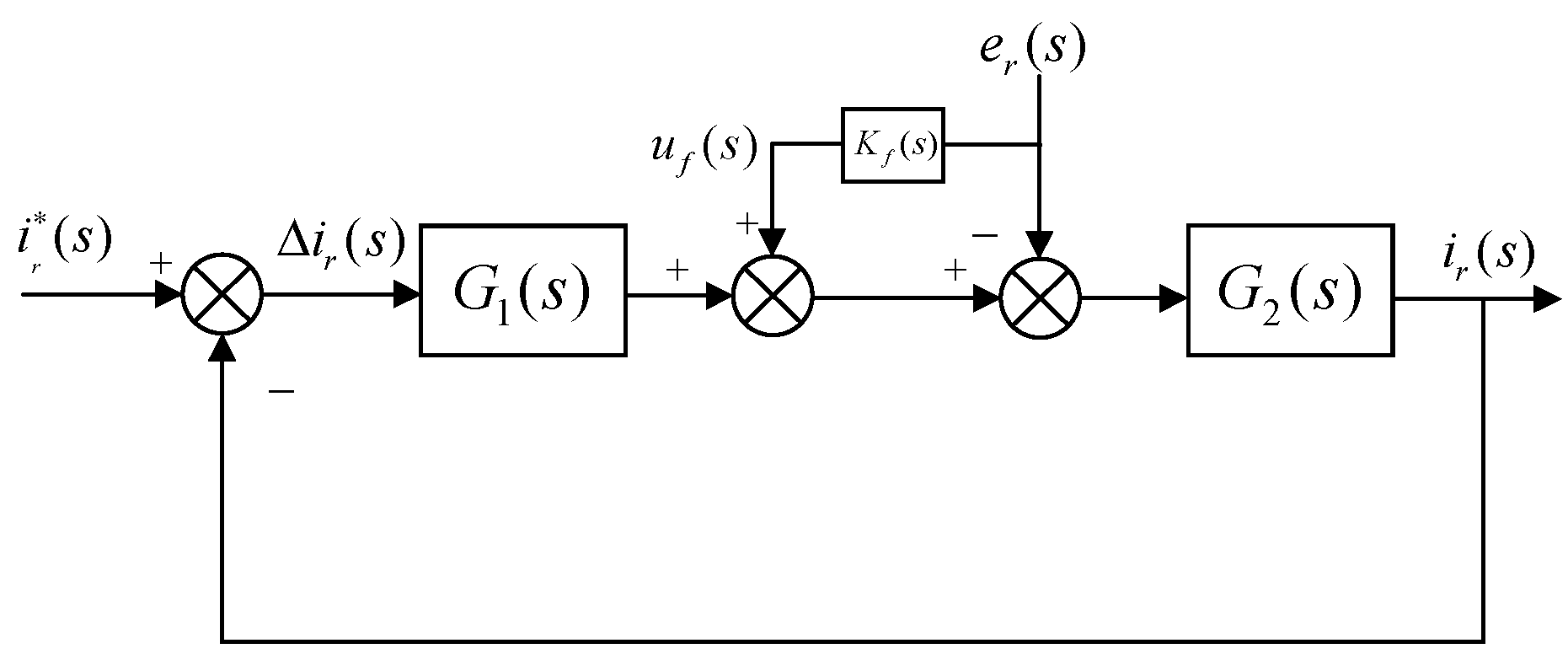
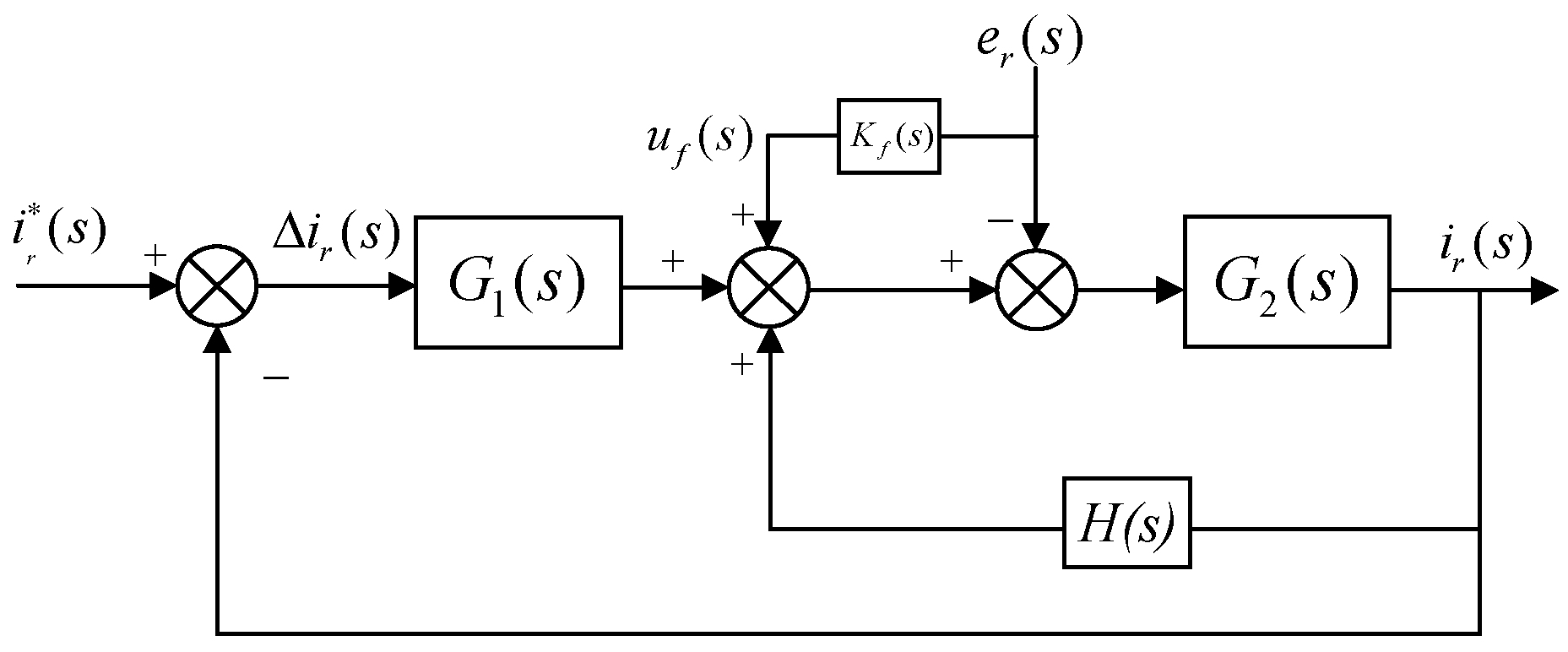
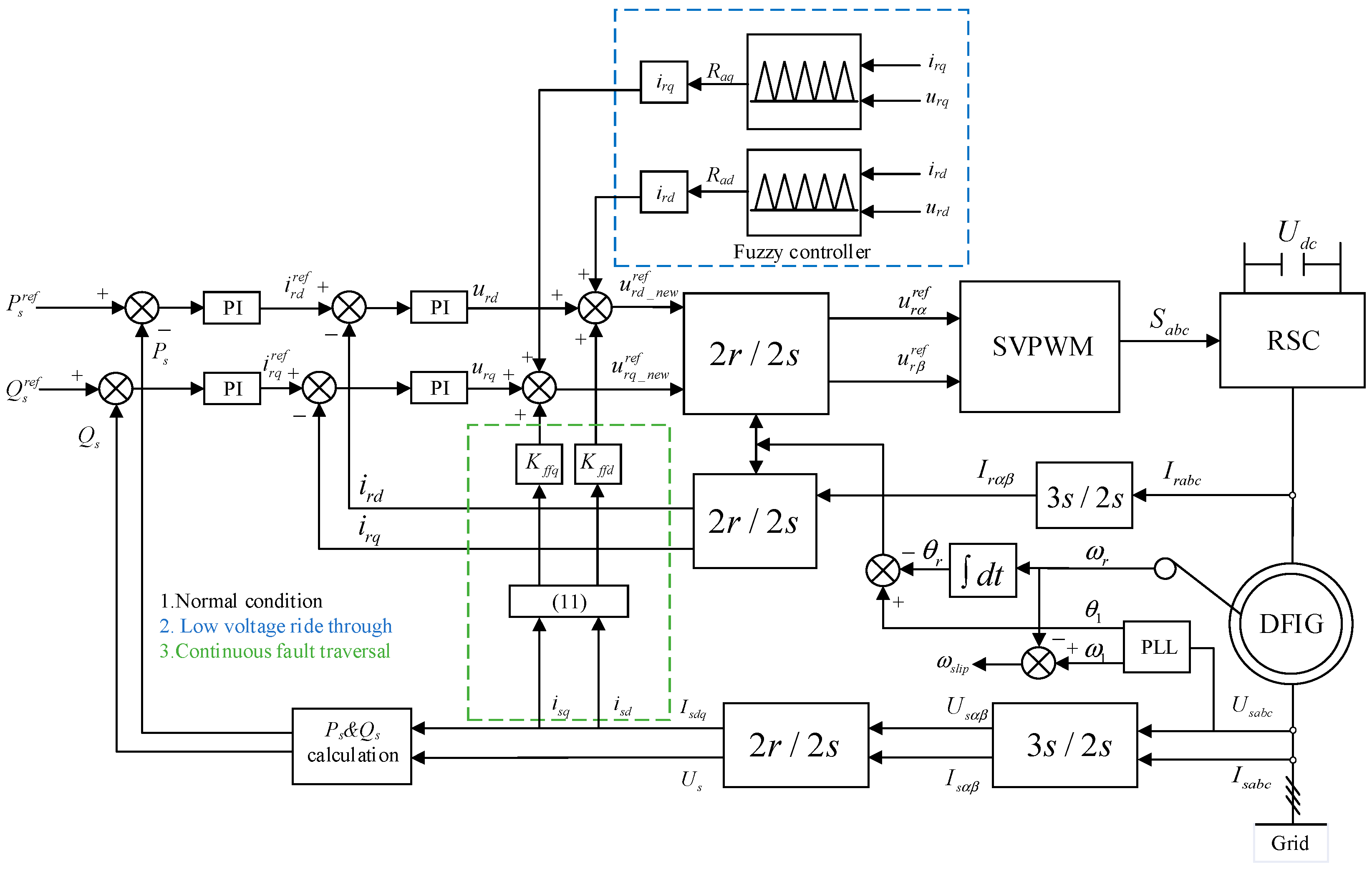
3.2.1. Control System Incorporating Feedforward and Virtual Resistance
3.2.2. Design of Fuzzy Adaptive Link
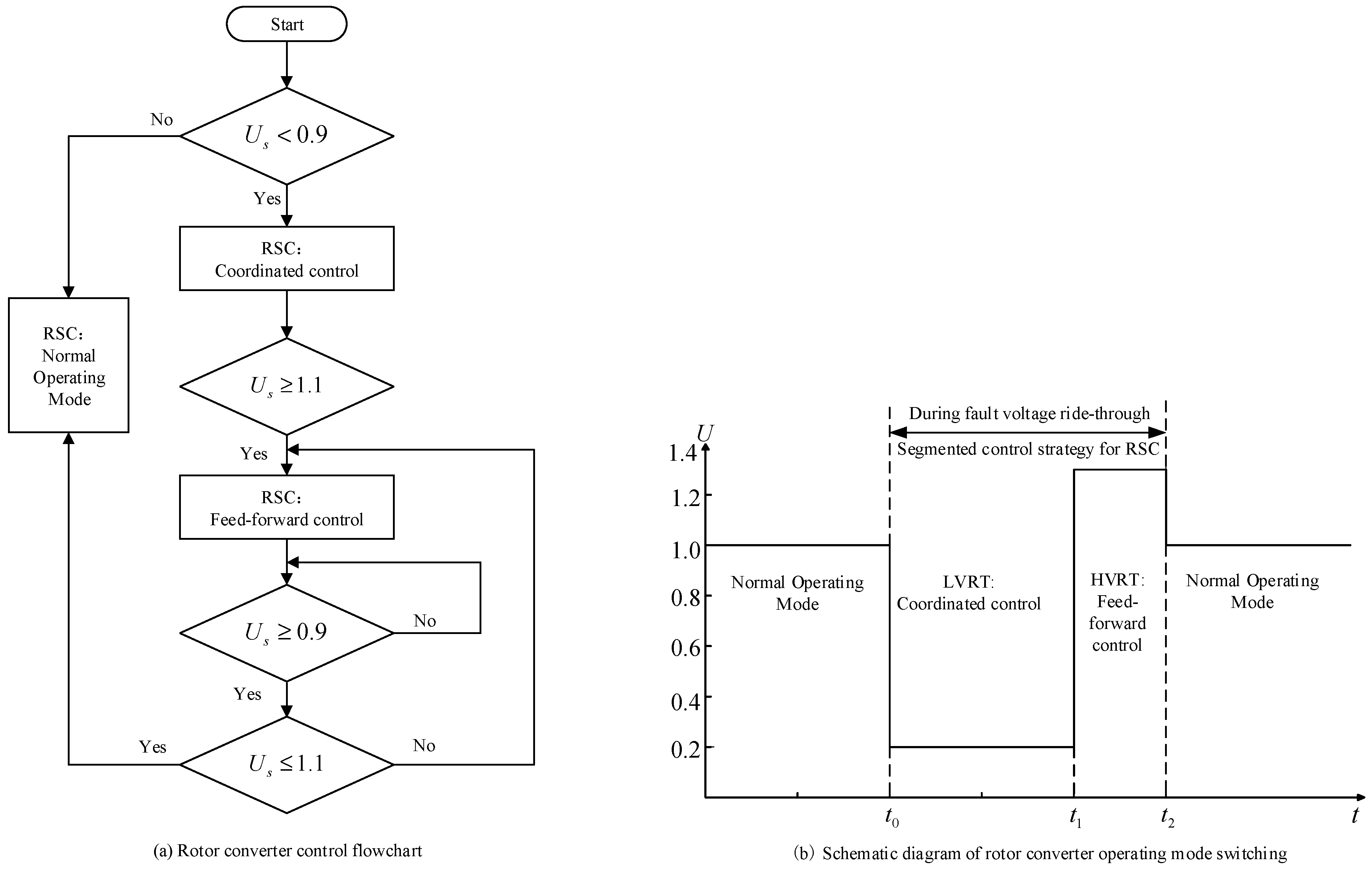
3.3. Segmented Control Strategy
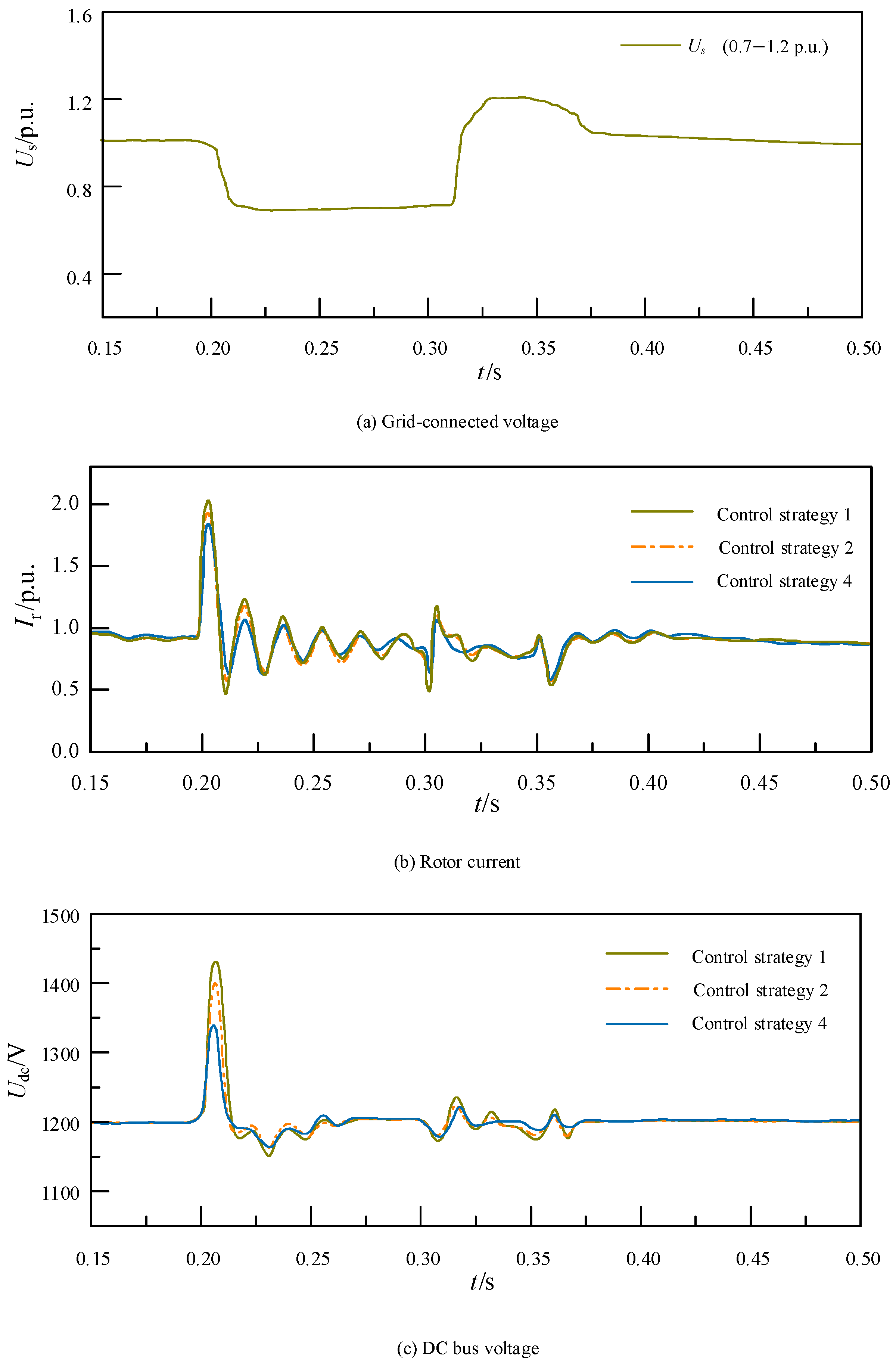
4. Simulation Analysis
4.1. Deep Fault
4.2. Mild Fault
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, W.; Chao, P.; Liang, X.; Ma, J.; Xu, D.; Jin, X. A practical equivalent method for DFIG wind farms. IEEE Trans. Sustain. Energy 2017, 9, 610–620. [Google Scholar] [CrossRef]
- Liu, X.; Li, C.; Shahidehpour, M.; Chen, X.; Yi, J.; Wu, Q.; Sun, K.; Zhou, B. Fault current mitigation and voltage support provision by microgrids with synchronous generators. IEEE Trans. Smart Grid 2020, 11, 2816–2831. [Google Scholar] [CrossRef]
- Zhou, C.; Wang, Z.; Xin, H.; Ju, P. A PQ coordination based model predictive control for DFIG high-voltage ride through. IEEE Trans. Energy Convers. 2021, 37, 254–263. [Google Scholar] [CrossRef]
- Maheshwari, Z.; Kengne, K.; Bhat, O. A comprehensive review on wind turbine emulators. Renew. Sustain. Energy Rev. 2023, 180, 113297. [Google Scholar] [CrossRef]
- Tian, S.; Chen, W.; Wang, P. Continuous voltage ride-through segmentation control strategy for PMSG-based wind power integrated systems with dynamic reactive current scale factor. Proc. Chin. Soc. Electr. Eng. 2024, 44, 7671–7684. [Google Scholar]
- Onishi, K.; Li, Y.; Koiwa, K.; Liu, F.; Zanma, T.; Liu, K.-Z. Analysis on the operation of crowbar in doubly fed induction generators. Electr. Power Syst. Res. 2023, 215, 108950. [Google Scholar] [CrossRef]
- Xiao, F.; Xia, Y.; Zhang, K.; Zhang, Z.; Yin, X. Fault characteristics analysis of DFIGWT in whole LVRT process considering control strategy switching between RSC and Crowbar. Int. J. Electr. Power Energy Syst. 2023, 145, 108615. [Google Scholar] [CrossRef]
- Ali, M.A.S. Improved Transient Performance of a DFIG-Based Wind-Power System Using the Combined Control of Active Crowbars. Electricity 2023, 4, 320–335. [Google Scholar] [CrossRef]
- Wei, J.; Li, C.; Wu, Q.; Zhou, B.; Xu, D.; Huang, S. MPC-based DC-link voltage control for enhanced high-voltage ride-through of offshore DFIG wind turbine. Int. J. Electr. Power Energy Syst. 2021, 126, 106591. [Google Scholar] [CrossRef]
- Lai, J.; Liu, Y.; Yin, X.; Wang, Y.; Hu, J.; Yin, X.; Zhou, K. A novel hybrid interlinking transformer-integrated DFIG wind power and energy storage system with flexible control strategy. Int. J. Electr. Power Energy Syst. 2025, 168, 110641. [Google Scholar] [CrossRef]
- Tabosa da Silva, P.L.; Rosas, P.A.C.; Castro, J.F.C.; Marques, D.d.C.; Aquino, R.R.B.; Rissi, G.F.; Neto, R.C.; Barbosa, D.C.P. Power Smoothing Strategy for Wind Generation Based on Fuzzy Control Strategy with Battery Energy Storage System. Energies 2023, 16, 6017. [Google Scholar] [CrossRef]
- Ahmed, M.; Kandil, T.; Ahmed, E. Enhancing Doubly Fed Induction Generator Low-Voltage Ride-through Capability Using Dynamic Voltage Restorer with Adaptive Noise Cancellation Technique. Sustainability 2022, 14, 859. [Google Scholar] [CrossRef]
- Rafiee, Z.; Heydari, R.; Rafiee, M.; Aghamohammadi, M.R.; Blaabjerg, F. Enhancement of the LVRT capability for DFIG-based wind farms based on short-circuit capacity. IEEE Syst. J. 2022, 16, 3237–3248. [Google Scholar] [CrossRef]
- Zhu, D.; Zou, X.; Dong, W.; Jiang, C.; Kang, Y. Disturbance feedforward control for type-3 wind turbines to achieve accurate implementation of transient control targets during LVRT. Int. J. Electr. Power Energy Syst. 2020, 119, 105954. [Google Scholar] [CrossRef]
- Sun, L.; Wang, Y. Analysis and performance evaluation for transient whole process of improved control strategy for doubly-fed induction generator during high voltage ride-through. High Volt. Eng. 2019, 45, 593–599. [Google Scholar]
- Zhu, R.; Chen, Z.; Tang, Y.; Deng, F.; Wu, X. Dual-loop control strategy for DFIG-based wind turbines under grid voltage disturbances. IEEE Trans. Power Electron. 2015, 31, 2239–2253. [Google Scholar] [CrossRef]
- Xiang, D.; Ran, L.; Tavner, P.J.; Yang, S. Control of a doubly fed induction generator in a wind turbine during grid fault ride-through. IEEE Trans. Energy Convers. 2006, 21, 652–662. [Google Scholar] [CrossRef]
- Shen, Y.W.; Ke, D.P.; Qiao, W.; Sun, Y.Z.; Kirschen, D.S.; Wei, C. Transient reconfiguration and coordinated control for power converters to enhance the LVRT of a DFIG wind turbine with an energy storage device. IEEE Trans. Energy Convers. 2015, 30, 1679–1690. [Google Scholar] [CrossRef]
- Hu, S.; Lin, X.; Kang, Y.; Zou, X. An improved low-voltage ride-through control strategy of doubly fed induction generator during grid faults. IEEE Trans. Power Electron. 2011, 26, 3653–3665. [Google Scholar] [CrossRef]
- Zhou, D.; Blaabjerg, F. Optimized demagnetizing control of DFIG power converter for reduced thermal stress during symmetrical grid fault. IEEE Trans. Power Electron. 2018, 33, 10326–10340. [Google Scholar] [CrossRef]
- Cheng, P.; Nian, H.; Zhu, Z. Control technique of DFIG based on virtual resistance under symmetrical grid fault. Electr. Mach. Control 2014, 18, 1–8. [Google Scholar]
- Xie, Z.; Zhang, X.; Zhang, X.; Yang, S.; Wang, L. Improved ride-through control of DFIG during grid voltage swell. IEEE Trans. Ind. Electron. 2015, 62, 3584–3594. [Google Scholar] [CrossRef]
- Li, S.; Wang, W.; Wang, R.; Sun, Y.; Chen, C. Control strategy and experiment of high voltage ride-through for DFIG-based wind turbines. Autom. Electr. Power Syst. 2016, 40, 76–82. [Google Scholar]
- Chen, W.; Xu, D.; Zhu, N.; Chen, M.; Blaabjerg, F. Control of doubly-fed induction generator to ride-through recurring grid faults. IEEE Trans. Power Electron. 2015, 31, 4831–4846. [Google Scholar] [CrossRef]
- Jiang, H.; Wang, S.; Li, X.; Xiao, R. Accurate analysis of transient characteristics and ride-through scheme under DFIG low and high voltage cascading fault. Power Syst. Technol. 2021, 45, 4076–4083. [Google Scholar]
- State Administration for Market Regulation; Standardization Administration of the People’s Republic of China. GB/T 19963.1-2021, Technical Specification for Connecting Wind Farm to Power System—Part 1: On Shore Wind Power; Standards Press of China: Beijing, China, 2021. [Google Scholar]
- López, J.; Sanchis, P.; Roboam, X.; Marroyo, L. Dynamic behavior of the doubly fed induction generator during three-phase voltage dips. IEEE Trans. Energy Convers. 2007, 22, 709–717. [Google Scholar] [CrossRef]
- López, J.; Sanchis, P.; Gubía, E.; Ursua, A.; Marroyo, L.; Roboam, X. Control of doubly fed induction generator under symmetrical voltage dips. In Proceedings of the IEEE International Symposium on Industrial Electronics, Cambridge, UK, 30 June–2 July 2008; pp. 2456–2462. [Google Scholar]
- Kovacic, Z.; Bogdan, S. Fuzzy Controller Design: Theory and Applications; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Wang, S.; Shang, L. Fault ride through strategy of virtual-synchronous-controlled DFIG-based wind turbines under symmetrical grid faults. IEEE Trans. Energy Convers. 2020, 35, 1360–1371. [Google Scholar] [CrossRef]
- Ziane, D.; Deffaf, B.; Belaid, S.L.; Belkhier, Y.; Bajaj, M.; Blazek, V. Fuzzy logic-enhanced direct power control for wind turbines with doubly fed induction generators. Results Eng. 2024, 24, 103557. [Google Scholar] [CrossRef]

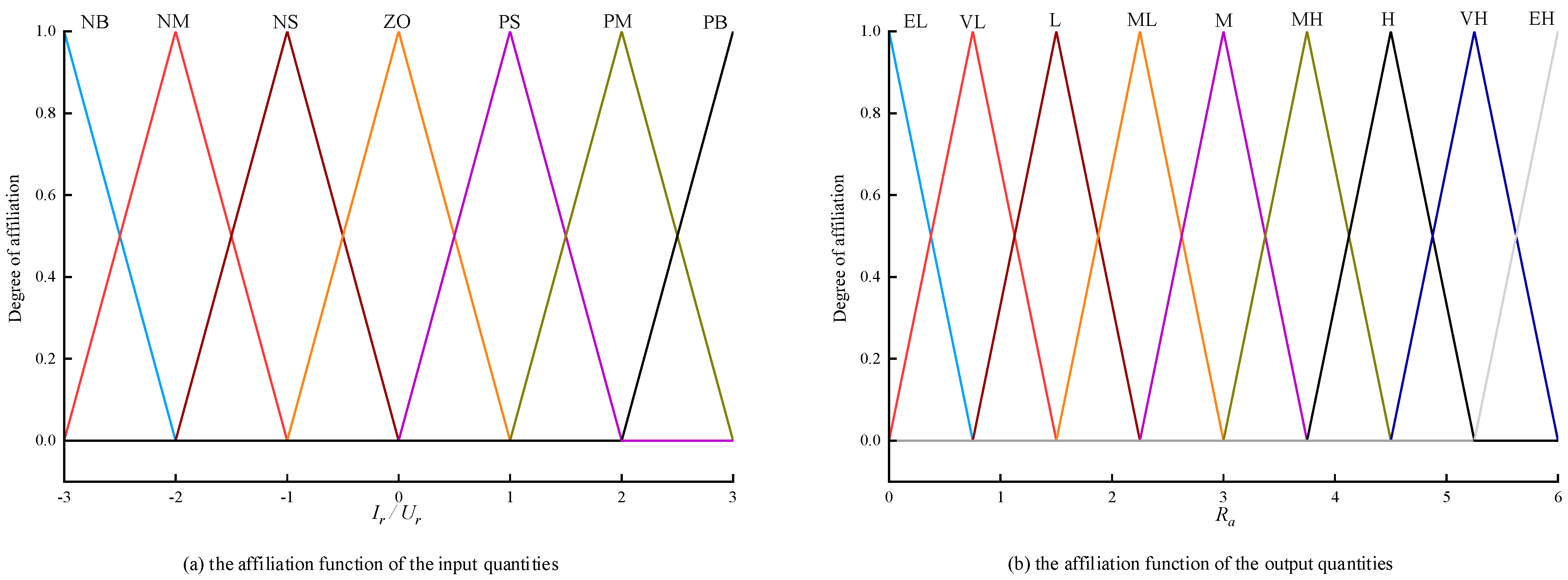

| NB | NM | NS | Z | PS | PB | PM | ||
| NB | M | H | VH | EH | VH | H | M | |
| NM | ML | MH | H | EH | H | MH | ML | |
| NS | VL | ML | ML | VH | ML | ML | VL | |
| Z | EL | VL | ML | M | ML | VL | EL | |
| PS | VL | ML | ML | VH | ML | ML | VL | |
| PM | ML | MH | H | EH | H | MH | ML | |
| PB | M | H | VH | EH | VH | H | M | |
| Parameters | Numerical Value | Parameters | Numerical Value |
|---|---|---|---|
| Rated power/MW | 1.5 | Rated voltage/kV | 0.69 |
| DC bus voltage/V | 1200 | slippage rate | −0.2 |
| Stator resistance (p.u.) | 0.0054 | Rotor Resistance(p.u.) | 0.0062 |
| Stator Leakage Inductance (p.u.) | 0.10 | Rotor Leakage Inductance (p.u.) | 0.11 |
| Mutual inductance (p.u.) | 3.0 | number of pole pairs | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.; Xu, Y.; Liu, Y.; Ren, J.; Fan, Y. Improved Segmented Control Strategy for Continuous Fault Ride-Through of Doubly-Fed Wind Turbines. Energies 2025, 18, 3845. https://doi.org/10.3390/en18143845
Chen T, Xu Y, Liu Y, Ren J, Fan Y. Improved Segmented Control Strategy for Continuous Fault Ride-Through of Doubly-Fed Wind Turbines. Energies. 2025; 18(14):3845. https://doi.org/10.3390/en18143845
Chicago/Turabian StyleChen, Tie, Yifan Xu, Yue Liu, Junlin Ren, and Youyuan Fan. 2025. "Improved Segmented Control Strategy for Continuous Fault Ride-Through of Doubly-Fed Wind Turbines" Energies 18, no. 14: 3845. https://doi.org/10.3390/en18143845
APA StyleChen, T., Xu, Y., Liu, Y., Ren, J., & Fan, Y. (2025). Improved Segmented Control Strategy for Continuous Fault Ride-Through of Doubly-Fed Wind Turbines. Energies, 18(14), 3845. https://doi.org/10.3390/en18143845





