A Review of Electromagnetic Wind Energy Harvesters Based on Flow-Induced Vibrations
Abstract
1. Introduction
2. Electromagnetic Wind Energy Harvesters Based on Different FIV Phenomena
2.1. Based on Vortex-Induced Vibration
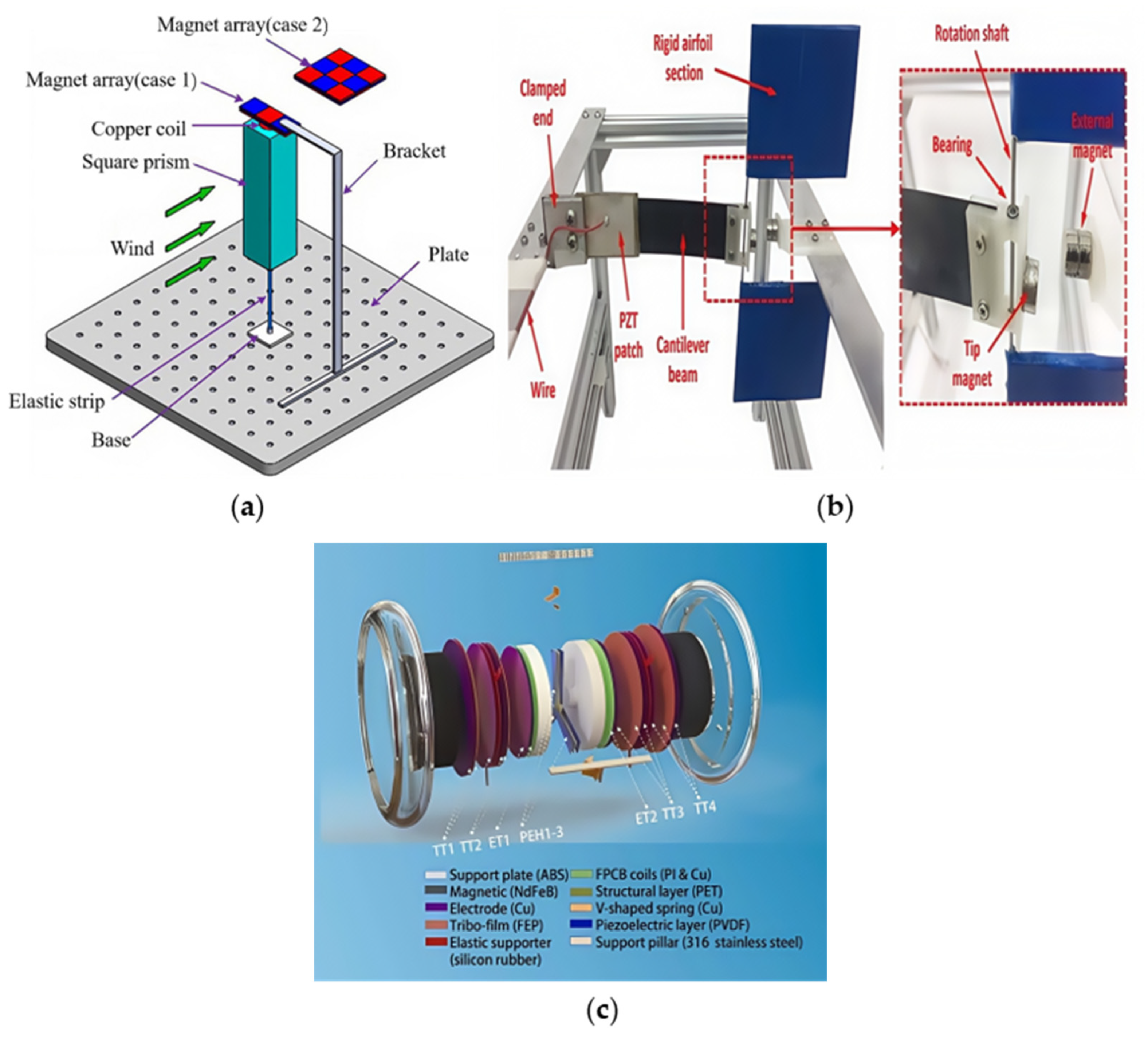
2.2. Based on Galloping
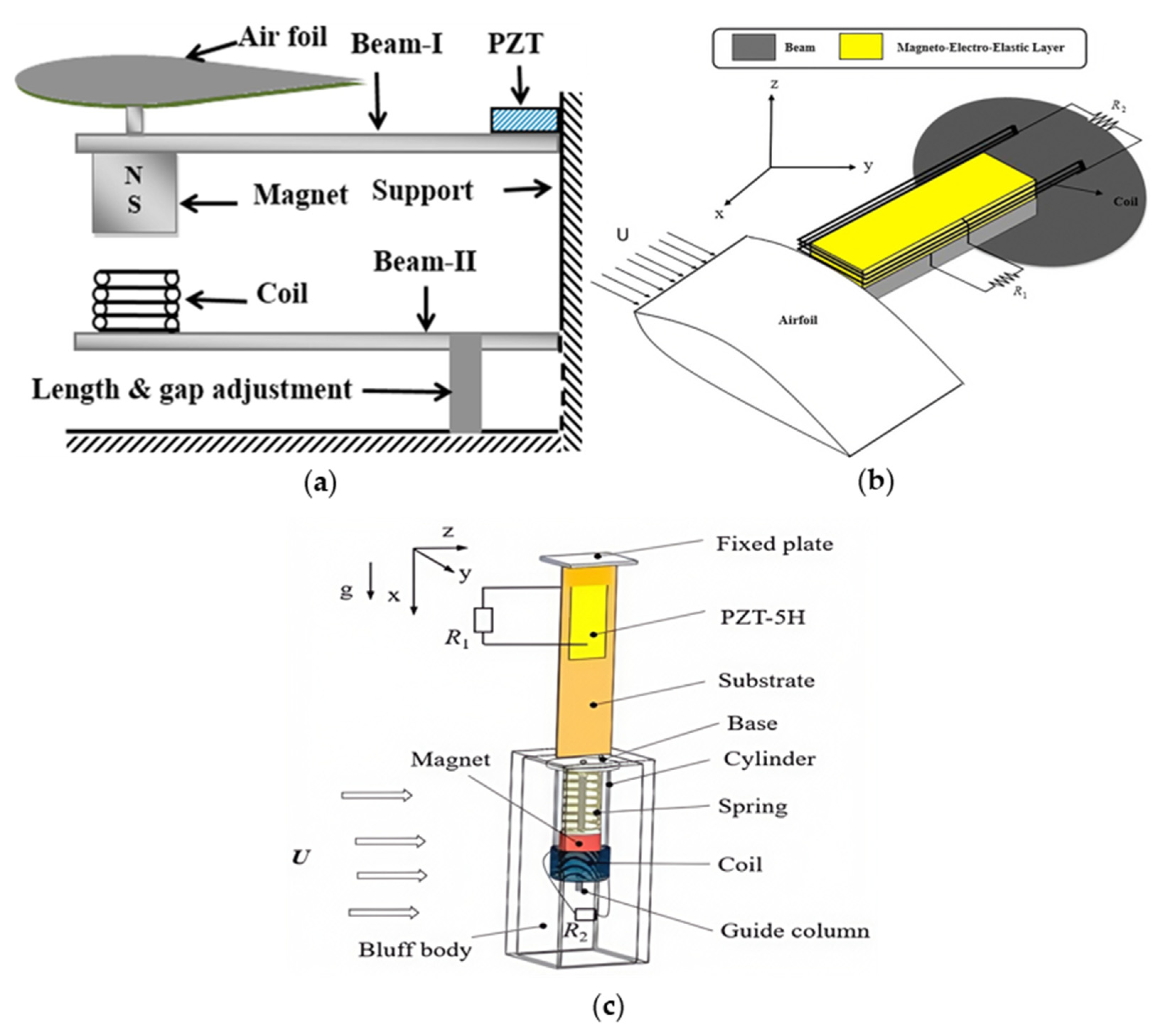
2.3. Based on Flutter
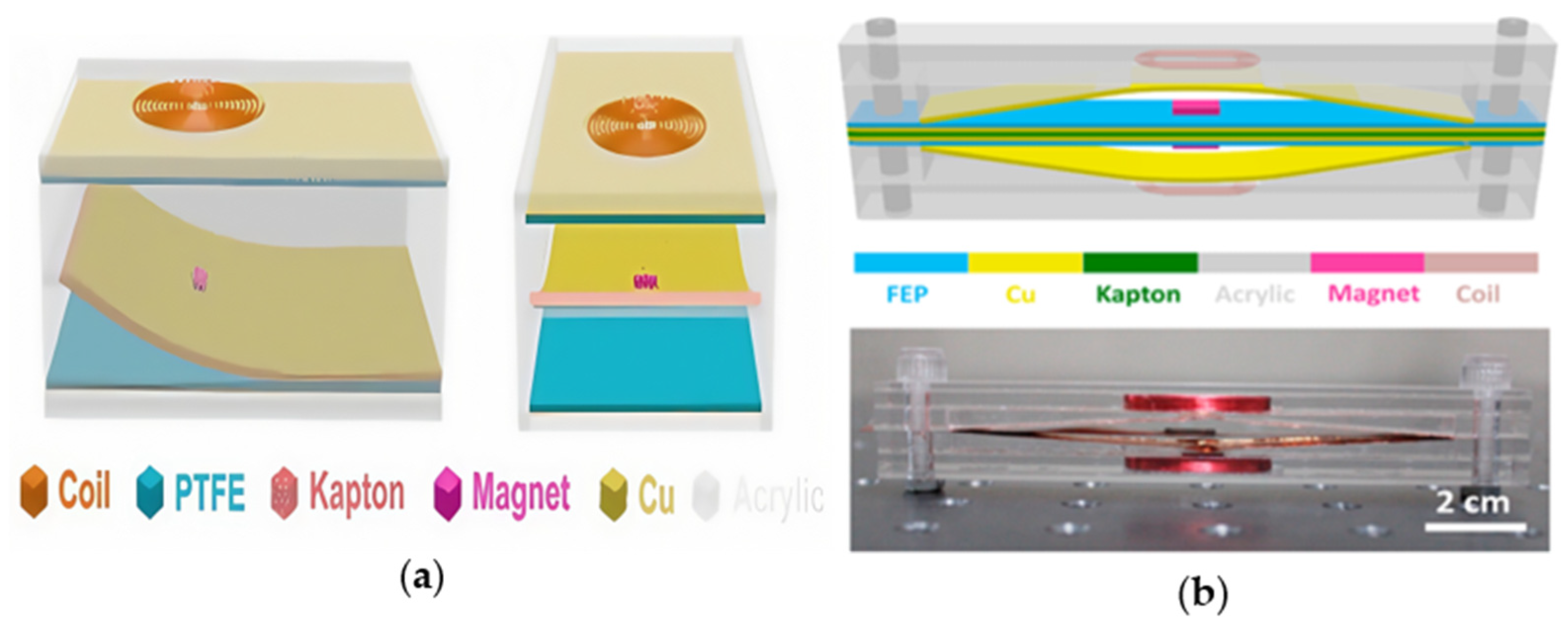
2.4. Based on Wake Galloping
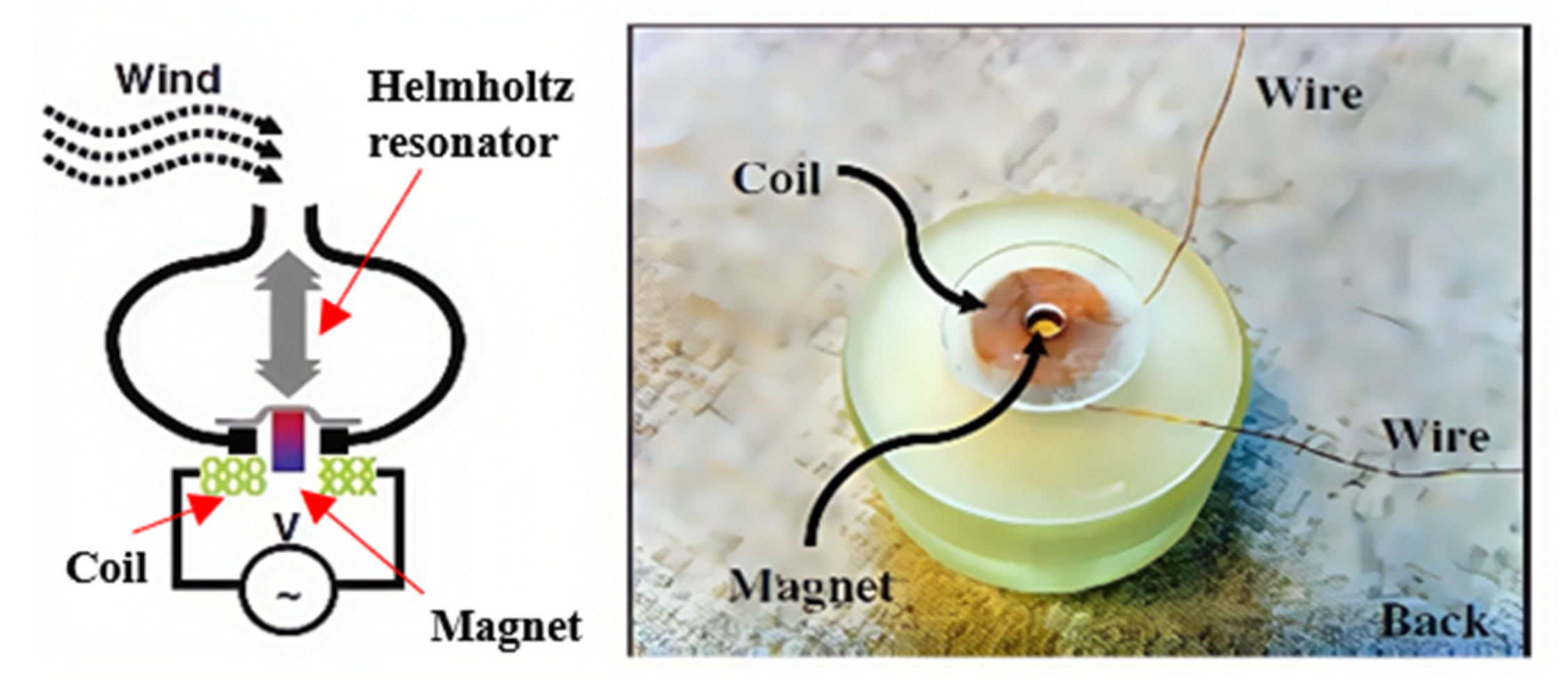
2.5. Based on Helmholtz Resonator
2.6. Comparisons Among Electromagnetic WEHs Based on Different FIV Phenomena
3. Performance Enhancement Methods
3.1. Output Power Enhancement
3.1.1. Hybrid Electromechanical Conversion
3.1.2. Nonlinear Effects
3.2. Operational Wind Speed Range Expansion
3.3. Operational Wind Direction Range Expansion
3.4. Durability Enhancement
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FIV | Flow-Induced Vibration |
| WEHs | Wind Energy Harvesters |
| FIVs | Flow-Induced Vibrations |
| VIV | Vortex-Induced Vibration |
| CFD | Computational Fluid Dynamics |
| LCO | Limit Cycle Oscillations |
| ET | Electromagnetic Transducer |
| PT | Piezoelectric Transducer |
| TENGs | Triboelectric Nanogenerators |
| EMGs | Electromagnetic Generators |
| FEP | Fluorinated Ethylene Propylene |
| EMC | Electromagnetic Compatibility |
| EMI | Electromagnetic Interference |
References
- Jia, R.; Zhang, H. Wireless sensor network (WSN) model targeting energy efficient wireless sensor networks node coverage. IEEE Access 2024, 12, 27596–27610. [Google Scholar] [CrossRef]
- Jamshed, M.A.; Ali, K.; Abbasi, Q.H.; Imran, M.A.; Ur-Rehman, M. Challenges, applications, and future of wireless sensors in Internet of Things: A review. IEEE Sens. J. 2022, 22, 5482–5494. [Google Scholar] [CrossRef]
- Chen, M.; Yu, Y.; Ouyang, D.; Weng, J.; Zhao, L.; Wang, J.; Chen, Y. Research progress of enhancing battery safety with phase change materials. Renew. Sustain. Energy Rev. 2024, 189, 113921. [Google Scholar] [CrossRef]
- Maka, A.O.; Alabid, J.M. Solar energy technology and its roles in sustainable development. Clean Energy 2022, 6, 476–483. [Google Scholar] [CrossRef]
- Opolot, M.; Zhao, C.; Liu, M.; Mancin, S.; Bruno, F.; Hooman, K. A review of high temperature (≥ 500 °C) latent heat thermal energy storage. Renew. Sustain. Energy Rev. 2022, 160, 112293. [Google Scholar] [CrossRef]
- Zhou, S.; Lallart, M.; Erturk, A. Multistable vibration energy harvesters: Principle, progress, and perspectives. J. Sound Vib. 2022, 528, 116886. [Google Scholar] [CrossRef]
- Roga, S.; Bardhan, S.; Kumar, Y.; Dubey, S.K. Recent technology and challenges of wind energy generation: A review. Sustain. Energy Technol. Assess. 2022, 52, 102239. [Google Scholar] [CrossRef]
- Shepherd, D.G. Historical Development of the Windmill; (No. NASA-CR-4337); NASA: Washington, DC, USA, 1990. [Google Scholar]
- Ackermann, T.; Söder, L. Wind energy technology and current status: A review. Renew. Sustain. Energy Rev. 2020, 4, 315–374. [Google Scholar] [CrossRef]
- Ackermann, T.; Söder, L. An overview of wind energy-status 2002. Renew. Sustain. Energy Rev. 2002, 6, 67–127. [Google Scholar] [CrossRef]
- Smil, V. World history and energy. Encycl. Energy 2004, 6, 549–561. [Google Scholar]
- Wang, H.; Xiong, B.; Zhang, Z.; Zhang, H.; Azam, A. Small wind turbines and their potential for internet of things applications. iScience 2023, 26, 107674. [Google Scholar] [CrossRef]
- Antonini, E.G.; Virgüez, E.; Ashfaq, S.; Duan, L.; Ruggles, T.H.; Caldeira, K. Identification of reliable locations for wind power generation through a global analysis of wind droughts. Commun. Earth Environ. 2024, 5, 103. [Google Scholar] [CrossRef]
- Zhang, L.B.; Abdelkefi, A.; Dai, H.L.; Naseer, R.; Wang, L. Design and experimental analysis of broadband energy harvesting from vortex-induced vibrations. J. Sound Vib. 2017, 408, 210–219. [Google Scholar] [CrossRef]
- Barrero-Gil, A.; Alonso, G.; Sanz-Andres, A. Energy harvesting from transverse galloping. J. Sound Vib. 2010, 329, 2873–2883. [Google Scholar] [CrossRef]
- Olivieri, S.; Boccalero, G.; Mazzino, A.; Boragno, C. Fluttering conditions of an energy harvester for autonomous powering. Renew. Energy 2017, 105, 530–538. [Google Scholar] [CrossRef]
- Alhadidi, A.H.; Daqaq, M.F. A broadband bi-stable flow energy harvester based on the wake-galloping phenomenon. Appl. Phys. Lett. 2016, 109, 033904. [Google Scholar] [CrossRef]
- Covaci, C.; Gontean, A. Piezoelectric energy harvesting solutions: A review. Sensors 2020, 20, 3512. [Google Scholar] [CrossRef] [PubMed]
- Zhu, D.; Beeby, S.P.; Tudor, M.J.; White, N.M.; Harris, N.R. Novel Miniature Airflow Energy Harvester for Wireless Sensing Applications in Buildings. IEEE Sens. J. 2013, 13, 691–700. [Google Scholar] [CrossRef]
- Fan, F.-R.; Tian, Z.-Q.; Lin Wang, Z. Flexible triboelectric generator. Nano Energy 2012, 1, 328–334. [Google Scholar] [CrossRef]
- Khaligh, A.; Onar, O.C. Energy Harvesting: Solar, Wind, and Ocean Energy Conversion Systems; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Priya, S.; Song, H.C.; Zhou, Y.; Varghese, R.; Chopra, A.; Kim, S.G.; Kanno, I.; Wu, L.; Ha, D.S.; Ryu, J.; et al. A review on piezoelectric energy harvesting: Materials, methods, and circuits. Energy Harvest. Syst. 2019, 4, 3–39. [Google Scholar] [CrossRef]
- Dong, X.; Liu, Z.; Yang, P.; Chen, X. Harvesting wind energy based on triboelectric nanogenerators. Nanoenergy Adv. 2022, 2, 245–268. [Google Scholar] [CrossRef]
- Yan, J.; Tang, Z.; Mei, N.; Zhang, D.; Zhong, Y.; Sheng, Y. Research progress on the application of triboelectric nanogenerators for wind energy collection. Micromachines 2023, 14, 1592. [Google Scholar] [CrossRef] [PubMed]
- Williamson, C.H.K.; Govardhan, R. A brief review of recent results in vortex-induced vibrations. J. Wind. Eng. Ind. Aerodyn. 2008, 96, 713–735. [Google Scholar] [CrossRef]
- Lupi, F.; Niemann, H.-J.; Höffer, R. Aerodynamic damping model in vortex-induced vibrations for wind engineering applications. J. Wind. Eng. Ind. Aerodyn. 2018, 174, 281–295. [Google Scholar] [CrossRef]
- Francis, S.; Swain, A. Modelling and harnessing energy from flow-induced vibration, particularly VIV and galloping: An explicit review. Ocean Eng. 2024, 312, 119290. [Google Scholar] [CrossRef]
- Fukushima, H.; Yagi, T.; Shimoda, T.; Noguchi, K. Wake-induced instabilities of parallel circular cylinders with tandem and staggered arrangements. J. Wind. Eng. Ind. Aerodyn. 2021, 215, 104697. [Google Scholar] [CrossRef]
- Chai, Y.; Gao, W.; Ankay, B.; Li, F.; Zhang, C. Aeroelastic analysis and flutter control of wings and panels: A review. Int. J. Mech. Syst. Dyn. 2021, 1, 5–34. [Google Scholar] [CrossRef]
- Xu, C.; Zhao, L. Internal resonance in galloping, VIV, and flutter for concurrent wind and base vibration energy harvesting. In Active and Passive Smart Structures and Integrated Systems XVI; SPIE: Bellingham, WA, USA, 2022; Volume 12043, pp. 227–237. [Google Scholar]
- Hasheminejad, S.M.; Masoumi, Y. Dual-functional synergetic energy harvesting and flow-induced vibration control of an electromagnetic-based square cylinder integrated with a flexible bimorph piezoelectric wake splitter plate. Renew. Energy 2023, 216, 119133. [Google Scholar] [CrossRef]
- Ma, X.; Zhou, S. A review of flow-induced vibration energy harvesters. Energy Convers. Manag. 2022, 254, 115223. [Google Scholar] [CrossRef]
- Feng, C.C. The Measurement of Vortex Induced Effects in Flow Past Stationary and Oscillating Circular and D-Section Cylinders. Ph.D. Dissertation, University of British Columbia, Vancouver, BC, Canada, 1968. [Google Scholar]
- Jeon, D.; Gharib, M. On circular cylinders undergoing two-degree-of-freedom forced motions. J. Fluids Struct. 2001, 15, 533–541. [Google Scholar] [CrossRef]
- Jauvtis, N.A.; Williamson, C.H.K. The effect of two degrees of freedom on vortex-induced vibration at low mass and damping. J. Fluid Mech. 2004, 509, 23–62. [Google Scholar] [CrossRef]
- Zhu, D.; Beeby, S.; Tudor, J.; White, N.; Harris, N. A novel miniature wind generator for wireless sensing applications. In Proceedings of the SENSORS, 2010 IEEE, Waikoloa, HI, USA, 1–4 November 2010; pp. 1415–1418. [Google Scholar]
- Wang, D.A.; Chiu, C.Y.; Pham, H.T. Electromagnetic energy harvesting from vibrations induced by Kármán vortex street. Mechatronics 2012, 22, 746–756. [Google Scholar] [CrossRef]
- Xu-Xu, J.; Barrero-Gil, A.; Velazquez, A. A theoretical study of the coupling between a vortex-induced vibration cylindrical resonator and an electromagnetic energy harvester. Smart Mater. Struct. 2015, 24, 115009. [Google Scholar] [CrossRef]
- Atrah, A.B.; Ab-Rahman, M.S.; Salleh, H.; Nuawi, M.Z.; Mohd Nor, M.J.; Jamaludin, N.B. Karman vortex creation using cylinder for flutter energy harvester device. Micromachines 2017, 8, 227. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Zhong, T. Hydrokinetic energy harvesting from flow-induced vibration of a hollow cylinder attached with a bi-stable energy harvester. Energy Convers. Manag. 2023, 278, 116718. [Google Scholar] [CrossRef]
- Moradi Gharghani, F.; Bijarchi, M.A.; Mohammadi, O.; Shafii, M.B. An experimental investigation into a novel small-scale device for energy harvesting using vortex-induced vibration. Int. J. Low-Carbon Technol. 2021, 16, 317–325. [Google Scholar] [CrossRef]
- Abdelkefi, A. Aeroelastic energy harvesting: A review. Int. J. Eng. Sci. 2016, 100, 112–135. [Google Scholar] [CrossRef]
- Dai, H.L.; Yang, Y.W.; Abdelkefi, A.; Wang, L. Nonlinear analysis and characteristics of inductive galloping energy harvesters. Commun. Nonlinear Sci. Numer. Simul. 2018, 59, 580–591. [Google Scholar] [CrossRef]
- Zhang, L.B.; Dai, H.L.; Abdelkefi, A.; Lin, S.X.; Wang, L. Theoretical modeling, wind tunnel measurements, and realistic environment testing of galloping-based electromagnetic energy harvesters. Appl. Energy 2019, 254, 113737. [Google Scholar] [CrossRef]
- Xing, J.; Rezaei, M.; Dai, H.; Liao, W.-H. Investigating the effect of surface protrusions on galloping energy harvesting. Appl. Phys. Lett. 2023, 122, 153902. [Google Scholar] [CrossRef]
- Kim, H.; Kim, S.; Xue, K.; Seok, J. Modeling and performance analysis of electromagnetic energy harvester based on torsional galloping phenomenon. Mech. Syst. Signal Process. 2023, 195, 110287. [Google Scholar] [CrossRef]
- Le, H.D.; Kwon, S.-D. An electromagnetic galloping energy harvester with double magnet design. Appl. Phys. Lett. 2019, 115, 133901. [Google Scholar] [CrossRef]
- Le, H.D.; Kwon, S.D. Design and experiments of a galloping-based wind energy harvester using quadruple halbach arrays. Energies 2021, 14, 6094. [Google Scholar] [CrossRef]
- Su, B.; Wang, Y.; Li, J.; Guo, T.; Cheng, G.; Sun, W. A novel elastic strip suspension-based bi-directional electromagnetic wind energy harvester designed specifically for wind energy factories. Mech. Syst. Signal Process. 2024, 208, 111059. [Google Scholar] [CrossRef]
- Xiong, L.; Gao, S.; Jin, L.; Guo, S.; Sun, Y.; Liu, F. The Design and Experiment of a Spring-Coupling Electromagnetic Galloping Energy Harvester. Micromachines 2023, 14, 968. [Google Scholar] [CrossRef]
- Xiong, L.; Gao, S.; Jin, L.; Sun, Y.; Du, X.; Liu, F. Study on the Influence of Coil Arrangement on the Output Characteristics of Electromagnetic Galloping Energy Harvester. Micromachines 2023, 14, 2158. [Google Scholar] [CrossRef]
- Theodorsen, T. General Theory of Aerodynamic Instability and the Mechanism of Flutter (No. NACA-TR-496). 1979. Available online: https://ntrs.nasa.gov/citations/19800006788 (accessed on 3 June 2025).
- Li, Z.; Zhou, S.; Yang, Z. Recent progress on flutter-based wind energy harvesting. Int. J. Mech. Syst. Dyn. 2022, 2, 82–98. [Google Scholar] [CrossRef]
- Abdelkefi, A.; Nayfeh, A.H.; Hajj, M.R. Modeling and analysis of piezoaeroelastic energy harvesters. Nonlinear Dyn. 2012, 67, 925–939. [Google Scholar] [CrossRef]
- Park, J.; Morgenthal, G.; Kim, K.; Kwon, S.-D.; Law, K.H. Power evaluation of flutter-based electromagnetic energy harvesters using computational fluid dynamics simulations. J. Intell. Mater. Syst. Struct. 2004, 25, 1800–1812. [Google Scholar] [CrossRef]
- Dinh Quy, V.; Van Sy, N.; Tan Hung, D.; Quoc Huy, V. Wind tunnel and initial field tests of a micro generator powered by fluid-induced flutter. Energy Sustain. Dev. 2016, 33, 75–83. [Google Scholar] [CrossRef]
- Chawdhury, S.; Morgenthal, G. Numerical simulations of aeroelastic instabilities to optimize the performance of flutter-based electromagnetic energy harvesters. J. Intell. Mater. Syst. Struct. 2018, 29, 479–495. [Google Scholar] [CrossRef]
- Liu, S.; Li, P.; Yang, Y. On the design of an electromagnetic aeroelastic energy harvester from nonlinear flutter. Meccanica 2018, 53, 2807–2831. [Google Scholar] [CrossRef]
- Lu, Z.; Wen, Q.; He, X.; Wen, Z. A flutter-based electromagnetic wind energy harvester: Theory and experiments. Appl. Sci. 2019, 9, 4823. [Google Scholar] [CrossRef]
- Vinayan, V.A.; Yap, T.C.; Go, Y.I. Design of Aeroelastic Wind Belt for Low-Energy Wind Harvesting. IOP Conf. Ser. Earth Environ. Sci. 2019, 268, 012069. [Google Scholar] [CrossRef]
- Zakaria, N.M.; Zulkifli, M.S.; Mukhtar, A. The Potential of Flutter-Based Windbelt for Energy Generation in Low-Wind-Speed Regions: A Case Study in Malaysia. J. Adv. Res. Fluid Mech. Therm. Sci. 2023, 107, 125–141. [Google Scholar] [CrossRef]
- Kumar, S.K.; Bose, C.; Ali, S.F.; Sarkar, S.; Gupta, S. Investigations on a vortex induced vibration based energy harvester. Appl. Phys. Lett. 2017, 111, 243903. [Google Scholar] [CrossRef]
- Tokoro, S.; Komatsu, H.; Nakasu, M.; Mizuguchi, K.; Kasuga, A. A study on wake-galloping for stay cables of extradosed bridges employing full aeroelastic cable model. In Proceedings of the Wind Engineering into The 21st Century, Copenhagen, Denmark, 21–24 June 1999; pp. 1055–1062. [Google Scholar]
- Jung, H.-J.; Lee, S.-W.; Jang, D.-D. Feasibility Study on a New Energy Harvesting Electromagnetic Device Using Aerodynamic Instability. IEEE Trans. Magn. 2009, 45, 4376–4379. [Google Scholar] [CrossRef]
- Sumner, D. Two circular cylinders in cross-flow: A review. J. Fluids Struct. 2010, 26, 849–899. [Google Scholar] [CrossRef]
- Zhou, Y.; Mahbub Alam, M. Wake of two interacting circular cylinders: A review. Int. J. Heat Fluid Flow 2016, 62, 510–537. [Google Scholar] [CrossRef]
- Wang, L.; Alam, M.M.; Zhou, Y. Two tandem cylinders of different diameters in cross-flow: Effect of an upstream cylinder on wake dynamics. J. Fluid Mech. 2018, 836, 5–42. [Google Scholar] [CrossRef]
- Zhou, Y.; Hao, J.; Alam, M.M. Wake of two tandem square cylinders. J. Fluid Mech. 2024, 983, A3. [Google Scholar] [CrossRef]
- Jung, H.-J.; Lee, S.-W. The experimental validation of a new energy harvesting system based on the wake galloping phenomenon. Smart Mater. Struct. 2011, 20, 055022. [Google Scholar] [CrossRef]
- Sarviha, A.; Barati, E.; Zarkak, M.R. Electromagnetic energy harvesting via flow-induced vibration of flexible diaphragm in the presence of square cylinders at varied incidence angles: An experimental investigation. Mech. Syst. Signal Process. 2023, 202, 110696. [Google Scholar] [CrossRef]
- Sarviha, A.; Barati, E.; Zarkak, M.R.; Derakhshandeh, J.F.; Alam, M.M. Experimental investigations on the wake-induced vibration of an electromagnetic energy-harvesting system. Int. J. Energy Res. 2024, 2024, 7072340. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, J.; Xue, K.; Seok, J. Development of a novel wake-induced rotational galloping wind energy harvester and the identification of its working mechanism. Mech. Syst. Signal Process. 2025, 224, 112019. [Google Scholar] [CrossRef]
- Kim, S.-H.; Ji, C.-H.; Galle, P.; Herrault, F.; Wu, X.; Lee, J.-H.; Choi, C.-A.; Allen, M.G. An electromagnetic energy scavenger from direct airflow. J. Micromechanics Microengineering 2009, 19, 094010. [Google Scholar] [CrossRef]
- Du, Z.G.; He, X.F. Micro piezoelectric wind energy harvester with a resonant cavity. Chin. J. Sensors Actuators 2012, 25, 748–750. [Google Scholar]
- Li, X.; Li, Z.; Liu, Q.; Shan, X. Study on the critical wind speed of a resonant cavity piezoelectric energy harvester driven by driving wind pressure. Micromachines 2019, 10, 842. [Google Scholar] [CrossRef]
- Iqbal, M.; Khan, F.U. Hybrid vibration and wind energy harvesting using combined piezoelectric and electromagnetic conversion for bridge health monitoring applications. Energy Convers. Manag. 2018, 172, 611–618. [Google Scholar] [CrossRef]
- Javed, U.; Abdelkefi, A. Characteristics and comparative analysis of piezoelectric-electromagnetic energy harvesters from vortex-induced oscillations. Nonlinear Dyn. 2019, 95, 3309–3333. [Google Scholar] [CrossRef]
- Li, X.; Li, Z.; Liu, B.; Zhang, J.; Zhu, W. Numerical research on a vortex shedding induced piezoelectric-electromagnetic energy harvester. J. Intell. Mater. Syst. Struct. 2022, 33, 105–120. [Google Scholar] [CrossRef]
- Abdehvand, M.Z.; Seyed Roknizadeh, S.A.; Mohammad-Sedighi, H. Modeling and analysis of novel coupled magneto-electro-aeroelastic continuous system for flutter-based energy harvesting system. Energy 2021, 230, 120742. [Google Scholar] [CrossRef]
- Li, X.; Bi, C.; Li, Z.; Liu, B.; Wang, T.; Zhang, S. A piezoelectric and electromagnetic hybrid galloping energy harvester with the magnet embedded in the bluff body. Micromachines 2021, 12, 626. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Tang, W.; Han, C.; Fan, F.; Wang, Z.L. Theoretical Comparison, Equivalent Transformation, and Conjunction Operations of Electromagnetic Induction Generator and Triboelectric Nanogenerator for Harvesting Mechanical Energy. Adv. Mater. 2014, 26, 3580–3591. [Google Scholar] [CrossRef] [PubMed]
- Zi, Y.; Guo, H.; Wen, Z.; Yeh, M.H.; Hu, C.; Wang, Z.L. Harvesting low-frequency (<5 Hz) irregular mechanical energy: A possible killer application of triboelectric nanogenerator. ACS Nano 2016, 10, 4797–4805. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Hasan, M.A.M.; Wu, H.; Yang, Y. Electromagnetic–triboelectric hybridized nanogenerators. Energies 2021, 14, 6219. [Google Scholar] [CrossRef]
- Wang, X.; Wang, S.; Yang, Y.; Wang, Z.L. Hybridized Electromagnetic–Triboelectric Nanogenerator for Scavenging Air-Flow Energy to Sustainably Power Temperature Sensors. ACS Nano 2015, 9, 4553–4562. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Yang, Y. Effective energy storage from a hybridized electromagnetic-triboelectric nanogenerator. Nano Energy 2017, 32, 36–41. [Google Scholar] [CrossRef]
- Kim, W.J. Development of Hybrid Generator Using Triboelectric-Electromagnetic Components for Scavenging Wind and Water Wave Energy. Ph.D. Dissertation, Jeju National University Graduate School, Jeju City, Republic of Korea, 2022. [Google Scholar]
- Li, X.; Ma, T.; Liu, B.; Wang, C.; Su, Y. Experimental Study on Magnetic Coupling Piezoelectric–Electromagnetic Composite Galloping Energy Harvester. Sensors 2022, 22, 8241. [Google Scholar] [CrossRef]
- Li, K.; Yang, Z.; Zhou, S. Performance enhancement for a magnetic-coupled bi-stable flutter-based energy harvester. Smart Mater. Struct. 2020, 29, 085045. [Google Scholar] [CrossRef]
- He, X.; Yang, X.; Jiang, S. Enhancement of wind energy harvesting by interaction between vortex-induced vibration and galloping. Appl. Phys. Lett. 2018, 112, 33901. [Google Scholar] [CrossRef]
- Wang, J.; Gu, S.; Zhang, C.; Hu, G.; Chen, G.; Yang, K.; Li, H.; Lai, Y.; Litak, G.; Yurchenko, D. Hybrid wind energy scavenging by coupling vortex-induced vibrations and galloping. Energy Convers. Manag. 2020, 213, 112835. [Google Scholar] [CrossRef]
- Del Priore, E.; Romano, G.P.; Lampani, L. Coupled electro-aeroelastic energy harvester model based on piezoelectric transducers, VIV-galloping interaction and nonlinear switching circuits. Smart Mater. Struct. 2023, 32, 075012. [Google Scholar] [CrossRef]
- Shan, X.; Tian, H.; Cao, H.; Xie, T. Enhancing performance of a piezoelectric energy harvester system for concurrent flutter and vortex-induced vibration. Energies 2020, 13, 3101. [Google Scholar] [CrossRef]
- Dong, L.; Hu, G.; Tang, Q.; Zhao, C.; Yang, F.; Yang, Y. Advanced Aerodynamics-Driven Energy Harvesting Leveraging Galloping-Flutter Synergy. Adv. Funct. Mater. 2025, 35, 2414324. [Google Scholar] [CrossRef]
- Sun, W.; Seok, J. Novel galloping-based piezoelectric energy harvester adaptable to external wind velocity. Mech. Syst. Signal Process. 2021, 152, 107477. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, Y.; Li, Z.; Lin, S.; Zhang, Z.; Kan, J. Design and characteristic analysis of a performance-enhanced piezoelectric wind energy harvester with a transformable Y-type bluff body. IEEE Sens. J. 2024, 24, 25360–25368. [Google Scholar] [CrossRef]
- Chen, S.; Zhao, L. A quasi-zero stiffness two degree-of-freedom nonlinear galloping oscillator for ultra-low wind speed aeroelastic energy harvesting. Appl. Energy 2023, 331, 120423. [Google Scholar] [CrossRef]
- Liu, F.R.; Zhao, L.C.; Yan, G.; Zhang, W.M.; Wu, Z.Y.; Zhang, X.L. Performing Magnetic Boundary Modulation to Broaden the Operational Wind Speed Range of a Piezoelectric Cantilever-Type Wind Energy Harvester. Micromachines 2024, 15, 1286. [Google Scholar] [CrossRef]
- Zhang, H.; Sui, W.; Yang, C.; Zhang, L.; Song, R.; Yang, X. Scavenging wind induced vibration by an electromagnet energy harvester from single to multiple wind directions. Ferroelectrics 2021, 577, 170–180. [Google Scholar] [CrossRef]
- Li, J.; Wang, G.; Yang, P.; Wen, Y.; Zhang, L.; Song, R.; Hou, C. An orientation-adaptive electromagnetic energy harvester scavenging for wind-induced vibration. Energy 2024, 286, 129578. [Google Scholar] [CrossRef]
- Li, S.; Chen, Z.; He, X.; Ye, Y.; Wan, S.; Dong, L. High performance hybrid omnidirectional wind energy harvester based on flutter for wireless sensing and hydrogen production applications. Nano Energy 2024, 132, 110403. [Google Scholar] [CrossRef]
- Zhang, M.; Hu, G.; Wang, J. Bluff body with built-in piezoelectric cantilever for flow-induced energy harvesting. Int. J. Energy Res. 2020, 44, 3762–3777. [Google Scholar] [CrossRef]
- Wang, S.; Liao, W.; Zhang, Z.; Liao, Y.; Yan, M.; Kan, J. Development of a novel non-contact piezoelectric wind energy harvester excited by vortex-induced vibration. Energy Convers. Manag. 2021, 235, 113980. [Google Scholar] [CrossRef]
- Li, S.; He, X.; Li, J.; Feng, Z.; Yang, X.; Li, J. An in-plane omnidirectional piezoelectric wind energy harvester based on vortex-induced vibration. Appl. Phys. Lett. 2022, 120, 43901. [Google Scholar] [CrossRef]
- Li, S.; Feng, Z.; He, X.; Ye, Y.; Li, J. An in-plane omnidirectional flutter piezoelectric wind energy harvester. Mech. Syst. Signal Process. 2023, 200, 110637. [Google Scholar] [CrossRef]
- Li, X.; He, X. Preparation of Superhydrophobic Coating with Silica Powder on Flexible Substrates. Nanosci. Nanotechnol. Lett. 2018, 10, 554–558. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, J.; Zhao, Y.; Ding, X.; Chen, J.; Liu, Z.; Liu, Z.; Zhu, Y. Lotus leaf-inspired superhydrophobic piezoelectric nanofiber films for moisture-proof pressure sensing and energy harvesting. Chem. Eng. J. 2025, 504, 158874. [Google Scholar] [CrossRef]
- Citroni, R.; Mangini, F.; Frezza, F. Efficient integration of ultra-low power techniques and energy harvesting in self-sufficient devices: A comprehensive overview of current progress and future directions. Sensors 2024, 24, 4471. [Google Scholar] [CrossRef]
- Harb, A. Energy harvesting: State-of-the-art. Renew. Energy 2011, 36, 2641–2654. [Google Scholar] [CrossRef]



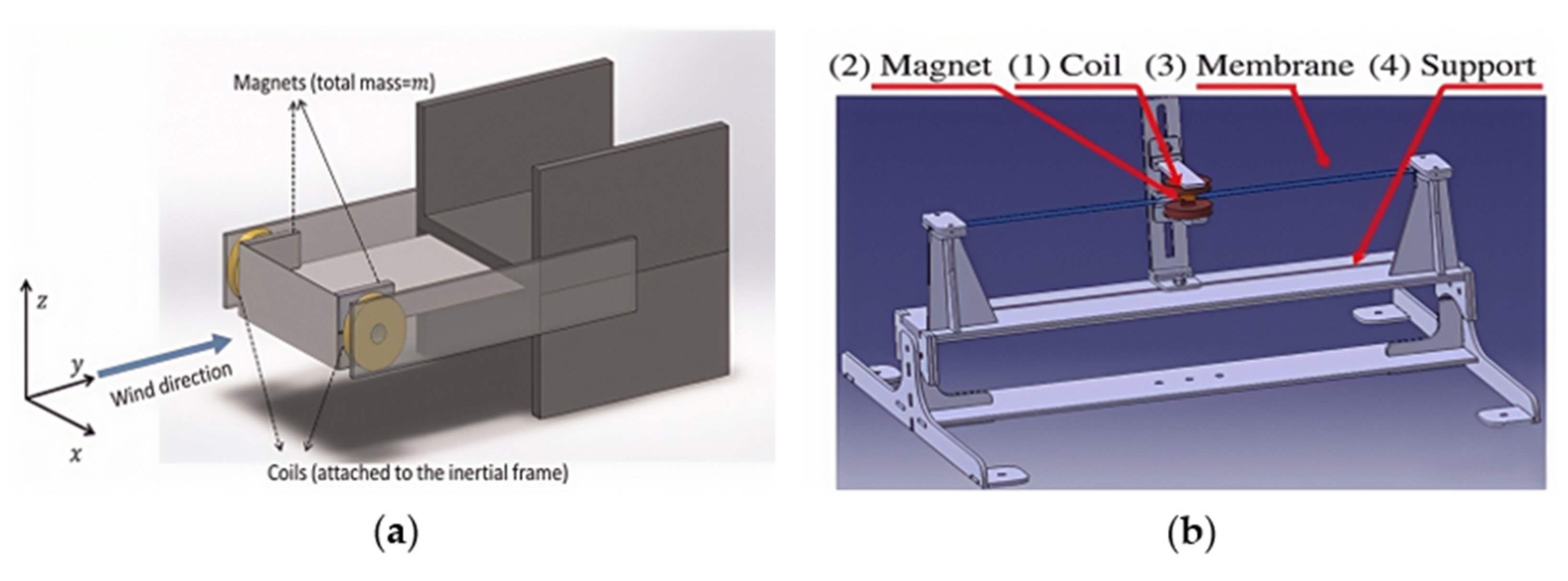
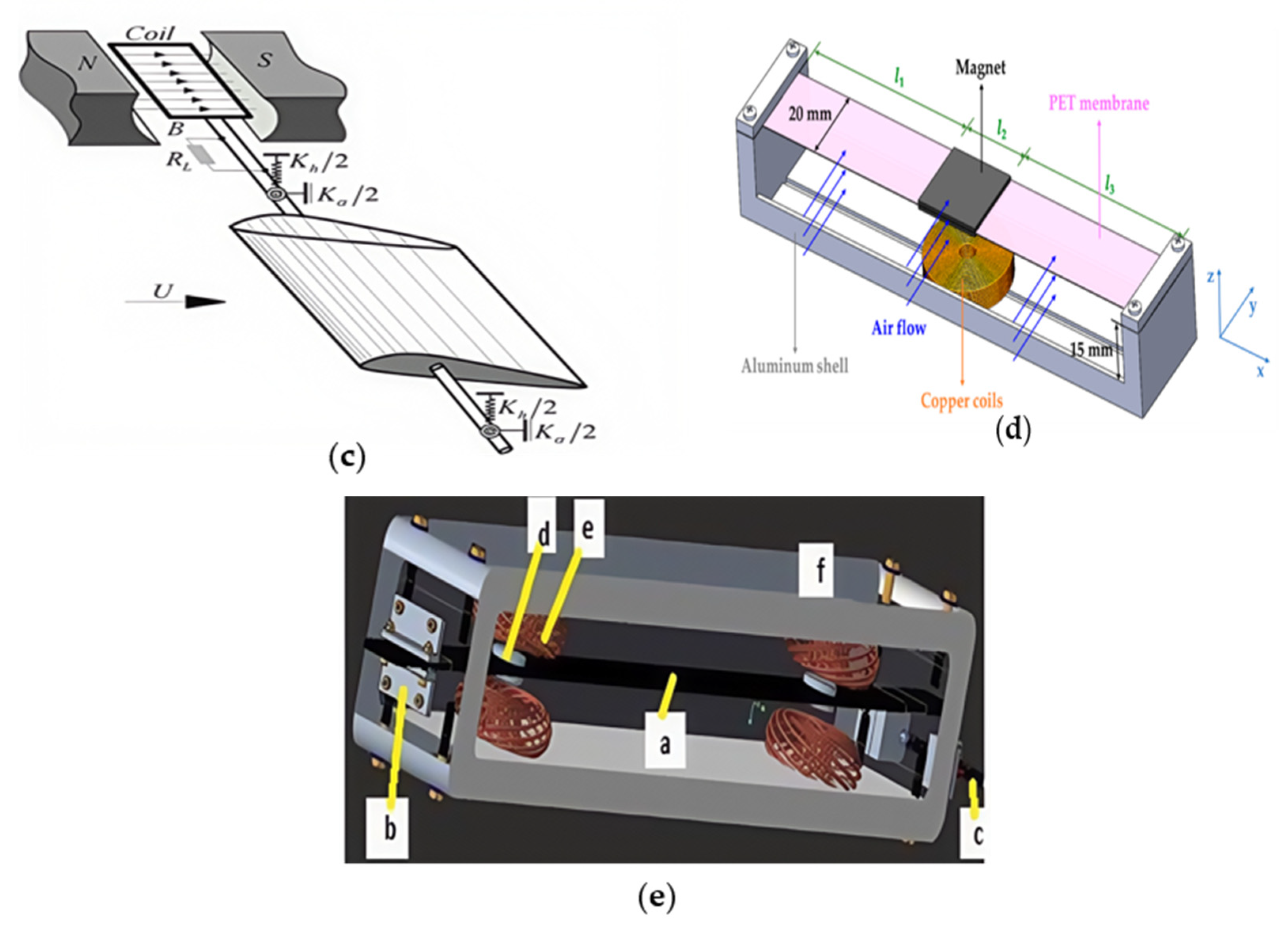
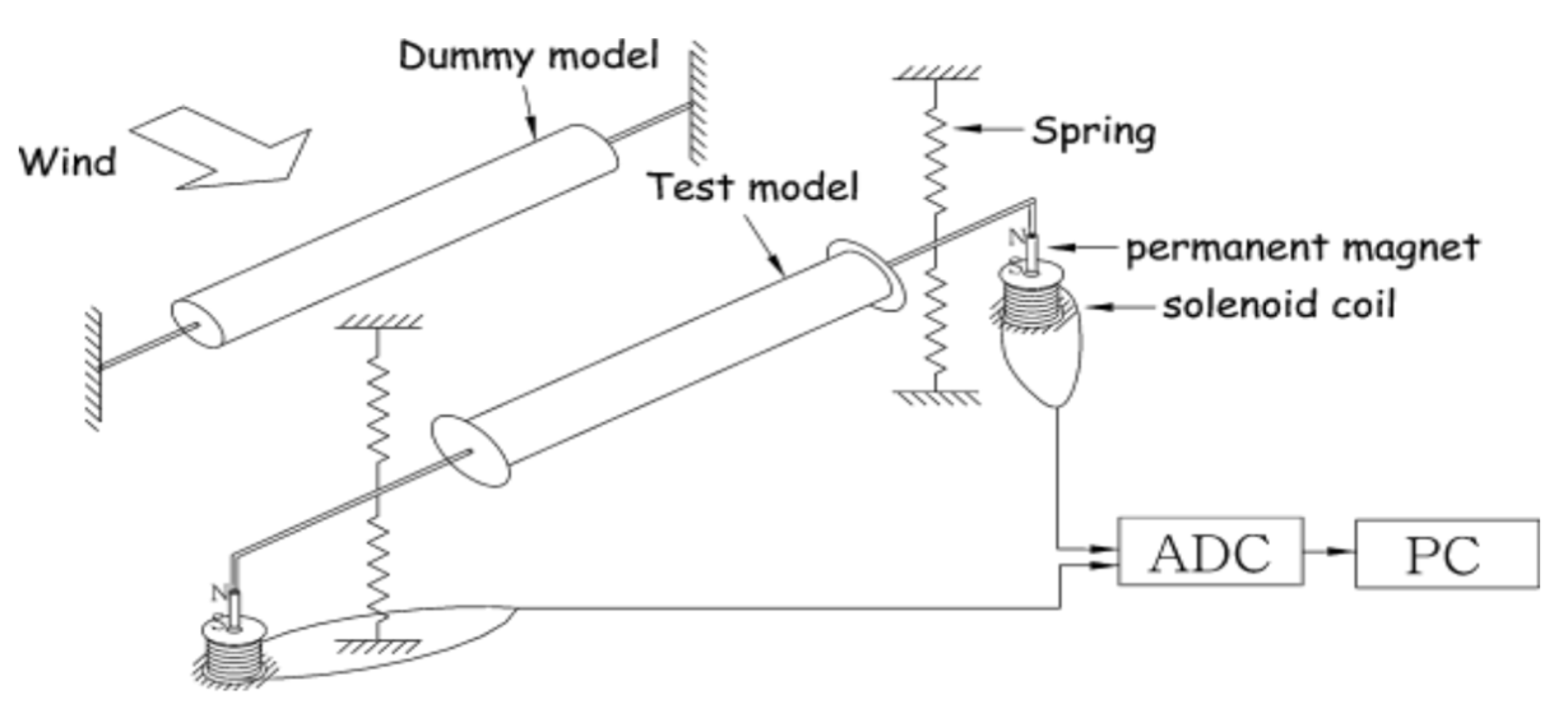
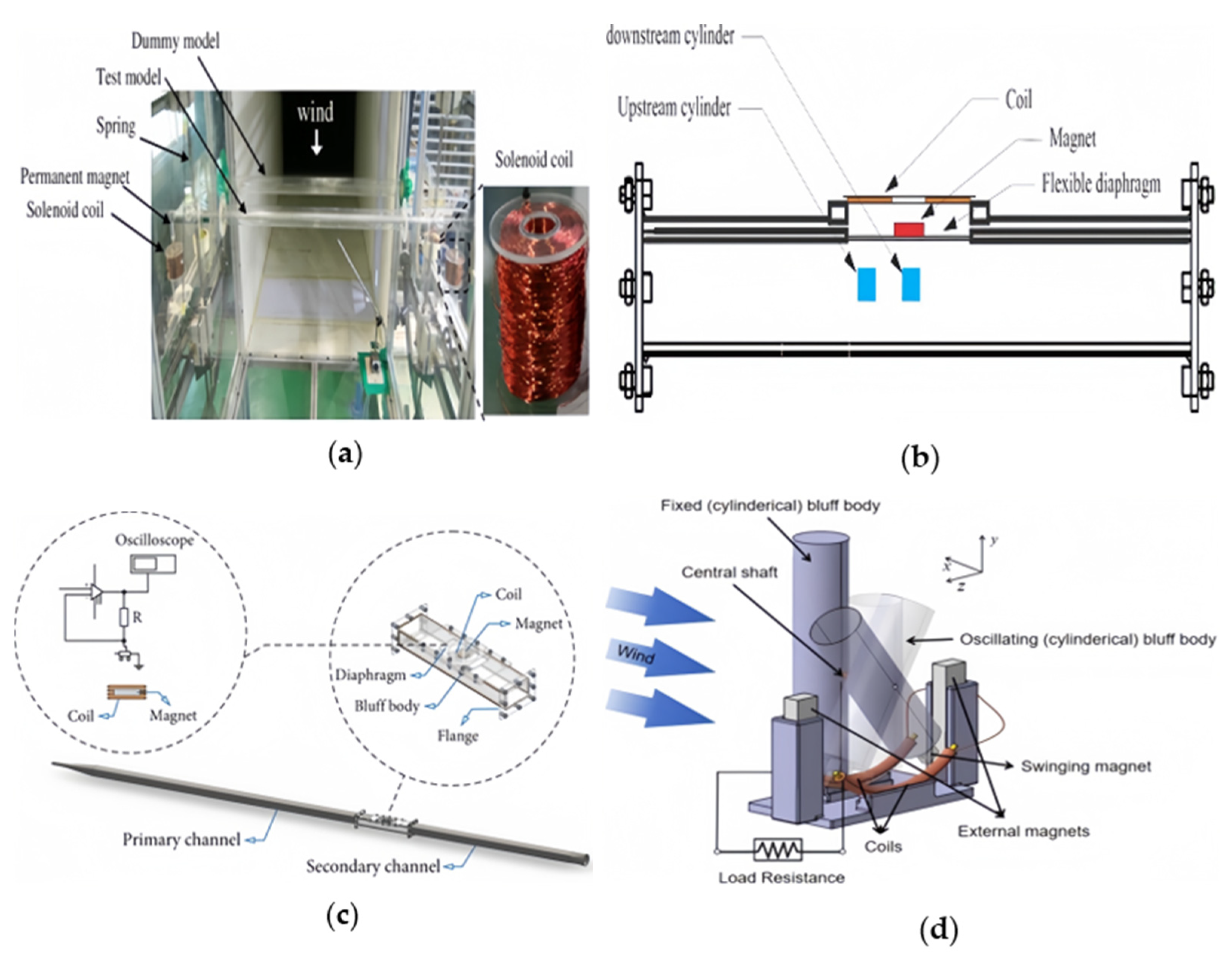
| Ref. | FIV Type | Cut-In Speed (m/s) | Wind Speed (m/s) | Output Voltage (V) | Output Power (mW) |
|---|---|---|---|---|---|
| [36] | VIV | 2.5 | 5 | − | 1.6 |
| [37] | VIV | − | − | − | 0.00177 |
| [44] | galloping | 1.5 | 4 | − | 2.5 |
| [46] | galloping | 2.75 | 10 | 0.118 | 0.31 |
| [47] | galloping | 1.5 | 4 | − | 1.41 |
| [48] | galloping | − | 12 | − | 8 |
| [49] | galloping | 2 | 4 | 3.20 | 7.8 |
| [50] | galloping | 7.5 | 14 | 0.1032 | 0.79 |
| [56] | flutter | 3 | 8 | 3 | 100 |
| [57] | flutter | 4 | 8 | − | 5.3 |
| [59] | flutter | 3 | 10 | − | 0.705 |
| [60] | flutter | 2 | 12 | 21.00 | 346.08 |
| [69] | wake-galloping | 1 | 4.5 | − | 370 |
| [71] | wake-galloping | − | − | 0.08 | 0.00202 |
| [72] | wake-galloping | 2.95 | 10 | 0.2 | 9.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Li, S.; Wang, W.; Zen, P.; Li, C.; Ye, Y.; He, X. A Review of Electromagnetic Wind Energy Harvesters Based on Flow-Induced Vibrations. Energies 2025, 18, 3835. https://doi.org/10.3390/en18143835
Zhang Y, Li S, Wang W, Zen P, Li C, Ye Y, He X. A Review of Electromagnetic Wind Energy Harvesters Based on Flow-Induced Vibrations. Energies. 2025; 18(14):3835. https://doi.org/10.3390/en18143835
Chicago/Turabian StyleZhang, Yidan, Shen Li, Weilong Wang, Pengfei Zen, Chunlong Li, Yizhou Ye, and Xuefeng He. 2025. "A Review of Electromagnetic Wind Energy Harvesters Based on Flow-Induced Vibrations" Energies 18, no. 14: 3835. https://doi.org/10.3390/en18143835
APA StyleZhang, Y., Li, S., Wang, W., Zen, P., Li, C., Ye, Y., & He, X. (2025). A Review of Electromagnetic Wind Energy Harvesters Based on Flow-Induced Vibrations. Energies, 18(14), 3835. https://doi.org/10.3390/en18143835







