Abstract
Maintenance scheduling of hydropower units is essential for ensuring the operational security and stability of large-scale cascaded hydropower systems and for improving the efficiency of water energy utilization. This study takes the Cascaded Hydropower System of the Lower Jinsha River (CHSJS) as a representative case, identifying four key challenges facing maintenance planning: multi-dimensional influencing factor coupling, spatial and temporal conflicts with generation dispatch, coordination with transmission line maintenance, and compound uncertainties of inflow and load. To address these issues, four strategic recommendations are proposed: (1) identifying and quantifying the impacts of multi-factor influences on maintenance planning; (2) developing integrated models for the co-optimization of power generation dispatch and maintenance scheduling; (3) formulating coordinated maintenance strategies for hydropower units and associated transmission infrastructure; and (4) constructing joint models to manage the coupled uncertainties of inflow and load. The strategy proposed in this study was applied to the CHSJS, obtaining the weight of the impact factor. The coordinated unit maintenance arrangements of transmission line maintenance periods increased from 56% to 97%. This study highlights the critical need for synergistic optimization of generation dispatch and maintenance scheduling in large-scale cascaded hydropower systems and provides a methodological foundation for future research and practical applications.
1. Introduction
1.1. Motivation
Large-scale cascaded hydropower systems form a cornerstone of China’s clean energy framework. In addition to supplying vast amounts of low-carbon electricity, they serve as essential flexible resources supporting long-distance, inter-provincial, and cross-regional power transmission [1]. It is of vital importance to determine reasonable maintenance schedules of hydropower units because this work significantly affects the power generation, dispatching, and operation safety and stability of power grids [2,3,4].
As illustrated in Figure 1, the Cascaded Hydropower System of the lower Jinsha River (CHSJS), located in the southwest of China, represents the most prominent mainstream hydropower system in the country. It comprises four mega-scale hydropower stations with a total installed capacity of 46.46 GW, approximately 11% of China’s total hydropower capacity, and serves multiple receiving provinces that jointly account for nearly one-third of the national Gross Domestic Product (GDP) [5]. Owing to its scale, operational complexity, and strategic importance, the CHSJS plays a pivotal role in both China’s hydropower sector and its broader energy security architecture [6].
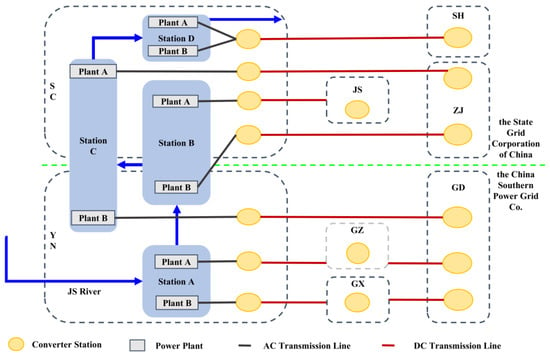
Figure 1.
Cascaded hydropower station-to-province power transmission network.
In the past, most research on the CHSJS has focused on generation scheduling optimization, with relatively little attention given to maintenance planning. However, the operational context is evolving rapidly. On the one hand, the secure functioning of the CHSJS is foundational to the high-penetration integration of wind and solar power in southwest China, where large-scale renewable bases are built around hydropower hubs for flexibility support [7]. It also underpins the stability of clean energy corridors that couple hydro, wind, solar, and storage resources across entire river basins. On the other hand, with the rapid development of multi-level electricity markets in China, there is increasing potential to exploit the heterogeneity in load characteristics across different receiving provinces. By coordinating preventive maintenance with variations in regional load and market conditions, it becomes possible to not only alleviate the pressure on hydropower stations during peak supply periods but also to enhance the economic returns of cascade operations through better market alignment [8,9,10].
However, the maintenance scheduling of the CHSJS is currently facing several critical challenges. First, the feasibility of maintenance is heavily constrained by a multitude of complex factors, including inflow conditions, generation obligations, transmission capacity, local grid characteristics, electricity consumption requirements, and broader social benefits. The influence of these factors is not only uneven but also insufficiently quantified, making it difficult to formulate rational and adaptive maintenance strategies. Second, there are often spatial and temporal mismatches between maintenance needs and dispatch priorities [11,12,13,14,15]. These conflicts are particularly acute during periods of high demand or low inflow, when taking units offline may jeopardize supply adequacy or result in the inefficient use of water resources. Third, coordination between unit maintenance and transmission lines maintenance is often lacking. Without integrated planning, simultaneous maintenance could significantly limit the capacity to deliver clean energy to receiving grids. Lastly, increasing variability in hydrological inflows and uncertainty in load patterns—especially in systems with high renewable energy penetration—further complicate the identification of reliable maintenance windows, as short-term peak demands may shift unexpectedly and alter the available generation margins [16].
In response to these challenges, this study analyzes the actual engineering characteristics of the CHSJS and summarizes the key constraints and drivers of maintenance scheduling [17]. Combining the team’s years of research experience in actual engineering projects of power grids and cascaded hydropower systems, from the aspects of identifying and quantifying multi-factor influences on maintenance availability, integrated co-optimization of dispatch and maintenance, coordinated maintenance of units and associated transmission infrastructure, and uncertainties in inflow and load, this paper outlines the research approaches for maintenance scheduling problems in cascaded hydropower systems and proposes corresponding technical methods. The outcomes are expected to provide both theoretical insights and practical tools for enhancing the synergy between generation dispatch and maintenance planning in large-scale cascaded hydropower systems under China’s evolving power system landscape [18,19,20].
1.2. Literature Review
In order to better sort out the existing research results, the relevant references were classified and organized according to the different research objects, as shown in Table 1.

Table 1.
Summary of the related literature.
The field of power system maintenance and dispatching has undergone a significant transformation from traditional experience-driven methods to intelligent optimization methods over the past few decades. In terms of methods, the research mainly focuses on the development of three core technical routes: The first is the optimization method based on decomposition, such as Benders decomposition, which effectively solves the computational complexity of large-scale maintenance scheduling problems. Second, the wide application of meta-heuristic algorithms, including genetic algorithms and particle swarm optimization, etc., has performed outstandingly in dealing with multi-objective and nonlinear optimization problems. The third is the precise solution of the mixed integer programming and linear programming methods, which has once again attracted attention as the performance of commercial solvers improves. The trend of technological development shows obvious characteristics of integration and intelligence: from single maintenance of power generation or transmission to coordinated maintenance of power generation and transmission; from deterministic optimization to random optimization considering the uncertainty of renewable energy; from single-objective optimization to multi-objective optimization; and at the same time, increasing emphasis is placed on the coordination of multiple stakeholders under environmental constraints and market environments.
2. Major Issues
2.1. Identification and Quantification of Maintenance-Influencing Factors
As the main power source of the power grid, the safe and stable operation of cascaded hydropower stations is extremely crucial, and their regulation capacity simultaneously affects the power supply of both the sending and receiving end power grids [21]. Therefore, arranging the preventive and restorative maintenance work of power station equipment reasonably and efficiently has become one of the core tasks of the dispatching and operation of cascaded hydropower stations in this basin.
However, as shown in Figure 2, due to the large scale of power generation, the wide range of power transmission, and the interrelationship between upstream and downstream power stations, the maintenance arrangements need to fully consider the impacts or demands of water inflow, power generation, power consumption, maintenance of the external transmission system, ecological dispatching tests, shipping, and the settlement of cascade reservoirs. In recent years, the large-scale integration of new wind and solar energy and the frequent occurrence of extreme weather have led to increasingly higher demands from the power grid for the regulation capacity of hydropower and its supply guarantee capacity during critical periods. As a result, the difficulty in arranging maintenance plans for cascade power stations has been growing. Therefore, how to systematically analyze the influence of these complex factors on maintenance arrangements, quantify their weights and interaction relationships, and rationally and efficiently formulate maintenance plans has become an urgent dispatching problem to be solved for giant cascaded hydropower station groups [21,22].
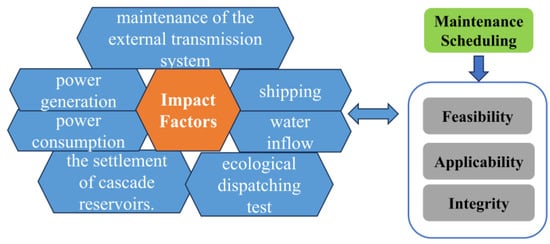
Figure 2.
Various factors affecting maintenance operations.
2.2. Spatiotemporal Coupling and Conflicts Between Maintenance and Generation Dispatch
As shown in Figure 3, in cascaded hydropower systems, maintenance and generation dispatch are inherently coupled in both spatial and temporal dimensions, making them prone to operational conflicts. This is primarily because both processes share the same hydropower operational capacity. On the one hand, generation dispatch reduces the available window for maintenance by occupying unit capacity to meet grid demands; on the other hand, maintenance scheduling limits the upper bound of generation by taking units offline [23].
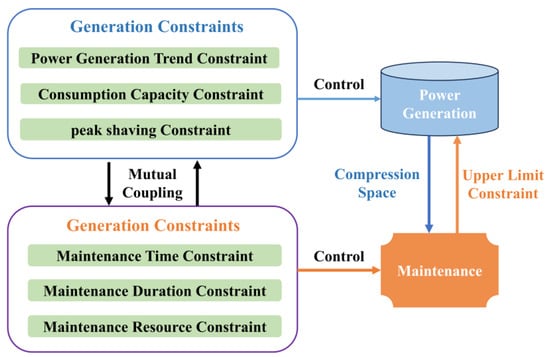
Figure 3.
Complex coupling between power generation and maintenance activities.
Moreover, the two processes operate under distinct scheduling logics and temporal constraints. Generation dispatch must simultaneously respond to short-term system needs, such as peak shaving and frequency regulation, and honor long-term obligations, including energy delivery targets and inter-provincial quotas. These are typically framed within a calendar-year cycle, aligning with market contracts and regulatory requirements.
However, maintenance scheduling is governed primarily by hydrological seasonality. Major maintenance tasks must be concentrated during the dry season, when inflows are low and reservoir drawdown is minimal. This window is further constrained by the limited availability of skilled personnel, equipment, and logistical resources, and often requires a multi-year planning horizon to ensure coordination across the cascade [24].
This mismatch in both scheduling timelines and planning rationales leads to frequent inconsistencies between dispatch and maintenance. The lack of alignment reduces the feasibility of concurrent optimization and increases the likelihood of operational compromises. In practice, maintenance plans are often postponed, compressed, or overridden to accommodate real-time dispatch needs, especially during tight supply conditions. Such adjustments, while necessary in the short term, undermine the long-term health and reliability of the generating equipment and increase the risk of unplanned outages that may prove more disruptive and costly.
2.3. Lack of Coordination Between Generator and Transmission Line Maintenance
A further challenge in the CHSJS arises from the insufficient coordination between the maintenance of hydropower units and their associated transmission lines, as shown in Figure 4. While the generator maintenance directly requires unit shutdowns, reducing available generating capacity, transmission line maintenance generally does not result in total line disconnection. However, in a large-scale cascaded hydropower system with ultra-high-voltage (UHV) transmission lines, even a small derating or route constraint may significantly restrict the power delivery capability [25].
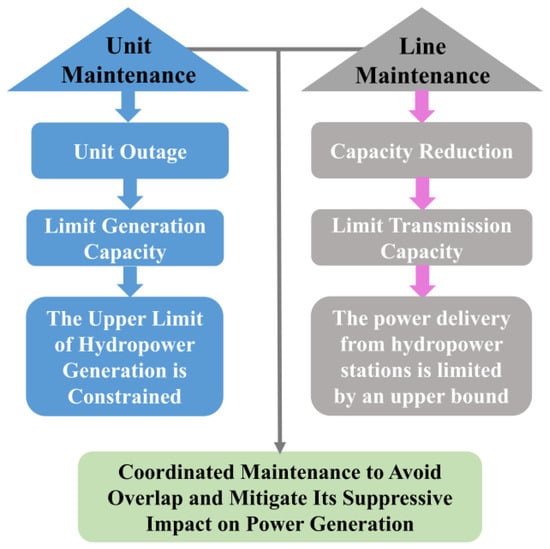
Figure 4.
Relationship between the unit and transmission line maintenance.
In a cascaded system with high-capacity ultra-high-voltage links, even partial derating can cause power curtailments or necessitate upstream water spillage if not matched with unit availability. Therefore, misaligned maintenance schedules lead to stranded capacity and economic inefficiency when a unit is operational but the corresponding transmission channel is constrained. Conversely, simultaneous outages of both generation and transmission components, if not well synchronized, may exacerbate system-level supply shortages or violate reliability margins.
The coordination difficulty stems from the following aspects:
- (1)
- The planning timelines for generator and transmission maintenance are often managed by different entities with distinct objectives and constraints, leading to siloed scheduling decisions.
- (2)
- The CHSJS involves multiple stakeholders and delivery endpoints across provinces, making it hard to achieve unified scheduling across regional grids.
- (3)
- Hydropower output is highly sensitive to inflow conditions, which vary inter-annually and seasonally, further complicating fixed maintenance planning.
- (4)
- Transmission outages require complex rerouting strategies, and their allowable outage windows are tightly constrained by grid security assessments, limiting scheduling flexibility.
Therefore, improving the coordination mechanism (e.g., through integrated optimization of unit and line maintenance schedules based on forecasted hydrological and load conditions) is crucial to enhance overall system efficiency and reliability.
2.4. Impact of Inflow and Load Uncertainty on Maintenance Scheduling
The fourth major issue pertains to the compounding effects of inflow and load uncertainty on maintenance feasibility, both in the short term and over seasonal horizons, as shown in Figure 5.
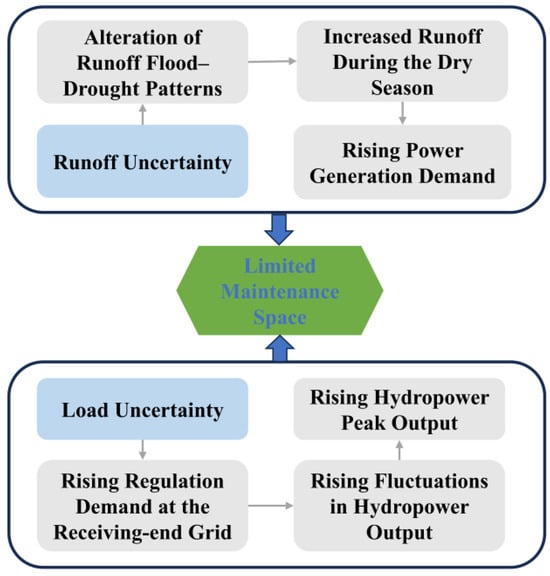
Figure 5.
Impact of Inflow and Load Uncertainty on Maintenance Scheduling.
On the inflow side, climate variability and extreme weather events have increased the unpredictability of hydrological regimes. Unexpected increases in inflow during the dry season can elevate power generation demand, narrowing the window for planned outages. This undermines the assumption that low inflow periods are naturally conducive to maintenance, especially in high-demand or water-scarce regions [26].
On the load side, rapid changes in demand profiles driven by weather conditions, renewable energy fluctuations, industrial activity, and regional market signals have made peak load periods increasingly volatile. This is particularly evident in hour-level dispatch, where hydropower often serves as the primary intraday balancing resource. As a result, real-time peak output from hydropower units becomes a direct constraint on the permissible maintenance space: any misjudgment in available capacity can result in dispatch failure or regulatory penalties.
The combined uncertainty in both inflow and load, therefore, requires planners to go beyond static assumptions. Robust maintenance planning must incorporate probabilistic modeling or scenario-based forecasting, enabling a more flexible definition of “available windows” for maintenance that ensures system security under multiple plausible futures.
3. Strategy Suggestion
3.1. Impact of Inflow and Load Uncertainty on Maintenance Scheduling
The CHSJS features massive hydropower capacity, a broad transmission range, and tightly coupled cascaded hydropower operations. Its maintenance planning must comprehensively account for a multitude of interacting factors, including water inflow, power generation, power consumption, maintenance of the external transmission system, ecological dispatching test, shipping, and the settlement of cascade reservoirs. In recent years, the large-scale grid integration of wind and solar energy, coupled with the increasing frequency of extreme weather events, has imposed growing demands on hydropower for flexibility and supply assurance during critical periods. These developments have significantly increased the difficulty of arranging effective maintenance schedules for cascade stations [27].
Consequently, along with the quantification of their relative weights and interaction mechanisms, a systematic analysis of these complex influencing factors has become essential for improving the quality and feasibility of maintenance scheduling across the CHSJS. As illustrated in Figure 6, explainable machine learning techniques can be applied to identify and quantify the importance of various maintenance influencing factors based on the operational characteristics of the cascade and its actual maintenance requirements. This data-driven approach enables planners to rationally prioritize scheduling decisions, reduce conflicts with power dispatch operations, and adapt maintenance planning to evolving system conditions in a more intelligent and efficient manner.
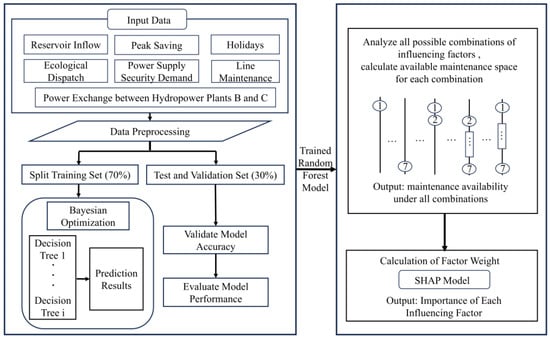
Figure 6.
Multi-factorial impact analysis workflow.
To effectively capture the complex, high-dimensional, and nonlinear relationships between multiple influencing factors and hydropower maintenance feasibility, this paper employs a Random Forest regression model, which is known for its robustness against overfitting and its strong performance in handling heterogeneous data. The model is used to learn the functional relationship between key operational variables and the available maintenance space. The implementation includes the following steps [28]:
Step 1: Input and Output Definition
Quantitative representations of various potential influencing factors (e.g., inflow, dispatch load, and line constraints) are defined as input features, while the output is the available maintenance space for hydropower units. Once trained, the model can estimate maintenance availability under new system conditions.
Step 2: Dataset Partitioning
Historical data are divided chronologically into training (70%), validation (15%), and testing (15%) sets to ensure generalization and avoid information leakage.
Step 3: Hyperparameter Optimization
Key parameters of the Random Forest model—such as the number of decision trees and maximum tree depth—are tuned using Bayesian Optimization techniques to enhance model performance and avoid local optima.
Step 4: Model Validation
Model performance is evaluated using three complementary metrics:
Coefficient of determination R2:
Symmetric Mean Absolute Percentage Error (SMAPE):
Mean Squared Logarithmic Error (MSLE):
where is the actual maintenance space, is the predicted value, is the average of the actual values, and n is the total number of samples.
To further interpret the model and quantify the contribution of each feature to the output, the SHAP (Shapley additive explanations) algorithm is applied. Rooted in cooperative game theory, SHAP assigns an importance value to each feature by computing its average marginal contribution across all possible feature coalitions. This framework provides both global interpretability (e.g., ranking overall feature importance) and local interpretability (e.g., explaining individual predictions), making it particularly suitable for complex systems like cascaded hydropower scheduling.
Mathematically, the Shapley value for feature i is calculated as follows:
where denotes the weight of the i-th influencing factor, S and N represent a subset of features and the full set of all influencing factors, respectively, with and being the number of elements in these sets, refers to the output of the Random Forest model using the feature subset S, denotes the model output when the i-th factor is added to subset S, and represents the output of the model when all influencing factors are included (i.e., the grand coalition).
To enhance transparency, SHAP values were computed for each prediction across the dataset. These were then aggregated to derive a global feature importance ranking. And it was determined that various factors (e.g., inflow, reservoir level, and turbine availability) had the most significant impact on maintenance decisions. This SHAP-based evaluation enables a detailed and interpretable quantification of each factor’s relative importance, offering insights for planners to prioritize maintenance decisions under various system conditions [29]. The combined use of Random Forest and SHAP ensures both accurate prediction and transparent attribution, forming a reliable foundation for intelligent maintenance scheduling in large-scale hydropower cascades.
3.2. Co-Optimization of Power Generation and Maintenance in Cascaded Hydropower Systems
As illustrated in Figure 7, the coordinated allocation of generation and maintenance in cascaded hydropower systems involves complex multi-dimensional and multi-scale spatiotemporal challenges. A key difficulty lies in the mismatch of scheduling cycles: generation planning is typically confined within annual or seasonal dispatch frameworks, whereas maintenance requirements often span across calendar years due to hydrological seasonality and resource constraints. The system must simultaneously address dispatch tasks over long-term, annual, and monthly horizons, while also adhering to diverse operational boundaries—including maintenance workforce availability, inflow uncertainty, power consumption quotas, and regulatory control on inter-provincial energy transmission.
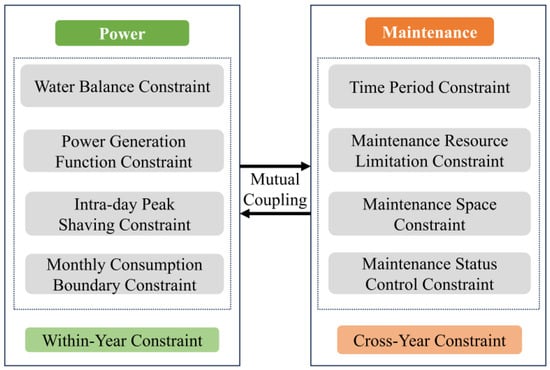
Figure 7.
Power generation and maintenance coordination method.
Spatially, generation and maintenance continuously compete for limited capacity. During dry seasons or high-load periods, the space available for maintenance is compressed by peak generation demands, while scheduled maintenance, in turn, imposes capacity restrictions that limit the achievable power output and flexibility of the system. This inherent spatial and temporal coupling creates significant operational tension between the two functions [30].
To address these issues holistically, this study proposes a novel two-year rolling optimization framework that integrates both power generation and maintenance scheduling. The extended time horizon allows for the resolution of inter-year conflicts and provides a common planning cycle to accommodate both the generation obligations and seasonal maintenance requirements of the cascade.
The model is formulated with the objective of maximizing total hydropower generation over the planning horizon, subject to a comprehensive set of constraints, including hydraulic balance, reservoir operation limits, and maintenance status. By embedding maintenance variables as decision points within the generation dispatch model, the approach enables the identification of globally optimal solutions that balance the trade-offs between energy output and equipment availability [31].
- (1)
- The objective function equation is as follows:where T represents the set time period, I represents the power station set, and represents the output of hydropower station i during period t.
- (2)
- Hydraulic constraints
- (1)
- The water balance equation is as follows:where and represent the initial and final water levels in the reservoir for the time period. and represent the inflow and outflow rates for the reservoir in the time period, measured in units.
- (2)
- The reservoir water level constraints equation is as follows:where , , and represent the water level of the reservoir in the time period and its upper and lower limits, measured in m units.
- (3)
- The power generation constraints equation is as follows:where , , and represent the power generation of the reservoir in the time period and its upper and lower limits, measured in units.
- (4)
- The outflow constraints equation is as follows:
- (5)
- Additionally, the following equation was employed:where , , and represent the outflow of the reservoir in the time period and its upper and lower limits, measured in units.
- (6)
- The output constraints equation is as follows:where , , and represent the output of the reservoir in the time period and its upper and lower limits; represents the capacity of the lines connected to power station I, measured in units.
- (7)
- The power generation function equation is as follows:where represents that the output of hydropower is related to the flow rate and storage capacity.
- (8)
- The power generation function equation is as follows:where represents the generator set of hydropower station i; represents the output of unit g of hydropower station i.
- (3)
- Maintenance constraints of the hydropower unit
- (1)
- The maintenance status constraint equation is as follows:where represents the maintenance status variable of unit g of hydropower station i, which results in 0–1 variables, where 0 represents the non-maintenance status and 1 represents the maintenance status.
- (2)
- The maintenance space constraint equation is as follows:where represents the capacity of unit g of hydropower station i, and represents the installed capacity of hydropower station i.
3.3. Co-Optimization of Generation Units and Transmission Line Maintenance
In cascaded hydropower systems, both generation units and transmission lines are subject to regular preventive maintenance. Although transmission line maintenance typically does not require a complete line shutdown, it often leads to a significant reduction in transmission capacity, which can restrict the ability of the system to deliver hydropower to receiving regions and result in clean energy curtailment, as illustrated in Figure 8. Simultaneously, generator maintenance requires unit outages, directly limiting the available generation capacity during the maintenance period.
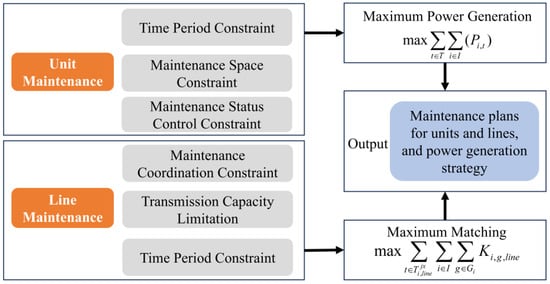
Figure 8.
Unit and transmission line maintenance coordination method.
Compounding these issues are operational constraints on the transmission side. For example, multiple transmission lines that deliver power to the same receiving province or grid region are generally prohibited from being maintained simultaneously to preserve system security and avoid bottlenecks in cross-provincial power flows. These operational and spatial dependencies introduce additional complexity in maintenance planning, as the coordinated availability of both generation and delivery infrastructure is required to ensure reliable system performance.
Given these interactions, the coordinated optimization of maintenance scheduling across both generation units and transmission lines is of paramount importance. This coordination can minimize the total impact on power delivery capacity and enhance the utilization of hydropower during maintenance windows [31].
To this end, a mathematical optimization model is proposed to jointly determine the optimal timing of generator and line maintenance activities. The model considers hydraulic constraints, transmission topology, delivery targets, and maintenance status, and is formulated to minimize energy loss or maximize energy utilization across the cascade while satisfying all system constraints. The structure of the model is as follows:
- (1)
- Objective function
- (1)
- Maximize power generation:Consistent with the objective in Section 3.2.
- (2)
- Maximize the matching degree between the maintenance of the unit and the line:where represents the set of maintenance periods for the transmission lines connected to hydropower station i; represents the matching degree between the maintenance of unit i of the hydropower station and the maintenance of its connected transmission line in the time period.
- (2)
- Hydraulic constraints:
Consistent with hydraulic constraints in Section 3.2.
- (3)
- Maintenance constraints of the hydropower unit:
Consistent with the maintenance constraints of the hydropower unit in Section 3.2.
- (4)
- Maintenance constraints of the transmission line:
- (1)
- The line maintenance status equation is as follows:where represents the maintenance status variable of the transmission lines connected to hydropower station i, which results in 0–1 variables, where 0 is the non-maintenance status and 1 is the maintenance status. , represent the rated capacity of the line and the capacity during maintenance, respectively.
- (2)
- The matching of the degree of unit line maintenance equation is as follows:where represents the matching degree between the maintenance of unit i of a hydropower station and the maintenance of its connected transmission line in the time period, which results in 0–1 variables, where 0 is simultaneous matching and maintenance of the unit and the line and 1 is non-simultaneous maintenance of the unit and the line.
This model can link the maintenance of generating units and transmission lines together and make them cooperate with each other. In the traditional power system maintenance arrangement, the maintenance of generating units and transmission lines is carried out independently, and there is a lack of evidence that their cooperation can bring positive benefits. The proposal of this model can serve as a support for the joint optimization mode of the two, promoting the system optimization of the maintenance of generating units and transmission lines.
3.4. Strategies for Addressing Multi-Source Uncertainties in Inflow and Multi-Network, Multi-Scale Load Demand
In large-scale cascaded hydropower systems such as the CHSJS, maintenance scheduling is increasingly constrained by the intertwined uncertainties of hydrological inflows and power system loads. These uncertainties manifest across multiple spatial and temporal dimensions: inflows are subject to both inter-annual and intra-annual climatic variability, while electricity demand fluctuates across different provinces and at different time scales (e.g., yearly, monthly, and daily). In the case of the CHSJS, which delivers power to seven receiving provinces, each province presents distinct load characteristics and flexibility requirements, further complicating maintenance planning [32].
To effectively capture these dynamics, this study proposes a joint probabilistic modeling approach that integrates hydrological inflow uncertainty with multi-regional, multi-scale load variability. Rather than relying on deterministic assumptions, we adopt a scenario-based framework to reflect the spatiotemporal coupling between river inflow conditions and provincial-level load demand.
As illustrated in Figure 9, the proposed inflow–load joint scenario generation method comprises three core steps:
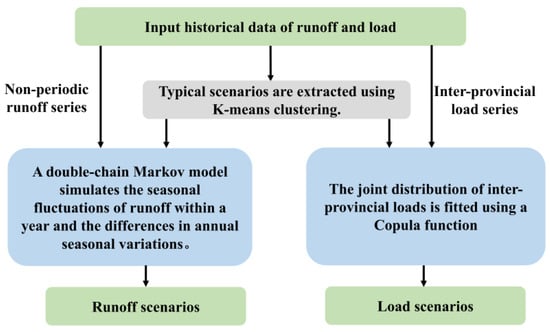
Figure 9.
Runoff and load scenario generation workflow.
- (1)
- K-means clustering is applied to historical inflow and load data to extract annual joint fluctuation patterns. This method enables the identification of typical and extreme hydrological-demand scenarios in a data-driven way. It has been widely applied in the energy and water sectors due to its simplicity and computational efficiency. However, its limitation lies in the lack of temporal continuity and the need to predefine the number of clusters, which may affect classification stability.
- (2)
- A dual-chain Markov model is used to simulate the seasonal evolution of inflows. Compared to traditional single-chain models, the dual-chain structure allows for a more accurate representation of hydrological variability within the year, especially in capturing transitions between dry, normal, and wet seasons. This model has been applied in river flow forecasting and reservoir management. Its main advantage lies in modeling time series progression and transition probabilities, though it assumes Markovian properties and may require recalibration under non-stationary climate conditions.
- (3)
- A copula-based model is employed to characterize the statistical dependencies among the loads of different receiving provinces. Copula models are prioritized for their ability to capture nonlinear and tail dependencies, which are often observed in multi-provincial power load data but cannot be effectively represented by traditional linear correlation methods such as Pearson or Spearman coefficients. By leveraging the flexibility of copula functions to model diverse marginal distributions and complex interdependencies, the approach enables a more realistic joint simulation of inter-provincial load correlation structures, while preserving regional heterogeneity and improving scenario representativeness. Nonetheless, their application requires careful selection of copula families and estimation of marginal distributions, which may increase computational complexity.
By integrating these stochastic inflow–load scenarios into long-term maintenance planning models, it becomes possible to define robust and flexible outage windows that better reflect real-world operating conditions. This joint uncertainty modeling also provides a critical foundation for the development of multi-scale optimization frameworks, enabling more adaptive scheduling of preventive maintenance under complex and uncertain system dynamics [33].
The generated scenarios were evaluated from three aspects: randomness, volatility, and correlation. The three characteristics were evaluated, respectively, by using the three indicators of Average Euclidean Distance (AED), coverage rate, and Average Pearson Correlation Coefficient (APCC).
Randomness refers to the deviation between the actual scene and the generated scene set on the time cross-section. The AED metric evaluates scenarios based on distance, and its formula is as follows:
where is the sequence of the first scene; is a sequence of actual scenes; and is the L2 norm of the difference between two sequences. The smaller the AED value is, the closer the generated scene is to the actual output sequence.
The generated scene should include the fluctuation range of the actual scene as much as possible. Based on this, the coverage rate, a volatility evaluation index, is proposed. The coverage rate is a positive number. The larger its value, the greater the probability that the actual scene falls within the range of the generated scene. Its formula is as follows:
where indicates the coverage rate; is a binary variable. If the condition within the parentheses is met, its value is 1; otherwise, it is 0. and , respectively, represent the minimum and maximum values of all scenes at the first moment.
The larger the average value of the Pearson correlation coefficient of the generated scene is, the higher the degree of correlation between the generated scene and the actual scene. The expression of the APCC indicator is as follows:
where is the covariance of two sequences; is the standard deviation of the sequence.
3.5. Analysis of Calculation Examples
To validate the effectiveness and practicality of the proposed method, this study employs the CHSJS cascaded hydropower stations as a case study and systematically evaluates the advantages of the proposed collaborative optimization strategy over traditional methods through empirical analysis.
3.5.1. Impact of Inflow and Load Uncertainty on Maintenance Scheduling
This study utilizes actual operational data from four CHSJS cascaded hydropower stations spanning 2020–2024 to validate the effectiveness of the explainable machine learning method in analyzing the primary factors influencing cascaded hydropower maintenance.
The research compiled key characteristic variables, including cascade reservoir inflow variations, receiving-end grid peak regulation demands, holidays, ecological dispatching trials, energy exchanges between Station B and Station C, outgoing transmission line maintenance, and power supply security requirements. Through numerical processing, authentic data distributions over five years were obtained. Applying the influence factor weight calculation strategy proposed in this study, quantitative results are presented in Table 2.

Table 2.
Quantified impact weights of factors influencing maintenance planning (cascade level).
The analysis results reveal that the three most influential factors affecting cascade maintenance scheduling are inflow (52.89%), peak regulation demand (20.95%), and holidays (10.86%). This finding aligns with the actual operational patterns of hydropower stations: inflow directly determines the generation capacity and available maintenance space of hydropower stations, while peak regulation demand and holidays indirectly affect hydropower station output through load variations, thereby influencing the flexibility of maintenance scheduling. These analytical results are highly consistent with theoretical understanding in the existing literature, validating the rationality of the proposed method.
3.5.2. Co-Optimization of Power Generation and Maintenance in Cascaded Hydropower Systems
To objectively evaluate the proposed collaborative optimization strategy, this study employs actual inflow data and engineering requirements from the CHSJS during 2022–2023 to validate the effectiveness of the proposed two-year rolling optimization framework. Taking Station C as an example, the optimization results shown in Figure 10 demonstrate the following:
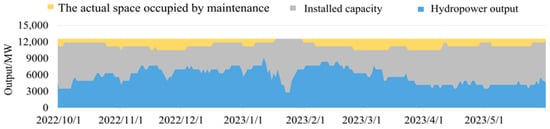
Figure 10.
Power generation and maintenance power generation process diagram.
As illustrated in Figure 10, Station C exhibits cross-year maintenance units, proving that the proposed model can effectively address the mismatch between maintenance and scheduling cycles through a two-year rolling optimization framework that integrates generation and maintenance scheduling. Furthermore, excellent spatial coordination is achieved between generation and maintenance, with no spatial conflicts, thereby avoiding the problem of spatial competition between generation and maintenance.
3.5.3. Co-Optimization of Generation Units and Transmission Line Maintenance
To further validate the effectiveness of the collaborative optimization model, this study compares fixed transmission line maintenance scenarios (Model 1) with collaborative optimization of generating units and transmission line maintenance (Model 2). Taking Station D as an example, the maintenance space utilization conditions are illustrated in Figure 11 and Figure 12.
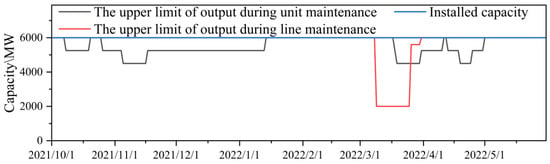
Figure 11.
Space diagram of unit and line maintenance of Model 1.
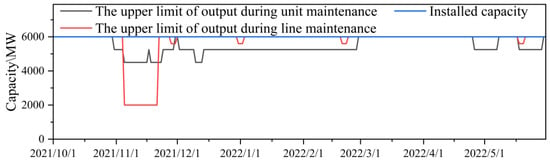
Figure 12.
Space diagram of unit and line maintenance of Model 2.
The comparative analysis reveals a substantial improvement in maintenance coordination effectiveness. In the traditional approach (Model 1), only 56% of transmission line maintenance periods accommodate coordinated unit maintenance arrangements, indicating significant waste of maintenance resources. In contrast, the proposed collaborative optimization approach (Model 2) achieves coordinated arrangements for 97% of the time slots, representing a remarkable enhancement in maintenance coordination efficiency. This collaborative optimization strategy substantially reduces the impact of maintenance activities on generation space utilization, enhances the rational allocation of space resources during transmission line maintenance periods, and effectively minimizes the adverse effects of both unit and transmission line maintenance on overall generation performance.
3.5.4. Summary
Through comprehensive comparative analysis with traditional methods, this study validates the effectiveness of the proposed collaborative optimization strategy in enhancing generation efficiency, improving water resource utilization efficiency, and strengthening system flexibility. The application results of actual engineering cases demonstrate that the proposed method possesses significant practical value and promising prospects for widespread application.
4. Future Research Directions for Maintenance Optimization in Large-Scale Cascaded Hydropower Systems
Considering the increasing complexity and strategic importance of large-scale cascaded hydropower systems, particularly the CHSJS, future research on maintenance scheduling must respond to evolving operational, hydrological, and system-level demands. Building on the challenges and strategic insights highlighted in this study, the following directions outline a coherent research roadmap for maintenance optimization [34]:
- (1)
- Quantitative modeling of multi-dimensional influencing factors
Future studies should focus on systematically identifying and quantifying the key factors that affect maintenance feasibility, such as reservoir inflows, ecological constraints, load-following obligations, inter-station hydraulic coupling, and unit availability. Developing unified evaluation frameworks and sensitivity analysis tools will help to capture the heterogeneous and time-varying impacts of these factors, enabling more adaptive and robust maintenance planning.
In particular, the integration of AI algorithms, such as machine learning models for inflow forecasting or fault prediction, could enhance the accuracy and responsiveness of such quantitative evaluations.
- (2)
- Integrated optimization of generation dispatch and maintenance scheduling
Considering the deep coupling between preventive maintenance and generation tasks in cascaded systems, optimization models that jointly determine unit outages and dispatch profiles are essential. These models should capture the physical and operational interdependence among upstream and downstream stations, account for water balance and energy conversion constraints, and ensure that maintenance activities do not compromise overall power generation efficiency or water resource utilization [35,36].
Future research may explore AI-driven co-optimization models that leverage real-time operational data and predictive analytics to dynamically adjust outage plans in line with generation targets.
- (3)
- Spatiotemporal conflict resolution mechanisms
Maintenance windows often clash with high-demand periods or low-inflow seasons, particularly in complex hydrological years. Future research should explore mechanisms to resolve temporal and spatial conflicts between maintenance needs and dispatch priorities. This includes the design of multi-scenario simulation platforms that evaluate trade-offs across different maintenance sequences, as well as the development of decision-support tools that recommend optimal timing and coordination strategies under variable operating conditions. Digital twin technology can provide a virtual, real-time replica of the hydropower system, enabling simulation-based validation of scheduling decisions and proactive conflict avoidance.
- (4)
- Joint scheduling of hydropower units and supporting infrastructure
Maintenance coordination should not be limited to generating units but extended to associated infrastructure, such as lines. In large cascades with tightly coupled station operations, the reliability of auxiliary systems directly affects the feasibility and safety of maintenance activities. Research is needed to establish joint scheduling frameworks that co-optimize maintenance across different system components while respecting hydropower system operational constraints [37,38]. Applying AI-based diagnostic systems and predictive maintenance technologies can help monitor equipment health status and optimize inspection cycles.
- (5)
- Uncertainty-aware planning under variable inflow and load conditions
Inflow variability and multi-grid load fluctuations introduce significant uncertainty into the planning of maintenance activities. Future methodologies should incorporate stochastic programming, robust optimization, or scenario-based planning techniques to identify resilient maintenance schedules. Emphasis should be placed on methods that can adapt to near-term hydrological updates and grid demand forecasts while preserving the long-term safety and efficiency of the system. The combination of digital twins and AI-based forecasting tools can further improve uncertainty modeling, allowing for continuous re-optimization as new information becomes available.
In summary, future research on maintenance optimization in large-scale cascaded hydropower systems should aim to build unified, flexible, and forward-looking frameworks that reconcile the need for reliable maintenance with the increasingly dynamic and multi-dimensional operation of modern hydropower systems. Aligning with global industry trends such as digitalization, intelligent monitoring, and predictive analytics, technologies like digital twins and AI-driven maintenance will be instrumental in achieving smarter and more resilient hydropower system management. The Cascaded Hydropower System of the Lower Jinsha River, as a representative case, offers valuable insights and serves as a foundation for generalized methodologies applicable to other large-scale hydropower systems worldwide.
5. Conclusions
The reliable and efficient scheduling of preventive maintenance is fundamental to ensuring the long-term safety, stability, and performance of large-scale cascaded hydropower systems. Meanwhile, maintenance planning faces a series of extremely challenging theoretical and technical problems.
This study focuses on the Cascaded Hydropower System of the Lower Jinsha River and achieved the following important contributions in the field of preventive maintenance scheduling optimization:
- (1)
- Systematically analyzed the influence of complex factors on maintenance arrangements, quantifying their weights and interaction relationships.
- (2)
- Proposed a novel two-year rolling optimization framework that integrates both power generation and maintenance scheduling, coordinating the allocation of generation and maintenance.
- (3)
- Established a mathematical optimization model to jointly determine the optimal timing of generator and transmission line maintenance activities.
- (4)
- Constructed robust planning models under uncertainty conditions, effectively addressing the constraints of intertwined uncertainties from hydrological inflow and power system load.
Future research should further advance these directions by developing adaptive, uncertainty-aware, and data-driven frameworks capable of handling the growing operational complexity of modern hydropower systems. Joint modeling approaches and conflict-resolution mechanisms will be critical for maintaining flexibility in the face of increasing variability in hydrological and demand conditions. The Cascaded Hydropower System of the Lower Jinsha River, given its scale and strategic role, offers valuable lessons and opportunities for testing advanced maintenance optimization approaches applicable to other major hydropower systems worldwide.
In conclusion, strengthening the integration between maintenance scheduling and hydropower system operation is essential to unlocking the full flexibility potential of large-scale cascades and supporting the broader goals of clean energy security and sustainable system development.
Author Contributions
Conceptualization, Y.H. and Y.W.; methodology, Y.H., J.S., and Y.W.; software, L.L., Z.X., X.W., and Y.L.; validation, Y.H., L.L., and Y.W.; formal analysis, Y.W. and X.W.; investigation, L.L.; resources, Y.L.; data curation, Z.X.; writing—original draft preparation, Y.H.; writing—review and editing, L.L. and X.W.; visualization, Y.W. and Z.X.; supervision, Y.L. and J.S.; project administration, J.S.; funding acquisition, J.S. All authors have read and agreed to the published version of the manuscript.
Funding
This achievement was funded by the scientific research project of China Yangtze Power Co., Ltd. (Contract No.: Z242302025).
Acknowledgments
The authors would like to thank the editors and reviewers for their valuable comments and suggestions that helped improve the quality of this manuscript.
Conflicts of Interest
Authors Le Li, Yuanyuan Han, Xingye Wu, Yan Luo were employed by the company China Yangtze Power Co., Ltd. The authors declare that this research was conducted as part of work affiliated with China Yangtze Power Co., Ltd., which also provided funding for this study. However, the research was conducted with scientific rigor and objectivity, and the conclusions presented are based solely on the data and analysis without bias from the funding source.
References
- Cheng, C.T.; Wu, X.Y.; Shen, J.J.; Liao, S.; Liu, B. Hydropower dispatching problems and progress in the era of 100 million kilowatts in China. J. Hydraul. Eng. 2019, 50, 112–123. (In Chinese) [Google Scholar]
- Abirami, M.; Ganesan, S.; Subramanian, S.; Anandhakumar, R. Source and transmission line maintenance outage scheduling in a power system using teaching learning based optimization algorithm. Appl. Soft Comput. 2014, 21, 72–83. [Google Scholar] [CrossRef]
- Geetha, T.; Shanti Swarup, K. Coordinated preventive maintenance scheduling of GENCO and TRANSCO in restructured power systems. Int. J. Electr. Power Energy Syst. 2009, 31, 626–638. [Google Scholar] [CrossRef]
- Kim, J.; Geem, Z.W. Optimal scheduling for maintenance period of generating units using a hybrid scatter-genetic algorithm. IET Gener. Transm. Distrib. 2015, 9, 22–30. [Google Scholar] [CrossRef]
- Moslemi, N.; Kazemi, M.; Abedi, S.M.; Khatibzadeh-Azad, H.; Jafarian, M. Maintenance Scheduling of Transmission Systems Considering Coordinated Outages. IEEE Syst. J. 2018, 12, 3052–3062. [Google Scholar] [CrossRef]
- Norozpour Niazi, A.; Badri, A.; Khoshnoud, S. Annual coordinated generation and transmission maintenance scheduling considering network constraints and energy not supplied. Int. Trans. Electr. Energ. Syst. 2015, 25, 1831–1847. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Z.; Shahidehpour, M.; Wu, L.; Guo, C.; Zhu, B. Stochastic co-optimization of midterm and short-term maintenance outage scheduling considering covariates in power systems. IEEE Trans. Power Syst. 2016, 31, 4795–4805. [Google Scholar] [CrossRef]
- Mollahassani-Pour, M.; Rashidinejad, M.; Pourakbari-Kasmaei, M. Environmentally constrained reliability-based generation maintenance scheduling considering demand-side management. IET Gener. Transm. Distrib. 2019, 13, 1153–1163. [Google Scholar] [CrossRef]
- San Martin, L.S.; Yang, J.; Liu, Y. Hybrid NSGA III/dual simplex approach to generation and transmission maintenance scheduling. Int. J. Electr. Power Energy Syst. 2022, 135, 107498. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, X.; Cao, B.; Wang, X.; Wang, B. An efficient generator maintenance scheduling model based on unit clustering and linear relaxation. Electr. Power Syst. Res. 2024, 230, 110300. [Google Scholar] [CrossRef]
- Zhang, W.; Hu, B.; Xie, K.; Shao, C.; Niu, T.; Yan, J.; Peng, L.; Cao, M.; Su, Y. Short-term transmission maintenance scheduling considering network topology optimization. J. Mod. Power Syst. Clean Energy 2021, 10, 883–893. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, M.; Xie, M.; Dong, P. A mathematical programming–based heuristic for coordinated hydrothermal generator maintenance scheduling and long-term unit commitment. Int. J. Electr. Power Energy Syst. 2023, 147, 108833. [Google Scholar] [CrossRef]
- Zhong, Z.; Fan, N.; Wu, L. Multistage stochastic optimization for mid-term integrated generation and maintenance scheduling of cascaded hydroelectric system with renewable energy uncertainty. Eur. J. Oper. Res. 2024, 318, 179–199. [Google Scholar] [CrossRef]
- Sadeghian, O.; Mohammadpour Shotorbani, A.; Mohammadi-Ivatloo, B. Generation maintenance scheduling in virtual power plants. IET Gener. Transm. Distrib. 2019, 13, 2584–2596. [Google Scholar] [CrossRef]
- Bahrami, F.; Moazzami, M. Long-term generation maintenance scheduling with integration of pumped storage units. Int. J. Renew. Energy Res. 2019, 9, 1694–1704. [Google Scholar] [CrossRef]
- Shen, J.J.; Cheng, C.T.; Cao, R.; Lu, J. Key issues and research progress of large-scale hydropower consumption and peak regulation scheduling. Autom. Electr. Power Syst. 2018, 42, 174–183. (In Chinese) [Google Scholar]
- Lusby, R.; Muller, L.F.; Petersen, B. A solution approach based on Benders decomposition for the preventive maintenance scheduling problem of a stochastic large-scale energy system. J. Sched. 2013, 16, 605–628. [Google Scholar] [CrossRef]
- Gao, J.; Liu, W.Y.; Wang, X.L.; Wang, X.F. Practical research on optimization of power generation system maintenance planning. Northwest Electr. Power Technol. 2002, 1, 22–26. (In Chinese) [Google Scholar]
- Zheng, X.B.; Zhang, Y.K.; Bie, Z.H.; Liu, Y. Assessment of power system maintenance reserve capacity considering uncertainty of maintenance requirements. Electr. Power Autom. Equip. 2014, 34, 144–149. (In Chinese) [Google Scholar]
- Garver, L.L. Adjusting maintenance schedules to levelize risk. IEEE Trans. Power Appar. Syst. 1972, 91, 2057. [Google Scholar] [CrossRef]
- Feng, C.; Wang, X.; Li, F. Optimal maintenance scheduling of power producers considering unexpected unit failure. IET Gener. Transm. Distrib. 2009, 3, 460–471. [Google Scholar] [CrossRef]
- Chen, S.H.; Yang, P. Application of genetic algorithm in planned maintenance of thermal power units. J. Wuhan Univ. Hydraul. Electr. Eng. 1999, 5, 35–37. (In Chinese) [Google Scholar]
- Liao, S.L.; Cheng, C.T.; Li, G.; Xie, Y.G.; Cai, H.X. Minimum power shortage model for unit maintenance optimization. Power Syst. Technol. 2010, 34, 38–42. (In Chinese) [Google Scholar]
- Subramanian, S.; Anandhakumar, R.; Ganesan, S. Generator maintenance management using bio-inspired search algorithm. Int. J. Energy Sect. Manag. 2011, 5, 522–544. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, L.Z.; Jiang, Y.; Cai, H.; Li, X.; Wu, Y.; Qi, X. Bi-level optimization model for medium and long-term scheduling and maintenance planning of cascaded hydropower stations in electricity market environment. Power Syst. Technol. 2018, 42, 1541–1549. (In Chinese) [Google Scholar]
- Ge, X.L.; Shu, J.; Zhang, L.Z. Medium and long-term optimal scheduling method of hydro-thermal power coordination considering maintenance planning. Proc. CSEE 2012, 32, 36–43. (In Chinese) [Google Scholar]
- Yu, V.F.; Nguyen Truc, Q.V.; Ngoc Minh, N. Integrated maintenance scheduling for generators and transmission lines considering renewable energy sources and energy storages. Electr. Power Syst. Res. 2025, 246, 111696. [Google Scholar] [CrossRef]
- Wang, J.; Cheng, C.T.; Shen, J.J.; Wu, X.; Cao, R. Nonlinear global optimization method for optimal operation of hydropower station groups. Proc. CSEE 2018, 38, 5107–5117. (In Chinese) [Google Scholar]
- Cheng, C.; Wang, J.; Wu, X. Hydro unit commitment with a head-sensitive reservoir and multiple vibration zones using MILP. IEEE Trans. Power Syst. 2016, 31, 4842–4852. [Google Scholar] [CrossRef]
- Shen, J.; Cheng, C.; Zhang, X.; Zhou, B. Coordinated operations of multiple-reservoir cascaded hydropower plants with cooperation benefit allocation. Energy 2018, 153, 509–518. [Google Scholar] [CrossRef]
- Niu, W.J.; Shen, J.J.; Cheng, C.T.; Wu, X.Y.; Feng, Z.K.; Guo, Y.A. Multi-objective optimization scheduling hybrid search method for cascaded hydropower stations coupling peak regulation and navigation demands. Proc. CSEE 2016, 36, 2331–2341. (In Chinese) [Google Scholar]
- Zhang, Z.; Zhang, H.; Yue, S.; Zeng, W. A Review of Icing and Anti-Icing Technology for Transmission Lines. Energies 2023, 16, 601. [Google Scholar] [CrossRef]
- Cai, J.; Guo, S.; Liao, S.; Chen, X.; Miao, S.; Li, Y. Optimization Model of Key Equipment Maintenance Scheduling for an AC/DC Hybrid Transmission Network Based on Mixed Integer Linear Programming. Energies 2020, 13, 1011. [Google Scholar] [CrossRef]
- Mazidi, P.; Tohidi, Y.; Sanz-Bobi, M.A. Strategic Maintenance Scheduling of an Offshore Wind Farm in a Deregulated Power System. Energies 2017, 10, 313. [Google Scholar] [CrossRef]
- Arafat, M.Y.; Hossain, M.J.; Li, L. Advanced Deep Learning Based Predictive Maintenance of DC Microgrids: Correlative Analysis. Energies 2025, 18, 1535. [Google Scholar] [CrossRef]
- Karki, R.; Hu, P.; Billinton, R. Reliability Evaluation Considering Wind and Hydro Power Coordination. IEEE Trans. Power Syst. 2010, 25, 685–693. [Google Scholar] [CrossRef]
- Basaran, U.; Kurban, M. The Strategy for the Maintenance Scheduling of the Generating Units. In Proceedings of the Large Engineering Systems Conference on Power Engineering, Montreal, QC, Canada, 7–9 May 2003; pp. 172–176. [Google Scholar]
- Grudz, V.; Grudz, Y.; Pavlenko, I.; Liaposhchenko, O.; Ochowiak, M.; Pidluskiy, V.; Portechyn, O.; Iakymiv, M.; Włodarczak, S.; Krupińska, A.; et al. Ensuring the Reliability of Gas Supply Systems by Optimizing the Overhaul Planning. Energies 2023, 16, 986. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).