1. Introduction
District systems offer a rational solution to efficiently meet the energy demand of an aggregation of users [
1]. Alongside district heating [
2] and cooling [
3] networks delivering thermal energy to customers mostly in the residential and commercial building sectors, steam networks are widespread in industry to provide process heat up to 250 °C [
4,
5] and are typically supplied by burning fossil fuels [
6]. As electric heating technologies reach commercial maturity, their use in conjunction with clean electricity is becoming a more attractive way to supply steam with lower associated emissions and, potentially, greater demand-side flexibility [
7]. However, many industries operate on tight margins [
8] and require a constant, on-demand steam supply to avoid costly downtime. Any flexible, electricity-based steam generation must therefore meet strict operational requirements.
Heat pumps use electricity to upgrade heat from a source to a higher-temperature sink. They are well-established for space heating applications, where the same unit can provide heating or cooling, alternatively [
9]. In this context, flexible heat pump use has been shown to reduce peak electricity demand significantly [
10] whilst maintaining occupants’ comfort [
11] and offering benefits to various agents across the power system [
12]. Suitable device control strategies [
13] and optimised refrigerant circuitry [
14] have proven effective in improving heat pump performance outside rated operating conditions, containing costs and emissions.
A high-temperature heat pump (HTHP) works on the same principle but can deliver heat above 100 °C [
15], which makes these devices suitable for industrial steam generation. Several HTHP pilot projects have been tested [
16], with multiple manufacturers worldwide and applications in sectors like paper, food, and chemicals [
17]. As with space heating, operating HTHPs flexibly in industry could bring wider system benefits, as well as offer an improved business case for practitioners, compared to fixed operation [
18]. However, variations in power input affect thermodynamic states along the HTHP cycle [
19], which in turn alter steam flow and temperature.
Steam accumulators (SAs) are commonly used in industry to balance short-term mismatches between steam supply and demand [
20]. These devices operate as sliding pressure vessels where saturated water vapour and liquid are in thermodynamic equilibrium. During charging, injected steam increases vessel pressure and some vapour condenses, raising the liquid level; during discharging, this process is reversed [
21]. Acting as a buffer between steam supply and demand, SAs help ensure a more stable steam delivery and reduce fluctuations.
To date, most studies on flexible HTHP operation have focused on the dynamics of internal system states [
22] and on control methods to keep performance near design conditions [
23]. Others have tested the HTHP response to upward and downward ramps in compressor power setpoints against the specifications for a grid balancing service provision [
24]. The effect of flexible HTHP operation on the heat supply and delivery to downstream processes remains largely unaddressed. Meanwhile, works on SAs—either experimental [
25], numerical [
26,
27], or combined [
28,
29]—consider SA in isolation and demonstrate strong dynamics. The input steam profiles used in these studies are case-dependent and unrelated to an upstream HTHP [
30,
31]. Overall, the steam supply dynamics from variable-power HTHPs, with or without a downstream SA, remain underexplored in sufficient detail. As such, a clear understanding of how SAs could support HTHP’s flexible operation and strengthen the case for their integration in industry is missing.
This paper bridges that gap by addressing the research question, “How does the flexible operation of an HTHP, alone or combined with a downstream SA, affect the flow and temperatures of the steam supplied?” The analysis proceeds as follows:
First, a single-stage HTHP is designed to supply 5 MWth of steam at 4 bar to some industrial processes, using steady-state modelling;
Then, the steam supply dynamics of both a standalone HTHP and an HTHP combined with an SA are examined during power turn-up and turn-down operation;
Finally, these insights are used to explore suitable SA sizing and discuss how flexibility incentives might justify the investment.
By shedding light on steam supply dynamics under flexible HTHP operation, this work supports cleaner, more flexible heat provision in low-to-medium-pressure industrial steam networks. The results can therefore assist clean technology uptake and development in industrial steam and district heating networks.
2. Methods
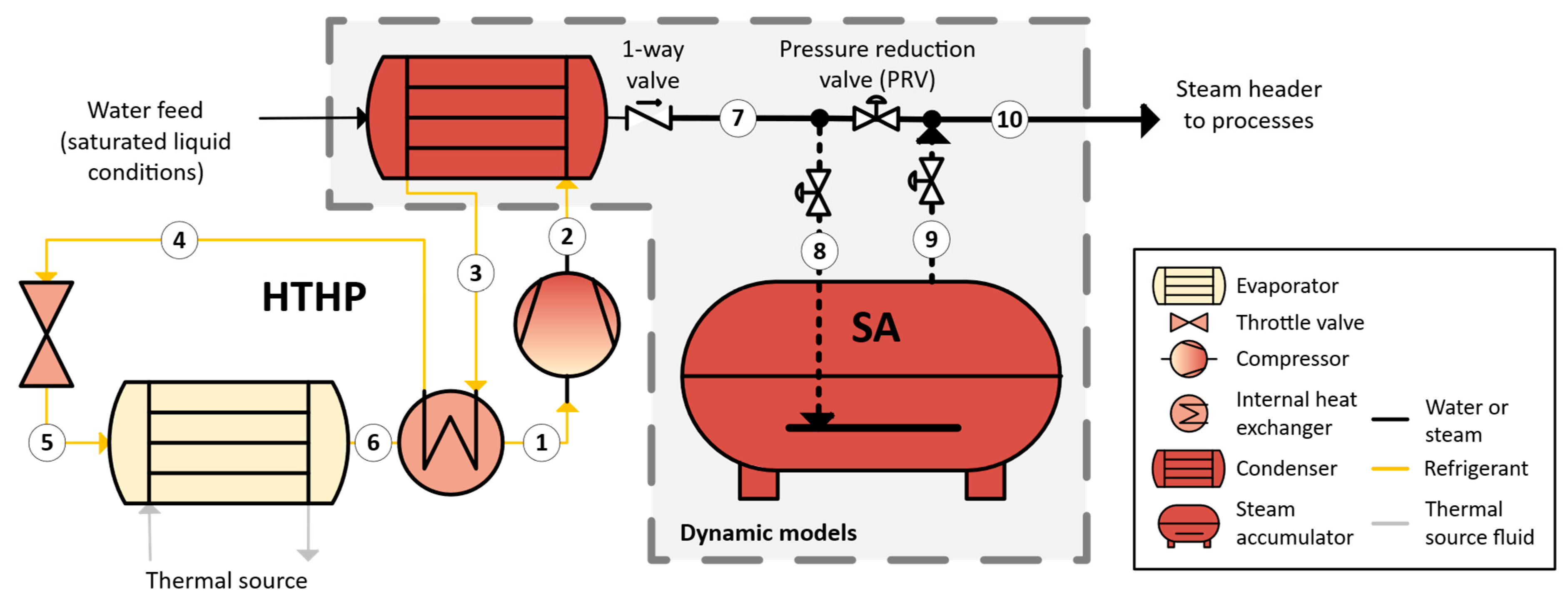
Figure 1 shows a schematic of the system studied. A single-stage, reverse vapour compression cycle HTHP is considered to supply a notional downstream industrial process via a 4-bar steam header. The HTHP uses the heat input from a thermal source and an electrical power input to supply thermal power at the condenser. This thermal power evaporates the water feed to generate steam, which is then injected through the main steam header to supply downstream industrial processes. This can happen directly (solid pipework in
Figure 1) or with an intermediate SA (dashed pipework in
Figure 1). Since the latter option requires a pressure difference between the header and the SA to allow for accumulator charging and discharging, two cases are considered:
In both cases, a pressure reduction valve (PRV) is needed on the steam supply line that leaves the HTHP condenser to maintain the desired header pressure.
A thermodynamic model of the HTHP was developed by applying steady-state mass, momentum, and energy balances to all components [
32]. The model included standard assumptions such as constant equipment efficiency, fixed pressure drops and pinch point temperature differences in the heat exchangers, and saturated liquid conditions of the water feed to the condenser. The selected refrigerant was n-Pentane due to its favourable thermodynamic properties and low environmental impact [
33]. However, the presented modelling framework is equally suitable to study HTHP using other refrigerants in the same system layout. Input parameters to the steady-state HTHP thermodynamic model are reported in
Table 1.
The model was used to design a 5 MW
th HTHP intended to supply steam at 4 bar (approximately 145 °C), using an 80 °C heat source with a temperature difference of 10 °C. These conditions were chosen to reflect the needs of several industrial applications [
34] and, given the resulting 65 °C temperature lift, also align with the operating range of many commercial units [
17]. The size of individual components was then used as an input for the dynamic models of the HTHP condenser and SA, both developed in OpenModelica [
35] and described in detail hereafter. These and other HTHP component models, together with the integrated system models used to generate the results in this work, are available on GitHub (
https://github.com/AndreOlds/HTHP.git, accessed on 26 May 2025).
2.1. Dynamic Modelling of the Condenser
A finite-volume, segmented approach was adopted to account for thermal dynamics in the HTHP condenser [
36]. Dynamic, lumped-parameter energy conservation equations were specified for each of the fluid and wall control volumes along the heat exchanger. Under the considered counterflow arrangement, and for each segment
, these were expressed as follows:
In Equations (1) to (3),
superscripts indicate wall control volumes; fluid control volumes are denoted by
and
superscripts, as the equations apply regardless of which one of them is the hot and which one the cold fluid. Since the flow direction is known, internal fluid states in each segment were assumed to equate the upstream values at the segment boundaries, using an upwind scheme. A 2nd-order, centred finite difference scheme was used to discretise space derivatives in Equation (3). Furthermore, fluid properties in the above equations vary as a function of the thermodynamic state, as described by equations of state implemented in CoolProp and accessed through the ExternalMedia library [
37].
A fixed refrigerant pressure loss over each segment was considered for each segment, which yielded an overall pressure drop
across the component:
Local convective heat transfer coefficients,
values, were estimated for each fluid stream based on the Prandtl number and a mean Reynolds number computed over a channel cross-section of hydraulic diameter
:
Appropriate convective heat transfer correlations were computed for each segment. Gnielinski’s correlation was used for fully developed, turbulent, internal single-phase flow [
38]. As both fluids can experience phase change, two correlations proposed by Shah for flow boiling through a pipe [
39] and internal condensation [
40] were used for heat transfer coefficient estimations in the case of, respectively, local evaporation and condensation in each condenser segment.
The model was solved by imposing mass flow rates and suitable temperature and pressure boundary conditions at fluid inlets, alongside fixed initial temperature conditions. It is worth noting that the presented modelling approach is also suitable to capture the operation of a counterflow evaporator.
2.2. Dynamic Modelling of the Steam Accumulator
The modelling of the SA follows the approach presented by Desideri et al. [
41]. Under the common assumption of thermodynamic equilibrium between the liquid and vapour phase, the dynamic mass and energy conservation equations for the component read as follows:
The liquid level in vessel
was introduced, which allows for characterising the properties within the SA as a linear combination of those for saturated liquid and vapour conditions, both depending on SA internal pressure:
Equations (8) and (9) were then substituted into Equations (6) and (7) and suitably manipulated. This allowed for expressing dynamic mass and energy balances as a function of tank pressure and liquid level as the two independent variables:
Derivatives of fluid thermodynamic properties in Equations (10) and (11) were returned by the ExternalMedia library [
37].
Outlet conditions from the SA depend on the liquid level inside the accumulator. For an outlet flange located at a level
,
The model was complemented by assuming an adiabatic vessel () and solved by specifying boundary conditions on the inlet and outlet pressures, which drive the respective mass flow rates, and the initial pressure and liquid level inside the SA.
2.3. Model Validation
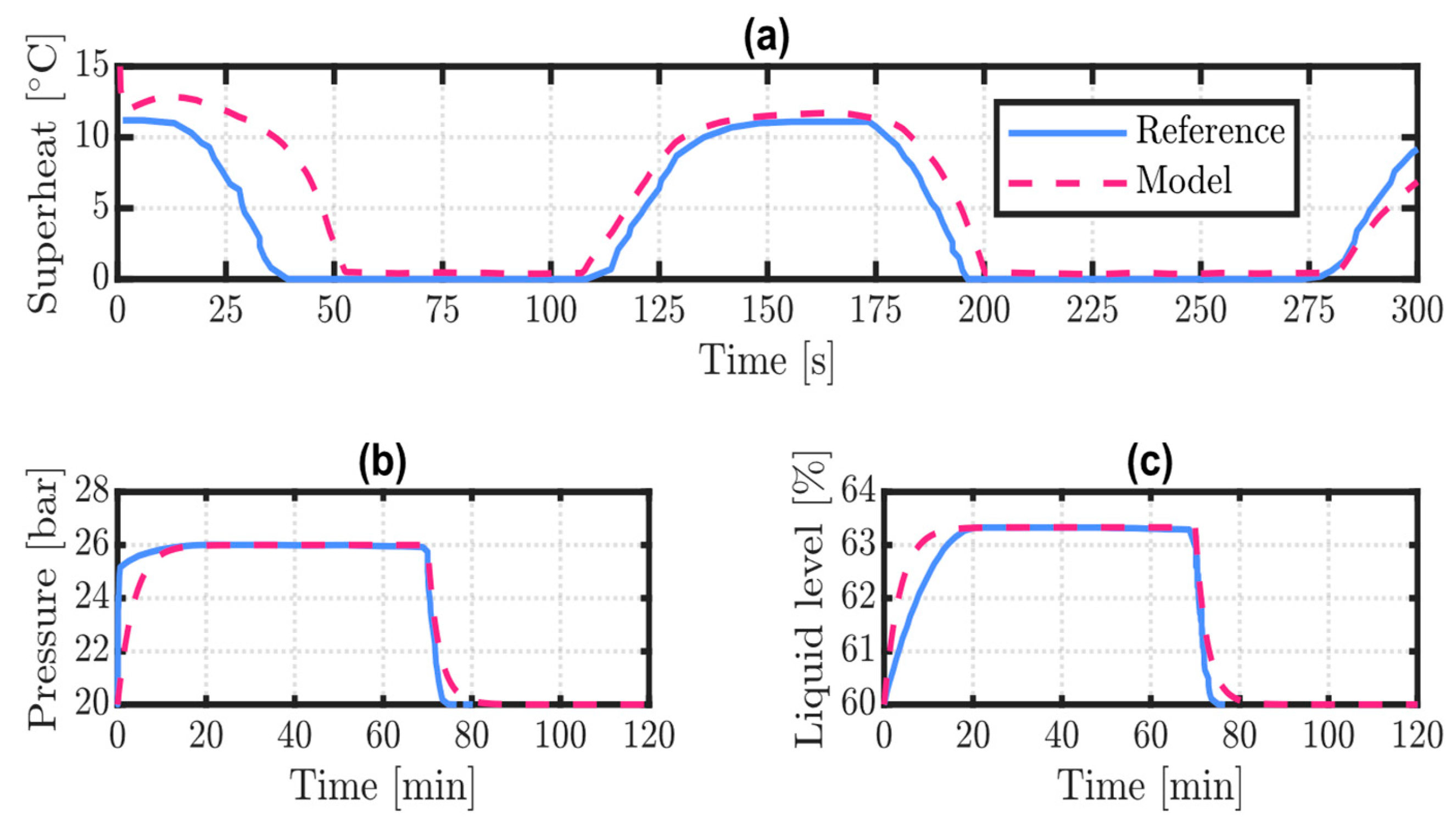
This section describes the validation of the two dynamic models presented against data from the literature. Given the lack of condenser-specific references reporting both component features and test conditions, dynamic simulation results for an evaporator using R-404A refrigerant were selected to validate the model from
Section 2.1 [
42]. As mentioned, the proposed modelling is indeed broadly applicable to counterflow heat exchangers. For constant mass flow rates and inlet temperatures of both fluids,
Figure 2a illustrates the degree of superheating at the refrigerant outlet, which follows changes to the inlet pressure of the secondary fluid. Twelve segments were used to discretise the component as a result of prior grid independence tests performed.
For the validation of the SA model, pressure and liquid level evolution inside a 26 m
3 vessel were compared against the results by Niknam and Sciacovelli [
30], using their profile of inlet and outlet mass flow rates over a 120 min charge/discharge cycle. The results are presented in
Figure 2b,c. Both the heat exchanger and the SA models exhibit a very close match with the reference in steady-state conditions and overall satisfactory behaviour during transients.
2.4. Flexible HTHP Operation
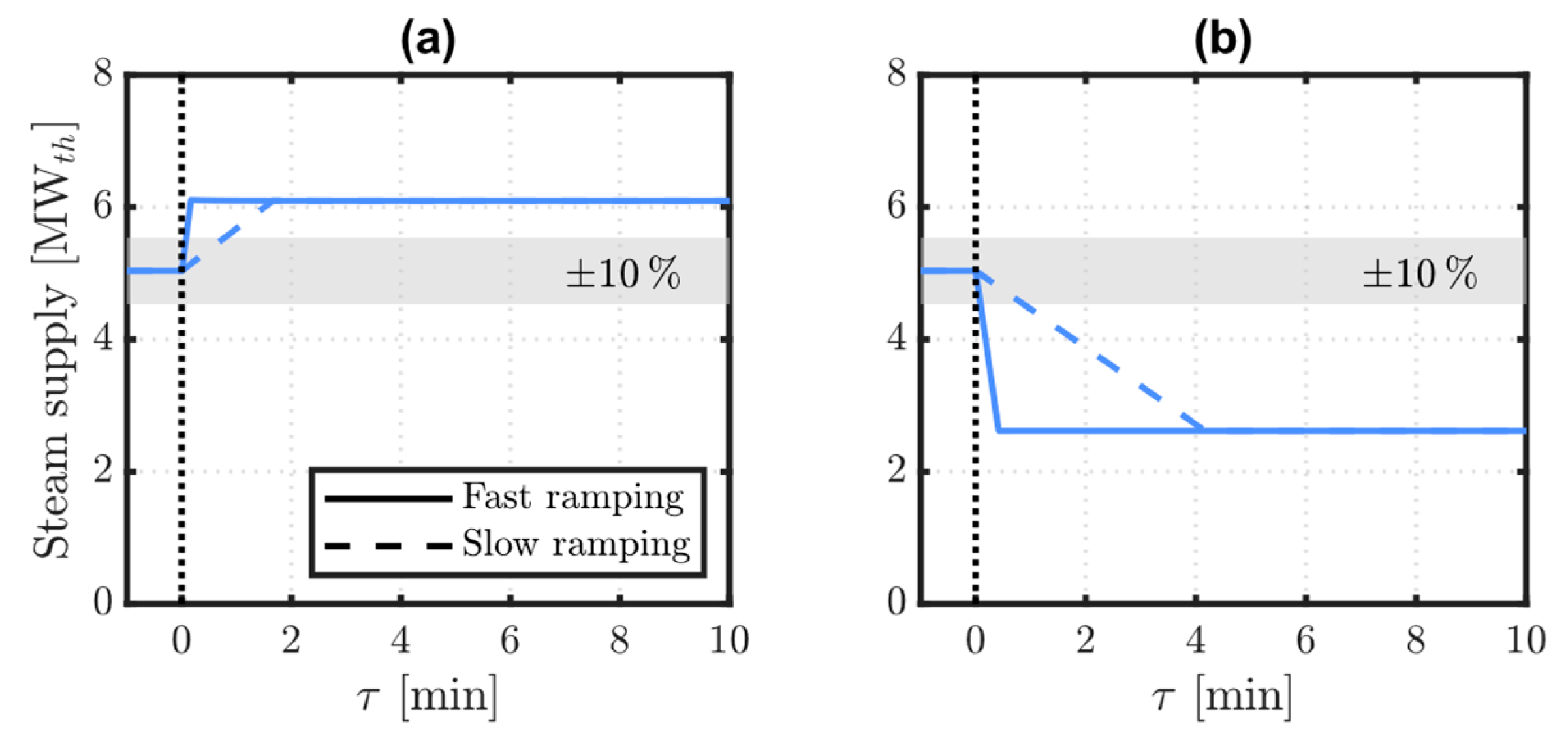
Flexible HTHP operation in this work involves the adjustment of HTHP power input at values other than the rated setpoints to suit some external signal. Three operating conditions were tested:
Rated: HTHP power input in rated conditions;
Turn-up: HTHP power input increased to 120% of the rated setpoint for 1 h;
Turn-down: HTHP power input decreased to 50% of the rated setpoint for 1 h.
Although this modelling could equally simulate more specific demand-side response signals in both HTHP power input and duration, the operating conditions tested aim to uncover the underlying phenomena that broadly apply to flexible HTHP operation. Power turn-up mimic periods of high renewable generation and/or low energy demand present, for instance, in the middle of the day (see [
43]). Power turn-down could be used to enable partial load shedding at peak demand times or when renewable generation is lacking (see [
44]). Rated conditions, on the other hand, serve mainly as a baseline.
Deviations in the HTHP power input require control of the HTHP cycle to maintain thermodynamic states within feasibility. Drawing from relevant work on heat pump control [
10,
23,
45], the following strategies were assumed:
A pressure vessel maintains a constant pressure in the low-pressure segment of the system;
Adjustment of secondary-side flow in the evaporator maintains a fixed inlet temperature under compressor suction and avoids wet conditions;
Adjustment of the secondary-side flow in the condenser is proportional to the refrigerant mass flow.
A variable frequency drive was considered to achieve HTHP power input variations. Two verified ramp rates from HTHP control studies in the literature were used to study dynamic responses under fast and slow ramping, as per
Table 2. These indirectly account for response delays due to rotational and other inertial terms in the compressor and throughout the HTHP cycle. They also represent two limiting cases for HTHP regulation speed and, since other dynamic studies report ramp rates within these limits, are deemed to provide a reasonable estimate of the system response range over time. The refrigerant conditions at the compressor outlet under a fixed inlet pressure and temperature were then determined from the
instantaneous value of compressor isentropic efficiency,
, and compression ratio,
.
Instantaneous values of isentropic efficiency and compression ratio were expressed as a function of the corrected rotational speed,
, and mass flow rate,
, via off-design performance maps [
46]:
Table 2.
Feasible ramp rates verified by HTHP control studies and adopted in this work.
Table 2.
Feasible ramp rates verified by HTHP control studies and adopted in this work.
| Ramping | Ramp Rate [%/s] | Ref. | Note |
|---|
| Fast | 2 | [19] | 0.2–0.6%/s verified for large-scale ammonia heat pumps [23] |
| Slow | 0.2 | [24] |
2.4.1. Model Runs Performed
Table 3 summarises the model run performed, whose results are presented later on.
2.4.2. Performance Assessment
A primary performance indicator is the HTHP coefficient of performance,
, which expresses the ratio between the heat delivered at the condenser and the power input to the compressor:
For each run, the thermal power supplied to the downstream processes by the steam header was also computed, considering a return liquid stream in saturated liquid conditions, with specific enthalpy
. Steam supply conditions (
) were evaluated at point 10 (
Figure 1):
Both
and
assess an instantaneous performance and therefore vary as a function of time. Conversely, the unserved steam demand,
, was evaluated by integrating the thermal power supplied over the full duration of flexible HTHP operation and normalising by the value in rated conditions:
4. Discussion
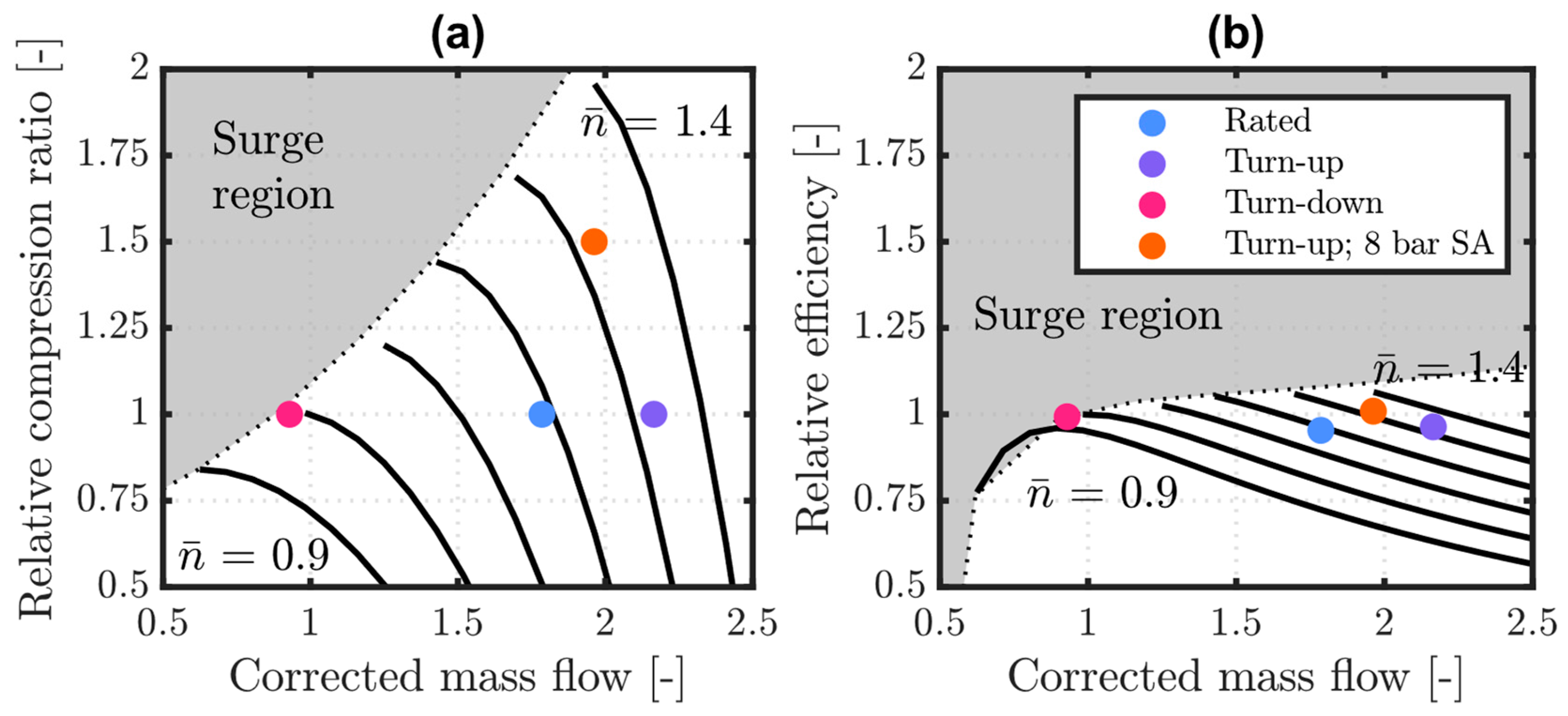
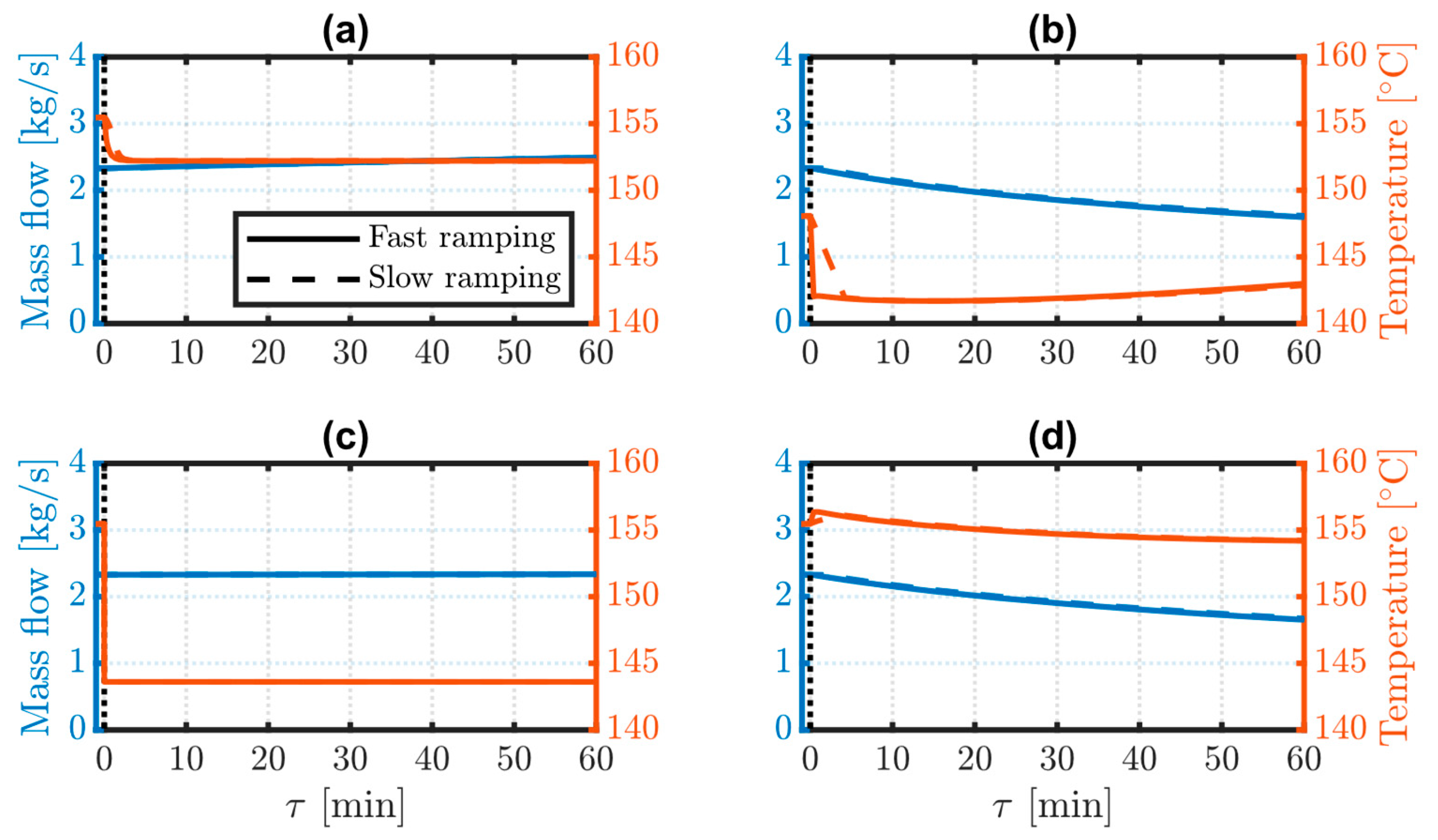
The results so far demonstrate the importance of compressor characteristics and selection in enabling flexible HTHP operation. Power input flexibility comes at the expense of HTHP performance at rated conditions. Indeed, a slightly higher was found for both the turn-down and the turn-up cases compared to rated conditions, which results from the discussed need to select a nominal compressor operating point that allows a wide enough power adjustment.
Once the nominal operating point is selected, off-design compressor characteristics determine the refrigerant mass flow rate and outlet temperature from the compressor. These drive dynamic changes in system and steam supply performance, which depend largely on fluid-dynamic transients and the compressor ramp-up/down capability, and with minimal contribution of thermal dynamics in the condenser.
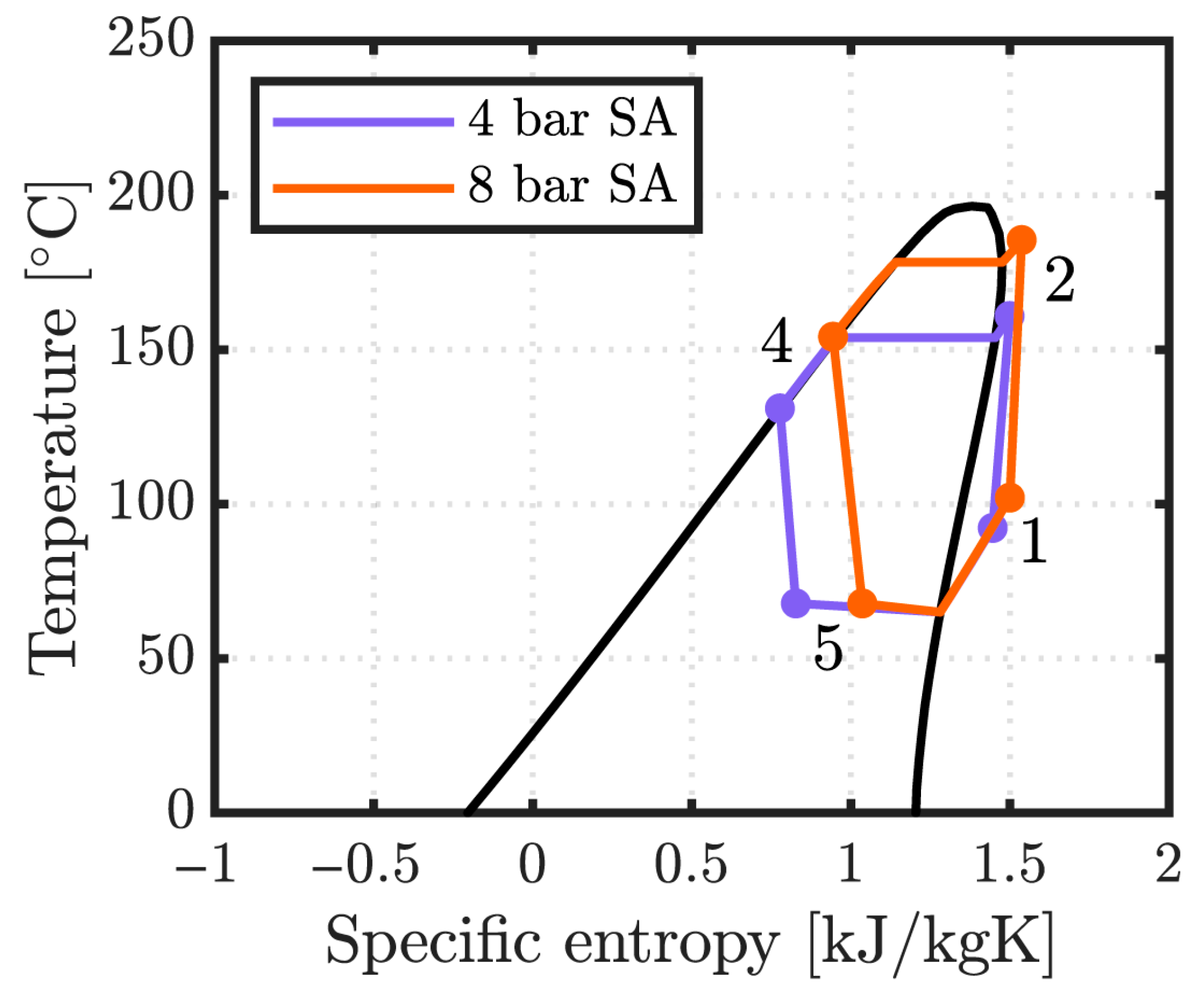
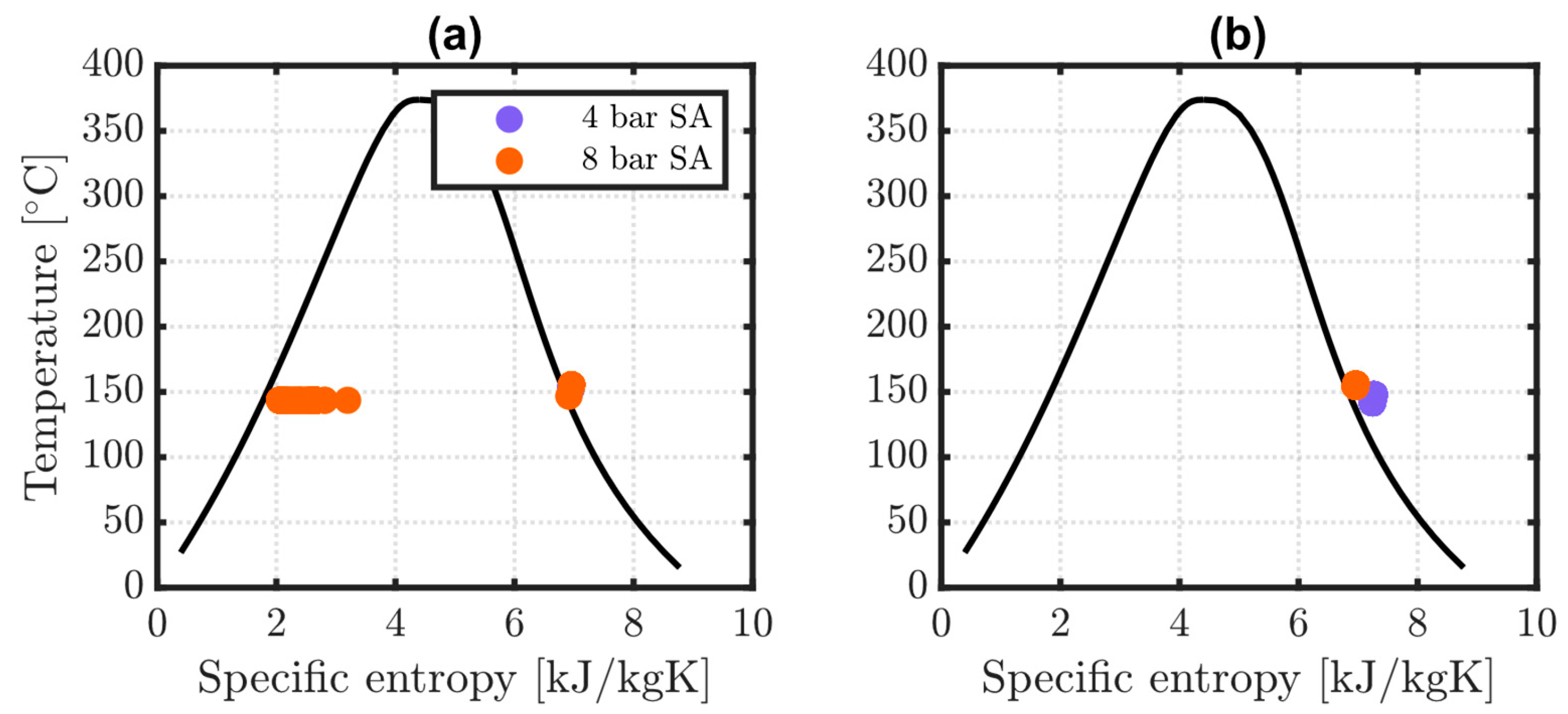
By smoothing steam supply variations, and subject to temperature and thermal power deviations’ acceptability in the downstream processes, SA may ensure their continuous operation along with flexible adjustment of HTHP power. However, SA integration also requires either increasing the pressure level of the water feed or decreasing that of the steam header. These findings suggest that the former should be avoided as it significantly impacts HTHPs capacity to supply the downstream processes. The latter leads to much smaller variations in HTHP and steam delivery performance, and only during power turn-down, with the extent to which the steam header pressure can be decreased to be assessed case by case.
Therefore, the following section concludes by focusing on steam delivery during HTHP power turn-down operation and with a 4-bar downstream SA. Accounting for the dynamic phenomena discussed, guidelines are derived for SA sizing at different levels of HTHP turn-down setpoints and duration. These allow us to contain the unserved steam demand within acceptability and should guide the assessment of this technical solution in various cases.
4.1. SA Sizing Guidelines for a Reliable Steam Supply
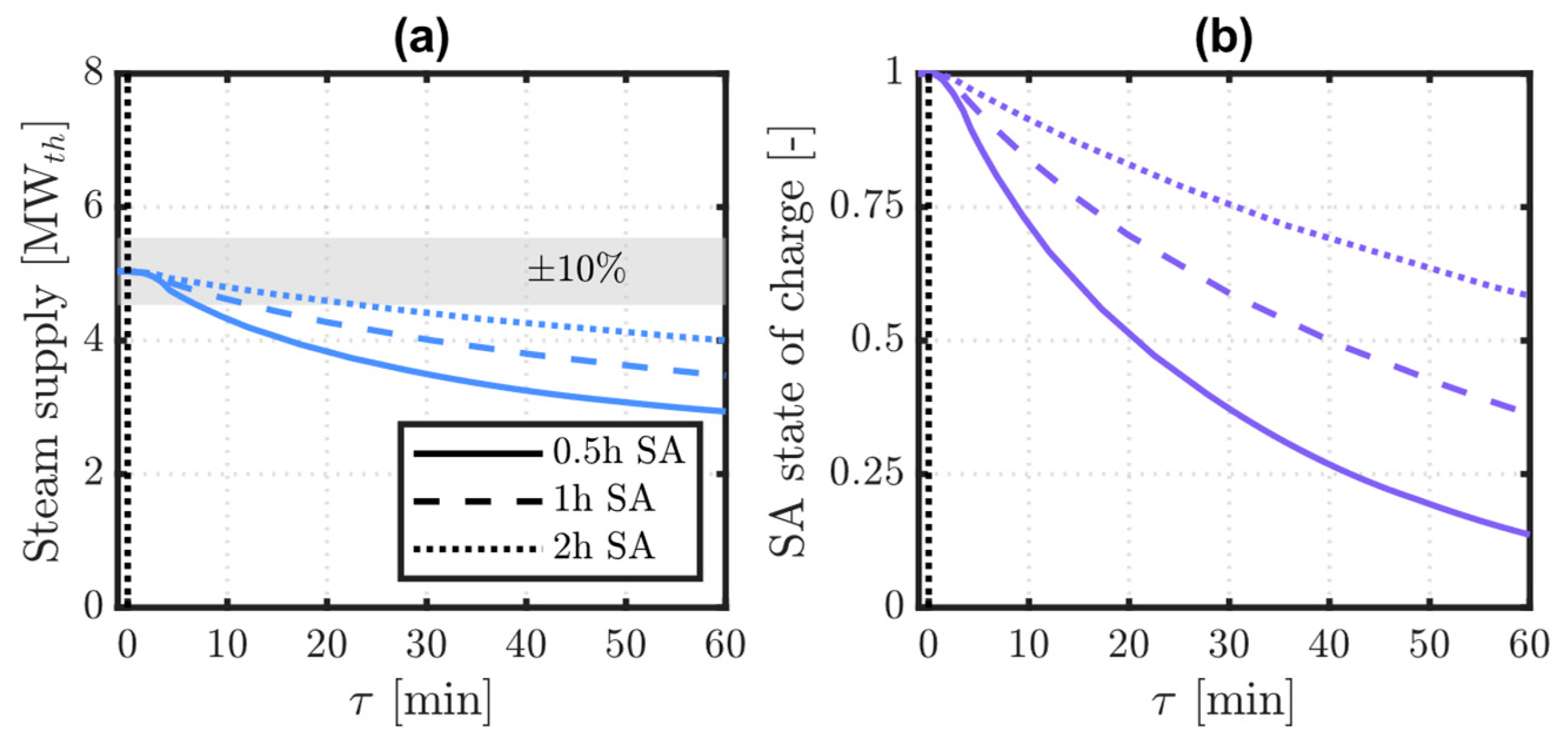
Figure 10 shows the thermal power of steam supplied with three SAs of different design capacities and the evolution in SA state of charge. Departure from the rated thermal power of steam supplied is mitigated by a downstream SA, to an extent that depends on SA capacity. The computed values of unserved steam demand to the industrial processes,
, are 27%, 18%, and 11%, respectively, for a 0.5, 1, or 2 h tank capacity. As bigger SAs are shown to reduce
, as well as the steam supply departure from rated thermal power values, it must be possible to size SA so that the steam supply is kept within the acceptability range. Depending on the specific application, the unserved steam demand to the industrial processes or the instantaneous thermal power could be chosen as the most suitable indicator to quantify this acceptability range. Choosing the former entails setting a lower bound for the thermal energy delivered over a certain period and therefore seems more significant, for instance, when other backup steam generation technologies are available on-site. Choosing the thermal power delivered, on the contrary, involves limiting the departure from rated values at each timepoint throughout a certain period, which is generally a stricter requirement. Hence, it seems more relevant to a standalone application.
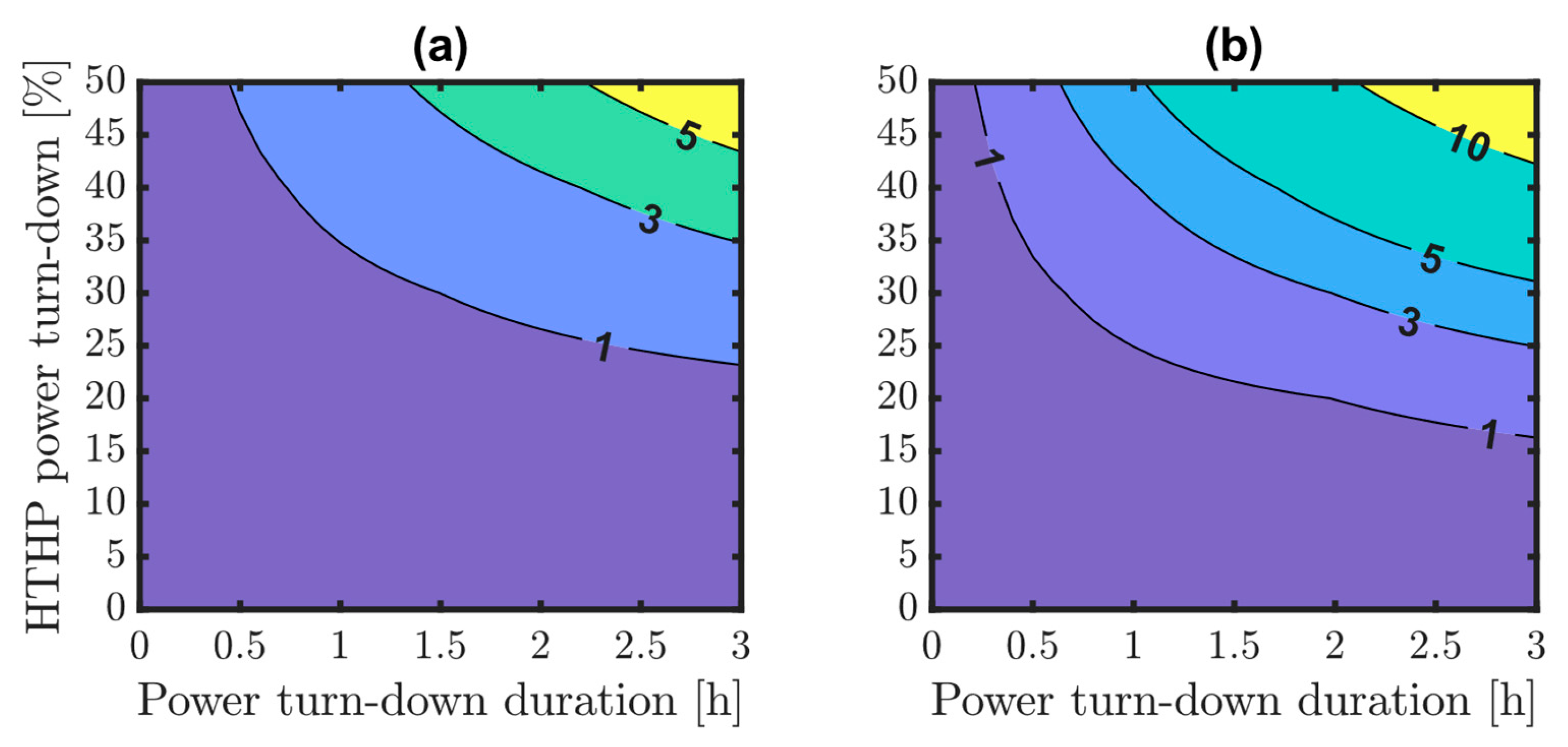
Figure 11 presents the actual SA supply time to be used for SA sizing in the integrated HTHP + SA systems; panel (a) assumes a maximum 10% drop in
to be acceptable and panel (b) a maximum 10% drop in the thermal power supplied. Both figures show that SA sizing depends on the desired level of power reduction during HTHP turn-down operation (y-axis), as well as its duration (x-axis). At up to 20% power turn-down, HTHP and steam departure from rated conditions is small, and SAs of up to 1 h are found sufficient for a reliable operation of the downstream industrial processes. However, a wider HTHP flexibility necessitates larger SA capacities; the desired level of power reduction during HTHP turn-down affects SA sizing much more than the expected turn-down duration. Comparing the actual SA supply time values from panels (a) and (b) in
Figure 11 also demonstrates how limiting the drop in thermal power supplied as opposed to the unserved steam demand is a stricter acceptability requirement and necessitates larger SA capacities.
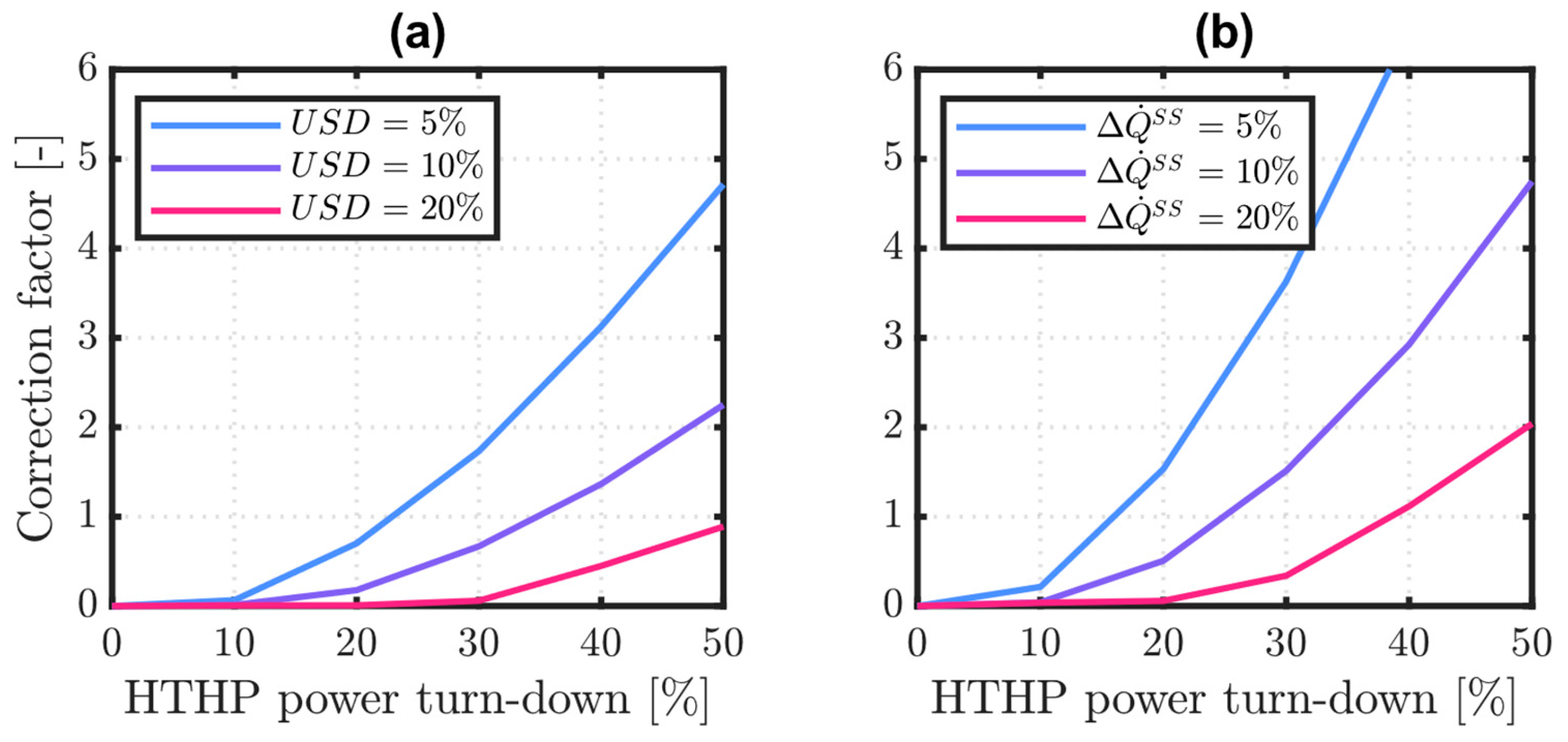
Finally, design correction factors for variable levels of the relevant acceptability threshold are presented in
Figure 12. These are multiplication factors on the SA tank capacity that will be needed to match a certain duration of HTHP turn-down operation. Again, in
Figure 12a, the threshold is applied to the drop in
and in
Figure 12b, to the drop in the thermal power supplied. Particularly at high levels of HTHP power turn-down, correction factors are above unit values. This indicates that a steady-state SA design not accounting for the integrated HTHP and SA dynamics can result in significantly undersized SAs. On the other hand, for minor reductions in HTHP power, correction factors are below the unit value. In these cases, a smaller SA may be needed compared to what traditional steady-state design would suggest. These sizing corrections could be considered, together with the revenues resulting from different schemes of demand–response and balancing services provided to the grid, to assess the economic viability of flexible HTHP operation and SA investments, case by case. Economic considerations are beyond the scope of this work, but a suggested area for follow-up work is to quantify the viability of this integrated solution for flexible HTHP operation in specific industrial applications.
4.2. Limitations of This Study
This work aims to position itself between technology- and system-level assessment. Thus, without developing a fully dynamic HTHP model, as carried out in existing studies on heat pump control [
10,
23,
45], it instead aims to capture, both
directly and
indirectly, and discuss only those dynamics that are relevant for system-level technology integration. Accordingly, a relatively simple system configuration was considered to better characterise steam supply dynamics associated with flexible HTHP operation and their mitigation via a downstream SA.
Of course, alternative configurations of the steam supply networks will react to and tolerate deviations in steam supply differently. On-site availability of other backup technologies will also help to counteract variations. Moreover, it is possible that the many HTHP system layouts proposed [
33] will be more or less sensitive to power turn-up/down. Nonetheless, acknowledging their extent will ultimately be case-dependent. This work uncovers dynamic effects and technical considerations that will be encountered when providing steam with flexible HTHP operation and downstream storage in an SA.
5. Conclusions
This study examined steam supply using both HTHP alone and in combination with a downstream SA, testing two alternative pressure intervals for the SA. It revealed both steady-state and dynamic effects that should be considered for suitable design and reliable system operation.
Even in a steady state, enabling demand-side flexibility from HTHP operation impacts the coefficient of performance achievable in rated conditions, to an extent that mainly depends on the technical features of the compressor. Furthermore, operating HTHPs flexibly was proven to result in changes to both the temperature and mass flow rate of the steam supplied to downstream processes. For a 20% increase in power consumption, a 21% higher thermal power could be delivered, while for a 50% reduction, the steam power supplied dropped to 48%. Alternative HTHP cycle layouts may present a technically feasible operation for different power turn-up and turn-down regions and therefore vary in suitability for flexible HTHP use. Yet, changes to the downstream steam supply are still to be expected.
A downstream SA between the HTHP and the processes supplied was proven effective in smoothing these fluctuations in the thermal power of steam delivered. Provided that the associated steam temperature variations are acceptable, the results demonstrated that the combined HTHP and SA system ensures a continuous steam supply to the downstream processes within acceptability, and it can be considered to enact a demand-side response. However, while the HTHP dynamic response to ramps in power input is resolved in a few minutes, longer-term dynamics in the order of hours are introduced by the SA. These are intrinsic to the sliding-pressure operation of SAs. Considering these dynamics for the appropriate design of the SA is shown to be paramount for a reliable steam supply.