Abstract
The permanent magnet integrated motor (PMIM) for ball mills has the problems of difficult assembly and poor air gap uniformity adjustment due to the magnetic pull force in the conventional magnetic assembly. In this study, a non-magnetic assembly technology based on the installation of a permanent magnet after assembly was first proposed, and the analytical models of conventional magnetic assembly and non-magnetic assembly were established. On this basis, combined with the finite element method, the mechanical performance difference between the two assembly methods in the assembly, lifting, and centering stages were compared and analyzed. In addition, a device for adjusting the air gap was designed for the non-magnetic assembly technology, and the stress and deformation of the structure of this device were analyzed. The results showed that the total assembly load by using the non-magnetic assembly technique was significantly reduced by 71.8%, the maximum stress in the assembly process was reduced by 66.3%, and the maximum deformation was reduced by 66.7%, which significantly reduced the difficulty of assembly. Finally, a 210 W permanent magnet integrated motor for ball mills was designed and successfully assembled, which proves the effectiveness of the assembly technology.
1. Introduction
The PMIM for ball mills improves the transmission efficiency of a system by using an integrated drive, but it also increases the difficulty of motor production, and the structure of the PMIM for ball mills is shown in Figure 1.
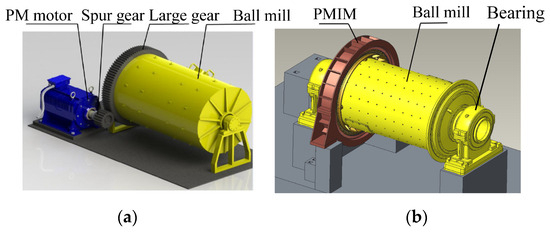
Figure 1.
Ball mill drive system. (a) Traditional drive mode. (b) PMIM direct drive.
Currently, the research on the PMIM for ball mills primarily concentrates on electromagnetic design and enhancing heat dissipation. In [1,2], a modular combination stator structure based on coil removal for the PMIM for ball mills was proposed. This design meets the installation requirements for this type of motor, allowing each stator module to operate independently while exhibiting excellent fault tolerance. In [3], a temperature cycle method based on a three-dimensional equivalent thermal network was proposed to address the uneven distribution of the overall water circuit and the challenges associated with calculating the temperature rise in the PMIM for ball mills. This method simplifies the temperature rise calculation for the motor. In [4], a torque distribution method for efficiency optimization was proposed to address the issue of significant power redundancy in the PMIM for ball mills. This method enhances both system efficiency and reliability. The assembly problem has consistently posed significant challenges that hinder the widespread adoption of this type of motor, and it remains unresolved to date.
The PMIM for ball mills is assembled on-site, and there is no end cover constraint between the stator and the rotor, making it susceptible to the influence of the permanent magnet’s magnetic field [5]. Currently, the PMIM for ball mills utilize conventional low-speed permanent magnet motor assembly technology, which suffers from magnetic attraction during assembly, severely affecting assembly accuracy [6]. To address this issue, a method utilizing high-precision guide rods was introduced [7]. This method controls the coaxiality between the stator and rotor via the guide rods, effectively suppressing magnetic attraction during the assembly process of permanent magnet motors. However, the guide rods must support the entire weight of the motor rotor, imposing high stiffness requirements. In [8], a vertical pressing rotor assembly technology was employed, wherein the stator is fixed and the rotor is moved. This design ensures uniformity of the air gap between the stator and rotor through the guide rods, which do not bear the rotor’s weight. Furthermore, in [9], a vertical pressing stator assembly technology was proposed that utilizes the stator’s own weight to counteract magnetic attraction.
The above assembly is a magnetic assembly, where magnetic attraction plays a crucial role in the process of assembling the stator and rotor. Consequently, researchers have proposed a general assembly approach that involves first assembling the permanent magnet, followed by the magnetization process. In [10,11,12], a stator-assisted magnetization technique was proposed, which involves pre-assembly followed by the overall magnetization of small-power permanent magnet motors. In [13], the relationship between motor dimensions and the process requirements for assembly was first derived and then overall magnetization was derived, and the experimental verification was conducted with a 400 W prototype machine. In [14], it was pointed out that the distributed winding is more suitable for application in integral magnetization than the concentrated winding, through the magnetization results of the simulations and experiments of two 20 kW permanent magnet motors with different winding forms. In [15,16], a post-magnetization assembly process system was proposed and applied to a 10 kW permanent magnet motor. In [17,18], a coupled field-circuit numerical model for the assembly of the permanent magnet followed by magnetization was established. This model systematically completed the mechanical characteristics analysis during the assembly process. The interior rotor structure significantly influences the magnetic field permeability in the technology of initial assembly followed by integral magnetization, rendering it unsuitable for high-power permanent motors [15]. In [19,20,21,22], the permeability of the external magnetic field was enhanced by developing a stator auxiliary magnetization device, which involved first assembling the built-in components and then applying the overall magnetization technology to the 160 kW motor application scenarios. It can be seen that the technology of assembling the permanent magnet first and then magnetizing is only applicable to small-power motors at present, and there are significant technical implementation barriers to the existing assembly scheme for special application scenarios such as ball mill permanent magnets, which have large power and must be assembled on-site.
In this study, a non-magnetic assembly technology with an inserting permanent magnet after the installation of the PMIM for ball mills was developed. Mathematical analysis models were established for both the conventional magnetic assembly and the proposed non-magnetic assembly methods. On this basis, the advantages of non-magnetic assembly technology in terms of mechanical properties are compared and analyzed in detail from multiple perspectives. Finally, a 210 kW PMIM for ball mills was designed and assembled to verify the correctness of this assembly technology.
2. Structure and Non-Magnetic Assembly Technology of PMIM for Ball Mills
The 3D structural diagram of the PMIM for ball mills is shown in Figure 2.
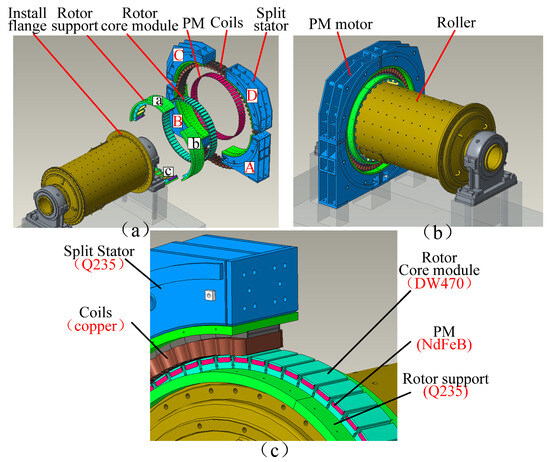
Figure 2.
The 3D structural diagram of the PMIM for ball mills. (a) Explosion diagram. (b) Overall diagram. (c) Local enlargement diagram.
Due to the pre-arrangement of the roller on-site, all components of the motor are installed around the roller, leading to the modular design of the PMIM for ball mills. As shown in Figure 1, the rotor support is mounted on the flange in a split configuration (with the rotor support divided into parts a, b, and c). The rotor core is affixed to the outer circumference of the rotor support, while the permanent magnet (PM) is inserted into the rotor iron core. The stator is also installed on the foundation in a split form, as depicted in the illustration, which shows the stator divided into parts A, B, C, and D.
The non-magnetic assembly process of the PMIM for ball mills is shown in Figure 3, and the three-dimensional structural diagram of the non-magnetic assembly process is shown in Figure 4.
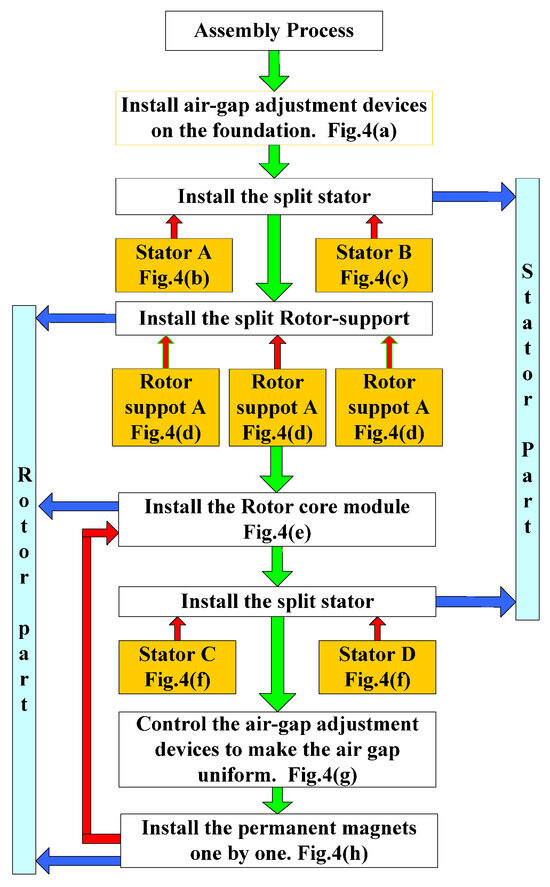
Figure 3.
Non-magnetic assembly process flow.
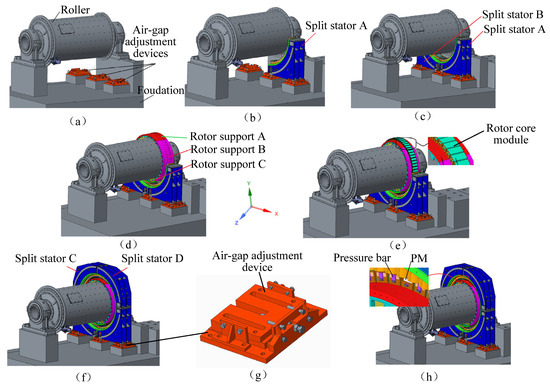
Figure 4.
Schematic diagram of 3D structure of non-magnetic assembly. (a) Install air-gap adjustment devices (b) Install split stator A (c) Install split stator B (d) Install rotor support (e) Install rotor core (f) Install split stator C and D (g) The structural of air-gap adjustment devices (h) Install PM.
The complete process flow of the non-magnetic assembly technology is described as follows:
- (1)
- Install air gap adjustment device
First, the air gap adjustment device is installed on the base of the platform, as shown in Figure 4a, and the air gap adjustment device is used to adjust the spatial position of the stator.
- (2)
- Assembly of split stators A and B
Assemble the split stators A and B on the air gap adjustment device, as shown in Figure 4b,c.
- (3)
- Assembly of rotor support and rotor core
Assemble the rotor support A, B, and C on the roller flange to form the overall rotor support, as shown in Figure 4d, and install the rotor core modular on the rotor support, as shown in Figure 4e.
- (4)
- Complete stator and air gap adjustment
Assemble the split stators C and D with the split stators A and B into a complete stator as shown in Figure 4f. At this time, the air gap between the stators and rotors is in a non-uniform state. By controlling the air gap adjustment device, the spatial position of the stator is adjusted to make the air gap uniform, as shown Figure 4g.
- (5)
- Assembly of PM
Finally, install the PM and the PM pressing bar one by one to complete the motor assembly.
3. Analytical Modeling of Magnetic and Non-Magnetic Assembled Stator Loads
The assembly models of the PMIM for ball mills include both magnetic and non-magnetic assemblies, as illustrated in Figure 5. The magnetic assembly model comprises four main components: the guide bar, stator segments, rotor with permanent magnets (PMs), and an installation platform. In contrast, the non-magnetic assembly model substitutes the rotor with one that lacks permanent magnets. In the magnetic assembly configuration, the guide bar serves not only as a guide but also provides support to the stator segments to counteract the electromagnetic attraction between the stator and rotor. Conversely, in the non-magnetic assembly, the guide bar functions solely as an alignment guide. It is noteworthy that, during magnetic assembly, the electromagnetic attraction force (F) between the upper stator segment and the rotor with PM gradually increases as the stator approaches the rotor, necessitating the guide bar to bear the resultant indirect load. In the non-magnetic assembly state, the upper stator segment is solely subjected to its own gravitational force (GS), allowing it to descend smoothly along the guide bar and complete the closure.
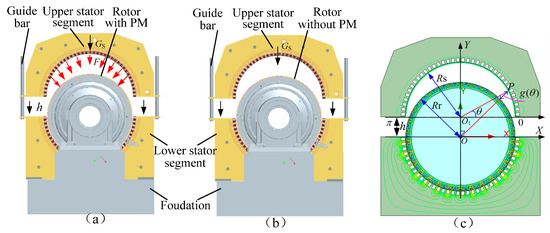
Figure 5.
The model of assembly. (a) Magnetic assembly. (b) Non-magnetic assembly. (c) Geometric model.
The magnetic assembly process can be effectively modeled as the transition of the upper stator of the motor from an eccentric position to a uniform air gap configuration. Initially, the lower stator is assembled first, ensuring a uniform air gap (g = g0) with the rotor. During the assembly process, the upper stator gradually approaches the lower stator, resulting in a progressive decrease in the assembly distance h (when h = 0, the air gap returns to g = g0). For any point P on the inner surface of the upper stator, its coordinates relative to the center O can be expressed as follows:
where RS is the stator inner radius, θ is the angle between point P and X-axis, and h is stator mating interface gap.
The air gap value at any arbitrary point on the upper stator can be expressed as follows:
The air gap magnetic flux density at any arbitrary point on the upper stator can be expressed as follows:
where Rr is the rotor outer radius, B0 is the air gap magnetic flux density when the air gap is uniform, and g0 is the uniform air gap.
According to Maxwell’s stress tensor method, the magnetic pull force at point P can be calculated as follows:
The component of magnetic pull force along the Y-axis can be expressed as follows:
The total magnetic pull force along the Y-axis can be expressed as follows:
The total stator load during magnetic assembly and non-magnetic assembly can be calculated, respectively, as follows:
where GS is the gravity of upper stator.
A comparison between analytical and finite element analysis results of the total magnetic pull force F during magnetic assembly at different assembly distances h is shown in Figure 6. The total magnetic pull force of the stator, as calculated by the analytical solution, aligns closely with the results obtained from the finite element method. The magnetic pull force acting on the stator increases as the distance h decreases and reaching its maximum when assembly is completed. When h/g > 25, the magnetic pull force on the upper stator approaches zero; when h/g < 25, the magnetic pull force on the upper stator begins to increase rapidly and the influence of magnetic forces must be considered in design and assembly.
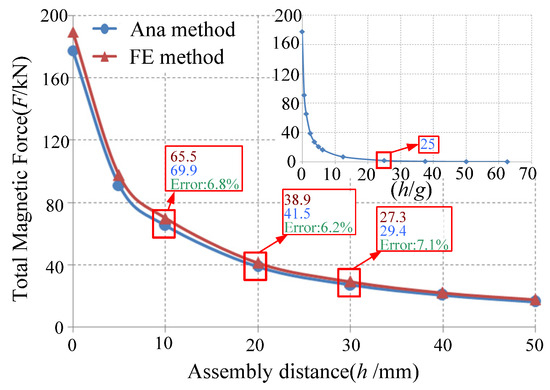
Figure 6.
Total magnetic pull distribution at different assembly distances.
Figure 7 illustrates the distribution of magnetic pull forces at any point on the inner surface of the upper stator. It is observed that the load on the inner surface of the upper stator initially decreases and then increases within the range of 0 to π when h ≠ 0, exhibiting symmetry on both sides. Conversely, when h = 0, the load on the inner surface of the upper stator remains constant across the range of 0 to π.
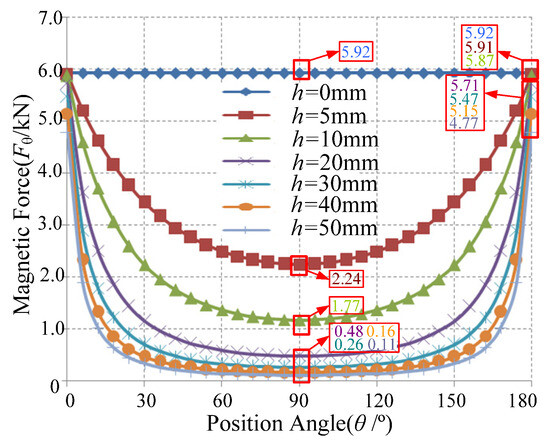
Figure 7.
Magnetic pull distribution at different position angles.
4. Mechanical Performance Analysis of Magnetic and Non-Magnetic Assembly
4.1. Mechanical Analysis of Stator During Assembly
The distribution of the total load on the upper stator at varying assembly distances (h) under both magnetic and non-magnetic assembly conditions is illustrated in Figure 8. It is evident that, under magnetic assembly conditions, a decrease in the assembly distance (h) leads to a significant increase in the total load on the stator. In contrast, under non-magnetic assembly conditions, the total load remains stable. Specifically, as the assembly distance is reduced from 50 mm to 0 mm, the load for non-magnetic assembly remains constant at 70 kN, while the total load for magnetic assembly fluctuates between 86 kN and 24 kN. Comparative analysis reveals that non-magnetic assembly can reduce the total load by 18.6% to 71.8% relative to magnetic assembly.
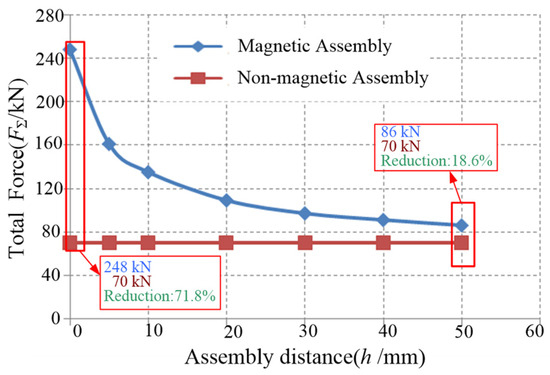
Figure 8.
Total force comparison at different assembly distances.
The distribution curves of stress and deformation at various hoisting distances (h) are illustrated in Figure 9 and Figure 10. It is evident that the distribution trends of both stress and deformation align with the overall load variation. When the hoisting distance is decreased from 50 mm to 0 mm, the maximum stress of the non-magnetic assembled stator decreases by 15.5% to 66.3% compared to that of the magnetic assembled stator, while the deformation accounts for only 9.0% to 66.7% of that of the magnetic assembled stator.
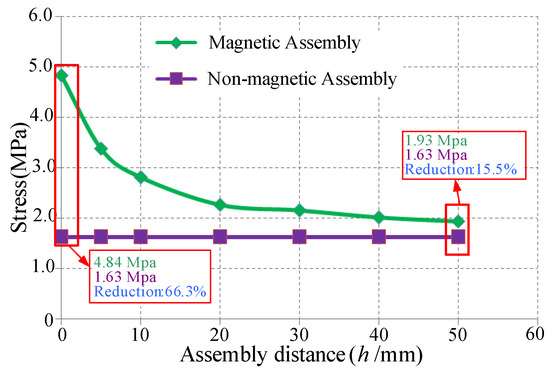
Figure 9.
Stress comparison at different assembly distances h.
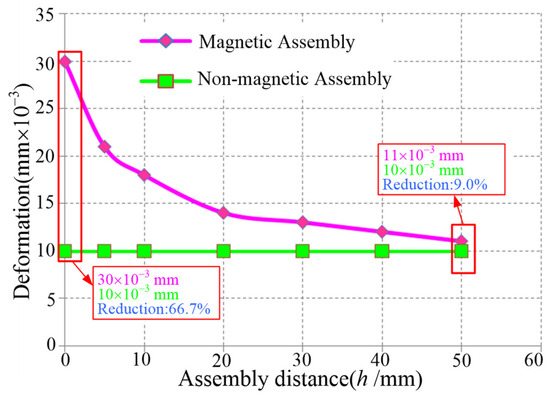
Figure 10.
Deformation comparison at different assembly distances h.
The stress and deformation finite element distribution cloud map of magnetic assembly and non-magnetic assembly are shown in Figure 11.
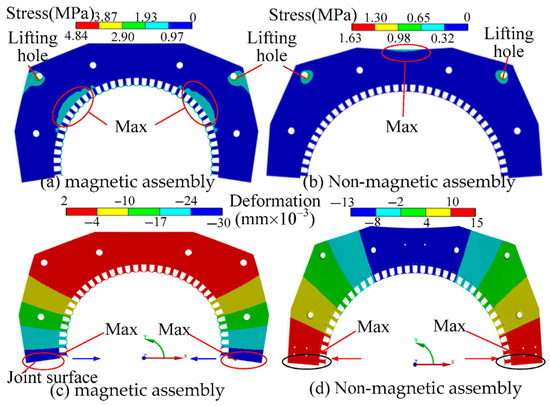
Figure 11.
The stress and deformation distribution cloud map (h = 0 mm).
In the case of the magnetic assembly, magnetic drag serves as the primary load, with the maximum stress concentrated around the stator tooth corresponding to the lifting hole, as illustrated in Figure 11a. The maximum deformation occurs at the joint surface, with the deformation direction pointing toward the center of the circle, consistent with the magnetic drag, as shown in Figure 11c. Conversely, for the non-magnetic assembly, it is solely subjected to gravitational load, resulting in the maximum stress distributed at the upper part of the stator, as depicted in Figure 11b. The maximum deformation is also located at the joint surface; however, the direction of deformation radiates outward. This phenomenon can be attributed to the arch structural characteristics of the stator: under the influence of self-weight, the load is transmitted through the arch path, producing an outward load component at the joint surface and causing outward deformation, as shown in Figure 11d.
4.2. Stator Deformation Analysis at Different Lifting Positions
The finite element analysis results of magnetic and non-magnetic assemblies at different lifting positions A, B, and C are presented in Figure 12. It is evident that the displacement of the non-magnetic assembly is consistently less than that of the magnetic assembly across all lifting positions. Specifically, the non-magnetic assembly technology reduces the deformation of the stator assembly by 48% to 85%. As the lifting point descends, the deformation of the upper stator exhibits a significant decreasing trend. By optimizing the position of the lifting point, the adverse deformation of the stator generated during the motor assembly process can be effectively mitigated, thereby enhancing the accuracy and quality of the assembly.
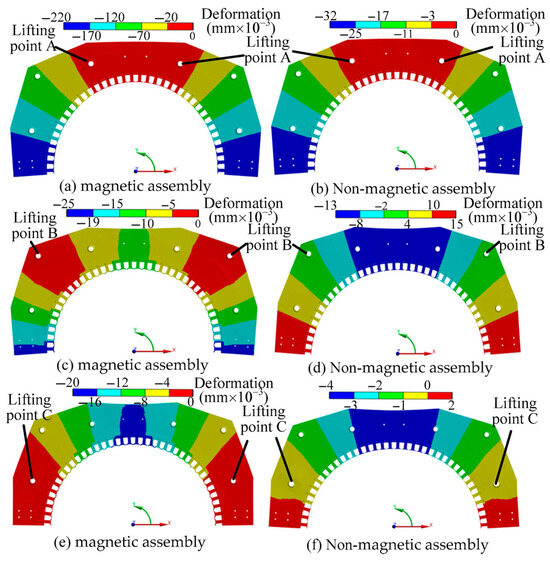
Figure 12.
The deformation contour cloud in different lifting positions.
4.3. Mechanical Analysis of the Stator During Centering
When the stator is assembled, there is still a certain degree of eccentricity between the stator and the rotor. At this time, the eccentricity of the assembled stator needs to be adjusted by using the air gap adjustment device (refer to Section 5 for details). The total load that needs to be overcome in the adjustment of the air gap with magnetic can be expressed as follows:
where FM is the unbalanced magnetic pull, GS1 is the gravity of upper and lower stators, L is the length of the stator core, and ε is the eccentricity of the motor.
The total load to be overcome in the adjustment of the air gap without magnetic is as follows:
It can be seen from Equations (10) and (11) that the total load to be overcome in the magnetic adjustment process is the force of the unilateral magnetic pull and the weight of the stator, and only the weight of the stator needs to be overcome in the non-magnetic adjustment process. The load required for the magnetic and non-magnetic adjustment with different eccentricities is shown in Figure 13.
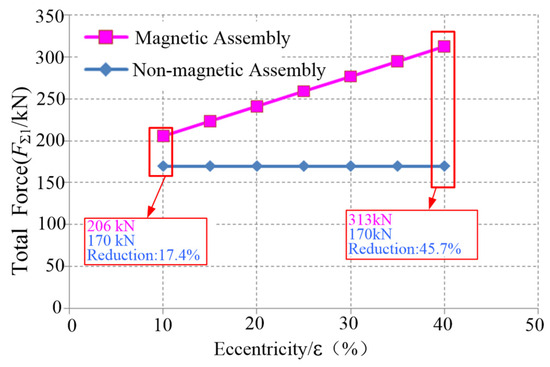
Figure 13.
The comparison of total stator force at different eccentricities.
As illustrated in Figure 13, the total load required for adjusting the stator increases with the eccentricity during magnetic adjustment, while it remains constant during non-magnetic adjustment. Specifically, when the eccentricity varies from 10% to 40%, the total load for non-magnetic adjustment consistently stays at 70 kN. In contrast, the total load required for magnetic adjustment escalates from 206 kN to 313 kN. Notably, the load that must be overcome during non-magnetic adjustment constitutes only 17.4% to 45.7% of the load experienced during magnetic adjustment.
The distribution curves of the stress and deformation of the motor stator at different eccentricities are shown in Figure 14 and Figure 15.
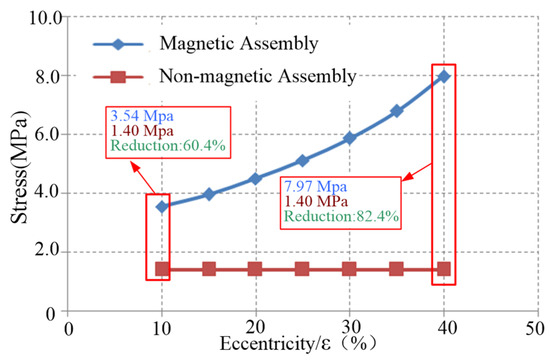
Figure 14.
The stress comparison of the stator at different eccentricities.
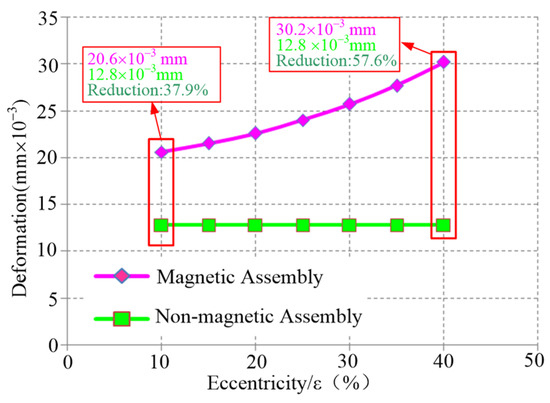
Figure 15.
The deformation comparison of the stator at different eccentricities.
As illustrated in Figure 14 and Figure 15, when the eccentricity varies from 10% to 40%, the maximum stress of the stator without magnetic adjustment is 60.4% to 2.4% lower than that with magnetic adjustment. Additionally, the maximum deformation of the stator is between 37.9% and 57.6% of that observed with magnetic adjustment.
The stress and deformation finite element distribution cloud map with magnetic air gap adjustment and without magnetic gap adjustment are shown in Figure 16.
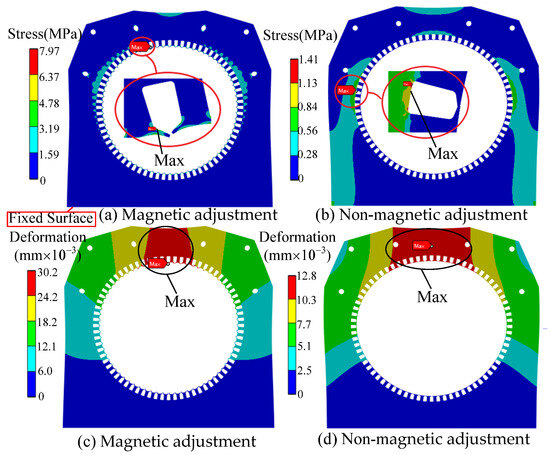
Figure 16.
The comparison of stress and deformation distribution cloud map (eccentricity = 40%).
As illustrated in Figure 16, the constraint position is located at the bottom surface of the stator during air gap adjustment. The maximum stress, resulting from the combined effects of magnetic pull and gravity, occurs at the stator tooth during magnetic air gap adjustment, as depicted in Figure 16a. In the absence of magnetic air gap adjustment, the maximum stress is observed at the tooth root due to gravitational forces, as shown in Figure 16b. Furthermore, owing to the bottom surface constraint, the top surface of the stator is the most susceptible to deformation. Notably, the maximum deformation, both during magnetic air gap adjustment and without it, occurs at this location, illustrated in Figure 16c,d. It is important to note that the stress and deformation experienced without magnetic air gap adjustment are significantly lower than those observed with magnetic air gap adjustment.
From the above analysis, it can be concluded that the mechanical properties of the motor stator are unaffected by assembly distance and eccentricity during non-assembly, remaining constant and consistently lower than those observed in magnetic assembly. Consequently, non-magnetic assembly technology can simplify the assembly process of the PMIM for ball mills.
5. Construction and Analysis of Air Gap Adjustment Device
5.1. Construction of Air Gap Adjustment Device
The spatial positioning of the stator in the X, Y, and Z directions of the PMIM for ball mills is modified using an air gap adjustment device. This device enhances the uniformity of the air gap. The three-dimensional structure of the air gap adjustment device is illustrated in Figure 17.
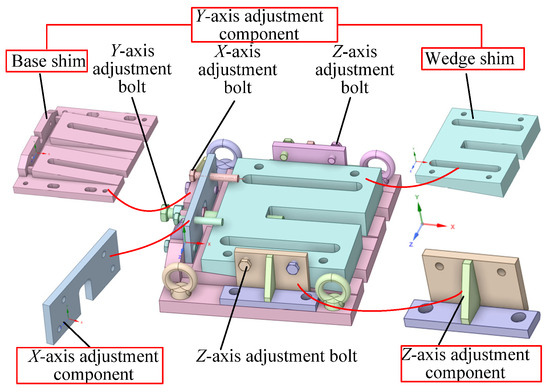
Figure 17.
The air gap adjustment device.
As illustrated in Figure 17, the air gap adjustment device comprises three primary components: the X-axis adjustment component, the Y-axis adjustment component, and the Z-axis adjustment component. The adjustment and control of the air gap are achieved by configuring adjustment bolts in each direction. Notably, the Y-axis adjustment component consists of a base shim and a wedge shim.
5.2. Mathematical Model of Air Gap Adjustment Device
- (1)
- Non-magnetic adjustment
During non-magnetic adjustment, the frictional resistance force generated by the weight of the stator is supported by the air gap adjustment device. The X-axis and Z-axis adjustment components are responsible for adjusting the horizontal position of the stator, and the frictional resistance force they experience can be expressed as follows.
The Y-axis adjustment component is used to adjust the height of stator, and the adjustment principle is shown in Figure 18.
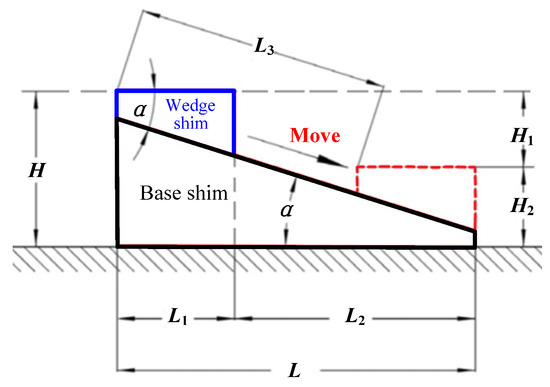
Figure 18.
The schematic diagram of Y-axis adjustment.
As illustrated in Figure 18, the contact surface between the base shim and the wedge shim forms an inclined plane with an angle α. The base shim remains fixed while the position of the wedge shim along the inclined plane is adjusted to modify the height of the stator. The frictional resistance force experienced by the Y-axis adjustment component during upward and downward adjustments is expressed as follows:
where m1 is the mass of the stator, m2 is the mass of the wedge shim, g is the acceleration of gravity, and μ is the coefficient of sliding friction.
- (2)
- Magnetic adjustment
With magnetic adjustment, the force borne by the air gap adjusting device is the friction resistance force due to the weight of the stator and the magnetic pull on it. When adjusting the horizontal position of the stator, the friction resistance force of X-axis adjustment component and Z-axis adjustment component can be expressed as follows:
The friction resistance force of the Y-axis adjustment component when adjusting downward and upward can be expressed, respectively, as follows:
It can be seen from Equations (12)–(17) that the friction resistance of each component is less for the non-magnetic adjustment than the magnetic adjustment. When adjusting the stator height, the friction resistance encountered during the upward adjustment is greater than that during the downward adjustment.
5.3. Analysis of Mechanical Properties of Air Gap Adjustment Device
- (1)
- Mechanical performance analysis of X-axis adjustment component
Figure 19 illustrates the stress and deformation distribution of the X-axis adjustment component under both non-magnetic and magnetic adjustment conditions. The trends in stress and deformation for both adjustment methods are similar. Specifically, the maximum stress observed during non-magnetic adjustment is 42.2 MPa, accompanied by a maximum deformation of 90 × 10−3 mm. In contrast, the magnetic adjustment yields a maximum stress of 60.0 MPa and a maximum deformation of 130 × 10−3 mm. Notably, the maximum stress during non-magnetic adjustment is reduced by 29.6%, while the maximum deformation is decreased by 30.1%.
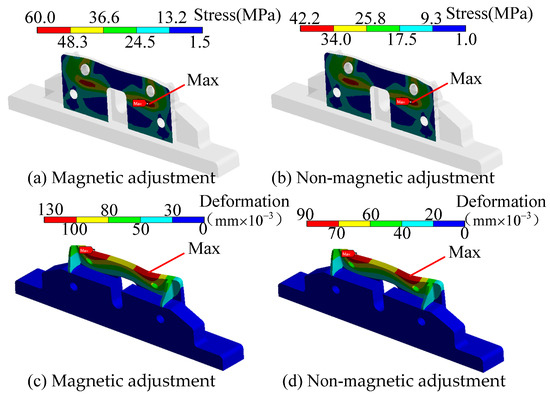
Figure 19.
Stress and deformation contour map of X-axis adjustment component.
- (2)
- Mechanical performance analysis of Y-axis adjustment component
During upward adjustment, the adjustment component experiences the maximum load. Figure 20 illustrates the stress and deformation distribution of the adjustment component along the Y-axis during both the non-magnetic and magnetic adjustments. It can be observed that the maximum stress during the non-magnetic adjustment is 88.9 MPa, while the maximum deformation is 120 × 10−3 mm. In contrast, the maximum stress during the magnetic adjustment reaches 125.8 MPa, with a maximum deformation of 170 × 10−3 mm. Consequently, the maximum stress during the non-magnetic adjustment is reduced by 36.9%, and the maximum deformation is decreased by 29.4%.
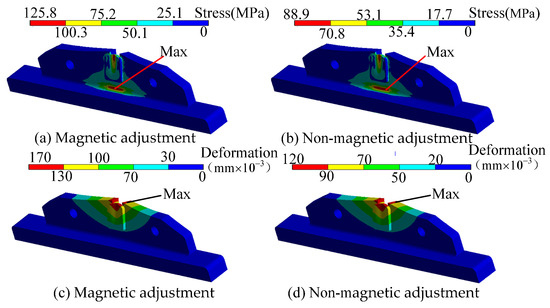
Figure 20.
Stress and deformation contour map of Y-axis adjustment component.
- (3)
- Mechanical performance analysis of Z-direction adjustment component
The stress distribution of the Z-axis adjustment component under both the non-magnetic and magnetic adjustment conditions is illustrated in Figure 21. It is evident that the maximum stress during non-magnetic adjustment reaches 82.4 MPa, while the maximum stress during magnetic adjustment is significantly lower, i.e., 17.1 MPa. This indicates a reduction of 29.6% in the maximum stress when employing the magnetic adjustment.
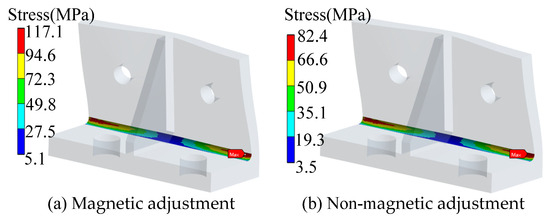
Figure 21.
Stress contour map of Z-axis adjustment component.
6. Result Discussion
Table 1 shows the summary of mechanical properties under different assembly states, using the non-magnetic technology and magnetic technology. The observations made are as follows:
(1) The non-magnetic assembly technology has been employed, which eliminates the presence of a permanent magnet on the motor rotor. Consequently, the system is not subjected to magnetic pull forces during stator assembly, significantly reducing the overall load, stress, and deformation.
(2) In the case of the PMIM for ball mills, the stator and rotor are independent of each other, leading to substantial air gap eccentricity post-assembly (with mechanical properties exhibiting a 40% eccentricity). As illustrated in Figure 12, Figure 13 and Figure 14, the load, stress, and deformation of the system progressively increase with rising eccentricity during the magnetic centering process. It is important to note that the system consistently bears the constant weight of the stator throughout the non-magnetic centering process, thereby maintaining stable mechanical properties.
(3) During assembly without magnetism, the upper and lower stators remain separate; however, they merge into a single unit during the non-magnetic centering, enhancing their resistance to stress and deformation. Although the load significantly increases compared to scenarios without magnetic assembly, the stress and deformation remain relatively unchanged.
(4) Furthermore, the stress and deformation induced by the motor are highly sensitive to the structural shape and size alterations, while the magnetic pull force within the motor remains unaffected by these factors. This paper primarily analyzes the trends in mechanical properties when the non-magnetic assembly technology is utilized, highlighting its advantages. It is worth noting that the structural shape and size have not been optimized, and the selection of stator dimensions must consider the stator slot and magnetic circuit saturation, resulting in minimal stress and deformation in the stator.

Table 1.
Comparison of non-magnetic technology and magnetic technology.
Table 1.
Comparison of non-magnetic technology and magnetic technology.
| Component | Assembled State | Force /kN | Stress /MPa | Deformation /mm × 10−3 |
|---|---|---|---|---|
| Stator | Non-magnetic assembly | 70.0 | 1.6 | 10.0 |
| Magnetic assembly | 248.0 | 4.8 | 30.0 | |
| Stator | Non-magnetic centering | 170.0 | 1.4 | 12.8 |
| Magnetic centering | 313.0 | 8.0 | 30.2 | |
| X-direction adjustment | Non-magnetic adjustment | 34.0 | 42.2 | 90.0 |
| Magnetic adjustment | 62.6 | 60.0 | 130.0 | |
| Y-direction adjustment | Non-magnetic adjustment | 49.3 | 88.9 | 185.0 |
| Magnetic adjustment | 116.9 | 125.8 | 231.0 | |
| Z-direction adjustment | Non-magnetic adjustment | 34.0 | 82.4 | 120.0 |
| Magnetic adjustment | 62.6 | 117.1 | 170.0 |
7. Prototype and Assembly
The manufacturing and assembly of a PMIM for ball mills was completed using the non-magnetic processing technology. The design parameters of the motor are listed in Table 2, and a physical photo is shown in Figure 22.

Table 2.
Design parameters of PMIM for ball mills.

Figure 22.
Prototype of 210 kW PMIM for ball mills.
The photographs depicting the on-site assembly without permanent magnets are presented in Figure 23. Figure 23a illustrates the installation of the air gap adjustment device and the lower stator surrounding the roller. Figure 23b,c depict the assembly of the rotor support, the rotor module, and the lifting of both the upper and lower stators for assembly. At this stage, the rotor does not contain permanent magnets; thus, the assembly process is unaffected by magnetic attraction. As shown in Figure 23b, it is unnecessary to establish a guiding device to prevent the attraction of the stator and rotor during assembly; the process can be completed using only a single crane. Figure 23d displays the air gap adjustment device. The motor can be maneuvered in all directions by adjusting the bolts, thereby enhancing the uniformity of the air gap within the motor.
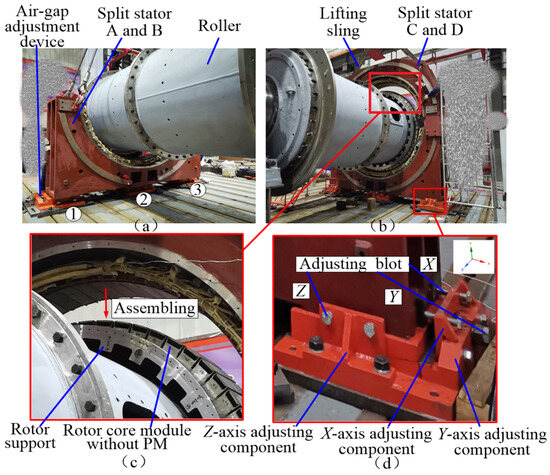
Figure 23.
Physical photographs of non-magnetic assembly for 210 kW PMIM for ball mills. (a) Install air-gap adjustment devices and Stator (b) Assembling (c) Enlarged detail view for assembling (d) Enlarged detail view for air-gap adjustment devices.
The motor assembly is completed, and the air gap is adjusted evenly before assembling the permanent magnet (PM). The assembly of the PM is shown in Figure 24.
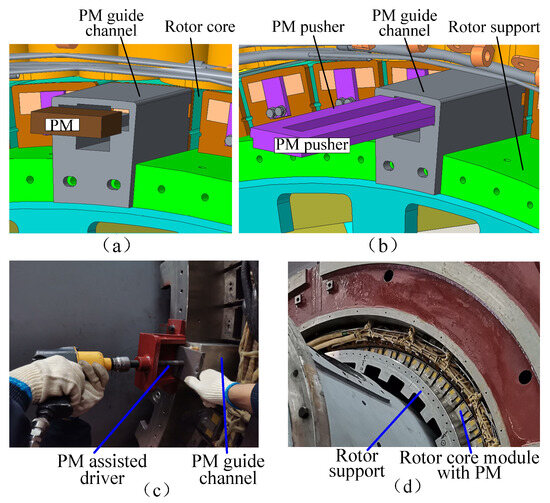
Figure 24.
Photographs of PM assembly. (a) Insert PM (b) Push PM into position (c) PM fixation (d) PM assembly completed.
As shown in Figure 24a, a PM guide channel is implemented during assembly to eliminate magnetic interference from stator/rotor structures on PM installation. As shown in Figure 24b,c, using a PM pusher and PM-assisted driver, the permanent magnets are sequentially mounted into rotor core modules through the PM guide channel. Figure 23d displays the fully assembled motor with all permanent magnets installed. It is important to note that the material of the permanent magnet push rod is nylon, while the material of the permanent magnet pipeline is stainless steel. Additionally, the clearance between the permanent slot and the permanent magnet must be maintained within a range of 0.1 to 0.2 mm.
8. Conclusions
To address the assembly challenges of the PMIM for ball mills, in this study, a non-magnetic assembly technology is proposed. Through theoretical analysis, numerical calculations, and structural optimization, it systematically resolves the field assembly difficulties of large segmented permanent magnet integrated motors. The main conclusions are as follows:
- (1)
- A post-assembly permanent magnet installation technique based on non-magnetic principles is proposed. By deferring the magnet mounting to the final stage of motor assembly, this innovative approach effectively eliminates the magnetic attraction issues between the stator and rotor encountered in conventional methods. The implementation results demonstrate a remarkable 71.8% reduction in the total assembly load, significantly simplifying the assembly process while enhancing operational safety.
- (2)
- By comparing the mechanical characteristics of magnetic and non-magnetic assembly, it is confirmed that the stress and deformation of the motor stator under non-magnetic assembly are significantly reduced. The maximum stress in the assembly stage is reduced by 66.3%, and the maximum deformation is reduced by 66.7%. The adjustment load in the air gap adjustment stage is not affected by the amount of eccentricity, and the stress and deformation increase with the growth of eccentricity. When the eccentricity is 40%, the maximum stress of the stator is reduced by 82.4%, and the maximum deformation is reduced by 57.6%. The maximum stress and deformation of each component of the air gap adjustment device during the non-magnetic adjustment stage are all reduced by about 30%.
- (3)
- The non-magnetic assembly process, combined with an air gap adjustment device, significantly reduces the on-site assembly difficulty of the PMIM for ball mills, providing a feasible technical solution for the assembly of large permanent magnet integrated motors.
- (4)
- Currently, the process technology for assembling 210 kW and 24 r/min and 540 W and 24 r/min ball mill permanent magnet motors has been successfully completed. The author’s future research in this field is anticipated to explore the scalability limits of motor size, particularly focusing on larger input power scales. Additionally, this paper did not consider the influence of motor axial eccentricity on the X-direction regulation; this aspect will be addressed in future work.
Author Contributions
Conceptualization, J.G. and Z.Y.; methodology, J.G. and Z.A.; software, J.G.; validation, J.G., X.H. and Z.A.; formal analysis, J.G. and X.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by the Liaoning Provincial Department of Science and Technology of China [Grant No. 2023JH2/101700273].
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| Gs | gravity of upper stator |
| GS1 | gravity of upper and lower stators |
| m1 | mass of upper and lower stators |
| m2 | mass of wedge shim |
| P | any point on inner surface of upper stator |
| RS | stator inner radius |
| Rr | rotor outer radius |
| θ | angle between point P and X-axis |
| h | mating interface gap between upper and lower stators |
| B0 | air gap magnetic flux density when air gap is uniform |
| Bg(θ) | air gap magnetic flux density at any arbitrary point on upper stator |
| g | acceleration of gravity |
| g0 | air gap value when air gap is uniform |
| g(θ) | air gap value at any arbitrary point on upper stator |
| P(θ) | magnetic pull force at point P |
| Py(θ) | magnetic pull force along Y-axis at point P |
| total magnetic pull force along Y-axis | |
| total stator load, during magnetic assembly ( = + Gs), and during non-magnetic assembly ( = Gs) | |
| total load that needs to be overcome in air gap with magnetic adjustment | |
| unbalanced magnetic pull | |
| friction resistance force of X-axis adjustment component during non-magnetic adjustment | |
| friction resistance force of Z-axis adjustment component during non-magnetic adjustment | |
| friction resistance force of Y-axis adjustment component during non-magnetic adjustment (downward) | |
| friction resistance force of Y-axis adjustment component during non-magnetic adjustment (upward) | |
| friction resistance force of X-axis adjustment component during magnetic adjustment | |
| friction resistance force of Z-axis adjustment component during magnetic adjustment | |
| friction resistance force of Y-axis adjustment component during magnetic adjustment (downward) | |
| friction resistance force of Y-axis adjustment component during magnetic adjustment (upward) | |
| L | length of stator core |
| ε | eccentricity of motor |
| μ | coefficient of sliding friction (μ = 0.2) |
| μ0 | vacuum permeability (μ0 = 4π × 10−7 H/m) |
References
- Xu, Y.Y.; Zhang, B.Y.; Feng, G.H. Analysis of Unwinding Stator Module Combined Permanent Magnet Synchronous Machine. IEEE Access 2020, 8, 191901–191909. [Google Scholar] [CrossRef]
- Niu, Y.L.; Zahng, B.Y.; Pei, Z. Stress analysis and optimization of transmission structure of permanent magnet direct drive ball mill. In Proceedings of the International Conference on Mechanisms and Robotics (ICMAR 2022), Zhuhai, China, 25–27 February 2022. [Google Scholar] [CrossRef]
- Xu, Y.Y.; Zhang, B.Y.; Feng, G.H. Electromagnetic Design and Thermal Analysis of Module Combined Permanent Magnet Motor with Wrapped Type for Mine Ball Mil. IET Electr. Power Appl. 2022, 16, 139–157. [Google Scholar] [CrossRef]
- Xu, Y.Y.; Zhang, B.Y.; Feng, G.H. Research on Efficiency Optimal Torque Distribution of Stator Module Combined Permanent Magnet Synchronous Machine. IET Electron. Power Appl. 2022, 16, 236–247. [Google Scholar] [CrossRef]
- Qiu, X.; Bai, J.; Sui, Y.; Xiao, Q.; Li, G.; Liu, Y. Design and Analysis of a Free-Piston PM Linear Motor Considering the Influence of Processing and Assembly. In Proceedings of the 2023 26th International Conference on Electrical Machines and Systems (ICEMS), Zhuhai, China, 5–8 November 2023; pp. 4909–4913. [Google Scholar] [CrossRef]
- Chen, M.; Zhang, B.; Li, H.; Gao, X.; Wang, J.; Zhang, J. Lifetime Prediction of Permanent Magnet Synchronous Motor in Selective Compliance Assembly Robot Arm Considering Insulation Thermal Aging. Sensors 2024, 24, 3747. [Google Scholar] [CrossRef] [PubMed]
- Matejić, M.; Matejić, M.; Miletić, I.; Marić, D.; Milojević, S.; Stojanović, B. Efficiency Calculation of Cycloid Reducer with Plastic Meshing Elements. Tehnički Vjesnik 2025, 32, 748–755. [Google Scholar] [CrossRef]
- Wu, S.; Li, Z.; Tong, W. Research on thermal calculation and end winding heat conduction optimization of low speed high torque permanent magnet synchronous motor. CES Trans. Electr. Mach. Syst. 2023, 7, 397–403. [Google Scholar] [CrossRef]
- Hu, Y.; Li, L.; Guo, W.; Wang, S. Study on the Rotor Strength of High-Speed Permanent Magnet Motor Considering the Influence of Assembly Pressing Force. Symmetry 2021, 13, 2161. [Google Scholar] [CrossRef]
- Lee, C.K.; Kwon, B.I.; Kim, B.T.; Woo, K.I.; Han, M.G. Analysis of magnetization of magnet in the rotor of line start permanent magnet motor. IEEE Trans. Magn. 2003, 39, 1499–1502. [Google Scholar] [CrossRef]
- Lee, C.K.; Kwon, B.I. Study in the post-assembly magnetization method of permanent magnet motors. Int. J. Appl. Electromagn. Mech. 2004, 20, 125–131. [Google Scholar] [CrossRef]
- Lee, C.K.; Kwon, B.I. Design of post-assembly magnetization system of line start permanent-magnet motors using FEM. IEEE Trans. Magn. 2005, 41, 1928–1931. [Google Scholar]
- Hsieh, M.F.; Hsu, Y.C.; Dorrell, D.G. Design of Large-Power Surface-Mounted Permanent-Magnet Motors Using Postassembly Magnetization. IEEE Trans. Ind. Electron. 2010, 57, 3376–3384. [Google Scholar] [CrossRef]
- Hsieh, M.F.; Hsu, Y.C.; Chen, P.T. Analysis and Experimental Study of Permanent Magnet Machines with In-Situ Magnetization. IEEE Trans. Magn. 2013, 49, 2351–2354. [Google Scholar] [CrossRef]
- Wang, Q.; Ding, H.; Zhang, H.; Lv, Y.; Guo, H.; Li, L. Study of a Post-Assembly Magnetization Method of a V-Type Rotor of Interior Permanent Magnet Synchronous Motor for Electric Vehicle. IEEE Trans. Appl. Supercond. 2020, 30, 5206205. [Google Scholar] [CrossRef]
- Fu, W.N.; Chen, Y. A Post-Assembly Magnetization Method for a Line-Start Permanent-Magnet Motor. IEEE Trans. Appl. Supercond. 2016, 26, 2535968. [Google Scholar] [CrossRef]
- Zhu, Z.-A.; Wang, Y.-C.; Qin, X.-F.; Yao, L.; Gyselinck, J.; Shen, J.-X. Optimal Design Method of Post-Assembly Magnetizing Device with Field–Circuit Coupling Analysis. Actuators 2023, 12, 383. [Google Scholar] [CrossRef]
- Kwon, S.-J.; Lee, B.-H.; Kim, K.-S.; Jung, J.-W. Design Process of Post-Assembly 3-Times Magnetizer for 10-Poles of Flux Concentrated Rotor Considering Eddy Current Effect. IEEE Access 2023, 11, 34476–34485. [Google Scholar] [CrossRef]
- Hyun-Soo, S.; Tak, J.; Hyun-Woo, J.; Ju, L.; Dong-Woo, K. Design of 3-Times Magnetizer and Rotor of Spoke-Type PMSM Considering Post-Assembly Magnetization. IEEE Trans. Magn. 2017, 53, 2707593. [Google Scholar] [CrossRef]
- Lv, Y.; Wang, G.; Li, L. Post-assembly magnetization of a 100 kW high speed permanent magnet rotor. Rev. Sci. Instrum. 2015, 86, 034706. [Google Scholar] [CrossRef] [PubMed]
- Seol, H.-S.; Kim, J.-Y.; Liu, H.-C.; Kang, D.-W.; Lee, J. Design Strategy of Magnetizer for Post-Assembly Magnetization of Spoke-Type Ferrite Magnet Motor. J. Electron. Mater. 2018, 48, 1368–1374. [Google Scholar] [CrossRef]
- Tu, Z.; Lv, Y.; Li, X.; Xu, W.; Peng, T.; Han, X.; Ding, H.; Li, L. Design and Experiment of Post-assembly Magnetization System for a 160-kW Interior Permanent-magnet Motor. IEEE Trans. Appl. Supercond. 2024, 34, 3364132. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).