Coupled Productivity Prediction Model for Multi-Stage Fractured Horizontal Wells in Low-Permeability Reservoirs Considering Threshold Pressure Gradient and Stress Sensitivity
Abstract
1. Introduction
2. Mathematical Model for Productivity of Multi-Stage Fractured Horizontal Wells
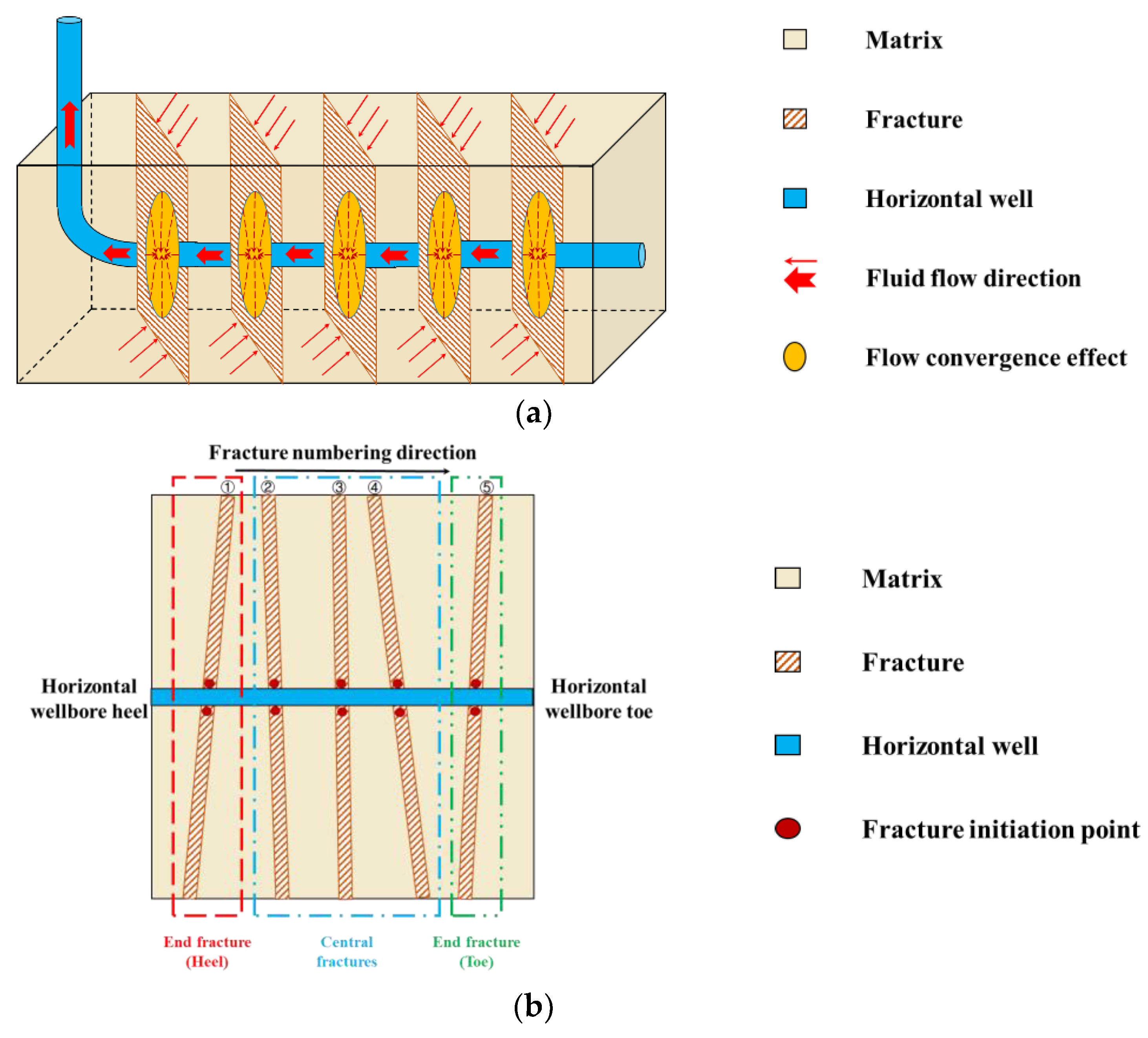
2.1. Physical Model and Assumptions
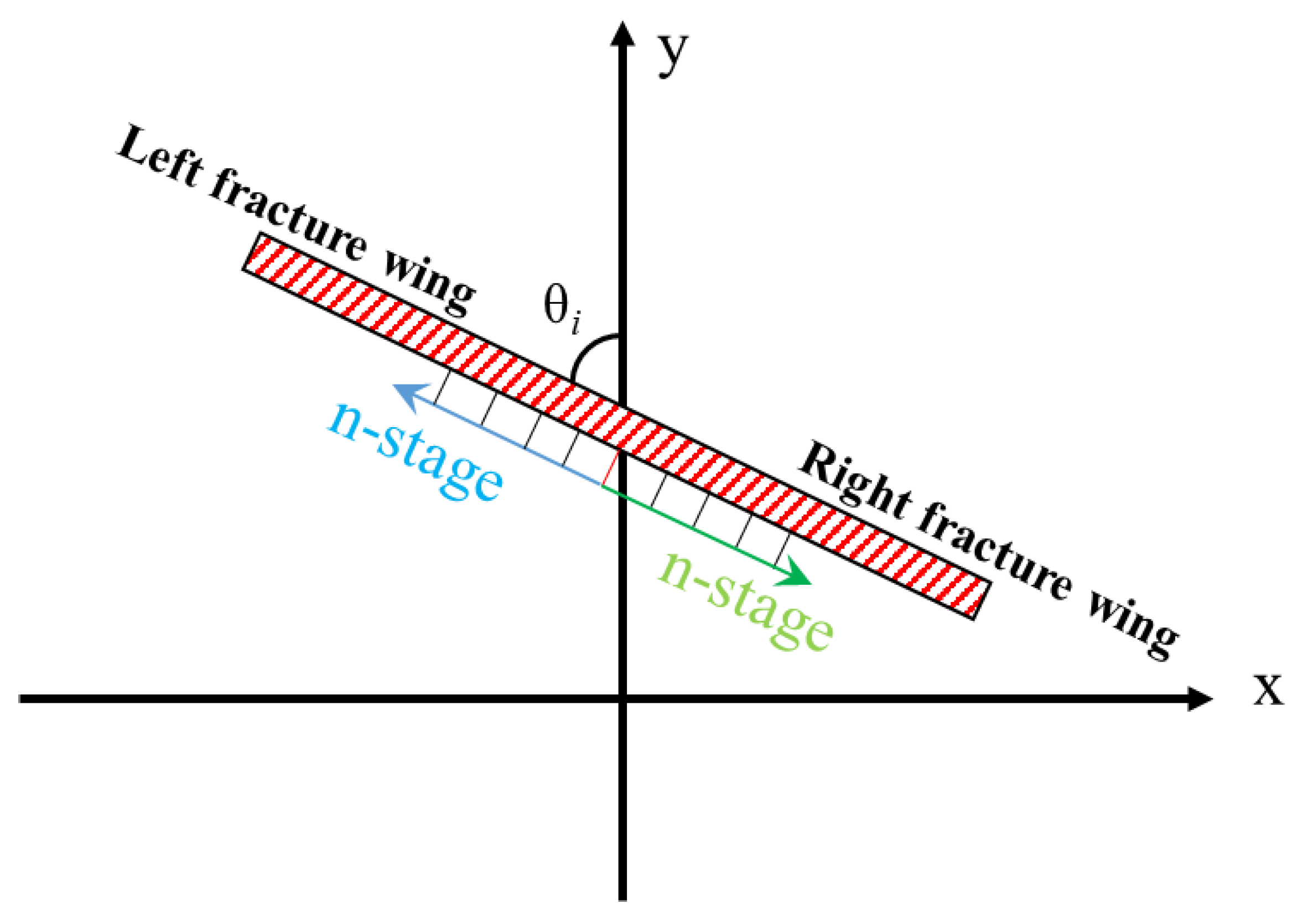
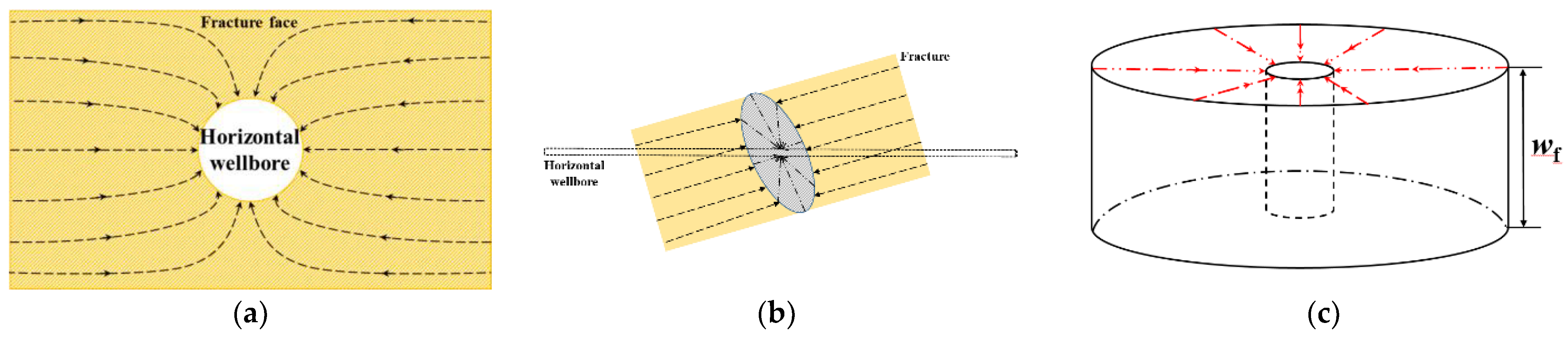
2.2. Matrix–Fracture Flow Model
- (1)
- Pressure Drop Model at Any Point in the Matrix
- (2)
- Matrix–Fracture Flow Model
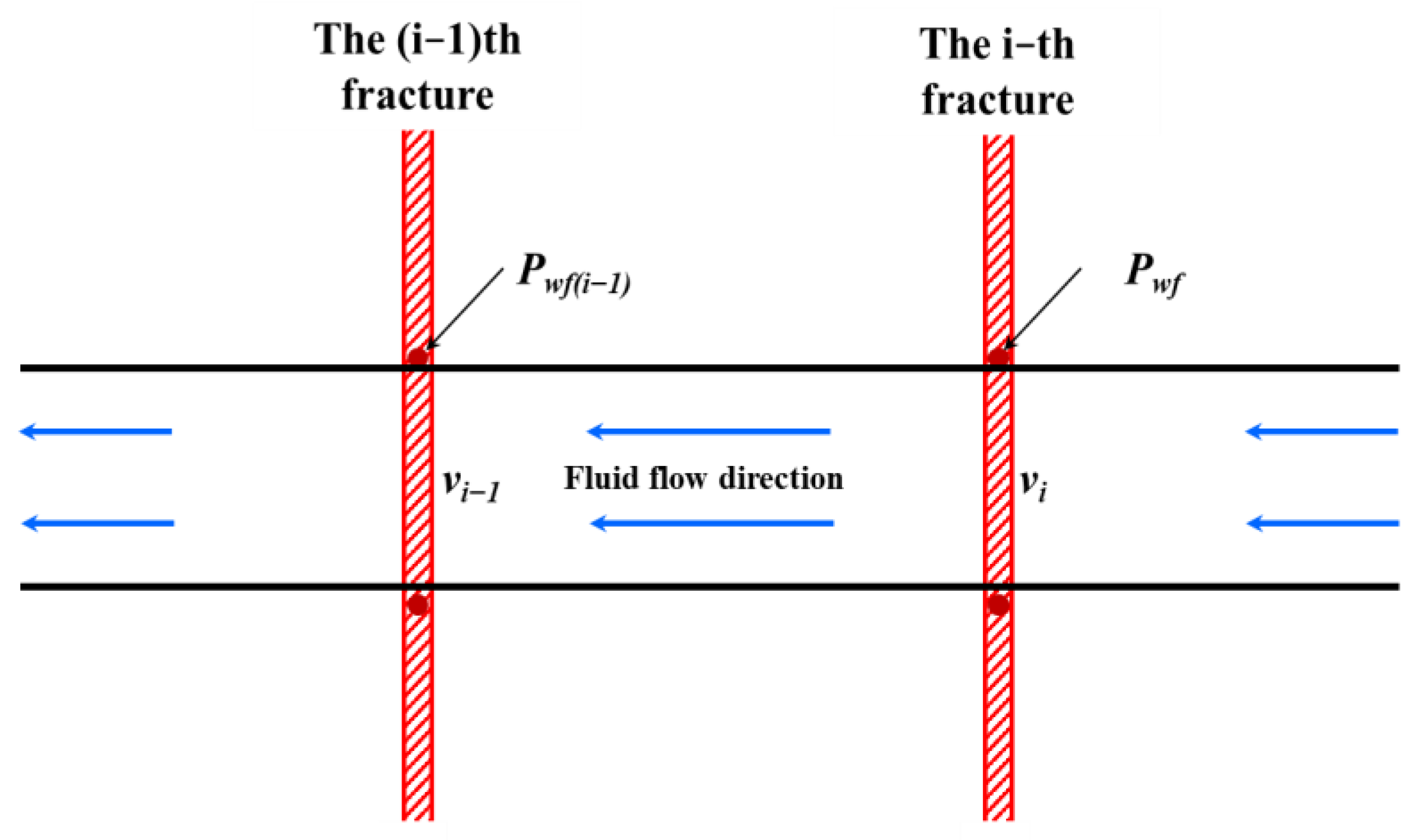
2.3. Fracture–Wellbore Flow Model
2.4. Wellbore Fluid Flow Model
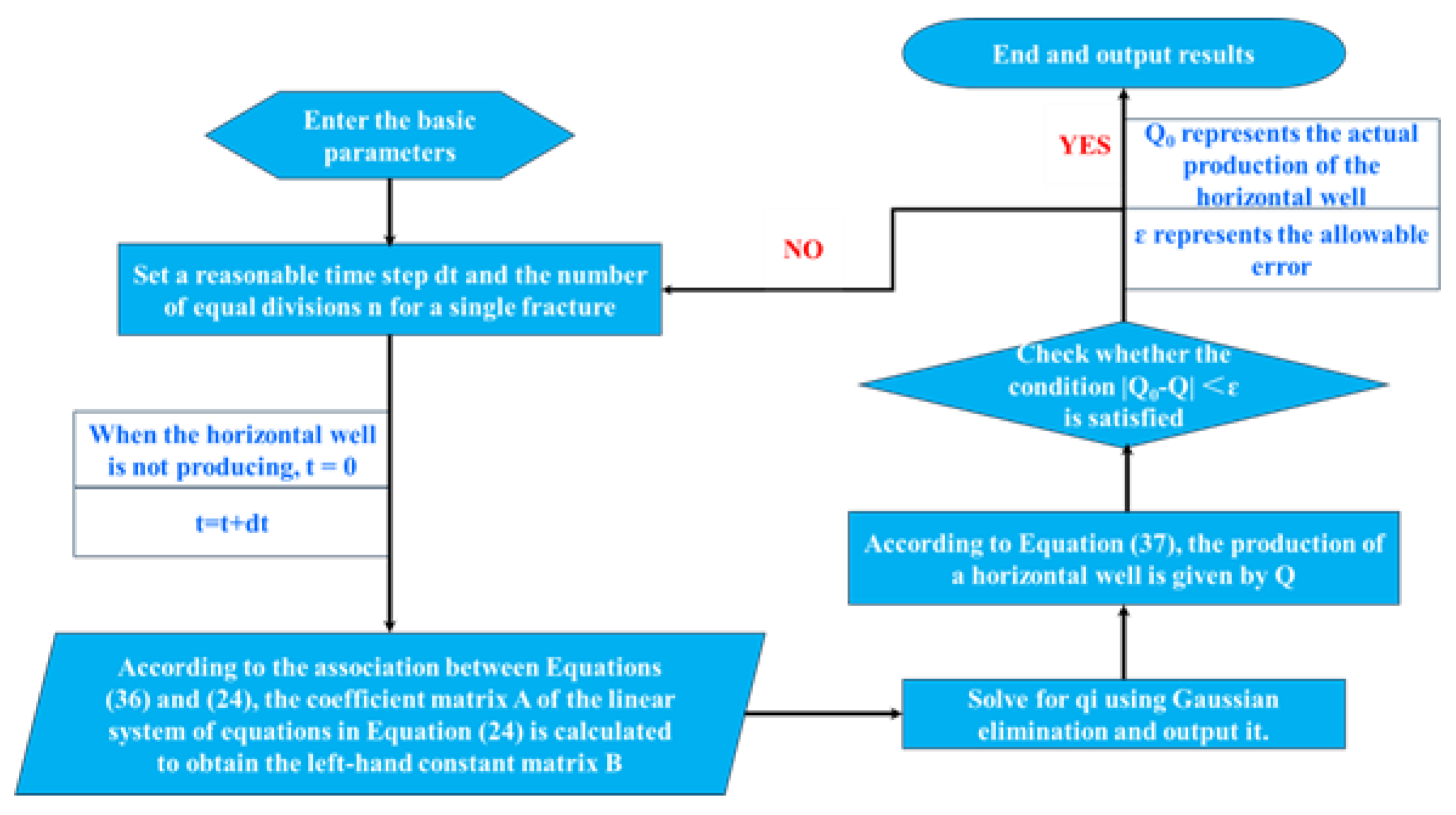
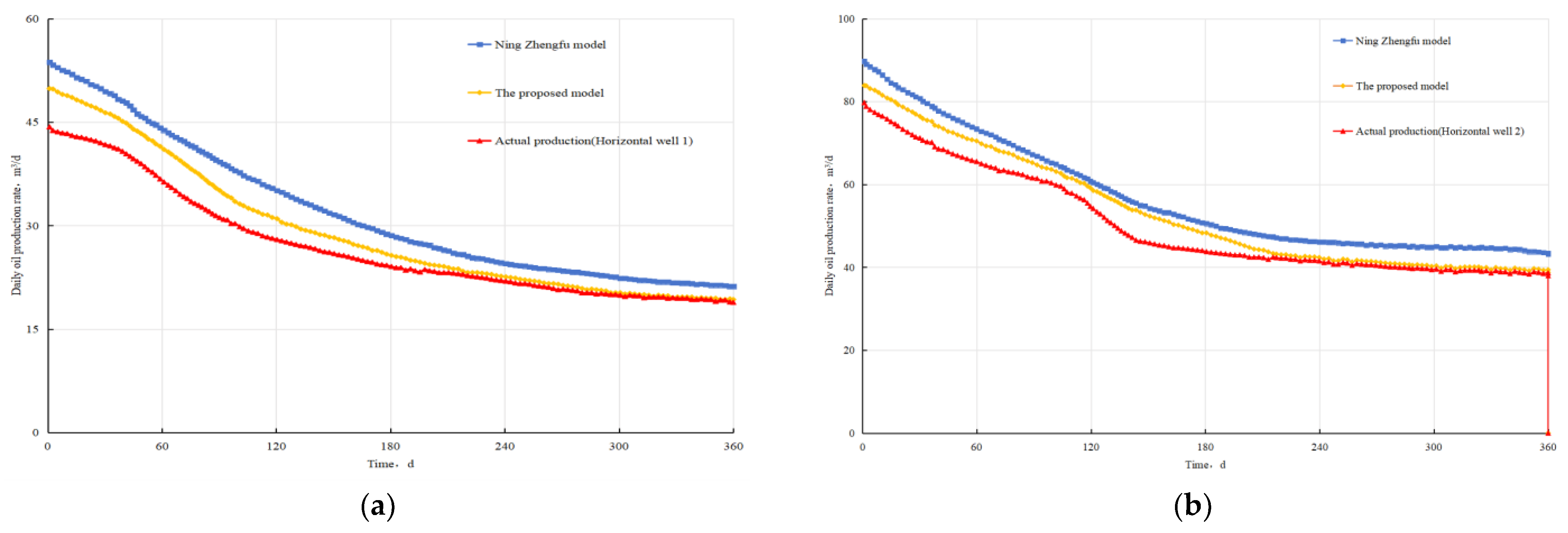
3. Model Validation
4. Sensitivity Analysis of Productivity Influencing Factors
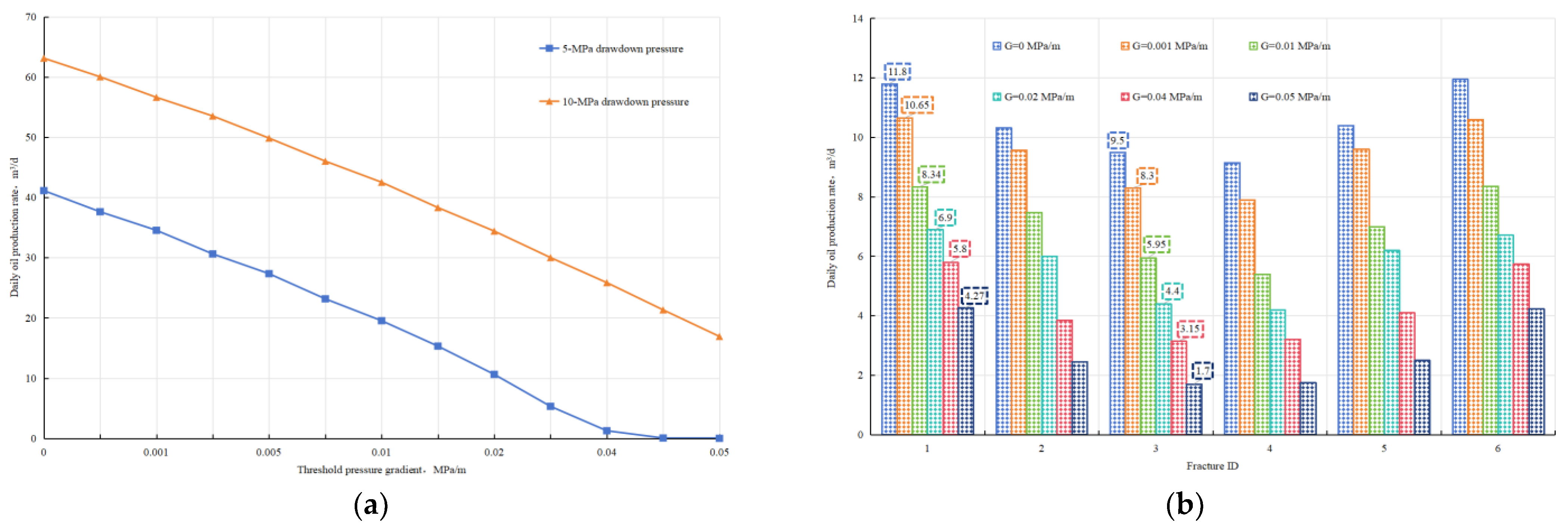
4.1. Threshold Pressure Gradient
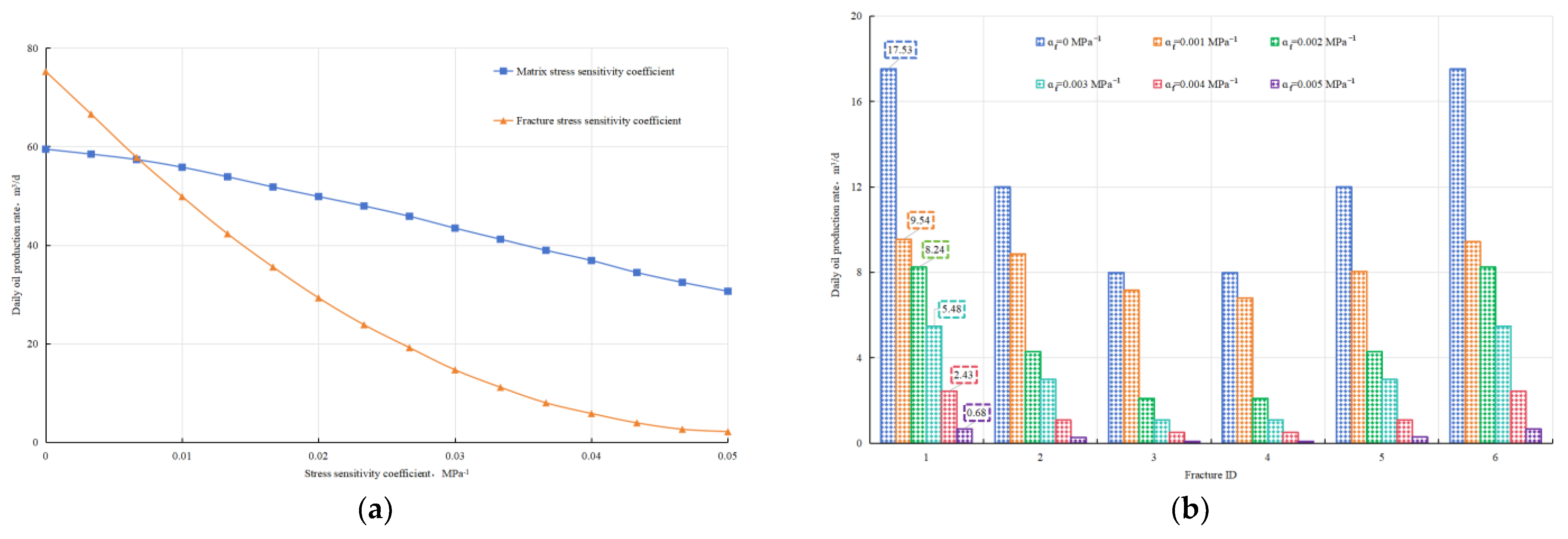
4.2. Stress Sensitivity Coefficients
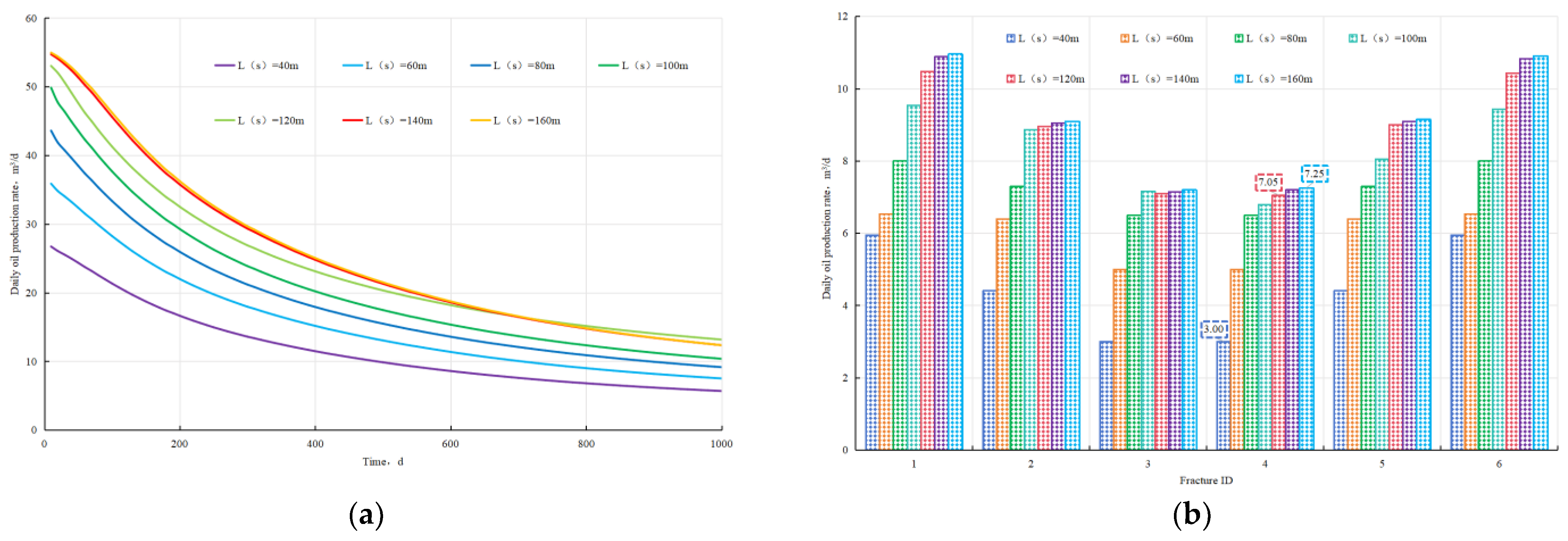
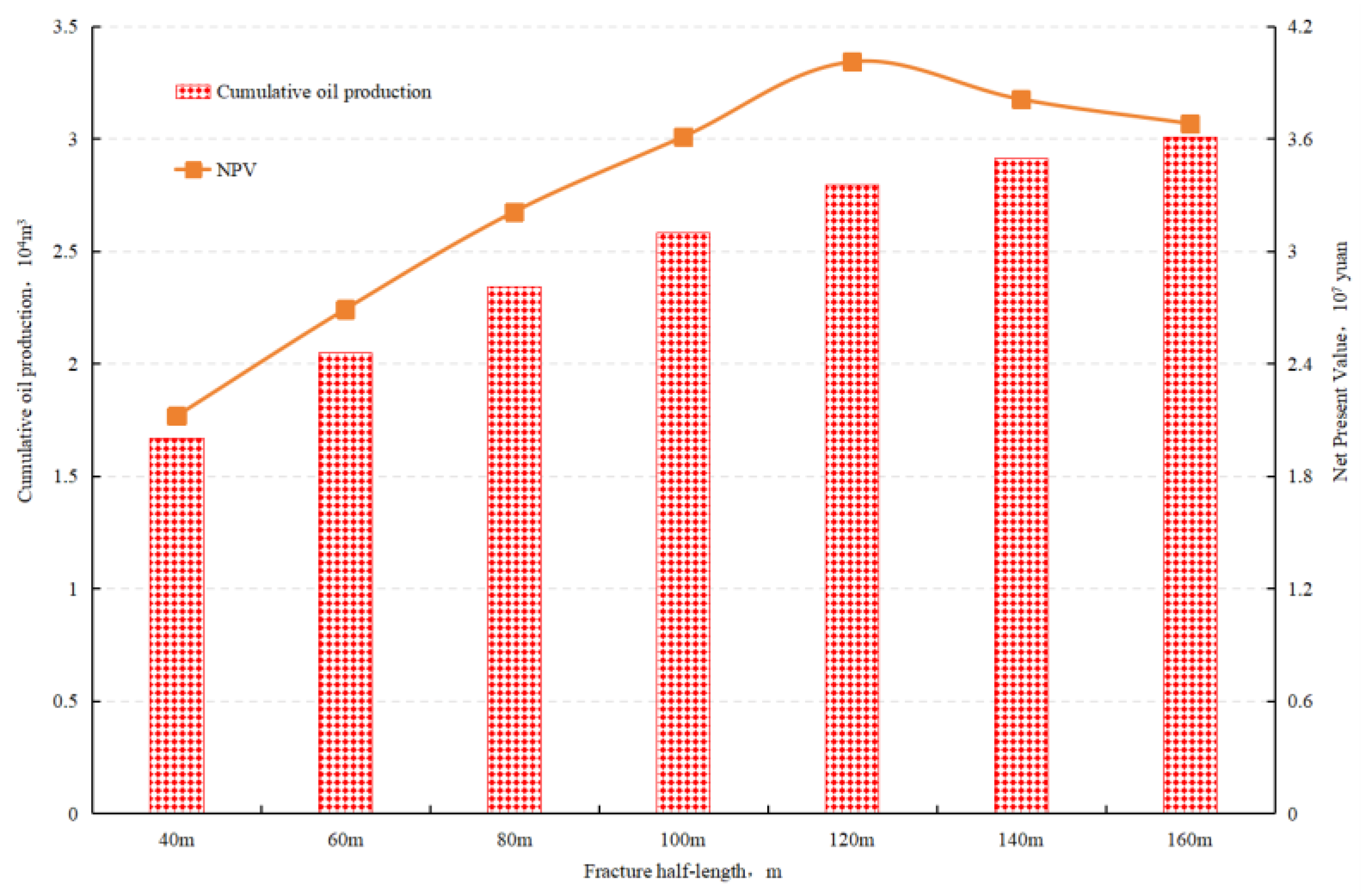
4.3. Fracture Half-Length
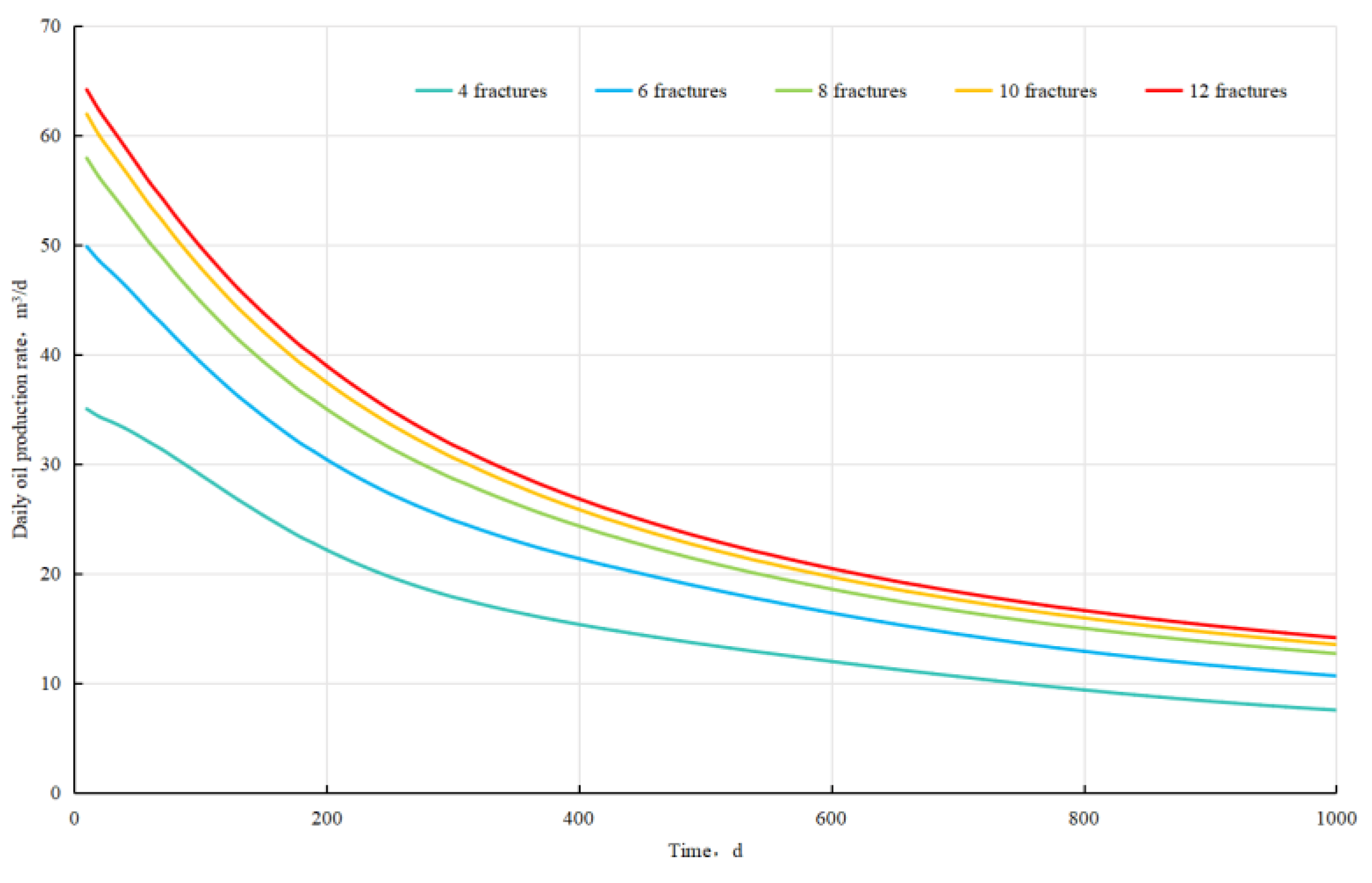
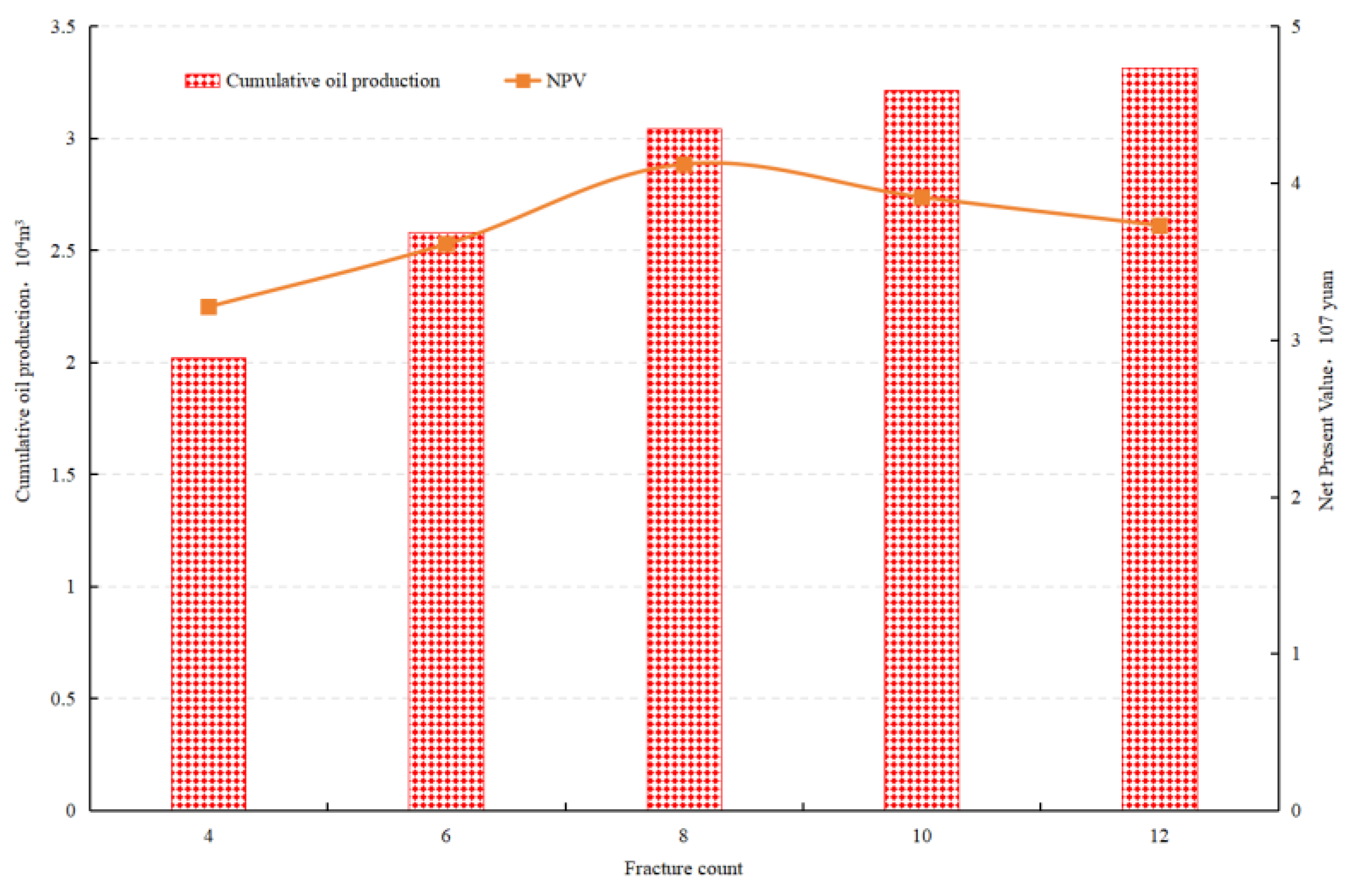
4.4. Number of Fractures
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Han, D. Status and challenges for oil and gas field development in China and directions for the development of corresponding technologies. Strateg. Study CAE 2010, 12, 51–57. [Google Scholar]
- Fan, T. Development process, key technologies and research directions of China’s offshore low-permeability oil and gas fields. China Offshore Oil and Gas 2024, 36, 95–109. [Google Scholar]
- Chen, H.; Liu, Q.; Sun, L.; Yu, H. Status and prospects of low carbon development in offshore oil and gas industry. Pet. Reserv. Eval. Dev. 2024, 14, 981–989. [Google Scholar]
- Miller, B.; Paneitz, J.; Yakely, S.; Evans, K. Unlocking tight oil: Selective multi-stage fracturing in the bakken shale G. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 21–24 September 2008; SPE 116105. pp. 1–5. [Google Scholar]
- Zhu, J. Practice and reflection on the strategy of engineering technology to cope with the regional development of offshore oil and gas fields. China Offshore Oil Gas 2014, 26, 35–39. [Google Scholar]
- Yang, Z.; Chen, Q.; Li, X. A Method to Predict Productivity of Multi -stage Multi-cluster Fractured Horizontal Wells in Tight Oil Reservoirs. Spec. Oil Gas Reserv. 2017, 24, 73–77. [Google Scholar]
- Liu, L.; Ran, Q.; Wang, X.; Li, R. Method of optimizing the spacing betweenvolumetric fracturing stages in horizontal wells in tight reservoir. Oil Drill. Prod. Technol. 2015, 37, 84–87. [Google Scholar]
- Pu, C.; Zheng, H.; Yang, Z.; Gao, Z. Research status and development trend of the formation mechanism of complex fractures by staged volume fracturing in horizontal wells. Acta Pet. Sin. 2020, 41, 1734–1743. [Google Scholar]
- Stalgorova, K.; Mattar, L. Analytical model for unconventional multifractured composite systems. SPE Reserv. Eval. Eng. 2013, 16, 246–256. [Google Scholar] [CrossRef]
- Li, Q.; Li, Q.; Wang, F.; Xu, N.; Wang, Y.; Bai, B. Settling behavior and mechanism analysis of kaolinite as a fracture proppant of hydrocarbon reservoirs in CO2 fracturing fluid. Colloids Surf. A Physicochem. Eng. Asp. 2025, 724, 137463. [Google Scholar] [CrossRef]
- Li, Q.; Wu, J.; Li, Q.; Wang, F.; Cheng, Y. Sediment Instability Caused by Gas Production from Hydrate-Bearing Sediment in Northern South China Sea by Horizontal Wellbore: Sensitivity Analysis. Nat. Resour. Res. 2025, 34, 1667–1699. [Google Scholar]
- Liu, X.; Guo, P.; Ren, J.; Wang, Z.; Tu, H. Productivity Model for Multi-Fractured Horizontal Wells with Complex Fracture Networks in Shale Oil Reservoirs Considering Fluid Desorption and Two-Phase Behavior. Energies 2024, 17, 6012. [Google Scholar] [CrossRef]
- Li, Z.; Wu, X.; Han, G.; Wang, R.; Zheng, L. Semi-analytical model of multi-stage fractured horizontal well productivityconsidering time-dependent fracture conductivity. Oil Drill. Prod. Technol. 2019, 41, 354–362. [Google Scholar]
- Sun, R.; Hu, J.; Zhang, Y.; Li, Z. A semi-analytical model for investigating the productivity of fractured horizontal wells in tight oil reservoirs with micro-fractures. J. Pet. Sci. Eng. 2020, 186, 106781. [Google Scholar] [CrossRef]
- Sun, R.; Zhang, Y.; Zhang, X. Productivity prediction model and parameter analysis for fractured horizontal wells in doublemedium tight oil reservoirs. Sci. Technol. Eng. 2019, 19, 89–96. [Google Scholar]
- Gao, X.; Guo, K.; Chen, P.; Yang, H.; Zhu, G. A productivity prediction method for multi-fractured horizontal wells in tight oil reservoirs considering fracture closure. J. Pet. Explor. Prod. Technol. 2023, 13, 865–876. [Google Scholar] [CrossRef]
- Tian, F.; Wang, J.; Xu, Z.; Xiong, F.; Xia, P. A nonlinear model of multifractured horizontal wells in heterogeneous gas reservoirs considering the effect of stress sensitivity. Energy 2023, 263, 125979. [Google Scholar] [CrossRef]
- Zhang, H.Y.; He, S.L.; Luan, G.H.; Lu, Q.; Mo, S.Y.; Zhang, Z.; Lei, G. Influence of Fracture Parameters on the Productivityof Fractured Horizontal Well Based on Fluid Mechanics in Tight Gas Reservoir. Adv. Mater. Res. 2014, 886, 452–455. [Google Scholar] [CrossRef]
- Hu, J.; Chen, Q.; Yu, G.; Lü, Y. Hydraulic Parameter Optimization of Dual Horizontal Well in Tight Oil Reservoirs. Geoscience 2021, 35, 1880–1890. [Google Scholar]
- Liu, S.; Wang, K.; Xie, M.; Feng, S.; Li, L.; Gao, Y. A Production Prediction Model for Fractured Horizontal Wells with Irregular Fracture Network in Low Permeability Reservoirs. Chin. J. Comput. Phys. 2024, 41, 503–514. [Google Scholar]
- Chen, L.; Bai, Y.; Xu, B.; Li, Y.; Dong, Z.; Wang, S. An Efficient and Robust Method to Predict Multifractured Horizontal Well Production in Shale Oil and Gas Reservoirs. Geofluids 2021, 2021, 1–11. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, L.; Lu, X.; Luo, Y.; Liu, Q. Deliverability analysis of fractured horizontal wells in low permeability fractured reservoir. Sci. Technol. Eng. 2014, 14, 41–48. [Google Scholar]
- Zhang, Y.; Chen, J.; Wu, Z.; Xiao, Y.; Xu, Z.; Cheng, H.; Zhang, B. Effect Evaluation of Staged Fracturing and Productivity Prediction of Horizontal Wells in Tight Reservoirs. Energies 2024, 17, 2894. [Google Scholar] [CrossRef]
- Li, L.; Yao, J.; Li, Y.; Wu, M.; Zeng, Q.; Lu, R. Productivity calculation and distribution of staged multi-cluster fractured horizontal wells. Pet. Explor. Dev. 2014, 41, 457–461. [Google Scholar] [CrossRef]
- Ji, J.; Yao, Y.; Huang, S.; Ma, X.; Zhang, S.; Zhang, F. Analytical model for production performance analysis of multi-fracturedhorizontal well in tight oil reservoirs. J. Pet. Sci. Eng. 2017, 158, 380–397. [Google Scholar] [CrossRef]
- Fang, W.; Jiang, H.; Li, J.; Wang, Q.; Killough, J.; Li, L.; Peng, Y.; Yang, H. A numerical simulation model for multi-scale flow in tight oil reservoirs. Pet. Explor. Dev. 2017, 44, 446–453. [Google Scholar] [CrossRef]
- Rashid, F.; Hussein, D.; Lorinczi, P.; Glover, P. The effect of fracturing on permeability in carbonate reservoir rocks. Mar. Pet. Geol. 2023, 152, 106240. [Google Scholar] [CrossRef]
- Ji, B.; Fang, J. An overview of efficient development practices at low permeability sandstone reservoirs in China. Energy Geosci. 2023, 4, 100179. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, H.; Wu, Z. Study and application of self-diverting fracturing fluid containing highly deformabletemporary plugging agents. Drill. Fluid Complet. Fluid 2022, 39, 114–120. [Google Scholar]
- Fan, L. Study on Productivity Prediction of Fractured Horizontal Well in Tight Oil Reservoirs. Master’s Thesis, China University of Geosciences, Wuhan, China, 2018. [Google Scholar]
- Li, Q.; Cheng, Y.; Li, Q.; Ansari, U.; Liu, Y.; Yan, C.; Lei, C. Development and verification of the comprehensive model for physical properties of hydrate sediment. Arab. J. Geosci. 2018, 11, 325. [Google Scholar] [CrossRef]
- Li, C. Stress Sensitivity influence on oil well productivity. J. Southwest Pet. Univ. (Sci. Technol. Ed.) 2009, 31, 170–172+200. [Google Scholar]
| Parameter Name | Value | Parameter Name | Value |
|---|---|---|---|
| Reservoir Thickness1/2, m | 25/33.5 | Wellbore Radius, m | 0.1 |
| Formation Permeability1/2, mD | 1.5/14.4 | Fracture Width, m | 0.005 |
| Formation Porosity1/2, % | 12/15.8 | Angle between Fracture and Horizontal Well, ° | 90 |
| Compressibility Coefficient, MPa−1 | 8 × 10−5 | TPG Coefficient1/2 | 0.82/0.53 |
| Formation Pressure1/2, MPa | 29.05/45.34 | TPG1/2, MPa/m | 0.005/0.003 |
| Bottomhole Flowing Pressure1/2, MPa | 19.05/25.34 | Number of Fractures | 6 |
| Horizontal Well Length1/2, m | 400/500 | Fracture Half-Length, m | 100 |
| Crude Oil Viscosity1/2, mPa·s | 1.29/0.21 | Fracture Permeability, mD | 100 |
| Density of Crude Oil, g/cm3 | 0.68/0.59 | Biot Number | 0.8 |
| Volume Coefficient1/2 | 1.34/1.84 | Matrix Stress Sensitivity Coefficient1/2, MPa−1 | 0.02/0.01 |
| Absolute Roughness of the Wellbore Wall | 0.00002 | Fracture Stress Sensitivity Coefficient, MPa−1 | 0.01 |
| Horizontal Well Zone | Fracture-Contributed Production (m3/d) | Fieldwide Total Production (m3/d) | Actual Production (m3/d) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Fracture ID | 1 | 2 | 3 | 4 | 5 | 6 | |||
| Horizontal well 1 | The comparison model | 9.28 | 8.87 | 8.69 | 8.70 | 8.89 | 9.26 | 53.69 | 44.3 |
| The proposed model | 9.65 | 8.87 | 7.05 | 6.8 | 8.05 | 9.43 | 49.85 | ||
| Horizontal well 2 | The comparison model | 15.03 | 14.93 | 14.89 | 14.91 | 14.91 | 15.06 | 89.73 | 77.74 |
| The proposed model | 14.9 | 13.98 | 12.98 | 13.06 | 14.04 | 14.9 | 83.86 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, L.; Yue, P.; Yang, H.; Guo, W.; Qu, S.; Yao, H.; Meng, L. Coupled Productivity Prediction Model for Multi-Stage Fractured Horizontal Wells in Low-Permeability Reservoirs Considering Threshold Pressure Gradient and Stress Sensitivity. Energies 2025, 18, 3654. https://doi.org/10.3390/en18143654
Xiao L, Yue P, Yang H, Guo W, Qu S, Yao H, Meng L. Coupled Productivity Prediction Model for Multi-Stage Fractured Horizontal Wells in Low-Permeability Reservoirs Considering Threshold Pressure Gradient and Stress Sensitivity. Energies. 2025; 18(14):3654. https://doi.org/10.3390/en18143654
Chicago/Turabian StyleXiao, Long, Ping Yue, Hongnan Yang, Wei Guo, Simin Qu, Hui Yao, and Lingqiang Meng. 2025. "Coupled Productivity Prediction Model for Multi-Stage Fractured Horizontal Wells in Low-Permeability Reservoirs Considering Threshold Pressure Gradient and Stress Sensitivity" Energies 18, no. 14: 3654. https://doi.org/10.3390/en18143654
APA StyleXiao, L., Yue, P., Yang, H., Guo, W., Qu, S., Yao, H., & Meng, L. (2025). Coupled Productivity Prediction Model for Multi-Stage Fractured Horizontal Wells in Low-Permeability Reservoirs Considering Threshold Pressure Gradient and Stress Sensitivity. Energies, 18(14), 3654. https://doi.org/10.3390/en18143654





