A Fully Coupled Numerical Simulation Model for Bottom-Water Gas Reservoirs Integrating Horizontal Wellbore, ICD Screens, and Zonal Water Control: Development, Validation, and Optimization Strategies

Abstract

To address the challenges of water coning and early water breakthrough commonly encountered during the development of bottom-water gas reservoirs, this study establishes a fully coupled numerical simulation model integrating a horizontal wellbore, inflow control device (ICD) screens, and a zonal water control system. A novel “dual inflow performance index” method is introduced for the first time, enabling separate calculation of the pressure drops induced by gas and water phases flowing through the ICDs, thereby improving the accuracy of pressure simulations throughout the production lifecycle. The model divides the entire production system into four physically distinct subsystems, the bottom-water gas reservoir, ICD screens, production compartments, and the horizontal wellbore, which are dynamically coupled through transient interflow exchange. Based on geological parameters from the SPE10 dataset, the model simulates realistic production scenarios. The results show that the proposed model accurately captures the time-dependent increase in ICD pressure drop as fluid properties evolve during production. Moreover, the zonal water control method outperforms the single ICD-based control strategy in water control performance, achieving a 23% reduction in cumulative water production. Additionally, the water control intensity of the ICD screens increases nonlinearly with the reduction in the number of openings. In highly heterogeneous reservoirs with significant permeability contrast, effective suppression of water coning can only be achieved by setting a minimal number of openings in the high-permeability compartments, resulting in up to a 15% reduction in cumulative water production. The timing of production compartment shutdown exerts a significant influence on water control performance. The optimal strategy is to first identify the water breakthrough point through unconstrained production simulation as production with all eight ICD screen openings fully open and then shut down the high-permeability production compartment around this critical time. This approach can suppress cumulative water production by up to 27%. Overall, the proposed model offers a practical and robust tool for optimizing completion design and water control strategies in complex bottom-water gas reservoirs.

1. Introduction

China is currently undergoing rapid economic development, with a continuously increasing demand for energy. Among various energy sources, natural gas has become an increasingly important component of the country’s primary energy mix due to its high calorific value, low environmental impact, and wide applicability. To meet the growing demand for natural gas, the development of complex and challenging gas reservoirs not only aligns with China’s “resource expansion and cost reduction” policy but also plays a crucial role in ensuring national energy security. Consequently, it has become a key focus in oil and gas exploration and development research [1]. In recent years, several bottom-water gas reservoirs have been developed in China’s major gas-producing regions, including the Upper Permian Changxing Formation in the Yuanba gas field of the Sichuan Basin [2], the second member of the Dengying Formation in the Gaoshiti–Moxi area of the Anyue gas field, and the Tazhong I and Dina 2 gas fields in the Tarim Basin. These reservoirs exhibit substantial production potential and large development scales, indicating a promising future for natural gas exploitation in China. However, one of the persistent engineering challenges in the development of bottom-water gas reservoirs is water invasion. The reservoir rocks in such systems are primarily composed of carbonates and clastic rocks [3], which often feature fracture–porosity and fracture–cavity structures [4]. These formations lead to local high-permeability channels and strong reservoir heterogeneity. Moreover, due to the strong aquifer drive and significant gas–water viscosity contrast, bottom-water reservoirs are prone to water cresting in high-permeability compartments and regions with steep pressure gradients [5], resulting in early water breakthrough. Water invasion is one of the main factors affecting development performance in bottom-water gas reservoirs [6]. Once water invades, gas relative permeability is significantly reduced due to two-phase flow, compared to single-phase gas flow, leading to a sharp decline in well productivity—and in severe cases, complete well shut-in due to water loading [7]. Additionally, the presence of water segments the continuity of gas distribution in the reservoir, creating large “water-blocked gas” compartments that reduce the recoverable reserves [8]. Therefore, evaluating different water control strategies through numerical simulation prior to production has become an essential research direction for ensuring sustainable gas output from bottom-water reservoirs.

Traditional water control techniques are generally developed based on geological and flow characteristics of specific reservoirs. For example, to address microfracture development, techniques such as water channel blocking, bottom-water fracturing isolation, and low-rate/high-pressure control are employed. To mitigate the viscosity contrast between gas and water, methods like CO₂ injection, polymer-based selective plugging [9], and downhole gas–water separation have been applied. However, these methods are often case-specific and lack generalizability across different bottom-water reservoirs, leading to limited overall effectiveness. Recently, advanced completion technologies—such as inflow control devices (ICDs), autonomous ICDs (AICDs), and zonal water control—have offered new perspectives for managing water in bottom-water gas reservoirs [10]. ICD screens function by introducing additional pressure drops in high-permeability compartments, balancing the pressure gradient between the reservoir and the wellbore, thereby reducing radial water inflow [11]. ICD screen-based water control has been successfully applied in numerous oil wells worldwide [12]. Zonal water control divides the horizontal production section into multiple isolated compartments, and the flow rate in each compartment can be individually adjusted via control valves, reducing inter-compartmental interference and improving reservoir utilization [13]. The combination of ICD screens and zonal control enables flexible adjustment of the number of ICD ports and compartment divisions based on permeability distribution, gas–water saturation, bottom-water proximity, pressure differential, segmentation intensity, and economic factors [14], thus offering strong adaptability to various reservoir conditions. As this technology modifies only near-wellbore completion components, it is operationally simpler and more cost-effective compared to conventional approaches, showing excellent potential for field application.

In terms of modeling, previous studies treated the reservoir, ICD screen, and horizontal wellbore as three independent systems, connected via interface flow, to construct an integrated coupled simulation model for bottom-water oil reservoirs with ICD completions [15]. And employed an approximate method to simulate steady-state single-phase flow in horizontal wells within anisotropic reservoirs [16]. However, directly applying this model to bottom-water gas reservoirs introduces significant inaccuracies. Specifically, in oil reservoirs, the pressure drop caused by the oil–water mixture passing through ICDs can be reliably computed using a fixed inflow performance index (IPI), as viscosity changes are minimal throughout production [17]. In oil reservoirs, the viscosity of oil–water mixtures changes minimally, so using a fixed productivity index yields production pressure drops that closely match actual values. However, in bottom-water gas reservoirs, the gas–water mixture properties vary significantly over time—high flow rates and low viscosity in early stages, and reduced flow with higher viscosity later. This leads to large deviations between simulated and actual pressure drops if a fixed index is used. Therefore, separate productivity indices for gas and water must be introduced to ensure accuracy throughout the production period. For zonal water control simulation, current models typically segment the ICD screen into multiple parts, each representing an individual compartment [18]. However, this does not reflect the real field configuration, where compartmentalization is achieved by inserting internal tubing within the ICD screen. To replicate this accurately, a separate production compartment system must be defined and coupled with the reservoir, ICD screen, and horizontal wellbore systems via flow exchange.

This study, for the first time, divides the bottom-water gas reservoir into four physically distinct systems—reservoir domain, ICD screen system, production compartment system, and horizontal wellbore system—based on spatial structure. Compared to previous models developed for oil reservoirs, we introduce a novel dual-IPI formulation to separately compute gas- and water-induced pressure drops across ICDs, establishing a fully coupled numerical simulation model specifically for bottom-water gas reservoirs. The model closely matches real production performance, maintaining computational accuracy within acceptable limits. Based on this model and realistic permeability distribution, we further evaluate the water control effectiveness under various ICD port configurations and production compartment shutdown timings, aiming to identify the optimal combination for specific reservoir conditions. The results provide new theoretical and technical support for water control design in complex bottom-water gas reservoirs.

2. Development and Solution of Fully Coupled Numerical Simulation Model for Horizontal Wellbore–ICD Screen–Zonal Water Control Completion

2.1. Physical Model

To reasonably simplify the complex flow processes in bottom-water gas reservoirs, a fully coupled physical model integrating the horizontal wellbore, inflow control device (ICD) screens, and zonal water control system is established. This model enables clear delineation of each stage of gas–water flow from the reservoir into the wellbore. Each stage corresponds to an independent spatial domain characterized by distinct flow mechanisms and physical behaviors. These spatial domains are physically decoupled but interact through transient interflow (mass transfer), which serves as the coupling condition. Therefore, separate mathematical models must be constructed for each domain based on the physical characteristics of gas and water flow and then integrated using the interflow terms to achieve unified simulation of the entire production process.

The fluid flow patterns in the newly proposed water control strategy—combining ICD screens with zonal control—differ significantly from those in traditional single-mode control approaches such as standalone ICD-based or zonal water control. In the conventional ICD-only system, the ICD screens are deployed in the annulus, often segmented using packers or filled with plugging particles [19]. When packers are used, the annulus is physically isolated, and reservoir fluids can only enter the wellbore radially through the ICD screens [20]. In the case of particle-filled annuli, although limited axial seepage may occur through the porous particle pack, radial inflow remains the dominant flow pattern. In zonal water control systems, packers directly divide the horizontal wellbore into several isolated production compartments. Fluids first enter the annulus and then flow radially into the horizontal well through the assigned compartments.

Regardless of the specific conventional control method used, radial flow is the predominant pathway for reservoir fluid entry into the wellbore. Therefore, enhancing water control efficiency requires addressing radial inflow mechanisms. The proposed hybrid strategy combines ICD control with zonal compartmentalization by installing packers inside the ICD screen assembly to define multiple production compartments. In this configuration, reservoir fluids first enter the annulus; whether axial flow occurs depends on whether the annulus is packed with particles or sealed with packers. For most fluids that preferentially select radial flow paths, the flow sequence is as follows: ICD screen → production compartment → horizontal wellbore. However, in annuli filled with granular packing, a small portion of the fluids may follow an alternative path due to the limited permeability of the packing material, granular media → ICD screen → production compartment → horizontal wellbore, as illustrated in Figure 1. The fluid flow process through the packed granular materials is illustrated in Figure 2. This serial coupling of ICD-based and zonal water control mechanisms results in a two-stage pressure drop: one across the ICD screen and another across the compartment interface. Compared to conventional single-mode control systems, this configuration significantly reduces water inflow while enhancing gas inflow, thereby effectively suppressing bottom-water coning and improving overall water control performance.

2.2. Mathematical Model

2.2.1. Mathematical Model for Bottom-Water Gas Reservoir Flow

Tight sandstone bottom-water gas reservoirs have become a major focus in reservoir development research due to their widespread distribution and the availability of extensive geological data. Consequently, constructing a flow model based on the geological characteristics of tight sandstone reservoirs and governed by the principles of mass conservation and Darcy’s law offers significant advantages in terms of applicability and generalizability, making it suitable for most field production scenarios. These reservoirs typically exhibit an average permeability of less than 1 × 10⁻⁴ μm² and are characterized by strong heterogeneity, multi-layered structures, and high irreducible water saturation [21].

Although microfractures are widely developed in tight sandstones, to reduce model complexity while maintaining computational accuracy, these microfractures are integrated with matrix pores and treated as a unified element referred to as the matrix block. The matrix block functions both as the primary storage medium and as the main flow channel. Therefore, a single-porosity, single-permeability model is adopted as the foundational framework. In the single-porosity, single-permeability model, the tight sandstone is divided into several matrix blocks, with the matrix block’s porosity and permeability representing the combined properties of both the matrix pores and microfractures. The fluid flow within the matrix pores and microfractures can be approximated as occurring within the matrix block. This simplification allows for an efficient model calculation while still reflecting the true flow behavior of the system. During production, due to the stress sensitivity of tight sandstone formations, reservoir permeability and porosity gradually decline as pressure drops with continued fluid extraction. To realistically capture this behavior, a poroelastic flow–stress coupling mechanism is introduced into the simulation. Based on these considerations, the following assumptions are applied in formulating the mathematical model for fluid flow in tight sandstone bottom-water gas reservoirs:

(1) Geological medium assumption: The reservoir is modeled as a homogeneous, continuous, isotropic porous elastic medium.

(2) Flow behavior assumption: Darcy’s law is used to describe gas flow within the matrix block system. The gas–water transfer between the matrix and ICD system is assumed to be in quasi-steady-state. To simplify the flow calculations, the model does not account for non-Darcy flow.

(3) Flow path assumption: The flow sequence for gas and water is as follows: matrix block → ICD screen → production compartment → horizontal wellbore.

(4) Mechanical response assumption: Reservoir stress sensitivity is considered. Rock deformation is assumed to be small-strain and satisfies the Terzaghi effective stress theory.

(5) Fluid property assumption: Natural gas is treated as a single-phase, isothermal fluid; capillary pressure effects are neglected.

(6) Reservoir property assumption: Properties such as Young’s modulus and Poisson’s ratio are constant. The influence of gravity on natural gas flow was neglected due to its low density.

(7) Analytical aquifer assumption: The intrusion of bottom-water during production is modeled using the Getkovich analytical water influx model, assuming continuous injection from the aquifer at the reservoir base [22].

This model simplifies the computational process while incorporating the critical physical characteristics of tight sandstone bottom-water reservoirs, providing a robust theoretical foundation for subsequent numerical simulations and water control optimization.

Connectivity between matrix blocks is established through microfractures, which serve as essential channels for two-phase gas–water flow. Thus, the model explicitly incorporates inter-block gas and water transfer. Additionally, due to the pronounced stress sensitivity of tight sandstones, both porosity and permeability are dynamically updated as functions of pressure, which in turn affects the fluid flow. Based on these physical behaviors, the gas-phase and water-phase flow control equations in bottom-water gas reservoirs are developed using the principles of mass conservation and Darcy’s law [23], and are formulated as follows:

$${\displaystyle \frac{\partial }{\partial t}}({\displaystyle \frac{{\phi }_{\mathrm{m}}{S}_{\mathrm{gm}}}{B_{\mathrm{gm}}}})=\nabla (T_{g\mathrm{m}}\nabla U_{g\mathrm{m}})-W{I}_{\mathrm{m}-\mathrm{ICD}}{\lambda }_{\mathrm{gm}}(P_{\mathrm{gm}}-P_{\mathrm{ICD}})$$

(1)

$${\displaystyle \frac{\partial }{\partial t}}({\displaystyle \frac{{\phi }_{\mathrm{m}}{S}_{\mathrm{wm}}}{B_{\mathrm{wm}}}})=\nabla (T_{w\mathrm{m}}\nabla U_{w\mathrm{m}})-W{I}_{\mathrm{m}-\mathrm{ICD}}{\lambda }_{\mathrm{wm}}(P_{\mathrm{wm}}-P_{\mathrm{ICD}})$$

(2)

where Φ_m is the porosity of the matrix block, calculated using the method proposed by Davies; S_gm and S_wm are the gas and water saturations in the matrix block, respectively; B_gm and B_wm are the formation volume factors of gas and water in the matrix block, respectively; T_gm and T_wm are the transmissibilities of gas and water in the matrix block, in m³/(MPa·s), calculated using the method proposed by Terzaghi; U_gm and U_wm are the gas and water potentials in the matrix block, in MPa; WI_m–ICD is the well index between the matrix block and the ICD screen, calculated using the method proposed by Moinfar et al. [24], in m³; λ_gm and λ_wm are the gas and water mobilities in the near-well matrix region, in MPa⁻¹·s⁻¹.

Due to the low density of natural gas, the effect of gravity on the gas potential can be neglected. Therefore, based on Darcy’s law, the expressions for gas and water potentials are modified as follows:

$$U_{\mathrm{g}}=\nabla P_{\mathrm{gm}}$$

(3)

$$U_{\mathrm{w}}=\nabla P_{\mathrm{wm}}-{\rho }_{\mathrm{w}}g\nabla z$$

(4)

where P_gm and P_wm are the gas and water pressures in the matrix block, respectively, in MPa; z is the vertical elevation of the water phase within the matrix block, in meters (m).

2.2.2. Mathematical Model for Flow in ICD Screen and Zonal Water Control System

Based on their internal flow path structures, ICD screens can be categorized into several types, including channel-type, nozzle-type, venturi-type, labyrinth-type, and hybrid-type configurations. Despite their structural differences, all ICD screens operate under a common flow control mechanism: as fluids pass through the screen, a pressure drop is generated due to localized flow resistance, which is correlated with the flow rate. This mechanism enables the regulation of production rates and suppression of water invasion. In the actual development of bottom-water gas reservoirs, the produced fluid typically consists of a gas–water mixture. If a single inflow performance index (IPI) is used to calculate the pressure drop across the ICD screen throughout the entire production cycle, the result may deviate significantly from reality. Specifically, during the early production stage, gas production dominates and the pressure drop is mainly attributed to gas flow through the ICD screen. In contrast, in the later stage, water production becomes dominant, and the pressure drop primarily results from water flow. Therefore, the conventional single-IPI approach fails to accurately capture the dynamic pressure response and productivity changes over time. To improve the predictive accuracy of the ICD model, a dual inflow performance index approach is proposed. This method assigns separate IPIs for gas and water phases, allowing for the dynamic calculation of phase-specific pressure contributions based on their relative proportions at each production stage. Such an enhancement ensures better alignment with actual flow behavior in the reservoir and improves the reliability and practical value of the numerical simulation. On this basis, the two-phase flow control equation for the ICD screen system with packer segmentation is modified as follows:

$$\begin{array}{l}LC{I}_{\mathrm{g}}\sqrt{P_{\mathrm{ICD}}-P_{\mathrm{PC}}}+LC{I}_{\mathrm{w}}\sqrt{P_{\mathrm{ICD}}-P_{\mathrm{PC}}}=\\ W{I}_{\mathrm{m}-\mathrm{ICD}}{\lambda }_{\mathrm{gm}}(P_{\mathrm{gm}}-P_{\mathrm{ICD}})+W{I}_{\mathrm{m}-\mathrm{ICD}}{\lambda }_{\mathrm{wm}}(P_{\mathrm{wm}}-P_{\mathrm{ICD}})\end{array}$$

(5)

$$LC{I}_{\mathrm{g}}=\sqrt{{\displaystyle \frac{1}{[K_{\mathrm{ICD}}]{\rho }_g}}}$$

(6)

$$LC{I}_{\mathrm{w}}=\sqrt{{\displaystyle \frac{1}{[K_{\mathrm{ICD}}]{\rho }_w}}}$$

(7)

where LCI_g and LCI_w are the gas and water inflow performance indices for the ICD screen, in m³/(Pa^0.5*s); [K_ICD] is the ICD screen strength coefficient obtained by experimental fitting, in m⁻⁴; ρ_g and ρ_w are the gas and water densities, respectively, in kg/m³; P_ICD is the pressure within the ICD screen, in Pa; and P_PC is the pressure within the production compartment, in Pa.

In ICD screen systems packed with granular materials, the annulus is filled with spherical particles resembling gravel, forming a continuous medium with limited axial permeability. Due to the presence of micro-voids between the particles, a portion of the fluid may undergo axial Darcy flow through the packed layer under the influence of a pressure gradient. This behavior is significantly different from that of ICD systems with packers, where axial flow in the annulus is almost completely blocked. To accurately represent the flow behavior in particle-packed systems, an additional axial flow term must be incorporated into the previously established control equations for the packer-segmented ICD system. This term accounts for the pressure drop induced by gas and water flow through the granular medium in the axial direction. For computational simplicity, the pressure differential across the particle-packed layer is approximated by the pressure differential across the ICD screen itself—that is, the pressure drop along the granular layer is assumed to be equivalent to that across the ICD screen body. This approximation is generally valid under conditions of limited reservoir thickness and moderate pressure gradient and is considered suitable for engineering applications. Accordingly, the two-phase flow control equations for the particle-packed ICD screen system are expressed as follows:

$$\begin{array}{l}LC{I}_{\mathrm{g}}\sqrt{P_{\mathrm{ICD}}-P_{\mathrm{PC}}}+LC{I}_{\mathrm{w}}\sqrt{P_{\mathrm{ICD}}-P_{\mathrm{PC}}}+{\displaystyle \frac{k_{\mathrm{p}}A}{{\mu }_{\mathrm{g}}L}}\mathrm{\Delta }{P}_{\mathrm{ICD}}+{\displaystyle \frac{k_{\mathrm{p}}A}{{\mu }_{\mathrm{w}}L}}\mathrm{\Delta }{P}_{\mathrm{ICD}}=\\ W{I}_{\mathrm{m}-\mathrm{ICD}}{\lambda }_{\mathrm{gm}}(P_{\mathrm{gm}}-P_{\mathrm{ICD}})+W{I}_{\mathrm{m}-\mathrm{ICD}}{\lambda }_{\mathrm{wm}}(P_{\mathrm{wm}}-P_{\mathrm{ICD}})\end{array}$$

(8)

where A is the cross-sectional area of the annulus between the ICD screen and the horizontal wellbore, in m²; k_p is the permeability of the particle-packed layer, in m²; μ_g and μ_w are the viscosities of the gas and water phases, respectively, in Pa·s; and L is the length of the water control completion assembly, in meters (m).

In the ICD screen–zonal water control completion system, the operating mechanism of the production compartment is essentially analogous to that of an ICD screen. As fluid flows through the compartment, local throttling and structural restrictions generate an additional pressure drop that is correlated with the flow rate [25]. This added pressure drop affects gas and water phases differently, particularly during bottom-water gas reservoir production, where the gas–water ratio evolves significantly over time. Therefore, using a single inflow performance index (IPI) throughout the entire production period is insufficient for accurately characterizing the pressure behavior. To improve the accuracy of the production compartment model, independent gas and water IPIs must be introduced into the compartment’s flow control equation. These allow for the separate calculation of pressure drops induced by natural gas and water, ensuring that the simulated productivity remains consistent with actual trends. Additionally, since the annular space between the ICD screen and the production compartment is isolated by packers, no axial flow occurs in this region. Hence, axial flow terms are excluded from the compartment flow model, and only radial pressure differential is considered. Accordingly, the two-phase flow control equations for the production compartment are given by

$$\begin{array}{l}PC{I}_{\mathrm{g}}\sqrt{P_{\mathrm{PC}}-P_{\mathrm{Well}}}+PC{I}_{\mathrm{w}}\sqrt{P_{\mathrm{PC}}-P_{\mathrm{Well}}}=\\ LC{I}_{\mathrm{g}}\sqrt{P_{\mathrm{ICD}}-P_{\mathrm{PC}}}+LC{I}_{\mathrm{w}}\sqrt{P_{\mathrm{ICD}}-P_{\mathrm{PC}}}\end{array}$$

(9)

$$PC{I}_{\mathrm{g}}=\sqrt{{\displaystyle \frac{1}{[K_{\mathrm{PC}}]{\rho }_g}}}$$

(10)

$$PC{I}_{\mathrm{w}}=\sqrt{{\displaystyle \frac{1}{[K_{\mathrm{PC}}]{\rho }_w}}}$$

(11)

where PCI_g and PCI_w are the gas and water inflow performance indices for the production compartment, in m³/(Pa^0.5*s); [K_PC] is the strength coefficient of the production compartment obtained through experimental fitting, in m⁻⁴; and P_Well is the bottomhole flowing pressure of the horizontal well, in Pa.

If the production compartment openings are replaced using the equivalent valve approach, the corresponding gas–water two-phase flow control equation for the production compartment can be expressed as follows:

$$\begin{array}{l}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}(PC{I}_{\mathrm{g}}^{\mathrm{i}}\sqrt{P_{\mathrm{PC}}-P_{\mathrm{Well}}}+PC{I}_{\mathrm{w}}^{\mathrm{i}}\sqrt{P_{\mathrm{PC}}-P_{\mathrm{Well}}}})=\\ LC{I}_{\mathrm{g}}\sqrt{P_{\mathrm{ICD}}-P_{\mathrm{PC}}}+LC{I}_{\mathrm{w}}\sqrt{P_{\mathrm{ICD}}-P_{\mathrm{PC}}}\end{array}$$

(12)

Since the pressure drop generated by the equivalent valve is assumed to be identical to that of the original configuration, the following expression can be derived based on the valve pressure drop equation:

$$PC{I}_{\mathrm{g}}^{\mathrm{i}}={\displaystyle \frac{1}{n}}\sqrt{{\displaystyle \frac{1}{[K_{\mathrm{PC}}]{\rho }_g}}}$$

(13)

$$PC{I}_{\mathrm{w}}^{\mathrm{i}}={\displaystyle \frac{1}{n}}\sqrt{{\displaystyle \frac{1}{[K_{\mathrm{PC}}]{\rho }_w}}}$$

(14)

where PCI_gⁱ, PCI_wⁱ represent the gas-phase and water-phase inflow performance indices of each equivalent valve, in m³/(Pa^0.5*s); and n denotes the number of equivalent valves.

2.3. Coupled Solution Method

At each time step during the production process, the gas–water two-phase flow control equations for the bottom-water gas reservoir, ICD screens, and production compartments can be discretized according to their respective governing variables. Given that each set of control equations involves different primary variables—such as matrix block pressure, water saturation, ICD pressure, and compartment pressure—it is necessary to construct independent spatial and temporal discretization schemes for each sub-model. Once discretized, the resulting linear algebraic equations are assembled into subsystem-specific matrix equations. These matrices are then embedded into a unified coupled matrix system according to the physical structure and interconnections of the components, as illustrated in Figure 3—a process referred to as “matrix padding.” This ensures accurate numerical coupling and effective information transfer among the physical subsystems. The final coupled system is solved using an implicit Jacobi iteration scheme [26], enabling dynamic updates of gas–water flow states at each time step throughout the production period. This approach ensures both numerical stability and convergence, satisfying the requirements for engineering-scale simulations.

In the gas–water two-phase flow control equations for the bottom-water gas reservoir, the primary unknowns are the reservoir pressure P_m and the water saturation S_wm. These control equations can be transformed into a form suitable for numerical solution through a discretization process. The following expressions illustrate the discretization of the two-phase flow equations at each time step ∆t:

$$\begin{array}{l}({\displaystyle \frac{1}{\mathrm{\Delta }t}}({\displaystyle \frac{S_{\mathrm{gm}}}{B_{\mathrm{gm}}}}{\displaystyle \frac{\partial {\phi }_{\mathrm{m}}}{\partial P_{\mathrm{m}}}}-{\displaystyle \frac{{\phi }_{\mathrm{m}}{S}_{\mathrm{gm}}}{B_{\mathrm{gm}}^2}}{\displaystyle \frac{\partial B_{\mathrm{gm}}}{\partial P_{\mathrm{m}}}})-\nabla ({\displaystyle \frac{\partial T_{\mathrm{gm}}}{\partial P_{\mathrm{m}}}}\nabla U_{\mathrm{gm}}+T_{\mathrm{gm}})+(W{I}_{\mathrm{m}-\mathrm{ICD}}{\displaystyle \frac{\partial {\lambda }_{\mathrm{gm}}}{\partial P_{\mathrm{m}}}}(P_{\mathrm{gm}}-P_{\mathrm{ICD}})+W{I}_{\mathrm{m}-\mathrm{ICD}}{\lambda }_{\mathrm{gm}}))\partial P_{\mathrm{m}}\\ +(-{\displaystyle \frac{1}{\mathrm{\Delta }t}}{\displaystyle \frac{{\phi }_{\mathrm{m}}}{B_{\mathrm{gm}}}}-\nabla ({\displaystyle \frac{\partial T_{\mathrm{gm}}}{\partial S_{\mathrm{wm}}}}\nabla U_{\mathrm{gm}})+W{I}_{\mathrm{m}-\mathrm{ICD}}{\displaystyle \frac{\partial {\lambda }_{\mathrm{gm}}}{\partial S_{\mathrm{wm}}}}(P_{\mathrm{gm}}-P_{\mathrm{ICD}}))\partial S_{\mathrm{wm}}\\ -W{I}_{\mathrm{m}-\mathrm{ICD}}{\lambda }_{\mathrm{gm}}\partial P_{\mathrm{ICD}}=0\end{array}$$

(15)

$$\begin{array}{l}({\displaystyle \frac{1}{\mathrm{\Delta }t}}({\displaystyle \frac{S_{\mathrm{wm}}}{B_{\mathrm{wm}}}}{\displaystyle \frac{\partial {\phi }_{\mathrm{m}}}{\partial P_{\mathrm{m}}}}-{\displaystyle \frac{{\phi }_{\mathrm{m}}{S}_{\mathrm{wm}}}{B_{\mathrm{wm}}^2}}{\displaystyle \frac{\partial B_{\mathrm{wm}}}{\partial P_{\mathrm{m}}}})-\nabla ({\displaystyle \frac{\partial T_{\mathrm{wm}}}{\partial P_{\mathrm{m}}}}\nabla U_{\mathrm{wm}}+T_{\mathrm{wm}})+(W{I}_{\mathrm{m}-\mathrm{ICD}}{\displaystyle \frac{\partial {\lambda }_{\mathrm{wm}}}{\partial P_{\mathrm{m}}}}(P_{\mathrm{wm}}-P_{\mathrm{ICD}})+W{I}_{\mathrm{m}-\mathrm{ICD}}{\lambda }_{\mathrm{wm}}))\partial P_{\mathrm{m}}\\ +({\displaystyle \frac{1}{\mathrm{\Delta }t}}{\displaystyle \frac{{\phi }_{\mathrm{m}}}{B_{\mathrm{wm}}}}-\nabla ({\displaystyle \frac{\partial T_{\mathrm{wm}}}{\partial S_{\mathrm{wm}}}}\nabla U_{\mathrm{wm}})+W{I}_{\mathrm{m}-\mathrm{ICD}}{\displaystyle \frac{\partial {\lambda }_{\mathrm{wm}}}{\partial S_{\mathrm{wm}}}}(P_{\mathrm{wm}}-P_{\mathrm{ICD}}))\partial S_{\mathrm{wm}}\\ -W{I}_{\mathrm{m}-\mathrm{ICD}}{\lambda }_{\mathrm{wm}}\partial P_{\mathrm{ICD}}=0\end{array}$$

(16)

In the gas–water two-phase flow control equations for the ICD screen, the primary unknown is the ICD pressure P_ICD. The following expressions represent the discretization of the two-phase flow control equations for the packer-segmented ICD screen at each time step ∆t:

$$\begin{array}{l}((LC{I}_{\mathrm{g}}+LC{I}_{\mathrm{w}}){\displaystyle \frac{0.5}{\sqrt{P_{\mathrm{ICD}}-P_{\mathrm{PC}}}}}+W{I}_{\mathrm{m}-\mathrm{ICD}}{\lambda }_{\mathrm{gm}}+W{I}_{\mathrm{m}-\mathrm{ICD}}{\lambda }_{\mathrm{wm}})\partial P_{\mathrm{ICD}}+\\ (-W{I}_{\mathrm{m}-\mathrm{ICD}}{\displaystyle \frac{\partial {\lambda }_{\mathrm{gm}}}{\partial P_{\mathrm{m}}}}(P_{\mathrm{gm}}-P_{\mathrm{ICD}})-W{I}_{\mathrm{m}-\mathrm{ICD}}{\lambda }_{\mathrm{gm}}-W{I}_{\mathrm{m}-\mathrm{ICD}}{\displaystyle \frac{\partial {\lambda }_{\mathrm{wm}}}{\partial P_{\mathrm{m}}}}(P_{\mathrm{wm}}-P_{\mathrm{ICD}})-W{I}_{\mathrm{m}-\mathrm{ICD}}{\lambda }_{\mathrm{wm}})\partial P_{\mathrm{m}}+\\ (-(LC{I}_{\mathrm{g}}+LC{I}_{\mathrm{w}}){\displaystyle \frac{0.5}{\sqrt{P_{\mathrm{ICD}}-P_{\mathrm{PC}}}}})\partial P_{\mathrm{PC}}=0\end{array}$$

(17)

The following expressions represent the discretization of the gas–water two-phase flow control equations for the particle-packed ICD screen at each time step ∆t:

$$\begin{array}{l}((LC{I}_{\mathrm{g}}+LC{I}_{\mathrm{w}}){\displaystyle \frac{0.5}{\sqrt{P_{\mathrm{ICD}}-P_{\mathrm{PC}}}}}+W{I}_{\mathrm{m}-\mathrm{ICD}}{\lambda }_{\mathrm{gm}}+W{I}_{\mathrm{m}-\mathrm{ICD}}{\lambda }_{\mathrm{wm}}+{\displaystyle \frac{k_{\mathrm{p}}A}{L}}({\displaystyle \frac{1}{{\mu }_{\mathrm{g}}}}+{\displaystyle \frac{1}{{\mu }_{\mathrm{w}}}}))\partial P_{\mathrm{ICD}}+\\ (-W{I}_{\mathrm{m}-\mathrm{ICD}}{\displaystyle \frac{\partial {\lambda }_{\mathrm{gm}}}{\partial P_{\mathrm{m}}}}(P_{\mathrm{gm}}-P_{\mathrm{ICD}})-W{I}_{\mathrm{m}-\mathrm{ICD}}{\lambda }_{\mathrm{gm}}-W{I}_{\mathrm{m}-\mathrm{ICD}}{\displaystyle \frac{\partial {\lambda }_{\mathrm{wm}}}{\partial P_{\mathrm{m}}}}(P_{\mathrm{wm}}-P_{\mathrm{ICD}})-W{I}_{\mathrm{m}-\mathrm{ICD}}{\lambda }_{\mathrm{wm}})\partial P_{\mathrm{m}}+\\ (-(LC{I}_{\mathrm{g}}+LC{I}_{\mathrm{w}}){\displaystyle \frac{0.5}{\sqrt{P_{\mathrm{ICD}}-P_{\mathrm{PC}}}}})\partial P_{\mathrm{PC}}=0\end{array}$$

(18)

In the gas–water two-phase flow control equations for the production compartment, the primary unknown is the compartment pressure P_PC. The following expressions represent the discretization of the compartment flow control equations at each time step ∆t:

$$\begin{array}{l}((PC{I}_{\mathrm{g}}+PC{I}_{\mathrm{w}}){\displaystyle \frac{0.5}{\sqrt{P_{\mathrm{PC}}-P_{\mathrm{Well}}}}}+(LC{I}_{\mathrm{g}}+LC{I}_{\mathrm{w}}){\displaystyle \frac{0.5}{\sqrt{P_{\mathrm{ICD}}-P_{\mathrm{PC}}}}})\partial P_{\mathrm{PC}}+\\ (-(PC{I}_{\mathrm{g}}+PC{I}_{\mathrm{w}}){\displaystyle \frac{0.5}{\sqrt{P_{\mathrm{PC}}-P_{\mathrm{Well}}}}})\partial P_{\mathrm{Well}}+(-(LC{I}_{\mathrm{g}}+LC{I}_{\mathrm{w}}){\displaystyle \frac{0.5}{\sqrt{P_{\mathrm{ICD}}-P_{\mathrm{PC}}}}})\partial P_{\mathrm{ICD}}=0\end{array}$$

(19)

The fully coupled numerical simulation model for horizontal wellbore–ICD screen–zonal water control completion integrates the bottom-water gas reservoir flow model with the ICD screen and zonal compartment flow model, using the horizontal well gas production rate as the coupling point. At each solution time step, a balance check is performed to ensure that the entire system reaches convergence within every Newton iteration cycle. The computational flowchart is illustrated in Figure 4, and the detailed steps are as follows:

(1) During each Newton iteration, determine whether coupling is required for the current step. If coupling is needed, use the parameters from the previous iteration step to independently solve the bottom-water reservoir flow model and the ICD–compartment flow model.

(2) Check whether the solutions of both models have converged.

(3) If convergence is achieved, extract the horizontal well gas production rate computed at the current iteration step and compare it with the target gas production rate.

(4) If there is a deviation between the calculated and the prescribed gas production rate, adjust the bottomhole flowing pressure and re-solve the coupled models for the reservoir and the completion system.

(5) Once the computed gas production rate matches the prescribed value, the current time step is considered complete, and the computation proceeds to the next time step.

3. Application of Fully Coupled Numerical Simulation Model for Horizontal Wellbore–ICD Screen–Zonal Water Control Completion

3.1. Field-Scale Production Simulation

The fully coupled numerical simulation model for horizontal wellbore–ICD screen–zonal water control completion developed in this study is based on data from the SPE10 dataset. This dataset is constructed from three-dimensional geostatistical models of the Jurassic Brent formation in the North Sea and includes representative geological characteristics of major oilfields such as Statfjord, Gullfaks, Oseberg, and Snorre. The relevant reservoir parameters are listed in

Table 1. Basic reservoir parameters.

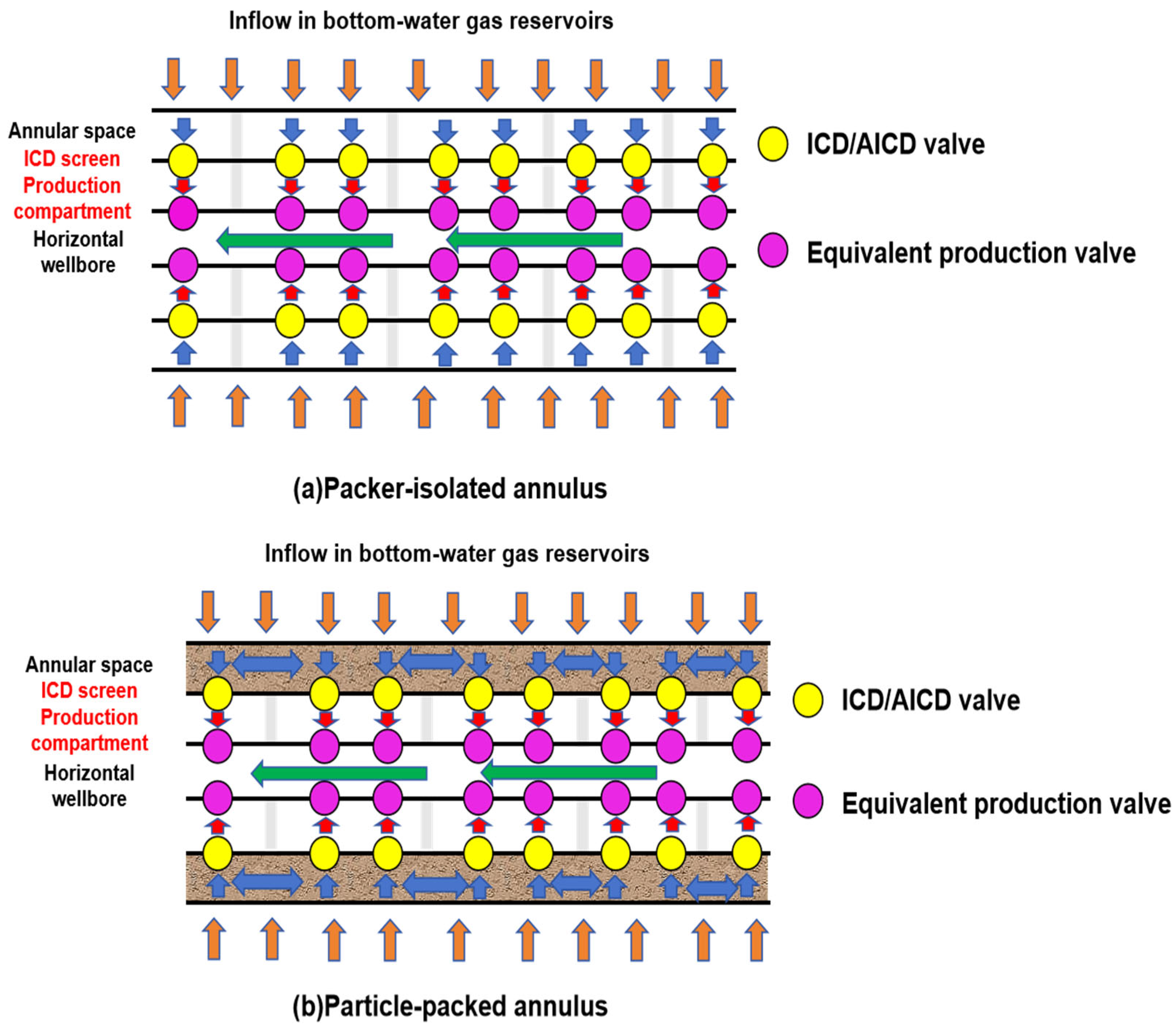
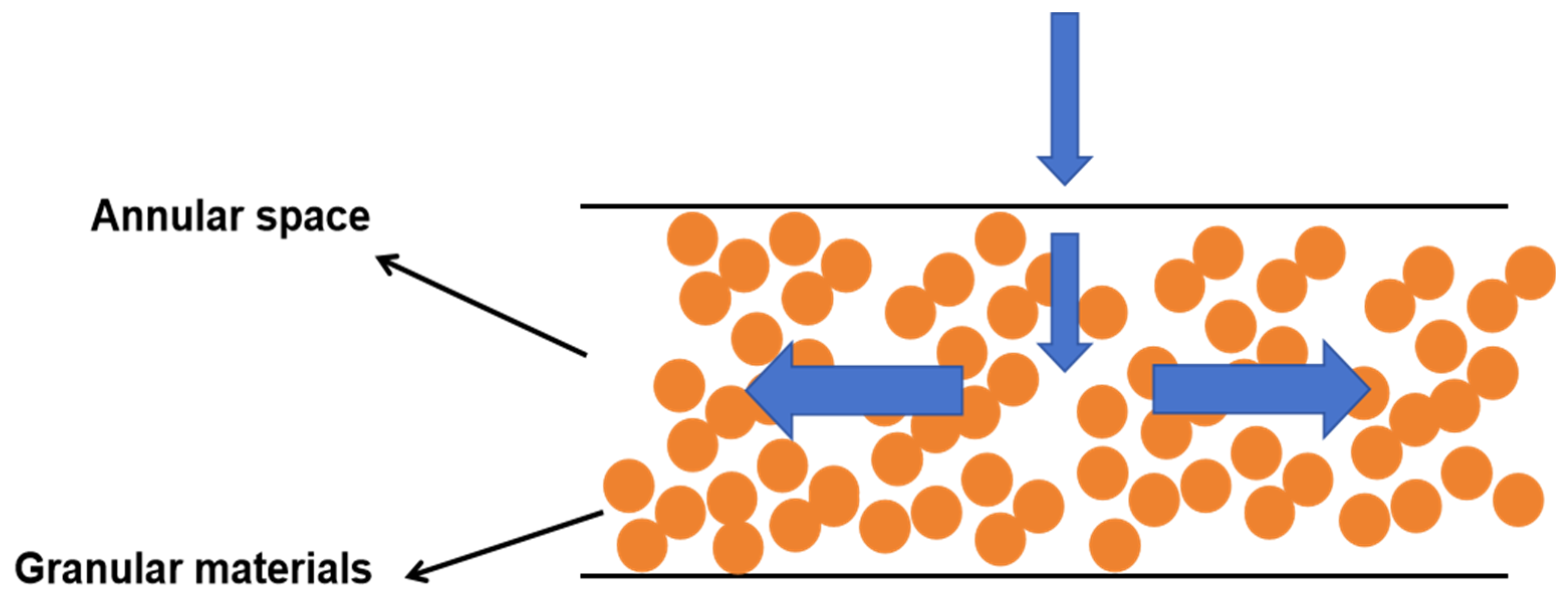
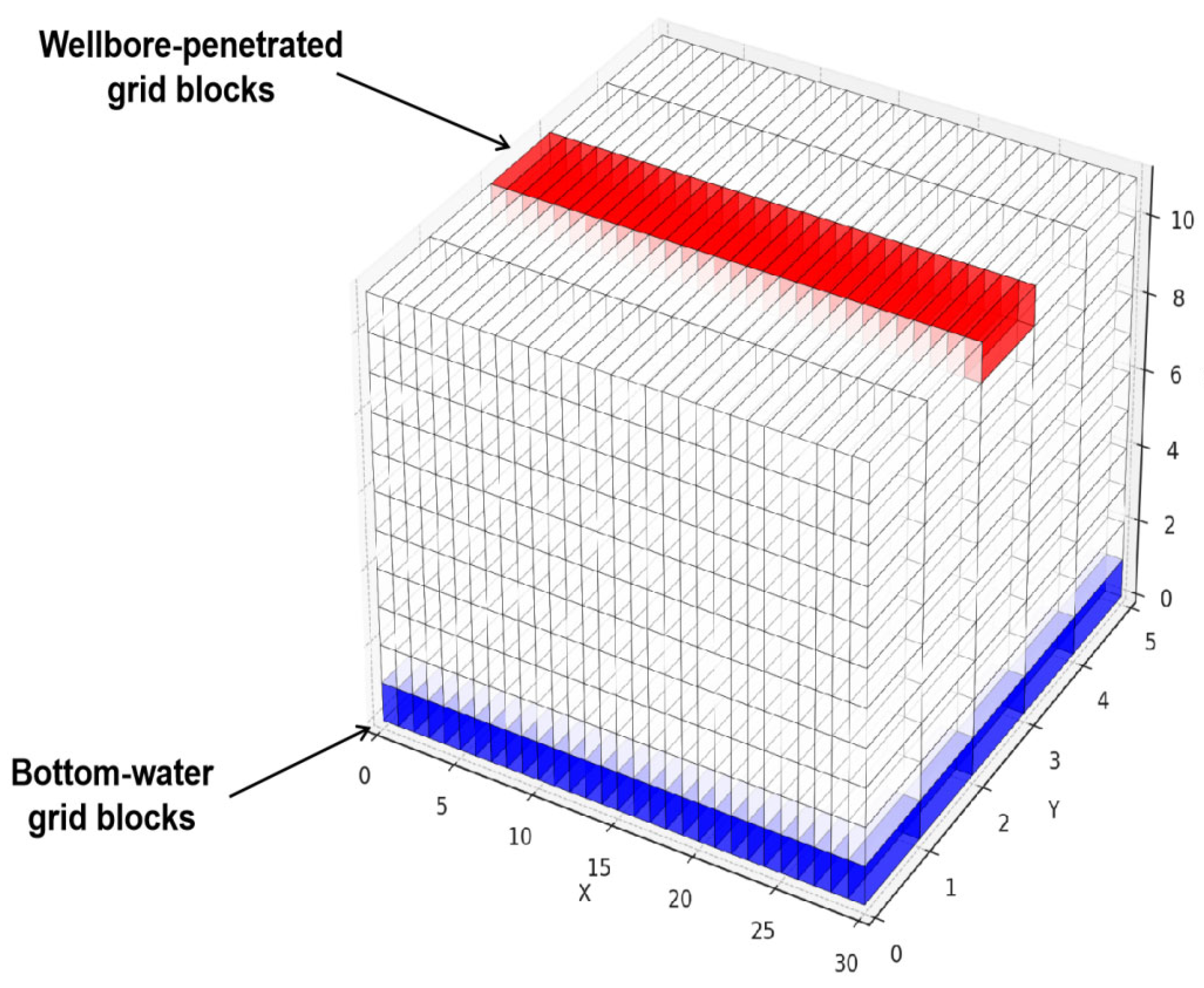
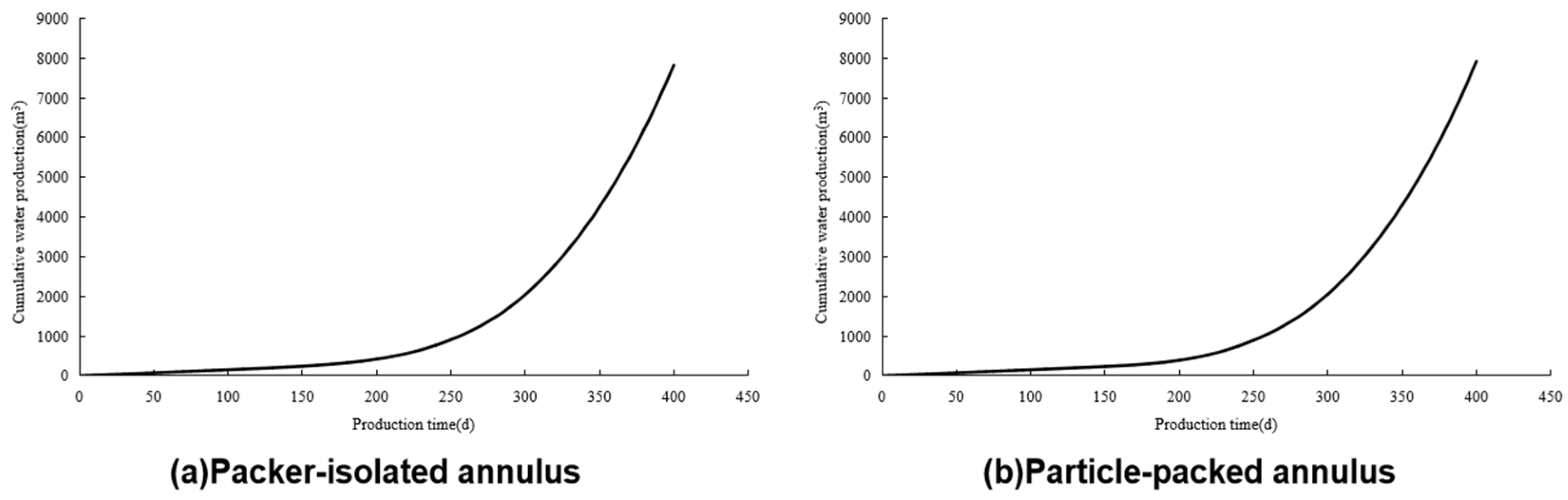
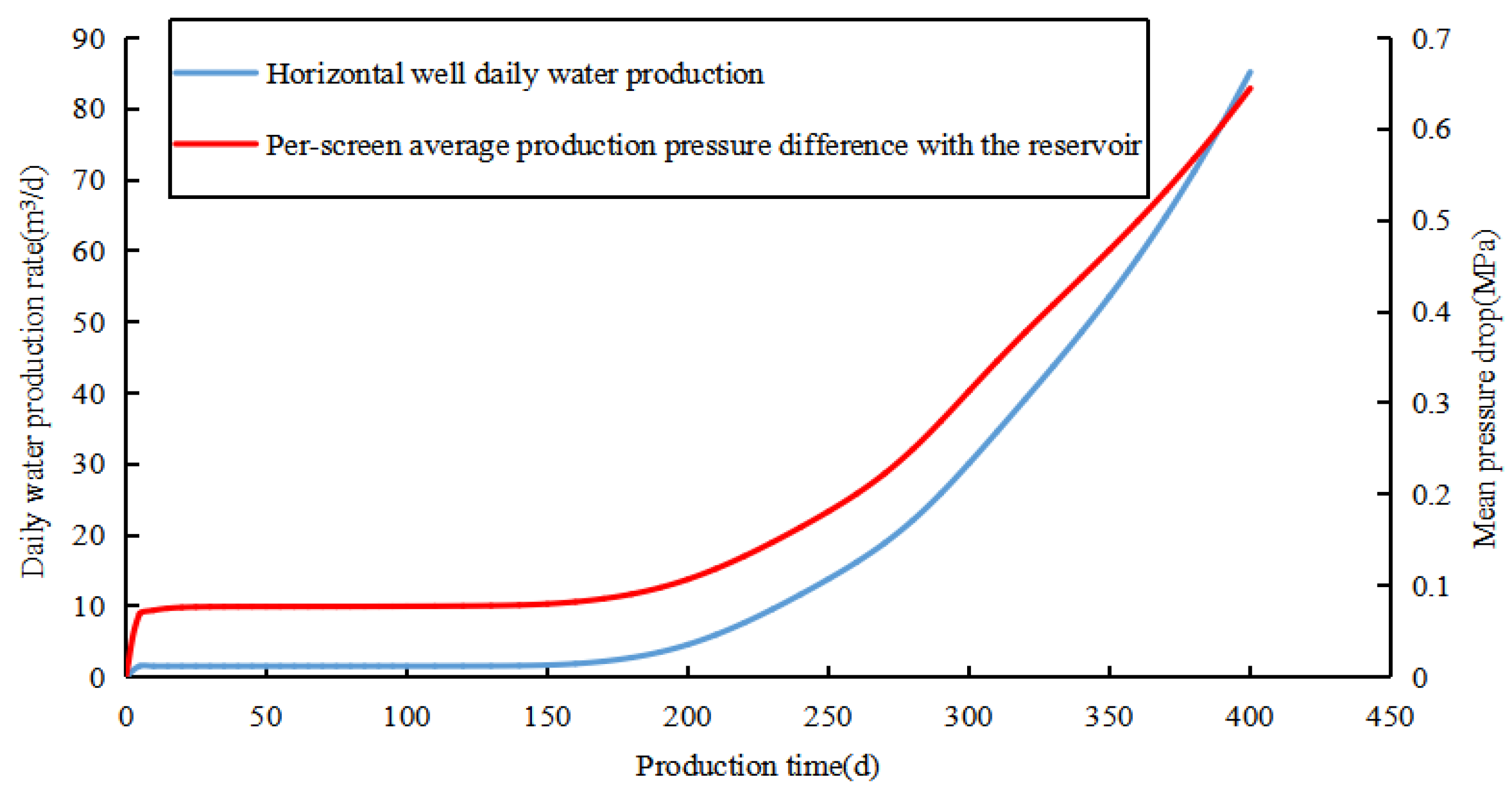
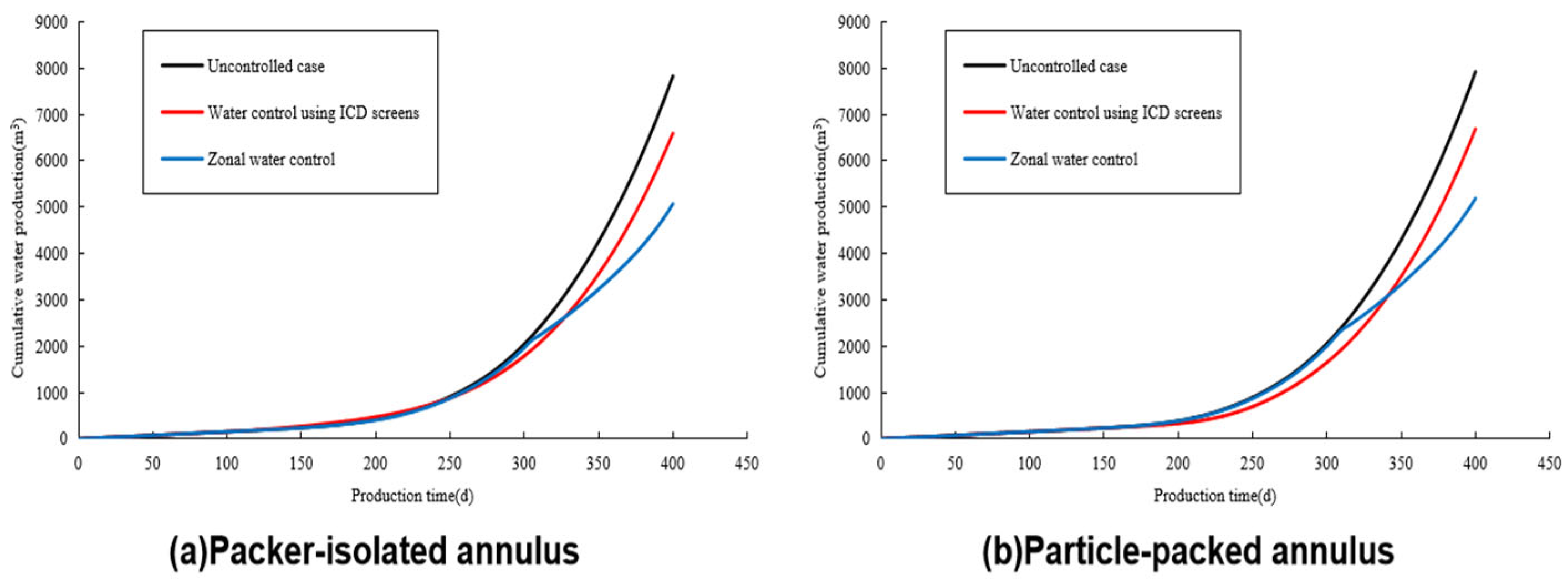
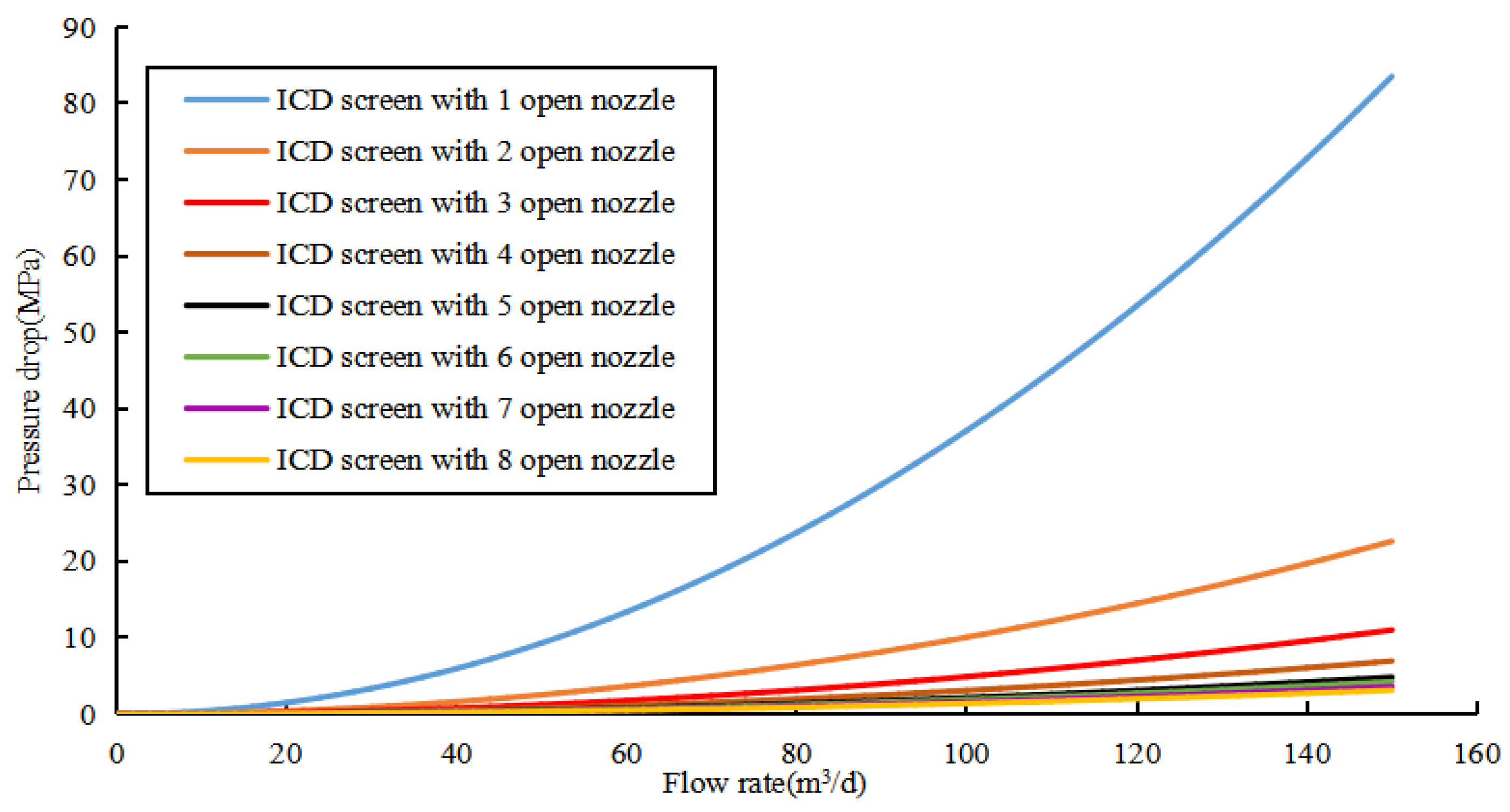
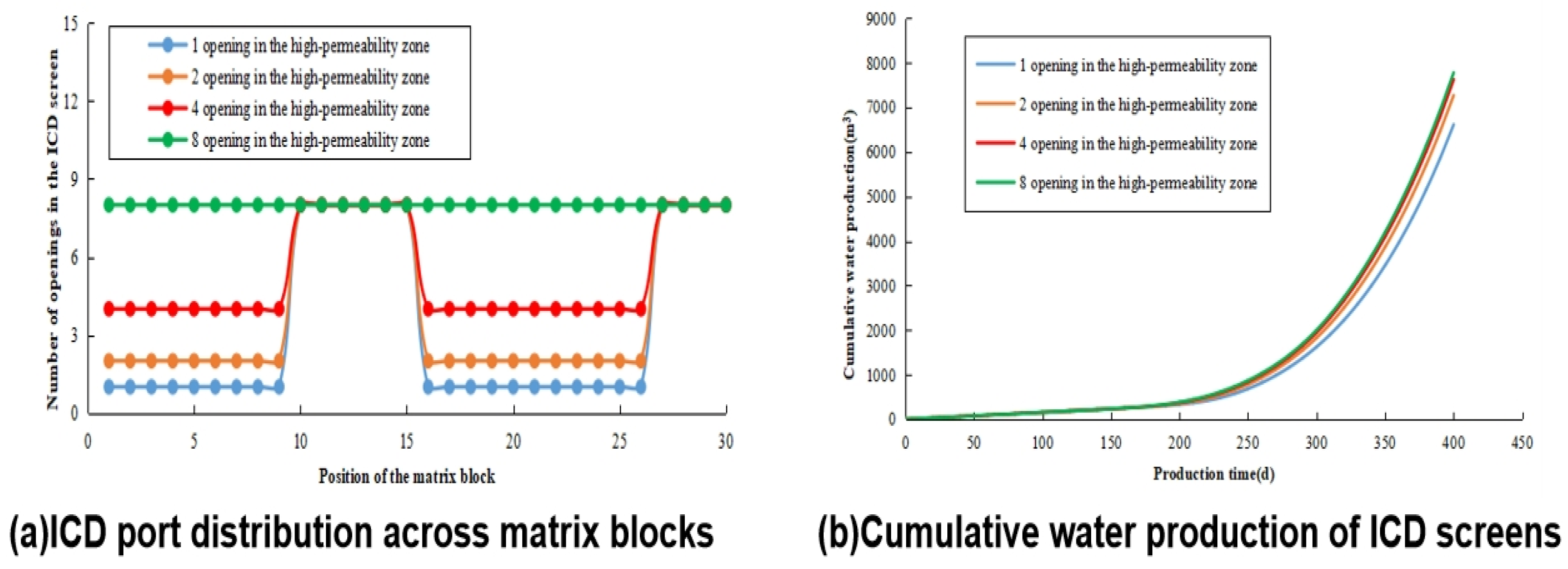
Parameters (Unit)	Value	Parameters (Unit)	Value
Area (m2)	339 × 250	Reservoir thickness (m)	12
Initial water saturation (%)	50	Reservoir pressure (MPa)	20
Reservoir porosity (%)	6.7	Reservoir depth (m)	2000
Distance to bottom-water (m)	6	Average reservoir permeability (10−3 μm2)	31.2
Vertical-to-horizontal permeability ratio	0.1	Permeability of the particle-packed layer (10−3 μm2)	40,000

.

The construction steps for the fully coupled numerical simulation model of horizontal wellbore–ICD screen–zonal water control completion are as follows:

(1) The matrix domain is discretized into 30, 5, and 10 grid blocks in the x, y, and z directions, respectively. Each matrix block has dimensions of 11.3 m (length), 50 m (width), and 1.2 m (height). The initial reservoir parameters—permeability, porosity, and water saturation—are assigned to each block according to the values listed in Table 1.

(2) An additional layer is established below the z = 10 layer, designated as z = 11, to represent the bottom-water intrusion layer. The Getkovich analytical aquifer model is applied to simulate bottom-water influx. This layer is assigned the same reservoir permeability and water saturation as the z = 10 layer, but with a porosity of 1% and a matrix height of 6 m. The purpose of this layer is to provide a vertical flow pathway for bottom-water intrusion without contributing to storage capacity.

(3) A horizontal wellbore is placed at z = 1, aligned along the x direction and positioned at y = 3, simulating a top-well deployment strategy commonly used in bottom-water gas reservoir development to mitigate water coning.

Based on the data in Table 1 and the steps described above, the structure of the fully coupled horizontal well–ICD screen–zonal water control numerical model is illustrated in Figure 5.

When the ICD screen is configured with eight openings, the production pressure drop across the ICD becomes negligibly small, indicating a flow regime effectively equivalent to production without ICD control. A coupled numerical simulation model integrating the horizontal wellbore, ICD screen, and compartmentalized water control completion was established. The ICD screen was configured with eight perforations, and no shut-in period was set for the production compartments, thereby simulating an unrestricted production scenario without screens or compartments. Assuming a constant gas production rate of 3000 m³/d over 400 days, the cumulative water production was obtained under two conditions: (1) annulus packed with gravel, and (2) annulus isolated by packers. The results are shown in Figure 6.

The fully coupled numerical simulation model for horizontal wellbore–ICD screen–zonal water control completion is configured to operate under a constant gas production rate of 3000 m³/d over a production period of 400 days. Based on the simulation results, the daily water production curve and the average production pressure differential between the bottom-water reservoir and the ICD screens are obtained, as illustrated in Figure 7.

As shown in Figure 7, the daily water production curve exhibits a transition from a relatively stable trend to a rapid increase over the course of production. A similar trend is observed in the curve of average production pressure differential between the bottom-water reservoir and the ICD screens. During the first 150 days of production, the daily water output remains stable at approximately 1.5 m³/d with only minor fluctuations. After day 150, however, water production rises sharply—from 1.5 m³/d to 85.2 m³/d. During the first 150 days of production, the average production pressure differential remained stable at approximately 0.077 MPa with only minor fluctuations. However, after day 150, it increased rapidly from 0.077 MPa to 0.644 MPa. This reflects the production behavior of a bottom-water gas reservoir: in the early stage, gas saturation is high and water invasion is minimal, supporting stable production at low water rates; in the later stage, as the gas content declines, water invasion accelerates, leading to bottom-water coning and a rapid increase in water production. The production pressure differential between the reservoir and the ICD screen results from the combined pressure drops generated by gas and water flow through the ICD. While the gas production rate remains constant throughout the simulation, the water production rate varies over time. Consequently, the trend of the average pressure differential aligns closely with that of water production. This demonstrates that the use of a dual inflow performance index enables the ICD screen to accurately reflect the dominant phase contributing to pressure drop: gas in the early production stage and water in the later stage. Therefore, the model effectively captures the dynamic shift in pressure sources over time.

To further investigate the influence of different water control strategies, two coupled models were established—one with a particle-packed annulus and the other with a packer-isolated annulus—within the horizontal well–ICD–zonal completion framework. Both models were simulated under a constant gas production rate of 3000 m³/d over a period of 400 days. The zonal water control strategy involves shutting down the production compartment located in the high-permeability compartment at day 300. The cumulative water production curves obtained from the simulations are presented in Figure 8.

As shown in Figure 8, both the ICD screen and zonal water control strategies lead to a significant reduction in cumulative water production after 400 days, regardless of whether the annulus is filled with particles or isolated with packers. Compared to the case without any water control measures, these strategies effectively suppress bottom-water invasion and reduce water output. Compared with the ICD screen-based water control method, the zonal water control strategy reduced the cumulative water production by 23%. Notably, the zonal water control approach demonstrates superior performance relative to the ICD screen alone. This is attributed to its dual control mechanism: in addition to generating additional pressure drop as gas–liquid mixtures flow through the control valve, the system allows for the selective shutdown of individual production compartments with high water output. By doing so, the remaining open compartments maintain lower water production rates while sustaining gas output, thereby reducing water entry into the horizontal wellbore. Furthermore, for a given water control method, the difference in cumulative water production between particle-packed and packer-isolated annuli is minimal. This indicates that particle packing is effective in blocking axial flow within the annulus and can achieve a comparable water control effect to that of mechanical packers, confirming its feasibility as an alternative completion technique for bottom-water control.

3.2. Prediction of Water Control Performance

(1)

Influence of ICD Screen Opening Number on Water Control Performance

The valve characteristic curves of the ICD screen with different numbers of openings under water flow conditions are shown in Figure 9. These curves illustrate the relationship between the flow rate and production pressure drop for various opening configurations. By analyzing the flow–pressure response under different conditions, the strength coefficient of the ICD screen can be determined accordingly.

Based on the fully coupled numerical simulation model for horizontal wellbore–ICD screen–zonal water control completion, a series of tests was conducted using known reservoir data. In the low-permeability compartments, the ICD screen was configured with eight openings, while in the high-permeability compartments, various opening numbers were applied to evaluate their effects. The simulations assumed a constant gas production rate of 3000 m³/d over a 400-day production period. Figure 10 presents the spatial distribution of ICD screen opening numbers across the reservoir and shows the corresponding cumulative water production curves under different opening configurations. By comparing these curves, the impact of ICD opening number on water production can be assessed. This analysis provides a basis for optimizing ICD screen design, enhancing water control effectiveness, and mitigating bottom-water invasion.

As shown in Figure 10, the water control performance of the ICD screen improves progressively as the number of openings is reduced, with the enhancement exhibiting a nonlinear trend. When the number of openings in the high-permeability section is reduced from 8 to 4, the cumulative water production decreases slightly from 7778 m³ to 7624 m³—a reduction of only 2%, indicating a marginal improvement in water control. However, when the number of openings is further reduced from 4 to 1, cumulative water production drops significantly from 7624 m³ to 6612 m³, corresponding to a 13% reduction, demonstrating a much more pronounced control effect. Compared to the 8-port ICD screen, the 1-port ICD screen configuration can reduce cumulative water production by up to 15%, demonstrating a significantly enhanced water control capacity. This nonlinear behavior can be attributed to the valve characteristic curves associated with different ICD opening configurations. The ICD strength coefficient increases slowly at first as the number of openings rises but then accelerates significantly. As a result, ICDs with a higher number of openings generate only minor additional pressure drops, whereas those with fewer openings impose a much larger pressure differential. Moreover, the reservoir under investigation exhibits a permeability contrast ratio of 89.4, indicating strong heterogeneity. In such formations, excessive ICD openings in high-permeability compartments fail to produce sufficient resistance to bottom-water coning. Instead, a more effective water control strategy involves minimizing the number of openings in high-permeability regions to promote balanced production across the reservoir.

(2)

Influence of Production Compartment Shutdown Timing on Water Control Performance

Based on the established fully coupled numerical simulation model for horizontal wellbore–ICD screen–zonal water control completion, and taking into account the reservoir permeability distribution, the formation was divided into four independent production compartments. A constant gas production rate of 3000 m³/d was assumed over a 400-day production period. To evaluate the impact of shutdown timing on water control effectiveness, the production compartment located in the high-permeability compartment was selectively shut down at different production time points. Figure 11 presents the cumulative water production curves under various shutdown scenarios, providing a comparative assessment of the effectiveness of dynamic intervention strategies for mitigating bottom-water invasion in high-permeability compartments.

As shown in Figure 11, the water control performance of the production compartment exhibits a “first-improving-then-declining” trend with the postponement of its shutdown timing. When the shutdown time is delayed from Day 100 to Day 250, the cumulative water production decreases from 7272 m³ to 5330 m³—a 27% reduction—indicating a significant improvement in water control. However, further delaying the shutdown to Day 350 results in an increase in cumulative water production to 6148 m³, representing a 15% rise and a decline in control effectiveness. This phenomenon can be explained as follows: if the compartment is shut down too early, the high-permeability compartment is likely not yet affected by water invasion and still has strong gas productivity. Premature shutdown shifts the production burden to low-permeability compartments, which have limited capacity. To maintain the target gas production rate, the system increases the drawdown pressure, thereby promoting bottom-water coning along the low-permeability paths and weakening the overall control effect. Conversely, if the shutdown is executed too late, the high-permeability compartment has already experienced severe water invasion driven by long-term pressure gradients. At this point, water production from the horizontal well has significantly increased, and shutting down the compartment becomes less effective at preventing further bottom-water breakthrough. Therefore, an optimal time window should be selected for shutting down the high-permeability production compartment. By examining the cumulative water production curve without compartment shutdown, it is observed that water production starts to rise sharply after Day 250, indicating intensified water intrusion and substantial gas depletion in the reservoir—clear signs of bottom-water coning. It is thus recommended to close the high-permeability compartment around Day 250 to maximize water control effectiveness. For reservoirs with uncertain bottom-water behavior, open production simulations can first be conducted using the fully coupled horizontal well–ICD–zonal water control model. By identifying the onset of bottom-water breakthrough, the optimal shutdown timing for high-permeability compartments can be determined, thereby enabling a more effective water management strategy.

4. Conclusions

This study introduces, for the first time, a dual inflow performance index (IPI) approach to improve the conventional pressure drop calculation method for ICD screens. Based on this improvement, a fully coupled numerical simulation model was developed that integrates the bottom-water gas reservoir flow model with an enhanced ICD screen and zonal water control system. Using reservoir parameters from the SPE10 dataset, field-scale simulations were conducted under realistic production conditions. The main findings are summarized as follows:

(1) The proposed fully coupled horizontal well–ICD screen–zonal water control model accurately captures the dynamic increase in pressure drop across the ICD screen as production progresses. Comparative analysis indicates that the compartmentalized water control method exhibits superior water control performance compared to the ICD screen approach, with an improvement of approximately 23% in water control efficiency.

(2) The water control strength of the ICD screen exhibits a nonlinear relationship with the number of openings. In highly heterogeneous reservoirs with large permeability contrasts, minimizing the number of ICD openings in high-permeability compartments is essential to generate sufficient additional pressure drop and effectively suppress bottom-water coning, thereby promoting balanced production. Reducing the number of ICD screen openings from eight to one leads to a 15% improvement in water control performance.

(3) The shutdown timing of production compartments has a significant impact on water control effectiveness and should be optimized based on reservoir-specific characteristics. By analyzing the cumulative water production curve under an open production scenario, the inflection point at which water production surges can be identified as the onset of bottom-water breakthrough. Scheduling compartment shutdown operations around this point allows for a more effective water management strategy and improved reservoir performance. Selecting an appropriate shut-in duration for the production chamber can improve water control effectiveness by 27%.